Abstract
Background
Phylogeography improves our understanding of spatial epidemiology. However, application to practical problems requires choices among computational tools to balance statistical rigor, computational complexity, sensitivity to sampling strategy and interpretability.
Methods
We introduce a fast, heuristic algorithm to reconstruct partially-observed transmission networks (POTN) that combines features of phylogenetic and transmission tree approaches. We compare the transmission network generated by POTN with existing algorithms (BEAST and SeqTrack), and discuss the benefits and challenges of phylogeographic analysis on examples of epidemic and endemic diseases: Ebola virus, H1N1 pandemic influenza and polio.
Results
For the 2014 Sierra Leone Ebola virus outbreak and the 2009 H1N1 outbreak, all three methods provide similarly plausible transmission histories but differ in detail. For polio in northern Nigeria, we discuss performance trade-offs between the POTN and discrete phylogeography in BEAST and conclude that spatial history reconstruction is limited by under-sampling.
Conclusions
POTN is complementary to available tools on densely-sampled data, fails gracefully on under-sampled data and is scalable to accommodate larger datasets. We provide further evidence for the utility of phylogeography for understanding transmission networks of rapidly evolving epidemics. We propose simple heuristic criteria to identify how sampling rates and disease dynamics interact to determine fundamental limitations of phylogeographic inference.
Keywords: Computational biology, Ebola virus, Epidemiology, Influenza, Phylogeography, Polio
Introduction
Inadequate understanding of the spatial epidemiology of infectious diseases limits our ability to assess risk, allocate resources, respond to and suppress epidemics and reduce global disease burden.1 Spatial epidemiology is difficult because sampling rates are often low and sampling strategies in the field are rarely clearly defined. Furthermore, the spatial autocorrelation induced by the disease transmission dynamics (that we are interested in) can be difficult to control for in statistical models that only consider case dates and locations.2 One route to improved spatial epidemiology is molecular epidemiology and phylogeographic inference.3 For rapidly evolving pathogens, genetic correlations among pathogens record imprints of the chains of transmission, and phylogeography offers tools to systematically use the information contained in genetic sequences to infer underlying spatial patterns of disease transmission.4,5
With steady declines in cost and the future promise of field-deployed sequencing technology, an open question is how best to apply current and future phylogeography tools to datasets that vary in size, sampling strategy and underlying molecular dynamics when one needs to balance statistical rigor, computational cost and interpretability. A brief survey of existing tools reveals three families of phylogeographic analysis. Cladistic approaches correlate genetic distances with spatial distribution to identify evidence of spatial structure, but they do not offer an explicit model of transmission history and so are difficult to interpret in an epidemiological context.6 Bayesian phylogenetic models,6 including discrete phylogeography in BEAST,7,8 and structured coalescent models,9 provide transmission history reconstructions, inferred transmission models and statistical rigor. However, with typical desktop computing power, they are computationally prohibitive for datasets with more than a few hundred sequences.10 Transmission tree algorithms infer ancestry solely among observed cases11–14 and so require minimal inference of unobserved spatial data to reconstruct transmission history. However, transmission trees are most appropriate for densely-sampled data in which many ancestor-descendent pairs are present in the sample.11
To better understand when various phylogeographic analyses a likely to be useful and as a first attempt to identify an alternate path to compromise among complexity, rigor and interpretability, we introduce a heuristic algorithm to reconstruct partially-observed transmission networks (POTN) that retain features of both transmission tree and phylogenetic models. Using likelihood ratio tests based on sample dates, genetic distances and a pre-specified molecular clock, the method identifies pairs of sequences that are consistent with relationship by direct descent and excludes pairs that are consistent with relationship by an unobserved common ancestor. The set of all pairs consistent with direct descent forms a transmission history network containing only the connected components best supported by the data. To our knowledge, an algorithm of this type has not been described previously.
In the Methods section, we describe the POTN algorithm and its properties. Next, we assess the accuracy of the POTN algorithm on simulated data where true ancestry is known. Then we demonstrate the POTN algorithm on a relevant problem for which phylogeography has enormous potential to add to our understanding of the disease, the Ebola virus outbreak in Sierra Leone,15–17 and compare with discrete phylogeography in BEAST8 and transmission tree reconstruction in SeqTrack.11 We then discuss phylogeographic data exploration using the POTN for the 2009 H1N1 outbreak.11,18–20 We conclude with an analysis of the vaccine-derived polio outbreak in Nigeria21–23 that demonstrates fundamental limitations of phylogeographic inference. To summarize our experiences, we propose a simple heuristic for when phylogeographic analysis is likely to be informative about the spatial epidemiology of infectious diseases.
Materials and methods
Partially-observed transmission network (POTN)
For a pair of cases with sample dates t1 and t2 , we denote the time to the most recent common ancestor (tMRCA) prior to t1 as . In pairs for which the case at time t1 is a direct ancestor of the case at t2, the tMRCA is . Pairs that are related by unobserved common ancestry have . The genetic distance between the pair is d12 (measured in nucleotides using any appropriate distance metric). We assume a Poisson model for mutation with constant mutation rate μ (measured in nucleotides per unit time). The Poisson likelihood for the tMRCA of a pair is
| (1) |
where is the gamma function continuation of the factorial to allow for non-integer d12.
To identify pairs for which the genetic distance and time between cases is consistent with relationship by direct descent and to reject pairs that are better explained by relationship through an unobserved common ancestor, we perform a likelihood ratio test to compare the hypotheses of (null) and :
| (2) |
where is the maximum likelihood estimate of the tMRCA. The p-value for each likelihood ratio is calculated from the χ2 distribution with one degree of freedom. We use the false discovery rate (FDR) paradigm with FDR=0.05 to set the significance threshold for rejecting the null hypothesis and thus exclude pairs from the network.24 See Figure 1 for a graphical depiction of the POTN.
Figure 1.
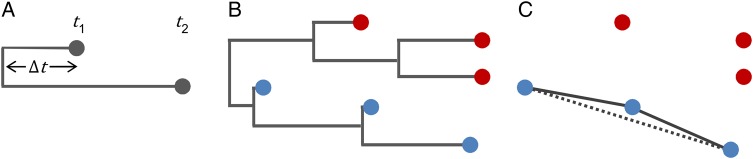
Description of the partially-observed transmission networks (POTN) algorithm. (A) Example sampled pair with candidate parent case at time t1 and candidate child at time t2. The time to the most recent common ancestor (tMRCA) is , and so the cumulative time elapsed for genetic evolution between the cases is , as in Equation (1). (B) Example phylogenetic tree describing the genetic relationships among six cases sampled at different times. For each pair of the blue cases, , while for each pair of the red cases and each pair consisting of one red and one blue case, is greater than zero. (C) The POTN corresponding to the phylogenetic tree in panel B. The POTN algorithm identifies ancestral links between the blue cases where , while it leaves the red cases disconnected because there are no observed direct ancestors of the red cases. For the blue cases, the dashed link indicates a redundant grandparent-child link that is removed by the triangle pruning algorithm.
The result of this procedure is the basic POTN. The network is ‘partially-observed’ because cases with no direct ancestors in the sample have unobserved ancestry and are excluded from the network, and because we make no claim that the ancestors are immediate and there may be many unobserved generations along the ancestral lineages. The pairwise algorithm assumes that genetic distances are independent. It is thus common to identify redundant ancestry (grandparent-parent, parent-child, grandparent-child) because the pairwise algorithm is unable to detect when deeper relationships are better explained by an intermediate ancestor. To remove this redundancy, we prune the network to remove all significant links for which there is an intermediate observed ancestor (remove grandparent-child; keep grandparent-parent and parent-child). The pruning algorithm is described in the Supplementary information. Multiple, conflicting ancestries are preserved by this pruning step if they are present. The researcher is also free to apply additional pruning steps to support specific analyses. For example, to emphasize geographic relationships in a densely sampled network, one can remove links for which both end nodes are in the same location, leaving only location-changing links. Further pruning into a transmission tree is possible by keeping only the ancestral link to each case that has the shortest time duration. This will force a single ancestry when the data suggest multiple conflicting ancestries between observed cases, but it may be appropriate when the generation time is shorter than the typical time between sampled cases.
The transmission history reconstruction by the POTN is subject to sequence alignment and mutation rate uncertainty. To identify robust links, one can use the bootstrapping procedure developed for phylogenetic trees25,26 with a prior distribution for the mutation rate. The procedure is as follows: run the POTN algorithm repeatedly on bootstrap-resampled alignments with mutation rates drawn from the prior. The percent of realizations in which a link appears defines the robustness of the link with respect to sequence and rate uncertainty.
As described previously, POTN identifies the ancestry links with . The ancestry identified by the POTN is perhaps best thought of in terms of the coalescent model.27 In the haploid coalescent with effective population size Ne, the likelihood of the pairwise effective population size is
| (3) |
for .28 The pairwise effective population size is a measure of the size of the breeding population responsible for the pair of cases. When , the vanishing size of the breeding population indicates that the earlier case is a direct ancestor of the later case. The maximum likelihood estimate for Ne is , and so direct ancestry, , corresponds to the limit of . In other words, the links that the POTN identifies with are lines of direct descent for which there is minimal genetic diversity along their lineage, and observed cases that are disconnected from the POTN indicate the existence of genetic diversity that is not observed in the sampled cases. Note that our definition of the effective population size is related to the definition in BEAST v1.8.17 by the following relation: , where θ corresponds to the BEAST variable.27 In the Supplementary information, we discuss how the ability to identify direct ancestry changes with sampling rates through the variance of the effective population size. Additional methodological details, asymptotic properties of the POTN, code and data needed to reproduce our results are also available in the Supplementary information.
Results
Simulation study to assess reconstruction accuracy
To demonstrate the performance of the algorithm on data where the true ancestral relationships are known, we tested the POTN algorithm with grandparent-child triangle pruning against simulated outbreak data generated by haploGen from the R package adegenet v1.4–2.11 Briefly, haploGen is an individual-based simulation of an outbreak. Each simulation starts from an infection with a random haplotype. New infections are created from each previous one in proportion to the previous individual's reproduction number. Mutations accumulate between transmissions at a Poisson rate. For our simulations, genomes were 10 000 bases long, each individual had a reproduction number randomly chosen between 2 and 4, the generation time was random with distribution 1 +Pois(0.5) and the mutation rate was set at either 1e-4, 3e-4, or 10e-4 per unit time. On each haploGen sequence alignment, we ran the POTN algorithm and pruned redundant grandparent-child links as described in the supplement. The R script to run this analysis is available in the Supplemental data.
We examined POTN links that are exactly correct parent-child links and links that are valid reconstructions of deeper ancestor-child relationships but that miss intermediate parent nodes. For the highest mutation rate, µ=10e-4 per unit time, the expected number of mutations between generations is 15 and so we expect high accuracy. On average, we found that 66% of the exact true parent-child links are recovered by the POTN and >99% of links in the POTN are valid ancestor-child links. Thus, for high mutation rates, almost all links in the POTN indicate true ancestry, although one-third of the most immediate ancestors are missed. For µ=3e-4 per unit time, when the expected number of mutations between generations is 4.5, we again find 66% of exact true parent-child links and 93% of all links are valid ancestor-child links. For µ=1e-4 per unit time (1.5 expected mutations per generation), we find 53% of exact true parent-child links and 70% of all links are valid ancestor-child links. As expected, performance falls off when lower mutation rates produce low genetic diversity such that multiple possible ancestors have the same haplotype.
From the observation that only two-thirds of exact parent-child links can be recovered even with high mutation rate data, we observe that the POTN is a biased, conservative estimator of transmission network. For data with sufficient genetic diversity, we can expect that most POTN links are true, but that some true links will be missed. The bias occurs because the false-discovery rate procedure for selecting links can reject true links if the maximum likelihood estimate of the tMRCA is sufficiently earlier than the date of the parent case; this can occur when the observed genetic distance between true pairs is longer than the expected genetic distance given the time between samples in the pair.
The Ebola virus outbreak in Sierra Leone
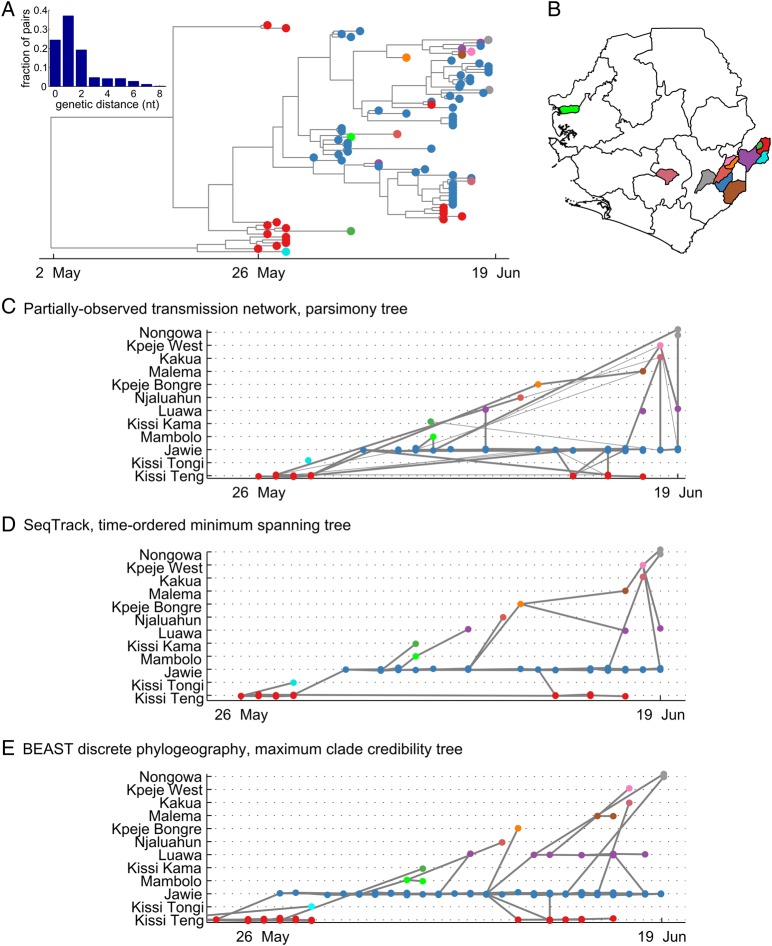
We examined the phylogeography in the early stages of the Ebola virus outbreak in Sierra Leone. Sequences are available for 78 of an estimated 136 cases prior to 19 June 2014.15,29 The sequenced cases occurred in 12 chiefdoms. Figure 2 shows summaries of the genetic and location data, and the transmission history reconstructions from the POTN, SeqTrack11 and the discrete phylogeographic continuous-time Markov chain model in BEAST.8
Figure 2.
Three methods for phylogeographic reconstruction of the initial phase of the 2014 Ebola virus outbreak in Sierra Leone. (A) Maximum clade credibility phylogenetic tree; cases (tips) labeled by color according to location, as shown on the map in panel B; inset: histogram of pairwise genetic distances. The earliest cases are in Kissi Teng, Kailahun (red), and the majority of cases prior to 19 June 2014 were in Jawie, Kailahun (blue). (B) Chiefdom colormap of Sierra Leone, location of cases analysed in panel A are depicted in corresponding colors on the map. (C) Partially-observed transmission network: cases labeled by color according to location, gray lines indicate POTN links between case pairs, thick gray lines indicate the parsimonious transmission tree representing a single consistent ancestry that results from pruning to keep only the ancestral link to each case with the shortest duration. (D) SeqTrack minimum spanning tree: cases labeled by color according to location, gray lines indicate POTN links between case pairs. (E) BEAST discrete phylogeography, maximum clade credibility tree, projected as a transmission network: cases labeled by color according to location with internal nodes colored by highest posterior probability location, gray lines indicate POTN links between case pairs.
All three networks tell the same primary story: the outbreak first took hold in Sierra Leone in Kissi Teng, spread to Jawie and was repeatedly exported from Jawie. All approaches also reveal repeated multiple overlapping importation pathways. For example, there are at least two independent exportations from Jawie to Luawa and the two cases in Nongowa, detected only 1 day apart, are due to two separate importations. The ability to disentangle independent chains of transmission on a local scale shows the promise of phylogeography applied to a densely-sampled outbreak with complex spatial dynamics.
However, the reconstructed transmission histories disagree in key respects. For example, SeqTrack and POTN suggest that the case in Kpeje Bongre is on the transmission chain to Malema while BEAST infers that it is a separate branch from transmission in Jawie. The uncertainty arises because there are no cases on the backbone of the clade to anchor the inference (Figure 2A). For the case in Kissi Tongi near the start of the outbreak, BEAST and SeqTrack root the case to Kissi Teng. However, the POTN leaves the Kissi Teng case disconnected from the network because the relatively deeper root in the phylogeny indicates that the genetic diversity that sourced the case in Kissi Tongi was not observed in the sample.
Much of the disagreement between the three methods we observe arises because we are not accounting for uncertainty. For example, the transmission history cannot be fully resolved with low genetic diversity data in which samples taken at different times have the same haplotype. In the POTN, this uncertainty is represented as multiple conflicting ancestries (Figure 2C) where a child node has multiple plausible parents. Any algorithm that reduces the network to a single consistent transmission tree hides this uncertainty. BEAST also naturally characterizes uncertainty through its ability to sample the posterior of phylogenetic tree topology space, but the difficulty of marginalizing over tree topology uncertainty makes visualization and interpretation challenging30 and so it is common to only visualize a single tree. Easy visualization of uncertainty is a feature of the POTN since multiple conflicting ancestries can be laid out simultaneously.
The 2009 H1N1 influenza pandemic
In Figure 3, we show the POTN for the first few months of the 2009 H1N1 outbreak using case information from Jombart et al.11 Consistent with prior work,11,18–20 the outbreak started in Mexico, went global first from the United States and then from all over the Americas, Europe and Asia. An important feature of the network is that many transmission pathways are traversed multiple times. In this situation, models that try to find a minimally-connected network to explain the data are likely to be misleading. For example, POTN has many short links that directly connect China with North America, contrary to earlier results using BEAST with Bayesian stochastic search variable selection that explain the linkage between North America and China through indirect transmission via Europe.31 In Figure 4, we show the three largest connected components of the POTN within the United States. The three components likely result from three separate importations from Mexico. The components display incomplete geographic segregation (American Southwest, east of the Mississippi) and unsurprisingly reveal a highly-connected USA. Within each component, the multiple conflicting lines of ancestry indicate low genetic diversity (Figure 4D) and an inability of the data to resolve the transmission history in finer detail. In Figure 4C, there are clear signatures of exportation events. For example, the Texas case on 22 May is closely related to New York City cases at the end of May and is not a descendent of the earlier Texas case in April.
Figure 3.
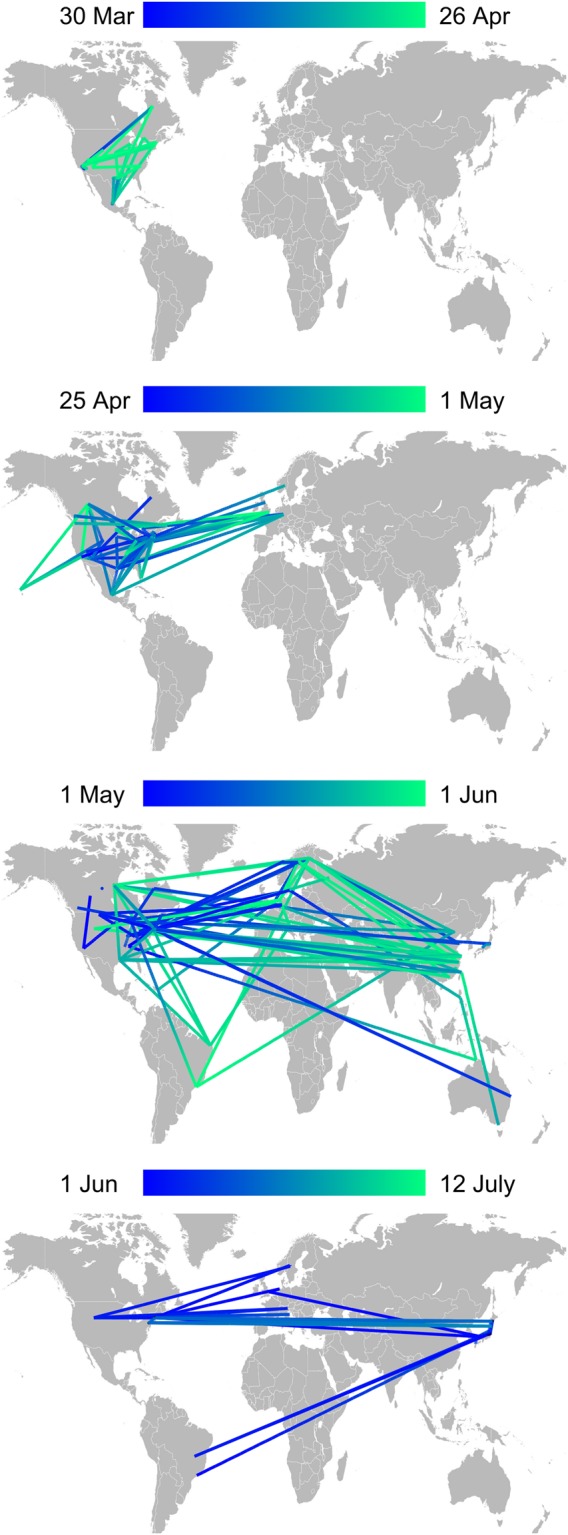
Progression through time of the partially-observed transmission network for the 2009 H1N1 influenza outbreak. Each panel shows the links between cases during the time interval indicated above; color gradient from blue to green goes from early to late. As described previously,11,18,19 the outbreak started in Mexico and went global first from the USA and then from Europe. Many exportation paths between locations are traversed multiple times over the 4 month period spanned by this dataset. The median link duration is 2 days.
Figure 4.
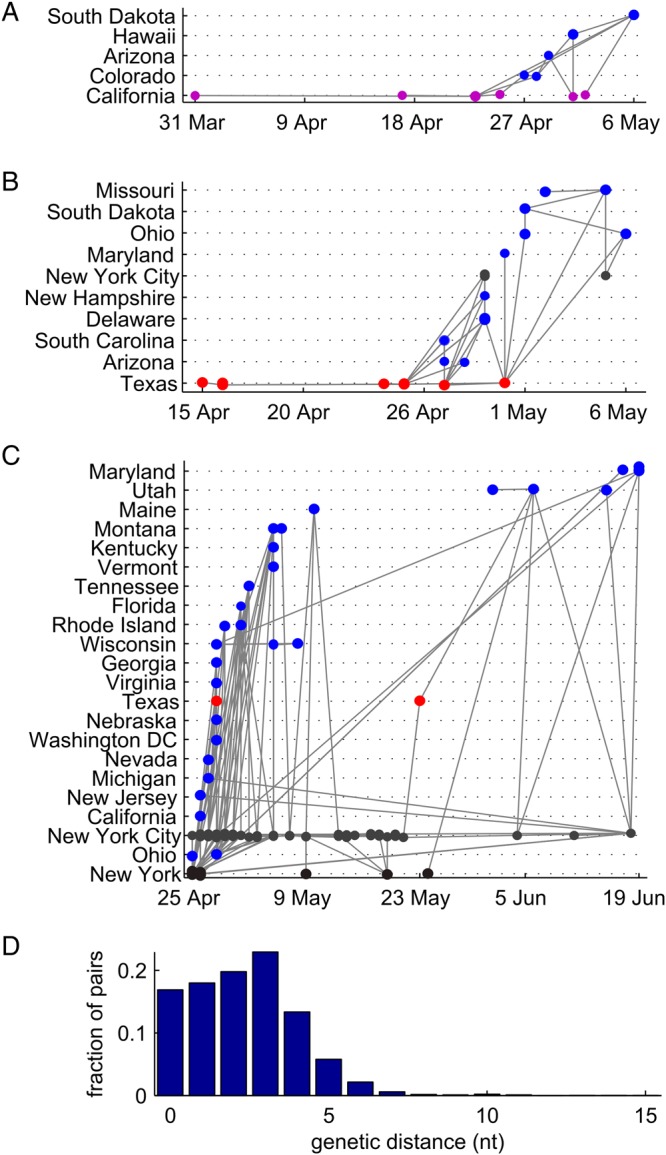
Phylogeographic data exploration with the partially-observed transmission network. The three largest connected components within the USA, rooted in: (A) California (purple), (B) Texas (red, all panels) and (C) New York City (gray, all panels) and New York state (black), with non-root locations (blue, all panels). (D) Pairwise genetic distance histogram for the entire global dataset.
The connected components also show examples of issues that arise from non-representative sampling. The number of samples available grows rapidly in late April upon growing awareness of the burgeoning pandemic.32 While the attribution of New York City (and the eastern region of the USA and Canada) as the driving force of the global epidemic is plausible because of its central role in the global transportation network, within the United States we cannot rule out that the algorithm is attributing transmission to New York and not the surrounding states simply because there is more data for New York. For example, see the Maryland cases in Figure 4C. The rate of available sequences nationwide drops at the end of April, and the lack of related cases over a 7 week interval provides essentially no information about transmission history. A benefit of the POTN for data exploration is that this consequence of incomplete data is easy to see.
Vaccine-derived polio in northern Nigeria
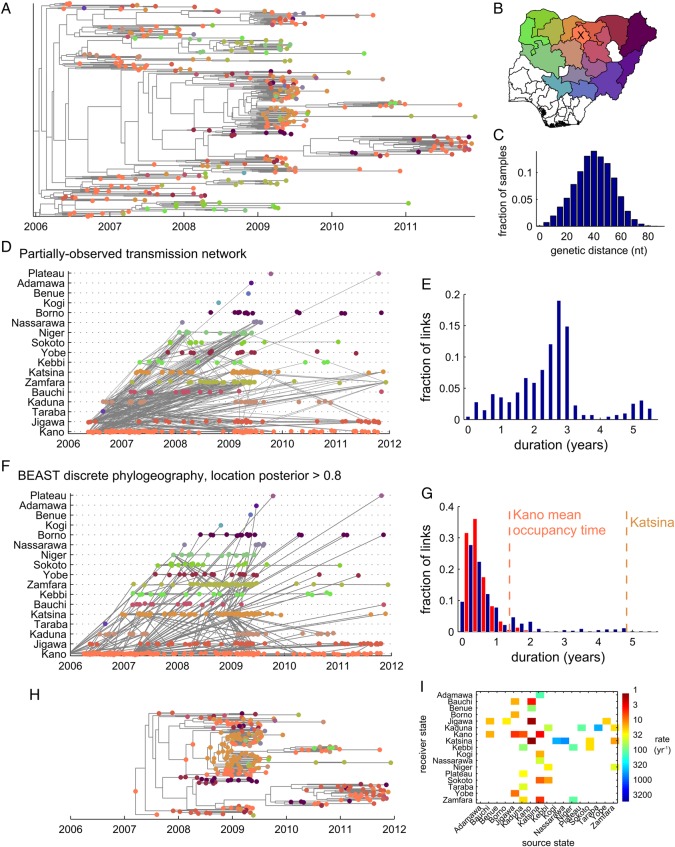
We are interested in making use of viral sequence data to better understand the subnational transmission pattern of polio in Nigeria. Due to operational challenges, vaccine cost, supply constraints and complex sociopolitical dynamics, improved risk assessment and the efficient targeting of limited resources are critical if poliovirus is to be eradicated in the remaining reservoirs.22,23 Here, we focus on the outbreak of type 2 vaccine-derived polio in Nigeria, known as Nigeria 2005–8.21 The outbreak 2005–8 was first detected in 2006, established itself as endemic by 2007, produced 358 poliomyelitis cases through to the end of 2011 and persists today.21
Figure 5 shows the results of our analysis. The POTN is unable to provide a useful reconstruction of the transmission history. Any direct ancestor was inferred for only 26% (93 of 358) cases, the majority of links are years in length and the geographic specificity is poor (many cases have ancestral links in multiple states at similar times). Entire states are disconnected, indicating that no plausible ancestry was observed at any time. We consider this a graceful failure in that the analysis takes minutes to run and it is obvious that it is not likely to be informative.
Figure 5.
Phylogeography of polio in Nigeria. (A) Maximum clade credibility tree with poliomyelitis cases (tips) colored by state, as shown on the map in panel B. (B) State colormap. Cases most commonly occur in Kano (center, bright orange, labeled with ‘x’). (C) Genetic distance histogram. (D) Partially-observed transmission network (POTN): cases labeled by color according to location, gray lines indicate POTN links between case pairs. (E) Link duration histogram. The POTN is not informative because links are long compared to the timescale over which the locations are changing in the data and the majority of nodes are disconnected. (F) BEAST discrete phylogeography, maximum clade credibility tree: gray lines indicate POTN links between case pairs; cases labeled by color according to location with internal nodes colored by highest posterior probability location (internal branches have been collapsed to span nodes with posterior location probability >0.8). (G) Link duration histogram. All branches in tree (red); collapsed links between nodes with posterior location probability >0.8 (blue). Shortest mean occupancy times estimated for the continuous-time Markov chain model are from central states Kano and Katsina. (H) Highlight of the clade that dominates after 2010, traced back to the only confident root in Kano in 2007; internal nodes colored by posterior location probability (>0.8 shown). BEAST produces a fully-connected network, but many of the links that extend after 2009 indicate years with no confident ancestral location reconstruction. (I) Mean transition rate matrix. The continuous-time Markov chain model timescales are long compared to the branching and tip location changing timescales, which limits the ability to infer ancestral locations.
We also analyzed the outbreak using the discrete phylogeographic model with Bayesian stochastic search variable selection implemented in BEAST.8 BEAST provides a fully-connected network by construction, but we can see that it suffers many of the same limitations as the POTN. The transition rate inferences are supported on the multi-year intervals between clades (Figure 5I). Within periods of high incidence, when spatial epidemiology could have policy impact, the model predicts roughly equal probabilities for all allowed transitions. Within periods of low incidence, where it would be useful to better understand the reservoirs that allow the disease to persist, there is insufficient data to anchor estimates of the reservoir locations. The low sampling rate of roughly 1 per 2000 infections33 is too sparse to resolve the interlaced patterns of transmission at the inter-state level. The only strong conclusion one can draw is that the central northern states (Kano, Katsina and Jigawa) are critical for sustaining and exporting polio, but that is unambiguous from the case count data alone.
Comparison of the POTN performance across diseases
As discussed in the methods section, the precision by which the POTN can identify ancestry can be quantified in terms of the pairwise effective population size. For both Ebola virus and H1N1, the median pairwise effective population size, , for pairs in the POTN is . The effective population size describing the entire outbreak for Ebola virus grows from roughly 30 to 60 over the course of the data (BEAST exponential coalescent)7,27 and for H1N1, the epidemic-wide effective population size of order 107 ( from).31 For both outbreaks, the POTN connects over 80% of nodes into relationships between pairs with much less genetic diversity than between randomly chosen pairs. In contrast, for polio the median pairwise effective population size is and the epidemic-wide population size is of order 103 (BEAST Bayesian skyline).34 For polio, only 38% (155 of 358) of nodes are connected and the ancestry is less well resolved as measured by the pairwise relative to the total effective population size. Thus, the ancestry in the POTN is less precise and more incomplete for polio than for Ebola virus and influenza.
Discussion
For Ebola virus in Sierra Leone, our analysis is consistent with the observations from contact tracing in Guinea:17 the epidemic consists of a highly-localized series of outbreaks characterized by within-chiefdom transmission, linked closely in time by traveling individuals, as evinced by the vertical links in the POTN between cases in different locations with zero genetic distance and zero difference in time to onset. This one example centered in Jawie also suggests that the rate of long-distance exportation from a focal outbreak cluster increases with the size of the cluster. We expect that the multi-national Ebola virus outbreak is built from many local chains like this early one for which data is available. Insofar as it is possible, additional sequencing of Ebola cases needs to be completed and made publically available with corresponding case timing and location data, so that epidemiologists and public health officials can learn patterns of Ebola virus transmission to help anticipate how to terminate this epidemic and to limit the extent of the next epidemic. For pandemic influenza, we reiterate that phylogeography is informative about transmission patterns between cities. However, we note that transmission history reconstruction is sensitive to unrepresentative sampling. For polio in northern Nigeria, our epidemiological question about transmission between states on timescales of months was poorly matched to the data and no algorithm is likely to provide a meaningful transmission history on those scales.
Ping-back behavior in which transmission routes are traversed multiple times in both directions is a common occurrence in all three diseases studied here. This can be an important mechanism for sustaining endemic disease,35 and its ubiquity indicates the value of intervening along links that have already been traversed once early in an outbreak to suppress further disease transmission.
Ancestry reconstruction and phylogeography are most likely to be useful when genetic evolution is faster than the spatial process and when the typical time between sampled cases is short compared to the correlation time of the spatial process. Figure 6 provides a graphical description of this intuition. For estimating the genetic and sampling timescales, we propose two simple heuristics. A researcher faced with a new dataset can expect the genetics to be able to resolve ancestry with little ambiguity on timescales longer than the mean time for a substitution to occur, . To estimate if the sampling rate is sufficient to resolve the spatial history, consider the disease dynamics along an ancestral lineage in the POTN. During an exponential epidemic, new infections accumulate along a lineage like , where R is the effective reproductive number and τ is the generation time. Thus, the typical time interval between cases on a lineage sampled at rate ρ per infection is approximately . For an endemic disease , the typical time is inverse in the sampling rate, . When the sampling time is shorter than the spatial correlation time, such that typical ancestor-descendent pairs are in the same or similar locations, then properties of the spatial dynamics can be inferred.
Figure 6.
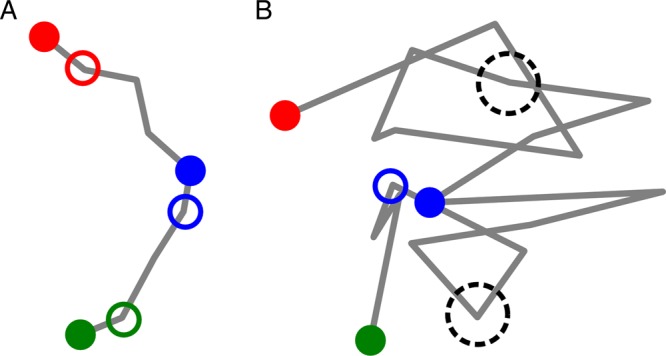
Phylogeographic inference is most informative when genetic evolution is faster and when the spatial observations are more densely sampled in time than the correlation time of the spatial process. Observed case/inferred ancestor are depicted as solid/open circles; circle size corresponds to the precision of genetic ancestor inference; location is indicated by color; unobserved spatial pathway is indicated by the gray line. (A) Cartoon of a well-resolved situation. The spatial process is densely sampled in time and the genetics provide precise estimation of ancestry. (B) Cartoon of an under-sampled situation. Much of the spatial process is unobserved and genetic distances are long. The genetics provide less precise estimates for ancestry and there is little information to infer spatial history.
For Ebola virus in Sierra Leone, the mutation timescale with whole-genome sequencing is roughly 10 days. The expected sampling timescale from the formula with sampling rate 78/136 and growth rate based on the sequenced cases of (10 days)−1 is days. The observed mean link duration in the POTN is 4 days. For the 2009 H1N1 influenza pandemic, the genetic timescale using the neuraminidase gene only is roughly 50 days and the observed link duration in the POTN is 1 week. For polio, the equivalent is 40 days, and 2.5 years. These numbers capture our experiences. For the available Ebola virus and H1N1 sequences, sampling is dense enough to provide useful spatial information on the timescale of weeks and the uncertainty in the history reconstruction is dominated by the lack of genetic diversity. For polio, the low sampling rate and more closely linear transmission dynamics leave little information about spatial mixing on policy-relevant timescales.
Furthermore, in epicenters of outbreaks experiencing exponential growth, the time interval between phylogenetically-linked cases is only logarithmically-sensitive to the sampling rate and so phylogeographic analysis is likely to be somewhat insensitive to a sampling strategy that is not stable or well-defined. In contrast, for an endemic disease, the time interval between phylogenetically-linked cases is linear in the sampling rate and therefore low sampling rates and unmeasured changes to the sampling strategy can increase susceptibility to sampling bias.
These examples demonstrate that the partially-observed transmission network has similar ability to generate plausible hypotheses for transmission history as the leading statistically rigorous approach implemented in BEAST and as the easily-interpreted heuristic transmission tree finding algorithm, SeqTrack.
We see two primary use cases for use of an algorithm like the POTN. The first is data exploration. The POTN is fast to compute in comparison to more rigorous models, it facilitates visualizing uncertainty in transmission history reconstruction and it fails gracefully when the data are uninformative. The second use is for disease surveillance in a future where field-deployable sequencing technology leads to massive expansion of near-real-time sequencing capability. By virtue of being a pairwise algorithm, the POTN can be easily extended to allow for the assimilation of new data into an existing network without having the reprocess all data.
Conclusions
With data adequate to address the epidemiological questions of interest, multiple routes to phylogeography are likely to be informative and available methods support and complement each other. As sequencing continues to become more ubiquitous, phylogeography will become an increasingly valuable tool, but research into how to match field sampling strategies, analysis methods and epidemiological needs to obtain reliable and useful results requires continued attention.
Supplementary data
Acknowledgments
Authors' contributions: HH and MF designed the POTN algorithm. MF wrote the code, performed all data analyses and drafted the manuscript. Both authors read, revised and approved the final manuscript. MF is guarantor of the paper.
Acknowledgements: We thank Dr Cara Burns (CDC) for providing linking information for the polio sequences and Dr Cara Burns, Dr Matthew Behrend and Dr Edward Wenger for motivating interest and helpful feedback throughout this project.
Funding: This work was supported by the Bill & Melinda Gates Foundation through the Global Good Fund, Bellevue, WA, USA.
Competing interests: None declared.
Ethical approval: Not required.
References
- 1.Ostfeld RS, Glass GE, Keesing F. Spatial epidemiology: an emerging (or re-emerging) discipline. Trends Ecol Evol. 2005;20:328–36. doi: 10.1016/j.tree.2005.03.009. [DOI] [PubMed] [Google Scholar]
- 2.Beale L, Abellan JJ, Hodgson S, Jarup L. Methodologic issues and approaches to spatial epidemiology. Environ Health Perspect. 2008;116:1105–10. doi: 10.1289/ehp.10816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Archie EA, Luikart G, Ezenwa VO. Infecting epidemiology with genetics: a new frontier in disease ecology. Trends Ecol Evol. 2009;24:21–30. doi: 10.1016/j.tree.2008.08.008. [DOI] [PubMed] [Google Scholar]
- 4.Faria NR, Suchard M, Rambaut A, Lemey P. Toward a quantitative understanding of viral phylogeography. Curr Opin Virol. 2011;1:423–9. doi: 10.1016/j.coviro.2011.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Holmes EC. Evolutionary history and phylogeography of human viruses. Annu Rev Microbiol. 2008;62:307–28. doi: 10.1146/annurev.micro.62.081307.162912. [DOI] [PubMed] [Google Scholar]
- 6.Bloomquist EW, Lemey P, Suchard MA. Three roads diverged? Routes to phylogeographic inference. Trends Ecol Evol. 2010;25:626–32. doi: 10.1016/j.tree.2010.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Drummond A, Suchard M, Xie D, Rambaut A. Bayesian Phylogenetics with BEAUti and the BEAST 1.7. Mol Biol Evol. 2012;29:1969–73. doi: 10.1093/molbev/mss075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lemey P, Rambaut A, Drummond A, Suchard MA. Bayesian phylogeography finds its roots. PLoS Comput Biol. 2009;5:e1000520. doi: 10.1371/journal.pcbi.1000520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Volz EM, Koelle K, Bedford T. Viral phylodynamics. PLoS Comput Biol. 2013;9:e1002947. doi: 10.1371/journal.pcbi.1002947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ayres DL, Darling A, Zwickl DJ, et al. BEAGLE: an application programming interface and high-performance computing library for statistical phylogenetics. Syst Biol. 2012;61:170–3. doi: 10.1093/sysbio/syr100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jombart T, Eggo RM, Dodd PJ, Balloux F. Reconstructing disease outbreaks from genetic data: a graph approach. Heredity (Edinb) 2011;106:383–90. doi: 10.1038/hdy.2010.78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ypma RJ, van Ballegooijen WM, Wallinga J. Relating phylogenetic trees to transmission trees of infectious disease outbreaks. Genetics. 2013;195:1055–62. doi: 10.1534/genetics.113.154856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Cottam EM, Thébaud G, Wadsworth J, et al. Integrating genetic and epidemiological data to determine transmission pathways of foot-and-mouth disease virus. Proc Biol Sci. 2008;275:887–95. doi: 10.1098/rspb.2007.1442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Morelli MJ, Thébaud G, Chadœuf J, et al. A bayesian inference framework to reconstruct transmission trees using epidemiological and genetic data. PLoS Comput Biol. 2012;8:e1002768. doi: 10.1371/journal.pcbi.1002768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gire SK, Goba A, Andersen KG, et al. Genomic surveillance elucidates Ebola virus origin and transmission during the 2014 outbreak. Science. 2014;345:1369–72. doi: 10.1126/science.1259657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Aylward RB, Barboza P, Bawo L, et al. Ebola virus disease in west Africa - the first 9 months of the epidemic and forward projections. N Engl J Med. 2014;371:1481–95. doi: 10.1056/NEJMoa1411100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Baize S, Pannetier D, Oestereich L, et al. Emergence of Zaire Ebola virus disease in Guinea - preliminary report. N Engl J Med. 2014;371:1418–25. doi: 10.1056/NEJMoa1404505. [DOI] [PubMed] [Google Scholar]
- 18.Lemey P, Suchard M, Rambaut A. Reconstructing the initial global spread of a human influenza pandemic: A Bayesian spatial-temporal model for the global spread of H1N1 pdm. PLoS Curr. 2009;1:RRN1031. doi: 10.1371/currents.RRN1031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Rambaut A, Holmes E. The early molecular epidemiology of the swine-origin A/H1N1 human influenza pandemic. PLoS Curr. 2009;1:RRN1003. doi: 10.1371/currents.RRN1003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Viboud C, Nelson MI, Tan Y, Holmes EC. Contrasting the epidemiological and evolutionary dynamics of influenza spatial transmission. Phil Trans R Soc Lond B Biol Sci. 2013;368:20120199. doi: 10.1098/rstb.2012.0199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Burns CC, Shaw J, Jorba J, et al. Multiple independent emergences of type 2 vaccine-derived polioviruses during a large outbreak in northern Nigeria. J Virol. 2013;87:4907–22. doi: 10.1128/JVI.02954-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Upfill-Brown AM, Lyons HM, Pate MA, et al. Predictive spatial risk model of poliovirus to aid prioritization and hasten eradication in Nigeria. BMC Med. 2014;12:92. doi: 10.1186/1741-7015-12-92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Grassly N. The final stages of the global eradication of poliomyelitis. Phil Trans R Soc Lond B Biol Sci. 2013;368:20120140. doi: 10.1098/rstb.2012.0140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Verhoeven K, Simonsen K, McIntyre L. Implementing false discovery rate control: increasing your power. Oikos. 2005;108:643–7. [Google Scholar]
- 25.Felsenstein J. Confidence limits on phylogenies: an approach using the bootstrap. Evolution. 1985;39:783–91. doi: 10.1111/j.1558-5646.1985.tb00420.x. [DOI] [PubMed] [Google Scholar]
- 26.Nei M, Kumar S. Oxford: Oxford University Press; 2000. Molecular evolution and phylogenetics; pp. 171–175. [Google Scholar]
- 27.Nordborg M. Coalescent Theory. In: Balding DJ, Bishop M, Cannings C, editors. Handbook of Statistical Genetics. Chichester: Wiley; 2004. pp. 179–212. [Google Scholar]
- 28.Rodrigo A, Felsenstein J. Coalescent approaches to HIV population genetics. In: Crandall K, editor. The evolution of HIV. Baltimore: Johns Hopkins University Press; 1999. pp. 233–274. [Google Scholar]
- 29.WHO. Geneva: World Health Organization; 2014. Ebola virus disease, West Africa – update. Disease Outbreak News. http://www.who.int/csr/don/2014_06_22_ebola/en/ [accessed 20 Oct 2014]. [Google Scholar]
- 30.Bouckaert RR. DensiTree: making sense of sets of phylogenetic trees. Bioinformatics. 2010;26:1372–3. doi: 10.1093/bioinformatics/btq110. [DOI] [PubMed] [Google Scholar]
- 31.De Silva E, Ferguson NM, Fraser C. Inferring pandemic growth rates from sequence data. J R Soc Interface. 2012;9:1797–808. doi: 10.1098/rsif.2011.0850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Fraser C, Donnelly CA, Cauchemez S, et al. Pandemic potential of a strain of influenza A (H1N1): early findings. Science. 2009;324:1557–61. doi: 10.1126/science.1176062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Nathanson N, Kew OM. From emergence to eradication: the epidemiology of poliomyelitis deconstructed. Am J Epidemiol. 2010;172:1213–29. doi: 10.1093/aje/kwq320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Drummond A, Rambaut A, Shapiro B, Pybus OG. Bayesian coalescent inference of past population dynamics from molecular sequences. Mol Biol Evol. 2005;22:1185–92. doi: 10.1093/molbev/msi103. [DOI] [PubMed] [Google Scholar]
- 35.Grenfell B, Bjørnstad ON, Kappey J. Travelling waves and spatial hierarchies in measles epidemics. Nature. 2001;414:716–23. doi: 10.1038/414716a. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.