Abstract
This computational study integrates anatomical and physiological data to assess the functional role of the lateral excitatory connections between layer 2/3 (L2/3) pyramidal cells (PCs) in shaping their response during early stages of intracortical processing of a whisker deflection (WD). Based on in vivo and in vitro recordings, and 3D reconstructions of connected pairs of L2/3 PCs, our model predicts that: 1) AMPAR and NMDAR conductances/synapse are 0.52 ± 0.24 and 0.40 ± 0.34 nS, respectively; 2) following WD, connection between L2/3 PCs induces a composite EPSPs of 7.6 ± 1.7 mV, well below the threshold for action potential (AP) initiation; 3) together with the excitatory feedforward L4-to-L2/3 connection, WD evoked a composite EPSP of 16.3 ± 3.5 mV and a probability of 0.01 to generate an AP. When considering the variability in L4 spiny neurons responsiveness, it increased to 17.8 ± 11.2 mV; this 3-fold increase in the SD yielded AP probability of 0.35; 4) the interaction between L4-to-L2/3 and L2/3-to-L2/3 inputs is highly nonlinear; 5) L2/3 dendritic morphology significantly affects L2/3 PCs responsiveness. We conclude that early stages of intracortical signaling of WD are dominated by a combination of feedforward L4–L2/3 and L2/3–L2/3 lateral connections.
Keywords: barrel cortex, compartmental model, cortical circuits, synaptic integration, whisker deflection
Introduction
The cortical column, in particular that of the barrel field in the somatosensory cortex of rodents (Woolsey and Van der Loos 1970), with its ∼15 000–20 000 neurons distributed over 6 layers, has attracted in recent years an intense experimental attention (da Costa and Martin 2010; Meyer et al. 2010). Novel anatomical, electrophysiological, optical, and molecular techniques have provided new information about the pattern of neuronal connectivity, reliability, and efficacy of synaptic connections and the electrical and morphological types of neurons that constitute the cortical column (Markram et al. 1997a, 1997b; Reyes and Sakmann 1999; Lübke et al. 2000, 2003; Petersen and Sakmann 2000; Schubert et al. 2001; Feldmeyer et al. 2002, 2005, 2006; Holmgren et al. 2003; Silver et al. 2003; Shepherd et al. 2005; Song et al. 2005; Le Bé and Markram 2006; Le Be et al. 2007; Lefort et al. 2009). In vivo recordings in both anesthetized animals (Brecht and Sakmann 2002; Brecht et al. 2003; de Kock et al. 2007; Kerr et al. 2007; Sato et al. 2007) and recently also in awake animals (Crochet and Petersen 2006; Huber et al. 2008; Poulet and Petersen 2008) provide a wealth of information regarding the dynamics of the response within the column following sensory stimulation. With the accumulation of these new data, the need to understand how the structural and physiological details give rise to the dynamics of the cortical column, and eventually to its function, becomes more acute. A modeling framework that enables one to integrate the accumulating body of experimental data about the cortical column is therefore essential.
Recently, we have proposed a comprehensive computational approach for constructing an in silico model of the neocortical column (Sarid et al. 2007). This systematic approach is based on modeling basic building blocks (connection “modules”) of a column, by combining in vitro paired recordings and anatomical reconstruction and in vivo recordings from the respective projection and target cells of a connection. We started by focusing on the synaptic connection between layer 4 (L4) spiny stellate cells and layer 2/3 (L2/3) pyramidal cells (PCs) in rat somatosensory cortex (Feldmeyer et al. 2002). We constructed this L4–L2/3 module based on the parameters found from pair recordings of connected L4-to-L2/3 neurons, together with the spatial distribution and number of L4 synapse on L2/3 dendrites (Lübke et al. 2003) and the average in vivo spiking probability (the poststimulus time histogram, PSTH) of L4 spiny neurons (Brecht and Sakmann 2002) evoked by single whisker deflection (WD). The model predicts that, when using the average PSTH of L4 neurons as an input, synaptic signals arriving via the L4–L2/3 connection, on their own, do not reach the spiking threshold of L2/3 PCs. However, taking into account that some of the spiking L4 spiny neurons are more responsive than others, we showed that L2/3 PCs are likely to spike at low frequency following WD, as observed experimentally (Brecht et al. 2003).
We extended this work by constructing another major cortical module—the excitatory synaptic connection between intracolumnar pairs of L2/3 PCs (Fig. 1a). This model is based on the parameters found from pair recordings of synaptically connected L2/3–L2/3 PCs, the total number of L2/3 synapses converging on the dendrites of a single L2/3 neuron (270 axons, 2.8 contacts per axon) and their spatial distribution over the dendritic field (Lübke et al. 2003), and the average in vivo spiking probability of L2/3 PCs following WD (Brecht et al. 2003). The model predicts that the intralaminar (lateral) connection between L2/3 and L2/3 PCs is weaker than that of the feedforward L4–L2/3 connection. It cannot on its own initiate a spread of activity in the L2/3 network.
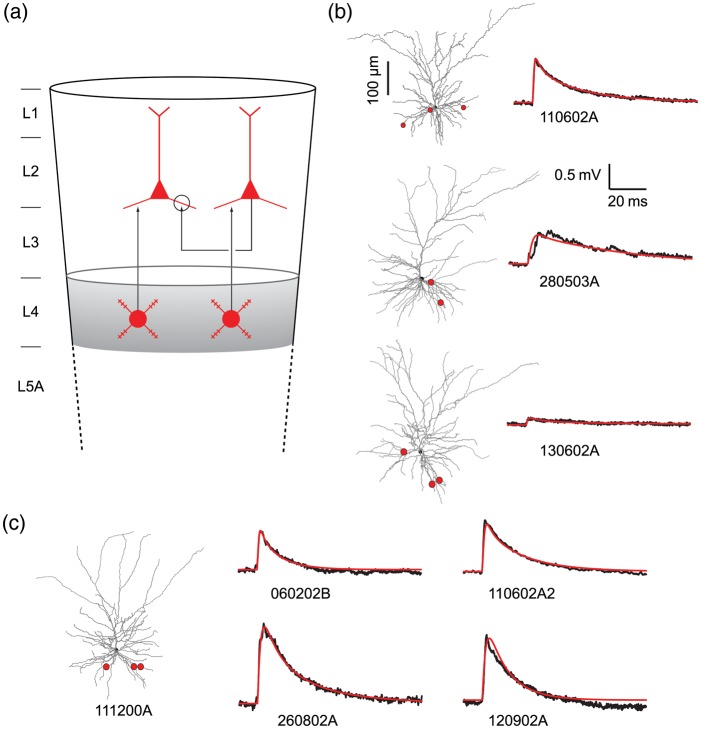
Figure 1.
Extracting synaptic parameters through fitting model to experiments. (a) Schematic drawing depicting the cortical modules modeled in this study. Shown are the feedforward excitatory connection between L4 spiny stellate and L2/3 pyramidal cells and the lateral excitatory connection between L2/3 and L2/3 pyramidal cell pairs (circle). (b) The postsynaptic cell from each connected pair of L2/3 pyramidal cells is shown in gray together with the putative synaptic contacts (red dots) originated from the corresponding presynaptic cell. For each case, black trace at right is the average EPSP (n = 62, 20, 91, from top to bottom) resulting from a single presynaptic spike; modeled EPSP is depicted in red. The corresponding values for Rin (MΩ), Rm (Ω × cm2), and Cm (µF/cm2) in these modeled cells are, respectively, 88, 16 000, 0.91 (top cell); 75, 15 000, 1.1 (middle cell), and 46, 6000, 2.0 (lower cell) with Ri = 150 Ω × cm in all cases. (c) Experimental average EPSP (n = 20, black line) measured in 4 other connected L2/3–L2/3 pyramidal cells pairs that were not morphologically reconstructed. In these cases, the morphology of a typical reconstructed L2/3 pyramidal neuron was used for modeling (gray cell at the left; see Materials and Methods section) with location of synaptic contacts as shown by red dots. For this case, Rin, Rm, and Cm are 74, 14 000, and 0.89, respectively.
Next, we combined the 2 modules by computing the voltage response of the modeled L2/3 PC following the firing of both the presynaptic L4 spiny cell population and of the presynaptic L2/3 PCs population as measured in vivo following whisker stimulation (Brecht et al. 2003). This enabled us to assess the contribution of the nonlinear interaction between these 2 major excitatory input sources in shaping the response of L2/3 PCs to WD. The model predicts that the activation of both inputs is expected to generate low probability of spiking in L2/3 PCs as was indeed found experimentally (Brecht et al. 2003). We also found that the specific morphology of L2/3 PCs (assuming a constant number of synapses and the same spatial distribution of synapses for all modeled cells) has a significant impact on their response to WD. This study brings us yet one step closer to understanding how the unique “hardware” composing a cortical column enables the processing of sensory input within the column.
Materials and Methods
Compartmental Modeling
Modeling was carried out using NEURON 6.2.1 simulator (Hines and Carnevale 1997). 3D reconstructions of 3 synaptically connected L2/3–L2/3 pairs of PCs in which the putative location of the synaptic connection is also available, were obtained using a NEUROLUCIDA system (Microbrightfield, Colchester VT, USA) and converted to NEURON format (Fig. 1a). For the simulations in Figures 2–5, the prototypical model cell (111200A, Fig. 1b, see complete description for this cell in Sarid et al. 2007) was used, whereas in Figure 7 the above cell plus 5 additional reconstructed L2/3 PCs were used. Dendritic sections were subdivided into compartments; each dendritic compartment was shorter than 20 μm. This yields between 515 and 1182 compartments per neuron. The integration time step for the simulations was 0.025 ms.
Figure 2.
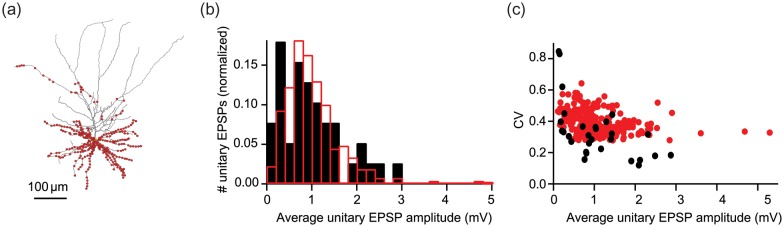
Distribution of synaptic contacts and unitary EPSP histogram of a L2/3 pyramidal cell population converging onto a single L2/3 pyramidal cell. (a) Distribution of 756 L2/3–L2/3 synaptic contacts (red dots) from 270 axons (average of 2.8 contacts per axon) onto the dendritic domain of the modeled prototypical L2/3 pyramidal cell (see Materials and Methods section). Due to overlap, each dot may represent more than one synaptic contact. (b) Distribution of the average amplitude of the 270 modeled unitary EPSPs (red) superimposed on the experimental distribution of the average unitary EPSPs (black). (c) The coefficient of variation (CV) plotted as a function of the EPSP peak amplitude (model in red, experiment in black).
Figure 5.
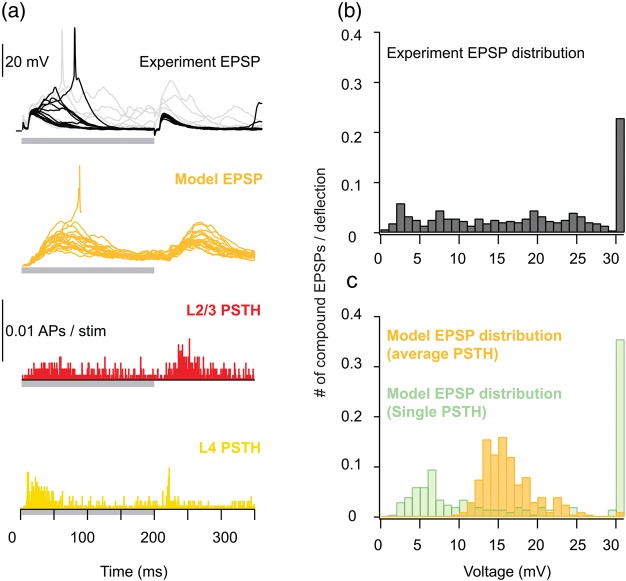
Distribution of compound PSP amplitudes following whisker deflection—experiment versus model with both L2/3 + L4 activated. (a) Top: 20 experimental responses of a barrel-related L2/3 cell to principal whisker deflection (courtesy of M. Brecht). Black traces are responses from the Down state. Orange trace: Records of 20 model responses to whisker deflection; note an occasional spike (truncated). Activation of modeled synaptic inputs was drawn from both the average PSTH recorded in vivo from L2/3 pyramidal cells (red histogram, n = 26) as well as from the average PSTH recorded from L4 spiny neurons (lower yellow histogram, n = 25). Gray bars below voltage traces and PSTHs indicate the onset and offset of whisker deflection. (b) Experimental distribution of PSPs amplitude from the Down state, following whisker deflection. (c) Model prediction of the distribution of composite PSPs amplitude following whisker deflection. Orange histogram depicts the case whereby the average PSTHs shown in (a) were used as input. The green histogram illustrates the case in which the input was drawn from individual PSTHs of the 3 L2/3 pyramidal cells depicted in Figure 3a (purple) and the PSTHs of 6 individual L4 spiny neurons (Fig. 7a, in Sarid et al. 2007). Spikes are evoked in the model and in experiments for PSPs larger than 30 mV (rightmost bar).
Figure 7.
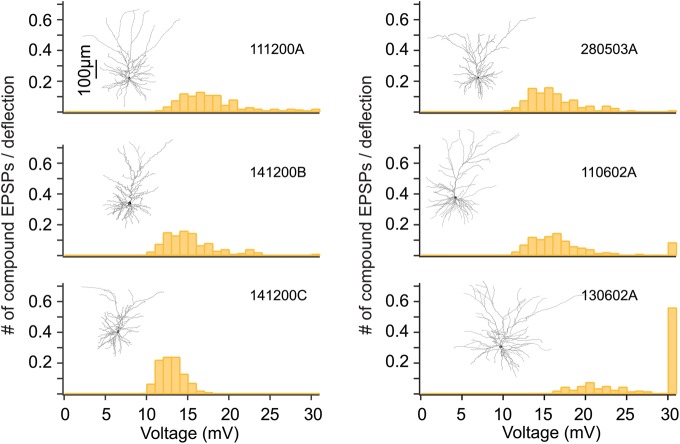
Response variability to whisker deflection due to difference in morphology of L2/3 pyramidal cells. The dendritic arbor of modeled cells is depicted in the inset of each panel and the corresponding distribution of composite PSPs amplitude following whisker deflection predicted by the model is shown in orange. Modeled synapses were activated based on the average PSTHs measured in vivo from both L2/3 and L4 neurons (red and yellow PSTHs in Fig. 5a bottom). In all 6 neurons modeled, the same specific Rm, Cm, and Ri values were used with identical number of synapses activated and same statistics for their spatial distribution over the dendritic tree (see Materials and Methods section). The only difference between these cases is in the morphology of the modeled postsynaptic L2/3 pyramidal cells. Details are provided in Table 2.
Passive Cable Model of L2/3 Pyramidal Cells and Properties of L2/3-to-L2/3 Synaptic Connection
The procedure for estimating the specific passive, Rm, Cm, and Ri for each of the modeled L2/3 PCs was as previously described (Sarid et al. 2007). Dendritic spines were incorporated globally into the modeled neuron as outlined in Sarid et al. (2007).
Excitatory synaptic responses at L2/3 PCs have both AMPAR and NMDAR components (Busetto et al. 2008). We used the standard equation to describe the synaptic conductance associated with both of these components (for a detailed description, see Sarid et al. 2007). The target for model fitting was the experimental average unitary EPSP recorded in each of the 3 morphologically reconstructed L2/3 PCs for which the location of the putative synapses is also known (Fig. 1). Additional targets for the model fit were unitary EPSPs from 4 additional synaptically connected L2/3–L2/3 PC pairs that were not morphologically reconstructed (and hence the dendritic location of synaptic contacts was not defined, Fig. 1b). In this case, the location of contacts was randomly chosen according to the probability of a synapse to be at a certain branch order (Feldmeyer et al. 2006); the average distance of these modeled contacts was 90 µm from the soma as was found experimentally (Feldmeyer et al. 2006). A genetic algorithm, implemented in NEURON, was used for estimating the synaptic parameters for both AMPA and NMDA components that provide the best fit for the target experimental EPSPs (Vanier and Bower 1999; Druckmann et al. 2007).
Neuron Model Parameters for the in Vivo Condition
Under in vivo conditions (measured in anesthetized animals), Rin is ≈ 40% of that measured in vitro, yet the membrane time constant remains essentially the same in both conditions (Waters and Helmchen 2006; Sarid et al. 2007). Therefore, for our in vivo simulations (Figs 3 and 5–7), we have used a Rm value of 4500 Ωcm2 and a Ri value of 150 Ωcm, so that the model Rin is reduced by a factor of 2.5 compared with that measured in vitro. To maintain the same time constant, Cm was multiplied by the ratio between the in vitro and the in vivo Rm (Cm = 2.3 μF/cm2). Nonlinear membrane properties of L2/3 neurons were also modeled are as previously described (Sarid et al. 2007).
Figure 3.
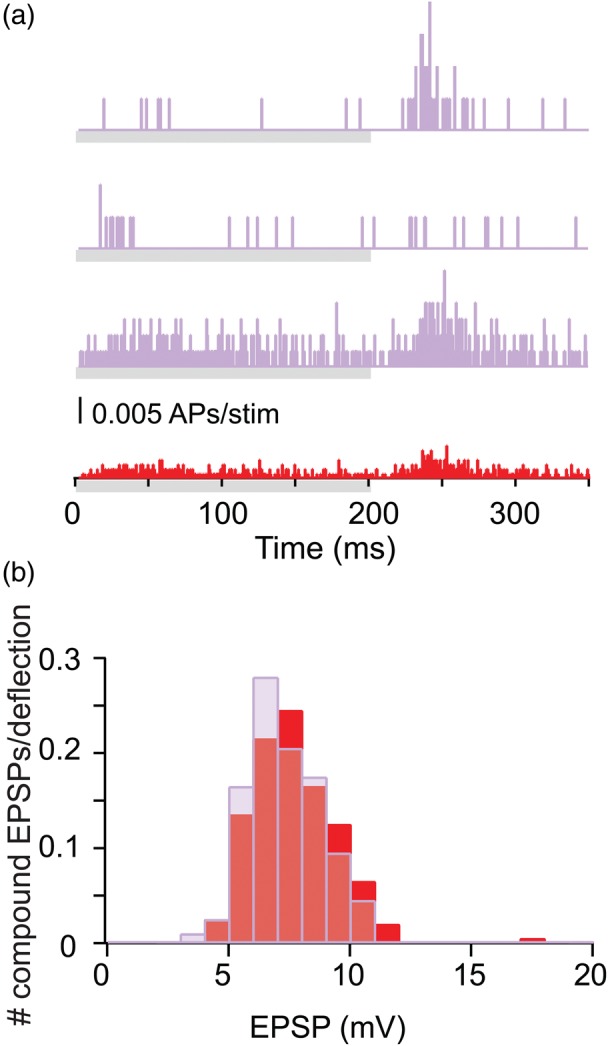
Model prediction for the distribution of compound EPSP's resulting from L2/3–L2/3 pyramidal cell connection following whisker stimulation. (a) Three individual PSTHs measured in vivo from 3 L2/3 pyramidal cells following whisker deflection (purple); the average PSTH in shown in red (n = 25 cells). Gray bars below the PSTHs indicate the onset and offset of the whisker deflection. (b) Composite EPSP amplitude distribution following whisker deflection predicted by the model based either on the 3 individual PSTH shown in a (purple histogram, n = 200) or on the average PSTH (corresponding red histogram, n = 200), see Materials and Methods section. In both cases, AP threshold was not reached.
L2/3 Pyramidal Cells Population Converging Onto a Single L2/3 Pyramidal Cell
On average 270 L2/3 PCs converge onto a single L2/3 PC (Feldmeyer et al. 2006). Each L2/3 PC establishes about 2.8 synaptic contacts on the target L2/3 PC (Feldmeyer et al. 2006). Therefore, on average, 756 synaptic contacts are formed by the presynaptic L2/3 PCs on a single postsynaptic L2/3 PC. The distribution of synaptic inputs over the dendritic surface of a L2/3 neuron was taken from Table 1 in Feldmeyer et al. (2006). To check the validity of this distribution, we activated individually 270 axons (each composed of 2–4 randomly chosen synaptic contacts, out of 756). Each contact was activated 100 times, using the synaptic parameters that were found to fit the experimental unitary EPSP (Table 1). For each synapse activated, the maximal conductance for the AMPA and NMDA receptors was chosen at random from a lognormal distribution, with a mean of 0.52 ± 0.24 nS for the AMPAR and 0.40 ± 0.34 nS for the NMDA receptor (see Table 1). The release probability at each synaptic contact was 0.71, calculated from the failure probability and the number of synaptic contacts per pair given in Feldmeyer et al. (2006).
Table 1.
Model predictions for L2/3–L2/3 synaptic parameters
| Cell | gAMPA (nS) | τ1 (ms) | τ2 (ms) | gNMDA (nS) | τ1 (ms) | τ2 (ms) |
|---|---|---|---|---|---|---|
| 110602A | 0.71 | 0.33 | 0.33 | 0.39 | 0.23 | 31 |
| 280503A | 0.21 | 0.99 | 2.0 | 1.0 | 5.0 | 46 |
| 130602A | 0.25 | 0.060 | 0.63 | 0.13 | 0.79 | 97 |
| 120902A | 0.46 | 0.26 | 2.0 | 0.22 | 1.6 | 7.6 |
| 060202B | 0.67 | 0.41 | 0.41 | 0.0010 | 4.1 | 12 |
| 110602A2 | 0.51 | 0.45 | 0.77 | 0.40 | 2.0 | 22 |
| 260802A | 0.84 | 0.020 | 1.8 | 0.69 | 3.2 | 34 |
| Average | 0.52 | 0.36 | 1.1 | 0.40 | 2.4 | 36 |
| S.D | 0.24 | 0.32 | 0.75 | 0.34 | 1.7 | 30 |
gAMPA and gNMDA are the maximal conductance for the AMPA- and NMDA-receptor channels at individual synaptic contact; τ1 and τ2 are the time constants that govern the double exponent function describing the receptor's kinetics. Equations used are as in Sarid et al. (2007). Shaded area is for the 4 EPSPs depicted in Figure 1b for which the morphology of the postsynaptic cell is not available.
Simulating Responses of L2/3 Neuron to Whisker Deflection
WDs that induced compound EPSPs and occasionally the generation of APs in the modeled L2/3 PC were simulated by activating synapses originating either from both L2/3 PCs and L4 spiny neurons or from each source separately. For the intralaminar L2/3–L2/3 input, in each simulation, the number of presynaptic L2/3 PCs was randomly chosen from a normal distribution with a mean of 270 ± 16 (Feldmeyer et al. 2006). Axons were activated according to the average probability for the generation of an AP (the average peristimulus time histogram, PSTH) measured using whole-cell recordings in vivo (Brecht et al. 2003) in L2/3 PCs following WD (n = 23, with 20 repetition per cell). Additional PSTHs obtained from recordings from other 3 individual L2/3 PCs with 160 repetitions per neuron were also used either individually or as part of the average PSTH (Fig. 3). The resulting simulated compound PSPs were compared with the experimental PSPs, measured from the Down state in 16 L2/3 PCs (Brecht et al. 2003) and from 4 additional recordings of L2/3 PCs responding to WD (Fig. 5). For simulations in which both L4 spiny neurons and L2/3 PCs contributed to L2/3 PC activation, L4 spiny neurons were activated as described previously (Sarid et al. 2007); see also Figures 5–7.
Results
Passive Model for L2/3 Pyramidal Cells
Passive models were constructed for 3 connected pairs of L2/3 PCs that were physiologically characterized and morphologically reconstructed including the identification of putative synaptic contacts (Fig. 1b, red dots). For the 3 postsynaptic L2/3 PCs modeled, the apical dendrite extended between 609 and 639 µm and the basal dendritic tree between 187 and 294 µm. The mean surface area of the dendritic arbor (including the estimation of dendritic spines area; see Materials and Methods section) was 18 974 ± 1155 µm2.
Input resistance (Rin) measured in vitro was, on average, 70 ± 21 MΩ, and the membrane time constant was 14 ± 1.7 ms (Fig. 1, legend). Adjustment between model and experiments yielded estimates for the specific membrane resistivity, Rm, and membrane capacitance, Cm, of around 12 000 Ω × cm2 and 1.3 μF/cm2, respectively, assuming an axial resistance, Ri of 150 Ωcm.
Time Course of a Unitary L2/3–to–L2/3 EPSP
Seven experimentally measured L2/3–L2/3 unitary EPSPs (Fig. 1b,c, black traces) were used as targets for estimating the magnitude and time course of the synaptic conductance mediated by both AMPA receptors (AMPAR) and NMDA receptors (NMDAR; see Materials and Methods section). Three pairs were fully reconstructed and their morphology and location of putative synaptic contacts (red dots) are known (Fig. 1b). The mean unitary EPSP amplitude (0.87, 0.65, and 0.14 mV, top to bottom in Fig. 1b) for these neurons was smaller than the mean unitary EPSP for all 7 pairs (1.0 ± 0.7 mV; see Feldmeyer et al. 2006). Consequently, we expanded our dataset by adding 4 unitary EPSPs recorded from connected L2/3–L2/3 PCs for which the location of synaptic contacts and dendritic morphology were not known (Fig. 1c). The mean amplitudes of these 4 unitary EPSPs were 1.5, 1.3, 1.0, and 0.83 mV.
Estimation of synaptic parameters by matching a model to the experimental data requires both the dendritic morphology and cable properties of the postsynaptic cells, and the location of the synaptic contact onto their dendritic arbor. As this information is missing for the latter 4 ESPSP's, we chose 1 L2/3 PC that was fully reconstructed as the prototypical cell (Fig. 1c and previously used in Sarid et al. 2007). We show that the passive and synaptic parameters measured in this cell are close to the average of L2/3 PC population. In the model, the locations of synaptic contacts (red dots) were selected such that they agree with the experimentally determined statistical distribution (branch order and average distance from soma of 90 μm) of these synaptic contacts (Feldmeyer et al. 2006). The red lines in Figure 1b,c depict an excellent fit of the model EPSPs to the experimentally recorded EPSPs (black traces). Synaptic parameters obtained via this matching procedure are shown in Table 1.
The average amplitude of the AMPAR conductance for the 7 cells modeled was 0.52 ± 0.24 nS; the peak value for NMDAR conductance was 0.40 ± 0.34 nS. These values are within the range reported previously (McBain and Dingledine 1992; Spruston et al. 1995). Notably, these values are almost twice those found for the L4–L2/3 connection (Sarid et al. 2007). This is expected since 1) the average unitary EPSP amplitude for L2/3–L2/3 connections is larger than the unitary EPSP measured for L4–L2/3 connections (1.0 ± 0.7 vs. 0.7 ± 0.6 mV, respectively; Feldmeyer et al. 2002, 2006); 2) the number of synaptic contacts per axon is smaller for L2/3–L2/3 connections than for L4–L2/3 connections (2.8 ± 0.7 vs. 4.5 ± 0.5; Feldmeyer et al. 2002, 2006); 3) the average distance of synaptic contacts from the soma is larger for L2/3–L2/3 connections than of for L4–L2/3 connections (91 ± 47 vs. 67 ± 34 μm; Feldmeyer et al. 2002, 2006). In other words, despite the smaller number of contacts per connection and their more distant dendritic location, an individual L2/3–L2/3 connection is stronger than an individual L4–L2/3 connection, because the synaptic conductance associated with each contact is larger in the former.
Population of Unitary EPSPs at the L2/3–L2/3 Connection: Model Versus Experiments
Fitting L2/3 model to the experimental data obtained from L2/3 to L2/3 pair recordings provided an estimate for properties of individual synaptic contacts (Table 1; Fig. 1). Next, 756 synaptic contacts from 270 axons (average of 2.8 contacts per axon, see Feldmeyer et al. 2006 and Materials and Methods section) were distributed over the modeled L2/3 PC at the appropriate dendritic innervation domain of the L2/3–L2/3 connection (Fig. 2a; Feldmeyer et al. 2006). The 270 presynaptic L2/3 “axons” were activated individually and the distribution of the resulting simulated EPSPs was measured (see Materials and Methods section). On average, the amplitude of the model unitary EPSP was 1.0 ± 0.6 mV (Fig. 2b, red) with corresponding coefficient of variation (CV) of 0.39 ± 0.07 (Fig. 2c, red), in excellent agreement with the experimental data (amplitude of 1.0 ± 0.7 mV, Fig. 2b black dots, and CV of 0.33 ± 0.18, Fig. 2c, black, respectively; Feldmeyer et al. 2006). These results show that our model of the L2/3–L2/3 connection and the dendritic domain for the synaptic contacts is “realistic”. This model was further used to explore the contribution of the L2/3–L2/3 connection to the response of L2/3 PCs following WD.
Simulation of Whisker Deflection: Input from Layer 2/3 Alone
In the simulation illustrated in Figure 3, the input to the modeled L2/3 PC was sampled either from the average spiking probability (PSTHs) of L2/3 PCs following WD measured experimentally (Brecht et al. 2003; Fig. 3a, red) or from the PSTHs of 3 individual L2/3 PCs (measured by R. Bruno, unpublished results, Fig. 3a, purple). Figure 3b depicts the composite EPSPs amplitude distribution following WD predicted by the model, based either on using the 3 individual PSTHs (purple) as the model input or on the average PSTH (red), see Materials and Methods section. There is no significant difference between the 2 cases; in both, the distribution of the voltage amplitude of the compound EPSP about the mean is relatively narrow. For the case based on the average PSTH (red), 122 axons out of the total of 270 (i.e., 259 synaptic contacts, assuming a release probability of 0.71, calculated based on the results in Feldmeyer et al. 2006) were activated on average per WD (ranging between 97 and 154 axons, corresponding to 201–325 synaptic contacts). The average amplitude of the compound EPSP is 7.6 ± 1.7 mV (range between 4.1 and 17.0 mV). For the individual PSTHs case (purple), on average 117 axons (i.e., 215 synaptic contacts, assuming release probability of 0.71) were activated per WD (ranging between 91 and 147 axons, corresponding to 161–267 synaptic contacts). In this case, the average amplitude of the compound EPSP is 7.2 ± 1.4 mV (range between 3.4 and 10.9 mV). In both cases, the AP threshold was not reached in the modeled L2/3 PC [spike threshold is near 30 mV above the resting potential in both model and experiments (Brecht et al. 2003)].
We conclude that the contribution of the intracolumnar lateral L2/3–L2/3 connections, on its own, is significantly below threshold for initiating a spike in L2/3 PCs. Therefore, this intracolumnar connection is too weak to trigger the lateral spread of activity within this layer. However, this may be substantially different during UP states of cortical activity, during which the excitability of excitatory neurons is significantly enhanced (McCormick et al. 2003; Crochet and Petersen 2006; Castro-Alamancos 2009; Constantinople and Bruno 2011; Hirata and Castro-Alamancos 2011).
Simulation of Whisker Deflection: Input from Both L2/3 and L4
Before modeling the combined impact of both feedforward L4–L2/3 and the lateral L2/3–L2/3 connections on L2/3 PCs (based on experimental recordings from both L4 as well as L2/3 responses to whisker stimulation), we show (Fig. 4) the distribution of synaptic contacts over the dendritic field of L2/3 PC of these input sources (L2/3 input is in red and input from L4 spiny neurons is in yellow, see Lübke et al. 2003; Feldmeyer et al. 2006). Notably, synaptic inputs from both sources overlap to a significant degree. There are about 2-fold more contacts converging from L4 spiny neurons onto a single L2/3 PC than those arising from L2/3 (1575 vs. 756 on average, respectively). Synaptic contacts from L2/3 PCs are, on average, more distal than synaptic contacts from L4 spiny neurons (90 vs. 70 µm; Feldmeyer et al. 2002, 2006); both types of synaptic input avoid the distal parts of L2/3 dendrites.
Figure 4.
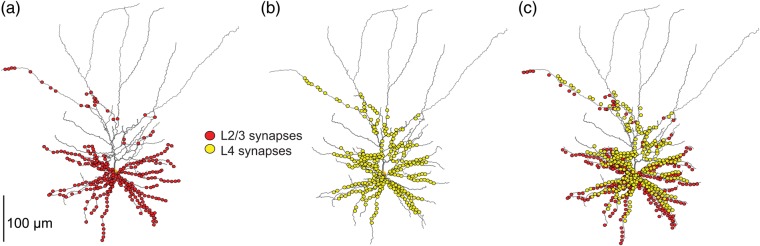
Comparison of the dendritic innervation of L2/3 pyramidal neuron by synaptic inputs arising either from lateral L2/3 pyramidal cells or from feedforward L4 spiny stellate cells. (a) 756 synaptic contacts (red dots) established by 270 L2/3 pyramidal cells axons (average of 2.8 contacts per axon). (b) 1575 synaptic contacts (yellow dots) established by 350 L4 spiny stellate cells axons (average 4.5 contacts per axon). (c) Superposition of synaptic contacts converging from the 2 input sources. Each dot may represent more than one synaptic contact; red and yellow dots were slightly shifted from each other to avoid overlap.
Figure 5 compares the distribution of experimentally measured compound PSPs in L2/3 PCs following WD and those predicted by the model, with model inputs drawn from sources in both layer 4 and 2/3. The experimental average PSTH measured in L4 spiny neurons (Fig. 5a, yellow histogram; Brecht and Sakmann 2002) and that in L2/3 PCs served as an input to the model (Fig. 5a, red histogram; Brecht et al. 2003; and see also Sarid et al. 2007). Experimentally, a broad distribution of compound PSPs was found (Sarid et al. 2007), with average amplitude of 18 ± 10 mV (Fig. 5b). In this case, the rightmost bin (30 mV) is the contribution of mostly one cell (which is over-represented with 149 traces of a total of 424 traces from a total of 20 cells) that tended to spike with high probability (0.53 APs per stimulus). With this neuron included, the experimentally determined spiking probability is 0.23 APs per stimulus, whereas without this neuron, the average amplitude of the compound PSPs was 17 ± 9 mV, and the corresponding firing probability was only 0.06 APs per stimulus.
The corresponding average amplitude of the modeled compound EPSP in the simulations (n = 200) was 16.3 ± 3.5 mV (Fig. 5c, orange), with a distribution that is narrower than the experimental one (see Fig. 5b), but broader than the distribution obtained when the input arises from either L2/3 PCs or L4 spiny neurons alone (Figs 2 and 5 in Sarid et al. 2007). When both input sources were activated, the model L2/3 PC does generate APs with a probability of 0.01 APs per stimulus (Fig. 5c, right most orange bin).
Figure 5a (top trace) depicts 20 experimental responses of 1 barrel-related L2/3 cell to principal WD (courtesy of M. Brecht); black traces are responses from the Down state. The corresponding orange traces below are 20 modeled compound EPSPs in response to WD; the stimulations for these traces were drawn from the average (L4 + L2/3 histogram, as in Fig. 5c); this explains the somewhat more smeared and slow simulated versus the experimental compound EPSPs.
In another set of simulations, in which the PSTH of 6 individual L4 spiny cells (Fig. 6a in Sarid et al. 2007) and of PSTH of 3 individual L2/3 PCs (Fig. 2a, purple) were used to sample the input for the model L2/3 neurons, the distribution of compound EPSPs was much broader (Fig. 5c, green), more closely resembling the experimental distribution. In this case, the average amplitude is 17.8 ± 11.2 mV and the spiking probability is 0.35 APs/stimulus.
Figure 6.
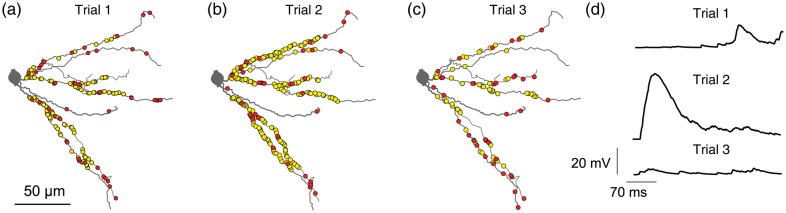
Spatial distribution of activated synaptic contacts on L2/3 dendrites following whisker deflection predicted by the model. Three realizations (trial 1, 2, and 3) of the model following whisker deflection are shown (a–c); only a subset of the basal dendrites of the modeled neuron given in Figure 4 is shown (see also Varga et al. 2011). Statistics of activation of synaptic contacts was drawn from the corresponding red and yellow PSTHs shown in Figure 5a. Red dots are activated synaptic contacts established by L2/3 pyramidal cells and yellow dots are activated synaptic contacts established by L4 spiny neurons. The corresponding composite EPSPs are shown in d.
Based on the total length of the dendritic domain of the modeled L2/3 PC (7933 µm) and on the total number of synapses from excitatory L2/3 and L4 neurons converging on the modeled cell (2331), the estimated density of synaptic contacts from these 2 input sources is one contact per 3.4 µm length of L2/3 dendrites in close agreement with (Varga et al. 2002). Apparently, these 2 input sources establish only very few if any synaptic contacts with the distal portion of the L2/3 dendrites (Fig. 4). Hence, the actual synaptic contact density of L2/3 and L4 inputs in the dendritic domain of L2/3 PCs is larger than calculated above. In Figure 6, we compute the trial-to-trial variability in the number and the spatial organization of the activated synapses following WD. Superimposed on a selected L2/3 dendritic branch are dots indicating the activated synapses per trial; red dots are for synapses originating from L2/3 PCs and yellow dots are synapses established by L4 spiny neurons. The variability of activated synapses between trials is relatively large. For trial 1, 2, and 3, the total number of activated synapses was 133, 115, and 69 for the L2/3 input and 298, 696, and 124 for the L4 input, respectively. Only a portion of these activated contacts are shown in the dendritic branch depicted in Figure 6. The result of this trial-to-trial variability in the number and location of activated synapses is reflected by the large variability in the corresponding composite EPSP amplitudes (Fig. 6d).
Effect of L2/3 Pyramidal Cell Morphology on the Response to Whisker Deflection
For these simulations, we have used one reconstructed L2/3 PC as the prototypical model cell (Fig. 7 top cell on the left). However, L2/3 PCs show some variability in their dendritic branching pattern and dimensions (Fig. 7 insets; Feldmeyer et al. 2006; Helmstaedter et al. 2008; Bruno et al. 2009). These morphological differences are likely to affect the response behavior to WD of these neurons. We examined this possibility by modeling the response to WD in 6 different L2/3 PCs for which full morphological reconstructions were obtained in vitro. These model L2/3 PCs were stimulated using both L2/3 and L4 inputs while keeping all parameters identical (passive and active membrane properties, average number of synapses converging on the dendrites and the statistics of their activation, and their spatial distribution over the dendritic field). Figure 6 suggests that the response variability among cells is rather large; some L2/3 PCs tend to spike with high probability in response to this input (cell at lower right) whereas, for other cells, the voltage response is well below threshold for spiking (e.g., cell at lower left).
We found that the average amplitude of the compound PSPs and the probability to generate an AP are strongly correlated with the input resistance of the cells (r = 0.94 and r = 0.84, respectively) and both are less correlated with the cell's surface area (r = −0.69 and r = −0.82, respectively; see summary for these 6 cells in Table 2). The average probability r for generating an action potential (AP) in the modeled 6 L2/3 PCs is 0.11 ± 0.22 APs per stimulus. Another source of variability in somatic PSPs and spiking probability (assuming that the only difference is the dendritic morphology while all other parameters are constant) is the expected variability in the effective cable distance (different cable filtering) for the synapses with the change in dendritic morphology/branching pattern. Indeed, cable theory for dendrites shows that the same synapse located at the same branch order and distance from the soma, but on cells with different dendritic morphologies, might result in different somatic EPSP.
Table 2.
Calculated input resistance and surface area for the 6 modeled cells shown in Figure 7
| Cell | Rin (MΩ) | Surface area (µm2) | Firing probability (APs/stim.) | Average EPSP amplitude (mV) |
|---|---|---|---|---|
| 111200A | 33 | 18 997 | 0.01 | 16.3 |
| 141200B | 28 | 21 810 | 0.01 | 15.4 |
| 141200C | 28 | 21 146 | 0.00 | 12.9 |
| 110602A | 35 | 19 142 | 0.02 | 18.0 |
| 280503A | 32 | 20 036 | 0.09 | 17.4 |
| 130602A | 41 | 17 744 | 0.56 | 26.1 |
| Average | 33 | 19 812 | 0.11 | 17.7 |
| S.D | 5 | 1497 | 0.22 | 4.5 |
Input resistance (Rin) was calculated using identical Rm and Ri that fit the in vivo condition (see Materials and Methods section).
We conclude that the inherent morphological difference between L2/3 PCs population can, on its own, explain the experimental finding as to why some L2/3 PCs seem to spike more readily than others following WD (Fig. 3a; Brecht and Sakmann 2002; Brecht et al. 2003). Clearly, other parameters not studied here, such as different in number and spatial distribution of converging synapses among cells, are expected to have a strong impact on the somatic PSP's and on AP firing probability for different L2/3 PCs. This calls for caution when using a “prototypical” cell for representing, via a model, the L2/3 population, as the mere morphological inhomogeneity within the same cortical layer could be responsible, to a large extent, for the observed differences in their response properties (see Discussion section).
Discussion
In this experimentally based computational study, we explored the contribution of the intracolumnar lateral excitatory L2/3–L2/3 connection to the spiking probability of L2/3 PCs following WD. In addition to modeling, the L2/3–L2/3 cortical “module,” we incorporated this module to another “module” the feedforward L4–L2/3 excitatory connection (Sarid et al. 2007). This enabled us to evaluate the interplay between the 2 excitatory inputs in shaping the response of L2/3 PCs to WD.
Sensory excitation via L4 spiny neurons together with lemniscal thalamococortical afferents to layer 3 (Jensen and Killackey 1987; Arnold et al. 2001) initiates lateral excitation between L2/3 PCs (Laaris et al. 2000; Brecht et al. 2003; Petersen et al. 2003). In order to study the impact of this connection on the response to WD, we first used in vitro data from connected L2/3–L2/3 pairs with identified locations of their synaptic contacts. The average EPSP amplitude of 1.0 mV in this connection (with 2.8 contacts per connection; Feldmeyer et al. 2006) and with a total of 270 axons from L2/3 PCs converging onto a single L2/3 PC, this input is expected to contribute significantly to the response of these neurons. However, the model predicts that the lateral input from other L2/3 PCs is not strong on its own; it is expected to produce a compound EPSP of 7.6 ± 1.7 mV following WD. This is below the (very positive) threshold for spike generation in L2/3 PCs (∼ −35 mV). Thus, the lateral L2/3–L2/3 connection alone cannot drive L2/3 PCs following a WD. Yet, together with the direct feedforward excitatory input from layer 4 (350 axons, each generating an EPSP of 0.7 mV with 4.5 contacts per connection) a firing probability that ranges between 0.10 and 0.35 APs/stimulus was obtained, which is in good agreement with the experimental finding measured in vivo in rats (Kerr et al. 2007) and in mice (Sato et al. 2007).
One conclusion that arises from our simulation is that the often used process of averaging neural APs should be handled with great care. We demonstrated that when using the average PSTH (of both L4 and L2/3 population) as the model input, the resultant composite EPSP is significantly smaller and narrower (and thus the probability of spiking is smaller) than when the PSTH of individual presynaptic cells was used (Fig. 5, orange vs. green histogram). Furthermore, in most of our earlier simulations, we used a prototypical (or averaged) L2/3 PC as our postsynaptic target. However, as in the experimental recordings in which the results are summed over many cells, we repeated our simulation in 6 fully reconstructed L2/3 PCs and found that the morphology (and corresponding input resistance) of the neuron is highly correlated with their responsiveness. The subpopulation of L2/3 PCs with a smaller membrane area (larger input resistance) is expected to be more responsive to whisker stimulation; these cells will then recruit (together with the input from L4 cells) additional L2/3 PCs. This result further supports our argument concerning the pitfalls of using average parameters (e.g., “prototypical” morphology) and may explain some of the mismatch observed between model and experiments.
Although the spiking probability obtained in our model following WD is consistent with the experimental result (de Kock et al. 2007; Kerr et al. 2007), the model lacks both feedforward and lateral and/or feedback inhibition that operates in parallel with the excitatory pathway (Helmstaedter et al. 2008). Furthermore, it is possible that L4 spiny neurons may more efficiently recruit L2/3 interneurons than L2/3 PCs (Helmstaedter et al. 2008) suggesting that inhibition is initiated in L2/3 PCs in a narrow (1–3 ms) window following excitation. This suggest that the model for L2/3 PCs not only lacks inhibitory input sources but also additional excitatory input sources, such direct input from the thalamus (Jensen and Killackey 1987; Arnold et al. 2001) or from deep cortical layers (Bureau et al. 2006; Lefort et al. 2009).
Two points regarding the role of inhibition in shaping whisker response are worth noting. First, the close similarity of the simulated voltage traces in our L2/3 model and those recorded in vivo indicates that, in fact, the 2 excitatory modules included in our present modeling capture much of the in vivo response to whisker stimulation. Second, some of the impact of inhibition within the barrel network is indirectly included in our modeling study, because the PSTHs measured in vivo (both from L4 and L2/3 cells) is already affected by inhibition within the network. How much of the whisker response is fine-tuned by inhibition requires further modeling study which we plan to pursue in our future efforts.
Moreover, other factors were not taken into account, such as second-order synchrony among L4 and/or L2/3 cells, as well as the possibility for the existence of functional subgroups (Sarid et al. 2007) or possible functional differences relating to the position of L2/3 pyramidal neurons above barrels, septa or neighboring barrels, respectively (Kerr et al 2007; Lang et al 2011; Oberlaender et al 2012). Other factors that influence the excitability of cortical neurons are neuromodulators such as acetylcholine or noradrenaline (Eggermann and Feldmeyer 2009; Constantinople and Bruno 2011). Nevertheless, this study brings us one step closer to understanding how the unique “hardware” composing the cortical column enables the processing of sensory input within the column. Specifically, it addresses the question how the different modules of the barrel column shape the response to whisker stimulation. Once we have a faithful in silico model for the barrel column, we can explore it to highlight the key components that determine its different computational functions.
Funding
I.S. is supported by a grant from the Gatsby Charitable Foundation, the German Israeli Foundation (1124-143.1/2010) and the Max Planck Hebrew University Centre for Sensory Processing of the Brain in Action; D.F. by Helmholtz Initiative for System Biology (SP 14) and the Deutsche Forschungsgemeinschaft—Swiss National Science Foundation Research Group on Barrel Cortex Function (BaCoFun Fe/4-1). Funding to pay the Open Access publication charges for this article was provided by a grant from the Hebrew University-Max Planck Centre.
Notes
Conflict of Interest: None declared.
References
- Arnold PB, Li CX, Waters RS. Thalamocortical arbors extend beyond single cortical barrels: an in vivo intracellular tracing study in rat. Exp Brain Res. 2001;136:152–168. doi: 10.1007/s002210000570. [DOI] [PubMed] [Google Scholar]
- Brecht M, Roth A, Sakmann B. Dynamic receptive fields of reconstructed pyramidal cells in layers 3 and 2 of rat somatosensory barrel cortex. J Physiol (Lond) 2003;553:243–265. doi: 10.1113/jphysiol.2003.044222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brecht M, Sakmann B. Dynamic representation of whisker deflection by synaptic potentials in spiny stellate and pyramidal cells in the barrels and septa of layer 4 rat somatosensory cortex. J Physiol (Lond) 2002;543:49–70. doi: 10.1113/jphysiol.2002.018465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruno RM, Hahn TTG, Wallace DJ, De Kock CPJ, Sakmann B. Sensory experience alters specific branches of individual corticocortical axons during development. J Neurosci. 2009;29:3172–3181. doi: 10.1523/JNEUROSCI.5911-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bureau I, Von Saint Paul F, Svoboda K. Interdigitated paralemniscal and lemniscal pathways in the mouse barrel cortex. PLoS Biol. 2006;4:e382. doi: 10.1371/journal.pbio.0040382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Busetto G, Higley MJ, Sabatini BL. Developmental presence and disappearance of postsynaptically silent synapses on dendritic spines of rat layer 2/3 pyramidal neurons. J Physiol (Lond) 2008;586:1519–1527. doi: 10.1113/jphysiol.2007.149336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castro-Alamancos MA. Cortical up and activated states: implications for sensory information processing. Neuroscientist. 2009;15:625–634. doi: 10.1177/1073858409333074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Constantinople CM, Bruno RM. Effects and mechanisms of wakefulness on local cortical networks. Neuron. 2011;69:1061–1068. doi: 10.1016/j.neuron.2011.02.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crochet S, Petersen CCH. Correlating whisker behavior with membrane potential in barrel cortex of awake mice. Nat Neurosci. 2006;9:608–610. doi: 10.1038/nn1690. [DOI] [PubMed] [Google Scholar]
- Da Costa NM, Martin KAC. Whose cortical column would that be? Front Neuroanat. 2010;4:16. doi: 10.3389/fnana.2010.00016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Kock CPJ, Bruno RM, Spors H, Sakmann B. Layer- and cell-type-specific suprathreshold stimulus representation in rat primary somatosensory cortex. J Physiol (Lond) 2007;581:139–154. doi: 10.1113/jphysiol.2006.124321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Druckmann S, Banitt Y, Gidon A, Schürmann F, Markram H, Segev I. A novel multiple objective optimization framework for constraining conductance-based neuron models by experimental data. Front Neurosci. 2007;1:7–18. doi: 10.3389/neuro.01.1.1.001.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eggermann E, Feldmeyer D. Cholinergic filtering in the recurrent excitatory microcircuit of cortical layer 4. Proc Natl Acad Sci USA. 2009;106:11753–11758. doi: 10.1073/pnas.0810062106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldmeyer D, Lübke J, Sakmann B. Efficacy and connectivity of intracolumnar pairs of layer 2/3 pyramidal cells in the barrel cortex of juvenile rats. J Physiol (Lond) 2006;575:583–602. doi: 10.1113/jphysiol.2006.105106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldmeyer D, Lübke J, Silver RA, Sakmann B. Synaptic connections between layer 4 spiny neurone-layer 2/3 pyramidal cell pairs in juvenile rat barrel cortex: physiology and anatomy of interlaminar signalling within a cortical column. J Physiol (Lond) 2002;538:803–822. doi: 10.1113/jphysiol.2001.012959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldmeyer D, Roth A, Sakmann B. Monosynaptic connections between pairs of spiny stellate cells in layer 4 and pyramidal cells in layer 5A indicate that lemniscal and paralemniscal afferent pathways converge in the infragranular somatosensory cortex. J Neurosci. 2005;25:3423–3431. doi: 10.1523/JNEUROSCI.5227-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Helmstaedter M, Staiger JF, Sakmann B, Feldmeyer D. Efficient recruitment of layer 2/3 interneurons by layer 4 input in single columns of rat somatosensory cortex. J Neurosci. 2008;28:8273–8284. doi: 10.1523/JNEUROSCI.5701-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hines ML, Carnevale NT. The NEURON simulation environment. Neural Comput. 1997;9:1179–1209. doi: 10.1162/neco.1997.9.6.1179. [DOI] [PubMed] [Google Scholar]
- Hirata A, Castro-Alamancos MA. Effects of cortical activation on sensory responses in barrel cortex. J Neurophysiol. 2011;105:1495–1505. doi: 10.1152/jn.01085.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmgren C, Harkany T, Svennenfors B, Zilberter Y. Pyramidal cell communication within local networks in layer 2/3 of rat neocortex. J Physiol (Lond) 2003;551:139–153. doi: 10.1113/jphysiol.2003.044784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huber D, Petreanu L, Ghitani N, Ranade S, Hromádka T, Mainen Z, Svoboda K. Sparse optical microstimulation in barrel cortex drives learned behaviour in freely moving mice. Nature. 2008;451:61–64. doi: 10.1038/nature06445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen KF, Killackey HP. Terminal arbors of axons projecting to the somatosensory cortex of the adult rat. II. The altered morphology of thalamocortical afferents following neonatal infraorbital nerve cut. J Neurosci. 1987;7:3544–3553. doi: 10.1523/JNEUROSCI.07-11-03544.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerr JND, De Kock CPJ, Greenberg DS, Bruno RM, Sakmann B, Helmchen F. Spatial organization of neuronal population responses in layer 2/3 of rat barrel cortex. J Neurosci. 2007;27:13316–13328. doi: 10.1523/JNEUROSCI.2210-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laaris N, Carlson GC, Keller A. Thalamic-evoked synaptic interactions in barrel cortex revealed by optical imaging. J Neurosci. 2000;20:1529–1537. doi: 10.1523/JNEUROSCI.20-04-01529.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lang S, Dercksen VJ, Sakmann B, Oberlaender M. Simulation of signal flow in 3D reconstructions of an anatomically realistic neural network in rat vibrissal cortex. Neural Netw. 2011;24:998–1011. doi: 10.1016/j.neunet.2011.06.013. [DOI] [PubMed] [Google Scholar]
- Le Bé J-V, Markram H. Spontaneous and evoked synaptic rewiring in the neonatal neocortex. Proc Natl Acad Sci USA. 2006;103:13214–13219. doi: 10.1073/pnas.0604691103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Be J-V, Silberberg G, Wang Y, Markram H. Morphological, electrophysiological, and synaptic properties of corticocallosal pyramidal cells in the neonatal rat neocortex. Cereb Cortex. 2007;17:2204–2213. doi: 10.1093/cercor/bhl127. [DOI] [PubMed] [Google Scholar]
- Lefort S, Tomm C, Floyd Sarria J-C, Petersen CCH. The excitatory neuronal network of the C2 barrel column in mouse primary somatosensory cortex. Neuron. 2009;61:301–316. doi: 10.1016/j.neuron.2008.12.020. [DOI] [PubMed] [Google Scholar]
- Lübke J, Egger V, Sakmann B, Feldmeyer D. Columnar organization of dendrites and axons of single and synaptically coupled excitatory spiny neurons in layer 4 of the rat barrel cortex. J Neurosci. 2000;20:5300–5311. doi: 10.1523/JNEUROSCI.20-14-05300.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lübke J, Roth A, Feldmeyer D, Sakmann B. Morphometric analysis of the columnar innervation domain of neurons connecting layer 4 and layer 2/3 of juvenile rat barrel cortex. Cereb Cortex. 2003;13:1051–1063. doi: 10.1093/cercor/13.10.1051. [DOI] [PubMed] [Google Scholar]
- Markram H, Lübke J, Frotscher M, Roth A, Sakmann B. Physiology and anatomy of synaptic connections between thick tufted pyramidal neurones in the developing rat neocortex. J Physiol (Lond) 1997a;500(Pt 2):409–440. doi: 10.1113/jphysiol.1997.sp022031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markram H, Lübke J, Frotscher M, Sakmann B. Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science. 1997b;275:213–215. doi: 10.1126/science.275.5297.213. [DOI] [PubMed] [Google Scholar]
- McBain C, Dingledine R. Dual-component miniature excitatory synaptic currents in rat hippocampal CA3 pyramidal neurons. J Neurophysiol. 1992;68:16–27. doi: 10.1152/jn.1992.68.1.16. [DOI] [PubMed] [Google Scholar]
- McCormick DA, Shu Y, Hasenstaub A, Sanchez-Vives M, Badoual M, Bal T. Persistent cortical activity: mechanisms of generation and effects on neuronal excitability. Cereb Cortex. 2003;13:1219–1231. doi: 10.1093/cercor/bhg104. [DOI] [PubMed] [Google Scholar]
- Meyer HS, Wimmer VC, Oberlaender M, De Kock CPJ, Sakmann B, Helmstaedter M. Number and laminar distribution of neurons in a thalamocortical projection column of rat vibrissal cortex. Cereb Cortex. 2010;20:2277–2286. doi: 10.1093/cercor/bhq067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oberlaender M, Ramirez A, Bruno RM. Sensory experience restructures thalamocortical axons during adulthood. Neuron. 2012;74.4:648–655. doi: 10.1016/j.neuron.2012.03.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petersen CCH, Hahn TTG, Mehta M, Grinvald A, Sakmann B. Interaction of sensory responses with spontaneous depolarization in layer 2/3 barrel cortex. Proc Natl Acad Sci USA. 2003;100:13638–13643. doi: 10.1073/pnas.2235811100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petersen CC, Sakmann B. The excitatory neuronal network of rat layer 4 barrel cortex. J Neurosci. 2000;20:7579–7586. doi: 10.1523/JNEUROSCI.20-20-07579.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poulet JFA, Petersen CCH. Internal brain state regulates membrane potential synchrony in barrel cortex of behaving mice. Nature. 2008;454:881–885. doi: 10.1038/nature07150. [DOI] [PubMed] [Google Scholar]
- Reyes A, Sakmann B. Developmental switch in the short-term modification of unitary EPSPs evoked in layer 2/3 and layer 5 pyramidal neurons of rat neocortex. J Neurosci. 1999;19:3827–3835. doi: 10.1523/JNEUROSCI.19-10-03827.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarid L, Bruno R, Sakmann B, Segev I, Feldmeyer D. Modeling a layer 4-to-layer 2/3 module of a single column in rat neocortex: interweaving in vitro and in vivo experimental observations. Proc Natl Acad Sci USA. 2007;104:16353–16358. doi: 10.1073/pnas.0707853104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato TR, Gray NW, Mainen ZF, Svoboda K. The functional microarchitecture of the mouse barrel cortex. PLoS Biol. 2007;5:e189. doi: 10.1371/journal.pbio.0050189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schubert D, Staiger JF, Cho N, Kötter R, Zilles K, Luhmann HJ. Layer-specific intracolumnar and transcolumnar functional connectivity of layer V pyramidal cells in rat barrel cortex. J Neurosci. 2001;21:3580–3592. doi: 10.1523/JNEUROSCI.21-10-03580.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shepherd GMG, Stepanyants A, Bureau I, Chklovskii D, Svoboda K. Geometric and functional organization of cortical circuits. Nat Neurosci. 2005;8:782–790. doi: 10.1038/nn1447. [DOI] [PubMed] [Google Scholar]
- Silver RA, Lubke J, Sakmann B, Feldmeyer D. High-probability uniquantal transmission at excitatory synapses in barrel cortex. Science. 2003;302:1981–1984. doi: 10.1126/science.1087160. [DOI] [PubMed] [Google Scholar]
- Song S, Sjöström PJ, Reigl M, Nelson S, Chklovskii DB. Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS Biol. 2005;3:e68. doi: 10.1371/journal.pbio.0030068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spruston N, Jonas P, Sakmann B. Dendritic glutamate receptor channels in rat hippocampal CA3 and CA1 pyramidal neurons. J Physiol (Lond) 1995;482(Pt 2):325–352. doi: 10.1113/jphysiol.1995.sp020521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanier MC, Bower JM. A comparative survey of automated parameter-search methods for compartmental neural models. J Comput Neurosci. 1999;7:149–171. doi: 10.1023/A:1008972005316. [DOI] [PubMed] [Google Scholar]
- Varga Z, Jia H, Sakmann B, Konnerth A. Dendritic coding of multiple sensory inputs in single cortical neurons in vivo. Proc Natl Acad Sci USA. 2011;108:15420–15425. doi: 10.1073/pnas.1112355108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varga C, Sík A, Lavallée P, Deschênes M. Dendroarchitecture of relay cells in thalamic barreloids: a substrate for cross-whisker modulation. J Neurosci. 2002;22:6186–6194. doi: 10.1523/JNEUROSCI.22-14-06186.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waters J, Helmchen F. Background synaptic activity is sparse in neocortex. J Neurosci. 2006;26:8267–8277. doi: 10.1523/JNEUROSCI.2152-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woolsey TA, Van der Loos H. The structural organization of layer IV in the somatosensory region (SI) of mouse cerebral cortex. The description of a cortical field composed of discrete cytoarchitectonic units. Brain Res. 1970;17:205–242. doi: 10.1016/0006-8993(70)90079-X. [DOI] [PubMed] [Google Scholar]