Competitive Hydrogen Atom Migrations Accompanying Cascade Dissociations of Peptide Cation-Radicals of the z^+• Type

Abstract

We report a combined experimental and computational study of energy-resolved collision-induced dissociation (ER-CID) and time-resolved infrared multiphoton dissociation (TR-IRMPD) of z₄ ions prepared by electron transfer dissociation of peptide (Ala-Ala-Asn-Ala-Arg + 2H)²⁺ ions. The z₄ cation-radicals, ^•ANAR⁺, undergo competitive dissociations by backbone cleavage and loss of a CONH₂ radical from the Asn side chain. The backbone cleavage proceeds by radical-assisted dissociation of the Asn C_α—CO bond, forming an x₂ ion intermediate which rapidly dissociates by HNCO elimination to yield a stable z₂ fragment ion, ^•AR⁺. The ER-CID and TR-IRMPD data were consistent with the consecutive nature of the backbone dissociation but showed different branching ratios for the two major fragmentations. The ER-CID data showed branching ratios 0.6-1.0 for the side-chain and backbone cleavages whereas the TR-IRMPD data showed an earlier onset for the latter dissociation. Computational analysis of the potential energy surface with density functional theory and ab initio calculations was carried out to provide structures and energies for the reactant ions as well as several intermediates, products, and transition states. Dissociation pathways for cis and trans amide conformers were distinguished and their energies were evaluated. The threshold dissociation energies for the backbone and side-chain dissociations were similar in accordance with the experimental ER-CID branching ratio. The TR-IRMPD data were interpreted by different absorbances of intermediates produced by hydrogen atom migrations along the dissociation pathways.

Introduction

Electron attachment to multiply charge peptide ions is a highly exothermic process that fundamentally changes the gas-phase peptide ion chemistry by converting even electron ions to cation-radicals [1,2]. This, and the internal excitation of the charge-reduced peptide cation-radicals, results in extensive dissociation that is utilized for peptide sequencing [3]. The primary dissociations of charge-reduced peptide cation-radicals, the so-called hydrogen-rich ions [1], proceed by loss of a hydrogen atom and radical-driven cleavages of covalent bonds between the ammonium or amide nitrogen atoms and the adjacent backbone carbon atoms in the α-positions, N—C_α bond cleavage for short. N—C_α bond cleavages in peptide cation-radicals typically are thermoneutral or exothermic and require very low activation energies to proceed [4]. The resulting C-terminal fragments represent de-aminated peptide radicals which, if carrying a charging proton, are called z^+• ions and belong to the category of electron-deficient peptide cation-radicals [1]. Depending on the mode of activation, the z^+• ions can either be stable to allow being detected or undergo further radical or charge induced dissociations. Spontaneous dissociation of z^+• ions is often observed in electron capture dissociation mass spectra [5] where secondary reactions, termed cascade dissociations [6], give rise to a variety of backbone and side chain cleavages [7-12] as well as hydrogen atom migrations between the incipient fragments [13]. Stable z^+• ions are produced by electron transfer dissociation [14] and their further fragmentations can be induced by collisional activation [15-18]. Radical-driven dissociations are also observed upon collisional activation of electron-deficient peptide cation-radicals produced by photodissociation of iodinated tyrosine residues [19].

A specific feature of z^+• ion dissociations is that they are accompanied by hydrogen atom migrations involving multiple intermediates and connecting transition states [20-22]. The outcome of these rearrangements depends on the nature of the side-chain groups in the affected amino acid residues (X and B in Scheme 1). Side-chain groups that have readily transferrable benzylic (F, Y, W, H) or tertiary (V, I) β-hydrogen atoms (X in Scheme 1) can form radical intermediates that undergo backbone cleavage yielding lower sequence fragments. Other side-chain groups (C, M, L, K, R) readily lose radicals by β,γ-bond cleavage in C_α radical intermediates, forming even-electron secondary fragments. Both kinds of dissociations are useful for the characterization of either the peptide sequence or the amino acid residues in the vicinity of the radical site in the primary z^+• ion [15, 21].

Scheme 1.

Generic mechanisms for side-chain and backbone cleavages triggered by hydrogen atom migrations in peptide radicals.

An interesting case occurs when H_α and H_β transfers occur in competition, resulting in a branching of the dissociation pathways. We now report a combined experimental and computational study of such a system, i.e., z₄^+• ions from electron transfer dissociation of (AANAR + 2H)²⁺ peptide ions. These ions are protonated on the arginine residue and the respective z₄^+• ions (denoted ^•ANAR⁺) are produced by N—C_α bond cleavage and loss of the N-terminal alanine amide.

EXPERIMENTAL

Materials and Methods

The AANAR peptide was custom-synthesized by NEOPeptide Laboratories (Cambridge, MA) and used as received. ETD mass spectra were measured on a Thermo Fisher (San Jose, CA, USA) LTQ XL quadrupole linear ion trap (QLT) instrument, outfitted with a chemical ionization source for the production of fluoranthene anion radicals as ETD reagent. The ion-ion interaction time was varied between 100 and 300 ms. The 200 ms spectra are reported. IRMPD and energy-resolved CID experiments were carried out on a modified dual cell QLT outfitted with a chemical ionization source for the generation of fluoranthene anion radicals, as described previously [23]. The mass spectrometer was modified to allow for the introduction of IR photons to the ion trapping region of the QLT. IR photons were generated using a Firestar T-100 Synrad 120-W CO₂ continuous wave laser (Mukilteo, WA, USA). Doubly protonated peptide precursor ions were produced by electrospray and subjected to ETD (~70 ms reaction with 5 × 10⁵ fluoranthene radical anions) to form z₄ ions. The z₄ ions were re-isolated and activated by using resonant excitation (CID) within the high-pressure QLT (bath gas He). For the energy-resolved experiments, CID normalized collision energies (NCE) of zero to 50 correspond roughly to supplemental AC excitation voltages of 0 to ~2.5 V. Infrared multiphoton dissociation was carried out by operating the laser in a mode whereby the laser was externally triggered via a TTL pulse from pin14 of the J1 connector. Laser power was set as indicated in the text.

Calculations

All electron structure calculations were performed using the Gaussian 09 suite of programs [24]. Ion geometries were optimized with density functional theory calculations using the hybrid B3LYP [25,26] and M06-2X [27] functionals in the spin-unrestricted format and the 6-31+G(d,p) basis set. The geometries in the Cartesian coordinate format (standard orientation) are available from the corresponding author upon request. The optimized structures were confirmed as local energy minima or first-order saddle points by harmonic frequency calculations. Three sets of single-point energies were calculated using the larger 6-311++G(2d,p) basis set and the B3LYP, M06-2X, and mPW1PW91(K) [28] functionals. The last functional has been claimed to give improved transition state energies for kinetic calculations [29]. The performance of the M06-2X functional in radical energy calculations has been evaluated [30]. In addition, Møller-Plesset theory [31], UMP2(frozen core), with the 6-311++G(2d,p) basis set was used to obtain single-point energies, which were corrected for contribution of higher spin state by the standard spin annihilation procedure [32,33]. The UB3LYP and PMP2 single-point energies were averaged (B3-PMP2), as reported previously [34-36]. Unimolecular rate constants were calculated for reactions occurring on the calculated B3-PMP2 and M06-2X potential energy surfaces, including zero-point vibrational energy corrections, using the Rice-Ramsperger-Kassel-Marcus (RRKM) theory [37]. These RRKM calculations used a modified [38] program by Zhu and Hase and [39] that allows one to deal with larger molecular systems with up to 1000 atoms and run the calculations under Windows operation systems. The RRKM rate constants were obtained by direct count of quantum states at internal energies that were increased in 2 kJ mol^-1 steps from the transition state up to 400 kJ mol^-1 above the reactant. Rotations were treated adiabatically, and the calculated microscopic rate constants k(E,J,K) were then Boltzmann-averaged over the thermal distribution of rotational states at 298 K.

RESULTS AND DISCUSSION

z₄ Ion Formation by ETD

Electron transfer dissociation of the (AANAR + 2H)²⁺ ion at m/z 251.6390 resulted in complete dissociation so that no charge-reduced precursor cation-radicals were detected (Figure 1a). The residual ions appearing at nominal m/z 503 (m/z 503.2741 and 503.2682) represent the respective ¹³C and ¹⁵N isotope satellites of the (M + H)⁺ ion at m/z 502.2705, as established from the high-resolution ETD mass spectrum (Figure S1, Supplementary Data). Backbone dissociations formed a series of z₁ through z₄ fragment ions (Figure 1a) whose elemental compositions were confirmed by accurate mass measurements in high-resolution ETD mass spectra. Competing with backbone dissociations were loss of ammonia (m/z 486.252) and cleavages of the arginine side chain (loss of CH₃N₂ and CH₅N₃). These are all typical dissociations of peptide dications induced by electron transfer.

Figure 1.

(a) ETD mass spectrum of (AANAR + 2H)²⁺ at m/z 251.6 obtained at 200 ms ion-ion reaction time. (b) CID-MS³ mass spectrum of the ^•ANAR⁺ z₄ ion at m/z 415.

Collision-Induced and Infrared Photodissociation

Mass selected z₄ ions at m/z 415.2153 were subjected to resonant excitation that resulted in collision-induced dissociation (CID) producing the MS³ spectrum shown in Figure 1b. The spectrum is dominated by the m/z 371.2014 fragment ion due to loss of CONH₂ (44.0136 Da) which most likely originates from the Asn side chain. The other abundant fragment ion is at m/z 230.1363, corresponding to a z₂ ion. The z₂ ion is accompanied by an x₂ ion which appears at a low m/z 272.67 in the low-resolution ETD spectrum (Figure 1b). The x₂ ion appears at the correct m/z 273.1418 in the high resolution ETD-CID-MS³ spectrum although at much reduced relative intensity. The mass difference (43.0055 Da) fits CHNO and is consistent with the x₂ → z₂ relationship. This x₂ ion has been generated from several other arginine terminated z₄ ions, as reported previously [21,22], and its unusual shape and m/z shift were assigned to its metastability [16,20,21,40].

The dependence on the Normalized Collision Energy (NCE) of the major CID-MS³ fragment ion intensities is plotted as a breakdown diagram in Figure 2. The breakdown diagram shows a rapid decrease of the m/z 415 precursor ion intensity at NCE >10. The m/z 371 and x₂ (m/z 273) ions show onsets at similar NCE, whereas that for the z₂ ion is shifted to higher NCE. The x₂ ion relative intensity peaks at NCE ≈ 16 and then declines. This is consistent with the x₂ ion being an intermediate that undergoes further dissociation at higher excitations. The m/z 371 and 230 ion relative intensities show a crossover at NCE ≈ 20. The m/z 371 relative intensity slightly decreases at excitation energies of NCE > 23. We note that an energy resolved scan obtained on an Orbitrap instrument showed nearly identical relative intensities of the m/z 371 and 230 ions from NCE = 20 to NCE = 35 (Figure S2, Supplement). Hence, it is safe to conclude that the loss of CONH₂ and the backbone cleavage leading to the formation of the z₂ fragment ion are closely competitive at NCE ≥ 20.

Figure 2.

Energy-resolved CAD spectrum of the ^•ANAR⁺ z₄ ion. The traces for energy-dependent intensities of the precursor and fragment ions are color coded as shown in the legend.

Different results were obtained for time-resolved infrared multiphoton dissociation of the z₄ ions. Figure 3 shows that upon irradiation at 35% of the laser power, the m/z 415 intensity gradually decreased with time to reach near zero at ca. 25 ms. The slope of the depletion curve became more steeply descending at a higher laser power (40%, Figure S3x, Supplementary Data). The intensities of the m/z 273 and 230 photodissociation products showed nearly identical onsets. The curve for the m/z 273 ion passed an early maximum at 7 ms and then dropped to zero at ca. 20 ms. This behavior is consistent with m/z 273 being an intermediate that is depleted at higher excitations. The m/z 230 curve also showed a maximum at 15 ms and then decreased, although it did not completely dropped to zero even at long irradiation times (50 ms). In contrast, the m/z 371 ion intensity showed a late onset and a shallower increase compared to those for the m/z 273 and 230 ions. The m/z 371 ion intensity reached a maximum at ca. 20 ms and stayed roughly constant at longer irradiation times up to 50 ms. The photodissociation curve for the m/z 371 ion that was obtained at a higher laser power did show a slow decrease after passing a maximum (Figure S3, Supplementary Data). It should be noted that IR photodissociation is not selectively applied to the m/z 415 precursor ion, because all the fragments are exposed to the IR beam in the ion trap and may absorb IR photons to drive their further dissociation.

Figure 3.

Time-resolved IRMPD mass spectrum of the ^•ANAR⁺ z₄ ion obtained at 35% laser power. The traces for energy-dependent intensities of the precursor and fragment ions are color coded as shown in the legend.

Ion Structures and Dissociation Energetics

The dissociations sketched in Scheme 1 are accompanied by hydrogen atom transfers to produce reactive radical intermediates that activate the respective C_α—CO and C_β—CO bonds for cleavage. The reactants, intermediates, products, and transition states were investigated by electron structure calculations to obtain structures and energies that were used to assess the dissociation kinetics of vibrationally excited ions. Relative energies were obtained at four levels of theory including three density functionals and a Moller-Plesset second order perturbation treatment with valence-electron only excitations. The M06-2X/6-311++G(2d,p) relative energies are discussed in the text. The other energies are compiled in Table 1. The z₄ ion was presumed to be initially formed as an all-trans amide conformer 1a (Scheme 2).

Table 1.

Relative Energies of ^•ANAR⁺ z₄ Ions.

Relative Energya,b
Species	B3LYPc	M062Xc	B3LYPd	MP2d	B3-MP2e	M062Xf	mPW1mPW91Kd
	6-31+G(d,p)		6-311++G(2d,p)
1a	0	0	0	0	0	0	0
1b	3	−0.1	3	3	3	0.3	−6
1c	56	−7	56	12	34	−2
2	31	13	30	20	25	13	23
3a	−2	−20	−3	−3	−3	−21	−10
3b	3	−57	3	−33	−15	−54
4	48	20	48	30	39	20
5	68	64	64	83	73	62
6	9	−11	9	−3	3	−12	0.3
7	78	52	77	63	70	51	71
8	102	102	97	97	97	97	112
9 + CONH2•	139	147	131	142	136	140	148
x2 + 10	117	153	110	160	135	146	129
11	16	−15	15	6	11	−12
TS1	124	82	126	79	103	86	109
TS2	158	95	160	116	138	100
TS3	150	104	146	119	133	104
TS4	111	97	112	87	100	100	97
TS5	130	119	131	111	121	120	118
TS6	135	131	130	129	129	127	141
TS7	150	160	146	157	151	155	158
TS8	147	97	148	97	123	100	133
TS9	181	141	183	139	161	145

^aIn kJ mol-1.

^bIncluding B3LYP/6-31+G(d,p) zero-point energies and referring to 0 K.

^cFully optimized structures.

^dSingle point energies on B3LYP optimized structures.

^eAveraged B3LYP and spin-projected MP2 energies.

^fSingle point energies on M06-2X optimized structures.

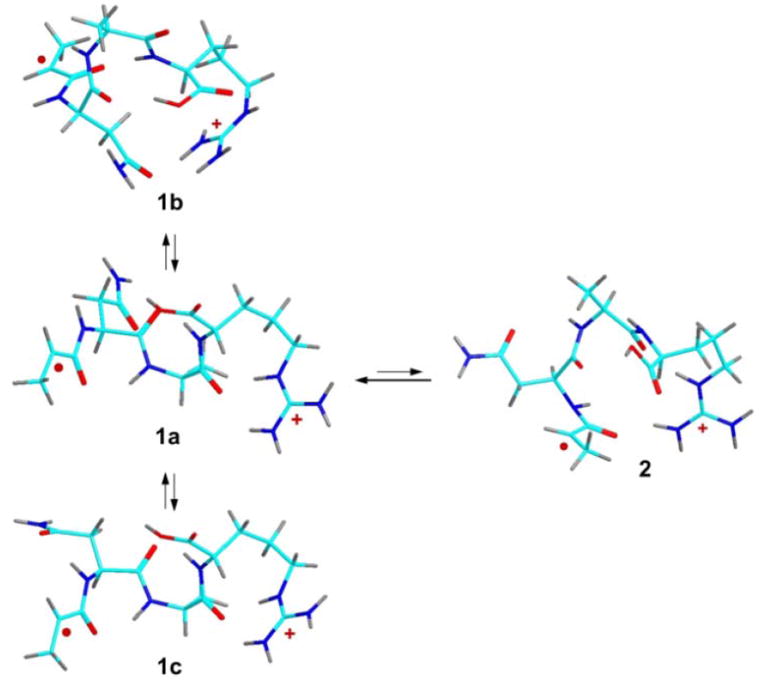
Scheme 2.

M06-2X/6-31+G(d,p) optimized structures of trans and cis isomers of ^•ANAR⁺ z₄ ions. Atoms are distinguished by color coding as follows: turquoise green = C, blue = N, red = O, gray = H.

Other trans-amide conformations were investigated. Structure 1b had a different folding pattern than 1a whereby the Arg side chain developed a hydrogen bond to the Asn side-chain amide group. Structure 1c had just the Asn side chain refolded while maintaining the 1a hydrogen bonding of the charged Arg group. Table 1 data indicate that conformers 1a-1c had very similar energies when based on the M06-2X calculations, whereas B3LYP disfavored structure 1c. Flipping the terminal Ala amide to a cis configuration formed a higher-energy cis-amide isomer 2. The activation energy for the trans-cis isomerization was not determined for this particular system. Previous studies of z cation radicals indicated that the barriers for analogous cis-trans amide isomerizations were rather low (30-60 kJ mol^-1) when they concerned the amide group in the vicinity of the radical site [20].

Structure 1a was the reactant for the transfer of the Arg C_α hydrogen atom forming the Arg C_α radical 3a (Scheme 3). The pertinent macrocyclic transition state (TS1) shows the migrating Arg C_α hydrogen atom about midway between the Arg and terminal C_α atoms. The TS1 energy was 86 kJ mol^-1 above 1a and the isomerization was 21 kJ mol^-1 exothermic. Ion 3a can exothermically refold to structure 3b (−54 kJ mol^-1 relative to 1a) in which the Arg C_α carbon is close to the β-CH² group of the Asn side chain. A β-hydrogen atom transfer in TS2 forms the Asn β-radical 4 at 20 kJ mol^-1 relative to 1a. The TS2 energy was 100 kJ mol^-1 relative to 1a. The β-carbon radical activates the C_α—CO bond to undergo homolytic cleavage in TS3 (104 kJ mol^-1 relative to 1a), forming a complex (5, 62 kJ mol^-1 relative to 1a) of the incipient x₂ fragment ion and its neutral counterpart (10). Fragment separation in 5 is endothermic, reaching the dissociation threshold at 146 kJ mol^-1 relative to 1a. A salient feature of this dissociation pathway is that the 3b → 4 and 4 → 5 steps are endothermic and thus reversible with rate constants favoring the reverse reactions. Radical 3b is the lowest energy structure in this pathway that can be activated by resonant collisional excitation or infrared absorption.

Scheme 3.

M06-2X/6-31+G(d,p) optimized structures of z₄ ion 1a, isomerization products 3a, 3b, 4, transition states TS1-TS3 and dissociation products 5, x₂ and 10. The atom color coding is as follows: turquoise green = C, blue = N, red = O, gray = H.

The cis-isomer 2 was a reactant for competitive pathways leading to the formation of the x₂ ion and loss of a CONH₂ radical from the Asn side chain (Scheme 4). Note that the facile 1a → 2 interconversion is conducive to establishing an equilibrium that favors the lower energy isomer 1a. When produced from 1a, radical 2 can further isomerize by exothermic Asn α-hydrogen migration forming ion 6 (−12 kJ mol^-1 relative to 1a). The migration proceeds through a five-membered transition state (TS4) whose energy is very close to that for TS2. Ion 6 has the appropriate electronic structure to undergo homolytic cleavage of the Asn C_β—CO bond to produce a complex (8) of the CONH₂ radical and the fragment ion (9) at 97 kJ mol^-1 above 1a. Fragment separation in 8 is endothermic forming ion 9 at 140 kJ mol^-1 relative to 1a. Note that the dissociation thresholds for the formation of (x₂ + 10) and (9 + CONH₂) were very similar at our best levels of theory, which were M06-2X and combined B3-PMP2.

Scheme 4.

M06-2X/6-31+G(d,p) optimized structures of cis-z₄ ion 2, isomerization product 6, dissociation products 8, 9, and transition states TS4 and TS6. The atom color coding is as follows: turquoise green = C, blue = N, red = O, gray = H.

cis-Amide 2 can undergo a competitive isomerization by migration of an Asn β-hydrogen atom to the N-terminal radical site, forming ion 7 which is 38 kJ mol^-1 above 2 (51 kJ mol^-1 relative to 1a, Scheme 5). The isomerization proceeds through a six-membered transition state (TS5) which is at 120 kJ mol^-1 relative to 1a and its energy is similar to that for TS6, but higher than for the analogous TS1 in the trans-dissociation pathway. Ion 7 is an Asn β-radical that has a suitable electronic configuration to undergo homolytic C_α—CO bond dissociation. However, the pertinent transition state (TS7) is at a relatively higher energy when compared to the analogous TS3 in the trans-dissociation pathway.

Scheme 5.

M06-2X/6-31+G(d,p) optimized structures of cis-z₄ ion 2, isomerization product 7, and transition states TS5 and TS7. The atom color coding is as follows: turquoise green = C, blue = N, red = O, gray = H.

Yet another hydrogen atom migration in 2 (Scheme S1, Supplementary Data) involves the Ala₄ α-hydrogen atom, forming ion 11 which is isoenergetic with 6. This isomerization proceeds through an eight-membered transition state (TS8, 100 kJ mol^-1 relative to 1a) whose energy is also similar to that for TS4. Ion 11 does not have an obvious dissociation pathway to the (x₂ + 10) and (9 + CONH₂) products and can be considered a kinetic cul-de-sac. Finally, it should be noted that intermediates 3a and 6 in the two major competing pathways are connected by a macrocyclic transition state (TS9) for the direct α-hydrogen atom migration between the Arg and Asn residues (Scheme S2, Supplement). However, the TS9 energy (145 kJ mol^-1 relative to 1a) was rather high and thus this isomerization may not be competitive with the other reactions. One of the reasons for the high TS9 energy is the distortion of Asn amide dihedral angle to 137° to bring together the Arg and Asn α-carbons for the hydrogen transfer to occur.

Dissociation Kinetics

To gain some insight in to the dissociation kinetics we obtained RRKM unimolecular rate constants for selected competitive isomerizations and dissociations reactions in the trans and cis dissociation pathways occurring on the M06-2X/6-311++G(2d,p) potential energy surface (PES). The PES for the trans pathway is shown in Figure 4 (top panel). The RRKM data for the trans pathway (Figure 4, bottom panel) indicated that the slow steps in the isomerization/dissociations sequences required substantial excitation to reach rate constants allowing the reactions to occur on the time scale of the experiment (t = 30 ms, k = 11.3 s^-1 for 50% conversion). These are denoted as kinetically relevant values in the following text. According to the PES in Figure 4, the two main dissociation channels have comparable threshold energies at 140 and 146 kJ mol^-1, respectively. Furthermore, the slow isomerization step in the trans pathway corresponds to the 3b → 4 isomerization. This step has a rate constant (k₂, Figure 4, bottom panel) that reaches kinetically relevant values only at substantial excitations in 1a. This indicates that a large kinetic shift of >450 kJ mol^-1 may be necessary for a kinetically relevant reaction.

Figure 4.

Top panel: M06-2X/6-311++G(2d,p) potential energy diagram for ^•ANAR⁺ z₄ ion isomerizations and dissociations. The energies are in kJ mol^-1 and include zero-point vibrational corrections. Bottom panel: RRKM rate constants for reversible hydrogen atom migrations through TS1 and TS2. The broken line indicates the rate constant needed for 50% conversion at 30 ms.

Analysis of the RRKM kinetics in the cis pathway indicates a fast reversible isomerization of the C_α radicals 2 and 6 through TS4 (Figure 5, top panel). The pertinent rate constants (k₄ and k_-4) reach the kinetically relevant values at internal energies of >180 kJ mol^-1 (Figure 5, bottom panel). In contrast, the competing isomerization of 2 to 7 through TS5 has smaller rate constants (k₅) and is outcompeted by the much faster reverse isomerization (k_-5). A similar kinetic effect can be expected for the 6 → 8 isomerization where the rate constant for the forward reaction (k₆) is likely to be much smaller than the pertinent rate constant for the reverse reaction. The final dissociation step leading to backbone cleavage is slow (k₇) and requires internal energies of >300 kJ mol^-1 in 2 to achieve kinetically relevant rates.

Figure 5.

Top panel: M06-2X/6-311++G(2d,p) potential energy diagram for ^•ANAR⁺ z₄ ion isomerizations and dissociations starting from the cis-amide 2. The energies are in kJ mol^-1 and include zero-point vibrational corrections. Bottom panel: RRKM rate constants for reversible hydrogen atom migrations through TS4, TS5, and TS6 and dissociation through TS7. The broken line indicates the rate constant needed for 50% conversion at 30 ms.

We note that a more detailed analysis of the reaction kinetics, including calculations of all rate constants, is hampered by the complexity of this kinetic system and the uncertainty regarding the TS energies. While the relative TS energies obtained at our best levels of theory are similar and consistent, the absolute values vary and these variations have a very large effect on the calculated rate constants. The consecutive dissociation by loss of HNCO from the x₂ ions requires a low-energy (70 kJ mol^-1) in the transition state and proceeds exothermically to a complex (−38 kJ mol^-1 relative to x₂) and finally to the z₂ ion (−13 kJ mol^-1 relative to x₂)[22].

The energy-resolved CID (Figure 2) and time-resolved photodissociation (Figure 3) breakdown diagrams showed different branching ratios for the backbone cleavage and loss of CONH₂ dissociations. In CID, all species of the same m/z (e.g., 1-8) are resonantly excited, so there is no excitation selectivity among the cis and trans isomers 1a ands 2 and the intermediates along the isomerization-dissociation pathways. Presumably, the branching ratio is determined by the thermochemical thresholds for the competitive dissociations.

In contrast, kinetic effects were indicated by the different branching ratios in the time-resolved photodissociation curves where the backbone cleavage occurred prior to the loss of CONH₂. Absorption of at least thirteen 10.6 μm photons of the 0.117 eV (11.3 kJ mol^-1) energy is needed to reach the 146 kJ mol^-1 threshold dissociation energy and, according to the RRKM kinetics, an even larger number of photons (>40) is needed to accomplish the dissociation on the millisecond time scale. The preferential backbone photodissociation can be explained by different absorbance at 10.6 μm (943 cm^-1) of the reactants and stable intermediates along the isomerization pathways, e.g., 1a, 2, 3b, 6, and 4. Figure S4 shows that there are differences among the isomers in absorbance at the laser main line (943 cm^-1). When allowed for a red shift due to anharmonic corrections [41-43], the best overlap with the 10.6 μm laser line is obtained for 1a and 3b. Hence, it is plausible to assume that the dissociation pathway involving 3b receives additional photoexcitation to drive a kinetically preferred backbone cleavage. However, quantitation of this effect is difficult. All the z₄ isomers (1-8) show 14-16 absorption bands in the 400-600 cm^-1 region that could give rise to overtones or combination bands overlapping with the laser excitation line. A rigorous analysis of such non-linear effects is beyond the scope of this work.

The different rates of photodissociation of the m/z 371, 273, and 230 fragment ions are also attributable to different absorbance of the main laser line, but must also reflect different threshold energies for their dissociations. Figure S5 (Supplementary Data) shows that the m/z 273 (x₂) and 230 (z₂) ions have IR absorption bands close to the 943 cm^-1 laser line to absorb energy and undergo facile photodissociation. The other factor favoring dissociation is the smaller number of internal degrees of freedom in the x₂ and z₂ ions, 108 and 96 d.o.f., respectively, compared to the z₄ ion (168 d.o.f.), which diminishes the kinetic shift for the smaller ions.

CONCLUSIONS

Results from this combined experimental and computational study allowed us to arrive at the following conclusions. Cation-radical z₄ ions from ETD of (AANAR + 2H)²⁺ dissociate by two major pathways, a backbone cleavage and a loss of side-chain CONH₂ radical, that involve radical isomerization with multiple consecutive hydrogen atom transfers. The hydrogen atom migrations can proceed in two reaction sequences involving cis and trans amide isomers. The isomerizations were calculated to have very similar transition state energies and can proceed reversibly. Dissociations leading to fragment ion and neutral products have similar threshold dissociation energies and occur competitively upon collisional activation. The dissociation kinetics are affected by infrared multiphoton activation that results in preferential backbone cleavage.

Highlights.

• Time-resolved IRMPD and energy-resolved CID spectra of peptide cation-radicals

• Ab initio theory and RRKM calculations of peptide cation-radical dissociations

• Combination of experiment and theory provides improved mechanistic insight