Local statistics allow quantification of cell-to-cell variability from high-throughput microscope images

Abstract

Motivation: Quantifying variability in protein expression is a major goal of systems biology and cell-to-cell variability in subcellular localization pattern has not been systematically quantified.

Results: We define a local measure to quantify cell-to-cell variability in high-throughput microscope images and show that it allows comparable measures of variability for proteins with diverse subcellular localizations. We systematically estimate cell-to-cell variability in the yeast GFP collection and identify examples of proteins that show cell-to-cell variability in their subcellular localization.

Conclusions: Automated image analysis methods can be used to quantify cell-to-cell variability in microscope images.

Contact: alan.moses@utoronto.ca

Availability and Implementation: Software and data are available at http://www.moseslab.csb.utoronto.ca/louis-f/

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Quantitative characterization of variability in gene expression has been a major area of research in systems biology (Pelkmans 2012; Snijder and Pelkmans 2011). Time-lapse movies of reporter genes in live-cell fluorescence microscopy demonstrated differences in protein expression between genetically identical cells (Elowitz et al. 2002; Levine et al. 2013). Cell-to-cell variability in protein abundance was measured for most yeast proteins (Newman et al. 2006) using high-throughput flow cytometry of the GFP collection (Huh et al. 2003). Time-lapse fluorescence microscopy experiments have also revealed examples of proteins that show cell-to-cell variability in subcellular localization (Cai et al. 2008). For example, the yeast stress-response transcription factors Msn2 and Msn4 have been observed to continuously shuttle between the cytoplasm and nucleus (Jacquet et al. 2003).

To our knowledge, cell-to-cell variability in subcellular localization has not been systematically characterized. Here, we set out to test whether cell-to-cell variability in protein abundance and subcellular localization could be systematically extracted from large image collections from automated microscopy. Still images have been used to quantify cell-to-cell variability in yeast protein abundance (Li et al. 2010), and advances in automated genetics and microscopy have led to large collections of yeast images (Huh et al. 2003; Riffle and Davis 2010). Recently, we and others have showed that quantitative measurements of protein localization and abundance can be extracted for single cells in these images (Handfield et al. 2013; Loo et al. 2014). However, it is not obvious how to define a metric that allows meaningful comparison of variability between different proteins. In particular, proteins localized to different subcellular compartments may show cell-to-cell variability simply due to imaging artefacts (small organelles might be missed from cells) or due to cell-to-cell variability in organelle size and shape. For example, yeast mitochondria have highly variable size and shape (Okamoto et al. 1998); proteins localized there will have more cell-to-cell variability than cytoplasmic proteins simply because of the underlying morphological variability. Another important complication is due to differential protein regulation during the cell-cycle that creates cell-to-cell variability in asynchronously growing cells. Previous studies of cell-to-cell variability in subcellular localization have used protein specific measures. For example, a study of Crz1 quantified bursts of nuclear localization using the median intensity of the five brightest pixels in each cell (Cai et al. 2008). While effective for that case, that approach is unlikely to generalize to other proteins or be quantitatively comparable between proteins of differing subcellular localizations.

As in efforts to analyze image-based measurements of morphological variability (Levy and Siegal 2008; Yvert et al. 2013), we define a local measure of variability, which we call ‘Relative Variability’ (RV) and show that it can be used to compare variability in both protein abundance and spatial pattern between proteins with different subcellular localization classes. We compare our image-based cell-to-cell variability estimates for protein abundance (cell-to-cell variability in total fluorescence intensity) with previous measurements from flow cytometry and find reasonable agreement. Because our analysis is based on images, we can also measure variability in the subcellular localization pattern (which we quantify using the spatial spread of the fluorescence in each cell), which is not possible using conventional flow cytometry. We identify examples of proteins that show cell-to-cell variability in their spatial distribution within the cells. To our knowledge, this represents the first systematic measurement of cell-to-cell variability in subcellular localization.

2 Methods

2.1 Image processing

High-resolution images of the yeast GFP collection were acquired and analyzed by an automated pipeline described previously (Handfield et al. 2013). Briefly, a highly expressed cytoplasmic RFP was introduced into the GFP collection to facilitate automated image analysis. High-resolution digital images (1331 × 1017, 12 bit) were obtained of unsynchronized log phase cultures using confocal fluorescence microscopy (Opera, PerkinElmer) with a water-immersion 63× objective and image depth of 0.6 µm. Object contours were identified automatically using a combination of geometric ellipse fits and watershed approach. Budded cells are fit by two ellipses, and the cell stage of the pair is estimated using the size of the bud cell. Each identified cell is assigned a confidence score w_c that represents that probability that it is a yeast cell (and not an artefact or misidentified a cell). We used the same single cell data from ∼0.4 million mother–bud pairs that we extracted for our previous study (Handfield et al. 2013). The single cell data are available for download (along with the image processing pipeline) at the author’s website.

2.2 Feature profiles for protein expression patterns

To define a local measure of cell-to-cell variability, we need to quantify the similarity between each protein (represented by images of a GFP-tagged strain) in our collection. To do so, we assign to each protein, p, a profile, ${{\displaystyle \overrightarrow{u}}}_p$ of features. In principle, any image features (or other measurements) that adequately capture the pattern can be used, as long as the same features can be calculated for each protein and proteins can be compared quantitatively in the feature space. Here, we use four simple features (GFP intensity, expected distance to GFP centre of mass, expected distance to cell periphery and expected distance to bud neck) calculated in five discrete bins of bud cell size (to capture change over the cell cycle) that we previously showed can be used to recover most previously recognized subcellular localization patterns in our yeast image collection (Handfield et al. 2013). For a given feature, X, for each protein, feature measurements from mother and bud cells are assigned to different bins, so that a total of 10 means ($E[X]$) and variances ($\text{Var}[X]$) are computed. Elements of ${{\displaystyle \overrightarrow{u}}}_p$ have the form

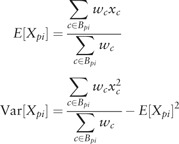(1)

where x_c is a feature measurement for the cell, c, that has been assigned the ith bin B_pi. To ensure that our estimates of variance were reasonably accurate, strains that have less than five cells assigned to any cell cycle bin are filtered out for the analysis, leaving 2860 proteins in the analysis (1144 out of 4003 filtered).

2.3 Subcellular ‘spread’ feature

Although the local method we propose to measure variability can be applied to any image feature (or more generally any observation of interest), in this study we chose a single feature to measure spatial variability, the ‘expected distance to GFP centre of mass’ (Handfield et al. 2013). An empirical probability distribution f_c for the subcellular position of GFP protein can be obtained by normalizing the GFP signal at each pixel coordinate ${\displaystyle \overrightarrow{z}}=(z_x,z_y)$ by the total GFP signal in the area of the cell (T_c), such that

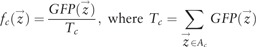(2)

where A_c is the set of pixel coordinates of a cell area. From the above, we then define the coordinates of the GFP pattern centre of mass, 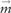, as the intensity weighted average of pixel coordinates. We then define ‘expected distance to GFP centre of mass’, which we refer to here as ‘subcellular spread’, by evaluating the distance to centre of mass under the empirical probability distribution:

(3)

where the $||{\displaystyle \overrightarrow{a}}-{\displaystyle \overrightarrow{b}}||$ represents the Euclidean distance between vectors ${\displaystyle \overrightarrow{a}}$ and ${\displaystyle \overrightarrow{b}}$, and summations in each case are over all the pixels, ${\displaystyle \overrightarrow{z}}$, within the area of the cell.

2.4 Co-efficient of variation

The variability in positive quantities (such as protein abundance) is usually quantified using the co-efficient of variation (CV, Newman et al. 2006), given by the standard deviation divided by the mean. Because we divided the cells into five cell-cycle bins, for mother and bud cells, we took the geometric mean of the CV over the 10 bins for protein, p.

$$\begin{array}{c}{\log }_2({\text{CV}}_p)=\frac{1}{10}{\displaystyle \sum _{i=1}^{10}\frac{1}{2}}{\log }_2\left(\frac{\text{Var}[X_{pi}]}{E{[X_{pi}]}^2}\right)\end{array}$$ (4)

In this equation, ${\log }_2(y)$ represents the base-2 logarithm of y and $E[X]$ and $\text{Var}[X]$ are the mean and variance of the expected distance to centre of mass as defined above.

2.5 Relative variability

Our main methodological contribution is to introduce an alternative method to estimate cell-to-cell variability in a feature measurement. Specifically, we define the ‘relative variability’ as the log ratio of the observed variance to the expected variance based what is observed in ‘similar’ proteins in the image collection (Fig. 1). To compute this local expected variance, we use a so-called conditional variance estimator (CVE, Auestad and Tjøstheim 1990; Hardle 1990). To compute the CVE, we first variance standardize the profiles, ${\displaystyle \overrightarrow{u}}$, such that $\text{cov}({{\displaystyle \overrightarrow{u}}}_1,\dots ,{{\displaystyle \overrightarrow{u}}}_{|C|})=I$ (Scott and Sain 2004), where C indicates the set of all proteins in the collection and $|C|$ indicates the size of the set C. We then use a multivariate Gaussian kernel, $K_{h_p}$, to weight each protein q based on its similarity to the protein of interest p.

$$K_{h_p}({{\displaystyle \overrightarrow{u}}}_p-{{\displaystyle \overrightarrow{u}}}_q)=\frac{1}{{(h_p\sqrt{2\pi })}^d}\exp \left[-\frac{1}{2h_p{}^2}{({{\displaystyle \overrightarrow{u}}}_p-{{\displaystyle \overrightarrow{u}}}_q)}^T({{\displaystyle \overrightarrow{u}}}_p-{{\displaystyle \overrightarrow{u}}}_q)\right]$$ (5)

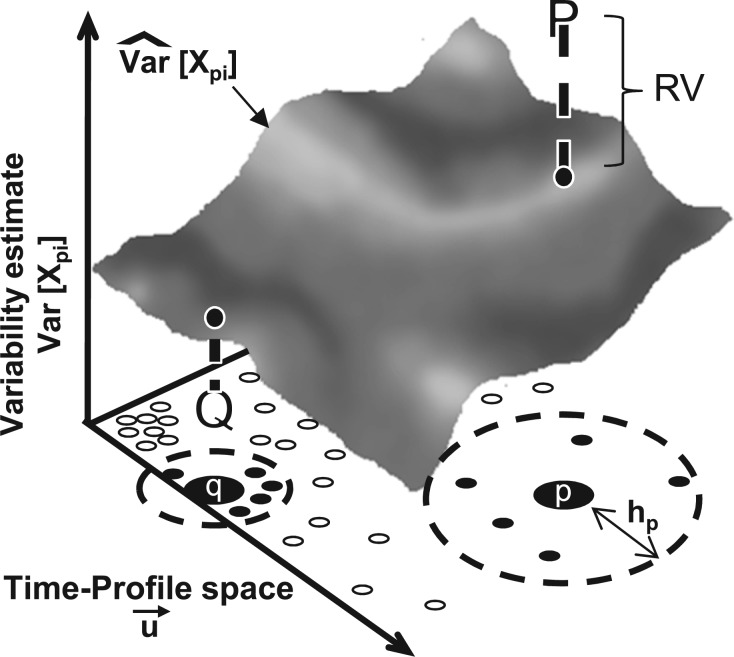
Fig. 1.

RV. A conditional variance estimate ($\widehat{\text{Var}}[]$) is computed for a feature, X, at every point in the feature space based on the nearby data points. For points of interest (corresponding to proteins, indicated by p and q), a bandwidth parameter h_p is computed based on the density of points (proteins with similar localization patterns) in that region of the space. The RV compares the conditional variance estimate (surface) to the observed variability (bold P and Q). In this example, the observed variability is high for protein p (P is above the surface) and is low for q (Q is below the surface)

Where h_p is a bandwidth parameter (discussed below) and d is the dimensionality of the feature space (length of 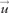, Scott and Sain 2004). We then compute the CVE, $\widehat{\text{Var}}[X]$, for each protein, p, based on the observed variability of all other proteins, q. We have:

$$\begin{array}{c}\widehat{E}[X_{pi}]=\frac{{\displaystyle \sum _{q\in C\mathrm{\setminus }\left\{p\right\}}{K}_{h_p}}({{\displaystyle \overrightarrow{u}}}_p-{{\displaystyle \overrightarrow{u}}}_q){\displaystyle \sum _{c\in B_{qi}}{w}_c}{x}_c}{{\displaystyle \sum _{q\in C\mathrm{\setminus }\left\{p\right\}}{K}_{h_p}}({{\displaystyle \overrightarrow{u}}}_p-{{\displaystyle \overrightarrow{u}}}_q){\displaystyle \sum _{c\in B_{qi}}{w}_c}}\\ \widehat{\text{Var}}[X_{pi}]=\frac{{\displaystyle \sum _{q\in C\mathrm{\setminus }\left\{p\right\}}{K}_{h_p}}({{\displaystyle \overrightarrow{u}}}_p-{{\displaystyle \overrightarrow{u}}}_q){\displaystyle \sum _{c\in B_{qi}}{w}_c}{x}_c^2}{{\displaystyle \sum _{q\in C\mathrm{\setminus }\left\{p\right\}}{K}_{h_p}}({{\displaystyle \overrightarrow{u}}}_p-{{\displaystyle \overrightarrow{u}}}_q){\displaystyle \sum _{c\in B_{qi}}{w}_c}}-\widehat{E}{[X_{pi}]}^2\end{array}$$ (6)

where, once again, x_c is a feature measurement for the cell, c, that has been assigned the ith bin for protein q, B_qi and $\widehat{E}[X]$ indicates the kernel regression (the conditional mean, Hardle 1990) of a feature X, in our case the subcellular spread feature or GFP intensity. We note that Equation (6) differs from the standard formulas (Auestad and Tjøstheim 1990) because we carry through the cell confidence, w_c, so that, e.g. we do not normalize by the total number of proteins, but rather the ’expected number’, 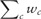. We compute the CVE for each protein, p, in each cell cycle bin, i. Because the data are non-uniformly distributed in the feature space, we use a locally adaptive bandwidth parameter (Altman 1992; Simonoff 1996), h_p, which we evaluate at each protein p (Fig. 1). This scales the kernel width to use a consistent number of ’similar’ proteins to evaluate $\widehat{\text{Var}}[X]$, so that the RV estimate for each protein is somewhat independent of scale of the differences in the local neighbourhood of ‘similar’ proteins (Breiman et al. 1977). To choose the bandwidth for each protein, a fixed point iterative procedure was used find the bandwidth, h_p, such that:

(7)

where once again C indicates the set of all proteins in the collection and d is the dimensionality of the feature space. By choosing h_p to satisfy equation (7), the number of neighbours considered for the local estimate is a fixed fraction of the whole protein collection (Breiman et al. 1977). In the following, we used 0.05% of the data, but we found that as long as the fraction was small enough, there was little overall effect on the RV distribution (Supplementary Information).

Previous studies have used deviations from LOESS regression (Hastie and Loader 1993) of the variance on the mean to quantify variability in image features (Levy and Siegal 2008; Yvert et al. 2013), which is also a local approach using a univariate measure of the difference between proteins. In principle, many choices of similarity measures between proteins could be used to compute the CVE. We explored using lower dimensional measures, such as similarity based only on the subcellular spread feature measurement and found that this also yielded more comparable variability estimates than the CV. However, we found that using the full feature profile further improved the distributions of variability estimates for different localization classes (Supplementary Information).

We define the RV for protein p as the log of a geometric mean over the 10 bins.

$$\begin{array}{c}{\text{RV}}_p=\frac{1}{10}{\displaystyle \sum _{i=1}^{10}\frac{1}{2}}\left[{\log }_2(\text{Var}[X_{pi}])-{\log }_2(\widehat{\text{Var}}[X_{pi}])\right]\end{array}$$ (8)

We note that, rather than dividing the cell cycle into discrete bins, it is also possible to use a kernel-based approach to estimate an RV using all of the cells, weighted by their cell stage estimates. We also implemented such an approach (see Supplementary Information) and find that it gives overall qualitatively similar results to the binning strategy we used here. However, we consider treating the cell stage as a series of independent categories to be a more generally applicable approach, because in other applications, there are likely to be high-dimensional, correlated sets of feature measurements, but these might not be related by time. For example, the discrete categories of features might be genetic or environmental perturbations.

3 Results and discussion

Overview: We sought to quantify cell-to-cell variability from images. Although the CV has been used previously to quantify variation in protein abundance, we find that the CV for our image-derived measurements systematically varies between proteins in different subcellular localization classes, particularly when used to quantify variability in spatial spread of protein expression. This means that identifying highly variable proteins based on CV might be biased towards identifying certain classes of proteins (such as nucleolar and mitochondrial proteins). We show that this bias is much less pronounced for the RV and test whether bona fide cell-to-cell variable proteins can be identified by ranking proteins based on the RV.

3.1 Quantifying cell-to-cell variability in protein abundance from images

To test whether we could quantify cell-to-cell variability in protein abundance from high-throughput images, we first extracted GFP intensity measurements (which reflect protein abundance) from each cell for each protein, computed the CV for the cells in each cell cycle bin and averaged these. The CV is a standard measure of variability for protein abundance (Bar-Even et al. 2006). We compared the results to high-throughput variability estimates for the yeast GFP collection based on flow cytometry (Newman et al. 2006). For example, variable proteins identified previously, such as Pry3, appear highly variable in our images (Fig. 2a). We note that technically we are not detecting Pry3 but rather the GFP-tagged fusion protein, Pry3-GFP. However, for brevity, we omit the ‘-GFP’ throughout when referring to our images; our images always show tagged fusion proteins. Overall, we found a correlation of 0.333 with the deviation to the median (DM) estimates of ‘noise’ (Newman et al. 2006). Although this correlation far exceeds what could be expected by chance ($P<{10}^{-10}$), there are many factors that we expect to affect the agreement of the image measurements with the previous estimates (Newman et al. 2006), such as different typical sample sizes, different treatment of the cell cycle, correction for autofluorescence, etc.

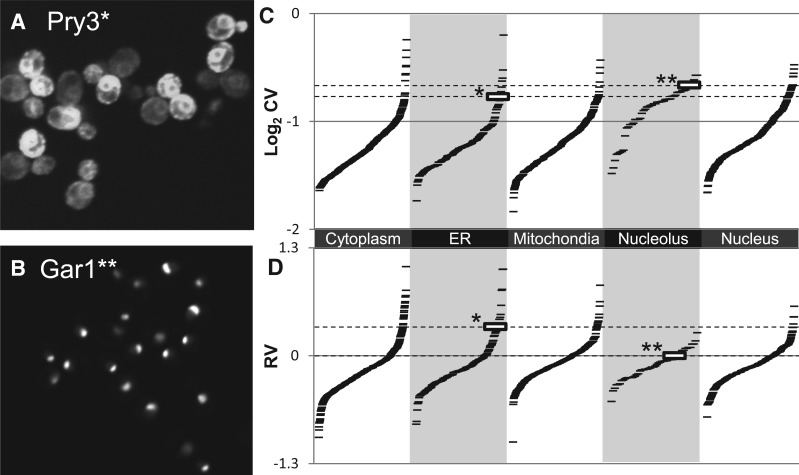
Fig. 2.

Variability in protein abundance. (A) Pry3 shows high cell-to-cell variability in protein abundance. (B) Gar1 shows a nucleolar localization pattern but little cell-to-cell variability in abundance. (C) CVs for nucleolar proteins are systematically biased relative to other localization classes. Each ‘-’ symbol represents the cell-to-cell variability for GFP fluorescence intensity for a single strain (tagged protein) in the collection. Gar1 (indicated by **) shows a higher CV than Pry3 (indicated by *). (D) RV estimates show much less bias between classes. Pry3 (indicated by *) shows a much higher RV than Gar1 (indicated by **). Example cell images are contiguous sections cropped from larger images. Contrast settings for Gar1 were adjusted to highlight the nucleolar pattern

We were particularly interested in the effect that differences in subcellular localization might have on the variability in protein abundance inferred from images. To test this, we plotted our CV estimates for all the proteins in several localization classes defined based on manual inspection of the original images of the GFP collection (Huh et al. 2003). We found that certain classes (e.g. nucleolus; Fig. 2b) display skewed distributions of CVs (Fig. 2c). This variability could be due to our imaging, as the nucleoli might be randomly missing from the focal plane or to variability in organelle shape. Regardless of the underlying reason, it is not fair to compare a variability estimate from a nucleolar protein to an estimate from a cytoplasmic protein, which will (almost) always be included in the focal plane or whose shape variation is better accounted for by the cell segmentation.

We designed the RV measure (see Section 2) to correct for differences in subcellular localization by comparing proteins’ variability to ‘similar’ proteins in our protein expression feature space (Handfield et al. 2013). Therefore, if the measure works correctly, the variability of a nucleolar protein will be compared with other nucleolar proteins, because they display ‘similar’ protein expression patterns. Consistent with this prediction, the distributions of RV measurements for nucleolar proteins are much more similar to the other classes than the CVs (Fig. 2d). For example, Pry3 shows dramatic cell-to-cell variability in our images (Fig. 2a) but has a CV that is lower than 13 nucleolar proteins that do not appear highly variable (e.g. Gar1, Fig. 2b). This is because ER proteins are biased to appear less variable than nuclear and nucleolar proteins based on the CV (Fig. 2c). In contrast, using the RV, Pry3 maintains its rank within the ER subcellular location class but ranks higher than any nucleolar protein (Fig. 2d). That the overall distributions of RVs for proteins in previously defined subcellular localization classes (Huh et al. 2003) are more similar than the CVs is supports the idea that a local estimate of variability is better suited to identify examples of unusually variable proteins. Furthermore, the correlation between RV and the DM estimates (Newman et al. 2006) is 0.398, such that RV explains nearly 5% more of the variance in the flow cytometry measured variability (DM) than does the image-based CV.

3.2 Quantifying cell-to-cell variability in subcellular localization from images

We next sought to test whether we could quantify the cell-to-cell variability in the spatial component of protein expression pattern. We computed the subcellular spread (see Section 2) for each cell and plotted its CV and RV (see Section 2) for several large classes of proteins based on their subcellular localization as defined through inspection of the original GFP collection images (Huh et al. 2003). As expected, we found even more pronounced biases in the CV between classes, such that classes with variable morphology (such as mitochondria; Fig. 3 a) and small organelles that might be out of the focal plane (such as nucleolus) showed very different distributions of CVs. Once again, we found that the RV effectively corrected these distributions, so that proteins with outstanding variability in each class were now ranked near the extremes of the entire RV distribution (Fig. 3b). For example, Spo12 shows cell-to-cell variability in subcellular localization (varying between the cytoplasm and nucleus, Fig. 3c) but is buried behind 330 proteins according to the CV. However, in the RV distribution, it is ranked $27\text{th}$ in the collection. The similarity of the RV distributions for proteins with very different spatial patterns of GFP expression indicates that comparison with nearby proteins yield comparable variability estimates, despite the heterogeneity in subcellular localization patterns.

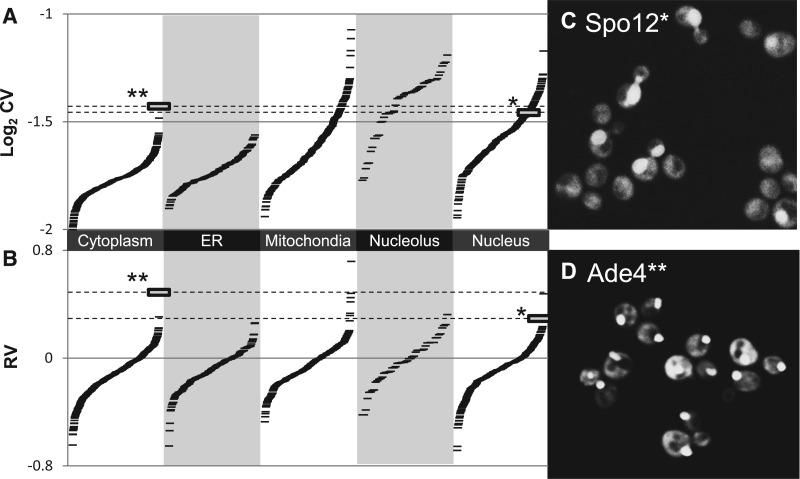
Fig. 3.

Variability in protein subcellular localization. (A) CVs for a spatial feature are systematically biased by localization class. (B) RV estimates show much less bias between classes. Each ‘-’ symbol represents the cell-to-cell variability for GFP spatial spread for a single strain (tagged protein) in the collection. (C) Spo12 shows cell-to-cell variability between nuclear and cytoplasmic localization. It has a typical CV for a nuclear protein (indicated by * in A and B) but has a high RV. (D) Ade4 shows cell-to-cell variability in localization and is the most variable cytoplasmic protein, but it falls below many nucleolar and mitochondrial proteins according to the CV. In contrast, according to the RV, it is one of the most highly variable proteins (indicated by ** in A and B)

We note that given the annotations of subcellular localization for each protein, it is possible to quantify cell-to-cell variability using the CV (Figs. 2 and 3). For example, the most variable protein cytoplasmic protein, in CV and RV, is Ade4 (Fig. 3d) and appears to exhibit punctae of varying intensity, probably reflecting a response to adenine starvation (Narayanaswamy et al. 2009). Indeed, proteins at the extreme of the distribution for each class tend to be bona fide variable proteins. However, this relies on the prior subcellular categorization of proteins (Huh et al. 2003). In practice, proteins may display localization to multiple organelles, have been annotated as ambiguous or change their localization over the cell cycle (Handfield et al. 2013) and therefore may not always fall into a single localization class. Therefore, it is not possible to identify variable examples systematically using the CV. Because the RV compares each protein to those most similar to it (as defined using quantitative image features, see Section 2), it can be applied regardless of the subcellular localization and therefore can be applied to the whole collection.

3.3 Systematic search for cell-to-cell variable proteins

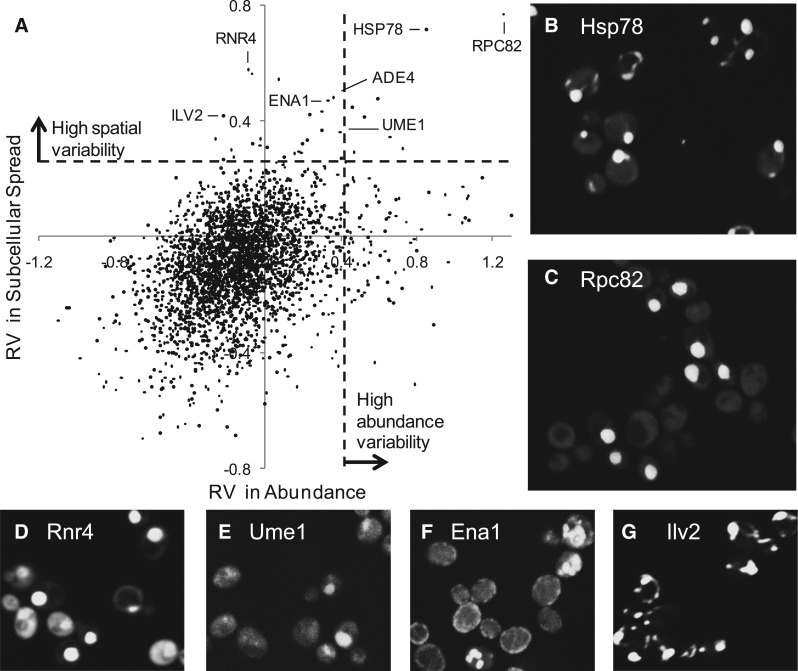
We next tested whether the RV (see Section 2) could systematically identify proteins that show cell-to-cell variability in both intensity and spatial spread in our images. We plotted the RV in subcellular localization against the RV in protein abundance (Fig. 4), as we expect variability in one aspect to influence the other. We chose arbitrary cutoffs (dashed lines in Fig. 4a) to identify predicted proteins likely to be variable in abundance, subcellular localization, both or neither. The most extreme examples were Hsp78 (Fig. 4b) and Rpc82 (Fig. 4c), which are identified as both abundance and subcellular variable. Rpc82 shows bright nuclear localization in some cells and very little fluorescence in others, whereas Hsp78 shows very bright dots mixed with a much dimmer mitochondrial pattern, which is barely visible at the contrast settings used to clearly display the bright dots).

Fig. 4.

Systematically identifying variable proteins. (A) RV estimates for subcellular localization vs. protein abundance. Each dot represents one protein. The dashed lines represent thresholds for defining proteins with high variability in either protein abundance or subcellular spread. (B–G) Examples of proteins with variability in subcellular localization

Previous studies have identified a few yeast transcription factors that stochastically translocate from the cytoplasm to the nucleus (Cai et al. 2008; Jacquet et al. 2003). These proteins have been studied in time-lapse movies, and it is currently unknown how many other proteins of this type exist and whether cell-to-cell variability in subcellular localization other than cytoplasm and nucleus can exist. Consistent with the prevalence of nuclear-cytoplasmic variability, we found several other proteins with high RV exhibiting nuclear localization in a subset of the cell population (Fig. 4d and e, Table1). Because the environment of the cells in our images is expected to be constant, these represent new candidates for stochastic nuclear-cytoplasmic translocation but could also represent static variability in the cellular response to the growth conditions.

Table 1.

Most spatially variable proteins

RV#	CV#	Name	Subcellular localization	Cells
1	10	RPC82a	Cytoplasm, nucleusb	155
2	3	HSP78a	Mitochondrionc	86
3	7	RNR4a	Cytoplasm, nucleusd	145
4	39	ERG6	Lipid particle	83
5	137	LEU4	Cytoplasm, mitochondrion	195
6	2	ATP2	Mitochondrion	130
7	4	CBF1a	Nucleusb	72
8	146	ADE4a	Cytoplasm	71
9	6	ALD5a	Mitochondrion	123
10	230	ENA1a	Cell periphery	130
11	129	DAD3	Spindle pole	192
12	32	ILV2a	Mitochondrion	77
13	56	GIN4	Ambiguous, bud neck, cytoplasm, bud	182
14	151	BCY1a	Cytoplasm, nucleusc	198
15	437	UME1a	Cytoplasm, nucleusd	164
16	398	SRD1a	Cytoplasm, nucleus	200
17	302	ACE2	Cytoplasm, nucleus, bud	148
18	274	VPS54	Punctate composite, early Golgi	95
19	21	LYS4	Mitochondrion	107
20	9	NET1	Nucleolus	206
21	266	EDE1	Punctate composite	168
22	1	ATP1	Mitochondrion	57
23	82	SPC34	Spindle pole	82
24	517	SNO1	Cytoplasm	66
25	80	MCM6	Cytoplasm, nucleus	100
26	247	TGL4	Lipid particle	159
27	331	SPO12a	Nucleus	153
28	466	SEC10	Ambiguous, bud neck, cell periphery, bud	164
29	102	DAD1	Spindle pole	185
30	22	GCV2	Mitochondrion	56

The top 30 spatially variable proteins ranked by RV (RV#) are listed. Their ranks according to the CV (CV#) are also included for comparison. Subcellular localization categories as defined previously (Huh et al. 2003) are also indicated. The total number of mother–bud pairs available for the analysis (Cells) is also indicated. A complete listing of all proteins we analyzed is available as Supplementary Information.

^aProteins that actually appear variable upon visual inspection of the images.

^bSubsequent experiments indicated that variability is due to mixed genotypes.

^cSubsequent experiments were inconclusive.

^dSubsequent experiments confirmed variability in genetically identical cells.

In addition to nuclear-cytoplasmic variability, the most variable 30 proteins according to RV (Table 1) include many subcellular locations. Some of these are rare and have a strong cell-stage dependence (bud neck, spindle pole and bud specific), so that it is difficult to visually assess cell-to-cell variability. Still, Ade4 (Fig. 2b) and Ena1 (Fig. 4f) appear to represent clear examples of spatial variability. Visual inspection suggests that Ena1 is localized to the cell periphery or to several punctae inside the cell. Ade4 (Fig. 3d) shows a bright dot or bright cytoplasmic intensity. We were particularly interested to identify proteins like Hsp78, Ena1 and Ade4, because they show that spatial variability other than nuclear-cytoplasmic is in principle possible; this type of variability can only be identified using microscopy, and our analysis represents the first systematic effort to identify these. That many classes of cell-to-cell variability could be identified using the RV in a single-feature measurement suggests that prior knowledge of subcellular location is not needed to detect unusual heterogeneity in spatial pattern.

To obtain a more objective measure of the power of our new measure (RV) to identify cell-to-cell variability in subcellular localization pattern, we examined images for the top 30 most spatially variable proteins according to the RV and CV. The main difference is that seven proteins with nuclear-cytoplasmic variability are found in the group of 30 proteins with highest RV, whereas only three of them are found using CV. In addition, two variable proteins (Ena1 and Ade4) with other localization patterns are identified by the RV but not by the CV. Among the 10 proteins found in both rankings, 6 are localized to the mitochondria. The mitochondrion is an organelle with a complex tubular network morphology but often also may show a punctate pattern (Okamoto et al. 1998). Among mitochondrial proteins with highest CV or RV, several showed a punctate pattern, but only Ald5 and Ilv2 (Fig. 4g) show a punctate pattern with a brightness comparable to Hsp78. All three have high rank for RV and CV (Table 1) consistent with the bias in the CV estimates for mitochondrial proteins (Fig. 3A). Overall, based on our inspection of the images, 12 true positives are found in the 30 most variable proteins using RV and only 5 are found using CV. This means that the RV analysis has positive predictive power of ∼40% compared with ∼17% for the CV.

False negatives are difficult to quantify, as a set of known ‘spatially variable’ proteins is difficult to define. For instance, Crz1 localizes to the nucleus if cells are treated with calcium (Cai et al. 2008) and Msn2 localizes to the nucleus as a general stress response (Jacquet et al. 2003). For Msn2 and Crz1, only one and four cells are found having protein with nuclear localization (out of 257 and 347 cells, respectively) in our images, likely because they were taken of cells in standard growth conditions. RV and CV both fail to detect this scarce variability (all ranks above 1400 out of 2860 proteins). For this experiment, where the nuclear localization was not induced, it is unclear whether to consider Crz1 and Msn2 false negatives.

An important limitation of the RV is that the local estimate of the variance level for a given protein relies on ‘similar’ proteins. If a protein has a pattern that has little similarity to any other protein (e.g. due to cell-stage dependencies or unusual protein abundance distributed into multiple subcellular locations), the local estimate of the variance may not be a good estimate for that protein. Indeed, several of the proteins we identify as most cell-to-cell variable in subcellular localization are either known to show cell-cycle regulated localization [Mcm6, Nguyen et al. (2000) and Ace2, O’Conalláin et al. (1999)] or are cell-cycle regulated proteins whose subcellular localization has not been characterized [Spo12, Tomson et al. (2009) and Net1, Visintin et al. (1999)] These proteins may be examples of proteins with unusual cell-cycle patterns. However, it is also possible that our simple strategy of binning cells according to bud size does not fully capture the cell-cycle variation in their protein expression.

The correspondence of our statistical approach and our examination of images (Fig. 4) confirms our computational methodology but does not provide confirmation of biological relevance of the cell-to-cell variability we identified. Because the microscope setup, medium composition, long-term storage of strain collections and other factors can affect the consistency of GFP-patterns, we first reimaged several of the variable proteins identified (Hsp78, Cbf1, Rpc82, Bcy1, Rnr4 and Ume1) and confirmed that the images in our high-throughput collection accurately reflected the GFP collection (Supplementary Information). Because high-throughput analysis of the GFP collection is typically done using automated liquid handling from 384-well plates, we next sought to confirm that the observed variability was indeed due to differences in protein expression among genetically identical cells. We tested this by streaking out individual colonies from the variable strains and imaging the resulting cultures. In several cases, we found that individual cultures did not recapitulate the variable pattern observed in the collection strain. For example, individual colonies from Rpc82 and Cbf1 showed homogeneous subcellular localization patterns (nuclear or cytoplasmic, but never both, Table 1 and Supplementary Information) strongly suggesting that the strains in the collection represent mixtures: the variability we observe is due to genetic differences and is not due to ‘noise’ in protein expression. We note that the variability for Rpc82 is clearly visible in the original GFP collection images (Huh et al. 2003), indicating that the mixture of strains has persisted. On the other hand, individual colonies from Rnr4 and Ume1 recapitulated the variability observed in the image collection and showed variability even in cells with buds in the same size range (Table 1 and Supplementary Information). Consistent with our observations, a mixed cytoplasmic and nuclear localization pattern for Rnr4 has been noted in response DNA damage (Yao et al. 2003). Ume1 may represent a new example of a protein with variable subcellular localization pattern. Nevertheless, we note that the variability we observe may simply be due to insufficient nutrients or other cultivation conditions (Narayanaswamy et al. 2009). Further experiments will be needed to determine the biological causes and consequences of the variability we have identified. Taken together, these experiments confirm that statistical analysis of high-throughput microscopy images can identify proteins with variability in subcellular localization.

4 Conclusion

We defined a local statistic to compare cell-to-cell variability, which alleviates potential biases arising from heterogeneity of subcellular localization of proteins. We performed the first systematic search for the most spatially variable proteins and found several examples of proteins that show variability in their subcellular localization pattern. These include new classes of cell-to-cell variability, where cytoplasm, mitochondria and cell periphery are mixed with the occurrence of bright punctae. This demonstrates that a statistical analysis of still images can be used to quantify cell-to-cell variability in protein abundance and subcellular localization pattern. We believe that local statistics will be useful for other high-throughput data analysis applications, where data are highly heterogeneous, but clear boundaries between classes cannot be defined.

Funding

This work was supported by the National Sciences and Engineering Research Council of Canada (to L.F.H. and B.S.); Canadian Institutes of Health Research [MOP-119579 to A.M.M.]; infrastructure grants from the Canada Foundation for Innovation (to A.M.M. and Brenda Andrews) and by grants from the Canadian Institutes for Health Research (to Y.T.C.).

Conflict of Interest: none declared.