Concepts in solid tumor evolution

Abstract

Evolutionary mechanisms in cancer progression give tumors their individuality. Cancer evolution is different from organismal evolution, however, and here we discuss where concepts from evolutionary genetics are useful or limited in facilitating an understanding of cancer. Based on these concepts we construct and apply the simplest plausible model of tumor growth and progression. Simulations using this simple model illustrate the importance of stochastic events early in tumorigenesis, highlight the dominance of exponential growth over linear growth and differentiation, and explain the clonal substructure of tumors.

Evolution seems so familiar

Everybody knows what evolution is. Right? One hundred fifty-six years after the first modern treatment of evolution [1], and 53 years after discovery of ‘the’ molecular clock [2], most biologists have an intuitive feel for evolution. Evolution is a popular subject for science education, it is taught with passion in college and graduate courses, and mentioning it in scientific papers is de rigueur even if the study has nothing to do with evolution. After all, (i) every single biological process is the product of evolution and therefore, (ii) nothing in biology makes sense except in the light of evolution [3].

Despite its popularity as a subject, however, evolution is surprisingly difficult to study, and every field that begins to embrace evolutionary thought and gather evolutionarily relevant data is faced with the tension between studying something so seemingly familiar and producing actually meaningful and novel insight. This tension is now emerging in cancer, where technological advances are enabling the generation of sufficient data to address which general evolutionary principles apply, and how cancer-specific mechanisms extend them.

Cancer repeats, the tree of life does not

The most obvious difference between cancer and organismal evolution is that the substrate of the former is a somatic cell, whereas the latter is a germline process. Cancer is a dead end whether or not it kills its host, whereas germline-based organismal evolution forever marches on. Natural selection over the billions of generations since the last common ancestor of all life has produced an enormous range of organisms but there is only one tree of life; life on earth is the realization of a single experiment that will never repeat. By contrast, each kind of human cancer is an experiment that is repeated over and over with similar initial conditions among the trials and a limited range of possible evolutionary trajectories, constrained by the specific molecular biology of the originating cell and by the human genome. See Box 1 for a discussion of driver mutations.

BOX 1. Identification of driver genes.

The limited range of evolutionary trajectories is the basis for the identification of cancer driver genes, now accomplished by large-scale sequencing projects that identify recurrently mutated genes. In many cancers, mutations in a limited number of genes act as the most common drivers [4–10]. Gain of function changes in oncogenes (e.g., ERBB2, KRAS, or IDH1) tend to be caused by a small set of mutations that recur, but as a class these are rarer than loss of function mutations in tumor suppressors (e.g., TP53, RB, or VHL). Because there are so many ways to inactivate a gene (loss of function point mutations, frameshifts, deletions, etc.), searches for driver mutations have been broadened to the gene level and do not require the exact same nucleotides to be recurrently mutated [11–12]. These searches have revealed that many cancers exhibit mechanistic commonalities, mostly along the lines of tissue of origin, but some crossing those lines as well [13].

Thus, in cancer, evolution really does repeat itself, and that is its Achilles’ heel: recurrently mutated genes are used in screening and diagnosis, inform treatment choice, and are potential targets for drug discovery. It also means that certain evolutionary principles are likely operational, some of which are already discernible at this early stage of our understanding of cancer.

Tumors are clonal

Two lines of evidence from tumor genome sequencing studies support the view that all tumor cells (either primary or metastatic) are derived from a single ancestral cell that acquired proliferative potential [14]. The first is that alternate allele frequencies of SNVs, and the prevalence of larger genomic aberrations such as aneuploidies, are frequently consistent with all tumor cells carrying the changes [10,15]. If cells within a tumor carry a number of shared somatic changes, then they must derive from a single ancestral cell that harbored these changes. This is because the probability of two or more cells independently acquiring the same set of somatic mutations is infinitesimally small.

The second, broader line of evidence supporting the presence of subclones and the clonal origin of metastases comes from phylogenetic studies of distinct samples in the same patients [16–20]. In these studies, somatic mutations serve as unequivocal lineage markers to construct bifurcating trees. Branch points represent cell divisions that gave rise to two proliferating daughter lineages that eventually expand into subclones.

Cancer cells are not a mating population and their genomes do not recombine

Cancer cells arise by mitotic division and therefore do not exchange genetic material, neither with each other nor with the cells of the microenvironment. A comparison to organismal life, which forms the basis for our intuition about populations, provides an illustrative contrast. Organismal species, including bacteria, constantly exchange genetic variation through mating or other mechanisms. This has the paradoxical effect of maintaining variation but binding the genomes of all individuals together such that as a whole the species evolves concertedly.

Cancer is entirely different. Once a cancer cell divides, the two daughters’ genomes are on a future path of absolute independence (Fig. 1A). Without mating and recombination, mutations that occur in one lineage have no bearing on another lineage. The variants carried by a cell occurred in a specific order in its ancestral lineage only, back to the zygote (Fig. 1B). Similarly, the context in which a new mutation arises is the totality of all previous mutations across the entire genome that occurred before it (Fig. 1C). As a consequence, some driver mutations will only provide an advantageous phenotype if the cell previously acquired another driver that allows the new driver to have an effect. This explains why mutations in some pathways tend to occur early in tumor evolution, and others late [20–22].

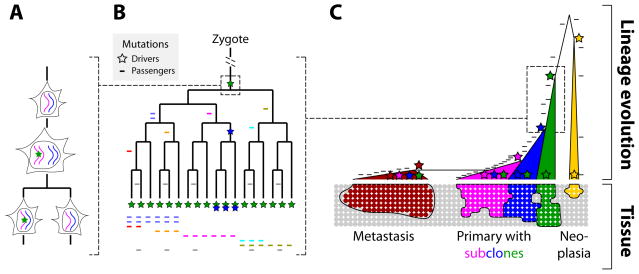
Figure 1.

Passenger mutations serve as lineage markers, and driver mutations lead to subclones whose size is a function of strength and timing of the driver. A. Mutations (star) that arise during DNA replication will be passed on in heterozygous state to one of the daughter cells. Mutations that arise during interphase (not shown), such as incorrectly repaired DNA damage, will likely be passed on to both daughter cells. B. Mutations serve as lineage markers because they are passed on to only their progeny and are not horizontally transferred. C. Drivers initiate proliferation and then increase the growth rate, which leads to subclones (or metastases) that are marked by ever increasing numbers of mutations. When the ancestor is old, as in slowly-growing neoplasias such as columnar cell lesions in breast, the number of mutations that are shared by all cells of the neoplasia is comparatively lower than the number of mutations in a fast-growing tumor whose ancestral cell is more recent. Note that, in the primary tumor, the subclones (blue and magenta) have to grow sufficiently more quickly to be detectable compared to the already existing and still-expanding original clone (green).

Cell autonomy rules

Driver mutations act cell-autonomously, that is, they confer a growth advantage on the cell in which they arose. That’s how they make themselves more frequent. A non-cell-autonomously acting mutation confers a growth advantage on cells that do not harbor it, and therefore cannot cause an increase of its own frequency in the cancer cell population. The vast majority of cancer-causing mutations that have been functionally studied exhibit cell-autonomous activity via processes such as intracellular signaling, cell-cycle control or cell death. Note that mutations that cause a tumor cell to interact with its microenvironment, for example via VEGF to stimulate vascularization, are considered cell-autonomous because they provide their growth benefit to the originating cells.

There are some exceptions to the cell-autonomy rule, however, such as in prostate cancer, where non-cell-autonomous signaling by androgens is permissive for tumor development. Androgen-deprivation therapy can lead to remission, but eventually, the cancer overcomes its dependence by cell-autonomous mechanisms [23]. Similarly, anti-EGFR antibody therapies in colorectal cancer have been shown to be eventually rendered ineffective by preexisting (cell-autonomously acting) KRAS mutations [24]. In a novel mouse cancer model, non-cell-autonomous drivers lead to unstable tumor growth and can result in tumor collapse [25]. Finally, the accumulation of genomic change that in some solid tumors culminates in hypermutation and chromothripsis [26,27], as well as the accumulation of driver mutations in the ancestral lineages of tumor cells, is difficult to reconcile with non-cell-autonomous mechanisms. These examples illustrate that non-cell-autonomous mechanisms exist and play a role in cancer, but it is cell-autonomy that make cancer the disease of relentless cell proliferation.

Cell autonomy has profound implications on our understanding of the relationship between subclones within a tumor. Much cancer literature implies or asserts that clones compete with one another, as if cells within a clone behave concertedly and and gang up on all the cells of another clone [e.g., 28]. Concerted behavior, such as slowing of growth rates in larger tumors due to lower nutrient availability and accumulation of toxic byproducts, is likely due to the microenvironment and not due to common ancestry. Cells of a clone behave independently from one another due to their cell-autonomy. The growth rates of the cells in any given clone may be similar because of common ancestry, and they may be greater than the growth rates of cells of another clone, but there is no reason to think that the cells of earlier clones stop growing and dividing just because new clones come along.

Mutations do not fix, selection neither sweeps nor purifies

Clonal mitotic growth, cell-autonomy, and lack of recombination/mating combine to produce population genetic and evolutionary effects in cancer that are distinct from, and simpler than, those in germline evolution. Most importantly, the somatic variants present in the cancer cell ‘population’ are locked into each individual cell such that allele frequencies are dependent on ‘population size’ (the number of cells in a tumor). In organismal populations, allele frequency is generally independent of population size, but in cancer, variants can only rise in frequency as a result of clonal (‘population’) growth, and ‘positive selection’ cannot take an allele to high frequency without increasing the number of cells that carry it. Similarly, genetic drift (the stochastic process that changes the frequency of neutral variants in the population) is largely irrelevant because neutral variants (passenger mutations) deterministically change frequency as a function of the cell growth caused by drivers.

Purifying selection, a useful term in population genetics describing the loss of an allele because of lower fitness, has little relevance to cancer growth because cells with a decreased growth rate trivially end up contributing negligible mass to a tumor. Perhaps cancer therapies can be thought of as agents of purifying selection, but the regimen is so different from the usual action of organismal purifying selection that there is little to be learned by the analogy. Organismal purifying selection acts to gradually reduce allele frequencies in a population, whereas the goal in cancer therapy is to achieve a 100% kill rate and eliminate the entire population of tumor cells.

The forced application of terms and concepts from organismal population genetics can distract from the fundamental simplicity of cancer evolution. For example, calling a driver an ‘advantageous allele’ or invoking ‘natural selection’ instead of clonal proliferation, can lead to unnecessary conceptual complications, like in the case of discussions about ‘fixation of advantageous alleles’. Fixation refers to the rise of a variant in frequency in the population, to 100%. In cancer, fixation would mean that all cells of a tumor carry a particular somatic variant, such as a strong driver mutation. But because mutations in cancer generally work cell-autonomously, sibling cells lacking a new driver mutation continue replicating, albeit at the original slower rate. Understanding these dynamics without confounding concepts from organismal population genetics is key to understanding the reasons for tumor heterogeneity.

Tumor heterogeneity is clonal (and virtually infinite)

Cancer genome data unequivocally demonstrate that the bulk of the tumor (excepting stroma and other ‘normal’ cells) derives from a single ancestral cell, and that there are not parallel lineages originating from several initially normal cells that proliferate at a similar rate to give a heterogeneous mass. Instead, tumor heterogeneity is generated by occasional, individual tumor cells that acquire increased proliferative potential and whose greater growth rate leads to a mass within a mass (see above; Fig. 1C). Amongst the cells of each clone, there is additional genomic heterogeneity, as evidenced by single-cell sequencing [29–31]. It is due, especially at later stages of tumor growth when mutator drivers have taken hold, to mutagenic potential in every cell division.

These two types of intratumor heterogeneity (among clones vs. among cells within a clone) are best kept conceptually separate. The former embodies the proven proliferative capability due to drivers that caused the clones to grow, and although drivers are vastly outnumbered by passengers, they are guaranteed to be present. In the latter, the private mutations present in individual cells of a clone are not enriched for drivers. Among the tremendous number of rare (i.e., not ancestrally shared) variants present in the billion or more cells that may make up a growth are mutations that do confer a proliferative advantage. However, overall the variation in an individual cell that is not shared with most other cells of a clone is highly enriched for irrelevant genomic changes that do not confer a proliferative advantage. One practical implication of this is that sequencing samples of larger numbers of cells may be preferable in many circumstances because it conveniently identifies those mutations that arose in their common ancestral lineage, which are comparatively enriched for the drivers that made those cells proliferate.

Heterogeneity is key to understanding a tumor’s response to drug treatment. Even in the absence of accelerated mutation rates, the genomic diversity present in the billions of cells of a moderate-sized tumor can harbor mutations conferring drug resistance, resulting in the high rates of relapse following chemotherapy typical of many types of cancer [32].

Models of tumor growth

Many mathematical models of tumor evolution have been proposed, of varying levels of complexity [33–37]. Our intent here is to explore the simplest possible model that gives interpretable results that are consistent with known dynamics of tumor evolution. Our uncontroversial premise is that in all tissues of the adult, homeostatic (non cell-autonomous) mechanisms keep bulk cell growth in check such that the number of new cells roughly equals the number of cells that die. Cancer begins when the nonautonomous mechanisms suppressing cell growth are overruled by cell-autonomous changes (driver mutations) in the genome of the founding cancer cell.

Given that cells grow by binary division there are two opposite, extreme scenarios that bound plausible models of how tumors grow: we refer to these as the Strict Stem Cell (SSC) model, and the Perfectly Proliferating Cell (PPC) model. In the SSC model, a true stem cell’s division regenerates a stem cell and one nondividing, differentiated daughter cell. In this model, one division produces one additional cell and growth is linear with the number of cell divisions. By contrast, the PPC model is perfectly exponential where every daughter cell divides and the number of cells doubles in each mitotic generation. Both models have biological underpinnings. Stem cells exist in many natural systems, and the PPC occurs in cell culture.

Under the SSC, the number of cell divisions required to produce n cells is n. It would take a million consecutive cell divisions of one stem cell lineage to generate a 1 mm³ neoplasm. This is impossible within a human lifespan. More generally, it is linear growth that makes the SSC or relaxed versions of it implausible. Allowing some limited proliferative potential of the non-stem daughter cells does not change the linearity of stem cell models. For example, if each of the non-stem daughter cells produce a hundred progeny, the number of stem cell divisions would still have to be 10⁶/10² = 10⁴ for a 1mm³ neoplasm, or 10⁷ for a 1cm³ tumor. Thus, relaxing the SSC does not yield a plausible variant of the model, fundamentally because it is linear.

At the other extreme, the PPC model implies rapid tumor growth: a million cells would be generated by a mere 20 cell divisions. This in itself does not make the model implausible as the time between divisions could be very long, but cell death (or terminal differentiation) decreases the growth rate from a perfect doubling per generation, making the PPC in its extreme form implausible. However, its essential feature is exponential growth, a much more plausible dynamic than linear growth.

A simple and interpretable model of proliferation

Cell-autonomy and mitotic division suggest a biologically straight-forward and parsimonious view of tumor cell divisions: tumor cells divide symmetrically to give rise to daughter cells that are very much like their mother cell, not in a deterministic but in a probabilistic sense. Daughter cells inherit their probability of division from their mother. This probability of division is cell-autonomously set by the genome and epigenome, and new drivers increase this probability. When homeostatic mechanisms are in place, an average daughter cell has a 0.5 probability of dividing again or dying. If instead of dying, the cell lives, growth is stem-cell-like and linear because only half of the daughters of a generation will divide again, just like in an asymmetric stem cell division. At the other end of the extreme, a daughter that has a 1.0 probability of dividing again is a PPC because the cell number doubles in every generation. Let’s call this probability f, for fraction of cells in a generation that will go on to divide again. A similar, slightly more complex model has been shown to accurately model the progression of known tumor types [33].

First stochasticity, then determinism

Homeostatic mechanisms initially keep f at 0.5. The first driver must set f > 0.5, meaning that the next cell division has a somewhat higher probability to give two proliferating daughters rather than just one. But the first driver occurs in a single cell, and there is a chance that this cell does not divide (equal to 1−f), or, if it divides, that neither daughter divides (equal to (1−f)²), in which case the driver is lost. Therefore, the chance that the driver is still around in the third generation is only f(1−(1−f)²), or, for example, 0.44 if f = 0.55. The consequence is that, if f is close to 0.5, it takes many independent occurrences for a first driver to succeed, as some simple simulations show. We explored f’s parameter space above 0.50 to find the number of tries it takes to eventually generate a neoplasm of 10⁶ cells, or roughly 1mm³ in volume. These simulations show that it takes 25 tries at f = 0.51 and still almost 3 tries at f = 0.6 (Fig. 2A). We found that a simple transformation of the probability of a driver’s survival in a previous model [33] gives exactly the same results.

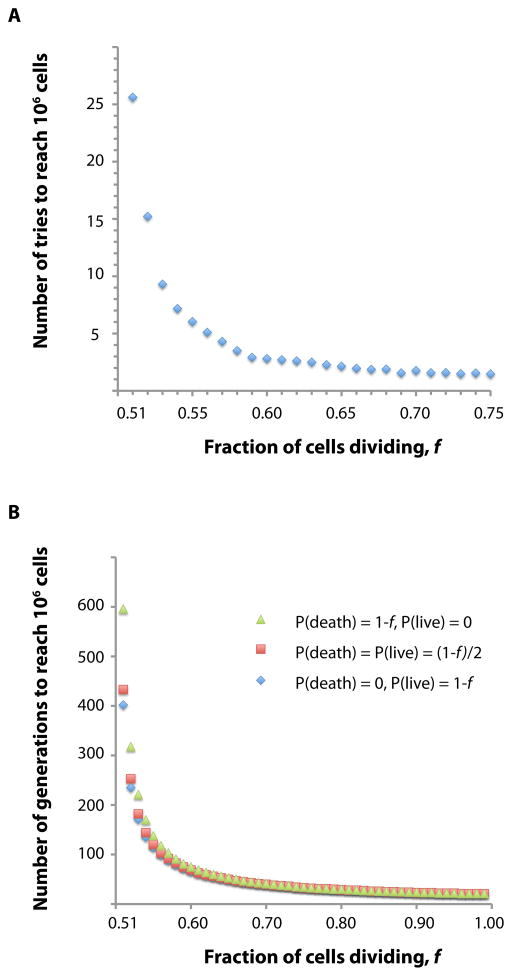
Figure 2.

Simulations of tumor growth based on a simple model of proliferation. A. Stochasticity in the initial phase of tumor growth, illustrated by the number of tries it takes (Y axis) for a clone to grow to one million cells (as opposed to going extinct), as a function of the strength of the initial driver mutation (X axis). B. Results from a simulation exploring the effect of the balance between cell death and ‘terminal differentiation’ of nondividing cells. Only when drivers are weak (X axis) is there an appreciable difference in the number of generations it takes to reach one million cells.

The universe of candidate driver mutations is comprised of drivers with a range of effect sizes [38]. Some may tweak f ever so slightly, some much more. And the same driver mutation may well behave differently in different individuals, depending on genetic background. So, depending on genetic background and the effect of candidate driver mutations, cancers with a strong inherited component and some sporadic cancers with strong-effect drivers develop early, whereas some individuals without predisposition or better somatic luck will never develop a tumor.

Once a large enough number of cells is produced, the stochastic process of tumor growth gradually approximates a deterministic one because there are enough cells that the population practically never goes extinct. And with an average f ≫ 0.5 and a large number of cells, a tumor is eventually guaranteed.

To be or not to be, it appears to matter not

Now let us consider the path that has generated an incipient tumor mass of 1mm³. Intuition suggests that f is not the only important parameter that determines how many cell generations it takes to produce the mass, but that it might also matter whether the nondividing cells live or die. Thus, the simple model of dividing vs. nondividing cells can be extended to dividing vs. dying vs. nondividing cells, such that f + d + l = 1, where d is the probability that a cell dies and l is the probability that a cell lives but does not divide. We performed simulations where f again ranges from 0.5 to 1, under three different d: d = 0 (no death, all live), d=l=(1−f)/2 (equal probability of dying and living), and d=1−f (certain death, if destined to not divide).

The results confound the intuition that the balance between cell death and terminal differentiation must be an important parameter (Fig. 2b). Only when the probability of division is close to 0.5 does it matter whether the nondividing cells live or die, and even then it does not matter much. At f = 0.51, it takes 400 cell generations to produce 10⁶ cells if all nondividing cells live and 600 generations if all of them die. At f = 0.55, it takes 138 and 114 generations, respectively. At f = 0.60, the difference practically disappears. Why is this? Consecutive cell division is an exponential process and the growth of every generation progressively and dramatically diminishes previous generations’ contribution to total cell numbers. The dividing cells are those that matter; the nondividing cells statistically disappear even if they live, so whether they die makes no difference. The greater the probability of division, the greater the fraction of dividing cells in the next generation, and the greater is the irrelevance of the nondividing cells.

Time

So far we have only considered the number of cell generations required to produce a certain number of cells, not actual time. That’s because real time and generation time are related linearly, and for the above discussions it is less confusing to just model cell generations than to bring in the time per generation. So how long in real time would it take to produce a clone of a certain size, and are these estimates consistent with what happens in cancer? We let t, the average time between divisions, range from two per week to one per month and calculated the number of weeks it takes to form a clone of 10³, 10⁶, or 10⁹ cells in the same range of f as before. For simplicity we set d=l=(1−f)/2, that is, we let the same number of nondividing cells live and die, and started with a single cell as before.

The resulting times are entirely within the range of plausible values [39]. On the slow end, a clone with f = 0.55 and t = 4 weeks/division takes 3.2 years to produce 10³ cells, or 8.9 years to produce 10⁶ cells. In the middle, a clone with f = 0.65 and t = 2 weeks/division takes 22 months to produce 10⁶ cells, or 34 months to produce 10⁹ cells. An aggressive clone with f = 0.75 and t = 2 divisions/week takes 16 weeks to produce 10⁶ cells, or 25 weeks to produce 10⁹ cells.

In principle, this simple model could also accommodate the increase in mutation rates many tumors experience (via genome instability or other mechanisms) at later stages of progression, or mutator phenotypes. Increasing mutation rates decrease the wait time to a driver mutation appearing somewhere in the clone, whether they are caused by genetic predisposition (Lynch syndrome), the environment (carcinogens in lung cancer), or somatic events in the course of tumor development (mutagenic drivers like APOBEC3 [40]). In the interest of simplicity, we chose here not to model mutation rates because their increase only compresses clock time between drivers and not the fundamental cell biology of drivers themselves.

Progression (Evolution)

Constraints on the cellular machinery and the robustness of biological networks suggest that the first successful driver is likely to set f to be just a little above 0.5, as opposed to immediately increasing the probability of division to a high value [33]. Subsequent drivers may continue to increase f, but a decrease in t would also cause a higher proliferative rate, and for each subsequent driver to succeed it has to either increase f or decrease t. The cells carrying these new drivers will only contribute substantially to the tumor mass if the magnitude of the change is great enough, because the earlier genotype has a head start in the number of cells that carry it (Fig. 3). Thus, unless drivers occur in very rapid succession, functional heterogeneity due to differential presence of drivers (not just lineage heterogeneity, which involves accumulation of passengers and happens regardless of drivers; Fig 1B), is ensured within the tumor (FIg 1C).

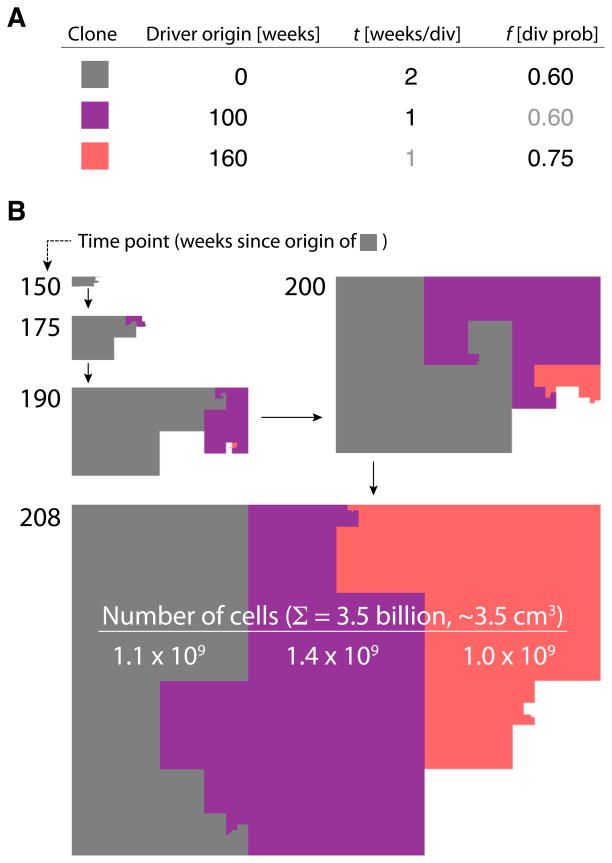
Figure 3.

Visual representation of evolution and resulting clonal heterogeneity in a tumor that grows to 3.5 billion cells over the course of three driver mutations that occur within four years. A. Parameters of the simulation. The grey clone originates with the first driver mutation that sets f = 0.60, and t = 2 weeks. 100 weeks later the purple clone originates due to a driver that decreases t to 1 week (f does not change). A further 60 weeks later, the orange clone arises by a driver that sets f to 0.75. B. Five time points of this tumor’s evolution. Area sizes are proportional to the number of cells in each clone. After four years (208 weeks), each clone is approximately the same size, 1 billion cells each, comprising a solid tumor of about 3.5 cubic centimeters.

That tumor evolution (progression) should follow this simple scenario, which explains intratumor heteroeneity, is entirely consistent with the nature of driver mutations. As comprehensively explored in a recent review on cancer [39], decades of functional studies as well as recent genome sequencing efforts have shown that there is a limited number, perhaps between 2 and 8, of large-effect driver genes in most tumors. There is still ascertainment bias towards point mutations and very-large chromosomal changes, such as recurrent chromosome 1q gain in ER-positive breast cancers, so the number may be higher once all genomic changes are reliably identified. There may also be a large number of small-effect drivers that are sometimes lucky enough to help generate a clone [11]. However, the fact that there are unlikely to be many more large-effect driver changes per cancer is consistent with the idea that in any given cell type there is a limited number of pathways that when mutated confer a big growth advantage. Small-effect drivers may also accumulate, but by definition they will not contribute the majority of the tumorigenic phenotype.

Simplicity of basics, complexity of instantiations

Cancer is a dumb disease, a disease of just cell numbers and their uncontrolled growth, a regression to a more primitive state that overcomes the intricate homeostatic mechanisms that have evolved in multicellular organisms. Perhaps it is not surprising that a very simple model with just two parameters, f and t, can provide an explanatory basis for its progression. Cancer is also capricious, however, because mutation is random and even the process of clonal growth is governed by stochasticity as each driver mutation is not guaranteed to be successful in causing a sufficient number of cell divisions to make a persisting clone. Synthetic interactions among drivers, or between drivers and genetic background, add genetic variance. Microenvironment, its interaction with genetics, local nutrient supply, and other organismal factors add further stochasticity. As a consequence, the variation in cancer incidence, speed of progression, likelihood of recurrence or metastasis, and eventual outcome is huge. But while every tumor is an individual experiment in evolution’s morbid playground, basic principles apply and the finite number of underlying mechanisms give hope that an exact 100% kill rate, not rounded up, will be achieved reliably in the future.