3D Surface Imaging of the Human Female Torso in Upright to Supine Positions

Abstract

Three-dimensional (3D) surface imaging of breasts is usually done with the patient in an upright position, which does not permit comparison of changes in breast morphology with changes in position of the torso. In theory, these limitations may be eliminated if the 3D camera system could remain fixed relative to the woman’s torso as she is tilted from 0 to 90 degrees. We mounted a 3dMDtorso imaging system onto a bariatric tilt table to image breasts at different tilt angles. The images were validated using a rigid plastic mannequin and the metrics compared to breast metrics obtained from 5 subjects with diverse morphology. The differences between distances between the same fiducial marks differed between the supine and upright positions by less than one percent for the mannequin, whereas the differences for distances between the same fiducial marks on the breasts of the 5 subjects differed significantly and could be correlated with body mass index and brassiere cup size for each position change. We show that a tilt table - 3D imaging system can be used to determine quantitative changes in the morphology of ptotic breasts when the subject is tilted to various angles.

1. Introduction

Many authors have advocated three-dimensional (3D) surface imaging of the breasts of women to facilitate preoperative patient education,^1–4 to assist the surgeon with surgical planning,^2–6 and to objectively document pre- and postoperative breast metrics for outcomes analysis.^{1–3, 5–21} Typically, image acquisition occurs with the patient in an upright, standing pose.^{1–9,11, 14–21} A standing pose is optimal for imaging with the routine configuration of 3D camera systems and because this is the standard position for subjective evaluation of breast aesthetics.

Some authors have employed a sitting pose to acquire 3D surface images of the patient’s breasts.^10,12 Catanuto et al.¹⁰ had the patient recline back 45 degrees from the upright sitting posture, presumably in an attempt to visualize the undersides of the breasts. Ericksen et al.¹² likewise employed a sitting pose to study breast volume.

3D surface imaging can be used to determine most breast metrics with the woman in standing and sitting poses, provided the woman has minimal or no ptosis (the extent that the nipple sags below the level of the inframammary fold [IMF] and lower contour of the mammary gland and breast skin [Table 1]).²² However, the undersides of the breasts of women with moderate to severe ptosis are not completely visible in these positions and, therefore, cannot be imaged. The inability to measure the entire surface of the breast can lead to errors when trying to determine breast volume.² To overcome this problem, Hensler et al., advocated having the patient bend over a custom-made positioning frame in a prone-like, almost horizontal position to facilitate the complete capture of the surface of the breast.¹³ However, this position is not very useful for determining other breast metrics required for patient education, surgical planning, or outcomes analysis and cannot be compared to the findings of other studies.

Table 1.

Regnault Classification of Breast Ptosis²²

Ptosis Grade	Definition
01	Nipple, lower contour of the gland and skin brassiere lie above the IMF
1	Nipple lies at the level of the IMF, above the lower contour of the gland and skin brassiere
2	Nipple lies below the level of the IMF but remains above the lower contour of the gland and skin brassiere
3	Nipple lies below the level of the IMF and at the lower contour of the gland and skin brassiere

¹Regnault did not actually describe a grade 0 ptosis but it is frequently used by plastic surgeons when describing ptosis grade.

IMF, inframammary fold

A better alternative to the standing pose position may be a combination of standing and supine poses. Data acquired with the patient in different positions can be used to precisely outline the position of the IMF, especially for women with ptosis.²³ Moreover, the data could also have potential new benefits, such as fusing information from different positions to determine breast volume.

In addition, biomechanical breast models have been developed with the aim of investigating the changes in the shape of the breast that occur due to a change in the position of the subject, such as from the prone or supine to upright position. These models take into consideration that with changes in position the breast is subjected to gravity load, thereby altering breast shape.^24–27 Measuring changes to the shape of the breast under different gravitational loads could be used to develop a physics-based model of the breast to predict how different surgical procedures would alter its shape. Many current software packages available for analyzing 3D surface images of the breast are based on geometric models that compare shapes but do not allow for deformability, gravitational loading, and other physical effects.

An imaging system that enables the determination of breast metrics in different positions, especially in women with ptosis, could be used to plan and facilitate surgery and quantify breast aesthetic outcomes postoperatively and may facilitate the development of a proper physics-based calculation of breast shape under different loading conditions. In this paper we introduce a new 3D surface imaging system to image a patient’s breasts in positions ranging from standing to supine, validate its accuracy, and discuss its capabilities and limitations.

2. Methods

2.1. Equipment Design

3D surface images were obtained using a commercially available camera system (3dMDtorso™ Imaging System, 3dMD^® LLC, Atlanta, GA, http://www.3dMD.com), which for our purposes was custom designed by 3dMD to mount on a bariatric motorized tilt table. This imaging system enabled acquisition of 3D surface images of the subject’s breasts while she was tilted in a range of positions from standing to reclining at various angles, including supine.

2.2. 3dMDtorso Imaging System

The 3dMDtorso imaging system, referred to subsequently as the imaging system, utilizes a software-driven technique called active stereophotogrammetry to calculate the 3D surface image from a series of individual photographs generated from the system’s array of machine vision cameras synchronized by a trigger and control circuit. The imaging system incorporates four modular camera units (MCUs), and external white light flash units, positioned around the subject’s frontal torso region to achieve optimal surface coverage. The following components are mounted in each MCU: two monochrome stereo cameras, one color camera, an internal white light flash unit, and one white light speckle projector. To generate the 3D anatomical shape information, the software utilizes the photographs taken with the monochrome stereo cameras in conjunction wi th a random white light speckle pattern projected on the subject. To produce the associated color texture information, the software utilizes the photographs taken with the color cameras in conjunction with the external and internal white light flash units illuminating the subject. In the imaging system, all four of the MCUs and external white light flash units are synchronized for a 1.5 millisecond capture window. First the four white light speckle projectors are simultaneously triggered with the four pairs of monochrome stereo cameras. A half millisecond later, the four color cameras located in the center of each MCU are triggered in conjunction with the external and internal white light flash units. The active stereophotogrammetry technique software uses proprietary stereo triangulation algorithms to identify and match unique external surface features recorded by each pair of monochrome cameras, enabling the system to yield a single 3D surface image. Once the 3D anatomical shape contour information has been generated, another software algorithm then matches and merges the images from the color cameras to generate a corresponding texture map. The system automatically generates a continuous 3D polygon surface mesh with a single x, y, z coordinate system from all synchronized stereo pairs of the image. Depending on the mode the resultant 3D image in conjunction with the measurement software has been verified to consistently record a geometric accuracy of <0.2 mm RMS (root mean square).²⁸

2.3. Tilt Table

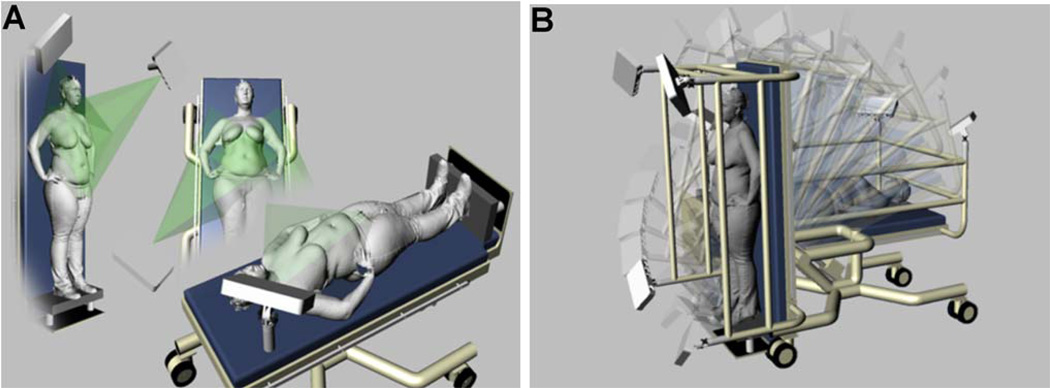
A Tri W-G TG2732 bariatric motorized tilt table (Tri W-G, Valley City, ND) was used to change the subject’s position prior to image capture. The table is 0.79 m wide, 2.07 m long and has a table top height of 0.88 m when the table is tilted at 0 degrees. The head of the table is 0.88 m from the floor when the table is tilted to 0 degrees and 2.07 m from the floor when tilted to 90 degrees with the subject in the standing (upright) position. The table frame is made of 0.0762 cm tubular heavy gauge steel, giving the table a weight capacity of 340 kilograms. Changes in table position are controlled by a handheld switch that activates an electric motor to tilt the table through a range of tilt angles. Patients stand on an attached footplate when the table is tilted to the 90-degree position (Figures 1A and B).

Figure 1.

(A) MCU positioning and projected coverage of the subject’s torso. (B) Customized imaging system can position the subject from supine (0 degrees) to standing (90 degrees) and any position in between.

2.4. Tilt Table Modifications

In order for the imaging system to acquire images of the subject’s torso at various inclines without needing to be recalibrated after each change in table position, a 0.0762 m tubular steel frame was designed, fabricated, and installed on the table to secure each MCU tightly in the desired position (Figure 1B).

The frame was designed to position an MCU at each corner of the table so that the subject’s breasts could be viewed and imaged from stereo viewpoints (Figure 1A). Each MCU was attached to adjustable, telescoping pivot mounts so that the MCU could be positioned for optimal viewing of the subject’s torso; this adjustability was especially important for women with a large abdomen and breasts.

2.5. Adjustable Platform to Accommodate Subject Height

The image volume of capture remains in the same location irrespective of the tilt angle of the table. To obtain optimum images of the torsos of short subjects, an actuator platform was added to the footplate of the tilt table, which can raise the subject as much as 0.1016 m. If the subject is less than 1.63 m in height, a detachable foot piece can be added to the actuator platform to raise them an additional 0.1016 m.

2.6. System Calibration

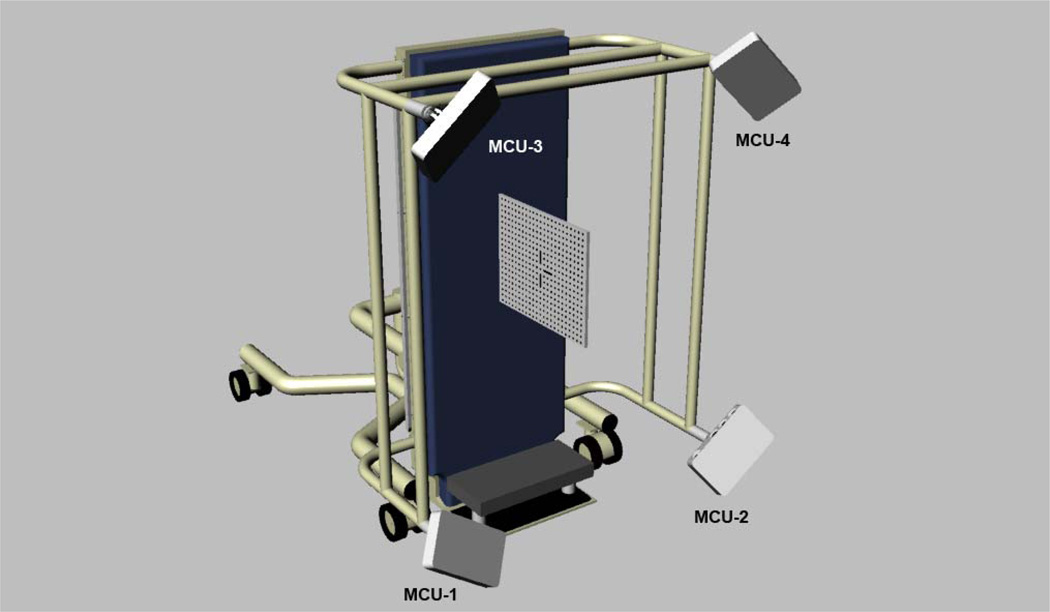
The imaging system was calibrated by having the algorithms use a known target, the 3dMD calibration plate, to compute all the parameters necessary to triangulate physical world points into digital 3D xyz coordinates. The calibration plate is 0.4826 m × 0.0696 m and the front is marked with a grid of precision dots and a central glyph. During the calibration routine (Figure 2), the imaging system acquires four image sets of the calibration plate positioned perpendicular to the tilt table with the front facing: (1) MCUs 1 and 2, (2) MCUs 2 and 4, (3) MCUs 3 and 4, and (4) MCUs 1 and 3. Next, the 3dMD acquisition software calculates the spatial coordinates of the cameras and notifies the operator that the system is ready for use. If for some reason the camera positions are outside of the necessary tolerances, the process is terminated, the operator is allowed to realign the cameras and the calibration, and the process is repeated.

Figure 2.

System calibration is obtained by acquiring 4 image sets of the 3dMD calibration plate positioned perpendicular to the tilt table in the upright (90 degree) tilt position. The front of the calibration plate is oriented for obtaining an image with MCUs 1 and 3. The orientation of the calibration plate is changed for acquiring images with the other MCUs as described in section 2.6 System Calibration.

The system was calibrated each day before images were obtained in case it had been moved during an unattended period. Calibration was not required between position changes on the table, as determined by previous trials.

2.7. Validation of 3D Surface Images Obtained from Tilt Table-Camera System

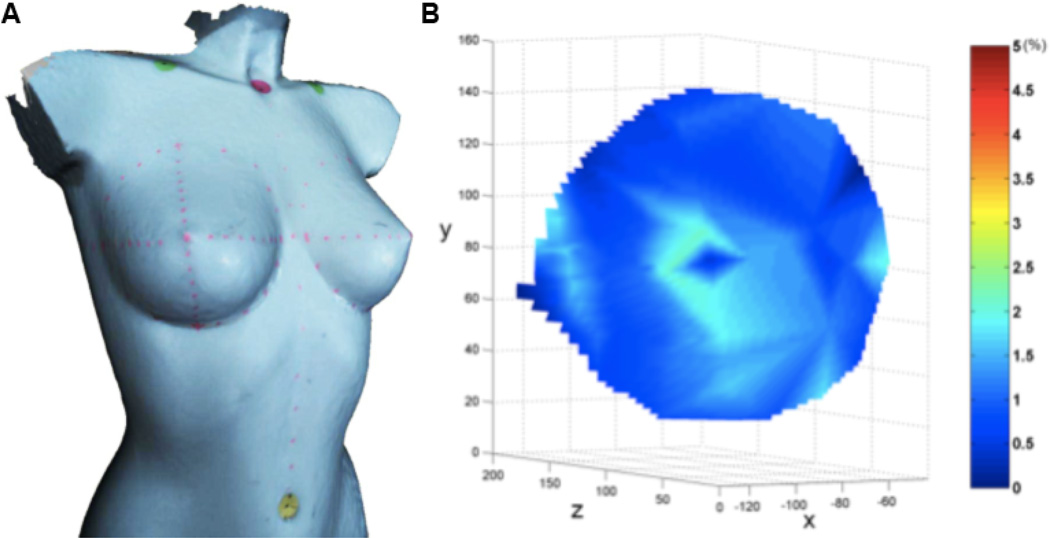
The accuracy of the registration of 3D images taken with the table tilted in different orientations was thoroughly tested using a hard plastic mannequin (Figure 3A). Unlike the human breast, the mannequin’s “breasts” do not change shape with changes in orientation of the tilt table. Similarly, the volume of the breasts should be constant at the varying positions. Thus, any differences in distances between fiducial points placed on the surface of the mannequin between images obtained in the upright and supine positions or in the volume estimates would arise from intrinsic errors in the measuring system as a whole; that is, errors from the camera, operator, image discretization, or computational measurements (e.g., those introduced by differences in picking fiducial marks for the images at the varying positions, for distance and/or volumes).

Figure 3.

(A) A 3D image of a rigid plastic mannequin in the upright position with marked breasts. (B) The percentage variation of error on the mannequin’s right breast, defined as the difference between distances of the same fiducial marks in the supine and upright positions normalized by the distance in the supine position that resulted from the comparison of 3D images in supine and upright positions.

The mannequin’s breasts were marked with a regular dot pattern (fiducial marks) and the mannequin was strapped to the tilt table with the patient safety straps. 3D images (point cloud + texture) of the mannequin were acquired in the supine through upright positions. The point-cloud density was increased using a Poisson reconstruction, which decreases the average distance between any two adjacent points from approximately 2 mm to 0.2 mm. Then, the positions of these same marks from each of the two 3D images corresponding to the supine and upright positions were identified and correlated. The marks selected on the surface of the mannequin’s breasts were used to calculate the error, defined as the differences in distance between the same fiducial marks in the supine and upright positions normalized by the distance between marks in the supine position (which is the average engineering strain along the line connecting the two points). Figure 3B shows the variation of this error on the surface of the mannequin’s right breast; the error is shown as contour plots projected on the upright image. Since marks were placed only sparsely on the mannequin, interpolation was used to determine the position identification error at other locations; this procedure results in greater errors in the regions with larger curvatures (such as near the nipple) and in geometric patterns as an artifact. These results point to the need to obtain position information at more closely spaced points on the breast. In the absence of shape changes in a rigid mannequin, this error should be zero; the error was indeed small, averaging less than one percent. This calculation of the error was repeated for images corresponding to other orientations between supine and upright, and the error was always within one percent.

2.8. Validation using Commissioned Volunteers (Subjects)

The torso anatomies of five female volunteer subjects were used for preliminary evaluation of the tilt table imaging system. None of the subjects were lactating or pregnant. The age, race, and other demographics of the female participants are listed in Table 2.

Table 2.

Demographics and Characteristics of Volunteer Subjects

	Subject A	Subject B	Subject C	Subject D	Subject E
Age	21	53	45	44	21
Race/Ethnicity	White/NH	White/NH	White/NH	White/NH	White/H
Height	1.65 m	1.65 m	1.59 m	1.59 m	1.55 m
Weight	55 kg	54 kg	66 kg	66 kg	87 kg
BMI	19	19.8	27	27	36
BFI	20.7	N/M	32.7	34.2	39.2
Bra size	32B	36B	34D	36C	38DD
Ptosis Grade	0	0	3	2	2
Previous Breast	None	Left breast	None	None	None
Surgery		TRAM flap

NH, Non-Hispanic or Latino; H, Hispanic; BMI, body mass index; BFI, body fat index; N/M, Not Measured

To determine the change in breast dimensions between fiducial marks, the surface of the breast was marked with a surgical marking pen in a regular pattern of radial lines emanating from the nipple, a set of circles nearly concentric with the areola, and a random pattern of dots, dashes, and lines.

2.8.1 Image Acquisition

The table was tilted 90 degrees from the horizontal position so that the subject could step onto the adjustable platform and face forward with her head, back, and shoulders placed firmly against the table pad (Figure 1A).

In addition to direct visualization of the subject on the table, the optimal imaging position was verified by visual inspection of the subject’s torso in the live camera views from each MCU, which provided additional guidance for optimal positioning before image acquisition. Each image was captured with the subject’s hands resting on her hips. Multiple 3D images of the torso of each subject were acquired with the table tilted at 0-, 45-, and 90-degree angles.

2.8.2 Quantitative Analysis of Breast Morphology

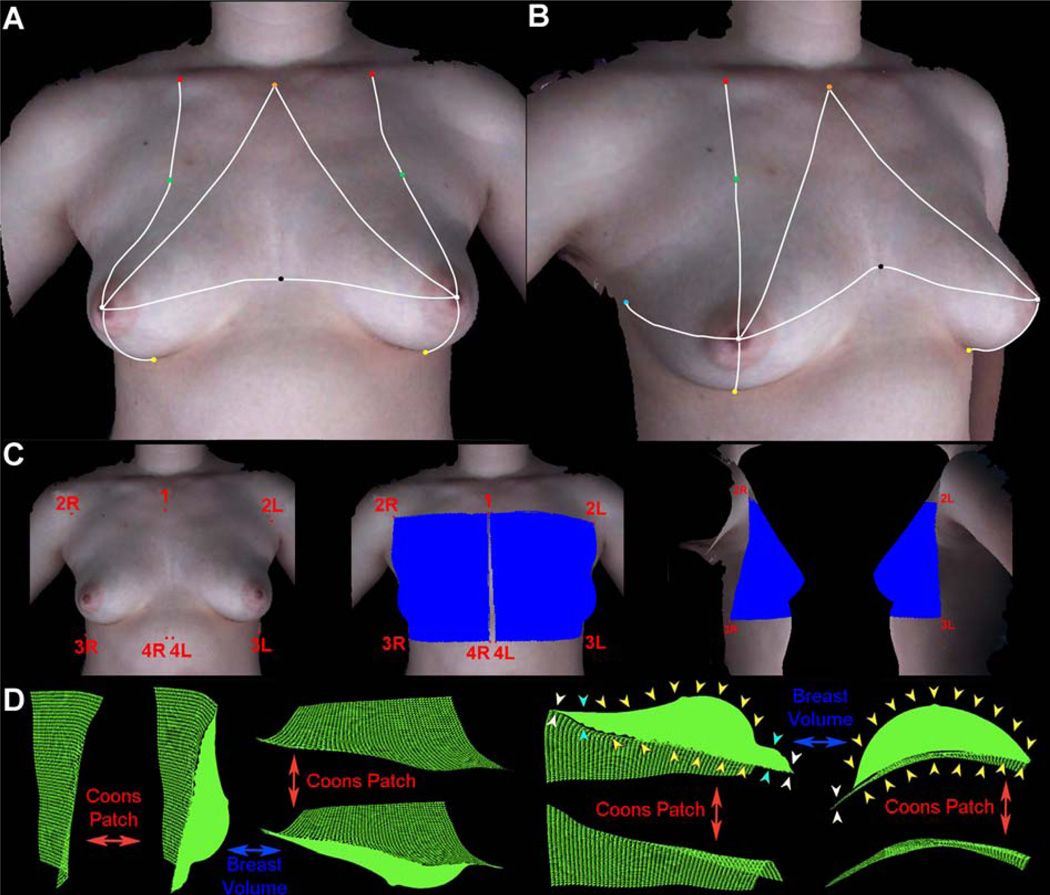
Distance measurements between pairs of six different fiducial marks, at the nipple (N), sternal notch (SN), midclavicle (MC), transition point (TP), lateral point (LP), and midline point (MP), were performed on the 3D surface images at different tilt positions to determine the effect of the tilt angle on breast morphometry. Distances were measured between the following fiducial marks: SN-N, MC-N, MC-TP, LP-N, and MP-N. Fiducial points for distance and landmark points for volume computation were manually annotated on the images by a student research assistant (JA) under the direction of the first author, and the contoured distances between the points and breast volume were measured using a customized software package as shown in Figures 4 a, b, & c. Our team has developed software for visualization, manipulation, and analysis of 3D surface data.^9,16,20,21 The analysis modules allow for manual annotation (via mouse click) of fiducial points on 3D images and computation of both distance (line-of-sight and contoured) and volume measurements. The visualization framework permits free full 360° rotation of the torso, thereby enabling the annotation of fiducial points with ease. Contoured distances were measured as the shortest geodesic path along the 3D surface of a subject’s torso between two points and computed using the “continuous Dijkstra” algorithm described by Mitchell et al.²⁹

Figure 4.

(A) Anterior-posterior view of a 3D image of Subject B in the supine position with fiducial points used in plastic surgery. (B) Left oblique view of a 3D image of Subject B in the supine position with fiducial points used in plastic surgery. The white lines indicate the geodesic distances between fiducials. Orange: sternal notch (SN), Red: midclavicle (MC), Green: transition point (TP), White: nipple (N), Black: midline point (MP), Yellow: inframammary fold point at the meridian (IMFp), and Light blue: lateral point (LP). The other marks on the image were used in a companion study³² to examine the variation of skin deformation at different regions of the breast. (C) Computation of breast volume. Landmark points for right (1, 2R, 3R, 4R) and left (1, 2L, 3L, 4L) used to delineate the region encompassing the breast mound. The blue regions show the surface area selected for breast volume determination in the front, right lateral, and left lateral views. (D) Different views of the region of the right breast extracted for volume determination are shown with the corresponding Coons patch. The Coons patch (green mesh) is a curved surface that parallels the surface curvature of the chest wall to establish the base of the breast mound. The computed volume comprises the volume of the space enclosed between the Coons patch and the surface of the breast mound (solid green silhouette). The yellow arrows on two of the views indicate the region between the surface of the breast and the underlying Coons patch that constitutes the volume. Note that the volume includes the region of the breast mound that projects above the underlying Coons patch, gradually increasing from the transition point (see cyan arrows), and then tapers off to zero at the area below the inframammary fold where the coons patch and the chest wall are flush against each other (see white arrows).

Volume measurements were made by first delineating the surface area of the breast mound via four landmark points located at the four corners enclosing the breast (see Figure 4c), as follows: (1) midline at the level of the TP (labeled 1), (2) axillary point at the level of the TP (labeled 2R and 2L), (3) a point at a level lower than the lowest visible point of the breast on the axillary side (labeled 3R and 3L), and (4) a point at paramedian, i.e., on either side of midline and an equal distance from midline, at a level below the lowest visible point of the breast (labeled 4R and 4L). These four points define four boundary curves, which are then used to computationally estimate a parametric surface known as “Coons patch”³⁰, which is widely used in computer aided graphic design³¹.

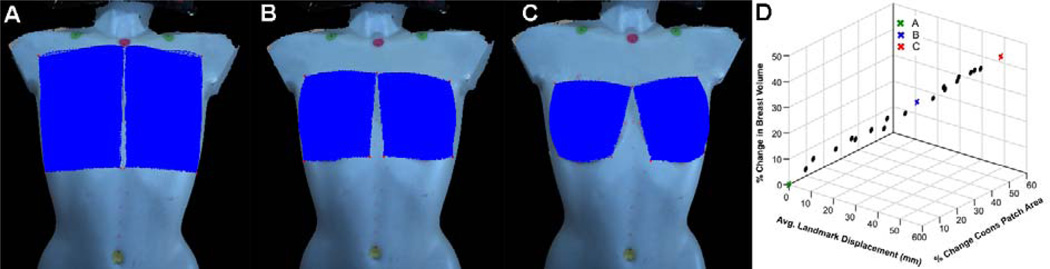
The computationally determined Coons patch is a 3D surface that parallels the surface curvature of the chest wall, thereby simulating the base of the breast (see Figure 4d). The total volume is then computed as the volume from the Coons patch to the skin surface of the breast.³² As seen in Figure 4d, only those regions of the breast that are raised above the Coons patch are included in volume computation. We evaluated the influence of landmark point placement for the Coons patch, on volume measurement. The volume of the right breast of the mannequin (Figure 5a) was computed by picking the four landmark points as described earlier (Figure 4c). Subsequently, the placement of the four landmark corner points was changed by choosing landmark points to create a series of inscribed patches of decreasing size. This analysis showed that an average displacement of approximately 3 cm for each of the four landmark points resulted in a 32.9% reduction in the surface area of the Coons patch, with a 29.2% decrease in volume (see Figures 5b and d), whereas an average displacement of approximately 5.5 cm for each of the four landmark points result in a 52.6% reduction in the surface area of the Coons patch, with a 45.9% decrease in volume (see Fig 5c and d).

Figure 5.

Effect of landmark point selection for Coons patch on the computed volume. (A) Volume computation with baseline Coons patch. (B) Coons patch reduced in surface area by 32.9% by an average displacement of ~3 cm for each of the four landmark points. (C) Coons patch reduced in surface area by 52.6% by an average displacement of ~5.5 cm for each of the 4 landmark points. (D) Plot of percent change in volume of breast and surface area of Coons patch, versus the average displacement of each of the four landmark points.

3. Results

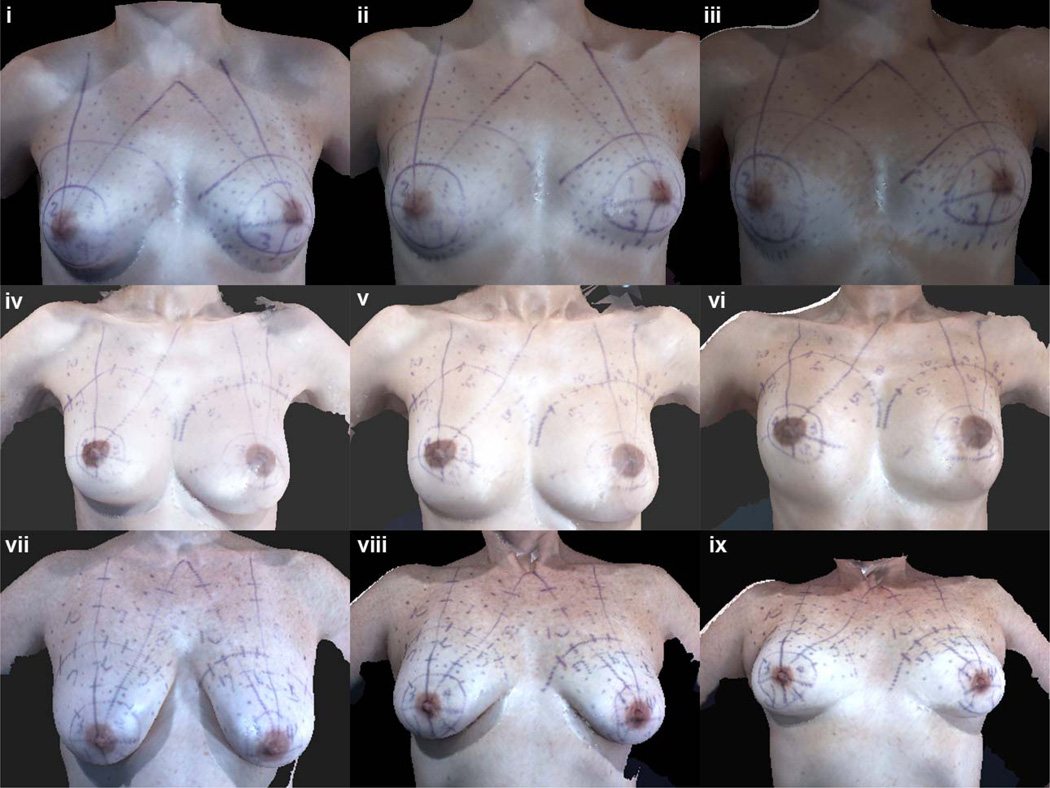
Typically, quantitative assessments of breast morphology include the use of distances between fiducial points to define appearance in terms of measures such as symmetry and ptosis. We evaluated the influence of the different tilt positions on breast morphometry by comparing the distances between fiducial points. Visualization of the torso images at different tilt angles indicated shape changes in breasts due to the displacement of the soft tissues of the breast (see Figures 6 i–ix). Note that the IMF is visible in images at the upright position in Subjects A and B with no ptosis, whereas in Subject C, the IMF is visible only in the supine position.

Figure 6.

Frontal views of 3D images of women with different degrees of breast ptosis and histories of breast surgery. For each subject, the left image was taken with the table tilted to 90° (upright), the center image was taken with the table tilted to 45°, and the right image was taken with the table tilted to 0° (supine). As seen here, the inframammary fold is only visible for the subjects with no ptosis in the upright position. For Subject C, with grade 3 ptosis, the inframammary fold can only be visualized in the supine position. (i–iii) Subject A (no history of breast surgery, grade 0 ptosis), (iv–vi) Subject B (history of TRAM flap reconstruction of left breast, grade 0 ptosis), and (vii–ix) Subject C (no history of breast surgery, grade 3 ptosis).

As the subjects were tilted from 90 to 0 degrees in Figure 6, their breasts became more rounded, the entire IMF became visible, there was more upper pole fullness between the nipple and clavicle as shown by a change in the shape of the MC to N line from straight or concave to convex as the distance between MC and N decreases, and there was a decrease in the amount of breast projection. Additionally, the breasts shifted superiorly toward the clavicles and laterally to some degree, as noted by the increased distance between the nipples.

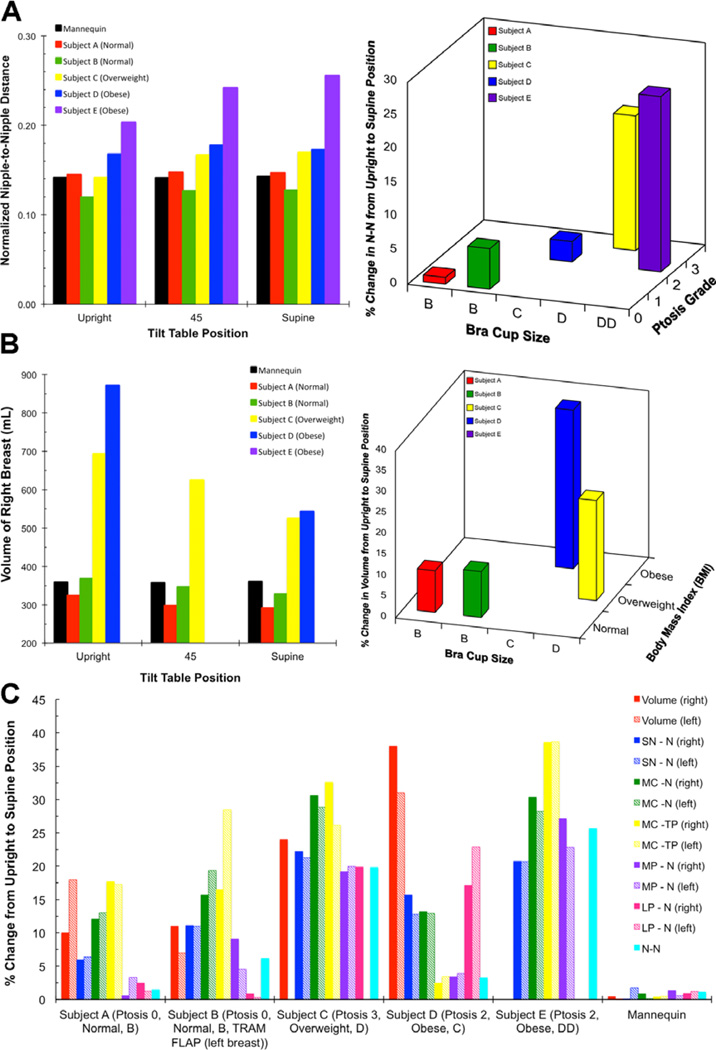
The morphometric measurements indicated changes (percentage increase or decrease) in the distances between fiducial marks as the torso was moved from the upright to the supine position. Figure 7 shows plots of various distance and volume measurements on the mannequin and subjects. Both the distance (Figure 7a) and the volume (Figure 7b) measurements of the mannequin were relatively constant across the varying tilt positions, whereas in the subjects’ differences were observed for both measures at various tilt positions (Figure 7a–c). One would expect a patient’s actual breast volume to remain unchanged at different tilt positions, whereas changes in the distance measures are expected as fiducial points on soft tissues are displaced as the subject is moved from the upright to the supine position. As seen in Figure 6 and 7, the breast changes in both the distance and volume measures with position change. Two factors contribute to changes in volume with position change: (1) the soft tissue comprising the volume of the breast is displaced both superiorly and laterally with position change, and (2) it is not always feasible to completely capture the displaced tissue within the landmark points used to delineate the breast for volume measurements.

Figure 7.

(A) Left: Plot of N-N distance measured at three different tilt angles in the mannequin and the 5 subjects, Right: Plot of the percentage change in N-N distance from upright to supine position with respect to the bra cup size and ptosis grade. (B) Left: Plot of volume of right breast measured at three different tilt angles in the mannequin and 4 subjects (volume for Subject D at 45° and volume for Subject E at all positions could not be determined due to image artifacts related to large size of breast), Right: Plot of the percent change in volume of left breast from upright to supine position with respect to the bra cup size and BMI. (C) Plot of percent change from upright to supine position for all distances and volumes measured on the 5 subjects and the mannequin. The exceptions for volume measured are for the left breast of Subject C (all positions) and those listed in 7 B above.

Morphometric features of the breast, such as size and ptosis, and the subject’s body mass index (BMI) influenced the amount of change observed with position change for both the geodesic distance and volume measures. The larger the breast, the more dramatic the change for each metric measured. For example, Figure 7a presents a plot of the N-N geodesic distance measured at different tilt positions (left panel) and the percent change in the N-N distance between the upright and supine positions with respect to the ptosis grade and bra cup size of the subjects (right panel). Note that the largest change in the N-N dist ance was observed for subject E, who had a bra cup size of DD. Similarly, there was a measured decrease in breast volume from the upright to the supine position for subjects A–D. As seen in Figure 7b, the percent change in the breast volume from the upright to the supine position was found to be relatively constant, in the range of 10–15%, for subjects with a BMI that was normal (18.5–24.5 kg/m²). However, with an increase in BMI (overweight [25–29.9 kg/m²] or obese [>30 kg/m²]), the percent change in volume was almost twice as high, in the range of 30–40%. Unfortunately, the breast volume for subject E could not be determined due to image artifacts related to the size of her breasts.

Figure 7c provides a plot of the percent change in all of the distance measures and all but one of the volume measures from the upright to the supine position for all subjects and the mannequin. It can be seen that both breast aesthetics (such as size and ptosis) and the subject’s BMI can influence the distance and volume metrics. We observed higher fold differences in the distance measures across the different tilt positions for those distances that involved the fiducial points located on soft tissues such as the nipple. These findings conform to our visual observation of the nipple being displaced as the subject is tilted (Figure 6). Similarly, for distances that included a relatively stationary fiducial point such as MC, which is located over a bony landmark, the change in distance from upright to 45 degrees was less striking.

4. Discussion

We have shown t hat a 3D imaging system mounted to a tilt table can be used to reliably capture images of the human female torso in the upright to supine positions without needing to recalibrate between position changes. Reliability was established by demonstrating image registration of mannequin images to within 1% error, and distance and breast volume measurements to within 2% variation in two tilt positions. This study also shows that the distances between specific fiducial points and the nipple can change dramatically with respect to the change in the subject’s position and that the metrics with the subject standing can be correlated to the same metrics in the supine position and positions in between.

Provided the shoulders stay in the same fixed position, the changes in breast morphology that occur with position change of the torso are caused by changes in the vector of body orientation with respect to gravitational load. Displacement of the normal non-lactating breast with position change of the torso is limited primarily by breast volume, biomechanical qualities of the anatomical structures comprising the human breast, and to some degree, the retromammary space, a gliding plane between the posterior side of the breast and the anterior side of the superficial layer of the fascia of the pectoralis major muscle. This became evident from both the visible changes in Figure 5 and the linear and volume changes measured with position change observed in Figure 6 of this study.

Although the actual volume of the breast should remain the same irrespective of the change in position, the “apparent” change in breast volume as the subject’s torso changes from the upright to supine position appears to be due primarily to the movement of the breast tissue superiorly towards the clavicle and posteriorly towards and into the axilla. As shown in Figure 5, we validated that smaller variations in landmark placement do not influence volume computation. For example, an average displacement of approximately 5 mm for each of the four landmark points resulted in only a 3.5% reduction in the surface area of the Coons patch, with a 5.9% decrease in volume. Annotating landmark points for volume computation for both the upright and supine positions are highly unlikely to result in point placement discrepancies > 1 cm. Thus, the percent change in volume of 30–40% in subjects with a high BMI can be attributed to changes in mammary gland tissue movement rather than landmark point placement. It should also be noted that the computationally determined breast volume includes the volume enclosed between the estimated curved surface of the chest wall at the base of the breast to the imaged surface of the breast. Typically, the computationally estimated volume underestimates the actual volume since it is not feasible to include the breast volume from behind the Coons patch to the underlying pectoralis major muscle and ribs.

The qualitative displacement of the breast toward the clavicle that can be seen in images of the subjects in Figure 6 was also quantitatively confirmed by a decrease in breast volume in Figure 7b and a decrease in distances between the fiducials SN-N, MC-N, and MC-TP in Figure 7c. The lateral displacement of the breast towards and into the axilla can be seen by an increase in nipple displacement laterally in Figure 7a and the fiducials MP-N in Figure 7c. These displacements can be attributed to the corresponding displacement of fiducial points such as N and TP when moving from the upright to the supine position, since these points are anatomically located on the soft tissues of the breasts. Distances measured between fiducial points that are on soft tissues, such as the N-N distance, are more susceptible to change with change in position than distances between fiducial points that are located on anatomically bony landmarks, such as MC-MC, which are relatively stable between the upright and supine position.

Breast volume and linear distances between fiducial points are usually measured preoperatively with the patient in a standing position and arms at her sides. Conversely, breast surgery is performed with the patient in the supine position and arms abducted from about 45 to 90 degrees from the torso. Prior to this study, a patient’s breast metrics obtained in a standing position could not be correlated well with her breasts when she was supine and, thus, were of limited use to the plastic surgeon during surgery. Although the patient can be placed upright on the operating table by flexing the hips to 90 degrees^33,34, most anesthesiologists will not sit the patient up more than about 60–70 degrees from the supine position due to concerns about patient safety. Additionally, when the hips of obese patients are flexed to 90 degrees from the supine position, the protuberant abdomen usually interferes with breast position, especially if the patient has pendulous breasts. Thus, the ability to correlate the breast metrics taken in the standing position to other positions may facilitate cosmetic and reconstructive breast surgery.

As this is the first time that a tilt table-3D camera system has been described, there are no other studies in the literature with which to compare findings. Studies by Catanuto et al.¹⁰ and Ericksen et al.¹² used only the upright sitting position for the 3D surface imaging.

Limitations of the tilt table-3D camera system are still being determined. Prior to using the tilt table, we imaged the torsos and breasts of patients in the standard upright position and noticed problems visualizing the IMF of most patients with ptosis grade 2 or higher, the lower sternal areas of some patients with large breasts, and the lateral breast and upper abdomen of some obese patients with a BMI of about 30 or higher. With the tilt table-3D camera system, we did have some problems visualizing the IMF of subjects C, D, and E in the upright and 45-degree positions, but not in the supine position. Although we did not have problems visualizing the lower midsternal area for subject E, we did have image artifacts associated with the lateral breast area for this subject in the standing and 45-degree positions. This has led us to begin testing other arm placements during imaging, such as arms abducted 45 degrees with forearms and palms flat against the table and arms abducted 90 degrees from the torso, similar to surgery. Further research needs to be done to determine the limitations of this imaging system when imaging women with ptotic pendulous breasts and obese women with large bra cup sizes. However, it should be noted that imaging artifacts associated with imaging women with larger BMIs are not specific to the tilt table system described in this study but are also inherent with the conventional 3dMD Torso system.

In conclusion, this study presents a new tool that allows researchers to acquire 3D images of the human breast in upright through supine positions. By using established fiducial marks, researchers can reliably obtain accurate measurements between fiducials and use the data for surgical planning in breast surgery. These images also enhance the potential to develop a physics-based finite element model of the human breast. A physics-based model of the breast has been the goal of many researchers who want to simulate the mechanical deformations of the breast that occur with imaging procedures used in the evaluation of breast cancer. Working toward that goal, we have examined the movement of numerous closely-spaced Lagrangian fiducial markers placed on the breast and identified the spatial variation of skin deformation in different portions of the breast resulting from a change from supine to upright.³⁵

Highlights.

• A 3D camera-tilt table (system) was used to image breasts at different angles.

• We describe the methods used to validate the imaging system.

• The system can determine quantitative changes in breast morphology.