Abstract
A five-state model of myofilament contraction was integrated into a well-established rabbit ventricular myocyte model of ion channels, Ca2+ transporters and kinase signaling to analyze the relative contribution of different phosphorylation targets to the overall mechanical response driven by β-adrenergic stimulation (β-AS). β-AS effect on sarcoplasmic reticulum Ca2+ handling, Ca2+, K+ and Cl− currents, and Na+/K+-ATPase properties were included based on experimental data. The inotropic effect on the myofilaments was represented as reduced myofilament Ca2+ sensitivity (XBCa) and titin stiffness, and increased cross-bridge (XB) cycling rate (XBcy). Assuming independent roles of XBCa and XBcy, the model reproduced experimental β-AS responses on action potentials and Ca2+ transient amplitude and kinetics. It also replicated the behavior of force-Ca2+, release-restretch, length-step, stiffness-frequency and force-velocity relationships, and increased force and shortening in isometric and isotonic twitch contractions. The β-AS effect was then switched off from individual targets to analyze their relative impact on contractility. Preventing β-AS effects on L-type Ca2+ channels or phospholamban limited Ca2+ transients and contractile responses in parallel, while blocking phospholemman and K+ channel (IKs) effects enhanced Ca2+ and inotropy. Removal of β-AS effects from XBCa enhanced contractile force while decreasing peak Ca2+ (due to greater Ca2+ buffering), but had less effect on shortening. Conversely, preventing β-AS effects on XBcy preserved Ca2+ transient effects, but blunted inotropy (both isometric force and especially shortening). Removal of titin effects had little impact on contraction. Finally, exclusion of β-AS from XBCa and XBcy while preserving effects on other targets resulted in preserved peak isometric force response (with slower kinetics) but nearly abolished enhanced shortening. β-AS effects on XBCa vs. XBcy have greater impact on isometric vs. isotonic contraction, respectively.
Keywords: β-adrenergic, myocyte model, contractile model, Ca2+ sensitivity, cross-bridge cycling
1. Introduction
β-adrenergic stimulation (β-AS) is an important physiological modulator of cardiac activity, increasing peak force (inotropy) and the rate of force development and relaxation (lusitropy). β-AS raises intracellular cAMP levels, activating protein kinase A (PKA), which in turn phosphorylates key proteins involved in excitation-contraction (E–C) coupling. These include the L-type Ca2+ channel [1, 2] and phospholamban (PLB), respectively increasing Ca2+ entry into the cytoplasm and sarcoplasmic reticulum (SR) Ca2+ reuptake by the SR Ca2+-ATPase2a (SERCA2a) [3, 4], and these effects contribute to increased SR Ca2+ content, inotropy and lusitropy. High SR Ca2+ load also increases Ca2+ leak and fractional Ca2+ release during E-C coupling [5]. β-AS can increase the probability of ryanodine receptor Ca2+ release channel (RyR2) opening in response to cytosolic Ca2+ [6], but that may be mediated more by Ca2+/calmodulin-dependent protein kinase II (CaMKII) activation, downstream of nitric oxide synthase (nNOS) or Epac (exchange protein activated by cAMP) [7–11]. K+ channels are also targets of PKA phosphorylation and can shorten action potential (AP) duration (APD) [12, 13] during β-AS.
At the myofilaments, PKA phosphorylates troponin I (TnI) and myosin binding protein-C (MyBP-C) [14–17]. Although experimental studies have attempted to link specific contractile effects of β-AS to specific TnI and MyBP-C phosphorylation sites, precise roles in altering myofilament Ca2+ sensitivity (XBCa) and cross-bridge (XB) cycling rate (XBcy) are still debated. Some studies have suggested that PKA phosphorylation of TnI predominates in both decreased XBCa and enhanced XBcy [18], and the optimization of cardiac function at different heart rate, load and inotropic state [19]. Conversely, it was postulated that TnI and MyBP-C phosphorylation have separate effects on XBCa and XBcy [20, 21], a shared responsibility in PKA-dependent decrease of XBCa [22, 23], or a central role of MyBP-C in the PKA-dependent increased XBcy kinetics [22]. However, the relative PKA effects of these two proteins on twitch contractions, Ca2+ transients and APs is lacking. A computational model, as we describe here, can be a valuable complementary tool for further analysis of the impact of XBCa and XBcy and their interaction during β-AS induced inotropy.
Myocyte models have evolved from mathematical descriptions of ion channels to detailed formulations of Ca2+ transport mechanisms [24, 25], cell compartmentalization [25, 26], cell signaling pathways [27–30], metabolic processes [31], and pH regulation [32]. Even though mechanical models of the cardiac muscle have been developed [33], they have typically been divorced from electrical/Ca2+ handling models [34–37]. Some studies have begun to fill this gap, including descriptions of length and force-dependent processes of Ca2+-induced XB formation [38] and length-dependent activation [39], but most have been limited to myocyte ion handling and electrophysiological descriptions [27, 29, 40].
The purpose of this study is three-fold: (1) to help clarify unresolved questions of how altered Ca2+ sensitivity and XB cycling rate interact during β-AS in ventricular myocytes (and how putative TnI and MyBP-C effects may interact), (2) to provide a new quantitative framework to study the complex interaction of β-AS dynamic effects on Ca2+ transient, AP, and contractile properties, which are not well resolved, and (3) to provide a freely available new tool for all investigators to further study these aspects. We have built the β-AS effect on our prior detailed contraction model [37] and incorporated that into an updated Soltis-Saucerman model [29], which integrates the Shannon-Bers Ca2+-electrophysiological myocyte model [25] with dynamic descriptions of CaMKII and PKA signaling pathways [28, 41] and dynamic target phosphorylation.
2. Methods
2.1 Generation of XB force
Our previously described mechanical model [37] has been slightly modified. It represents a muscle or myocyte as a series arrangement of units, each defined by the half-sarcomere length and the muscle cross-sectional area. The half-sarcomere is composed of inextensible thick and thin filaments in parallel with an internal elastic load (Fig. 1A). The thick (ThF) and thin filaments (Tf) can slide past each other defining a zone of overlap where XBs can attach to the thin filament. According to the XB theory, attached XBs act as independent force generators, occupying different states in the XB cycle [42]. Individual XB force is fi = a × hi, where a is the elastic constant of one attached XB and hi = XB elongation. Then, total XB force (Ft) is:
| (1) |
where N is number of attached XBs, N × a represents the elastic constant corresponding to the pool of attached XBs and h is the mean elongation of all XBs. Thus, Ft is the force of an equivalent XB, representing all attached XBs, and h is the equivalent XB length.
Figure 1.
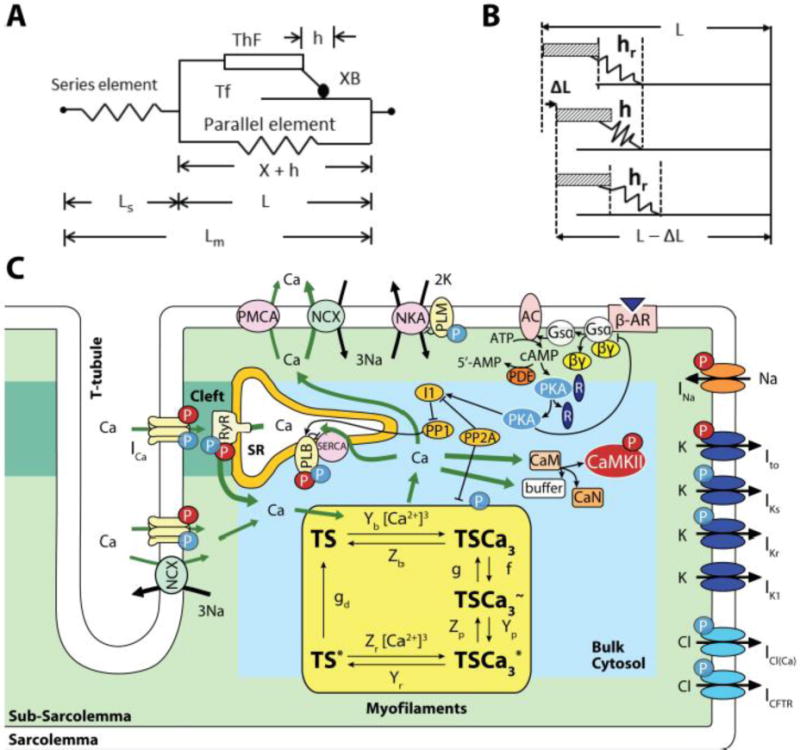
Model. A: Constitutive muscle unit, consisting of half-sarcomere length (L) composed of thick (ThF) and thin (Tf) filaments in parallel with an elastic element. The equivalent cross-bride (XB) representing all attached cross-bridges is part of the ThF. It attaches to the Tf by the mobile end of its elastic structure, with h elongation, defining an inextensible half-sarcomere length X = L − h. A series elastic element with length Ls accounts for compliant muscle ends and together with L make up total muscle length (Lm). B: Cross-bridge dynamics showing steadystate XB elongation (hr), its decrease due to ΔL and later return to hr at shorter half-sarcomere length (L-ΔL). C: Four compartment myocyte model: Bulk Cytosol, Cleft, sarcoplasmic reticulum (SR) and subsarcolemmal space (Sub-SL) [25, 29] with ion currents as described by these authors. This model is coupled to the myofilament force development model consisting of 5-state troponin systems (TS) with Ca2+ binding. Each TS is composed of three adjacent troponin–tropomyosin regulatory units able to act cooperatively to bind Ca2+ in three successive steps. Troponin systems are: free TS; Ca2+ bound to TS without attached XBs (TSCa3), Ca2+ bound to TS with attached XBs in the weak state (TSCa3~), Ca2+ bound to TS with attached XBs in the power state (TSCa3*), and TS without Ca2+ with attached XBs in the power state (TS*). Baseline mechanical parameters and all changes used for ISO are in Table 1.
Total XB force is normalized for cross-sectional area (Fb) measured at a defined reference state:
| (2) |
where reference area = volr/Lr with volr = half-sarcomere volume of myoplasmic compartment (Bulk Cytosol) containing the mechanical elements and Lr = half-sarcomere slack length, i.e, resting conditions for force close to zero. Then, substituting Eq. 1 into Eq. 2 gives:
| (3) |
Since N = Avogadro’s number (A) × (moles of attached XBs), it can be expressed as:
where [XB] is total attached XB concentration (see Ca2+ kinetics). Replacing N in Eq. 3:
Grouping A × a × Lr and changes in concentration units into Ae, results in:
| (4) |
The equivalent XB is considered to be situated at the free end of the half myosin filament. Consequently, in the model, half-sarcomere length (L) has two components: an elastic component (h) and a non-elastic component (X) formed by the half-sarcomere thick filament and the parts of the thin filament not overlapping either with the thick filament or h (Fig. 1A). Then:
| (5) |
We assume that individual XBs attach and detach cyclically and asynchronously from the thin filament, but the equivalent XB remains attached while there is at least one attached XB. In steady state conditions, the equivalent XB has a constant length hr and during a quick sarcomere shortening equal to ΔL, h instantly absorbs this length change (Fig. 1B), so: h = hr − ΔL.
The equivalent XB then detaches and reattaches in a different position along the thin filament to return to hr. This is represented as sliding of the point of attachment of the equivalent XB to reproduce the asynchronous behavior of individual XBs. Thus, the return to hr produces a change in X expressed as the differential equation:
| (6) |
and substitution by Eq. 5 gives:
| (7) |
where dX/dt is the velocity of motion of the mobile equivalent XB end and B is the involved parameter [43]. The sliding movement can also be expressed from the derivation of Eq. 5 and substitution by Eq. 7 as:
| (8) |
Thus, once shortening ends, dL/dt = 0 and in Eq. 8 returns h exponentially to hr. Similar criteria apply to the description of muscle stretching and concomitant XB elongation.
Similarly to our previous model [37], two states of attached XBs are defined: XBw (weak state, with h = hw), a state in which the equivalent XB is attached to the filament but has not yet developed the power stroke, and XBp (power state, with h = hp), a state in which the equivalent XB can develop the power stroke [36]. Contrary to XBp, XBw elongation hwr is assumed close to zero in steady state conditions. However, when the muscle shortens or stretches, the XBw elastic element is passively stretched, hw ≠ 0, and XBw respectively contributes negatively or positively to Fb. Then, according to Eq. 4, total XB force becomes:
| (9) |
where Aw and Ap are elastic constants for the weak and power states. According to this assumption Eq. 5 becomes:
and
showing that for the same L, the inextensible X lengths and the equivalent XB elastic lengths differ according to the XB state. Similarly, from Eq. 8, the two equivalent XB kinetic equations are:
| (10) |
| (11) |
where Bw and Bp are the weak and power parameters.
2.2 Parallel and series elasticity
As shown in Fig. 1A, the muscle unit includes an undamped parallel elastic element that symbolizes the sum of the non-linear titin and the linear cellular passive element components attributed to intermediate filaments (Fig. S1); then, parallel elastic force (Fp) results as:
| (12) |
where Ke and Le, respectively represent titin and cellular element elasticities for Fp normalized by cross-sectional area, and Lo is slack length (L for Fp = 0). Then, total muscle force (Fm) is the sum of Fb plus the force needed to stretch Fp:
An elastic element in series with the muscle (Fig. 1A) is added to describe compliant muscle ends, producing elastic force Fs:
| (13) |
where α and β are parameters defining the elastic relation and Ls is series elastic length, showing that changes in Fm produced by Fb elicit changes in Ls. Then, total muscle length (Lm) results as:
Therefore, according to the model, in isometric conditions, changes in Fm produced by Fb generation trigger changes in Ls and hence in L because Lm is constant. Variations in L then lead to h changes whose return to hr is achieved through Eq. 6. In isotonic conditions, where Fm is constant, Fb and Fp change due to L variations, and again these L changes lead to h adjustments with the ensuing return to hr through Eq. 6. Finally, in isosarcometric contractions L is constant, Ls = 0, and consequently Lm = L [37].
2.3 Myofilament Ca2+ kinetics
Ca2+ kinetics is represented by five states of troponin systems (TS) (Fig. 1C), which is a slight simplification of the prior six state model [37], by condensing an intermediate state (TS~) into the TS* to TS transition. Each TS is defined as 3 adjacent troponin-tropomyosin regulatory units (RU) [36], so that each can bind one Ca2+ ion (TSCa, TSCa2, TSCa3). In this scheme, Ca2+ binding to the three RU within one TS is cooperative, and we assume that all three Ca2+ bind in one step (so only TSCa3 is indicated) driven by the on- and off-rate constants (Yb and Zb, Fig. 1C), where [Ca2+]i is free Ca2+ concentration in the bulk cytosol. It is further postulated that XB attachment takes place when Ca2+ RUs are fully activated and driven by the forward (f) and reverse (g) rate constants. The five TS states are thus: TS (free); TSCa3 (Ca2+ bound to TS, without XB attachment), TSCa3~ (weak binding XB (XBw) with Ca2+ bound to TS), and TS* (attached XBs in the power state (XBp) involving TS without Ca2+). Because force depends on attached [XB], Eq. 9 results as:
| (14) |
and redefining Ap and Aw to include the common factor 3 gives:
| (15) |
Rates of change of TS states (Fig 1C) are described by the following differential equations:
| (16) |
| (17) |
| (18) |
| (19) |
and introducing [TSt] as total concentration, the five TS can be expressed as:
| (20) |
where Yb, Zb, f, g, Yp, Zp, Yr, Zr, and gd are reaction rate parameters with subscripts b, p, r and d respectively related to binding of Ca2+, power state transition, reversal of Ca2+ binding and dissociation of XB (Fig 1C).
The model utilizes three length-dependent reaction rate parameters. The first is the sarcomere attachment rate function which accounts for XB attachment in the zone of overlap between thick and thin filaments [42]:
| (21) |
where La is the optimal overlap length for maximum XB attachment, Ya is maximum f for L = La and Ra commands the kurtosis of the curve, changing the effective zone of overlap between thin and thick filaments [37, 43]. The second is the redefined velocity-dependent XB detachment rate constant g, with the asymmetrical detachment behavior postulated by Huxley [42] (Fig. 2A):
| (22) |
where Yh is the detachment function characterized as
Figure 2.
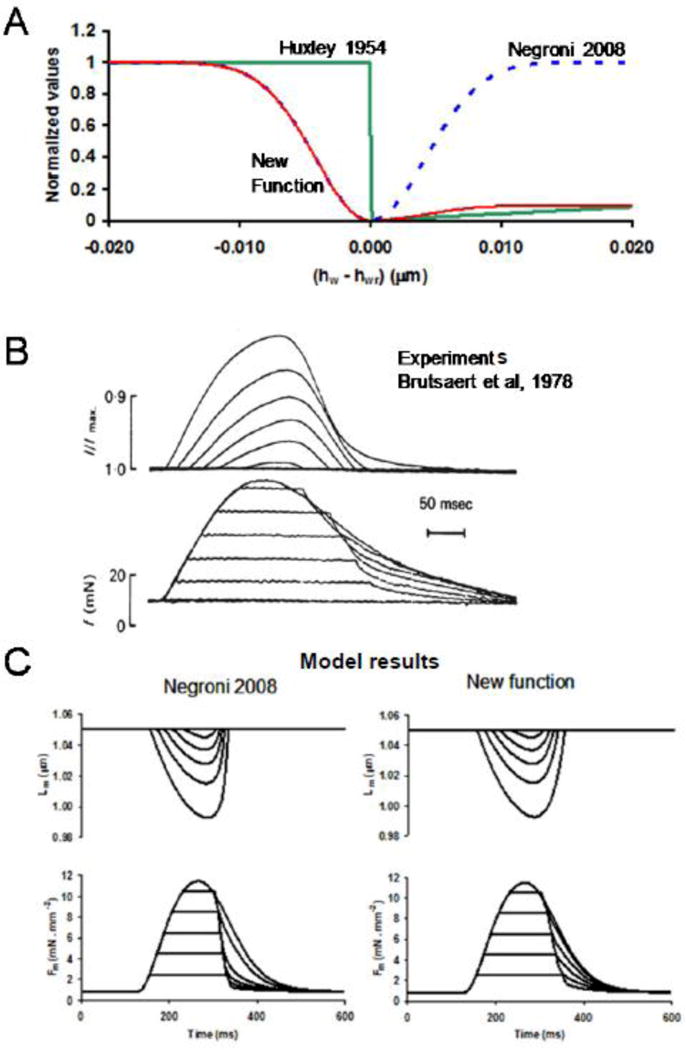
Asymmetrical detachment function validated by its effect on afterloaded contractions. A: Normalized detachment as a function of the difference between weak (hw) and steady state weak (hwr) XB length. The previous symmetrical detachment function [37] based on the proposition of Slawnych et al. [44] was corrected, incorporating the asymmetry (New function) postulated by Huxley [42]. B: Experimental afterloaded contractions from Brutsaert et al. [86]. C: Simulation of myocyte afterloaded contractions with Negroni et al. detachment function [37] and the new detachment function, resembling more accurately the experimental reports.
| (23) |
In Eq. 23, (1 – e−γ(hw – hwr)) represents the symmetrical detachment function used by Slawnych et al. [44] where γ defines the kurtosis of the curve and sarcomere L velocity dependence through (hw-hwr), Fh provides asymmetry [42] (with Fh = 0.1 or Fh = 1 for hw > hwr or hw < hwr, respectively), Yv amplifies the detachment effect, and Za is a constant representing the value of g when hw = hwr. This more accurate g description resulted in improved simulation of afterloaded contractions (Fig. 2B). The third is the sarcomere length-dependent rate function of XB detachment from TS* to TS given by:
| (24) |
where Lc determines the range of sarcomere length around which gd varies, Yc defines the rate of change of gd, and Yd is the value of gd for L = Lc. This equation represents the lattice space effect on the rate of XB detachment whereby gd decreases at larger lengths reducing lattice space [45].
To express Ca2+ binding and buffering by myofilaments, the low affinity troponin C (TnClow) Ca2+ buffer in the Soltis-Saucerman model [29] (from the Shannon-Bers model [25]) was interpreted as the sum of change of all TS bound to Ca2+:
| (25) |
expressing buffer action dependence on the contractile machinery and hence on Lm and Fm and the mode of contraction.
Table 1 shows the classification of contractile parameters. One group of parameters is structural (Strct). A second group of parameters corresponds to XBCa, involving the rate constants Yb, Zb, Yr and Zr acting in transitions where there are only changes in Ca2+ binding to TS with no modifications in the XB force generating capacity. The third group of parameters comprises XBcy rate constants Zp and Yp, and parameters related to rate functions g, f, and gd, acting in transitions of XB attachment and detachment, altering the force generating capacity and cycling rate without producing changes in Ca2+ binding to TS.
Table 1.
Mechanical parameter classification and values.
| Role | Symbol | Defining Eq. | Units | Value | Effect of 100 nM [ISO] |
|---|---|---|---|---|---|
| Strct | Ap | 9, 14, 15 | mN mm−2 μm−1 μM−1 | 2700 | |
| Strct | Aw | 9, 14, 15 | mN mm−2 μm−1 μM−1 | 540 | |
| Strct | α | 13 | mN mm−2 | 0.5 | |
| Strct | β | 13 | μm−1 | 80 | |
| Strct | Ke | 12 | mN mm−2 μm−5 | 105000 | 50% decrease [56] |
| Strct | Le | 12 | mN mm−2 μm−1 | 10 | |
| Strct | Lo | 12 | μm | 0.97 | |
| Strct | [TSt] | 20 | μM | 23 | |
|
| |||||
| XBCa | Yb | 16 | μM−3 ms−1 | 0.1816 | |
| XBCa | Yr | 18, 19 | ms−1 | 0.1397 | 2.2-fold increase [18–22, 63] |
| XBCa | Zb | 16 | ms−1 | 0.1397 | 4.2-fold increase [18–22, 63] |
| XBCa | Zr | 18, 19 | μM−3 ms−1 | 7.2626 | 80% increase [18–22, 63] |
|
| |||||
| XBcy | Bw | 10 | ms−1 | 0.35 | 3.4-fold increase [18–22, 63] |
| XBcy | Bp | 11 | ms−1 | 0.5 | 3.4-fold increase [18–22, 63] |
| XBcy | hpr | 11 | μm | 0.006 | |
| XBcy | hwr | 10, 23 | μm | 0.0001 | |
| XBcy | Fh | 23 | adimensional | 0.1 or 1 | |
| XBcy | γ | 23 | μm−2 | 28000 | |
| XBcy | La | 21 | μm | 1.15 | |
| XBcy | Lc | 24 | μm | 1.05 | |
| XBcy | Ra | 21 | μm−2 | 20 | 40% decrease (model fit) |
| XBcy | Ya | 21 | ms−1 | 0.0023 | 24% increase [18–22, 63] |
| XBcy | Yc | 24 | μm−1 | 4 | 40% decrease (model fit) |
| XBcy | Yd | 24 | ms−1 | 0.028 | 2.2-fold increase (model fit) |
| XBcy | Yp | 17, 18 | ms−1 | 0.1397 | 2.2-fold increase [18–22, 63] |
| XBcy | Yv | 23 | ms−1 | 0.9 | 60% increase (model fit) |
| XBcy | Za | 22 | ms−1 | 0.0023 | 24% increase [18–22, 63] |
| XBcy | Zp | 17, 18 | ms−1 | 0.2095 | 2.2-fold increase [18–22, 63] |
2.4 Integrated ionic, contractile, and β-AS model
We embedded the contraction model with the Soltis-Saucerman model [29], and updated the formulation of target phosphorylation by PKA in several ways (detailed in the Supplement): (1) IKs phosphorylation kinetics were slowed, as done previously [46] in accordance with recent experimental observations [47]; (2) phosphorylation of phospholemman (PLM) to increase Na+–K+-ATPase (NKA) affinity for internal Na+ [48] was added as done previously [30, 46, 49, 50]; (3) PKA-dependent modulation of IKr was introduced based on experiments by Harmati et al. [51] with kinetics that we used for IKs phosphorylation previously [52]; (4) formulation of PKA-dependent modulation of ICl(Ca) [53] was added with the same kinetics as for CFTR phosphorylation. Figure S2 shows the responses of ionic PKA targets to isoproterenol (ISO), and Table 2 describes the effects of 100 nM [ISO] administration; (5) PKA-dependent effects on contraction were added, with phosphorylation extent and kinetics as was formulated for TnI in the Soltis-Saucerman model. Table 1 reports all changes to myofilament model parameters induced by 100 nM [ISO] administration. PKA phosphorylation has been reported to reduce stiffness (attributed to titin) [54] and XBCa [55], in addition to increasing XBcy [18, 20–22]. The maximal ISO-induced reduction of titin stiffness was represented by decreasing the parallel element elasticity (Ke) by 50% to explain sarcomere passive force reduction with β-AS [56] (see Supplement and Fig. S3). To reproduce PKA effects on contractile targets, XBCa was adjusted by increasing the rate constants Zb, Yr and Zr to reduce Ca2+ affinity and alter the ratio of Ca2+ binding over unbinding rate parameters (Yb/Zb and Yr/Zr) favoring Ca2+ release. The ISO effect on XBcy was represented by modifying the rate constants Zp, Yp and parameters involved in g, f, and gd to increase the rate constants implicated in XB attachment and detachment (Fig. 1C).
Table 2.
Effect of β-AS on ionic model parameters.
| Target | Effect of β-AS | Effect of 100 nM [ISO] |
|---|---|---|
| ICaL | Enhanced channel opening probability and increased fraction of available channels | 8% of channels in gating mode 2 and 29% increase in channel availability |
| RyR | Enhanced channel opening probability | 53% increase in koSRCa |
| PLB | Enhanced Ca2+-sensitivity of SERCA | 68% reduction of forward mode Kmf |
| PLM | Enhanced NKA activity due to increased affinity for [Na+]i | KmNaip reduced from 11 to 8 mM |
| IKs | Enhanced channel availability and left-shifted current-voltage relationship | 2.8-fold increase in channel availability and 15-mV shift |
| IKr | Enhanced channel availability and left-shifted current-voltage relationship | 30% increase in channel availability and 10-mV shift |
| ICFTR | Graded current activation | Total conductance gCFTR increased to 0.0043 A/F |
| ICl(Ca) | Increased Ca2+-affinity of the channel | 30% reduction in KdClCa |
All simulations were performed in MATLAB (The MathWorks, Natick, MA, USA) using the stiff ordinary differential equation solver ode15s. The model code is available for download at: https://somapp.ucdmc.ucdavis.edu/Pharmacology/bers/.
3. Results
3.1 β-AS behavior at imposed [Ca2+]
Figures 3 and 4 and Table 3 show results of control and β-AS at fixed [Ca2+]i, to assess PKA effects on XBCa and XBcy separately, independent of [Ca2+]i changes. We compared simulations to experiments done in transgenic animals in which PKA phosphorylation on TnI or MyBP-C sites was prevented. To this end, abrogation of the ISO-induced XBCa desensitization was simulated by eliminating ISO effects on parameters involved in XBCa (ISO-XBCa), and to suppress ISO-increased XBcy we removed ISO effects on XBcy parameters (ISO-XBcy). Simulations were compared with skinned fiber data in the literature. Fig. 3A illustrates experimental (top) [20] and model (bottom) for XB force (Fb) vs. [Ca2+]i relationships at halfsarcomere length of 1.05 μm. Skinned fibers often exhibit higher half-activating [Ca2+]i ([Ca2+]50) vs. measurements in intact fibers or myocytes, due partly to supra-physiological free [Mg2+] in the former [57], which would prevent contraction for normal myocyte Ca2+ transients (below 1 μM). Our control half-activating [Ca2+]50 = 0.79 μM and apparent Hill coefficient (3.6) agrees with baseline data in intact muscle. From this baseline, ISO produced a rightward shift of the force-[Ca2+] relationship, as seen experimentally. ISO-XBcy behavior was comparable to that of ISO, as reported in transgenic mice expressing non-phosphorylatable MyBP-C [20]. ISO-XBCa reversed the ISO relationship towards control as observed by Kentish et al. in mice expressing non phosphorylatable TnI [18]. In simulation-generated values fitted to the Hill equation [37, 58], ISO caused a rightward shift of 51% in [Ca2+]50 with only slight changes in Hill coefficient (nH) and Fb(max), in agreement with experimental studies in mouse skinned cardiac muscle [18, 20], ferret papillary muscle [59] and rat trabeculae [60].
Figure 3.
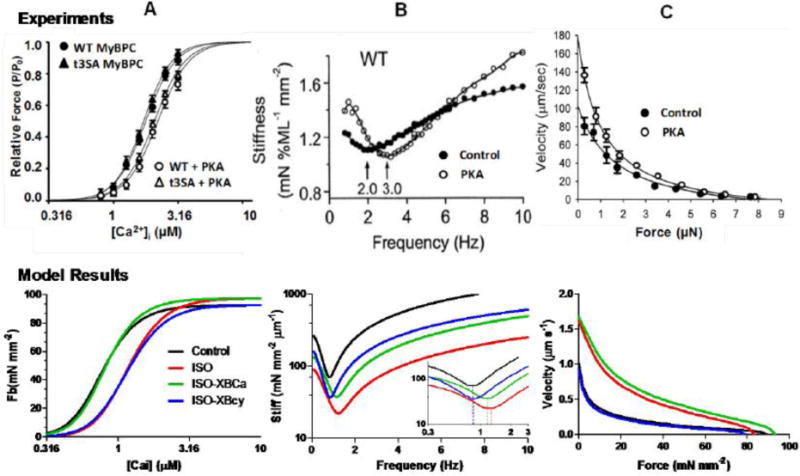
Experimentally reported (upper panels) and model simulated (lower panels) contractile response at fixed [Ca2+]i. A: Model simulated XB force (Fb) – [Ca2+]i relationships depict rightward shift in ISO (100 nM) and ISO-XBcy, but comparable to control in ISO-XBCa, as seen in experimental results with PKA in WT or non phosphorylatable MyBPC (cMyoBP-C(t3SA)) mice [20]. B: Stiffness-frequency relationship simulations exhibit a shift of minimum stiffness towards higher frequency in ISO (see inset), as seen in experimental data with ISO in WT mice [18]. This effect is partially abolished in ISO-XBCa, though the effect is less than in TG experiments, and is eliminated in ISO-XBcy. C: force-velocity curves built from isotonic shortening velocities at imposed loads starting at isometric force (Lm = 1.05 μm). Shifts with ISO are comparable to experimental responses [63]. ISO-XBCa was similar to ISO and ISO-XBcy analogous to control, suggesting force-velocity dependence mainly on XBcy (see Table 3 for simulation numerical values).
Figure 4.
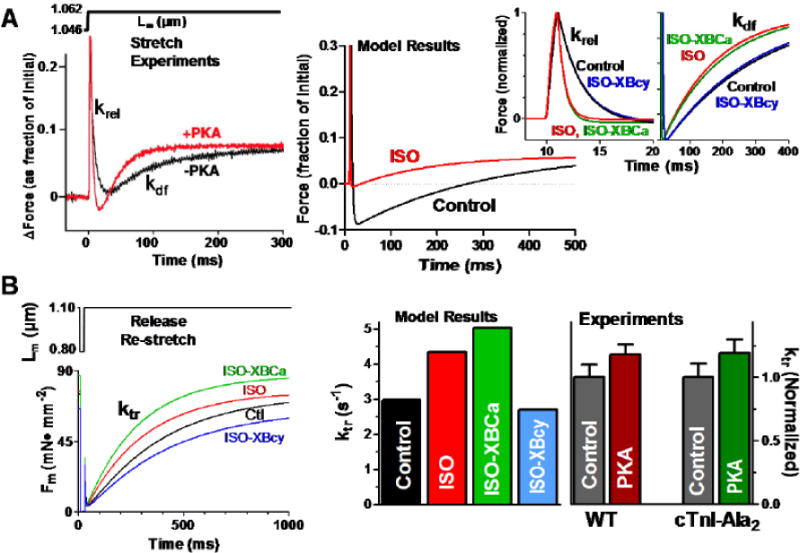
Contractile response to stretch at fixed [Ca2+]i. A: Experimental (left, [21]) and simulated (right) force response to a length step. Simulations at expanded time scale show that the 100 nM [ISO] effect on krel is comparable to the experimental response in WT mice [21]. ISO-XBCa and ISO-XBcy simulations (insets) evidence a comparable response with non-phosphorylatable TnI (cTnI-Ala2, [21]) and non-phosphorylatable MyBPC (cMyoBP-C(t3SA), [20]) (experimental data not shown). B: Simulated force response following a release and restretch pulse (left panel), and simulated and experimental rates of force redevelopment (ktr, right panel). ktr increases in ISO and ISO-XBCa, equivalent to the behavior observed in WT and cTnI-Ala2 mice [23], and decreases in ISO-XBcy (see Table 3 for simulation numerical values).
Table 3.
Contractile response at imposed [Ca2+]i in control, ISO, ISO-XBCa, ISO-XBcy, ISO-XBCa-XBcy, and ISO-titin.
| Index | Units | Control | ISO | ISO-XBCa | ISO-XBcy | ISO-XBCa-XBcy | ISO-titin |
|---|---|---|---|---|---|---|---|
| nH | adimensional | 4.03 | 4.00 | 4.22 | 3.74 | 4.03 | 4.00 |
| [Ca2+]50 | μM | 0.765 | 1.154 | 0.801 | 1.141 | 0.765 | 1.154 |
| Fb(max) | mN mm−2 | 92.5 | 97.2 | 97.2 | 92.5 | 92.5 | 97.2 |
| krel | s−1 | 39.6 | 101.9 | 100.4 | 40.3 | 39.8 | 101.9 |
| kdf | s−1 | 4.15 | 9.3 | 8.09 | 4.48 | 4.15 | 9.31 |
| ktr | s−1 | 2.98 | 4.34 | 5.02 | 2.69 | 2.98 | 4.34 |
| Stiff.min | mN mm−2 μm−1 | 70.6 | 22.2 | 37.6 | 36.9 | 70.6 | 22.2 |
| Fr(Stiff.min) | Hz | 0.85 | 1.20 | 1.12 | 0.85 | 0.85 | 1.20 |
| Vmax | μs−1 | 1.01 | 1.62 | 1.67 | 0.93 | 1.01 | 1.53 |
The Fb-[Ca2+]i relationship is characterized by nH, [Ca2+]50 and Fb(max) of the Hill equation. krel and kdf describe the response to a length step, and ktr depicts the reaction to a length pulse. Minimum stiffness (Stiff.min) and frequency (Fr) at minimum stiffness (Fr(Stiff.min)) describe the stiffness-frequency relationship, and Vmax characterizes the response of the force-velocity relationship.
Figure 3B (top) shows an experimental stiffness-frequency relationship [18] reflecting actively cycling XB kinetics and Fig. 3B (bottom) depicts simulation results. Simulation of experimental stiffness-frequency relationships [61] has been previously described [37, 43]. These were obtained at steady-state with sinusoidal oscillations from a constant basal L (Lbas) to give an input L(t) = Lbas + ΔL sin(2π freq t), where ΔL (< 1% of Lbas) is the amplitude and freq the frequency of the applied oscillations. The stiffness modulus is defined as ΔF/ΔL, where ΔF is the amplitude of the resulting force oscillations. Stiffness simulations showed a minimum at 0.85 Hz frequency in control conditions. ISO produced a 41% rightward shift of this relationship, within the range experimentally reported (19% [62] and 63% [18]). ISO-XBCa only slightly limited the ISO effect (32% vs. 41% rightward shift vs. control), a change that was less pronounced than that seen in non-phosphorylatable TnI mice [18]. Conversely, ISO-XBcy completely abrogated the shift in stiffness minimum, suggesting that XBcy is more important than XBCa in the dynamic stiffness response to ISO.
Figure 3C shows the effect of β-AS on XB kinetics assessed by force-velocity relationships. Similarly to experimental results (top panel) [63], simulated isotonic shortening velocities during force clamps at constant [Ca2+]i (2 μM) (bottom panel) showed that ISO enhanced shortening velocity at every force value. Maximal velocity at Fm = 0 increased by 60%, comparable to experiments in cat papillary muscle with norepinephrine [64] and rat myocytes with PKA stimulation [63]. ISO-XBCa produced a similar result (65% increase with respect to control) while ISO-XBcy abolished the ISO-induced response, suggesting that, like the dynamic stiffness behavior, XBcy predominates on the force-velocity reaction in enhanced inotropic state.
Figure 4A (top, left) shows experimental muscle force (Fm) response to 1% step increase in muscle length (Lm) [21]. Following the length step the apparent rate constant of force decay (krel) indicates rates of detachment/reattachment of strongly bound XBs, and the apparent rate constant of force redevelopment (kdf) indicates XB recruitment into the force-generating state. Simulation results (Fig. 4A, right) show Fm responses to a similar 1% stretch. The insets illustrate more clearly that ISO increased krel by 157% and kdf by 124% (Table 3). As expected, a similar response was observed for ISO-XBCa, comparable to reported effects in wild type and non-PKA phosphorylatable TnI transgenic mice [21]. On the other hand, ISO-XBcy reversed the response towards control, suggesting major XBcy involvement in the krel response, in accordance with the behavior observed in mice with non-phosphorylatable MyBP-C sites [20].
XB kinetics were also assessed during release-re-stretch (20%) from half-sarcomere length = 1.05 μm, lasting 20 ms at [Ca2+]i = 0.75 μM, as done experimentally [23, 65] (Fig. 4B, bottom right). The rate of force redevelopment (ktr) following the length pulse (determined at half-time force recovery [66], upper panel) was 2.98 s−1 in control, similar to the linear slope of two phase ktr-pCa Hill plots (3.21–1.83 s−1) reported in similar conditions in isolated rat myocytes [65]. ISO increased ktr by 46% and further enhanced it by 68% in ISO-XBCa, comparable to experiments on PKA-treated wild type and non-phosphorylatable TnI rat ventricular trabeculae Fig 4B, right) [23]. Preventing the cycling rate effect (ISO-XBcy) abolished the ISO-induced increase in ktr, which was decreased even below control. Taken together, these results suggest that both XBCa and XBcy influence ktr.
3.2 β-AS effect on action potentials, Ca2+ transients and contractions
Figures 5 and 6 and Tables 4 and S1 show effects of β-AS on 1 Hz steady state AP, Ca2+ transients and contractions for intact myocyte twitches. We separately assessed the impact of each PKA target. ISO (100 nM) decreased APD only slightly (from 211 to 204 ms), consistent with some experimental data [67, 68]. This is due to a balance of effects on ICaL and PLM which would prolong APD vs. IKs which would shorten APD. That is, in Fig. 5A, switching off the ICaL effect (blue AP) allows ISO to shorten APD, whereas disabling the IKs effect allows ISO to prolong APD (Fig 5D). Removing the PLM effect allows [Na+]i to rise and increases outward (repolarizing) Na+-pump current Fig 5C). ISO effects on PLB (Fig. 5B), RyR, IKr, ICFTR and ICl(Ca) (Fig. S5) or myofilaments (Fig. 6A) had no appreciable effects on APD.
Figure 5.
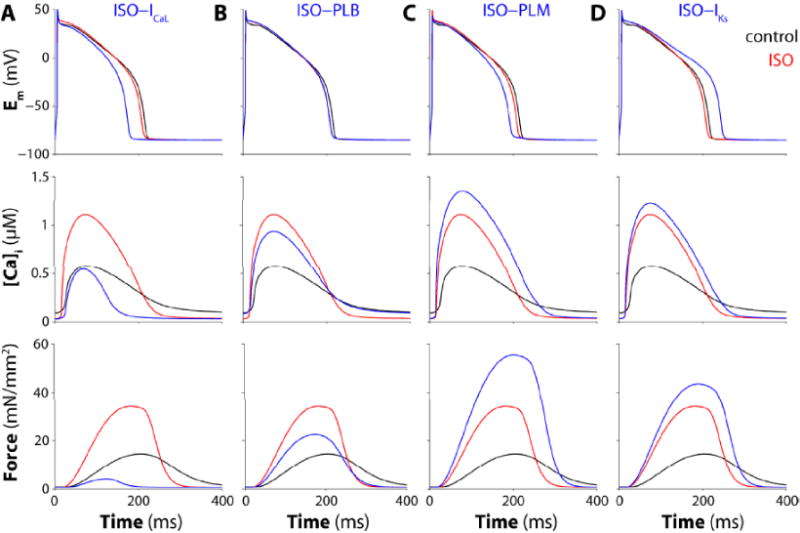
Effects of PKA-phosphorylation on individual ion channel and transporter targets. Time courses of membrane potential (top panels), Ca2+ transient (middle) and isometric force (bottom) during steady state 1-Hz stimulation are shown before (black), with 100 nM [ISO] (red) an with ISO, but with PKA effects on the indicated transporter disabled, for ICaL (A), PLB (B), PLM (C), and IKs (D).
Figure 6.
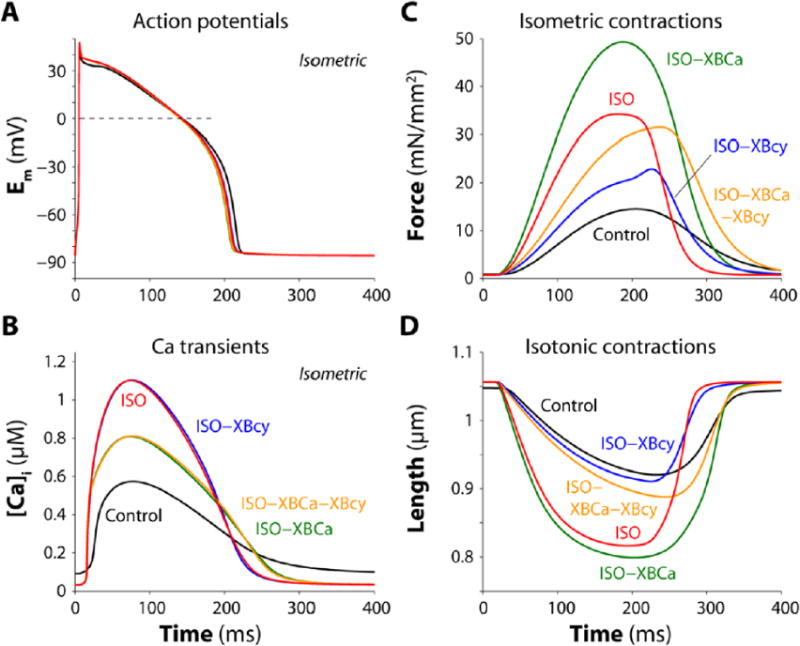
Simulation of AP, [Ca2+]i and isometric or isotonic twitches. Results are shown for control, ISO (100 nM), and ISO with suppression of different target effects (ISO-XBCa, ISO-XBcy and ISO-XBCa-XBcy). A: ISO slightly reduces APD, a response seen in all β-AS conditions. B: ISO and ISO-XBcy increase peak [Ca2+]i, its velocity of rise and faster decline (TCa50 and TCa90), while abrogation of conditions involving XBCa decrease the peak [Ca2+]i. C–D: ISO increases isometric force and isotonic shortening which is further enhanced upon eliminating ISO effect from XBCa (ISO-XBCa). Abrogation of ISO effect on XBcy (ISO-XBcy) blunts inotropy for force and shortening, while removing ISO effect on both contractile targets (ISO-XBCa-XBcy) allows the inotropic increase in force but not shortening (see also Table 4).
Table 4.
Isometric and isotonic twitch responses to ISO, ISO-XBCa, ISO-XBcy, ISO-XBCa-XBcy, ISO-titin, and ISO-Cytofl.
| Feature | Units | Control | ISO | ISO-XBCa | ISO-XBcy | ISO-XBCa-XBcy | ISO-titin | ISO-Cytofl |
|---|---|---|---|---|---|---|---|---|
|
Isometric contractions (Lm = 1.05 μm)
| ||||||||
| APD90 | Ms | 211.3 | 204.3 | 201.2 | 204.9 | 201.9 | 204.2 | 212.1 |
| [Ca2+]CL(max) | μM | 77.0 | 228.4 | 277.7 | 223.5 | 272.1 | 228.4 | 69.7 |
| [Ca2+]SL(max) | μM | 5.94 | 10.00 | 11.60 | 9.84 | 11.41 | 10.00 | 5.61 |
| [Ca2+]i(max) | μM | 0.577 | 1.110 | 0.814 | 1.111 | 0.816 | 1.110 | 0.780 |
| [Ca2+]i(min) | μM | 0.091 | 0.031 | 0.033 | 0.031 | 0.032 | 0.031 | 0.090 |
| TCa(max) | Ms | 77.3 | 75.4 | 73.5 | 75.3 | 76.6 | 74.0 | 75.2 |
| TCa50 | Ms | 114.6 | 105.6 | 125.7 | 109.0 | 125.6 | 107.3 | 88.0 |
| TCa90 | Ms | 213.2 | 157.2 | 192.7 | 154.0 | 186.5 | 159.4 | 167.6 |
| Fm(max) | mN mm−2 | 14.5 | 34.3 | 49.3 | 22.9 | 31.5 | 34.3 | 12.8 |
| Fm(min) | mN mm−2 | 0.91 | 0.76 | 0.77 | 0.76 | 0.77 | 0.83 | 0.78 |
| TP50 | Ms | 107.3 | 87.4 | 89.5 | 109.3 | 110.6 | 88.0 | 85.2 |
| RT50 | Ms | 93.4 | 66.2 | 82.2 | 46.7 | 65.4 | 65.8 | 68.5 |
| T90 | Ms | 378.5 | 280.7 | 314.2 | 325.1 87 | 363.1 | 279.8 | 275.4 |
|
| ||||||||
|
Isotonic contraction (Fm = 0.87 mN mm−2)
| ||||||||
| APD90 | Ms | 211.9 | 205.5 | 202.2 | 206.0 | 202.2 | 205.4 | 212.7 |
| [Ca2+]i(max) | μM | 0.580 | 1.109 | 0.813 | 1.106 | 0.810 | 1.110 | 0.787 |
| [Ca2+]i(min) | μM | 0.091 | 0.031 | 0.032 | 0.031 | 0.032 | 0.031 | 0.090 |
| TCa(max) | Ms | 79.6 | 77.5 | 77.3 | 77.9 | 77.8 | 77.2 | 76.3 |
| TCa50 | Ms | 115.8 | 108.6 | 128.0 | 109.6 | 129.4 | 108.7 | 90.0 |
| TCa90 | Ms | 203.6 | 148.9 | 182.8 | 146.7 | 181.7 | 149.8 | 162.2 |
| % short | % | 12.1 | 22.7 | 24.3 | 13.8 | 15.9 | 21.0 | 18.3 |
| RT50 | Ms | 73.9 | 73.2 | 105.3 | 49.5 | 63.8 | 78.6 | 70.6 |
APD90, APD at 90% repolarization; [Ca2+]CL(max) and [Ca2+]SL(max), peak in cleft and sub-sarcolemmal [Ca2+]; [Ca2+]i(max) and [Ca2+]i(min), peak and minimum in bulk cytosolic [Ca2+]; TCa(max), time to [Ca2+]i(max); TCa50 and TCa90, time to 50% and 90% [Ca2+]i decay; TP50, time from the stimulus to 50% peak force; RT50, time from peak force or peak shortening to 50% relaxation; T90, time from the stimulus to 90% muscle force (Fm) relaxation; Fm(max) and Fm(min), maximum and minimum Fm; % short, percent shortening expressed as the percentage of the difference between maximum and minimum muscle length divided by maximum muscle length.
ISO had the expected effects on Ca2+ transients and contraction, increasing the amplitude and rising rate of both and also greatly accelerating [Ca2+]i decline and relaxation (TCa50 and TCa90 in Table 4) [59, 62]. The ISO effects on ICaL and PLB were important to the increase in Ca2+ transients and contraction amplitude, because preventing either (especially ICaL) reduced peak [Ca2+]i and inotropy (Fig. 5A–B). Conversely, the ISO effects on PLM (by limiting [Na+]i) and IKs (by limiting APD) both diminish Ca2+ loading, Ca2+ transient increases and the inotropic effect seen with ISO (Fig. 5C–D). As expected, PLB effects are important for the ISO-induced acceleration of [Ca2+]i decline and relaxation. None of the other ion transporters (RyR, IKr, CFTR, ICl(Ca)) contribute substantially to the effects of ISO on [Ca2+]i or contraction (Fig. S5).
3.3 β-AS effect on twitch contractions driven by action potentials
Figure 6B shows that the ISO-induced increase in peak [Ca2+]i and kinetics of the Ca2+ transient was unaltered in ISO-XBcy. However, preventing the ISO-induced decrease in myofilament Ca2+ affinity (ISO-XBCa and ISO-XBCa-XBcy) reduced peak [Ca2+]i in response to ISO by 27%, and thus blunted the ISO-induced increase in [Ca2+]i by 55%. This emphasizes the quantitative impact of myofilament Ca2+ buffering during the normal Ca2+ transient [69, 70], and that part of the normal ISO-induced increase in Ca2+ transients is caused by the reduction in myofilament Ca2+ buffering. Thus greater myofilament Ca2+ binding in ISO-XBCa (vs. ISO) results in higher force development (Fig. 6C).
Rapid buffering of cytosolic Ca2+ is dominated by TnC and SERCA, which are present at 70 and 47 μM respectively [69]. Notably, ISO reduces TnC affinity and increases SERCA affinity for Ca2+. So, with respect to overall cytosolic Ca2+ buffering these two effects would tend to partially offset each other, as shown experimentally [70]. Consequently, ISO may have little net effect on cytosolic Ca2+ buffering. But with only the SERCA effect (ISO-XBCa) net Ca2+ buffering is increased so the same amount of total SR Ca2+ release will produce less rise in free [Ca2+]i (ISO-XBCa vs. ISO in Fig. 6B).
APs were almost identical in ISO vs. ISO-XBCa (APD90 = 204 vs. 201 ms; Table 4), despite the much smaller Ca2+ transient in ISO-XBCa. Given the importance of Ca2+-dependent currents (e.g. ICaL, Na+-Ca2+ exchanger (NCX) current (INCX), and ICl(Ca)) the superimposable APs are surprising. The reason is that the change in myofilament Ca2+ binding is relatively isolated from the cleft and subsarcolemmal space (Sub-SL, Fig. 1C). During ICaL and SR Ca2+ release, the cleft [Ca2+] ([Ca2+]CL) is almost uninfluenced by the difference in TnC Ca2+ buffering, but rather depends mainly on Ca2+ fluxes into the cleft, local buffering in the cleft and diffusion out to the Sub-SL (see Supplement and Fig. S4). Note that the amount and kinetics of Ca2+ released in ISO and ISO-XBCa are almost identical. The Sub-SL (where all non-cleft Ca2+-sensitive channels and transporters are) is only somewhat less isolated than the cleft from the myofilaments. That is, during release [Ca2+]CL drives up [Ca2+] in the Sub-SL ([Ca2+]SL, which is unaltered by TnC buffering), while diffusion from the Sub-SL to bulk cytosol is only slightly slowed by the higher [Ca2+]i in ISO vs. ISO-XBCa. Most of the diffusional driving force ([Ca2+]SL – [Ca2+]i) comes from the high [Ca2+]SL. The result is that the altered myofilament buffering has no effect on cleft Ca2+ channels (ICaL and RyR) and only slight effects on non-cleft Ca2+-dependent currents like INCX. If we double the diffusion constants for Ca2+ and Na+ from Sub-SL to cytosol, then [Ca2+]SL is still almost unchanged. In contrast, if we reduce SR Ca2+ release by 50%, that produces strong and relatively proportional decreases in [Ca2+]CL, [Ca2+]SL and [Ca2+]i (and of course ICaL inactivation, INCX and APD).
Figure 6C shows isometric twitch force (Fm) at 1 Hz stimulation and Lm = 1.05 μm. ISO increased peak Fm 2.4 fold, and accelerated relaxation, reducing RT50 (time from peak to 50% decline) by 29% and T90 (time from stimulus to 90% relaxation) by 26%, similar to results obtained in rat trabeculae [71]. As noted above, peak Fm was further enhanced in ISO-XBCa vs. ISO, but the ISO-induced lusitropy was partially reversed, suggesting that ~59% of the lusitropic effect may be due to XBCa effects, while the remaining 41% may be due to PLB-SERCA effects. That is consistent with the 11% acceleration of [Ca2+]i decline with ISO-XBCa vs. Control, and the slowing of [Ca2+]i decline and relaxation when PLB phosphorylation is blocked (Fig. 6B). Thus, both myofilament Ca2+ desensitization and enhanced SERCA pumping contribute to ISO-induced lusitropy.
Preventing the ISO-induced increase in XB cycling (ISO-XBcy) attenuated the ISO-induced inotropy, despite the normal increase in peak [Ca2+]i. ISO-XBcy also exhibited faster relaxation. This emphasizes not only the critical role of enhanced XB cycling to ISO-induced inotropy, but also that it may slightly limit lusitropy (which seems counter-intuitive). When both cycling and Ca2+ binding were suppressed (ISO-XBCa-XBcy) peak force was similar to that with ISO (2.2-fold increase), but contraction duration (both rise and fall) was substantially delayed vs. ISO (TP50 was near the control value). The result is that the negative inotropic effect of reduced myofilament Ca2+ sensitivity with ISO is compensated by the faster XB cycling, allowing larger and faster isometric contraction, and both factors contribute to faster relaxation with ISO.
Figure 6D shows isotonic contractions (at Fm = 0.87 mN.mm−2), where ISO increased maximal shortening (by 88%) and caused faster relaxation, as seen experimentally [72]. Compared to the isometric case, ISO-XBCa only slightly enhanced shortening vs. ISO, and the main effect was a prolongation of contraction time. Thus, the ISO-induced reduction in myofilament Ca2+ sensitivity is less limiting for isotonic shortening (at low load) than it is for isometric force. Failure to boost XB cycling (ISO-XBcy) blunted shortening rate and extent vs. ISO (as with Fm), but in this case the combination ISO-XBCa-XBcy was unable to appreciably restore maximum shortening to the ISO level (unlike the isometric case).
Elimination of ISO effects on titin stiffness while preserving it on the other targets (ISO-titin) (Tables 3 and 4) only affected passive force Fm(min) in isometric twitches, with only very slight slowing of force development and decline compared with ISO. In isotonic conditions where force was the imposed variable (and was constant), ISO-titin slowed relengthening by ~7%. These results are consistent with a contribution of titin phosphorylation to restoring force as seen in experimental and simulation restoring force studies [56] (see Supplement and Fig. S6).
Removing the effect of ISO from all myocyte ion fluxes while preserving its effect on myofilaments (ISO-Cytofl) abolished inotropy; in fact, peak force was 12% lower than control. This emphasizes the importance of enhanced Ca2+ transients for ISO-induced inotropy. It also shows that the reduced XB Ca2+ affinity with ISO slightly supersedes the enhanced XB cycling with respect to isometric force development. Note also that peak [Ca2+]i is higher than control for ISO-Cytofl, mainly because of the lower Ca2+ buffering by myofilaments. For the isotonic case, the ISO-enhanced shortening (88%) was only partially reduced (51%) in ISO-Cytofl. This again emphasizes that enhanced XB cycling is particularly important for ISO effects on isotonic shortening at low load. Obviously as the load increases the isotonic results would gradually shift to be more like the isometric case.
3.4 Kinetics and dose-dependence of β-AS effect on twitch contractions
Figure 7 illustrates the time course (panels A–D) and steady-state (panels E–H) cell responses to instantaneous application of 20 and 100 nM [ISO], where the former is roughly half-maximally activating for most of the PKA targets. As previously shown experimentally [73] and in models [49], we observed a rise of Ca2+ transient amplitude and force to a peak that subsided to a slightly lower steady state level during maintained ISO exposure. The secondary sag from the maximum was concurrent with the gradual decline in [Na+]i which is more evident at higher [ISO]. Notably, APD rapidly prolonged upon ISO (due to faster enhancement of ICaL vs. IKs [46]), and subsequently shortened to a variable extent. APD shortening was less marked at higher [ISO], in part because the lower [Na+]i drives smaller outward INKA (repolarizing) compared to 100 nM [ISO]. There is also higher Na+ influx rate at higher [ISO]. That is because the Ca2+ influx and transients are larger, and in the steady state that greater Ca2+ influx must be balanced by greater Ca2+ efflux via NCX, resulting in greater Na+ influx.
Figure 7.
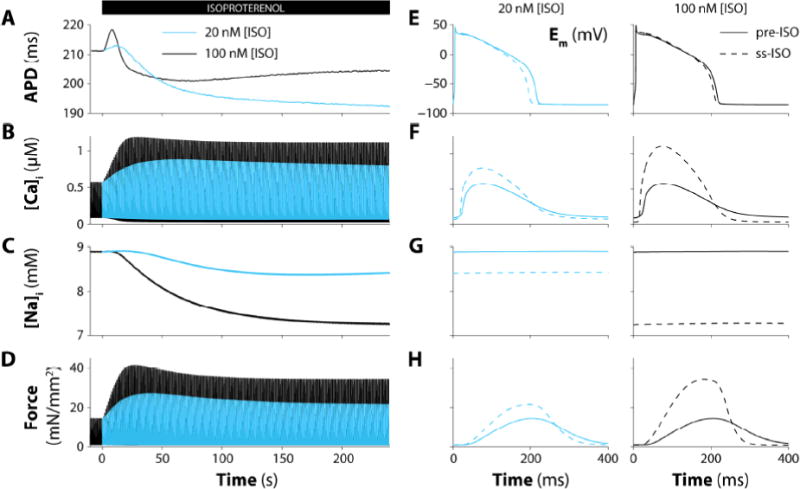
Time-course and graded effect of β-AS. Simulated action potential duration (A), [Ca2+]i (B), [Na+]i (C), and isometric force (D) in virtual myocyte paced at 1 Hz during 4 min exposure to ISO (20 and 100 nM; black and blue). Expanded time scales for membrane potential (E), [Ca2+]i (F), [Na+]i (G), and isometric force (H) before (solid) and after (dashed) 20 nM (left) and 100 nM (right) [ISO] administration.
4. Discussion
We incorporated a new contractile model into a robust electrophysiological, Ca2+ handling, and β-AS signaling myocyte model [25, 29]. This provides a new quantitative framework to dynamically study complex interactions of β-AS effects on Ca2+ transient, AP and contractile properties. This allowed us to start to clarify unresolved questions about the interaction of altered XB Ca2+ sensitivity and XB cycling rate during β-AS in ventricular myocytes. This may also provide a useful resource for other investigators for related studies (the model is freely available).
The contractile model exhibited appropriate fundamental mechanical properties with respect to experimental data (Figs. 2–4). This includes asymmetric XB detachment (which improved fit to experimental afterloaded contraction kinetics), force-[Ca2+]i relationship, frequency-dependence of stiffness, force-velocity curves and kinetic responses to abrupt stretch and release-stretch protocols. These properties and the effects of PKA were validated against critical experimental results, including data from mice with either non-phosphorylatable TnI or MyBP-C, to help analyze relative roles of XBCa and XBcy (as well as TnI and MyBP-C) in the response of twitch isometric and isotonic contractions. When embedded in a well-established electrophysiology/Ca2+ handling/signaling model [25, 29] the composite model produced normal APs, Ca2+ transients and isometric and isotonic contractions, as well as ISO responses for each.
4.1 Model assumptions
Three key changes were incorporated into our prior 6-element Ca2+ kinetic model [37]. First, we simplified this to a recently used 5-element version [74]. Because [TS~] in the original model, which was in the transition from TS* to TS (weak XB, Ca2+-free), was <5% of the total attached XBs, the irreversible pathway from TS* to TS was combined into a single step (eliminating TS~; Fig. 1C). Second, we changed the velocity-dependent detachment function from a symmetrical to an asymmetrical function, a behaviour originally postulated by Huxley [42]. Third, we changed the sarcomere length-dependent lattice spacing effect on the rate function gd from a parabolic description to an exponential representation [74], better accounting for gd changes at any L. These changes preserved results from the previous model [37] (<10% difference in index values of Fb-[Ca2+]i, stiffness-frequency and Fm-velocity, not shown). The newer model here has fewer differential equations and improved simulation of afterloaded contractions.
Incorporating the contractile model into the Soltis-Saucerman model [29] allowed replacing the passive Ca2+-buffering by TnC with the bi-directionally coupled Ca2+-XB model (Fig. 1C). Thus, length-dependent force generation is coupled to Ca2+ kinetics, and incorporates cooperativity between nearest-neighbor troponin complexes (within a TS). This coupling also provides inherent feedback from length and force to Ca2+ binding (and cytosolic buffering) by influencing transitions between states that have different Ca2+ affinity. Moreover, the model reproduces the classical observation [75] that abrupt shortening step during the AP causes release of Ca2+ from myofilaments due to the length-dependent decrease in Ca2+ affinity (Fig. S7). The ISO-induced reduction in TnC Ca2+ affinity also reduces myofilament Ca2+ binding, and allows peak [Ca2+]i to reach a significantly higher level for almost the same amount of Ca2+ supplied by ion channels (Fig. 6B). Indeed, a potentially surprising emergent result from the model was that changes in cytosolic (or myofilament) Ca2+ buffering alone had almost no effect on the AP shape, ionic currents or Ca2+ release and extrusion function. As discussed above, this is because the cleft and Sub-SL regions (where all Ca2+ transporters and channels are located) are partially isolated from the cytosolic buffering. Also the most rapid changes in [Ca2+]CL and [Ca2+]SL, which drive current changes, occur very early in the AP, and although high [Ca2+]i may reduce inward ICaL in the Sub-SL, it also increases inward INCX eliminating Ca2+. This raises the intriguing possibility that therapeutic approaches aimed at selective alteration of cytoplasmic buffering to accelerate twitch [Ca2+]i decline [76], may have relatively modest effects on the cardiac AP and arrhythmias. This, of course, is fundamentally different for primary changes in ICaL or SR Ca2+ release, which will have large and relatively proportional effects on Ca2+-dependent currents, their electrophysiological consequences and on contractile properties (apparent in the ISO cases in Fig. 6 and Table 4).
The model characterizes the separate effect of β-AS on TnI and MyBP-C as independent changes in the Ca2+ kinetic parameters involving XBCa and XBcy, respectively. This assumption was based on data suggesting relative dominance of PKA-dependent TnI phosphorylation on XBCa and of MyBP-C phosphorylation on XBcy [20, 21]. However, the exclusivity of this target-function arrangement is not universally accepted. Although emerging evidence suggests that MyBP-C may be primarily responsible for changes in XBcy in response to phosphorylation [21, 22, 77, 78] it may also contribute to XBCa when regulatory light chain phosphorylation has been reduced [22], or when basal levels of phosphorylation are decreased by propranolol pretreatment [23]. Conversely, there is also some evidence that TnI phosphorylation by PKA is critical for XBcy effects [18]. While our model is consistent with a separate influence of β-AS on XBCa and XBcy, the model itself may be instrumental in further elucidation of the functional interaction between TnI and MyBP-C phosphorylation sites.
ISO effects on ion currents and Ca2+ transport were mostly as in the Soltis-Saucerman model [29], with modifications based on experimental data and our recent theoretical studies [46, 52] and indicated in Methods. In addition, ICl(Ca) was slightly enhanced by ISO [53], whereas INCX properties were not altered [79, 80], despite earlier data suggesting such modulation [81]. The set of myofilament parameters and ISO-induced shifts was adequate to mimic experimental findings in wild type and transgenic mice with non-phosphorylatable TnI or MyBP-C. That enabled predictions of relative XBCa and XBcy participation in isometric and isotonic twitch behavior. Although some relative shifts were inferred from transgenic mice, these were imbedded in the Soltis-Saucerman model that is based on the Shannon-Bers rabbit myocyte framework. This was motivated, in part, by the likely more direct extension to the human ventricular myocyte regarding electrophysiology and Ca2+ handling [82]. The model creates a template that will allow newer data to be added to improve its accuracy for both rabbit and human tissue. Also, our model allows simulating variable degrees of β-AS, as demonstrated in Fig. 7.
4.2 β-AS effects on contractility
We systematically switched off the β-AS effect from each of 11 individual targets to analyze their relative impact on contractility. Preventing β-AS effects on ICaL or PLB limited Ca2+ transients and contractile responses in parallel, while blocking PLM and K+ channel (IKs) effects enhanced Ca2+ and inotropy. These results are all consistent with the expected effects of these individual targets. But the integrated model here allows a relative assessment of the impacts of each process to β-AS induced inotropy and lusitropy. Four other ion transporters (RyR, IKr, CFTR, ICl(Ca)) are modulated by PKA effects in the model, but their net effects on Ca2+ transients and contraction were minimal.
The satisfactory simulation of Fb-[Ca2+]i relationships [18, 20, 83], release-restretch [20, 21] and length step [23] experiments at fixed [Ca2+]i, demonstrates the adequate behavior of the present model. These results enabled the dissection of the ISO twitch response (Table 4 and Fig. 6) to understand the separate role of XBCa and XBcy on contractility. Results of Ca2+ transient and isometric and isotonic twitches suggest that enhanced XBcy is essential to explain the twitch inotropic response, and without that the larger Ca2+ transient appears only able to offset the intrinsic negative inotropic effect of ISO-induced reduced myofilament Ca2+ sensitivity (XBCa). The larger and faster Ca2+ fluxes are also essential, because without them ISO would have a slightly negative or a reduced inotropic effect for isometric and isotonic contractions, respectively (Table 4; ISO-Cytofl). The absence of both XBCa and XBcy effects does not prevent inotropic and lusitropic effects of ISO, due to the larger and faster Ca2+ transients (although the lack of XBcy greatly limits inotropy in the isotonic case). The reduced XBCa contributes to faster relaxation and shorter time to peak, and the enhanced XBcy amplifies the inotropic effect (but also slows kinetics). Notably, the XBcy effect is especially critical for isotonic contraction during sarcomere shortening, because without that ISO reduces shortening vs. control despite the much larger Ca2+ transients. Looking at this another way, the ISO-induced increase in Ca2+ transient offsets the reduced XBCa, resulting in little difference in force or shortening vs. control, whereas enhanced XBcy drives the net enhancement of contraction.
For isometric force, enhanced XBcy and Ca2+ cycling contribute roughly equally to force development, whereas for isotonic contraction enhanced XBcy is more critical than enhanced Ca2+ cycling for maximal shortening. With respect to kinetics, the situation differs. Both faster Ca2+ kinetics and reduced XBCa contribute to the shorter time to peak and faster relaxation, and both work against the enhanced XBcy (which by itself slows relaxation).
4.3 Limitations
Our contraction model is based on cardiac data from multiple species (frog, guinea pig, rabbit, ferret and cat), whereas the ionic and Ca2+ handling model is based more explicitly on rabbit data. In both cases temperature-dependent parameters were adapted to 37°C [25, 37]. Ideally, all model parameters should be derived from rabbit at 37°C. However, as is often the case in model development [84], there is limited rabbit data at 37°C to constrain the mechanical model. So, we used available data from various species, including seminal rabbit data [35, 37] and from genetically modified mice, which are of unique value in distinguishing effects of TnI and MyBP-C phosphorylation sites. We think the model is a very good approximation, but this necessary compromise is a model limitation. Of course the model can be further tuned as additional relevant data becomes available with respect to any of the model assumptions.
The model also includes CaMKII signaling, and there is known to be some cross-talk between β-AS and CaMKII signaling. We tested how much CaMKII effects might contribute to the acute ISO effects reported here (Fig. S8 vs. Fig. 7). Turning off CaMKII effects had only slight effects on acute ISO effects, so the ISO effects we report here are almost entirely PKA-dependent. That agrees with data showing that ISO-induced inotropic and lusitropic effects are preserved in CaMKIIδ knockout mice [85].
4.4 Conclusions
We have developed a useful model to study the interplay of mechanical, Ca2+ handling and electrophysiological properties of cardiac myocytes. Here we have used it to improve our understanding of how XBCa and XBcy effects of ISO interact with each other during both isometric and isotonic contractions. Coupling the contractile and Ca2+-AP models allowed us to study how ion channel and Ca2+ changes influence contraction dynamically, and also how the contractile process feeds back to influence [Ca2+]i. An emergent finding was that changes in myofilament Ca2+ buffering can influence [Ca2+]i, but at the same time have little direct impact on ionic currents and the AP shape. Both increased XBcy and Ca2+ transients contribute to enhanced contractility during β-AS isometric systole, whereas XBcy may be more critical during cardiac ejection when sarcomere shortening occurs. The model may also be useful for both further study of these AP-Ca2+-XBCa-XBcy interactions and incorporation into multicellular or intact heart models.
Supplementary Material
Highlights.
β-AS effects on cardiac contraction are analyzed with a new computer model.
The model reproduces a range of experiments involving force and length changes.
Impact of PKA targets to ®-AS effects on AP, Ca2+ and contraction is studied.
ICa, PLB, PLM and IKs effects dominate in the ®-AS increase in Ca2+ transients.
Increased XBcy compensates for lower myofilament Ca2+ sensitivity during inotropy.
Acknowledgments
This research was supported by ANPCyT PICT08–0340-grant (JAN, ECL), by a Postdoctoral fellowship from the American Heart Association (SM), and NIH grants R01–HL096819 (AVG), R01–HL105242 and R37–HL30077 (DB).
Abbreviations
- AP
Action potential
- APD
AP duration
- CaMKII
Ca2+/calmodulin-dependent protein kinase II
- E–C
Excitation-contraction
- Fm
Muscle force
- ICaL
L-type Ca2+ channel current
- ICFTR
CFTR-mediated Cl− current
- ICl(Ca)
Ca2+-dependent Cl− current
- IKr
Rapid delayed rectifier K+ current
- IKs
Slow delayed rectifier K+ current
- INa
Fast Na+ current
- INCX
Na+-Ca2+ exchanger current
- INKA
Na+-K+-ATPase current
- ISO
Isoproterenol
- ISO-Cytofl
ISO effect without β-AS on parameters involved in cytosolic fluxes
- ISO-titin
ISO effect without β-AS on parameters involved in titin
- ISO-XBCa
ISO effect without β-AS on parameters involved in XBCa
- ISO-XBCa-XBcy
ISO effect without β-AS on parameters in XBCa and XBcy
- ISO-XBcy
ISO effect without β-AS on parameters involved in XBcy
- kdf
Rate of force redevelopment (response to a length step)
- krel
Rate of force decay
- ktr
Rate of force redevelopment (response to a length pulse)
- Lm
Muscle length
- MyBP-C
Myosin binding protein-C
- NCX
Na+-Ca2+ exchanger
- NKA
Na+-K+-ATPase
- PKA
Protein kinase A
- PLB
Phospholamban
- PLM
Phospholemman
- RyR
Ryanodine receptor
- SERCA
SR Ca2+-ATPase
- SR
Sarcoplasmic reticulum
- TnC
Troponin C
- TnI
Troponin I
- XB
Myofilament cross-bridge
- XBCa
XB Ca2+ sensitivity
- XBcy
XB cycling rate
- β-AS
un β-adrenergic stimulation
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Disclosures: None declared.
References
- 1.McDonald TF, Pelzer S, Trautwein W, Pelzer DJ. Regulation and modulation of calcium channels in cardiac, skeletal, and smooth muscle cells. Physiol Rev. 1994;74:365–507. doi: 10.1152/physrev.1994.74.2.365. [DOI] [PubMed] [Google Scholar]
- 2.Tsien RW, Bean BP, Hess P, Lansman JB, Nilius B, Nowycky MC. Mechanisms of calcium channel modulation by beta-adrenergic agents and dihydropyridine calcium agonists. J Mol Cell Cardiol. 1986;18:691–710. doi: 10.1016/s0022-2828(86)80941-5. [DOI] [PubMed] [Google Scholar]
- 3.Lindemann JP, Jones LR, Hathaway DR, Henry BG, Watanabe AM. beta-Adrenergic stimulation of phospholamban phosphorylation and Ca2+-ATPase activity in guinea pig ventricles. The Journal of biological chemistry. 1983;258:464–71. [PubMed] [Google Scholar]
- 4.Hunter DR, Haworth RA, Berkoff HA. Modulation of cellular calcium stores in the perfused rat heart by isoproterenol and ryanodine. Circulation research. 1983;53:703–12. doi: 10.1161/01.res.53.5.703. [DOI] [PubMed] [Google Scholar]
- 5.Shannon TR, Ginsburg KS, Bers DM. Quantitative assessment of the SR Ca2+ leak-load relationship. Circulation research. 2002;91:594–600. doi: 10.1161/01.res.0000036914.12686.28. [DOI] [PubMed] [Google Scholar]
- 6.Shan J, Kushnir A, Betzenhauser MJ, Reiken S, Li J, Lehnart SE, et al. Phosphorylation of the ryanodine receptor mediates the cardiac fight or flight response in mice. The Journal of clinical investigation. 2010;120:4388–98. doi: 10.1172/JCI32726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Curran J, Hinton MJ, Rios E, Bers DM, Shannon TR. Beta-adrenergic enhancement of sarcoplasmic reticulum calcium leak in cardiac myocytes is mediated by calcium/calmodulin-dependent protein kinase. Circulation research. 2007;100:391–8. doi: 10.1161/01.RES.0000258172.74570.e6. [DOI] [PubMed] [Google Scholar]
- 8.Li Y, Kranias EG, Mignery GA, Bers DM. Protein kinase A phosphorylation of the ryanodine receptor does not affect calcium sparks in mouse ventricular myocytes. Circulation research. 2002;90:309–16. doi: 10.1161/hh0302.105660. [DOI] [PubMed] [Google Scholar]
- 9.Bers DM. Ryanodine receptor S2808 phosphorylation in heart failure: smoking gun or red herring. Circulation research. 2012;110:796–9. doi: 10.1161/CIRCRESAHA.112.265579. [DOI] [PubMed] [Google Scholar]
- 10.Curran J, Tang L, Roof SR, Velmurugan S, Millard A, Shonts S, et al. Nitric oxide-dependent activation of CaMKII increases diastolic sarcoplasmic reticulum calcium release in cardiac myocytes in response to adrenergic stimulation. PloS one. 2014;9:e87495. doi: 10.1371/journal.pone.0087495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pereira L, Cheng H, Lao DH, Na L, van Oort RJ, Brown JH, et al. Epac2 mediates cardiac beta1-adrenergic-dependent sarcoplasmic reticulum Ca2+ leak and arrhythmia. Circulation. 2013;127:913–22. doi: 10.1161/CIRCULATIONAHA.12.148619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sanguinetti MC, Jurkiewicz NK, Scott A, Siegl PK. Isoproterenol antagonizes prolongation of refractory period by the class III antiarrhythmic agent E-4031 in guinea pig myocytes. Mechanism of action. Circulation research. 1991;68:77–84. doi: 10.1161/01.res.68.1.77. [DOI] [PubMed] [Google Scholar]
- 13.Koumi S, Backer CL, Arentzen CE, Sato R. beta-Adrenergic modulation of the inwardly rectifying potassium channel in isolated human ventricular myocytes. Alteration in channel response to beta-adrenergic stimulation in failing human hearts. The Journal of clinical investigation. 1995;96:2870–81. doi: 10.1172/JCI118358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Li L, Desantiago J, Chu G, Kranias EG, Bers DM. Phosphorylation of phospholamban and troponin I in betaadrenergic-induced acceleration of cardiac relaxation. Am J Physiol Heart Circ Physiol. 2000;278:H769–79. doi: 10.1152/ajpheart.2000.278.3.H769. [DOI] [PubMed] [Google Scholar]
- 15.Sadayappan S, Gulick J, Klevitsky R, Lorenz JN, Sargent M, Molkentin JD, et al. Cardiac myosin binding protein-C phosphorylation in a {beta}-myosin heavy chain background. Circulation. 2009;119:1253–62. doi: 10.1161/CIRCULATIONAHA.108.798983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kranias EG, Garvey JL, Srivastava RD, Solaro RJ. Phosphorylation and functional modifications of sarcoplasmic reticulum and myofibrils in isolated rabbit hearts stimulated with isoprenaline. The Biochemical journal. 1985;226:113–21. doi: 10.1042/bj2260113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Garvey JL, Kranias EG, Solaro RJ. Phosphorylation of C-protein, troponin I and phospholamban in isolated rabbit hearts. The Biochemical journal. 1988;249:709–14. doi: 10.1042/bj2490709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kentish JC, McCloskey DT, Layland J, Palmer S, Leiden JM, Martin AF, et al. Phosphorylation of troponin I by protein kinase A accelerates relaxation and crossbridge cycle kinetics in mouse ventricular muscle. Circulation research. 2001;88:1059–65. doi: 10.1161/hh1001.091640. [DOI] [PubMed] [Google Scholar]
- 19.Layland J, Solaro RJ, Shah AM. Regulation of cardiac contractile function by troponin I phosphorylation. Cardiovascular research. 2005;66:12–21. doi: 10.1016/j.cardiores.2004.12.022. [DOI] [PubMed] [Google Scholar]
- 20.Tong CW, Stelzer JE, Greaser ML, Powers PA, Moss RL. Acceleration of crossbridge kinetics by protein kinase A phosphorylation of cardiac myosin binding protein C modulates cardiac function. Circulation research. 2008;103:974–82. doi: 10.1161/CIRCRESAHA.108.177683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Stelzer JE, Patel JR, Walker JW, Moss RL. Differential roles of cardiac myosin-binding protein C and cardiac troponin I in the myofibrillar force responses to protein kinase A phosphorylation. Circulation research. 2007;101:503–11. doi: 10.1161/CIRCRESAHA.107.153650. [DOI] [PubMed] [Google Scholar]
- 22.Chen PP, Patel JR, Rybakova IN, Walker JW, Moss RL. Protein kinase A-induced myofilament desensitization to Ca2+ as a result of phosphorylation of cardiac myosin-binding protein C. The Journal of general physiology. 2010;136:615–27. doi: 10.1085/jgp.201010448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bardswell SC, Cuello F, Rowland AJ, Sadayappan S, Robbins J, Gautel M, et al. Distinct sarcomeric substrates are responsible for protein kinase D-mediated regulation of cardiac myofilament Ca2+ sensitivity and crossbridge cycling. The Journal of biological chemistry. 2010;285:5674–82. doi: 10.1074/jbc.M109.066456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Puglisi JL, Wang F, Bers DM. Modeling the isolated cardiac myocyte. Prog Biophys Mol Biol. 2004;85:163–78. doi: 10.1016/j.pbiomolbio.2003.12.003. [DOI] [PubMed] [Google Scholar]
- 25.Shannon TR, Wang F, Puglisi J, Weber C, Bers DM. A mathematical treatment of integrated Ca dynamics within the ventricular myocyte. Biophys J. 2004;87:3351–71. doi: 10.1529/biophysj.104.047449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Nordin C, Ming Z. Computer model of current-induced early afterdepolarizations in guinea pig ventricular myocytes. Am J Physiol. 1995;268:H2440–59. doi: 10.1152/ajpheart.1995.268.6.H2440. [DOI] [PubMed] [Google Scholar]
- 27.Saucerman JJ, Brunton LL, Michailova AP, McCulloch AD. Modeling beta-adrenergic control of cardiac myocyte contractility in silico. The Journal of biological chemistry. 2003;278:47997–8003. doi: 10.1074/jbc.M308362200. [DOI] [PubMed] [Google Scholar]
- 28.Saucerman JJ, Bers DM. Calmodulin mediates differential sensitivity of CaMKII and calcineurin to local Ca2+ in cardiac myocytes. Biophys J. 2008;95:4597–612. doi: 10.1529/biophysj.108.128728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Soltis AR, Saucerman JJ. Synergy between CaMKII substrates and beta-adrenergic signaling in regulation of cardiac myocyte Ca2+ handling. Biophys J. 2010;99:2038–47. doi: 10.1016/j.bpj.2010.08.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Morotti S, Edwards AG, McCulloch AD, Bers DM, Grandi E. A novel computational model of mouse myocyte electrophysiology to assess the synergy between Na+ loading and CaMKII. J Physiol. 2014;592:1181–97. doi: 10.1113/jphysiol.2013.266676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Cortassa S, Aon MA, O’Rourke B, Jacques R, Tseng HJ, Marban E, et al. A computational model integrating electrophysiology, contraction, and mitochondrial bioenergetics in the ventricular myocyte. Biophys J. 2006;91:1564–89. doi: 10.1529/biophysj.105.076174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Crampin EJ, Smith NP. A dynamic model of excitation-contraction coupling during acidosis in cardiac ventricular myocytes. Biophys J. 2006;90:3074–90. doi: 10.1529/biophysj.105.070557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hunter PJ, McCulloch AD, ter Keurs HE. Modelling the mechanical properties of cardiac muscle. Prog Biophys Mol Biol. 1998;69:289–331. doi: 10.1016/s0079-6107(98)00013-3. [DOI] [PubMed] [Google Scholar]
- 34.Chin L, Yue P, Feng JJ, Seow CY. Mathematical simulation of muscle cross-bridge cycle and force-velocity relationship. Biophys J. 2006;91:3653–63. doi: 10.1529/biophysj.106.092510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Peterson JN, Hunter WC, Berman MR. Estimated time course of Ca2+ bound to troponin C during relaxation in isolated cardiac muscle. Am J Physiol. 1991;260:H1013–24. doi: 10.1152/ajpheart.1991.260.3.H1013. [DOI] [PubMed] [Google Scholar]
- 36.Rice JJ, Stolovitzky G, Tu Y, de Tombe PP. Ising model of cardiac thin filament activation with nearest-neighbor cooperative interactions. Biophys J. 2003;84:897–909. doi: 10.1016/S0006-3495(03)74907-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Negroni JA, Lascano EC. Simulation of steady state and transient cardiac muscle response experiments with a Huxley-based contraction model. J Mol Cell Cardiol. 2008;45:300–12. doi: 10.1016/j.yjmcc.2008.04.012. [DOI] [PubMed] [Google Scholar]
- 38.Noble D, Varghese A, Kohl P, Noble P. Improved guinea-pig ventricular cell model incorporating a diadic space, IKr and IKs, and length- and tension-dependent processes. Can J Cardiol. 1998;14:123–34. [PubMed] [Google Scholar]
- 39.Rice JJ, Wang F, Bers DM, de Tombe PP. Approximate model of cooperative activation and crossbridge cycling in cardiac muscle using ordinary differential equations. Biophys J. 2008;95:2368–90. doi: 10.1529/biophysj.107.119487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Heijman J, Volders PG, Westra RL, Rudy Y. Local control of beta-adrenergic stimulation: Effects on ventricular myocyte electrophysiology and Ca2+-transient. J Mol Cell Cardiol. 2011;50:863–71. doi: 10.1016/j.yjmcc.2011.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Saucerman JJ, McCulloch AD. Mechanistic systems models of cell signaling networks: a case study of myocyte adrenergic regulation. Prog Biophys Mol Biol. 2004;85:261–78. doi: 10.1016/j.pbiomolbio.2004.01.005. [DOI] [PubMed] [Google Scholar]
- 42.Huxley AF. Muscle structure and theories of contraction. Progress in biophysics and biophysical chemistry. 1957;7:255–318. [PubMed] [Google Scholar]
- 43.Negroni JA, Lascano EC. A cardiac muscle model relating sarcomere dynamics to calcium kinetics. J Mol Cell Cardiol. 1996;28:915–29. doi: 10.1006/jmcc.1996.0086. [DOI] [PubMed] [Google Scholar]
- 44.Slawnych MP, Seow CY, Huxley AF, Ford LE. A program for developing a comprehensive mathematical description of the crossbridge cycle of muscle. Biophys J. 1994;67:1669–77. doi: 10.1016/S0006-3495(94)80639-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Metzger JM, Moss RL. Shortening velocity in skinned single muscle fibers. Influence of filament lattice spacing. Biophys J. 1987;52:127–31. doi: 10.1016/S0006-3495(87)83197-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Xie Y, Grandi E, Puglisi JL, Sato D, Bers DM. beta-adrenergic stimulation activates early afterdepolarizations transiently via kinetic mismatch of PKA targets. J Mol Cell Cardiol. 2013;58:153–61. doi: 10.1016/j.yjmcc.2013.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Liu GX, Choi BR, Ziv O, Li W, de Lange E, Qu Z, et al. Differential conditions for early afterdepolarizations and triggered activity in cardiomyocytes derived from transgenic LQT1 and LQT2 rabbits. J Physiol. 2012;590:1171–80. doi: 10.1113/jphysiol.2011.218164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Despa S, Bossuyt J, Han F, Ginsburg KS, Jia LG, Kutchai H, et al. Phospholemman-phosphorylation mediates the beta-adrenergic effects on Na/K pump function in cardiac myocytes. Circulation research. 2005;97:252–9. doi: 10.1161/01.RES.0000176532.97731.e5. [DOI] [PubMed] [Google Scholar]
- 49.Yang JH, Saucerman JJ. Phospholemman is a negative feed-forward regulator of Ca2+ in beta-adrenergic signaling, accelerating beta-adrenergic inotropy. J Mol Cell Cardiol. 2012;52:1048–55. doi: 10.1016/j.yjmcc.2011.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Moreno JD, Yang PC, Bankston JR, Grandi E, Bers DM, Kass RS, et al. Ranolazine for congenital and acquired late INa-linked arrhythmias: in silico pharmacological screening. Circulation research. 2013;113:e50–61. doi: 10.1161/CIRCRESAHA.113.301971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Harmati G, Banyasz T, Barandi L, Szentandrassy N, Horvath B, Szabo G, et al. Effects of beta-adrenoceptor stimulation on delayed rectifier K(+) currents in canine ventricular cardiomyocytes. British journal of pharmacology. 2011;162:890–6. doi: 10.1111/j.1476-5381.2010.01092.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Xie Y, Grandi E, Bers DM, Sato D. How does beta-adrenergic signalling affect the transitions from ventricular tachycardia to ventricular fibrillation? Europace: European pacing, arrhythmias, and cardiac electrophysiology: journal of the working groups on cardiac pacing, arrhythmias, and cardiac cellular electrophysiology of the European Society of Cardiology. 2014;16:452–7. doi: 10.1093/europace/eut412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Zygmunt AC, Gibbons WR. Calcium-activated chloride current in rabbit ventricular myocytes. Circulation research. 1991;68:424–37. doi: 10.1161/01.res.68.2.424. [DOI] [PubMed] [Google Scholar]
- 54.Kruger M, Linke WA. Titin-based mechanical signalling in normal and failing myocardium. J Mol Cell Cardiol. 2009;46:490–8. doi: 10.1016/j.yjmcc.2009.01.004. [DOI] [PubMed] [Google Scholar]
- 55.Robertson SP, Johnson JD, Holroyde MJ, Kranias EG, Potter JD, Solaro RJ. The effect of troponin I phosphorylation on the Ca2+-binding properties of the Ca2+-regulatory site of bovine cardiac troponin. The Journal of biological chemistry. 1982;257:260–3. [PubMed] [Google Scholar]
- 56.Fukuda N, Wu Y, Nair P, Granzier HL. Phosphorylation of titin modulates passive stiffness of cardiac muscle in a titin isoform-dependent manner. The Journal of general physiology. 2005;125:257–71. doi: 10.1085/jgp.200409177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Gao WD, Backx PH, Azan-Backx M, Marban E. Myofilament Ca2+ sensitivity in intact versus skinned rat ventricular muscle. Circulation research. 1994;74:408–15. doi: 10.1161/01.res.74.3.408. [DOI] [PubMed] [Google Scholar]
- 58.Dobesh DP, Konhilas JP, de Tombe PP. Cooperative activation in cardiac muscle: impact of sarcomere length. Am J Physiol Heart Circ Physiol. 2002;282:H1055–62. doi: 10.1152/ajpheart.00667.2001. [DOI] [PubMed] [Google Scholar]
- 59.Okazaki O, Suda N, Hongo K, Konishi M, Kurihara S. Modulation of Ca2+ transients and contractile properties by beta-adrenoceptor stimulation in ferret ventricular muscles. J Physiol. 1990;423:221–40. doi: 10.1113/jphysiol.1990.sp018019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Varian KD, Raman S, Janssen PM. Measurement of myofilament calcium sensitivity at physiological temperature in intact cardiac trabeculae. Am J Physiol Heart Circ Physiol. 2006;290:H2092–7. doi: 10.1152/ajpheart.01241.2005. [DOI] [PubMed] [Google Scholar]
- 61.Shibata T, Hunter WC, Yang A, Sagawa K. Dynamic stiffness measured in central segment of excised rabbit papillary muscles during barium contracture. Circulation research. 1987;60:756–69. doi: 10.1161/01.res.60.5.756. [DOI] [PubMed] [Google Scholar]
- 62.Hongo K, Tanaka E, Kurihara S. Alterations in contractile properties and Ca2+ transients by beta-and muscarinic receptor stimulation in ferret myocardium. J Physiol. 1993;461:167–84. doi: 10.1113/jphysiol.1993.sp019507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Herron TJ, Korte FS, McDonald KS. Power output is increased after phosphorylation of myofibrillar proteins in rat skinned cardiac myocytes. Circulation research. 2001;89:1184–90. doi: 10.1161/hh2401.101908. [DOI] [PubMed] [Google Scholar]
- 64.Sonnenblick EH. Force-velocity relations in mammalian heart muscle. Am J Physiol. 1962;202:931–9. doi: 10.1152/ajplegacy.1962.202.5.931. [DOI] [PubMed] [Google Scholar]
- 65.Vannier C, Chevassus H, Vassort G. Ca-dependence of isometric force kinetics in single skinned ventricular cardiomyocytes from rats. Cardiovascular research. 1996;32:580–6. [PubMed] [Google Scholar]
- 66.Patel JR, Fitzsimons DP, Buck SH, Muthuchamy M, Wieczorek DF, Moss RL. PKA accelerates rate of force development in murine skinned myocardium expressing alpha- or beta-tropomyosin. Am J Physiol Heart Circ Physiol. 2001;280:H2732–9. doi: 10.1152/ajpheart.2001.280.6.H2732. [DOI] [PubMed] [Google Scholar]
- 67.Ng GA, Mantravadi R, Walker WH, Ortin WG, Choi BR, de Groat W, et al. Sympathetic nerve stimulation produces spatial heterogeneities of action potential restitution. Heart rhythm: the official journal of the Heart Rhythm Society. 2009;6:696–706. doi: 10.1016/j.hrthm.2009.01.035. [DOI] [PubMed] [Google Scholar]
- 68.Malfatto G, Rocchetti M, Zaza A. The role of the autonomic system in rate-dependent repolarization changes. Heart rhythm: the official journal of the Heart Rhythm Society. 2010;7:1700–3. doi: 10.1016/j.hrthm.2010.05.029. [DOI] [PubMed] [Google Scholar]
- 69.Bers DM. Excitation-contraction coupling and cardiac contractile force. The Netherlands: Kluwer Academic Publishers; 2001. [Google Scholar]
- 70.Briston SJ, Dibb KM, Solaro RJ, Eisner DA, Trafford AW. Balanced changes in Ca buffering by SERCA and troponin contribute to Ca handling during beta-adrenergic stimulation in cardiac myocytes. Cardiovascular research. 2014;104:347–54. doi: 10.1093/cvr/cvu201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Layland J, Kentish JC. Myofilament-based relaxant effect of isoprenaline revealed during work-loop contractions in rat cardiac trabeculae. J Physiol. 2002;544:171–82. doi: 10.1113/jphysiol.2002.022855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Spurgeon HA, Stern MD, Baartz G, Raffaeli S, Hansford RG, Talo A, et al. Simultaneous measurement of Ca2+, contraction, and potential in cardiac myocytes. Am J Physiol. 1990;258:H574–86. doi: 10.1152/ajpheart.1990.258.2.H574. [DOI] [PubMed] [Google Scholar]
- 73.Despa S, Tucker AL, Bers DM. Phospholemman-mediated activation of Na/K-ATPase limits [Na]i and inotropic state during beta-adrenergic stimulation in mouse ventricular myocytes. Circulation. 2008;117:1849–55. doi: 10.1161/CIRCULATIONAHA.107.754051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Lascano EC, Said M, Vittone L, Mattiazzi A, Mundina-Weilenmann C, Negroni JA. Role of CaMKII in post acidosis arrhythmias: a simulation study using a human myocyte model. J Mol Cell Cardiol. 2013;60:172–83. doi: 10.1016/j.yjmcc.2013.04.018. [DOI] [PubMed] [Google Scholar]
- 75.Allen DG, Kurihara S. The effects of muscle length on intracellular calcium transients in mammalian cardiac muscle. J Physiol. 1982;327:79–94. doi: 10.1113/jphysiol.1982.sp014221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Wang W, Barnabei MS, Asp ML, Heinis FI, Arden E, Davis J, et al. Noncanonical EF-hand motif strategically delays Ca2+ buffering to enhance cardiac performance. Nature medicine. 2013;19:305–12. doi: 10.1038/nm.3079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Colson BA, Patel JR, Chen PP, Bekyarova T, Abdalla MI, Tong CW, et al. Myosin binding protein-C phosphorylation is the principal mediator of protein kinase A effects on thick filament structure in myocardium. J Mol Cell Cardiol. 2012;53:609–16. doi: 10.1016/j.yjmcc.2012.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Mamidi R, Gollapudi SK, Mallampalli SL, Chandra M. Alanine or aspartic acid substitutions at serine23/24 of cardiac troponin I decrease thin filament activation, with no effect on crossbridge detachment kinetics. Archives of biochemistry and biophysics. 2012;525:1–8. doi: 10.1016/j.abb.2012.05.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Ginsburg KS, Bers DM. Isoproterenol does not enhance Ca-dependent Na/Ca exchange current in intact rabbit ventricular myocytes. J Mol Cell Cardiol. 2005;39:972–81. doi: 10.1016/j.yjmcc.2005.09.005. [DOI] [PubMed] [Google Scholar]
- 80.Lin X, Jo H, Sakakibara Y, Tambara K, Kim B, Komeda M, et al. Beta-adrenergic stimulation does not activate Na+/Ca2+ exchange current in guinea pig, mouse, and rat ventricular myocytes. American journal of physiology Cell physiology. 2006;290:C601–8. doi: 10.1152/ajpcell.00452.2005. [DOI] [PubMed] [Google Scholar]
- 81.Ruknudin A, He S, Lederer WJ, Schulze DH. Functional differences between cardiac and renal isoforms of the rat Na+-Ca2+ exchanger NCX1 expressed in Xenopus oocytes. J Physiol. 2000;529(Pt 3):599–610. doi: 10.1111/j.1469-7793.2000.00599.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Grandi E, Pasqualini FS, Bers DM. A novel computational model of the human ventricular action potential and Ca transient. J Mol Cell Cardiol. 2010;48:112–21. doi: 10.1016/j.yjmcc.2009.09.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Ramirez-Correa GA, Cortassa S, Stanley B, Gao WD, Murphy AM. Calcium sensitivity, force frequency relationship and cardiac troponin I: critical role of PKA and PKC phosphorylation sites. J Mol Cell Cardiol. 2010;48:943–53. doi: 10.1016/j.yjmcc.2010.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Niederer SA, Smith NP. At the heart of computational modelling. J Physiol. 2012;590:1331–8. doi: 10.1113/jphysiol.2011.225045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Neef S, Sag CM, Daut M, Baumer H, Grefe C, El-Armouche A, et al. While systolic cardiomyocyte function is preserved, diastolic myocyte function and recovery from acidosis are impaired in CaMKIIdelta-KO mice. J Mol Cell Cardiol. 2013;59:107–16. doi: 10.1016/j.yjmcc.2013.02.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Brutsaert DL, de Clerck NM, Goethals MA, Housmans PR. Relaxation of ventricular cardiac muscle. J Physiol. 1978;283:469–80. doi: 10.1113/jphysiol.1978.sp012513. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


