Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2016 Apr 1.
Published in final edited form as: J Pediatr. 2015 Jan 31;166(4):960–964.e2. doi: 10.1016/j.jpeds.2014.12.037

Comparison of Formulas for Calculation of the Corrected QT Interval in Infants and Young Children

Derek Q Phan 1, Michael J Silka 2, Yueh-Tze Lan 3, Ruey-Kang R Chang 1
PMCID: PMC4380641  NIHMSID: NIHMS651183  PMID: 25648293

Abstract

Objective

To compare four heart rate correction formulas for calculation of the rate corrected QT interval (QTc) among infants and young children.

Study design

R and QT intervals were measured from digital electrocardiograms. QTc were calculated with the Bazett, Fridericia, Hodges, and Framingham formulas. QTc versus RR graphs were plotted, and slopes of the regression lines compared. Slopes of QTc-RR regression lines close to zero indicate consistent QT corrections over the range of heart rates.

Results

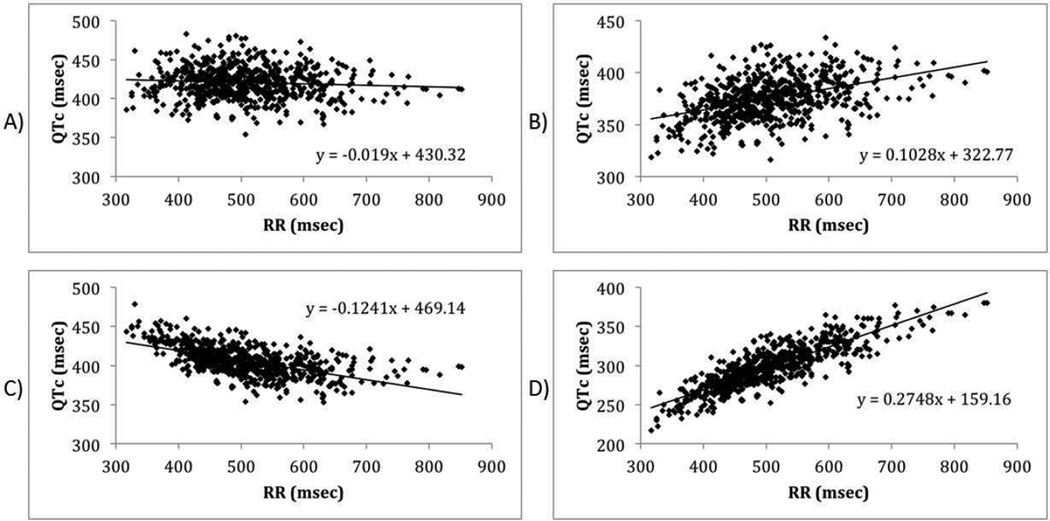
We reviewed electrocardiograms from 702 children, with 233 (33%) <1 year of age and 567 (81%) <2 years. The average heart rate was 122 ±20 bpm (median 121 bpm). The slopes of the QTc-RR regression lines for the four correction formulas were: −0.019 (Bazett); 0.1028 (Fridericia); −0.1241 (Hodges); and 0.2748 (Framingham). With the Bazett formula, a QTc >460 ms was 2 standard deviations above the mean, compared with “prolonged” QTc values of 414, 443, and 353 ms for the Fridericia, Hodges, and Framingham formulas, respectively.

Conclusions

The Bazett formula calculated the most consistent QTc; 460 msec is the best threshold for prolonged QTc. The study supports continued use of the Bazett formula for infants and children and differs from the use of the Fridericia correction during clinical trials of new medications.

Keywords: Electrocardiography, Long-QT syndrome, Rate corrected QT, Children

The congenital long QT syndrome (LQTS) has an estimated prevalence of 1:2000 among infants, and potentially accounts for 10% of sudden infant deaths (1, 2, 3). Early diagnosis of LQTS is important, in order to initiate therapies that prevent arrhythmic events and death (4). One method of establishing a clinical diagnosis of the LQTS is based on the Schwartz score, which assigns points for the presence of electrocardiographic (ECG) findings (i.e., heart rate corrected QT interval [QTc], T wave morphology, bradycardia, torsades de pointes), symptoms (i.e., syncope, congenital deafness), and family history. A total score of 3.5 or higher is taken to indicate a high probability for LQTS (5–8).

In clinical scoring for diagnosis of LQTS, the most crucial determinant among the ECG findings is an accurately measured QTc, which estimates the corresponding QT interval at a heart rate of 60 / minute. Several formulas have been proposed to calculate the QTc, and multiple studies have compared these formulas among adults (9–20). Most pediatric studies have involved adolescents. Few studies have compared the formulas among infants and young children (10, 11, 15–17). As ECG screening for LQTS in newborns is a topic of much debate among physicians and policy makers (21–25), it is useful to examine which QTc correction formula is most appropriate for infants and young children.

Although the Bazett formula is the most widely used correction method in clinical practice, the Fridericia formula is recommended by the U.S. Food and Drug Administration (FDA) for clinical trials on drug safety (26). It is unclear whether the Bazett or the Fridericia formula provides a more consistent QT correction in infants and young children. In addition, there are two other formulas (Hodges and Framingham) which have been proposed for calculation of the QTc. Our goal was to compare four QTc formulas -- to determine which formula provides the most consistent QT interval correction across the wide range of heart rates present in infants and young children.

METHODS

We conducted this study utilizing digital recordings of standard 12-lead ECGs obtained from children ≤6 years old who had sensorineural hearing loss and underwent ECG screening for LQTS (3). The study received approval from the Institutional Review Board at Los Angeles Biomedical Research Institute at the Harbor-UCLA Medical Center.

ECGs were reviewed and analyzed using IQ Manager software v8.3.1 (Midmark Corporation, Versailles, OH). The QT and RR intervals were measured manually, by use of digital calipers at a 4× zoom. Measurements were taken in lead II. If significant artifacts or indiscernible intervals were present in lead II, measurements were instead taken in lead V5, with more distinct waveforms and fewer artifacts. Three consecutive measurements of the QT and preceding RR intervals were taken. In ECGs where the return of the T wave to base line was not easily discernable in either lead II or V5, the end of the T wave was defined as the intersection of a tangent line (drawn along the steepest part of descending portion of the T wave) with the isoelectric line. For each subject, the QT and RR intervals were used to calculate the QTc by use of four different heart rate correction formulas: Bazett (QTc=QT/RR); Fridericia (QTc=QT/RR3); Hodges [QTc = QT + 1.75 *(HR-60)]; and Framingham [QTc = QT + 0.154*(1-RR)].

The QTc and RR intervals were then graphed on a scatter plot, with the QTc on the y-axis (in ms) and the RR interval on the x-axis (also in ms). Four different QTc-RR interval scatter plots were generated, one for each QTc formula. The slope of QTc-RR regression line for each QTc formula was determined and used to compare QTc formulas. Regression line slopes close to zero indicate consistency in calculating QTc values across the range of heart rates.

Subjects were also stratified by age, sex, and heart rate, according to the following groups: Ages: ≤ 6, < 2, and < 1 year; Heart rate: ≥ 130 and < 130; and Sex: males and females. QTc-RR scatter plots, means, standard deviations, and ranges were evaluated for each group, as described above.

RESULTS

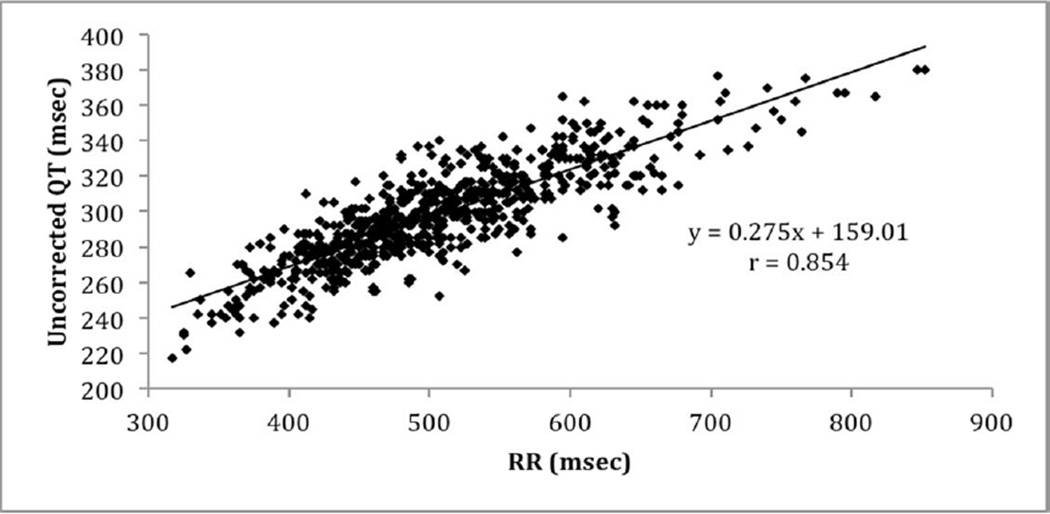
Our data consisted of ECGs from 702 infants and young children (mean age, 26 ± 19 months; Table I). Almost all ECGs measurements were taken from lead II, with only 10 from lead V5 (1.4%). Correlation coefficients between uncorrected QT intervals and heart rates, between heart rates and age, and between uncorrected QT intervals and age were −0.854, −0.625, and 0.595, respectively. As expected, the QT interval correlated inversely with heart rate, with shorter QT duration at higher heart rates. Heart rate and age were also inversely correlated, with slower rates in older children. Table II (available at www.jpeds.com) summarizes these results among the seven sub-groups.

Table 1.

Demographics of Sample Cohort

Characteristic Value
Number of subjects 702
Average Age 26 ± 19.8 months
Age Range 1–72 months
Male (%) 382 (54%)
Female (%) 320 (46%)
Race/Ethnicity
  Caucasian (%) 147 (21%)
  African-American (%) 28 (4%)
  Hispanic (%) 414 (59%)
  Asian (%) 56 (8%)
  Other (%) 57 (8%)
Open in a new tab

QTc based on the four heart rate correction formulas for each of the sub-groups and values for each QTc correction formula at which <2.5% (2 standard deviations) of the individuals have greater QTc are shown in Table III. The Fridericia formula gave the narrowest range of QTc values across the different age categories and among males. The Hodges formula gave the narrowest range of QTc values across heart rates (≥130 and <130) and among females. The Bazett formula gave a range of QTc values of 158 ms, with a range of 325 ms to 483 ms. The Framingham gave the lowest overall QTc at 217 ms with a range of 163 ms.

Table 3.

Calculated QTc (msec) values for All Sub-Groups

Formula Age ≤6 yo Age < 2 yo Age < 1yo HR ≥ 130 HR < 130 Male Female
Bazett QTc
  Mean 421 420 422 422 420 420 421
  Std Dev 20 21 21 20 20 21 19
  Min-Max 354–483 354–483 354–483 373–483 354–479 354–479 374–483
  Range 129 129 129 110 125 125 109
  2 SD threshold 460 461 464 461 460 462 459
Fridericia QTc
  Mean 375 368 368 365 380 375 374
  Std Dev 20 19 20 18 19 21 18
  Min-Max 316–434 316–427 316–421 318–427 316–434 316–434 318–427
  Range 118 111 105 109 118 118 109
  2 SD threshold 414 407 408 402 417 417 411
Hodges QTc
  Mean 406 411 415 419 400 406 407
  Std Dev 18 19 20 17 16 18 18
  Min-Max 353–478 354–478 354–478 371–478 353–446 353–478 359–460
  Range 125 124 124 107 93 125 101
  2 SD threshold 443 449 455 452 431 442 444
Framingham QTc
  Mean 298 284 281 275 311 299 297
  Std Dev 27 23 22 18 23 28 26
  Min-Max 217–380 217–362 217–350 217–337 273–380 222–380 217–375
  Range 163 145 133 120 133 158 158
  2 SD threshold 353 330 326 311 356 356 349
Open in a new tab

Figure 1 (available at www.jpeds.com) shows the inverse relationship between the uncorrected QT intervals and RR intervals, for all subjects [r = 0.88 (Pearson), P < 0.001]. Figures 2 demonstrates the QTc-RR interval scatter plots and regression lines based on the Bazett, Fridericia, Hodges, and Framingham formulas. The Bazett formula gave a regression line with a slope closest to zero (−0.019), indicating the best consistency across heart rates. The slopes of the QTc-RR regression lines for the other correction formulas were Fridericia (+0.1028); Hodges (−0.1241); and Framingham (+0.2748). The Bazett formula was also the most consistent for the variables of sex and age (Table IV; available at www.jpeds.com). The Fridericia formula was second best in five of seven sub-groups, being surpassed by the Hodges formula for HR <130 and among males.

Figure 1.

Figure 1

Open in a new tab

Uncorrected QT-RR Scatter Plot of all subjects.

Figure 2.

Figure 2

Open in a new tab

QTc-RR Scatter Plot of all subjects: (a) Bazett, (b) Fridericia, (c) Hodges, (d) Framingham formulas. A linear regression slope closer to zero indicates better QT correction across different heart rates (RR intervals).

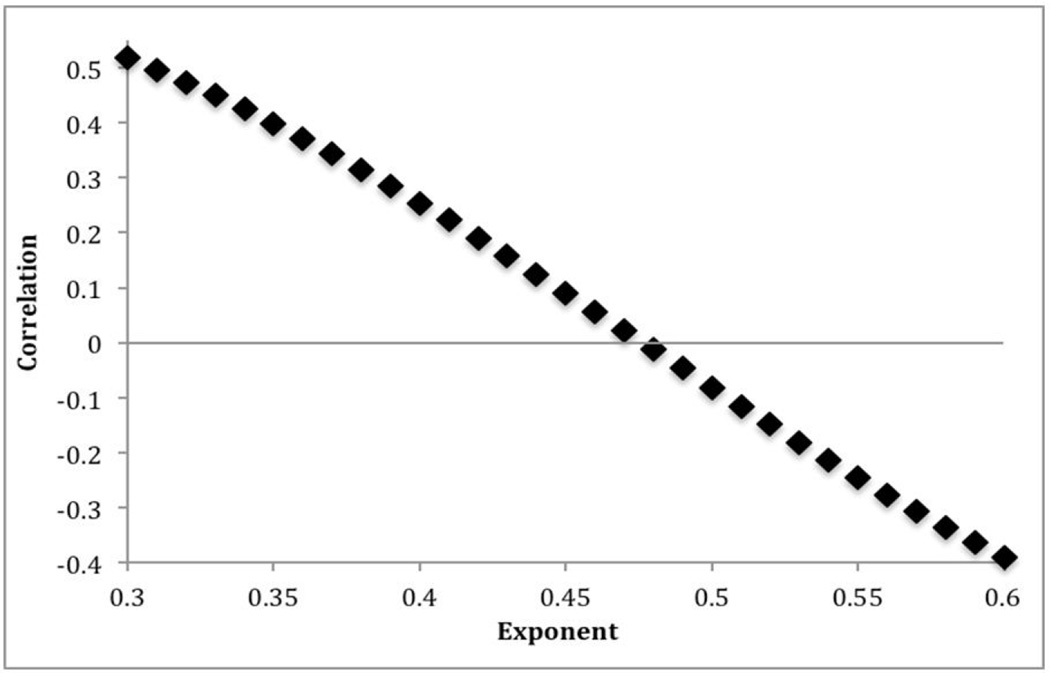
The Bazett and Fridericia methods calculate the corrected QT intervals through different values of an exponent (e) in the correction formula (QTc = QT/RRe, where e = 0.5 for the Bazett correction and 0.33 for Fridericia). Therefore, we computed slopes of QTc-RR regression lines for different values of e (from 0.3 to 0.6). An e value of 0.48 resulted in a regression line with a slope equal to zero (Figure 3; available at www.jpeds.com). Results of these slope calculations further support the conclusion that the Bazett formula provides the greatest consistency in QTc values across heart rates seen in infants and children.

Figure 3.

Figure 3

Open in a new tab

Correlation coefficient between QTc and RR with various correction factor exponents. The correction factor exponent e in the formula QTc = QT/RRe is varied across the values of 0.3 – 0.6.

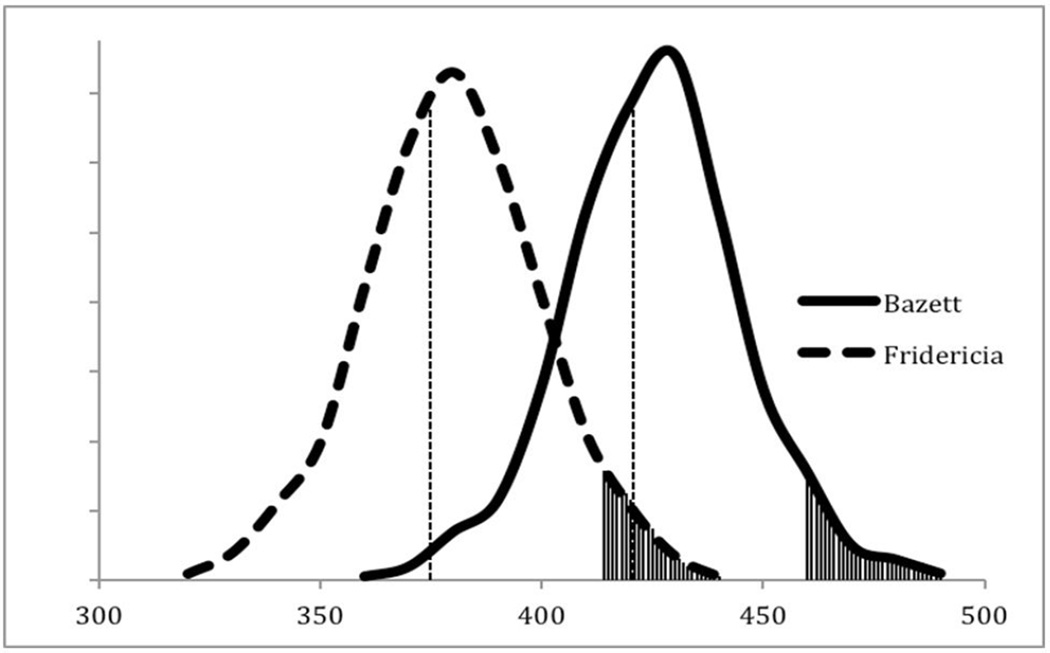
Figure 4 depicts two super-imposed curves of distribution comparing the QTc values computed with data from our subjects by the Bazett and Fridericia formulas, respectively. As can be seen from this graph, using a threshold of 460 ms as definition for “prolonged QT” (>2SD above the mean), calculation of the QTc based on the Fridericia formula will lead to an increased number of false negatives. Likewise using an absolute threshold of 414 ms while calculating QTc based on the Bazett formula will lead to an increased number of false positives. Thus, the definition of “potentially prolonged QT” is dependent on the formula used and needs to be clearly stated.

Figure 4.

Figure 4

Open in a new tab

Two superimposed distribution curves comparing the QTc values computed by the Bazett vs Fridericia formulas. The X-axis denotes QTc values in msec. The vertical line represents the mean for each formula, and the shaded area under the curve represents values > 2SD, for each respective formula.

DISCUSSION

Several formulas have been proposed for heart rate corrections of QT intervals, each with limitations. For example, the Bazett formula has been reported to over-correct the QT interval at faster heart rates and under-correct at slower rates (12, 15, 18, 27–29). Conversely, the Fridericia formula has been shown to do the opposite -- under-correct at faster and over-correct at slower rates (12,13,15). Our data are consistent with these limitations, as indicated by negative and positive values of the slopes of regression lines for the Bazett and Fridericia QTc-RR plots, respectively. However, almost all of these studies are limited to adolescents or adults in resting states with an upper limit of heart rates of 100 bpm (12, 15, 18, 27, 29). Furthermore, use of the terms overcorrection and undercorrection in the absence of an accepted absolute correction factor, may be questioned.

Because of these limitations, many studies across a range of age groups have been done, to identify new heart rate correction formulas or validate established methods (12, 14, 15, 27,29–31). However, new formulas may lack the simplicity needed for routine clinical use (31). Moreover, most studies have been done on adults, and of the pediatric studies, most represent the adolescent age group, with less attention on infants and young children (10, 11, 15–17).

Previous work comparing various heart rate correction formulas have produced conflicting results. One study examined 24-hour Holter monitors from adults (36–76 years of age) and found no significant differences among five formulas (9). Another study on individuals <20 years of age showed that the Bazett formula yields the most consistent results across heart rates and ages (10). A study on children and adolescents 6–17 years of age found the best heart rate correction QT formula to be QTc = QT/RR0.38, which is close to the Fridericia formula (QTc = QT/RR0.33) (11). Given these inconsistencies, some investigators have suggested that separate rate correction formulas may be appropriate for different heart rate ranges, creating a “bin-method” for analysis of the QTc (32).

We found the Bazett formula not only provides the most consistent correction across a wide range of high heart rates, it is consistent with clinical practice of 460 ms as threshold for identifying infants and children at risk for LQTS. In a study of ECGs obtained at 3 or 4 days of age in over 30,000 infants, the Bazett formula demonstrated consistent correlation of the QT and RR intervals and correctly defined infants with a QTc > 440 ms as 2 SD above the mean and at significant risk for sudden death (4). Furthermore, in another large study of ECG screening of newborns 15–25 days of age, Schwartz and co-workers again used the Bazett formula to identify potential cases of LQTS based on a QTc >460 ms with subsequent genetic confirmation (1). Our findings provides further evidence for the continued use of the Bazett formula in light of increasing debate on newborn ECG screening.

A strength of our study is the large sample size (n=702) and population-based recruitment of subjects which reflects the general demographics of the newborn and infant population in the state of California (3). Furthermore, to our knowledge, it is one of the few studies to compare four commonly used QTc formulas among infants and young children. Additionally, this study was performed with digital electrocardiography with amplification of the initial ECG data to allow more precise measurements than previously possible with standard ECG recordings. Although the original study was designed to identify individuals with sensorineural hearing loss and possible LQTS, very few potentially affected children were found. Therefore, we are unable to evaluate the various formulas for use in LQTS diagnosis. We recognize that there are several limitations to precise measurement of QT intervals on the ECG which are inherent to the basic technology. These include QT variance or dispersion among various leads, where leads V2–V3 may have longer QT duration due to onset of the QRS 20 ms earlier than limb leads. Another limitation inherent to QT measurement occurs when the T and U wave are superimposed or cannot be separated, or when the T and P waves are superimposed. Use of the tangent method was required in a small number of cases in this study, with recognition that this method may shorten the QT interval in patients with a delayed return of the T wave to the baseline, as in patients with LQTS type 1. However, the analyses performed in this study were performed in accordance with current Recommendations for the Standardization and Interpretation of the ECG (32).

Our study population was predominantly Hispanic (59%). However, this is similar to the demographics of births in California (51% Hispanics, according to 2009 vital statistics).

Our findings may have implications for the pharmaceutical industry and clinical trials. The FDA currently recommends use of the Fridericia formula, due to the under-correction of the Bazett formula at slower heart rates. The Fridericia correction may work well for adults, in whom average heart rates tend to be 60–90 bpm. However, children, especially infants, tend to have average heart rates well above 100 bpm. Therefore, the Bazett correction may be more appropriate for drug safety trials and clinical studies involving infants and young children. When the Fridericia formula is used in evaluation of new drugs, a QTc of 414 ms should be viewed as the threshold for significant QTc prolongation. On the other hand, a QTc of 460 ms appears to be an appropriate threshold for potentially significant QTc prolongation when the Bazett formula is used. Consistent use of the Bazett formula by clinicians as well as the FDA may be needed to avoid confusion as to what value constitutes a prolonged QTc in a young child. This is an important topic which will require further study and validation. Regardless, definition of “potentially prolonged QT” is dependent on the formula used for calculation of this value and needs to be clearly stated.

Supplementary Material

01

ACKNOWLEDEGMENTS

The authors would like to thank Henry J. Lin, MD (Harbor-UCLA Medical Center), for critical review of this manuscript. We appreciate assistance of Sandra Sedano, Eva Villa, Arturo Martinez, Erica Flore, and Robin Wu (all from Harbor-UCLA Medical Center), who performed all the ECGs on the study subjects.

Supported by National Institutes of Health (1RC1HL100114-01 [part of the American Recovery and Reinvestment Act program, to Los Angeles Biomedical Research Institute, to R.-K.C.] and 1UL1-RR033176 [to the UCLA CTSI]).

Abbreviations

ECG

Electrocardiogram

LQTS

Long QT Syndrome

QTc

Corrected QT

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

The authors declare no conflicts of interest.

REFERENCES

  • 1.Schwartz PJ, Stramba-Badiale M, Crotti L, Pedrazzini M, Besana A, Bosi G, Gabbarini F, Goulene K, Insolia R, Mannarino S, Mosca F, Nespoli L, Rimini A, Rosati E, Salice P, Spazzolini C. Prevalence of the congenital long-QT syndrome. Circulation. 2009;120:1761–1767. doi: 10.1161/CIRCULATIONAHA.109.863209. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Arnestad M, Crotti L, Rognum TO, Insolia R, Pedrazzini M, Ferrandi C, Vege A, Wang DW, Rhodes TE, George AL, Jr, Schwartz PJ. Prevalence of long-QT syndrome gene variants in sudden infant death syndrome. Circulation. 2007;115:361–367. doi: 10.1161/CIRCULATIONAHA.106.658021. [DOI] [PubMed] [Google Scholar]
  • 3.Chang RK, Lan YT, Silka MJ, Morrow H, Kwong A, Smith-Lang J, Wallerstein R, Lin HJ. Genetic variants for long QT syndrome among infants and children from a statewide newborn hearing screening program cohort. J Pediatr. 2014;164:590–595. doi: 10.1016/j.jpeds.2013.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Schwartz PJ, Stramba-Badiale M, Segantini A, Austoni P, Bosi G, Giorgetti R, Grancini F, Marni ED, Perticone F, Rosti D, Salice P. Prolongation of the QT Interval and the sudden infant death syndrome. N Engl J Med. 1998;338:1709–1714. doi: 10.1056/NEJM199806113382401. [DOI] [PubMed] [Google Scholar]
  • 5.Schwartz PJ. Idiopathic long QT syndrome: progress and questions. Am Heart J. 1985;109:399–411. doi: 10.1016/0002-8703(85)90626-x. [DOI] [PubMed] [Google Scholar]
  • 6.Schwartz PJ, Moss AJ, Vincent GM, Crampton RS. Diagnostic criteria for the long QT syndrome. An update. Circulation. 1993;88:782–784. doi: 10.1161/01.cir.88.2.782. [DOI] [PubMed] [Google Scholar]
  • 7.Schwartz PJ. The congenital long QT syndromes from genotype to phenotype: clinical implications. J Intern Med. 2006;259:39–47. doi: 10.1111/j.1365-2796.2005.01583.x. [DOI] [PubMed] [Google Scholar]
  • 8.Schwartz PJ, Crotti L. QTc Behavior during exercise and genetic testing for the long-QT syndrome. Circulation. 2011;124:2181–2184. doi: 10.1161/CIRCULATIONAHA.111.062182. [DOI] [PubMed] [Google Scholar]
  • 9.Molnar J, Weiss J, Zhang F, Rosenthal J. Evaluation of five QT correction formulas using a software-assisted method of continuous QT measurement from 24-Hour Holter recordings. Am J Cardiol. 1996;78:920–926. doi: 10.1016/s0002-9149(96)00468-7. [DOI] [PubMed] [Google Scholar]
  • 10.Qiu H, Bird GL, Qu L, Vetter VL, White PS. Evaluation of QT interval correction methods in normal pediatric resting ECGs. Comput Cardiol. 2007;34:431–434. [Google Scholar]
  • 11.Wernicke JF, Faries D, Breitung R, Girod D. QT correction methods in children and adolescents. J Cardiovasc Electrophysiol. 2005;16:76–81. doi: 10.1046/j.1540-8167.2005.03520.x. [DOI] [PubMed] [Google Scholar]
  • 12.Aytemir K, Maarouf N, Gallagher MM, Yap YG, Waktare JE, Malik M. Comparison of formulae for heart rate correction of QT interval in exercise electrocardiograms. Pacing Clin Electrophysiol. 1999;22:1397–1401. doi: 10.1111/j.1540-8159.1999.tb00635.x. [DOI] [PubMed] [Google Scholar]
  • 13.Indik JH, Pearson EC, Fried K, Woosley RL. Bazett and Fridericia QT correction formulas interfere with measurement of drug-induced changes in QT interval. Heart Rhythm. 2006;3:1003–1007. doi: 10.1016/j.hrthm.2006.05.023. [DOI] [PubMed] [Google Scholar]
  • 14.Luo S, Michler K, Johnston P, Macfarlane PW. A comparison of commonly used QT correction formulae: the effect of heart rate on the QTc of normal ECGs. J Electrocardiol. 2004;37(Suppl):81–90. doi: 10.1016/j.jelectrocard.2004.08.030. [DOI] [PubMed] [Google Scholar]
  • 15.Benatar A, Decraene T. Comparison of formulae for heart rate correction of QT interval in exercise ECGs from healthy children. Heart. 2001;86:199–202. doi: 10.1136/heart.86.2.199. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Yoshinaga M, Ushinohama H, Seiichi S, Nobuo T, Horigome H, Takahashi H, Sumitomo N, Kucho Y, Shiraishi H, Nomura Y, Shimizu W, Nagashima M. Electrocardiographic screening of 1-month-old infants for identifying prolonged QT intervals. Circ Arrhythm Electrophysiol. 2013;6:932–938. doi: 10.1161/CIRCEP.113.000619. [DOI] [PubMed] [Google Scholar]
  • 17.Yoshinaga M, Kato Y, Nomura Y, Hazeki, Yasuda T, Takahashi K, Higaki T, Tanaka Y, Wada A, Horigome H, Takahashi H, Ueno K, Suzuki H, Nahashima M. The QT intervals in infancy and time for infantile ECG screening for long QT syndrome. J Arrhythmia. 2011;27:193–201. [Google Scholar]
  • 18.Musat D, Adhaduk M, Preminger M, Arshad A, Sichrovsky T, Steinberg J, Mittal S. Correlation of QT interval correction methods during atrial fibrillation and sinus rhythm. Am J Cardiol. 2013;112:1379–1383. doi: 10.1016/j.amjcard.2013.06.027. [DOI] [PubMed] [Google Scholar]
  • 19.Wong S, Kervio G, Altuve M, Francois Carre, Carrault G. Comparing six QT correction methods in an athlete population. Computing in Cardiology. 2012;39:585–588. [Google Scholar]
  • 20.Chiladakis J, Kalogeropoulos A, Arvanitis P, Koutsogiannis N, Zagli F, Alexopoulos D. Preferred QT correction formula for the assessment of drug-induced QT interval prolongation. J Cardiovasc Electrophysiol. 2010;21:905–913. doi: 10.1111/j.1540-8167.2010.01738.x. [DOI] [PubMed] [Google Scholar]
  • 21.Chang RK, Rodriguez S, Gurvitz MZ. Electrocardiogram screening of infants for long QT syndrome: survey of pediatric cardiologists in North America. J Electrocardiol. 2010;43:4–7. doi: 10.1016/j.jelectrocard.2009.07.004. [DOI] [PubMed] [Google Scholar]
  • 22.Van Langen IM, Wilde AA. Con: Newborn screening to prevent sudden cardiac death? Heart Rhythm. 2006;3:1356–1359. doi: 10.1016/j.hrthm.2006.07.015. [DOI] [PubMed] [Google Scholar]
  • 23.Schwartz PJ. Pro: Newborn ECG screening to prevent sudden cardiac death. Heart Rhythm. 2006;3:1353–1355. doi: 10.1016/j.hrthm.2006.07.016. [DOI] [PubMed] [Google Scholar]
  • 24.Saul JP, Schwartz PJ, Ackerman MJ, Triedman JK. Rationale and objectives for ECG screening in infancy. Heart Rhythm. 2014 doi: 10.1016/j.hrthm.2014.09.047. pii: S1547-5271(14)01039-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Skinner JR, VanHare GF. Routine ECG screening in infancy and childhood should not be performed. Heart Rhythm. 2014 doi: 10.1016/j.hrthm.2014.09.046. pii: S1547-5271(14)01038-8. [DOI] [PubMed] [Google Scholar]
  • 26.U.S. Food and Drug Administration. E14 Clinical Evaluation of QT/QTc Interval Prolongation and Proarrhythmic Potential for Non-Antiarrhythmic Drugs - Questions and Answers (R1) [Accessed August 22, 2014];2012 Oct; Available at: http://www.fda.gov/downloads/Drugs/GuidanceComplianceRegulatoryInformation/Guidan ces/UCM073161.pdf.
  • 27.Sagie A, Larson MG, Goldberg RJ, Bengtson JR, Levy D. An improved method for adjusting the QT interval for heart rate (the Framingham Heart Study) Am J Cardiol. 1992;70:797–801. doi: 10.1016/0002-9149(92)90562-d. [DOI] [PubMed] [Google Scholar]
  • 28.Funck-Brentano C, Jaillon P. Rate-corrected QT interval: techniques and limitations. Am J Cardiol. 1993;72:17B–22B. doi: 10.1016/0002-9149(93)90035-b. [DOI] [PubMed] [Google Scholar]
  • 29.Rowlands DJ. Graphical representation of QT rate correction formulae: an aid facilitating the use of a given formula and providing a visual comparison of the impact of different formulae. J Electrocardiol. 2012;45:288–293. doi: 10.1016/j.jelectrocard.2012.01.003. [DOI] [PubMed] [Google Scholar]
  • 30.Sarma JS, Sarma RJ, Bilitch M, Katz D, Song SL. An exponential formula for heart rate dependence of QT interval during exercise and cardiac pacing in humans: reevaluation of Bazett's formula. Am J Cardiol. 1984;54:103–108. doi: 10.1016/0002-9149(84)90312-6. [DOI] [PubMed] [Google Scholar]
  • 31.Van de Water A, Verheyen J, Xhonneux R, Reneman RS. An improved method to correct the QT interval of the electrocardiogram for changes in heart rate. J Pharmacol Methods. 1989;22:207–217. doi: 10.1016/0160-5402(89)90015-6. [DOI] [PubMed] [Google Scholar]
  • 32.Rautaharju PM, Surawicz B, Gettes LS. AHA / ACCF / HRS recommendations for the standardization and interpretation of the electrocardiogram. J Am Coll Cardiol. 2009;53:982–9133. doi: 10.1016/j.jacc.2008.12.014. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

01
NIHMS651183-supplement-01.pdf (57.5KB, pdf)

RESOURCES