Dynamic quantification of antigen molecules with flow cytometry

Abstract

Traditional methods for estimating the number of expressed molecules, based on the detection of target antigens bound with fluorescently labeled antibodies, assume that the antigen-antibody reaction reaches equilibrium. A calibration procedure is used to convert the intensity of the fluorescence signal to the number of target molecules. Along with the different limitations of every calibration system, this substantially limits the applicability of the traditional approaches especially in the case of low affinity antibodies.

We address this problem here with studies in which we demonstrate a new approach to the antigen molecule quantification problem. Instead of using a static calibration system, we analyzed mean fluorescence values over time by flow cytometry during antibody-antigen binding. Experimental data obtained with an LSRII cytometer were fitted by a diffusion-reaction mathematical model using the Levenberg–Marquardt nonlinear least squares curve-fitting algorithm in order to obtain the number of target antigen molecules per cell. Results were compared with the Quanti-BRITE calibration system.

We conclude that, instead of using experiment-specific calibration, the value of the binding rate constant for each particular antibody-antigen reaction can be used to quantify antigen molecules with flow cytometry. The radius of CD8 antibody molecule binding site was found, that allows recalculating the binding rate constant for other conditions (different sizes of reagent molecules, fluorescent label, medium viscosity and temperature). This approach is independent of specially prepared calibration beads, antibody reagents and the specific dye and can be applied to both low and high affinity antibodies, under both saturating and non-saturating binding conditions. The method was demonstrated on a human blood sample dataset investigating CD8α antigen on T cells in stable binding conditions.

1 Introduction

Flow cytometry is a powerful tool for the identification of cell populations based on the expression level of target molecules on cells. Flow cytometry users operate with relative fluorescence intensity (FI) values for the cell subset of interest, which makes it almost impossible to directly compare (without normalization on shared control samples) different flow cytometers and even different experiments on the same machine. Flow cytometers settings, in terms of lasers and optical alignment, light collection, optical filters and photodetector sensitivity [1] have not been successfully standardized. In addition, different dye conjugates are often available for a given antibody, antibody preparations with the same fluorochrome vary from vendor to vendor, and differences in sample processing (e.g., the incubation time) generate additional variability.

In order to overcome these difficulties, there have been various efforts to quantitate the FI of beads (or cells), i.e. to estimate the number of expressed molecules. Traditional methods for estimating the number of expressed molecules on cells, based on the detection of target antigens bound with fluorescently labeled antibodies, assume that the antigen-antibody reaction reaches equilibrium and hence that the amount bound correctly reports the amount of antigen on the cell. However, at a minimum, a calibration procedure with carefully prepared reagents is needed to convert the intensity of the fluorescence signal to the number of target antigens [2]. For instance, among the currently marketed technologies there are three that are well known: Quantum Simply Cellular beads (QSC) designed to bind any fluorochrome-labeled murine monoclonal antibody [3]; Quantitative Immunofluorescence Intensity beads (QIFI kit) [4] for indirect immunofluorescence; and the Quanti-BRITE assay [5]. Although the calibration bead-based technologies seem to be a straightforward and easy-to-use approach for quantitative fluorescence flow cytometry, the on-site comparison of these three technologies [2] has revealed their limitations.

The QSC bead-based data were found to be comparable only if they were obtained using a single strictly uniform approach [6,7]. Additionally, the use of the QSC assay with FITC and PE reagents revealed substantially different estimates of cellular binding sites [2]. The use of QIFI calibration kit is restricted since it is marketed with a single manufacturer-defined fluorescent antibody. In its turn, the Quanti-BRITE assay is specified for use of specially-prepared equimolar (1 antibody molecule:1 PE molecule) reagents only. Speaking in general, these approaches are not applicable to labeling with lower affinity antibodies and/or to labeling under non-equilibrium conditions. The choice of calibrator, fluorochrome conjugates and details of sample handling can affect the determination of antigen concentration on beads or cells.

If target sites are very mobile (i.e. the surface diffusion of the sites on the cell membrane is fast in comparison with the 3-dimension diffusion of the ligand molecules in the medium) or sufficiently close to each other (i.e. the distance between sites are equal or less than the radius of the sites) for some IgG antibodies to bind divalently, the number of effective antibody binding sites will be lower than the number of target antigens. This is a common limitation of the antibody-based methods mentioned above and of the method presented here, and special approaches like use on univalent antibodies are needed to resolve this issue.

We previously showed that flow cytometry data for antigen-antibody interactions can be analyzed as a temporal evolution of the cellular fluorescence profile to get information on the cellular distribution of the surface antigens, as well as the association and dissociation rate constants per antigen [8,9] with the use of calibrators. Here we further developed and optimized a kinetic approach to antigen quantification on beads and cells which can be applied to both low and high affinity antibodies, under both saturating and non-saturating binding conditions, and independently of the conjugated fluorochrome. The major step forward from our 2011 work [8] is that now, instead of using a static calibration system, we analyzed the mean fluorescence dynamics of the population of interest measured by flow cytometry only, in order to evaluate the amount of surface antigens. Experimental data obtained with the LSRII cytometer was fitted by the diffusion-reaction mathematical model for stable binding conditions (the solution for the general case, applied to both low and high affinity antibodies, was described in [8]) using the Levenberg–Marquardt nonlinear least squares curve-fitting algorithm in order to obtain the number of target antigens per bead/cell. As a result, we proved that the binding rate constant for each particular antibody-antigen reaction can be used instead of calibrators in order to quantify antigen molecules per cell with flow cytometry.

The applicability of our approach was demonstrated for the quantification of CD8α antigen concentration on human T cells in stable binding conditions. Moreover, in order to prove the adequacy of the method, we compared the results with those obtained with the Quanti-BRITE calibration system.

2 Materials and Methods

2.1 Monoclonal antibodies

FITC-labeled anti-CD3 IgG mouse monoclonal antibody (BD Pharmingen, Cat # 555332, Lot # 30100) was used in experiments with human blood cells.

PE-labeled RPA-T8 (anti-CD8α) IgG mouse monoclonal antibody (BioLegend, Cat # 301008, Lot # B137490) was used for all kinetic experiments. The manufacturer claims the concentration of 1.9×10¹³ 1/mL (3×10⁻⁸ M). This lot was prepared to consist almost exclusively of 1:1 PE-to-antibody conjugates.

2.2 Calibration beads

Quanti-BRITE PE Beads (Becton Dickinson, Cat # 340495, Lot # 30746, Lot # 77602) were used in accordance with the protocol [10] to relate the measured signal to the number of PE-antibody molecules. The signal per PE-antibody molecule was determined in each experiment.

2.3 Microbeads

Antibody capture (compensation) beads coupled with anti-Mouse Ig kappa (Becton Dickinson, Cat # 552843, Lot # 2230632) were used in the kinetic experiments as described below.

2.4 Human blood sample preparation

18 ml of peripheral blood was drawn from a healthy volunteer with informed consent by venipuncture and placed into a polystyrene tube containing the potassium salt of ethylene diamine tetraacetic acid (EDTA). We transferred the blood into a 50 ml conical tube, rinsed with 1x PBS and refilled to 50 ml with 1× PBS. We placed 25 ml of the mixture on 15 ml Ficoll (2 tubes) (Lymphoprep, Cat # 07801) and centrifuged 20 min at 700 g, 20°C. We aspirated the upper phase and transferred the zone containing PBMCs (Peripheral blood mononuclear cells) into a new 50 ml tube with 10 ml 1× PBS (2× Ficoll into one 50 ml tube). This was filled to 50 ml with 1× PBS (with 10% FCS) and centrifuged 10 min at 450 g, 20C. The supernatant was discarded and the pellet resuspended in 1 ml 1× PBS, filled up to 50 ml and centrifuged 10 min at 200 g, 20C. The supernatant was discarded and the pellet resuspended in 100 µL of PBS and 10 ul of FITC-labeled CD3 antibody and further incubated on ice for 20 minutes in the dark. Then we washed the cells in PBS (with 10% FCS) by centrifugation for 10 min at 450 g, 20C. The supernatant was discarded and the pellet resuspended in 1 ml of Phosflow™ Lyse/Fix Buffer (Becton Dickinson, Cat# 558049) and in 3 ml PBS (with 10% FCS) and further incubated at 20C for 20 minutes. Then, we repeated the washing step. Excess supernatant was aspirated off prior to the kinetic experiment, and cells were resuspended in 450 µL of PBS (with 10% FCS). Then, we proceeded with the kinetic experiment as described below.

2.5 Kinetic experiment overview

Time series of mean fluorescence intensity (MFI), hereinafter referred to as kinetics, were measured as follows. A volume v₂ of anti-Mouse Ig kappa bead suspension (described in Sec. 2.3) or human blood cell suspension (described in Sec. 2.4) was resuspended in buffer (50 and 40 µL of PBS, respectively). Then, volume v₁ of PE-labeled antibody (described in more details in Sec. 2.1) was added to the mixture of microbeads or cells to initiate the antigen-antibody binding reaction. Then, at certain time points (0.16 min, 1 min, 3 min, 9 min, 27 min and 81 min) 8 µL of the mixture were resuspended in a relatively large volume of PBS (300 µL) in order to stop the reaction. After all sampling was completed, the microbeads or cells were analyzed with the flow cytometer. The reactions and measurements were carried out at room temperature.

The reaction kinetics of the microbeads and of the cells were measured for five different combinations of microbead-antibody and nine combinations of cell-antibody concentrations (i.e., 5 or 9 v₁, v₂ combinations). The resulted antibody concentrations varied from 1.5×10⁻¹⁰ M to 1×10⁻⁸ M.

2.6 Instrument and Data acquisition

We collected 3000 microbeads at each time point, and 30,000 cells at each time point for the human blood sample, using an LSRII digital flow cytometer with 5 lasers (355, 405, 488, 561, and 640 nm), 2 light scatter detectors, and 14 fluorescent detectors utilizing DiVa software (BD Biosciences). MFIs in the PE fluorescence channel for microbeads were calculated in each measured sample for single microbeads as gated in a forward light scattering (FSC) versus side light scattering (SSC) cytogram. MFIs in the PE fluorescence channel for the CD3⁺CD8⁺ subset of cells were obtained by gating the lymphocytes singlets in the light scattering (FSC, SSC) cytograms and the CD3⁺CD8⁺ lymphocyte subset in CD3 versus CD8 cytograms.

The LSR-II electronics includes both analog and digital baseline restoration that prevents free dye in the samples from affecting the MFIs of the microbeads or cell populations.

In order to evaluate the concentrations of beads and cells in samples we performed volumetric measurements using the sample flow rate described in the datasheet for the LSRII digital flow cytometer [11]. All the measurements were made at a medium speed of about 100 particles per second. The stability of flow rate was confirmed by the linearity of number of events versus time (R²=0.9988).

3 Theory

3.1 Acceleration of the reaction during mixing

In our experiments the diffusion-limited condition assumed in the reaction model only becomes applicable after the initial mixing of microbeads or cells with antibody. A substantial amount of antibody binding occurs during this initial mixing, leading to relatively large MFIs at the earliest time points. This accelerated reaction before the first time point can be accommodated in the model by adding a time shift parameter t₀ for the difference between the apparent and the actual starting times. The fitted values for t₀ will also adjust for small effects like cell autofluorescence and possible incomplete stopping of the reaction after the final dilution.

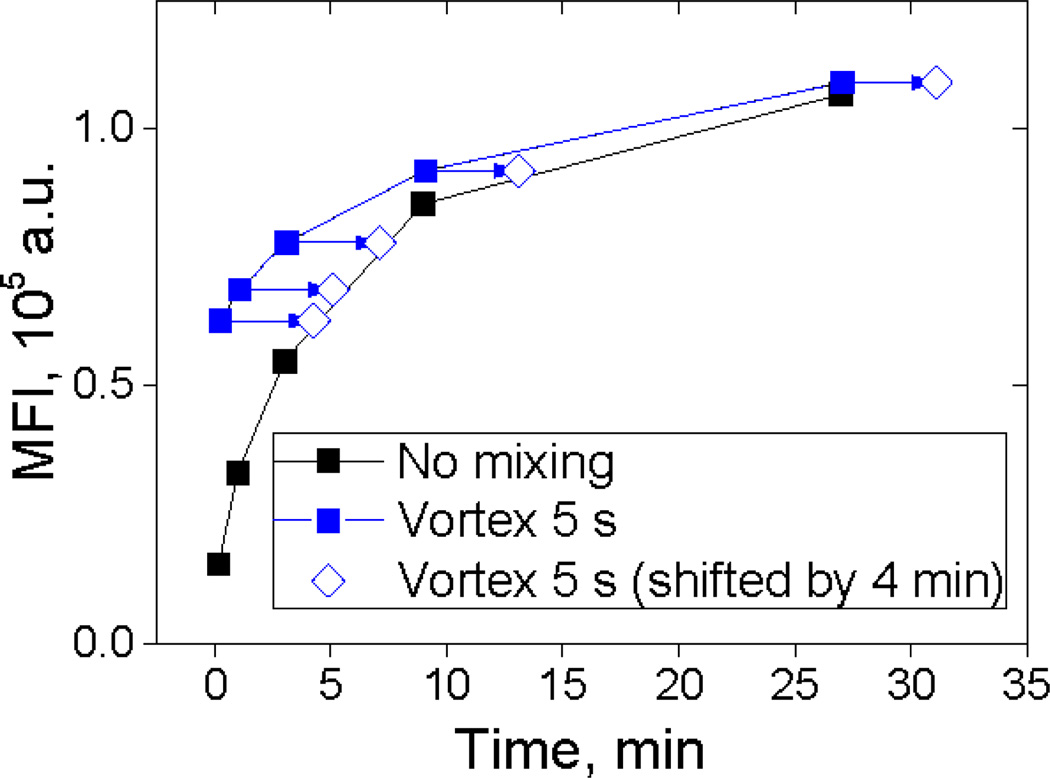
To test the hypothesis of reaction acceleration during mixing, we measured a time-series of MFIs with the same concentrations of reagents with and without additional mixing (Fig. 1). Evidently, adding 5 seconds vortexing after minimal initial mixing results in an effective time shift t₀ of about 4 minutes.

Fig. 1.

An example of MFI kinetics for Anti-Mouse Ig kappa microbeads binding IgG mouse monoclonal antibody (described in Sec. 2.1, 2.3). Time-series of MFI measured with and without additional mixing. Arrows represent time shift of 4 min.

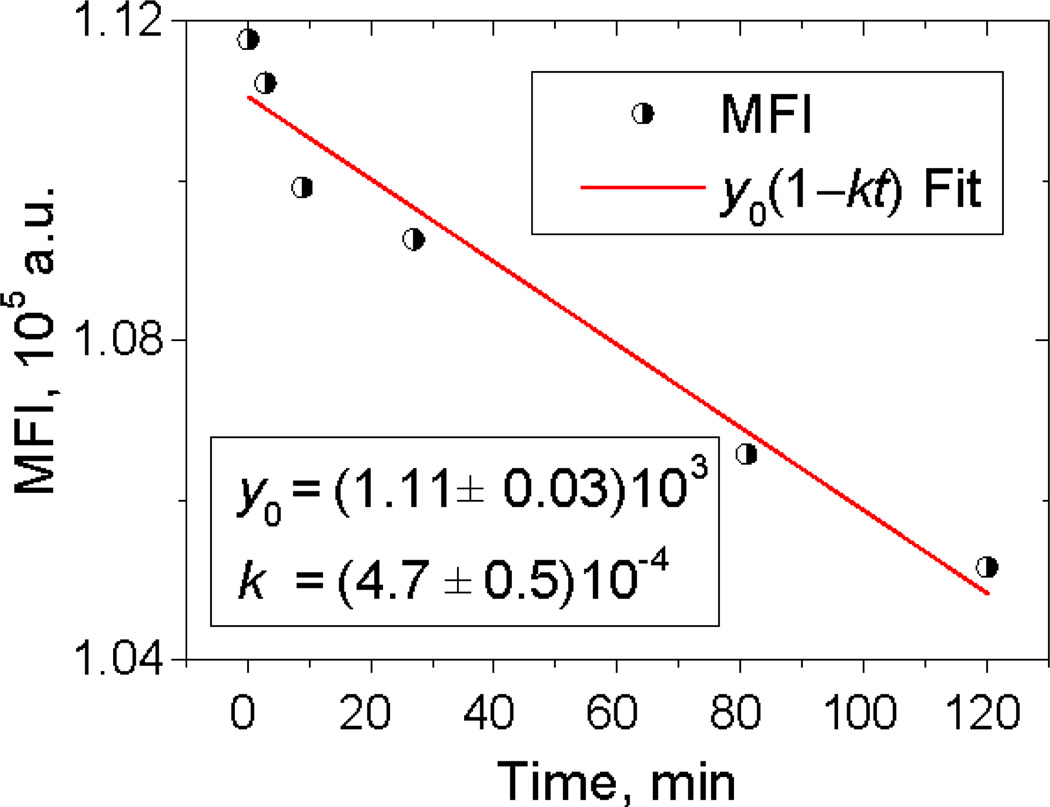
After final dilution by a certain factor, the reaction rate slows down by the same factor. In the case of a long delay between dilution and measurements, continuing slow reaction can contribute to time shift effect. However, this effect can be minimized by optimization of the dilution and measurement procedures. Ideally, the MFI should be measured just after dilution, but this can be impractical, especially when using flow cytometer in a shared research laboratory. Instead, we performed the dilutions for all of the time points and measured all of the samples in a short time at the end. In this case, the recommendation is to minimize the gap between the end of the kinetics sequence and the start of measurements. In our experiments, this gap was about one hour, which changes the MFI value by no more than 4% (see Fig. 2). The stopping procedure might be improved by including an excess of unconjugated antibody in the dilution medium.

Fig. 2.

The decrease in MFI after 25-fold dilution of the reaction mixture after the incubation of 10⁻⁹ M of receptors (tethered to beads) with 10⁻⁸ M of antibody during 81 min. Linear fitting was used to evaluate the rate constant of this decrease k, which is an estimate of reverse reaction rate constant k₋.

3.2 General equation for the Temporal evolution of MFI

To describe the temporal evolution of the fluorescence profile, we used the mathematical model for reversible antibody-antigen binding published elsewhere [8]. The model is applicable for independent binding sites, i.e., when the size of the binding site is much less than the distance between binding sites [12]. We extended the model by accounting for time shift t₀ (Sec. 3.1). This model allows one to analyze the temporal evolution of MFI (ȳ) with respect of the following parameters: fluorescence signal per antibody molecule α, concentration of particles (beads or cells, for instance) c, total concentration of binding sites X₀, total concentration of antibody A₀, reaction rate constant k₊ and the equilibrium constant K:

$$\overline{y}=\alpha \frac{A_0}{c}\frac{y_1^{\prime }{y}_2^{\prime }·[\text{exp}(k_{+}{A}_0(y_1^{\prime }-y_2^{\prime })(t+t_0))-1]}{y_1^{\prime }·[\text{exp}(k_{+}{A}_0(y_1^{\prime }-y_2^{\prime })(t+t_0))-1]-y_2^{\prime }},$$ (1)

$$y_{1,2}^{\prime }=\frac{1}{2}(1+\frac{X_0}{A_0}+\frac{K}{A_0})\pm \frac{1}{2}\sqrt{{(1+\frac{X_0}{A_0}+\frac{K}{A_0})}^2-4\frac{X_0}{A_0}}$$

In the present work, although some experiments included kinetics series in non-saturating conditions, the reverse reaction has small influence on the kinetics. We confirmed this with the following observations: after dilution of beads incubated with the excess of antibody (~10⁻⁹ M of antibody to ~10⁻¹⁰ M of receptors) for 81 min, the MFI decreases in time with the initial relative rate near 5·10⁻⁴ min⁻¹ (Fig. 2). Since the decrease is due to the reverse reaction, this value is an estimate for the reverse reaction rate constant. Together with the measured reaction rate constant (see Sec. 4.4) this gives the equilibrium constant K in order of 10⁻¹² M. We numerically tested Equation (1) for this value of K and the experimental conditions used in this work with the result that the reverse reaction makes a negligible contribution, changing the saturation value by less than 0.5%.

3.3 Irreversible binding: relationship between parameters

Hereinafter we neglect the reverse reaction, i.e., consider the dissociation constant to be zero (K→0). In this case, Eq. (1) can be reduced as follows. First, we rewrite all the parameters with respect to the concentration of particles c: n=X₀/c − mean number of binding sites per particle (the parameter of interest, which is to be determined), a₀= A₀/c, ǩ₊= k₊c. This leads to the following simplified equation:(1):

$$\overline{y}=\alpha n\frac{\text{exp}\left({\stackrel{(}{k}}_{+}{a}_0\right(1-\frac{n}{a_0})(t+t_0))-1}{\text{exp}\left({\stackrel{(}{k}}_{+}{a}_0\right(1-\frac{n}{a_0})(t+t_0))-\raisebox{1ex}{$n$}\!\left/ \!\raisebox{-1ex}{$a_0$}\right.}=P_1\frac{\text{exp}[P_2(1-P_3)(t+P_4)]-1}{\text{exp}[P_2(1-P_3)(t+P_4)]-P_3},$$ (2)

where P₁ = αn, P₂ = ǩ₊a₀, P₃ = n/a₀ and P₄ = t₀. The equation (2) is function of 4 parameters, and they can be determined by fitting experimental kinetics data. The MFI evolution itself is in general controlled by t₀ and 4 parameters of interest (α, n, ǩ₊ and a₀). Therefore, we need to know at least one of the 4 parameters independently to determine other ones.

Consider that we want to determine the number of binding sites per cell n (antigen quantification) given the measured kinetics. Let all the parameters P₁ – P₄ be determined by fitting. Three situations would allow us to complete the evaluation:

1. The fluorescence signal generated per antibody molecule α is known from calibration.

   This situation is the most typical. In this case, the number of binding sites n can be found as P₁/α. Moreover, n can be estimated from just the last kinetics point, assuming that saturation is achieved at that time. However, the present work is aimed at avoiding routine calibration.

2. The antibody concentration A₀ is known/previously measured.

   In this case n=P₃a₀= P₃A₀/c. The antibody concentration is usually provided in the datasheet; however, the accuracy of this value is rarely given, and it should be double-checked by other methods prior to use for antigen quantification. Furthermore, the concentration is subject to variation over time due to antibody aggregation.

3. The rate constant k₊ for the given binding reaction is known/previously measured.

   In this case n=P₃P₂/ǩ₊= P₃P₂/k₊c. Reaction rate constants are known for relatively few antigen-antibody pairs; however, once the rate constant is known, it allows one to measure n independently of instrument settings, reagent concentrations and time. In this sense, k₊ is the most universal parameter. However, n is determined by the combination of two model parameters instead of one, which could result in slightly larger uncertainty compared to previous cases.

We emphasize here that fitting by Eq. (2) allows one to quantitate the antigen on target particles as soon as one other parameter of the system is known. This could be the signal per antibody molecule α, the antibody concentration a₀ or reaction rate constant ǩ₊. In this sense, the time-consuming repetitive calibration procedure is equivalent to just knowing the rate constant, which is the universal characteristic of the interacting molecules. Application of the rate constant approach is limited by the lack of measured k₊ values for most antigen-antibody pairs of interest. Therefore, preliminary experiments to evaluate k₊ are likely to be necessary. Ideally, vendors would measure the value of k₊ in house using an α value calibration once for each specific lot of antibody and provide this information in product description. Another limitation is the dependence of the reaction rate constant on temperature, pH and other parameters, which, however, can be controlled during the measurement.

Determination of model parameters by fitting constitutes the solution of non-linear regression problem, which gives values of P₁ – P₄ together with their precision. The latter depends on the experimental conditions. For instance, in antibody excess Eq. (2) tends to ȳ =αn (i.e., independent of a₀ and ǩ₊), which results in large errors in determining these parameters. A similar situation will occur in the case of receptors excess.

The model (2) was used to fit the experimental kinetics of MFI. In each experiment the time shift t₀ was determined separately for each kinetics time series, and other parameters (P₁– P₃) were the same with adjustments for different dilutions. Fitting was made with OriginLab Origin 9.1 using Levenberg–Marquardt algorithm. We did a multistart procedure, i.e. ran the fitting many times at different initial values of the parameters and observed one solution that agreed visually with experiment and had the squared error norm much less than others. It also gave parameters consistent with our preliminary estimates. The script used is available upon request.

4 Results and discussion

4.1 Anti Kappa beads: multi-kinetics fitting

We first performed kinetic experiments as described in Sec. 2.5 with anti-Mouse Ig-kappa capture beads (Sec. 2.3). The fluorescently-labeled monoclonal antibody (anti-CD8α-PE, Sec. 2.1) was added to the bead suspension to initiate antibody-antigen binding. The mean fluorescence intensity (MFI) of ~3000 beads was measured for each time point (0.16, 1, 3, 9, 27 and 81 min).

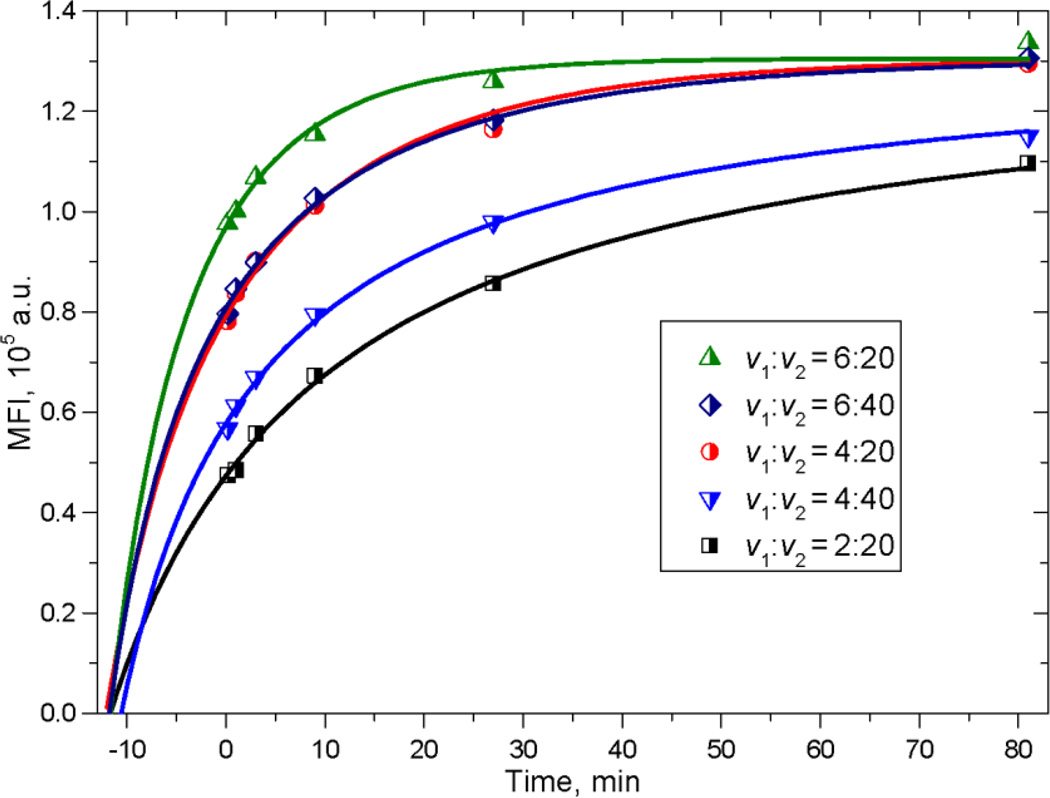
We measured 5 time-series of the MFI (kinetics) for different ratios of antibody:antigen by mixing different volumes of reagents, i.e., 2 to 6 µL of antibody and 20 to 40 µL of beads. This was done to span a range of saturating and non-saturating conditions. Five measured kinetics series are shown in Fig. 3. We carried out composite fitting of these data with the theoretical expression for the evolution of mean fluorescence over time in Equation (2) with appropriate adjustments for v₁ and v₂ of each time series. The corresponding curves are shown as solid lines.

Fig. 3.

Measured time-series of MFI (dots) and theoretical curves (solid lines) obtained by fitting. The fitting parameters together with their errors are shown in Table 1. Volumes v₁ and v₂ of antibody and beads, respectively, were added to a constant volume of the reaction suspension (see Sec. 2.5).

Fitted parameters corresponding to v₁:v₂ = 1:1 are presented in Table 1 together with their precision, which is quite good: 0.7% for α·n, 6% for ǩ₊·a₀ and 4% for n/a₀. P₃ = n/a₀ = 9.5·10⁻² adjusted for the actual values of v₁:v₂ = 4:40 and 2:20 gives an antibody/binding site ratio (a₀/n) of 1.05 which does not label to saturation in 81 minutes (see Figure 3) while the highest curve with v₁:v₂ = 6:20 has a₀/n = 3.15 and is very close to saturation at 27 minutes. The values of initial time t_0i are essentially the same for all kinetics (~12 min), indicating reproducibility in the mixing procedure.

Table 1.

Parameters of fitting and their standard errors.

Parameter	Value	Standard Error
P1 = α·n	1.30×105	1·103
P2 = ǩ+·a0, min−1	1.7	0.1
P3 = n/a0	9.5·10−2	4·10−3
t01, min	12	1
t02, min	12	1
t03, min	12	1
t04, min	11	1
t05, min	12	1

4.2 Reaction rate constant instead of calibration?

The parameters shown in Table 1 can be evaluated by fitting without calibration, but they are not enough for antigen quantitation. We used Quanti-BRITE beads to obtain the signal per antibody molecule α = 1.99±0.01 as described in Sec. 2.2. Using the fitted value of P₁ = α·n = (1.30 + 0.01)·10⁵, we obtain the amount of antigen per bead n = 65.6·10³. Then we can calculate a₀ = 69·10⁴ and ǩ₊ = 2.5·10⁻⁶ min⁻¹.

Given the value of α and assuming that the maximal fluorescence intensity observed in Figure 3 represents full labeling, one can evaluate n without any fitting and obtain the similar result of n = 67.2·10³. This standard approach to antigen quantitation confirms the fitting results, but it does not provide the other parameters of interest.

The idea of the present work is to avoid direct calibration. Since the relationship between fitting parameters P₁–P₃ and physical parameters α, a₀, ǩ₊ and n is unambiguous, one can use α, a₀ or ǩ₊ equivalently to find n. Imagine that the signal per antibody molecule α is not measured, but another parameter is known and has the value shown in Table 2. The values of other parameters would be unchanged but expressed by different combinations of P_i. For instance, if α is known, n = P₁/α; if ǩ₊ is known, n = P₃·P₂/ǩ₊. However, the precision would be different in these cases, since each P_i has its own uncertainty, as well as the uncertainty in the known parameter. In the case of small uncertainties, the overall precision can be approximated by adding the relative errors. The corresponding standard errors (assuming that the known parameter is absolutely accurate) are shown in Table 2 for all three situations discussed in Sec. 3.3. The largest relative errors are about 10%.

Table 2.

Values of parameters determined from fitting and calibration. Precision of parameters for three different situations are also shown.

Parameter	Value	SE (α is known)	SE (a0 is known)	SE (ǩ+ is known)
A	1.99	-	0.1	0.2
a0	69·104	3·104	-	4·104
ǩ+, min−1	2.5·10−6	0.3·10−6	0.1·10−6	-
N	65.6·103	0.4·103	2.8·103	6.6·103

The idea of using reaction rate constant ǩ₊ instead of the signal per antibody molecule α as the known parameter for evaluating the others is very attractive. First, the rate constant is independent of the specific instrument and can be recalculated for different fluorochrome labels (using the theory published in [12]).We emphasize that no experiment-specific calibration would be needed. Second, the rate constant is determined only by the interacting antibody-antigen pair (assuming that the temperature and pH are controlled). This suggests that it would be valuable to develop a database with rate constants for different couples of specific molecules. The only limitation is that concentration of cells must be known to relate k₊ and ǩ₊. The concentration, however, can be estimated without any additional measurements by using a cytometer with volumetric sample delivery or by the approach discussed in Sec. 2.6. The concentration of beads amounted to 6.4·10⁶ ml⁻¹; the corresponding absolute values k₊ and A₀ are presented in Table 4.

Table 4.

Absolute values for the microbeads and T-cells. Estimated values and their standard errors are given in parentheses.

Parameter	Microbeads (anti-mouse κ)	T-cells (CD8)
N	(65.6±0.4)·103	(28.8±0.6)·103
c0, mL−1	6.4·106	4.0·106
A0, mL−1	(4.4±0.2)·1012	(5.6±0.5)·1012
k+, M−1min−1	(2.3±0.3)·108	(3.1±0.4)·108

4.3 Is one-kinetics fitting possible?

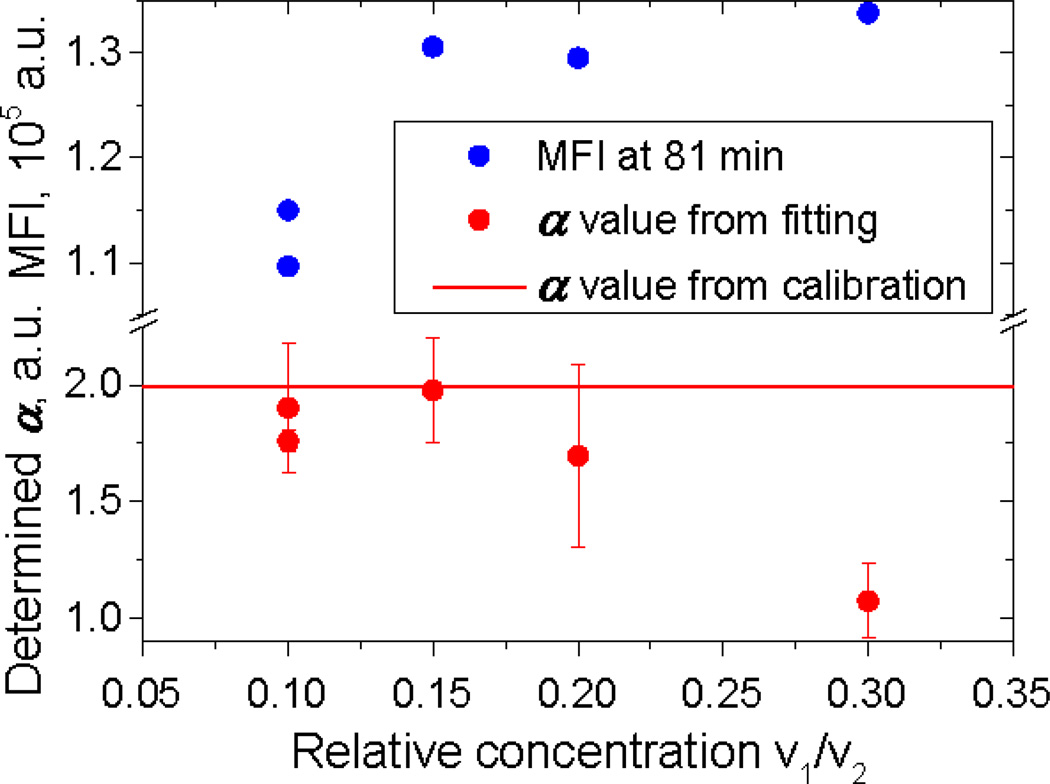
From a practical point of view, it is undesirable to measure several kinetics since it is time-consuming. On the other hand, unfortunately, one curve is not sufficiently informative to give four parameters with small errors. Therefore, the question arises whether it is possible to obtain at least α and n without calibration using only one time series. The rate constant and the antibody concentration (or one of them and their product P₂) are considered known, i.e., determined from preliminary experiments. For this example, we used the rate constant and P₂ values from multi-kinetics fitting (Table 1). Fixing these values, we performed fitting for each of the measured kinetics separately.

The closest match to the calibrated α value and the lowest standard error were found for v₁/v₂ = 0.15 where the antibody/binding site ratio is about 1.6. The fits for v₁/v₂ = 0.10 and 0.20 have higher standard errors, and the highest concentration fit misses the calibrated value entirely. Therefore, single kinetics fitting is useful only if the antibody/binding site ratio is quite close to the optimum.

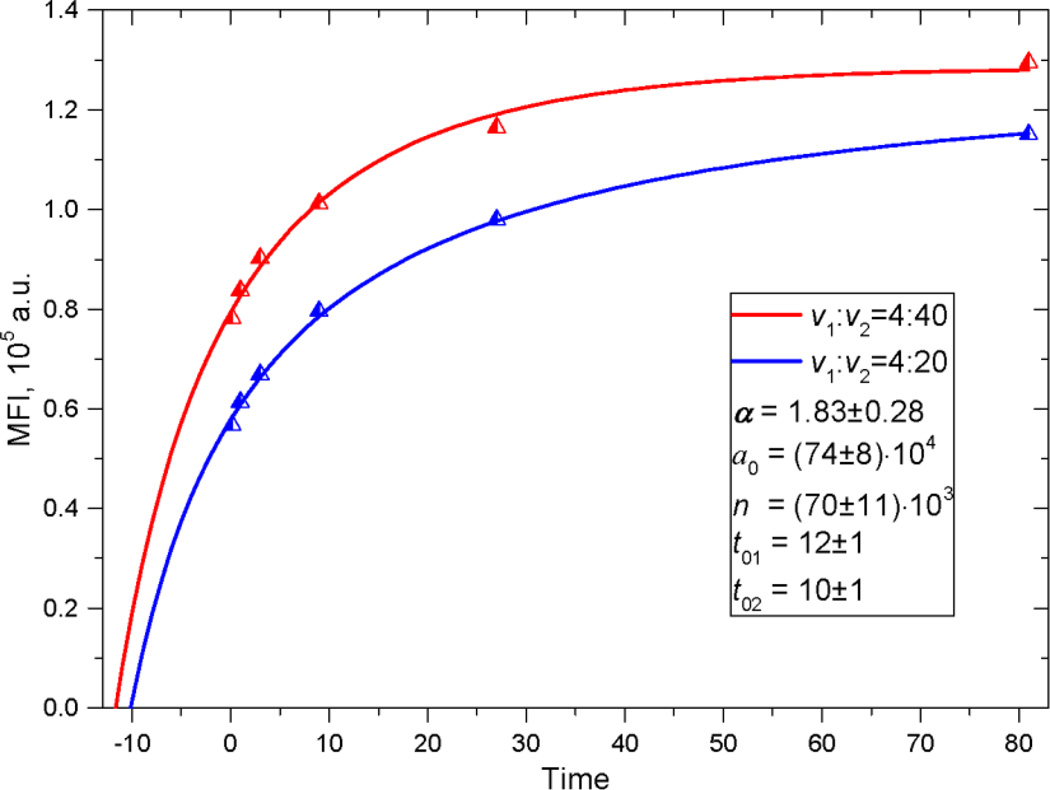
Another possibility is to use two kinetics on opposite sides of the optimal ratio. With two curves we can evaluate all parameters simultaneously, without fixing P₂. The example of fitting is shown in Fig. 5. The value of 1.83±0.28 is well within one standard error of the calibrated value, but this is not as good as the standard error estimated for the full composite fit of 0.2 (see Table 2).

Fig. 5.

The example of double-kinetics fitting. The rate constant has been fixed (taken to be known a priori)

4.4 Human T cells

In this section, we study human cytotoxic T-cells. They interact with antigen-presenting cells through TCR receptors that bind MHC-I tetramer.

The CD8 co-receptor plays critical role for this binding [13]. The CD8 increases the binding rate by two orders of magnitude, approximately up to the CD8-MHC I reaction rate constant. The latter is in the order of 10⁵ M⁻¹ s⁻¹ [14]. The cooperative effect is also confirmed by the fact that anti-CD8 antibody blocks TCR-MHC I binding [15]. This implies that the CD8-anti-CD8 reaction rate is much faster; however, as far as we know, this reaction has not been well characterized, i.e., the rate constant is not available in the literature. By contrast, the number of CD8 co-receptors on the T-cell surface n was measured by flow cytometry [16] and amounted to ~2.5·10⁴.

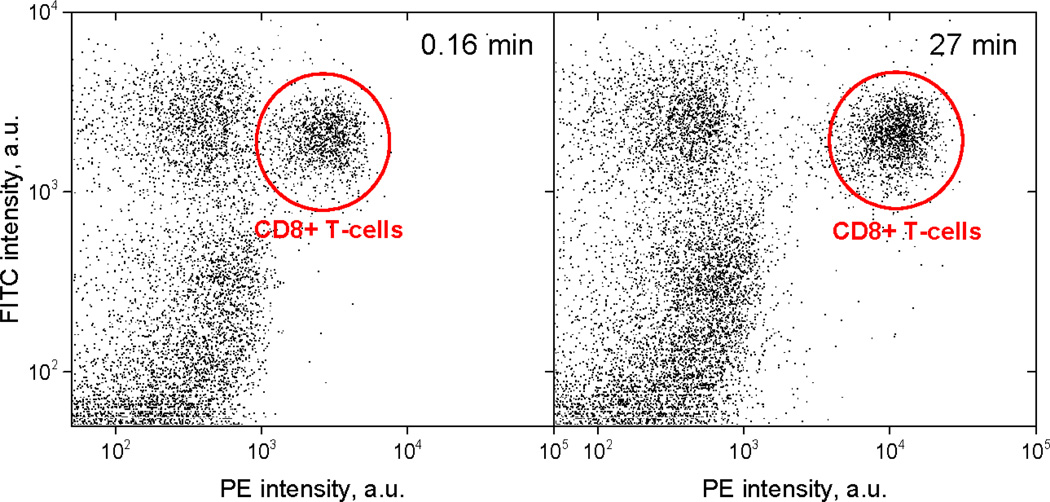
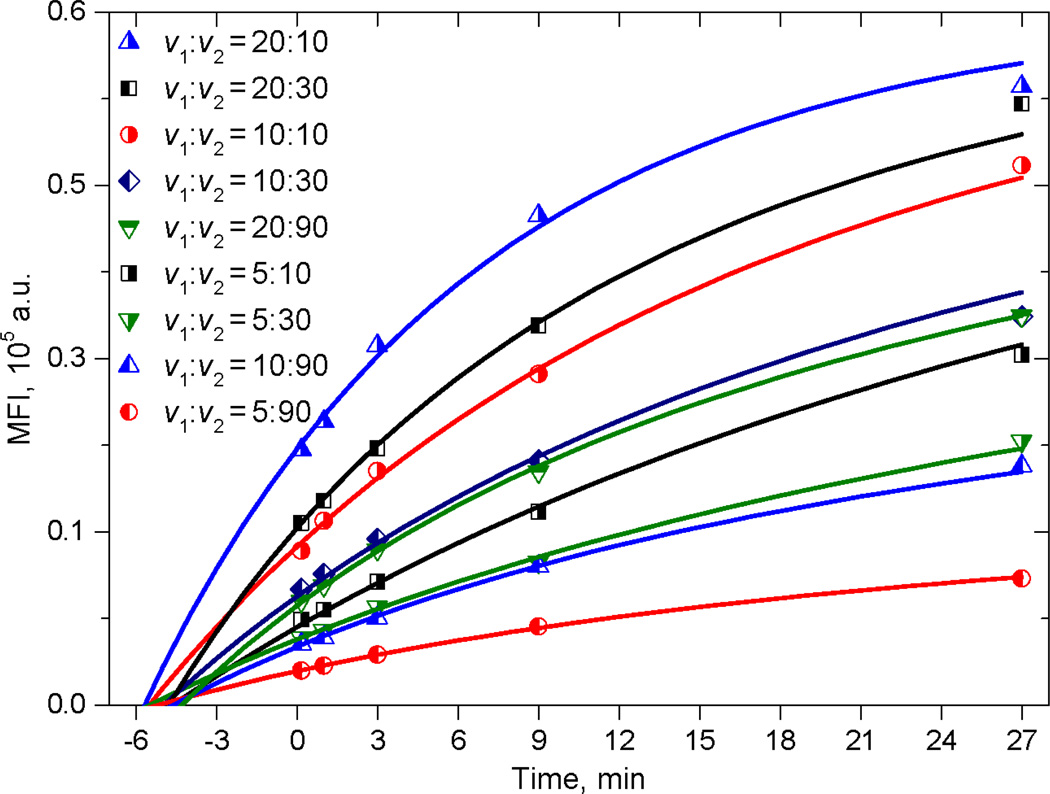
Kinetics experiments for CD8-antiCD8α binding were carried out as described in Sec. 2.5. The evolution of the CD8+ T-cell fluorescence intensity is illustrated in Fig.6. The similarity of the CD3+CD8− populations at about 400 MFI in both the 0.16 min and 27 min panels indicates that non-specific binding is negligible in this system. We measured kinetics for 9 combinations of antibody and cell concentration (Fig. 7) and limited the time series to 27 min instead of 81 min to make the measurement more practical. Each of the kinetics consists of 5 time points – 0.16, 1, 3, 9 and 27 min. We made a 10-fold pre-dilution of the antibody to provide antibody in the range of maximum sensitivity in convenient volumes.

Fig. 6.

The growth of mean PE intensity of the population of human cytotoxic T-cells over time: (left) 0.16 min and (right) 27 min after addition of IgG PE-labeled antibodies specific to CD8α. Each plot includes cells in the lymphocyte peak as gated on a plot of FSC versus SSC. The axes: Y is the fluorescence intensity in the FITC channel (FITC-labeled CD3 antibody, see Sec. 2.1); X is the fluorescence intensity in the PE channel (PE labeled CD8α antibody, see Sec. 2.1). Each dot corresponds to one cell.

Fig. 7.

Kinetic experiment for T-cells (dots) and theoretical curves obtained by fitting. Volumes v1 and v2 of antibody and cells, respectively, were added to a constant volume of the reaction buffer (see Sec. 2.5)

The results of fitting are shown in Table 3. First, we used the signal per antibody molecule α=2.10±0.02 obtained from Quanti-BRITE calibration and the cell concentration obtained as described in Sec 2.6 to measure the mean number of receptors per cell n, the antibody concentration A₀ and rate constant k₊. All of the obtained values are shown in Table 4 (right column) together with values obtained in experiments with microbeads (left column).

Table 3.

Parameters of fitting and their precision.

Parameter	Value	Standard Error
α·n	61·103	1·103
ǩ+·a0, min−1	0.29	0.02
n:a0	2·10−2	2·10−3
t01, min	5	1
t02, min	5	1
t03, min	6	1
t04, min	5	1
t05, min	5	1
t06, min	5	1
t07, min	5	1
t08, min	5	1
t09, min	4	1

The determined A₀ is close to but slightly larger than the value obtained in the microbead experiment. However, both determined A₀ values are approximately 5 times lower than specified in the reagent documentation (Sec. 2.1), which can be related to, e.g., degradation of antibody over time or aggregation and sedimentation of molecules in the bottle.

The rate constant k₊ has a reasonable value, which is about one third higher than that of Ab-beads reaction. The difference can be related to the different binding sites of the antibody since the reaction rate is approximately proportional to the third power of the size of binding site [8].

Considering the variability among human subjects, the number of receptors per cell is in good agreement with the literature [16].

The binding rate constant k₊ can also be used in this case instead of calibration. Parameter values and their standard errors for three different situations (see Sec. 3.3) are presented in Table 5. We conclude that the knowledge of the reaction rate constant can completely replace the repetitive calibration procedure.

Table 5.

Values of parameters determined from fitting and calibration. Precision of parameters for three different situations are also shown.

Parameter	Value	SE (α is known)	SE (a0 is known)	SE (ǩ+ is known)
A	2.10	-	0.2	0.4
a0	141·104	13·104	-	10·104
ǩ+, min−1	2·10−6	0.3·10−6	0.1·10−6	-
N	28.8·103	0.6·103	3·103	5·103

From the binding rate constant k₊, it was possible to estimate the radius b of the binding site (a circular approximation of the shape of the site placed on a spherical reagent) using following expression [12]:

$$k_{+}=N_1{N}_2\frac{k_{B}T{b}^3}{12\eta }{(\frac{1}{R_1}+\frac{1}{R_2})}^3$$ (3)

where η is the viscosity of the media, k_B is the Boltzmann constant, T is the temperature; R₁ and R₂ are radii, N₁ and N₂ are valences of the first and second reactants, correspondingly. It should be noted that equation (3) is applied if bond formation is diffusion limited, - this is not necessary the general case, but this is true for many particular antibodies. The radius of the beads in our experiments was 3 µm (approximately the same as the radius of the cells). The radius of antibody molecules can be estimated from the diffusion coefficient using Stokes–Einstein equation [12]:

$$D=\frac{k_{B}T}{6\pi \eta R}$$ (4)

Since the shape of the antibody molecule is not spherical (the diffusion coefficient depends also on the shape), equation (4) is an approximation that can be used to estimate the radius of the equivalent spherical particle (which has the same diffusion coefficient as the antibody molecule). On the other hand, the diffusion coefficient of the molecule can be estimated using the known relationship [17] between the diffusion coefficient (in cm² s⁻¹) and the molar mass (in Da), M, of a protein (in water at room temperature)

$$\mathit{\text{Log}}M=-16.88-3.51\mathit{\text{Log}}D$$ (5)

It is known that anti-CD8a molecule is the 150 kDa type IgG immunoglobulin with the valence N=2, and PE is the protein with approximate molecular weight of 240 kDa. Therefore, the molar mass of the IgG-PE complex is about 390 kDa that corresponds to the diffusion coefficient D_IgG-PE = 4.0·10⁻⁷ cm²s⁻¹ according to equation (5). Substituting this value of the diffusion coefficient into equation (4) one can estimate the radius of the IgG-PE complex R_IgG-PE = 5.4 nm that gives the binding site radius b=1.26±0.05 according to equation (3), since the binding rate constant k₊=(3.1±0.4)·10⁸ M⁻¹min⁻¹ (from Table 4), the valence of the ligand is 2 and the valence of the receptor is 1. It should be noted that the value of binding site radius b is more convenient constant of the antigen-antibody interaction, since it is independent on sizes of reagents, the type of fluorescent label and the medium properties (viscosity and temperature). The binding contant k₊ can be recalculated for other medium conditions, reagents and fluorescent labels using equation (3), if the value of the binding site radius b is known. Then the recalculated binding rate constant k₊ can be used instead of calibration for the modified system.

5 Conclusions

In keeping with the increasing importance of flow cytometry in biology and medicine, the number and data acquisition power of flow cytometry instruments has expanded greatly in the last few years [18,19]. Modern flow cytometry is particularly useful for disease diagnostic purposes because it enables simultaneous measurement of up to 20 markers on the inside and surface of each of a very large number of cells in a sample.

In particular, differences in antigen expression on small subsets of cells may be informative relative to clinical outcomes such as drug response, disease susceptibility and prognosis. Thus, subsets of cells identified by flow cytometry are frequently compared to find such differences. Specifically, comparisons between a disease sample and control, different genetically modified organisms, or samples that have undergone stimulations provide fundamental information [20, 21, 22]. Therefore, it is important to have appropriate methods to characterize these differences in a quantitative and useful way. However, while flow instrumentation has improved markedly to meet these needs, there is still a lack of appropriate methods for clinically useful quantitation of differences between subsets of cells in routine and high-throughput analyses. Here we demonstrate a new approach to the solution of the antigen number quantification problem. This work confirms that, instead of using calibrators in each experiment, the value of binding rate constant for the particular antibody-antigen reaction can be used in order to quantify the number of antigen molecules by flow cytometry. This approach is independent of specially prepared calibration beads and antibody reagents and can be applied to both low and high affinity antibodies, under both saturating and non-saturating binding conditions.

Fig. 4.

Titration curve (blue dots) and the signal per antibody molecule estimates α (red dots) with their precision (error bars). Volumes v₁ and v₂ of antibody and beads, respectively, were added to a constant volume of buffer (see Sec. 2.5). The α value closest to the real one is achieved at the transition point, i.e. when n≈a₀.