SEDPHAT – a platform for global ITC analysis and global multi-method analysis of molecular interactions

Abstract

Isothermal titration calorimetry experiments can provide significantly more detailed information about molecular interactions when combined in global analysis. For example, global analysis can improve the precision of binding affinity and enthalpy, and of possible linkage parameters, even for simple bimolecular interactions, and greatly facilitate the study of multi-site and multi-component systems with competition or cooperativity. A pre-requisite for global analysis is the departure from the traditional binding model, including an ‘n’-value describing unphysical, non-integral numbers of sites. Instead, concentration correction factors can be introduced to account for either errors in the concentration determination or for the presence of inactive fractions of material. SEDPHAT is a computer program that embeds these ideas and provides a graphical user interface for the seamless combination of biophysical experiments to be globally modeled with a large number of different binding models. It offers statistical tools for the rigorous determination of parameter errors, correlations, as well as advanced statistical functions for global ITC (gITC) and global multi-method analysis (GMMA). SEDPHAT will also take full advantage of error bars of individual titration data points determined with the unbiased integration software NITPIC. The present communication reviews principles and strategies of global analysis for ITC and its extension to GMMA in SEDPHAT. We will also introduce a new graphical tool for aiding experimental design by surveying the concentration space and generating simulated data sets, which can be subsequently statistically examined for their information content. This procedure can replace the ‘c’-value as an experimental design parameter, which ceases to be helpful for multi-site systems and in the context of gITC.

Introduction

Isothermal titration calorimetry (ITC) is a powerful, first-principles based technique to study molecular interactions label-free in solution with wide-spread applications in many scientific disciplines [1]. Unique among biophysical techniques, it observes directly the heat change ΔQ of a solution associated with a change of composition {Δc_i} during the titration of a macromolecular component in the cell with increasing amounts of its binding partner(s) [2,3]. The differences in heat between chemical equilibria along discrete steps of the titration are measured as the integral of the differential power applied to keep a sample and reference solution at the same temperature. As has been reviewed elsewhere in detail [2–6], the shape and midpoint of the resulting titration isotherm yields information on the association constant K_A, and therefore the free energy of binding, as well as information on the binding stoichiometry. The amplitude of such titration isotherms contains information on the molar enthalpy changes ΔH of molecular complex formation, which in turn may be interpreted in the context of structural thermodynamics. For systems with multi-site binding, ITC can provide information on stoichiometry and cooperativity of molecular complexes [7–14].

Unfortunately, similar to most binding saturation curves, individual titration isotherms usually have relatively low intrinsic information content, due to the shallow concentration dependency of complex formation predicted by mass action law [15 (this volume)]. Furthermore, dependent on the interaction enthalpies, even for multi-site systems only a single transition may be observed. Thus, the number of binding parameters of an interacting system can quickly exceed what can be confidently determined from the given data. This can be true even for ‘simple’ bimolecular reactions with 1:1 stoichiometry, if constraints in the available concentration and amounts of material hinder the implementation of optimal experimental conditions, if limitations in the sensitivity of the calorimeter require application of suboptimal conditions (such as high ‘c-values’ for high-affinity systems leading to essentially stoichiometric binding), or if uncertainties in the experimental concentrations exist. The relatively low information content of many ITC isotherms also often causes models with different binding mechanisms to describe the data equally well. In this case, independent knowledge (or assumptions) of the number and composition of complexes formed, their symmetry, and possible site-interactions is required for the justification of a particular model.

Strategies have been developed recently in several laboratories to enhance the information content of ITC, for example, related to experimental design [16,17], the improvement of the precision of isotherm data through advanced integration of the differential power trace [18,19], or the exploitation of kinetic data in the injection shapes [20]. Global strategies combine multiple experiments in global analyses of ITC (gITC) [9,21–28] and in global multi-method analysis (GMMA), the combination of ITC data with data from complementary biophysical disciplines [29–32,82]. Beyond merely organizing separate complementary experiments into a hierarchical, multi-stage interpretation, global analysis takes full advantage of all possible constraints of the model and the full statistics of the data by simultaneously and directly fitting all experimental data with one explicit global model. Natural applications of gITC analysis are multi-site binding processes of homo- and hetero-oligomerizing macromolecules [9–11,13,14,15 (this volume),23,33–37], displacement experiments [22,38,39], and protonation-linked and other linked binding analyses varying temperature to determine heat capacity changes or buffer composition to determine salt or other co-factor linkage [24,26,28].

SEDPHAT is a computational platform for global analysis of data from various biophysical techniques, including gITC, which has been widely adopted in ITC applications [11–14,15 (this volume),17,19,24,33–62]. Distinguishing aspects of SEDPHAT in comparison with other gITC platforms include the absence of data-specific or model-specific programming by the user, allowing for seamless combination of titration experiments in a graphical user interface, and offering many different pre-programmed multi-site models for two- and three-component systems [9]. For fully exploiting the advantages of gITC, the concept of an empirical ‘n-value’ as a combined parameter for concentration errors and numbers of sites [2] must be abandoned. In contrast, SEDPHAT exclusively allows for integral numbers of binding sites, and introduces explicit parameters accounting for errors in active concentrations, which may be shared among different experiments in the same global analysis [9].

The present communication has two goals: First, it reviews several extensions of SEDPHAT for the analysis of ITC data included since the original introduction [9]. Among those are a method for the unbiased, high-precision integration of the differential power trace [18], implemented in the companion program NITPIC [18,19 (this volume)] that we have developed to interface with SEDPHAT and automatically provide total heat changes including error estimates separately for each injection. Another companion program, GUSSI (by Dr. Chad Brautigam), can be spawned by SEDPHAT for improved presentation and publication quality graphs of the results of ITC and gITC. Further, greater flexibility in the treatment of concentration errors was introduced by distinguishing between inactive fractions and pure concentration errors. To allow more convenient statistical characterization of the analysis of ITC isotherms, automated methods to explore the error surface of the fit using F-statistics [63] were added. They include automated determination of confidence intervals of binding parameters (propagated from the error bars of the individual injection heats), the computation of error surface projections, as well as the display of two-dimensional error projections highlighting parameter correlations [30]. Finally, with the development of GMMA and the associated statistical tools in SEDPHAT, significant enhancement of ITC analyses became possible by incorporation of complementary data from orthogonal techniques [29–32]. A second goal of the present communication is to provide examples for gITC of single-site and multi-site interactions to demonstrate the potential of gITC. Since the design of experiments for multi-site systems is often non-trivial, we describe a new tool to simulate ITC and other types of data in SEDPHAT that will help to predict which experiments would be most useful to be combined in global analysis.

Methods

SEDPHAT Basic Principles and Resources

The input for SEDPHAT consists of tables of integrated heats and injection schedules, after peak integration of the raw thermograms. The peak integration can be accomplished in the stand-alone software NITPIC, which creates or appends a pre-formed SEDPHAT configuration. Alternatively, the input data can be created manually by exporting integrated data tables from instrument-specific software. (Data from a two-part experiment where the syringe is reloaded in between can be ‘stiched’ together simply by combining data rows of the integrated heat tables.) From the table of integrated heats (saved as “.dat”-file), SEDPHAT automatically creates a unified data file (‘xp’-file) including all necessary ancillary parameters. Global analysis is achieved simply be loading more than one data set, each of the same kind or of different kinds, including different titration configurations or data collected by methods other than ITC. This may be achieved by drag-and-drop of ‘xp’-files, by using the SEDPHAT loading menu functions, or by allowing NITPIC to extend an existing SEDPHAT configuration.

For a given interaction model and binding parameters, SEDPHAT calculates the populations of free and bound species on the basis of mass action law prior and after each injection, the finite differences between these equilibrium populations, and the associated changes in total heat content of the solution [9]. Differential equation based approaches [64–66] are not used due to the discrete nature of the injections. This affects the fit lines connecting the fitted values between each data point – in SEDPHAT these are linearly interpolated segments between the data points; this is a question solely of graphical representation without consequence for the data analysis and molecular binding parameters.

Independent of the interaction model, different approaches are available for the treatment of superimposed signals from heats of dilution (not including heats of pre-formed complexes, which are explicitly accounted for in the model): As default option, they are modeled as a constant baseline contribution to all isotherm points, to be refined in the fit. Alternatively, the baseline can be fixed, constrained to remain within a certain range of values (a new option added in SEDPHAT v.12.1) or eliminated and heats from a blank experiment with matching injections may be subtracted. (In addition, an option for a sloping baseline is available.)

To account for total concentration of components after each injection, values supplied from an instrument software, from NITPIC, or those calculated by SEDPHAT from the cell volume and injection schedule can be used, the latter assuming a full fixed-volume cell with either mixed or unmixed neck (which can accommodate different kinds of instruments, the default being the Microcal configuration). Any configuration of initial concentrations in cell and syringe may be used (and different ones in different experiments of the global analysis), accounting for pre-formed complexes that may be present in the syringe prior to injections.

Importantly, no non-integral binding sites are allowed. Rather, concentration errors can be treated explicitly for each component separately with concentration correction factors (which may be smaller or larger than 1.0), for example, corresponding to errors in the extinction coefficients if used for measuring concentrations. Alternatively, incompetent fractions (which are constrained to between 0 and 1) can be used to describe, for example, partially folded and therefore inactive fractions of proteins. In order to exploit existing constraints, these correction factors can optionally be shared between different selected experiments of the global analysis (e.g., concentration errors that originate from extinction coefficient errors may be linked to be equal in different experiments). They can also be constrained by user-defined bounds. (For example, assigning errors arising in amino acid based extinction coefficients bounds of +/−20% may seem reasonable [67].)

For global analysis, from a set of global binding parameters, which comprise those governing chemical equilibria and macromolecular properties, in combination with local parameters (which apply only to individual data sets, such as an optional baseline offset) and shared local parameters, a prediction for the binding isotherm is generated, and compared with the data of each experiment. A weighted global χ² of the fit is determined

$${\chi }_{r,\mathit{\text{glob}}}^2={\left(\sum _{e=1}^E{N}_e\right)}^{-1}\sum _{e=1}^E{w}_e^{-2}\sum _{i=1}^{N_e}\frac{{(y_{e,i}-f_{e,i}(\left\{p_{\mathit{\text{glob}}}\right\},\left\{p_{\mathit{\text{loc}},e}\right\}\left)\right)}^2}{{\sigma }_{e,i}^2}$$ (1)

(where E denotes the total number of experiments, N_e the total number of data points in experiment e, w_e a weight assigned to experiment e; y_e,i and ▯_e,i are data points and statistical errors of data acquisition, respectively, and f_e,i represents the fitting function dependent on the experiment type, interaction model, and the global and local parameters p_glob and p_loc,e, respectively) [29], which in its dependence on all adjustable parameters constitutes the error surface to be minimized to find the globally best fit. For fitting, the simplex, the Marquardt-Levenberg, and a simulated annealing approach are available.

The error analysis can be carried out either with a Monte-Carlo approach, or, more rigorously, with F-statistics based contours of the error surface [63,68]. In this method, one, or for a cross-correlation map two, parameters are fixed and all remaining adjustable parameters are optimized to allow a statistical comparison of the best-fit obtained under these constraints with the overall best-fit. An automated function to create these error projections is available; however, for difficult error surfaces it may be necessary to verify each fitting step and proceed manually with a series of optimizations incrementing the parameter of interest. For global analyses, cross-validation approaches are implemented to examine the information content of different data sets, as described in [29].

SEDPHAT v. 12.1 can be freely downloaded from sedfitsedphat.nibib.nih.gov/software, and an extensive web-based help system is available at analyticalultracentrifugation.com/sedphat. The companion programs NITPIC and GUSSI by Chad Brautigam – the latter used in the present work for all ITC graphs – can be downloaded freely from http://biophysics.swmed.edu/MBR/software.html. An email listserv-based user group is at https://list.nih.gov/cgi-bin/wa.exe?A0=SEDPHAT-L, and workshops on biophysical methods for protein interactions with a strong component of ITC analysis in SEDPHAT are held regularly at the National Institutes of Health, Bethesda, MD, and international locations (sedfitsedphat.nibib.nih.gov/workshop).

Simulation Tools

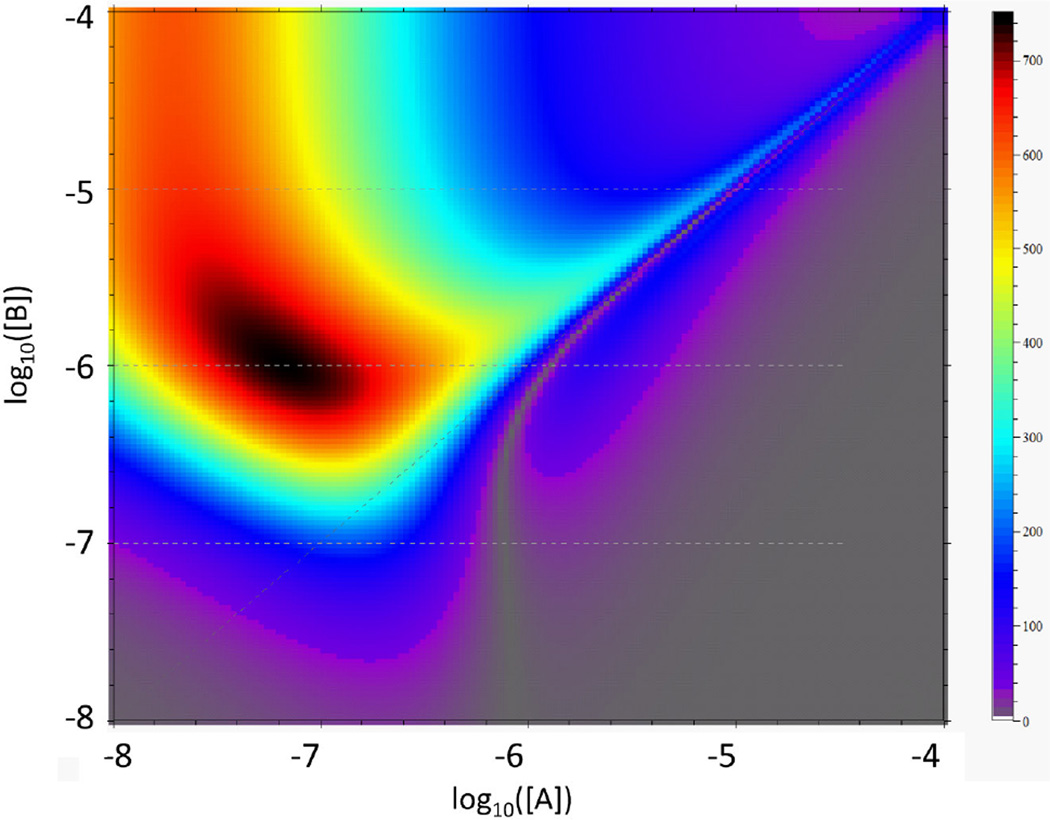
A recurring observation for multi-site binding processes is the difficulty in intuitively predicting the populations of the different complexes as a function of loading concentrations, which is required for the effective experimental design. To facilitate this process, mass action law calculator functions and species population plots were already previously implemented in SEDPHAT. To enhance experimental planning, we have now introduced functions to simulate experimental data from different biophysical methods and to graphically depict their information content [30]. We have adapted these tools to account for the particular experimental setup of an ITC titration, to allow a comprehensive survey of experimental conditions, binding isotherms, and calorimetric signal contributions: Cell and syringe concentrations can be selected from within a graphical representation of the binding isotherm as a function of total concentrations of all components {c,_tot}. The visualization displays color-coded values of the isotherms of various selected quantities. For two-component systems, these quantities are depicted on a grid of log-spaced total concentrations of the two components plotted in the abscissa and ordinate, respectively (Fig. 1A). For three-component systems (with components referred to as ‘A’, ‘B’, and ‘C’), the isotherm of interest is a three-dimensional volume, which is plotted along a stack of two-dimensional cross-sections that can be navigated with a slider or arrow keys. The cross-sections can be cut through the volume along constant c_tot,C, or diagonally with constant molar ratio of c_tot,C/c_tot,A, c_tot,C/c_tot,B, or c_tot,B/c_tot,A.

Figure 1.

Panel A: Screenshot of the SEDPHAT ITC visualization tool of the differential heats dQ/dc_A,tot for the titration of a component A into another component B (K_D = 0.1 µM, ΔH = −10 kcal/mol), which are shown in the form of a two-dimensional heat map (large negative enthalpy changes in gray/purple/magenta/blue, and small heat changes in red to black). The screenshot was modified to enhance the axis labels. In the plot, the plane of total concentrations (ranging logarithmically from 0.01 to 100 µM in each dimension) is cropped to the region that reflect experimentally observable concentrations if the maximum stock concentration of each component is 100 µM, provided a cell volume of 1400 µl and a total syringe volume of 300 µl. A left-to-right swipe with the mouse allows to delineate an experimental titration trajectory, indicated by the yellow circles connected by the black line, here reflecting 30 injections at 10 µl each of 45.6 µM A into the cell with initially 6.2 µM B – information that is provided after any trajectory is graphically entered. Additionally, the small inset shows the shape of heat changes of a putative experiment along this titration. The bank of buttons on the right allows depicting any fractional population of free or complex species in any component (light blue), as well as the fractional contribution of each species to the total heat changes (green). The bank of buttons on the left allows to switch the titration type, crop the display, pick another experimental trajectory, change binding parameters, switch to a differencing mode, and exit this display to simulate data for the trajectory shown. Panel B: Analogous isotherm for the same system for the injection of B into A, with an experimental trajectory of titrating 56.9 µM B into 5.7 µM A. Panel C: ITC data generated along the trajectories shown in Panel A and B.

The quantities that can be displayed in this concentration space include: the fractional population of each component in the free or any of the bound states; the differential changes in total heat content dQ/dc_tot in the cell along a titration; and the fractional contributions to dQ/dc_tot due to changes in any particular complex concentration. Due to the differential nature of the titration with increasing concentrations of one of the components, the surface of dQ/dc will assume different shapes dependent on the orientation of the titration, which can be switched by the user to simulate different experimental configurations (e.g., A into B and B into A for two-component experiments, and C into a mixture of A and B, or a pre-mixed solution of A and C injected in C, or many other permutation for three-component experiments).

In contrast to the species population and the heat content of the solution in the cell, which are state functions and can therefore be depicted unequivocally in the concentration space, any contributions from heats of dilution of preformed complexes in the syringe are trajectory dependent, since they are dependent on the total syringe concentrations. To address this for systems and experimental configurations where such pre-formed complexes can exist, an expected approximate syringe concentration can be specified upfront, which allows estimates for the heats of dilution from preformed complexes to be calculated. After selection of a suitable trajectory, the total syringe concentration for this trajectory may be selected to achieve a refined display of the total differential heats in concentration space. On the other hand, the added heat content from injection of pre-formed complexes are constant (for constant injection volumes) and lead to uniform offsets to the heat change throughout the entire isotherm. Therefore, they will not contribute to features in the isotherm display, and may usually be neglected in the exploration of experimental designs.

In the plots of titration isotherms in the concentration space, as illustrated in Fig. 1A and B, typically a diagonal transition can be discerned where saturation occurs, which increases in sharpness with higher concentrations of the component in the cell. This conforms well to the expectation of steeper saturation for conditions of higher c-value. The graphical representation, however, is more general and more informative than a single c-value, since it can visualize more complex features of the binding isotherms of multi-site systems (such as the cooperative ligand-linked dimerization in Fig. 3 below). Due to the directionality of the injection and the quantity dQ/dc_tot, the plot will look different for different injection strategies (compare Fig. 1A showing dQ/dc_A,tot and Fig. 1B showing dQ/dc_B,tot). The isotherm plot can be cropped such as to omit regions that are experimentally not feasible, as determined from user-provided maximum stock concentrations of either component and given cell and syringe volumes. This will constrain the feasible region in different ways, dependent on the directionality of the titration experiment.

Figure 3.

Relative species populations of complexes, weighted by the respective heat content, for a ligand-linked dimerization system where A exhibits weak self-association (K_D = 10 µM, ΔH_AA = −10 kcal/mol), and has a binding site for B (K_D = 1 µM, ΔH_AA = −5 kcal/mol) which cooperatively induces 10fold stronger self-association in A when liganded (ΔH_AAB − ΔH_AB = −2 kcal/mol). Shown are partial screenshots of the SEDPHAT display generated in the simulation function after pressing the species display buttons.

For the generation of simulated titration data, upon dragging the mouse horizontally (for A into B titrations) or vertically (for B into A titrations), a particular experimental trajectory can be mapped into the isotherm plot (black line in Fig. 1A), with user-selected number of injections, which are used as the basis for simulating a titration data set that is subsequently automatically loaded into the SEDPHAT analysis configuration (Fig. 1C). This simulated data set will appropriately account for any path-dependent contributions, such as the continuous change of total solution volume, how it is expelled from a fixed volume calorimeter, any dilution of pre-formed complexes, etc., just as in the fitting models for experimental data. Analogously, any experimental data set can be displayed as a trajectory in the isotherm plot for context (by using the small button ‘s’ below the quadratic button in the upper right corner of each experiment indicating the experimental number in the SEDPHAT window, or by using the corresponding Display menu function).

A graphical difficulty arises from the fact that the concentration space is plotted logarithmically, whereas the titrations are approximately linear, as determined by consecutive addition of fixed injection volumes. To aid in the graphical selection of titration conditions, after a trajectory is specified, and before it is committed to a simulation, a small plot showing the corresponding titration isotherm will appear (insets in Fig. 1A and B). The trajectory can then be refined if desired. After creation of a new simulated data set, if the existing configuration already contains a data set, then the newly simulated data will be added alongside, as an extension into a global ITC analysis. This allows one to examine the statistical properties of the new extended analysis, and helps to judge whether or not such an experiment provides significant new information and is worth carrying out.

As a further aid to guide the selection of optimal experimental conditions, the given plot data can be saved as a reference to be subtracted from the isotherms calculated for modified conditions. For example, by displaying finite differences in the plot after a small change of the parameter of interest, this tool can highlight which region of the isotherm will be particularly informative on a certain parameter,. Essentially, this provides an approximation of the derivative d(dQ/dc_tot)/dK, where K can be any binding parameter of interest. This is shown in Fig. 4 below to illustrate the sensitivity isotherms of differential heat to the cooperativity parameter for a simulated ligand-induced dimerization system. Similarly, it is possible to compare the isotherms from different binding modes, such as single-site vs two-site binding, and assess which concentration range would be expected to be most sensitive to an additional site.

Figure 4.

Different titration data sets created in SEDPHAT for the ligand-linked dimerization system of Fig. 3. Shown are screenshots of the SEDPHAT display of four loaded ITC titration experiments, represented in different quadrants, showing titration data points with best-fit lines in the customary plot as a function of molar ratio (Panel A), and in the context of the isotherms of differential heats (Panel B). All experiments simulate injections of A into B, except that in the upper right quadrant which is for injection of B into A. Concentrations were 7.1 µM B in the cell and 49.8 µM A in the syringe (upper left quadrant), 5.3 µM A in the cell and 55.6 µM B in the syringe (upper right quadrant), 1.4 µM B in the cell and 5.7 µM A in the syringe (lower left quadrant), and 2.5 µM B in the cell and 135.1 µM A in the syringe (lower right quadrant).

Overview of the Workflow for Data Simulation

Briefly, the sequence of user-driven actions for using the above simulation tool is as follows: First, the model needs to be selected to match the molecular interaction to be studied. Expected parameter values should be entered, including molecular weights, and unknown parameters to be refined in the analysis should be checked. Next, after selecting the function “ITC xp” in the “Generate” menu, basic ITC parameters (including cell volume) and expected noise can be entered, and the plots are generated. They can be visually inspected, and different quantities and different titration configurations can be selected using the on-screen buttons. The plot can also be centered to a different concentration range. The concentration space can be cropped to the available mg/ml concentrations of the samples. Setting a plot as “reference”, changing one (or more) parameter incrementally using the “new parameters” button, followed by “difference” will allow finite difference plots to be created, to show changes induced by modified parameter values. A swipe with the mouse, keeping the right mouse button pressed, will create a putative trajectory, provide concentration information for cell and syringe, and display a small inset with the shape of the resulting titration. The trajectory can be redrawn until it shows the desired properties. Finally, the “exit and simulate” button will leave the simulation tool and add the newly created titration data to the existing SEDPHAT configuration. An execution of the “Fit” function will calculate the best-fit to the simulated data, including any other data sets that may already have existed in the SEDPHAT configuration and have not been deactivated. Finally, the “automated confidence interval search w. projection method” found in the “Statistics” menu will create the report of the confidence intervals of the parameters of interest.

Results and Discussion

General Global Analysis Strategies of ITC titrations: Fragments, Replicates, and Concentration Errors

In most cases there are multiple simple opportunities to combine data into a global analysis. As most biophysical methods, unless the system under study has already been very well characterized, ITC typically requires some amount of experimentation so as to iteratively adjust the experimental conditions, including binding partner concentrations in cell and syringe, and the number of injections. In this process, often multiple isotherm data sets that are sub-optimal for a standard analysis are inadvertently produced. However, barring any preparative problems, this data still reports faithfully on the molecular interaction of interest, and when combined into a gITC analysis, they can significantly enhance the results.

This is illustrated in the data of α-chymotrypsin being titrated with soybean trypsin inhibitor, which has two binding sites (Fig. 2) [29]. When the analysis is confined to the single well-formed titration shown in red, for example, the 68% confidence interval for the enthalpy change ΔH_AB of the first site is 2.9 – 19.6 kcal/mol. However, when titrations that have either too high or too low ratio of syringe-to-cell concentration are added into a global analysis, the error interval shrinks considerably to 3.4 – 6.3 kcal/mol. Even better results are achieved after incorporating a replicate of the well-formed titration, and independent data (below and [29]).

Figure 2.

Titration experiments of α-chymotrypsin (CT) in 200 µl cell of an ITC200 MicroCal calorimeter (GE Healthcare) being titrated with 1.8 µl aliquots of soybean trypsin inhibitor (SBTI) [29]. With 20 µM CT in the cell and 83.7 µM SBTI in the syringe (red), a well-formed transition is observed. By contrast, with 22.7 µM CT in the cell (allowing locally for a concentration error) and 68.4 µM SBTI in the syringe no saturation is achieved, whereas with 3 µM CT in the cell and 83.7 µM SBTI in the syringe saturation is achieved too quickly. It is advantageous to include all experiments into a gITC analysis (solid lines), rather than solely analyzing the single well-formed data set, as reflected in the narrower confidence intervals of the binding parameters. For example, the confidence interval for ΔH_AB of the first site is 2.9 – 19.6 kcal/mol based on the red trace alone, and 3.4 – 6.3 kcal/mol for the joint analysis of all traces (see text).

It is often possible to carry out one or more replicates of an experiment. Unfortunately, averaging best-fit K_D-values from individual analyses of replicate experiments produces an ill-defined average, and taking their standard deviation as a measure of the uncertainty of K_D can vastly underestimate the true error. By contrast, the combination of all replicates into one gITC analysis is rigorous and fully exploits the statistical advantage of the additional data points, and the small number of ITC dta points makes this approach particularly advantageous.

In comparison with side-by-side analysis of replicates, the combination of different experiments usually offers a chance to implement constraints that improve the determination of binding parameters. If the concentrations of the interacting molecules are determined with the same method, or originate from the same stock solution (for example, proteins from the same batch of preparation), then it is reasonable to assume that the concentration errors (or incompetent fractions, respectively) are identical in each experiment. This opportunity can be further exploited in gITC by thoughtfully planning the preparation of adequate stock solutions to allow carrying out the entire sequence of experiments with the same material. If such relationships between the samples cannot be established, then concentration errors have to be treated as separate unknowns for each experiment in gITC.

Variation of Experimental Conditions

The possibility to carry out multiple experiments naturally offers the potential to enhance the analysis through the variation of experimental conditions. It can be expected that the combination of data from different experimental conditions becomes increasingly important with increasing number of binding sites and increasing complexity of the system. This is due to the fact that the binding isotherm will generally exhibit more features, which must be sampled along different paths to allow the full characterization of the system.

For simple bimolecular single-site systems, the best ‘c-value’ (the ratio of cell concentration to K_D) for optimal experiments has been much discussed [2,17,69–71]. As described out by Freiburger et al., it can be highly advantageous to analyze titrations obtained for multiple c-values (i.e., at multiple cell concentrations) jointly in gITC. This can naturally be accomplished in SEDPHAT, for any of the implemented binding models. This can allow, for example, the combination of an experiment with very low c-value, not carrying much information on the enthalpy change, with an experiment at very high c-value, where the steep transition does not carry much information on the binding constant, into a joint gITC analysis producing well-determined parameters. Broecker et al. have pointed out that in the analysis of data sets with different cell concentrations, it must be considered that the relative experimental noise decreases with increasing concentration (due to the larger heats) [17]. When using NITPIC for integration of the raw thermograms, error bars of the heat changes for each injection will be passed on to SEDPHAT, such that the appropriate relative statistical weights of the different data sets are obtained.

Another highly useful variation of experimental condition is the orientation of the injection, which was described earlier [9]. This may not always be feasible, dependent on the available stock concentrations of the binding partners. (If a separate pre-concentration step is required to bring a protein to sufficiently high concentrations to be placed in the syringe, then it should be noted that the concentration error parameter may be different after pre-concentration due to losses or partial aggregation.)

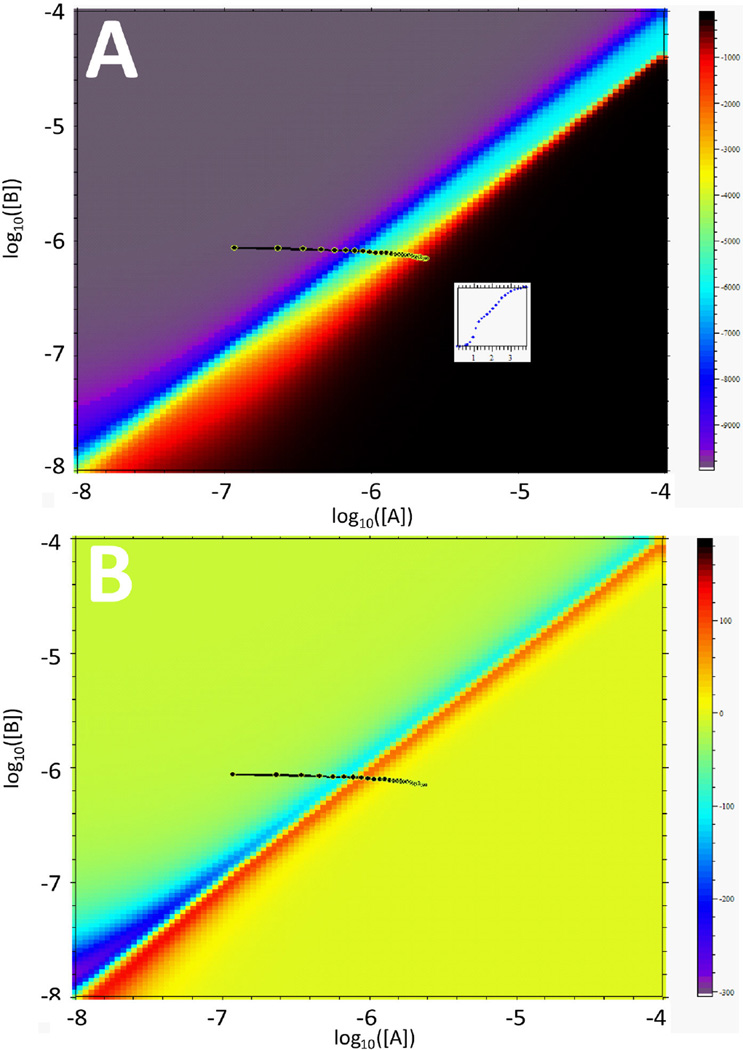
As an example of a more complicated interaction, we consider a system of ligand-linked dimerization, where binding of a ligand B to a molecule A enhances the dimerization of A by 10fold, but without cooperativity between the sites for B on A. This includes three affinity constants: binding of B to the monomer of A (K_AB), the dimerization of A in the absence of ligand (K_AA), and the cooperativity factor which can be expressed equivalently as the relative change in the affinity for B of the dimer vs monomer of A, (i.e., K_AA-B/K_AB where K_AA-B is the affinity of the A dimer for B), or the ratio dimerization constants of A in the liganded vs unliganded form (i.e., K_(AB)−(AB)/K_AA). In most SEDPHAT models, parameters are expressed in macroscopic units, and statistical factors present the default value of binding parameters. An overview of the population of different species, generated as an optional output of the simulation function in SEDPHAT, is shown in Fig. 3.

To simulate ITC data, data were generated first using the simulation tool along standard paths, both titrating A into B and B into A, as shown in the upper two quadrants of the SEDPHAT window in Fig. 4A. They have a ‘classical well-formed shape’ of a single transition; these titrations would have c-values of 7 and 5 if based on the binding constant of B to the monomer of A, or 70 and 50 if based on the binding to the dimer of A. However, it is clear that the concept of a c-value loses its meaning in the context of multiple sites and ceases to be helpful, whereas the graphical depiction of the isotherm used here can still serve as a guide for experimental design. If these two data sets are analyzed together, the 68% confidence interval for the cooperativity factor ranges from 6.9 to 292.

However, even the most cursory visual inspection of the two-dimensional isotherms will reveal fundamental differences in their shape in comparison to the simple 1:1 binding isotherms of Fig. 1 when titrating A into B, with additional features in the middle and lower concentration range of B. It is reasonable to assume these will need to be sampled with experimental titration trajectories for the binding parameters to be well determined. Since in our view the cooperativity parameter is the most interesting aspect of this interaction, we used the differentiation tool in the isotherm display to highlight regions where the binding isotherm changes most with a small change in the cooperativity factor (Fig. 5). The most informative region coincides with the ‘anomalies’ in the ~ 1 µM range of B and the ~ 0.1 range of A (black region in the color scale of Fig. 5). Therefore, a third titration experiment was simulated to cover this region, predicted to exhibit a minimum in the measured heats (lower left quadrant of Fig. 4B). An additional unusual feature of the binding isotherm of the ligand-linked dimerization model is the drop in heat change at constant concentration of B and increasing concentrations of A. This was sampled through a fourth simulated titration experiment (lower right quadrant of Fig. 4B). The global analysis now led to a 68% confidence range of the cooperativity factor reduced to 5.4 – 22, corresponding to a ~2.3fold reduction of the uncertainty in ΔΔG. To some extent, merely the increase in the number of data points will lead to an improvement in the confidence intervals (see above). However, simple duplication of the first two ‘classical’ titration isotherms would have led to a 68% confidence interval for the cooperativity factor of 8.6 – 57.2, highlighting that a substantial improvement arises here from the variation of the conditions, sampling the characteristic features of the binding isotherm.

Figure 5.

Differences of dQ/dc_A,tot from two isotherms titrating A into B as shown in Fig. 4B, upon a small change in the cooperativity parameter. This indicates regions in the parameter space that will depend most on this parameter, i.e., are most informative for its precise quantitative determination. In the present case, the largest changes occur for conditions where c_A,tot ≈ 0.1 µM and c_B,tot ≈ 1 µM, as indicated in black.

In the above analysis of the data for the ligand-linked dimerization, the model allowed for up to 20% global concentration errors in both components A and B, as would be reasonable to allow for even relatively large errors in protein extinction coefficients [67]. (This can be conveniently implemented in SEDPHAT by choosing fixed concentration correction factors of 1.2 in all experiments, compensated by global incompetent fractions for both components to be refined in the fit within the constraints from 0.0 to 0.4.) It is well-known that a single-experiment analysis of a single-site interaction does not allow refinement of concentration errors of both reactants simultaneously, since all binding parameters would be completely correlated with the unknown concentration factors. However, the global analysis of multi-site interactions contains features that are independent of the concentration scale, including cooperativity factors that reflect the ratio of binding constants. (Similarly, proton linkage analysis in gITC can be carried out with unknown incompetent fractions of binding partners [24].) These can be extracted from gITC analysis if, for each component, the concentration errors can be constrained to be identical for all experiments. Other quantities that directly depend on the concentration scales, such as the binding constants K_AB and K_AA, would be completely indeterminate in this analysis and require fixing at least one of the concentration factors. Alternatively, applying constraints to the concentration error, here ±20% translates, for example, to a 68% confidence limit for K_AB of 0.52 – 2.1 µM.

Multi-Component Systems

The characterization of multi-component systems is a natural application of gITC, as it usually requires multiple titration experiments. For example, the study of three-component interactions typically involves the combination of experiments with binary mixtures and with ternary mixtures. In comparison with a hierarchical analysis with apparent binding constants extracted from each single titration as intermediate steps, the global analysis can provide a model that is often more accurate and always more stringent. As discussed above, it allows rigorous statistical error propagation from error bars of individual injections of all titrations towards final parameter errors. Further, it allows implementing powerful constraints with regard to uncertainties in active concentration of reactants that are unavailable in individual analyses, and often prove essential.

Displacement experiments are a special case of three-component interaction, with the goal of extending the dynamic range of affinities between two reactants that can be studied by ITC [22,38,72–75, and 76 (this volume)]. Various configurations are possible, and all can be analyzed with the SEDPHAT model “A + B + C ←→ AB + C ←→ AC + B, competing B and C for A” with different titration orientations as appropriate for different experiments. For example, gITC of a simulated series consisting of titrations of a high-affinity ligand B into A, a titration of a low-affinity ligand C into A, and the titration of the high-affinity ligand B into a mixture of A and C with pre-formed weak complexes is shown in Fig. 6. Even for configurations where a single titration will exhibit two transitions and in principle allows a full analysis [38,72,76 (this volume)], it can be expected that such experiments would usually be based on prior knowledge and follow at least some initial experiments characterizing binary mixtures, which can be included into a gITC analysis [38]. For any given system with known or hypothesized binding parameters, SEDPHAT can display stacks of slices through the three-dimensional concentration space with color-temperature coded values for dQ/dc_tot (along a specified titration orientation) and its derivative with respect to a certain parameter of interest. This is illustrated in Fig. 7 for the case of a titration of a protein into a mixture of high- and low-affinity ligands, which creates the characteristic bi-phasic titration data. In this way, benefits and drawbacks of different designs for titration experiments, as well as the combination of multiple titrations, can be efficiently explored for a given system.

Figure 6.

GUSSI plot of the gITC analysis in SEDPHAT of a simulated displacement experiment, titrating 300 µM of a high-affinity ligand (K_AB = 1 nM) into 20 µM protein (purple), 355 µM of a low-affinity ligand (K_AC = 1 µM) into 34 µM protein (blue), and the titration of 250 µM of the high-affinity ligand into a mixture of 20 µM protein with low-affinity ligand in 10fold molar excess (parameters after [81]). The inset shows the 1-dimensional error contour projection for the high-affinity binding constant as generated by an SEDPHAT statistics function, highlighting confidence levels at 1 (purple) and two (red) standard deviations, which leads to a 68% confidence interval of 0.57 – 1.4 nM.

Figure 7.

Panel A: Graphical depiction of the differential binding isotherm in the three-dimensional concentration space for a titration of a protein A (abscissa) into a mixture of a high-affinity B (K_D = 1 nM, ΔH = −10 kcal/mol) and a low-affinity ligand C (K_D = 100 nM, ΔH = −6 kcal/mol), showing the section at molar ratio of C/A = 1.359 (ordinate). SEDPHAT allows the user to scroll through different sections of the volume, and create simulated experimental titration trajectories (black dotted line, and small inset). Planes at constant molar ratio C/B in the cell exhibit the typical bi-phasic transition at high concentrations. Panel B: Differentiation of the isotherm in A with respect to the high-affinity binding constant. Red and blue areas highlight areas with largest sensitivity toward changes in K_AB. The isotherm can also be explored by scrolling through different slices in this differential form. In both panels, the connected black dots depict, in different context, the trajectory of the same isotherm, simulated experimental data of which are shown in the inset of panel A.

Global Multi-Method Analysis

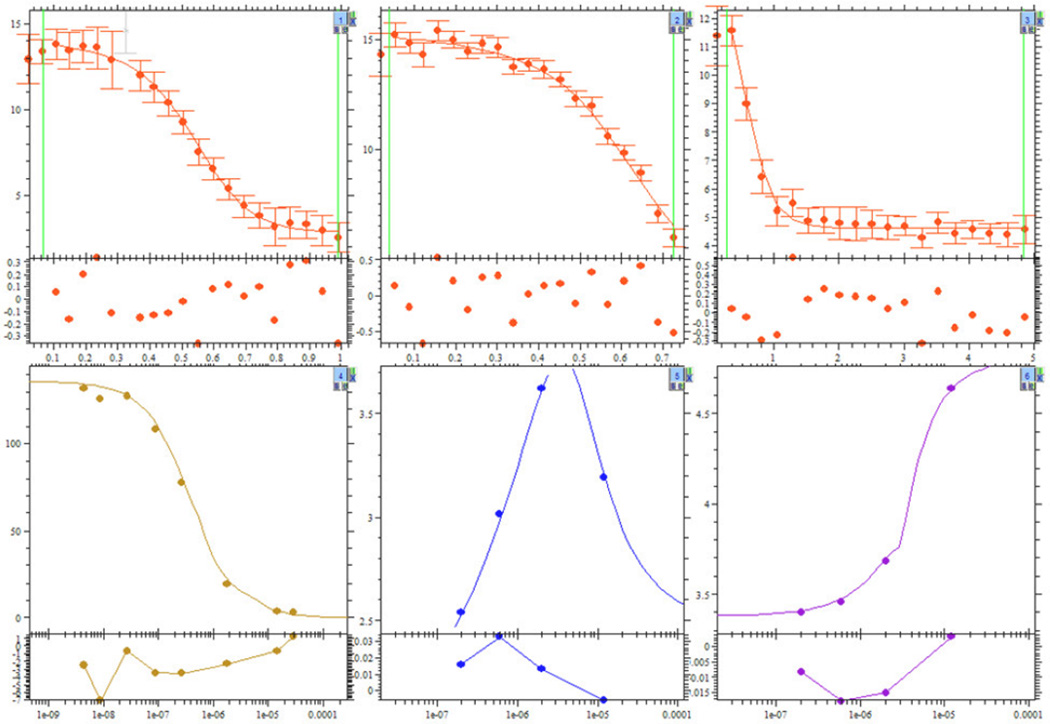
A key feature of gITC in SEDPHAT is the possibility for including side-by-side data from different biophysical techniques in a global multi-method analysis (GMMA) [29]. This is illustrated in Fig. 8 for the data shown in Fig. 2 on the interaction of α-chymotrypsin with soybean trypsin inhibitor [29]. Remarkably, even though the data sets added stem from techniques that do not report on reaction enthalpies – surface plasmon resonance solution competition and sedimentation velocity analytical ultracentrifugation – their inclusion can improve the error estimate of the reaction enthalpies. For example, with the data shown in Fig. 8 the confidence interval of ΔH_AB of the first site shrinks by 31%, as compared to the three ITC data sets alone, to a range of 3.2 – 4.8 kcal/mol. The mechanism by which this happens is the decrease of correlation between the two binding sites afforded by the additional data (Fig. 9), which in turn allows the experimentally observed enthalpies to be better decomposed into the contributions of the different sites.

Figure 8.

Screenshot of the global multi-method analysis of the interaction of α-chymotrypsin (CT) with soybean trypsin inhibitor (SBTI), extending the data shown in Fig. 2 (shown here in the top row) by a surface plasmon resonance experiment in solution competition configuration (lower left), and sedimentation velocity experiment in a dilution series yielding an isotherm of signal-weighted average sedimentation coefficients of the interacting system (lower middle) and of the reaction boundary (lower right) [29].

Figure 9.

Parameter correlations between the two binding sites K₁ and K₂ of SBTI for CT for different experiments:(A) SPR alone (as shown in bottom left of Fig. 8); (B) a single well-formed ITC experiment (replicate of that shown in top left panel of Fig. 8); (C) a dilution series in SV (lower middle and lower right in Fig. 8); (D) GMMA jointly of the same data sets. Two-dimensional projections of the parameter error surface are generated as color-temperature map by the SEDPHAT statistics function, highlighting the one and two standard deviation contour (red and magenta lines). (Reproduced from Fig. 8 of [29].)

Just like the simulation of ITC data, the simulation tool allows the creation of data sets for the other techniques, such that useful combination can be explored as part of the GMMA design [30]. The particular data format for the data from other techniques can be conveniently copied from the simulated data files, or be retrieved from the online help system of SEDPHAT.

Conclusions

In the present communication we have reviewed different opportunities for global analysis of ITC titrations, and highlighted the resulting improvement in the data analysis of single- and multi-site systems. gITC analysis can be carried out conveniently in SEDPHAT by simply loading multiple data sets, without requiring any data-dependent or model-dependent programming.

Global analysis is the most stringent approach to test a model and to apply it to the interpretation of experimental data in their entirety. Unless there is a reason to consider experiments to be mutually inconsistent due to experimental imperfections (which may sometimes be revealed by unsatisfactory global analysis) the joint interpretation of all data sets is always statistically advantageous. This is often crucial, in particular for the multi-site systems. The gITC method is not only useful to improve the precision of binding parameters, but more fundamentally, can help to verify whether a certain binding model is appropriate for the given interacting system. gITC has a far greater power to discriminate different binding models than individual analyses, a feature that is further enhanced in the extension to GMMA. For complex systems, often a superior starting point for determining the binding mechanism may be structural considerations, in combination with sedimentation velocity analytical ultracentrifugation and multi-signal sedimentation velocity [12,77], owing to its potential for hydrodynamic and spectral separation of the different species and their complexes.

For several reasons, it is highly desirable to combine gITC with the automated shape analysis of experimental thermograms in NITPIC, which provides error estimates for the heat changes of individual titration data points: First, this allows for experimental titration data to be properly weighted relative to each other in gITC. Second, due to the generally low number of data points, adventitious large uncertainties in heat changes from individual injections due to unusual baseline fluctuations can have an impact on the results of the ITC analysis, in particular if the injections in question are located in the transition region. Third, manual user-dependent interference in what is considered the experimental data should be avoided as much as possible to rule out bias, and this can be accomplished automatically and reliably with the peak shape analysis and truncated singular value decomposition algorithms in NITPIC [18]. First examples for the application of the NITPIC-SEDPHAT analysis strategy can be found in [35,38,48,53–62,66,78–80]. By letting the thermogram integration software NITPIC feed data into SEDPHAT, errors from the individual injections are honored and carried through to yield rigorous final parameter uncertainties in gITC.

Since ITC experiments are often costly in terms of time and material, it is of practical importance to design efficient and informative experiments by proper choice of the titration configuration and of concentrations in the cell and syringe. Historically, this was accomplished by considering a ‘c-value’, but this concept ceases to be very useful for multi-site systems and in the context of global analysis. This presents the motivation for the introduction of simulation tools in the current paper. They include a graphical depiction of the differential heats in two- or three-dimensional concentration space, which can generate visual cues to regions in parameter space that are both feasible – given existing stock solutions – and information rich. This can be followed by a statistical analysis of the error surface with the automated confidence interval search for a certain parameter of interest.

In future work, it may be possible to improve the simulation tool by accounting for signal/noise limitations directly in the isotherm display. Currently different noise levels have to be anticipated prior to the simulations for each data set. It would be desirable, however, to crop the display to regions that are not only feasible on the basis of available sample concentrations, but also exceed lower threshold of heat changes per titration step dependent on the instrument sensitivity. The goal would be to upfront exclude from consideration such designs that would provide only highly noisy titrations.

For more complex multi-site systems, it may not always be possible to identify satisfactory conditions and combinations of ITC data. For example, the accuracy or level of available reactant concentrations may be limiting, highlighting the potential importance of efforts to improve aspects of sample preparation prior to the ITC experiments. Similarly, in some cases it may be anticipated through the simulation that the combination with other biophysical data in a global multi-method analysis (GMMA) will be crucial. Examples for such cases can be found in two-site and three-site systems [29,78]. In this way, the new simulation tools can be used to consider ITC in the broader experimental context.

Highlights.

• We review principles and opportunities for global analysis of ITC titrations

• SEDPHAT provides a seamless graphical user interface for global ITC analysis

• We present a new tool for the design of ITC experiments

• The global analysis can be extended to multi-method analysis