Phase Cycling Schemes for finite-pulse-RFDR MAS Solid State NMR Experiments

Abstract

The finite-pulse radio frequency driven dipolar recoupling (fp-RFDR) pulse sequence is used in 2D homonuclear chemical shift correlation experiments under magic angle spinning (MAS). A recent study demonstrated the advantages of using a short phase cycle, XY4, and its super-cycle, XY4¹₄, for the fp-RFDR pulse sequence employed in 2D ¹H/¹H single-quantum/single-quantum correlation experiments under ultrafast MAS conditions. In this study, we report a comprehensive analysis on the dipolar recoupling efficiencies of XY4, XY4¹₂, XY4¹₃, XY4¹₄, and XY8¹₄ phase cycles under different spinning speeds ranging from 10 to 100 kHz. The theoretical calculations reveal the presence of second-order terms (T₁₀T_2,±2, T_1,±1T_2,±1, etc.) in the recoupled homonuclear dipolar coupling Hamiltonian only when the basic XY4 phase cycle is utilized, making it advantageous for proton-proton magnetization transfer under ultrafast MAS conditions. It is also found that the recoupling efficiency of fp-RFDR is quite dependent on the duty factor (τ₁₈₀/τ_R) as well as on the strength of homonuclear dipolar couplings. The rate of longitudinal magnetization transfer increases linearly with the duty factor of fp-RFDR for all the XY-based phase cycles investigated in this study. Examination of the performances of different phase cycles against chemical shift offset and RF field in homogeneity effects revealed that XY4¹₄ is the most tolerant phase cycle, while the shortest phase cycle XY4 suppressed the RF field inhomogeneity effects most efficiently under slow spinning speeds. Our results suggest that the difference in the fp-RFDR recoupling efficiencies decreases with the increasing MAS speed, while ultrafast (>60 kHz) spinning speed is advantageous as it recouples a large amount of homonuclear dipolar couplings and therefore enable fast magnetization exchange. The effects of higher-order terms and cross terms between various interactions in the effective Hamiltonian of fp-RFDR are also analyzed using numerical simulations for various phase cycles. Results obtained via numerical simulations are in excellent agreement with ultrafast MAS experimental results from the powder samples of glycine and L-alanine.

Introduction

With the recent developments in NMR instrumentation, solid-state NMR spectroscopy is playing a crucial role in determining atomic-level structural and dynamics information for a variety of non-soluble and non-crystalline solids of chemical and biological molecules [1–4]. In particular, the recent development of ultrafast magic-angle-spinning (MAS) probes has enabled the development of proton-detected radio-frequency (RF) pulse sequences [5–14] and multidimensional techniques [15–19]. Increasing number of studies utilize ultrafast MAS techniques to study chemical [20–25], biological [26–35] and material [36–39] systems. A recent study demonstrated the feasibility of recoupling proton-proton dipolar couplings at ultrafast MAS frequencies by using the finite-pulse radio frequency-driven dipolar recoupling (fp-RFDR) sequence [40]. fp-RFDR, composed of a single 180° pulse at the center of each rotor period, recouples zero-quantum homonuclear dipolar couplings [41–46]. In addition to the spinning speed and the 180° pulse width, the dipolar recoupling efficiency of fp-RFDR depends on chemical shift offset, RF field inhomogeneity, and the interference of chemical shift anisotropy (CSA) and heteronuclear dipolar couplings that are especially significant for low-γ (for example, ¹³C) nuclei [41]. XY-based phase cycling for the 180° pulse has been shown to overcome these limitations of the fp-RFDR sequence [41, 47]. A recent study demonstrated that, for 2D ¹³C/¹³C chemical shift correlation experiments, the best performance of fp-RFDR under fast MAS could be achieved by a super phase cycle XY8¹₄ [47]. On the other hand, our recent study demonstrated that, for proton-based homonuclear correlation experiments, the fp-RFDR pulse sequence had the highest recoupling efficiency when a short phase cycle, XY4, or its super-cycle, XY4¹₄, was used under ultrafast MAS frequencies [40]. It should be noted that XY4 and XY4¹₄ phase cycles corresponding to ${[R{4}_4^{-1}]}_{45}$ and $\{{[R{4}_4^{-1}]}_{45}\}{4}^1$ symmetry, respectively, recouple zero-quantum homonuclear dipolar couplings [48–50]. As demonstrated in our previous study [40], XY4 and XY4¹₄ render a superior performance when compared to XY8 (corresponding to the ${[R{4}_4^{-1}R{4}_4^1]}_{45}$ symmetry) and XY8-based super-cycles such as XY16 and XY8¹₄ corresponding to $[{(R{4}_4^{-1}R{4}_4^1)}_{45}]2^1$ and $[{(R{4}_4^{-1}R{4}_4^1)}_{45}]4^1$ symmetry, respectively. This fact is further demonstrated by performing fp-RFDR based experiments on U-¹³C-glycine at 60 kHz MAS for all the phase cycling schemes including XY4¹₃ and the results are shown in Figure S1. These results are in excellent agreement with the experimental results obtained from alanine at higher MAS speeds [40]. In this paper, we mainly analyze the recoupling efficiencies of XY4 based super cycling schemes and XY8¹₄.

Though the performances of these phase cycling schemes have been experimentally demonstrated, reasons for the inefficient performance of XY8 and superior performances of XY4 and XY4¹₄ for ¹H-based RFDR experiments are not well understood. The factors affecting the performance of an RFDR sequence could vary with the choice of nuclei under investigation, while the RF field inhomogeneity effect is common for all nuclei but dependent on the type of MAS probe used in the study. For example, the performance of ¹³C-based RFDR experiments could highly depend on the large chemical shift anisotropy of ¹³C nuclei, chemical shift offset, heteronuclear dipolar couplings, and higher order terms among these interactions. Whereas, even under ultrafast MAS conditions, the very large ¹H-¹H dipolar couplings affect the performance of ¹H-based RFDR experiments. For example, unlike for ¹³C nuclei, the loss of ¹H magnetization in fp-RFDR with XY8 or its super cycles is significant [40]. In addition, higher-order terms in the effective Hamiltonian of fp-RFDR as well as the cross-terms such as dipolar-dipolar interactions, dipolar coupling - offset, and dipolar coupling - RF field inhomogeneity could affect the performance of a phase cycling scheme used in a ¹H-based RFDR experiment. In this study, we systematically analyze the performance of fp-RFDR, based on various XY-based phase cycling schemes, at different magic angle spinning speeds. The transfer of longitudinal magnetization via homonuclear dipolar couplings recoupled by fp-RFDR is calculated using SIMPSON [51, 52] for various phase cycling schemes to compare their performances against RF field inhomogeneity, chemical shift offset, chemical shift anisotropy (CSA) and duty factor (defined as the ratio of the 180° pulse length to the rotor period, f = τ₁₈₀/τ_R). Numerical simulations on three spin ½ and two spin ½ systems were carried out to evaluate the effects of higher-order terms as well as the cross-terms in the effective Hamiltonian of fp-RFDR. Experimental results obtained under ultrafast MAS are also included.

Experimental

All proton NMR experiments at 60 kHz MAS were performed on a Agilent/Varian 600 MHz solid-state NMR spectrometer equipped with a 1.2 mm ultrafast MAS probe, while a 600 MHz JNMECA600II solid-state NMR spectrometer (JEOL RESONANCE Inc., Tokyo, Japan) equipped with a 0.75 mm ultrafast MAS probe was used to perform experiments at 90 kHz MAS. U-¹³C-glycine and U-¹³C-¹⁵N-L-alanine were purchased from Cambridge Isotope Laboratory (Andover, MA), and were used as received without any further purification for comparing the fp-RFDR efficiencies under different phase cycling schemes. All other experimental conditions used in this study are given in figure captions.

Simulations

All numeric simulations were performed using the SIMPSON software [51, 52]. For the three spin ½ model system used in this study, three nuclei (represented as H1, H2 and H3) with equal inter-spin distances were considered in the simulations under 10, 20, 40, 60, and 100 kHz MAS. The magnetization of one of the nuclei (H1) is selectively prepared first and then its longitudinal magnetization is allowed to evolve under the recoupled homonuclear dipolar couplings to calculate the build-up of the longitudinal magnetization of H2 as a function of fp-RFDR mixing time. The homonuclear dipolar coupling was varied from 1 to 29.3 kHz to evaluate the efficiency of fp-RFDR under various conditions. For simulations on a two spin ½ system, the two spin 1/2 nuclei H1 and H2 are considered and other parameters are the same (or similar) as used for the three spin ½ system. The RF field strength was deliberately misset to evaluate the effect of RF field inhomogeneity. The simulated results are valid for any nuclei, but defined by the strength of homonuclear dipolar coupling: a strong homonuclear dipolar coupling correspond to high-γ nuclei (like ¹H, ¹⁹F or ³¹P) present in a rigid solid whereas a weak homonuclear dipolar coupling can be associated with either high-γ nuclei (like ¹H, ¹⁹F or ³¹P) present in a mobile solid or low-γ nuclei (like ¹³C) present in a rigid solid. Chemical shift anisotropy and chemical shift offset were set to zero in simulations unless otherwise specific values are mentioned. To compare the efficiencies of different phase cycling schemes against CSA, we also used a three ¹³C spin system with a ¹³C-¹³C dipolar coupling of 1 kHz for each spin pair. In fact, a recent study reported the performances of XY8, XY16 and XY8¹₄ against CSA in RFDR-based 2D ¹³C/¹³C chemical shift correlation experiments [47].

Theoretical analysis of the fp-RFDR pulse sequence

To better understand the difference in recoupling efficiencies of various RFDR phase cycling schemes investigated in this study, symmetry based theoretical analysis of the effective Hamiltonian is given in this section [48]; a detailed derivation process is included in the Appendix. All RFDR phase cyclings can be categorized into the (super-cycled) symmetry based sequence. The symmetry based theory can be used to identify the terms recoupled in the first-order and in the higher-order average Hamiltonian. RFDR with XY4 can be written by the basic building block, ${(R{4}_4^{-1})}_{45}$, which comes from phase shift of $R{4}_4^1$. Based on the symmetry selection rules, $R{4}_4^1$ can recouple the first order average Hamiltonian of (l, m, λ, μ) = (2,±2,2,0) and (2,±1,2,0), where l and λ represents space rank and spin rank of the tensors, while m takes any integer which satisfy |m|≤ l and μ with |μ| ≤ λ. The phase inversion of all RF pulses makes the sequence $R_4^{-1}$. The average Hamiltonian ${\overline{H}}_{{\mathrm{\Lambda }}_K‥{\mathrm{\Lambda }}_1}^{(K)}(R{4}_4^{-1})$ can be written as

$${\overline{H}}_{{\mathrm{\Lambda }}_K\dots {\mathrm{\Lambda }}_1}^{(K)}(R{4}_4^{-1})=(-1)\sum _{Q=1}^K{\lambda }_{Q}R(\pi ,x){\overline{H}}_{{\mathrm{\Lambda }}_K‥{\mathrm{\Lambda }}_1}^{(K)}(R{4}_4^1)R{(\pi ,x)}^{†}$$ (1)

where ${\overline{H}}_{{\mathrm{\Lambda }}_K‥{\mathrm{\Lambda }}_1}^{(K)}(R{4}_4^1)$ is the Kth order average Hamiltonian of interactions Λ_Q(Q = 1,2,3…K) with λ_Q representing the rank of the interaction, R(θ, p) describes the θ rotation of Hamiltonian H along the p axis through R(θ, p)HR(θ, p)^†. The first-order average dipolar Hamiltonian can be written as

$${\overline{H}}_{DD}^{(1)}(R{4}_4^{-1})={(-1)}^{2}R(\pi ,x){\overline{H}}_{DD}^{(1)}(R{4}_4^1)R{(\pi ,x)}^{†}$$ (2)

Since the first-order average Hamiltonian of $R{4}_4^1$ is zero-quantum dipolar interactions, the Hamiltonian is invariant for rotations along the x axis:

$${\overline{H}}_{DD}^{(1)}(R{4}_4^{-1})={\overline{H}}_{DD}^{(1)}(R{4}_4^1).$$ (3)

The second order homonuclear dipolar × CSA cross terms of (l₁, m₁, λ₁, μ₁) = (2,±2,2,0) and (2,±1,2,0) with arbitrary sets of (l₂, m₂, λ₂, μ₂) are symmetry allowed term. This also applies to homonuclear dipolar × isotropic chemical shift. The term with μ₂ = 0 can be written as

$${\overline{H}}_{DD\times CS(A){\mu }_2=0}^{(2)}(R{4}_4^{-1})=-{\overline{H}}_{DD\times CS(A){\mu }_2=0}^{(2)}(R{4}_4^1).$$ (4)

The ϕ rotation of all RF pulses of $R{4}_4^1$ gives the average Hamiltonians of

$${\overline{H}}_{{\mathrm{\Lambda }}_K\dots {\mathrm{\Lambda }}_1}^{(K)}({(R{4}_4^1)}_{\varphi })=R(\varphi ,z){\overline{H}}_{{\mathrm{\Lambda }}_K‥{\mathrm{\Lambda }}_1}^{(K)}(R{4}_4^1)R{(\varphi ,z)}^{†}$$ (5)

Basically, ϕ step super cycling such as XY4¹_n removes the terms which has nonzero μ. Since the first-order average Hamiltonian of $R{4}_4^1$ is composed of μ = 0 terms, the Hamiltonian is invariant to rotations. Thus, ${(R{4}_4^1)}_{\phi }$, which is given by ϕ shift of all RF pulses of $R{4}_4^1$, results in the average Hamiltonian:

$${\overline{H}}_{DD}^{(1)}\left({(R{4}_4^1)}_{\phi }\right)={\overline{H}}_{DD}^{(1)}(R{4}_4^1)$$ (6)

Therefore, the first-order average Hamiltonians are the same for XY4, $\mathrm{X}\mathrm{Y}{4^1}_2([{(R{4}_4^{-1})}_{45}]2^1),\mathrm{X}\mathrm{Y}{4^1}_3([{(R{4}_4^{-1})}_{45}]3^1),\mathrm{X}\mathrm{Y}{4^1}_4([{(R{4}_4^{-1})}_{45}]4^1)$, and $\mathrm{X}\mathrm{Y}8({(R{4}_4^{-1}R{4}_4^1)}_{45})$. On the other hand, the higher-order average Hamiltonians differ. $R{4}_4^1$ has many symmetry allowed second order CSA × CSA terms of H̅_{l1m1λ1μ1l2m2λ2μ2} with m₁ + m₂ = 0,±1,±2,±3,±4 and (μ₁, μ₂) = (±1,∓1). All these cross terms results in spin operators of T_1,0(∝ I_z) in the spin part of the Hamiltonian. These cross terms interfere the magnetization transfer process in the RFDR pulse sequence. However, the cross terms can be removed by combining with phase-inverted RF pulses such as XY8. XY8 also removes the homonuclear × CS(A) cross terms with μ₂ = 0, as demonstrated in Eq. (4). The terms with μ₂ ≠ 0 can be removes by XY8¹₄ super cycling. These are the reason why the super phase cycle XY8¹₄, based on XY8, works well in RFDR-based ¹³C-¹³C dipolar recoupling in spite of the presence of large ¹³C CSA and offset. On the other hand, there are many higher-order terms in the effective Hamiltonian that could assist the magnetization transfer process. For example, dipolar × dipolar cross terms that involve (l₂, m₂, λ₂, μ₂) = (2,±2,2,0) and (2,±1,2,0) could play a role in the magnetization transfer during fp-RFDR. These dipolar × dipolar cross terms involve zero-quantum and double-quantum homonuclear terms can be removed by the super phase cycles. Therefore, the shortest phase cycle, XY4, gives a high dipolar recoupling efficiency in proton-based RFDR homonuclear correlation experiments when the ¹H-¹H dipolar coupling is large as observed in our experiments on glycine (Figure S1) and alanine [40]. For the benefit of readers, a detailed derivation of first-order and higher-order terms in the effective Hamiltonian using the average Hamiltonian theory is given in the Appendix.

Results and Discussion

A recent study on fp-RFDR based 2D ¹H/¹H SQ/SQ correlation experiments under ultrafast MAS conditions proposed XY4, XY4¹₄ and XY8¹₄ phase cycling schemes for an efficient transfer of longitudinal proton magnetization, whereas other phase cycling schemes like XY8, XY16, XY32 and XY64 were found to be inefficient [40]. In the present study, we systematically investigate and compare the efficiency of the fp-RFDR pulse sequence by employing XY4, XY4¹₂, XY4¹₃, XY4¹₄ and XY8¹₄ phase cycling schemes. The magnetization transfer efficiency of fp-RFDR depends on a combination of various factors including the magnitude of homonuclear dipolar couplings present in the system, spinning speed, duty factor, RF field inhomogeneity, chemical shift offset, and chemical shift anisotropy. While it is difficult to fully understand the role of each of these factors from experimental results alone, numerical simulations are used in this study to evaluate independent effects of these factors by calculating the magnetization transfer efficiency of the fp-RFDR sequence. In addition, numerical simulations were carried out to understand the effects of higher-order terms as well as the effects of cross terms between various interactions present in the effective Hamiltonian of fp-RFDR.

Spinning speed dependence

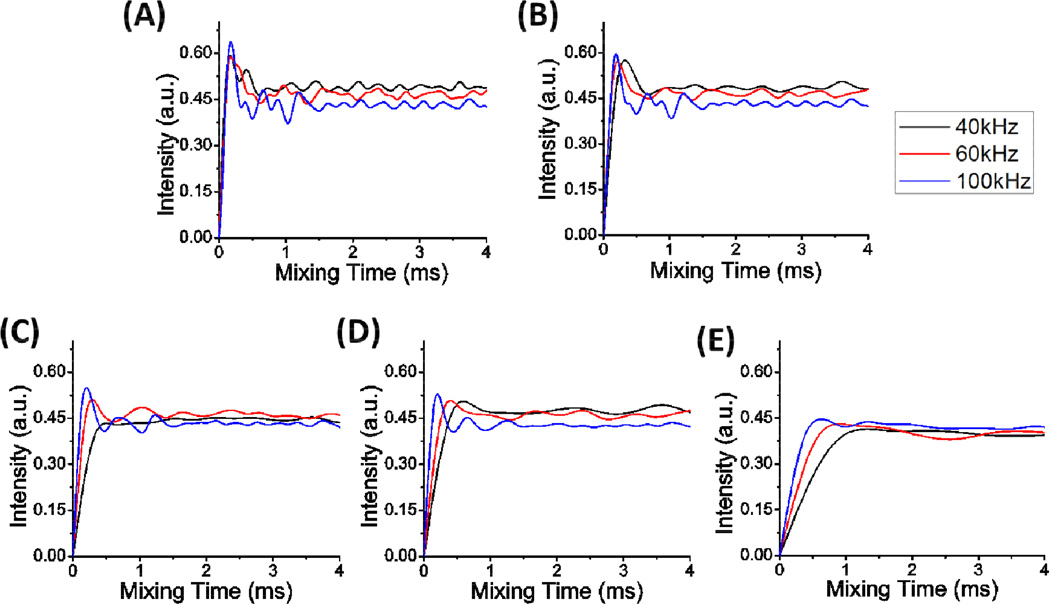
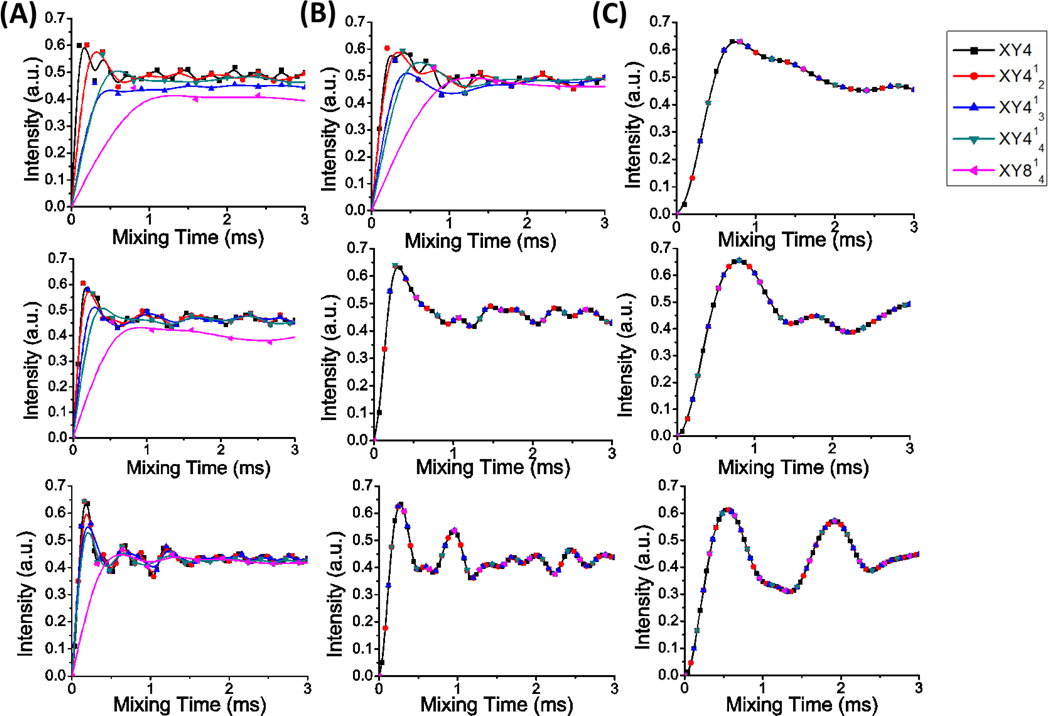
Longitudinal magnetization transfer efficiencies of fp-RFDR employing XY4, XY4¹₂, XY4¹₃, XY4¹₄ or XY8¹₄ phase cycling schemes for various spinning speeds were evaluated by numerical simulations using SIMPSON and the results are shown in Figures 2 and S2. These results indicate that the rate of magnetization transfer increases with the MAS speed. The decay of H1 magnetization as well as the buildup of H2 magnetization are induced only when π pulses have a finite pulse width as explained in the literature [41]. For a constant RF field strength used for the 180° pulse in the fp-RFDR sequence, the duty cycle of the π pulse in a rotor period increases with the increasing spinning speed, indicating a longer spin evolution time during the RF field within a rotor period. Therefore, the magnitude of the recoupled dipolar coupling between protons is increased and therefore the build-up rate of the longitudinal magnetization transfer is enhanced with the MAS speed. This effect is clearly seen from the simulated results for a strongly dipolar coupled spin system in Figure 2. The rate of magnetization transfer for all phase cycling schemes is fast under fast spinning speeds with the following order: 100 > 60 > 40 kHz. In addition, the simulated results presented in Figure 2 show that the shorter the phase cycling period, the faster the rate of magnetization transfer. However, it is due to the strong ¹H-¹H dipolar coupling (29.3 kHz) used in the simulation, that result in a rapid magnetization transfer to reach the maximum within just one phase cycle period. If the polarization buildup intensity is monitored after every four rotor periods for all the phase cycling schemes, then it is found that the buildup rate is the same (as shown in Figure S3). In the case of a weakly dipolar coupled spin system, all the phase cycles have the same buildup rate as shown in Figure 4. However, the final equilibrium intensity reflecting the magnitude of magnetization transfer is different indicating the difference in the recoupling efficiencies of different phase cyclings.

Figure 2.

The dependence of the longitudinal magnetization transfer efficiency, from one proton to another in a three-proton spin system, on the fp-RFDR mixing time at the indicated spinning speeds obtained using various phase cycling schemes: (A) XY4, (B) XY4¹₂, (C) XY4¹₃ (D) XY4¹₄ and (E) XY8¹₄. The radio-frequency field strength used for the 180° pulse was 250 kHz. In the numerical simulations using SIMPSON, the homonuclear dipolar couplings between H1 and H2, H2 and H3, and H1 and H3 nuclei were set to 29.3 kHz. Simulations for 10 and 20 kHz MAS and the dependence of magnetization transfer up to 15 ms mixing time are included in Figure S2 of the supporting information.

Figure 4.

Longitudinal magnetization transfer efficiency from H1 to H2 for the three spin ½ system under different phase cycles as indicated at a MAS speed of 40 (top row), 60 (middle row), and 100 (bottom row) kHz for a homonuclear dipolar coupling of (A) 29.3 kHz, (B) 20 kHz and (C) 10 kHz. The radio-frequency field strength used for the 180° pulse was 250 kHz. Simulations for 10 and 20 kHz MAS and the dependence of magnetization transfer up to 15 ms mixing time are included along with simulations for a strongly dipolar coupled spin system in Figure S4 of the supporting information.

Dependence on the duty factor

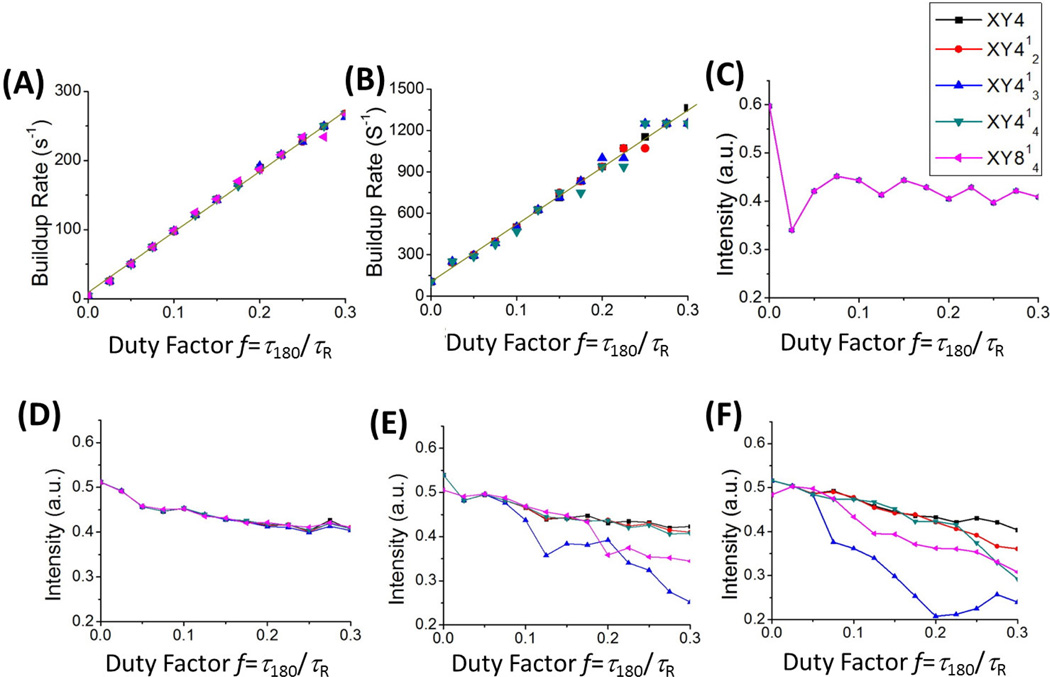
As mentioned earlier, the recouping efficiency of fp-RFDR also depends on the duty factor f=τ₁₈₀/τ_R. To better understand this effect, numerical simulations were used to calculate the dependence of the longitudinal magnetization build-up (or transfer) rate – that is the inverse of the mixing time needed to reach the maximum magnetization transfer – as a function of the duty factor of the fp-RFDR sequence for various phase cycles and the results are shown in Figure 3. Since the build-up rate is very fast as compared to the phase cycling time for a homonuclear dipolar coupling larger than 5 kHz, we restricted our calculations to dipolar coupling values of 1 and 5 kHz; even a 5 kHz dipolar coupling is too fast for a long phase cycling like XY8¹₄. It is interesting to find that the magnetization buildup rates are basically the same for different phase cycling schemes under 60 kHz MAS (Figure 3A and 3B). Similar results were also observed for other MAS speeds (results are not shown). Simulations also show that the magnitude of the transferred longitudinal magnetization at a mixing time of 100 ms is very similar for different phase cycling schemes (Figure 3C–F) except that XY4¹₃ and XY8¹₄ exhibit a decreasing amount of magnetization transfer for large duty factors (>0.1) when the homonuclear dipolar coupling is large (>20 kHz) as shown in Figure 3(E and F). Overall, the calculated build-up rate increases linearly with the duty factor of the fp-RFDR pulse sequence as shown in Figure 3(A and B). It seems that the duty factor is the only parameter that determine the magnetization buildup rate (or the transfer efficiency) and the extent of magnetization transfer. In principle, this is understandable based on the theoretical analysis reported in the literature [41] as the magnetization transfer occurs only when π pulses have a finite pulse width and the homonuclear dipolar recoupling is actually dependent on the spin evolution during the π pulse. However, for a given spinning speed and RF field strength used for the π pulse, the recoupling efficiency of the fp-RFDR sequence is different for different phase cycling schemes as shown in Figure 2 (and Figure S2). Therefore, these results suggest that the fp-RFDR dipolar recoupling efficiency is quite dependent on the strength of homonuclear dipolar couplings present in the spin system as shown in Figure 3(C–F).

Figure 3.

The dependence of the longitudinal proton magnetization build-up rate in a three-proton spin system against the duty factor of the fp-RFDR pulse sequence, f=τ₁₈₀/ τ_R, at 60 kHz MAS for different phase cycling schemes. The buildup rate is defined as the inverse of mixing time needed for the transferred magnetization intensity to reach the maximum. In the simulations using SIMPSON, a three spin ½ system was considered with 1 kHz (A) and 5 kHz (B) homonuclear dipolar couplings. The final equilibrated magnetization intensity, obtained at a mixing time of 100 ms, as a function of fp-RFDR duty factor for a homonuclear dipolar coupling of 1 (C), 10 (D), 20 (E) and 29.3 kHz (F). The duty factor was adjusted by changing the RF field strength used for the 180° pulse in the fp-RFDR pulse sequence.

Dependence on the homonuclear dipolar coupling

As mentioned above, the magnetization transfer efficiency of the fp-RFDR pulse sequence also depends on the strength of homonuclear dipolar couplings present in the system in addition to its dependence on the duty factor. To better explain this effect, simulations were performed for spin systems that differ in homonuclear dipolar couplings at different spinning speeds and the results are shown in Figures 4 and S4. The simulated results indicate that the rate of magnetization transfer depends on the spinning speed as well as on the phase cycling scheme used. As discussed above (Figures 2 and S3), the buildup rates for different phase cycling schemes are the same. The difference seen in Figure 4 only results from the difference in the phase cycling periods, as the buildup intensity is calculated after each phase cycling period. However, there is a small difference in the final equilibrium intensity, which decreases with decreasing magnitude of homonuclear dipolar coupling.

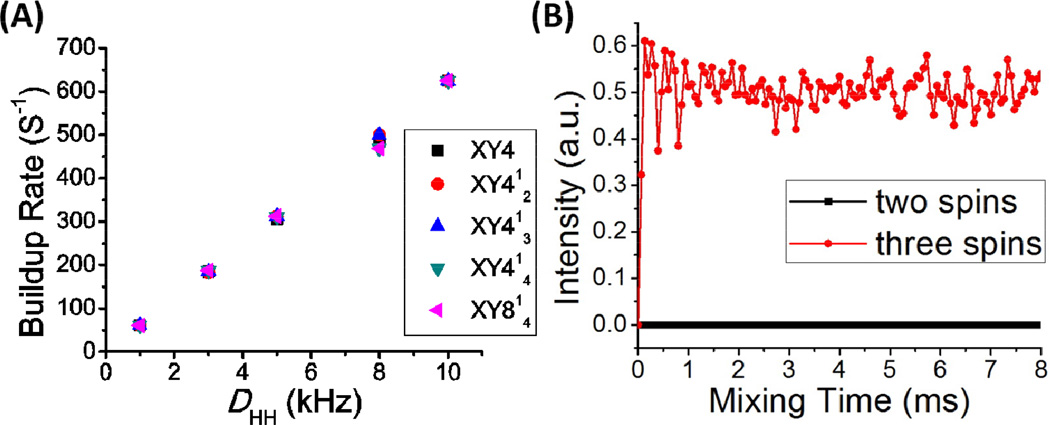
Simulated results also suggest that the rate of magnetization transfer obtained for a given homonuclear dipolar coupling is the same for a two spin ½ system under different phase cycles as shown in Figure 5A. It is surprising that even when the 180° pulse width is infinitely small, the magnetization transfer occurs for a three spin ½ system but not in the case of a two spin ½ system, as shown in Figure 5B. This result indicates that the higher-order homonuclear dipolar interactions introduced by the third spin (as also explained in the theoretical section) do play a major role in the magnetization transfer process as discussed below.

Figure 5.

(A) Simulated magnetization buildup rate as a function of homonuclear dipolar coupling for a two spin ½ nuclei under 60 kHz MAS. The duty factor was set as 0.1 and a 300 kHz RF field strength was used in simulations. The buildup rate is not possible to calculate when the homonuclear dipolar coupling is >10 kHz as the maximum magnetization transfer is attained just in one cycle time. (B) Longitudinal magnetization transfer efficiency as a function of fp-RFDR mixing time for two and three spin ½ systems with a short XY4 phase cycling. The ¹H-¹H dipolar coupling was 29.3 kHz and the RF field strength was set at 500,000 kHz in the simulations.

Effects of higher-order dipolar-dipolar terms in the effective Hamiltonian of fp-RFDR

The calculated build-up rates for different phase cycles were basically the same as shown for a two (Figure S5) and three (Figure 3 (A and B)) spin ½ systems; the use of a very strong dipolar coupling (>10 kHz) resulted in a maximum magnetization transfer in just one fp-RFDR cycle. The build-up rates for different phase cycles are the same for a given homonuclear dipolar coupling and duty factor as indicated in Figure 5A. These results seem to suggest that the effects of higher-order terms in the effective Hamiltonian of fp-RFDR are negligible. However, the buildup rate for a three spin ½ case is faster than that for the two spin ½ system (Figure S6). Therefore, the presence of higher-order dipolar-dipolar cross terms does enhance the magnetization transfer efficiency during fp-RFDR mixing time as explained in the theoretical section. Actually, the second-order term is much smaller than the first-order term, and the super cycles are efficient in suppressing most of the second-order terms, rendering it less prominent especially when the dipolar coupling is weak. This explains why XY8 based cycles perform well for low γ nuclei like ¹³C that have weak homonuclear dipolar couplings unlike protons [47].

Chemical shift offset effect

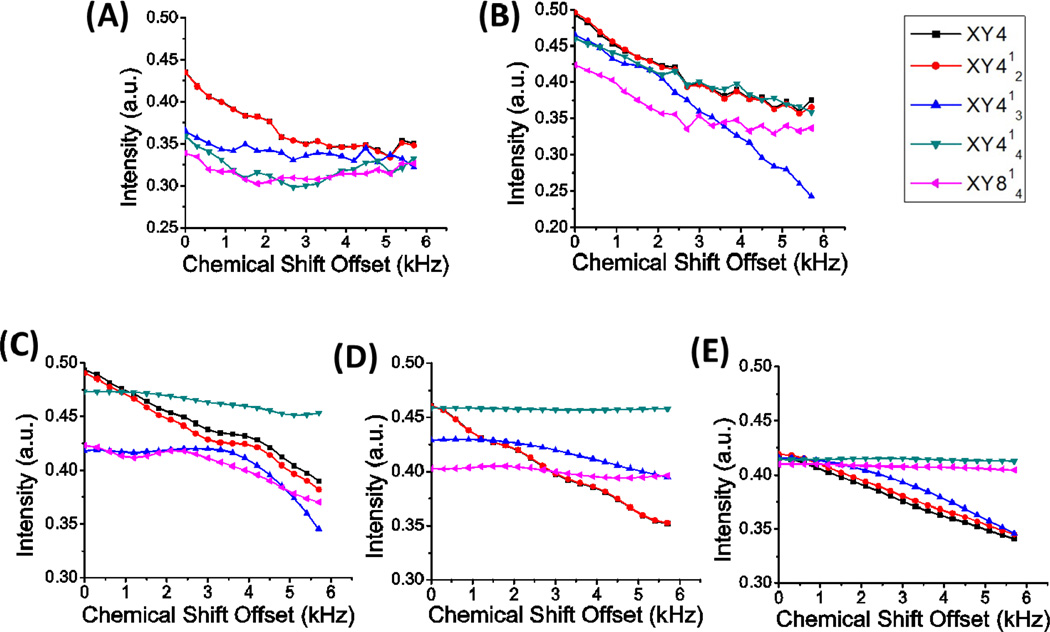
Since the span of chemical shift increases with the applied magnetic field, it is important to evaluate the efficiency of the fp-RFDR pulse sequence against the offset frequency. SIMPSON simulations were performed on a three spin ½ system to evaluate the transfer of longitudinal magnetization via homonuclear dipolar couplings recoupled by the fp-RFDR pulse sequence for different offset frequencies. As shown in Figure 6, simulated results show that fp-RFDR gains better tolerance to the chemical shift offset with increasing MAS speed. Overall, the super cycles XY4¹₄ and XY8¹₄ are more effective in suppressing the chemical shift offset effect, while short phase cycles XY4 and XY4¹₂ are more effective at on-resonance and for small offset values (~ 1 kHz). XY4¹₄ renders the most robust performance, which is in complete agreement with our previously reported experimental results [40].

Figure 6.

Effect of chemical shift offset on the longitudinal magnetization transfer at a mixing time of 8 ms fp-RFDR for different phase cyclings as indicated at a magic angle spinning speed of: (A) 10 kHz, (B) 20 kHz, (C) 40 kHz, (D) 60 kHz and (E) 100 kHz. A 250 kHz RF strength for the 180° pulse and a three spin ½ system as defined in the simulation section were used in SIMPSON simulations. The dipolar coupling is 29.3kHz for each proton spin pair.

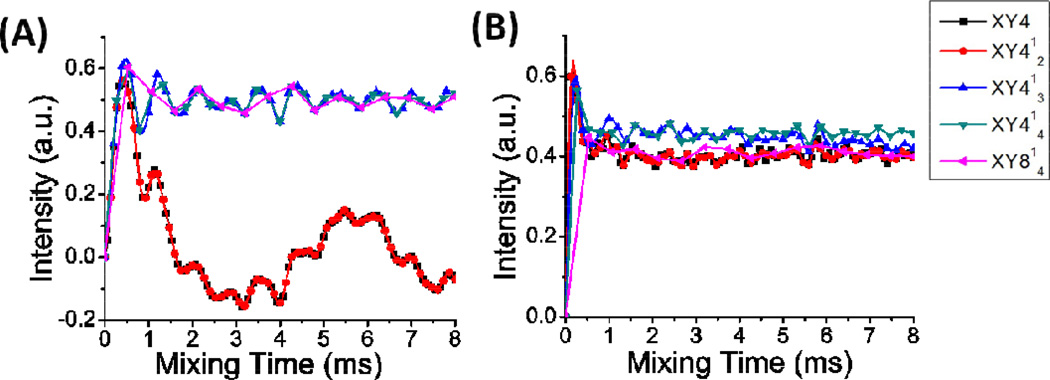
To examine the effect of a cross term between the dipolar coupling and chemical shift offset, numerical simulations were carried out using SIMPSON on a two spin ½ system and compared with that obtained from a three spin ½ system, as shown in Figure 7. The simulated results on a two spin ½ system revealed that only the short phase cycles XY4 and XY4¹₂ exhibit a significant dependence on the offset frequency (Figure 7A), while a 3 kHz chemical shift offset has a negligible effect on the fp-RFDR’s efficiency of magnetization transfer in a three spin ½ system for all phase cycles (Figure 7B). These results suggest that the super cycles are successful in overcoming the effects of offset and dipolar-offset cross terms. Whereas, it is interesting to note that the offset dependences of short phase cycles XY4 and XY4¹₂ (Figure 7A) are suppressed by the presence of the dipolar-dipolar cross term introduced by the third spin (Figure 7B). But, as shown in Figure 6, large offsets (>3 kHz) significantly affect the performance of short phase cycles.

Figure 7.

Magnetization transfer as a function of mixing time with different phase cycles as indicated for two spin ½ (A) and three spin ½ (B) systems. The spinning rate is 60 kHz and the dipolar coupling is 29.3 kHz for each proton pair. A 3 kHz chemical shift offset was set for the observed proton spin.

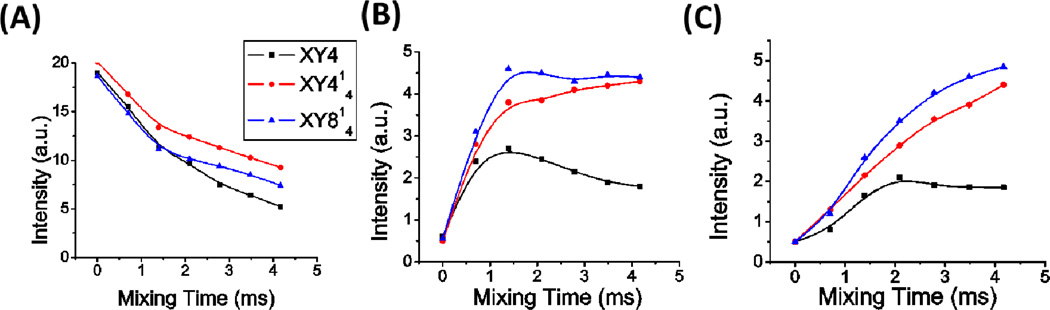
Since the ¹³C-¹³C dipolar coupling is small, the dipolar – dipolar cross term is negligible in a 2D ¹³C/¹³C fp-RFDR correlation experiment. Therefore, XY4 is expected to have a lower efficiency than the super-cycles XY4¹₄ and XY8¹₄ when a large chemical shift offset is present. An experimental demonstration of the performances of XY4, XY4¹₄ and XY4¹₈ phase cycles on U-¹³C-¹⁵N L-alanine under 90 kHz MAS is shown in Figures 8 and S7. Since the ¹³C chemical shifts of ¹³CH₃ to ¹³CH and ¹³COOH groups are quite different, alanine is an excellent system to demonstrate the offset-compensating efficiencies of the phase cycles used for the fp-RFDR sequence. The loss of longitudinal magnetization and the magnetization transfer as a function of fp-RFDR mixing time were measured from 2D ¹³C/¹³C chemical shift correlation experiments. As shown in Figures 8A and S7, the loss of ¹³CH₃ magnetization is similar for all the three phase cycles during a short fp-RFDR mixing time (<3 ms), but for long mixing times XY4¹₄ renders the best performance. The transfer of longitudinal ¹³C magnetization was measured from the intensities of cross peaks observed in 2D ¹³C/¹³C spectra as a function of the fp-RFDR mixing time for different phase cycles. Sample spectral slices extracted from 2D ¹³C/¹³C spectra and the corresponding cross peak intensities are shown in Figure S7. Results presented in Figures 8(B and C) and S7 show that the ¹³C longitudinal magnetization transfer from the ¹³CH₃ to ¹³CH and ¹³COOH resonances (Figure 8(B and C)) under XY4¹₄ and XY8¹₄ phase cycles are similar and better than that obtained using the XY4 phase cycle for the fp-RFDR sequence; the performance of XY8¹₄ is slightly better that that of XY4¹₄ for longer mixing times. These results demonstrate that XY4¹₄ and XY8¹₄ phase cycles efficiently suppress the effects of chemical shift offset whereas XY4 is inefficient. These results are in agreement with previously reported experimental studies [40, 47].

Figure 8.

Variation of peak intensity experimentally measured as a function of fp-RFDR mixing time obtained using XY4, XY4¹₄, and XY8¹₄ phase cycles at an RF field strength of 118 kHz on U-¹³C-¹⁵N L-alanine under 90 kHz MAS. 2D ¹³C/¹³C chemical shift correlation experiments were carried out using fp-RFDR mixing on a 600 MHz JEOL solid-state NMR spectrometer using a 0.75 mm ultrafast MAS probe. Peak intensities were measured from the spectral slices extracted at the resonance frequency of ¹³CH₃ group along the indirect frequency dimension of 2D ¹³C/¹³C spectra: (A) diagonal peak of ¹³CH₃, (B) cross peak between ¹³CH₃ and ¹³CH, and (C) cross peak between ¹³CH₃ and ¹³COOH. Spectral slices are given in the supporting information (Figure S7). Since the trends obtained from spectral slices corresponding to ¹³CH and ¹³COOH resonances are similar, they are not included.

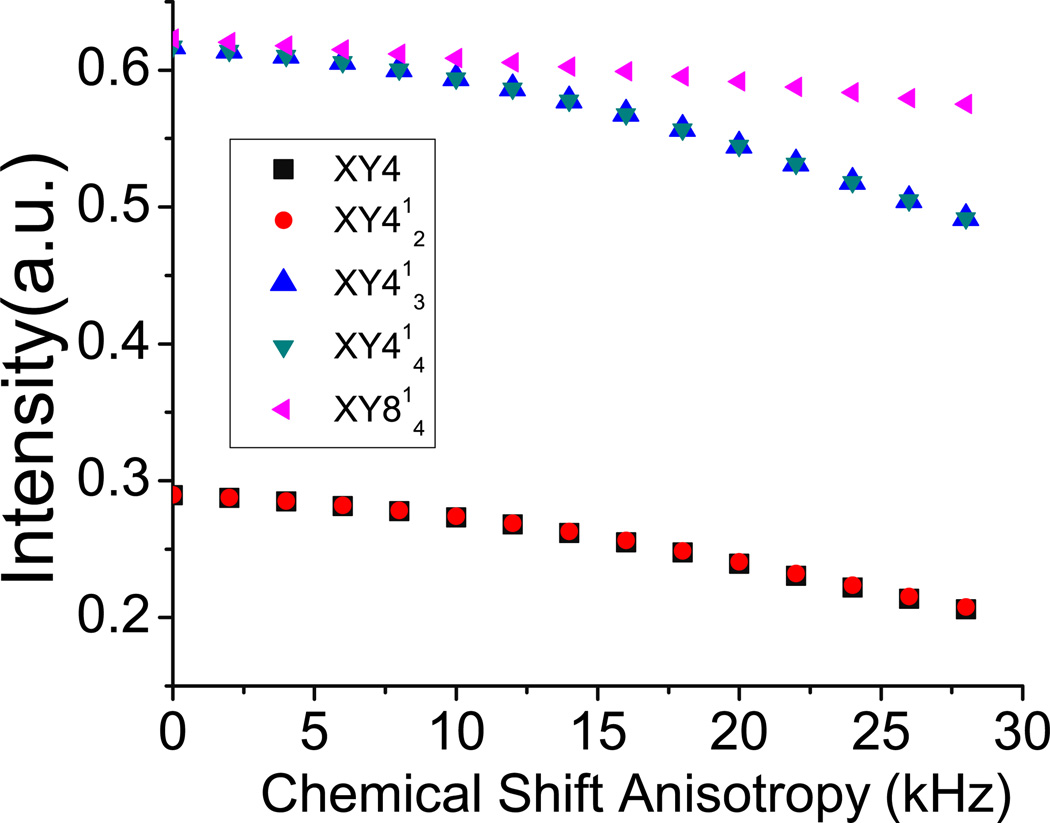
Chemical Shift Anisotropy effect

The small size proton CSAs are usually averaged out by MAS, and therefore they do not affect the performance of the fp-RFDR pulse sequence for 2D ¹H/¹H homonuclear correlation experiments. However, for low-γ nuclei, such as ¹³C, chemical shift anisotropy may not be completely suppressed even under ultrafast MAS conditions. Therefore, we examine the performance of the RFDR phase cycling schemes against CSA, and the results are shown in Figure 9. Three ¹³C spins, with 1 kHz ¹³C-¹³C dipolar coupling for each spin pair, were used in the simulation. The chemical shift offset was set at 12 kHz (~80 ppm in a 600 MHz NMR spectrometer). As shown by the simulated results in Figure 9, XY4 and XY4¹₂ have low recoupling efficiencies, as the dipolar-dipolar cross term is too small to compensate the chemical shift offset effect as explained above. In contrast, the super-cycles XY4¹₃, XY4¹₄ and XY8¹₄ exhibit high recoupling efficiencies as well as tolerance to CSA. Overall, XY8¹₄ exhibits the best performance against CSA in good agreement with experimental data shown in Figure 8.

Figure 9.

Effect of chemical shift anisotropy on the longitudinal magnetization transfer by fp-RFDR at a mixing time of 100 ms for different phase cyclings as indicated at a magic angle spinning speed of 60 kHz. Three ¹³C spins are used as explained in the main text. A 12 kHz chemical shift offset was used for the observed spin.

RF field inhomogeneity effect

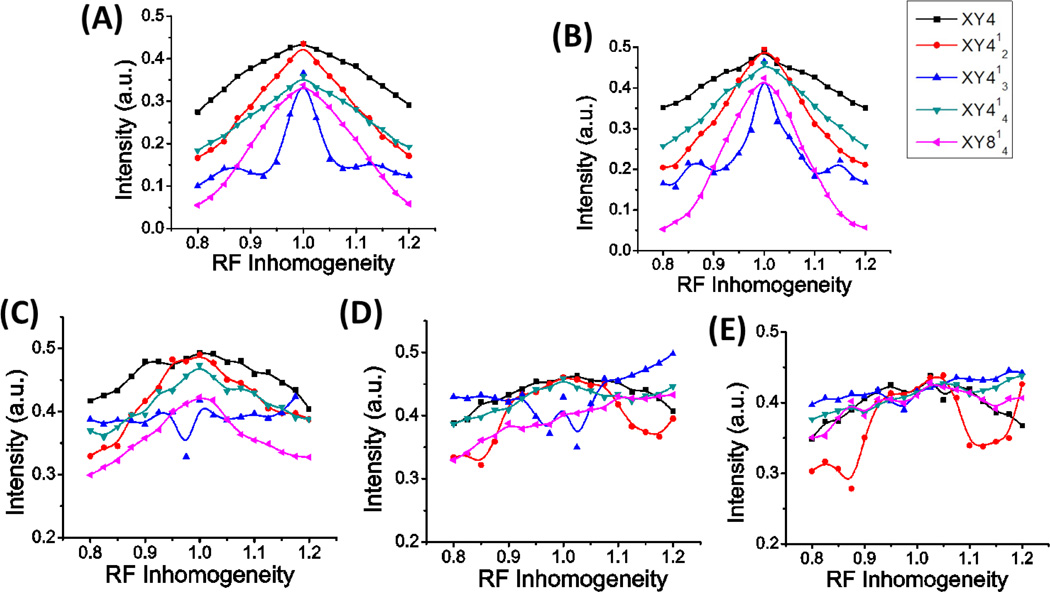
SIMPSON simulations were carried out to evaluate the transfer of longitudinal magnetization via the homonuclear dipolar couplings recoupled by the fp-RFDR pulse sequence for different RF field inhomogeneity values. As shown in Figure 10, the fp-RFDR pulse sequences have better tolerance to the RF field inhomogeneity with increasing MAS speed. However, it is interesting to find that the shortest phase cycle XY4 renders the most robust performance against the RF field inhomogeneity as compared to other super-cycles at lower spinning speeds (up to 40 kHz), whereas at 100 kHz MAS most phase cycling schemes exhibit the same efficiency against the RF field inhomogeneity except XY4¹₂. These results for lower spinning speeds are unexpected, as the super-cycles XY4¹₄ and XY8¹₄ are expected to compensate the effect of RF field inhomogeneity better than that of a basic phase cycling unit like XY4, as reported in the ¹³C/¹³C fp-RFDR-based correlation experiments [47].

Figure 10.

Effect of RF field inhomogeneity on the longitudinal magnetization transfer at a mixing time of 8 ms fp-RFDR for different phase cycles as indicated for a three spin 1/2 system at a MAS speed of: (A) 10 kHz, (B) 20 kHz, (C) 40 kHz, (D) 60 kHz and (E) 100 kHz. The value on the x-axis indicates the ratio of the applied RF field strength to the accurate RF field strength (i.e., 250 kHz). The homonuclear dipolar coupling was set as 29.3 kHz.

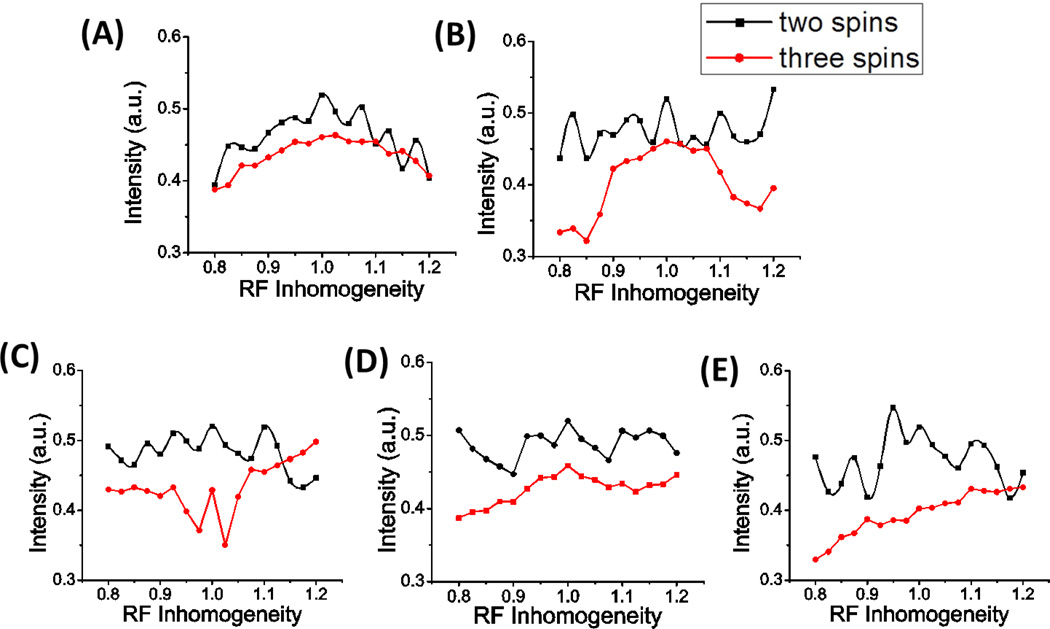
A comparison of the performances of different phase cycles against the RF inhomogeneity for two and three spin ½ systems would be beneficial to evaluate the effect of dipolar coupling - RF field inhomogeneity cross terms in the effective Hamiltonian of fp-RFDR. The RF field inhomogeneity effect for a two spin ½ system shown in Figure S8 suggests a similar overall performance for all the different phase cycles under different MAS speeds. However, the tolerance to the RF field inhomogeneity for a two spin ½ system is quite different from that for a three spin ½ system as shown in Figure 11. The simulated results reveal that the dipolar coupling - RF field inhomogeneity cross terms introduced by the presence of the third spin significantly reduced the magnetization transfer efficiency for all the phase cycles.

Figure 11.

Effect of RF field inhomogeneity on the longitudinal magnetization transfer at a 8 ms fp-RFDR mixing time for two and three spin ½ systems as indicated under 60 kHz MAS with a phase cycle of: (A) XY4, (B) XY4¹₂, (C) XY4¹₃, (D) XY4¹₄ and (E) XY8¹₄. The value on the x-axis indicates the ratio of the applied RF field strength to the accurate RF field strength (i.e., 250 kHz). The homonuclear dipolar coupling was set as 29.3 kHz.

An examination of the RF inhomogeneity effect for a rather weakly dipolar-coupled system is shown in Figures S9 and S10, where all the phase cyclings exhibit similar performances against the RF inhomogeneity. The comparison of the RF inhomogeneity effect for two and three spin-1/2 systems in Figure S10 also shows that the dipolar coupling - RF field inhomogeneity cross terms introduced by the presence of the third spin significantly reduced the magnetization transfer efficiency for all phase cycles.

Conclusion

In this study, recoupling efficiencies of XY-based phase cycling schemes - XY4, XY4¹₂, XY4¹₃, XY4¹₄, and XY8¹₄ - for the fp-RFDR pulse sequence under different MAS speeds were analyzed using the average Hamiltonian theory with second-order terms and SIMPSON simulations on two and three spin-½ systems with strong and weak homonuclear dipolar couplings. The average Hamiltonian reveals the presence of certain second-order terms that are not suppressed by the super cycles. In particular, the presence of $T_{1,0}^i{T}_{2,\pm 2}^{ij}$ and $T_{1,\pm 1}^i{T}_{2,\pm 1}^{ij}$ (as well as $T_{2,\pm 2}^{ij}{T}_{1,0}^i$ and $T_{2,\pm 1}^{ij}{T}_{1,\pm 1}^i$)terms makes the XY4 phase cycle a good choice for proton-based fp-RFDR homonuclear correlation experiments. In addition, simulated results revealed that the recoupling efficiency of fp-RFDR is quite dependent on the duty factor (τ₁₈₀/τ_R) of the sequence as well as on the strength of homonuclear dipolar couplings in the system. The rate of magnetization transfer was found to increase linearly with the duty factor for all phase cycles. At fast MAS frequencies (40 – 100 kHz), the recoupling efficiencies of all the phase cycles were found to be very similar for a weakly dipolar coupled system, while XY4 and XY4¹₄ are better than XY8¹₄ for a strongly coupled system. Furthermore, at slow spinning speeds (10 and 20 kHz), the short phase cycling scheme, XY4, could be preferable as it has a high recoupling efficiency and tolerance to the RF field inhomogeneity if offset is not large (like in protons); otherwise, a super-cycling scheme, XY4¹₄, is recommended as it overcomes the effect of chemical shift offset and RF field inhomogeneity effects. Finally, the effect of higher-order dipolar coupling terms and the cross terms between various interactions (such as dipolar coupling, chemical shift offset, and RF field inhomogeneity) were also evaluated using numerical simulations. The higher-order dipolar-dipolar coupling terms were found to enhance the magnetization transfer efficiency during fp-RFDR mixing time, and suppress the offset effects for short phase cycles, whereas the dipolar coupling - RF field inhomogeneity cross term reduced the magnetization transfer efficiency. Overall, these findings are in excellent agreement with our experimental findings for experiments under ultrafast MAS conditions.

Figure 1.

(A) The radio-frequency pulse sequence for the 2D ¹H/¹H chemical shift correlation experiment using the fp-RFDR dipolar recoupling sequence in the mixing period t_mix; the basic unit of the RFDR sequence is: τ − 180° − τ = one MAS rotor period. The 90° and 180° pulses are indicated with the blank and solid rectangles, respectively. The relevant phase cycling (ϕ_i) for the 90° pulses and receiver are given below the pulse sequences. (B) A list of phase cycling schemes used for the 180° pulse in fp-RFDR in the present study.

Highlights.

• Efficiencies of XY-based phase cycles for fp-RFDR experiments are investigated.

• Effects of higher-order terms and cross terms in fp-RFDR Hamiltonian are analyzed.

• XY4¹₄ is recommended based on its best performance under all conditions.

• RFDR efficiency depends on the scaling factor and homonuclear dipolar couplings.

  • Higher-order dipolar coupling terms enhance magnetization transfer efficiency.

Appendix

The derivation of first-order effective Hamiltonian, as given by Ishii [41], and the calculation of second-order terms are presented. Following the derivation given in reference [41], the time-dependent interaction Hamiltonian in the RF interaction frame of RFDR pulse sequence is given as:

$${\tilde{H}}_{\text{int}}(t)=\text{exp}(i{\mathrm{\Phi }}_n{I}_z)[{(-1)}^{n-1}{\tilde{H}}_{CS}(\mathrm{\Delta }t)+{\tilde{H}}_D(\mathrm{\Delta }t)]\text{exp}(-i{\mathrm{\Phi }}_n{I}_z)$$ (A1)

$${\tilde{H}}_{CS}(\mathrm{\Delta }t)=\sum _j{\mathrm{\Omega }}_j(\mathrm{\Delta }t)\{\text{cos}\beta T_{10}^j+i\text{sin}\beta [\text{cos}\gamma (T_{1,1}^j+T_{1,-1}^j)+i{\rho }_n\text{sin}\gamma (T_{1,1}^j-T_{1,-1}^j)]/\sqrt{2}\}$$ (A2)

$${\tilde{H}}_D(\mathrm{\Delta }t)=\sum _{j<k}\frac{\sqrt{6}}{2}\pi D^{jk}(\mathrm{\Delta }t)\{(3{\text{cos}}^2\beta -1)T_{2,0}+i\sqrt{3/2}\text{sin}2\beta [\text{cos}\gamma (T_{2,1}^{jk}-T_{2,-1}^{jk})+i{\rho }_n\text{sin}\gamma (T_{2,1}^{jk}+T_{2,-1}^{jk})]-\sqrt{3/2}{\text{sin}}^2\beta [\text{cos}(2\gamma )(T_{2,2}^{jk}+T_{2,-2}^{jk})+i{\rho }_n\text{sin}(2\gamma )(T_{2,2}^{jk}+T_{2,-2}^{jk})]\}$$ (A3)

Δt = t − (n − 1)τ_R, and (n − 1)τ_R ≤ t < nτ_R. ρ_n = (−1)ⁿ σ_n, σ_n is the symmetry sign of the nth pulse. β and γ are the Euler angles which define rotation in spin space. Ω_j(t) is the sum of isotropic and time-dependent anisotropic chemical shifts for nuclei j, while D^jk(t) is a time-dependent dipolar coupling constant between spins j and k. Also,

$${\mathrm{\Phi }}_n={(-1)}^{n+1}{\varphi }_n+2\sum _{j=1}^n{(-1)}^j{\varphi }_j$$ (A4)

ϕ_n is the phase for the nth π pulse in a fp-RFDR cycle.

The above equations are valid for an fp-RFDR sequence that employs phase/amplitude modulation or composite π pulses. In present study only rectangle π pulses without any phase/amplitude modulations are used; therefore, γ=0, β=ω₁ τ at the end of π pulse. ω₁ is the RF field strength for the π pulses, and τ is the π pulse width. As a result, the time-dependent chemical shift and homonuclear dipolar coupling Hamiltonians given in equations (A2) and (A3) can be simplified as:

$${\tilde{H}}_{CS}(\mathrm{\Delta }t)=\sum _j{\mathrm{\Omega }}_j(\mathrm{\Delta }t)[\text{cos}\beta T_{10}^j+i\text{sin}\beta (T_{1,1}^j+T_{1,-1}^j)/\sqrt{2}]$$ (A5)

$${\tilde{H}}_D(\mathrm{\Delta }t)=\sum _{j<k}\frac{\sqrt{6}}{2}\pi D^{jk}(\mathrm{\Delta }t)[(3{\text{cos}}^2\beta -1)T_{2,0}+i\sqrt{3/2}\text{sin}2\beta (T_{2,1}^{jk}-T_{2,-1}^{jk})-\sqrt{3/2}{\text{sin}}^2\beta (T_{2,2}^{jk}+T_{2,-2}^{jk})]$$ (A6)

Using equations (A1), (A5) and (A6), and the following relations,

$$\text{exp}(-i\phi I_z)I_x\text{exp}(i\phi I_z)=I_x\text{cos}\phi +I_y\text{sin}\phi$$ (A7a)

$$\text{exp}(-i\phi I_z)I_y\text{exp}(i\phi I_z)=I_y\text{cos}\phi -I_x\text{sin}\phi$$ (A7b)

$$\text{exp}(-i\phi I_z)I^{+}\text{exp}(i\phi I_z)=\text{exp}(-i\phi )I^{+}$$ (A7c)

$$\text{exp}(-i\phi I_z)I^{-}\text{exp}(i\phi I_z)=\text{exp}(i\phi )I^{-}$$ (A7d)

the Hamiltonian in the RF interaction frame can be written as:

$${\tilde{H}}_{\text{int}}(t)={\tilde{H}}_{CS}^{RF}(\mathrm{\Delta }t)+{\tilde{H}}_D^{RF}(\mathrm{\Delta }t)$$ (A8)

$${\tilde{H}}_{CS}^{RF}(\mathrm{\Delta }t)=\sum _j{\mathrm{\Omega }}_j(\mathrm{\Delta }t)*{(-1)}^{n-1}[\text{cos}\beta T_{10}^j+i\text{sin}\beta (e^{i{\mathrm{\Phi }}_n}{T}_{1,1}^j+e^{-i{\mathrm{\Phi }}_n}{T}_{1,-1}^j)/\sqrt{2}]$$ (A9)

$${\tilde{H}}_D^{RF}(\mathrm{\Delta }t)=\sum _{j<k}\frac{\sqrt{6}}{2}\pi D^{jk}(\mathrm{\Delta }t)[(3{\text{cos}}^2\beta -1)T_{2,0}+i\sqrt{3/2}\text{sin}2\beta (e^{i{\mathrm{\Phi }}_n}{T}_{2,1}^{jk}-e^{-i{\mathrm{\Phi }}_n}{T}_{2,-1}^{jk})-\sqrt{3/2}{\text{sin}}^2\beta (e^{i2{\mathrm{\Phi }}_n}{T}_{2,2}^{jk}+e^{-i2{\mathrm{\Phi }}_n}{T}_{2,-2}^{jk})]$$ (A10)

According to the average Hamiltonian theory [53, 54], the effective Hamiltonian can be obtained using the Magnus expansion as given below.

$${\overline{H}}_{\text{int}}^{\mathit{\text{eff}}}(t)={\overline{H}}_{\text{int}}^{(1)}(t)+{\overline{H}}_{\text{int}}^{(2)}(t)+{\overline{H}}_{\text{int}}^{(3)}(t)+\cdots$$ (A11)

where

$${\overline{H}}_{\text{int}}^{(1)}(t)=\frac{1}{t_c}{\int }_0^{t_c}d{t}_1{\tilde{H}}_{\text{int}}(t_1)$$ (A12)

$${\overline{H}}_{\text{int}}^{(2)}(t)=\frac{-i}{2t_c}{\int }_0^{t_c}d{t}_1{\int }_0^{t_1}d{t}_2[{\tilde{H}}_{\text{int}}(t_1),{\tilde{H}}_{\text{int}}(t_2)]$$ (A13)

$${\overline{H}}_{\text{int}}^{(3)}(t)=\frac{-1}{6t_c}{\int }_0^{t_c}d{t}_1{\int }_0^{t_1}d{t}_2{\int }_0^{t_2}d{t}_3\{[{\tilde{H}}_{\text{int}}(t_1),[{\tilde{H}}_{\text{int}}(t_2),{\tilde{H}}_{\text{int}}(t_3)]+[{\tilde{H}}_{\text{int}}(t_3),[{\tilde{H}}_{\text{int}}(t_2),{\tilde{H}}_{\text{int}}(t_1)]\}$$ (A14)

The interaction Hamiltonian fulfills the periodic condition:

$${\tilde{H}}_{\text{int}}(t)={\tilde{H}}_{\text{int}}(t+t_c)$$ (A15)

t_c is the cycle period for the fp-RFDR pulse sequence.

Therefore, the first-order average interaction Hamiltonian in the RF interaction frame is:

$${\overline{H}}_{\text{int}}^{(1)}={\overline{H}}_{CS}^{(1)}+{\overline{H}}_D^{(1)}$$ (A16)

$${\overline{H}}_{CS}^{(1)}=\frac{1}{L}\sum _{n=1}^L[\sum _j\sum _{m=-1}^1{i}^m{(-1)}^{n-1}\text{exp}(i\mathrm{m}{\mathrm{\Phi }}_n){\mathrm{\Omega }}_m^j{\mathrm{T}}_{1,m}^j]$$ (A17)

$${\overline{H}}_D^{(1)}=\frac{1}{L}\sum _{n=1}^L[\sum _{j<k}\sum _{m=-2}^2{i}^m\text{exp}(i\mathrm{m}{\mathrm{\Phi }}_n)D_m^{jk}{\mathrm{T}}_{2,m}^{jk}]$$ (A18)

where L is the number of π pulses in a fp-RFDR cycle. With XY4 phase cycling (or its super cycles or XY8¹₄) as the phase cycling scheme for fp-RFDR, ${\overline{H}}_{CS}^{(1)}$ is averaged to zero due to the presence of the prefactor (−1)ⁿ⁻¹ exp(imΦ_n), while ${\overline{H}}_D^{(1)}$ contains only the zero-quantum term T_2,0, as the prefactor exp(imΦ_n) is constant (i.e. 1 for m=0) for T_2,0 terms. The effective Hamiltonian at different time periods in fp-RFDR do not commute with each other. As a result, cross terms in the second-order average Hamiltonian, such as chemical shift-dipolar coupling cross terms, zero quantum-double quantum (ZQ-DQ) dipolar coupling cross terms, and so on, are present.

The effective chemical shift and dipolar coupling Hamiltonians in the RF interaction frame can be written as follows:

$${\tilde{H}}_{CS}^{RF}(\mathrm{\Delta }t)={\tilde{H}}_{CS1}(\mathrm{\Delta }t)+{\tilde{H}}_{CS2}(\mathrm{\Delta }t)$$ (A19)

$${\tilde{H}}_D^{RF}(\mathrm{\Delta }t)={\tilde{H}}_{D1}(\mathrm{\Delta }t)+{\tilde{H}}_{D2}(\mathrm{\Delta }t)+{\tilde{H}}_{D3}(\mathrm{\Delta }t)$$ (A20)

where

$${\tilde{H}}_{CS1}(\mathrm{\Delta }t)=\sum _j{\mathrm{\Omega }}_j(\mathrm{\Delta }t)*{(-1)}^{n-1}\text{cos}\beta T_{10}^j$$ (A21a)

$${\tilde{H}}_{CS2}(\mathrm{\Delta }t)=\sum _{j}i{\mathrm{\Omega }}_j(\mathrm{\Delta }t)*{(-1)}^{n-1}\text{sin}\beta (e^{i{\mathrm{\Phi }}_n}{T}_{1,1}^j+e^{-i{\mathrm{\Phi }}_n}{T}_{1,-1}^j)/\sqrt{2}$$ (A21b)

$${\tilde{H}}_{D1}(\mathrm{\Delta }t)=\sum _{j<k}\frac{\sqrt{6}}{2}\pi D^{jk}(\mathrm{\Delta }t)(3{\text{cos}}^2\beta -1)T_{2,0}^{jk}$$ (A21c)

$${\tilde{H}}_{D2}(\mathrm{\Delta }t)=\sum _{j<k}i\frac{\sqrt{6}}{2}\pi D^{jk}(\mathrm{\Delta }t)\sqrt{3/2}\text{sin}2\beta (e^{i{\mathrm{\Phi }}_n}{T}_{2,1}^{jk}-e^{-i{\mathrm{\Phi }}_n}{T}_{2,-1}^{jk})$$ (A21d)

$${\stackrel{\sim }{H}}_{D3}(\mathrm{\Delta }t)=\sum _{j<k}-\frac{\sqrt{6}}{2}\pi D^{jk}(\mathrm{\Delta }t)\sqrt{3/2}{\text{sin}}^2\beta (e^{i2{\mathrm{\Phi }}_n}{T}_{2,2}^{jk}+e^{-i2{\mathrm{\Phi }}_n}{T}_{2,-2}^{jk})$$ (A21e)

Therefore, for a two spin-1/2 system, the effective Hamiltonian is:

$${\tilde{H}}_{\mathit{\text{eff}}}^{RF}(\mathrm{\Delta }t)=\sum _{i=1}^2({\tilde{H}}_{CS1}^i(\mathrm{\Delta }t)+{\tilde{H}}_{CS2}^i(\mathrm{\Delta }t))+{\tilde{H}}_{D1}^{12}(\mathrm{\Delta }t)+{\tilde{H}}_{D2}^{12}(\mathrm{\Delta }t)+{\tilde{H}}_{D3}^{12}(\mathrm{\Delta }t)$$ (A22)

As mentioned above, every term with a prefactor of (−1)ⁿ⁻¹ exp(imΦ_n) will be averaged to zero over all RFDR phase cycling schemes used in this study, except for the XY4 phase cycling. The terms with a prefactor of (−1)ⁿ⁻¹ exp(±i2Φ_n) survives for the XY4 phase cycling. The terms with a prefactor of exp(imΦ_n) for m=0 as well as cross-terms without a prefactor also survive. As a result, the second-order terms in the Hamiltonian are averaged to zero for a two spin-1/2 system, except the commutator $[{\tilde{H}}_{CS1}^i(\mathrm{\Delta }t),{\tilde{H}}_{D3}(\mathrm{\Delta }t)],[{\tilde{H}}_{CS2}^i(\mathrm{\Delta }t),{\tilde{H}}_{D2}(\mathrm{\Delta }t)]$ that correspond to $[T_{1,0}^i,T_{2,\pm 2}],[T_{1,\pm 1}^i,T_{2,\pm 1}]$ terms, respectively, when the XY4 phase cycling is used.

On the other hand, for a three spin-1/2 system, the effective Hamiltonian in the RF interaction frame is complicated and also different from the two spin-1/2 case as shown below.

$${\stackrel{\sim }{H}}_{\mathit{\text{eff}}}^{RF}(\mathrm{\Delta }t)=\sum _{i=1}^3({\stackrel{\sim }{H}}_{CS1}^i(\mathrm{\Delta }t)+{\stackrel{\sim }{H}}_{CS2}^i(\mathrm{\Delta }t))+\sum _{i<j,i,j=1}^3({\stackrel{\sim }{H}}_{D1}^{ij}(\mathrm{\Delta }t)+{\stackrel{\sim }{H}}_{D2}^{ij}(\mathrm{\Delta }t)+{\stackrel{\sim }{H}}_{D3}^{ij}(\mathrm{\Delta }t))$$ (A23)

All the second-order terms are averaged to zero, except the commutators: $[{\tilde{H}}_{CS2}^i(\mathrm{\Delta }t),{\tilde{H}}_{CS2}^j(\mathrm{\Delta }t)],[{\tilde{H}}_{D1}^{ij}(\mathrm{\Delta }t),{\tilde{H}}_{D1}^{ij}(\mathrm{\Delta }t)],[{\tilde{H}}_{D2}^{ij}(\mathrm{\Delta }t),{\tilde{H}}_{D2}^{ij}(\mathrm{\Delta }t)],[{\tilde{H}}_{D3}^{ij}(\mathrm{\Delta }t),{\tilde{H}}_{D3}^{ij}(\mathrm{\Delta }t)]$, corresponding to $[T_{1,1}^i,T_{1,-1}^j],[T_{2,0}^{ij},T_{2,0}^{jk}],[T_{2,1}^{ij},T_{2,-1}^{jk}],[T_{2,2}^{ij},T_{2,-2}^{jk}]$, respectively. These higher-order terms contribute to the magnetization transfer under fp-RFDR especially when the homonuclear dipolar coupling is large (like in the case of protons), as reflected in the numerical simulations shown in Figure 5. In particular, when the XY4 phase cycling is used, the terms with a prefactor of (−1)ⁿ⁻¹ exp(±i2Φ_n), (i.e. $[T_{1,0}^i,T_{2,\pm 2}^{ij}]$ and $[T_{1,\pm 1}^i,T_{2,\pm 1}^{ij}]$ terms), are non-zero. Both the terms contain the double-quantum operators ($I_i^{+}{I}_j^{+}$ and $I_i^{-}{I}_j^{-}$), that contribute to the magnetization transfer efficiency rendered by the XY4 phase cycling. This explains the faster build-up rate observed for the fp-RFDR pulse sequence that utilizes the XY4 phase cycling when compared to the super cycling schemes as reported in our experimental analyses of proton-based RFDR under ultrafast-MAS conditions [40].