Abstract
Bone mineral density (BMD) measurements from Dual-energy X-ray Absorptiometry (DXA) alone cannot account for all factors associated with the risk of hip fractures. For example, the inhomogeneity of bone mineral density in the hip region also contributes to bone strength. In the stochastic assessment of bone inhomogeneity, the BMD map in the hip region is considered as a random field and stochastic predictors can be calculated by fitting a theoretical model onto the experimental variogram of the BMD map. The objective of this study was to compare the ability of bone mineral density and stochastic assessment of inhomogeneous distribution of bone mineral density in predicting hip fractures for postmenopausal women. DXA scans in the hip region were obtained from postmenopausal women with hip fractures (N=47, Age: 71.3±11.4 years) and without hip fractures (N=45, Age: 66.7±11.4 years). Comparison of BMD measurements and stochastic predictors in assessing bone fragility was based on the area under the receiver operating characteristic curves (AUC) from logistic regression analyses. Although stochastic predictors offered higher accuracy (AUC=0.675) in predicting the risk of hip fractures than BMD measurements (AUC=0.625), such difference was not statistically significant (p=0.548). Nevertheless, the combination of stochastic predictors and BMD measurements had significantly (p=0.039) higher prediction accuracy (AUC=0.748) than BMD measurements alone. This study demonstrates that stochastic assessment of bone mineral distribution from DXA scans can serve as a valuable tool in enhancing the prediction of hip fractures for postmenopausal women in addition to BMD measurements.
Keywords: Bone mineral density (BMD), osteoporosis, experimental variogram, DXA, stochastic method
Introduction
The bone mineral density (BMD), measured from dual-energy X-ray absorptiometry (DXA), has become the gold standard for the diagnosis of osteoporosis and the assessment of fracture risk (WHO, 2003). However, BMD alone is not sufficient to account for all spectra of fracture risks. The overlap of BMD has been observed for subjects with hip fractures and without hip fractures (Hui et al., 1988; Kanis et al., 2005; Kanis et al., 2007). Therefore, bone quality measures, including architecture, turnover, damage accumulation and mineralization, have been proposed as additional features in predicting bone fractures (NIH, 2000). New techniques, such as fractal texture analysis (Majumdar et al., 1993; Benhamou et al., 1994; Buckland-Wright et al., 1994; Majumdar et al., 2000; Pothuaud et al., 2000; Chappard et al., 2001; Messent et al., 2005; Apostol et al., 2006; Lespessailles et al., 2008; Le Corroller et al., 2012), topological analysis (Boehm et al., 2007; Boehm et al., 2008), hip structure analysis (Beck, 2003; Beck, 2007), finite element analysis (Langton et al., 2009), and trabecular bone score based on the experimental variogram (Pothuaud et al., 2008; Pothuaud et al., 2009; Hans et al., 2011; Winzenrieth et al., 2013), have been introduced to enhance the prediction of bone fractures from DXA images by providing additional information of bone quality.
Fractal analysis of texture in two-dimensional images is a useful imaging technique that has been successfully applied to high-resolution radiography images to extract the hidden geometric and microstructure parameters of trabecular bone in both clinical studies and in vitro studies (Majumdar et al., 1993; Benhamou et al., 1994; Buckland-Wright et al., 1994; Majumdar et al., 2000; Pothuaud et al., 2000; Chappard et al., 2001; Messent et al., 2005; Apostol et al., 2006; Lespessailles et al., 2008; Le Corroller et al., 2012).
Topological analysis is another example of image processing tools that have been applied to two-dimensional DXA images (Boehm et al., 2007). An in vitro study of 100 hip specimens demonstrated that the topology-based parameter from DXA images had a strong correlation with the failure strength of the specimens (Boehm et al., 2008).
Both hip structural analysis and finite element analysis of X-ray images have attempted to directly extract stiffness and strength of bone from DXA scans. In hip structural analysis, bone strength is estimated by extracting the total surface area of bone in a cross-sectional slice, the cross-sectional moment of inertia, and the buckling ratio from DXA scan data (Beck, 2003; Beck, 2007). In the finite element analysis of X-ray images, a 3D proximal femur shape can be generated from 2D radiographic images and used to construct the 3D finite element models (Langton et al., 2009).
In recent years, the Trabecular Bone Score (TBS) has gained the attention of researchers in the assessment of fracture risk (Bousson et al., 2012; Silva et al., 2014). TBS is a new parameter determined from the grayscale analysis of DXA images (Pothuaud et al., 2008). The value of TBS is calculated as the slope at the origin of the log-log representation of the experimental variogram of DXA images (Pothuaud et al., 2009; Hans et al., 2011; Winzenrieth et al., 2013). In ex vivo studies, TBS has been found to correlate with microarchitecture parameters of trabecular bone, such as bone volume fraction, mean bone thickness, degree of anisotropy and structure model index (SMI) (Pothuaud et al., 2008; Roux et al., 2013; Winzenrieth et al., 2013). TBS has also been used in numerous clinical studies (Pothuaud et al., 2009; Rabier et al., 2010; Winzenrieth et al., 2010; Hans et al., 2011; Bousson et al., 2012; Leib et al., 2013; Leslie et al., 2014; Silva et al., 2014).
Among these enhanced techniques for DXA scans, TBS may have the most potential to be used for improving the prediction of bone fractures. However, there are several challenges to be addressed before the trabecular bone score can be extensively used in clinical situations. First, the physical meaning of TBS is still vague at this time. TBS evaluates the variations of grayscale values in DXA images through experimental variograms. The use of grayscale values does not characterize the exact distribution of bone mineral density, and grayscale values in DXA images may be easily changed by varying the brightness and the contrast of these images. Second, TBS only reflects the initial trend, rather than the global trend, of the experimental variogram since it is defined as the initial slope of log-log representation of the experimental variogram. A more appropriate model needs to be used to describe the variation of bone mineral distribution from DXA scans.
To this end, we proposed a novel stochastic approach based on random field theory (Dong et al., 2010; Dong et al., 2013) to extract the stochastic parameters from the inhomogeneous distribution of bone mineral density of DXA scans. The objectives of this study were: (1) to generate a map of bone mineral density in terms of gram per unit area from DXA scans using the raw data of dual-energy X-ray attenuation; (2) to create the experimental variogram of bone mineral density map and extract the stochastic parameters from theoretical models that represent the global trend of experimental variograms; (3) to apply this stochastic assessment of bone mineral distribution to the risk prediction of hip fractures for postmenopausal women.
Materials and Methods
Recruitment of human subjects
In this retrospective study, two groups of human subjects, i.e. patients with fracture and control, were examined from postmenopausal women over the age of 50 who had visited the Department of Radiology at UT Health Northeast. Among these subjects, the fracture group (N=47, Age: 71.3±11.4 years old) included subjects with a history of osteoporotic hip fractures whereas the control group (N=45, Age: 66.6±9.9 years old) consisted of subjects without osteoporotic fractures. In the fracture group, only the patients with a hip fracture in the left side and an intact hip in the right side were chosen for this study. Women with traumatic fractures, such as secondary to an automobile accident, were excluded. The approval of IRB from participating institutions was obtained for this study.
DXA scan
Images of DXA scans were obtained from 92 postmenopausal women using a Hologic densitometer (QDR Discovery A, Bedford, MA) by a technologist certified by the International Society for Clinical Densitometry. Prior to scanning each day, an anthropometric Spine phantom supplied by the manufacturer was scanned to monitor scanner precision. For the fracture group, all fractures occurred at the left hip and the contralateral hip (i.e., right hip) was scanned. For the control group, the left hip was scanned. The subject was first positioned on the scanning table by the technologist such that the X-ray beam projection was from posterior to anterior direction. Next, the Hip mode was selected to scan the hip. Finally, the total hip BMD was reported with a unit of g/cm2, and a T-score value was also reported by the Hologic scanner.
BMD maps extracted from DXA scans
The BMD map, expressed in terms of gram per cm2 at the total hip region was calculated using the raw data from DXA scans of Hologic densitometers (i.e., R files) consisting of the attenuation of X-ray beams at two distinct energies. Details of obtaining the BMD map from DXA scans are available in the literature (Blake et al., 1992; Blake and Fogelman, 1997; Blake et al., 1999) and are included in the Appendix.
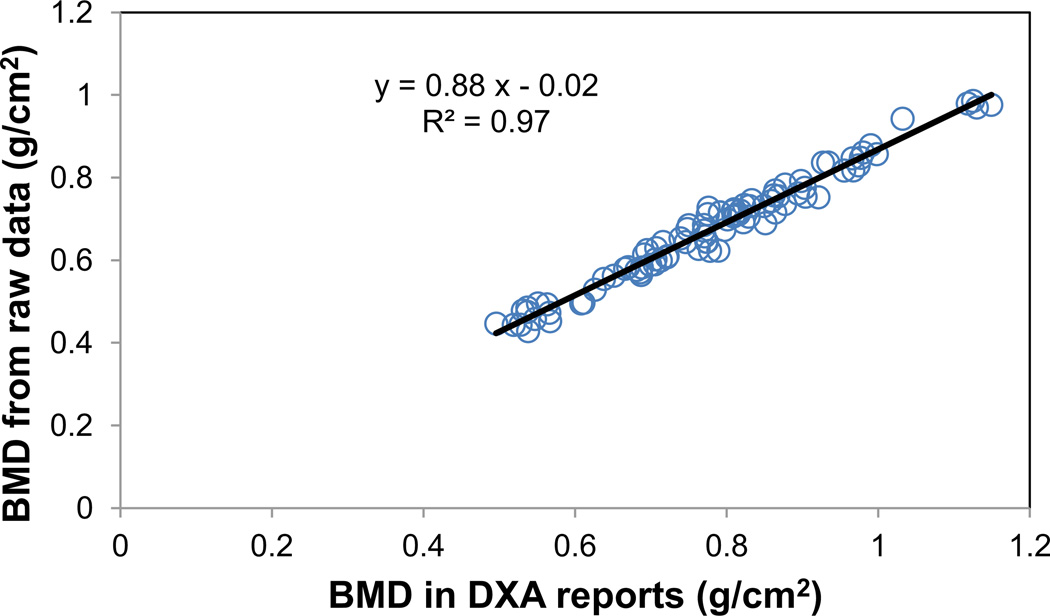
The current method of extracting the bone map from DXA scans was validated by performing a linear regression analysis of the mean values of the BMD map in the hip region and the total hip BMD values in the same region of interest provided by the Hologic densitometer in the DXA reports. A total number of 92 subjects were used in the regression analysis. The Rsquared value of the linear regression was 0.97, indicating a significantly (p<0.001) linear relationship between the calculated BMD values from the BMD map and the total hip BMD values reported by the densitometer manufacturer (Figure 1).
Figure 1.
Validation of BMD maps from raw data of DXA scans. For a cohort of 92 postmenopausal women, linear regression was performed between the BMD values reported in Hologic densitometers and the BMD values calculated as the average of the BMD map at the same total hip region from the raw data of DXA scans. Significant (p<0.001) linear relationship was observed between the reported and calculated BMD values with the R-squared value of 0.97.
Stochastic predictors from the experimental variogram of the BMD map
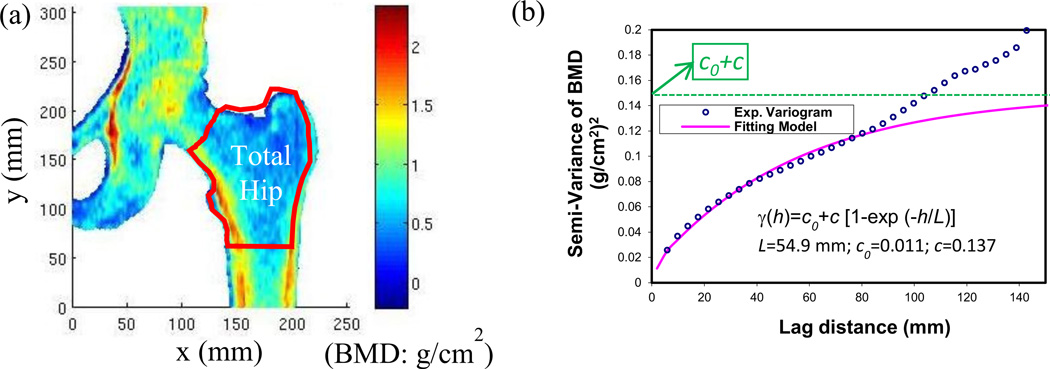
The spatial variation of the BMD map (Figure 2a) from DXA scans was characterized using an experimental variogram (Figure 2b). The concept of experimental variograms is briefly described here. A semi-variance, γ(h), is defined as the half of the expected squared differences of bone mineral density between any two locations with a lag distance of h.
| (1) |
where Z(x) is a function to describe the random field of bone mineral density; Both x and h are vectors; x is the spatial coordinates of the data location. Lag distance, h, represents the Euclidean distance and direction between any two locations within the hip region.
Figure 2.
Calculation of stochastic predictors from the BMD map. (a) A typical BMD map obtained from the raw data of DXA hip scans; (b) An experimental variogram of BMD distribution at the total hip region and an exponential fitting model of the experimental variogram. The stochastic predictors, correlation length (L), sill variance (c) and nugget variance (c0), were extracted from the exponential model.
The experimental variogram is calculated as an average of semi-variance values at different locations that have the same value of lag distance (h).
| (2) |
where m(h) is the number of data pairs for the observations with a lag distance of h.
A simple mathematical function, known as an authorized model, can be used to describe the underlying stochastic process of experimental variograms (Mcbratney and Webster, 1986). An exponential model was used to fit over the experimental variogram of the BMD map with the least square curve fitting (Dong et al., 2010; Dong et al., 2013). The ordinary least square estimation was implemented in MATLAB (MathWorks, Natick,MA) with the function “lsqcurvefit”. The stochastic predictors in the exponential model can be estimated by minimizing the residual sum of squares for semi-variance.
The semi-variance (γ) with an exponential model can be represented by the following formula:
| (3) |
where γ(h) is the semi-variance of bone mineral density as a function of lag distance (h). L, correlation length, is a distance parameter defining the spatial extent of the model. Correlation length is an important parameter to describe the spatial variation of a random field. A large correlation length implies a smooth variation whereas a small correlation length corresponds to rapid changes in the property over the spatial domain. c, sill variance, is the a priori variance of the random field. The experimental variogram may reach its sill variance asymptotically. c0, nugget variance, is the positive intercept on the axis of semi-variance. Any apparent nugget variance usually arises from errors of measurement and spatial variation within the shortest sampling interval (Webster and Oliver, 2001). The sum of sill variance and nugget variance is the converging value of variance when the lag distance approached infinity (i.e. the global variance in the BMD map), which gives rise to a measure of magnitude of spatial variation of BMD map.
In this study, we used the stochastic parameters at the global level to characterize the BMD map in the total hip region for both control and fracture groups of postmenopausal women.
Statistical analyses
Statistical analyses were performed with SPSS (IBM, Armonk, NY) with a significance level of p<0.05. Comparisons of BMD and stochastic predictors between control and fracture group were conducted using Student’s t-tests. Logistic regression models were used to estimate the contribution of BMD and stochastic predictors on the risks of hip fracture (Vittinghoff, 2012). The outcome of logistic regression models was represented by a receiver operator characteristic curve (ROC). The area under the ROC curve (AUC) indicated the accuracy of the logistic regression model (Vittinghoff, 2012). The comparison of ROC curves was based on Delong’s test using pROC: an open-source package for R specifically dedicated to ROC analysis (DeLong et al., 1988; Robin et al., 2011).
Results
No significant differences in height (p=0.309), weight (p=0.522), or body mass index (p=0.783) were found between control and fracture groups (Table 1). However, significant (p=0.038) difference in age was observed between control and fracture groups (Table 1).
Table 1.
Comparisons of the age, height, weight and body mass index (BMI) between postmenopausal women with hip fractures (fracture group) and without hip fractures (control group) recruited in this study. Data were reported as mean ± standard deviation. The p-values were results from the comparisons using Student-t tests.
| Age (year) |
Height (inch) |
Weight (lb) |
BMI (kg/m2) |
|
|---|---|---|---|---|
| Control (N=45) | 66.7±9.9 | 64.4±2.8 | 165±40.2 | 28.2±6.2 |
| Fracture (N=47) | 71.3±11.4 | 63.8±3.0 | 159±44.9 | 27.9±7.6 |
| p-value | 0.038* | 0. 309 | 0.522 | 0.783 |
The p-value was significant.
The bone mineral density of postmenopausal women in the fracture group was significantly (p=0.042) lower than that of the control group (Table 2). Consequently, the T-score in the fracture group was significantly (p=0.040) less than the T-score in the control group (Table 2). On the other hand, no significant differences in the bone mineral content (p=0.182) and the bone area (p=0.894) of the total hip region were observed between control and fracture groups (Table 2).
Table 2.
Comparisons of bone mineral density (BMD), bone mineral content (BMC), area, and T-score in the total hip region reported from Hologic densitometers for both control and fracture groups. Data were reported as mean ± standard deviation. The p-values were results of comparisons between control and fracture groups using Student-t tests.
| BMD (g/cm2) |
BMC (g) |
Area (cm2) |
T-Score | |
|---|---|---|---|---|
| Control (N=45) | 0.802±0.124 | 26.4±4.81 | 33.0±4.30 | −1.12±1.01 |
| Fracture (N=47) | 0.740±0.161 | 24.8±6.71 | 33.2±4.87 | −1.69±1.33 |
| p-value | 0.042* | 0.182 | 0.894 | 0.040* |
The p-value was significant.
Among stochastic predictors, correlation length was significantly higher (p=0.024) in the control group than in the fracture group whereas no significant differences of sill variance (p=0.452) and nugget variance (p=0.852) were observed between control and fracture groups (Table 3).
Table 3.
Comparison of stochastic predictors (correlation length, sill variance, and nugget variance) calculated from DXA scans between control and fracture groups. Data were reported as mean ± standard deviation. The p-values were results of comparisons between control and fracture groups using Student-t tests.
| Correlation Length (mm) |
Sill Variance (g/cm2)2 |
Nugget Variance (g/cm2)2 |
|
|---|---|---|---|
| Control (N=45) | 65.1±19.9 | 0.161±0.047 | 0.020±0.011 |
| Fracture (N=47) | 55.2±21.2 | 0.152±0.056 | 0.020±0.015 |
| p-value | 0.024* | 0.427 | 0.852 |
The p-value was significant.
Logistic regression models were used to examine the relationship between the risk of hip fractures and BMD and stochastic predictors (correlation length, sill variance and nugget variance) for postmenopausal women (Table 4). When the BMD alone was used as the predictor variable, significant (p=0.047) relationship between the fracture risk and BMD measurements was observed. When only stochastic predictors were used as predictor variables, the risk of hip fractures had significant relationships with the correlation length (p=0.009), but not the sill variance (p=0.908) and the nugget variance (p=0.083). When a combination of BMD measurements and stochastic predictors was used, the sill variance (p=0.147) was the only predictor variable without significant relationship with the risk of hip fractures (Table 4).
Table 4.
Logistic regression models for predicting the risk of hip fractures from bone mineral density (BMD), stochastic predictors (correlation length, sill variance and nugget variance), and a combination of BMD and stochastic predictors, respectively. L was correlation length; c was sill variance; and c0 was nugget variance.
| Model | Variables | Coef. (a) | Std.Error(b) | Wald(c) |
Odds Ratio |
p-value(d) |
|---|---|---|---|---|---|---|
| Fracture ~ BMD | BMD | −3.047 | 1.531 | 3.960 | 0.048 | 0.047* |
| cons | 2.393 | 1.201 | 3.970 | 10.951 | 0.046* | |
| Fracture ~ L + c + c0 | L | −0.039 | 0.015 | 6.779 | 0.962 | 0.009* |
| c | −0.634 | 5.492 | 0.013 | 0.530 | 0.908 | |
| c0 | 43.133 | 24.888 | 3.004 | 5.400E+18 | 0.083 | |
| cons | 1.631 | 0.817 | 3.988 | 5.110 | 0.046* | |
| Fracture ~ BMD + L + c + c0 | BMD | −5.958 | 2.189 | 7.407 | 0.003 | 0.006* |
| L | −0.056 | 0.018 | 10.192 | 0.946 | 0.001* | |
| c | 10.061 | 6.944 | 2.099 | 23142.703 | 0.147 | |
| c0 | 57.327 | 27.031 | 4.498 | 7.884E+24 | 0.034* | |
| cons | 5.257 | 1.625 | 10.469 | 191.903 | 0.001* | |
The regression coefficients from the multiple logistic regression models. The coefficient labeled cons in the table is the intercept of the fitting logistic model.
The standard error of the coefficients
AWald test is used to test the statistical significance of each coefficient in the model. The ratio of the coefficients to their standard errors forms the Wald test statistic for the hypothesis that the true coefficients are different than zero (Vittinghoff, 2012).
The p-value was computed under the Ward test statistic (Vittinghoff, 2012).
The p-value was significant.
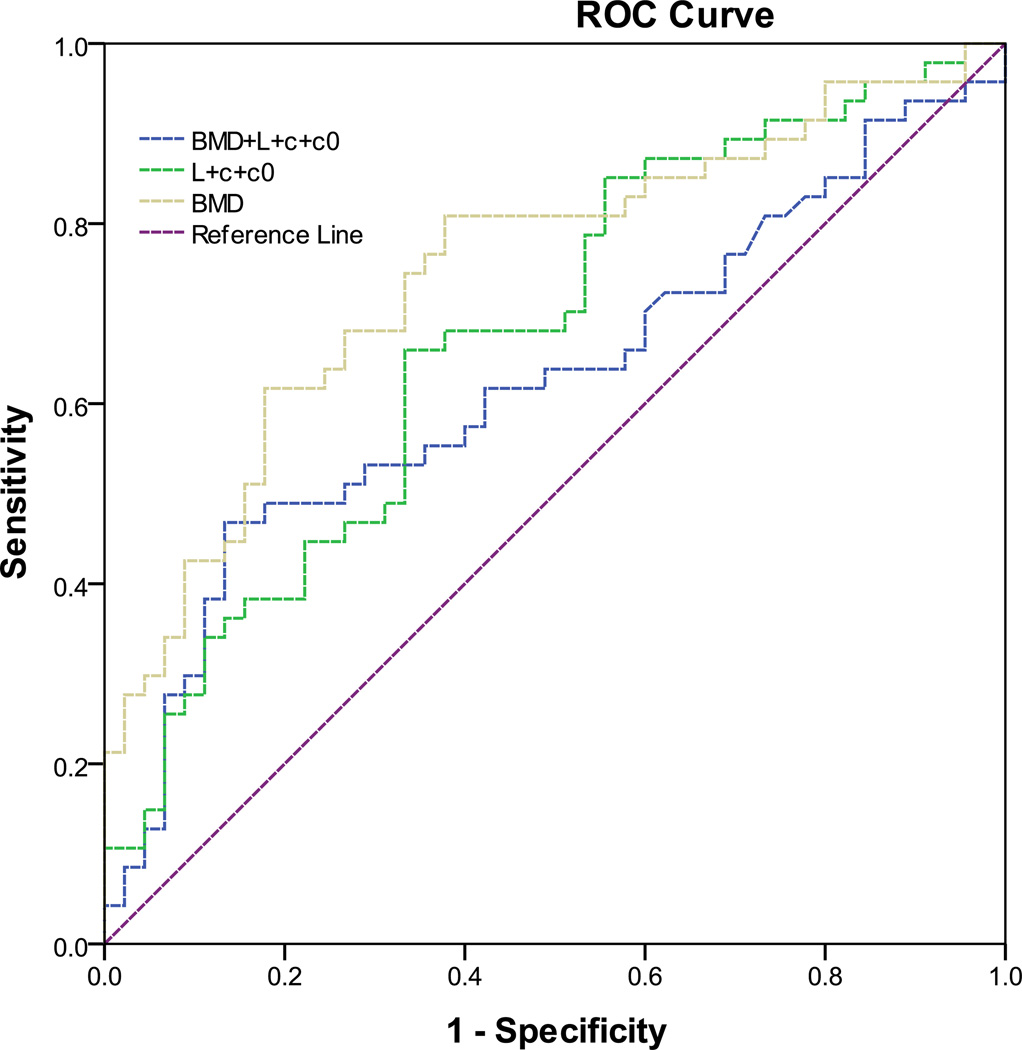
The accuracy of logistic regression models was characterized by the area under receiver operating characteristic (ROC) curves (Figure 3 and Table 5). The area under the ROC curve for the logistic regression model with only BMD measurements (AUC=0.625) was smaller than that with only stochastic predictors (AUC=0.675). However, this difference was not statistically significant (p=0.548). The logistic regression model with a combination of BMD and stochastic predictors had the greatest area under curve (AUC=0.748) with a lower bound of 0.647 and an upper bound of 0.849 at the 95% confidence level (Figure 3 and Table 5). The AUC of the logistic model with a combination of BMD and stochastic predictors was significantly (p=0.039) greater than the AUC of logistic model with only the BMD measurements. This indicated that a combination of BMD measurements and stochastic predictors enhanced the prediction of the risk of hip fractures, compared to the BMD measurement alone.
Figure 3.
The receiver operating characteristic (ROC) curves from logistic regression models for the prediction of hip fractures from the BMD measurements, stochastic predictors including correlation length (L), sill variance (c) and nugget variance (c0), and a combination of BMD measurements and stochastic predictors.
Table 5.
The accuracy of logistic regression models for predicting the risk of hip fractures from bone mineral density (BMD), stochastic predictors (correlation length, sill variance and nugget variance), and a combination of BMD and stochastic predictors, respectively. L was correlation length; c was sill variance; and c0 was nugget variance.
| Model | AUC(a) | Std.Error(b) | p-value(c) | Lower(d) Bound |
Upper(d) Bound |
|---|---|---|---|---|---|
| Fracture ~ BMD | 0.625 | 0.059 | 0.040* | 0.509 | 0.740 |
| Fracture ~ L + c + c0 | 0.675 | 0.056 | 0.004* | 0.565 | 0.784 |
| Fracture ~ BMD + L + c + c0 | 0.748 | 0.051 | 0.001* | 0.647 | 0.849 |
AUC represented the area under a receiver operating characteristic curve from the logistic regression model.
The standard error of the AUC was calculated under the nonparametric assumption.
The p-value was computed under the null hypothesis in which the true area equals to 0.5.
The lower and upper bounds were reported from the asymptotic 95% confidence interval.
The p-value was significant.
Discussion
We described a procedure to extract stochastic predictors from the bone mineral distribution of DXA scans. Such a procedure was applied to postmenopausal women with hip fractures and without hip fractures. The combination of BMD and stochastic predictors had stronger prediction power than the BMD alone.
Measurements of BMD for postmenopausal women in control and fracture groups were in agreement with existing literature. For example, previous studies (Boehm et al., 2007; Whitmarsh et al., 2012) also reported that measurements of BMD and T-score in postmenopausal women with hip fractures were significantly lower than those in postmenopausal women with no fractures. Additionally, we calculated the area under the receiver operating characteristic curve (AUC) for the contribution of BMD to hip fractures (AUC=0.625, Figure 3 and Table 5,). This value was within the range reported from other studies in which the AUC for BMD varied from 0.58 (Boehm et al., 2007) to 0.719 (Whitmarsh et al., 2012).
Similar to the stochastic technique of this study, TBS was also obtained from experimental variograms of DXA scans. In previous studies, TBS has been used for risk prediction of spine fractures, showing that the AUC for the prediction of vertebral fractures ranged from 0.662 to 0.721 (Rabier et al., 2010). In addition, spine TBS has also been used to predict hip fractures with the AUC calculated as 0.680 (Leslie et al., 2014). The stochastic approach can be distinguished from the TBS method in the following aspects:
First, the original definition of TBS is based on the variation of the grayscale values of DXA images (Pothuaud et al., 2008; Pothuaud et al., 2009), rather than a property with direct physical meaning. The modified definition of TBS is based on a black-box algorithm using the variogram after its log-log transformation (Hans et al., 2011). However, it is not clear how the variogram is calculated when the TBS is redefined (Bousson et al., 2012). On the other hand, stochastic predictors are based on the variation of bone mineral density values from the BMD map of DXA scans. The value of bone mineral density at each location was obtained from the raw data of DXA scans (i.e., R files in Hologic densitometers) using the equations of mass attenuation for dual-energy X-ray absorptiometry (Stein, 1989; Blake et al., 1992) (see Appendix). The use of BMD maps may facilitate the comparison of results when multicenter studies are conducted to predict osteoporotic fractures.
Second, TBS describes only one aspect of experimental variograms whereas the stochastic predictors we proposed represent a comprehensive view of experimental variograms. Experimental variograms are mostly used in geostatistics (Mcbratney and Webster, 1986; Atkinson and Lloyd, 2007) and have recently been introduced in the field of bone mechanics (Pothuaud et al., 2008; Pothuaud et al., 2009; Dong et al., 2010; Dong et al., 2013). TBS is calculated as the slope at the origin of the log-log representation of experimental variograms (Pothuaud et al., 2008; Pothuaud et al., 2009; Hans et al., 2011; Winzenrieth et al., 2013). The initial trend of the experimental variogram may be described by the TBS. However, the final trend in the experiment variogram is not represented by the TBS. On the other hand, stochastic predictors are derived from a theoretical model of random fields that captures the global trend of the experimental variogram. In this study, correlation length, sill variance and nugget variance are obtained by fitting an exponential model of random fields into the experimental variogram (Figure 2b).
This study has several limitations that should be mentioned. First, this is a retrospective case-control study by comparing patients known to have fractures with individuals known to be free of fractures. Although stochastic assessment of bone mineral distribution has shown to be very promising in predicting bone fragility, lack of baseline measurements for these patients is a disadvantage for this study. Therefore, a prospective study will be carried out in the future to examine patients with baseline measurements and subsequent follow-up. In addition, the retrospective analysis did not discriminate among the 5 common types of hip fracture (i.e, subcapital, basicervical, transcervical, intertrochanteric, and subtrochanteric). Many patients had those fractures diagnosed at other facilities, and all had them treated elsewhere, since UT Health Northeast did not have an orthopedic surgeon during the time frame in question.
The second limitation is that age may be a confounding variable because significant differences of age have been observed between the control group and the fracture group for postmenopausal women (Table 1). Therefore, we have examined the influence of age on the prediction of risk of hip fractures using logistic regression models (Table 6). With the introduction of age in the logistic regression models, the relationship between BMD and the risk of fracture was not statistically significant (p=0.086, Table 6), indicating that age may be a confounding variable for the prediction of risk of hip fractures using BMD measurements. The inclusion of age in the logistic regression models slightly increased the prediction accuracy for the logistic regression model with either BMD measurements (AUC=0.679, Table 6) or stochastic predictors (AUC=0.695, Table 6). However, the comparison of AUC from the ROC curves (DeLong et al., 1988; Robin et al., 2011) demonstrated that such changes were not statistically significant (p>=0.265). With the presence of age, there was no change for the AUC of the logistic regression model (AUC=0.748, Table 6) with the combination of BMD measurements and stochastic predictors.
Table 6.
The influence of age on the predicting the risk of hip fractures from bone mineral density (BMD), stochastic predictors (correlation length, sill variance and nugget variance), and a combination of BMD and stochastic predictors, respectively.
| Model | Variables | Coef.(a) | Std.Error(b) | Wald(c) |
Odds Ratio |
p- value(d) |
AUC(e) |
|---|---|---|---|---|---|---|---|
| Fracture ~ Age + BMD | Age | 0.038 | 0.021 | 3.163 | 1.038 | 0.075 | 0.679 |
| BMD | −2.729 | 1.587 | 2.956 | 0.065 | 0.086 | ||
| cons | −0.446 | 1.983 | 0.051 | 0.640 | 0.822 | ||
| Fracture ~ Age + L + c + c0 | Age | 0.037 | 0.022 | 2.787 | 1.039 | 0.095 | 0.695 |
| L | −0.035 | 0.015 | 5.211 | 0.966 | 0.022* | ||
| c | −2.152 | 5.714 | 0.142 | 0.116 | 0.706 | ||
| c0 | 42.605 | 25.910 | 2.704 | 3.184E+18 | 0.100 | ||
| cons | −0.901 | 1.693 | 0.283 | 0.406 | 0.594 | ||
| Fracture ~ Age + BMD + L + c + c0 | Age | 0.017 | 0.024 | 0.521 | 1.017 | 0.470 | 0.748 |
| BMD | −5.391 | 2.295 | 5.520 | 0.005 | 0.019* | ||
| L | −0.052 | 0.018 | 8.238 | 0.949 | 0.004* | ||
| c | 8.483 | 7.268 | 1.362 | 4830.020 | 0.243 | ||
| c0 | 54.572 | 27.405 | 3.965 | 5.016E+23 | 0.046* | ||
| cons | 3.695 | 2.651 | 1.943 | 40.253 | 0.163 | ||
The regression coefficients from the multiple logistic regression models. The coefficient labeled cons in the table is the intercept of the fitting logistic model.
The standard error of the coefficients.
AWald test is used to test the statistical significance of each coefficient in the model. The ratio of the coefficients to their standard errors forms the Wald test statistic for the hypothesis that the true coefficients are different than zero (Vittinghoff, 2012).
The p-value was computed under the Ward test statistic (Vittinghoff, 2012).
AUC represented the area under a receiver operating characteristic curve from the logistic regression model.
The p-value was significant.
Another limitation is that we have made assumptions that the BMD map at the hip region is a stationary and isotropic random field when extracting the stochastic predictors from the experimental variogram. By stationarity, we mean that the distribution of the random field has certain attributes that are the same everywhere (Stoyan et al., 1995). Specifically, second-order stationarity (i.e., weak stationarity) indicates the constancy of mean, variance, and covariance that depends only on lag distance and not on absolute positions (Webster and Oliver, 2001). The wavelet-based test of stationarity for locally stationary random fields is available in the R software package (Eckley et al., 2010; Nunes et al., 2014). By isotropy, we mean that the characteristics of the random field are invariant in all directions (Stoyan et al., 1995). Specifically, we can examine the isotropic assumption by generating the experimental variograms in every direction (Webster and Oliver, 2001). If the variation is anisotropic, we need to take into account such anisotropy by certain transformations (Webster and Oliver, 2001). The stationarity and anisotropy of the BMD map at the hip region as a random field need further investigation.
Finally, the influence of scanner resolution, scan mode and noise on the stochastic predictors from DXA scans needs to be investigated in the future study.
Conclusion
This study demonstrates that stochastic assessment of bone mineral distribution from DXA scans combined with BMD measurements can serve as a valuable tool in enhancing the prediction of osteoporotic fractures for postmenopausal women. Clinically, this may become an economic prognostic tool to enable individuals and their doctors to make informed judgments about the actual risk of fracture and to allow for steps to be taken to reduce that risk.
Acknowledgements
This study was supported by the National Institute of Arthritis and Musculoskeletal and Skin Disease of the National Institutes of Health under Award Number R15AR061740. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. In addition, this work received computation support from Computational System Biology Core at the University of Texas at San Antonio, funded by the National Institute on Minority Health and Health Disparities (G12MD007591) from the National Institutes of Health. Finally, we thank the support of Mr. Zhiwei Wang at the University of Texas at San Antonio.
Appendix
It is noted that most of contents in this appendix have already been avaiable at various places scattered in the literature (Stein, 1989; Blake et al., 1992; Blake and Fogelman, 1997; Blake et al., 1999). Nevertheless, they are presented here as one piece for the convienience of the readers who would like to generate the BMD map directly from the raw data of Hologic densitometers (i.e., R files).
1. A brief introduction to dual-energy X-ray absorptiometry (DXA)
A basic understanding of the interaction of X-ray photons and absorber materials is beneficial for us to learn about the principles of DXA. When an X-ray beam passes through an absorber material, the incident energy of X-ray photons is exponentially attenuated by photon interactions with absorber materials due to Compton scattering and photoelectric collision (Blake et al., 1999). The degree of attenuation is a function of the initial photon energy of the X-ray beam, the mass attenuation coefficient of the absorber material, and the mass per unit area of the absorber material. For a homogeneous absorber material like bone mineral, the transmitted intensity is related to the incident intensity according to the following formula:
| (A.1) |
where I is the transmitted X-ray beam intensity, I0 is the incident photon intensity, μ is the mass attenuation coefficient of bone mineral, and M is the mass per unit area (g/cm2) of bone mineral.
Although a single energy X-ray source is able to measure the areal density of a homogeneous absorber material, a dual-energy X-ray source is required to determine the area densities of an absorber with two components. For example, a human body consists of soft tissue and bone mineral. Two distinct X-ray energy beams can be used to measure bone mineral density by accounting for variations in the amount of overlaying soft tissue in human bodies. The aforementioned transmission equation A.1 can be extended to two transmission equations. One equation is for the low-energy beam and the other for the high-energy beam.
| (A.2) |
| (A.3) |
where and IL are the intensity of incident and transmitted low-energy photons, and IH are the intensity of incident and transmitted high-energy photons, and are the mass attenuation coefficients of soft tissue at the low and high energies, and are the mass attenuation coefficients of bone mineral at the low and high energies, Ms and Mb are the area densities (g/cm2) of soft tissue and bone mineral.
By taking the logarithm function on both sides of the equations A.2 and A.3, we have the following equations:
| (A.4) |
| (A.5) |
where JL and JH are the logarithmic transmission factors at the low and high energies ( and ).
If the values of the four attenuation coefficients are known, the area density of bone mineral (BMD) can be calculated by solving a simultaneous set of two linear equations A.4 and A.5. The following equation is the foundation for the determination of BMD in DXA.
| (A.6) |
2. Internal reference systems for Hologic densitometers
The assumption for the aforementioned equation A.6 is that the attenuation coefficients for soft tissue and bone mineral are known at low and high energies. However, it is not possible to give predetermined values of mass attenuation coefficients of soft tissue ( and ) since the composition of soft tissue varies from individual to individual. In addition, the values of mass attenuation coefficients of bone mineral ( and ) are affected by body thickness and composition due to beam hardening (Blake et al., 1992). Therefore, commercial densitometers from Hologic (Bedford, MA) have used an internal reference system that enables the accommodation of drift in the X-ray tube, differences in patient thickness and other system variations (Stein, 1989).
The internal reference system includes a rotating filter wheel that is synchronized with the main power supply of densitometers. There are three sectors in the filter wheel containing an open air gap, a soft tissue equivalent material made of epoxy resin, and a bone mineral equivalent material made of hydroxyapatite. The bone equivalent material has a BMD value of 1.0 g/cm2. There are high- and low-energy cycles in each sector. Therefore, each location in the DXA scan contains six transmission measurements that record the X-ray attenuation signals at the high and low energies through the air, bone and soft tissue sectors.
An important feature of the internal reference system is its ability to calculate the mass attenuation coefficients of soft tissue and bone mineral on every scan line and provide continuous calibration of the densitometer. It is important for this calibration to pass through at least some portions of the patient having only flesh adjacent to the spine.
3. Calculate the BMD value at each pixel from DXA scans
3.1 Calculation of mass attenuation coefficients of soft tissue and bone mineral
The raw data from DXA scans of Hologic densitometers (i.e., R files) consist of the attenuation of X-ray beams at two distinct energies. In each DXA scan file, each pixel consists of six transmission measurements through the patient’s body made through the air, soft tissue, and bone sectors of the reference wheel at high and low x-ray energies, respectively.
First, the mass attenuation coefficients of soft tissue and bone mineral are calculated from the six logarithmic transmission factors for air, soft tissue and bone sectors in the reference wheel. Let be the low-energy logarithmic transmission factors for the air, soft tissue and bone sectors, and let be the corresponding high energy factors.
Measurements through the air sector give the attenuation through the patient’s body
| (A.7) |
| (A.8) |
Measurements through the bone sector give the following equations
| (A.9) |
| (A.10) |
where MCB denotes the area density of the bone mineral equivalent filter, and are the mass attenuation coefficients of bone mineral equivalent filter at the low and high energies.
Measurements through the soft tissue sector give the following equations
| (A.11) |
| (A.12) |
where MCS denotes the area density of the soft tissue equivalent filter, and are the mass attenuation coefficients of soft tissue equivalent filter at the low and high energies.
The increases in attenuation when the bone sector of the reference wheel rotates into the X-ray beam are governed by
| (A.13) |
| (A.14) |
Similarly, the changes in attenuation when the soft tissue sector of the calibration wheel rotates into the X-ray beam can be calculated by
| (A.15) |
| (A.16) |
Therefore, the effective values of the four attenuation coefficients in Equation A.6 are obtained by assuming that the attenuation coefficients of soft tissue and bone mineral are equal to that of soft tissue equivalent and bone mineral equivalent in the reference wheel.
| (A.17) |
| (A.18) |
| (A.19) |
| (A.20) |
3.2 Calculation of the BMD value at each pixel with no beam hardening
After replacing the attenuation coefficients in equation A.6 with the aforementioned equations A.17–20, we have the following formula:
| (A.21) |
We can simplify the aforementioned equation A.21 by using
| (A.22) |
where k is the ratio of the attenuation coefficient of soft tissue for the low energy beam to that of the high energy beam. The average k value is normally available in DXA reports for Hologic densitometers.
| (A.23) |
| (A.24) |
where the average value of d0 is also available in the DXA report from Hologic densitometers. Therefore, we obtain
| (A.25) |
The Equation A.25 is the formula to calculate the bone mineral density at each pixel when there is no beam hardening.
3.3 Correction of the BMD value due to beam hardening
Due to the effects of beam hardening through soft tissue, the value of Q in equation A.25 is not zero for beam paths that pass through only the soft tissue (Blake et al., 1992). Therefore, the value of Mb for each pixel given by Equation A.25 does not equal to the actual BMD value at that point.
We have made two major changes to address the issue of beam hardening. First, we compute the values of k and d0 at each scan line by taking their average values only at the region of soft tissue for each scan line (Blake et al., 1999). The reason is that a large amount of 28 fluctuations are present at the values of k and d0 in the bone pixels due to quantum noise and beam hardening.
Second, the Q values at the bone pixels are corrected by a baseline value Qs equal to the average value at the region of soft tissue for each scan line (Blake et al., 1999). Consequently, the value Q in equation A.25 is replaced by Q − Qs. We can also replace the area density MCB with the bone density value of the reference wheel, BMDref. Finally, we can obtain for the BMD value of each pixel in DXA scans:
| (A.26) |
4. A software package for calculating stochastic predictors from DXA scans
We have developed a software package to obtain the BMD map for DXA scans from Hologic densitometers and calculate the stochastic predictors. The software package is able to calculate the stochastic predictors for both hip and spine scans. For the hip scan, the software package can calculate the stochastic predictors for the total hip region as well as the sub regions including the femoral neck, trochanter and inter-trochanter. For the spine scan, the software package can report the stochastic predictors for the individual vertebra from L1 to L4 as well as the whole lumbar spine. The choice of region of interest in the hip and spine is the same as indicated by the DXA reports from Hologic densitometers.
The software package is currently available for Windows, Mac and Linux operating systems. Although the software package is developed under the MATLAB environment, the acquisition of MATLAB (Mathworks, Natick, MA, USA) is not required to run the software package. The software package will be available for research use upon the request of readers who are interested in the package.
One limitation of the software package is that it is specifically developed for Hologic scanners at this time. However, the software package may be extended to densitometers from other manufacturers such as GE Lunar in the future.
References
- Blake GM, Fogelman I. Technical principles of dual energy x-ray absorptiometry. Semin Nucl Med. 1997;27:210–228. doi: 10.1016/s0001-2998(97)80025-6. [DOI] [PubMed] [Google Scholar]
- Blake GM, McKeeney DB, Chhaya SC, Ryan PJ, Fogelman I. Dual energy x-ray absorptiometry: the effects of beam hardening on bone density measurements. Med Phys. 1992;19:459–465. doi: 10.1118/1.596834. [DOI] [PubMed] [Google Scholar]
- Blake GM, Wahner HW, Fogelman I. The evaluation of osteoporosis: dual energy x-ray absorptiometry and ultrasound in clinical practice. London: Martin Duntiz; 1999. [Google Scholar]
- Stein JA. No. 4,811,373. U. S. Patent and Trademark Office; U.S. Patent. 1989
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of Interest Statement
Each author in this manuscript does not have and will not receive benefits in any form from a commercial party related directly or indirectly to the content in this manuscript.
The authors declare that they have no competing financial interests.
References
- Apostol L, Boudousq V, Basset O, Odet C, Yot S, Tabary J, Dinten JM, Boiler E, Kotzki PO, Peyrin F. Relevance of 2D radiographic texture analysis for the assessment of 3D bone micro-architecture. Med Phys. 2006;33:3546–3556. doi: 10.1118/1.2211727. [DOI] [PubMed] [Google Scholar]
- Atkinson PM, Lloyd CD. Non-stationary variogram models for geostatistical sampling optimisation: An empirical investigation using elevation data. Computers & Geosciences. 2007;33:1285–1300. [Google Scholar]
- Beck T. Measuring the structural strength of bones with dual-energy X-ray absorptiometry: principles, technical limitations, and future possibilities. Osteoporos Int. 2003;14(Suppl 5):S81–S88. doi: 10.1007/s00198-003-1478-0. [DOI] [PubMed] [Google Scholar]
- Beck TJ. Extending DXA beyond bone mineral density: understanding hip structure analysis. Curr Osteoporos Rep. 2007;5:49–55. doi: 10.1007/s11914-007-0002-4. [DOI] [PubMed] [Google Scholar]
- Benhamou CL, Lespessailles E, Jacquet G, Harba R, Jennane R, Loussot T, Tourliere D, Ohley W. Fractal organization of trabecular bone images on calcaneus radiographs. J Bone Miner Res. 1994;9:1909–1918. doi: 10.1002/jbmr.5650091210. [DOI] [PubMed] [Google Scholar]
- Blake GM, Fogelman I. Technical principles of dual energy x-ray absorptiometry. Semin Nucl Med. 1997;27:210–228. doi: 10.1016/s0001-2998(97)80025-6. [DOI] [PubMed] [Google Scholar]
- Blake GM, McKeeney DB, Chhaya SC, Ryan PJ, Fogelman I. Dual energy x-ray absorptiometry: the effects of beam hardening on bone density measurements. Med Phys. 1992;19:459–465. doi: 10.1118/1.596834. [DOI] [PubMed] [Google Scholar]
- Blake GM, Wahner HW, Fogelman I. The evaluation of osteoporosis: dual energy x-ray absorptiometry and ultrasound in clinical practice. London: Martin Duntiz; 1999. [Google Scholar]
- Boehm HF, Horng A, Notohamiprodjo M, Eckstein F, Burklein D, Panteleon A, Lutz J, Reiser M. Prediction of the fracture load of whole proximal femur specimens by topological analysis of the mineral distribution in DXA-scan images. Bone. 2008;43:826–831. doi: 10.1016/j.bone.2008.07.244. [DOI] [PubMed] [Google Scholar]
- Boehm HF, Vogel T, Panteleon A, Burklein D, Bitterling H, Reiser M. Differentiation between post-menopausal women with and without hip fractures: enhanced evaluation of clinical DXA by topological analysis of the mineral distribution in the scan images. Osteoporos Int. 2007;18:779–787. doi: 10.1007/s00198-006-0302-z. [DOI] [PubMed] [Google Scholar]
- Bousson V, Bergot C, Sutter B, Levitz P, Cortet B. Trabecular bone score (TBS): available knowledge, clinical relevance, and future prospects. Osteoporos Int. 2012;23:1489–1501. doi: 10.1007/s00198-011-1824-6. [DOI] [PubMed] [Google Scholar]
- Buckland-Wright JC, Lynch JA, Rymer J, Fogelman I. Fractal signature analysis of macroradiographs measures trabecular organization in lumbar vertebrae of postmenopausal women. Calcif Tissue Int. 1994;54:106–112. doi: 10.1007/BF00296060. [DOI] [PubMed] [Google Scholar]
- Chappard D, Chennebault A, Moreau M, Legrand E, Audran M, Basle MF. Texture analysis of X-ray radiographs is a more reliable descriptor of bone loss than mineral content in a rat model of localized disuse induced by the Clostridium botulinum toxin. Bone. 2001;28:72–79. doi: 10.1016/s8756-3282(00)00438-5. [DOI] [PubMed] [Google Scholar]
- DeLong ER, DeLong DM, Clarke-Pearson DL. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics. 1988;44:837–845. [PubMed] [Google Scholar]
- Dong XN, Luo Q, Sparkman DM, Millwater HR, Wang X. Random field assessment of nanoscopic inhomogeneity of bone. Bone. 2010;47:1080–1084. doi: 10.1016/j.bone.2010.08.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong XN, Shirvaikar M, Wang X. Biomechanical properties and microarchitecture parameters of trabecular bone are correlated with stochastic measures of 2D projection images. Bone. 2013;56:327–336. doi: 10.1016/j.bone.2013.05.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckley IA, Nason GP, Treloar RL. Locally stationary wavelet fields with application to the modelling and analysis of image texture. Journal of the Royal Statistical Society Series C-Applied Statistics. 2010;59:595–616. [Google Scholar]
- Hans D, Barthe N, Boutroy S, Pothuaud L, Winzenrieth R, Krieg MA. Correlations between trabecular bone score, measured using anteroposterior dual-energy X-ray absorptiometry acquisition, and 3-dimensional parameters of bone microarchitecture: an experimental study on human cadaver vertebrae. J Clin Densitom. 2011;14:302–312. doi: 10.1016/j.jocd.2011.05.005. [DOI] [PubMed] [Google Scholar]
- Hans D, Goertzen AL, Krieg MA, Leslie WD. Bone microarchitecture assessed by TBS predicts osteoporotic fractures independent of bone density: the Manitoba study. J Bone Miner Res. 2011;26:2762–2769. doi: 10.1002/jbmr.499. [DOI] [PubMed] [Google Scholar]
- Hui SL, Slemenda CW, Johnston CC., Jr Age and bone mass as predictors of fracture in a prospective study. J Clin Invest. 1988;81:1804–1809. doi: 10.1172/JCI113523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanis JA, Borgstrom F, De Laet C, Johansson H, Johnell O, Jonsson B, Oden A, Zethraeus N, Pfleger B, Khaltaev N. Assessment of fracture risk. Osteoporos Int. 2005;16:581–589. doi: 10.1007/s00198-004-1780-5. [DOI] [PubMed] [Google Scholar]
- Kanis JA, Oden A, Johnell O, Johansson H, De Laet C, Brown J, Burckhardt P, Cooper C, Christiansen C, Cummings S, Eisman JA, Fujiwara S, Gluer C, Goltzman D, Hans D, Krieg MA, La Croix A, McCloskey E, Mellstrom D, Melton LJ, 3rd, Pols H, Reeve J, Sanders K, Schott AM, Silman A, Torgerson D, van Staa T, Watts NB, Yoshimura N. The use of clinical risk factors enhances the performance of BMD in the prediction of hip and osteoporotic fractures in men and women. Osteoporos Int. 2007;18:1033–1046. doi: 10.1007/s00198-007-0343-y. [DOI] [PubMed] [Google Scholar]
- Langton CM, Pisharody S, Keyak JH. Comparison of 3D finite element analysis derived stiffness and BMD to determine the failure load of the excised proximal femur. Med Eng Phys. 2009;31:668–672. doi: 10.1016/j.medengphy.2008.12.007. [DOI] [PubMed] [Google Scholar]
- Le Corroller T, Halgrin J, Pithioux M, Guenoun D, Chabrand P, Champsaur P. Combination of texture analysis and bone mineral density improves the prediction of fracture load in human femurs. Osteoporos Int. 2012;23:163–169. doi: 10.1007/s00198-011-1703-1. [DOI] [PubMed] [Google Scholar]
- Leib E, Winzenrieth R, Aubry-Rozier B, Hans D. Vertebral microarchitecture and fragility fracture in men: A TBS study. Bone. 2013;62C:51–55. doi: 10.1016/j.bone.2013.12.015. [DOI] [PubMed] [Google Scholar]
- Leslie WD, Aubry-Rozier B, Lix LM, Morin SN, Majumdar SR, Hans D. Spine bone texture assessed by trabecular bone score (TBS) predicts osteoporotic fractures in men: The Manitoba Bone Density Program. Bone. 2014;67C:10–14. doi: 10.1016/j.bone.2014.06.034. [DOI] [PubMed] [Google Scholar]
- Lespessailles E, Gadois C, Kousignian I, Neveu JP, Fardellone P, Kolta S, Roux C, Do-Huu JP, Benhamou CL. Clinical interest of bone texture analysis in osteoporosis: a case control multicenter study. Osteoporos Int. 2008;19:1019–1028. doi: 10.1007/s00198-007-0532-8. [DOI] [PubMed] [Google Scholar]
- Majumdar S, Link TM, Millard J, Lin JC, Augat P, Newitt D, Lane N, Genant HK. In vivo assessment of trabecular bone structure using fractal analysis of distal radius radiographs. Med Phys. 2000;27:2594–2599. doi: 10.1118/1.1319375. [DOI] [PubMed] [Google Scholar]
- Majumdar S, Weinstein RS, Prasad RR. Application of fractal geometry techniques to the study of trabecular bone. Med Phys. 1993;20:1611–1619. doi: 10.1118/1.596948. [DOI] [PubMed] [Google Scholar]
- Mcbratney AB, Webster R. Choosing Functions for Semi-Variograms of Soil Properties and Fitting Them to Sampling Estimates. Journal of Soil Science. 1986;37:617–639. [Google Scholar]
- Messent EA, Buckland-Wright JC, Blake GM. Fractal analysis of trabecular bone in knee osteoarthritis (OA) is a more sensitive marker of disease status than bone mineral density (BMD) Calcif Tissue Int. 2005;76:419–425. doi: 10.1007/s00223-004-0160-7. [DOI] [PubMed] [Google Scholar]
- NIH. Osteoporosis prevention, diagnosis, and therapy. NIH Consens Statement. 2000;17:1–45. [PubMed] [Google Scholar]
- Nunes MA, Taylor SL, Eckley IA. A Multiscale Test of Spatial Stationarity for Textured Images in R. R Journal. 2014;6:20–30. [Google Scholar]
- Pothuaud L, Barthe N, Krieg MA, Mehsen N, Carceller P, Hans D. Evaluation of the potential use of trabecular bone score to complement bone mineral density in the diagnosis of osteoporosis: a preliminary spine BMD-matched, case-control study. J Clin Densitom. 2009;12:170–176. doi: 10.1016/j.jocd.2008.11.006. [DOI] [PubMed] [Google Scholar]
- Pothuaud L, Benhamou CL, Porion P, Lespessailles E, Harba R, Levitz P. Fractal dimension of trabecular bone projection texture is related to three-dimensional microarchitecture. J Bone Miner Res. 2000;15:691–699. doi: 10.1359/jbmr.2000.15.4.691. [DOI] [PubMed] [Google Scholar]
- Pothuaud L, Carceller P, Hans D. Correlations between grey-level variations in 2D projection images (TBS) and 3D microarchitecture: applications in the study of human trabecular bone microarchitecture. Bone. 2008;42:775–787. doi: 10.1016/j.bone.2007.11.018. [DOI] [PubMed] [Google Scholar]
- Rabier B, Heraud A, Grand-Lenoir C, Winzenrieth R, Hans D. A multicentre, retrospective case-control study assessing the role of trabecular bone score (TBS) in menopausal Caucasian women with low areal bone mineral density (BMDa): Analysing the odds of vertebral fracture. Bone. 2010;46:176–181. doi: 10.1016/j.bone.2009.06.032. [DOI] [PubMed] [Google Scholar]
- Robin X, Turck N, Hainard A, Tiberti N, Lisacek F, Sanchez JC, Muller M. pROC: an open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinformatics. 2011;12:77. doi: 10.1186/1471-2105-12-77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roux JP, Wegrzyn J, Boutroy S, Bouxsein ML, Hans D, Chapurlat R. The predictive value of trabecular bone score (TBS) on whole lumbar vertebrae mechanics: an ex vivo study. Osteoporos Int. 2013;24:2455–2460. doi: 10.1007/s00198-013-2316-7. [DOI] [PubMed] [Google Scholar]
- Silva BC, Leslie WD, Resch H, Lamy O, Lesnyak O, Binkley N, McCloskey EV, Kanis JA, Bilezikian JP. Trabecular bone score: a noninvasive analytical method based upon the DXA image. J Bone Miner Res. 2014;29:518–530. doi: 10.1002/jbmr.2176. [DOI] [PubMed] [Google Scholar]
- Stein JA. No. 4,811,373. U. S. P. a. T. Office; U.S. Patent. 1989
- Stoyan D, Kendall WS, Mecke J. Stochastic geometry and its applications. New York, Wiley: Chichester; 1995. [Google Scholar]
- Vittinghoff E. Regression methods in biostatistics : linear, logistic, survival, and repeated measures models. New York: Springer; 2012. [Google Scholar]
- Webster R, Oliver MA. Geostatistics for environmental scientists. New York: John Wiley & Sons; 2001. [Google Scholar]
- Whitmarsh T, Fritscher KD, Humbert L, Del Rio Barquero LM, Roth T, Kammerlander C, Blauth M, Schubert R, Frangi AF. Hip fracture discrimination from dual-energy X-ray absorptiometry by statistical model registration. Bone. 2012;51:896–901. doi: 10.1016/j.bone.2012.08.114. [DOI] [PubMed] [Google Scholar]
- WHO. Prevention and management of osteoporosis. World Health Organ Tech Rep Ser. 2003;921:1–164. [PubMed] [Google Scholar]
- Winzenrieth R, Dufour R, Pothuaud L, Hans D. A retrospective case-control study assessing the role of trabecular bone score in postmenopausal Caucasian women with osteopenia: analyzing the odds of vertebral fracture. Calcif Tissue Int. 2010;86:104–109. doi: 10.1007/s00223-009-9322-y. [DOI] [PubMed] [Google Scholar]
- Winzenrieth R, Michelet F, Hans D. Three-dimensional (3D) microarchitecture correlations with 2D projection image gray-level variations assessed by trabecular bone score using high-resolution computed tomographic acquisitions: effects of resolution and noise. J Clin Densitom. 2013;16:287–296. doi: 10.1016/j.jocd.2012.05.001. [DOI] [PubMed] [Google Scholar]