Multiscale Modeling of a Conditionally Disordered pH-Sensing Chaperone

Abstract

The pH-sensing chaperone HdeA promotes the survival of enteropathogenic bacteria during transit through the harshly acidic environment of the mammalian stomach. At low pH, HdeA transitions from an inactive, folded, dimer to chaperone-active, disordered, monomers to protect against the acid-induced aggregation of periplasmic proteins. Toward achieving a detailed mechanistic understanding of the pH response of HdeA, we develop a multiscale modeling approach to capture its pH-dependent thermodynamics. Our approach combines pK_a calculations from all-atom constant pH molecular dynamics simulations with coarse-grained modeling, and yields new, atomic-level, insights into HdeA chaperone function that can be directly tested by experiment. “pH triggers” that significantly destabilize the dimer are each located near the N-terminus of a helix, suggesting that their neutralization at low pH destabilizes the helix macrodipole as a mechanism of monomer disordering. Moreover, we observe a non-monotonic change in the pH-dependent stability of HdeA, with maximal stability of the dimer near pH 5. This affect is attributed to the protonation Glu37, which exhibits an anomalously high pK_a value and is located within the hydrophobic dimer interface. Finally, the pH-dependent binding pathway of HdeA comprises a partially unfolded, dimeric intermediate that becomes increasingly stable relative to the native dimer at lower pH values and displays key structural features for chaperone-substrate interaction. We anticipate that the insights from our model will help inform ongoing NMR and biochemical investigations.

Introduction

The severely acidic environment of the mammalian stomach acts as a natural line of defense against invading pathogens before they enter the intestine. The low pH surroundings can cause protein unfolding and aggregation, jeopardizing the survival of bacterial pathogens such as Escherichia coli and Shigella flexneri. To combat the potentially lethal acidic conditions of the stomach, enteropathogenic bacteria have evolved several acid resistance mechanisms¹. For example, enteric bacteria can maintain the cytosol at a moderate pH through the removal of intracellular protons^2,3. In contrast, the periplasmic space of gram-negative bacteria quickly equilibrates with environmental pH due to the porous composition of the outer membrane⁴. To protect against acid-induced aggregation, the chaperone HdeA senses changes in environmental pH and binds to unfolded proteins^1,5.

During non-stress conditions (neutral pH), HdeA exists as a well-folded, inactive homodimer (Fig. 1a). Upon entrance of the bacteria into the low pH environment of the stomach, HdeA dissociates into chaperone-active, disordered monomers^6,7. Thus, HdeA belongs to a recently discovered class of “conditionally disordered” chaperones that lose structure to gain function^8–10. The highly flexible chaperone-active state likely allows HdeA to address a broad range of client proteins through hydrophobic interactions^7,11. During acid stress, HdeA can also form mixed aggregates with client proteins to assist in sustaining the aggregates in a soluble form¹². After the bacteria pass through the stomach and return to a neutral pH environment in the small intestine, HdeA facilitates the return of client proteins to a functional form by releasing them in a folding competent state¹³.

Figure 1.

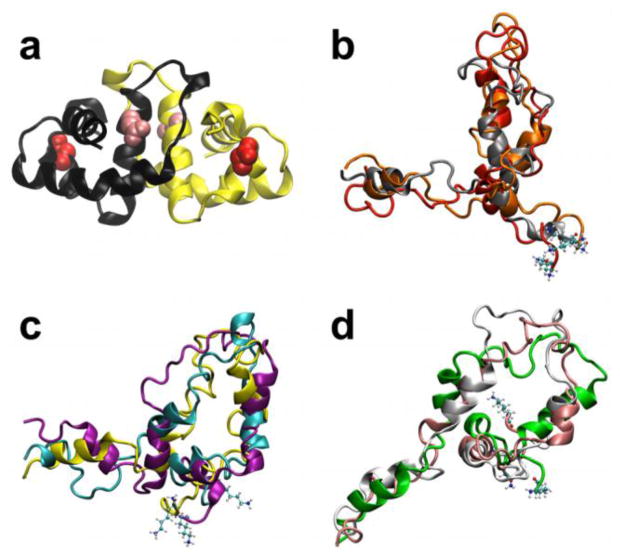
Folded dimer and unfolded monomer structures of HdeA. (a) Crystal structure of the HdeA homodimer (PDB ID: 1BG8)⁴⁷. The acidic residues that exhibit the most significant destabilizing (Asp20, red) and stabilizing (Glu37, pink) effects on HdeA upon protonation at low pH are denoted as van der Waals spheres. (b–d) Representative conformers of the unfolded ensemble of the HdeA monomer from clustering of the coarse-grained ensemble. The corresponding clusters have the following fractional population sizes: (b) 0.24 (c) 0.41, and (d) 0.35. The N-terminal residue in each unfolded conformer is denoted in CPK representation.

Given that enteropathogenic bacteria experience a pH gradient during transit through the mammalian gut, it is important to delineate the atomic-level structural details of HdeA over a range of pH values to achieve a comprehensive understanding of its acid stress-sensing mechanism. Toward this aim, the first NMR measurements on HdeA showed that the chaperone is well folded but undergoes a notable conformational change from pH 5 to 3.5, while adopting an unfolded conformation at pH 2.5⁶. Consistent with this study, we recently showed that the HdeA dimer becomes significantly destabilized below pH 3.5 using a combination of umbrella sampling and all-atom constant pH molecular dynamics (CpHMD) simulations¹⁴. pK_a calculations from this study identified key acidic residues for dimer dissociation and led to the computationally informed design of an HdeA mutant that was demonstrated to be partially unfolded, monomeric, and chaperone-active at neutral pH^15,16. A more recent NMR study showed that while HdeA remains dimeric from pH 6 down to pH 3, changes in amide protection during hydrogen/deuterium exchange measurements indicated that the protonation of acidic residues results in the progressive destabilization of tertiary and quaternary structure over this pH range¹⁷. Although NMR and simulation have revealed several important details of the acid stress response of HdeA, our understanding of the pH-dependent thermodynamics that facilitate enterobacterial pathogenicity remains incomplete.

We previously characterized the mechanism of HdeA dissociation and unfolding with a structure-based model at a constant pH¹⁸. To account for the large-scale, pH-dependent conformational dynamics of HdeA, here we develop a multiscale approach (Fig. 2). Our model reveals that HdeA is maximally stable under mildly acidic conditions and that a partially unfolded dimeric intermediate may contribute to chaperone-substrate interaction. Both of these predictions can be directly tested by experiment. More generally, our approach presents a practical avenue to the prediction of changes in large-scale functional dynamics in response to environmental pH.

Figure 2.

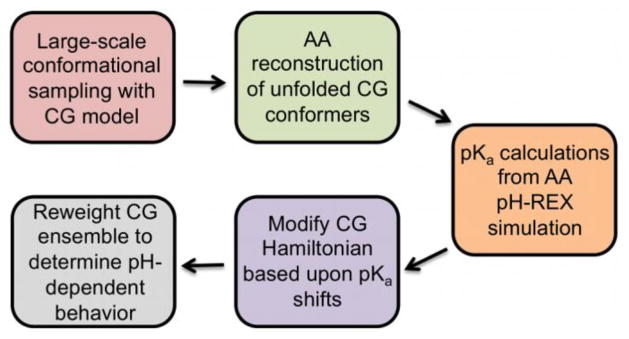
Outline of the multiscale modeling approach to describe the large-scale, pH-dependent thermodynamics of HdeA. CG and AA refer to the coarse-grained and all-atom models, respectively.

Results

Unfolded Monomer Models

Representative conformers of the unfolded monomer ensemble exhibit a range of global conformations (Fig 1b–d). The fraction of helicity (f_H) in the unfolded ensemble is 0.2–0.25 (Fig. S1), which agrees well with the helicity estimated for unfolded HdeA from CD spectroscopy (f_H ≈ 0.15)¹⁵. None of the structures exhibits a fully random coil conformation. This observation is consistent with fluorescence measurements showing that HdeA is not fully unfolded at low pH⁷ and is likely due the presence of an intramolecular disulfide bond.

pK_a Values from pH-Replica Exchange (pH-REX) CpHMD Simulation

pK_a values for acidic residues in the dimer and monomer are shown in Table 1. From pH-REX, Asp20 and Glu37 exhibit the largest pK_a shifts between the dimer and monomer species (−1.1 and +1.9, respectively). Glu37, which is largely buried near the hydrophobic dimer interface, exhibits an elevated pK_a (6.4) in the dimer. Overall, the acidic residue pK_a values predicted for the folded dimer from pH-REX show a two-fold improved agreement to NMR compared to those computed from temperature replica exchange (T-REX) calculations¹⁴, changing from an AUE of 0.29 to 0.60 (Table SI) and indicating better convergence of the pH-REX calculations. Nevertheless, the pK_a shifts from both the pH-REX and T-REX simulations show the same trend for over half of the residues (R² = 0.64), and Asp20 and Glu37 exhibit the largest pK_a shifts in both approaches. pK_a values from pH-REX of the unfolded monomer models do not significantly deviate from the model compound values (4.0 for Asp and 4.4 for Glu¹⁹) and are somewhat closer than the dimer pK_a values to NMR measurements (Table SI). The AUE of the dimer and monomer pK_a values from pH-REX when compared to the NMR values all fall within the estimated uncertainty of 0.5 pK_a units from measuring pK_a values by various NMR methods²⁰. This observation implies that just a handful of acidic residues exhibit anomalous protonation behavior and thus act as key “pH triggers” during HdeA chaperone activation.

Table 1.

Comparison of pK_a values for acidic residues in HdeA

Residuea	NMR (dimer)b	pH-REX dimer	pH-REX monomer	ΔpH-REXc	T-REX dimerd	T-REX monomerd	ΔT-REXc
Glu19	4.38	4.1	4.3	−0.2	3.7	3.8	−0.1
Asp20	3.66	3.1	4.2	−1.1	2.6	3.8	−1.2
Asp25	3.71	3.1	3.8	−0.7	3.1	2.7	0.4
Glu26	4.57	4.0	4.5	−0.5	4.35	4.0	0.35
Glu37	N/Ae	6.4	4.5	1.9	6.7	5.3	1.4
Asp43	3.87	3.9	3.6	0.3	2.85	3.7	−0.85
Glu46	4.07	3.8	4.3	−0.5	3.45	3.7	−0.25
Asp47	4.14	4.4	4.1	0.3	3.85	4.2	−0.35
Asp51	3.83	3.2	3.7	−0.5	2.8	3.8	−1.0
Asp69	3.74	3.7	3.6	0.1	3.5	3.8	−0.3
Asp76	3.75	3.5	3.8	−0.3	2.75	3.5	−0.75
Glu81	4.23	4.3	4.5	−0.2	4.1	4.0	0.1
Asp83	3.97	3.6	4.0	−0.4	3.1	3.7	−0.6

^aResidues observed in crystal structure⁴⁷ (10–85) are modeled during simulation, and thus Asp2, Asp8, and Asp88 at the disordered N- and C-termini are not considered for the pK_a calculations.

^bpK_a values from NMR were measured by Garrison and Crowhurst¹⁷.

^cpK_a shifts (Δ) from pH-REX and T-REX are computed as pK_dimer – pK_monomer.

^dpK_a values from T-REX simulation are from Zhang et al.¹⁴.

^eThe pK_a of Glu37 could not be determined from experiment.

Contribution of Acidic Residues to HdeA Binding Stability

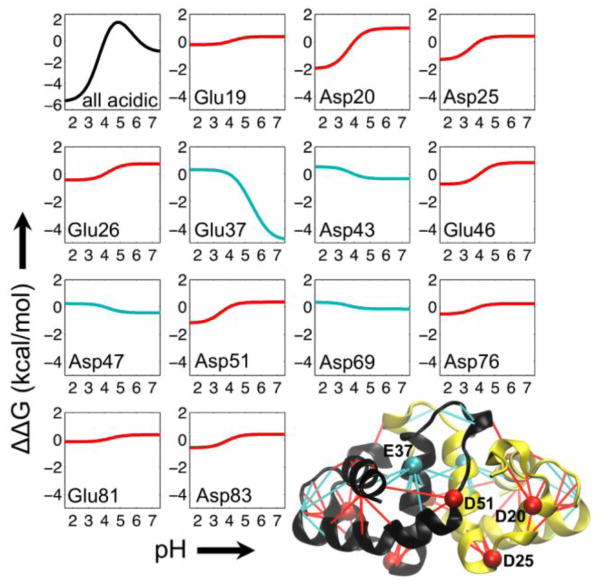
We use the pK_a values obtained from all-atom pH-REX along with Wyman-Tanford linkage theory to estimate pH-dependent changes in the binding stability (ΔΔG(pH)) of HdeA (see Eq. 3 in Materials and Methods). Larger pK_a shifts (ΔpH-REX, Table 1) between the dimer and monomer states correspond to larger changes in ΔΔG(pH) (Fig. 3). ΔΔG(pH) is maximal at pH 5 (~2 kcal/mol) and decreases by ~7 kcal/mol to a minimum at low pH (Fig. 3, black curve). Decomposing ΔΔG(pH) into the contributions from individual acidic residues provides insight into the pH triggers important for HdeA stability. The majority of the acidic residues (9 of 13) destabilize the dimer upon protonation at low pH, thus favoring dissociation and disordering to the active-state monomer (Fig. 3, red curves). Destabilizing interactions are located throughout the monomer as well as across the dimer interface (Fig. 3, red lines in the dimer cartoon). Asp20 is located near the beginning of an N-terminal helix and exhibits the largest destabilizing contribution (ΔΔG(pH)^pH7→1.5 of −2.9 kcal/mol). Asp25 and Asp51 are also both situated near the N-terminus of a helix, and are the only other two residues that contribute a destabilizing effect larger in magnitude than ~1.5 kcal/mol from pH 7 to 1.5. The remaining four acidic residues stabilize the dimer under acidic conditions (Fig. 3, cyan curves). Glu37 displays the most notable stabilizing effect (ΔΔG(pH)^pH7→1.5 of +4.9 kcal/mol) and is located at the dimer interface. No other acidic residue shows a significant stabilizing effect (increase in ΔΔG(pH) from pH 7 to 1.5). Stabilizing interactions occur in separate regions of the dimer: at the dimer interface and farther away at the opposite end of the subunits (Fig. 3, cyan lines in the cartoon), indicating the coupled nature of interface formation and monomer folding in HdeA¹⁸.

Figure 3.

Contribution of acidic residues to the pH-dependent binding stability of HdeA. In the binding stability curves, ΔΔG = 0 at the reference pH (pH_ref = 4). A decrease in ΔΔG from pH_ref to a given target pH represents destabilization of the dimer complex and thus favors the monomeric state. An increase in ΔΔG from pH_ref to a target pH stabilizes binding in the complex and thus favors the dimeric state. The black curve in the upper left corresponds to the binding stability profile with the contributions from all acidic residues in the dimer. Red and cyan curves denote acidic residues that destabilize and stabilize the dimer upon protonation at low pH, respectively. In the bottom right is a cartoon representation of the HdeA dimer crystal structure⁴⁷. In the structure, lines are drawn between residue pairs that are in close contact in the crystal structure and that involve an acidic amino acid. Red and cyan lines denote contacts involving acidic residues that destabilize and stabilize, respectively, the dimer at low pH. The location of the acidic residues that exhibit the largest destabilizing and stabilizing contributions are denoted by red (Asp20, Asp25, and Asp51) and cyan (Glu37) beads, respectively. For clarity, labels for these residues are only shown in one of the two monomers. Asp2, Asp8, and Asp88 are not resolved in the HdeA crystal structure, and thus were not considered in our calculations.

pH-Dependent Binding Pathway in HdeA

We next considered ΔΔG(pH) for each acidic residue in modifying the energy function of the coarse-grained model. We used the modified energy function with the “Hamiltonian mapping” reweighting formalism^21,22 (see Materials and Methods and supplementary information) to describe pH-dependent thermodynamic behavior of the system. We first computed the dimer dissociation constant (K_d) at different pH values (Table 2). The simulated and experimental K_d values show good agreement, with both sets spanning two orders of magnitude (10⁻⁵ to 10⁻⁷ M) between pH 2 and 7. From simulation, the weakest and tightest binding is predicted to occur at pH 2 and 5, respectively.

Table 2.

Comparison of experimental and simulated dimer dissociation constants

pH	Kd Exp. (μM)a	Kd Sim. (μM)b
7	0.25	1.5
5	N/Ac	0.7
4	1	2.5
2	45	84

^aExperimental K_d values are interpreted from values plotted from analytical ultracentrifugation measurements at 298 K⁵.

^bThe K_d values from simulation are computed at 298 K (0.98 T_m) using Equation 1.

^cNo experimental value is available.

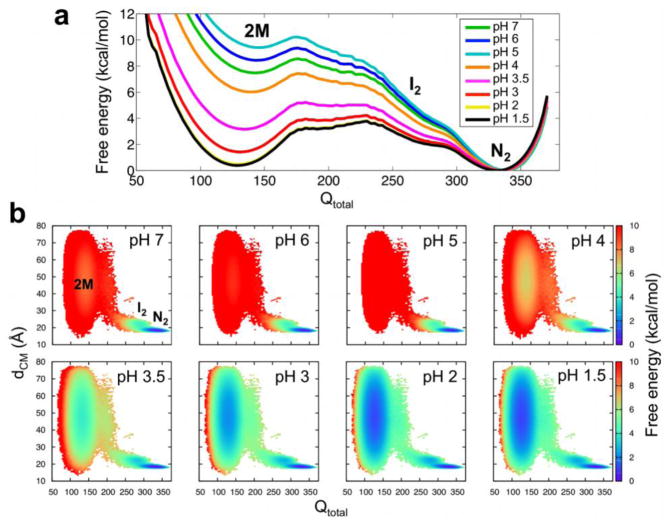
We further analyzed changes in conformational stability as a function of pH by analyzing the free energy as a function of the total number of native contacts (Q_total; Fig. 4a). The potentials of mean force in Figure 4 exhibit three minima corresponding to Q_total ≈ 340 (folded dimer; N₂), Q_total ≈ 275 (a partially unfolded, dimeric intermediate; I₂), and Q_total ≈ 135 (unfolded monomers; 2M). In the present paragraph, we refer to the free energy differences (ΔG) as the change between the free energy values at these values of Q_total. Interestingly, we observe a non-monotonic change in the stability of HdeA with decreasing pH values. As the pH drops from pH 7 to pH 5, the stability of N₂ relative to 2M (ΔG^N2-2M) actually increases by ~2 kcal/mol. This observation is consistent with the lower K_d value at pH 5 compared to pH 7 (Table 2). ΔG^N2-2M then sharply decreases by ~4 kcal/mol from pH 5 to pH 4 and by ~3 kcal/mol from pH 4 to pH 3.5, the pH ranges corresponding to the pK_a values for the majority of the acidic residues (Table 1). While ΔG^N2-2M is further diminished as the pH is lowered, the dimer is still ~2 kcal/mol more stable than the monomer, in agreement with NMR measurements in which HdeA persists as a dimer structure from pH 6 to pH 3¹⁷. Even at pH 2 and pH 1.5, N₂ is still slightly more stable than 2M. The dimer remains the dominant species at all pH values in our model due to the high local concentration of protein used in simulation (4.6 mM compared to NMR measurements performed with protein concentrations of 0.5 mM⁶ and ~1.0 to 1.7 mM¹⁷) to facilitate binding events. Moreover, the stability gap between the partially unfolded, dimeric intermediate, I₂, and N₂ (ΔG^N2-I2) decreases by ~3 kcal/mol from higher to lower pH values, indicating that an increased fraction of the dimeric population exhibits local unfolding at lower pH values. Compared to the native dimer (N₂), the I₂ state exposes an additional ~1100 Ų/~650 Ų of total/hydrophobic surface area (Fig. 5a), which is roughly half the size of the HdeA dimer interface and comparable in size to many small protein-protein interfaces²³.

Figure 4.

pH-dependent binding pathway in HdeA. (a) Free energy profiles as a function of Q_total at different pH values. The basins corresponding to the native dimer (N₂), partially unfolded dimeric intermediate (I₂), and unfolded monomers (2M) are indicated above their respective basins. (b) The free energy projected onto the plane of Q_total and the distance between the monomer centers of mass (d_CM). The conformational basins are labeled on the pH 7 surface and follow the same abbreviations as in (a). The colorbars indicate the free energy in units of kcal/mol computed at 0.98 T_m.

Figure 5.

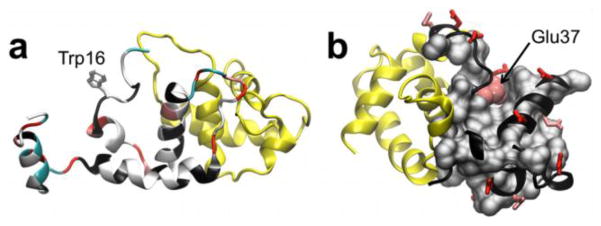
Proposed key structural features for HdeA chaperone activity. (a) Representative conformation of the partially unfolded, dimeric intermediate (I₂). Hydrophobic residues (white), lysines (cyan), glutamates (pink), and aspartates (red) are indicated on the cartoon backbone. The side chain of Trp16, which becomes exposed upon the formation of I₂, is highlighted. (b) HdeA dimer with Glu37 (pink van der Waals spheres) depicted in the context of hydrophobic residues (grey surface). All other acidic residues are displayed in stick representation (Glu residues in pink and Asp residues in red). In both panels, the labeled monomer is colored black and the neighboring subunit is shown in yellow.

The pH-dependent binding pathway of HdeA is also analyzed by projecting the free energy onto the plane of Q_total and the center-of-mass distance between the two monomers (d_CM) (Fig. 4b). The surfaces show three minima: N₂ at high Q_total/low d_CM and 2M at low Q_total/varying d_CM, with the basin for I₂ appended to the N₂ minimum at slightly lower Q_total and higher d_CM values. Similar to Fig. 4a, the relative stability of these species exhibits a non-monotonic trend as pH is lowered, i.e., N₂ is maximally stable at pH 5 and ΔG^N2-2M and ΔG^N2-I2 decrease at low pH.

Discussion

Modeling changes in the thermodynamics as a function of pH offers new insights into the chaperone mechanism of HdeA. The pH-dependent stability of HdeA shows that Asp20, Asp25, and Asp51 significantly contribute to dimer dissociation and disordering upon protonation at low pH. Asp20, Asp25, and Asp51 are each located at the N-terminus of a helix (Fig. 3), suggesting that the protonation of these pH triggers acts to destabilize the helix macrodipole as a mechanism for monomer disordering. Indeed, mutation of Asp20 and Asp51 to charge-neutral alanine resulted in a significantly destabilized, partially unfolded, monomeric, and constitutively active HdeA¹⁵. On the other hand, the protonation of Glu37 under acidic conditions stabilizes the folded dimer. Glu37 is highly conserved among HdeA sequences¹⁵ and situated near the hydrophobic dimer interface (Fig. 5b). Neutralization of its negative charge appears to notably stabilize the dimer at lower pH values (Fig. 3). Consistent with this observation, mutating Glu37 to alanine increased the melting temperature of HdeA by 5 °C¹⁵. Mutation to charge-neutral glutamine would more directly mimic the protonation of Glu37, and a tighter binding affinity and/or increased melting temperature of such a mutant would support the predicted role of Glu37 in stabilizing the inactive HdeA dimer as the pH is lowered. Moreover, the pK_a of Glu37 in the dimer (6.4) is at least two units higher than the pK_a of any other acidic residue. Thus, we attribute the non-monotonic change in pH-dependent stability of HdeA in our model (Fig. 4) to Glu37: HdeA is maximally stable near pH 5, where Glu37 is protonated and the other acidic residues predominantly reside in their deprotonated form. Maximal stability at pH 5 coincides with the increase in protection factors measured by NMR for several residues at pH 5 compared to those values at pH 6¹⁷. Increased stability of HdeA under mildly acidic conditions may act to tightly regulate chaperone activity by preventing dimer dissociation at elevated pH values, and contribute to the optimal function of HdeA and its structurally related, periplasmic acid-response chaperone HdeB at different pH values²⁴.

Further insight into HdeA chaperone activity from our model stems from the increased stability of a partially unfolded, dimeric, intermediate relative to the fully folded dimer at lower pH values. In the intermediate, unfolding occurs near the C-terminus of one monomer and results in a notable increase in the exposure of hydrophobic surface area (Fig. 5a). The presence of an intermediate species is consistent with the change in NMR chemical shifts between pH 5 and 3.5⁶, and can be further tested by measuring Cα and Cβ chemical shifts to detect changes in local structure near the C-terminus. Partial unfolding¹⁵ and the exposure of hydrophobic surfaces^6,7 are key functional requirements of HdeA, indicating that the dimeric intermediate could act as an alternate substrate binding mode. This hypothesis is supported by chaperone-substrate binding assays in which a modest quenching affect was observed for a non-interfacial tryptophan residue (Trp16) located in the exposed region of the intermediate (Fig. 5b).⁷ Further binding experiments with a crosslink introduced within the HdeA dimer interface to prevent dissociation would directly test the ability of a dimeric species to act as a chaperone-active state. Substrate interaction with hydrophobic surfaces in addition to the exposed dimer interface region (i.e., the primary binding site) would facilitate the formation of soluble chaperone-client aggregates¹².

It is intriguing that the pK_a values for acidic residues measured by NMR¹⁷ for the dimer agree most closely with our calculated pK_a values for the disordered monomer. In NMR, hydrogen-deuterium exchange experiments show that the dimer structure becomes “loosened” at lower pH values, suggesting an increase in solvent exposure¹⁷. Such a change in dimer conformation is consistent with our observation of a partially unfolded, dimeric intermediate and would contribute to shifting the observed pK_a values closer to their model compound values. We determine pK_a values through all-atom constant pH simulations and do not observe significant conformational change in the dimer during these calculations (Fig. S2). Probing “microstate” pK_a values within the well-folded native dimer is most appropriate for our model of pH-dependent dynamics in HdeA, as it allows us to obtain pK_a shifts corresponding to the complete conformational transition from the fully folded dimer to the disordered monomer state.

Finally, multiscale modeling of HdeA conformational dynamics is a significant endeavor to push forward pH-dependent simulation methodology^25,26. While coarse-grained simulation can access the long-timescale dissociation and unfolding events critical for HdeA chaperone function, the absence of protons in many “minimalist” models necessitates novel approaches for incorporating pH effects. Electrostatic phenomena are commonly incorporated into coarse-grained potentials with unit charges assigned to ionizable residues^27–31. However, modulating unit charges to mimic “high” or “low” pH states represents a gross approximation to the pH-dependent behavior of the system. Capturing the natural pH response instead requires taking into account the interplay of the protonation equilibria of the individual titratable groups. Accordingly, O’Brien and co-workers recently incorporated pK_a information into a coarse-grained model to describe pH- and force-induced unfolding³². In a similar vein, we use pK_a shifts between bound and unbound states obtained from all-atom constant pH simulation to account for pH effects in a native topology-based model. This information is used to modulate the strength of native contacts involving acidic residues. While longer-range electrostatic²⁷ and hydrophobic³³ “non-native” interactions may be necessary to reproduce experimental folding data, such data, which could serve as a basis for analyzing whether the incorporation of similar non-native interactions in the model for HdeA is more appropriate than a native contact-only approach, is largely unavailable. Nevertheless, our model yields binding affinities at different pH values in good agreement with experiment (Table 2), indicating that our approach reasonably captures HdeA binding and folding.

Materials and Methods

Structure-Based Model of HdeA

Given the extensive conformational sampling of our previous coarse-grained simulations¹⁸, this ensemble serves as the starting point for the current study. In brief, we simulated a Cα-based Gō-like model that takes into account sequence effects³⁴ in combination with the temperature replica exchange enhanced sampling method³⁵ using 16 replicas spanning 0.95 T_m to 1.12 T_m (where T_m is 304 K). Native contacts in the system interact in accordance with the statistical residue pair potentials reported by Miyazawa and Jernigan³⁶. Further details concerning these simulations and the Gō-like model can be found in refs ^{18 and 34}, respectively.

To examine the balance of the intramolecular folding and intermolecular binding forces in the Gō-like model of HdeA, we determined the fraction of helicity (f_H) and the dimer dissociation constant (K_d), respectively^37,38. We estimated f_H of a given snapshot as the number of i and i+4 contacts formed divided by the total possible number of such contacts in the sequence. f_H values for the dimer and disordered monomers during simulation are in good agreement with the helicity suggested by circular dichroism (CD) spectroscopy¹⁵ (Fig. S1). The difference in the experimental and simulated f_H values are comparable with the error in estimating helical content from CD spectroscopy³⁹. The K_d is computed as

$$K_d=[\text{protein}]\frac{p_u^2}{1-p_u},$$ (1)

where p_u is the fraction of unbound species and [protein] is the concentration of protein in moles per liter. Configurations were considered as unbound if none of the intermolecular contacts were within 1 Å of their distance in the crystal structure. The K_d computed just below T_m is 2.5 μM, which agrees well with the experimental K_d of ~1 μM at pH 4⁵. Collectively, the correspondence of f_H and K_d to experiment indicates a reasonable balance of intra- and intermolecular forces in the model. Equation 1 is also used to compute K_d at different pH values from simulation (Table 2).

All-Atom Reconstruction

For all-atom reconstruction from Cα-only coarse-grained conformers, we first clustered 1400 members of the unfolded ensemble with a hierarchical clustering algorithm⁴⁰ implemented in the Multiscale Modeling Tools for Structural Biology (MMTSB) tool set⁴¹. The root-mean-square deviation (RMSD) of Cα coordinates served as the distance metric. Within the three clusters from the top clustering level, we selected three representative conformers as those with the lowest average pairwise Cα-RMSD to all other cluster members (Fig. 1b–d). Thus, there were nine total representative conformers of the unfolded ensemble. All-atom models were then built from these coarse-grained conformers using the MMTSB complete.pl script, which reconstructs the protein backbone with the rebuild program⁴¹ and adds the side chains with the SCWRL4 algorithm⁴². The resulting all-atom models were relaxed by 100 steps of steepest descent minimization using the CHARMM22 force field⁴³ with harmonic restraints applied to all Cα atoms (5 kcal mol⁻¹ Å⁻² force constant).

All-Atom Constant pH Molecular Dynamics (CpHMD) Simulations

CpHMD permits pH-dependent biomolecular behavior to be explored by coupling the conformational and protonation state sampling of the system^25,26. In our approach, continuous titration coordinates describe the protonation and tautomer interconversion of ionizable residues, and are propagated between protonated and unprotonated end states along with the atomic coordinates^44,45. In this study, we perform CpHMD in combination with the replica exchange (REX) algorithm in pH space. “pH-REX” is analogous to REX in temperature space³⁵, in which multiple copies of the system exchange between different temperature states to promote barrier crossing on the conformational energy landscape. In pH-REX, multiple replicas of the molecule are simultaneously simulated at different pH values to improve both conformational and protonation state sampling. The replicas exchange between pH windows based on a Monte Carlo acceptance criterion. We refer the reader to refs ^{44,45 and 46} for a detailed description of standard CpHMD and pH-REX, respectively.

A total of 12 independent “pH-REX” simulations were performed. The starting coordinates for the pH-REX simulations were either the folded dimer X-ray structure (PDB ID: 1BG8)⁴⁷ or the rebuilt all-atom unfolded monomers (see above). In total, we ran three independent pH-REX simulations for the dimer, and nine additional simulations for the monomer (one per representative all-atom structure). The following protocol was applied to both the dimer and monomer pH-REX simulations. The initial coordinates were relaxed with 50 steepest descent and 500 adopted basis Newton-Raphson minimization steps followed by a 200 ps equilibration with no pH exchanges at 298 K, matching the temperature of previous NMR experiments^6,17. For the production pH-REX runs, we used 12 pH windows separated by 0.5 pH units between pH 1.5–7. Exchange acceptance ratios ranged from 0.12 to 0.60 for the three dimer simulations and 0.27 to 0.84 for the nine monomer simulations. We employed the CHARMM22 force field⁴³ and the GBSW implicit solvent model⁴⁸ with a salt concentration of 150 mM. The distance cutoff for the energy evaluation of non-bonded interactions was 24 Å. Langevin dynamics were propagated at 298 K with a 2 fs time step using the SHAKE algorithm⁴⁹ to hold fixed all bonds involving hydrogens. pH state exchanges were attempted every 2 ps and the total simulation times were 3 ns and 5 ns for the dimer and monomer, respectively.

pK_a Calculations

In total, there are five Glu, eight Asp, and nine Lys residues per monomer in the HdeA crystal structure; no histidines or arginines are present. Over the simulated pH range during CpHMD, we titrate Asp and Glu residues, while Lys residues (with a model pK_a of 10.5) are assumed to remain protonated. For each Asp and Glu residue, we first computed the fraction of unprotonated states (S^unprot) in each pH window over the final 2 ns of simulation. S^unprot is well converged over this period (Fig. S3). For the three simulations of the HdeA dimer, we average S^unprot for the same residue in the six total folded monomers. For the nine simulations of the unfolded monomer, we weight S^unprot for the equivalent residue in each simulation by the fractional population size of the starting configuration, as determined by hierarchical clustering. We then plot the set of S^unprot values against their corresponding pH values to fit the pK_a and the Hill coefficient (n) to the Henderson-Hasselbalch equation:

$$S^{\mathit{unport}}=\frac{1}{1+{10}^{n\left({pK}_a-pH\right)}}.$$ (2)

The pK_a values for acidic residues in the HdeA dimer and monomer are listed in Table 1.

pH-Dependent Binding Stability

We use the dimer and monomer pK_a values to determine the binding free energy at a given pH relative to a reference pH based upon an equation derived from Wyman-Tanford linkage theory^50,51:

$$\mathrm{\Delta }\mathrm{\Delta }G(pH)=RT\sum _{i}ln\frac{\left(1+{10}^{{pK}_D(i)-pH}\right)\left(1+{10}^{{pK}_M(i)-{pH}_{\mathit{ref}}}\right)}{\left(1+{10}^{{pK}_M(i)-pH}\right)\left(1+{10}^{{pK}_D(i)-{pH}_{\mathit{ref}}}\right)}.$$ (3)

T is the absolute temperature, and R is the ideal gas constant in units of kcal K⁻¹ mol⁻¹. The sum is over all acidic residues, i. pK_D and pK_M are the pK_a values for an acidic residue in the dimer and monomer, respectively. pH_ref was set to 4, as determined by comparing the simulated and experimental K_d values (see above), and corresponds to ΔΔG(pH) = 0. Written in this form, an increase in ΔΔG(pH) from pH_ref to a target pH signals stabilization in the dimer complex and thus favors the dimeric state. Conversely, a decrease in ΔΔG(pH) from pH_ref to a given target pH denotes destabilization of the dimer and thus favors the monomeric state. The pH-dependent binding stability curves for the complex and for individual acidic residues are shown in Figure 3.

Incorporating pH Effects into the Structure-Based Model

From our Gō-like model simulations, pH effects were incorporated by adding a perturbation, x(pH), to the original Hamiltonian (H₀): H_m = H₀ + x(pH). H_m is the modified Hamiltonian and x(pH) takes the form

$$x(pH)=\sum _i{\alpha }_i(pH)\left\{V_{nb,i}\right\},$$ (4)

where the sum is over all acidic residues. V_nb,i corresponds to the potential energy for the set of native contacts involving the i^th acidic residue. α_i(pH) is a scaling factor that depends on the pH and governs the strength of these contacts. 0 ≤ α_i < 1 and α_i > 1 correspond to weakening and strengthening the native contacts, respectively. For each acidic residue, α_i(pH) is determined by its contribution to ΔΔG(pH) (Eq. 3). (See supplementary information for further details.)

We examine changes in the thermodynamic behavior of the system under H_m through the “Hamiltonian mapping” reweighting formalism^22,33, which builds upon the Weighted Histogram Analysis Method⁵². H_m (corresponding to a particular target pH) is considered along with H₀ (representing pH_ref = 4, from matching experimental and simulated K_d values (see above)) to reweight the original probability distribution for a given progress variable, r:

$$P_{\mathit{reweighted}}(r)=\frac{{\sum }_{k=1}^R{N}_k(r)exp\left[-\beta H_m^{pH}\right]}{{\sum }_{m=1}^R{n}_{m}exp\left[f_m-{\beta }_m{H}_0^{{pH}_{\mathit{ref}}}\right]},$$ (5)

where exp(−f_m) = Σ_rP_{reweighted, m}(r). R is the total number of simulations, which corresponds to the number of temperature windows from replica exchange simulation of the Gō-like model¹⁸. n is the total number of configurations and N is the histogram count for a particular configuration in the k^th simulation. We determine the free energy shifts, f_m, self-consistently⁵². The reweighted probability is computed across all R windows and evaluated at 298 K.

Highlights.

• The bacterial chaperone HdeA impedes acid-induced aggregation of periplasmic proteins

• Multiscale model captures the pH-dependent, order-to-disorder transition of HdeA

• HdeA is maximally stable under mildly acidic conditions

• A partially unfolded intermediate may contribute to substrate binding

• General framework for modeling large-scale, pH-induced conformational events

Abbreviations

CpHMD

constant pH molecular dynamics

pH-REX

pH replica exchange

pK_a

logarithmic acid dissociation constant

K_d

dimer dissociation constant

d_CM

distance between centers of mass

Q_total

total number of native contacts