Rapid search for tertiary fragments reveals protein sequence–structure relationships

Abstract

Finding backbone substructures from the Protein Data Bank that match an arbitrary query structural motif, composed of multiple disjoint segments, is a problem of growing relevance in structure prediction and protein design. Although numerous protein structure search approaches have been proposed, methods that address this specific task without additional restrictions and on practical time scales are generally lacking. Here, we propose a solution, dubbed MASTER, that is both rapid, enabling searches over the Protein Data Bank in a matter of seconds, and provably correct, finding all matches below a user-specified root-mean-square deviation cutoff. We show that despite the potentially exponential time complexity of the problem, running times in practice are modest even for queries with many segments. The ability to explore naturally plausible structural and sequence variations around a given motif has the potential to synthesize its design principles in an automated manner; so we go on to illustrate the utility of MASTER to protein structural biology. We demonstrate its capacity to rapidly establish structure–sequence relationships, uncover the native designability landscapes of tertiary structural motifs, identify structural signatures of binding, and automatically rewire protein topologies. Given the broad utility of protein tertiary fragment searches, we hope that providing MASTER in an open-source format will enable novel advances in understanding, predicting, and designing protein structure.

Introduction

The observed modularity of protein structure—that is, the frequent recurrence in nature of local structural patterns—has had a strong influence on methods of computational structural biology. Modularity is evident on the level of secondary structure, with reliable amino acid propensities emergent from structural databases,¹ assembly of secondary structural elements (SSEs),^2–5 and even conserved domains.⁶ Computational methods have taken advantage of this in a multitude of ways. The observed recurrence of compact folds in unrelated native proteins gave rise to various template-based structure prediction approaches.^7–9 Conformational sampling based on previously observed contiguous structural fragments has revolutionized both structure prediction^10–12 and protein design.^13–15 As the Protein Data Bank (PDB) continues to grow, more ambitious uses of fragment-based data, incorporating both secondary and tertiary information, are being proposed for design and prediction.^16–19

Given the increased use of protein substructure statistics, the problem of rapidly finding close matches to a structural motif is growing in significance. We find that a particularly useful flavor of this general problem is the identification of precise atom-for-atom matches to arbitrary constellations of disjoint backbone fragments. We refer to this as the atomistic tertiary fragment search (ATFS) problem, and propose an efficient method to solve it here. We believe ATFS is of high value for many applications in structural biology, and we carry out several computational experiments demonstrating this in this study. A particularly useful feature of ATFS is that it does not require sequence constraints, which enables the discovery of natural sequence–structure relationships, as we have shown previously^15,20 and further demonstrate here.

Numerous methods have been proposed under the general umbrella of the protein structure search problem.²¹ Most development has focused on searching for structural similarity on the level of whole proteins or domains,^22–28 with intended applications including function prediction and evolutionary inference. This is a challenging problem, because one needs to find good query–target alignments while simultaneously choosing the best subset and permutation of query residues upon which the alignment is based. Methods for identifying matches to smaller protein substructures have also been proposed.^20,29–32 Search techniques used can be broken down into either heuristics-based approaches or those looking for provably optimal matches based on a given similarity score. Heuristic methods have dominated because of computational demands of the problem.²¹ Further, a number of ad hoc similarity scoring functions have been proposed as researchers have attempted to codify the intuition inherent in comparing structures manually. Such functions often assume the importance of certain structural features, such as the presence of canonical SSEs. Although this may be appropriate in most cases when querying with native structures, it may not apply as readily to simulated conformations.

The ATFS problem we consider here differs from the generic substructure search in that it further stipulates that all residues in the query are to be matched and the query connectivity is to be preserved (i.e., residues bonded in the query must also be bonded in matches). These additional constraints potentially simplify the problem a great deal, such that heuristics may not be necessary and exact methods could be efficient. Surprisingly, however, relatively little effort has been directed toward addressing this problem explicitly, without additional restrictions (e.g., preservation of sequence patterns) or heuristic requirements (e.g., presence of SSEs). We arrived at the need for ATFS through our work on computational protein design,¹⁵ having since identified more applications, some of which we demonstrate here. Other researchers have also found it necessary to perform ATFS-like operations in protein design studies, devising tailored solutions on a case-by-case basis.^18,33 It is thus clear that there is a growing need for a robust ATFS engine based on a universally applicable similarity metric that does not a priori assume the importance of certain structural features.

To address this need, we have developed an efficient exact ATFS method based on backbone root-mean-square deviation (RMSD) as the similarity metric. The method, dubbed MASTER (Method of Accelerated Search for Tertiary Ensemble Representatives), takes as query a structural fragment composed of one or more disjoint segments and provably finds all fragments from a database matching the query to within a given RMSD threshold. The method is fast, enabling searches over the PDB in a matter of seconds (for realistic thresholds), with the running time in practice most sensitive to the number of matches falling below the RMSD cutoff. This supports the notion that heuristics may not be necessary for ATFS. In fact, we show that application of typical heuristic filters (based on intersegment distances or local RMSD) either moderately speeds up the search at the loss of some matches (when filters are stringent) or preserves all matches but fails to produce any speedup (when filters are loose).

We previously proposed a different ATFS method, MaDCaT, which used a distance map-based similarity score as the search metric.²⁰ Like MASTER, MaDCaT finds provably optimal matches, and we have used it extensively in both design and structural analysis applications.^15,20 In so doing, we have found backbone RMSD to be a much better structural similarity metric, as it orders matches much more in line with our structural intuition about their relative “closeness” to the query. Further, though MaDCaT was already highly optimized,²⁰ we found that its speed would be a limiting factor in higher-throughput applications (e.g., systematic exploration of motif geometries). The development of MASTER, motivated by the need for a fast RMSD-based search engine, resulted in at least an order of magnitude speedup relative to MaDCaT for most queries we have tested.

In this study, we elude to applications in protein design and structure prediction that we believe are enabled by rapid solutions to ATFS. We demonstrate that MASTER searches can be used to establish the apparent designability landscape of a structural motif as a function of its geometric parameters, and to provide detailed information on the sequence features necessary to encode different geometries. We show that ATFS easily lends itself to functional mining and annotation, illustrating that putative peptide binding sites can be rapidly identified with just one example of a binding motif. Further, we demonstrate that ATFS can be used to “fill in” missing pieces of structure, enabling the rapid redesign of topology. We are providing MASTER as an open-source C++ package in hopes that it will be useful to the community in tackling these and related applications and to stimulate the further development of efficient ATFS engines.

Results

An ATFS query is a structural fragment consisting of one or more disjoint segments, each representing a contiguous stretch of amino acids. A valid alignment of this fragment is a one-to-one correspondence between residues of the query and a subset of residues from a database structure, such that each query segment maps onto a sequence-consecutive segment in the database structure. A valid alignment is a match, when the resulting best-fit RMSD is below a prespecified threshold.

In developing MASTER we assumed that the RMSD of each individual query segment aligned onto each possible position in the database is easily computable. MASTER currently calculates these RMSDs explicitly on the fly (as needed), but much better performance can be achieved by taking advantage of the metric property of RMSD,³⁴ parallelization, and/or faster-to-compute RMSD bounds.^35,36 We decided not to focus on this aspect of the problem, choosing rather to pour our effort into addressing the issue making ATFS “difficult”—namely, the potential combinatorial explosion of possible alignments when the query structure is composed of multiple disjoint segments.

To contain this explosion, MASTER adopts a variant of the classical branch and bound approach, using backbone RMSD as the search metric (the current implementation searches by CA-atom RMSD, but the algorithm is easily generalizable to more than one atom per residue). The main idea behind MASTER is that once alignment positions are chosen for the first one or more segments, one can calculate exact bounds on the locations of the remaining unaligned segments (i.e., their distances relative to the aligned ones) and on their individual RMSDs (see Fig. 1). MASTER uses a tailored database format that allows it to take advantage of these bounds to very quickly retrieve the restricted set of possible alignments for currently unaligned segments, making the search very fast in practice.

Figure 1.

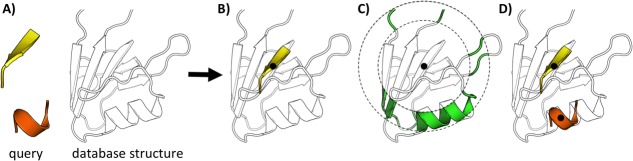
Schematic representation of the MASTER search algorithm. (A) The search query, consisting of two disjoint segments, is shown on the left, and a database structure on the right. (B) A potential location of a match for the first segment (black dot designates the central residue). Given this alignment, possible locations for aligning the second segment are limited, as shown in (C), by the distance from the central residue of the first segment [see Eq. (10)]. Further, the individual RMSD of aligning the second fragment is also constrained given the error already incurred in aligning the first [see Eq. (6)]; so, an even smaller set of possibilities is available for the second segment. One of these is shown in (D).

Algorithm

In the following description, RMSD will denote the root-mean-square deviation upon optimal superposition. MASTER defines a “central” residue for each of the disjoint segments in the query (a residue roughly in the middle of each segment; see Materials and Methods section) and limits the combinations of segment alignments by bounding center-to-center distances. Given a query, its segments are first sorted by number of residues in descending order. The first segment, of length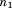, is considered for alignment onto all equally long sequence-consecutive segments from a given database structure, with the RMSD of each of these alignments calculated. We next apply a notion that is used repeatedly in the algorithm—namely that given a partial alignment of length n_p, if its RMSD is above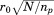, where 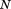is the length of the entire query and 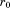is the requested overall RMSD cutoff, then this alignment can be safely eliminated as a possibility (i.e., it will never lead to a full alignment with RMSD below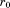). Thus, if the RMSD of the first segment is above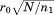, we can safely skip the corresponding alignment. If instead the alignment passes, we go on to consider alignments of the second segment. However, rather than checking all possibilities, we pursue only those that are at a distance from the first aligned region that is reasonably close to the distance between the first and second segments in the query (see Fig. 1). We use central residues to define intersegment distances and apply an exact bound to limit candidates. Specifically, as we prove in the Materials and Methods section, given a partial alignment with overall RMSD r_p and length n_p, the distance to the next segment considered for alignment cannot deviate by more than 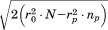from its value in the query. So, as the alignment grows accumulating length (and generally RMSD), the tolerance on distance deviations becomes lower. This is one of the main reasons for the efficiency of MASTER, allowing it to contain the potential combinatorial explosion of ATFS. Further, our disk-based database is designed to enable the quick retrieval of all atoms within a certain distance range of a given source atom (see Materials and Methods section). Together with the provable distance bound above, this produces a limited list of possible alignment locations for the second segment. Each of these locations is then visited, and three separate RMSD bounds are applied before continuing. First, the RMSD of the second-segment alignment on its own is checked against 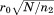(where 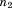is the length of the second segment). If it is above the bound, the alignment can be safely eliminated as an option for the second segment altogether. That is, it can be marked as invalid for the segment and will never have to be visited again as part of any combination. If the bound fails to eliminate, we then check the same RMSD against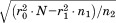. This bound requires no additional RMSD calculations and gives the potential to eliminate the alignment for the second segment in the context of the individual RMSD already accumulated by the first segment (though the former cannot be marked as invalid by itself). Finally, in the case where this bound does not apply, we check the total RMSD of segments 1 and 2 together against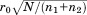. An RMSD above this value allows for the elimination of the partial alignment, though each of the alignments of segments 1 and 2 cannot be individually eliminated. If the partial alignment passes all bounds, the process repeats recursively for subsequent segments just as we described above for the second segment. When a valid alignment location is found for the last segment, the corresponding match is recorded. Taking this process until completion for the given structure will find all matches with RMSD below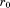. The pseudo-code of the method is outlined in Table I (omitting some details).

Table I.

Basic pseudo-code for the MASTER search algorithm (some time-saving features of the algorithm are omitted for clarity)

Input: query Q with L segments
Input: database structure T
Output: match list M
1 set C(k) to all residues in T, for k=1…L
2 set M to an empty set
3 set m to an empty match
4 return masterSearch(C,m,1)
5 masterSearch(C,m,k) {
6 for each i C(k) do
7 set r to RMSD(k,i)a
8 if r > maxA(k)b
9 eliminate i from the list C(k)
10 continue
11 end if
12 if (r > maxB(k)c) OR (cRMSD(k)d > maxC(k)e)
13 continue
14 end if
15 set m(k) to residue i
16 if (k == L)
17 insert match m into M
18 else
19 [dmin, dmax] = distBounds(k)f
20 C(k+1) = residues in T within [dmin, dmax] of m(k)
21 masterSearch(C,m,k+1)
22 end if
23 end for
24 }

^aComputes the individual RMSD of segment k when aligned onto T with position i corresponding to the central residue of k.

^bUpper bound on the RMSD of the k-th segment, assuming a perfect fit for all others [Eq. (5)].

^cUpper bound on the RMSD of k-th segment given the residuals already accumulated by segments 1..k − 1 [Eq. (6)].

^dComputes the cumulative RMSD incurred by the first k segments aligned together.

^eUpper bound on the joint RMSD of the first k segments assuming a perfect fit for the remainder [Eq. (7)].

^fComputes upper and lower bounds on the distance between k-th segment and the next one to be aligned, based on the currently accumulated residuals [Eq. (10)].

MASTER is fast in practice

To thoroughly test the practically relevant running time performance of MASTER, we applied it to search for matches to a highly diverse set of 50 substructure motifs under a range of RMSD cutoffs. The motifs varied in overall size (from 6 to 50 residues), topology (α-helical, β-sheet, noncanonical secondary structures in a variety of combinations), and number of disjoint segments (from 1 to 5; see Fig. 2). A nonredundant subset of the PDB, comprising 12,661 protein structures generated by using BLASTClust at 30% sequence identity, was used as the search database (hereafter referred to as nrPDB30).³⁷ Searches were performed under six different RMSD cutoffs: 0.4, 0.6, 0.8, 1.0, 1.5, and 2.0 Å.

Figure 2.

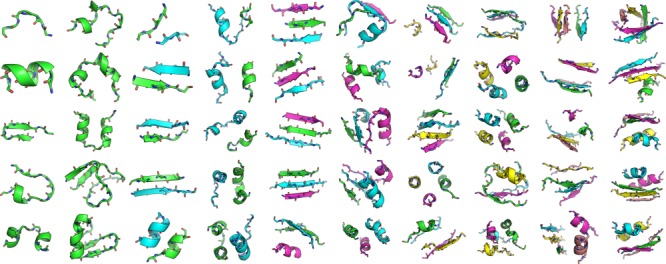
Fifty structural fragments used to test the performance of MASTER. Disjoint segments are designated with cartoon color; number of segments ranged from 1 to 5, with 10 motifs considered in each category. Within a given number of segments, motifs are ordered by increasing total number of residues, in column-major fashion.

Table II summarizes the search times (in seconds) for all motif–RMSD combinations as a function of two parameters that most influenced the performance—the number of disjoint segments in the query and the number of matches given the RMSD cutoff. Our implementation of the Kabsch algorithm³⁸ performs around a million superpositions per second (for up to ∼40-residue fragments; see Materials and Methods section); so, it took on the order of 3 sec to align a single segment onto every residue in our database. Because MASTER aligns the first query segment onto every possible database position, this is a lower bound for the search time. Remarkably, in most cases, the full search took not much longer, with significant exceptions corresponding to cases with very many matches (e.g., over 10⁶), large queries (e.g., four or five segments), or both. The single-segment searches can certainly be improved, given the metric property of RMSD³⁴ and the existence of efficient lower bounds.^35,36 However, our focus here was on containing the combinatorial explosion, and MASTER seems to do this well as even the large motifs under RMSD cutoffs that recover millions of hits run in seconds to 1–2 min. This is particularly impressive given that the MASTER database resides on disk, such that coordinates and other information are read on the fly as the search proceeds. However, because the database format was tailored around access patterns during a search (see Materials and Methods section), fraction of the total run time due to I/O was minor, ranging from 0.0% to 1.2%, with a median of 0.25%. Finally, the quoted times are for a single 2.7-GHz Intel Xeon processor. Because ATFS is an embarrassingly parallel problem, close-to-linear speedups can be expected from parallelizing the search by splitting the database. Thus, MASTER makes ATFS an easily manageable problem in practice, even for large motifs and very generous RMSD cutoffs.

Table II.

MASTER search times as a function of the number of disjoint fragments in the query and the number of returned matches (determined by the requested RMSD cutoff)

Matches	Segments
	1	2	3	4	5
0–10	3.1–4.6 (32)	2.5–6.3 (35)	2.7–21 (26)	2.7–35 (33)	2.8–21 (31)
101−102	3.7–4.4 (6)	3.0–7.5 (5)	2.9–9.4 (11)	2.9–72 (14)	9.5–41 (12)
102−103	3.3–4.2 (5)	3.0–6.4 (3)	3.5–28 (7)	3.4–90 (7)	17–119 (10)
103−104	3.2–3.8 (8)	3.7–57 (5)	5.0–58 (6)	5.4–146 (4)	90–210 (6)
104−105	3.4–3.8 (3)	5.2–22 (4)	9.4–37 (6)	41 (1)	482 (1)
105−106	3.8–4.8 (4)	7.7–37 (6)	57–103 (3)	143 (1)	(0)
106−107	5.5–5.7 (2)	43–82 (2)	162 (1)	(0)	(0)

Ranges of times are indicated in seconds and the number of different queries in each category is shown in parentheses. Cases with average running times over 1 min are shown in gray.

Despite the aforementioned time-saving techniques in MASTER, the problem still remains exponentially complex in nature, such that for large-enough motifs and generous-enough cutoffs, the time complexity will still become unmanageable. The beginning of this trend is seen even among the queries considered here (see Fig. 3). Importantly, however, the run time increases significantly only when the RMSD cutoff used produces very many matches (and only when the query motif has many disjoint segments; see Fig. 3). Arguably, this does not correspond to a practical use case, because one would not expect a large and complex motif to have millions of meaningful matches. In fact, in practice, this would indicate that the chosen RMSD cutoff was too loose. Because it is not always easy to anticipate the correct RMSD cutoff to use, MASTER offers an option to limit the number of matches to some integer N. This allows the initial RMSD cutoff to be set loosely, and once the number of found matches reaches N, the cutoff is lowered speeding up the search. The result is that the provably best-by-RMSD N matches are quickly found, without the need to know the right RMSD cutoff a priori.

Figure 3.

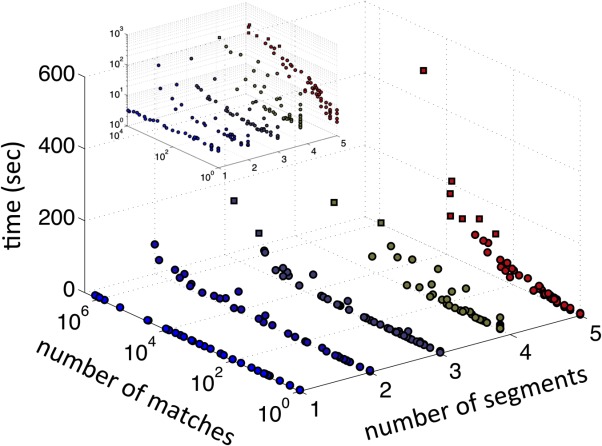
MASTER search time as a function of the number of disjoint segments in the query and the number of matches (determined by the RMSD cutoff used). Each dot corresponds to a single query–RMSD cutoff combination, with those taking more than a minute to search marked as squares. Queries with different numbers of segments are differentiated by color for clarity. The search slows down substantially only when the specified RMSD cutoff corresponds to a very large number of matches, and mostly with complex queries. Inset shows the same plot with the Z-axis in logarithmic scale.

Because in practice one rarely expects or needs more than 1000 matches, we repeated all test runs with N set to 1000 and the most loose RMSD cutoff considered (2.0 Å). The results summarized in Table III show that for the more complex motifs, this improves the running time by as much as an order of magnitude. Note that in practice, an RMSD cutoff of 2.0 Å would likely be too loose for most circumstances; so, practical running times would be even lower than these.

Table III.

Speedup of MASTER obtained by limiting the number of matches to the top 1000 and setting a loose initial RMSD cutoff of 2.0 Å

Matches	Segments
	1	2	3	4	5
103−104	1.0–1.0 (8)	1.0–1.6 (5)	1.0–1.3 (6)	1.0–1.5 (4)	1.0–1.6 (6)
104−105	1.0–1.1 (3)	1.2–2.9 (4)	1.4–4.0 (6)	1.7 (1)	2.3 (1)
105−106	1.2–1.5 (4)	1.8–7.3 (6)	7.0–10 (3)	5.4 (1)	(0)
106−107	1.7–1.7 (2)	9.6–9.6 (2)	22 (1)	(0)	(0)

Speedups are measured relative to searches with the same cutoff but without limiting the number of matches. Results are categorized according to the number of query segments and total number of matches under 2.0 Å. Queries for which there were fewer than 1000 matches under 2.0 Å were discarded for this analysis. Ranges of speedups in each category are indicated, with the number of examples shown in parentheses.

To our knowledge, no other ATFS approach offers such performance, while guarantying to find all matches and not requiring additional constraints (e.g., sequence filters). Our previously proposed method MaDCaT also finds all matches, but it uses a distance matrix-based metric. We have found that MASTER's search time consistently outperforms that of MaDCaT, in some cases by orders of magnitude. In particular, finding the top 1000 matches by RMSD using MASTER was, on average, 34 times faster (over all queries considered in Fig. 2) than finding the top 1000 matches by distance-map similarity with MaDCaT (maximal speedup was 220; Supporting Information Fig. S1 shows speedups for all queries).

Greedy heuristics provide only a limited performance boost

RMSD does not necessarily grow monotonically with increasing alignment size. Thus, many poor partial alignments cannot be provably eliminated because it is formally possible that the missing part of the alignment will bring the total RMSD below the desired cutoff. On the other hand, intuition suggests that alignments that start off very poorly will not generally result in good matches. We have considered three greedy rules one might apply to eliminate poor partial alignments early: (1) the accumulated residual for the partial alignment seems too high given the fraction of the alignment covered; (2) distances between disjoint segments in the partial alignment deviate too strongly from those in the query; (3) backbone dihedral  φ/ψ angles in the partial alignment differ significantly from those in the query. Application of such greedy filters would speed up the search, but may lead to some matches being missed. Further, the tradeoff between the speed gain and matches lost is a characteristic of the problem itself. If RMSD-based ATFS had considerable optimal substructure (with respect to the greedy filters), one would expect to gain significant speedups with little loss in match coverage. To test this characteristic, we implemented the three filters above in MASTER and repeated the running time analysis with each. Specifically, Heuristic 1 limited how quickly the RMSD of a partial alignment could grow with increasing alignment size via:

(1)

where r_o is the overall RMSD cutoff, r_p and n_p are the RMSD and length of the current partial alignment, respectively,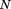 is the total query length, and is a tuning parameter determining the degree of greediness (higher values mean more greediness). With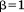, RMSD is required to grow no faster than linearly with query size and is perhaps the highest reasonable level of greediness. On the other hand, 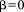corresponds to the case where the partial alignments are required to have an RMSD no worse than the overall cutoff r_o. Although this is a looser filter, it is still greedy because RMSD is not monotonic with alignment size; so, lower values of can be used to limit the degree to which local RMSD can be worse than the overall cutoff. For our experiments below, we used the fairly greedy value of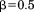. For Heuristic 2, a partial alignment was considered invalid if the deviation in any intersegment distance, with respect to that in the query, was above 4 Å. Note that this filter effectively limits the search radius for locating possible alignment options for a subsequent segment given a partial alignment [see Fig. 1(C)]. This is how the filter is implemented in MASTER, essentially using prespecified greedy bounds on intersegment distances in place of the provable ones in the original algorithm (function distBounds in Table I). Finally, Heuristic 3 stipulated that backbone  φ/ψ angles of corresponding query and matching residues had to be within 40° of each other, which was also used to a priori limit possible segment alignment locations.

Table IV summarizes the speedups generated by each heuristic (relative to the provable version) and the corresponding match recovery ratios, defined as the fraction of all matches below the specified RMSD recovered by the heuristic. Interestingly, the speedups are generally well below an order of magnitude, while a significant portion of matches is already lost in some cases. In fact, the speedups are most significant in cases with most matches lost. Experimenting with filter stringency showed that increased stringency does provide additional speedups in multisegment cases, but is quite problematic for coverage (data not shown). Although we have not considered all potential heuristics, these results nevertheless suggest that RMSD-based ATFS problem does not have a particularly optimal substructure in terms of properties of partial alignments. In turn, this means that one should generally not expect to gain substantial speedups of ATFS through greedy algorithms without losing considerable fractions of matches. On the other hand, in some cases it may be desirable to incorporate greedy filters as part of the definition of a match, which is enabled by MASTER's heuristic options.

Table IV.

Speedup and the fraction of matches recovered (recovery ratio) as a function of the number of disjoint segments in the query for three heuristic versions of MASTER (RMSD cutoff of 2.0 Å was used in all cases)

Heuristic	Segments
	1	2	3	4	5
Heuristic 1a	1.0 ± 0.03	1.1 ± 0.1	1.3 ± 0.3	1.6 ± 0.3	1.6 ± 0.1
Heuristic 2a	1.0 ± 0.04	1.6 ± 0.5	1.8 ± 0.6	2.2 ± 0.9	3.1 ± 0.8
Heuristic 3a	1.9 ± 0.3	2.6 ± 1.5	2.1 ± 1.0	3.0 ± 2.1	4.2 ± 2.0
Heuristic 1b	100 ± 0.0	100 ± 0.1	97.1 ± 3.0	93.3 ± 10.4	95.6 ± 1.9
Heuristic 2b	100 ± 0.0	98.5 ± 3.5	96.2 ± 4.8	94.9 ± 5.7	89.5 ± 7.6
Heuristic 3b	84.6 ± 19.4	69.2 ± 31.4	70.2 ± 22.9	72.1 ± 23.5	68.8 ± 18.2

^aValues given are average speedup ± standard deviation.

^bValues given are average recovery ratio (%) ± standard deviation (%).

Cases with average speedups over 2 or recovery ratio below 85% are shown in gray.

Designability landscapes are readily obtained from the PDB

We have previously argued that the number of unique natural examples of a structural motif should correlate with its designability.^3,20 We have also shown that mining native structural representatives of a motif can reveal important sequence features necessary for realizing it,²⁰ and we have used this concept in designing novel protein assemblies.¹⁵ To make mining the PDB for designability information a matter of routine requires a fast ATFS method. Furthermore, when comparing different motifs or geometries of the same motif, it is crucial to recover all matches; otherwise, relative statistics become difficult to interpret. MASTER does just this, and to ascertain the practicality of its use in designability analysis, we considered the simple α-helix/β-strand motif shown in Fig. 4(A). The motif is derived from an ideal-like structure de novo designed by Baker and coworkers¹³ (PDB ID 2KL8), and defined three parameters that can be varied to sample its geometry: (1) the separation between the two SSEs (ΔR), (2) the helical phase angle (Δφ), and (3) axial shift of the strand with respect to the helix [ΔZ; see Fig. 4(A)]. All values were defined relative to the original motif in 2KL8, and parameters were sampled to generate 13,671 structures. Specifically, ΔR was varied from −2.0 to 2.0 Å in 21 increments, Δφ was varied from −50° and 50° in 21 increments, and ΔZ was varied from −2 × 1.5 to 2 × 1.5 Å in 31 increments (1.5 Å is roughly the rise-per-residue for an ideal α-helix). Each generated structure was subjected to a search against nrPDB30 via MASTER, recovering all close matches (i.e., those within 0.5 Å CA RMSD and 0.5 Å full-backbone RMSD of the query).

Figure 4.

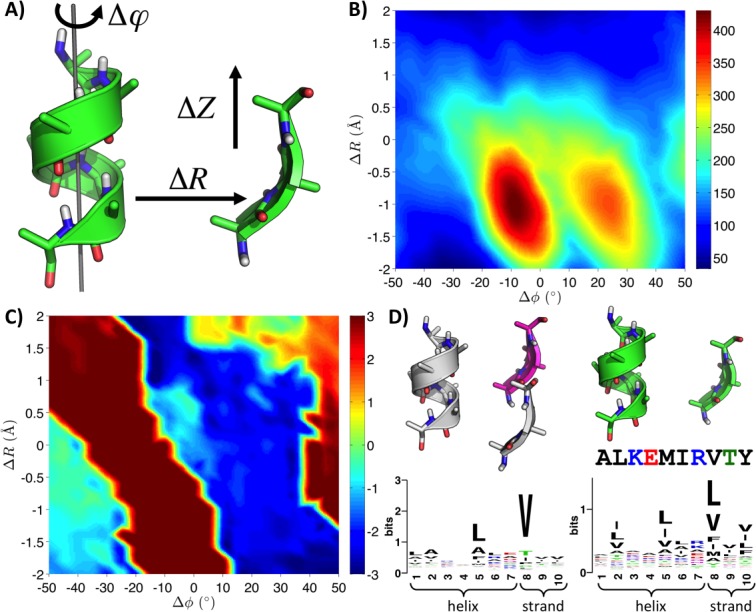
The designability landscape of a simple α/β motif. (A) The fragment was initially excised from PDB entry 2KL8 (residues 18–24 and 33–35) and idealized (to avoid bias in searching) by superimposing perfectly repeating α-helix ( φ/ψ angles of −57°/−47°, respectively) and β-strand ( φ/ψ angles of −135°/135°, respectively) elements onto the corresponding segments (total backbone-RMSD upon superposition was 0.25 Å; ideal version shown). The principal axis of the helix served to define the Z-axis (shown as a gray tube), with Δφ defined by rotating the helix around Z and ΔZ defined by translating the strand relative to the helix in the Z-direction. ΔR was defined as translations along the axis connecting the centroids of the helix and the strand (in the original structure). Positive directions of change are indicated with arrows for all three variables. (B) The number of matches within 0.5 Å in terms of both CA- and full-backbone RMSD, as a function of ΔR and Δφ. ΔZ is optimized for largest number of matches for each point, with the corresponding values shown in (C). (D) Structures and sequence logos corresponding to the two apparent maxima in the designability landscape (left) and the structure closest to the original motif (corresponding to ΔR = 0, Δφ = 0, and ΔZ = 0; right). Images in (B) and (C) are generated via cubic interpolation of the raw counts.

Figure 4(B,C) illustrates the resultant native designability landscape for this α/β motif. Figure 4(B) shows the number of close matches as a function of helical phase and intersegment separation (for each point, ΔZ is chosen to maximize the number of matches). The landscape shows that although the original geometry (corresponding to the origin in the figure) is within the well-designable region of the parameter space, there are two clearly identifiable maxima that exhibit closer approach between the two segments (lower values of ΔR). Figure 4(C) shows the optimal choice of ΔZ for each ΔR/Δφ combination, demonstrating substantial coupling between all three parameters. This reveals that the two pronounced designability maxima correspond to ΔZ values far from that in the de novo designed structure. On the other hand, the region corresponding to ΔR = 0/Δφ = 0 seems to be most designable among those for which optimal ΔZ is around zero. Thus, the parameters of the designed structure are well matched for one another.

In addition to estimating designability, the above analysis also reveals sequence preferences corresponding to different geometric parameters. Figure 4(D) compares sequence distributions of motifs matching either of the two detectable designability peaks as well as the ΔR = 0, Δφ = 0, ΔZ = 0 structure (closest to the designed geometry). Upon examining the structures of the two peaks [Fig. 4(D), top left] it is clear that they actually represent roughly the same packing geometry. The helical phase and ΔZ in the two structures adjust to compensate for one another, so that roughly the same close interdigitated packing of strand residue 1 or 3 [corresponding to the left and right peaks in Fig. 4(B), respectively] is observed in both cases (the slightly higher designability of the left peak is an artifact of limiting the range of ΔZ to [−3; 3] Å). Accordingly, the two structures show very similar sequence preferences [and thus only the sequence logo for the left peak is shown in Fig. 4(D)]. The sequence of the designed structure is in close agreement with its corresponding sequence preferences from the designability analysis [Fig. 4(D), right], with hydrophobic residues appearing at expected positions. The most designable geometries, however, do exhibit stronger sequence biases, especially for a Val or other β-branched amino acids in the strand position packing into the helix.

Important to the practicability of such analysis is its computational cost. We estimate that using just 100 parallel compute jobs, this entire analysis (including all search and postprocessing time) would be completed in under an hour. This performance is reasonable to enable the routine use of such calculations in protein design as a means of validating designed structures/sequences or at the stage of choosing a design template.

Searching with geometric signatures of binding

Binding sites and other functional regions of proteins are often characterized in terms of structural features that are understood to be essential for their function. For example, binding sites of PDZ domains involve a distinctive loop with exposed amides, essential for the accommodation of C-terminal backbone carboxylates of partnering peptides.³⁹ Antiapoptotic and proapoptotic Bcl-2 family members interact through a conserved helix-into-groove structural motif, which forms the basis for their control of apoptosis.⁴⁰ Many other essential structural features of protein modules with specific functions have been characterized. An interesting question is to what extent such structural features may be unique to these functions. For example, is the presence of a PDZ-like binding loop with exposed amides indicative of a PDZ domain? Or, are there grooves structurally similar to those in Bcl-2 family proteins that function in unrelated pathways? Such information would greatly help with the identification and classification of functional modules, as well as for inferring distant evolutionary and functional relationships.

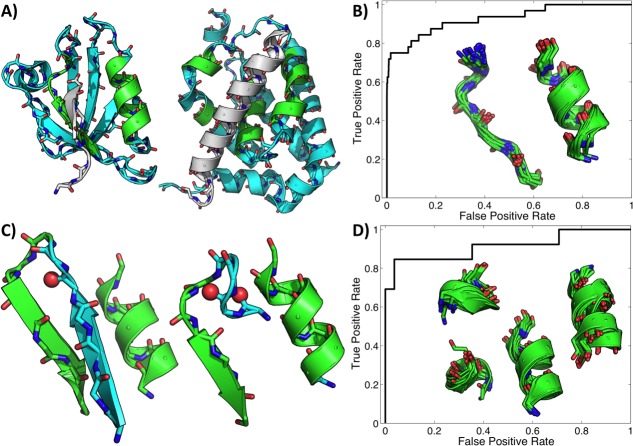
To demonstrate that MASTER can be used to quickly answer such questions, here we isolate binding-site fragments from single representatives of PDZ and Bcl-2 families and ask to what extent the mere presence of similar fragments in PDB proteins indicates membership in these families. For PDZ domains, the isolated motif consisted of the antiparallel α-helix/β-strand arrangement that typically houses bound peptides [Fig. 5(A), left]. Note that PDZ domains exhibit a great deal of variability in this general arrangement,⁴¹ whereas our fragment is based on just a single representative (first PDZ domain of MAGI-1, PDB ID 2I04). Further, the motif appears to be quite simple, comprising short stretches of common SSEs. Thus, it is not immediately obvious that such a motif would contain enough information to be necessarily indicative of PDZ-type binding function. Nevertheless, searching for this motif in nrPDB30 reveals that it is, in fact, highly indicative of PDZ domains. A total of 32 entries in the database contained PDZ domains. Further, by construction of nrPDB30, these 32 domains were highly different (having less than 30% sequence identity with each other). Eighteen out of these 32 (56%) are identified as the top hits by MASTER, without any interleaving non-PDZ domains. In fact, RMSD to the query motif is a nearly perfect classifier of PDZ domains, exhibiting the receiver operating characteristic curve shown in Figure 5(B) with an area under the curve of 0.93.

Figure 5.

Simple binding site fragments from single representatives of PDZ and Bcl-2 family members serve as signatures of function. (A) Shown are a PDZ domain (first PDZ domain of MAGI-1, PDB ID 2I04; left) and a Bcl-2 family member (Bcl-2-like protein 10, PDB ID 4B4S; right) bound to their cognate peptides (gray). The regions excised as potentially representative of the binding function are shown in green. Receiver operating characteristic curves of RMSD to the excised motifs as classifiers of family membership for PDZ and Bcl-2 domains are shown in (B) and (D), respectively, along with a superposition of close hits. Only matches below 2.0 Å were counted as predictions, and this set included all true domains in both cases. Shown in (C) are two common modes of protecting the PDZ binding loop by engaging the otherwise exposed amides in internal hydrogen bonds.

Equally interesting are matches that are close to the motif but are not PDZ domains. These tend to have structural features obstructing access to the site represented by the motif, with two common modes of obstruction illustrated in Figure 5(C). In these structures, the exposed amides of the PDZ binding loop are engaged in intrachain hydrogen bonding, using either α-helical or β-strand geometries. In effect, the proteins' own backbone carbonyls serve in place of the C-terminal carboxylate of a PDZ-bound peptide. This suggests that the PDZ-like α-helix/β-strand motif may have a strong innate binding tendency, such that it needs to be “protected” in proteins where the motif does not serve a binding function.

We performed a similar analysis for the Bcl-2/BH3 binding site, using a fragment from one family representative (Bcl-2-like protein 10, PDB ID 4B4S) as the query [see Fig. 5(D)]. The fragment, excised based on visual inspection of the structure to identify sites important for BH3 binding, consists of four helical segments, two of which contain just four residues. As with the PDZ domain example, here it is not obvious that this simple fragment could uniquely identify Bcl-2-type binding. In this case, nrPDB30 contained 18 highly diverse Bcl-2 family members, nine (50%) of which were identified as top hits by MASTER without any interleaving non-Bcl-2 proteins. Remarkably, the second non-Bcl-2 family hit (PDB ID 2JBY) was a viral protein previously found to mimic the structure and function of antiapoptotic Bcl-2 family members.⁴² As with the PDZ domain fragment, RMSD to the query motif here is also a nearly perfect classifier of Bcl-2 family members, achieving an area under the curve of 0.91 as shown in Figure 5(D).

Topology remodeling

The idea of assembling protein structures from fragments of known proteins has greatly impacted protein design and structure prediction,^10,11,13 and this constitutes an important application of ATFS. In recent work, Baker and coworkers demonstrated the principles of designing ideal proteins.¹³ By this, the authors meant proteins that are minimally frustrated, with all structural features (local and nonlocal) meant to optimize folding to a single unique conformational ensemble. To this end, they applied thorough structural sampling calculations to derive clear rules describing various junction geometries for consecutive SSEs, along with the preferred lengths and conformations of the corresponding connecting regions.¹³ Based on these the authors went on to successfully design five proteins containing six to eight mixed α/β SSEs arranged into different topologies.

An orthogonal method for arriving at structural preferences is mining the PDB. In fact, Baker and coworkers showed that loop length preferences emergent from their computed rules are well reflected in natural proteins.¹³ The continually growing PDB may now allow for the discovery of effective rules “on demand,” without the need for the a priori categorization of structural scenarios. Thus, it may be possible to discover unsuspected rules, as they are needed, during a design calculation (or even potentially a sampling simulation). This would require a fast solution to ATFS. Here, we demonstrate this idea using MASTER.

First, we consider the problem of loop remodeling. Loops and turns are not only crucial design elements for properly orienting SSEs,¹³ but they are also regions frequently targeted for mutations and insertions by bioengineers.^43–45 The problem of understanding the impact of different loop conformations, lengths, and sequences is thus of high relevance. As an example, we consider a loop in one of the proteins designed and structurally characterized by Baker and coworkers [PDB entry 2KL8; see Fig. 6(A)], asking: (1) whether its length is indeed ideal, as the authors suggest, (2) whether the designed sequence is indeed appropriate for it, and (3) whether the loop is a good location for an insertion point. We consider the disjoint motif composed of four α-helical and three β-strand residues up- and down-stream of the turn, respectively [Fig. 6(A)], using MASTER to find all of its close matches. We then categorize the matches by the length of the region between the two segments (matches where the strand comes before the helix in sequence were discarded). Remarkably, in all close matches, the length of the insert is two—exactly the length used by Baker and coworkers. Figure 6(B) shows how the fraction of two-residue inserts in the list of matches varies as a function of RMSD cutoff. Clearly, even at rather generous cutoffs (e.g., 0.8 Å for a seven-residue query), two residue turns still dominate. Further, clear sequence preferences of the turn and the surrounding regions emerge by analyzing close matches, and these agree quite well with the designed sequence [see inset in Fig. 6(A)]. Finally, a simple superposition of close matches reveals the tolerable conformational variation, showing limited flexibility [Fig. 6(A)]. Thus, by applying MASTER, in a matter of several seconds, we learn that the designed loop length and sequence are indeed rather appropriate for the geometry and that this is likely not a good location for insertions.

Figure 6.

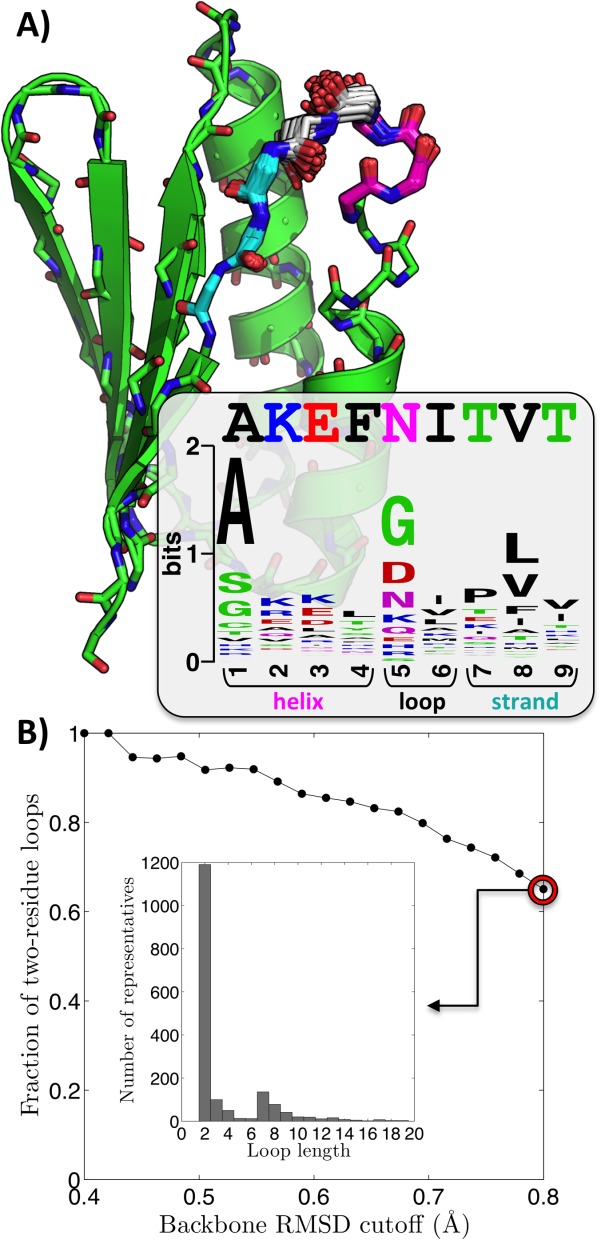
MASTER-based loop remodeling exercise. (A) Helical and strand segments shown in magenta and cyan, respectively, are used together as a query motif to rebuild the loop between them. Shown in gray are loop geometries from the top 100 matches (all under 0.5 Å full-backbone RMSD; five matches with different loop lengths were omitted for clarity; matches were fused with the query as detailed in Materials and Methods section). The inset shows a sequence logo diagram emergent from the sequences of these matches. (B) Fraction of two-residue loop matches as a function of full-backbone RMSD cutoff. The inset shows the distribution of loop lengths up to 20 residues for the least stringent cutoff. Two-residue loops still dominate, though other possibilities exist (e.g., seven-residue loops).

We next consider the problem of rewiring a protein's topology—that is, permuting the order of SSEs while maintaining their relative spatial packing. Circular permutation is a simple example of a topological rewiring, and this technique is often used to engineer protein variants with improved properties or enable a richer diversity of fusion proteins. Being able to rewire a protein's topology in an arbitrary fashion would enable much more flexibility in these and other bioengineering applications. Here, we demonstrate how PDB mining with MASTER can be used to automate the process of topology remodeling.

Continuing with the designed structure above, we remove three of its loops aiming to rewire its topology as shown in Figure 7. Thus, of five pairs of consecutive SSEs in the original topology, only two remain in the new one, whereas the 3D arrangement is unchanged. Given the structure with loops removed [Fig. 7(B)], we consider regions surrounding the desired insertion points (four residues for helical segments and three for strands), using MASTER to identify best ways of joining them. Thus, for each of the three connections to be designed, we quickly learn which connection lengths (and conformations) are most used natively [Fig. 7(D)]. Note that this information implicitly contains the relevant structural rules for segment joining. Picking the closest match from the most representative length for each loop, we can automatically generate the remodeled structure shown in Figure 7(C) (see Materials and Methods section). Further, close matches also provide information on any sequence features necessary to realize the different connection geometries—information crucial at the stage of sequence design.

Figure 7.

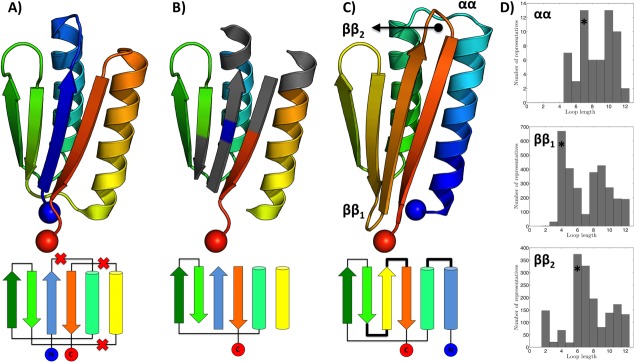
Topology remodeling using MASTER. All structures are colored blue-to-red in the N-to-C terminal direction. (A) PDB entry 2KL8 along with its topology (below). Crossed out connections in the topology correspond to loops marked for deletion. (B) The structure with loops removed. Gray areas designate segments that are used for finding connector regions to bridge gaps in the new topology. (C) Remodeled structure with its topology shown underneath. Blue and red spheres designate N- and C-termini, respectively. (D) Histograms of connector lengths among close matches corresponding to each of the three regions to be bridged. The most likely length, marked with an asterisk for each connector, was chosen to produce the remodeled structure (see Materials and Methods section).

Discussion

ATFS is a problem of growing importance in structural biology. This study presents and thoroughly validates an efficient and provably accurate ATFS approach, MASTER, demonstrating that it can rapidly generate plausible hypotheses with respect to designability and associated sequence features, emergent from the apparent modularity of protein structure in nature. Such insight can be of high value in protein design, structure prediction, and other structural biology applications.

We made several interesting observations with respect to the ATFS problem itself. It seems that despite its theoretically exponential complexity with the number of segments, a provable approach to the problem that uses simple RMSD and distance bounds to limit the search space is highly efficient in practice. The key to this apparent unexpected simplicity of the problem is that, unlike the search space, solution space does not generally grow with the number of segments. In fact, structural intuition suggests that for larger query motifs we expect fewer close hits (given a fixed-sized database). So, during a MASTER search, although having more segments leads to more combinatorial possibilities, it also means more constraints for the match to satisfy and thus a far smaller fraction of the search space surviving as matches. For this reason, given a fixed RMSD cutoff, MASTER search time varies little with query complexity. For example, for an RMSD cutoff of 1.0, the median and mean search times across all 50 queries were 4.4 and 8.1 sec, respectively, with a range from 3 to 30 sec (see Supporting Information Table S1). Of course, it is always possible to use such generous RMSD cutoffs that the solution space would grow uncontrollably as well. In fact, MASTER searches slow down significantly only in cases when the specified RMSD cutoffs result in very many solutions (and typically with larger motifs; see Table II). However, such situations are generally not of practical relevance. As the exact approach was already quite fast, heuristic methods failed to provide significant performance boosts. Further, even fairly conservative heuristic filters, based on local RMSD and intersegment distance deviations, invariably missed many matches (see Table IV). This suggests that though the problem is tractable in practice, it is still difficult and does not have a particularly optimal substructure.

The ability to explore the native variation around a given motif lends itself naturally to exploring plausible conformations. In principle, ATFS should be useful in identifying (and correcting) problematic regions in structural models, building novel templates for protein design, and revealing sequence–structure dependencies. The case studies in this work are demonstrations of some of these capabilities. In particular, we show that mining the PDB provides a detailed characterization of the apparent designability landscape of a small tertiary structural motif (see Fig. 4). Using MASTER, we were able to quickly verify that the geometry of this motif employed in a recently designed structure was indeed well designable, and that its sequence was appropriate for it. We further found that there were regions in the landscape of higher designability, albeit these required drastically different axial alignments. Given the high utility of such information to computational protein design, we think designability mapping will be an important application of ATFS.¹⁵ The provably correct aspect of MASTER is particularly important for this application, as it enables the unbiased comparison of natural abundance as a function of geometry.

Examples discussed in this work revolve around small tertiary motifs (e.g., Fig. 2). But do these carry sufficient structural context to be relevant? Using MASTER, we demonstrated that surprisingly small motifs can be indicative of function. For example, the typical α-helix/β-strand arrangement in the PDZ binding site seems to be highly characteristic of PDZ domains [Fig. 5(A,B)]. In fact, in essentially all cases where a similar motif occurs outside of the PDZ domain, the binding site is “protected” by a different part of the structure [Fig. 5(C)]. Similarly, for Bcl-2 family proteins, we found that a small motif consisting of four short helices is highly indicative of Bcl-2:BH3 binding function, even identifying a viral Bcl-2 mimic [Fig. 5(D)]. Thus, on the one hand, small tertiary motifs seem to be relevant for structure and function and on the other they are likely to be well sampled within the PDB at its present size. Statistics on such motifs, revealed by ATFS, may thus become a rich source of information for problems of structural biology.

To further explore the utility of ATFS for designing proteins, we consider problems of loop remodeling and topology rewiring (Figs. 6 and 7). We show that using MASTER it is possible to complete missing pieces of an existing structure in a way that respects any necessary natural structure and sequence rules. Importantly, these rules are discovered automatically, as needed. For example, by considering a single loop in a structure previously engineered by Baker and coworkers,¹³ we quickly verified that the chosen loop length is indeed quite optimal, with very few other options available (see Fig. 6). In fact, one might wonder what it is about the segments being joined [four helical and three strand residues; Fig. 6(A)] that so strongly constrains possible connector geometries and lengths. An expert structural biologist may detect upon visual inspection that the search query is two residues short of a turn in its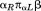 conformation,⁴⁶ and may proceed with designing such a structure accordingly. However, by mining the PDB, this rule and others can be discovered automatically, without the requirement of knowing a priori what the relevant structural features to look for might be. We further show that such insight can be used to remodel the topology of an existing structure in an automated fashion (Fig. 7). MASTER quickly identifies the most structurally appropriate means of wiring the existing SSEs so as to meet the desired topology, providing optimal connection lengths, conformations, and necessary sequence features. Importantly, these insights do not replace the need for accurate and predictive physical models of structure. Instead, results of ATFS-based mining should be seen as hypotheses generated on the basis of natural observations, to be verified experimentally or with accurate physical calculations. On the other hand, the ability to generate such plausible hypotheses easily on the fly is quite appealing for practical engineering or prediction applications.

Conclusions

Here, we argue that ATFS is a highly valuable tool for many problems in structural biology, but most applications require rapid searches. MASTER, a fast and provably correct ATFS engine, has the potential to address many existing needs. Specifically, we demonstrate that it can be used to characterize the apparent designability landscape of structural motifs, generate hypotheses on structural rules to aid in protein design, and establish connections between sequence and structure. Although it is certainly possible to further improve upon the performance of MASTER, importantly we have shown that despite the combinatorial complexity of the underlying problem, in practice search times are rather limited for realistic search criteria. Thus, given the broad relevance of ATFS to structural biology, MASTER and related search tools should significantly advance our ability to design and model protein structures.

Supplementary Material

Supplementary material is in supplement.docx, and it includes a detailed comparison of MASTER and MaDCaT running times (Supporting Information Fig. S1) and the listing of all running times and numbers of matches found for the main MASTER timing study (Supporting Information Tables S1 and S2; study results summarized in Table II).

Materials and Methods

RMSD bounds

Given two lists of atoms A and B of the same length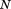 (e.g., CA traces of two protein structures), ordered according to the desired alignment, their best-fit RMSD is:

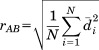(2)

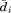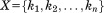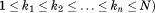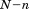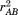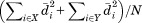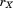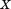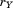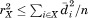where is the distance between the-th atom of A and B after the two structures are optimally superimposed. If we split each structure into two substructures, one with atoms and indices ( and the other with atoms and indices, we can write as. Let denote the RMSD upon optimal superposition of substructure from A and B, and denote the same for substructure. We can then say that and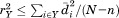. Combining this with Eq. (2), we get:

(3)

If we suppose that the overall RMSD of A and B must be below some specified cutoff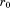 (i.e.,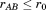), we can derive an upper bound for the individual RMSD of substructure:

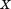(4)

where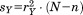 is the sum-squared residual upon optimal superposition of substructure from A and B.

In MASTER, we apply this bound in three scenarios. When evaluating the similarity between the-th query segment and its candidate match by itself, we assume the remaining part of the alignment to be perfect (i.e., the remaining residual is zero, so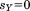). In this case, the upper bound on the RMSD of the-th,, is:

(5)

where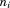 is the length of the segment and 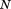the length of the entire query structure. We can also evaluate the similarity of the-th segment and its candidate match in the context of the previously aligned portion. In this case, the remaining unaligned portion is again assumed to have a perfect match, so that the residual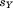 is bounded from below by the sum-squared residual from the previous alignment, and thus an upper bound on is:

(6)

where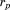 and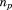 are the RMSD and total length of the previous alignment, respectively. Finally, when adding the-th segment to a previous alignment of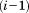 segments, we can derive a bound for the total RMSD of the resulting partial alignment,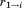, by once again assuming the unaligned portion to have a perfect match, so:

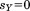(7)

where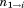 is the total length of the partial alignment that includes segments 1 through.

Intersegment distance bounds

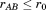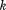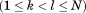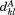Given the same A and B as above (and the same requirement), lets take and to be any two atoms in these structures. Let and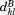 denote the distances between atoms 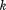and in A and B, respectively, and let us derive a limit on how different the two distances may be. We apply the bound from Eq. (4) by defining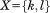 and thus:

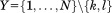(8)

where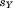 is the sum-squared residual from the optimal alignment of A and B without atoms 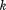and. Because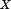 contains just two atoms, 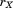is quite clearly simply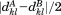. Combining this with the above equation, we obtain the desired bound:

(9)

In MASTER, we use this relationship to limit the admissible range of distances from the central residue of the last added-th segment to candidates for the central residue of the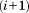-th segment. Thus, here 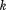and represent the central residues of the two segments, and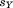 is the total accumulated residual without these two atoms. We assume that the presently unaligned portion may have a perfect match, and so the only contribution to 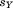comes from previously aligned atoms except the central residue of the last added fragment. Thus, the bound we apply is:

(10)

where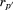 is the optimal RMSD of superimposing the previously aligned segments onto their corresponding matching regions without the central residue of the-th segment and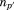 is the length of this alignment (i.e.,).

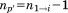MASTER database

The present implementation of MASTER uses a disk-based database. Each structure in the database has a corresponding file (a Protein Data Structure or PDS file), composed of several sections with different types of information. A strategy we have adopted throughout is to include “navigation” information within the file such that its different regions can be reached quickly. For example, the start of each file is a header that contains offsets for starting points of its composite sections, such that each can be reached with a single seek operation. Besides sections with atomic coordinate information (i.e., a section with CA atom coordinates and another with strings representing full ATOM records from the source PDB file), the files also store certain auxiliary precomputed data, which simplify the search. Some of these sections are detailed below.

Distance distribution

This section stores one record for each residue in the structure. The record for residue is generated by binning the distances from to all other residues in the structure, with each bin storing the list of residues within the corresponding range of distances (CA-to-CA distances are used; bin width and the maximal recorded distance are adjustable parameters with 5 and 25 Å, respectively, used in this study). Because the offset to each bin for each residue is stored in the header for this section, one can navigate to and read the list of residues within an arbitrary bin from an arbitrary residue with a handful of seek operations. Further, because several adjacent bins are often of interest, storing them consecutively in the file takes maximal advantage of block-based reading and disk caching.

Backbone dihedral angles distribution

To enable the rapid application of the backbone dihedral-based heuristic filter, we precompute and store the φ/ψ dihedral angles for each residue. To enable rapid lookup of this information, following an approach similar to that with distances, we create a series of bins for each type of dihedral angle (bin width is adjustable; 10° used here). Each bin stores the list of residues, with values of the dihedral angle falling within the corresponding range.

Central residue

For PDS files corresponding to query structures, we store the central residue of each segment and its dihedral angles. The central residue is defined as the residue with the lowest maximal distance to other residues in the structure. It has the property that a sphere centered at this residue can circumscribe the entire structure with the smallest possible radius, compared with spheres centered at other residues.²⁹

MASTER availability

The C++ source code for MASTER can be found at http://grigoryanlab.org/master and is available under the GPL v3.0 license.

Single-segment brute-force search

We have found that an efficient implementation of the Kabsch algorithm³⁸ can perform over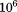 superpositions per second on a modern CPU (e.g., Intel Xeon 2.7 GHz) with structures of up to ∼40 residues (more for smaller segments). In our experience, the competing QCP approach⁴⁷ gives a similar performance. The PDB contains ∼7 × 10⁶ protein residues (when culled at 50% sequence identity); this means that a brute-force single segment search would take on the order of a second to several seconds on a single processor. MASTER performs single-segment searches (and alignments of the first segment in multisegment queries) in a brute-force manner, such that the speed of RMSD calculations provides a lower bound on its performance. The observation that multisegment searches frequently complete in roughly the same amount of time as single-segment ones suggests that the combinatorics of ATFS is handled well by MASTER and is often not the bottleneck. Thus, improvements in the speed of RMSD calculation would be expected to significantly improve not only single-segment, but also on multisegment searches.

Speed test

To measure MASTER's performance, each structure shown in Figure 2 was used as a query to search against nrPDB30 under six different RMSD cutoffs: 0.4, 0.6, 0.8, 1.0, 1.5, and 2.0 Å. Each query/RMSD cutoff combination was attempted three times, in random order of different combinations, on a single 2.7-GHz Intel Xeon processor with the database stored on a local disk. Total search times (i.e., wall times) were averaged over the three runs for each combination (standard deviations were also computed, but were negligible in all cases) and were used for analysis. CPU times (user and system) were also recorded and averaged, with the difference between wall and CPU time treated as an estimate of I/O time.

MASTER searches

Where matches are defined in terms of both CA and full-backbone RMSD, MASTER was first run to recover all hits below the given CA RMSD value, following which hits above the given full-backbone RMSD cutoff were discarded. To build nrPDB30, we downloaded the weekly BLASTClust³⁷ clustering of the PDB as of July 1, 2014, at 30% sequence identity, retaining the PDB entry of the first representative from each cluster. Of these, protein-containing entries solved by X-ray crystallography to a resolution below 2.6 Å constituted the final search database, with a PDS file generated for each corresponding biological entry. To limit the size of some very large biological entries (e.g., viral capsids), a feature was implemented in MASTER enabling the removal of structural redundancy (and near-redundancy) prior to the creation of a PDS file, while guaranteeing to capture all unique chains and unique interchain interfaces. For the sake of consistency, when comparing running times with MaDCaT, the same redundancy-removed biological entries were used to create the MaDCaT search database.

For designability and topology remodeling applications, the number of matches reported refers to the number of matches with unique matching-region sequences. Speedup in Tables III and IV is measured as the search time of the modified run (i.e., a run limiting the number of matches or a heuristic) divided by the search time of the standard exact version of MASTER.

Loop stitching

Loop geometries in Figure 6(A) and the topologically remodeled structure in Figure 7(C) were generated by fusing query regions with closely matching structures having desired insert lengths. To this end, the aligned regions between queries and matches were linearly recombined (after optimal superposition), enabling a transition from the designed structure to the identified PDB fragment. Specifically, the linear recombination was applied to non-hydrogen backbone atoms only, with a scale factor that itself varied linearly along the main chain. That is, the match and query were scaled by 0 and 1, respectively, at the termini farthest from the insert, and by 1 and 0, respectively, at termini immediately adjacent to the insert; the scale factors were linearly interpolated in between. Because only very close matches were used for such fusing (full backbone RMSDs ranged from 0.2 to 0.4 Å), this simple solution led to good backbone geometries of the fused structures.

Supporting Information

Additional Supporting Information may be found in the online version of this article.

Supplementary Information