The Intergenerational Effects of Changes in Women's Educational Attainments

Abstract

The effect of the socioeconomic characteristics in one generation on the socioeconomic achievement of the next generation is the central concern of social stratification research. Researchers typically address this issue by analyzing the associations between the characteristics of parents and offspring. This approach, however, focuses on observed parent–offspring pairs and ignores that changes in the socioeconomic characteristics of one generation may alter the numbers and types of intergenerational family relationships created in the next one. Models of intergenerational effects that include marriage and fertility as well as the intergenerational transmission of socioeconomic status yield a richer account of intergenerational effects at both the family and population levels. When applied to a large sample of Indonesian women and their families, these models show that the effects of women's educational attainment on the educational attainments of the next generation are positive. However, the beneficial effects of increases in women's schooling on the educational attainment of their children are partially offset at the population level by a reduction in the overall number of children that a more educated population of women bears and enhanced by the more favorable marriage partners of better educated women.

The study of intergenerational social mobility is centrally concerned with estimating the effects of the positions, statuses, and resources of a family on persons born and raised in the family. By showing who gets ahead in a society and the benefits to children of improvements in their parents' socioeconomic positions, these effects cast light on the persistence of social hierarchies, the rigidity of stratification, and the mechanisms of social change. For example, in a developing society, it is important to know the possible effects of parents' educational attainment on the education and general well-being of their children. These effects shape patterns of educational opportunity within the society and show the benefits to children of efforts to improve the education and socioeconomic level of their parents.

In this article, we argue that most studies of intergenerational mobility and the effects of parents on children offer an incomplete assessment of the intergenerational impact of socioeconomic characteristics. We propose alternative models that provide improved estimates of intergenerational effects. To elucidate these ideas and models, we focus on the effects of women's educational attainment on the education of the subsequent generation, although our argument applies to all aspects of family background that affect the life circumstances of the next generation. We show how to estimate the effects of changes in women's educational attainments in the maternal generation and how these effects work through marriage, fertility, and intergenerational transmission. This enables us to go beyond most other research, which relies on estimates of the effects of mothers' schooling that ignore the effects that accrue through changes in family formation and family size.

Researchers have explored social background effects and social mobility extensively, including variations across time, place, and dimensions of socioeconomic inequality (e.g., Erickson and Goldthorpe 1992; Featherman and Hauser 1978; Hout 1988; Mare 1981; Shavit and Blossfeld 1993; Treiman and Ganzeboom 1999). However, almost all discussions of intergenerational mobility give an incomplete account of how generations of men and women affect the socioeconomic attainment of subsequent generations. To see how parents' characteristics affect those of their offspring, it must be possible, in principle, to change those characteristics to yield an outcome different from what would otherwise occur. But conventional mobility studies are ill suited for assessing the effects of this type of intervention because these analyses typically measure the effect of parents' statuses on offspring's outcomes using existing parent–child combinations instead of accounting for changes in family size and structure that may intervene between the parent and offspring generations.

The study of observed family relationships fails to account adequately for the impact of the intervention on the formation of families. Existing mother–father or parent–child pairs depend on previous marital and fertility choices. However, changing the socioeconomic position of individuals in the parents' generation also may change their marital and fertility preferences and opportunities, which could, in turn, affect outcomes in the next generation as well. Thus, even if random assignment of children to families were somehow achieved, the resulting inferences from otherwise conventional approaches to the study of intergenerational relationships still may be of questionable value for practical and theoretical questions about the impact of family background on the next generation. Even in descriptive studies of intergenerational relationships, conventional approaches yield incomplete results. A more encompassing social and demographic model that shows the complex relationships between the characteristics of successive generations is needed for either causal inference or adequate description.

A New View of Intergenerational Effects

The intergenerational effects of changes in the socioeconomic characteristics of adults occur partly through individual- and family-level variables that intervene between those characteristics and the characteristics of the offspring generation (e.g., Blau and Duncan 1967; Jencks et al. 1972). Research on educational attainment and the transition to adulthood has focused on the role of social psychological factors (e.g., Sewell, Haller, and Portes 1969), family size (Blake 1989; Blau and Duncan 1967), family structure (e.g., Duncan and Duncan 1969; McLanahan and Sandefur 1994), the childrearing behavior of parents (e.g., Astone and McLanahan 1991), and families' strategic responses to incentives (e.g., Breen and Goldthorpe 1997) in efforts to show how families transmit their unequal positions, statuses, and resources to subsequent generations. Throughout this rich body of intergenerational research, these mechanisms are inferred from observed characteristics of parents and children in existing families. In this article, we refer to this approach as the standard approach. By themselves, these effects depend on existing mother–father and parent–child relationships. In the study of intergenerational occupational mobility, for example, researchers typically focus on the associations between the occupational classifications of fathers and sons. These relationships are based on observed father–son pairings.

Intergenerational effects, however, also may occur through mechanisms that alter the numbers and types of families in which children are raised. If changing the characteristics of people alters their propensity to marry, the types of persons they marry, whether they survive through their childbearing years, or the number of their children who survive to adulthood, these mechanisms will alter the distributions of socioeconomic outcomes in subsequent generations. These full effects, however, cannot be inferred from existing mother–father and parent–child relationships alone. A more complete analysis of the intergenerational reproduction of inequality requires that both the effects of families on children and the processes by which these families are formed be considered.¹

The Effects of Increases in Women's Educational Attainment

Consider the effect of a mother's educational attainment on the educational attainment of her child. Mother's schooling often is viewed as a key determinant of her children's welfare. In populations with low average maternal education or a large gap in education between men and women, it may be possible to improve the lives of both women and their children by removing barriers to their advancement in school (e.g., Caldwell 1986; King and Hill 1993; Schultz 2001; Summers 1994).² If a mother's attainment is a cause of her child's attainment, then one may ask: What is the effect on children of a policy that changes the schooling of an individual woman, an entire cohort of women, or some targeted subgroup of women?

This question raises important research design issues. Regression estimates based on samples of offspring, which are the most common tool for answering this type of question, can at best show the impact of changing a woman's schooling after she has given birth to a sampled child and, if the father's or other family characteristics are controlled in the analysis, after her marriage. Even if all important confounding family factors are controlled, these estimated effects may be quite unsatisfactory for many purposes, including their use to assess the effects of interventions in women's lives on subsequent generations. Women complete most of their schooling before childbearing and, in most societies, before marrying the fathers of their children. A change in a woman's educational attainment may alter whether, when, and whom she marries; the number and timing of the children she bears; how many of these children survive to adulthood; and the education of her surviving children. Thus, the estimated impact of a mother's education depends on whether it is assumed that she has already given birth, has not yet given birth but has formed a union with a child's (potential) father, or has not yet taken a partner.

It is impossible to discern the full impact of changing a woman's educational attainment without considering these demographic mechanisms. At the individual level, marriage and fertility are intervening mechanisms between a woman's educational attainment and the attainment of her children. At the population level, the impact of a change in the average level or the distribution of women's schooling must take into account both the intergenerational correlation of educational attainments and also the changes in population composition that result from the population renewal process. These processes alter the relative numbers of children who achieve various levels of educational attainment. For a given distribution of women's educational attainment and effects of mothers on children, the resulting distribution of offspring's schooling may differ between populations that have different patterns of differential fertility by mother's schooling. Thus, to assess the impact of a change in women's education in the parents' generation on the distribution of education in a later generation, it is necessary to examine its separate effects on marriage, childbearing, and the educational attainment of children.

In addition to fertility and marriage, differences among women in their timing of fertility, their rate of marital disruption, their rate of survival through the childbearing years, and their children's rate of survival to adulthood also are potentially important demographic factors that contribute to intergenerational reproduction. These mechanisms often depend on women's schooling as well, and are part of a full accounting of the intergenerational effect of women's educational attainment. In most societies, however, the fertility and marriage processes emphasized in this article are likely to be the most important demographic mechanisms governing the intergenerational impact of women's schooling. Although we have excluded the effects of fertility and marriage timing as well as differential mortality from our empirical analyses to make our models more tractable, each of these can be added to the models presented in this article.

Differential Fertility

An association between women's educational attainment and their levels of fertility is observed in virtually all societies (e.g., Bledsoe et al. 1999). The most prevalent relationship is a negative correlation, typically interpreted as arising from delays in marriage, improved labor market opportunities, increased use of contraception, and a weakening of women's traditional childbearing roles. Yet the strength and form of this relationship vary considerably across societies and over time. Some societies exhibit positive associations between women's educational attainment and their number of children ever born, whereas others have a nonmonotonic pattern in which women with some primary schooling have higher fertility rates than those who have either no education or secondary and tertiary schooling (Diamond, Newby, and Varle 1999; Jeejeebhoy 1995). These alternative patterns may reflect relatively low levels of family resources, poor health, or poor marriage prospects for women with very low levels of educational attainment.

For a given pattern of differential fertility, the impact of a change in the distribution of women's educational attainments occurs at two levels: the individual/family level and the population level. The well-being and eventual socioeconomic attainment of children in a family may be affected by variation in their mother's level of fertility because of the differential advantages and disadvantages associated with variations in the number of siblings. In most developed and low-fertility societies, children's attainments typically vary inversely with number of siblings, either because of the more severe resource constraints experienced by larger families (Blake 1989) or because of the trade-offs that parents make between having larger families with relatively lower social, economic, and cultural resources for each child and having smaller families with relatively higher resources for each child (Becker 1991). In less developed and higher fertility societies, the relationships between number of siblings and children's achievements are varied. Although having many siblings may limit the resources available to a child, it also may enhance family wealth and provide access to broader social networks for children. As a result, the association between number of siblings and children's schooling may be weak or even positive in these contexts (Lloyd 1994; Maralani 2004; Mueller 1984; Shavit and Pierce 1991). Whatever the context, a change in a woman's educational attainment may affect the educational attainment of her offspring because it may change her eventual fertility, her children's number of siblings, and the family resources available to each child.

Differential fertility also affects changes at the population level by altering the numbers and characteristics of male–female and mother–child relationships. Within a population, the effect of a change in the distribution of women's education on the educational attainment of the next generation may depend on whether this increases the relative numbers of children born to highly or less educated women. If fertility and educational attainment are negatively correlated, the beneficial effects of increases in women's schooling are dampened by the tendency of more educated women to have fewer children than their less educated counterparts.³ Thus, although an improvement in women's average educational attainment may benefit whatever children they bear, they may bear fewer children overall. This implies that the individual- and population-level effects of an improvement in women's schooling may be offsetting.

In contrast, if the relationship between education and fertility is nonlinear, the size of the effect of increasing women's education depends on where in the education distribution changes occur. For example, if fertility follows a nonmonotonic pattern in which women at intermediate levels of schooling have the highest birthrates, efforts to improve the attainment of those with little or no schooling to an intermediate level may have a twofold benefit for the next generation. This cohort of more educated women will bear more children, and these children will be more educated. In contrast, efforts to move women from intermediate to high levels of schooling may have offsetting effects at the individual and population composition levels. Thus, differential fertility among women with varying educational attainments may lead to a mixture of individual effects that depend on particular family relationships and population-level effects that work through relative numbers of different family sizes. A full assessment of intergenerational effects must take both of these processes into account.

Marriage and Assortative Mating

Marriage also affects the educational reproduction process in several ways. For individual families, the mother's marital status and the father's educational attainment affect the educational attainment of their offspring. A change in the characteristics of an individual woman may alter her opportunities and incentives for the timing of her marriage, the type of partner she marries, and the stability of her marriage. An increase in her attainment typically raises the educational attainment of the man she marries, which further increases the advantages that accrue to the couple's children.

At the population level, marriage alters the education distribution of the next generation both directly through changes in the joint distribution of mothers' and fathers' schooling and indirectly through its effect on levels and differentials in fertility. The size and direction of this effect, however, depends on the organization of the marriage market and how the men's educational distribution changes relative to improvements in women's educational status. If improvements in women's schooling are accompanied by increases in men's schooling as well, then the association between husband's and wife's schooling is unlikely to change. Both fathers and mothers become more educated, on the average, and the offspring generation benefits from average improvements in both parents' educational attainments. But women's educational gains may not be matched fully by corresponding gains of men if, for example, women benefit from targeted government subsidies or experience other improvements in their lives not enjoyed by men. In this case, the association between wife's and husband's educational attainments may change because at any given level of education, women may marry men with somewhat lower average attainment than would have been available had the number of more educated women remained unchanged. The resulting change in the joint distribution of mothers' and fathers' schooling and its impact on their children's schooling will depend on the shape of the men's educational distribution and where in the distribution of women's schooling the greatest changes occur.

The aggregate effect of marriage also affects the next generation through fertility. If nonmarital fertility is negligible, and highly educated women are relatively more likely to remain single or marry later, an increase in women's schooling reduces fertility and dampens the aggregate benefit for the next generation. Similarly, patterns of educational resemblance between women and their husbands may modify differential fertility patterns in a complex way, depending on the pattern of fertility among couples with varying levels of wives' and husbands' schooling. If the educational attainments of wives and husbands are strongly associated, an increase in women's average attainment may enhance or suppress the effects of women's educational differentials in fertility, depending on how the attainments of wives and husbands jointly affect the numbers and timing of children ever born.

Related Literature

Our effort to embed intergenerational mobility in a demographic model that includes fertility and marriage builds on prior research. Over the past 50 years, researchers have attempted to examine the implications of differential fertility for the study of social mobility and, conversely, to incorporate intergenerational mobility and assortative mating into the study of differential population growth (e.g., Duncan 1966; Mare 1997; Matras 1967; Mukherjee 1954). We extend this research by using a model of socioeconomic and demographic reproduction to develop new methods for estimating the effects of family socioeconomic background on educational attainment. That taking account of marriage and fertility may alter assessments of intergenerational effects is only implicit in these prior studies. By modeling these processes explicitly, we link standard sociological efforts to determine the effects of family background on achievement with formal demographic studies of intergenerational processes.

Empirical Context: Women's Education and Demographic Change in Indonesia

We investigate these issues using data for Indonesia, the world's fourth most populous nation. Indonesian women have historically obtained relatively low levels of schooling, although education levels have increased markedly in recent cohorts. Moreover, the historically large gap in schooling between men and women has all but closed in recent decades as a result of extensive school expansions, gender-specific government policies, and expansions in women's socioeconomic welfare. Indonesia has undergone huge demographic changes during the past 30 years, including massive declines in fertility and mortality rates and substantial rural-to-urban migration. Total fertility rates have declined from 5.6 children per woman in 1971 to 2.6 children in 1999 (Badan Pusat Statistik, Republik Indonesia 2004). Women's mean age at first marriage has increased from 19.3 years in 1971 to 21.6 years in 1990 (Jones 1994). Despite these changes, marriage remains nearly universal. In 1997, nearly 80 percent of 25- to 29-year-old women, 91 percent of 30- to 34-year-old women, and 96 percent of 35- to 39-year-old women were married (tabulations from the Indonesia Family Life Survey, described later in this article).

During this period, schooling levels and sex differences in schooling have changed dramatically as well. For example, 27 percent of men born from 1930 to 1934 had no formal schooling, and 92 percent had no more than primary school. Of the women in this cohort, 56 percent had no formal schooling and 97 percent had no more than primary school. In contrast, only 5 percent of men born from 1960 to 1964 had no formal schooling, and 36 percent had more than primary schooling. For women, these corresponding percentages were 10 and 23 percent, respectively (Cobbe and Boediono 1993). More recent cohorts show still higher levels of educational attainment and smaller differences between men and women.

Fertility in Indonesia varies by women's educational attainment, although it does not follow a simple inverse relationship. Among Indonesian women in the 1970s, fertility was highest for the women with a primary education, lowest for the small proportion of women with postsecondary schooling, and at an intermediate level for the women with no schooling or secondary schooling (Hirschman and Guest 1990). This nonmonotonic pattern has persisted in more recent years, albeit in a somewhat attenuated form, as shown later.

Although our approach is adaptable to any population, Indonesia is a good context for this research. Its comparatively low levels of educational attainment and historically large gender gap in attainment make it a realistic setting for considering the effects of hypothetical interventions to raise the educational attainment of women and improve the life chances of their children. Moreover, its near universal marriage, moderate mortality, and low nonmarital fertility rate make the relatively simple models of intergenerational effects considered in this article more realistic for the Indonesian population than for populations with either very high parental mortality rates during the childbearing years or high nonmarital fertility rates.

Models for the Intergenerational Effects of Women's Educational Attainment

We focus on how a population of women with varying amounts of schooling produces a generation of offspring who also varies in their educational attainments. We take into account three processes: (1) the intergenerational transmission of educational status; (2) differential fertility, as affected by mother's and father's education; and (3) marriage, focusing on whom women of varying education levels are likely to marry. Most research on intergenerational mobility is focused exclusively on 1, but 2 and 3 also are essential parts of the reproduction process.

In developing our models, we make a number of simplifying assumptions. We assume that all women marry. We ignore divorce, remarriage, mortality, and the timing of fertility and marriage, and assume that everything happens all at once for a given cohort or, equivalently, a generation at a time. We also ignore intercohort changes in the processes that we study. That unmarried women bear and raise children is obviously true in general, but occurs at such a low rate in Indonesia that is it safely ignored in this analysis. The remaining assumptions serve to show the workings of several basic demographic processes. These additional demographic effects, however, can be incorporated into the approach discussed in this article, albeit at the cost of increased complexity.

Our approach provides a way to assess the contribution of women and mothers to the reproduction of the population, but allows assortative marriage to affect fertility and intergenerational transmission. It is not a two-sex model because the marriage market is female dominated. For the purpose of estimating the model, we assume that whatever kind of man a woman wants, with respect to his schooling, she can get. As discussed later in this article, however, in estimating the effects of a change in women's schooling, we also explore the implications of alternative assumptions about how men's educational attainments change in response to improvements in women's status.⁴

We let C_j be the number of persons in the offspring generation with education level j. W_i be the number of women in the mother generation with education level i, and r_jk|i be the number of children who attain education level j, whose fathers have education level k per woman who has attained education level i. The term r_jk|i stands for the rates at which women at given levels of educational attainment marry men and produce children with various levels of educational attainment. These rates incorporate the effects of marriage, fertility, and intergenerational transmission on intergenerational reproduction. We let i = 1, …, 5; j = 1, …, 5, k = 1, …, 5. Thus, education has five discrete, but ordered levels. Then

$$C_j=\sum _{i=1}^5\sum _{k=1}^5{r}_{jk|i}{W}_i.$$ (1)

Given r_jk|i, we can compute the expected number of children with education level j born to a woman with education level i. If the processes governing r_jk|i are time invariant and we know the education distribution of women at a given date, then this equation can project the education distribution of offspring in successive generations. We also can simulate what would happen to the distribution of children's schooling (C_j) if the distribution of women's schooling (W_i) were modified.⁵

We can express how marriage, fertility, and intergenerational transmission affect r_jk|i as follows:

$$r_{jk|i}=p_{k|i}^H{r}_{ik}{p}_{j|ik}^C,$$ (2)

where $p_{j|ik}^C$ denotes the probability that a child with a mother at education level i and a father at education level k will attain education level j. The term r_ik is the expected number of children born to women in education category i who are married to men in education category k, and $p_{k|i}^H$ is the probability that a woman in education category i will be married to a man in education category k. We compute the components of Equation 2 as follows. We estimate the child's attainment probabilities $p_{j|ik}^C$ as an ordered logit model that includes the mother's and father's educational attainments and the child's sex as covariates. We compute the fertility rates r_ik using a Poisson regression model in which the covariates include the mother's and father's educational attainment. We estimate marriage probabilities $p_{k|i}^H$ using an ordered logit model in which the covariates include categories of women's educational attainment.⁶

These models are recursive in that (a) mother's schooling precedes marriage and father's schooling, which precedes fertility, which precedes offspring's schooling, and (b) the unobserved factors that affect the three processes are assumed to be independent. Thus, it is possible to estimate each of the three models separately. This specification assumes that individuals and families are homogeneous within categories of the independent variables included in the models, and that no common unmeasured variables affect marriage, fertility, and intergenerational transmission. Although recursive models are used in most studies of stratification processes, the assumption of uncorrelated errors often is violated. Extensions of our models that account for these complications are discussed at the conclusion of this article.⁷

Data and Methods

Indonesia Family Life Survey

Our analyses are based on the Indonesia Family Life Survey (IFLS), which first interviewed a longitudinal household sample in 1993, then followed up in 1997, 1998, and 2000. The IFLS is a comprehensive socioeconomic and health survey containing detailed information on demographic and socioeconomic characteristics, household economy, health, fertility and marriage histories, and child cognitive and health assessments. Almost everyone in the household was interviewed directly, although when necessary, the survey collected information by proxy. The survey represents an area that includes 83 percent of Indonesia's population. We use the public domain data from the 1993 and 1997 waves of the IFLS. The surveys achieved very high response and follow-up rates: 93 percent of the sampled households were successfully interviewed 1993, and 94 percent of the households interviewed in 1993 were reinterviewed in 1997. For documentation of the IFLS, see Frankenberg et al. (2000).

Our analytic samples include ever-married female respondents ages 41 years and older in 1997 and their adult children. For 1993 respondents not interviewed in 1997 (either because they died between the two waves or because the 1993 household was not located in 1997), we use information from 1993 whenever possible to retain these cases in our sample. For each ever-married woman, we assemble a full count of all live births, the schooling level of each living child age 20 years or older, and the schooling of her husband (either current or previous). Our analysis includes only observations with complete data on woman's, husband's, and children's schooling as well as woman's age, marital status, and fertility. Our samples of women and children are restricted in age to capture completed fertility and completed schooling. Our analyses use two interdependent subsamples of IFLS women and their offspring, described in the following section.

Husb and's Education/Fertility Sample

This sample includes 3,938 ever-married female respondents ages 41 years and older. These observations are used to assess the effects of women's educational attainment on the educational attainment of the men they married and their number of children ever born. For the approximately 30 percent of ever-married female respondents who married more than once, we use the educational attainment of the husband to whom she was married for the longest period between her ages of 15 and 40 years.⁸ When weighted, this sample is intended to represent ever-married Indonesian women ages 37 years and older in the target sample areas of the IFLS in 1993.⁹

Intergenerational Transmission Sample

This sample includes 10,820 offspring ages 20 years and older of ever-married female respondents ages 41 years and older. Some, but not all, of these offspring were themselves IFLS respondents. The offspring have a median age of 30 years, with an interquartile range of 25 to 36 years. The mothers of these sampled children are a subsample of the women included in the husband's education/fertility sample described earlier, namely those who had at least one surviving child age 20 years or older with valid information on the necessary variables. This corresponds to 3,236 of the 3,938 women included in the husband's education/fertility sample described earlier. Women with more than one eligible child contribute multiple observations to this offspring sample. When weighted, this sample is intended to represent approximately the offspring ages 20 years and older of ever-married women in the target sample areas of Indonesia in 1993.

For each respondent, the IFLS asks the highest level of school attended (no school, elementary, junior secondary, senior secondary, postsecondary), which is the education classification used in our analyses. Table 1 summarizes the education distributions of women, husbands, and children for each of the relevant samples. These distributions show the sizable education differences by gender and the intergenerational increase in educational attainment between parents and their adult children. Nearly half of the mothers in our sample have no formal schooling and less than 2 percent have any postsecondary education. In contrast, less than one third of the husbands have no formal schooling, whereas more than twice as many husbands as wives have postsecondary schooling. The children of these parents reach much higher levels of attainment: only 11 percent of adult female children and 6 percent of adult male children fail to attend any school, whereas 8 and 11 percent, respectively, go beyond secondary school. Although the gender gap in schooling remains in the sample of adult children, differences in schooling by sex diminish greatly between generations. The ratio of the proportion of women to men in each schooling category is closer to one in the offspring sample than in the parent sample at all levels of educational attainment except the lowest.

Table 1. Educational Attainment Distributions for Selected Indonesia Family Life Survey Samples.

	Marriage/Fertility Sample		Transmission Sample
	Woman	Husband	Woman	Husband	Woman/Husband	Daughter	Son	Daughter/Son
Educational Attainment (%)
None	47.2	29.2	48.0	29.2	1.64	11.0	6.2	1.77
Elementary	39.8	50.6	40.3	51.3	.79	47.5	42.2	1.13
Junior Secondary	6.1	8.7	6.2	8.7	.71	12.7	15.3	.83
Senior Secondary	5.3	8.1	4.5	7.9	.57	20.8	25.1	.83
Post Secondary	1.5	3.4	1.0	2.8	.34	7.9	11.2	.71
Total	99.9	100.0	100.0	99.9		99.9	100.0
Observations (n)	3,938	3,938	3,236	3,236		5,417	5,403

Note: Data are weighted to adjust for oversampling and attrition. Totals do not sum to 100 percent due to rounding.

Table 2 summarizes the distributions of the three outcome variables by women's educational attainment. The distribution of husband's educational attainment shows strong positive assortative mating on formal schooling in Indonesia, with a pronounced tendency for a woman to marry a man who has one level of schooling higher than hers. The fertility distribution reflects Indonesia's nonmonotonic pattern of fertility by the mother's educational attainment. The distribution of offspring's education shows a strong positive association between mother's and offspring's schooling, but also substantial upward intergenerational educational mobility.

Table 2. Distribution of Outcomes by Women's Educational Attainment.

	Husband's Education						Children Ever Born	Offspring's Education
	None	Elem	Jr Sec	Sr Sec	Post Sec	Total		None	Elem	Jr Sec	Sr Sec	Post Sec	Total
Women's Education (%)
None	51.8	44.6	2.2	1.3	.1	100.0	4.8	16.4	59.9	9.9	11.4	2.5	100.1
Elementary	11.5	69.2	12.0	5.8	1.4	99.9	5.2	1.9	39.1	19.8	30.7	8.6	100.1
Junior Secondary	2.4	23.4	32.4	35.9	5.9	100.0	5.0	.4	4.8	16.2	48.9	29.7	100.0
Senior Secondary	.3	7.3	14.1	49.2	29.2	100.1	4.1	.4	1.4	4.5	39.5	54.3	100.1
Post Secondary	.0	8.5	7.1	23.6	60.9	100.1	3.5	.0	.0	2.3	20.9	76.8	100.0
Total	29.2	50.6	8.7	8.1	3.4	100.0	4.9	8.6	44.8	14.0	23.0	9.6	100.0
Observations (n)				3,938			3,938				10,820

Note: Data are weighted to adjust for oversampling and attrition. Totals do not sum to 100 percent due to rounding. Elem = elementary; Jr Sec = junior secondary; Sr Sec = senior secondary; Post Sec = post secondary.

Estimation and Simulation

We estimate the statistical models for marriage, fertility, and offspring's educational attainment by maximum likelihood applied to each equation separately. We use the parameter estimates from our models in a series of simulations that compute the expected distributions of offspring's schooling implied by alternative assumptions about the education distribution of women and the ways that women's attainment affects marriage, fertility, and the attainment of children. We use predicted probabilities of a woman marrying a man at each level of educational attainment, predicted number of children born, and predicted probabilities of children achieving each level of educational attainment implied by parameter estimates and actual or hypothetical values of observed characteristics of women and their husbands. That is,

$${\widehat{r}}_{jk|i}={\widehat{p}}_{k|i}^H{\widehat{r}}_{jk}{\widehat{p}}_{j|ik}^C,$$ (3)

where ˆ denotes predicted values and all other notation is as defined above. Given r̂_jk|i for each woman in the initial generation, the expected number of persons in the offspring generation who attain the education level j is $C_j=\sum _i\sum _k{\widehat{r}}_{jk|i}{W}_i$. The component r̂_jk|i is computed for scenarios that vary by the change in the education distribution of the mothers' generation; the presence or absence of variation in the three components of r̂_jk|i included in Equation 3 (i.e., which of the women's education effects on marriage, fertility, and child's schooling are taken into account); and alternative assumptions about the marriage market.

Empirical Results

Parameter Estimates

Table 3 reports parameter estimates for the three parts of our model. Our samples include only married women older than 40 years or their adult children. Women's, husbands,' and children's schooling are measured in the five categories discussed earlier. In the fertility equation, the model assumes discrete, additive effects of women's and husband's schooling. We report ratios of coefficients to robust standard errors for all models. For the transmission model, we report ratios of coefficients to robust standard errors that also correct for clustering of multiple children born to the same woman. The equation for the educational attainment of offspring includes the additive effects of mother's and father's schooling plus an indicator for sex of offspring. Preliminary analyses indicated no important interactions of mother's and father's schooling in their effects on either fertility or the educational attainment of their children. The effect of father's educational attainment differs somewhat by sex of child. Contrasts between children of highly and moderately educated fathers are greater for female than for male offspring. Although these differences are of interest in a detailed analysis of Indonesian educational patterns, their inclusion does not affect our estimates of the effects of changes in women's educational attainments. For the sake of simplification, we base our calculations on the additive models shown in Table 3.¹⁰

Table 3. Parameter Estimates for Models of Intergenerational Transmission, Fertility, and Marriage.

	Offspring's Schooling (Ordered Logit)		Children Ever Born (Poisson)		Husband's Schooling (Ordered Logit)
	β	z	β	z	β	z
Women's Education
None (reference)
Elementary	0.936	12.8	0.008	0.3	2.014	24.3
Junior Secondary	1.725	14.0	−0.064	−1.6	4.072	31.2
Senior Secondary	2.346	16.4	−0.210	−4.5	5.571	35.5
Post Secondary	3.160	6.9	−0.418	−5.6	6.940	22.6
Husband's Education
None (reference)
Elementary	0.969	11.3	0.090	3.5	—	—
Junior Secondary	1.776	14.5	0.093	2.4	—	—
Senior Secondary	2.348	18.1	0.086	2.2	—	—
Post Secondary	3.362	14.6	0.019	0.3	—	—
Child's Sex (1 = girl)	−0.477	−12.4	—	—	—	—
Intercept	—	—	1.587	77.5	—	—
Observations (n)	10,820		3,938		3,938
Log Likelihood	−13155.2		−10161.7		−3944.0

Note: Ratios of coefficients to standard errors use robust standard errors. Cutpoint parameters in ordered logit models are not shown.

The educational attainments of both mothers and fathers have strong positive effects of approximately equal size on the attainments of their children. Moreover, the effects are relatively constant across parents' educational categories. On the average, the odds that children are in a higher rather than a lower category of schooling approximately double for each higher category of their mother's or father's schooling. The predicted probabilities of sons' and daughters' schooling by levels of mother's schooling, with father's schooling held constant, increase substantially with each successive level of mother's attainment. For example, approximately 55 percent of sons and 65 percent of daughters born to women with no education attain elementary school or less, whereas only 20 percent of sons and 30 percent of daughters born to women with senior secondary schooling have predicted levels of education this low. At the other end of the distribution, less than 5 percent of children whose mothers have no schooling are predicted to attend postsecondary schooling, as compared with nearly half of sons and about 40 percent of daughters whose mothers have postsecondary schooling themselves.

The estimates of the effects of parents' schooling on the number of children ever born follow the nonmonotonic pattern of differential fertility found in other research on Indonesia. Expected fertility is constant for the first three education categories, but decreases substantially for the two highest education categories. With husband's education held constant at the elementary level, women's expected number of children is approximately 5.0 for women with no schooling, primary education, or junior secondary education, and declines sharply to 3.7 for women with postsecondary education. The effect of husband's education on fertility is much smaller than the effect of wife's education. With women's educational attainment held constant, our estimates show that husbands with primary, secondary, or postsecondary schooling all have approximately 5.3 children, whereas men at the bottom of the education distribution average somewhat fewer children.

Indonesian couples show extremely strong evidence of positive assortative mating. The coefficients show that the odds of a woman marrying into the next highest husband's educational category are more than seven times greater both for women with elementary schooling compared to those with no schooling (exp[2.014]) and also for women with junior secondary schooling compared to those with elementary schooling (exp[4.072 – 2.014]). The odds of a woman marrying into the next highest husband's education category are about four times greater for women with senior secondary schooling than for those with junior secondary schooling (exp[5.571 – 4.072]), and also for women with postsecondary schooling than for those with senior secondary schooling (exp[6.94 – 5.571]). This model predicts that the proportion of women who marry men with at least a senior secondary education increases monotonically from less than 2 percent for women with no formal schooling to more than 90 percent for those with postsecondary schooling. Given the gender gap in educational attainment in Indonesia for this generation, women tend to marry men who have more schooling than they do. For example, the model predicts that among women with a senior secondary education, 30 percent marry men with postsecondary schooling. In contrast, among women with elementary schooling, only 12 percent marry men with no schooling.

These results provide a partial picture of the effect of mothers' educational attainment on their offspring's attainment. In most analyses of intergenerational effect, the parameters of equations predicting children's schooling from parents' schooling are used to evaluate the effect of a hypothetical change in mother's schooling on the schooling of her children. To assess the overall effect of an increase in women's educational attainment, however, it is necessary to take into account the joint compositional effects of fertility and marriage as well.

Simulations

We assess the effects of women's schooling on the education of the next generation through a series of simulations. The simulations use expected rates and probabilities, which correspond to the components of Equation 3, calculated from the parameter estimates shown in Table 3. Each simulation has three parts: (1) a hypothetical change in women's schooling (2) a selected subset of transmission, marriage, and fertility processes; and (3) whether men's schooling increases when women's schooling increases or whether the men's educational distribution is held fixed. We combine these parts as follows. For each simulation, we draw a random subsample of 5 percent of the women in the marriage/fertility sample (3938 × 0.05 = 197 women) subject to a hypothetical change in the women's education distribution that we consider. For example, to estimate the effect of moving 5 percent of the sample women from no schooling to elementary schooling, we randomly draw, without replacement, 197 women from the no schooling category and change their schooling from none to elementary. The other 95 percent of the women retain their observed educational attainments. Perturbing the education of 197 women can change the education of only the children of those 197 women. In models that assume fertility to be exogenous, this equals a maximum of exactly 5 percent of all the children. In models that assume fertility to be endogenous, this may be somewhat more or less than exactly 5 percent of the children because of differential fertility.¹¹

We then use the estimated parameters in Table 3 and the remaining assumptions of the scenario (specifically, whether fertility and/or marriage are taken into account and how the male education distribution may change) to predict the husbands' education distribution and the number of children born in each educational category in the subsequent generation. We form a ratio of the simulated offspring educational distribution to the baseline distribution predicted by our sample women's observed schooling to determine whether a given simulation increases or decreases the proportion of children at each schooling level, relative to no changes made in women's schooling. Although the simulations can alter the schooling of only about 5 percent of all the children, the size of the proportional changes in each education category varies greatly depending on the starting number of women and the daughters in each category.¹² We describe each component of the simulations in more detail in the following section.

Changes in Women's Education Distribution

We simulate the effect of changing women's schooling by computing the expected offspring education distribution under six scenarios for women's educational attainment. Scenario 1 is the education distribution of the sample women, as observed. In Scenarios 2 through 5, we move 5 percent of the sample women from one education category to the next one up while retaining observed values for the remaining 95 percent of the sample. For example, in Scenario 2, we randomly draw 197 women from education category 1 (no schooling) and reassign them to education category 2 (elementary schooling). In Scenario 6, we move 197 women from no schooling to postsecondary schooling. We compare each expected education distribution to the distribution of children's schooling predicted by the observed women's schooling represented by Scenario 1.

Combinations of Effects

Each of the scenarios discussed in the previous section is carried out for each of four combinations of processes using the components of Equation 3: (a) intergenerational transmission only, (b) intergenerational transmission plus differential fertility, (c) intergenerational transmission plus educational assortative mating, and (d) intergenerational transmission plus fertility plus educational assortative mating. Estimates from Combination a (transmission only) correspond to conventional estimates of the effect that mothers' schooling has on offspring's schooling based on the conditional joint distribution of parents' and offspring's schooling. Effects estimated from combinations b through d modify conventional estimates by taking into account fertility, marriage, or both.

Alternative Marriage Markets

The effect of a change in the distribution of women's schooling depends on changes in women's preferences and opportunities for marriage. How a change in women's attainment affects the next generation may depend on whether men's schooling changes as well because the men's educational distribution determines the possible combinations of men and women who marry, then bear and raise children. Consider two extreme possibilities. At one extreme, men's attainments are entirely endogenous to those of women. That is, the male educational distribution changes so as to maintain the prior conditional distributions of husband's educational attainment given wife's attainment. In this case, women's increased educational attainments do not constrain their marital opportunities. After a shift in women's attainments, women at each level of educational attainment have the same expected distribution of husband's educational attainment that their counterparts would have faced before the aggregate change. This extreme case is realistic only if men are given the same inducements and opportunities to increase their schooling as women. We call this market the “unconstrained marriage market.” For this model, the marriage probabilities are simply ${\widehat{p}}_{k|i}^H$, computed from our estimated ordered logit model for marriage.

At the other extreme, men's educational attainments are unaffected by shifts in the women's educational distribution. Instead, their marginal education distribution remains constant. In this case, women's marital opportunities are constrained by the available distribution of men. Under this assumption, an increase in women's educational attainments will make the conditional distribution of expected husbands' attainments, given wives' attainments, less favorable after the aggregate shift in women's attainment. This extreme case is realistic only if the norms, costs, and rewards connected with men's schooling are independent of women's educational status.¹³ We call this market the “constrained marriage market.” For this model, we constrain the marriage market by adjusting the predicted marriage probabilities from our model to conform to the existing men's educational distribution under the assumption that more educated women are more successful in marrying highly educated men than less educated women. If the predicted number of marriages within a category of men's schooling exceeds the number of men in that category in the original sample, we allow women in the higher education categories “first pick” of the most educated men. Depending on how many men remain in each education category, more poorly educated women may have to take husbands with less schooling than would be available in an unconstrained marriage market. We use an iterative algorithm to redistribute marriages in this way until equilibrium is reached. We then calculate the revised marriage probabilities implied by this redistribution and use these adjusted marriage parameters in the simulations. To show the range of possible effects of assortative marriage, we simulate the expected education distributions of offspring for both the unconstrained and constrained marriage markets.

Results

Taken together, these combinations of alternative hypotheses produce 48 simulations. We report key findings in Figures 1 and 2, and the full results in Appendix Tables A1 and A2. The figures show estimates for daughters in the next generation, but similar patterns are observed for sons (Table A2). Each line of Figures 1 and 2 corresponds to a single comparison (in the form of a ratio) of the expected proportion of offspring in each education category for a given simulation to the expected proportion in the absence of a shift in the education distribution of women (the baseline distribution). A ratio greater than 1.0 indicates an increasing proportion of offspring in that education category.

Figure 1. Effects of Redistributing Five Percent of Women from Senior Secondary Education to Postsecondary Education.

Note: Elem = elementary school; JrSec = junior secondary school; SrSec = senior secondary; PostSec = post-secondary.

Figure 2. Effects of Redistributing Five Percent of Women from No Education to Elementary Education.

Note: Elem = elementary school; JrSec = junior secondary school; SrSec = senior secondary; PostSec = post-secondary.

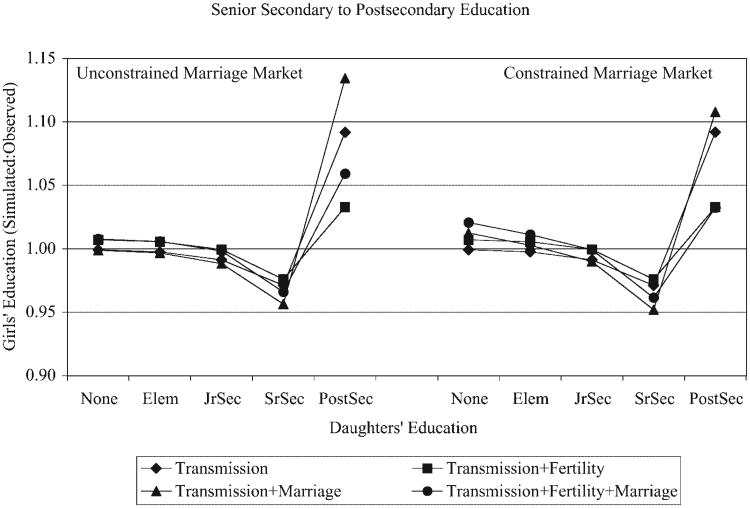
Figure 1 shows the estimated effects of moving 5 percent of all women (n = 197) from senior secondary to postsecondary schooling. Figure 2 shows estimated effects of moving 197 women from no education to the elementary school level. Moving 197 women from senior secondary to postsecondary schooling raises the proportion of children who themselves attain postsecondary schooling. The size of this effect, however, depends considerably on which aspects of the educational reproduction process are taken into account. In the unconstrained marriage market (left sides of Figures 1 and 2), the proportional change implied by the conditional intergenerational effect of mother's schooling on daughter's schooling is almost 10 percent (“transmission”).¹⁴ This is, however, an overestimate of the total effect because it ignores the offsetting effects of differential fertility. When the effects of both fertility and intergenerational transmission are included, the expected effect on the next generation is about 3 percent, only one third of the original estimate (transmission + fertility). In contrast, assortative mating tends to reinforce the effects of intergenerational transmission. Transmission and marriage together raise the proportion of daughters with postsecondary education by almost 13 percent (transmission + marriage). With all effects taken into account, the net impact of transferring 197 women from senior secondary to postsecondary schooling (a large proportional change in those education categories) is about a 6 percent increase in the proportion of the daughter generation with postsecondary schooling (transmission + fertility + marriage).

These patterns show that marriage, fertility, and intergenerational transmission combine to affect the next generation in a complex way. At the upper end of the women's education distribution, increases in attainment bode well for the next generation because more of these women will marry highly educated husbands, and these improvements in both mother's and father's education will benefit their children. These effects in the next generation, however, are offset by the reduced fertility of highly educated women. The net impact of the change in women's education is positive, but not nearly as great as an analysis of intergenerational transmission alone would imply.

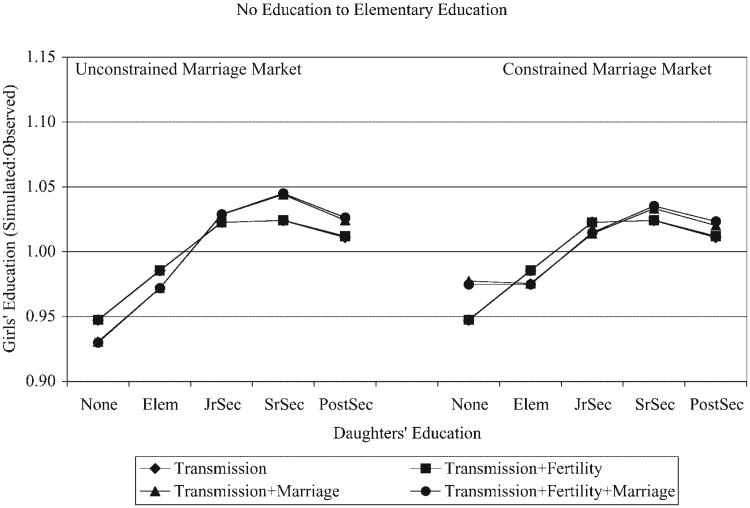
Moving the same number of women (197) from no education to elementary education also improves the education distribution of the next generation, but the pattern of effects is different in this case. In contrast to the top of the schooling distribution, where the effect is concentrated in a single education category, at the bottom of the distribution the effect is more modest and spread over several categories. In the unconstrained market, it reaches maximum values for those with no schooling, among whom the proportion of daughters is expected to decrease by about 7 percent, and for those with senior secondary schooling, among whom the proportion of daughters is expected to increase by approximately 5 percent. These results reflect the overall tendency for daughters to exceed the education level of women in the previous generation, which is reinforced by improvements in women's schooling at the bottom of the distribution. In contrast to the top of the education distribution, the estimated effects attributable to intergenerational transmission alone are similar to those when transmission, fertility, and marriage are considered together. Because women's fertility is nearly constant across the lower strata of women's educational attainment, the benefits to children of improvements in women's education in those strata are not offset by corresponding declines in fertility. In this simulation, differences in effects are driven by the improved marriage prospects that accrue to women when their educational attainment improves. This mechanism has a net positive effect on the education of the next generation, but these effects are small relative to those that occur with improvements at the top of women's education distribution.

The graphs on the right in Figure 1 show that in these simulations, the effects of improvements in women's status at either the top or the bottom of the education distribution are robust to alternative extreme assumptions about the marriage markets that women face. Our findings are generally similar whether or not we assume that men's schooling increases when we increase women's schooling. As expected, in the constrained marriage market, education effects are attenuated for scenarios that include marriage. The results for scenarios that do not include marriage remain unchanged. For example, in the simulation that moves women from senior secondary to postsecondary education, the proportion of daughters who obtain postsecondary education is reduced by nearly half when we consider all mechanisms in the constrained marriage market (3.2 vs. 5.9 percent). Nonetheless, the pattern of results is similar in the two marriage markets. The consistency across these alternative marriage market assumptions, which represent extremes in how the men's education distribution may change for a given increase in women's schooling, suggests that, at least for marginal changes in women's educational attainment, our pattern of results for Indonesia does not depend on specific marriage market assumptions.

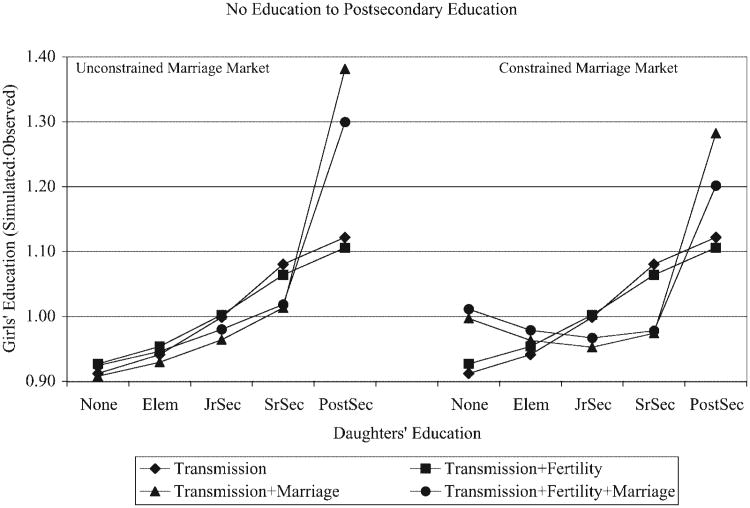
Figure 3 presents the estimated effects of a more extreme change in the distribution of women's educational attainment, namely a redistribution of 5 percent of sample women from the lowest (no education) to the highest (postsecondary education) category. This is tantamount to examining the effect of implementing simultaneously all four shifts of 5 percent of sample women to the next highest education category. Because this is a larger change in the distribution of women's schooling, the estimated effects are much larger, especially for the proportion of offspring that achieve postsecondary schooling. In the unconstrained marriage market, the expected proportion of offspring in the junior and senior secondary education categories implied by consideration of all the mechanisms combined (fertility, marriage, and intergenerational transmission) is lower than implied by intergenerational transmission alone. In contrast, at the postsecondary level, the combined effect of all three processes implies a much larger growth in the proportion of the next generation than the effect of intergenerational transmission alone (approximately 30 vs. 12 percent). This pattern of effects results from the reinforcing positive impact of assortative mating and the offsetting negative effect of fertility on the education of the next generation. The redistribution of 197 women from the lowest to the highest education category results in a very large increase in the expected educational attainment of their husbands. This implies much higher educational attainment for the couples' daughters. This effect, however, is offset to some degree by the lower fertility of these highly educated women. In the absence of fertility reductions for these women, the expected increase in the proportion of daughters achieving postsecondary schooling would be even higher (38 vs. 30 percent).

Figure 3. Effects of Redistributing Five Percent of Women from No Education to Postsecondary Education.

Note: Elem = elementary school; JrSec = junior secondary school; SrSec = senior secondary; PostSec = post-secondary.

In the constrained marriage market, the effect of redistributing 5 percent of sample women from the no education category to postsecondary schooling produces several notable differences. The educational attainments of daughters are dampened throughout the education distribution in scenarios that include marriage effects, especially at the highest and lowest education levels. This pattern results from the constrained marital opportunities implied by this simulation. The large redistribution of women's educational attainment combined with a fixed distribution of men's educational attainment implies that not all women will be able to marry the highly educated men they would otherwise expect to marry. Because women at the highest level of educational attainment get “first choice” in the constrained marriage market, the marriage opportunities for women in the lower education categories are made worse and their offspring's educational attainment is lowered more than they would experience in an unconstrained marriage market. This results in nearly no change in the distribution of girls in the no education category relative to the predicted baseline distribution (ratio of about 1 for “transmission + marriage” and “transmission + fertility + marriage”). When the marriage market is not constrained or when marriage effects are excluded in the constrained market, the predicted proportion of girls with no schooling is about 10 percent less than in the baseline distribution (ratio of about 0.9).¹⁵

Summary and Conclusions

How one views the effects of family background on socioeconomic attainment depends on how one thinks about assessing the consequences of changing the characteristics of individuals' families of origin. Many changes in the socioeconomic characteristics of parents, especially those that change the educational attainments of mothers or fathers, occur relatively early in their lives. These early changes affect their fertility and marriage as well as the attainments of their offspring. But changes that affect fertility and marriage cannot be adequately assessed from observations of parent and offspring socioeconomic characteristics alone. Changing women's schooling changes their fertility and marriage behavior, which alters the relative numbers of offspring born to women with varying education levels. Even in the absence of change in the individual-level effects of mother's schooling on offspring's schooling, these compositional effects alter the distribution of schooling in the offspring generation. Our models show how various components of intergenerational change contribute to the total effect of women's education on the education of the next generation.

The approach proposed in this article is only a single step in assessing the aggregate intergenerational effects that typically are ignored in standard analyses of parent–child associations. It can, however, be extended to take into account a richer set of mechanisms, including the timing of fertility and marriage, the instability of marriage, the mortality of parents and children, the sex-specific effects of family background characteristics on offspring, the unobserved factors that commonly affect both fertility and offspring's educational attainment, and the more complex marriage market effects. Increases in women's schooling may affect whether and when they marry, the timing of fertility, and whether they have children outside of marriage. These mechanisms may have relatively larger effects in low-fertility societies than the assortative mating and fertility-level effects considered in this article. In contrast, the impact of a change in women's schooling in poor high-fertility societies may affect the next generation through changes in the survival probabilities of both women and their children. Improving women's survival through their childbearing years increases their total exposure to child-bearing, the care they can provide for their children, and the likelihood that their children themselves will survive to adulthood. Additional individual and family effects may be important in some societies, including those of number of siblings and interactions between sex of child and sex of parent (Mare and Chang 2006; Thomas 1994). If mothers and fathers have distinct effects on their daughters and sons, then changes in women's educational attainments may, depending on the patterns of educational assortative marriage and the degree to which the supply of education is constrained, differentially alter the education distributions of men and women in the next generation.

Our analyses assume that, given the variables included in the models, the marriage, fertility, and intergenerational transmission processes are independent. If, however, women vary systematically on unmeasured factors that jointly affect marriage, fertility, and childrearing, then the estimated effects of parents' educational attainments on their offspring's schooling may be subject to a “selection bias” created by differential fertility (Winship and Mare 1992). If, for example, among women with the same educational attainment, those who can provide the best environments for their children are also those who, because of their other opportunities, have the fewest children, then the estimated effects of mother's schooling on offspring's schooling may be biased downward. Although we typically regard “family background” as exogenous to socioeconomic success, in this case it may be necessary to treat family background as jointly determined with the outcomes of family effects, such as offspring's educational attainment and economic success.

A full account of how marriage contributes to the intergenerational effects of a change in young women's schooling requires the development of two-sex models of marriage entry and assortative marriage that make explicit the interdependence of the male and female populations (Logan, Hoff, and Newton 2001; Mare 2000). Although our estimates of the effects of some changes in women's education distributions are robust to alternative assumptions about marriage markets, for other effects, alternative assumptions about marriage yield different predictions. A fuller understanding of these effects requires models that enable one to estimate rather than assume the parameters of the marriage process.

As with any statistical model, our estimates of effects assume that everything else is held constant. That is, our scenarios assume a fixed regime of intergenerational relationships. The historical change in educational attainment in Indonesia over this period has been a result of numerous economic, political, cultural, and demographic factors captured by our models only as gross effects (or in reduced form). However, our goal in this article has been to show that intergenerational processes depend on demographic mechanisms that generally are ignored in estimates of intergenerational effects rather than to calibrate a model that does full justice to the particulars of educational expansion in Indonesia.

Although the refinements and qualifications to our approach suggest many desirable lines of future investigation, our analysis demonstrates, in the Indonesian context, several important mechanisms of educational reproduction. The effects of women's educational attainment on the next generation are more complex than shown by conventional analyses of mother–offspring educational mobility. Positive educational assortative mating reinforces the beneficial effects of increased women's schooling. Better educated women advantage their children both directly and indirectly by marrying better educated men. At higher levels of educational attainment, however, education's dampening effects on fertility tend to offset the beneficial effects of marriage and women's education itself on the next generation. The long-term effects of interventions to raise women's schooling may depend on where in the education distribution these efforts are applied. For the Indonesian cohorts represented by our sample, interventions among the most poorly educated women appear to have an unalloyed benefit for both the current and future generations. Nonetheless, interventions at the top of the educational hierarchy produce the largest proportional changes in the offspring education distribution, despite the accompanying offsets produced by lowered fertility, because the women's baseline education distribution is relatively disadvantaged. In other contexts, interventions among better educated women may benefit them directly, but may have limited or even negative effects on the schooling of offspring if these are offset by other intergenerational mechanisms.

Unlike more conventional models of intergenerational transmission, our approach is suitable for assessing the long-term intergenerational consequences of interventions in the lives of teenagers and young adults. In low education populations, which still characterize large parts of the developing world and many immigrant groups in the developed world, the effort to increase women's education continues to be a promising avenue of human betterment. Models of the type presented in this article may prove to be a good way to assess these effects. But these contexts certainly are not the only ones to which our approach applies. Differences in marriage, fertility, and offspring's schooling by women's schooling also are important features of populations with relatively high levels of educational attainment. Finally, in addition to their descriptive and practical value, these models have the potential to advance mobility studies beyond a static focus on who gets ahead to a more dynamic view of how populations and societies change.

Biographies

Robert D. Mare is a Professor of Sociology at the University of California–Los Angeles. His ongoing research focuses on marriage markets and assortative mating, residential mobility and neighborhood change, and models for intergenerational social mobility.

Vida Maralani is a Ph.D. candidate in sociology at the University of California–Los Angeles. Her research interests include educational inequality, social stratification, and demography. Her dissertation examines the intergenerational processes that shape the distribution of schooling from one generation to the next using data from the United States and Indonesia.

Table A1: Ratios of Simulated to Observed Daughters' Education Distributions

	None	Elem	Jr Sec	Sr Sec	Post Sec
Simulation
Transmission Only
None to Elementary	.947	.985	1.023	1.024	1.011
Elementary to Junior Secondary	.988	.982	.992	1.026	1.033
Junior Secondary to Senior Secondary	.998	.994	.985	.993	1.064
Senior Secondary to Postsecondary	.999	.997	.991	.971	1.092
None to Postsecondary	.912	.941	.999	1.081	1.122
Transmission + Fertility
None to Elementary	.948	.986	1.023	1.024	1.012
Elementary to Junior Secondary	.990	.984	.991	1.024	1.037
Junior Secondary to Senior Secondary	1.004	1.000	.989	.987	1.049
Senior Secondary to Postsecondary	1.007	1.005	.999	.976	1.033
None to Postsecondary	.927	.954	1.003	1.064	1.106
Transmission + Marriage (unconstrained)
None to Elementary	.931	.972	1.029	1.044	1.024
Elementary to Junior Secondary	.982	.971	.973	1.037	1.087
Junior Secondary to Senior Secondary	.996	.990	.974	.976	1.136
Senior Secondary to Postsecondary	.999	.997	.988	.956	1.134
None to Postsecondary	.908	.930	.964	1.013	1.381
Transmission + Fertility + Marriage (unconstrained)
None to Elementary	.930	.972	1.029	1.045	1.026
Elementary to Junior Secondary	.985	.972	.973	1.035	1.096
Junior Secondary to Senior Secondary	1.004	.997	.980	.972	1.114
Senior Secondary to Postsecondary	1.008	1.006	.998	.966	1.059
None to Postsecondary	.924	.946	.980	1.019	1.300
Transmission + Marriage (constrained)
None to Elementary	.978	.976	1.014	1.033	1.020
Elementary to Junior Secondary	1.035	.978	.957	1.021	1.079
Junior Secondary to Senior Secondary	1.023	.999	.969	.965	1.115
Senior Secondary to Postsecondary	1.012	1.003	.990	.952	1.108
None to Postsecondary	.997	.963	.953	.974	1.282
Transmission + Fertility + Marriage (constrained)
None to Elementary	.975	.975	1.015	1.035	1.023
Elementary to Junior Secondary	1.035	.979	.958	1.020	1.088
Junior Secondary to Senior Secondary	1.030	1.006	.975	.960	1.093
Senior Secondary to Postsecondary	1.021	1.011	.999	.961	1.032
None to Postsecondary	1.011	.979	.967	.978	1.202

Note: Elem = elementary; Jr Sec = junior secondary; Sr Sec = senior secondary; Post Sec = postsecondary.

Table A2: Ratios of Simulated to Observed Sons' Education Distributions

	None	Elem	Jr Sec	Sr Sec	Post Sec
Simulation
Transmission Only
None to Elementary	.946	.976	1.015	1.025	1.013
Elementary to Junior Secondary	.988	.983	.984	1.015	1.035
Junior Secondary to Senior Secondary	.998	.995	.989	.987	1.054
Senior Secondary to Postsecondary	.999	.998	.994	.978	1.058
None to Postsecondary	.911	.932	.976	1.054	1.125
Transmission + Fertility
None to Elementary	.946	.977	1.015	1.025	1.014
Elementary to Junior Secondary	.990	.984	.984	1.014	1.038
Junior Secondary to Senior Secondary	1.004	1.001	.993	.984	1.039
Senior Secondary to Postsecondary	1.007	1.006	1.003	.985	1.011
None to Postsecondary	.926	.946	.985	1.044	1.106
Transmission + Marriage (unconstrained)
None to Elementary	.929	.961	1.013	1.042	1.028
Elementary to Junior Secondary	.983	.973	.966	1.014	1.088
Junior Secondary to Senior Secondary	.997	.993	.981	.969	1.108
Senior Secondary to Postsecondary	.999	.998	.993	.968	1.082
None to Postsecondary	.907	.924	.953	.993	1.305
Transmission + Fertility + Marriage (unconstrained)
None to Elementary	.928	.961	1.013	1.043	1.030
Elementary to Junior Secondary	.985	.975	.967	1.012	1.095
Junior Secondary to Senior Secondary	1.004	1.000	.988	.969	1.086
Senior Secondary to Postsecondary	1.008	1.006	1.002	.979	1.025
None to Postsecondary	.924	.940	.969	1.003	1.238
Transmission + Marriage (constrained)
None to Elementary	.979	.971	.999	1.030	1.023
Elementary to Junior Secondary	1.039	.987	.953	.997	1.078
Junior Secondary to Senior Secondary	1.024	1.004	.980	.959	1.089
Senior Secondary to Postsecondary	1.013	1.005	.995	.966	1.059
None to Postsecondary	1.000	.968	.954	.962	1.217
Transmission + Fertility + Marriage (constrained)
None to Elementary	.977	.970	.999	1.031	1.026
Elementary to Junior Secondary	1.039	.988	.954	.996	1.085
Junior Secondary to Senior Secondary	1.031	1.011	.986	.960	1.066
Senior Secondary to Postsecondary	1.021	1.013	1.004	.977	1.001
None to Postsecondary	1.015	.983	.969	.971	1.151

Note: Elem = elementary; Jr Sec = junior secondary; Sr Sec = senior secondary; Post Sec = post secondary.