Abstract
In vision, humans use summary statistics (e.g., the average facial expression of a crowd) to efficiently perceive the gist of groups of features. Here, we present direct evidence that ensemble coding is also important for auditory processing. We found that listeners could accurately estimate the mean frequency of a set of logarithmically spaced pure tones presented in a temporal sequence (Experiment 1). Their performance was severely reduced when only a subset of tones from a given sequence was presented (Experiment 2), which demonstrates that ensemble coding is based on a substantial number of the tones in a sequence. This precise ensemble coding occurred despite very limited representation of individual tones from the sequence: Listeners were poor at identifying specific individual member tones (Experiment 3) and at determining their positions in the sequence (Experiment 4). Together, these results indicate that summary statistical coding is not limited to visual processing and is an important auditory mechanism for extracting ensemble frequency information from sequences of sounds.
Keywords: statistical summary, ensemble coding, auditory perception, frequency, perception, visual perception
Humans frequently encounter ensembles or groups of objects (e.g., crowds of people, peaches at a fruit stall, cars in traffic) and are able to quickly process them with ease. However, the task of rapidly combining numerous features into a coherent percept is an incredible computational challenge. Because many natural scenes are composed of multiple objects that are similar and therefore highly redundant, it is more efficient for the visual system to compress these scenes by encoding information about summary statistics than to encode features of individual objects (for a review, see Alvarez, 2011). This ensemble coding has been shown to be important for perceiving the gist of visual scenes, and it occurs across an impressive variety of visual features. For example, when presented with a set of objects, humans can quickly extract the objects' average size (Ariely, 2001; Chong & Treisman, 2003), brightness (Bauer, 2009), orientation (Parkes, Lund, Angelucci, Solomon, & Morgan, 2001), location (Alvarez & Oliva, 2008), color (de Gardelle & Summerfield, 2011), speed (Watamaniuk & Duchon, 1992), and motion direction (Williams & Sekuler, 1984). Humans can even extract the mean emotion (Haberman & Whitney, 2007), gender (Haberman & Whitney, 2007), identity (de Fockert & Wolfenstein, 2009), and biological motion (Sweeny, Haroz, & Whitney, 2013) of a crowd of people. Summary statistics in vision are computed across both space and time (Albrecht & Scholl, 2010; Haberman, Harp, & Whitney, 2009), and certain temporal properties of a visual sequence (such as its overall duration) can affect its summary representation (Haberman et al., 2009).
Although ensemble coding is an important and widely studied phenomenon in vision, little is known regarding ensemble representation in other sensory domains. Auditory scene analysis is an extremely difficult task because the brain must segregate multiple streams of information and assign them to distinct objects, even though the streams often overlap in pitch, time, and space (Bregman, 1990; Bregman & Campbell, 1971; Micheyl & Oxenham, 2010). There is some evidence for statistical processing of auditory ensembles: Statistical information in tone sequences influences the phonetic categorization of subsequent speech sounds (Holt, 2006), and McDermott and Simoncelli (2011) have reported time-averaged statistical processing of sound textures in the auditory periphery (although at a very fine, subsecond timescale and involving statistics of activation of individual cochlear channels). In addition, humans can estimate the mean frequency of a series of tones (Albrecht, Scholl, & Chun, 2012), but it is not known how many of the tones subjects use to make their estimate and to what extent this ability is based on encoding of individual tones as opposed to a summary statistic. In particular, no previous studies have measured the efficiency of listeners' estimates of the mean frequency of auditory sequences and compared them with their memory of individual tones in the sequence. Given the importance of ensemble coding for vision, we hypothesized that it would also be present in auditory processing.
Research on auditory statistical learning has shown that listeners can acquire statistical information from tone sequences that are repeated multiple times (Loui, Wessel, & Hudson-Kam, 2010; Saffran, Johnson, Aslin, & Newport, 1999). In addition, many years of exposure to the statistics inherent in speech in a particular linguistic community can subsequently influence one's perceptual interpretation of ambiguous sounds, such as the tritone paradox (Deutsch, 1991; Dolson, 1994). However, this type of statistical learning is fundamentally distinct from statistical gist perception. The former involves the acquisition of statistical information from an assortment of sounds heard previously over a prolonged training period, whereas the latter refers to listeners' nearly instantaneous, moment-to-moment extraction of summary statistics from a given sensory environment. In an experimental setting, statistical summary perception of an auditory stimulus would occur within a single experimental trial.
We hypothesized that summary statistical representation of frequency information in auditory scenes may be an important property of auditory perception, and we designed several experiments to assess whether there is ensemble coding in audition. Specifically, we assessed whether listeners could extract the mean frequency (on a logarithmic scale) of a tone sequence despite limited access to information about the individual tones that comprise the sequence.
General Method
All experimental procedures were approved by the Committee for the Protection of Human Subjects at the University of California, Berkeley. All but 2 listeners were naive to the purpose of the experiments. Here, “naive” means that the listeners were given no information about the hypotheses, methods, or any other aspects of the study before beginning the experiment. Participants who completed more than one experiment were unaware of the methods of each individual experiment until the beginning of the experimental procedures and were not given information about the overall purpose or hypotheses of the study until data collection was complete. All listeners were affiliates of the University of California, Berkeley, who gave informed consent to participate and were compensated for their time. According to self-report, all of the participants had normal hearing, and none had absolute pitch.
To eliminate effects of experiment order on performance, we counterbalanced the order in which participants completed the different experiments (for subjects who participated in multiple experiments), except for 11 of the participants in Experiment 1, who were added after the original round of counterbalanced data collection and had already participated in Experiment 2. No feedback was provided in any of the experiments.
Experiment 1: Listeners Extract the Mean Frequency of Auditory Sequences
Method
Listeners
Twenty-three listeners (4 male, 19 female; age = 18–34 years) participated in the experiment. On average, listeners had 7.8 years of musical training (SD = 5.8) and initiated training at 7.7 years of age (SD = 2.8).
Stimuli and procedure
We assessed listeners' abilities to estimate the mean (log) frequency of a temporal sequence of 6 pure tones. All stimuli were sine-wave tones (Fig. 1) generated in MATLAB (The MathWorks, Natick, MA) and presented at a comfortable listening level via closed headphones. In each trial, the mean frequency of the sequence was randomly chosen from a range of 110 to 1174.7 Hz (A2 to D6). The 6 individual tones in each sequence were chosen from a wider range of 52 possible tones (82.4–1568 Hz; E2 to G6) and were always −5, −3, −1, +1, +3, and +5 semitones from the mean frequency. Thus, all tones in the sequence were separated by at least 2 semitones, an interval that greatly exceeds normal two-tone discrimination thresholds for successive pure tones (Moore, 2003), which we confirmed in a preliminary experiment. In addition, no two members of a sequence were ever more than one octave apart, thereby eliminating possible octave confusions. We chose a logarithmic (i.e., semitone, or musical) spacing between tones because auditory frequency discrimination of pure tones follows an approximately logarithmic scale (Moore, 2003), and results from a preliminary experiment indicated that listeners tend to report that the logarithmic mean sounds more like the true mean of a sequence of pure tones than the linear mean does. Thus, we use the term mean frequency to refer to mean frequency on a logarithmic (semitone) scale.
Fig. 1.
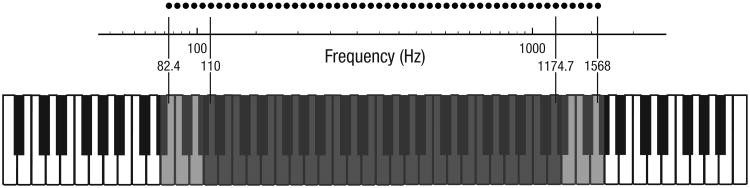
Tone stimuli used in the experiments. All stimuli were sine-wave tones spaced along a logarithmic (musical) scale; their frequencies corresponded to the pitches of piano keys. In each trial, the mean frequency of the sequence was chosen from the range of frequencies highlighted here with darker shading, and the individual tones composing the sequence were drawn from a wider range that spanned both the dark- and light-shaded regions. Black dots represent the frequencies of the full range of tones from which the individual tones in each sequence were drawn. Adjacent dots are separated by 1 logarithmic (semitone) unit.
Each trial consisted of a sequence and a test interval, which were always separated by a 500-ms silent interval. During the sequence interval, the six tones in the sequence were played in random order, each for 300 ms with a 100-ms pause between successive tones. In the subsequent test interval, a single comparison tone was played for 300 ms, and listeners reported whether this tone was higher or lower than the mean frequency of the sequence. Test tones differed from the true sequence mean by ±5, ±3, ±2, ±1, or ±0.5 semitones. Measuring discrimination between the mean frequency of the sequence and the test tone across this range of differences allowed us to determine how precisely listeners could estimate the mean frequency. The frequency difference between the test tone and the mean of the sequence was counterbalanced across trials. Listeners completed either 300 or 240 trials over two runs.
Results
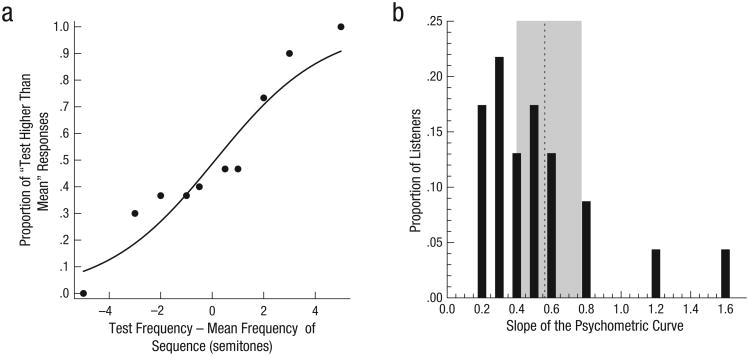
We fit a psychometric function to each listener's data (Fig. 2a) using a logistic equation. For each psychometric function, we generated a bootstrapped distribution of model-fitting parameter values by resampling the data with replacement 1,000 times and fitting a new curve for each iteration (as in Fischer & Whitney, 2011) to obtain a bootstrapped slope for each listener. This slope corresponded to the listener's sensitivity for estimating the mean frequency of the sequence. Higher slopes indicated better discrimination of mean frequency. If listeners were completely unable to discriminate the mean frequency of the sequence from the frequency of the test tone, the slope of the psychometric function would be zero. Every individual listener performed significantly above chance (least significant slope = .21, with more than 99% of the bootstrapped estimates > 0).
Fig. 2.
Results of Experiment 1. The psychometric curve in (a) shows the proportion of responses from a representative listener in which the frequency of the test tone was identified as higher than the mean frequency of the preceding tone sequence as a function of the difference (in semi-tones) between the test tone and the sequence mean. The histogram (b) shows the distribution of psychometric curve slopes across all 23 listeners. Chance performance corresponds to a slope of zero. The group mean is indicated by the vertical dashed line, and the gray shading indicates the 99% confidence interval (obtained by bootstrapping).
As a group, listeners performed above chance in reporting whether a test tone was higher or lower than the mean frequency of the preceding sequence (Fig. 2b; one-sample Wilcoxon signed-ranks test, p < .001, Cohen's d = 1.60). These data indicate that listeners could estimate the mean frequency of the sequence, which is consistent with the findings of Albrecht et al. (2012). However, it is unclear how many of the tones in the sequence contributed to this estimate and whether this estimate relied on explicit memory of each of the tones. Therefore, in Experiment 2, we determined the number of tones that contributed to listeners' mean estimates by varying the proportion of tones that were presented from each sequence. Further, in Experiments 3 and 4, we measured listeners' memory capacity for the frequency and position of individual tones in the sequence.
Experiment 2: Listeners' Estimates of the Mean Frequency Incorporate a Substantial Proportion of the Tones in a Sequence
In Experiment 2, we tested the hypothesis that listeners use multiple tones to estimate the mean frequency of a sequence of tones—a process known as ensemble coding. This experiment was necessary to rule out the possibility that in Experiment 1, listeners used only a single tone (and simply ignored or disregarded the other five tones) to estimate the average, which could have resulted in some ability to estimate mean frequency but would not constitute summary statistical perception. This concern has been important in the study of visual summary statistics (e.g., Myczek & Simons, 2008), and it was equally important in this investigation.
To directly test whether estimates were based on multiple tones, we restricted the number of tones that listeners could use to estimate the mean frequency of the full six-tone sequence. Specifically, we generated six-tone sequences as in Experiment 1, and on a given trial, either a subset of tones from the full sequence (one, two, or four) or all six tones were presented. We asked whether a listener's percept of the average frequency improves when more information about that average is available. If listeners' estimates of the mean frequency improve with increasing numbers of presented tones, this would indicate that they use those additional tones in their ensemble judgment. Because a single randomly selected tone from the sequence is a poor representative of the full six-tone sequence, we expected estimates of the mean to be poor when only one tone was presented. If listeners integrate multiple tones into an ensemble code, then estimates of mean frequency should improve when more tones are presented from the full sequence (e.g., two, four, or all six), as additional tones provide more information about the ensemble average. Alternatively, if listeners rely on only a single tone to estimate the mean even when more than one tone from the full sequence is presented, then behavioral performance should not vary as a function of the proportion of presented tones in each sequence.
Method
Listeners
Eleven listeners (2 male, 9 female; age = 24– 34 years) participated in the experiment. On average, listeners had 10.1 years of musical training (SD = 4.9) and initiated training at 7.0 years of age (SD = 1.8). All listeners also participated in Experiment 1, and all but 2 listeners were naive regarding the purpose of the experiment.
Stimuli and procedure
All sequences were generated as in Experiment 1 (with six tones), but we varied how many of those six tones were presented from each sequence—one, two, four, or all six of the tones. As in Experiment 1, each sequence was followed by a single test tone differing from the true mean of the full sequence of six tones by ±5, ±3, ±2, ±1, or ±0.5 semitones. The number of presented tones and the frequency difference between the test tone and the mean of the full sequence were counterbalanced across trials. Listeners were told to use any strategy to determine whether the test tone was higher or lower than the average frequency of the sequence. The correct mean was always defined as the mean of the full sequence; in trials with only one, two, or four tones, the full sequence included the tones that were not presented. On trials in which only one tone was presented, the correct mean was never equal to the single tone. All listeners completed 880 trials over four runs.
Results
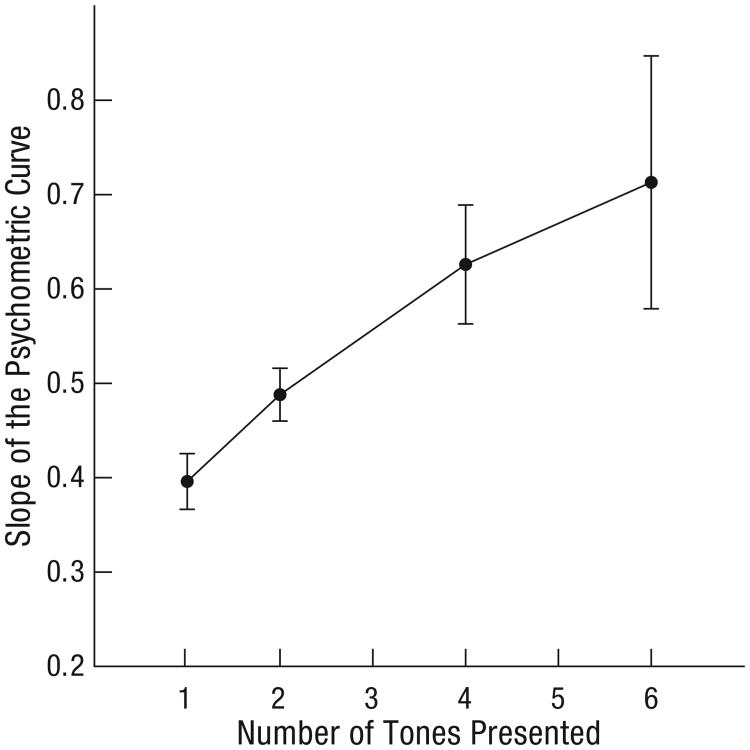
Listeners performed the same task as in Experiment 1, but only a subset of the full tone sequence was presented on each trial. We fit psychometric functions to the data for each of the four conditions (one, two, four, or six tones) using the same method as in Experiment 1 and compared slopes across the four conditions (Fig. 3). The average slope for the six-tone condition was significantly greater than the average slope for the one-tone condition (Wilcoxon signed-ranks test, p < .01, Cohen's d = 0.71) and the two-tone condition (p < .05, Cohen's d = 0.57), but it was not significantly greater than the average slope for the four-tone condition (p = .50). This indicates that listeners integrated a substantial number (at least three) of the tones, and it shows that encoding only one or two tones was insufficient to achieve optimal estimation of the mean frequency of the full six-tone sequence. In other words, listeners used an ensemble code to estimate the mean frequency of the sequence. For those listeners who participated in both Experiment 1 and Experiment 2, we found very high test-retest reliability of slopes for the identical six-tone conditions in the two experiments (Cronbach's α = .94; Cronbach, 1951).
Fig. 3.
Results of Experiment 2: slope of the psychometric curve as a function of the number of tones presented. Error bars represent ±1 SEM.
Experiment 3: Listeners Do Not Reliably Encode Individual Frequencies in a Sequence
Experiment 2 demonstrated that listeners used at least three tones to estimate mean frequency. It is possible that rather than computing a summary statistic, listeners estimated the mean frequency by employing an auditory working memory strategy that involved encoding the individual tones. Auditory working memory capacity has been widely studied (Crowder, 1993; Miller, 1956), and recency effects on tone memory are well-known and robust (Crowder, 1993). In Experiment 3, we used the same stimuli as in Experiment 1 but tested whether listeners could accurately identify individual tones they had just heard within the sequence. Poor performance on this task would suggest that the ensemble code is formed implicitly, without access to individual tones.
Method
Listeners
Ten listeners (6 male, 4 female; age = 18–33 years) participated in Experiment 3 (5 listeners from Experiment 1, 2 listeners from both Experiments 1 and 2, and 3 additional listeners). On average, listeners had 5.2 years of musical training (SD = 5.3) and initiated training at 7.4 years of age (SD = 3.6). All but 1 listener were naive to the purpose of the experiment.
Stimuli and procedure
The sequences were generated and presented in exactly the same way as in Experiment 1, except that each test interval contained two comparison tones (each with a 300-ms duration and separated by 100 ms). These comparison tones consisted of a member of the sequence and a new lure tone that differed by at least 1 semitone (well above the just-noticeable difference for frequency) from any member of the sequence. The temporal order of the lure and the target was counterbalanced across trials. Listeners reported which of the two tones was a member of the sequence in a two-alternative forced-choice task. All listeners completed 192 trials over two runs.
Results
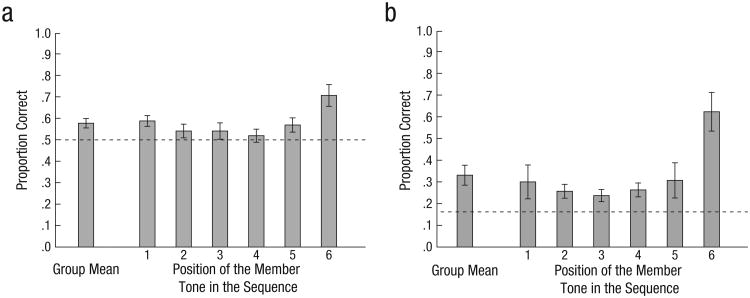
When asked to identify which of the two test tones was present in the preceding sequence, listeners performed significantly, but only slightly, above chance levels (Fig. 4a; one-sample Wilcoxon signed-ranks test, p < .05, Cohen's d = 1.12). This indicates that listeners had limited access to frequency information about individual tones in the sequence. We estimated the mean number of tones that were effectively accessible to the listener at the time of report, assuming a linear relationship between the number of remembered tones and the percentage of correct responses. Specifically, we calculated the difference between perfect performance and chance performance (100% − 50% = 50%) and divided this value by the number of tones in the sequence (six), which resulted in 8.3%. A performance level of 58.3%, or 8.3% above chance (8.3% + 50% = 58.3%), is consistent with representation of a single tone, performance of 66.6% (8.3% + 8.3% + 50% = 66.6%) corresponds to representation of two tones, and so forth. Our listeners' average accuracy rate was 57.7%, or 7.7% above chance. By dividing 7.7% by 8.3% (which corresponds to representation of one tone), we determined that, on average, listeners had access to approximately one of the individual tones in the sequence (0.93 tones, SEM = 0.26) at the time of report, a number that is insufficient to explain the mean discrimination accuracy in Experiments 1 and 2 (see the Discussion section).
Fig. 4.
Results of (a) Experiment 3 and (b) Experiment 4: mean proportion of correct responses when identifying which of two test tones was a member of the preceding sequence and reporting the temporal position of a given member tone, respectively, as a function of the position of the member tone in the preceding sequence. The group mean is also shown. The dashed lines indicate chance-level performance. Error bars represent ±1 SEM.
Experiment 4: Listeners Cannot Reliably Identify a Single Tone's Position Within a Sequence
Experiment 4 was similar to Experiment 3, except that we tested whether listeners could accurately identify the temporal position, rather than the frequency, of individual tones within the six-tone sequence. As in Experiment 3, poor performance would suggest that the ensemble code is formed implicitly, without access to individual tones.
Method
Listeners
Ten individuals from Experiment 1 (including 4 from Experiment 3 and none from Experiment 2) participated in Experiment 4 (2 male, 8 female; age = 18–24 years). On average, listeners had 4.3 years of musical training (SD = 5.6) and initiated training at 9.1 years of age (SD = 3.7). All listeners were naive to the purpose of the experiment.
Stimuli and procedure
The method of generating and presenting the sequences was the same as in Experiment 1, except that the test stimulus was always one of the tones from the preceding sequence. Listeners were asked to identify the position (one through six) of the test tone in the preceding six-tone sequence. Listeners completed 180 trials over two runs.
Results
Overall, listeners correctly identified the position of the test tone in the sequence 33.1% of the time, which is slightly but significantly above chance (Fig. 4b; one- sample Wilcoxon signed-ranks test, p < .01, Cohen's d = 1.14). As in Experiment 3, we estimated the mean number of tones that were accessible to the listener at the time of report. To do this, we again calculated the difference between perfect performance and chance performance (100% − 16.6% = 83.4%) and divided the result by the number of tones (six), which resulted in 13.9%. A performance level of 30.5%, or 13.9% above chance (13.9% + 16.6% = 30.5%), is consistent with representation of a single tone, performance of 44.4% (13.9% + 13.9% + 16.6% = 44.4%) corresponds to representation of two tones, and so forth. The fact that average performance was only 33.1% indicates that listeners had access to position information for approximately one of the individual tones in the sequence (1.18 tones, SEM = 0.33) at the time of report. This is remarkably consistent with the results of Experiment 3 (in particular, a bootstrapped permutation test indicated no significant difference between the mean number of accessible tones in the two experiments, p > .20). In conclusion, both Experiments 3 and 4 indicate that listeners had access to approximately one tone. This very limited auditory working memory capacity for the tone sequences we employed cannot account for the discrimination performance in Experiments 1 and 2 (see the Discussion section).
We also found a significant recency effect: Listeners were significantly more likely to successfully report the position of the test tone when it was the final tone in the sequence than when it was any of the first five tones (related-samples Wilcoxon signed-ranks test; after Bonferroni correction, p < .05 for all five comparisons). Together, the results of Experiments 3 and 4 indicate that listeners' ability to report information about individual tones in the sequence was severely limited.
Discussion
Our results provide the first direct evidence of ensemble coding in the auditory domain. Listeners reliably estimated the mean frequency of a sequence of six sine-wave tones. This ability was severely reduced when we restricted the proportion of these six tones that were presented to listeners, which indicates that ensemble coding occurred over a substantial number (at least three) of the tones in the sequence. This finding rules out cognitive strategies for estimating the mean frequency, such as basing judgments on a single tone in the sequence. Moreover, listeners performed poorly when asked to identify either the frequency or the position of individual tones in a sequence, which indicates that the ensemble code was not based on explicit memory of the individual tones that made up the sequence. Instead, listeners' representations of those tones were transformed into a concise summary representation of the mean frequency.
Previous work on visual statistical summary demonstrates that the number of items in a set that subjects can integrate is equal to approximately the square root of the total set size (Dakin, 2001). Experiment 2 showed that listeners used at least three out of the six tones in a sequence to estimate the mean, a value that is generally consistent with √N (i.e., √6 = ∼2.5). Future work using sequences with a greater number of tones will help elucidate whether, as in vision, this square-root relationship holds for various lengths of auditory sequences.
Auditory frequencies convey crucial information in various social contexts, and ensemble coding of frequency may provide a computationally efficient means of obtaining perceptual information that is essential for communication. Pitch is an important social cue in speech processing: It can indicate emotional tone (Curtis & Bharucha, 2010; Fairbanks & Provonost, 1939), level of interest (Wennerstrom, 2001), gender (Abitbol, Abitbol, & Abitbol, 1999), and even sexual infidelity (O'Connor, Re, & Feinberg, 2011). For instance, the frequency of a single pure tone can influence the perceived gender of a visually androgynous face (Smith, Grabowecky, & Suzuki, 2007). In the natural world, auditory information is broadband, containing multiple frequencies. In the present experiments, we showed that humans can accurately perceive ensemble frequency even when information about individual frequencies is not explicitly encoded. Given that natural environments and stimuli, including speech, contain complex sequences of pitches comprised of multiple frequencies, humans' ability to encode ensemble frequency may have evolved to facilitate perception of social stimuli.
Ensemble frequency encoding may also be a fundamental mechanism underlying music processing, even in individuals without music training. When people hear a tonal sequence (i.e., a melody in a particular key, such as E major), statistical likelihood and hierarchical pitch schemas constrain their understanding of which pitches belong in the sequence and which do not (Krumhansl, 1990; Krumhansl & Cuddy, 2010; Krumhansl & Kessler, 1982; Temperley, 2007). Even listeners without musical training can reliably judge how well a given tone fits into a particular key context (Krumhansl & Kessler, 1982). Our results extend these findings by showing that statistical mechanisms are also involved in the perception of sequences that are not traditionally tonal (i.e., not belonging to a single major or minor key). This gist encoding was independent of musical training (we found no significant correlation between musical training and performance in any of our experiments), which suggests the operation of a basic mechanism for rapidly perceiving an ensemble of tones.
We have shown that statistical summary is a powerful mechanism for perceiving the auditory environment, and we propose that perceiving auditory gist may be critical for social interactions and music perception. Our findings demonstrate that ensemble coding is a useful strategy beyond the visual domain and may be a general mechanism for efficient representation of the environment.
Acknowledgments
We thank Aaron Bloch for assistance with data collection and Jason Fischer for providing code for fitting psychometric curves.
Funding: This research was supported by the Department of Defense through a National Defense Science and Engineering Graduate Fellowship awarded to E. A. Piazza, by National Science Foundation Grant 1245461 to D. Whitney, and by National Eye Institute Core Grant EY003176.
Footnotes
Declaration of Conflicting Interests: The authors declared that they had no conflicts of interest with respect to their authorship or the publication of this article.
Author Contributions: E. A. Piazza developed the study concept. E. A. Piazza, T. D. Sweeny, D. Whitney, and D. Wessel contributed to the study design. Testing and data collection were performed by E. A. Piazza, who performed the data analysis and interpretation under the supervision of D. Whitney, T. D. Sweeny, and M. A. Silver. E. A. Piazza drafted the article, and D. Whitney, M. A. Silver, and T. D. Sweeny provided critical revisions.
References
- Abitbol J, Abitbol P, Abitbol B. Sex hormones and the female voice. Journal of Voice. 1999;13:424–446. doi: 10.1016/s0892-1997(99)80048-4. [DOI] [PubMed] [Google Scholar]
- Albrecht AR, Scholl BJ. Perceptually averaging in a continuous visual world: Extracting statistical summary representations over time. Psychological Science. 2010;21:560–567. doi: 10.1177/0956797610363543. [DOI] [PubMed] [Google Scholar]
- Albrecht AR, Scholl BJ, Chun MM. Perceptual averaging by eye and ear: Computing summary statistics from multimodal stimuli. Attention, Perception, & Psychophysics. 2012;74:810–815. doi: 10.3758/s13414-012-0293-0. [DOI] [PubMed] [Google Scholar]
- Alvarez G. Representing multiple objects as an ensemble enhances visual cognition. Trends in Cognitive Sciences. 2011;15:122–131. doi: 10.1016/j.tics.2011.01.003. [DOI] [PubMed] [Google Scholar]
- Alvarez G, Oliva A. The representation of simple ensemble visual features outside the focus of attention. Psychological Science. 2008;19:392–398. doi: 10.1111/j.1467-9280.2008.02098.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ariely D. Seeing sets: Representation by statistical properties. Psychological Science. 2001;12:157–162. doi: 10.1111/1467-9280.00327. [DOI] [PubMed] [Google Scholar]
- Bauer B. Does Steven's power law for brightness extend to perceptual brightness averaging? Psychological Record. 2009;59:171–186. [Google Scholar]
- Bregman AS. Auditory scene analysis. Cambridge, MA: MIT Press; 1990. [Google Scholar]
- Bregman AS, Campbell J. Primary auditory stream segregation and perception of order in rapid sequences of tones. Journal of Experimental Psychology. 1971;89:244–249. doi: 10.1037/h0031163. [DOI] [PubMed] [Google Scholar]
- Chong S, Treisman A. Representation of statistical properties. Vision Research. 2003;43:393–404. doi: 10.1016/s0042-6989(02)00596-5. [DOI] [PubMed] [Google Scholar]
- Cronbach LJ. Coefficient alpha and the internal structure of tests. Psychometrika. 1951;16:297–334. [Google Scholar]
- Crowder RG. Auditory memory. In: McAdams S, Bigand E, editors. Thinking in sound: The cognitive psychology of human audition. Oxford, England: Clarendon Press; 1993. pp. 113–145. [Google Scholar]
- Curtis ME, Bharucha JJ. The minor third communicates sadness in speech, mirroring its use in music. Emotion. 2010;10:335–348. doi: 10.1037/a0017928. [DOI] [PubMed] [Google Scholar]
- Dakin S. Information limit on the spatial integration of local orientation signals. Journal of the Optical Society of America A. 2001;18:1016–1026. doi: 10.1364/josaa.18.001016. [DOI] [PubMed] [Google Scholar]
- de Fockert J, Wolfenstein C. Rapid extraction of mean identity from sets of faces. The Quarterly Journal of Experimental Psychology. 2009;62:1716–1722. doi: 10.1080/17470210902811249. [DOI] [PubMed] [Google Scholar]
- de Gardelle V, Summerfield C. Robust averaging during perceptual judgment. Proceedings of the National Academy of Sciences, USA. 2011;108:13341–13346. doi: 10.1073/pnas.1104517108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deutsch D. The tritone paradox: An influence of language on music perception. Music Perception. 1991;8:335–347. [Google Scholar]
- Dolson M. The pitch of speech as a function of linguistic community. Music Perception. 1994;11:321–331. [Google Scholar]
- Fairbanks G, Provonost W. An experimental study of the pitch characteristics of the voice during the expression of emotion. Speech Monographs. 1939;6:87–104. [Google Scholar]
- Fischer J, Whitney D. Object-level visual information gets through the bottleneck of crowding. Journal of Neurophysiology. 2011;106:1389–1398. doi: 10.1152/jn.00904.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haberman J, Harp T, Whitney D. Averaging facial expression over time. Journal of Vision. 2009;9(11) doi: 10.1167/9.11.1. Article 1. Retrieved from http://www.journalofvision.org/content/9/11/1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haberman J, Whitney D. Rapid extraction of mean emotion and gender from sets of faces. Current Biology. 2007;17:751–753. doi: 10.1016/j.cub.2007.06.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holt L. The mean matters: Effects of statistically defined nonspeech spectral distributions on speech categorization. Journal of the Acoustical Society of America. 2006;120:2801–2817. doi: 10.1121/1.2354071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krumhansl CL. Cognitive foundations of musical pitch. New York, NY: Oxford University Press; 1990. [Google Scholar]
- Krumhansl CL, Cuddy LL. A theory of tonal hierarchies in music. In: Jones MR, Fay RR, Popper AN, editors. Music perception. New York, NY: Springer; 2010. pp. 51–87. [Google Scholar]
- Krumhansl CL, Kessler EJ. Tracing the dynamic changes in perceived tonal organization in a spatial representation of musical keys. Psychological Review. 1982;89:334–368. [PubMed] [Google Scholar]
- Loui P, Wessel DL, Hudson-Kam CL. Humans rapidly learn grammatical structure in a new musical scale. Music Perception. 2010;27:377–388. doi: 10.1525/mp.2010.27.5.377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDermott JH, Simoncelli EP. Sound texture perception via statistics of the auditory periphery: Evidence from sound synthesis. Neuron. 2011;71:926–940. doi: 10.1016/j.neuron.2011.06.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Micheyl C, Oxenham AJ. Pitch, harmonicity and concurrent sound segregation: Psychoacoustical and neurophysiological findings. Hearing Research. 2010;266:36–51. doi: 10.1016/j.heares.2009.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller GA. The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychological Review. 1956;63:81–97. [PubMed] [Google Scholar]
- Moore BCJ. An introduction to the psychology of hearing. 5th. San Diego, CA: Academic Press; 2003. [Google Scholar]
- Myczek K, Simons DJ. Better than average: Alternatives to statistical summary representations for rapid judgments of average size. Perception & Psychophysics. 2008;70:772–788. doi: 10.3758/pp.70.5.772. [DOI] [PubMed] [Google Scholar]
- O'Connor J, Re DE, Feinberg DR. Voice pitch influences perceptions of sexual infidelity. Evolutionary Psychology. 2011;9:64–78. [PubMed] [Google Scholar]
- Parkes L, Lund J, Angelucci A, Solomon J, Morgan M. Compulsory averaging of crowded orientation signals in human vision. Nature Neuroscience. 2001;4:739–744. doi: 10.1038/89532. [DOI] [PubMed] [Google Scholar]
- Saffran JR, Johnson EK, Aslin RN, Newport EL. Statistical learning of tone sequences by human infants and adults. Cognition. 1999;70:27–52. doi: 10.1016/s0010-0277(98)00075-4. [DOI] [PubMed] [Google Scholar]
- Smith EL, Grabowecky M, Suzuki S. Auditory-visual crossmodal integration in perception of face gender. Current Biology. 2007;17:1680–1685. doi: 10.1016/j.cub.2007.08.043. [DOI] [PubMed] [Google Scholar]
- Sweeny TD, Haroz S, Whitney D. Perceiving group behavior: Sensitive ensemble coding mechanisms for biological motion of human crowds. Journal of Experimental Psychology: Human Perception and Performance. 2013;39:329–337. doi: 10.1037/a0028712. [DOI] [PubMed] [Google Scholar]
- Temperley D. Music and probability. Cambridge, MA: MIT Press; 2007. [Google Scholar]
- Watamaniuk SNJ, Duchon A. The human visual system averages speed information. Vision Research. 1992;32:931–941. doi: 10.1016/0042-6989(92)90036-i. [DOI] [PubMed] [Google Scholar]
- Wennerstrom AK. The music of everyday speech: Prosody and discourse analysis. New York, NY: Oxford University Press; 2001. [Google Scholar]
- Williams DW, Sekuler R. Coherent global motion percepts from stochastic local motions. Vision Research. 1984;24:55–62. doi: 10.1016/0042-6989(84)90144-5. [DOI] [PubMed] [Google Scholar]