Abstract
Purpose
Reliably detecting MRI signals in the brain that are more tightly coupled to neural activity than BOLD fMRI signals could not only prove valuable for basic scientific research but could also enhance clinical applications such as epilepsy presurgical mapping. This endeavor will likely benefit from an improved understanding of the behavior of ionic currents, the mediators of neural activity, in the presence of the strong magnetic fields that are typical of modern-day MRI scanners.
Theory
Of the various mechanisms that have been proposed to explain the behavior of ionic volume currents in a magnetic field, only one—magnetohydrodynamic (MHD) flow—predicts a slow evolution of signals, on the order of a minute for normal saline in a typical MRI scanner.
Methods
This prediction was tested by scanning a volume-current phantom containing normal saline with gradient-echo EPI at 3 T.
Results
Greater signal changes were observed in the phase of the images than in the magnitude, with the changes evolving on the order of a minute.
Conclusion
These results provide experimental support for the MHD flow hypothesis. Furthermore, MHD-driven cerebrospinal fluid (CSF) flow could provide a novel fMRI contrast mechanism.
Keywords: neuronal currents, magnetohydrodynamic flow, ionic currents, CSF, fMRI, BOLD
Introduction
Understanding the behavior of ionic currents in the presence of strong magnetic fields could facilitate efforts to use MRI to detect signals that are more tightly coupled to neuronal activity than the hemodynamic response—efforts that, if successful, could have a tremendous impact on neuroscience and medicine. However, studies reporting the detection of such signals have been, for the most part, controversial and irreproducible (1, 2), with several reports of negative findings (3–11) conflicting with reports of positive findings (12–24). This lack of consensus is echoed in studies attempting to model or simulate these signals (25–35).
Even studies in simple phantoms are not without controversy: Truong et al. (36) investigated ionic volume currents in a spherical phantom scanned at 4 T, and observed a large apparent displacement of the currents in a direction orthogonal to the main magnetic field , an effect they explain with a simple mechanism incorporating the Lorentz force law and a drag term. However, Wijesinghe and Roth (37) pointed out that when realistic values of ion mobility are used in the model proposed by Truong et al., the predicted displacement of the volume currents by the magnetic field is negligible. They instead suggested that magnetohydrodynamic (MHD) flow effects, which are thought to explain the distortion of electrocardiogram (ECG) signals at high field strengths (38, 39), may offer a better explanation of the signals observed by Truong et al., but did not provide any experimental support for this hypothesis.
If phenomena such as those described by Truong et al. (36) are in fact due to MHD flow, then the observed signal changes should develop on a relatively slow time scale—on the order of a minute for normal (0.9%) saline in a 3 T magnetic field (see Theory). Our goal here was to test this prediction with a volume-current phantom containing normal saline, on which we obtained echo-planar imaging (EPI) magnitude and phase data at 3 T, as described in the Methods. As shown in the Results, we do indeed observe a slow evolution of phase changes, providing experimental support for detectable MHD effects in ionic-current phantoms scanned at these field strengths. In the Discussion, we compare our study to other MRI studies of electric-current phantoms, followed by a discussion of the source of phase contrast in our data and the sensitivity of phase versus magnitude image contrast to electric currents. We then compare the amplitude of the electric currents in our phantom experiments to the corresponding values for epilepsy, based on an estimate derived from previous reports of invasive electrophysiology measurements in humans. Finally, we consider the possibility that changes in the flow of cerebrospinal fluid (CSF) due to MHD effects might lead to a novel functional MRI contrast mechanism, especially in the context of epilepsy, where regions of high-amplitude electrical activity are often adjacent to large CSF spaces such as the lateral ventricles.
Theory
We take as our starting point the Navier-Stokes equation for a conducting fluid:
| [1] |
where ρ is the fluid density, is the fluid velocity, is the particle derivative (also known as the material derivative or the advective derivative), is the sum of all of the applicable non-electromagnetic (NEM) force density terms, such as those due to pressure gradients, viscosity and gravity, and is the electromagnetic (EM) force density, i.e., the Lorentz force in the continuum. For an electrically neutral fluid (containing an equal number of positive and negative charges),
| [2] |
where is the electric current density in the fluid and is the magnetic field. In addition to the equations above, we have Ohm’s law for a fluid, which is given by
| [3] |
where σ is the conductivity, is the electric field, and and are as above. Although not explicitly written, all of the physical quantities above are assumed to be functions of space and time t.
If we combine the three equations above, we obtain the following magnetohydrodynamic (MHD) equation of motion (as derived in the Appendix):
| [4] |
where and are the components of and , respectively, that are perpendicular to , and is the component of that is parallel to . Note that the flow parallel to is governed purely by the non-electromagnetic force term (40). On the other hand, the flow perpendicular to is driven by the term and damped by the σB2 term (where ), and therefore evolves on a time scale on the order of τ = ρ/(σB2)—a quantity known as the Joule or magnetic damping time (see refs. 40–42).
For normal (0.9%) saline or cerebrospinal fluid (CSF) at room temperature (25°C), ρ = 1000 kg/m3 and σ ≈ 1.5 S/m; in a 3 T scanner, this results in a value of τ ≈ 75 seconds. At body temperature (37°C), the conductivity of CSF increases to σ ≈ 1.8 S/m (43), resulting in a slightly lower value of τ ≈ 60 seconds. Therefore, we hypothesize that for such fluids and field strengths, signal changes due to MHD effects will take on the order of tens of seconds to develop—a hypothesis we test by passing long-duration currents through a pair of saline phantoms, as described in the Methods.
Methods
Ionic-current phantoms
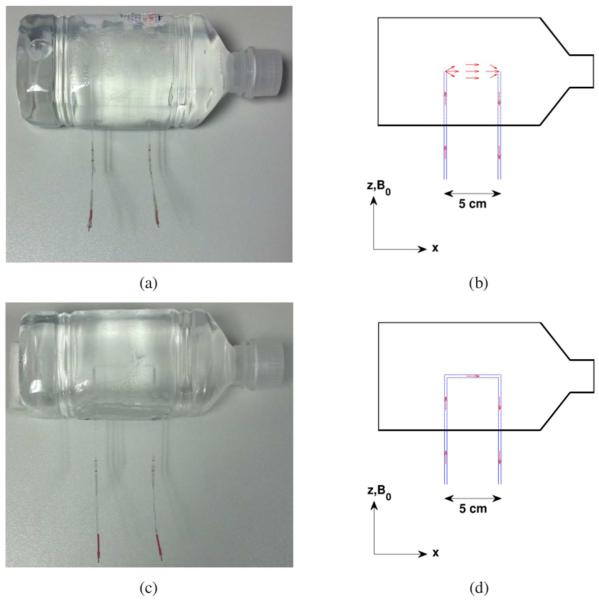
The volume-current phantom used in this study was constructed by embedding two glass capillary tubes (1.2 mm inner diameter, 1.6 mm outer diameter) inside a 9 × 9 × 22 cm plastic bottle, with the tubes spaced 5 cm apart and running parallel to the main magnetic field , as shown in Fig. 1(a). The bottle and the capillary tubes were filled with a solution of 1 L normal saline (0.9%) and 1 mL of gadopentetate dimeglumine (Magnevist, Berlex Laboratories). Chloridized silver electrodes, which are non-polarizing and therefore advantageous for the application of direct currents, were inserted into the two capillary tubes, in the section of these tubes that extended outside the bottle (and outside the imaging field-of-view). The two electrodes were connected to a twisted-pair cable leading to a signal generator (Rigol DG1022) and a 10 kΩ resistor, connected in series, in the scanner console room. The potential difference across the resistor was measured with an oscilloscope (Rigol DS1052E), allowing us to calculate the current running through the circuit. This setup allowed us to pass ionic direct currents of various amplitudes and durations through the volume of the phantom, from the end of one capillary tube to the other, as shown schematically in Fig. 1(b).
Fig. 1.
(a) Photograph of the volume-current phantom used in this study. (b) Diagram of the volume-current phantom, with the capillary tubes shown in blue. Positive ionic current (schematic red arrows) flows into and along the left capillary tube, through the volume of the phantom, and along and out of the right capillary tube. Photograph (c) and diagram (d) of the control phantom, which is nearly identical to the volume-current phantom, except for an additional capillary tube connecting the left and right capillary tubes of the original phantom. Consequently, ionic currents in this phantom (red arrows) are restricted to the interiors of the capillary tubes and do not flow through the volume of the phantom.
In addition, we constructed a control phantom that was nearly identical to the phantom described above, but which had no volume currents flowing through it. This was achieved by connecting the two capillary tubes with a third capillary tube inside the bottle, ensuring that any ionic currents would be contained within the three capillary tubes and not flowing through the volume of the phantom, as shown in Fig. 1(c) and Fig. 1(d).
MRI sequence parameters
All MRI data were acquired on a 3 T Siemens MAGNETOM Trio system (Siemens Healthcare, Erlangen, Germany) equipped with a 12-channel receive coil array for the head. A standard single-shot gradient-echo interleaved multi-slice EPI sequence was used, with the following parameters: TR/TE = 750/32 ms, flip angle = 20°, bandwidth = 2298 Hz/pixel, echo spacing = 0.5 ms, FOV = 220 × 220 mm, matrix = 64 × 64, slice thickness = 5 mm, and number of slices = 15, resulting in a 3.4 × 3.4 × 5 mm voxel size.
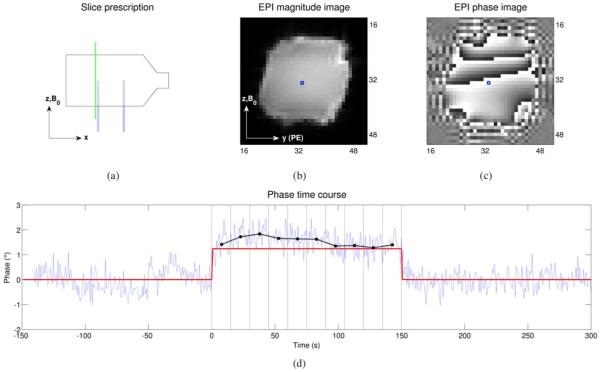
The slice-select gradient was chosen to be along the x-axis (i.e., in the left-to-right direction), resulting in images in the y-z plane (see Fig. 2). For the vast majority of the acquisitions, the phase-encode (PE) direction was chosen to be along +y, as shown in Fig. 2(b), with the readout (RO) direction along +z. However, for one set of acquisitions, the imaging gradients were reversed, with the PE direction along −y and the RO direction along −z, in order to investigate the sensitivity of the imaging gradients to fluid flow.
Fig. 2.
(a) The location of a slice in the y-z plane (a “sagittal” slice), slightly to the left of the left capillary tube in the volume-current phantom, is shown with the dashed green line. The corresponding EPI magnitude and phase DICOM images, as reconstructed by the scanner, are shown in (b) and (c), respectively (intensities are in arbitrary units, i.e., the 12-bit integer values typical of DICOM images). For the voxel marked with the blue square in (b) and (c), the phase time course (light blue) is shown in (d). The current is off for the first 150 seconds (the baseline period), on for the next 150 seconds (the ON period), and then off again for the last 150 seconds, as indicated by the red trace. The phase time course was quadratically detrended and the average value during the baseline period was subtracted out—in other words, the light blue trace shows the phase change (in degrees) relative to the baseline period, for this voxel. The ON period was divided into 15-second bins, indicated by the vertical black lines, and the average phase change (relative to baseline) for each bin was calculated and is shown by the black dots. This process was repeated for each voxel in order to generate the phase-change images shown in Fig. 3 and Fig. 4.
Data acquisition and analysis
Each EPI scan was acquired for 450 seconds which, given the TR of 750 ms, resulted in 600 time points per acquisition. Magnitude and phase images were reconstructed for each time point, as shown in Fig. 2(b) and Fig. 2(c). For the first 150 seconds (the baseline period) of the acquisition, currents were off; for the next 150 seconds, either positive or negative currents with an amplitude of 60 μA were turned on (the ON period); and for the last 150 seconds, currents were off again, as indicated by the red trace in Fig. 2(d).
For the phase data, the time course for each voxel was quadratically detrended (in order to discount the effects of any scanner drift) and the average baseline value was subtracted out, resulting in the phase change (in degrees) relative to baseline. The ON period was divided into 15-second bins and the average phase change within each bin was computed, in order to produce less noisy phase estimates, as shown in Fig. 2(d). Repeating this process for each voxel resulted in the phase-change images shown in Fig. 3 and Fig. 4.
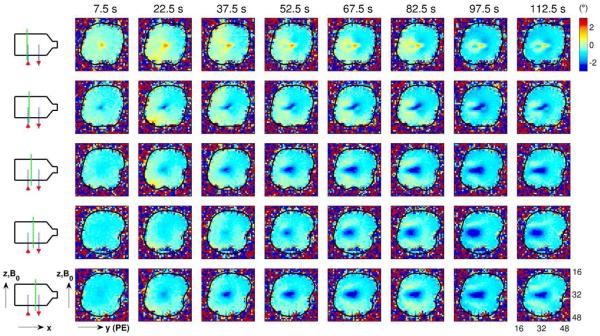
Fig. 3.
Using the process described in Fig. 2, images of phase change (in degrees) relative to the baseline time period were generated for several time bins and slice positions. Each column of images corresponds to a different time bin, with the time corresponding to the bin center shown at the top of each column (e.g., the center of the first time bin is 7.5 s after current onset). Each row of images corresponds to a different slice position, indicated by the dashed green line on the schematic diagram to the left of each row. Ionic current flows “up” the left capillary tube (in the positive z-direction), through the body of the phantom and “down” the right capillary tube (in the negative z-direction), as shown by the red arrows in the schematic diagrams. The black contour in the images indicates the boundary of the phantom. Note that the spatial pattern of phase changes develops over the course of tens of seconds, as is particularly evident in the images from the central slice (fourth row of images).
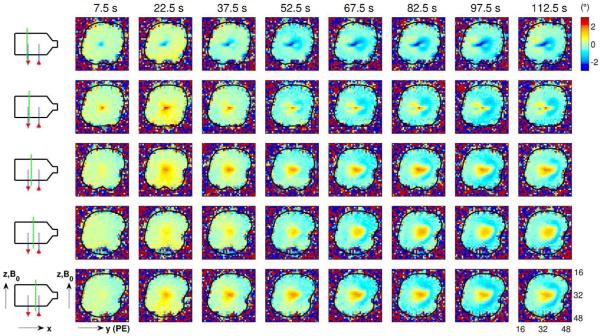
Fig. 4.
Phase-change images relative to baseline (in degrees) as in Fig. 3, but with the direction of the ionic currents reversed, i.e., current flows “up” the right capillary tube (in the positive z-direction), through the body of the phantom and “down” the left capillary tube (in the negative z-direction), as shown by the red arrows in the schematic diagrams. As with the results shown in Fig. 3, the spatial pattern of phase changes develops over the course of tens of seconds. However, unlike Fig. 3, the large region of phase change near the center of the phantom (e.g., see fourth row of images) is now positive (rather than negative), and migrates in the positive (rather than the negative) y-direction.
For the magnitude data, a similar procedure was followed. Here, however, the changes were computed as a percent difference from the average baseline value. Repeating this process for each voxel resulted in the magnitude-change images shown in Fig. 5.
Fig. 5.
Changes in the magnitude of the EPI images for the same current direction, time bins and slice positions as Fig. 3. The magnitude time course for each voxel was quadratically detrended and the percent change relative to the baseline time period was computed for each time bin, resulting in the magnitude-change images shown here. The black contour in the images indicates the boundary of the phantom.
Results
Phase-change images resulting from the application of a positive current (with 60 μA amplitude and 150 s duration) are shown in Fig. 3. A “positive” current here is arbitrarily designated as a current that flows “up” the left capillary tube (in the positive z-direction), through the body of the phantom and “down” the right capillary tube (in the negative z-direction). Note that, as hypothesized in the Theory, the spatial pattern of phase changes develops on a time scale of tens of seconds, as is particularly evident in the images from the central slice (fourth row of images in Fig. 3).
Reversing the current direction leads to the phase-change images shown in Fig. 4. Again, note that the spatial pattern takes tens of seconds to develop. However, the sign of the phase change is now reversed: instead of the predominantly negative phase changes seen in Fig. 3, we now see predominantly positive phase changes. Furthermore, note that the large zone of positive phase change seen near the center of the phantom (rows 3–5 in Fig. 4) appears to drift in the positive y-direction, whereas in Fig. 3, the corresponding central zone (with negative phase change) drifts in the negative y-direction.
Fig. 5 shows the magnitude-change images corresponding to the positive current direction. Although it is not straightforward to make direct comparisons between percent changes in magnitude and phase changes in degrees, it can nevertheless be argued that the changes are far less apparent in the magnitude data.
The control phantom (described in the Methods and Fig. 1) contains no volume currents, preventing MHD effects from developing in the phantom (other than inside the capillary tubes—well below the resolution of our EPI scans). This phantom was scanned under the same experimental conditions as the volume-current phantom, and the phase-change images for the central slice (in the positive-current condition) are shown in Fig. 6 (upper row). The corresponding phase-change images for the volume-current phantom are shown for comparison in the lower row. Note that, in the control phantom, the spatial pattern of phase changes develops immediately (i.e., by the first time bin), unlike the slow evolution seen in the volume-current phantom. Incidentally, the phase-change images for the control phantom have a very similar spatial pattern to that of the z-component of the magnetic field produced by a current in an infinite straight wire along x (i.e., the direction of the central capillary tube), as given by Ampère’s law.
Fig. 6.
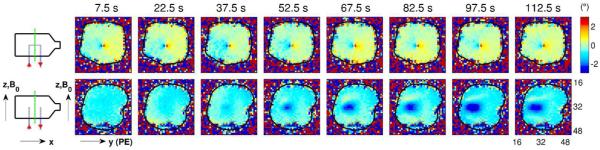
Phase-change patterns in the control phantom, in which there are no volume currents, versus the volume-current phantom (see Methods and Fig. 1 for a detailed description of the two phantoms). The upper row shows the spatial pattern of phase changes over time for the central slice through the control phantom. The lower row shows the corresponding phase changes in the volume-current phantom (note that this is a reproduction of the fourth row of images from Fig. 3). By comparing these two rows of images, we see that the spatial pattern of phase changes develops “immediately” in the control phantom (i.e., by the first time bin), but takes tens of seconds to develop in the volume-current phantom.
In order to quantify the pattern of phase changes seen in Fig. 6, we computed the root-mean-square-difference (RMSD) between the phase map for the first time bin and the phase map for each subsequent time bin, for both the control phantom and the volume-current phantom, excluding voxels lying outside the phantom. Plots of RMSD versus time are shown in Fig. 7, confirming the qualitative observations made from inspection of Fig. 6.
Fig. 7.
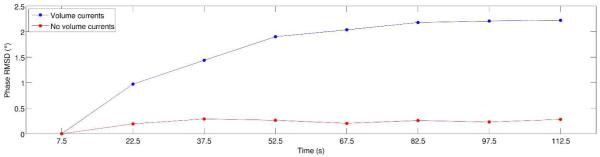
The root-mean-square-difference (RMSD) between the phase map for the first time bin and the phase map for each time bin is shown for the control phantom (red curve) and the volume-current phantom (blue curve). These plots support the result that can be observed qualitatively in Fig. 6, i.e., that the spatial pattern of phase changes develops immediately in the control phantom, which contains no volume currents, but takes on the order of a minute to develop in the volume-current phantom. (Note that, for both phantoms, the RMSD for the first time bin, centered at 7.5 seconds, is zero by definition.)
As described in the Methods, the imaging gradients were reversed in order to investigate the sensitivity of the acquired images to flow effects, and the resulting phase maps for the central slice through the volume-current phantom are shown in Fig. 8. Note the reversal of the sign of the main phase changes with the reversal of the gradients, even with the direction of the ionic currents kept unchanged. The implications of this result are discussed in greater detail in a later subsection (“The source of the observed MRI phase contrast”). Since the data shown in the lower rows of Fig. 6 and Fig. 8 were collected under the same conditions but several months apart, we remark as an aside that a comparison of these two rows also demonstrates the test-retest reliability of these measurements.
Fig. 8.
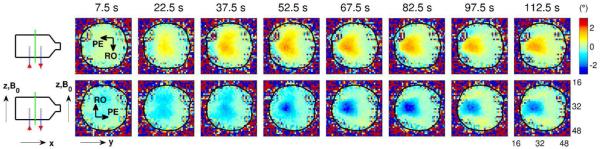
The effect of reversing the direction of the imaging gradients on the phase changes observed in the volume-current phantom. The upper row shows the spatial pattern of phase changes over time for the central slice through the phantom when the PE direction was along −y and the RO direction was along −z. The lower row shows the corresponding phase changes observed in the same phantom when the PE direction was along +y and the RO direction was along +z, as was the case for all previous results. Note that the direction of the ionic currents is the same for the two conditions, and for both conditions the large region of phase change migrates in the −y direction. However, the sign of the main phase changes reverses with the gradients, suggesting that these phase changes are predominantly due to flow effects.
Discussion and Conclusions
Comparison with other MRI studies of electric-current phantoms
Several reports on the detection of electric currents in phantoms with MRI have been published (12, 19,20, 44–54); in these studies, however, the currents were carried by either metal or carbon wires, neither of which are realistic conduits for neural currents (or, more generally, biological currents). On the other hand, the currents in the phantoms used by Scott and colleagues (55–59) were carried by ions in solution, as is the case with biological currents. However, the main goal of those studies was to demonstrate the use of MRI for noninvasively measuring static or periodic current densities, and thus the experiments were designed to minimize the effect of the main magnetic field on the current distributions (55). In other MR studies of phantoms carrying ionic currents, the influence of on the currents was similarly deemed insignificant given the experimental conditions (60, 61) or was not considered at all (3, 62, 63).
To the best of our knowledge, the only MRI studies that have investigated the effect of the main magnetic field on the behavior of ionic volume currents are the present study and that of Truong et al. (36), and we now describe the main differences between these two studies. With regard to the design and composition of the phantoms, Truong et al. used a spherical phantom containing copper sulphate (CuSO4) solution with a conductivity of 1.4 S/cm, whereas our phantoms had a roughly rectangular shape (see Fig. 1) and contained normal (0.9%) saline (i.e., NaCl solution), which has a conductivity of approximately 0.015 S/cm (64)—two orders of magnitude lower than the conductivity used by Truong et al. and a more realistic model of fluids in biological tissues and organs. Furthermore, the 60 μA currents that we passed through our phantoms have a plausible amplitude for epileptiform activity, as discussed in a later subsection (“The amplitude of epileptiform currents in humans”), whereas Truong et al. use currents as high as 5 mA (i.e., approximately two orders of magnitude higher).
With regard to pulse sequences, Truong et al. (36) used a modification of a conventional gradient-echo sequence, acquiring one line of k-space per RF excitation, rather than using a single-shot EPI readout that acquires all lines of k-space following each RF excitation, as we did. Consequently, it would have taken them 19.2 seconds (150 ms TR × 128 phase encoding steps) to acquire a single image (per slice position), whereas we acquired one image (per slice position) every 750 ms, allowing us to investigate signal evolution at time scales on the order of a second. It should be mentioned, however, that they obtained images with much higher in-plane resolution (0.5 mm) than ours (3.4 mm). Furthermore, Truong et al. did not look at phase images, as we did, and instead focused on magnitude images. In order to produce detectable signal changes in the magnitude images, they applied oscillating magnetic-field gradients in synchrony with the ionic-current pulses, thus amplifying the intra-voxel dephasing induced by the currents (for details, see reference 36).
In spite of all of these differences, signal changes primarily perpendicular to were observed both by Truong et al. (36) and by us. However, very different explanations of these observed signal changes are proposed in the two studies: we contend that the slow development of phase patterns, as seen in our study, provides experimental support for MHD effects as the underlying explanation of the phenomena observed in both studies, in agreement with the theoretical arguments made by Wijesinghe and Roth (37) and in contradiction to the explanation proposed by Truong et al. (36). Computer simulations (65) also provide support for MHD effects as the best explanation of the signals observed by Truong et al.
The source of the observed MRI phase contrast
Let ΔBz be the z-component of the average magnetic field change within a voxel due to the presence of electric currents within the object of interest. The resulting phase shift Δϕcurrent of the magnetization vector in this voxel (for a gradient-echo sequence) is given by
| [5] |
where γ is the gyromagnetic ratio (2π × 42.58 MHz/T for protons), TE is the echo time, ΔBz(t) is the z-component of the magnetic field due to the currents as a function of time, and t is time. If the currents, and therefore ΔBz(t), can be assumed to be static in the time interval between the application of the RF excitation pulse and the time at which the subsequent gradient echo forms (i.e., ΔBz(t) = ΔBz), the equation above simplifies to
| [6] |
Eq. 6 (or its generalization, Eq. 5) is typically invoked as the source of current-related MRI phase contrast (2, 3, 19, 26, 27, 29–31, 34, 35, 44, 48, 51, 62)—however, this fails to fully explain the phase changes seen in Fig. 6, as we discuss below.
Recall that the amplitude of the current passed through the two phantoms is the same (60 μA); in the control phantom, however, the current is contained within the central capillary tube, whereas in the volume-current phantom, the current can flow throughout the body of the phantom. Therefore, the current density should be much higher in the control phantom than in the volume-current phantom, resulting in greater values of ΔBz, as follows from the Biot-Savart law (40). We would therefore expect the maximum phase change to be far greater in the control phantom than in the volume-current phantom—however, close examination of Fig. 6 reveals that this is clearly not the case.
In order to account for the “extra” phase shifts seen in the volume-current phantom, we remark that MRI phase is sensitive to fluid flow, even in the absence of any current flow—a fact that is routinely exploited in velocity-encoding MRI techniques used for flow quantification (66–71). For a bipolar, rectangular gradient waveform, such that each of the two lobes has amplitude G and duration tδ, with the temporal separation between the positive lobe and the negative lobe given by tΔ, the phase shift Δϕflow of the magnetization vector within a voxel due to fluid flow is given by
| [7] |
where γ is again the gyromagnetic ratio, v is the average speed of the fluid within the voxel, and θ is the angle between the direction of the first gradient lobe and the direction of the average fluid velocity within the voxel (72). For flow quantification, velocity-encoding gradients are typically introduced into the pulse sequence in addition to the imaging gradients; however, even in the absence of explicit velocity-encoding gradients, the imaging gradients themselves will exhibit some sensitivity to fluid flow (unless flow-compensated imaging gradients are used). Although Eq. 7 is not directly applicable to EPI gradient waveforms, which are typically neither rectangular nor bipolar, it nevertheless serves to illustrate the relationship between magnetic-field gradients, fluid flow, and phase shifts in a simplified scenario.
Note that the phase change Δϕflow due to fluid flow could have the opposite sign as the phase change Δϕcurrent due to electric currents, leading to a (partial) cancellation of phase shifts within the voxel. However, the fact that we see such robust phase shifts in the volume-current phantom relative to the control phantom (Fig. 6) suggests that Δϕflow dominates Δϕcurrent (since the latter is expected to be much smaller in the volume-current phantom than the control phantom, based on the argument above). Reversing the direction of the EPI gradients and hence the sign of Δϕflow (but not that of Δϕcurrent) led to a reversal of the sign of the phase changes observed in the volume-current phantom (Fig. 8), confirming that Δϕflow is indeed the dominant source of phase contrast here.
Although greater contrast in phase images over magnitude images (in response to electric currents) has been reported in several studies (14, 16, 44, 62), arguments for magnitude contrast over phase contrast have also been made (13, 20, 21, 26, 31, 48). In our study, we see far greater contrast in the phase data than in the magnitude data (compare Fig. 3 and Fig. 5)—a result we attribute to flow-related phase shifts in the volume-current phantom, as discussed above.
The amplitude of epileptiform currents in humans
In this study, we applied 60 μA currents to the two ionic-current phantoms that were imaged, and we now consider the question of how this current amplitude compares to the amplitude of epileptiform currents in humans. Direct measurements of this nature are obviously hard to obtain and we therefore provide a “back-of-the-envelope” estimate of the relevant current amplitude, based in part on the strategy used by Kobayashi et al. (73) in their attempt to estimate the current dipole-moment density associated with epileptiform discharges.
Assume that we have a cylindrical patch of cortex with length l and circular cross-sectional area a, with current uniformly distributed throughout the cylinder and flowing along its main axis. Let v be the potential difference across the two circular faces of the cylinder and let ρ be the resistivity of cortex. The current amplitude i is then obtained via Ohm’s law:
| [8] |
Estimating i therefore requires knowledge of v, a, ρ, and l, and we turn to the epilepsy literature for these values: Alarcon et al. (74) studied interictal discharges in presurgical epilepsy patients implanted with intracranial electrodes and observed voltage differences of up to 750 μV between depth electrodes 2.5 mm apart. The area of cortex that needs to be synchronously active in order to generate an interictal spike on scalp EEG is believed to be at least 6 cm2 (73, 75) and the resistivity of cortex is approximately 3 Ωm (73, 74). Inserting these values (v = 750 × 10−6 V, l = 2.5 × 10−3 m, a = 6 × 10−4 m2, and ρ = 3 Ωm) into Eq. 8, we obtain an estimate of i = 6 × 10−5 A = 60 μA—the value we used in our phantoms.
We emphasize that 60 μA should not be taken as an exact figure for epileptiform current amplitudes. As mentioned above, 6 cm2 is a lower bound for the active area of cortex, leading to a possible underestimate of the current amplitude. On the other hand, a potential difference of 750 μV across 2.5 mm is at the high end of the published range (73, 74), leading to a possible overestimate. Furthermore, neural currents are unlikely to be modeled well by a simple homogeneous cylinder, with complicated conductivity boundaries between tissue and CSF more likely to be found in reality. Thus 60 μA is best seen as a “ballpark” figure, within approximately one order of magnitude of actual epileptiform current amplitudes.
MHD-driven CSF flow: a novel functional MRI contrast mechanism?
Functional magnetic resonance imaging (fMRI) based on the “blood-oxygen-level-dependent” (BOLD) signal is by far the most common functional neuroimaging technique in use today (76–80). However, other fMRI methods based on non-BOLD vascular signals are also worthy of mention, such as functional cerebral blood flow (CBF) changes measured with arterial spin labeling (ASL) techniques (81–85) or functional cerebral blood volume (CBV) changes measured with the VASO technique (86–88).
Considerable effort has gone into the search for fMRI signal changes that are non-vascular in origin, in the hope of finding signals that are more tightly coupled to neural activity than the vascular changes accompanying this activity. One avenue of research is based on 1–100 μT “ultra-low-field” MRI (89–91), where the proton Larmor frequencies overlap with the frequency bands of neural electrical activity, leading to the intriguing possibility that neural activity itself can serve as the excitation pulse in an ultra-low-field fMRI pulse sequence (92, 93). The extremely low signal-to-noise ratio (SNR) at these field strengths, however, poses a major challenge. At field strengths of 1.5 T or above, another avenue of research has been the investigation of high b-value diffusion changes associated with brain activation (94–97), hypothesized to be due to changes in cell structure during neural activity (98, 99). However, this hypothesis has been challenged by several groups (100, 101).
The non-vascular fMRI contrast mechanism that has to date received the greatest attention, however, is that based on changes of the phase of spins due to the magnetic fields generated by neuronal currents (see Eq. 5 and Eq. 6), resulting in either net phase shifts in activated voxels or in reductions of signal magnitude due to intra-voxel dephasing. Using this contrast mechanism, several groups have reported positive findings in humans (12–15, 19–24). However, this area of research is highly controversial, with several published reports of negative findings (3–11) or theoretical arguments (i.e., based on modeling and simulations) against the detectability of these signals with present-day MRI technology (29, 34, 35).
To this menagerie, we nevertheless propose adding a novel functional MRI contrast mechanism: MHD-driven changes in the flow of cerebrospinal fluid (CSF) in response to neural activity. To elaborate, consider a patch of cortex that, when activated, produces an electric field in the adjacent CSF. In the presence of a magnetic field , this will result in CSF flow driven by a force proportional to , as described in the Theory. Note that this MHD-driven flow of CSF should be distinguishable from the pulsatile flow of CSF (102–106), by virtue of being unrelated to the cardiac cycle. When high electric fields are generated, e.g., during epileptiform activity, the resulting MHD-driven CSF flow may be detectable with MR phase imaging methods, such as those used in this study. If so, this technique could prove useful in the presurgical evaluation of epilepsy patients, by assisting efforts to delineate the “epileptogenic zone”—the area of cortex that is responsible for the generation of seizures and which is consequently the target of surgical resection. However, the sensitivity, specificity, and localization accuracy of MHD-driven CSF flow as a functional MRI contrast mechanism—especially in comparison with well-established techniques such as BOLD fMRI—have yet to be determined.
Acknowledgments
The authors would like to thank Arnie Cyr for his help in conducting the experiments. This work was supported by a BCH-MIT Collaborative Fellowship Grant and NIH grants R21NS076859, P41EB015898 and P41EB015902.
Appendix
Our goal is to derive Eq. 4 in the Theory section. For convenience, we begin by rewriting Eq. 1 (the Navier-Stokes equation), Eq. 2 (the Lorentz force density), and Eq. 3 (Ohm’s law):
| [A1] |
| [A2] |
| [A3] |
Substituting Eq. A3 into Eq. A2, we obtain
| [A4] |
| [A5] |
The second term in Eq. A5 can be rewritten using a standard vector algebra identity:
| [A6] |
| [A7] |
where and is the unit vector in the direction of . Note that is the component of that is parallel to ; subtracting this component from (as in the square brackets above) leaves the component of that is perpendicular to .
Therefore, let , where is perpendicular to and is parallel to . Eq. A7 then becomes
| [A8] |
Substituting Eq. A8 into Eq. A5 leads to
| [A9] |
Note that all terms in are perpendicular to .
If we also let , where is perpendicular to and is parallel to , and substitute this expression and Eq. A9 into Eq. A1, we obtain the desired equation:
| [A10] |
References
- 1.Bandettini PA, Petridou N, Bodurka J. Direct detection of neuronal activity with MRI: Fantasy, possibility, or reality? Applied Magnetic Resonance. 2005;29(1):65–88. [Google Scholar]
- 2.Hagberg GE, Bianciardi M, Maraviglia B. Challenges for detection of neuronal currents by MRI. Magnetic Resonance Imaging. 2006;24(4):483–93. doi: 10.1016/j.mri.2005.12.027. [DOI] [PubMed] [Google Scholar]
- 3.Singh M. Sensitivity of MR phase shift to detect evoked neuromagnetic fields inside the head. IEEE Transactions on Nuclear Science. 1994;41(1):349–51. [Google Scholar]
- 4.Chu R, de Zwart JA, van Gelderen P, Fukunaga M, Kellman P, Holroyd T, Duyn JH. Hunting for neuronal currents: absence of rapid MRI signal changes during visual-evoked response. NeuroImage. 2004;23(3):1059–67. doi: 10.1016/j.neuroimage.2004.07.003. [DOI] [PubMed] [Google Scholar]
- 5.Parkes LM, de Lange FP, Fries P, Toni I, Norris DG. Inability to directly detect magnetic field changes associated with neuronal activity. Magnetic Resonance in Medicine. 2007;57(2):411–6. doi: 10.1002/mrm.21129. [DOI] [PubMed] [Google Scholar]
- 6.Mandelkow H, Halder P, Brandeis D, Soellinger M, de Zanche N, Luechinger R, Boesiger P. Heart beats brain: The problem of detecting alpha waves by neuronal current imaging in joint EEG-MRI experiments. NeuroImage. 2007;37(1):149–63. doi: 10.1016/j.neuroimage.2007.04.034. [DOI] [PubMed] [Google Scholar]
- 7.Tang L, Avison MJ, Gatenby JC, Gore JC. Failure to direct detect magnetic field dephasing corre sponding to ERP generation. Magnetic Resonance Imaging. 2008;26(4):484–9. doi: 10.1016/j.mri.2007.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Luo Q, Lu H, Lu H, Senseman D, Worsley K, Yang Y, Gao JH. Physiologically evoked neuronal current MRI in a bloodless turtle brain: Detectable or not? NeuroImage. 2009;47(4):1268–76. doi: 10.1016/j.neuroimage.2009.06.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rodionov R, Siniatchkin M, Michel CM, Liston AD, Thornton R, Guye M, Carmichael DW, Lemieux L. Looking for neuronal currents using MRI: An EEG-fMRI investigation of fast MR signal changes time-locked to frequent focal epileptic discharges. NeuroImage. 2010;50(3):1109–17. doi: 10.1016/j.neuroimage.2009.12.076. [DOI] [PubMed] [Google Scholar]
- 10.Luo Q, Jiang X, Gao JH. Detection of neuronal current MRI in human without BOLD contamination. Magnetic Resonance in Medicine. 2011;66(2):492–7. doi: 10.1002/mrm.22842. [DOI] [PubMed] [Google Scholar]
- 11.Huang J. Detecting neuronal currents with MRI: A human study. Magnetic Resonance in Medicine. 2014;71(2):756–62. doi: 10.1002/mrm.24720. [DOI] [PubMed] [Google Scholar]
- 12.Kamei H, Iramina K, Yoshikawa K, Ueno S. Neuronal current distribution imaging using magnetic resonance. IEEE Transactions on Magnetics. 1999;35(5):4109–11. [Google Scholar]
- 13.Xiong J, Fox PT, Gao JH. Directly mapping magnetic field effects of neuronal activity by magnetic resonance imaging. Human Brain Mapping. 2003;20(1):41–9. doi: 10.1002/hbm.10124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bianciardi M, Di Russo F, Aprile T, Maraviglia B, Hagberg GE. Combination of BOLD-fMRI and VEP recordings for spin-echo MRI detection of primary magnetic effects caused by neuronal currents. Magnetic Resonance Imaging. 2004;22(10):1429–40. doi: 10.1016/j.mri.2004.10.009. [DOI] [PubMed] [Google Scholar]
- 15.Liston AD, Salek-Haddadi A, Kiebel SJ, Hamandi K, Turner R, Lemieux L. The MR detection of neuronal depolarization during 3-Hz spike-and-wave complexes in generalized epilepsy. Magnetic Resonance Imaging. 2004;22(10):1441–4. doi: 10.1016/j.mri.2004.10.017. [DOI] [PubMed] [Google Scholar]
- 16.Konn D, Leach S, Gowland P, Bowtell R. Initial attempts at directly detecting alpha wave activity in the brain using MRI. Magnetic Resonance Imaging. 2004;22(10):1413–27. doi: 10.1016/j.mri.2004.10.012. [DOI] [PubMed] [Google Scholar]
- 17.Petridou N, Plenz D, Silva AC, Loew M, Bodurka J, Bandettini PA. Direct magnetic resonance de tection of neuronal electrical activity. Proceedings of the National Academy of Sciences of the United States of America. 2006;103(43):16015–20. doi: 10.1073/pnas.0603219103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Truong TK, Song AW. Finding neuroelectric activity under magnetic-field oscillations (NAMO) with magnetic resonance imaging in vivo. Proceedings of the National Academy of Sciences of the United States of America. 2006;103(33):12598–601. doi: 10.1073/pnas.0605486103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chow LS, Cook GG, Whitby E, Paley MNJ. Investigating direct detection of axon firing in the adult human optic nerve using MRI. NeuroImage. 2006;30(3):835–46. doi: 10.1016/j.neuroimage.2005.10.024. [DOI] [PubMed] [Google Scholar]
- 20.Chow LS, Cook GG, Whitby E, Paley MNJ. Investigation of MR signal modulation due to magnetic fields from neuronal currents in the adult human optic nerve and visual cortex. Magnetic Resonance Imaging. 2006;24(6):681–91. doi: 10.1016/j.mri.2006.01.005. [DOI] [PubMed] [Google Scholar]
- 21.Chow LS, Cook GG, Whitby E, Paley MNJ. Investigation of axonal magnetic fields in the human cor pus callosum using visual stimulation based on MR signal modulation. Journal of Magnetic Resonance Imaging. 2007;26(2):265–73. doi: 10.1002/jmri.21025. [DOI] [PubMed] [Google Scholar]
- 22.Chow LS, Dagens A, Fu Y, Cook GG, Paley MNJ. Comparison of BOLD and Direct-MR Neu ronal Detection (DND) in the human visual cortex at 3T. Magnetic Resonance in Medicine. 2008;60(5):1147–54. doi: 10.1002/mrm.21753. [DOI] [PubMed] [Google Scholar]
- 23.Xue Y, Chen X, Grabowski T, Xiong J. Direct MRI mapping of neuronal activity evoked by electrical stimulation of the median nerve at the right wrist. Magnetic Resonance in Medicine. 2009;61(5):1073–82. doi: 10.1002/mrm.21857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sundaram P, Wells WM, Mulkern RV, Bubrick EJ, Bromfield EB, Münch M, Orbach DB. Fast hu man brain magnetic resonance responses associated with epileptiform spikes. Magnetic Resonance in Medicine. 2010;64(6):1728–38. doi: 10.1002/mrm.22561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hatada T, Sekino M, Ueno S. Finite element method-based calculation of the theoretical limit of sensitivity for detecting weak magnetic fields in the human brain using magnetic-resonance imaging. Journal of Applied Physics. 2005;97(10E109):1–3. [Google Scholar]
- 26.Xue Y, Gao JH, Xiong J. Direct MRI detection of neuronal magnetic fields in the brain: Theoretical modeling. NeuroImage. 2006;31(2):550–9. doi: 10.1016/j.neuroimage.2005.12.041. [DOI] [PubMed] [Google Scholar]
- 27.Park TS, Lee SY. Effects of neuronal magnetic fields on MRI: Numerical analysis with axon and dendrite models. NeuroImage. 2007;35(2):531–8. doi: 10.1016/j.neuroimage.2007.01.001. [DOI] [PubMed] [Google Scholar]
- 28.Blagoev KB, Mihaila B, Travis BJ, Alexandrov LB, Bishop AR, Ranken D, Posse S, Gasparovic C, Mayer A, Aine CJ, Ulbert I, Morita M, Müller W, Connor J, Halgren E. Modelling the magnetic signature of neuronal tissue. NeuroImage. 2007;37(1):137–48. doi: 10.1016/j.neuroimage.2007.04.033. [DOI] [PubMed] [Google Scholar]
- 29.Cassarà AM, Hagberg GE, Bianciardi M, Migliore M, Maraviglia B. Realistic simulations of neuronal activity: A contribution to the debate on direct detection of neuronal currents by MRI. NeuroImage. 2008;39(1):87–106. doi: 10.1016/j.neuroimage.2007.08.048. [DOI] [PubMed] [Google Scholar]
- 30.Heller L, Barrowes BE, George JS. Modeling direct effects of neural current on MRI. Human Brain Mapping. 2009;30(1):1–12. doi: 10.1002/hbm.20484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Huang Y, Xiong H, Yao D. Direct MRI detection of the neuronal magnetic field: the effect of the dendrite branch. Physics in Medicine and Biology. 2010;55(18):5599–616. doi: 10.1088/0031-9155/55/18/022. [DOI] [PubMed] [Google Scholar]
- 32.Drobnjak I, Pell GS, Jenkinson M. Simulating the effects of time-varying magnetic fields with a realistic simulated scanner. Magnetic Resonance Imaging. 2010;28(7):1014–21. doi: 10.1016/j.mri.2010.03.029. [DOI] [PubMed] [Google Scholar]
- 33.Luo Q, Gao JH. Modeling magnitude and phase neuronal current MRI signal dependence on echo time. Magnetic Resonance in Medicine. 2010;64(6):1832–7. doi: 10.1002/mrm.22569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Luo Q, Jiang X, Chen B, Zhu Y, Gao JH. Modeling neuronal current MRI signal with human neuron. Magnetic Resonance in Medicine. 2011;65(6):1680–9. doi: 10.1002/mrm.22764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Jay WI, Wijesinghe RS, Dolasinski BD, Roth BJ. Is it possible to detect dendrite currents using presently available magnetic resonance imaging techniques? Medical and Biological Engineering and Computing. 2012;50(7):651–7. doi: 10.1007/s11517-012-0899-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Truong TK, Avram A, Song AW. Lorentz effect imaging of ionic currents in solution. Journal of Magnetic Resonance. 2008;191(1):93–9. doi: 10.1016/j.jmr.2007.12.005. [DOI] [PubMed] [Google Scholar]
- 37.Wijesinghe RS, Roth BJ. Lorentz effect imaging of ionic currents in solution using correct values for ion mobility. Journal of Magnetic Resonance. 2010;204(2):225–7. doi: 10.1016/j.jmr.2010.02.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Nijm GM, Swiryn S, Larson AC, Sahakian AV. Extraction of the magnetohydrodynamic blood flow potential from the surface electrocardiogram in magnetic resonance imaging. Medical & Biological Engineering & Computing. 2008;46(7):729–33. doi: 10.1007/s11517-008-0307-1. [DOI] [PubMed] [Google Scholar]
- 39.Frauenrath T, Fuchs K, Dieringer MA, Özerdem C, Patel N, Renz W, Greiser A, Elgeti T, Niendorf T. Detailing the use of magnetohydrodynamic effects for synchronization of MRI with the cardiac cycle: A feasibility study. Journal of Magnetic Resonance Imaging. 2012;36(2):364–72. doi: 10.1002/jmri.23634. [DOI] [PubMed] [Google Scholar]
- 40.Jackson JD. Classical electrodynamics. Wiley; New York, USA: 1975. [Google Scholar]
- 41.Davidson PA. An Introduction to Magnetohydrodynamics. Cambridge University Press; 2001. [Google Scholar]
- 42.Tillack MS, Morley NB. Magnetohydrodynamics. McGraw Hill; New York, USA: 1999. [Google Scholar]
- 43.Baumann SB, Wozny DR, Kelly SK, Meno FM. The electrical conductivity of human cerebrospinal fluid at body temperature. IEEE Transactions on Biomedical Engineering. 1997;44(3):220–3. doi: 10.1109/10.554770. [DOI] [PubMed] [Google Scholar]
- 44.Bodurka J, Jesmanowicz A, Hyde JS, Xu H, Estkowski L, Li SJ. Current-induced magnetic resonance phase imaging. Journal of Magnetic Resonance. 1999;137(1):265–71. doi: 10.1006/jmre.1998.1680. [DOI] [PubMed] [Google Scholar]
- 45.Song AW, Takahashi AM. Lorentz effect imaging. Magnetic Resonance Imaging. 2001;19(6):763–7. doi: 10.1016/s0730-725x(01)00406-4. [DOI] [PubMed] [Google Scholar]
- 46.Bodurka J, Bandettini PA. Toward direct mapping of neuronal activity: MRI detection of ultraweak, transient magnetic fields changes. Magnetic Resonance in Medicine. 2002;47(6):1052–8. doi: 10.1002/mrm.10159. [DOI] [PubMed] [Google Scholar]
- 47.Yang H, Cook GG, Paley MN. Mapping of periodic waveforms using the ghost reconstructed alter nating current estimation (GRACE) magnetic resonance imaging technique. Magnetic Resonance in Medicine. 2003;50(3):633–7. doi: 10.1002/mrm.10573. [DOI] [PubMed] [Google Scholar]
- 48.Pell GS, Abbott DF, Fleming SW, Prichard JW, Jackson GD. Further steps toward direct magnetic res onance (MR) imaging detection of neural action currents: Optimization of MR sensitivity to transient and weak currents in a conductor. Magnetic Resonance in Medicine. 2006;55(5):1038–46. doi: 10.1002/mrm.20857. [DOI] [PubMed] [Google Scholar]
- 49.Huang R, Posnansky O, Celik A, Oros-Peusquens AM, Ermer V, Irkens M, Wegener HP, Shah NJ. Measurement of weak electric currents in copper wire phantoms using MRI: influence of susceptibility enhancement. Magnetic Resonance Materials in Physics, Biology, and Medicine. 2006;19(3):124–33. doi: 10.1007/s10334-006-0035-1. [DOI] [PubMed] [Google Scholar]
- 50.Truong TK, Wilbur JL, Song AW. Synchronized detection of minute electrical currents with MRI using Lorentz effect imaging. Journal of Magnetic Resonance. 2006;179(1):85–91. doi: 10.1016/j.jmr.2005.11.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Brewer KD, Osberg BL, Rioux JA, D’Arcy RCN, Stroink G, Beyea SD. Is 4.0 T MRI advantageous for current source localization of weak magnetic fields? International Congress Series. 2007;1300:565–9. [Google Scholar]
- 52.Burac̆as GT, Liu TT, Buxton RB, Frank LR, Wong EC. Imaging periodic currents using alternating balanced steady-state free precession. Magnetic Resonance in Medicine. 2008;59(1):140–8. doi: 10.1002/mrm.21457. [DOI] [PubMed] [Google Scholar]
- 53.Halpern-Manners NW, Bajaj VS, Teisseyre TZ, Pines A. Magnetic resonance imaging of oscillating electrical currents. Proceedings of the National Academy of Sciences of the United States of America. 2010;107(19):8519–24. doi: 10.1073/pnas.1003146107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Burac̆as GT, Jung Y, Lee J, Buxton RB, Wong EC, Liu TT. On multiple alternating steady states induced by periodic spin phase perturbation waveforms. Magnetic Resonance in Medicine. 2012;67(5):1412–8. doi: 10.1002/mrm.23105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Scott GC, Joy MLG, Armstrong RL, Henkelman RM. Measurement of nonuniform current-density by magnetic resonance. IEEE Transactions on Medical Imaging. 1991;10(3):362–74. doi: 10.1109/42.97586. [DOI] [PubMed] [Google Scholar]
- 56.Scott GC, Joy MLG, Armstrong RL, Henkelman RM. Sensitivity of magnetic resonance current-density imaging. Journal of Magnetic Resonance. 1992;97(2):235–54. doi: 10.1002/mrm.1910280203. [DOI] [PubMed] [Google Scholar]
- 57.Scott GC, Joy MLG, Armstrong RL, Henkelman RM. RF current-density imaging in homogeneous media. Magnetic Resonance in Medicine. 1992;28(2):186–201. doi: 10.1002/mrm.1910280203. [DOI] [PubMed] [Google Scholar]
- 58.Scott GC, Joy MLG, Armstrong RL, Henkelman RM. Electromagnetic considerations for RF current-density imaging. IEEE Transactions on Medical Imaging. 1995;14(3):515–24. doi: 10.1109/42.414617. [DOI] [PubMed] [Google Scholar]
- 59.Scott GC, Joy MLG, Armstrong RL, Henkelman RM. Rotating-frame RF current-density imaging. Magnetic Resonance in Medicine. 1995;33(3):355–69. doi: 10.1002/mrm.1910330309. [DOI] [PubMed] [Google Scholar]
- 60.Holz M, Müller C. NMR measurements of internal magnetic field gradients caused by the presence of an electric current in electrolyte solutions. Journal of Magnetic Resonance. 1980;40(3):595–9. [Google Scholar]
- 61.Holz M, Lucas O, Müller C. NMR in the presence of an electric current. simultaneous measurements of ionic mobilities, transference numbers, and self-diffusion coefficients using an NMR pulsed-gradient experiment. Journal of Magnetic Resonance. 1984;58(2):294–305. [Google Scholar]
- 62.Konn D, Gowland P, Bowtell R. MRI detection of weak magnetic fields due to an extended current dipole in a conducting sphere: A model for direct detection of neuronal currents in the brain. Magnetic Resonance in Medicine. 2003;50(1):40–9. doi: 10.1002/mrm.10494. [DOI] [PubMed] [Google Scholar]
- 63.Witzel T, Lin FH, Rosen BR, Wald LL. Stimulus-induced rotary saturation (SIRS): A potential method for the detection of neuronal currents with MRI. NeuroImage. 2008;42(4):1357–65. doi: 10.1016/j.neuroimage.2008.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Haynes WM, Lide DR, Bruno TJ. CRC Handbook of Chemistry and Physics. 93rd edition CRC Press; Boca Raton, USA: 2012. [Google Scholar]
- 65.Pourtaheri N, Truong TK, Henriquez CS. Electromagnetohydrodynamic modeling of Lorentz Effect Imaging. Journal of Magnetic Resonance. 2013;236:57–65. doi: 10.1016/j.jmr.2013.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Bryant DJ, Payne JA, Firmin DN, Longmore DB. Measurement of flow with NMR imaging us ing a gradient pulse and phase difference technique. Journal of Computer Assisted Tomography. 1984;8(4):588–93. doi: 10.1097/00004728-198408000-00002. [DOI] [PubMed] [Google Scholar]
- 67.Dumoulin CL, Souza SP, Walker MF, Wagle W. Three-dimensional phase contrast angiography. Magnetic Resonance in Medicine. 1989;9(1):139–49. doi: 10.1002/mrm.1910090117. [DOI] [PubMed] [Google Scholar]
- 68.Guilfoyle DN, Gibbs P, Ordidge RJ, Mansfield P. Real-time flow measurements using echo-planar imaging. Magnetic Resonance in Medicine. 1991;18(1):1–8. doi: 10.1002/mrm.1910180102. [DOI] [PubMed] [Google Scholar]
- 69.Bernstein MA, Shimakawa A, Pelc NJ. Minimizing TE in moment-nulled or flow-encoded two-and three-dimensional gradient-echo imaging. Journal of Magnetic Resonance Imaging. 1992;2(5):583–8. doi: 10.1002/jmri.1880020517. [DOI] [PubMed] [Google Scholar]
- 70.Korosec FR, Grist TM, Polzin JA, Weber DM, Mistretta CA. MR angiography using velocity-selective preparation pulses and segmented gradient-echo acquisition. Magnetic Resonance in Medicine. 1993;30(6):704–14. doi: 10.1002/mrm.1910300608. [DOI] [PubMed] [Google Scholar]
- 71.Debatin JF, Leung DA, Wildermuth S, Botnar R, Felblinger J, McKinnon GC. Flow quantitation with echo-planar phase-contrast velocity mapping: In vitro and in vivo evaluation. Journal of Magnetic Resonance Imaging. 1995;5(6):656–62. doi: 10.1002/jmri.1880050607. [DOI] [PubMed] [Google Scholar]
- 72.Mulkern RV, Haker SJ, Maier SE. Complimentary aspects of diffusion imaging and fMRI: II. Elu cidating contributions to the fMRI signal with diffusion sensitization. Magnetic Resonance Imaging. 2007;25(6):939–52. doi: 10.1016/j.mri.2007.02.006. [DOI] [PubMed] [Google Scholar]
- 73.Kobayashi K, Yoshinaga H, Ohtsuka Y, Gotman J. Dipole modeling of epileptic spikes can be accurate or misleading. Epilepsia. 2005;46(3):397–408. doi: 10.1111/j.0013-9580.2005.31404.x. [DOI] [PubMed] [Google Scholar]
- 74.Alarcon G, Guy CN, Binnie CD, Walker SR, Elwes RD, Polkey CE. Intracerebral propagation of interictal activity in partial epilepsy: implications for source localisation. Journal of Neurology, Neu rosurgery and Psychiatry. 1994;57(4):435–49. doi: 10.1136/jnnp.57.4.435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Cooper R, Winter AL, Crow HJ, Walter WG. Comparison of subcortical, cortical and scalp activity us ing chronically indwelling electrodes in man. Electroencephalography and Clinical Neurophysiology. 1965;18(3):217–28. doi: 10.1016/0013-4694(65)90088-x. [DOI] [PubMed] [Google Scholar]
- 76.Ogawa S, Tank DW, Menon R, Ellermann JM, Kim SG, Merkle H, Uğurbil K. Intrinsic signal changes accompanying sensory stimulation: functional brain mapping with magnetic resonance imaging. Pro ceedings of the National Academy of Sciences of the United States of America. 1992;89(13):5951–5. doi: 10.1073/pnas.89.13.5951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Kwong KK, Belliveau JW, Chesler DA, Goldberg IE, Weisskoff RM, Poncelet BP, Kennedy DN, Hoppel BE, Cohen MS, Turner R. Dynamic magnetic resonance imaging of human brain activity during primary sensory stimulation. Proceedings of the National Academy of Sciences of the United States of America. 1992;89(12):5675–9. doi: 10.1073/pnas.89.12.5675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Bandettini PA, Wong EC, Hinks RS, Tikofsky RS, Hyde JS. Time course EPI of human brain function during task activation. Magnetic Resonance in Medicine. 1992;25(2):390–7. doi: 10.1002/mrm.1910250220. [DOI] [PubMed] [Google Scholar]
- 79.Logothetis NK, Pauls J, Augath M, Trinath T, Oeltermann A. Neurophysiological investigation of the basis of the fMRI signal. Nature. 2001;412(6843):150–7. doi: 10.1038/35084005. [DOI] [PubMed] [Google Scholar]
- 80.Mulkern RV, Balasubramanian M, Orbach DB, Mitsouras D, Haker SJ. Incorporating reversible and irreversible transverse relaxation effects into steady state free precession (SSFP) signal intensity ex pressions for fMRI considerations. Magnetic Resonance Imaging. 2013;31(3):346–52. doi: 10.1016/j.mri.2012.10.002. [DOI] [PubMed] [Google Scholar]
- 81.Wong EC, Buxton RB, Frank LR. Implementation of quantitative perfusion imaging techniques for functional brain mapping using pulsed arterial spin labeling. NMR in Biomedicine. 1997;10(4):237–49. doi: 10.1002/(sici)1099-1492(199706/08)10:4/5<237::aid-nbm475>3.0.co;2-x. [DOI] [PubMed] [Google Scholar]
- 82.Kim SG, Tsekos NV, Ashe J. Multi-slice perfusion-based functional MRI using the FAIR technique: comparison of CBF and BOLD effects. NMR in Biomedicine. 1997;10(4):191–6. doi: 10.1002/(sici)1099-1492(199706/08)10:4/5<191::aid-nbm460>3.0.co;2-r. [DOI] [PubMed] [Google Scholar]
- 83.Yang Y, Engelien W, Pan H, Xu S, Silbersweig DA, Stern E. A CBF-based event-related brain activa tion paradigm: Characterization of impulse-response function and comparison to BOLD. NeuroImage. 2000;12(3):287–97. doi: 10.1006/nimg.2000.0625. [DOI] [PubMed] [Google Scholar]
- 84.Duong TQ, Kim DS, Uğurbil K, Kim SG. Localized cerebral blood flow response at submillime ter columnar resolution. Proceedings of the National Academy of Sciences of the United States of America. 2001;98(19):10904–9. doi: 10.1073/pnas.191101098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Detre JA, Wang J. Technical aspects and utility of fMRI using BOLD and ASL. Clinical Neurophysi ology. 2002;113(5):621–34. doi: 10.1016/s1388-2457(02)00038-x. [DOI] [PubMed] [Google Scholar]
- 86.Lu H, Golay X, Pekar JJ, van Zijl PCM. Functional magnetic resonance imaging based on changes in vascular space occupancy. Magnetic Resonance in Medicine. 2003;50(2):263–74. doi: 10.1002/mrm.10519. [DOI] [PubMed] [Google Scholar]
- 87.Donahue MJ, Lu H, Jones CK, Edden RA, Pekar JJ, van Zijl PCM. Theoretical and experimental investigation of the VASO contrast mechanism. Magnetic Resonance in Medicine. 2006;56(6):1261–73. doi: 10.1002/mrm.21072. [DOI] [PubMed] [Google Scholar]
- 88.Jin T, Kim SG. Improved cortical-layer specificity of vascular space occupancy fMRI with slab inver sion relative to spin-echo BOLD at 9.4 T. NeuroImage. 2008;40(1):59–67. doi: 10.1016/j.neuroimage.2007.11.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Kraus RH, Jr., Volegov P, Matlachov A, Espy M. Toward direct neural current imaging by resonant mechanisms at ultra-low field. NeuroImage. 2008;39(1):310–7. doi: 10.1016/j.neuroimage.2007.07.058. [DOI] [PubMed] [Google Scholar]
- 90.Cassarà AM, Maraviglia B, Hartwig S, Trahms L, Burghoff M. Neuronal current detection with low-field magnetic resonance: simulations and methods. Magnetic Resonance Imaging. 2009;27(8):1131–9. doi: 10.1016/j.mri.2009.01.015. [DOI] [PubMed] [Google Scholar]
- 91.Höfner N, Albrecht HH, Cassarà AM, Curio G, Hartwig S, Haueisen J, Hilschenz I, Körber R, Martens S, Scheer HJ, Voigt J, Trahms L, Burghoff M. Are brain currents detectable by means of low-field NMR? A phantom study. Magnetic Resonance Imaging. 2011;29:1365–73. doi: 10.1016/j.mri.2011.07.009. [DOI] [PubMed] [Google Scholar]
- 92.Kraus RH, Jr., Espy MA, Volegov PL, Matlachov AN, Mosher JC, Urbaitis AV, Zotev VS. Toward SQUID-based direct measurement of neural currents by nuclear magnetic resonance. IEEE Transac tions on Applied Superconductivity. 2007;17:854–7. [Google Scholar]
- 93.Cassarà AM, Maraviglia B. Microscopic investigation of the resonant mechanism for the implemen tation of nc-MRI at ultra-low field MRI. NeuroImage. 2008;41(4):1228–41. doi: 10.1016/j.neuroimage.2008.03.051. [DOI] [PubMed] [Google Scholar]
- 94.Darquié A, Poline JB, Poupon C, Saint-Jalmes H, Le Bihan D. Transient decrease in water diffusion observed in human occipital cortex during visual stimulation. Proceedings of the National Academy of Sciences of the United States of America. 2001;98(16):9391–5. doi: 10.1073/pnas.151125698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Le Bihan D, Urayama Si, Aso T, Hanakawa T, Fukuyama H. Direct and fast detection of neuronal activation in the human brain with diffusion MRI. Proceedings of the National Academy of Sciences of the United States of America. 2006;103(21):8263–8. doi: 10.1073/pnas.0600644103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Yacoub E, Uludağ K, Uğurbil K, Harel N. Decreases in ADC observed in tissue areas during activation in the cat visual cortex at 9.4 T using high diffusion sensitization. Magnetic Resonance Imaging. 2008;26(7):889–96. doi: 10.1016/j.mri.2008.01.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Aso T, Urayama S, Poupon C, Sawamoto N, Fukuyama H, Bihan DL. An intrinsic diffusion response function for analyzing diffusion functional MRI time series. NeuroImage. 2009;47(4):1487–95. doi: 10.1016/j.neuroimage.2009.05.027. [DOI] [PubMed] [Google Scholar]
- 98.Andrew RD, Macvicar BA. Imaging cell volume changes and neuronal excitation in the hippocampal slice. Neuroscience. 1994;62(2):371–83. doi: 10.1016/0306-4522(94)90372-7. [DOI] [PubMed] [Google Scholar]
- 99.Stroman PW, Lee AS, Pitchers KK, Andrew RD. Magnetic resonance imaging of neuronal and glial swelling as an indicator of function in cerebral tissue slices. Magnetic Resonance in Medicine. 2008;59(4):700–6. doi: 10.1002/mrm.21534. [DOI] [PubMed] [Google Scholar]
- 100.Miller KL, Bulte DP, Devlin H, Robson MD, Wise RG, Woolrich MW, Jezzard P, Behrens TEJ. Evidence for a vascular contribution to diffusion FMRI at high b value. Proceedings of the National Academy of Sciences of the United States of America. 2007;104(52):20967–72. doi: 10.1073/pnas.0707257105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Jin T, Kim SG. Functional changes of apparent diffusion coefficient during visual stimulation investi gated by diffusion-weighted gradient-echo fMRI. NeuroImage. 2008;41(3):801–12. doi: 10.1016/j.neuroimage.2008.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.O’Connell JEA. The vascular factor in intracranial pressure and the maintenance of the cerebrospinal fluid circulation. Brain. 1943;66(3):204–28. [Google Scholar]
- 103.Bering EA., Jr. Choroid plexus and arterial pulsation of cerebrospinal fluid: Demonstration of the choroid plexuses as a cerebrospinal fluid pump. AMA Archives of Neurology and Psychiatry. 1955;73(2):165–72. doi: 10.1001/archneurpsyc.1955.02330080043012. [DOI] [PubMed] [Google Scholar]
- 104.Hamit HF, Beall AC, Jr., De Bakey ME. Hemodynamic influences upon brain and cerebrospinal fluid pulsations and pressures. The Journal of Trauma. 1965;5(2):174–84. doi: 10.1097/00005373-196503000-00005. [DOI] [PubMed] [Google Scholar]
- 105.Henry-Feugeas MC, Idy-Peretti I, Baledent O, Poncelet-Didon A, Zannoli G, Bittoun J, Schouman-Claeys E. Origin of subarachnoid cerebrospinal fluid pulsations: a phase-contrast MR analysis. Mag netic Resonance Imaging. 2000;18(4):387–95. doi: 10.1016/s0730-725x(99)00142-3. [DOI] [PubMed] [Google Scholar]
- 106.Alperin N, Mazda M, Lichtor T, Lee SH. From cerebrospinal fluid pulsation to noninvasive intracra nial compliance and pressure measured by MRI flow studies. Current Medical Imaging Reviews. 2006;2(1):117–29. [Google Scholar]