Transport of gases between the environment and alveoli – theoretical foundations

Abstract

The transport of oxygen and carbon dioxide in the gas phase from the ambient environment to and from the alveolar gas/blood interface is accomplished through the tracheobronchial tree, and involves mechanisms of bulk or convective transport and diffusive net transport. The geometry of the airway tree and the fluid dynamics of these two transport processes combine in such a way that promotes a classical fractionation of ventilation into dead space and alveolar ventilation respectively. This simple picture continues to capture much of the essence of gas phase transport. On the other hand, a more detailed look at the interaction of convection and diffusion leads to significant new issues, many of which remain open questions. These are associated with parallel and serial inhomogeneities especially within the distal acinar units, velocity profiles in distal airways and terminal spaces subject to moving boundary conditions, and the serial transport of respiratory gases within the complex acinar architecture. This chapter focuses specifically on the theoretical foundations of gas transport, addressing two broad areas. The first deals with the reasons why the classical picture of alveolar and dead space ventilation is so successful; the second examines the underlying assumptions within current approximations to convective and diffusive transport, and how they interact to effect net gas exchange.

I.1 Introduction

The primary purpose of the lung is the exchange of the respiratory gases O₂ and CO₂ between ambient air and blood. The site of exchange is in the alveoli, where blood and gas are brought into very close proximity, a matter of approximately 1 micron. This requires two conduits with appropriate pumps: the pulmonary vascular system driven by the right heart bringing mixed venous blood to the exchange region, and the tracheobronchial tree, with ventilation driven by the respiratory muscles exchanging gas between the alveolar space and the ambient air. The basic features of the latter are the subject of this chapter; its focus is specifically on the nature of gas transport between the ambient environment and the gas region within the alveolus.

We first note that the surface area of the lung specific to gas exchange is on the order of 100 m² (Gehr et al. 1978), and that gas is brought cyclically to this surface through the branching bronchial tree. Path lengths along the intrathoracic tree vary considerably, but range from 20–40 cm between the larynx and acini (with about 15 cm path length in the upper airways connecting nostrils to thoracic inlet). The geometric nature of the conduits comprising the bronchial tree that effect this transport is an important determinant of the relative contributions of fundamental mechanisms of gas transport and mixing.

The transport of any molecular species in the gas phase is governed by two primary mechanisms: convection and diffusion (here we focus primarily on oxygen, but similar considerations apply to carbon dioxide and any of the commonly used tracer gases). These two are fundamentally different in a number of ways, and the relative importance of each is determined in large measure by the flow regimes present at any given locus along the bronchial tree, which in turn is a fluid dynamical function of the geometry of branching and the interaction with serially distributed pressure drops. For reasons which will be explored below, there are some drastic simplifications that can be made, secondary to the striking characteristics of the geometry of the bronchial tree and acinar regions.

This chapter is divided into two sections: the first is phenomenologic and elementary – it is based on simple experimental evidence that characterizes traditional fractionation of ventilation between the so-called dead space and alveolar regions. This is important insofar as, despite its simplicity, such an approach in fact captures much of the essential features of gas transport in the gas phase. Following this, there is a survey of more sophisticated investigations into the nature of transport. These are dealt with not only in the specifics of what they offer in understanding the nature of particular features of gas transport, but more importantly, with the assumptions underlying these approaches – many of which are implicit, and few of which are well understood.

I.2 Phenomenology of dead space and alveolar space ventilation

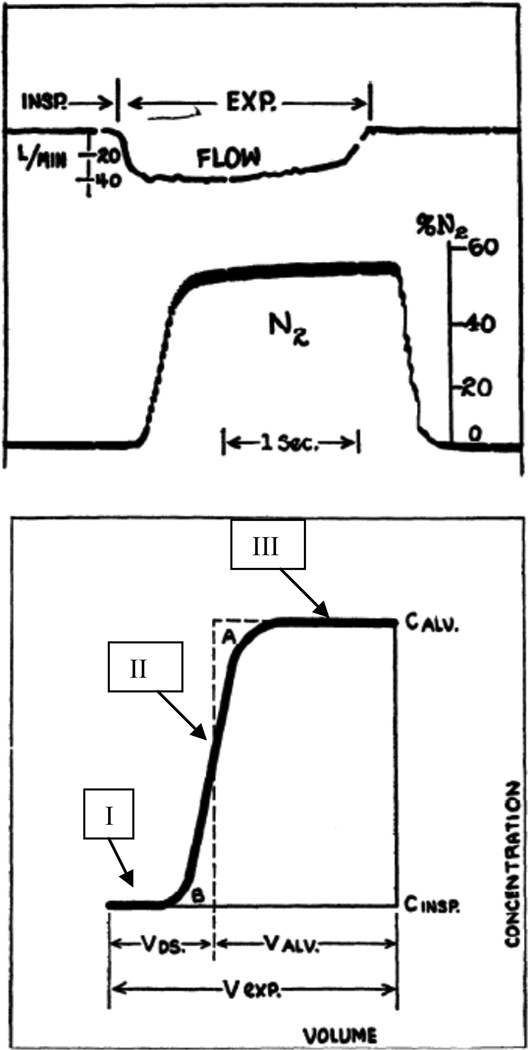
We begin with some simple phenomenology, of both intrinsic and historical interest. Alveolar gas concentrations are, in general, a time varying mixture of inspired gas, of ambient O₂ partial pressure and essentially zero CO₂ partial pressure, modulated by O₂ consumption and CO₂ production. The nature of this mixture has been debated for almost a century, dating back to foundation laid by Krogh and Lindhard (1917). One clear probe of this sense of mixing of ambient gas with metabolic sinks for O₂ and sources for CO₂ is in wash-in and wash-out tests of tracer gases. In particular, N₂, being a nonrespiratory gas, is a natural candidate. This leads to a simple probe of gas transport. A single breath N₂ washout test is conducted by inhaling a given volume of pure O₂ from some reference lung volume such as functional residual capacity (FRC), followed by an exhalation during which the N₂ concentration is measured as a function of time (or of cumulative volume). A classic example of this is given in Fig. 1, taken from seminal work by Fowler (1948). Roughly speaking, the expired concentration curve has several distinctive features, traditionally labeled as phases: Phase I is the early portion of the expirate, where there is essentially no N₂ present. This is followed by phase II, a sharply rising concentration towards phase III, approximated by a plateau (perhaps gently rising). Importantly, this is the concentration profile following a single breath interaction of a step change in N₂ concentration from ambient to zero, with whatever gas concentration distribution there may be along the bronchial tree and in the deep alveolar zone. Following the suggestion of C. Bohr, phase II can be sharpened to a single step, giving a measure of the volume point during exhalation that separates phases I and III; this is the Fowler dead space. Phase I corresponds to the volume of an equivalent portion of the conduit tree in which simple bulk transport takes place; Phase II is transitional, and Phase III corresponds to a reasonably well mixed region distal to the dead space.

Figure 1.

Single breath N₂ washout experiment, demonstrating the fractionation of the expirate into dead space and alveolar portions. Upper panel shows flow and N₂ concentration following an O₂ inspiration. Lower panel shows three phases of the washout, and the fractionation of ventilation into dead space and alveolar volumes. From Fowler, 1948.

Changes in this pattern can be observed with variations in inspired volumes, reference volumes at the beginning of the maneuver, flow rates, etc. But all of these point to a relatively sharp demarcation between regions dominated respectively by convection and diffusion. In essence, convection is simple bulk transport of volumes of gas from one location to another, with negligible mixing. By contrast, diffusion is the process by which gas concentrations mix, leading towards an equilibrium distribution wherein the concentrations are constant. An important difference between these mechanisms is that convection is fully reversible (to the extent that velocity profiles are reversible), whereas diffusion is strictly irreversible, being associated with the increase in entropy as gases mix. These observations then lead to a classical picture of the lung as a gas exchanger: a single equivalent conduit representing the bronchial tree, in which gas is transported simply by convection or bulk flow, and a single respiratory unit wherein the gas is uniformly mixed due to diffusion. To the extent that convection dominates throughout the phase I region, and as noted above is reversible, this volume constitutes the dead space V_D; the volume beyond the dead space comprises the alveolar space in which true mixing and net transport takes place. Support for this idea comes from the experimental observations that the magnitude of the dead space as operationally defined above varies little with flow rate, inspired volumes, or even carrier gas species. Why might this strikingly simplified picture obtain, and why should it be so faithful to the observed behavior of the lung? The answer lies in the geometry of the bronchial tree, and in the associated fluid dynamics that govern transport and mixing.

I.3 Geometry

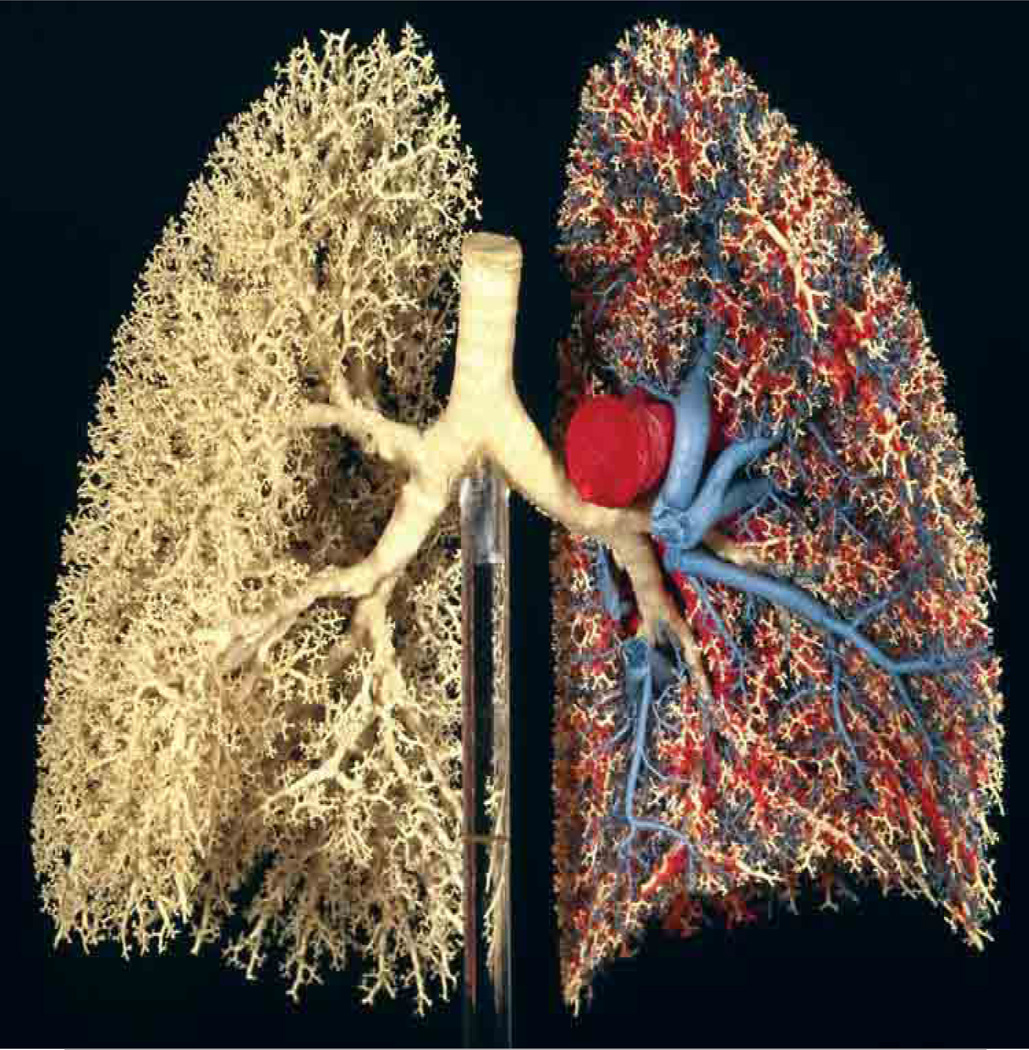
The structure of the bronchial tree can be appreciated most easily by examination of an extraordinary cast of the lung shown in Fig. 2 (Weibel, 1984, 1997; see also Weibel, 2009). In this stunning photograph, one can appreciate that in general, each airway branches into two daughter airways (dichotomous branching), which are roughly equal in diameter and lengths (regular branching). Careful studies (Horsfield et al., 1971, Horsfield et al., 1987, and Phalen and Oldham, 1983) on departures from this simple picture have quantified the extent of irregularity and asymmetry from parent to daughter branches, but the simple picture captures much of the essence of the nature of the tree. This 23 generation model is the original one put forth by Weibel almost a half century ago (Weibel, 1963). It has stood the test of time, retaining its significance in capturing the most important features of the geometry of the tree. The origins of the design of the bronchial tree, especially with respect to the nature and quantification of irregular branching and optimization criteria that may determine both the length ratios of parent branches to offspring as well as diameter ratios, are treated in depth in the Handbook chapter by Suki et al. (2010).

Figure 2.

Cast of the human bronchial and vascular trees. White resin corresponds to airways; red and blue resins correspond to pulmonary arterial and venous vascular trees respectively. From Weibel, 1984, 1997; color photograph courtesy E.R. Weibel, 2009.

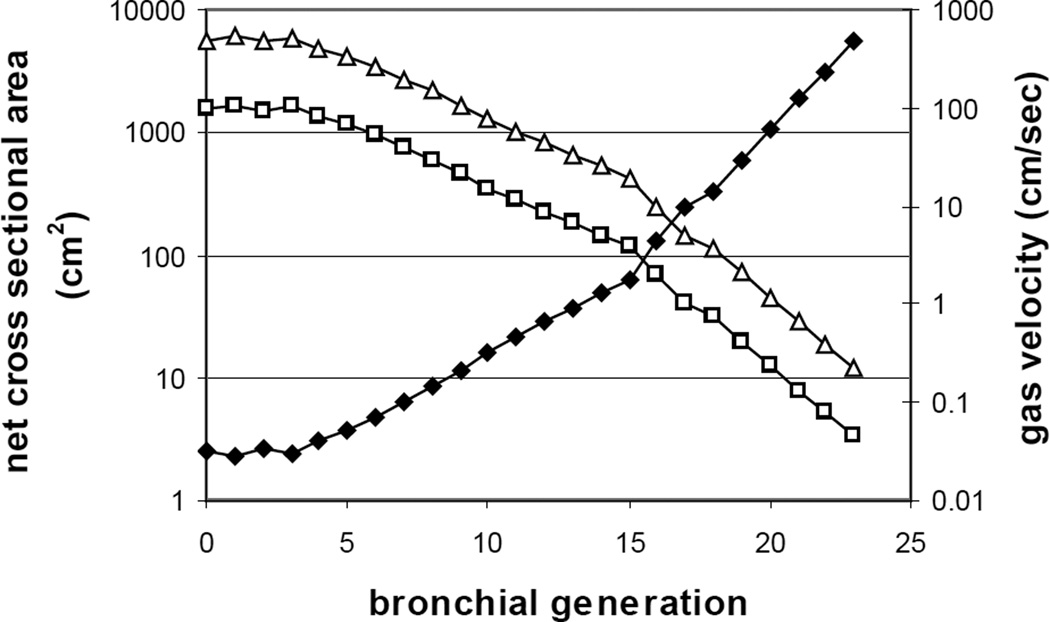
From the point of view of gas transport, it is essential to quantify the degree to which the cumulative cross sectional area changes as a function of generation number or of path length. This is because by conservation of volume (since absolute pressures do not vary from atmospheric pressure by more than a few percent), mean flow velocities are given by the ratio of volume flow to total cross section. Careful measurements of the nature of branching has been done (Weibel, 1963, see also Haefeli-Bleuer and Weibel, 1988, Pump, 1969, Schreider and Raabe, 1981, Hansen et al., 1975, Parker et al., 1971 and Hansen and Ampaya, 1975 for morphometric measurements in distal airways and within the pulmonary acinus; and Kitaoka et al., 2000, for algorithms generating realistic acinar geometries.). The results are shown in Fig. 3. The solid symbols correspond to the sharply increasing net cross sectional area of the tree at each generation, and the open squares to the local gas velocity for ventilation at rest. Here tidal volume has been set to 500ml, total respiratory period of 5 sec, and equal inspiratory and expiratory times. The open triangles denote gas velocities at moderate exercise, taken as 5× resting. Precise values of ventilatory parameters are not important to the essential point, which is that the important feature is the drastic increase in area and commensurate decrease in flow velocities; note that this figure is plotted with a semilogarithmic scale.

Figure 3.

Sharply increasing net area of the bronchial tree (closed symbols) with generation number in a Weibel model, and the reciprocal fall in gas velocities (open squares at rest, open triangles at moderate exercise) proceeding from proximal to distal airways. Data modified from Tsuda et al. 2008.

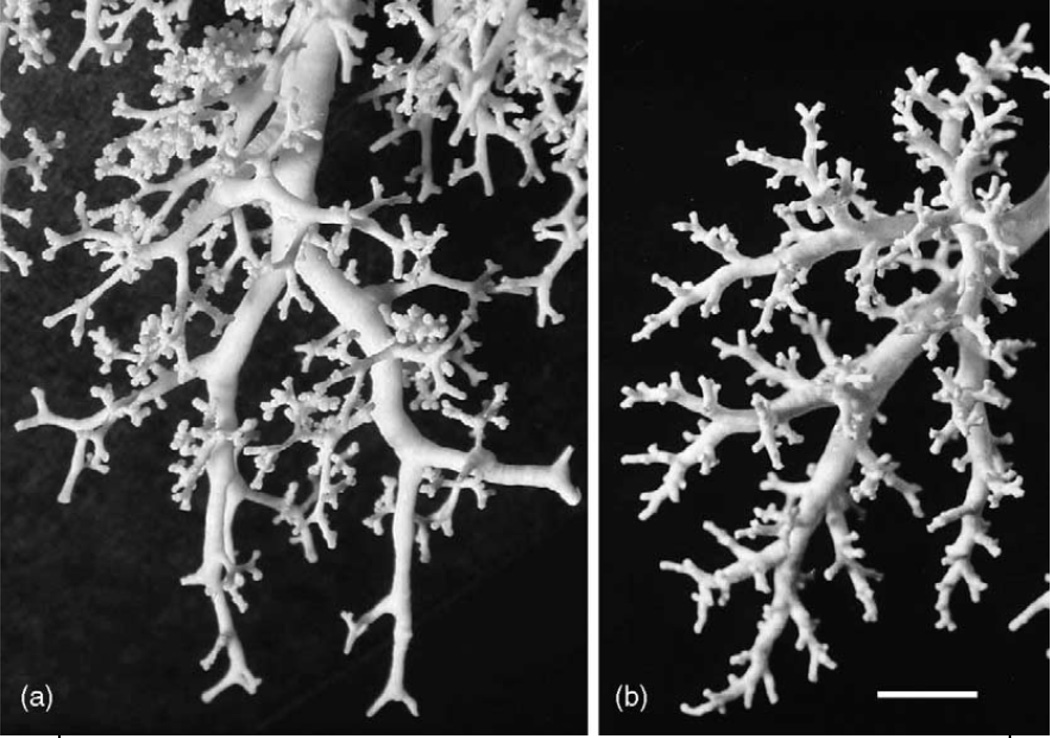
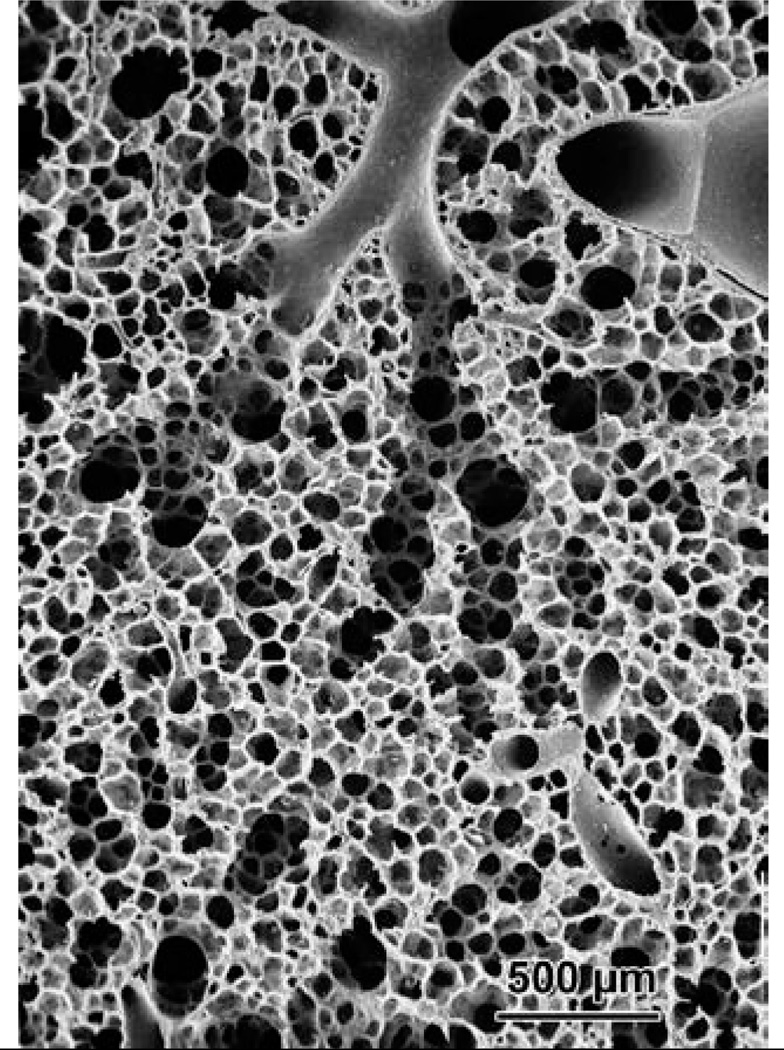
The conducting airways begin at the trachea (generation 0) through approximately generation 15 (terminal bronchioles); they are called conducting airways in the sense that there is no alveolation present. Beginning roughly at generation 16 there are alveolar units formed laterally on the airways (respiratory bronchioles), which then evolve a few generations later into alveolar ducts and alveoli, with some 8 additional branches. Fig. 4 shows casts of the peripheral conducting airways in human and rat, and Fig. 5 shows terminal conducting airways branching into alveolar ducts and alveoli, which in turn constitute the pulmonary acinus where gas exchange with the blood takes place.

Figure 4.

Casts of the peripheral conducting airways in (a): human and (b): rat. Scale bar = 5mm. From Weibel et al. 2005.

Figure 5.

A scanning EM picture of terminal bronchioles branching into respiratory bronchioles, ducts, and alveoli. Specimen from Weibel, 1984, image courtesy E.R. Weibel, 2009.

Of importance in the design and structure of the bronchial tree is its variation over the course of development from the fetal lung to the newborn and infant lung to the adult lung. Significant differences exist at the level of alveolation from a more primitive saccular stage to that of the fully alveolated human lung (see e.g. Boyden, 1971, Burri, 1974 and 2006, Hislop et al., 1986, Dunnill, 1962, and Zeltner et al., 1987). These developmental features are important, but are beyond the scope of this chapter.

I.4 Fluid dynamics and mixing

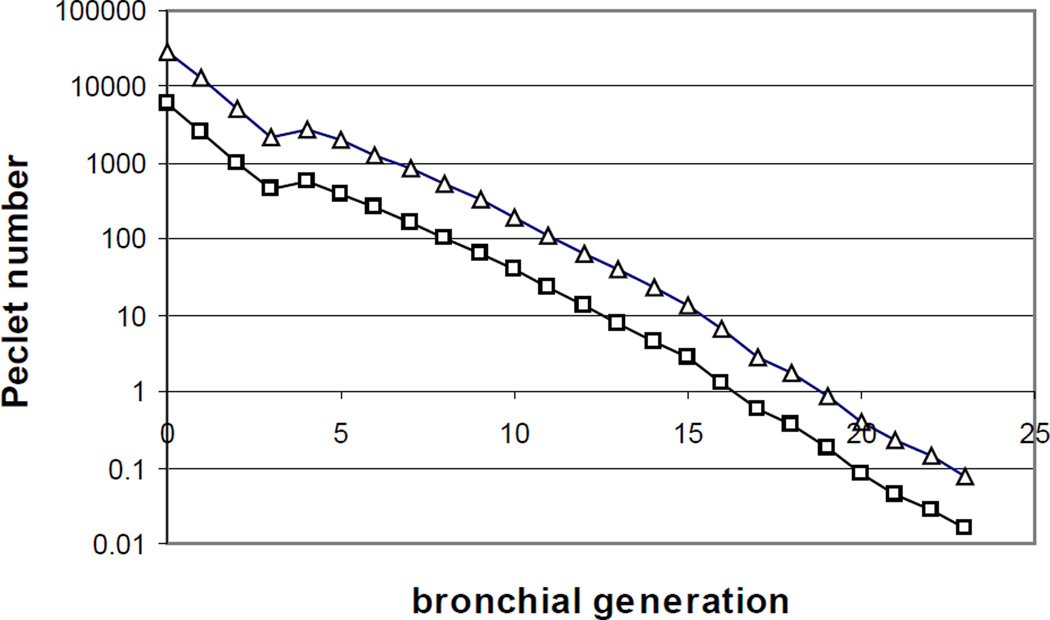
As noted above, there are two primary mechanisms for gas transport. The first is convective (and reversible); the second is diffusive (and irreversible). The essential physics of these mechanisms are different, and can be described as follows. We begin with an analogy: it is well known that the ratio of inertial to viscous forces determines the extent to which flows are laminar or turbulent; this ratio is the Reynolds number Re = ud / ν, where u and d are respectively a characteristic velocity and diameter (for tube flow), and ν is the kinematic viscosity given by the ratio of fluid viscosity to fluid density. A similar ratio occurs in consideration of the relative roles of convective and diffusive transport, and is commonly described by the Peclet number Pe = uL / D, where L is the characteristic length of a tube, and D is the molecular diffusivity. That Pe should represent the role of convection relative to diffusion can be appreciated by the following argument. The characteristic time for approach to diffusive equilibrium over a distance L is given by L² / D; the characteristic time for convective transport through the same tube is given by the residence time, L / u. The ratio of diffusive time to convection time is then just uL / D, the Peclet number. Functionally, when Pe is large, it means that residence times are short compared to diffusive times, and diffusion is too slow to effect significant transport. By contrast, when Pe is small, it means that diffusion times are short compared with convection times, and diffusion has sufficient time to effect significant transport (and hence irreversible mixing). Numerically, it turns out that for respiratory gases, both the kinematic viscosity and the molecular diffusivity are both on the order of ν ≈ D ≈ 0.2 cm²/sec. Moreover, since the bronchial length to diameter ratio is roughly 3 to 1 for most of the bronchial tree, we see that the numerical values of the Peclet number and Reynolds number are within a factor of 3 for any given generation of the tree. This is due to fact that the ratio Pe / Re = (uL / D) / (ud / ν) / ≈ L / D, which as noted is about 3 given that the kinematic viscosity and molecular diffusivity are approximately equal. Fig. 6 shows the Peclet number as a function of generation for the modified Weibel lung model, with open squares corresponding to resting ventilation, and open triangles to moderate exercise at 5× resting. As noted, it shares a numerical approximation to the Reynolds number, with an important difference in interpretation. The latter is unusual in that while most dimensionless numbers representing competing effects, the transition from laminar to turbulent flow occurs at a Re of several thousand. By contrast, the transition from transport domination by convection to diffusion in fact occurs near Pe ≈ 1; we see from this graph that at rest, for all generation up to 15 or 16, Pe > 1 (and for most of the conducting airways, Pe >> 1). Similarly, the region distal to the terminal bronchioles enjoys Pe < 1, and for most of the acinus, Pe << 1. Notice the important point that this transition occurs rather sharply. Figure 6 is plotted semilogarithmically; a few generations at most suffice to complete the transition. The same remarks apply during exercise, except that the convection/diffusion transition occurs a few generations distal compared to resting conditions. The fact that there is only a modest distal shift with even a five fold change in ventilation is further evidence of the sharply increasing cross sectional area of the bronchial tree with each generation, and of the commensurate fall in velocities.

Figure 6.

Peclet number, representing the relative magnitude of convective or bulk transport to diffusive transport, versus generation number. As in Fig. 3, open squares represent conditions at rest, and open triangles moderate exercise. Note the transition point Pe ≈ 1 around generation 16 at rest, and generation 19 at exercise. Data taken from Figure 3.

While the above is adequate to describe the bulk transport nature of ventilation within the dead space, further considerations are necessary to examine the behavior in the diffusion dominated alveolar region. As noted, the characteristic time for approach to equilibrium in simple diffusion is given by L² / D, where here L is any typical length scale, not necessarily the length of a conducting airway. Within the alveolar space, we may take typical dimensions to be on the order of 100μ or less (this argument is not sensitive to exact values, nor whether lengths are given by alveolar diameters, ductal diameters, or mean linear intercepts). It follows that characteristic diffusion times are less than 1 msec. This being significantly shorter than any times associated with breathing periods, it follows that to a very good approximation, the alveolar region is “well mixed” (but see below for issues associated with assuming a constant alveolar concentration versus a small but not negligible concentration gradient). In summary, the geometry of the bronchial tree, and importantly its rapidly increasing area with generation proceeding distally, implies a commensurately sharp fall in gas velocity. This is turn leads to a transition in the Peclet number from being >>1 proximally to <<1 distally. These observations, coupled with the rapid equilibration within the alveolar zone, are the reasons why the simple washout curve shown at the beginning displays its characteristic properties, and why, ultimately, the picture of the lung as a serial arrangement of conducting airways and a well-mixed alveolar space is so successful.

I.5 Alveolar and dead space ventilation

These ideas lead naturally to a fractionation of the tidal volume into that portion associated with the dead space, and that (major) portion entering the well mixed alveolar region. Simply multiplying dead space volume by breathing frequency yields dead space ventilation and alveolar ventilation respectively. This is an operational definition, based on an identifiable demarcation between the dead space and the alveolar space; equivalently, it can be written in terms of the dilution of the alveolar space with fresh gas leading to the alveolar plateau. This is commonly used with e.g. CO₂, which when coupled with metabolic production V̇_CO2, yields the simple relation that alveolar ventilation V̇_A = V̇_CO2 / F_A,CO2, where F_A,CO2 is the fractional concentration in expired gas at end expiration (or an estimate of its value over the alveolar plateau or from the use of arterial P_a,CO2). By extension, these ideas can also be used to define a functional dead space; this was introduced by C. Bohr more than a century ago (Bohr, 1891; see also Otis, 1964 and West, 2000), and is still of high value conceptually. Specifically, it can be shown that with the fractionation between conducting and well mixed regions, the ratio of dead space to tidal volume satisfies V_D / V_T = (F_A,CO2 − F_E,CO2) / F_A,CO2, where F_E,CO2 is the mixed expired CO₂ fraction. This so-called Bohr dead space is approximately equal to the Fowler type dead space described above in normals; it may depart substantially in individuals with pulmonary disease. As the Fowler-type dead space is structurally interpreted, and the Bohr-type dead space is functionally determined through gas exchange, these two are often called the anatomic and physiologic dead spaces, respectively. The important concept here is that it is only in these measurement senses that alveolar and dead space ventilations are actually defined. To be sure, there is value in thinking of alveolar ventilation as that gas which takes part in gas exchange, or as that portion of fresh gas which enters the alveoli, but it must be recognized that these concepts are simply constructs that arise from the fractionation picture itself (indeed, all gas everywhere is taking part in gas exchange, and limiting the distal region for gas transport to alveoli proper ignores irreversible mixing in the alveolar ducts, respiratory bronchioles, etc.)

II.1 Probing more deeply into the foundations of transport

There are at least two major features that the simple one-compartment picture above does not take into account, and which play a significant role especially in disease, and yet within each of these, the relative importance of various factors is not known. The first is the existence of parallel inhomogeneities – parallel pathways from the central airways to the exchange regions differ in the distribution of bronchial diameters, lengths, and hence flow resistances. Ventilatory volumes are known to be dominated by the distribution of local compliances in normals at rest, but this is not true in heavy exercise or in patients especially with chronic obstructive pulmonary disease. In these cases, the effect of parallel inhomogeneities in airways resistance leads to commensurate variations in flow and hence alveolar ventilation if the associated time constants (given by the product of pathway resistance and terminal compliance) become comparable to breathing periods. Measurement of the distribution of ventilation regionally has enjoyed a wide variety of techniques, including radioactive tracers (Milic-Emili, 2005), PET scans (Musch, 2002), the use of relatively radiodense Xe and computed tomography (Kreck et al. 2001), and the introduction of hyperpolarized noble gases in MRI (Kauczor et al., 2002, Butler et al., 2002, Patz et al., 2008).

The coupling of distributed ventilation V̇_A with the distribution of local capillary perfusion Q̇_c leads to specific predictions about the local values of alveolar gas concentrations and end capillary blood partial pressures; this is captured in the classic monograph of West (1965). There is an enormous literature on the distribution of ventilation/perfusion ratios, its role in both health and especially in disease, and its measurement especially through the multiple inert gas elimination technique (MIGET) of Wagner (1974, 2008), PET scans (Musch et al., 2002), and Xe CT (Kreck et al. 2001) but that is beyond the scope of this chapter.

The second major issue ignored in the strict fractionation scheme is the actual nature of transport axially, i.e. how does convection interact with diffusion along the pathways, being mindful of its convective dominance proximally and diffusive dominance distally. This requires casting the problem in terms of the physics of transport for these coupled mechanisms, which we now examine in some detail.

II.2 The convection-diffusion equation

Transport in general is described in terms of the relationship between a flux density of some molecular species j⃗ (say number of molecules per unit time crossing a unit area), the local concentration ρ of that species, and the motion of the carrier fluid given by the velocity field u⃗. Bulk or convective transport is elementary: j⃗_conv = ρu⃗, which simply states that a packet of gas with a given concentration moving with velocity u⃗ carries with it an associated mass or number of molecules. By contrast, diffusive transport relates the flux density j⃗_dif a concentration gradient and to the molecular properties of the species of interest within the carrier medium. Specifically, j⃗_dif = −D∇ρ, where D is the diffusion coefficient and ∇ is the gradient operator denoting respectively the partial derivatives (∂ / ∂x, ∂ / ∂y, ∂ / ∂z). This relation between the diffusive flux density and the concentration gradient is a local statement of Fick’s first law. The idea that a flux of some transportable quantity is linearly related to a gradient of an associated potential is the basis of a number of analogous relations, including Fourier’s law of heat transport and temperature gradients, and Ohm’s law of electrical currents and potentials. Finally, noting that fluxes are additive quantities, the final expression for the net flux, including the interaction of convective and diffusive terms, becomes j⃗ = j⃗_conv + j⃗_dif = ρu⃗ − D∇ρ.

There is a second relation between fluxes and concentrations; this is given by the equation of continuity expressing conservation of mass. This is expressed by ∂ρ / ∂t = −∇ · j⃗, which states that the rate of change of mass or number of molecules in a differential volume is exactly equal to rate entering less the rate leaving, this latter being given differentially by the negative of the gradient operator. Combining these two equations yields ∂ρ / ∂t = D∇² ρ − u⃗ · ∇ ρ, the classical convection-diffusion equation. (Note that in expanding ∇ · u⃗ρ = u⃗ ·∇ρ + (∇ · u⃗)ρ, we may safely drop the second term, insofar as gas flow in the lung is negligibly different from being isobaric and isothermal, and hence divergenceless.)

In principle, then, one can solve for mass transport in any given geometry by first solving the Navier-Stokes equations for the velocity field u⃗, and then solving the convection-diffusion equation for the concentration ρ, where both of these are functions of spatial position within the bronchial tree and acinus, and are functions of time during breathing. Unfortunately, however, no solutions are known for this problem except in highly restricted circumstances and approximations. In particular, the most common approach is to reduce the three dimensional problem to an approximation in one spatial (axial) dimension that is equivalent. Even here very little is known. The most widely appreciated example is that of diffusion interacting with convection in fully developed Poiseuille flow in straight circular pipes of constant radius, first solved by Taylor (1953). Here the velocity field is parabolic in the radial coordinate, and the axial velocity is coupled to radial diffusion. A reduction in dimensionality of the problem to that of a single mean bulk velocity p and a mean concentration over each cross section leads to a decoupling of the convective and diffusive terms. Specifically, Taylor found that mass transport averaged across a cross section in a coordinate system moving with the mean flow velocity was proportional to the mean concentration gradient. The prefactor, however, was not that of molecular diffusivity, but rather one that incorporated the simultaneous effects of velocity, radius, and molecular diffusivity. This has been known since as the effective diffusivity D_eff, which turns out to be quadratic in the flow velocity, and surprisingly, inversely proportional to the molecular diffusivity. This approach has been extended to include turbulent flow as well (Taylor, 1954) and oscillatory flow (Watson, 1983). It remains unclear whether such Taylor-type effective diffusivities are important in gas transport in the lung, with evidence supporting its importance in the uptake of carbon monoxide in the presence of SF₆ (Kvale et al., 1975), its potential importance in intermediate sized bronchi (Wilson and Lin. 1970), and with arguments suggesting Taylor diffusion is only of marginal significance (Worth et al., 1977). These are still open questions.

As noted above, one of the essential architectural features of the bronchial tree is its extraordinarily rapid expansion in net cross sectional area proceeding distally down the tree. In this case, a reduction of the full convection-diffusion equation to one dimension poses new and non-trivial issues. In particular, at any given cross section with area A(x), we write the mass flux as J(x), where x is the axial coordinate. Conservation of mass in this reduced coordinate system becomes ∂Aρ̅ / ∂t = −∂J / ∂x − α, where α represents the mass loss rate; it is typically taken to be negligible in the conducting airways for O₂ and CO₂ transport. For other gases, this may not be valid; airway gas exchange has recently been investigated with respect to gas exchange measurements probed with MIGET (Anderson and Hlastala, 2010; see also Hlastala 2003). They found significant effects of airway exchange (especially ether and acetone) on estimated ventilatory distributions, while perfusion distributions were relatively unaffected. The specific dependence of airway exchange on diffusivity has also been determined (Schimmel et al., 2004). Airway exchange is also important in analyzing breath tests for ethanol, which is largely exchanged within the airways (George et al., 1996, Anderson and Hlastala, 2007). For these gases which exchange mainly in the airways, α is a dominant term of mass loss axially along the airway tree; but note that to extent exchange is essentially complete within the conducting airways, difficulties noted below with respect to distal boundary conditions play little role. At the acinar level, realistic models of the transport of respiratory gases must also take into account mass loss within small acinar airways, insofar as the arrangement of ducts and alveoli include serial as well as parallel arrangements of gas exchange surfaces (see below).

The mass flux term J(x) can not be computed exactly within a dimensional reduction, but it can be approximated. Thus, by analogy with the additive nature of the actual convective and diffusive fluxes, one typically write J = J_conv + J_dif; the convective term is approximated by J_conv = Aūρ̅, where A is cross sectional area, and the overbar denotes areal averages over the cross section. (Note that the true mean flux density is a mean over the product of local velocity and concentration; the implicit assumption made here is that the mean of a product is equal to the product of the individual means.) For the diffusive term, it is common to invoke a Taylor-type behavior, and write J_diff = −D_eff A∂ρ̅ / ∂x. Here again, there is an implicit assumption that regardless of the nature of the interaction of the velocity field with concentration gradients, the net diffusive flux behaves as a simple one dimensional current with all complications buried in a common prefactor, D_eff, which is some a priori defined function of mean velocity, bronchial radius, and molecular diffusivity. Substitution of these expressions into the one dimensional version of the conservation of mass law leads to the one dimensional convection diffusion equation, ∂ρ̅ / ∂t = D_eff∂²ρ̅ / ∂x² − ūρ̅ / ∂x + A⁻¹ (∂D_eff A / ∂x)(∂ρ̅ / ∂x) − A⁻¹ ∂α / ∂x. The first two terms are precisely those that appear in the original and complete convection-diffusion equation. The third term arises explicitly because of the variation of area and D_eff with axial distance, and as noted above, the last term is required whenever there is serial exchange between gas and tissue or blood. Despite the fact that it looks more complicated that the complete 3 dimensional equation, the reduction in dimension makes this expression more tractable by far; it has been the basis of a number of studies. In addition to the axial dependences of A and D_eff, the latter especially is likely to be time dependent. That is, D_eff depends on the velocity profiles even at fixed flow rates, and thus during the course of breathing with nonconstant flows, D_eff will change. Perhaps more importantly, the differences in velocity profiles in inspiration and expiration imply that these two phases will inherit different effective diffusivities. The early work of Scherer (1975), explored this difference in inspiration and expiration in a bifurcating airway model, and is widely used to probe at least some aspects of irreversible transport associated with cyclic breathing. The effective diffusivities in these models satisfy relations approximated by D_eff = D_mol + 1.08ud and D_eff = D_mol + 0.37ud for inspiration and expiration respectively, and where u and d are mean velocities and diameters of the relevant airways. The general approach outlined above has been used in a variety of trumpet models of the expanding cross section of the bronchial tree (Scherer et al., 1972, Paiva, 1973, Darquenne and Paiva, 1994), and more recently extended to multinodal models of the tree and acinus proper (Dutrieue et al., 2000, and Tawhai and Hunter, 2001).

II.3 Boundary conditions

While the above description of the convection-diffusion equation applies locally in either its correct three dimensional version, or in its approximation to one dimensional transport with an effective diffusivity, its solutions depend on the assigned boundary conditions. These are problematic; an early description of appropriate boundary conditions is found in Chang et al. (1973). See also Engel (1983), Paiva and Engel (1987), Engel and Macklem (1977). In brief, the issues divide cleanly into those conditions imposed at, respectively, the proximal and distal ends of the entire airway tree from the airway opening to the terminal spaces including alveolar ducts and alveoli proper. At the distal end, one approach is to assume a particular volume of resident alveolar gas with a constant concentration of either O₂ or a relevant tracer. For single breath experiments and applications, this may be appropriate, given the millisecond time scale for approximate diffusive equilibration within the alveolar region. Extension of these ideas to the serial and parallel interaction of transport of tracers in multibreath washout and washin experiments, necessarily transient, has been extensively studied; see Section II.4 below and e.g. Verbanck et al. (1997) and Verbanck and Paive (2010).

For respiratory gases in steady state, a boundary condition of constant partial pressure (i.e. zero gradient) is of course not applicable insofar as there is continual uptake of O₂ and excretion of CO₂. In this circumstance, the net transport is equal to the product of the gas phase diffusion coefficient and the area weighted average of local concentration gradients at the gas - exchange surface interface. (Note that this construct is independent of tissue phase permeabilities; see Section II.5.) These gradients are very small, to be sure, but they are not negligible in steady state, just as the respiratory zone cannot be completely well-mixed with diffusive transport taking place. Similarly, the effective area over which transport takes place is correspondingly large. This leads to a delicate point insofar as the terminating area and gas phase concentration gradients at the air/tissue interface cannot be independently assigned. This is due to the fact that they are, in steady state, coupled through net O₂ consumption and CO₂ elimination at the level of the lung; they are not independently functions of the lung as a gas exchanger. That is, in steady state, this product of normal gradient and its corresponding area, summed over the lung, is a determined quantity based on the O₂ and CO₂ fluxes needed by the rest of the body. (For O₂ this is essentially determined by overall metabolic rate; for CO₂ account must be taken of excretion by renal pathways.) This is analogous to a current sink for O₂ and a current source for CO₂ servicing a relatively large capacitance in the alveolar volume through a small resistive pathway (equivalently a large diffusing capacity). Actual partial pressures of O₂ and CO₂ at this interface are therefore insensitive to details of morphometric areas – within some bounds (which are unknown); increased or decreased areas are associated with commensurately decreased or increased concentration gradients, such that the product is preserved to satisfy O₂ and CO₂ flux demands. In short, it is essential to pay careful attention to what is important – e.g. the net fluxes – and what is not important – e.g. the precise values of areas and gradients so long as they satisfy the net flux requirements. We emphasize that these arguments apply under steady state conditions at rest in normals, but with moderate to heavy exercise, metabolic requirements rise to levels at which local partial pressures of O₂ and CO₂ do become sensitive to actual areas; it is here that morphometric and physiologic measurements of pulmonary diffusing capacities are to be reconciled (Weibel, 1984). Similarly, the above arguments do not apply under non-steady state or transient conditions such as acute changes in gas concentrations in washout or washin experiments (see Section II.4) or under conditions of extreme breath-holding (see Section III).

At the proximal end, different problems arise. During inspiration, there is clearly no problem with assigning ambient concentrations of e.g. O₂ and CO₂ as fixed concentration boundary conditions at the airway opening. The conditions during expiration are more difficult. Thus, fixing concentrations to remain at ambient values leads to the buildup of an axial boundary layer during expiration, wherein the expired gas concentrations are, on the one hand, forced to match an artificial airway opening condition, and are, on the other hand, tending towards simple convective expiratory transport where the Peclet number is >>1. This is a serious problem for any quantitative analysis of steady state gas transport. Even a condition such as setting the diffusive flux at the airway opening to zero, secondary to the large value of Pe, also implies the existence of an axial boundary layer phenomenon, although not as extreme as the condition of a fixed concentration at the airway opening. To avoid such difficulties, it is possible to model the airway tree during expiration as an extended tree such that the artifacts associated with either form of boundary condition do not propagate upstream to any significant extent. This extension can be done in a finite manner by including a buffer zone (Pack, 1977), or even extending the location of the expiratory boundary past the airway opening to an artificial boundary condition at infinity (Butler, 1977).

With respect to boundary conditions on the velocity profiles, it is important to recognize that virtually all studies of the interaction of diffusion and convection have been done in models where the conduits are rigid, which is not true for real airways. Indeed, airway lengths and diameters cyclically expand and contract together with the lung parenchyma in a fashion satisfying approximate geometric similarity (Hughes et al., 1972). The consequence of this is that the imposition of the no-slip boundary condition is no longer zero velocity, as is the case in rigid conduits, but rather that the gas velocity match the material velocity of the local moving boundary of the bronchial wall. The effect of this is to change the character of the secondary flows that exist; whether this is important or not in gas transport and mixing at the level of the conducting airways is not known, but is almost certainly important at the level of the acinus (see below). Within the branches of the conducting airways, most approaches are based on convective flux boundary conditions that fractionate local average concentrations proportionate to mean volume flows at each airway bifurcation. This is a reasonable approach, but details of how secondary flows interact with concentration gradients are not known, especially with expanding and contracting airways during breathing.

The recent advent of advanced methods of numerical simulations of the solutions to the Navier Stokes equations have led to a deeper understanding of the nature of the velocity profiles, especially at bronchial bifurcations. Such computational fluid dynamical approaches are explored in detail elsewhere in the Handbook series (Tawhai, et al., 2010). In the more distal regions of the lung, particularly at the level of the pulmonary acinus, a variety of techniques have been used, both experimental and theoretical, to which we now turn.

II.4 Acinar transport—multibreath studies

Recall the simple description of a single breath washout, wherein there is an approximate alveolar plateau in phase III. This reflects the composition of mixed alveolar gas, where the average is taken over parallel units emptying. To the extent that each unit is well mixed, and importantly, the parallel units empty synchronously, phase III will be roughly constant. In normals this is true, but there may be significant deviations from this behavior in patients with pulmonary disease. Departures can arise either from asynchrony in emptying, associated with parallel inhomogeneities, or from failure within the acinus to achieve equilibration. These two phenomena have been studied in great detail by Verbanck (see e.g. Verbanck et al. 1997), following the introduction of the analytic technique by Paiva (1975). The importance of this approach is in its potential to estimate the sites of airway dysfunction in diseases ranging from chronic obstructive pulmonary disease to asthma, and in particular whether these sites are principally local to the acinus or higher up in the bronchial tree.

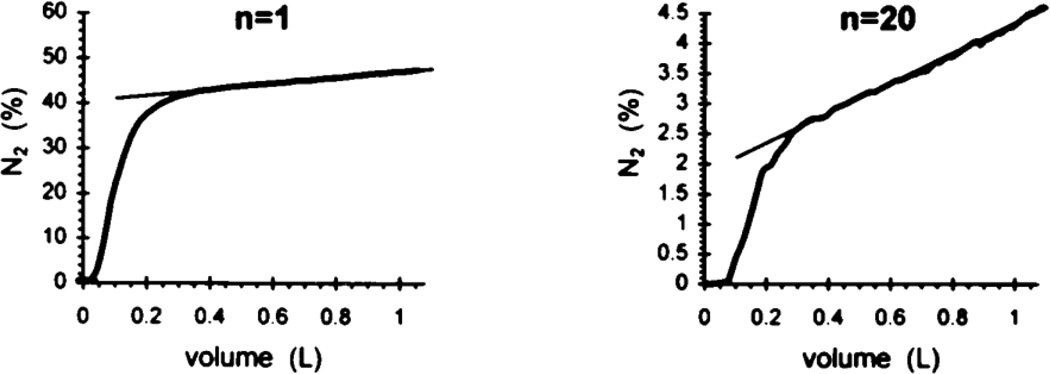
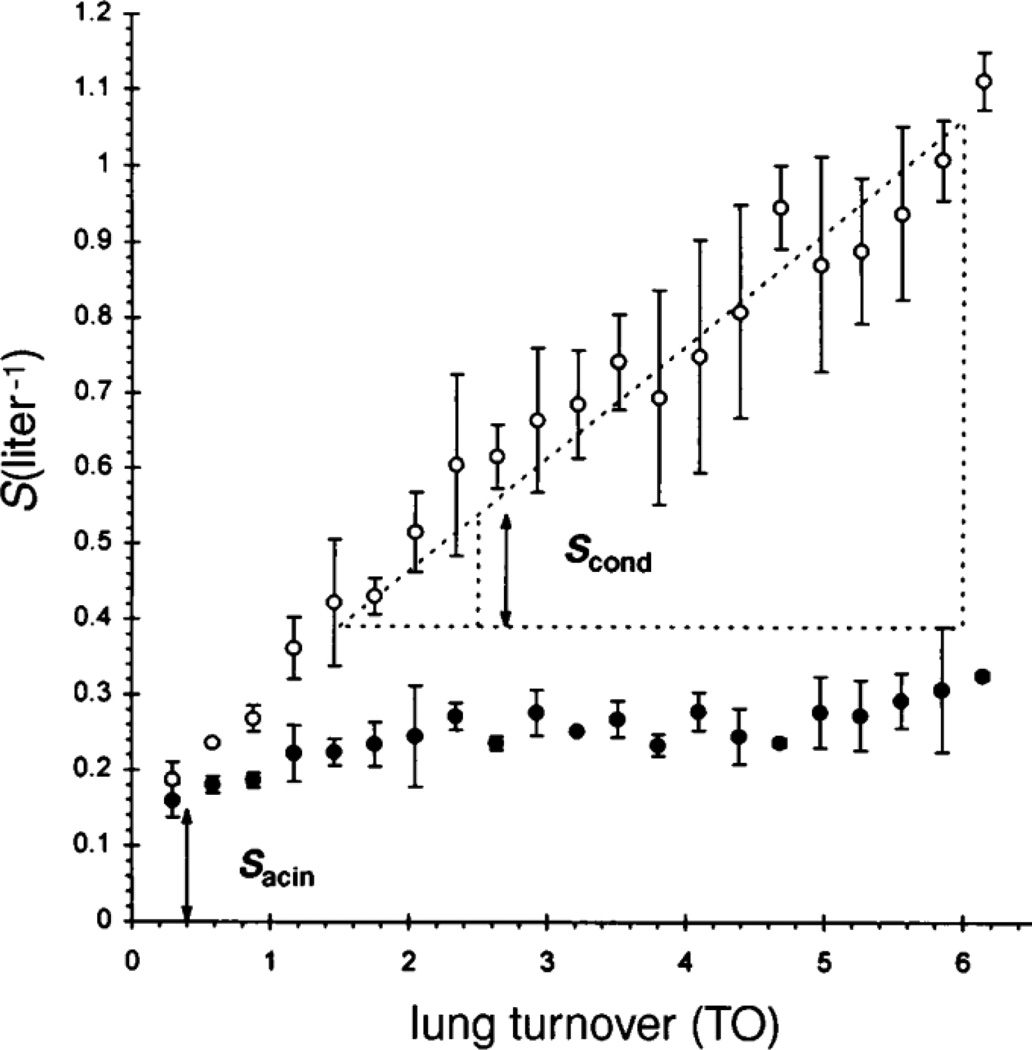
The basic argument rests on an analysis of the slope of phase III, and its evolution over time in a multibreath washout experiment. The slopes are normalized by mean concentrations within each phase III portion of each breath, and displayed as a function of turnover times (or, equivalently, breath number). Fig. 7 shows the first breath and the n=20^th breath from a multibreath N₂ washout experiment. The basic idea is that the contribution, breath by breath, of so-called diffusion-convection-dependent inhomogeneities associated with failure to reach equilibrium at the acinar level, is relatively constant throughout the procedure. By contrast, parallel contributions, referred to as convection-dependent ventilation inhomogeneities, sequentially cause an increase in the slope of phase III during the course of the multibreath maneuver. These are thought to arise from regional differences in local pressure/volume characteristics (as noted above, local compliances are the most important determinant of ventilation distribution to the extent that time constants do not reach the magnitude of breathing periods). These differences are necessary but not sufficient for this mechanism to contribute; importantly (and less well appreciated) is the fact that there must also be asynchrony in emptying of units with different N₂ concentrations. It is certainly true that, as a general rule, units with lower specific ventilation tend to empty later than those with higher ventilations; this is clearly true with respect to the overall behavior of mean N₂ concentrations over the multibreath maneuver, but it is an independent assumption for the within-breath behavior. In any event, given this foundation, one can then examine the explicit nature of the normalized slopes over the multibreath washout; an example is shown in Fig. 8, in a subject hyperresponsive to histamine provocation. Baseline evolution of the normalized slopes (shown as filled symbols) are roughly constant over the maneuver, consistent with the slopes being dominated by peripheral or acinar contributions. The magnitude of this normalized slope is conventionally denoted S_acin. During provocation, however, there is a marked change in the behavior. Normalized slopes progressively increase, consistent with more proximal inhomogeneities associated with regional variability in ventilation coupled with asynchrony in emptying. The rate of change of the normalized slopes with turnover number is denoted S_cond. Through these two indices, this method of analysis thus permits an approximate separation of the relative contributions of inhomogeneities resulting from primarily proximal convection-dependent mechanisms versus those resulting from more distal and intra-acinar diffusion-convection-dependent mechanisms.

Figure 7.

N₂ concentrations at the first and 20^th breath of a multibreath washout test. The slopes of phase III reflect the combined effects of convection-dependent parallel inhomogeneities in ventilation and diffusion-dependent inhomogeneities within the acinus. From Verbanck et al. (1997).

Figure 8.

Normalized slopes of phase III in a multibreath N2 washout study of a hyperresponsive subject, plotted as a function of lung turnover (proportional to breath number). Baseline slopes (solid symbols) vary but little over the maneuver, while there is a significant increase in slope following histamine provocation (open symbols). These are interpreted as reflecting diffusion (S_acin) and convection (S_cond) dominated inhomogeneities, respectively. From Verbanck et al., 1997.

II.5 Acinar transport—screening

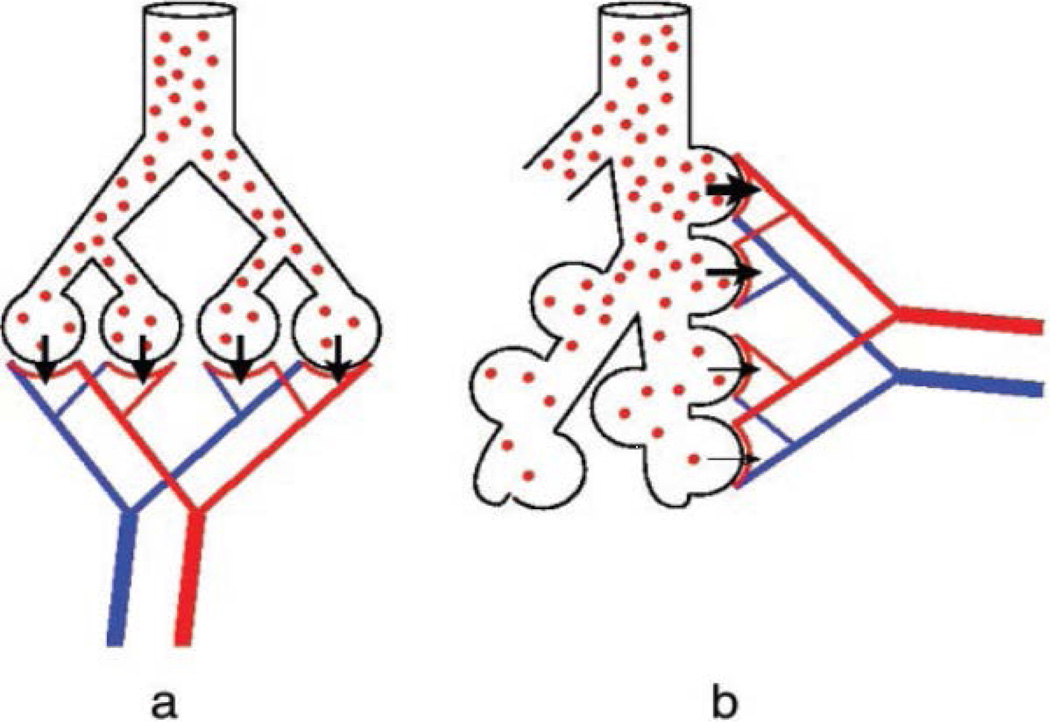
Examination of the scanning electron micrograph in Fig. 4 reveals that, particularly at the level of the acinus, the idea of a single equivalent conducting airway servicing a lumped, well-mixed alveolar region is a gross oversimplification. Indeed, the structures distal to terminal or transitional bronchioles not only have progressively increased levels of alveolation, but their serial arrangement along the respiratory bronchioles and alveolar ducts necessarily implies a serially distributed inhomogeneity even within the gas exchanging region. This is shown pictorially in Fig. 9, where panel a shows a conventional parallel distribution of ventilation and panel b shows the serial arrangement of alveoli along a respiratory bronchiole or duct. (In both cases, perfusion is distributed in a parallel fashion.) With the red dots representing local O₂ concentration, we note a relative uniformity in the parallel ventilation model, whereas in the more realistic picture with serially arranged alveoli, the O₂ concentration is systematically decreased distally within the acinus due to O₂ absorption in the proximal regions. The extent to which this may be significant forms the basis of an important advance in our understanding, introduced by Sapoval et al. (2002) and extended by Felici et al. (2003), and Felici et al. (2005). The concept is called “screening”, and specifically casts this issue in quantitative terms amenable to measurement. Note that to the extent that the screening concept applies to the serially arranged distribution of alveoli within the branching structure of the acinus, it is equivalent to a specific modeling approach to the concept of serial inhomogeneity, based on analytic scaling of the relevant parameters of O₂ exchange described below. The idea is elegant, and rests on consideration of two conductances for O₂, one from the acinar entrance (more specifically, in humans, the 1/8 subacinus, see Weibel et al. (2005) for a clear exposition of the distal branching patterns) to the air/tissue interface, and one crossing the tissue barrier to the erythrocyte. These are derived by consideration of the diffusivity for O₂ in the gas phase, D_O2,air and the permeability of the membrane separating gas from the erythrocyte, W_O2 (assumed to be a sink for O₂). The latter is given by W_O2 = β D_O2,tissue / τ, where β is the solubility of O₂ in tissue (here tissue includes cellular tissue and plasma; values do not differ significantly from those of water), and τ is the tissue barrier thickness between gas and red blood cell. The ratio of the gas phase diffusivity and the membrane permeability is denoted Λ = D_O2,air / W_O2 and has the dimensions of length. It is clear that when the gaseous diffusivity of O₂ is very high compared with membrane permeability, then O₂ concentrations are close to being uniform; when diffusivity is low compared with permeability, then there will be a significant decrease in O₂ partial pressures proceeding distally into the acinus as O₂ is lost to the more proximal alveolar exchange surfaces. Λ is thus a parameter that can be characterized as a screening length. In other words, if distances from the acinar entrance to the exchange surfaces are large compared with Λ, then significant screening takes place, with compromise to gas exchange; when distances are short compared with Λ, then screening is insignificant.

Figure 9.

Cartoon of gas exchange units with (a) parallel ventilation and (b) serial ventilation. Both pictures exhibit parallel perfusion. For O₂, in (a), gas concentrations are uniformly distributed across the parallel units, whereas in (b), O₂ concentrations are diluted distally due to O₂ uptake in more proximal acinar regions. From Sapoval et al., 2002.

With this foundation, one can then explicitly compare Λ (which depends only on physicochemical properties of O₂ and tissue) with morphometrically determined relevant distance scales. Now the conductance to reach a typical surface in the gas phase scales as D_O2,air L, where L is a characteristic length of the entire acinus or subacinus; the conductance at the membrane level is given by W_O2 S, where S is the total surface area available for transport. It follows that the ratio D_O2,air L / W_O2 S = Λ / (S / L) reflects the importance of screening in the actual acinus. Thus, whether Λ is large or small is in comparison with the morphometric length scale (S / L); the latter representing a morphometric perimeter length, Λ has been referred to as the “unscreened perimeter length”.

Quantitatively, both Λ and (S / L) are on the order of 30 cm in the human lung (the latter computed for the more functionally relevant 1/8 subacinus), and thus the fundamental ratio determining the contribution of screening Λ /(S / L) is of order unity. This is a most remarkable finding, and suggests that screening is indeed significant in gas transport at the acinar level, although not strongly so. On the other hand, the additional demands placed on the respiratory system during exercise imply that with higher ventilations (specifically higher tidal volumes), there is deeper penetration of fresh gas into the acinus, and so the effective distance L needed to reach an exchange surface is diminished. This in turn implies Λ /(S / L) increases, thus diminishing the effect of screening and promoting a more uniform distribution of local partial pressures of O₂.

II.6 Acinar transport – the velocity field

As noted above, the velocity profiles in the conducting airways is the subject of intense investigation, and is covered elsewhere in the Handbook (Tawhai et al., 2010). The velocity field within the acinus is in many ways a more difficult problem, insofar as the acinar architecture presents new and nontrivial complications (see e.g. geometric models such as Kitaoka et al. 2000, alveolar flow in a 3D alveolus model such as Haber et al. (2000), and a dynamic model with more realistic geometry such as Kumar et al., 2009). Here computational fluid dynamical methods can also be used, but specifying the model geometry is a delicate task. Importantly, the cyclic expansion and contraction of the gas exchange units, even if geometrically similar, imply that the location of the no-slip boundary conditions themselves are dynamic, and this leads to some unexpected and new phenomena that may prove significant in gas exchange.

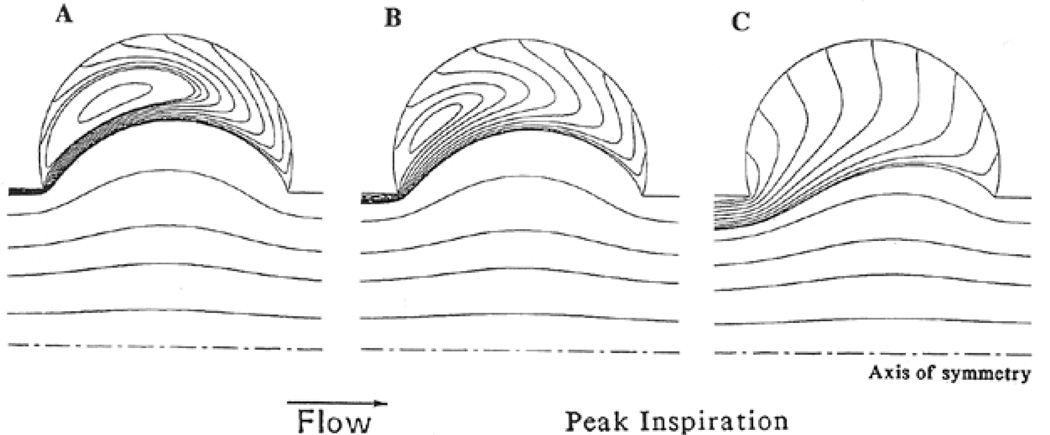
The flow fields in models of the alveoli and alveolar ducts illustrate these features. Fig. 10 shows the streamlines in one alveolar unit of a model acinus composed of a central duct surrounded by an axisymmetric alveolar region (Tsuda et al., 1995; and for a fully 3D spherical alveolus model, see Haber et al., 2000). As these are serially arranged along the duct, and with geometric similarity in alveolar expansion, it follows that the volume flow into each alveolus Q̇_a relative to the ductal flow Q̇_d must systematically increase as one proceeds distally down the duct. (That is, even with uniform Q̇_a among alveolar units, Q̇_d must service all distal units and thus is maximal at the proximal end and minimal at the distal end of the acinus; hence the ratio Q̇_a / Q̇_d is minimal proximally and maximal distally.) This ratio has been found to be a primary determinant of the flow patterns within each alveolar unit. As the Figure shows, those units which are more proximal (panels A and B), and hence with the lowest values of Q̇_a / Q̇_d, display the largest recirculation flows. This is also seen in the solutions to flows in similar geometries but where the walls are rigid. Importantly, however, note that the streamlines in this expanding/contracting model terminate at the alveolar boundaries, as they must to satisfy the no-slip condition at the moving boundaries. By contrast, at the most distal level, where Q̇_a / Q̇_d is the largest, the recirculation patterns disappear, and are replaced by simpler streamlines roughly following the expansion field. Importantly, in those circumstances with recirculatory flows, a stagnation “saddle” point in the velocity field exists near the proximal edge of the alveolus. This is true for panels A and B in Figure 10, although they cannot be easily visualized due to their proximity to the leading proximal edge. Saddle points are commonly found in chaotic flow, and imply extreme sensitivity to variations in upstream conditions. A consequence of this is the introduction of irreversibility in the kinematics (Henry et al., 2002), which in turn leads to further mixing within the alveolar region. The streamlines shown in the Figure are for inspiration; an interesting feature of this model is the observation the flow patterns are approximately the same during expiration as well (with sign reversal); this is a consequence of the low Reynolds number character of the flow regime. On the other hand, geometric hysteresis during breathing is another potentially important source of kinematic irreversibility in the flow fields (Haber et al., 2000; Butler and Tsuda, 2005) (for a converse, see Watson (1974) for a theorem regarding reversibility of velocity fields with reversible wall motion, and see also Taylor, 1960). Here geometric hysteresis refers to the configuration of airspaces, especially those in distal regions, which are different during inspiration and expiration at the same lung volume; it is not to be confused with stress hysteresis in which there are substantial differences in lung recoil during inspiration and expiration at isovolume points. While it is true that during quiet breathing, experiments show that pulmonary expansion is approximately reversible (Ardila, et al., 1974), but importantly, a small degree of geometric hysteresis has also been experimentally verified (Miki et al., 1993). Coupled with the presence of alveolar recirculation, this can in principle lead to significant intra-acinar mixing due to repeated folding of streamlines which do not retrace their trajectories.

Figure 10.

Streamlines within the alveolus and alveolar duct in an axisymmetric model of the acinus with expanding boundaries simulating parenchymal expansion during breathing. Panels A, B, and C show streamlines with increasing values of flow into the alveolus relative to flow in the central alveolar duct. From Tsuda, et al. 1995.

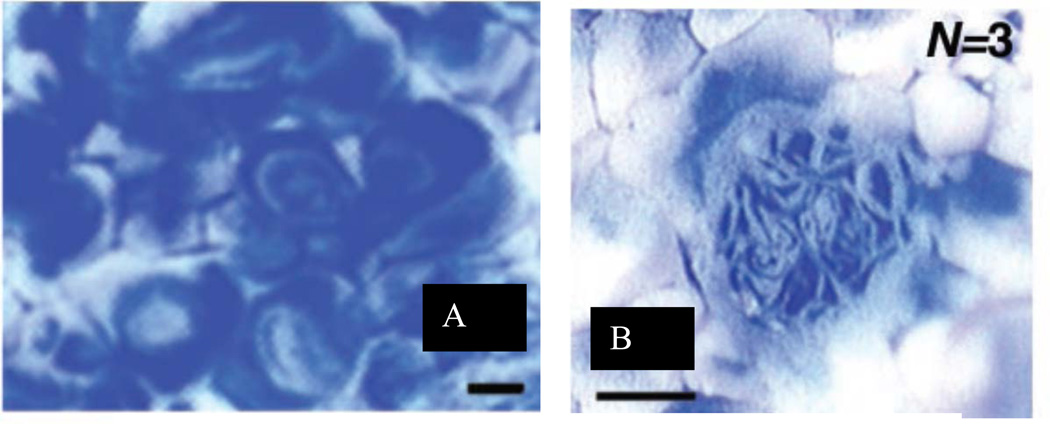
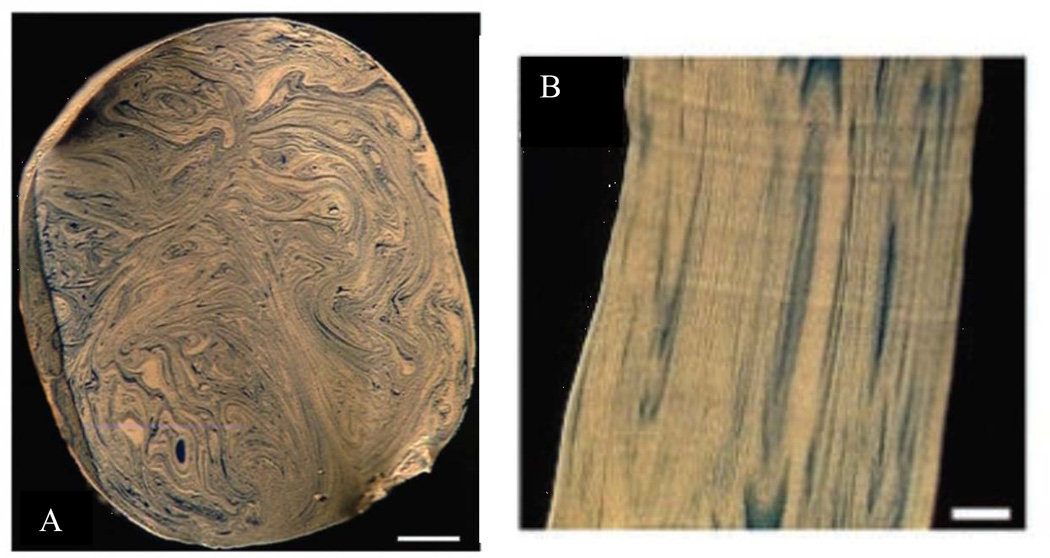
This interaction of irreversible flow kinematics, of whatever origin, in the expanding and contracting model of the acinus has led to predictions of sequential “stretch and fold” patterns (Butler and Tsuda (1997), Tsuda et al. (1995, 1999, 2002), wherein the expanding fronts of fluid following their Lagrangian trajectories do not time reverse, even with approximate reversibility in the material velocities of the boundaries. That is, even small amounts of irreversibility in the boundary motion, in addition to the sensitivity of velocities can lead to substantial irreversibilities in inspiration and expiration. A consequence of this is that the expanded fronts, tethered to bronchial or acinar walls by no-slip, do not retrace their configurations and lead instead to folds, increasing in complexity with each breath. An example of this is shown in Fig. 10, where the trajectories were visualized by using polymerizable silicones of different color, white for the initial resident fluid and blue for tidal volume. Panel A shows the striations in a transverse section of the trachea, illustrating the multiple folds seen in this preparation after just a single breath cycle. Panel B shows a longitudinal section at the level of a small bronchus of the 7^th generation, confirming the existence of the stretch and folded pattern arising from deep in the lung. Deep in the lung, complex trajectories are already evident within alveoli; Figure 12, Panel A shows the initial entry of blue tidal fluid into resident white fluid. There is marked heterogeneity in these images, which do not follow a simple convective ventilatory pattern with a blue tongue surrounded by a white annulus within each alveolus. With successive inspiratory/expiratory cycles, these do not simply retrace their original trajectories, and as in the larger airways shown above, lead to stretch and folded ventilatory patterns even in small airways. Figure 12, Panel B, shows the folded nature of trajectories after 3 breaths within a small acinar airway. These patterns, arising from alveolar recirculation and other potential origins of kinematic irreversibility are consistent with numerical simulations. The implications here are that even within the acinus, it is not sufficient to take these regions as “well mixed”; the velocity profiles remain complex and need to be considered in understanding the nature of gas transport at this level.

Figure 12.

Complex patterns of irreversible kinematics within the acinus. Panel A shows evidence of recirculation within alveoli, and Panel B shows significant folding patterns in a small intra-acinar airway. Scale bars = 100 μ, From Tsuda, et al., 2002.

This has been confirmed by recent numerical work (Kumar et al., 2009) investigating flow profiles in a realistic honeycomb model of the acinus with a central duct and surrounding alveoli, showing significant alveolar recirculation patterns particularly in the proximal alveoli in the acinus. In the more distal regions, significant alveolar entrainment of ductal flow leads to an absence of recirculation. This expands on and generalizes earlier work establishing complex profiles deep in the lung (Tsuda et al. 1995, Tsuda et al. 1999). The issues of secondary motions such as recirculation, particularly in the context of repeated breathing cycles, has a strong influence on the transport and deposition of fine and nanosize aerosol particles. Further details on acinar flow dynamics can be found in the “Particle transport and deposition” chapter in this series (Tsuda et al., 2010).

From these studies, both theoretical and experimental, it is apparent that the flow patterns within the acinus are far from simple, and that their very complexity has implications for gas mixing. Of particular interest is the potential link of these ideas with those principally focused on diffusional screening (Sapoval et al., 2002, Felici et al. 2003, Felici et al. 2005). In their work, ventilation per se is absent, and solutions to the static Laplace equation for concentrations serially changing secondary to serial uptake of O₂ are based on a fixed source term at the effective entrance to the acinus. As noted above, the effect of screening is thought to be largely ameliorated during exercise, as the inspired front of fresh gas penetrates deeper and deeper into the acinus proper. But even at rest, the stretching and folding patterns, including recirculation and entrainment, seen here imply a potentially very significant role for irreversible convective transport even within the acinus. As noted in the section on boundary conditions, in steady state transport of respiratory gases there cannot be true equilibrium within the alveolar space, the gradients are very small, to be sure, but are necessarily nonzero to satisfy metabolic requirements. The difficulty is that convection must also play a role in the establishment of these gradients, and will require a marriage of acinar kinematics with diffusive transport and screening within the known context of the serial disposition of gas exchange surfaces in the acinus. That is, a systematic exploration of the serial inhomogeneities that exist within the acinus will necessitate a commensurate and quantitative characterization of the velocity fields, which as noted above have been demonstrated both experimentally and with numerical simulations to involve significant secondary motions. The more recirculation, entrainment, and folding that occurs will tend to limit the development of serial inhomogeneities, thus tending to ameliorate any ventilation/perfusion inequalities that may occur even in normals. By contrast, in the absence of such secondary motions, simple kinematically reversible velocity fields will accentuate the effect of serial depletion of O₂ axially along the acinar pathways, and may lead to ventilation/perfusion mismatches. Quantifying these effects remain a major open area of research.

III. Summary and future directions

The classical description of gas transport from the ambient environment to the alveolar gas exchange region has been traditionally described in terms of a simple fractionation of the entire airway tree into a proximal region comprising a dead space, where transport takes place cyclically by convection, and a distal region comprising a well-mixed alveolar space, where transport is effected by diffusion from gas to blood. The former is in principle reversible, while the latter is intrinsically irreversible, and is associated with true net transport. This picture is simple, but surprising in its ability to accurately characterize most features of gas transport in normal lungs.

The reasons behind the success of this fractionation lie in the remarkable architectural features of the tracheo-bronchial tree, specifically its sharply increasing net cross sectional area at each bifurcation in the tree. This, coupled with appropriate quantitative measures of the relative importance of convection and diffusion, leads to an appreciation of why such a description is largely valid.

At a deeper level, there are a number of outstanding questions with a great array of experimental techniques to probe them. These fall into issues of the specific interaction and coupling of convective and diffusive transport mechanisms. Mechanisms include irreversibility in velocity profiles, velocity profiles in general with moving boundaries during breathing, parallel and serial inhomogeneities in gas concentrations and their combined effects on transport, and the new concepts of screening associated with serial gas exchange within the acinus proper.

These play into the larger physiologic questions of gas exchange in circumstances other than rest. One example is gas phase transport during exercise, where the distribution of perfusion is largely altered through vascular recruitment, thus changing potential diffusional screening. Moreover, the high velocities in the central airways imply a commensurate influence on intraluminal pressures through the Bernoulli effect thus changing airway caliber, resistance, and the distribution of ventilation. Another example is gas phase transport at altitude, where hypoxic vasoconstriction also changes the local uptake of O₂, with consequences to serial inhomogeneities again through changes in screening. Note further that these examples, and the concepts and issues presented in this chapter are all predicated on being in steady state. Transient phenomena are different, and will require different approaches, with attention to which mechanisms are important and which may be negligible. For example, at the opposite extreme from heavy exercise with high ventilations, in elite divers gas phase transport is largely unexplored during prolonged breath holds (which can exceed 10 min), and with lung volume excursions significantly in excess of traditional total lung capacity and below traditional residual volume (through glossopharyngeal pumping, see Sun et al. 2009, Loring et al. 2007, Muradian et al. 2010).

In all of these examples, the larger physiologic context will require the coupling of mechanics, dynamics, perfusion, local exchange at the blood/gas interface, and physiologic feedback mechanisms. This implies that an integrated approach is essential for significant progress; mechanisms isolated from the entire lung (and indeed from the entire body) are unlikely to provide a complete picture. Lastly, at the theoretical level, it must be stressed that both analytic approaches and numerical simulations each share strengths and weaknesses. The former’s strength is the explicit identification of the role of a limited number of primary variables, and how gas transport depends upon them. The small number of independent variables is also its greatest weakness—it cannot capture features that depend in complex ways on the complex geometry and kinematics of surface movements during breathing. Similarly, the strength of numerical simulations is that they can incorporate a large range of independent variables, typically associated with the complex geometry of the conducting airways and acini, including lengths, diameters, branching angles, and the correlation of planes of bifurcations between successive generations. This large number of independent variables is also the greatest weakness of numerical work; it is commensurately difficult to identify the essential features that contribute to gas transport, or to capture which features, while completely different in detail between individual representations of the airway and acinar trees, are the ones that characterize the commonality of lung structure and transport properties within a given taxon. By analogy to the argument above with respect to the need for an integrated approach to the various mechanisms contributing to gas transport, it is equally important that analytic and numerical approaches be integrated, such that the strengths of each may complement one another. The future holds great promise in integrating both fundamental mechanisms at various levels within the airway and acinar trees, their modulation in differing circumstances, how they scale across species, and importantly, how these are affected in disease.

Figure 11.

Panel A: Realization of multiple stretch and fold patterns in the trachea of a rat, after a single breath. Two colors of polymerizable silicone were used to visualize resident and tidal fluid. Scale bar = 500 μ. Panel B: Longitudinal striations in a small airway (7^th generation) showing the folded patterns originating from deep in the lung. Scale bar = 100 μ. From Tsuda, et al., 2002.