Wrinkled, wavelength-tunable graphene-based surface topographies for directing cell alignment and morphology

Abstract

Textured surfaces with periodic topographical features and long-range order are highly attractive for directing cell-material interactions. They mimic physiological environments more accurately than planar surfaces and can fundamentally alter cell alignment, shape, gene expression, and cellular assembly into superstructures or microtissues. Here we demonstrate for the first time that wrinkled graphene-based surfaces are suitable as textured cell attachment substrates, and that engineered wrinkling can dramatically alter cell alignment and morphology. The wrinkled surfaces are fabricated by graphene oxide wet deposition onto pre-stretched elastomers followed by relaxation and mild thermal treatment to stabilize the films in cell culture medium. Multilayer graphene oxide films form periodic, delaminated buckle textures whose wavelengths and amplitudes can be systematically tuned by variation in the wet deposition process. Human and murine fibroblasts attach to these textured films and remain viable, while developing pronounced alignment and elongation relative to those on planar graphene controls. Compared to lithographic patterning of nanogratings, this method has advantages in the simplicity and scalability of fabrication, as well as the opportunity to couple the use of topographic cues with the unique conductive, adsorptive, or barrier properties of graphene materials for functional biomedical devices.

1. Introduction

Patterning of surface topography is a powerful technique for controlling interfacial interactions between a material and its environment [1]. Topographical patterns can be created by etching or molding the surface of a single-component material, or through creation of heterostructures consisting of a substrate and a surface film with engineered texture. An emerging method for surface texturing is the creation of wrinkle patterns by controlled shrinkage of a stiff coating on a softer, compliant substrate [2–5]. This approach has been experimentally implemented in a variety of polymeric and inorganic material systems [6], and the wrinkle morphologies have been the subject of theoretical treatments of buckling instability [7–9]. An exciting new approach to the creation of these textured surface films is the growth or deposition of two-dimensional, sheet-like nanomaterials, such as graphene, whose atomically thin nature enables the creation of the ultrathin flexible films suitable for controlled wrinkling. Topographically patterned graphene has found numerous applications in optical and electronic devices, energy storage, and functional coatings [10–19].

Here we demonstrate another application area for graphene surfaces with engineered wrinkle structures: as functional substrates for cell and tissue engineering. Planar graphene and graphene oxide (GO) have already been explored as substrates for biological cells and tissues [20–22], and remarkably, mesenchymal stem cells, myoblasts and fibroblasts appear to display enhanced viability compared to conventional tissue culture substrates [23–27]. A limitation of conventional flat, uniform 2D cell culture substrates, however, is that they lack the complexity of structural architectures found in the extracellular matrix in living tissue. On planar 2D surfaces, cells adopt strongly flattened morphologies, and the resulting cellular behavior can deviate from the natural behavior observed in a physiological 3D context.

Modern nanopatterning approaches strive to create biomimetic features that are comparable in size and geometry with molecular elements of the natural microenvironment.[28–31] In particular, interstitial collagen in the extracellular matrix are bundled together with diameters from tens to hundreds of nanometers, as well as pore sizes or gaps on the order of 5–20 μm [32]. These anisotropic topographies can affect cell morphology and orientation, a phenomenon known as contact guidance [33]. Cell-substrate interactions that mimic this anisotropy using aligned grooves have been previously investigated on polymeric materials using controlled buckling [34–36] and micropatterning [37–41], revealing altered migration dynamics, proliferation, gene expression and differentiation. In this context, graphene substrates incorporating microscale topography are intriguing as functional substrates for cell and tissue engineering, but have not, to our knowledge, been previously examined. Overall, the design of biomaterial interfaces based on graphene represents an exciting approach for understanding fundamental cell biology, nanostructured scaffolds for tissue engineering and regenerative medicine as well as to promote biocompatibility and biointegration of functional medical implants in neuronal, cardiovascular or epidermal tissues.

In this article, we demonstrate the formation of wrinkled multilayer graphene surfaces using GO solution phase deposition on pre-stretched elastomeric substrates followed by relaxation and thermal stabilization. We find that the topography of these stabilized graphene oxide (s-GO) surfaces is maintained during thermal treatment, and displays exceptionally sharp features, whose spatial periodicity can be systematically tuned by simple variation of the GO concentration in the deposition suspension. We examine the effect of these wrinkled s-GO architectures on human and murine fibroblast cells, which attach and remain viable, and cause important changes in cell orientation, alignment, and morphology relative to cells on planar s-GO. This work establishes the feasibility of graphene wrinkle engineering for the fabrication of textured substrates for cell and tissue engineering and potential applications in biomedical implants.

2. Experimental

2.1. Fabrication of textured surfaces

GO suspensions were prepared by a modified Hummer’s method and purified and characterized as described previously [42]. These GO sheets are primarily in monolayer form in aqueous suspension and are 1–5 μm in lateral dimension with a C/O atomic ratio of approximately 1.8 [42]. The elastomeric substrates were silicone rubber sheets (McMaster-Carr) of 1/16″ thickness and either 50A or 20A hardness. The elastic modulus of the substrates was measured using an Instron 5882. The elastomer films were cut into 4×2 cm pieces, washed with deionized water, and fixed at one end to glass slides. The films were stretched uniaxially to a desired pre-strain (1.5%–50%) and secured with a fastener. A specific volume of GO aqueous suspension (typically 150 uL of 0.2 g/L GO) was pipetted onto the substrate, dried overnight, and relaxed to form the wrinkle patterns (Fig. 1A). For cell studies the films were rendered stable to re-dissolution in cell culture medium by mild thermal treatment through annealing overnight at 120 °C in air.

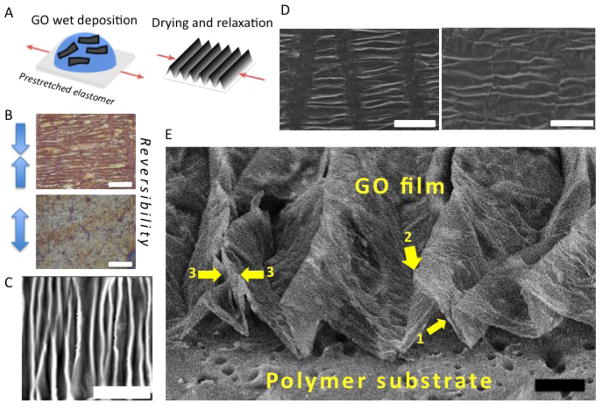
Figure 1.

Fabrication process and morphology characterization of wrinkled graphene-based multilayer films. (A) Illustration of the fabrication process for wrinkled GO multilayer films. (B) Demonstration of reversibility by re-stretching under an optical microscope, scale bar is 100 μm. (C) AFM image showing the basic morphology of parallel ridges with sharp crests (light) and broader valleys (dark). Film thickness is 20 nm and scale bar is 20 μm. (D) SEM showing longitudinal microcracks that form when simple uniaxial relaxation occurs (left image). These cracks can be suppressed (right image) if the substrate is constrained in the transverse direction during relaxation to prevent the expansion associated with the Poisson effect, scale bar 100 μm. (E) High-tilt SEM image of transverse profiles, which shows a delaminated buckle structure with nearly straight slopes (arrow 1) and curvature concentrated at the ridge tops (arrow 2). These wrinkles are high-amplitude buckled ridges in which some primary peaks have collapsed on neighbors to create double-ridges (arrow 3). Scale bar 20 μm. All samples in Fig. 1 unless noted use 50% pre-stretch and 200 ug/ml GO suspension that gives a nominal GO film thickness of 200 nm).

2.2. Morphology characterization

Morphologies of the textured surfaces were characterized by optical microscopy, atomic force microscopy (Asylum MFP-3D Origin AFM) in pulse mode, and field emission SEM (LEO 1530 VP) in the variable operating pressure mode without coating the samples, in top view (for wavelength determination) or high tilt (for transverse profiles). The characteristic wavelength of the wrinkle features were quantified by sampling grey-scale line profiles from the micrographs using Gatan DigitalMicrograph, followed by Fast Fourier Transformation in MATLAB (Mathworks).

2.3. Cell culture

NIH-3T3 mouse fibroblasts were a gift from Dr. Agnes Kane (Brown University), while normal human fibroblasts (NHF cells) derived from neonatal foreskin were a gift from Dr. Jeffrey Morgan (Brown University). Cells were cultured in high glucose, pyruvate Dulbecco’s Modified Eagle’s Medium (DMEM, Life Technologies # 11995) supplemented with 10% Fetal Bovine Serum (FBS), 100 units/mL penicillin, and 100 ug/mL streptomycin. Both cell lines were carried out under standard culture conditions: incubation at 37°C in a 5% CO₂ gaseous environment, which pairs with the DMEM’s sodium bicarbonate buffer system to maintain physiological pH, cells were cultured in T-25 flasks, and passaged at 70–80% confluence. Only low passage numbers were used in experiments (P5–P12 for NIH-3T3s and P4–P10 for NHFs).

2.4. Preparation of s-GO-coated substrates for cell culture experiments

Paired wrinkled and flat s-GO substrates were prepared as described previously. For cell culture, substrates were further processed by immersion and rinsing in DI water (Milli-Q, 18.2 MΩ) for at least 12 hours to remove debris and any contaminants. Substrates were then sterilized by UV exposure with a 30W lamp for 1 hour before transferring to a 24 well plate.

Once the s-GO materials were prepared and sterilized, cells cultured in T25 flasks were incubated with HyClone 0.05% Trypsin for detachment. Once cells were lifted off the flask, the suspension was transferred to a conical tube containing growth medium and centrifuged at 1000RPM for 5 minutes. The cell pellet was then re-suspended in culture medium, and cells were subsequently counted using an automated cell viability counter (Nexcelom Cellometer Auto 1000). Next, a 100uL droplet with a concentration of 40,000 cells/mL was deposited on the materials, allowed to settle for ~1 hour, and then the well was filled with 1 mL of culture media. After 48 h, the cell culture media was replenished.

2.5. Cell viability

After culturing cells on polystyrene, flat s-GO, and wrinkled s-GO substrates for 96 hours, culture medium was aspirated and replenished with media containing Hoechst (bis-Benzimide), diluted 1:2000. Cells were incubated for 30 minutes at 37°C in 5% CO₂ to label cell nuclei, the Hoechst-media was aspirated, and cells were rinsed with 1X phosphate buffered saline (PBS). To label dead cells, DRAQ7 (BioStatus), diluted 1:100 in culture medium, was added to each well. Cells were incubated for an additional 10 minutes, and then imaged using an inverted epifluorescence microscope (Nikon TiE). Images were acquired using a 10X Plan Fluor objective (NA 0.3, long working distance) with fluorescence illumination, provided by using a light-guide coupled Lumen Dynamics X-Cite 120 LED system. All images were acquired with 14-bit resolution using a sCMOS camera (Andor Neo). Care was taken to ensure that all images were recorded with identical acquisition parameters (exposure time, camera gain/gamma control and microscope aperture settings). To determine the percentage of viable cells in each condition, the total cell nuclei (Hoechst label) and dead cells (DRAQ7 label) were counted using CellProfiler (version 2.1, Broad Institute). Cell viability was defined by the ratio of live cells (Total nuclei count – Dead cell count) to the total number of cells (Total nuclei count); the results were plotted as bar graphs, with the use of MATLAB (Mathworks).

2.6. Immunostaining and fluorescence imaging

After 96 h of culture on wrinkled and flat s-GO substrates, cells were fixed using 4% paraformaldehyde in 1X PBS. Cells were then permeabilized with 0.1% Triton-X 100 in 1X PBS. For F-actin microfilament detection, cells were immunostained with a conjugated antibody, Alexa Fluor 647 Phalloidin (Invitrogen), diluted 1:80 in 1% nonfat dry milk in 1X PBS. Cell nuclei were also labeled by counterstaining with Hoechst (bis-Benzimide), diluted 1:5000 in 1X PBS. 1X PBS was added to the wells, and immunostained samples were placed upside down in a new 24 well plate for imaging using an inverted epifluorescence microscope (Nikon TiE). Images were acquired using a 10X Plan Fluor objective (NA 0.3, long working distance) or a 20X Super Plan Fluor objective (NA 0.45, extra long working distance). Fluorescence illumination was provided using a light-guide coupled Lumencore Sola white light excitation system. All images were acquired with 14-bit resolution using a sCMOS camera (Andor Neo). Care was taken to ensure that all images were recorded with identical acquisition parameters (exposure time, camera gain/gamma control and microscope aperture settings).

2.7. Image processing for quantification of cell morphology

CellProfiler (version 2.1, Broad Institute) was utilized for cell segmentation and analysis [43], with manual verification afterwards. First, fluorescently labeled nuclei were segmented as primary objects using maximum correlation thresholding (MCT) and clumped objects were resolved using shape and intensity. Next, based on the location of the nuclei, fluorescently labeled F-actin in the cell body was segmented as a secondary object. For wrinkled surfaces, secondary objects were best segmented by a robust background threshold and adaptive threshold strategy. Instead, for flat controls, secondary objects were best segmented using the Ostu thresholding method and global thresholding strategy. Finally, the “MeasureObjectSizeShape” module was employed to extract the following shape descriptors for the detected objects:

Area

The actual number of pixels in the region.

Eccentricity

The eccentricity of the ellipse that has the same second-moments as the region. The eccentricity is the ratio of the distance between the foci of the ellipse and its major axis length. The value is between 0 and 1. (0 and 1 are degenerate cases; an ellipse whose eccentricity is 0 is actually a circle, while an ellipse whose eccentricity is 1 is a line segment.)

Solidity

The proportion of the pixels in the convex hull that are also in the object, i.e. ObjectArea/ConvexHullArea. Equals 1 for a solid object (i.e., one with no holes or has a concave boundary), or <1 for an object with holes or possessing a convex/irregular boundary.

Orientation

The angle (in degrees ranging from −90 to 90 degrees) between the x-axis and the major axis of the ellipse that has the same second-moments as the region.

Compactness

The variance of the radial distance of the object’s pixels from the centroid divided by the area.

MinorAxisLength

The length (in pixels) of the minor axis of the ellipse that has the same normalized second central moments as the region.

MaxFeretDiameter

The Feret diameter is the distance between two parallel lines tangent on either side of the object (imagine taking a caliper and measuring the object at various angles). The maximum Feret diameter is the largest possible diameter, rotating the calipers along all possible angles.

We found that width of a cell was poorly approximated by the minor axis of an ellipse with equivalent second central moments, resulting in an overestimation of cell width. Instead, we defined an alternate metric:

Average Cell Width = Area/MaxFeretDiameter, which is based on the actual area of the cell.

2.8. Cell orientation and statistical analysis

A variety of circular statistical tests were applied using Oriana (Kovach Computing Services) to test whether cellular orientations were uniformly distributed (one-sample tests) or to compare the similarity of two distributions (multiple sample tests) [44]. Rao’s Spacing Test was used to evaluate the null hypothesis that a given circular dataset is uniformly distributed by checking if the differences between successive measurements are comparable to 180°/N, where N is the number of measurements. In addition, the Mardia-Watson-Wheeler test was used to evaluate the null hypothesis that two samples have identical distributions as a circular analogue of the two sample t-test. It should be noted that, for simplicity, the coordinate system for wrinkled materials was defined along the length of the wrinkles. Circular statistics were plotted in MATLAB (Mathworks) using ROSE.

For all other metrics of cell morphology, the statistical distributions were compared using the two-sample Kolmonogorov-Smirnov test in MATLAB (Mathworks). Statistical significance was determined by rejecting the null hypothesis at p ≤ 0.05 (5% significance level). Plots were also generated in MATLAB, as a combination of BOXPLOT, where the dividing line corresponds to the median, 25^th and 75^th percentiles are indicated by the box edges and whiskers correspond to 99.3% coverage, as well as PLOTSPREAD (MATLAB File Exchange), which displays data points representing individual cell measurements.

3. Results and discussion

3.1 Film fabrication and structure

The main objective of this research was to explore wrinkled GO surfaces as anisotropic cell attachment substrates for control of cell alignment and morphology in tissue engineering applications. We chose a fabrication route based on GO wet deposition and mild thermal treatment, which is a potentially practical and scalable method that is an attractive alternative to large-area coverage by pristine CVD graphene. Figure 1 shows the basic morphology of the wrinkled GO surfaces prior to thermal treatment created by relaxation of substrates with 50% uniaxial pre-strain and covered by 200 nm thick GO multilayer films. Relaxation produces a series of nearly parallel ridges with high-curvature crests separated by broader valleys (Fig. 1A and C). The wrinkle patterns can be removed by re-stretching to the initial state (Fig. 1B), and the process is reversible over multiple cycles. These features are similar to those observed previously for pristine few-layer graphene coatings undergoing similar uniaxial compression [16, 18]. The present films show longitudinal cracking (Fig. 1D left) during relaxation, which we suspected was due to Poisson expansion in the transverse direction. The cracks here did not appear to affect the periodic wrinkle textures, but do reveal the underlying substrate, which would be an undesirable feature in some applications. We therefore sought a solution, and found that the cracks could be suppressed by fixing the sides of the film during the pre-stretch to mechanically constrain its Poisson contraction, which then also suppresses its subsequent Poisson expansion during the relaxation and wrinkling process (Fig. 1D right).

The longitudinal cracks in the films fabricated in our early attempts without transverse pinning were undesired, but did make it possible to directly view the cross-section wrinkle profiles in detail (Fig. 1E). The wrinkles are delaminated buckled structures with nearly straight slopes and with curvatures concentrated at the ridge tops. The ridge tops have characteristic curvatures on the order of the film thickness, and are similar to the sharp ridges seen in crumpled graphene particles formed during isotropic compression [45, 46], which are 3D structures having both ridges and vertices. The films remain on the substrate through adhesion at the valley floor regions, and the local delamination produces cavities with triangular cross-sections between the substrate and film. This delamination buckling in multilayer GO has also been observed in pristine few-layer or multi-layer graphene films [16, 18], while amorphous carbon films fabricated by ion beam deposition from hydrocarbons do not show such local delamination when they undergo spontaneous buckling associated with growth-induced film compression [19]. The difference may reflect very different film-substrate bonding in the graphene-based films and the ion-beam deposited films.

3.2 Wavelength and amplitude tuning

For manipulation of cell alignment and morphology, it is desirable to control the amplitude and wavelength of the wrinkle patterns in our multilayer graphene films. Approaches to this control are readily suggested by the significant literature on the theoretical and experimental mechanics of stiff thin films on pre-stretched compliant substrates [15, 47–49]. The critical buckling strain is reported to be ${\epsilon }_c=1/4{\left[\frac{3E_s(1-{\nu }_f^2)}{E_f(1-{\nu }_s^2)}\right]}^{2/3}$, where E_f and E_s are the Young’s modulus of film and substrate, respectively, and ν_s and ν_f are the Poisson’s ratio of elastomer substrate and stiff film, respectively. When this strain is exceeded, wrinkles develop with a wavelength:

$${\lambda }_0=2\pi h_f{\left[\frac{E_f(1-{\nu }_s^2)}{3E_s(1-{\nu }_f^2)}\right]}^{1/3}$$ (1)

where, h_f is the film thickness. This theory is valid in the limit of small deformation. When the deformation is large, wavelength becomes strain-dependent [50], and consequently the corresponding wavelength is [49]

$$\lambda =\frac{{\lambda }_0}{(1+{\epsilon }_{\mathit{pre}}){(1+\xi )}^{1/3}}$$ (2)

where λ₀ is the wavelength based on small deformation theory, ε_pre is the pre-strain and a pre-stretch factor (1 + ε_pre)(1 + ξ)^1/3 is included with ξ = 5ε_pre(1 + ε_pre)/32. When ε_pre is constant, the superficial wavelength λ only depends on the thickness of the film.

Equation (1) suggests the use of film thickness or substrate stiffness to tune wavelength. The former is an attractive option for multilayer GO films, whose thickness can be easily and systematically altered by changing the concentration in the deposition fluid. The results of both methods for wavelength tuning are illustrated in Fig. 2. For a given substrate, wavelengths can be changed by an order of magnitude (e.g. 3 to 30 μm for the softer substrate) by varying GO film thickness from 20–200 nm through increasing GO suspension concentration from 0.02–0.2 mg/ml. Based on the work of Kunz et al [15], we anticipate the ability to extend to nanoscale features by using monolayer or few-layer s-GO, though it becomes increasingly difficult to fully cover the substrate with such ultrathin films made by tiling microscale GO sheets.

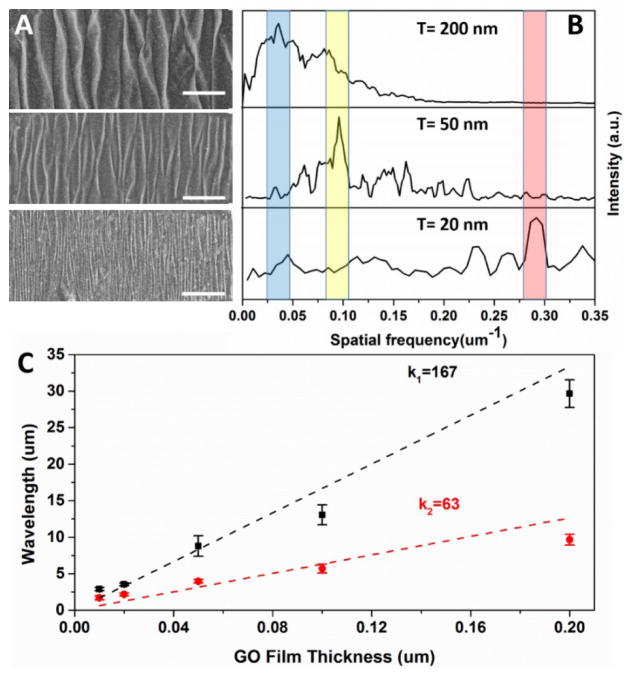
Figure 2.

Wavelength tunability through control of multilayer GO film and through substrate selection. (A) SEM images of wrinkled GO films of thickness from 10 nm to 200 nm on the softer elastomer (modulus 5·10⁴ Pa) and (B) their Fourier transform spectra with the dominant spatial frequency shaded. (C) Thickness-dependent wavelengths on softer (black squares) and stiffer elastomer (modulus 6·10⁵ Pa; red circles) with linear regression slopes $\frac{\lambda }{h_f}$ shown. The scale bars in (A) represent 50 nm.

The linear relationship between the wavelength and film thickness is consistent with Eq. 1, and can be used to estimate the Young’s modulus of the multilayer GO film. Taking ε_pre = 50%, ν_f = 0.197, [51] ν_s = 0.48, we can obtain from equation (1) and (2),

$$E_f=0.057E_s{(\frac{\lambda }{h_f})}^3$$ (3)

giving an estimate of the film modulus of 8.6–13.3 GPa, which is similar to published experimental results obtained by other methods [52, 53]. The wavelength of our wrinkle features decreases with increasing pre-stretch in agreement with Eq. 2 (Supplementary Information, Fig. S1).

In dynamic experiments under the optical microscope, we observe that the ridges do not all appear at once during relaxation, but rather in pairs separated by a distance corresponding to the characteristic wavelength. Upon further relaxation the ridge pairs migrate closer together in response to the substrate shrinkage and the characteristic periodic wrinkle structure becomes uniform over large areas. The amplitude of the sinusoidal wrinkles that appear at small deformation is predicted by theory to be $A_0=h_f\sqrt{\frac{{\epsilon }_{\mathit{pre}}}{{\epsilon }_c}-1}$, while for large defomation, Song et al. proposed [49]

$$A=\frac{A_0}{\sqrt{1+{\epsilon }_{\mathit{pre}}}{(1+\xi )}^{1/3}}$$ (4)

This suggests that both film thickness and pre-stretch can be used to control feature height. Though these relations are for adherent and elastically deformed films, they can be used as an estimate for the delaminated buckle structures observed here.

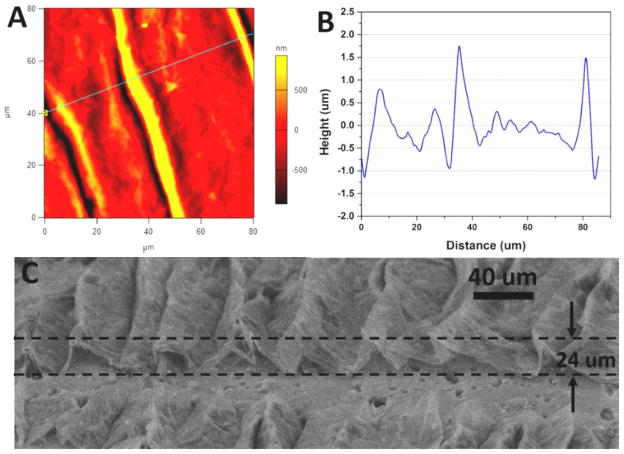
The height and periodicity of these buckled structures was quantified through the use of atomic force microscopy (AFM). A representative scan of a buckled structure formed after a small pre-strain (1.5%) is shown in Fig. 3A. The corresponding height profile for these structures shows a characteristic ridge height of ~2 μm (Fig. 2B). At moderate pre-strains (8.5 % or 25 %), increased ridge heights of approximately 7 and 12 μm were observed, respectively (Supplementary Information, Fig. S2). Finally, for large pre-strains (50%), the ridge heights became large enough that characterization with high-tilt SEM was more appropriate than AFM. These ridge heights were ~24 μm (Fig. 3C), with no correction for foreshortening needed to estimate these values at the high tilt angle used. Overall, pre-strain affects ridge amplitude much more than it affects wavelength (Supplementary Information, Fig. S1), so it is an effective and facile means to control feature height.

Figure 3.

Pre-strain provides effective control over wrinkle feature height. (A) AFM image of multilayer graphene oxide film after release of 1.5% pre-strain on the softer elastomer substrate. (B) Height profile along line marked in (A). (C) High-tilt SEM image of wrinkled graphene on the soft elastomer substrate with 50% pre-strain.

3.3 Mild thermal treatment for liquid phase stability

The data in Figs. 1–3 are for multilayer GO films in their as-produced, fully-oxidized state. We observed that these films were poorly suited for biological applications due to gradual redissolution of GO sheets in cell culture medium as well as instability in the feature heights in response to wetting and drying cycles. Infiltration of aqueous solutions into the delamination cavities between the film and substrate leads to peak collapse by capillary forces when the solution is driven out during the drying process (Supplementary Information, Fig. S3). We hypothesize this effect is due to the hydrophilicity of GO, and could be managed by partial deoxygenation. We could not fully reduce GO due to the limited thermal stability of the elastomer substrate, and therefore explored long-time, mild heating as a possible route to stabilization. After overnight heating at 120 °C in air, we found the GO samples lost absorption peaks at ~850 and ~1200 cm⁻¹ measured by Fourier transform infrared spectroscopy (Supplementary Information, Fig. S4), which are typically assigned to C-O vibrations and may be due to the removal or alteration of epoxides.[54] The reduced intensity of broad peak (O-H stretch) at ~3300 cm⁻¹ indicates the removal of interstitial water, which may also contribute to the stabilization of GO. Most importantly, the stabilized graphene oxide (s-GO) films showed good retention of the wrinkle features in GO and also good stability following water immersion and drying (Supplementary Information, Fig. S5). These s-GO films were therefore used exclusively in the cell studies below. We were also interested in whether the wrinkled s-GO films could be made if the thermal treatment was carried out prior to the relaxation step. We found that relaxing pre-thermally-treated films led to a less regular wrinkle pattern and a larger number of small cracks (Supplementary Information, Fig. 6). This may reflect stronger adhesion of s-GO to the substrate, but was not further investigated, and the higher quality films made by post-wrinkling thermal treatment were used in all of the cell studies.

3.4 Cell alignment on flat and wrinkled s-GO substrates

Based on previous studies of cellular interactions with anisotropic grooved substrates, we hypothesized that wrinkled s-GO substrates with wavelength λ ~ 25 μm would be sufficient for cell confinement and alignment through contact guidance mechanisms [28–31]. As a model system, we chose to study murine and human fibroblasts on matched samples of 25 μm wavelength and flat s-GO substrates. Cell viability was measured on wrinkled and flat s-GO substrates compared with conventional tissue culture plastic (polystyrene) using DRAQ7 (Biostatus), a far-red fluorescent DNA dye that only stains dead and membrane compromised cells [55]. These measurements showed that cell viability was consistently over 95% on wrinkled and flat s-GO substrates (Supplementary Figure S7 and S8), indicating excellent biocompatibility.

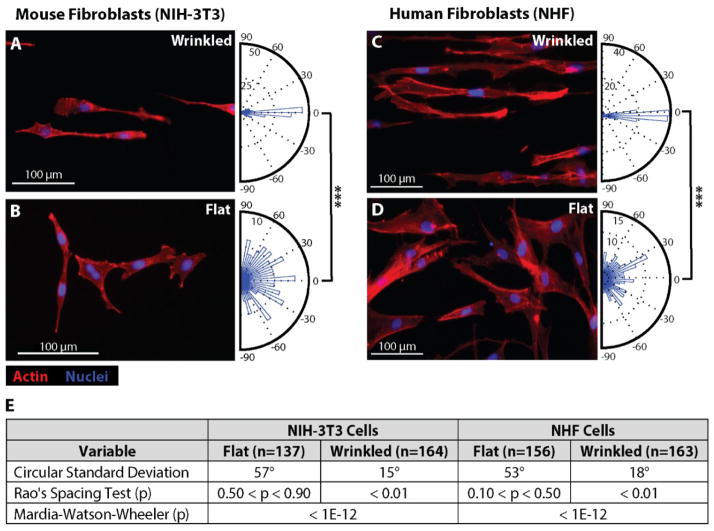
The angular orientation of NIH-3T3 mouse fibroblasts was then compared on wrinkled (~25 μm wavelength) and flat s-GO substrates after culture for 96 h. To better visualize the cell morphology, both the nuclei and F-actin cytoskeleton were immunostained with fluorescent markers (Fig. 4A,B). Qualitatively, NIH-3T3 fibroblasts appeared highly aligned on the wrinkled substrates (Fig. 4A) and randomly oriented on the flat substrates (Fig. 4B). To quantify this alignment, the cell morphology was automatically extracted using CellProfiler (Broad Institute) based on F-actin immunostaining. This software then determined an orientation based on the major axis of a best-fit ellipse to the cell morphology, which was manually verified. A circular histogram of these results are plotted as a rose plot for wrinkled (n = 164) and flat substrates (n = 137). The coordinate system for the wrinkled s-GO was defined so that 0° points along the wrinkle patterns (perpendicular to the axis of uniaxial stretch). NIH-3T3 fibroblasts on wrinkled substrates displayed a mean orientation angle of 0° with a standard deviation of 15°. In contrast, NIH-3T3 fibroblasts on flat substrates displayed a mean orientation angle of 13° and a standard deviation of 57°, which approximates a random orientation (with 0° mean, 52° standard deviation). To corroborate these results, primary human fibroblasts derived from neonatal foreskin (Normal Human Fibroblasts, NHF cells) were also cultured on these substrates. NHF cells also displayed qualitatively similar alignment on wrinkled substrates relative to flat substrates (Fig. 4C,D). Quantitatively, NHF cells on wrinkled substrates displayed a mean orientation angle of 0° with a standard deviation of 18°. In comparison, NHF cells on flat s-GO substrates displayed a mean orientation angle of 16° with a standard deviation of 53°, also approximating a random orientation distribution.

Figure 4.

Fibroblast culture on wrinkled graphene materials results in highly aligned cells. (A–D) Fluorescence images of Actin-phalloidin (red) and nuclei (blue) for NIH-3T3 and NHF cells cultured on 200 nm wrinkled s-GO substrates (~25 μm period) for 96 hours (A, C) and on paired flat graphene controls (B,D). Circular histograms of fibroblast orientation, ranging from −90° to 90°, for cells on wrinkled and flat materials are displayed as orientation rose plots to the right of each corresponding fluorescence image (A–D). (E) Table of statistics summarizing circular standard deviation, and statistical significance for uniformity (one-sample test) and distribution (two-sample test) using Rao’s spacing test and Mardia-Watson-Wheeler test, respectively.

The statistical significance of these results was assessed using two metrics. First, Rao’s Spacing Test was used to evaluate the null hypothesis that a given circular dataset is uniformly distributed (Fig. 4E). For both NIH-3T3 and NHF cells, the angular orientation on wrinkled substrates was non-uniform (p < 0.01), while the angular orientation on flat substrates was uniform (p > 0.10). Next, the Mardia-Watson-Wheeler test was used to evaluate the null hypothesis that two circular datasets have identical distributions. For both NIH-3T3 and NHF cells, the distribution of angular orientations of wrinkled and flat substrates were significantly different (p < 10⁻¹²).

3.5 Cell morphology on flat and wrinkled s-GO substrates

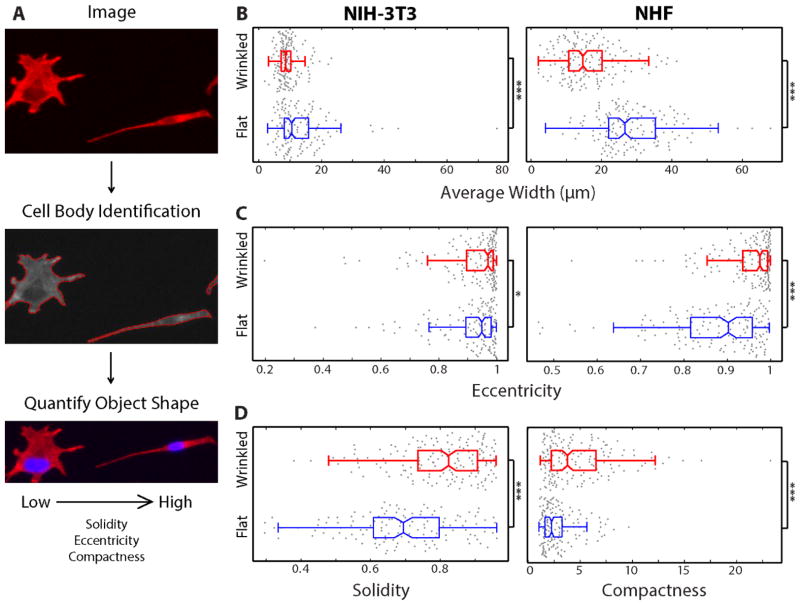
The morphology of NIH-3T3 and NHF cells was analyzed by extracting cell shape based on F-actin immunostaining. Briefly, CellProfiler was used to segment fluorescent nuclei in the blue fluorescent channel, which served as a starting point to segment the surrounding cell body in the red fluorescent channel (Fig. 5A). The morphology was then quantified using a number of geometric parameters.

Figure 5.

Image analysis of fibroblasts on graphene-based materials demonstrates distinct morphological features for different cell types on wrinkled vs. flat substrates. (A) Process flow for image analysis/cell segmentation: fluorescence images are split into separate channels for each color, CellProfiler outlines cells by distinguishing between pixels in the background and foreground, automated object shape features are calculated. (B–D) Boxplots of quantitative shape features for the fibroblasts were plotted with MATLAB. 25^th and 75^th percentiles are indicated by the box edges, the median value is displayed as the dividing line of the box, data not considered outliers are contained within the boxplot whiskers, and data points representing individual cell measurements are overlaid as plotted dots (Red boxplots= cells on wrinkled substrates, blue boxplots = cells on flat control substrates).(B) Comparison of average cell width for fibroblasts on wrinkled and flat substrates (as in Figure 4) for NIH-3T3 and NHF cells (left and right, respectively). (C) Comparison of eccentricity values for cells on wrinkled and flat substrates for NIH-3T3 and NHF cells (left and right, respectively). (D) Solidity values for NIH-3T3 cells on wrinkled and flat substrates (D, left) and compactness values for NHF cells on wrinkled and flat substrates (D, right). Statistical significance is indicated as follows: * p < 0.05; ** p < 0.01; *** p < 0.001

First, an average cell width was measured for NIH-3T3 and NHF cells on wrinkled and flat substrates. NIH-3T3 cells on wrinkled substrates displayed an average cell width of 9 μm and standard deviation of 3.3 μm, while cells on flat substrates had an average cell width of 13 μm and a standard deviation of 8.7 μm (Fig. 5B). In addition, NHF cells on wrinkled substrates display an average cell width of 16 μm with a standard deviation of 8.0 μm, while cells on flat substrates had an average cell width of 29 μm with a standard deviation of 10.3 μm (Fig. 5B). Overall, both fibroblast lines displayed narrower morphologies with smaller standard deviations on wrinkled substrates compared to flat substrates, with highly significant differences (p < 10⁻³). These narrower cell widths were comparable to the wrinkle spacing of ~25 μm, suggesting that the elongation reflects some degree of cell micro-confinement in the inter-ridge valley spaces.

Next, the relative elongation of these cells was assessed in terms of the eccentricity of the best-fit ellipse to the cell morphology. An eccentricity of 0 corresponds to a circle, while an eccentricity of 1 corresponds to a line. NIH-3T3 cells on wrinkled substrates displayed an average eccentricity of 0.921, compared to cells on flat substrates with an average eccentricity of 0.907 (Fig. 5C). These values, although similar, display a statistically significant difference (p < 0.05). NHF cells on wrinkled substrates displayed an average eccentricity of 0.947, compared to cells on flat substrates with an average eccentricity of 0.872. Interestingly, NHF cells on flat substrates display considerable variability in eccentricity, with a standard deviation of 0.112, compared to 0.069 for NHF on wrinkled substrates. Altogether, fibroblasts are intrinsically quite elongated on flat substrates, but are even more elongated on our wrinkled graphene surfaces, where they have eccentricity values close to 1, and the effect of the wrinkle texture is statistically significant. In order to further elucidate differences across these cell lines and conditions, several additional metrics were considered.

Qualitatively, NIH-3T3 fibroblasts may display multipolar, star-like morphologies, particularly on flat substrates. This shape was quantified in terms of the cell solidity metric, which describes an object shape based on the regularity of its boundaries. For example, a solid object with no holes has an area equal to the convex hull and thus has a solidity of 1, while an object with a very irregular boundary has a solidity that approaches 0. NIH-3T3 cells cultured on wrinkled substrates have an average solidity of 0.80 and a standard deviation of 0.12, while cells on flat substrates have an average solidity of 0.69 with a standard deviation of 0.16 (Fig. 5D). This data indicates that NIH-3T3 fibroblasts are biased towards bipolar morphologies on wrinkled substrates, compared to multipolar morphologies with more irregular boundaries on flat substrates. NHF cells (Supplemental Table 1) display similar solidities on both wrinkled and flat substrates, which may occur due to a more dominant bipolar phenotype.

Finally, NHF cells displayed the greatest variability in radial distance from the object center, known as compactness. NHF cells on wrinkled substrates displayed a mean compactness of 4.8, with a standard deviation of 3.4, and cells on flat substrates have a mean compactness of 2.8, with a standard deviation of 1.7 (Fig. 5D, right). On the other hand, NIH-3T3 cells did not display a significant difference for cell compactness between wrinkled and flat substrates. These differences likely arise from differences in cell size between NHF and NIH-3T3 cells. Since NHF cells are larger, they are more confined and elongated on wrinkled substrates but can be more spread out on flat substrates, resulting in larger differences in compactness.

In summary, NIH-3T3 and NHF fibroblasts on wrinkled substrates display reduced cell widths and increased eccentricity relative to cells on flat substrates. Furthermore, NIH-3T3 cells on wrinkled substrates display increased solidity, while NHF cells display increased compactness. These results indicate that the topography of these wrinkled graphene substrates can strongly influence cell morphology (summarized in Supplemental Table 1).

4. Conclusions

This study demonstrates the feasibility of wrinkled graphene as a surface texturing agent to direct cell alignment and morphology in tissue engineering. Wet deposition of graphene oxide multilayer tiled films on pre-stretched elastomers followed by relaxation and mild thermal treatment produces cell-culture-compatible textured substrates with long-range periodic topography in the form of parallel ridges and valleys. Both the spatial period and the wrinkle amplitude can by systematically tuned from 1 – 25 μm by selection of the substrate stiffness, by variation of pre-strain, and by alteration of the GO precursor concentration in the feed suspension. Fibroblasts are observed to attach to these textured s-GO surfaces and remain viable, while the wrinkles induce statistically significant cell alignment and elongation relative to flat s-GO substrates in a manner consistent with contact guidance on lithographically fabricated nanograting architectures. Together the results suggest that s-GO wrinkle engineering is a promising new approach for creation of functional surfaces and scaffolds in tissue engineering. In comparison with competing methods of patterning, wrinkled s-GO offers potential advantages in the ease, cost, and scale-up of fabrication. We envision a modular graphene-based platform for the application of orthogonal topographic stimuli, chemical stimuli (through functionalization or adsorption), electrical stimuli (enabled by conductive graphene), as well as dynamic mechanical actuation of topographic confinement. Furthermore, we believe these biologically inspired architectures will be widely applicable to other cell types, including neurons, skeletal, smooth muscle, cardiomyocytes and stem cells. These wrinkled s-GO architectures could potentially be integrated with soft, stretchable implantable devices such as neural prostheses, cardiac assist devices, catheters or epidermal electronics in order to enhance biocompatibility and biointegration [56, 57].