Abstract
Beam tracking with scanned carbon ion radiotherapy achieves highly conformal target dose by steering carbon pencil beams to follow moving tumors using real-time magnetic deflection and range modulation. The purpose of this study was to evaluate the robustness of target dose coverage from beam tracking in light of positional uncertainties of moving targets and beams. To accomplish this, we simulated beam tracking for moving targets in both water phantoms and a sample of lung cancer patients using a research treatment planning system. We modeled various deviations from perfect tracking that could arise due to uncertainty in organ motion and limited precision of a scanned ion beam tracking system. We also investigated the effects of interfractional changes in organ motion on target dose coverage by simulating a complete course of treatment using serial (weekly) 4DCTs from 6 lung cancer patients. For perfect tracking of moving targets, we found that target dose coverage was high (V̄95 was 94.8% for phantoms and 94.3% for lung cancer patients, respectively) but sensitive to changes in the phase of respiration at the start of treatment and to the respiratory period. Phase delays in tracking the moving targets led to large degradation of target dose coverage (up to 22% drop for a 15 degree delay). Sensitivity to technical uncertainties in beam tracking delivery was minimal for a lung cancer case. However, interfractional changes in anatomy and organ motion led to large decreases in target dose coverage (target coverage dropped approximately 8% due to anatomy and motion changes after 1 week). Our findings provide a better understand of the importance of each of these uncertainties for beam tracking with scanned carbon ion therapy and can be used to inform the design of future scanned ion beam tracking systems.
Keywords: beam tracking, robustness, ion, carbon, proton, therapy, motion, lung, uncertainty
1. Introduction
Actively scanned carbon ion beams have been used to safely treat a number of static tumors such as chordomas, chondrosarcomas, and osteosarcomas of the skull base, spine, and sacrum as well as adenoid cystic carcinomas of the salivary glands (Kraft, 2000; Schulz-Ertner et al., 2004; Schulz-Ertner and Tsujii, 2007). Given the relatively high tumor control rates and low toxicity observed for some of those patients (Schulz-Ertner et al., 2007), there are ongoing efforts to utilize the scanned carbon ion beam for new cancer sites, for example, gliomas and meningiomas (Rieken et al., 2012), pancreatic cancer (Combs et al., 2013), and hepatocellular carcinoma (Habermehl et al., 2013; Richter et al., 2014). Indeed, some of these sites have already been treated successfully with passively scattered carbon ion beams (Tsujii and Kamada, 2012). However, one of the obstacles to using scanned ion therapy is that the dose distributions in moving tissue may be highly sensitive to errors and uncertainties in treatment planning and treatment delivery. Simulation studies investigated the theoretical dosimetric advantages of using scanned carbon ion beam tracking for moving tumors, when treatment was delivered perfectly, i.e., with no errors (Bert and Rietzel, 2007; Lüchtenborg, 2011). Recently, Eley et al. (2014) demonstrated that 4D optimization could be used with scanned ion beam tracking to further improve target dose uniformity and reduce dose to avoidance regions near a moving target. In this work, we investigate the robustness of scanned carbon ion beam tracking in order to understand whether its theoretical benefits can persist in the presence of uncertainties in patient motion, also considering the limited precision of a scanned carbon ion beam tracking system.
Several investigators have studied the robustness of scanned ion therapy to uncertainties in treatment planning, treatment delivery, and patient alignment (Pflugfelder et al., 2007; Lomax, 2008a, b; Meyer et al., 2010). For example, if the patient is misaligned or exhibits a change in anatomy during a course of therapy, ion Bragg peaks may miss their planned target position, leading to potential underdosage of the target or overdose to critical structures outside of the target. If the target is moving, interplay effects between the target and a moving (scanning) beam (Lambert et al., 2005; Bert et al., 2008) can exacerbate this problem, potentially leading to treatment failure if adequate motion mitigation strategies are not used (Bert and Durante, 2011).
As reported by Bert et al. (2007), scanned carbon ion beam tracking relies on real-time motion state detection to apply tracking offsets to each scanned pencil beam coordinate for each motion state. In this way, beams are steered to follow motion of the target for all phases of respiration. In their particular approach, beam-tracking offsets are computed prior to treatment using a planning 4DCT. Deformable image registration vectors are calculated from this 4DCT to map the motion of tissues throughout the respiratory cycle, and these vector maps are used to compute tracking offsets required for each pencil beam for each phase of respiration. Similar to beam gating, this approach relies on the assumptions that the planning 4DCT adequately represents the internal motion of the patient’s organs during treatment delivery and that a correlation between the patient respiratory phase and the position of internal organs is reliable for the duration of treatment.
It is not yet known how robust scanned carbon tracking is against violations of these assumptions. For example, van de Water et al. (2009) studied beam tracking with scanned proton beams and reported deterioration of target dose coverage when simulated time delays or position errors were introduced to tracking simulations, which was improved by combining the principles of rescanning and beam tracking. To our knowledge, the robustness of target dose coverage to uncertainties in scanned carbon ion beam tracking therapy for moving tumors has not been reported in the literature.
The purpose of this study was to evaluate the robustness of target dose coverage to motion uncertainties for scanned carbon ion beam tracking therapy of moving targets. To accomplish this, we simulated scanned carbon ion beam tracking for moving targets in both water phantoms and a sample of lung cancer patients using a research treatment planning system for ion radiotherapy. We modeled various deviations from perfect tracking that could arise due to uncertainty in organ motion and limited precision of a scanned ion beam tracking system in operation at GSI Helmholtzzentrum für Schwerionenforschung GmbH (GSI) (Darmstadt, Germany). We calculated 4D dose to moving targets for many combinations of these modeled uncertainties. We also investigated the effects of interfractional changes in organ motion on target dose coverage by simulating treatment using multi-week 4DCT images from 6 lung cancer patients. This study seeks to quantify the reliability, efficacy, and safety of scanned carbon ion beam tracking, which might one day be used to deliver scanned ion therapy to patients with thoracic tumors.
2. Methods
2.1. Influence of Errors in Beam Tracking on Target Dose Coverage for Phantoms
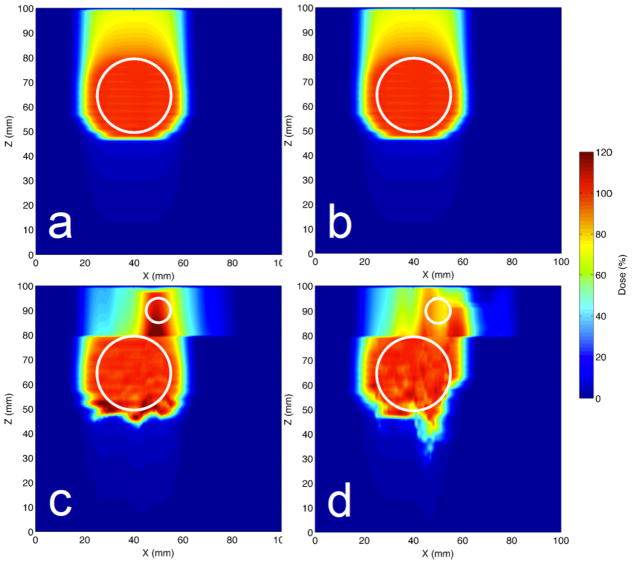
We designed 4 mathematical phantoms with increasing degrees of complexity to evaluate scanned carbon ion beam tracking. The phantoms are shown in Figure 1. Phantoms 1 and 2 were inspired by patients with liver cancer, i.e., a moving tumor in relatively homogeneous tissue, and Phantoms 3 and 4 were inspired by patients with lung cancer, i.e., a moving tumor in heterogeneous tissue. All phantoms were 10 × 10 × 10 cm3, consisting of cubic voxels with dimension 1 × 1 × 1 mm3. In all phantoms, a 3-cm diameter spherical target oscillated with sinusoidal motion, with displacement s as a function of time t expressed as s = A sin4(πt/τ) (Lujan et al., 1999). We studied respiratory periods τ of 3, 4, and 5 s. In Phantom 1, the sphere oscillated along the x-axis, perpendicular to the beam axis (z), in a homogeneous water box with amplitude (A) of Ax = 2 cm, i.e., no depth changes. In Phantom 2, the sphere moved in 3 dimensions, again in a homogeneous water box, with Ax = 2 cm, Ay = 0.5 cm, and Az = 1 cm, with depth changes up to 1 cm along the z-axis. In Phantom 3, the target moved along the x-axis in water as in Phantom 1, but a simulated rib heterogeneity was positioned upstream of the target in water to introduce changes in radiological depths of the target voxels. The rib was approximated as a cylinder with 1-cm diameter, inferred from anatomical cross-section measurements of human ribs reported by Mohr et al. (2007), and 10-cm length parallel to the y-axis with uniform Hounsfield value of 750 (Schneider et al., 2000). In Phantom 4, the rib heterogeneity of Phantom 3 was replaced by an air cavity with identical dimensions to the rib cylinder, but with uniform Hounsfield value of −1000. For each phantom, we generated target contours, 4DCT data, and image registration vector maps to use in treatment planning, corresponding to their unique geometry and motion characteristics.
Figure 1.
Schematic drawings of phantoms. In Phantom #1 (a), a 3-cm spherical target (black circle) moves sinusoidally along the x-axis (Ax = 2 cm) with no change in depth in a uniform water phantom. In Phantom #2 (b), another such sphere moves sinusoidally in 3D (Ax = 2 cm, Ay = 0.5 cm, Az = 1 cm) with 1-cm change in depth in a uniform water phantom. In Phantoms #3 and #4 (c), another sphere moves sinusoidally along the x-axis (Ax = 2 cm) in a water phantom, but a heterogeneity (grey shaded area) is modeled upstream of the target as a cylinder (1-cm diameter, 10-cm length) parallel to the y-axis. For Phantom #3, the cylinder has uniform Hounsfield value of 750, to approximate a rib. For Phantom #4, the cylinder has uniform Hounsfield value of −1000, to represent an air cavity.
Treatment planning and 4D dose calculation for scanned carbon ion beam tracking was performed using the TRiP4D research treatment planning system (TPS) code (Richter et al., 2013) as follows.
3DCT images and 3D target contours for a reference motion state were loaded into the TPS.
A 3D scanned treatment field was planned to irradiate the target in the reference motion state. A focal spot size of approximately 6.5 mm, full-width at half-maximum (FWHM), was planned for each pencil beam. In our study, the focal spot size was defined as the lateral beam width in air of a single pencil beam at the isocenter of the treatment room, i.e., at the origin of the beam coordinate system. Pencil beam Bragg peaks were regularly spaced on a 2-mm Cartesian grid within each isoenergy layer. Pencil beam energies were selected to provide a 3-mm water-equivalent depth spacing between isoenergy layers, and a 3-mm ripple filter (Weber and Kraft, 1999) was used to blur the carbon Bragg peaks in the depth direction. A radial target margin of 1.1 × FWHM, i.e., perpendicular to the beam central axis, was used to ensure sufficient lateral-scatter-equilibrium to achieve target dose coverage at the off-axis target boundary. A distal target margin of 4-mm water-equivalent thickness was used to achieve target dose coverage at the distal target boundary.
The numbers of carbon ions in each beam spot were optimized to achieve uniform relative-biological-effectiveness- (RBE) weighted dose to the target for the 3D static case in the reference motion state. An RBE value of 1 was used for phantom studies.
4DCT images and 4D image registration vectors were loaded into the TPS.
Following the methods of Bert and Rietzel (2007), beam tracking offsets were calculated for each pencil beam for each motion state so that each pencil beam Bragg peak would arrive at its planned local anatomic subvolume of the target regardless of the motion state presented during irradiation (see Figure 2). Lateral tracking offsets, i.e., x- and y-offsets orthogonal to the beam central axis, were calculated by projecting 4D image registration vectors onto an xy-plane perpendicular to the beam central axis (z). Range-tracking offsets, i.e., z-offsets, were calculated to compensate changes in the radiological depth of the target at points coinciding with the Bragg peak position for each pencil beam. First, 4D image-registration vectors were used to map the movement of a subvolume in the target (e.g., a single voxel containing a pencil beam Bragg peak) from its position in the reference motion state to its position for all other motion states. Second, the radiological depth of that (moving) subvolume was calculated uniquely for each motion state using an existing ray-tracing algorithm in TRiP4D and using the appropriate 3DCT subset of the 4DCT. Finally, a range-tracking offset was calculated based on the change in radiological depth of the subvolume (containing the Bragg peak coordinate) for all motion states.
Idealized patient respiratory motion trace signals, i.e., with constant respiratory period, were loaded into the TPS. These motion signals were used to simulate those that would be monitored in real-time during treatment delivery, for example using a respirometer.
Beam-tracking 4D delivery was simulated. Based on the patient respiratory motion trace signal (e.g., period and starting phase), the required particles per pencil beam, and the availability of particles from the accelerator spill sequence (characteristic of the current GSI synchrotron), temporal characteristics of 4D delivery were simulated by binning each pencil beam into the motion state in which it would most likely be irradiated (Richter et al., 2013). The corresponding tracking offsets (from Step 5) were added to each pencil beam Bragg peak coordinate depending on the motion state into which it was binned. Using new TPS codes developed in this work, errors were added to the x, y, and z components of each tracking offset to simulate the effect of motion uncertainties, described in further detail below.
Finally, 4D RBE-weighted dose was calculated by accumulating dose to voxels from all pencil beams for all discrete motion states (Richter et al., 2013). Coordinates of the target voxels were transformed for each motion state using the deformable image registration vectors to allow summation of 4D dose to the moving voxels.
Figure 2.
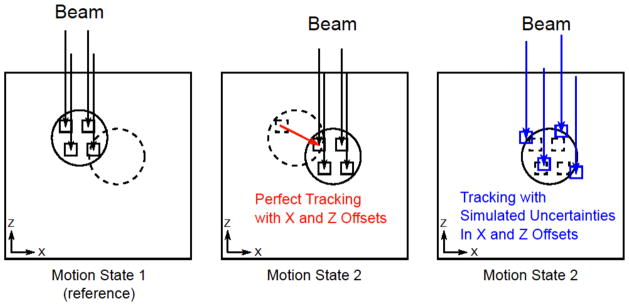
Diagram of perfect beam tracking and beam tracking with simulated motion uncertainties. For perfect tracking, a set of ion pencil beams (arrows) are distributed throughout a target volume (circle) in the reference Motion State 1 (left) with individual Bragg peaks located in subvolumes of the target (small squares). After the target moves to Motion State 2 (middle), each pencil beam also moves to track the subvolumes. To simulate the effect of motion uncertainties, we offset individual pencil beam positions (right). The offset pencil beams (right) are shown to irradiate new subvolumes (small squares) that partially or fully miss their planned subvolumes in the target (dashed small squares), usually leading to deterioration of the planned target dose coverage.
For perfect tracking, we simulated 18 motion scenarios for each phantom with variation in motion trace signals with period, τ = 3, 4, and 5 s, and starting respiratory phase at beginning of irradiation, ϕ = 0, 60, 120, 180, 240, and 300 degrees. Our rationale for these multiple motion scenarios was that, even when pencil beams perfectly track target motion and depth changes, some deviations in off-axis dose contributions for individual pencil beams are expected (van de Water et al., 2009). By sampling these 18 scenarios of motion, we avoided the chance that our findings would be confounded by a single “lucky” or “unlucky” choice of τ or ϕ.
We modeled both systematic and random positional uncertainties as well as temporal lags during beam tracking therapy. Ultimately, uncertainties were simulated by shifting pencil beam coordinates and modifying target motion signals prior to 4D dose calculation as illustrated in Figure 2. For each individual uncertainty modeled, we also included 18 motion scenarios of respiration with variable period and starting phase as described for the perfect tracking case above. A list of modeled uncertainties and a brief description of our rationale and implementation in our TPS is given below.
A. Phase Delays in Beam Tracking
Rationale: Delays in applying tracking offset to individual pencil beams for given motion states might be caused either by delays in the motion state detection system or by delays in the beam tracking control system or beam delivery system.
Implementation: Delays were simulated by loading both an internal motion signal (i.e., representing the “true” tumor motion) and an external motion signal (e.g., that could represent motion of an external surrogate marker) into the TPS (Richter et al., 2013). The internal motion signal was used to synchronize the temporal delivery of pencil beams to their appropriate 4DCT motion state for 4D dose calculation (see Step 7 above), but the external motion signal was used to determine a given beam-tracking offset. By delaying the external motion signal, we caused tracking offsets to be applied from an incorrect motion state, depending on the amount of delay.
Variables Simulated: Phase delays of 0, 5, 10, and 15 degrees were simulated.
B. Random Errors in Bragg Peak Coordinates
Rationale: Random errors in Bragg peak coordinates during beam tracking might be caused by limited precision of the beam tracking system, i.e., scanner magnets and range-tracking wedge.
Implementation: Random errors were sampled from Gaussian distribution with a user specified width (σ) using a random number generator and added to beam-tracking offsets prior to 4D dose calculation.
Variables Simulated: We applied 1D random errors independently to x, y, and z with σ of 0, 0.5, 1.0, and 1.5 mm. We also applied combined 3D random errors to x, y, and z with σ values of 0, 0.5, 1.0, and 1.5 mm.
C. Systematic Errors in Bragg Peak Coordinates
Rationale: Systematic errors in Bragg peak coordinates during beam tracking therapy might be caused by misalignment of the patient, patient shifting after setup, or by weight change of the patient.
Implementation: Systematic errors were added to pencil-beam tracking offsets prior to 4D dose calculation.
Variables Simulated: We applied 1D errors of 0, 1, 2, 3, and 4 mm independently to x, y, and z pencil beam coordinates. We also applied combined 3D errors of 0, 1, 2, 3, and 4 mm simultaneously to x, y, and z pencil beam coordinates.
D. Limited Acceleration of Range-tracking Wedge System
Rationale: When a motion state change occurs or a new pencil beam begins irradiation, a new range-tracking offset must be applied. The tracking system at GSI uses a passive acrylic wedge system mounted on linear drive motors that move material in or out of the beam path. This motorized system has a finite acceleration of 8 g (1 g = 9.81 m/s2), i.e., in water-equivalent range changes, (Saito et al., 2009) that delays immediate application of the range-tracking offset.
Implementation: We implemented equations for 1D motion of the range-tracking wedge pair under the influence of constant acceleration, constant deceleration, or no acceleration into our TPS. When a new tracking range-offset was requested during treatment simulation, e.g., when a new pencil beam started irradiation or a motion state change occurred, we considered the current position and velocity of the range-tracking wedge and simulated its trajectory that would allow it to most quickly reach and stop at the desired new position. From this trajectory we determined the mean wedge-position for each pencil beam for each motion state and used that mean position as the range-tracking offset for our simulations.
Variables Simulated: We simulated range-tracking wedge acceleration values of 0.001, 0.01, 0.1, 1, 8, 10, and 100 g and a hypothetical wedge with infinite acceleration. The infinite acceleration wedge was used for our reference case simulations. These acceleration values correspond to acceleration of beam range along the beam central axis (z), i.e., in terms of changing water-equivalent thickness of the acrylic wedge in the beam path.
All 4D dose distributions were transformed to a reference 3D motion state for analysis. For each phantom and each variable studied, we combined the target dose distributions for the 18 scenarios of possible respiratory patterns. From these combined distributions, we prepared box-whisker plots to allow easy visualization of the entire distribution of target dose expected for a single modeled uncertainty. We also determined the volume of the target receiving at least 95% of the prescribed dose (V95), the volume of target receiving greater than 107% of the prescribed dose (V107), and D5-D95, the difference between the highest dose in the target, after excluding 5% of the target volume receiving the very highest dose, and the lowest dose in the target, after excluding 5% of the target volume receiving the very lowest dose. V95 was used to quantify target dose coverage, V107 was used to quantify target overdosage, and D5-D95 was used to quantify target dose homogeneity. For select cases, we plotted 2D cuts from the dose distributions as colorwash overlaying the phantom and target contours.
2.2. Influence of Errors in Beam Tracking on Target Dose Coverage for Lung Treatment
We simulated the impact of motion uncertainties on target dose coverage for one lung patient (Lung Patient #1), who was previously enrolled in a research study at The University of Texas MD Anderson Cancer Center (UTMDACC) (Houston, TX) and who had a peak-to-peak tumor motion amplitude of 25 mm. For this lung cancer patient, treatment planning for scanned carbon beam tracking was similar to that described for the water phantoms in Section 2.1, with the following differences. Instead of 1 field, we used the 4-field irradiation protocol developed at NIRS for hypofractionated lung cancer therapy with carbon beams (Miyamoto et al., 2007). We used gantry angles of +20, −20, −70, and −110 degrees that corresponded to the angles used at NIRS. For reference, in TRiP4D, 0 degrees represents a lateral beam and −90 degrees represents an AP beam. The couch angle was −90 degrees, hence all beams fell in an axial plane. We used the Local Effect Model Version IV at GSI (Scholz et al., 1997; Elsässer et al., 2010) along with TRiP4D to optimize and calculate RBE-weighted carbon dose distributions, i.e., for the biological endpoint of lung tumor control. For this, we used an α/β ratio of 6 Gy for lung tumor control (α = 0.021 Gy−1, β = 0.0035 Gy−2, DT = 10 Gy) (Lüchtenborg, 2011). We planned 8.2 Gy (RBE) for each of the 4 fields for a total RBE-weighted dose of 32.8 Gy (RBE) to the target. We used a combination of both rigid image registration vectors and deformable image registration vectors to plan beam-tracking offsets and to calculate 4D accumulated dose, respectively. Lüchtenborg et al. (2011) demonstrated that keeping a rigid spacing between neighboring pencil beams can provide a more homogeneous target dose for beam tracking, since a deforming grid can lead to bunching and dispersion of pencil beams that causes local overdosing and underdosing within the target, respectively. Thus, we used rigid vectors to plan beam-tracking offsets, but we used deformable image registration vectors in the 4D dose calculations. For calculation of rigid image registration vectors, we only considered motion of tissue within the CTV boundary. For calculation of deformable image registration vectors, we used the entire 4DCT data set.
For Lung Patient #1, motion uncertainties and beam tracking uncertainties were simulated identical to those described for the water phantom studies in Section 2.1. Analysis of target dose distributions was similar to that described for the water phantoms. In all cases, the 4D RBE-weighted dose distributions from the combined 4 fields were transformed to a 3D reference motion state at end-exhale for analysis. In addition, we also plotted the full distribution of beam tracking offsets required for each pencil beam and each motion state.
2.3. Influence of Interfractional Changes in Organ Motion on Target Dose Coverage for Lung Treatment
One serious criticism of scanned ion beam tracking is that the approach currently assumes true periodic organ motion and that there exists a perfect correlation between the patient respiratory phase and the motion of internal anatomy. For example, if only external motion surrogates, such as markers fixed to the sternum, were monitored during treatment delivery, an uncorrelated or poorly correlated internal motion deviation might not be detected. If drifts in absolute tissue position would occur, e.g., due to muscle relaxation over the course of several minutes, then respiratory phase alone may not accurately be used to predict the position of internal organs. In addition, weight changes of the patient during a course of treatment likely leads to changes in the range of ion pencil beams in tissue. Therefore, we sought to better understand the dosimetric consequences of relying on these assumptions by simulating scanned carbon ion beam tracking therapy using an initial 4DCT for treatment planning and then using a multiple-week series of 4DCT images, acquired for the same set of patients, to simulate treatment and delivery of 4D dose distributions to the patients at later time points.
To study the effects of interfractional changes in organ motion on target dose coverage for scanned carbon beam tracking, we selected 6 lung cancer patients who were previously enrolled in a research study at UTMDACC and had undergone multi-week serial 4DCT imaging. These patients received a 4DCT imaging sequence each week following the methods of (Pan et al., 2004), with images binned into 10 phases of their respiratory cycle. Our approach was to prepare a scanned carbon ion beam tracking treatment plan using the first 4DCT image set and, then, to simulate treatment delivery without any subsequent adaptation using the later 4DCT image sets.
We used the software program Plastimatch using B-splines (Shackleford et al., 2010) to calculate deformable image registration vectors for each patient for each 4DCT image series to use in 4D dose calculation. We calculated rigid image registration vectors for all phases of the first 4DCT set to plan beam tracking offsets as described in Section 2.2. In addition, we rigidly registered the patient position at a reference state of end-exhale throughout all weeks of 4DCT images. From this, we rigidly offset the CT voxel coordinates when simulating treatment on later week 4DCTs. This concept is similar to aligning the patient before each treatment, e.g., using an onboard imaging device such as orthogonal x-ray planar images or cone-beam CT images. Treatment plans were prepared as described in Sections 2.1 and 2.2, again using 4 fields and 32.8 Gy (RBE) total dose. For patients with targets in the right lung, the couch angle was changed from −90 to 90 degrees. For calculation of dose on later 4DCTs, the correct 4DCT and corresponding deformable image registration vector map was loaded into the TPS just before calculating 4D dose. For 6 patients, we calculated dose on 3 4DCTs, i.e., week 0, 1, and 2. For Lung Patient #1, we also used a second 4DCT scan from week 0 to investigate interfractional motion changes that might occur during a single day, however, this data was not available for the other 5 patients in our study. For each treatment simulation, we used 18 different respiratory motion signals with variable period and starting phase as described in Section 2.1.
Analysis of target dose distributions was similar to that described for the water phantoms. In all cases, the 4D dose distributions from the combined 4 fields were transformed to a 3D reference motion state at end-exhale for analysis.
3. Results
Robustness of target dose coverage for scanned carbon ion beam tracking was found to be sensitive to errors in beam tracking. The major qualitative findings are as follows. As expected, robustness was generally poorer when heterogeneities were present near the target. However, robustness was generally better for patient plans, where we used 4 equal-weight beams, compared to the mathematical phantom plans with simulated heterogeneities, where we used only a single beam. Overall, coverage was found to be most sensitive to phase delays in beam tracking, systematic spatial errors in tracking, and interfractional changes in organ motion. Limited acceleration of the range-tracking wedge was found to have a moderate impact on target dose coverage, particularly for the lung patient. Random errors in beam tracking arising from the limited precision of beam steering magnets and the precision of the range-tracking wedge system were found to have minimal impact on target dose coverage.
In the following sections, we detail our quantitative findings for the robustness of scanned carbon ion beam tracking for each modeled error. First, we present dose-colorwash plots to illustrate our treatment plans for perfect tracking scenarios. Then, we present dose-volume statistics for the moving targets for all cases of simulated errors in beam tracking. We also present tables to summarize the robustness of V95, our main metric for target coverage, as a function of the simulated errors in beam tracking. Finally, we present the robustness of target dose coverage to interfractional changes in organ motion for 6 lung cancer patients.
3.1. Influence of Errors in Beam Tracking on Target Dose Coverage for Phantoms
For our simulations of perfect beam tracking (for the motion scenario with τ = 4 s and ϕ = 0 degrees), we found a highly uniform and nearly identical target dose for Phantoms #1 and #2 with mean target doses of 100 ± 1 %, i.e., percent of the prescribed target dose, for both phantoms. However, we found slightly less-uniform target dose for Phantoms #3 and #4, which both had a cylindrical heterogeneity upstream of the moving target, with mean target doses of 100 ± 3 % and 99 ± 5 %, respectively. Dose distributions are shown as 2D colorwash cuts in the XZ plane in Figure 3 for perfect tracking. Dose-volume statistics for perfect tracking are shown in Figure 4, at points where the phase delay was 0 degrees (i.e., no delay). We observed that the target dose coverage for perfect tracking for Phantoms #1 and #2 was not affected by respiratory period or starting phase, and all 18 data points (for the 18 scenarios of respiratory motion with variable period (τ) and starting phase (ϕ)) overlay exactly. However, for Phantoms #3 and #4, we observed differences in target dose coverage for those 18 scenarios depending on the respiratory period and respiratory starting phase. Thus, even for perfect tracking, target dose coverage was found to be degraded by heterogeneous tissue upstream of the moving target.
Figure 3.
Perfect beam tracking dose distributions in XZ plane shown for a reference scenario (τ = 4 s and ϕ = 0 degrees) for Phantom #1 (a), Phantom #2 (b), Phantom #3 (c), and Phantom #4 (d). Target indicated by large white circle. Beam direction was −z. For Phantoms #3 and #4, a proximal slab (z in 80–100 mm) did not move and contained the rib cylinder and air cylinder heterogeneities, respectively, indicated by the small white circles. Irregular dose distributions are seen in the target for Phantoms #3 and #4 even for perfect tracking.
Figure 4.
Robustness of target dose coverage to phase delays in tracking shown for the 4 phantoms. Each box-whisker plot (top left) summarizes the minimum, first quartile, median, third quartile, and maximum target dose (values are percent of prescribed dose) over all 18 scenarios of motion (with variable period τ and starting phase ϕ) for each value of phase delay. Dose-volume statistics for each of the 18 individual motion scenarios are shown by the markers for V95, V107, and D5-D95 for each value of phase delay. Dose and volume values are reported as percent of prescribed target dose and percent of total target volume, respectively. Markers are offset slightly (Phantoms #1-#4 presented left to right, respectively) to ease viewing. For all phantoms, target dose coverage (V95) degrades rapidly with increasing phase delays in beam tracking.
The robustness of target dose coverage to simulated phase delays in beam tracking is shown in Figure 4. A rapid degradation of target dose coverage (V95) with increasing phase delay is seen for all 4 phantoms. For an example, if the respiratory period were 4 s, these phase delays of 5, 10, and 15 degrees would correspond to temporal delays of 56, 111, and 167 ms, respectively. Such phase delays in beam tracking could potentially arise from lags in real-time detection of a patient’s current motion state or lags in real-time application of tracking offsets with the beam delivery system. Future countermeasures against these delays could include increasing the processing speed in motion-state-detection electronics and possibly implementing predictive algorithms.
The impact of random spatial errors in beam tracking on target dose coverage was found to be minimal (V95 changed less than 1%) when errors were sampled from Gaussian distributions with σ ≤ 0.5 mm. Furthermore, only slight degradation of target dose coverage was seen with random errors sampled with σ values up to 1.5 mm (cf. Table 1). For reference, the precision in lateral x and y pencil beam spot position for beam tracking, as determined by the dipole scanning magnets and position feedback system, is approximately 0.16 mm for the GSI carbon ion synchrotron including positional feedback loop, and the precision in the z range-tracking offsets, determined by the water-equivalent pathlength through the range-tracking wedge system, is approximately 0.25 mm (Saito et al., 2009). Thus, we infer that the precision of the current beam delivery system at GSI is already slightly better than needed and that further efforts to improve spatial precision in beam delivery will likely not improve robustness for beam tracking.
Table 1.
Robustness of target dose coverage <V95> to tracking errors for 4 phantoms. <V95> is the mean V95 for 4 phantoms and 18 motion scenarios. Changes in target coverage (Δ) more than 5% indicated in boldface.
| Variable (units) | Magnitude | <V95> (%) | Δ (%) |
|---|---|---|---|
| Perfect Tracking | - | 94.8 | - |
| Phase Delay (deg) | 5 | 83.1 | −11.7 |
| 10 | 76.4 | −18.4 | |
| 15 | 72.8 | −22.0 | |
| Random X Offset (mm) | 0.5 | 93.9 | −0.9 |
| 1.0 | 90.7 | −4.1 | |
| 1.5 | 86.2 | −8.6 | |
| Random Y Offset (mm) | 0.5 | 93.9 | −0.8 |
| 1.0 | 90.9 | −3.9 | |
| 1.5 | 86.5 | −8.2 | |
| Random Z Offset (mm) | 0.5 | 95.2 | 0.5 |
| 1.0 | 95.6 | 0.9 | |
| 1.5 | 95.7 | 0.9 | |
| Random XYZ Offset (mm) | 0.5 | 93.3 | −1.5 |
| 1.0 | 87.1 | −7.6 | |
| 1.5 | 80.6 | −14.2 | |
| Systematic X Offset (mm) | 1 | 93.1 | −1.6 |
| 2 | 90.8 | −3.9 | |
| 3 | 88.0 | −6.8 | |
| 4 | 84.3 | −10.4 | |
| Systematic Y Offset (mm) | 1 | 94.7 | 0.0 |
| 2 | 94.5 | −0.2 | |
| 3 | 93.4 | −1.4 | |
| 4 | 90.9 | −3.9 | |
| Systematic Z Offset (mm) | 1 | 94.5 | −0.3 |
| 2 | 94.0 | −0.8 | |
| 3 | 93.0 | −1.7 | |
| 4 | 91.1 | −3.7 | |
| Systematic XYZ Offset (mm) | 1 | 92.7 | −2.0 |
| 2 | 88.8 | −5.9 | |
| 3 | 82.3 | −12.5 | |
| 4 | 74.3 | −20.5 | |
| Wedge Acceleration (g) | 0.001 | 75.6 | −19.2 |
| 0.01 | 81.3 | −13.5 | |
| 0.1 | 86.0 | −8.8 | |
| 1 | 93.1 | −1.6 | |
| 8 | 94.6 | −0.2 | |
| 10 | 94.6 | −0.2 | |
| 100 | 94.7 | 0.0 |
Target dose coverage was found to be highly sensitive to systematic spatial errors in beam tracking. Errors up to 4 mm led to an approximately 21% drop in target coverage V95, averaged over all phantoms. Figure 5 shows the robustness of target dose coverage to combined systematic errors in tracking x-, y-, and z-coordinates. For Phantoms #1 and #2, minimal effect on target dose was seen until the errors were greater than 2 mm, with visible drops in coverage at errors of 3 and 4 mm, likely caused when the scanned ion field edge moves very close to the target boundary. In contrast, for Phantoms #3 and #4, loss of target dose coverage was seen even for 1 mm systematic spatial errors and increased with the amount of error. This effect was dominated by lateral (x-axis) errors in tracking (cf. Table 1), since relatively small lateral shifts introduced comparably large changes in radiological depth of the target due to the cylindrical heterogeneities present upstream of the target for Phantoms #3 and #4. Therefore, the robustness of beam tracking to systematic spatial errors was poorer when heterogeneities were present.
Figure 5.

Robustness of target dose coverage to systematic errors in tracking x-, y-, and z-coordinates shown for the 4 phantoms. Markers are offset slightly (Phantoms #1-#4 presented left to right, respectively) to ease viewing. A rapid deterioration of target dose coverage (V95) with increasing offset is seen for Phantom #4 and, to a lesser extent, Phantom #3 even for offsets as little as 1 mm. Phantoms #1 and #2 showed a greater robustness to systematic errors but target dose coverage also degraded with shifts greater than 2 mm.
For the 4 phantoms, we found target dose coverage to be mostly insensitive to wedge acceleration for a ≥ 8 g (1 g = 9.81 m/s2). However, for acceleration less than 1 g, target dose coverage deteriorated with decreasing acceleration. Note that the direction of acceleration is reported not in the direction of wedge motion but rather in the beam direction, i.e., quantifying the change in water-equivalent pathlength through the acrylic wedge. Figure 6 shows the robustness of target dose coverage when we simulated variable acceleration of the range-tracking wedge system. Our reference case of perfect tracking was modeled with infinite wedge acceleration. To put these numbers in perspective, the range tracking wedge system implemented at GSI can modify the beam range with an acceleration of approximately 8 g (Saito et al., 2009).
Figure 6.

Robustness of target dose coverage to to limited acceleration of the range-tracking wedge shown for the 4 phantoms. Markers are offset slightly (Phantoms #1-#4 presented left to right, respectively) to ease viewing. Note that Phantom #1 (black markers) did not require any range tracking, and, therefore, dose coverage does not depend on range-tracking acceleration. (1 g = 9.81 m/s2)
3.2. Influence of Errors in Beam Tracking on Target Dose Coverage for Lung Treatment
The robustness of target dose coverage to tracking errors in patient cases can be better understood by looking at an exemplary distribution of tracking parameters needed for a lung tumor moving in heterogeneous tissue. Figure 7 shows the distribution of beam tracking offsets required for Lung Patient #1 for Field #1 (gantry angle of −20 degrees) for all pencil beams and all motion states for perfect tracking. The x tracking offsets compensated SI motion of up to approximately 25 mm, while y tracking offsets compensated mainly AP motion up to approximately 5 mm. The z offsets compensated changes in radiological depth of the target tissue, requiring up to 25 mm of range-compensation in some motion states, with large variations in range tracking needed for different pencil beams within single motion states. These large fluctuations in range-tracking offset values put high technical demands on the treatment delivery system for patient cases, e.g., when a tumor moves in heterogeneous lung tissue, and are a concerning factor for tracking robustness.
Figure 7.
Perfect beam tracking offsets for Lung Patient #1 for Field #1. Pencil beam x-offsets (green/light grey), y-offsets (blue/dark grey), and z-offsets (red/medium grey) are shown for each pencil beam for each motion state. Note the x-offsets of up to approximately 25 mm correspond directly to SI target motion. z-offsets (i.e., range-offsets) exhibit a more complex pattern due to motion of the target in heterogeneous tissue. The reference motion state was 5.
Our treatment plan for Lung Patient #1 is shown in Figure 8(a) with a 2D cut of 4D RBE-weighted dose overlaying a CT image in the reference motion state at end-exhale for perfect beam tracking (τ = 4 s and ϕ = 0 degrees). We observed a uniform target dose coverage of 32.7 ± 1.1 Gy (RBE) with a rapid falloff of dose outside the target volume. Dose-volume statistics for perfect tracking (for all 18 scenarios of variable respiratory period and starting phase) are shown in Figure 9, at points where the offset is 0.0 (i.e., no offset). Similar to Phantom #3 with the rib heterogeneity, some dependence of target dose coverage on respiratory period and starting phase is seen even for perfect tracking, though not as much as that seen for Phantom #4 with the air heterogeneity. These 18 dose distributions provide our baseline estimate of target dose coverage (V̄95 = 95.5%) for perfect beam tracking for Lung Patient #1, against which we compare our dose distributions with simulated errors in tracking, discussed in the remainder of this section and summarized in Table 2.
Figure 8.
Axial view of RBE-weighted dose overlaying CT shown for Lung Patients #1 - #6, indicated by (a) – (f), respectively, for perfect tracking for a reference case with τ = 4 s and ϕ = 0 degrees. 4D RBE-weighted dose and CT data are shown in the reference motion state at end-exhale. The CTV boundary is indicated by the white curve. The prescribed target dose was 32.8 Gy (RBE). This figure gives a view of our treatment plans and shows the variation in patient anatomy and tumor size for our 6 lung patients.
Figure 9.
Robustness of target dose coverage to systematic errors in tracking x-, y-, and z-coordinates shown for Lung Patient #1. A more dramatic decrease in V95 and increase in D5-D95 is seen, compared to systematic offsets in 1D only (cf. Table 2).
Table 2.
Robustness of target dose coverage <V95> to tracking errors for Lung Patient #1. <V95> is the mean V95 for 18 motion scenarios. Changes in target coverage (Δ) more than 5% indicated in boldface.
| Variable (units) | Magnitude | <V95> (%) | Δ (%) |
|---|---|---|---|
| Perfect Tracking | - | 95.5 | - |
| Phase Delay (deg) | 5 | 86.9 | −8.7 |
| 10 | 79.2 | −16.3 | |
| 15 | 77.2 | −18.3 | |
| Random X Offset (mm) | 0.5 | 95.5 | 0.0 |
| 1.0 | 95.6 | 0.1 | |
| 1.5 | 95.4 | −0.1 | |
| Random Y Offset (mm) | 0.5 | 95.4 | −0.1 |
| 1.0 | 95.2 | −0.3 | |
| 1.5 | 94.9 | −0.7 | |
| Random Z Offset (mm) | 0.5 | 95.9 | 0.3 |
| 1.0 | 96.4 | 0.9 | |
| 1.5 | 96.6 | 1.1 | |
| Random XYZ Offset (mm) | 0.5 | 95.8 | 0.3 |
| 1.0 | 96.1 | 0.6 | |
| 1.5 | 95.9 | 0.4 | |
| Systematic X Offset (mm) | 1 | 95.0 | −0.5 |
| 2 | 94.1 | −1.4 | |
| 3 | 92.5 | −3.0 | |
| 4 | 90.4 | −5.2 | |
| Systematic Y Offset (mm) | 1 | 95.4 | −0.1 |
| 2 | 94.9 | −0.6 | |
| 3 | 93.6 | −1.9 | |
| 4 | 91.6 | −3.9 | |
| Systematic Z Offset (mm) | 1 | 95.6 | 0.0 |
| 2 | 95.2 | −0.3 | |
| 3 | 94.5 | −1.0 | |
| 4 | 93.6 | −1.9 | |
| Systematic XYZ Offset (mm) | 1 | 94.9 | −0.6 |
| 2 | 92.7 | −2.8 | |
| 3 | 87.7 | −7.8 | |
| 4 | 79.6 | −15.9 | |
| Wedge Acceleration (g) | 0.001 | 79.0 | −16.5 |
| 0.01 | 79.7 | −15.8 | |
| 0.1 | 87.5 | −8.0 | |
| 1 | 90.3 | −5.2 | |
| 8 | 90.5 | −5.0 | |
| 10 | 90.7 | −4.8 | |
| 100 | 95.2 | −0.3 |
Target dose coverage was found to be highly sensitive to phase delays in beam tracking. Phase delays up to 15 degrees led to drops in target dose coverage (V̄95) up to 18%. These findings were similar to and confirm those of our phantom study (cf. Figure 4). Thus, phase delays in tracking were a major detriment to target dose coverage for beam tracking for both phantom and patient cases.
The impact of random spatial errors in beam tracking on target dose coverage for Lung Patient #1 was found to be minimal (V̄95 changed less than 1%) when errors were sampled from Gaussian distributions with σ ≤ 1 mm (cf. Table 2). Compared with the phantoms, even less effect was seen in Lung Patient #1, likely due to averaging effects for the 4 beams. As discussed in Section 3.1, the precision in beam tracking is better than 0.3 mm for the experimental system at GSI. We determined that random spatial errors in beam tracking had negligible impact on target dose coverage for the precision of our tracking system.
Target dose coverage was found to be highly sensitive to systematic spatial errors in beam tracking. Errors up to 4 mm led to an approximately 16% drop in target coverage V95, averaged over all phantoms. Figure 9 shows the robustness of target dose coverage to combined systematic errors in tracking x-, y-, and z-coordinates. Only minimal effect on target dose (< 3% change in V̄95) were seen until the errors were greater than 2 mm, with larger drops in target dose coverage and slight loss of dose homogeneity for errors of 3 and 4 mm, as the scanned ion field edge approaches the target boundary. The drop in target coverage V95 due to systematic errors for Lung Patient #1 was less dramatic than for either of the phantoms with heterogeneities (cf. Figure 5), likely explained by blurring out of dose errors by the 4 fields. Overall, the robustness of beam tracking to systematic errors was better for the patient case compared to the phantoms but still a major concern.
For Lung Patient #1, target dose coverage was degraded due to limited acceleration of the range tracking wedge, except for very high wedge acceleration (e.g., a > 100 g). Figure 10 plots the robustness of target dose coverage to limited acceleration of the range-tracking wedge for the patient. The reference case of perfect tracking was represented by infinite wedge acceleration. Simulation of 100 g wedge acceleration produced nearly identical target dose coverage to that with infinite wedge acceleration. For wedge acceleration of 1 to 10 g, similar target dose coverage V95 is seen approximately 5% lower than that seen for perfect tracking (cf. Table 2). At wedge accelerations below 1 g, target dose coverage deteriorates even further with decreasing wedge acceleration. The range-tracking wedge system implemented for experiments at GSI has an acceleration of approximately 8 g and, thus, might not achieve the dose coverage needed for patients.
Figure 10.
Robustness of target dose coverage to limited acceleration (a) of the range-tracking wedge shown for Lung Patient #1. A moderate drop in target dose coverage V95 is seen for a < 100 g and further worsening is seen for a < 1 g.
3.3. Influence of Interfractional Changes in Organ Motion on Target Dose Coverage for Lung Treatment
Target dose coverage was found to deteriorate greatly due to interfractional changes in organ motion 1 and 2 weeks post-planning, as studied for 6 lung cancer patients using multi-week 4DCTs. To give an overview of these patients and the variety of lung tumors studied, Figure 8 shows our treatment plans overlaying CT images from the initial planning 4DCT (week 0), i.e., for perfect tracking (τ = 4 s and ϕ = 0 degrees). Figure 11 shows the robustness of target dose coverage to interfractional motion changes for the 6 lung patients. The median target dose remained stable for all patients, within 4% of the prescribed dose, even up to 2 weeks after planning. However, more importantly, the target dose coverage (V95) deteriorated with time post-planning. Averaged for all 6 patients (and for the 18 motion scenarios), V̄95 dropped from 94.3% at week 0 to 85.9% and 86.2% for treatment simulated 1 and 2 weeks after planning, a mean decrease in V̄95 of 8.4% and 8.1%, respectively. Target dose coverage deteriorated more with time post-planning for Patients #1 and #2, who had the greatest motion amplitudes (up to 25 mm). Overall, target dose coverage (V95) was significantly degraded by interfractional changes in organ motion though median target dose was not.
Figure 11.
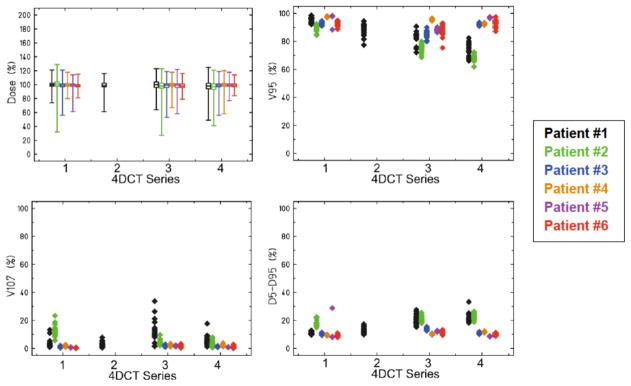
Robustness of target dose coverage to interfractional motion changes shown for the 6 lung patients. Markers are offset slightly (Patients #1-#6 presented left to right, respectively) to ease viewing. All treatment plans were prepared for an initial 4DCT Series #1, and dose was also calculated using the later 4DCTs. 4DCT Series #2 was acquired for only Patient #1 on the same day as the initial 4DCT. For all patients, 4DCT Series #3 was acquired 1 week after the initial 4DCT, and 4DCT Series #4 was acquired 2 weeks after the initial 4DCT. Target dose coverage V95 deteriorated with time post-planning, dropping approximately 8% after 1 week.
3.4. Summary of Results
For simulations of perfect scanned beam tracking of moving targets in heterogeneous matter, we found that dose distributions were sensitive to the phase of respiration at the start of irradiation and to the respiratory period. Even when the pencil beam Bragg peaks perfectly tracked the moving target, off-axis dose contributions from individual pencil beams were affected by variation in tissue upstream of the moving target and dose was degraded. This finding confirms the finding of van de Water et al. (2009).
Phase delays in tracking the moving targets led to large degradation of target dose coverage. This finding supports the need for predictive algorithms for motion tracking and fast, i.e., few ms, hardware to apply beam-tracking parameters in real time during treatment.
Random tracking errors sampled from a Gaussian distribution with σ < 0.5 mm had negligible effect on target dose coverage.
Systematic errors in beam tracking, which could be caused by patient misalignment, baseline drifts in target position, or errors in image registration used for planning, caused two distinct ill effects on target dose coverage. First, simple misalignment of the target with the radiation field boundary led to underdosage of the target, as the target moved near the dose falloff region. This degradation was observed with errors greater than 2 mm and could likely be addressed simply by using treatment margins, similar to a PTV concept (margins were purposefully omitted from this study). Second, a more complex relation was seen in heterogeneous tissue, and even relatively small, e.g., 1 mm, lateral positional errors led to degraded dose, likely since the radiological thickness of tissue upstream of the target can vary greatly off axis. Thus, lateral misalignment of a pencil beam can manifest as an incorrect depth of its Bragg peak in a complex manner.
The limited acceleration of the range-tracking wedge led to minimal degradation of target dose when acceleration was ≥ 8 g for phantoms. We observed an inflection and rapid worsening of target dose when acceleration was ≤ 1 g. Our patient simulations suggest that a higher wedge acceleration > 10 g might be required to improve target dose coverage, but our data do not suggest the need for acceleration greater than 100 g. If very fast range-tracking is needed in the future, the method of Chaudhri et al. (2010), which uses magnetic beam deflection and a static wedge degrader, might be preferable to the mechanically actuated wedge system assumed in this study.
For the 6 lung cancer patients in our study with multi-week 4DCTs, interfractional changes in organ motion did not lead to large changes in the median target dose, i.e., median dose was within 4% of that prescribed, even up to 2 weeks after planning. However, as expected, dose coverage (V95) worsened with time, dropping approximately 8% after 1 week post-planning. Larger degradation of dose coverage was observed for patients with greater tumor motion. For Lung Patient #1, V95 dropped approximately 7% due to variation in organ motion occurring during a single day.
4. Discussion
In this study, we evaluated the robustness of target dose coverage to motion uncertainties for 3D-optimized scanned carbon ion beam tracking therapy for moving targets. We implemented new algorithms in a research TPS to allow simulation of a number of deviations from perfect tracking. Additionally, we investigated the robustness of beam tracking to interfractional changes in organ motion using multiweek 4DCTs for a sample of lung patients. We found target dose coverage for scanned carbon ion beam tracking therapy to be sensitive to a number of motion uncertainties. Sensitivity was minimal for the lung cancer case against technical uncertainties of beam delivery. Higher sensitivity was seen with respect to changes of anatomy as studied in the multiweek analysis. Our findings can be used to inform the design specifications of future scanned ion beam tracking systems and to inspire future motion mitigation strategies.
One major strength of this work is that this approach gives a view of the motion problem that cannot be explored using commercial treatment planning systems. By the thousands (nearly 4000 dose calculations were reported in this work) of 4D dose calculations possible using a research TPS and a research computing cluster, we were able to isolate motion uncertainties related to beam tracking and to test the robustness of target dose coverage independently to these uncertainties. Another strength is that many of these methods are general and might also be used to simulate the effect of motion uncertainties on dose for future motion-mitigation strategies for scanned ion therapy, such as breath hold, beam gating, or rescanning. In this work, we evaluated the robustness of target dose coverage for moving phantoms and lung patients without using setup or motion margins, i.e., no “PTV-type” margins, which could have masked underlying changes to the desired dose distribution caused by small errors in beam tracking. This means that our results can be used to understand the baseline robustness of scanned carbon beam tracking and also be used to decide margins and positional precision requirements that best ensure robustness of target dose coverage for future patient treatments.
Our finding of imperfect target dose coverage even for perfect tracking confirms that reported by van de Water et al. (2009). However, their study did not include patient simulations, whereas we found target dose coverage to be more robust to tracking errors in patient anatomy compared with our mathematical phantoms. These heterogeneous phantoms could be viewed as a worst-case example since such cylindrical geometries with discrete edges are rarely found in patients. Since we found target dose coverage to depend on patient starting phase and respiratory period, even for perfect tracking, we expect that rescanning with beam tracking, as suggested by van de Water et al. (2009), would likely provide a more robust dose coverage for targets moving in heterogeneous tissue.
Our study had several limitations. One limitation was that we only investigated robustness to technical (i.e., beam delivery system) uncertainties for one lung patient, who had the highest motion amplitude in our sample of 6 patients. Thus, we might overestimate the sensitivity of target dose coverage to errors in tracking compared to that possible for patients with less tumor motion. Another limitation of this work was that we simulated temporal aspects of beam delivery using a spill-intensity profile typical of the SIS 18 synchrotron at GSI. Thus some of our findings, mainly those regarding the impact of limited wedge acceleration, would likely change for accelerators with spill-intensity (temporal) profiles vastly different from that of the GSI synchrotron. To coarsely understand this, we repeated a small part of our study using a hypothetical spill-intensity profile, which was identical to our original profile, but simulated to occur 10 times faster. Those results (cf. Supplementary Data) show some differences but encourage that the spill intensity profile does not have a large influence on our major findings. A full analysis of that problem needs to be addressed in future studies. Another limitation was that we optimized the particle fluence for a single reference motion state, e.g., at end-exhale, prior to calculating the beam tracking offsets for each pencil beam for each motion state. That is, we did not account for all motion states in the planning of particle numbers, which partially explains some of our degraded target dose coverage seen even for perfect tracking. These limitations are being addressed in ongoing studies in our laboratory (Eley et al., 2014); however, they did not prevent us from achieving our objective, which was to evaluate the robustness of target dose coverage to motion uncertainties for scanned carbon ion beam tracking therapy of moving targets.
Based on our findings, we propose the following future studies. First, we suggest that appropriate beam-specific margins be designed to mitigate range errors introduced by lateral target misalignment, similar to the approach of Park et al. (2012), but also including motion margins needed to cover the deforming tissue during respiration (Graeff et al., 2012). To investigate this, we briefly repeated part of our study using beam-specific, robust (range-proof) margins and, indeed, found some improvements to the median target coverage for Patient #1, which appeared to persist for treatment simulated at 1 and 2 weeks after treatment planning (cf. Supplementary Data). However, this improvement did not exist for all scenarios of respiratory period and starting phase, which indicates that margins alone will likely not provide a comprehensive solution due to persisting interplay effect in the target. Nonetheless, we speculate the ideal field margins could be a “center-of-mass ITV,” which covers any range changes (i.e., changes in radiological depth of the target boundary) and lateral deformations for all motion states, specifically considering the deviations in the center-of-mass frame and likewise using the center of mass as the beam tracking target centerpoint. Such a center-of-mass ITV concept could also be used with motion detection systems that directly determine the tumor location, instead of surrogate detection. Thus, lateral beam tracking parameters could be determined in real time and would not need to rely on a planning 4DCT. The remaining issue of range tracking might still be addressed using vectors derived from a planning 4DCT or, alternatively, range tracking might be abandoned entirely, which might also achieve acceptable target dose coverage (Lüchtenborg, 2011), especially when multiple beam angles are used. In addition, based on the findings of van de Water et al. (2009), we expect that rescanning combined with beam tracking will offer improved robustness.
Strategies to improve robustness have already been developed for both photon therapy (Bortfeld et al., 2008; Unkelbach et al., 2009) and particle therapy (Unkelbach, 2007; Pflugfelder et al., 2008; Chen et al., 2012; Liu et al., 2012). Many of these strategies incorporated uncertainties in plan optimization to improve probability of tumor control in the presence of patient setup uncertainty, though, to our knowledge, do not yet explicitly address organ motion for particle therapy. Theoretically, robust 4D optimization could be used to optimize particle numbers that are both optimal for all motion states and robust to motion uncertainties, which would be beneficial, since, for this beam tracking approach, it is unknown prior to treatment in which motion state a pencil beam will be irradiated.
In summary, we developed a new method to model the impact of motion uncertainties for scanned ion beam tracking and implemented our work in a 4D research treatment planning system. We quantified the sensitivity of target dose to several uncertainties present in scanned carbon ion beam tracking for moving tumors using both mathematical phantom studies and retrospective lung cancer patient studies. Our results provide a better understanding of the importance of each of these uncertainties for beam tracking with scanned carbon ions.
Supplementary Material
Acknowledgments
We thank George Starkschall for helpful scientific discussions regarding uncertainties in lung motion. Portions of this work were funded by the Deutscher Akademischer Austausch Dienst, the Rosalie B. Hite Fellowship, the National Cancer Institute Award 1 R01 CA 131463-01A1, Northern Illinois University through a subcontract of the Department of Defense Award W81XH-08-1-0205, and the POFII Program of the Helmholtz Gemeinschaft.
Contributor Information
John Gordon Eley, Email: jeley@som.umaryland.edu.
Christoph Bert, Email: christoph.bert@uk-erlangen.de.
References
- Bert C, Durante M. Motion in radiotherapy: particle therapy. Phys Med Biol. 2011;56:R113–44. doi: 10.1088/0031-9155/56/16/R01. [DOI] [PubMed] [Google Scholar]
- Bert C, Grozinger SO, Rietzel E. Quantification of interplay effects of scanned particle beams and moving targets. Phys Med Biol. 2008;53:2253–65. doi: 10.1088/0031-9155/53/9/003. [DOI] [PubMed] [Google Scholar]
- Bert C, Rietzel E. 4D treatment planning for scanned ion beams. Radiat Oncol. 2007:2. doi: 10.1186/1748-717X-2-24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bortfeld T, Chan TCY, Trofimov A, Tsitsiklis JN. Robust management of motion uncertainty in intensity-modulated radiation therapy. Oper Res. 2008;56:1461–73. [Google Scholar]
- Chaudhri N, Saito N, Bert C, Franczak B, Steidl P, Durante M, Rietzel E, Schardt D. Ion-optical studies for a range adaptation method in ion beam therapy using a static wedge degrader combined with magnetic beam deflection. Phys Med Biol. 2010;55:3499–513. doi: 10.1088/0031-9155/55/12/015. [DOI] [PubMed] [Google Scholar]
- Chen W, Unkelbach J, Trofimov A, Madden T, Kooy H, Bortfeld T, Craft D. Including robustness in multi-criteria optimization for intensity-modulated proton therapy. Phys Med Biol. 2012;57:591–608. doi: 10.1088/0031-9155/57/3/591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Combs SE, Habermehl D, Kieser M, Dreher C, Werner J, Haselmann R, Jakel O, Jager D, Buchler MW, Debus J. Phase I study evaluating the treatment of patients with locally advanced pancreatic cancer with carbon ion radiotherapy: the PHOENIX-01 trial. BMC Cancer. 2013;13:419. doi: 10.1186/1471-2407-13-419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eley JG, Newhauser WD, Luchtenborg R, Graeff C, Bert C. 4D optimization of scanned ion beam tracking therapy for moving tumors. Phys Med Biol. 2014;59:3431–52. doi: 10.1088/0031-9155/59/13/3431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elsässer T, Weyrather WK, Friedrich T, Durante M, Iancu G, Kramer M, Kragl G, Brons S, Winter M, Weber KJ, Scholz M. Quantification of the relative biological effectiveness for ion beam radiotherapy: direct experimental comparison of proton and carbon ion beams and a novel approach for treatment planning. Int J Radiat Oncol Biol Phys. 2010;78:1177–83. doi: 10.1016/j.ijrobp.2010.05.014. [DOI] [PubMed] [Google Scholar]
- Graeff C, Durante M, Bert C. Motion mitigation in intensity modulated particle therapy by internal target volumes covering range changes. Med Phys. 2012;39:6004–13. doi: 10.1118/1.4749964. [DOI] [PubMed] [Google Scholar]
- Habermehl D, Debus J, Ganten T, Ganten MK, Bauer J, Brecht IC, Brons S, Haberer T, Haertig M, Jakel O, Parodi K, Welzel T, Combs SE. Hypofractionated carbon ion therapy delivered with scanned ion beams for patients with hepatocellular carcinoma - feasibility and clinical response. Radiat Oncol. 2013;8:59. doi: 10.1186/1748-717X-8-59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraft G. Tumor therapy with heavy charged particles. Prog Part Nucl Phys. 2000;45(S2):S473–S544. [Google Scholar]
- Lambert J, Suchowerska N, McKenzie DR, Jackson M. Intrafractional motion during proton beam scanning. Phys Med Biol. 2005;50:4853–62. doi: 10.1088/0031-9155/50/20/008. [DOI] [PubMed] [Google Scholar]
- Liu W, Zhang X, Li Y, Mohan R. Robust optimization of intensity modulated proton therapy. Med Phys. 2012;39:1079–91. doi: 10.1118/1.3679340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lomax AJ. Intensity modulated proton therapy and its sensitivity to treatment uncertainties 1: the potential effects of calculational uncertainties. Phys Med Biol. 2008a;53:1027–42. doi: 10.1088/0031-9155/53/4/014. [DOI] [PubMed] [Google Scholar]
- Lomax AJ. Intensity modulated proton therapy and its sensitivity to treatment uncertainties 2: the potential effects of inter-fraction and inter-field motions. Phys Med Biol. 2008b;53:1043–56. doi: 10.1088/0031-9155/53/4/015. [DOI] [PubMed] [Google Scholar]
- Lüchtenborg R. Technische Universität Darmstadt. 2011. Real-time dose compensation methods for scanned ion beam therapy of moving tumors. [Google Scholar]
- Lujan AE, Larsen EW, Balter JM, Ten Haken RK. A method for incorporating organ motion due to breathing into 3D dose calculations. Med Phys. 1999;26:715–20. doi: 10.1118/1.598577. [DOI] [PubMed] [Google Scholar]
- Meyer J, Bluett J, Amos R, Levy L, Choi S, Nguyen QN, Zhu XR, Gillin M, Lee A. Spot scanning proton beam therapy for prostate cancer: treatment planning technique and analysis of consequences of rotational and translational alignment errors. Int J Radiat Oncol. 2010;78:428–34. doi: 10.1016/j.ijrobp.2009.07.1696. [DOI] [PubMed] [Google Scholar]
- Miyamoto T, Baba M, Sugane T, Nakajima M, Yashiro T, Kagei K, Hirasawa N, Sugawara T, Yamamoto N, Koto M, Ezawa H, Kadono K, Tstyii H, Mizoe JE, Yoshikawa K, Kandatsu S, Fujisawa T. Carbon ion radiotherapy for stage I non-small cell lung cancer using a regimen of four fractions during 1 week. J Thorac Oncol. 2007;2:916–26. doi: 10.1097/JTO.0b013e3181560a68. [DOI] [PubMed] [Google Scholar]
- Mohr M, Abrams E, Engel C, Long WB, Bottlang M. Geometry of human ribs pertinent to orthopedic chest-wall reconstruction. J Biomech. 2007;40:1310–7. doi: 10.1016/j.jbiomech.2006.05.017. [DOI] [PubMed] [Google Scholar]
- Pan T, Lee TY, Rietzel E, Chen GT. 4D-CT imaging of a volume influenced by respiratory motion on multi-slice CT. Med Phys. 2004;31:333–40. doi: 10.1118/1.1639993. [DOI] [PubMed] [Google Scholar]
- Park PC, Zhu XR, Lee AK, Sahoo N, Melancon AD, Zhang L, Dong L. A beam-specific planning target volume (PTV) design for proton therapy to account for setup and range uncertainties. Int J Radiat Oncol. 2012;82:e329–36. doi: 10.1016/j.ijrobp.2011.05.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pflugfelder D, Wilkens JJ, Oelfke U. Worst case optimization: a method to account for uncertainties in the optimization of intensity modulated proton therapy. Phys Med Biol. 2008;53:1689–700. doi: 10.1088/0031-9155/53/6/013. [DOI] [PubMed] [Google Scholar]
- Pflugfelder D, Wilkens JJ, Szymanowski H, Oelfke U. Quantifying lateral tissue heterogeneities in hadron therapy. Med Phys. 2007;34:1506–13. doi: 10.1118/1.2710329. [DOI] [PubMed] [Google Scholar]
- Richter D, Saito N, Chaudhri N, Hartig M, Ellerbrock M, Jakel O, Combs SE, Habermehl D, Herfarth K, Durante M, Bert C. Four-dimensional patient dose reconstruction for scanned ion beam therapy of moving liver tumors. Int J Radiat Oncol Biol Phys. 2014;89:175–81. doi: 10.1016/j.ijrobp.2014.01.043. [DOI] [PubMed] [Google Scholar]
- Richter D, Schwarzkopf A, Trautmann J, Kramer M, Durante M, Jäkel O, Bert C. Upgrade and benchmarking of a 4D treatment planning system for scanned ion beam therapy. Med Phys. 2013;40:051722. doi: 10.1118/1.4800802. [DOI] [PubMed] [Google Scholar]
- Rieken S, Habermehl D, Haberer T, Jaekel O, Debus J, Combs SE. Proton and carbon ion radiotherapy for primary brain tumors delivered with active raster scanning at the Heidelberg Ion Therapy Center (HIT): early treatment results and study concepts. Radiat Oncol. 2012;7:41. doi: 10.1186/1748-717X-7-41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saito N, Bert C, Chaudhri N, Gemmel A, Schardt D, Durante M, Rietzel E. Speed and accuracy of a beam tracking system for treatment of moving targets with scanned ion beams. Phys Med Biol. 2009;54:4849–62. doi: 10.1088/0031-9155/54/16/001. [DOI] [PubMed] [Google Scholar]
- Schneider W, Bortfeld T, Schlegel W. Correlation between CT numbers and tissue parameters needed for Monte Carlo simulations of clinical dose distributions. Phys Med Biol. 2000;45:459–78. doi: 10.1088/0031-9155/45/2/314. [DOI] [PubMed] [Google Scholar]
- Scholz M, Kellerer AM, Kraft-Weyrather W, Kraft G. Computation of cell survival in heavy ion beams for therapy - The model and its approximation. Radiat Environ Bioph. 1997;36:59–66. doi: 10.1007/s004110050055. [DOI] [PubMed] [Google Scholar]
- Schulz-Ertner D, Karger CP, Feuerhake A, Nikoghosyan A, Combs SE, Jakel O, Edler L, Scholz M, Debus J. Effectiveness of carbon ion radiotherapy in the treatment of skull-base chordomas. Int J Radiat Oncol Biol Phys. 2007;68:449–57. doi: 10.1016/j.ijrobp.2006.12.059. [DOI] [PubMed] [Google Scholar]
- Schulz-Ertner D, Nikoghosyan A, Thilmann C, Haberer T, Jakel O, Karger C, Kraft G, Wannenmacher M, Debus J. Results of carbon ion radiotherapy in 152 patients. Int J Radiat Oncol Biol Phys. 2004;58:631–40. doi: 10.1016/j.ijrobp.2003.09.041. [DOI] [PubMed] [Google Scholar]
- Schulz-Ertner D, Tsujii H. Particle radiation therapy using proton and heavier ion beams. J Clin Oncol. 2007;25:953–64. doi: 10.1200/JCO.2006.09.7816. [DOI] [PubMed] [Google Scholar]
- Shackleford JA, Kandasamy N, Sharp GC. On developing B-spline registration algorithms for multi-core processors. Phys Med Biol. 2010;55:6329–51. doi: 10.1088/0031-9155/55/21/001. [DOI] [PubMed] [Google Scholar]
- Tsujii H, Kamada T. A review of update clinical results of carbon ion radiotherapy. Jpn J Clin Oncol. 2012;42:670–85. doi: 10.1093/jjco/hys104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Unkelbach J. Including geometrical uncertainties in IMRT and IMPT optimization. Radiother Oncol. 2007;84:S90–S. [Google Scholar]
- Unkelbach J, Bortfeld T, Martin BC, Soukup M. Reducing the sensitivity of IMPT treatment plans to setup errors and range uncertainties via probabilistic treatment planning. Med Phys. 2009;36:149–63. doi: 10.1118/1.3021139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van de Water S, Kreuger R, Zenklusen S, Hug E, Lomax AJ. Tumour tracking with scanned proton beams: assessing the accuracy and practicalities. Phys Med Biol. 2009;54:6549–63. doi: 10.1088/0031-9155/54/21/007. [DOI] [PubMed] [Google Scholar]
- Weber U, Kraft G. Design and construction of a ripple filter for a smoothed depth dose distribution in conformal particle therapy. Phys Med Biol. 1999;44:2765–75. doi: 10.1088/0031-9155/44/11/306. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.