Communication of brain network core connections altered in behavioral variant frontotemporal dementia but possibly preserved in early-onset Alzheimer’s disease

Abstract

Diffusion imaging and brain connectivity analyses can assess white matter deterioration in the brain, revealing the underlying patterns of how brain structure declines. Fiber tractography methods can infer neural pathways and connectivity patterns, yielding sensitive mathematical metrics of network integrity. Here, we analyzed 1.5-Tesla whole-brain diffusion-weighted images from 64 participants – 15 patients with behavioral variant frontotemporal dementia (bvFTD), 19 with early-onset Alzheimer’s disease (EOAD), and 30 healthy elderly controls. Using whole-brain tractography, we reconstructed structural brain connectivity networks to map connections between cortical regions. We evaluated the brain’s networks focusing on the most highly central and connected regions, also known as hubs, in each diagnostic group – specifically the “high-cost” structural backbone used in global and regional communication. The high-cost backbone of the brain, predicted by fiber density and minimally short pathways between brain regions, accounted for 81–92% of the overall brain communication metric in all diagnostic groups. Furthermore, we found that the set of pathways interconnecting high-cost and high-capacity regions of the brain’s communication network are globally and regionally altered in bvFTD, compared to healthy participants; however, the overall organization of the high-cost and high-capacity networks were relatively preserved in EOAD participants, relative to controls. Disruption of the major central hubs that transfer information between brain regions may impair neural communication and functional integrity in characteristic ways typical of each subtype of dementia.

1. INTRODUCTION

Brain connectivity studies are becoming increasingly popular for investigating the communication patterns of the normal and diseased brain. Connectivity analyses combine concepts from neuroscience and engineering to characterize the brain in terms of its structural and functional connections. Diffusion-weighted imaging (DWI) is used in structural brain connectivity studies to assess the global and local breakdown of network integration in degenerative disease. In addition, there are immediate applications of analysis methods such as graph theory – a branch of mathematics that can be used to model the topological organization of the brain’s networks. These forms of analysis have recently been applied to neurological diseases, for instance, to test the long-standing hypothesis that each focal neurodegenerative syndrome targets specific large-scale networks [1].

Behavioral variant frontotemporal dementia (bvFTD) and early-onset Alzheimer’s disease (EOAD) are the two common forms of early-onset dementia in patients less than 65 years of age, and are often characterized by dysfunctional connectivity [2]. Here, we studied 15 bvFTD participants and 19 early-onset amnestic AD (EOAD) participants, and compared them to 30 healthy age-matched participants using advanced structural connectivity measures to define some of the differentiating factors between the diagnostic groups. bvFTD is a neurodegenerative disease that affects mainly the anterior cingulate cortex and frontoinsular regions of the brain [1], while EOAD is another neurodegenerative disease with dysfunctions predominantly in the hippocampal-cingulo-temporal parietal network [2].

In this study, we analyzed the EOAD and bvFTD neural networks, and compared them to those of healthy controls, to evaluate them in terms of their structural network efficiency. To do this, we defined the densely and mutually interconnected networks in the brain – also known as hubs – consisting of ‘nodes’, represented by segmented regions of interest (ROIs), and edges, interconnecting these ROIs. Often, edges - or connections that link a pair of ROIs - may be assigned a ‘weight’, for instance, the density of fibers extracted from tractography or the shortest fiber path between the ROIs. These two weights can be multiplied together to define a measure of the communication cost, which provides information on a network’s spatial layout in the brain. Previous studies showed that densely connected pathways of connections in the brain’s network are expected to contribute highly to a network’s cost and the communication capacity of cortico-cortico connections [3]. Here, we hypothesized that (1) relative to healthy controls, both degenerative diseases will show impaired communication cost in brain networks, and (2) there would be different patterns of disruption among network components, between the disorders, with greater frontal lobe disruption in bvFTD.

2. METHODS

2.1 Participant Demographics and Imaging Parameters

We analyzed diffusion-weighted images (DWI) from 30 healthy controls and 34 dementia patients – 15 patients with bvFTD and 19 with EOAD (Table 1). All 64 participants underwent whole-brain MRI scanning on a 1.5-Tesla Siemens Avanto scanner, at the MRI Center at the University of California, Los Angeles. Standard anatomical T1-weighted (T1w) sequences were collected (256×256 matrix; voxel size=1×1×1 mm³; TI=900, TR=2000 ms; TE=2.89 ms; flip angle=40°), along with diffusion-weighted images (DWI) using a single-shot multi-section spin-echo echo-planar pulse sequence with the following parameters: 144×144 matrix; voxel size: 2×2×3 mm³; TR=9800 ms; TE=97 ms; flip angle=90°; scan time=5 min 38 s. 31 separate images were acquired for each DWI sequence: 1 T2-weighted image with no diffusion sensitization (b₀ image) and 30 diffusion-weighted images (b=1000 s/mm2). This protocol has been previously implemented in diffusion imaging studies [4–6].

Table 1.

Demographic information from the 30 healthy controls, 15 bvFTD and 19 EOAD patients with brain imaging. The mean age and sex are listed for each diagnostic group.

	CTL	bvFTD	EOAD	Total
Age	59.5 ± 9.6 SD	61.3 ± 10.8 SD	57.9 ± 4.3 SD	59.5 ± 8.7 SD
Sex	13M/17F	7M/8F	7M/12F	27M/37F

2.2 Image Analysis

Tractography from DWIs was combined with an automatically labeled set of brain regions from the high-resolution T1w MRI to map the brain’s fiber connections and create the cortical connectivity networks. To do this, we linearly aligned the DWI to the T1w images and performed whole-brain tractography on them using the Hough voting method on orientation distribution functions (ODFs) reconstructed based on a constant-solid angle method as described in [7]. Each subject’s dataset contained ~10,000 useable fibers (3D curves) in total. Then, 34 cortical labels per hemisphere, from the Desikan-Killiany atlas [8], were automatically extracted from all aligned T1w structural MRI scans using FreeSurfer version 5.0 (http://surfer.nmr.mgh.harvard.edu/) [9]. The resulting T1w images and cortical models were aligned to the original T1w input image space and down-sampled to the space of the DWIs (we assume that the anatomical scan serves as a relatively undistorted anatomical reference).

Considering the white matter tractography and the cortical parcellations, fibers connecting each pair of ROIs were enumerated into a matrix. From this, a 68×68 connectivity matrix was created for each subject with 34 ROIs in each hemisphere. In this paper, we use the word fiber to denote a single curve, or “streamline”, extracted via tractography; if no participants had detected fibers connecting two regions (i.e., all participants had a 0 count at a specific matrix element), then that connection was considered invalid, or not consistent enough in the population, and was not included in the analysis.

2.3 Connectivity matrices representing communication cost within the brain network

In graph theory, an NxN connectivity matrix may be compiled to describe the network [5, 10]. To do this, we traced all the fibers that connected all pairs of nodes in the network and saved the total counts of fibers connecting the regions under an element-wise 68×68 fiber density connectivity matrix. The network’s nodes are typically defined as ROIs, in our case on the cortex, segmented from anatomical T1w images. Network nodes are linked by ‘edges’ whose weights denote some measure of connectivity between the two regions. In structural connectivity studies, the edges are often represented by the density or integrity of fiber tracts connecting the regions [5, 10].

The most basic measure that describes the connectedness of the nodes in the connectivity matrix is nodal degree – the number of edges (binary elements of the matrix) that connect to a node. The most densely interconnected nodes of the brain form hubs, which are thought to disseminate large proportions of signal among central and remote nodes of the network [3]. Most often, hubs are defined using k – nodes that have high values of k are considered to be part of the hub network, while nodes with low values of k are not. Here, we defined the network hubs by calculating the k-core network using a decomposition algorithm that reveals the hierarchical structure of the network components [3, 5, 11, 12]. The nodal degree serves as a threshold to define the largest sub-networks of the brain with mutually and highly interconnected ‘central cores’. For example, to compute the ‘26-core’ (k=26) of the network, all nodes contained within a sub-network with k=26 or higher will be retained, while all other connections (with k<26) will be set to zero. At k=26, nodes of the sub-network are connected to at least 39% of the other 67 nodes that make up the brain’s entire network (26/68=38.8% while at 100% one node connects to all 67 nodes in the network). For more details on the k-core decomposition, please see [5, 11].

To remove unreliable tracts that may arise from tractography errors (i.e., false fibers), we thresholded the connectivity matrices at k=12 where 18% of the nodes in each sub-network are required to be connected among themselves. These thresholded connectivity matrices were used for all statistical analyses.

Next, we defined the most centrally interconnected hubs of the brain in each diagnostic group by selecting the k level prior to the one where all connections were purged. In controls and EOAD participants, this thresholding level was k=26 (at k=27 or 40%, no sub-networks were formed in either diagnostic groups). Whereas in bvFTD participants, this nodal threshold was lower – k=22 (33%), possibly due to a greater loss in network connections. To confirm the presence of a high degree hub in each subject’s brain, we computed a global value, R, also known as the ‘rich club’ coefficient [13], describing the fraction of edges that connect nodes of nodal degree k. R was computed for each k-core for both the non-randomized and randomized networks in each subject:

$$R(k)=\frac{E_{>k}}{N_{>k}(N_{>k}-1)}$$ (1)

We randomized R using random networks of the same size (68×68) and similar nodal degree distribution as the true brain networks:

$$R_n(k)=\frac{R(k)}{R_r(k)}$$ (2)

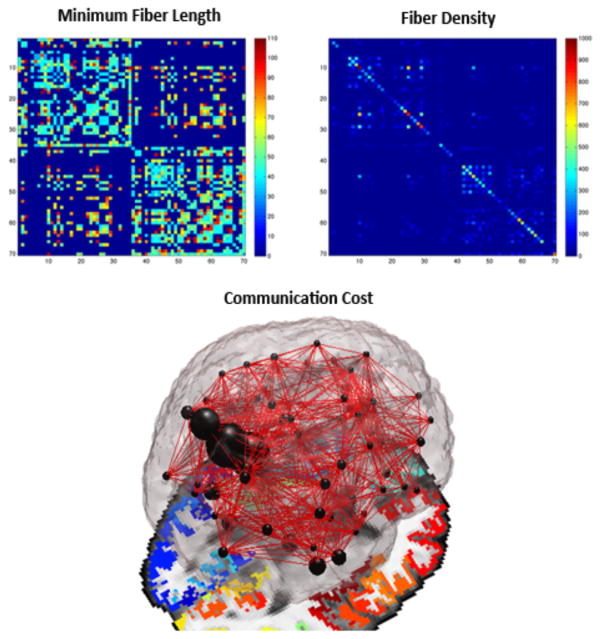
It is important to randomize R as the absolute values vary greatly with the size and density of each individual network, and therefore – it provides limited information on network integration [10, 13]. In this dataset, we verified that R_n was greater than 1 to indicate the presence of a rich club organization (i.e., formation of hubs) in the brain networks [3, 10, 13]. For each subject’s connectivity matrix, we assessed the weighted communication cost [3] among a pair of nodes and saved this information under the form of a 68×68 matrix, where each element of the matrix reflected the multiplication between the normalized fiber density and the minimum physical fiber length connecting a pair of nodes. To further explain this, we normalized each element of the fiber density connectivity matrices by the total number of fibers extracted per brain and multiplied it with the minimum physical length describing the fiber, extracted directly from tractography. This fiber was considered to support communication between two ROIs via the shortest fiber path. Finally, the local communication cost – which is intended to describe an aspect of communication related to the network’s spatial embedding (Fig. 1) [3], was defined as:

$$C_{ij}={\sum }_{i,j\in N}{L}_{ij}{\rho }_{ij}$$ (3)

where C_ij is the total minimum communication cost between nodes i and j, L_ij is the shortest physical fiber bundle length between nodes i and j, and ρ_ij is the density of the edges used for information transfer between nodes i and j [3].

Figure 1.

A local network ‘communication cost’ can be defined between a pair of ROIs. Here we define the cost as the multiplication between the normalized fiber density and the minimum physical fiber length among a set of white matter bundles connecting ROIs, thus describing an aspect of communication related to the network’s spatial embedding.

To test for group differences in local cost communication in bvFTD vs. controls, EOAD vs. controls and bvFTD vs. EOAD, we ran a linear regression (i.e., with disease coded as 1 and controls coded as 0), and covaried for age and sex. We used the False Discovery Rate (FDR) to correct for the multiple tests performed. Then, we computed the nodal degree – the sum of all edges connecting to a node, and tested in a linear regression for differences between the nodal degree in bvFTD vs. controls and EOAD vs. controls. We also covaried for age and sex.

3. RESULTS

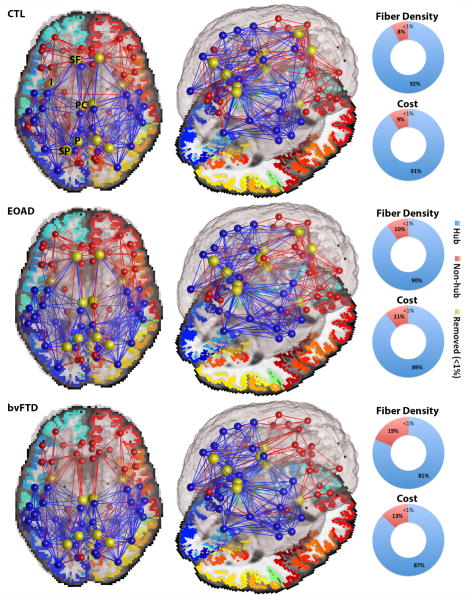
In this study we examined the topological organization of hub connections in healthy and diseased brains to reveal aspects of their local cost, as indexed by their volume (i.e., fiber density) and their capacity (i.e., shortest communication paths between nodes). As stated in the introduction, we hypothesized that degenerative disease would impair the communication networks especially in the frontal lobe of bvFTD participants. The brain networks in all diagnostic groups formed high-cost and high-capacity hubs, also known as rich club networks – where network components are more interconnected among themselves than would be expected by chance [3]. These rich club networks accounted for 89–92% of the total network cost and fiber density in controls and EOAD participants (Fig. 2); in bvFTD, they accounted for 87% of the total network cost and 81% of the total network density. Cost and density network metrics may be reduced in disease leading to an altered global topology as seen in bvFTD participants (as expected), but not in EOAD. Alterations of global topology may impair the organization of a focal network, through which components of the brain’s network are thought to receive and integrate information from functionally diverse regions (hubs and non-hubs) [3].

Figure 2. Average set of nodes illustrating the structural backbone of the brain’s networks, averaged across healthy controls (CTL), bvFTD and EOAD participants.

Blue edges indicate connections that are part of the network hub (k=26 for CTL and EOAD, and k=22 for bvFTD), while red edges describe low-degree non-hub connections (<1% of unreliable connections were removed). The local cost, fiber density and minimum fiber length were computed for each network type (hub and non-hub) in all groups. Hubs accounted for 89–92% of the total network cost and fiber density in CTL and EOAD; in bvFTD, they accounted for 87% of the total network cost and 81% of the total network density. The centrally positioned hubs (yellow nodes) describe the superior frontal (SF), insula (I), posterior cingulate (PC), precuneus (P) and superior parietal (SP). Note that the SF is no longer a hub in bvFTD, yet all major hubs remain in EOAD.

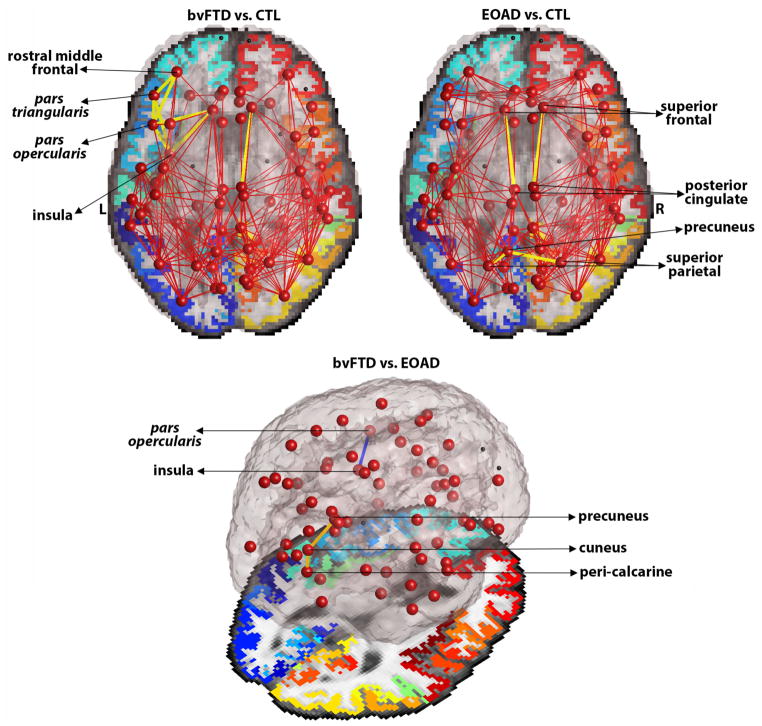
As hypothesized, the local communication cost networks differed significantly between the disease groups and healthy controls (Fig. 3). Our findings show that in bvFTD, relative to controls, the local cost decreased among left hemisphere connections between language processing areas – pars triangularis and pars opercularis, and their connections with the insula and frontal cortical areas (i.e., rostral middle frontal) (FDR critical p-value=4.1×10⁻³). Studies have previously shown language impairments in bvFTD [14, 15] and frequent frontal lobe and insular impairments [1]. On the other hand, in EOAD participants, relative to controls, we found a decrease in the local communication cost among connections between the left precuneus – a region known to atrophy in AD [16], and the left and right superior parietal regions (FDR critical p-value=2.0×10⁻³). Local cost between the posterior cingulate and superior frontal regions was also found to decrease in EOAD in both hemispheres (FDR critical p-value=2.0×10⁻³). Interestingly, when compared to each other, the disease groups showed an alternating pattern of impairment among regions known to be specific to each disease. bvFTD participants were found to have a decreased local cost between the left insula and left pars opercularis, relative to EOAD; however, EOAD participants had a decreased local cost in the right hemisphere between the precuneus and cuneus, and cuneus and peri-calcarine regions (FDR critical p-value=9.0×10⁻⁴) (Fig. 3). Although the current structural study does not directly address functional network organization, our findings are in line with functional studies that show the same alternating patterns; regions of the Salience Network (SN; i.e., frontoinsula) are more impaired in bvFTD than in AD, while regions of the Default Mode Network (DMN; i.e., precuneus, posterior, posterior cingulate) are more impaired in AD than bvFTD [2].

Figure 3. Group comparisons for bvFTD vs. controls, EOAD vs. controls and bvFTD vs. EOAD participants.

Upper: Yellow edges indicate connections between nodes in the bvFTD and EAOD networks where local communication cost was lower than in controls. Bottom: Blue connection indicates decreased local cost in bvFTD, relative to EOAD; Orange connections indicate decreased local cost in EOAD, relative to bvFTD participants.

We defined the most highly interconnected hubs of the brain, as previously reported [3, 10, 17], as the superior frontal (SF), posterior cingulate (PC), precuneus (P), insula (I) and superior parietal (SP) (Fig. 2). These regions were shown to form the central communication backbone in both human [3] and non-human studies of the macaque and cat cortical network [10, 17]. In this study, we found that in bvFTD participants, the nodal degree in the superior frontal and posterior cingulate regions were significantly lower, relative to controls (FDR critical p-value=0.02). Particularly in the superior frontal cortical region, there was a large loss in connectivity that ultimately led to this region being removed from the hubs of the bvFTD brain connectome (Fig. 2). Disruptions of the rich club network may lead to global topological alterations, and possibly to inefficient integration of information between parts of the brain. Meanwhile, no differences were found for nodal degree between EOAD and controls. Although locally weighted cost functions of the network organization also indicate impairment in EOAD, the global organization of the brain’s network in EOAD is relatively preserved.

4. CONCLUSION

Our findings suggest that the centrally located hub connections form a core for global brain communication that may have a higher concentration of lesions when disease strikes. It is important to note that hubs may appear more affected in disease due to their higher topological value (larger nodal degree), which is possibly when diseases become symptomatic [18] and more easily detectable with neuroimaging approaches. In bvFTD especially – we found a large loss in connections among central regions of the brain (i.e, superior frontal) that eventually may turn hub regions into non-hub regions. Meanwhile, in EOAD, although network hubs were affected in their local communication with other regions, their high connectedness was relatively preserved at global level, and the hub regions were not eliminated from the core network, as seen in bvFTD (Fig. 2). Our analyses suggest that in bvFTD, hub vulnerability is characterized by a locally propagating white matter disorder focused on the regions of the frontal cortex, whereas in EOAD, hub vulnerability may be a globally propagating white matter disorder where low-degree nodes are removed from the overall brain network. These connectome alterations may cause the structural and potentially functional damages, most evident in the later stages of the disease.