Standardized beam bouquets for lung IMRT planning

Abstract

The selection of the incident angles of the treatment beams is a critical component of IMRT planning for lung cancer due to significant variations in tumor location, tumor size and patient anatomy. We investigate the feasibility of establishing a small set of standardized beam bouquets for planning. The set of beam bouquets were determined by learning the beam configuration features from 60 clinical lung IMRT plans designed by experienced planners. A k-medoids cluster analysis method was used to classify the beam configurations in the dataset. The appropriate number of clusters was determined by maximizing the value of average silhouette width of the classification. Once the number of clusters had been determined, the beam arrangements in each medoid of the clusters were designated as the standardized beam bouquet for the cluster. This standardized bouquet set was used to re-plan 20 cases randomly selected from the clinical database. The dosimetric quality of the plans using the beam bouquets was evaluated against the corresponding clinical plans by a paired t-test. The classification with 6 clusters has the largest average silhouette width value and hence would best represent the beam bouquet patterns in the dataset. The results shows that plans generated with a small number of standardized bouquets (e.g. 6) have comparable quality to that of clinical plans. These standardized beam configuration bouquets will potentially help improve plan efficiency and facilitate automated planning.

1. Introduction

Intensity modulated radiation therapy (IMRT) has demonstrated evidence as an effective technique for cancer treatment in the thorax with reduced toxicity (Liao et al., 2010; Shirvani et al., 2013; Ji et al., 2014; Harris et al., 2014). Due to variations in tumor location, tumor size and patient anatomy, selection of the incident angles of the treatment beams is a critical component of IMRT planning as it offers another dimension to maximize organ sparing. In clinical practice, beam angles are often selected based on the planner’s experience and adjusted through a trial-and-error process to find an optimal set of beam bouquet.

Approaches to aid the selection of beam angles in IMRT planning have been reported (Das et al., 2003; Wang et al., 2005; Jia et al., 2011; Zhang et al., 2013; Pugachev et al., 2001; Li et al., 2004; Zhang et al., 2011; Breedveld et al., 2012). The beam angle optimization in IMRT planning is a large scale combinatorial optimization problem due to the large search space of possible beam angle combinations and the coupling of beam orientation optimization and the beam intensity optimization for each beam. In order to find the optimized beam angles within a clinically practical timeframe, these studies utilized a number of global optimization methods with consideration of time efficiency, including simulated annealing (Pugachev et al., 2001), the genetic algorithm (Li et al., 2004), sparse optimization (Jia et al., 2011) and nested partition method (Zhang et al., 2013). However, a significant amount of time is still required to perform the iterative beam angle optimization process using these methods. For example, two to a few hours of planning time for head-and-neck plans using un-optimized computing architectures has been reported (Zhang et al., 2013; Jia et al., 2011).

Other studies approximated the combinatorial beam angle optimization problem by sequentially eliminating single candidate beam directions from the treatment plan (Zhang et al., 2011) or by adding one to the treatment plan (Breedveld et al., 2012) in an iterative procedure. Zhang et al. (Zhang et al., 2011) developed an automatic beam angle elimination method in an automatic lung IMRT planning process. In this method, the frequency distributions of the beam angles used for three major tumor locations (left, right and middle) are extracted from a set of prior plans. The 19 most frequently used beam angels are selected as initial angles for each tumor location. During beam intensity optimization, these beams are eliminated sequentially if it does not reduce the plan quality. In Breedveld et al. (Breedveld et al., 2012), starting from an empty plan with no beams selected, each not yet selected candidate beam direction is temporarily added to the plan during each iteration and the beam intensity optimization problem is solved. The process is stopped if adding more beams no longer improves plan quality.

Several studies have developed population-based beam bouquets (i.e., entire beam configuration settings) for certain treatment sites (Schreibmann and Xing, 2004; Abraham et al., 2013). In the study by Schreibmann et al., beam bouquets with 3 to 9 beams for prostate IMRT planning were demonstrated by averaging the beam directions for all the patients under study (Schreibmann and Xing, 2004). In another study by Abraham et al., simulated annealing is used to classify a set of clinical liver plans into two beam bouquets, each with five beams (Abraham et al., 2013).

In the present study, we investigate the feasibility of establishing a small set of standardized beam bouquets for lung IMRT planning. The bouquets were determined by learning the patterns from the multi-dimensional beam configuration features of prior clinical plans using a cluster analysis method. The validity of these bouquets was assessed by re-planning 20 clinical cases with these bouquets and evaluating the dosimetry against original clinical plans.

2. Methods and Materials

Sixty (60) lung IMRT plans with prescription doses ranging from 45 Gy to 70 Gy were retrospectively studied under an IRB approved research protocol. The plans have six to eleven co-planar beam angles, with an average beam number of eight. The dataset has a wide range of tumor size (from 12 to 4432 cm³, mean 502 cm³) and locations. The tumor locations in the dataset are distributed as follows: 26 cases in the right lung, 23 in the left lungs, 8 in the mediastinums and 3 in the chest walls.

We use an unsupervised cluster analysis method to classify the beam angle features of the training data to realize a set of standardized beam bouquets. The method involves three major steps: 1) defining a dissimilarity measure between two beam bouquets, 2) determining a suitable number of clusters and classifying the beam angle settings using the k-medoids classification algorithm and finally, 3) establishing the standardized beam bouquets from the resulting clusters.

2.1 Defining the dissimilarity measure between two beam bouquets

First, we define a dissimilarity measure between two beam bouquets. The dissimilarity measure is computed as the sum of angle separations between each pair of corresponding beams in the two bouquets. It takes into account the permutation of beams within each bouquet when comparing two beams. Specifically, a distance is first defined between two angles a and b,

$$\delta (a,b)={min}_{k\in Z}\mid a-b+360k\mid ,$$

where k can take any value in the integer set Z and the 360k term accounts for the 360 degree modulo in the angle space. Then, the dissimilarity measure between two bouquets with the same number of beams x₁ = (x₁¹, x₂¹, ···, x_n¹) and x₂ = (x₁², x₂², ···, x_n²) is defined as (Abraham et al., 2013):

$$d^1(x_1,x_2)={min}_{\sigma \in \pi }{\sum }_{l=1}^n\delta (x_{\sigma (l)}^1,x_l^2),$$

where σ is any permutation π of the beam orders. In our dataset, the number of beams used in a plan ranges from 6 to 11, thus it is necessary to classify beam angle settings with different number of beams, by defining the dissimilarity measure between bouquets with different number of beams. If two bouquets x₁ and x₂ have different numbers of beams n₁ and n₂ and assume n₁> n₂ without losing generality, we define the dissimilarity as the sum of two terms:

$$d(x_1,x_2)={min}_{x_1^{\prime }\subseteq x_1}{d}^1(x_1^{\prime },x_2)+{min}_{x_2^{\prime }\subseteq x_2}{d}^1(x_1\backslash x_1^{\prime },x_2^{\prime }),$$

where $x_1^{\prime }$ is a subset of x₁ which has the same number of beams as x₂ and $x_2^{\prime }$ is a subset of x₂ with beam number n₁− n₂. The first term compares n₂ beams in both x₁ and x₁ to calculate the distance, while the second term compares the remaining n₁− n₂ beams in x₁ with x₂. This step ensures that every beam in the plan is taken into account when calculating the dissimilarity between two bouquets with different number of beams.

The dissimilarity needs to be evaluated between each of the two beam bouquets in the training dataset. The calculation of the dissimilarity involves the permutation of all beam angles in one configuration, which is equivalent to solving a Linear Assignment Problem (LAP). A fast algorithm for LAP, the Jonker-Volgenant Algorithm is used in this step to save the computation time (Jonker and Volgenant, 1987).

2.2 Establishing the standardized beam bouquets

After the dissimilarity (or distance) is calculated between each pair of the beam bouquets, a k-medoids method is used to sort the beam angle configurations into clusters (Kaufman and Rousseeuw, 2009). A medoid is defined as the object in a cluster, with the average distance to all the other objects in the same cluster (within-cluster distance) being the minimal. Thus the medoid of a cluster is the most representative beam angle configuration of all cases within the cluster. The set of all medoids characterizes the major types of beam angle settings frequently used in clinical lung IMRT plans and they are designated as the standardized beam bouquets. The medoid case that corresponds to a standardized beam bouquet is designated as the reference case of this bouquet.

In the k-medoids method, the final classification result is dependent on the selection of k objects as the initial medoids to start the classification iteration. To avoid the iteration from being trapped in a local minimum, the classification procedure is repeated multiple times, beginning with a different set of randomly selected initial medoids at each time, to find the final medoids with the lowest sum of within-cluster distance.

A class solution needs to include sufficient number of beam bouquets in order to cover a wide variety of clinical cases with minimal error. On the other hand, the number of bouquets should not be too large so that the most suitable bouquet can be selected quickly and it is representative of certain clinical case characteristics. We investigate the appropriate number of beam bouquets by generating classifications with 3 to 8 clusters and calculating the average silhouette width s̄ for each classification. In general, a higher average silhouette width value indicates better overall cluster separation in the classification (Kaufman and Rousseeuw, 2009).

The average silhouette width s̄ is the average of the silhouette index s(i) over all the data points in the dataset. The silhouette index measures how close each point in one cluster is to the data points in the neighboring clusters. For a data point i in cluster A, let a(i) be the average distance of i to all other points in cluster A, d(i, C) be the average distance of i to all the data points in another cluster C. the silhouette index is defined as:

$$s(i)=1-\frac{a(i)}{\underset{C\ne A}{min}d(i,C)}$$

The silhouette index s(i) has a numerical value from +1 to −1. Large positive value indicates the point in one cluster is far from neighboring clusters, while negative value indicates the point may be assigned to a wrong cluster. A silhouette plot can be used to visualize how well separated the resulting clusters are. It plots the silhouette index s(i) for each data point as a horizontal bar. A wider silhouette plot indicates larger s(i) values.

2.3 Validating the standardized beam bouquets with clinical cases

20 additional lung cancer cases randomly selected from the clinical dataset were re-planned to assess the validity of using the standardized beam bouquets. For each case, a planner experienced in routine clinical lung IMRT planning manually matched a standardized beam bouquet to the patient anatomy based on his/her judgment of the similarity between the tumor location and patient anatomical features of the case and those of the reference cases. The planner had no knowledge of (i.e., was blinded to) the beam configurations used in the original clinical plans. After the beam bouquet was selected, inverse planning/optimization was performed using the same dose objectives as in the clinical plans.

In some cases, the PTV is large or consists of several sub-volumes which are located at different parts of the lung. A “blocking field” method was used to manually block part of the field (i.e., only part of PTV is exposed) by adjusting collimator positions in the beam’s-eye-view. This process mimics the routine clinical practice to spare critical organs such as heart in situations when tumor location changes in cranial-caudal direction. However, no adjustment to the beam angles was made once they had been selected from the standardized bouquets. The quality of the plans generated using the standard beam bouquets is evaluated by comparing the dosimetric parameters and DVHs of the bouquet-based plans with those of the original clinical plans. Paired t-tests were performed, with significance threshold set at 0.05.

To further evaluate the effect of the number of beam bouquets (i.e. the value of k) on plan quality, the 20 test cases were re-planned again using different numbers of bouquet options. The dosimetric quality of these plans was compared with those plans generated with the set of bouquets determined in the last section.

3. Results

3.1 Establishing the standardized beam bouquets

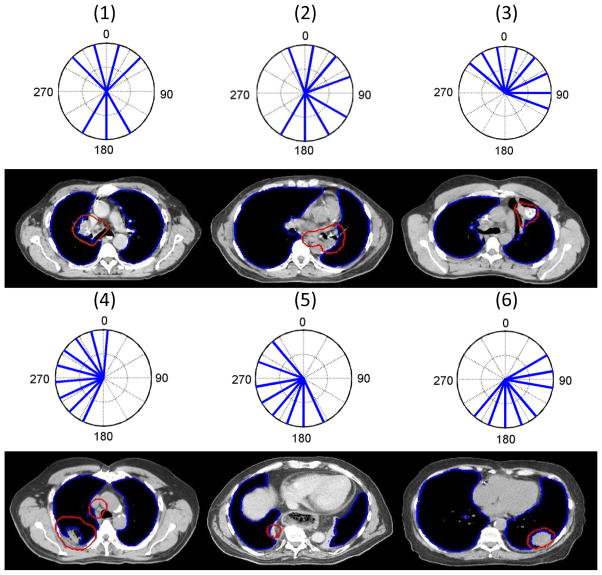
The beam settings in the training dataset were classified into 3 to 8 clusters by the k-medoids algorithm. The average silhouette width s̄ for each classification result is plotted against the number of clusters in Fig. 1(a). As shown in this figure, the classification with 6 clusters has the largest average silhouette width value of 0.39, which suggests that 6 bouquets best represent the beam configuration patterns in the dataset. The silhouette plot with 6 clusters is shown in Fig. 1(b). The all positive silhouette index values indicate that the beam configurations align well within their assigned clusters. The beam bouquets corresponding to the medoids of the 6 clusters are shown in Fig. 2. The number of beams in these bouquets ranges from 7 to 9, which reflects the number of beams used in the reference clinical plans. The representative axial CT image slices of these reference plans are also shown under each medoid in Fig. 2. As shown, these beam configurations reflect the gross anatomical and tumor location characteristics. For example, bouquet #1 and #2 consist of two groups of beams coming mostly from the anterior and posterior directions, corresponding to cases in which the tumors are mainly in the middle of the lungs, while the other bouquets consist of beams mainly from one side of the body aiming to minimize the contra-lateral lung dose. The beam arrangements for the left and right side tumors are not symmetric because of the need to spare the heart, as seen in Fig. 2. The relative position of the heart to the body and lung is not symmetric and more on the left side of the body. Hence, the left side bouquet tries to avoid the most anterior angle and to compensate that with additional posterior oblique angles.

Figure 1.

(a) The average silhouette width for the classifications with each given number of clusters. (b) The silhouette plot for the classifications with 6 clusters. Each horizontal bar indicates the silhouette index for an object, which is grouped according to its cluster assignment. The width of the bar represents the silhouette index value. The vertical axis numbers indicate the indices of the clusters.

Figure 2.

The 6 beam bouquets are shown in polar coordinates using IEC beam angle convention at the first and third rows. The solid radial lines indicate the beam directions. The number inside the parenthesis on top of each bouquet labels the ID of the bouquet. The representative axial CT image slices of the reference cases corresponding to the medoids of the 6 clusters are shown under each medoid at the second and fourth rows. The PTV is denoted by the red contours and the lung by the blue contours.

3.2 Lung IMRT planning using the standardized beam bouquets

The 20 validation cases were re-planned utilizing the standardized beam bouquets. The planner selected a bouquet for each case (with the tally listed in Table 1) by matching the reference cases’ tumor location and patient anatomical characteristics with those of the validation case. On average, the whole process of beam bouquet selection and plan optimization utilizing the standard beam bouquets took about 30 minutes for one case, during which the beam bouquet selection took about 2–3 minutes and optimization was run without adjusting the beam angles.

Table 1.

The IDs of the beam configuration bouquets which were chosen by the planner to re-plan the 20 validation cases.

Case ID	Bouquet ID	Case ID	Bouquet ID
1	5	11	2
2	1	12	2
3	3	13	5
4	6	14	1
5	3	15	4
6	1	16	1
7	1	17	3
8	2	18	1
9	5	19	1
10	2	20	1

In current clinical practice, an experienced planner needs to spend typically between one to a few hours to plan a lung IMRT case depending on the complexity of the case. This includes the time for initial beam bouquet design when the beams are manually selected, and subsequent adjustments of these angles after the planner reviews the dose distribution results from the optimization. The overall planning time is longer, due to the trial-and-error methodology of deciding between beam angle adjustment and optimization objective adjustment to further improve the dose distribution.

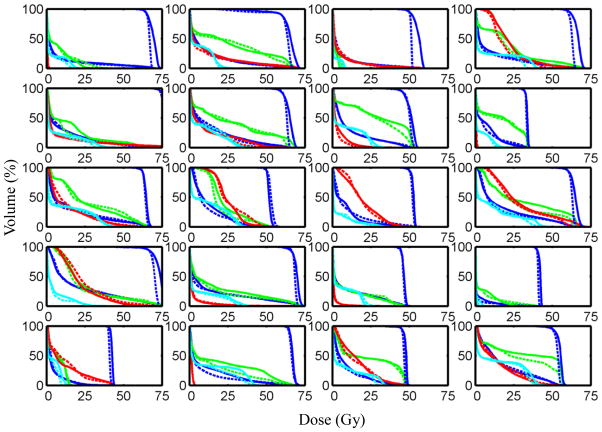
In three of these plans: #11, #12 and #13, the jaws for some beams were adjusted to block part of the field. They were used mainly to reduce the dose to the heart when the beam directly passing through it. The DVHs for the PTV and the OARs in the standardized bouquet based plans and those in the clinical plans are plotted in Fig. 3, while the mean DVHs of all the validation cases are shown in Fig. 4. Example dose distributions in both bouquet-based and original clinical plans for case #12 are shown in Fig. 5. As is shown, the 100% isodose line in the bouquet-based plan appears to better conform to the PTV than the clinical plan on the axial CT slice. The lung in the bouquet-based plan appears to have better dose sparing than the clinical plan on the coronal slice, and vice versa in the sagittal slice. The overall dose sparing for the lung is comparable between the two plans, as shown by the DVH plots (Fig. 3).

Figure 3.

DVHs of the lung (blue curves), esophagus (green curves), heart (red curves) and spinal cord (cyan curves) in the plans which used the beam bouquet bouquets are compared with those in the clinical plans. The clinical plans are represented by the solid curves and the plans using bouquets by the dashed curves. The PTV DVHs are represented by the blue curves on the high dose end of the plots. The panels are ordered sequentially top-down and left-to-right according to the case IDs.

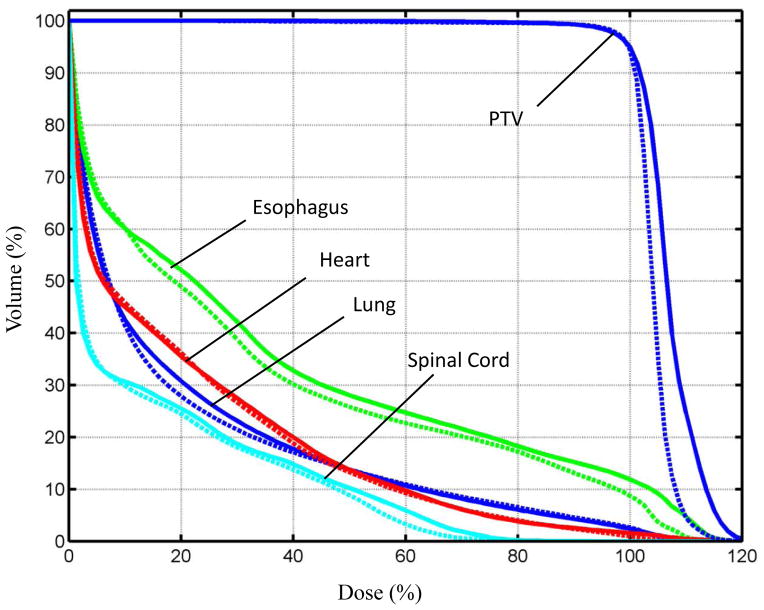
Figure 4.

The means of the DVHs for the PTV and OARs over all the validation cases. The clinical plans are represented by the solid curves and the plans using bouquets by the dashed curves.

Figure 5.

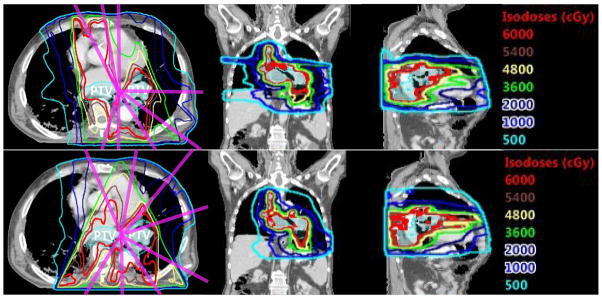
The isodose lines in case #12 are shown on the representative axial, coronal and sagittal CT image slices. The magenta lines indicate beam directions. Top row: clinical plan, bottom row: plan using beam angle bouquet. The Prescription dose to the PTV is 60 Gy.

Table 2 lists the mean and standard deviations of the dosimetric parameters in the bouquet-based and the clinical plans, as well as the paired t-test values. The lung V_10Gy, the esophagus mean dose, cord D_2% and PTV dose homogeneity defined as D_2%–D_99% are statistically better in bouquet-based plans (p-value<0.05), but the improvements (<5%) were small and may not be clinically significant. Other dosimetric parameters are not statistically different.

Table 2.

The mean and standard deviations (S.D.) of the dosimetric parameters in plans using 6 beam bouquets and those in the clinical plans. They are compared by paired t-tests.

OAR/PTV	Parameter	Plans using bouquets Mean ± S.D	Clinical plans Mean ± S.D	p-value
Lung	V10Gy (% OAR volume)	29.1±11.7	32±12.6	0.01
	V20Gy (% OAR volume)	18.3±8.1	18.9±8.7	0.44
	Mean dose (% Dx)	18.8±7.0	19.2±7.0	0.28
Esophagus	Mean dose (% Dx)	32.0±16.3	34.4±17.9	0.01
Heart	V60Gy(% OAR volume)	0.6±1.1	1.2±2.7	0.39
	Mean Dose (% Dx)	19.2±16.5	19.4±16.6	0.74
Spinal Cord	D2% (%Dx)	47.7±18.8	52.0±20.3	0.01
PTV	D2%–D99% (% Dx)	17.1±15.4	20.7±12.2	0.03

Abbreviations: OAR: organ at risk, PTV: planning target volume, Dx: prescription dose, S.D.: standard deviation, V_xGy: portion of OAR volume irradiated by dose higher than x Gy, D_x%: maximum dose covering at least x% of OAR volume.

3.3 Studying the effect of the number of standardized beam bouquets

In order to evaluate whether more standardized beam bouquets would further improve planning and fewer would deteriorate the plan quality, beam bouquets for the 5-bouquet and 7-bouquet options were determined by the classification algorithm using the number of clusters as 5 and 7, respectively. The results showed remarkable stability in the final classification. Careful inspection of the resulting medoids revealed that the only difference between the 6 bouquet and 7 bouquet options is the addition of one more beam bouquet choice in the 7 bouquet option, while the six other bouquet choices are identical. Similarly, the only change in the 5 bouquet option is that there is one beam bouquet choice that is eliminated from the 6 bouquets.

The same 20 validation cases were planned again using 5 and 7 standardized beam bouquets. Among all 20 cases, only in 3 cases (#4, #16, #17) different beam bouquets were chosen by the planner when the bouquet options were switched from 6- to 5-bouquet and from 6- to 7-bouquet. The dosimetric parameters in these cases are listed in Table 3. As shown, when the number of bouquets is changed from 7 to 6, there is no significant change in the dosimetric parameters. When the number of bouquets is further decreased from 6 to 5, the lung V_5Gy and the mean heart dose in case #4 are increased significantly.

Table 3.

Comparison of the dosimetric parameters in the plans which used beam configurations chosen from 5-, 6- and 7-bouquet options. The cases listed in the table are those for which different beam configurations were chosen when switching between different options.

OAR/PTV	Lung				Esophagus			Heart		Cord	PTV
Parameter	V5Gy	V10Gy	V20Gy	Dmean	V20Gy	V60Gy	Dmean	V60Gy	Dmean	D2%	D2% –D99%
Case #16
7 Bouquet	7.3	4.9	2.6	3.9	9.3	0.0	11.2	0.0	0.0	12.1	5.3
6 Bouquet	6.7	4.9	3.5	4.1	8.2	0.0	10.8	0.0	0.0	11.8	5.5
Case #17
7 Bouquet	29.2	16.4	6.7	13.1	2.4	0.0	20.2	0.0	29.1	31.9	8.8
6 Bouquet	24.0	12.1	4.4	11.2	0.0	0.0	17.9	0.0	30.0	23.7	7.4
Case#4
6 Bouquet	32.0	24.5	17.4	15.6	37.4	3.0	29.3	0.0	31.0	54.9	9.9
5 Bouquet	37.3	25.3	16.2	15.8	40.5	2.8	29.6	0.0	35.3	57.7	10.5

Abbreviations: OAR: organ at risk, PTV: planning target volume, V_xGy: portion of OAR volume irradiated by dose higher than x Gy (Unit: percentage of OAR volume), D_x%: maximum dose covering at least x% of OAR volume (Unit: percentage of prescription dose). D_mean: mean dose (Unit: percentage of prescription dose). 5,6 or 7 Bouquet: plans using beam configurations chosen from 5, 6 or 7 bouquet options, respectively.

4. Discussion

In this study, six bouquets were determined as the standardized beam bouquets to characterize the major types of beam angle settings used in clinical plans based on the average silhouette value. Validation test was performed by re-planning 20 clinical cases with these bouquets. The effect of the number of beam bouquets on plan quality were further evaluated by planning the 20 cases using 5 and 7 bouquets. It was found that the quality of the plans was not affected when the number of bouquets changed from 7 to 6, while the OARs would receive significantly higher dose in one of the test plan if the bouquet number was further reduced to 5. This exercise confirms that for the limited size of the dataset, the six beam angle bouquet option provides a good balance of plan quality and number of bouquets in lung IMRT planning. However, since the 7 bouquet option only adds one bouquet while keeping the other 6 bouquets identical to the 6 bouquet option, it will be a simple extension if additional clinical case complexity warrants more bouquet options in the future.

The number of beams used in the standardized bouquets ranges from 7 to 9. It reflects the variation of the number of treatment beams used in the clinical plans. It may be desirable to further standardize these bouquets by adopting equal number of beams, e.g. 7 beams in each bouquet. One approach to standardize these bouquets is to combine neighboring beams in the 8-beam and 9-beam plans. Further study is needed to determine the best approach for such standardization.

The beam bouquets reported in this study contain only coplanar angles as only the clinical plans using coplanar beam angles were included in the training dataset. It has been shown that non-coplanar beam angles can further improve the quality of the IMRT and SBRT plans for lung cancer treatment (Zhang et al., 2011; Dong et al., 2013). In clinical practice, because of the additional treatment setup time associated with the couch rotation and the risk of gantry-couch collision, non-coplanar beam angles are used less frequently and are often reserved for cases with complicated tumor geometries and patient anatomy, e.g., large centrally located tumors. Within the 72 lung IMRT cases we have studied, only 12 plans have used non-coplanar angles. Most of these non-coplanar beam configurations were chosen to achieve better sparing for the heart. Our future study will extend the standardized beam configuration bouquets to include non-coplanar beams.

In this study, although the beam bouquets were learned from a set of clinical plans from a single institution, the cases in the dataset cover a wide range of tumor location, tumor volume and patient anatomy. These plans were generated by multiple experienced dosimetrists and physicists for clinical treatment in our institution and have met all the physician’s dose constraint prescriptions. Hence the dataset represents the general clinical practice and knowledge of beam selection in lung IMRT planning. These bouquets represent general clinical beam angle preferences and the standardization may help improve the efficiency and quality consistency for lung IMRT planning. Using the 20 clinical cases, we showed that the plans generated with these bouquets have dosimetric qualities comparable to their manually generated clinical counterparts.

In order to simplify the plan quality comparison in this study, we didn’t allow any adjustment to the beam angles in the validation plans. However in clinical applications, minor adjustments to the beam angles around the bouquet directions can be made in order to further improve the dosimetry of the plan, thus the bouquets can be used as a near optimal starting point and can be fine-tuned with other local beam angle optimization methods (Craft, 2007). Further, the beam bouquet for a validation case is matched manually by comparing the anatomical features of the validation case with those of the reference cases. The next step in our study is to develop a method to automatically select the best bouquet from the standardized beam bouquets based on patient anatomical characteristics. Construction of these standardized bouquets is the first step toward the development of such method. A computerized algorithm can be developed to automatically assign beam bouquets based on optimal matching between cluster features and the patient anatomical features.

After the beam configurations are determined, the fluence map or MLC segments for each individual beam need to be optimized in the IMRT planning process based on a set of dose coverage and dose sparing objectives. Methods to automatically determine patient specific dose objectives in IMRT plans have been reported (Yuan et al., 2012; Appenzoller et al., 2012). A fully automatic planning method for lung IMRT plans can be developed by combining the automatic beam angle selection method with the automatic determination of dose objectives.

5. Conclusion

We have developed a novel approach to determining a standardized set of beam bouquets for lung IMRT planning. We showed that plans generated with these standardized beam bouquets have comparable quality to that of clinical plans based on conventional beam design methods. The use of a small number of standardized beam bouquets will potentially help improve planning efficiency and facilitate automated planning.