Magnetite Crystal Orientation in Magnetosome Chains

Abstract

One-dimensional magnetic nanostructures have magnetic properties superior to non-organized materials due to strong uniaxial shape anisotropy. Magnetosome chains in magnetotactic bacteria represent a biological paradigm of such magnet, where magnetite crystals synthesized in organelles called magnetosomes are arranged into linear chains. Two-dimensional synchrotron X-ray diffraction (XRD) is applied to cells of magnetotactic bacteria that are pre-aligned with a magnetic field to determine the crystallographic orientation of magnetosomes relative to the chain axis. The obtained pole figure patterns reveal a [111] fiber texture along the chain direction for magnetospirilla strains MSR-1 and AMB-1, whereas a [100] fiber texture is measured for Desulfovibrio magneticus strain RS-1. The [100] axis appears energetically unfavorable because it represents a magnetic hard axis in magnetite, but can be turned into an effective easy axis by particle elongation along [100] for aspect ratios higher than 1.25, consistent with aspect ratios in RS-1 magnetosomes determined earlier. The pronounced fiber textures can be explained either by a strain-specific biological control on crystal orientation at the chain level or by physical alignment effects due to intra-chain magnetic interactions. In this case, biological control of the axis of elongation would be sufficient to influence the crystallographic texture of the magnetosome chain.

1. Introduction

Due their unique magnetic properties, one-dimensional (1D) magnetic nanomaterials have recently become a focus of several research groups.[1] The key advantage of 1D structures over 3D structures is that they have maximum uniaxial anisotropy, which forces the magnetization to lie along the axis of the structure, pointing either up or down. Such a strict two-state system is interesting for a range of applications, for example, in magnetic memory devices.[2] From the point of view of material synthesis, it is noteworthy that the selective magnetic properties of 1D-nanomagnets also convey preferential interactions that promote further structural assembly and organization.[3]

The best example of a natural functional 1D nanostructured-magnet is found in the form of magnetosome chains in magnetotactic bacteria (MTB).[4,5] These organisms form magnetic crystals in intracellular organelles called magnetosomes. The magnetosomes comprise a ferrimagnetic crystal, typically magnetite, surrounded by lipid bilayer membrane. Evolutionary optimization is apparent at various hierarchical levels: i) The magnetosome crystals have the precise magnetite structure to obtain enhanced magnetic properties compared to other magnetic iron oxides.[6] ii) The crystal sizes (typically 40–100 nm) are just right to promote the magnetic single-domain state, which maximizes the magnetization per particle.[7] iii) The magnetosomes are arranged into chains such that their dipole moments sum up coherently to result in a magnetic moment strong enough to align the cell with the geomagnetic field.[7] The chain assembly process involves a combination of physical (magnetic)[8,9] and molecular (genetic)[10–12] processes, where the latter have a major role as recently shown in silico.[13] The same is true during cell division, where bacterial cytoskeletal filaments shuttle the chain to the division site and segregate the chain halves to the daughter cells.[14]

It is typically assumed that a dedicated trait of MTB is strict biological control on the aspect ratio and orientation of the magnetosome crystals such that the axis of elongation is aligned with the chain axis, and further, that they both correspond to a magnetic easy axis of magnetization (<111> in magnetite). A few transmission electron microscopy (TEM)[15–17] or electron holographic studies[18–20] have confirmed combined <111> elongation and chain orientation in those types of MTB that produce magnetite magnetosomes of symmetric morphology, such as MC-1, MV-1, and the magnetospirilla strains MS-1, AMB-1. The <111> trait as inferred from single-cell observations has been statistically confirmed by means of ferromagnetic resonance (FMR) measurements on bulk samples of MSR-1 and MV-1, where FMR spectra simulated for <111> oriented chains were in good, though not perfect agreement with the experimental spectra,[21,22] which suggests some degree of disorder and inhomogeneity. More surprisingly, however, elongations along various other crystallographic axes have been observed in MTB with magnetosomes of irregular morphology.[23–27] In these cases, the chain architecture often is less regular, which makes it difficult, if not impossible to determine on the single cell level the typical relationship between crystal axes and chain structure. It is therefore desirable to have an experimental method to quantitatively determine the crystallographic orientation of magnetosome chains with high statistical significance.

X-ray diffraction (XRD) is a powerful technique to study structure and texture of polycrystalline materials. In transmission geometry, a monochromatic light (with wavelength λ) hits the polycrystalline sample and the scattered radiation will form Debye rings on a 2-dimensional detector plate according to Bragg's law. In case the distribution of crystallographic orientations is not random but textured, the Debye rings will show azimuthal intensity variations. One type of texture is the so-called fiber texture,[28] where the crystals tend to align one crystallographic axis with a specific direction, while there is no preferred orientation in the plane perpendicular to this “fiber” direction. This technique is thus well-suited to study the anisotropic distribution of crystal axes.

In this work, we performed XRD on pre-aligned magnetotactic bacteria from different strains that are established models for magnetite biomineralization and for which the crystallographic orientation of the chain axis might differ. We show that a strain specific superstructure can indeed be observed, where the magnetosomes are consistently aligned along a <111> crystallographic axis in magnetospirilla, but along a <100> axis in Desulfovibrio magneticus strain RS-1.

2. Results

The magnetotactic bacteria were deposited either on a transmission electron microscoy (TEM) grid for imaging or on a Kapton foil for XRD analysis and dried in the presence of a magnetic field of 100 mT. TEM images (Figure 1) show that the cell bodies are oriented such that their magnetosome chains are aligned with the externally applied magnetic field, resulting in samples in which all magnetosome chains were close to parallel to each other.

Figure 1.

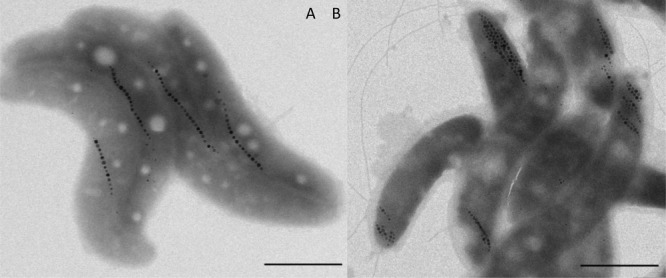
TEM images of wildtype (A) and ΔmamJ mutant (B) cells of MSR-1 dried in the presence of a magnetic field, scale bars represent 1 μm.

Aligned bacteria of different strains (the wildtype and a ΔmamJ mutant of Magnetospirillum gryphiswaldense MSR-1, Magnetospirillum magneticum AMB-1, and Desulfovibrio magneticus RS-1) and isolated magnetosomes of the MSR-1 strain were investigated with high-resolution X-ray diffraction. The diffraction pattern of MSR-1 is shown in Supplementary Figure 1. As expected, the positions of the diffraction rings, displayed as peaks in the diffractogram (azimuthally integrated I(Q), Q = 4π sin (θ)/λ, where 2θ corresponds to the scattering angle and λ is the wavelength of the beam), can be indexed to magnetite (Figure 2). Importantly, the Debye rings show systematic variations in their azimuthal intensity distribution (AID), indicating a non-random orientation of the crystals within the sample.

Figure 2.

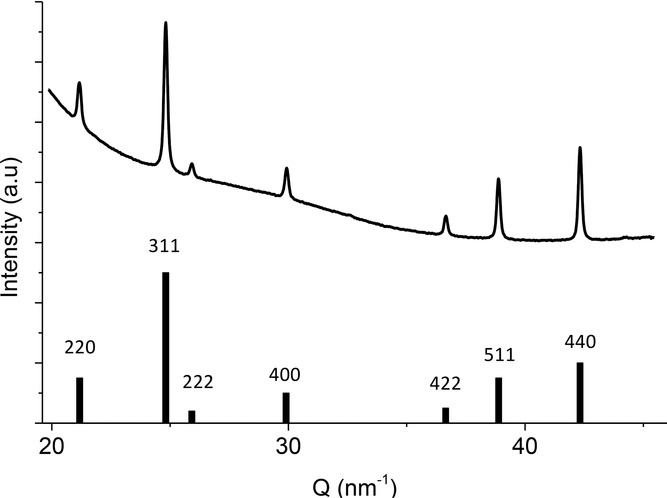
One dimensional diffractogram I(Q) of wildtype MSR-1 cells, obtained by azimuthal integration, compared with the reference pattern of magnetite.

Upon projecting the 2D XRD pattern onto a Cartesian grid (azimuthal angle γ vs Q), the diffraction rings become straight lines and the AID along the rings can be recognized more easily (Figure 3). The AID I_hkl(γ) of the diffraction ring for a certain set of planes {hkl} were obtained by radial integration of the 2D-pattern and a localized background subtraction (see SI). The AID I_hkl(γ) of four Debye rings are shown in Figure 3B. I_hkl(γ) represents the normalized directional distributions of the hkl lattice in the sample. The symmetry of the pattern can be observed in the intensity distribution of the different planes. All the AID display line (mirror) symmetry at the angles indicated by the dashed lines at γ = 2°, 92°, 182° and 272°. In the 2D-XRD pattern, these angles correspond to the plane parallel to the direction of bacterial alignment (92° and 272°, blue line in Figure 3) and to the plane perpendi­cular to it (2° to 182°).

Figure 3.

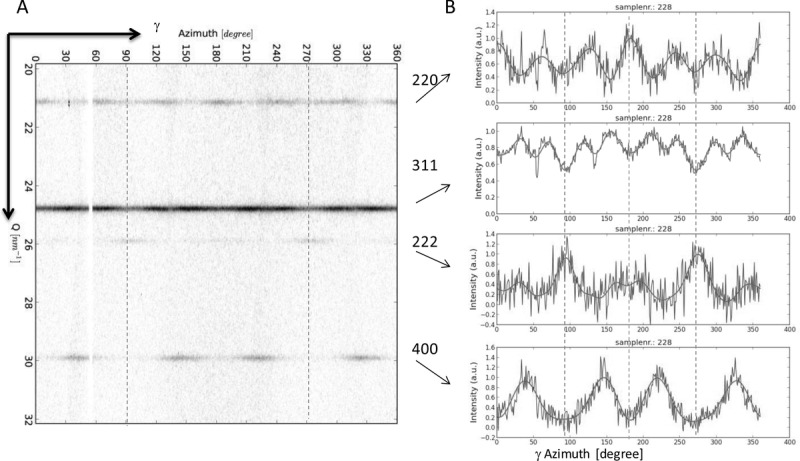
(A) Background subtracted Cartesian plot of Q vs γ of the inner rings of the XRD pattern; (B) normalized azimuthal intensity variations I_hkl(γ) for different rings, dashed lines indicate symmetry angles, blue dashed lines are along the direction of the bacteria alignment and therefore the fiber axis.

A further analysis of the AID reveals the type of fiber texture: The crystallographic direction parallel to the fiber axis can be determined from the I_hkl(γ) plots. The fact that the intensity maxima in the I₂₂₂(γ) are parallel to the fiber axis indicates that the texture is a [111] fiber texture. To confirm this, we determined the angular difference between the fiber axis and the maxima in the I_hkl(γ). For example, the I₄₀₀(γ) shows intensity maxima at about γ_max = 38° and 146°. This leads to an angular difference of α = |γ_max − ψ| ≈ 54° between [400] and the fiber axis at ψ = 92°. This angle matches with the angle between the [100] and [111] directions in the cubic crystal. The angle between two crystallographic directions [uvw] and [hkl] can be calculated by 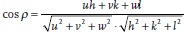[38] and leads in this particular case to 54.74°. The positions of the maxima in the I_hkl(γ) for the other lattice planes also correspond well with their expected positions for a [111] fiber texture (see SI for value of expected positions of the maxima).

As a measure for the dispersion in the fiber texture, we determined the half width at half maximum (HWHM) of the peaks in the AID. The HWHM is in the range of 15°, compared to a full width of 0.15° in the radial direction, the latter reflecting instrumental broadening (resulting from beam divergence and detector point spread) and grain-size related broadening (in nanoparticles, crystallite size correlates inversely with peak width). Since the effects of instrumental and grain size related broadening are equal in azimuthal and radial direction, the observed HWHM in azimuthal direction of about 15° reflects deviations from perfect crystal alignment. This deviation has two contributions, one from intra-chain scatter of [111] orientations, the other from cell-to-cell variations in the axial orientation of the magnetosome chains, as can be observed in the TEM image (Figure 1).

Not surprisingly, a [111] fibre texture with similar HWHM was also observed for cells of the AMB-1 strain (Figure 4). This strain, too, forms cubooctahedral magnetosome crystals, albeit with slightly larger elongation than MSR-1 does, and assembles the magnetosome in a similar, although more fragmented chain arrangement. The magnetosome crystals of this strain also assemble with their [111] direction along the chain axis and thus along the bacterial pole to pole direction.

Figure 4.

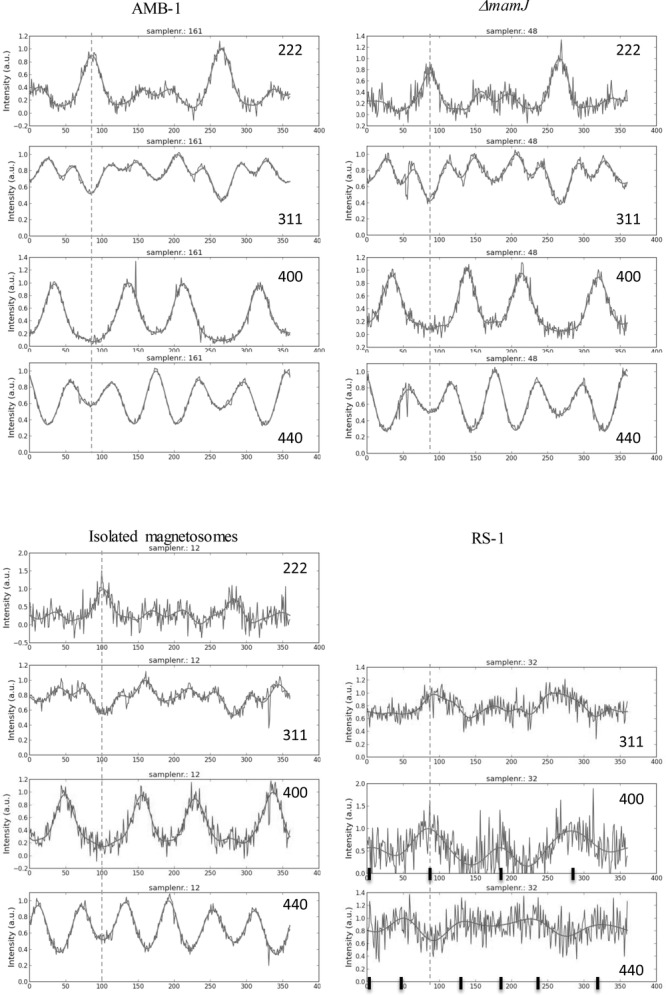
AID of different Debye rings of cells of AMB-1, a ΔmamJ mutant of MSR-1, RS-1 cells and isolated magnetosomes from MSR-1. The direction of the magnetic field applied during the drying process is indicated by dashed lines. In the RS-1 graphs, the black lines indicate expected intensity maxima for a [100] fiber texture (see SI for their calculations).

A [111] fiber texture has also been observed for a mutant of the MSR-1 strain, which lacks the anchor protein MamJ (Figure 4) and displays therefore no linear chain structures but clustered magnetosome arrangements. In a magnetic field, the cell bodies of ΔmamJ mutants are practically not aligned, which is reflected by a strongly reduced C_mag (C_mag = 0.05 for ΔmamJ and C_mag = 0.64 for wildtype). C_mag primarily measures the ease with which an elongated cell body, ideally with pole-to-pole running magnetosome chain, aligns with the external magnetic field, so that a sample consisting of many aligned cells produces strongly anisotropic light scattering, and therefore a C_mag value close to unity. In mutants where the magnetosome chain is not anchored to the cell body, the chain aligns with the field without co-aligning the cell body, and the resulting C_mag is close to zero. The C_mag therefore does not indicate the level of chain alignment in the mutants, which despite the low C_mag is good, as can be seen on the TEM image (Figure 1). A closer look at the image reveals the effect of the magnetic field on the ΔmamJ mutant: Magnetosome clusters become elongated in the field direction, which supports the concept that magnetosomes within these cells can move freely: the unbound magnetosomes can rearrange into an energetically more favorable disposition that is elongated along the field. Isolated magnetosomes from the MSR-1 strain resulted in the same [111] fiber texture. Clearly, in this case again, the magnetosomes are free to move and to rearrange. In this case, the interaction with the external magnetic field forces them to orient along their [111] easy axis, which results in the observed fiber texture.

The cells of the RS-1 strain, which produce magnetosomes of irregular shape, showed a completely different behavior. To begin with, RS-1 cells produce less magnetosomes so that the magnetic dipole moment per cell is too small for efficient alignment of the cells (C_mag = 0.14). The reduced number of magnetosomes also resulted in a diminished XRD signal intensity of the magnetite. Only three diffraction rings displayed variations in the AID (Figure 4). These AID differ strongly form those observed for the other samples. The higher intensities in the AID of the {400} planes along the direction of the magnetic field and perpendicular to it, as well as the higher intensities in the AID of the {440} planes at angular differences of 45° with respect to the direction of the magnetic field, suggests a [100] orientation of the magnetosomes in RS-1 cells. However, since the AID for {311} has a maximum along the direction of the zero field, too, albeit less pronounced than that for {400}, a [311] fiber orientation needs to be taken in consideration, too. Therefore, we performed pole-figure simulations, which for an assumed HWHM of 25° around the [100] fiber axis resulted in a satisfying fit of all the experimentally observed AIDs for [311], [400], and [440]. In contrast, the simulations for a [311] fiber orientation fail to explain the observed AIDs. Therefore, RS-1 has a [100] fiber axis.

3. Discussion

The observed fiber texture in 2D-XRD measurements originated from millions of magnetosome crystals in oriented bacteria and therefore enables a more generalized statement on the orientation of the magnetosome crystals within MTB than from single-cell analysis in TEM. Also, the 2D-XRD technique allows measurements to be conducted at ambient conditions, which could give access to study crystal orientation in living organisms, and therefore overcome problems due to chain bending artefacts induced by drying effects[39] or due to crystal tilting by the energy from the electron beam. The ferromagnetic resonance (FMR) technique, a statistical method like 2D-XRD on bulk samples, also allows to determine the predominant crystallographic orientation of magnetosomes with respect to the chain axis.[21,22] However, it represents a major challenge to extract the degree of intra-chain orientational disorder from a measured FMR spectrum. Inhomogeneity effects, such as variations in crystal spacing, magnetosome size and shape as well as inhomogeneous stray fields due to sharp crystal truncation faces, make a significant contribution to the observed FMR line broadening. In this respect, magnetic hysteresis curves have the same limitation, and are even further complicated by effects due the thermal fluctuations. Thus, the advantage of 2D-XRD is its insensitivity to both magnetic inhomogeneity and thermofluctuation effects so that HWHM derived from 2D-XRD pole figures reflect solely intra-chain orientational disorder and dispersion of axis orientations in the sample. It may be possible in future FMR studies to separate inhomogeneity effects from disordered crystal alignment by analyzing the angular dependence of the anisotropy field in samples prepared by drying MTB cells in a strong magnetic field. Cells of AMB-1 pre-aligned this way were recently found to display a distinct angular dependency in their hysteresis properties.[17] The standard deviation for the chain orientation angle was determined as 20° from scanning electron micrographs,[17] which is comparable with our HWHM values of 15° determined from 2D-XRD pole figures.

The fibre textures obtained here by 2D-XRD are in good agreement with previous TEM studies, which revealed that the <111> direction of the magnetosome crystals in AMB-1 is mostly parallel to the chain axis,[17,40] while it appears to be the <100> direction in RS-1.[25] We are not aware of similar TEM work on MSR-1, which here was shown to have a <111> fiber texture as well. This confirms the hierarchical optimization principle mentioned earlier, because one of the four intrinsic easy magnetic axes in <111> textured chains is aligned with the uniaxial anisotropy axis imparted by the chain structure. This mutual stabilizing effect is particularly important in MSR-1, which produces relatively small magnetosomes (ca. 40 nm) of isometric shape, which are separated by a nonmagnetic spacer layer that is thick compared to the crystal size. The latter implies a diminished externally imparted uniaxial anisotropy, the former proneness to thermal fluctuation induced magnetic instability. Thermal fluctuation effects still have adverse effects on magnetic hysteresis properties of MSR-1, as can be seen in bulk magnetic measurements on samples of MSR-1 cells with mature chains,[41–43] but the <111> fibre texture at least guarantees a coherent along-axis magnetization in MSR-1 magnetosome chains and therefore effective magnetotaxis behavior.

The RS-1 strain with its [100] fibre texture appears to violate the hierarchical optimization principle, because the <100> axis are magnetic hard axes in magnetite and therefore energetically unfavorable. Yet, in contrast to Magnetospirillum strains, RS-1 produces magnetosomes that in the mature stage are clearly nonequidimensional[32] with an elongation most probably along a <100> axis.[25] The shape anisotropy for an aspect ratio of 1.25 or greater is sufficient to turn the <100> axis of elongation into an effective easy axis and therefore overrides the intrinsic <111> easy axis (see SI for details). Hence an energetically stable chain configuration can be achieved by aligning RS-1 magnetosomes with their <100> elongation axes along the chain axis, as seen in the texture analysis. However, only roughly a third of the analyzed magnetosomes of RS-1[25] have an aspect ratio that exceeds the critical value of 1.25, whereas most magnetosomes have aspect ratios between 1 and 1.25, which implies a continuum of effective easy axis orientations between [111] to [001] (see SI, Figure S5). Indeed, the [100] texture orientation in RS-1 is not so well developed compared to the [111] texture in the magnetospirilla strains (Figure 4). The smaller degree of texture in RS-1 may reflect diminished alignment with the external field, but also an overlay of different crystal orientations due to magnetosomes in different stages of maturity, from isometric <111> oriented crystals in the early stage to mature crystals highly elongated along <100>, with a continuum of hybrid states in between. This is supported by the TEM work of Li et. al.,[27] who described both equidimensional crystals (up to 30 nm edge length) and <100> elongated crystals (up to 160 nm length but only 40 nm in width) in cells of uncultivated strain Myr-1, and divided the crystal formation process in two stages: isotropic growth of the particle, followed by anisotropic growth along the 100 direction.[27] The lower degree of texture observed for RS-1 could therefore be a result of isometric, transitional, and mature crystal morphologies.

It is not known, however, if the fiber texture, whether directed along <111> as in magnetospirilla or <100> as in RS-1, is strictly controlled by a biomineralization template (as it was suggested for an uncultured coccoid MTB,[44] or rather a result of magnetically enforced mechanical rotation of the easy axis into alignment with the chain axis caused by magnetostatic interactions among the crystals in the chain, because a magnetosome that is not oriented with its (effective) easy axis along the chain would represent no stable minimum and therefore would be subject to a torque. Physically enforced easy-axis alignment in the wildtype is consistent with our observation that FWHM values are similar for wild type MSR-1, its ΔmamJ mutant, and even isolated magnetosomes of MSR-1. This agreement in FWHM indicates that the deviation from a perfect crystal alignment with the field does not depend on the spatial configuration of the magnetosomes (chains versus clusters). The fact that non-chain bound magnetosomes aligns with their easy axes along an external magnetic field, as seen in the <111> fiber texture, demonstrates the great potential of physical alignment forces. From an experimental point of view, it may not be simple to distinguish between <111> template-controlled and physically-induced alignment, except perhaps at early growth stages, when magnetosome crystals are too small to strongly interact magnetically with each other. Once the first crystal is mature, however, a newly nucleating magnetosome particle next to it will be subject to magnetic orientation forces, that in silico were shown to promote consistent crystallographic orientation.[8]

RS-1 with its switch from isometric to anisotropic crystal growth appears to be a better candidate to test the physical alignment hypothesis. In a fresh cell culture of RS-1, a good proportion of crystals would be isometric and should then be aligned with one of their [111] axes, and thereby reduce the strength of the [100] fiber texture due to [100] elongated crystals that are already present. Over time, anisotropic growth along one of the <100> axes would rotate the [100] axis of elongation into alignment with the chain axis [100], so that the [100] fiber orientation should become more pronounced with time.

4. Conclusions

We have shown that synchrotron 2-dimensional X-ray diffraction is a powerful tool to study the crystallographic orientation of magnetosomes and the texture of magnetosome chains in magnetotactic bacteria. From our analysis, we can draw three main conclusions on the biological organization of magnetic nanoparticles in 1D. First, when building a nanostructured 1D magnet from a magnetically soft material like magnetite (low magnetocrystalline anisotropy compared to stray field energy), it is not obligatory to align the crystals with their intrinsic easy axis of magnetization (<111> in magnetite) along the chain axis, even though it would represent the optimum for a given particle geometry. A stable 1D magnet can be obtained as well on the basis of elongated crystals (aspect ratio > 1.25) aligned with their elongation axis along the chain axis. This can be seen in RS-1 and other strains that produce magnetosomes with elongations along axes other than <111>, thereby imparting a new effective easy axis on the crystals. In these cases, the crystallographic axis of elongation is species specific, which implies a high level of genetic control on the biomineralization mechanism. This contrasts with the straightforward design principle found in magnetospirilla, in particular with strain MSR-1, where the crystals are nearly isometric, and aligned with one of their intrinsic easy <111> axes. Our results on isolated magnetosomes show that the <111> orientation is the default case for isometric crystals and we conclude that the <111> texture in wildtype cells of MSR-1 may be the result of physical effects (e.g., torques), not of an underlying genetic blueprint.

We suggest that magnetic forces/torques generally have an important role on the chain texture and remove the need for bacteria to actively control the texture. Just by controlling the direction of elongation, they can affect the crystallographic orientation of the magnetosomes with respect to the chain direction. Of course, as opposed to the crystallographic texture of the chain, the very assembly of it requires biological control, as shown by the fact that linear chains are no longer observed in ΔmamJ mutant[11] and by theoretical approaches showing biological determinants at least helped stabilizing the chain.[13]

This can directly be used to draw our last conclusion. Indeed, there are currently debates in the microbiological community about evolution in bacteria in general and in particular about bacterial origin[45] and in the geological community about evolution in rocks.[46] We might in addition introduce a physico-chemical argument for such evolutionary perspective: Since the orientation of magnetosomes observed in the magnetospirilla may not require biological intervention, which in turn is necessary to explain the pattern observed in RS-1, the spirilla strategy certainly is less energy-demanding and would therefore be catalogued as chemically advantageous.

5. Experimental Section

Bacterial Strains and Growth: In this work, different strains of magnetotactic bacteria were studied: Magnetospirillum magneticum ABM-1[29] Magnetospirillum gryphiswaldense MSR-1,[30] a ΔmamJ mutant of MSR-1[11] and Desulfovibrio magneticus RS-1.[31] The RS-1 cells were grown in in rubber sealed culture tubes under anaerobic conditions in RS-1 growth medium.[32] The cells of the other strains were grown under microaerobic conditions in MSR-1 standard medium.[33] The tubes were inoculated with 10% v/v of a preculture and incubated under gentle shaking (100 rpm) at 28 °C for 24 h. A UV-spectrophotometer (UV-1201V, Shimadzu, Kyoto, Japan) was used to determine the growth by measuring the optical density (OD) at 565 nm. The average magnetic orientation of the cells was calculated using the equation 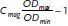The optical density was measured with a bar magnet (of about 50 mT) placed parallel (OD_min) and perpendicular to the beam (OD_max).[34] Isolated magnetosomes were obtained from MSR-1 cells following the procedure described in the literature.[33]

Transmission Electron Microscopy: Bacteria grown in culture medium were washed twice by centrifuging at 6000g for 5 min and resuspending the pellet in water. A small drop was deposited on a Cu grid with an amorphous carbon support film in the presence of a magnetic field of 100 mT parallel to the substrate. The magnetic field was created by a permanent magnet placed below the sample. This way the bacteria aligned with the magnetic field lines, also during drying at room temperature. Transmission electron micrographs were acquired on a Zeiss EM Omega 912 at an acceleration voltage of 120 kV.

X-ray Diffraction: Bacteria were prepared following an already published procedure[6] with additional alignment. Briefly, the cells were washed twice as above. After the third centrifugation, a concentrated bacteria solution was pipetted on a thin Kapton film (Breitlander GmbH, Hamm, Germany) in the presence of a magnetic field of 100 mT generated by a permanent magnet. Transmission high flux X-ray diffraction was performed at the μ-Spot beamline of the synchrotron facility BESSY II, Helmholtz Zentrum Berlin, Germany.[35] The monochromatic X-ray beam had a size of 30 μm and the energy was set up to 15 keV (λ = 0.82656 Å) by a Si (111) monochromator. A MarMosaic 225 detector (Mar USA, Evanston, USA), consisting of nine independent charge-coupled device cameras recorded the diffraction patterns. The detector was oriented with its surface normal parallel to the beam direction behind the sample (transmission geometry). The resolution of the detector was 3072 × 3072 pixels over a diameter of 225 mm. The distance between sample and detector was about 160 nm, which formally corresponds to a scattering event of 2θ ∼ 50° at λ = 0.82656 Å and ensures that the magnetite peaks of interest (220–400, at 2θ ∼ 16−22.7°) can be collected with high intensity (low geometric spread), but still well separated from the directly transmitted beam.

Diffraction patterns from a α-quartz reference sample (NIST standard reference 1878a) were used to determine the sample-detector separation and to correct for the tilt of the detector and beam center calibration. Exposure times were between 120 and 180 s. The pre-oriented cell samples were oriented with their long axis (fiber axis) perpendicular to the beam.

XRD Data Analysis: FIT2D[36] and custom written Python based codes were used for the analysis of the two dimensional XRD patterns. The images were integrated azimuthally in order to simulate a one dimensional diffractogram I(Q), (Intensity versus Q, Q = 4π sin(θ)/λ, where 2θ corresponds to the scattering angle and λ is the wavelength of the beam). Radial integrations were performed to obtain the azimuthal intensity variations (AID, or pole figures) I_hkl(γ) (where γ is azimuthal angle on the detector starting in the horizontal plane (see Supporting Information Figure S2)) along the diffraction ring of a specific set of planes. The background was subtracted locally from the intensity of the diffraction ring I_ring(γ). In particular, the background was linearly interpolated between the Q-values just above and just below the Bragg-peak (see SI). The obtained signal was low-pass filtered for better visualization of the pole figures, and normalized to the maximum intensity. Pole figure simulations were made with the software package ANAELU[37] to model angular diffraction intensity patterns and determine the degree of scatter in the fiber texture.

Supporting Information

Supporting Information is available from the Wiley Online Library or from the author.