Abstract
Purpose
Nicotinamide adenine dinucleotide (NAD), in oxidized (NAD+) or reduced (NADH) form, plays key roles in cellular metabolism. Intracellular NAD+/NADH ratio represents the cellular redox state; however, it is difficult to measure in vivo. We report here a novel in vivo 31P MRS method for noninvasive measurement of intracellular NAD concentrations and NAD+/NADH ratio in the brain.
Methods
It uses a theoretical model to describe the NAD spectral patterns at a given field for quantification. Standard NAD solutions and independent cat brain measurements at 9.4 T and 16.4 T were used to evaluate this method. We also measured T1 values of brain NAD.
Results
Model simulation and studies of solutions and brains indicate that the proposed method can quantify submillimolar NAD concentrations with reasonable accuracy if adequate 31P MRS signal-to-noise ratio and linewidth were obtained. The NAD concentrations and NAD+/NADH ratio of cat brains measured at 16.4 T and 9.4 T were consistent despite the significantly different T1 values and NAD spectra patterns at two fields.
Conclusion
This newly established 31P MRS method makes it possible for the first time to noninvasively study the intracellular redox state and its roles in brain functions and diseases, and it can potentially be applied to other organs.
Keywords: in vivo 31P MRS, intracellular redox state, NAD+ and NADH, brain
Nicotinamide adenine dinucleotide (NAD), as an important coenzyme mediating cytosolic and mitochondrial biochemical processes, plays a key role in energy metabolism in all living cells (1,2). The conversion between its reduced form (NADH) and oxidized form (NAD+) occurs in all redox reactions catalyzed by NADH-dependent dehydrogenase, including the major metabolic pathways of glycolysis, tricarboxylic acid cycle, and electron transport chain. Besides regulating bioenergetics and maintaining mitochondrial function, accumulating evidence has suggested that NAD+ and NADH are also involved in other biological activities (3,4) such as calcium homeostasis (5,6), antioxidation and oxidative stress, gene expression, immunological functions, aging (7), and cell death (2,8). Several redox pairs, i.e., NAD+ and NADH, the oxidized and reduced forms of nicotinamide adenine dinucleotide phosphate (NADP) and those of glutathione, are involved in establishing the intracellular redox state. However, the significantly higher intracellular level of NAD under physiological conditions (4,9) makes NAD the dominant component in regulating intracellular redox state. Therefore, the concentration ratio of NAD+ and NADH (defined as RX = [NAD+]/[NADH]) is widely accepted as a major representation of the intracellular redox state; and its changes have been linked to alterations in energy metabolism under various physiopathological conditions including aging (10), diabetes, stroke, cancer, and epilepsy (11–13).
To date, there have been only two approaches used to assess the intracellular NAD+/NADH redox state: one is based on biochemical analysis and the other relies on the autofluorescence signal of the intracellular NADH. The biochemical analysis uses high-performance liquid chromatography (14), capillary electrophoresis (15), or enzymatic cycling assays (13), to measure the NAD+ and NADH contents and, thus, the NAD+/NADH ratio. This approach detects the total amount of cellular NAD+ or NADH content, including free and protein-bound forms, without distinguishing their subcellular compartmentation. Since the biochemical approaches require tissue biopsy and extraction, they are not suitable for longitudinal studies in intact organs. On the other hand, by measuring weak endogenous fluorescence signals, the autofluorescence approach can monitor the intracellular level of NADH, mainly from the mitochondria in living cells (16–19). However, this approach suffers from low detection sensitivity, limited penetration and difficulty in detecting the NADH signal from deep tissue or organs, NADH unrelated artifacts, and potential cell injury resulting from ultraviolet irradiation. Moreover, the autofluorescence approach is unable to detect the NAD+ form and it is difficult to provide absolute quantification of intracellular NADH concentration (16,17). These drawbacks have restricted its utility in quantitatively determining the intracellular NAD contents and the redox ratio in vivo. Although studies using novel genetically encoded fluorescent sensors have reported improved sensitivity of NADH detection (20,21), a noninvasive approach suitable for in vivo applications aiming to quantify intracellular NAD+ and NADH contents is still absent.
In vivo 31P MRS has been used to study cellular metabolism in intact cells and organs since the late 1970s (22), and it could be, in principle, a good candidate for studying cellular NAD metabolism and redox state since both NAD+ and NADH molecules have two phosphate spins. Unfortunately, although NAD signals have been identified in 31P spectra in vivo decades ago, it was generally believed that low concentration NAD metabolites were below the level of in vivo NMR detection. Another challenge is the difficulty in resolving individual NAD+ and NADH resonances from their overlapped signals in an in vivo 31P spectrum, particularly, at relatively low fields. In this study, by taking the advantages of high/ultra-high fields, we developed a novel 31P MRS-based quantification method capable of directly measuring and quantifying the intracellular NAD+ and NADH concentrations and their ratio in vivo. This approach is based on a theoretical NMR model for a description of the NAD phosphorus resonance signals and spectral patterns at a given field strength. By least-square fitting the model to the partially overlapped resonances of NAD+, NADH, and α-ATP in a 31P spectrum, the NAD+ and NADH concentrations and the RX value can be determined.
To test and evaluate this novel NAD quantification method, the following studies were designed and conducted: (i) model simulations mimicking the 31P MR spectra obtained under various measurement conditions; (ii) rigorous tests using a series of NAD standard solutions with known NAD+ and NADH concentrations and varied RX, pH, or free [Mg2+]; (iii) independent measurements of anesthetized healthy cat brains at two different magnetic fields (9.4 T vs. 16.4 T). The longitudinal (T1) and apparent transverse ( ) relaxation times of NAD+ and NADH in cat brains were also measured at 9.4 T and 16.4 T. Our results indicate, for the first time, that it is possible to reliably measure the intracellular NAD+ and NADH concentrations in an intact brain. The significance of this advancement includes providing noninvasive means for intracellular redox state evaluation in normal or diseased brains and the potential for translation to human application.
METHODS
Quantification Model
Structurally, NAD is similar to adenosine triphosphate (ATP), but the γ-phosphate group on the ATP molecule is replaced by one nucleotide consisting of a ribose ring with nicotinamide attached to the C1 position. The α-phosphate in ATP and the two phosphate groups in NAD share a similar chemical and electronic environment and consequently could have similar 31P NMR and chemical properties, such as chemical shifts, relaxation times, and resonance linewidths.
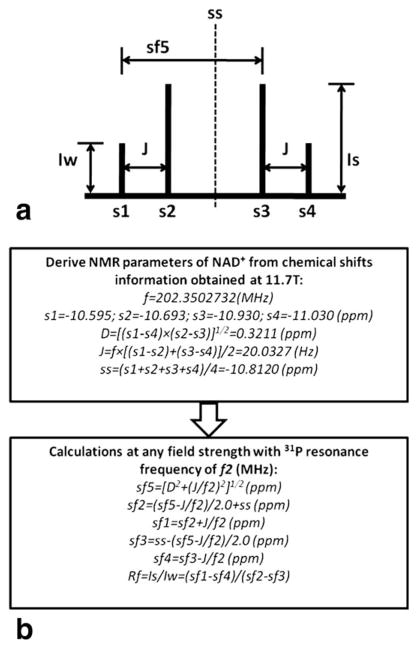
The molecular structures of NAD+ and NADH are almost identical; NAD+ differs from NADH by one H+ and two electrons. Consequently, NAD+ has an aromatic nicotinamide ring with partially delocalized electrons that NADH does not have. This subtle structural difference makes the nuclear spin shielding of the two phosphorus spins in the NAD+ molecule distinct from NADH. According to the NMR theory, NAD+ is a two-spin system and its 31P spectrum exhibits a quartet consisting of four resonances (Fig. 1a) as a result of the second-order coupling effect (23–25). In contrast, the two phosphorus spins in the NADH molecule have similar local magnetic fields induced by the currents of surrounding electrons, leading to a single peak with doubled peak height. Using the chemical shift information obtained from the high-resolution (HR) 31P NMR spectrum of NAD+ solution at 11.7 T in this study, frequency separation between the two phosphorus spins of NAD+ was determined (64.97 Hz) and it was found to be larger than the J coupling constant (J = 20.03 Hz, see Fig. 1), indicating a strong second-order coupling effect.
FIG. 1.
a: Diagram describes the NAD+ quartet with the two-spin system. b: The flow chart for spectrum prediction at any given field strength. The s1–s4 or sf1–sf4 represent the chemical shifts of NAD+ quartet at 11.7 T or any other field strength, respectively (set PCr at −2.5 ppm as reference); D is the true chemical shift separation of the NAD+ two-spin system; J is the coupling constant; ss is the center of the quartet; sf5 is the chemical shift difference between the first and third resonances at a given field strength; Rf represents the intensity ratio between the stronger peak (Is) and the weaker peak (Iw).
Based on the NMR theory of a two-spin system with a strong second-order coupling effect (23) and the chemical shift information extracted from the HR 31P spectrum of NAD+ solution, spectrum prediction of NAD+ can be made at any given field strength using a desired resonance linewidth and Lorentzian line shape (Fig. 1b). Therefore, a quantification model for description of all signals of NAD+, NADH, and α-ATP resonances with Lorentzian line shape at a magnetic field strength of interest was developed to quantify the NAD+ and NADH signals and concentrations using the α-ATP signal as an internal standard. With the assumptions of Lorentzian line shape and equal linewidth for α-ATP, NAD+, and NADH, their 31P resonance signals can be described by the following equations:
| [1] |
| [2] |
| [3] |
| [4] |
| [5] |
| [6] |
| [7] |
| [8] |
| [9] |
where represent the 31P NMR signals from four peaks of NAD+ quartet, Sα–ATP1 and Sα–ATP2 are the 31P NMR signals from two resonances of α-ATP doublet; SNAD+ and Sα–ATP are the linear summation of the NAD+ quartet and α-ATP doublet, respectively; SNADH is the signal of NADH singlet; INAD+ is the signal intensity of the weaker (or outside) peak in the NAD+ quartet; Rf is the intensity ratio of the stronger and weaker signals of NAD+ quartet; INADH and Iα–ATP are the signal intensities of NADH and α-ATP, respectively; HLW represents the half linewidth of a resonance in Hz; δ is the chemical shift in ppm; sfh and sfp are the chemical shift of NADH and center frequency of α-ATP doublet, respectively; Jα-ATP (= 15.5 Hz, experimentally determined at 11.7 T) is the J coupling constant between the α and β phosphorus spins in an ATP molecule; f2 is the Larmor frequency at a given magnetic field strength; four constants of sf1–sf4 can be calculated according to the scheme as described in Figure 1b.
Via least-square fitting of the model outputs to the resonance signals of NAD+, NADH, and α-ATP obtained from in vivo 31P spectrum, signal intensity and linewidth of each resonance can be determined. Only a small fraction of the 31P spectrum covering the NAD+, NADH, and α-ATP resonances within the chemical shift range of −9 to −11.5 ppm (with δPCr set at −2.5 ppm as the chemical shift reference) was applied to the spectral fitting and NAD quantification after phase and baseline corrections; thus, the effect of first order phase or baseline offset on the model fitting is negligible.
Due to the complex spectral patterns of NAD+, its strong field dependence, and the lack of flexibility and NAD spectral information in most available spectral fitting software, we developed a sophisticated program for NAD quantification in this study.
Preparation of NAD Standard Solution and 31P MRS Measurements
All prepared solutions contained phosphocreatine (PCr) as a chemical shift reference (set at −2.5 ppm). The chemical compounds used in the study were purchased from Sigma-Aldrich (St. Louis, MO) or Fisher Scientific (Pittsburgh, PA).
Two sets of standard solutions with known concentrations of ATP, MgCl2, NAD+, and NADH but varied NAD+/NADH ratios were prepared by dissolving the chemicals in deionized water, and the pH values of the solutions were adjusted to neutral condition (pH = 7.0 ± 0.1). One set of solutions contained 15 mM ATP, 16.2 mM [Mg2+], and total 5.0 mM of NAD, and the other set had 3.0 mM ATP, 3.2 mM [Mg2+], and total 1.0 mM of NAD. These solutions were used for methodology validation via comparing the true values of [NAD+], [NADH], and [NAD+]/[NADH] ratio (equivalent to RX) with the values determined by the 31P MRS-based quantification method.
Another group of solutions containing NAD+ and/or NADH, with or without ATP, were also prepared with varied pH (from 6.0 to 8.5) and free [Mg2+] (from 0.0 to 1.2 mM). These solutions were used to examine the chemical shift dependences of the NAD and ATP resonances on the pH and free (i.e., non-bound) [Mg2+], assuming magnesium is bound to ATP in 1:1 ratio.
The 31P MRS measurements of the NAD solutions were performed at 11.7 T (Varian Inova-500 vertical-bore spectrometer) using a Varian 5mm Broadband probe tuned to 31P frequency and 16.4 T (Varian horizontal-bore animal scanner) using the same surface coil probe as the cat studies (see the description below). The proton-decoupled HR 31P NMR spectra were acquired on 11.7 T with a single-pulse-acquire sequence, a nominal 90° excitation pulse, 6 kHz spectral width, 5k points (np) for each free induction decay data and repetition time (TR) of 5 s with 80 signal averages (NT). Before Fourier transformation, the free induction decay was processed by exponential filtering with various line broadening (LB) to demonstrate the changes in resonance patterns of the NAD+ quartet with different linewidth. The T1 values of NAD (≤ 1 s) and α-ATP (≤ 0.5 s) in solution at room temperature were estimated at 11.7 T for ensuring a fully relaxed acquisition with adequate TR. Temperature effects on the 31P resonances were also examined in one sample solution from 21 °C to 37 °C.
The acquisition parameters of 100 μs nominal 90° radiofrequency hard pulse, spectral width = 8 kHz, np = 1k, TR = 5 s, and NT = 160 were applied at 16.4 T for studying the NAD solutions. The 31P MR spectra of the NAD solutions were processed and analyzed with the proposed model fitting and quantification method. The chemical shifts and resonance linewidth of various phosphorus resonances in each 31P spectrum were also analyzed.
Model Simulation and Evaluation
Simulations of the NAD+ and NADH resonance signals and spectral patterns were conducted with various linewidths (12.5, 25, and 45 Hz) to match the experimentally measured 31P NMR spectra of NAD solution at 11.7 T with corresponding LB. To mimic the in vivo brain 31P MR spectra of NAD+ and/or NADH, model simulations were performed for the magnetic field strengths of 9.4 T and 16.4 T using the approximate in vivo linewidth values of α-ATP (42 Hz for 9.4 T and 52 Hz for 16.4 T) (26) and a predetermined RX value of 4 similar to that of a normal brain.
To evaluate the accuracy of the NAD model predictions and the sensitivity of the quantification method to the signal-to-noise ratio (SNR) of the α-ATP resonances in a 31P MR spectrum, five different levels of randomly generated white Gaussian noise were added to the simulated 31P spectra at 9.4 T and 16.4 T with known half linewidth (i.e., HLW) and RX values (10 trials for each noise level). The values of the parameters used in the simulation were similar to those of cat brains under normal physiological conditions: RX = 3, [NAD+] = 0.32 or 0.39 μmol/g brain tissue, [NADH] = 0.11 or 0.13 μmol/g brain tissue, HLW = 30 and 45 Hz for 16.4 T or 20 and 30 Hz for 9.4 T. By fitting the 31P spectra with different SNR of α-ATP (= 10, 20, 30, 40, and 50) and HLW, the model determined values (expressed as mean ± standard deviation of the 10 simulation trials) were compared with their true values to examine the accuracy and fitting error of the NAD quantification method and the requirement for the 31P spectral resolution and SNR.
Animal Preparation
Adolescent cats (weight 0.8–1.6 kg) were used for in vivo 31P MRS studies at 16.4 T and 9.4 T. Following the initial induction with a mixture of ketamine (15.0 mg/kg) and xylazine (2.5 mg/kg), oral intubation and mechanical ventilation (30 to 33 strokes/min) were applied. Cats were then switched to 0.9–1.2% isoflurane in a N2O/O2 (70:30 volume ratio) mixture for anesthesia throughout the experiment. The animals were placed in a cradle with head position restrained by a home-built holder integrated with mouth and ear bars to avoid head movement. Rectal temperature was maintained at 38.3 ± 0.3 °C using heated circulating water. The cats were maintained under physiological conditions during all the MR measurements via continuous monitoring of breathing patterns and the inhaled and exhaled air compositions (CO2, O2, and isoflurane); more information about animal preparation and maintenance can be found in the Ref. 27.
Most of the animals used in the study were prepared without any invasive procedures (e.g., artery/venous cannulas). Thus, after the completion of the MR measurements, the animals regained consciousness following discontinuation of anesthesia and were then returned to the animal facility. The Institutional Animal Care and Use Committee of the University of Minnesota approved all the procedures in this experimental protocol.
In Vivo 31P MRS Experiments
The in vivo 31P MRS measurements were conducted on either the 9.4 T/31 cm or the 16.4 T/26 cm horizontal-bore animal magnet (Magnex Scientific) interfaced to the VNMRJ console (Varian, Palo Alto, CA). Two passively decoupled 1H/31P dual-coil radiofrequency probes tuned to 9.4 T and 16.4 T Larmor frequencies, respectively, were used in the study and placed over the visual cortex of the cat brain. Each probe consisted of a one-turn, oval shaped single loop 31P surface coil (1.4 × 2 cm) for obtaining 31P MRS data and a quadrature 1H surface coil for shimming and anatomical images. The 1H decoupling was not applied during the 31P MRS acquisition of cat brain in this study.
Localized in vivo 31P MR spectra, in which the free induction decay signals were confined mainly in the cat brain by the sensitivity profile of the 31P radiofrequency coil B1 field, were acquired at either 162 MHz (9.4 T, N = 6) or 283 MHz (16.4 T, N = 6) using the single-pulse-acquire sequence with the following parameters: 100 μs hard pulse and a nominal 90° flip angle; TR = 16 s at 9.4 T and TR = 5 or 16 s at 16.4 T to ensure fully relaxed acquisition for NAD+, NADH, and α-ATP; spectral width = 5.2 kHz (9.4 T) or 8 kHz (16.4 T); acquisition time = 0.058 s (9.4 T) or 0.064 s (16.4 T); NT = 64 (9.4 T) or NT = 40 to 64 (16.4 T). Raw free induction decay signals were converted into frequency domain spectra by Fourier transformation using an exponential filter with LB = 10 Hz to enhance SNR.
Quantification of NAD+ and NADH Concentrations and the Redox State
The NAD quantification model for the field strength of 9.4 T or 16.4 T was applied to determine the signal intensities and linewidth of the NAD+, NADH, and α-ATP resonances by the least-square fitting of the model outputs with those resonances within −9 to −11.5 ppm of the in vivo 31P spectrum. Integrals of α-ATP, NAD+, and NADH signals were calculated based on the predicted spectrum of the least-square fitting.
The concentrations of NAD+ and NADH were quantified by normalizing their peak integrals to that of α-ATP, which has been known to have a stable pool size of 2.8 mM (equivalent to the unit of “μmol/ml brain tissue”) in a normal cat brain (28). In this study, we converted the unit of “μmol/ml brain tissue” to a more commonly used unit of “μmol/g brain tissue” assuming the brain tissue density of 1.1 g/ml, thus, [ATP] = 2.55 μmol/g. Consequently, the intracellular redox ratio RX and the total cerebral concentration of NAD ([NAD]total) were determined by the ratio of [NAD+] to [NADH] and the sum of [NAD+] and [NADH], respectively.
In Vivo Measurement of NAD+ and NADH Relaxation Times
The T1 values of the NAD+ and NADH were measured in cat brains using the inversion-recovery pulse sequence at both field strengths under fully relaxed condition with a pre-excitation delay of 16 s (5 cats at 16.4 T with NT = 16 or 24) or 20 s (7 cats at 9.4 T with NT = 12 or 16). A B1-insensitive hyperbolic secant inversion pulse was used to compensate the B1 inhomogeneity of the 31P surface coil (29,30). T1 values were determined by the least-square fitting of a single exponential function to the NAD signals, which were obtained from the model-fitting of the in vivo 31P spectra, with a total of nine different inversion-recovery times at each field (inversion-recovery times = 0.012, 0.02, 0.1, 0.3, 0.8, 2, 4, 10, and 20 s for 16.4 T; inversion-recovery times = 0.08, 0.16, 0.32, 0.64, 1.28, 2.56, 5.12, 10.24, and 20.48 s for 9.4 T). The value of the NAD+ or NADH was estimated via the relationship of .
The concentration unit of mM was used for standard solutions and μmol/g for in vivo brains. All results were presented as mean ± standard deviation (stdev). Comparisons were performed using unpaired Student’s t-test with the differences in mean values considered to be statistically significant at a probability level of <5%.
RESULTS
Model Simulation and Study of NAD Solutions
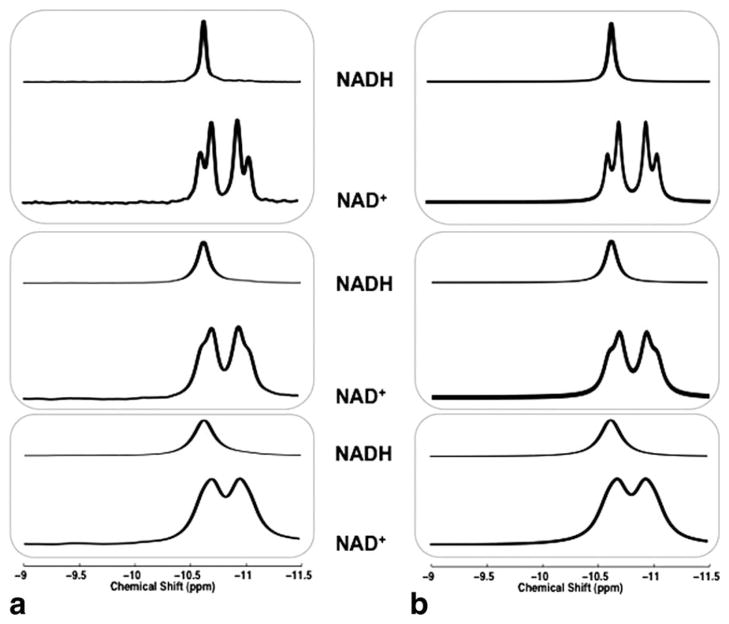
As shown in Figure 2, model simulations of NAD+ and NADH resonance signals (Fig. 2b) were highly comparable with the HR 31P NMR spectra of NAD+ and NADH solutions (Fig. 2a) measured at 11.7 T even with several fold variations in their resonance linewidths. The chemical shifts of the NAD+ quartet at 11.7 T were measured (see Fig. 1b for the list), and that of NADH was around −10.63 ppm. From the original linewidth of 8 Hz in the HR 31P spectra, NAD+ signal evolved into an apparent doublet with effective chemical shifts of −10.69 and −10.94 ppm (Δ = 0.25 ppm) when LB values of 4, 18 and 36 Hz were applied (Fig. 2a). Simulated 31P spectra with matched linewidths of 12.5, 25, and 45 Hz also demonstrated the same change in the NAD+ resonance pattern (Fig. 2b).
FIG. 2.
31P NMR spectra of the individual NAD+ and NADH solutions (a) and the corresponding model simulations (b) at 11.7 T with various LB effects. LB used (from top to bottom) in (a): 4, 18, and 36 Hz; Linewidth used for simulation (from top to bottom) in (b): 12.5, 25, and 45 Hz, for matching the apparent resonance linewidths between the NAD solution and simulated spectra.
Figure 3 illustrates the simulation result that mimicked the in vivo 31P spectra of NAD+ and NADH with appropriate linewidth at 9.4 T (Fig. 3a) and 16.4 T (Fig. 3b). It clearly shows a better separation between the two apparent NAD+ resonances at 16.4 T (effective chemical shifts: −10.67 and −10.96 ppm; Δ = 0.29 ppm) than that at 11.7 T (Δ = 0.25 ppm) or 9.4 T (effective chemical shifts: −10.70 and −10.92 ppm; Δ = 0.22 ppm). This improved spectral separation was also evident in the combined NAD+ and NADH signals at 16.4 T (Fig. 3b).
FIG. 3.
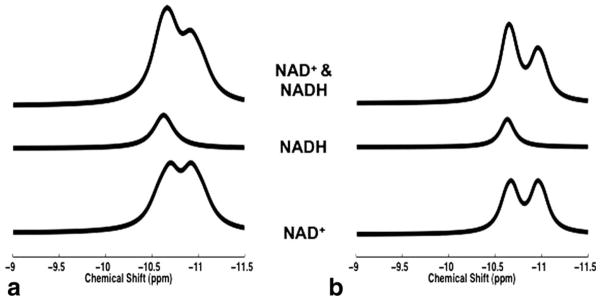
Model simulations of NAD+ (bottom traces), NADH (middle traces), and mixed NAD+ and NADH (top traces) signals at 9.4 T (a) and 16.4 T (b). Linewidth of 42 Hz (9.4 T) and 52 Hz (16.4 T), and predetermined RX value of 4 were used in the simulations.
Table 1 summarizes the results of the quantification method applied to the simulated 31P spectra of mixed NAD+, NADH, and α-ATP resonances with five levels of SNR and two sets of linewidth at both 9.4 T and 16.4 T. The values of the parameters (i.e., HLW, RX, [NAD+], [NADH], and [NAD]total) used in the simulation were predetermined for mimicking the in vivo 31P MRS of the animal brain. In general, excellent accuracy and reliability across a wide range of SNRα-ATP (from 10 to 50) were observed. The accuracy of the model quantification, defined as accuracy = 100 × abs(mean-real)/real, where “real” is the true value without added noise, were over 90% for all the parameters listed in the table when the SNR of α-ATP is equal or greater than 20. The fitting errors, i.e., error% = 100 × stdev/mean, of these parameters can also be calculated. It shows that when the SNR of α-ATP equals 30 or higher, the fitting errors can be lower than 1% for HLW, less than 5% for [NAD+] and [NAD]total, below 10% for [NADH], and within 13% for RX. A higher SNR led to a better accuracy and smaller fitting error. Although similar fitting results were observed for both linewidths and magnetic fields at a given SNR, results in Table 1 also suggest that narrower spectral linewidth or higher field strength can provide better fitting outcomes.
Table 1.
Model Simulation and Results (10 Trials Per Simulation)
| SNRα-ATP
|
10
|
20
|
30
|
40
|
50
|
w/o noise
|
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HLW used for simulations (Hz) | 20 | 30 | 20 | 30 | 20 | 30 | 20 | 30 | 20 | 30 | 20 | 30 | |
| 9.4 T | HLW (Hz) | 20.0 ± 0.7 | 29.5 ± 0.5 | 19.9 ± 0.3 | 29.7 ± 0.3 | 19.8 ± 0.1 | 30.0 ± 0.2 | 19.8 ± 0.2 | 29.9 ± 0.2 | 19.8 ± 0.1 | 29.9 ± 0.1 | 19.8 | 29.8 |
| RX | 2.66 ± 0.40 | 3.32 ± 1.14 | 3.01 ± 0.46 | 3.20 ± 0.77 | 3.11 ± 0.26 | 3.01 ± 0.38 | 3.02 ± 0.24 | 3.09 ± 0.26 | 3.04 ± 0.11 | 2.87 ± 0.22 | 3.00 | 2.99 | |
| [NAD+] (μmol/g) | 0.37 ± 0.02 | 0.40 ± 0.05 | 0.39 ± 0.02 | 0.39 ± 0.02 | 0.39 ± 0.01 | 0.39 ± 0.01 | 0.39 ± 0.01 | 0.39 ± 0.01 | 0.39 ± 0.01 | 0.38 ± 0.01 | 0.39 | 0.39 | |
| [NADH] (μmol/g) | 0.15 ± 0.02 | 0.13 ± 0.04 | 0.14 ± 0.01 | 0.13 ± 0.02 | 0.13 ± 0.01 | 0.13 ± 0.01 | 0.13 ± 0.01 | 0.13 ± 0.01 | 0.13 ± 0.00 | 0.14 ± 0.01 | 0.13 | 0.13 | |
| [NAD]total (μmol/g) | 0.52 ± 0.02 | 0.53 ± 0.02 | 0.53 ± 0.01 | 0.52 ± 0.01 | 0.52 ± 0.01 | 0.52 ± 0.01 | 0.52 ± 0.01 | 0.52 ± 0.01 | 0.52 ± 0.00 | 0.52 ± 0.01 | 0.52 | 0.52 | |
| HLW used for simulations (Hz) | 30 | 45 | 30 | 45 | 30 | 45 | 30 | 45 | 30 | 45 | 30 | 45 | |
| 16.4 T | HLW (Hz) | 30.1 ± 0.5 | 44.9 ± 1.3 | 29.7 ± 0.4 | 44.9 ± 0.4 | 29.9 ± 0.3 | 45.0 ± 0.3 | 29.9 ± 0.2 | 45.0 ± 0.3 | 29.9 ± 0.1 | 45.0 ± 0.1 | 29.9 | 44.9 |
| RX | 3.45 ± 1.28 | 2.97 ± 0.99 | 3.19 ± 0.48 | 3.06 ± 0.51 | 2.84 ± 0.22 | 3.31 ± 0.40 | 3.02 ± 0.13 | 2.83 ± 0.25 | 3.02 ± 0.18 | 3.00 ± 0.19 | 2.97 | 2.96 | |
| [NAD+] (μmol/g) | 0.33 ± 0.02 | 0.31 ± 0.03 | 0.33 ± 0.02 | 0.32 ± 0.02 | 0.32 ± 0.01 | 0.33 ± 0.02 | 0.32 ± 0.01 | 0.31 ± 0.01 | 0.32 ± 0.01 | 0.32 ± 0.01 | 0.32 | 0.32 | |
| [NADH] (μmol/g) | 0.10 ± 0.03 | 0.11 ± 0.03 | 0.11 ± 0.01 | 0.11 ± 0.01 | 0.11 ± 0.01 | 0.10 ± 0.01 | 0.11 ± 0.00 | 0.11 ± 0.01 | 0.11 ± 0.01 | 0.11 ± 0.01 | 0.11 | 0.11 | |
| [NAD]total (μmol/g) | 0.43 ± 0.02 | 0.43 ± 0.01 | 0.44 ± 0.01 | 0.43 ± 0.01 | 0.43 ± 0.01 | 0.43 ± 0.01 | 0.43 ± 0.01 | 0.43 ± 0.01 | 0.43 ± 0.00 | 0.42 ± 0.00 | 0.43 | 0.43 | |
Figure 4 compares the experimentally measured [NAD+], [NADH], and RX values of the standard NAD solutions with their corresponding true values. Figure 4a shows the comparison result based on the quantification of the 1H-decoupled HR 31P spectra acquired at 11.7 T. The 1H-decoupling applied in HR acquisition not only allowed accurate determination of chemical shifts and J-coupling constants of ATP and NAD but also eliminated potential error due to the 1H-31P coupling effect on the NAD+ lineshape observable in the HR spectra. The linear regression indicates excellent consistency between the true and measured values for all parameters studied (R2>0.99 and a linear slope of 1.00 ± 0.02). Figure 4b evaluates the 31P spectra of the standard solutions containing submillimolar NAD, which is similar to the NAD contents in normal cat brains, obtained at 16.4 T animal scanner. Strikingly, excellent agreement between the true and measured values was observed with R2>0.99 and a linear slope of 0.99 ± 0.02. The SNRα-ATP of the spectra in Fig. 4a,b was about 92–95. These results collectively validated the quantification model for analyzing the 31P spectra and providing reliable measures of [NAD+], [NADH], and RX.
FIG. 4.
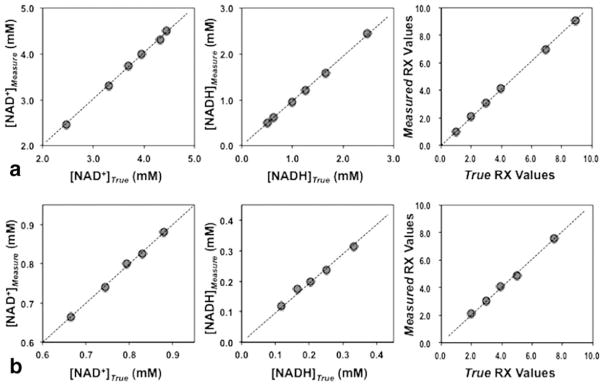
Comparison results of the standard NAD solutions between the true values of predetermined [NAD+], [NADH], and RX and the quantification method determined values based on 1H decoupled HR 31P MRS at 11.7 T (a) and conventional 31P MRS at 16.4 T animal scanner (b). The linear slope (S) and regression coefficient (R2) were: 1.01 and 1.00 for [NAD+], 0.98 and 1.00 for [NADH], 1.02 and 1.00 for RX in (a); and 1.00 and 1.00 for [NAD+], 0.96 and 0.99 for [NADH], 1.01 and 1.00 for RX in (b).
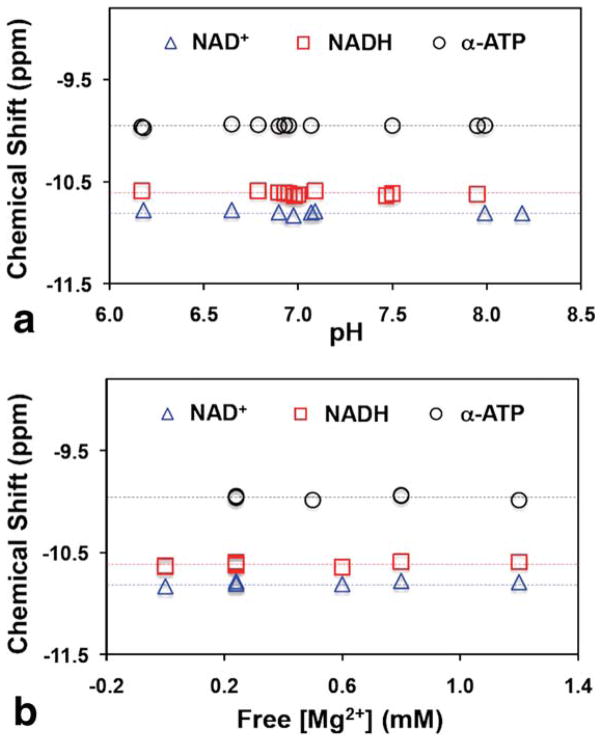
It has been known that the 31P chemical shift of the α-ATP is insensitive to the changes of pH and free [Mg2+] as compared to that of β-ATP and γ-ATP (31). Figure 5 clearly illustrates similar behaviors of the NAD+ and NADH chemical shifts as that of α-ATP, which are approximately independent on the pH change between 6.0 and 8.5 (Fig. 5a) and the free [Mg2+] change between 0 and 1.2 mM (Fig. 5b). The solutions used for this study covered a wide range of ATP and NAD concentrations ([ATP] = 0–15 mM, [NAD+] = 0.3–7.5 mM, and [NADH] = 0.1–7.5 mM). This NMR property greatly simplifies the NAD quantification model since the variation in the chemical shifts of the α-ATP, NAD+, and NADH under normal or pathological condition can be negligible.
FIG. 5.
Dependence of the chemical shifts of NAD+, NADH, and α-ATP resonances upon (a) pH values and (b) free [Mg2+] levels. The chemical shift of the NAD+ resonance is defined by the center frequency of the NAD+ quartet. Dashed lines display the mean values of chemical shifts. The free [Mg2+] levels in the solutions are estimated by subtracting [ATP] from the total [Mg2+] assuming that the ATP molecules are bound to Mg2+ in a 1:1 ratio. The concentrations of ATP, NAD+, and NADH in the solutions used for these measurements are: [ATP] = 0–15 mM, [NAD+] = 0.3–7.5 mM, and [NADH] = 0.1–7.5 mM.
In addition, the variation of the NAD+ and NADH chemical shifts due to the temperature changes was also negligible (less than 0.006 ppm when temperature increasing from 21 °C to 37 °C). The overall results demonstrate similar 31P NMR properties among the α-ATP, NAD+, and NADH resonances presumably owing to the similar environment of their 31P spins. More importantly, their chemical shifts are insensitive to pH, free [Mg2+], and tissue temperature in a physiologically relevant range.
In Vivo Studies of Brain NAD and Redox State at 9.4 T and 16.4 T
Figure 6 illustrates representative in vivo 31P spectra of normal cat brains acquired at 16.4 T (Fig. 6a) and 9.4 T (Fig. 6b), showing excellent spectral quality and high SNR. All the in vivo resonance signals of α-ATP, NAD+, and NADH were well fitted by the NAD quantification model at both field strengths, as reflected by the small residues between the original spectra and the model fittings (see the insets in Fig. 6). Similar to the simulation results shown in Figure 3, a better separation of the two merged peaks from combined NAD+ and NADH signals was also observed at 16.4 T compared to 9.4 T. Table 2 summarizes the independent measurement results of the RX, [NAD+], [NADH], [NAD]total, and values in cat brains measured at 16.4 T (N = 6) and 9.4 T (N = 6), showing RX = 2.61 ± 0.30, [NAD+] = 0.33 ± 0.03 μmol/g, [NADH] = 0.13 ± 0.02 μmol/g, [NAD]total = 0.46 ± 0.04 μmol/g, and at 16.4 T; and RX = 3.03 ± 0.98, [NAD+] = 0.35 ± 0.03 μmol/g, [NADH] = 0.12 ± 0.03 μmol/g, [NAD]total = 0.48 ± 0.03 μmol/g, and at 9.4 T. As expected, there were no statistically significant differences in all the measurements between 16.4 T and 9.4 T, except for , which is known to be field dependent. The accuracy and the error of these reported values can be estimated based on the simulation results in Table 1 and the SNR and linewidth of the α-ATP signal of the cat brain data (SNR = 38.1 ± 3.0 and HLW ≈ 20 Hz at 9.4 T; SNR = 54.2 ± 4.6 and HLW ≈ 30 Hz at 16.4 T with LB = 10 Hz), resulting in over 98% accuracy and less than 8% fitting error. Therefore, the SNR and spectra resolution achievable at high/ultrahigh field allows for reliable measurements of brain [NAD+], [NADH], and the redox ratio in vivo with small standard deviation and excellent consistency between two fields.
FIG. 6.
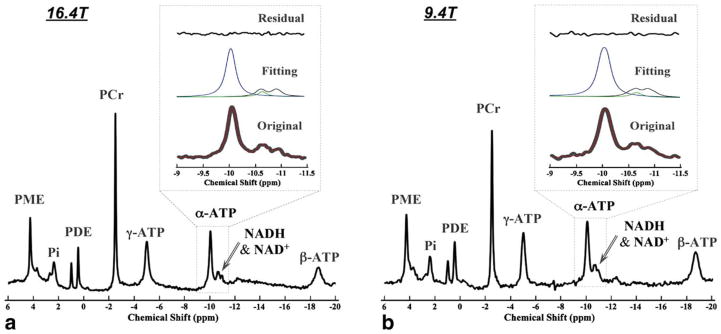
Representative surface-coil localized in vivo 31P MR spectra of normal cat brains at 16.4 T (a) and 9.4 T (b). Full spectra are shown below. Enlarged spectral regions (chemical shift from −9 to −11.5 ppm) with phase and baseline correction are shown in the bottom of the insets (gray lines), superimposed by the model predicted spectra (red lines). The model decomposed individual signals of NAD+ (black lines), NADH (green lines), and α-ATP (blue lines) are shown in the middle of the insets, and the residues of model fittings to the original 31P spectra are plotted in the top of insets.
Table 2.
Comparison of the RX, [NAD+], [NADH], [NAD]total, and Values in Cat Brains at 16.4 T and 9.4 T
| Cat | RX
|
[NAD+] (μmol/g)
|
[NADH] (μmol/g)
|
[NAD]total (μmol/g)
|
T2* (ms)
|
|||||
|---|---|---|---|---|---|---|---|---|---|---|
| 16.4 T | 9.4 T | 16.4 T | 9.4 T | 16.4 T | 9.4 T | 16.4 T | 9.4 T | 16.4 T | 9.4 T | |
| 1 | 3.05 | 3.75 | 0.37 | 0.37 | 0.12 | 0.10 | 0.49 | 0.47 | 6.70 | 11.50 |
| 2 | 2.71 | 2.02 | 0.35 | 0.30 | 0.13 | 0.15 | 0.48 | 0.45 | 6.20 | 10.00 |
| 3 | 2.62 | 2.73 | 0.34 | 0.37 | 0.13 | 0.14 | 0.46 | 0.51 | 6.00 | 10.70 |
| 4 | 2.26 | 4.62 | 0.30 | 0.37 | 0.14 | 0.08 | 0.43 | 0.45 | 6.20 | 10.30 |
| 5 | 2.28 | 2.78 | 0.35 | 0.38 | 0.15 | 0.14 | 0.50 | 0.53 | 6.60 | 10.30 |
| 6 | 2.73 | 2.27 | 0.30 | 0.32 | 0.11 | 0.15 | 0.41 | 0.46 | 6.80 | 9.70 |
| Mean | 2.61 ± 0.30 | 3.03 ± 0.98 | 0.33 ± 0.03 | 0.35 ± 0.03 | 0.13 ± 0.02 | 0.12 ± 0.03 | 0.46 ± 0.04 | 0.48 ± 0.03 | 6.42 ± 0.33 | 10.42 ± 0.63a |
p < 0.05.
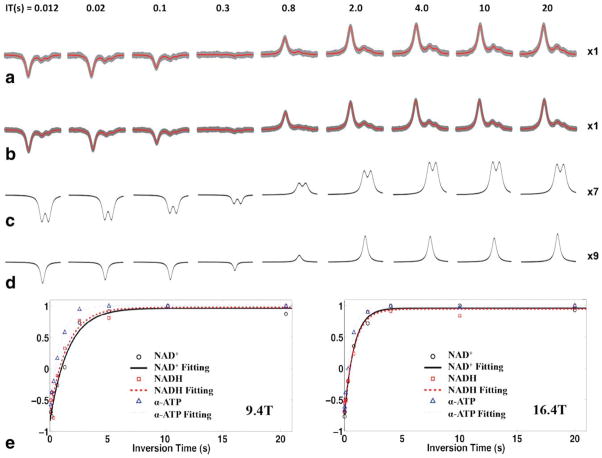
Because the proposed NAD quantification method has the ability to separate and extract individual resonance signals, it makes in vivo T1 measurement and quantification possible for NAD+ and NADH. Figure 7 shows the in vivo T1 measurements results at 16.4 T and 9.4 T. Figure 7a displays the original 31P spectra (gray lines) of a representative cat brain and the least-square fitting (red lines) using the NAD quantification model for the T1 measurement at 16.4 T. To further improve the SNR and the reliability of the T1 measurement, the in vivo 31P spectra of multiple animals was summed at each field (9.4 T: 7 cats and a total signal average of 88; 16.4 T: 5 cats and a total signal average of 96) and used for least-square fitting and NAD quantification. Figure 7b shows the summed in vivo 31P spectra (gray traces) acquired at 16.4 T and the excellent fittings (red traces). A slightly faster recovery for the α-ATP signal was observed when compared to that of NAD+ and NADH, while similar inversion-recovery processes are illustrated in Figure 7c for the NAD+ doublet (merged from quartets) and Figure 7d for the NADH singlet. Figure 7e displays the exponential fittings of the T1 measurements based on the summed 31P spectra of the NAD+, NADH, and α-ATP obtained at 9.4 T (left panel) and 16.4 T (right panel). The measured T1 values of NAD+, NADH, and α-ATP in normal cat brain were: 1.58, 1.50, and 0.90 s at 9.4 T; and 0.82, 0.87, and 0.57 s at 16.4 T, respectively. In addition, the T1 values determined from the 31P spectra of individual cat brains at 16.4 T summarized in Table 3 show how the mean T1 values from the measurements of five cat brains were consistent with the results of the summed spectra. In summary, as shown in Table 3, cerebral NAD+ and NADH had similar T1 relaxation times (0.84 ± 0.13 versus 0.91 ± 0.21 s at 16.4 T), which were significantly longer than that of α-ATP (0.59 ± 0.03 s at 16.4 T, P<0.05).
FIG. 7.
T1 measurements of NAD+, NADH, and α-ATP in normal cat brains with a total of nine different inversion-recovery time values acquired at 16.4 T and 9.4 T. a: Model fittings (red lines) to the in vivo 31P spectra (gray lines) of a representative cat brain with 24 signal averages obtained at 16.4 T. b: Model fittings (red lines) to the summed spectra (gray lines) from five cat brains with total 96 signal averages acquired at 16.4 T. c and d: Model decomposed individual signals of NAD+ (amplification × 7) and NADH (amplification × 9) from (b) (amplification × 1). e: Exponential fittings of the T1 data: based on the model fitting of summed spectra at 9.4 T (left, N = 7, total NT = 88) and 16.4 T (right, N = 5, total NT = 96). Measured T1 values of NAD+, NADH, and α-ATP are: 1.58, 1.50, and 0.90 s at 9.4 T; 0.82, 0.87, and 0.57 s at 16.4 T, respectively.
Table 3.
In Vivo T1 Measurement Results of Cat Brains at 16.4 T
| Cat | 1 | 2 | 3 | 4 | 5 | Mean | Summed spectra |
|---|---|---|---|---|---|---|---|
| T1,NAD+ (s) | 0.79 | 0.92 | 0.85 | 0.64 | 0.98 | 0.84 ± 0.13 | 0.82 |
| T1,NADH (s) | 0.70 | 0.93 | 0.73 | 1.23 | 0.94 | 0.91 ± 0.21 | 0.87 |
| T1,α-ATP (s) | 0.56 | 0.59 | 0.58 | 0.65 | 0.58 | 0.59 ± 0.03 | 0.57 |
DISCUSSION AND CONCLUSION
Although the total phosphorus signals of NAD (i.e., contribution of both NAD+ and NADH) have been detected by 31P NMR spectroscopy for decades, in the extracts of astrocytes (32), tumor cells (24,25), cortical slices (33), or healthy human brains (34), quantification of the RX or the individual NAD+ or NADH concentration has never been realized because of the challenges associated with decomposing overlapped resonance signals of NAD+, NADH, and α-ATP, especially for in vivo studies. For HR 31P NMR studies of extracted tissues or cells, in which strong oxidative chemicals such as perchloric acid are commonly used during the tissue extraction, a substantial amount of reduced NADH can be irreversibly converted to NAD+ and lead to large errors in the NAD quantification. In contrast, such errors are not a concern for the in vivo quantification of NAD+ and NADH.
In this study, we developed a novel 31P MRS-based method for quantification of the intracellular redox state via decomposition of individual signals of NAD+ and NADH from the overlapped in vivo 31P NAD spectrum of intact brains. Because of its noninvasive nature and exquisitely detailed information it provides, this in vivo 31P MRS method has the advantage of directly measuring the intracellular NAD+ and NADH concentrations, thus, determining the RX in intact organs (e.g., brain as studied herein) under normal and potentially pathological conditions. This method not only eliminates the major hurdle of the biochemical analysis, i.e., it requires tissue extraction and chemical processes, but also allows quantification of both intracellular NAD+ and NADH concentrations in vivo, which is not feasible with the autofluorescence approach.
Detectability of the Intracellular NAD at High Fields
The intracellular NAD contents of the normal brain tissue are less than a millimolar, which was generally believed to be under the in vivo 31P MRS detection limit. This probably was the case based on the spectral quality commonly obtained at low magnetic field and/or clinical scanner. However, as more high/ultrahigh field scanners become available for research in institutions worldwide, our understanding of the in vivo MRS detectability should be updated accordingly.
It has been found that the SNR of the in vivo 17O MRS signal almost quadruples with the B0 field strength, and the SNR obtained per unit time in the rat brain increases almost 12 times from 4.7 T to 16.4 T (35). For the in vivo 31P MRS, the improvements at high/ultra-high fields in terms of the sensitivity and spectra quality are demonstrated by (i) higher SNR, (ii) better spectral resolution, and (iii) shorter T1 relaxation time at higher fields (26,36,37). These improvements lead to a better than linear field-dependent enhancement of the in vivo 31P MRS detectability at higher field. In this study, we were able to obtain SNRα-ATP of 38 and 54 in the cat brain at 9.4 T and 16.4 T, respectively, which are equivalent to the SNRNADH of 3.8 and 5.4 in the same animal brain at the corresponding fields that were estimated by the concentration ratio of [ATP]/[NADH] ≈ 20 and the phosphate spin number ratio of 1:2 between the α-ATP and NADH. The SNR of the in vivo 31P NAD signals could be further improved if optimized acquisition parameters (e.g., using short TR and Ernst flip angle) were applied. Thus, detection of low concentrations of NAD+ and NADH metabolites becomes feasible at high field.
Validity of the NAD Quantification Method
Whether the NAD quantification method described herein is valid for providing reliable measurement of intracellular NAD and RX is an important question to answer before we can fully establish this novel MRS technique for in vivo applications. Due to the lack of in vivo approaches for directly measuring and quantifying intracellular NAD+, NADH, and NAD+/NADH ratio in an intact brain and the absence of in vivo brain studies reported in the literature, we took several steps to rigorously test and evaluate this method.
First, the ability of the method to reliably detect and quantify low concentrations of NAD+ and NADH in the standard NAD solutions was examined. The results shown in Figures 2–4 clearly demonstrate that not only can the theoretical model precisely describe and predict the 31P spectral patterns of the NAD at different field strengths (Figs. 2 and 3), the proposed NAD quantification method can also accurately determine the submillimolar NAD concentrations across a wide range of RX (Fig. 4).
Second, the accuracy of the quantification method and its dependence on the SNR and the spectral resolution of the 31P MRS data were estimated using the simulated spectra with added white noise to mimic the in vivo 31P spectra. As summarized in Table 1, the simulation results indicate that high accuracy and small fitting errors of the NAD and RX quantification can be achieved with the SNR of ≥20 for the α-ATP signal and linewidth obtainable at high/ultrahigh fields. In this sense, the high/ultrahigh field is advantageous for the NAD detection and quantification.
Third, independent in vivo 31P MRS studies of the same cat model were conducted at 9.4 T and 16.4 T, respectively; and the quantification method was applied to determine the intracellular [NAD+], [NADH], [NAD]total, and RX. The excellent spectra quality and sensitivity available at both fields (see Fig. 6 for example) allowed reliable measurement and quantification with data acquisition periods as short as a few minutes. The validity and reliability of the NAD quantification method were verified in the cat brains measured at 16.4 T and 9.4 T (Table 2) since the values of the RX, [NAD+], [NADH], and [NAD]total in normal cat brains should be same regardless the magnetic field applied in the study. The experimental results indicate that although the NAD spectra pattern and relaxation times (i.e., T1 and ) varied significantly at two fields, the measured NAD concentrations and RX values are indeed consistent.
Finally, we did not directly compare the in vivo 31P MRS measurements with biochemical analyses of the cat brain tissues used in this study. The concern is that NAD molecules, especially the NADH, are known to be unstable compounds and are very sensitive to the presence of acid, base, oxidative or reductive agents and even light (38); thus, the NAD levels are likely to change during the extraction and analysis if proper procedures and controls can not be implemented. Currently we do not have the capability to quickly freeze the entire cat brain, which is much larger than rat or mouse brain, or prevent NAD loss and conversion during the process. Nevertheless, we surveyed literature to gather information regarding the NAD concentrations and redox ratios of the brain tissue. The results are summarized in Table 4 (39–50), which also includes the results from this study for comparison. Most of the available data listed in the table was from biochemical assays of mouse or rat brains, which provide the necessary database for comparison. Despite certain discrepancies in the literature values of [NAD+] and RX, our results are well within the reported range. It is true that the [NADH], and thus, the [NAD]total levels in our studies are slightly higher than the literature reports, but they are still within the same magnitude. In fact, due to the instability of the NADH compound, we expect that the in vivo [NADH] level should be higher than that of tissue extraction although the use of an alternative extraction method based on organic solvents (51) might partially overcome this technical challenge.
Table 4.
Summarized Results of NAD Contents and NAD+/NADH Ratio Measurements in Brain Tissue
| Study | Method | Sample tissue | [NAD+] (μmol/g) | [NADH] (μmol/g) | [NAD]total (μmol/g) | RX |
|---|---|---|---|---|---|---|
| Present study | In vivo 31P MRS at 9.4 T | Cat visual cortex | 0.35 | 0.12 | 0.48 | 3.03 |
| Present study | In vivo 31P MRS at 16.4 T | Cat visual cortex | 0.33 | 0.13 | 0.46 | 2.61 |
| Ref. 39 | Fluorometric Assay | Rat Brain | 0.24 | 0.07 | 0.32 | 3.23 |
| Ref. 40 | Enzymatic Cycling Assay | Rat Brain | 0.32 | 0.10 | 0.42 | 3.39 |
| Ref. 41a | Enzymatic Analysis | Rat Brain | 0.33 | 0.04 | 0.37 | 9.41 |
| Ref. 42 | HPLC | Mouse Cortex | 0.19 | 0.05 | 0.24 | 3.52 |
| Ref. 43 | HPLC | Mouse Frontal Cortex | 0.39 | - | - | - |
| Ref. 44 | HPLC | Mouse Cortex | 0.34 | 0.05 | 0.39 | 6.80 |
| Ref. 45 | HPLC | Mouse Brain | 0.28 | - | - | - |
| Ref. 46 | Isotachophore Method | Rat Cortical Slice | - | - | - | 2.38 |
| Ref. 47 | HPLC | Mouse Cortex | 0.48 | - | - | - |
| Ref. 48 | Enzymatic Cycling Assay | Mouse Brain | 0.75 | - | - | - |
| Ref. 49b | Enzymatic Cycling Assay | Mouse Cortical Astrocytes | 0.33 | 0.09 | 0.42 | 3.66 |
| Ref. 50 | Commercial Kit, HPLC | Mouse Brain | 0.20 | 0.10 | 0.30 | 2.00 |
Molecular weight of 663.4 (NAD) and 709.4 (NADH) were used in unit conversion.
Assume ~11% protein in the tissue sample.
The results of this study and the preliminary findings of additional studies in ischemic rat brains and healthy human brains (52,53) collectively validate the model fitting for NAD quantification and suggest that the peaks we quantified vary appropriately and proportionally in accordance with the known knowledge of biochemistry and brain metabolism under normal and diseased conditions. The in vivo 31P MRS based NAD quantification method can provide reliable measures of the intracellular NAD contents and redox states.
Signal Source of the Measurement and Possible Contamination
The intracellular NADH and NAD+ can exist in both free and protein-bound forms and are compartmentalized into the cytosolic and mitochondrial spaces (54). To understand their roles in regulating cellular metabolism, it is important to clarify the signal source of the in vivo measurements. The ATP concentration previously measured in the cat brain by in vivo 31P MRS at 9.4 T (28) was in an excellent agreement with the literature reports based on the chemical/enzymatic assay analysis of extracted brain tissues (55). The consistency between in vivo and ex vivo results suggests that the 31P spins in the bound ATP still retain certain freedom of spin motion, thus, can attribute to the total NMR signal detected by the in vivo 31P MRS. Similar to the ATP molecule, we expect that the NAD molecules located in different subcellular compartments (for instance, in cytosolic or mitochondrial space) are also fully detectable by the in vivo 31P MRS. As demonstrated in Table 4, the intracellular NAD+ and NADH concentrations determined in vivo in this study were comparable to those of the biochemical measurements, where the NAD in different subcellular compartments or in free versus protein-bound form were not distinguishable. Therefore, it is likely that the in vivo 31P MRS measurement also detects the total intracellular NADH or NAD+ content from both free and protein-bound forms, in both cytosolic and mitochondrial pools.
The possible signal contributions of other phosphorous compounds to the chemical shift region of α-ATP and NAD and the potential error in the NAD quantification have been considered. The molecular structure of NADP (NADP+ and/or NADPH) is identical to that of NAD, except for an additional phosphate group on the 2′-position of the adenosine ribose ring. The HR 31P NMR data of the NADP+ solution at 11.7 T (data not shown herein) indicates that except for the additional 2′-phosphate resonance, it has similar chemical shift values and resonance patterns to that of the NAD+ solution. However, it is known that the 31P spectral pattern of free NADP is completely different from that bound to protein, which results in peak splitting and substantial changes of the chemical shifts in a biological system (56,57). In contrast, there is no significant change for NAD chemical shifts between free and bound forms (56). Moreover, the intracellular levels of NADP+ and NADPH in normal brains are only 10% or less of the NAD+ and NADH levels (4,9,40–42,44), thus, their signals in an in vivo brain 31P spectrum are well below the detectable limit and can be neglected. This notion was evident from the fact that the 2′-phosphate peak and other resonances of NADP+ or NADPH were not observable in the in vivo 31P MRS of this study.
The potential contamination of ADP (i.e., adenosine diphosphate) and UDPG (i.e., uridine diphosphoglucose) could also be neglected since the chemical shifts of the α-ADP and α-UDPG doublets were either downfield or not consistent with the resonances of α-ATP and NAD (58,59); thus, the NAD quantification model did not account them for. The ADP and UDPG levels in intact healthy brain tissue were very low; even if they were above the level of MR detection, their signals would be left in the fitting residue and, thus, unlikely to introduce a significant error to the NAD quantification although this aspect is open for more investigation.
31P MR Properties of the NAD Molecules
To understand the effects of Mg2+ bound to NAD+ and NADH and the influences of the pH and temperature changes on their 31P MR spectral patterns and chemical shifts, NAD solutions with various free [Mg+2], pH, and temperature were studied. Like with α-ATP, the spectral patterns (e.g., NAD+ quartet) and chemical shifts of NAD+ and NADH are strikingly insensitive to the changes of pH, free [Mg+2] and temperature covering various pathophysiological conditions (see Fig. 5) (60). This particular NMR property eliminates many confounding factors in the quantification of NAD+ and NADH concentrations in vivo.
The HR 31P spectra of the NAD+ quartet and the NADH singlet agreed well with the spectral predictions of the model simulation (Fig. 2). Based on the information in Figure 1b, the ratio between the frequency separation and the J coupling constant of the NAD+ phosphate spins was 3.24 at 11.7 T, indicating a strong second-order coupling effect, which leads to the spectral pattern of quartet. This ratio is field dependent and increases with the field strength (e.g., from 0.83 at 3 T to 4.54 at 16.4 T based on the model simulation). As the field strength increases, the chemical shift separation between the two NAD+ phosphate spins became larger, and the signal intensities of the weaker and stronger resonances in the NAD+ quartet become closer (data not shown). The four peaks of the quartet gradually merge into two apparent resonances when their linewidths become broader. The in vivo 31P signals of the NAD+ and NADH obtained in the cat brain at 9.4 T and 16.4 T confirmed a similar change in response to altered field strength (Fig. 6), which again supported the validity of the quantification model. Although the NADH resonance is highly overlapped with one apparent NAD+ peak, another NAD+ peak is well resolved in an in vivo brain 31P spectrum at high field (see Figs. 3 and 6). This distinct feature in the NAD spectral patterns significantly improves the reliability and statistical power of the NAD quantification model for decomposing the partially overlapped NMR signals of NAD+ and NADH, even though their brain concentrations are only in the submillimolar range.
Although the NAD detection method described in this study performs better with higher SNR and better spectral resolution (i.e., narrow linewidth), in which the ultrahigh field is obviously advantageous, its application should not be limited to ultrahigh fields. As long as a narrow linewidth and adequate SNR are achievable, this method can be extended to relatively lower fields and could be applied for assessing the human brain redox state, for instance, at 7 T (53). Moreover, this NAD quantification method can be combined with three-dimensional 31P MRS imaging techniques for mapping cerebral intracellular redox state and the spatial distribution of NAD+ and NADH in an intact brain (52).
According to the results of T1 measurements (Fig. 7 and Table 3), while longer T1 values were found at 9.4 T, there was no significant T1 difference between NAD+ and NADH in the cat brain at either 16.4 T or 9.4 T. This NMR property of similar NAD longitudinal relaxation process offers great flexibility in simplifying NMR experiment designs. If the purpose of the study is to investigate the intracellular redox state, that is to determine the RX value, a short TR with an Ernst flip angle can be used to gain SNR within a unit acquisition time without the need for correcting the magnetization saturation effect. In this case, the 31P signal ratio of NAD+ to NADH simply equals to the RX. In contrast, if the in vivo concentrations are desired, one can apply an Ernst flip angle based on the known in vivo T1 values of NAD+, NADH, and α-ATP to achieve an optimal SNR in a given amount of scan time, then calculate the NAD concentrations after the saturation correction using the known values of T1, flip angle, and TR.
In addition, we assumed equal linewidth for the α-ATP, NAD+, and NADH resonances in the quantification model. The HR 31P MRS data of the ATP-NAD solutions does confirm that the differences in their linewidth is within the small range of 2–4 Hz and, thus, negligible for in vivo 31P MRS studies at high/ultrahigh field owing to the much broader linewidths of the resonances. The assumption of Lorentzian lineshape in the model was verified by analyzing the cat brain spectra using a Gaussian lineshape or a mixed Lorentzian/Gaussian (Voigt) profile (61). The test results (data not shown herein) indicate that using Lorentzian lineshape resulted in much better fitting with smaller residuals than the use of Gaussian lineshape; and the mixed Lorentzian/Gaussian (Voigt) profile with high computation demand led to a fitting outcome almost identical to that of Lorentzian lineshape with less than 10% Gaussian contribution. Therefore, the Lorentzian lineshape applied to the NAD model fitting was justified. Using the endogenous α-ATP signal as an internal quantification standard in a normal cat brain should be reasonable and it is supported by an array of literature reports indicating stable ATP content in the healthy brain tissue (55,62). Nevertheless, potential alterations in cerebral α-ATP caused by pathological conditions should be considered in the absolute quantification of cerebral NAD concentrations, and an external reference with known phosphate concentration should prove to be valuable.
In summary, the findings of this study suggest that the 31P MRS approach described herein allows direct and reliable measurements of intracellular NAD+ and NADH concentrations in vivo; thus, their ratio RX, a measure of the intracellular redox state in an intact brain, can be calculated. This in vivo approach will provide an opportunity for noninvasively assessing the intracellular redox state associated with brain functions and diseases, and it has the potential to be applied to human brains, as well as other organs, under physiological and pathological conditions. In addition, this study also demonstrates the capability and utility of the high-field 31P MR spectroscopy technique for reliable measurement of low concentration metabolites in a living brain.
Acknowledgments
Grant sponsor: National Institute of Health; Grant numbers: NS041262; NS057560; NS070839; P41 RR008079; P41 EB015894 and P30 NS076408; S10 RR025031. Grant sponsor: Keck Foundation.
The authors would like to thank Professor Kamil Ugurbil for his support and Dr. Letitia J. Yao from the NMR Lab of Chemistry Department at the University of Minnesota for the help of HR spectra acquisition.
References
- 1.Berger F, Ramirez-Hernandez MH, Ziegler M. The new life of a centenarian: signalling functions of NAD(P) Trends Biochem Sci. 2004;29:111–118. doi: 10.1016/j.tibs.2004.01.007. [DOI] [PubMed] [Google Scholar]
- 2.Ying WH. NAD+ and NADH in cellular functions and cell death. Front Biosci. 2006;11:3129–3148. doi: 10.2741/2038. [DOI] [PubMed] [Google Scholar]
- 3.Belenky P, Bogan KL, Brenner C. NAD+ metabolism in health and disease. Trends Biochem Sci. 2007;32:12–19. doi: 10.1016/j.tibs.2006.11.006. [DOI] [PubMed] [Google Scholar]
- 4.Pollak N, Dolle C, Ziegler M. The power to reduce: pyridine nucleotides— small molecules with a multitude of functions. Biochem J. 2007;402:205–218. doi: 10.1042/BJ20061638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lee HC. Physiological functions of cyclic ADP-ribose and NAADP as calcium messengers. Ann Rev Pharmacol Toxicol. 2001;41:317–345. doi: 10.1146/annurev.pharmtox.41.1.317. [DOI] [PubMed] [Google Scholar]
- 6.Lee HC. Multiplicity of Ca2+ messengers and Ca2+ stores: a perspective from cyclic ADP-ribose and NAADP. Curr Mol Med. 2004;4:227–237. doi: 10.2174/1566524043360753. [DOI] [PubMed] [Google Scholar]
- 7.Ying WH. NAD+ and NADH in brain functions, brain diseases and brain aging. Front Biosci. 2007;12:1863–1888. doi: 10.2741/2194. [DOI] [PubMed] [Google Scholar]
- 8.Virag L, Szabo C. The therapeutic potential of poly(ADP-ribose) polymerase inhibitors. Pharmacol Rev. 2002;54:375–429. doi: 10.1124/pr.54.3.375. [DOI] [PubMed] [Google Scholar]
- 9.Ying WH. NAD+/NADH and NADP+/NADPH in cellular functions and cell death: regulation and biological consequences. Antioxid Redox Signal. 2008;10:179–206. doi: 10.1089/ars.2007.1672. [DOI] [PubMed] [Google Scholar]
- 10.Chen S, Whetstine JR, Ghosh S, Hanover JA, Gali RR, Grosu P, Shi Y. The conserved NAD(H)-dependent corepressor CTBP-1 regulates Caenorhabditis elegans life span. Proc Natl Acad Sci USA. 2009;106:1496–1501. doi: 10.1073/pnas.0802674106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Eto K, Tsubamoto Y, Terauchi Y, et al. Role of NADH shuttle system in glucose-induced activation of mitochondrial metabolism and insulin secretion. Science. 1999;283:981–985. doi: 10.1126/science.283.5404.981. [DOI] [PubMed] [Google Scholar]
- 12.Garriga-Canut M, Schoenike B, Qazi R, et al. 2-deoxy-D-glucose reduces epilepsy progression by NRSF-CtBP-dependent metabolic regulation of chromatin structure. Nat Neurosci. 2006;9:1382–1387. doi: 10.1038/nn1791. [DOI] [PubMed] [Google Scholar]
- 13.Zhang QH, Wang SY, Nottke AC, Rocheleau JV, Piston DW, Goodman RH. Redox sensor CtBP mediates hypoxia-induced tumor cell migration. Proc Natl Acad Sci USA. 2006;103:9029–9033. doi: 10.1073/pnas.0603269103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Yang HY, Yang T, Baur JA, et al. Nutrient-sensitive mitochondrial NAD+ levels dictate cell survival. Cell. 2007;130:1095–1107. doi: 10.1016/j.cell.2007.07.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Xie WJ, Xu AS, Yeung ES. Determination of NAD+ and NADH in a single cell under hydrogen peroxide stress by capillary electrophoresis. Anal Chem. 2009;81:1280–1284. doi: 10.1021/ac802249m. [DOI] [PubMed] [Google Scholar]
- 16.Chance B, Cohen P, Jobsis F, Schoener B. Intracellular oxidation-reduction states in vivo: the microfluorometry of pyridine nucleotide gives a continuous measurement of the oxidation state. Science. 1962;137:499–508. doi: 10.1126/science.137.3529.499. [DOI] [PubMed] [Google Scholar]
- 17.Kasischke KA, Vishwasrao HD, Fisher PJ, Zipfel WR, Webb WW. Neural activity triggers neuronal oxidative metabolism followed by astrocytic glycolysis. Science. 2004;305:99–103. doi: 10.1126/science.1096485. [DOI] [PubMed] [Google Scholar]
- 18.Patterson GH, Knobel SM, Arkhammar P, Thastrup O, Piston DW. Separation of the glucose-stimulated cytoplasmic mitochondrial NAD(P)H responses in pancreatic islet beta cells. Proc Natl Acad Sci USA. 2000;97:5203–5207. doi: 10.1073/pnas.090098797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Skala MC, Riching KM, Gendron-Fitzpatrick A, Eickhoff J, Eliceiri KW, White JG, Ramanujam N. In vivo multiphoton microscopy of NADH and FAD redox states, fluorescence lifetimes, and cellular morphology in precancerous epithelia. Proc Natl Acad Sci USA. 2007;104:19494–19499. doi: 10.1073/pnas.0708425104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hung YP, Albeck JG, Tantama M, Yellen G. Imaging cytosolic NADH-NAD+ redox state with a genetically encoded fluorescent biosensor. Cell Metab. 2011;14:545–554. doi: 10.1016/j.cmet.2011.08.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zhao YZ, Jin J, Hu QX, Zhou HM, Yi J, Yu ZH, Xu L, Wang X, Yang Y, Loscalzo J. Genetically encoded fluorescent sensors for intracellular NADH detection. Cell Metab. 2011;14:555–566. doi: 10.1016/j.cmet.2011.09.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Shulman RG, Brown TR, Ugurbil K, Ogawa S, Cohen SM, den Hollander JA. Cellular applications of 31P and 13C nuclear magnetic resonance. Science. 1979;205:160–166. doi: 10.1126/science.36664. [DOI] [PubMed] [Google Scholar]
- 23.Akitt JW. NMR and chemistry: an introduction to the fourier transform multinuclear era. New York: Chapman and Hall; 1983. [Google Scholar]
- 24.Navon G, Ogawa S, Shulman RG, Yamane T. High-resolution 31P nuclear magnetic resonance studies of metabolism in aerobic Escherichia coli cells. Proc Natl Acad Sci USA. 1977;74:888–891. doi: 10.1073/pnas.74.3.888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Navon G, Ogawa S, Shulman RG, Yamane T. 31P nuclear magnetic resonance studies of Ehrlich ascites tumor cells. Proc Natl Acad Sci USA. 1977;74:87–91. doi: 10.1073/pnas.74.1.87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhu XH, Chen W. Field dependence of PCr and ATP linewidths and its impact on in vivo 31P MRS studies. Proceedings of the 20th Annual Meeting of ISMRM; Melbourne, Australia. 2012. p. 1781. [Google Scholar]
- 27.Zhu XH, Zhang N, Zhang Y, Ugurbil K, Chen W. New insights into central roles of cerebral oxygen metabolism in the resting and stimulus-evoked brain. J Cereb Blood Flow Metab. 2009;29:10–18. doi: 10.1038/jcbfm.2008.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zhu XH, Zhang Y, Chen W. Absolute quantification of ATP and other high energy phosphate compounds in cat brain at 9.4T. Proceedings of the 17th Annual Meeting of ISMRM; Honolulu, Hawaii, USA. 2009. p. 4287. [Google Scholar]
- 29.Baum J, Tycko R, Pines A. Broad-band and adiabatic inversion of a 2-level system by phase-modulated pulses. Phys Rev A. 1985;32:3435–3447. doi: 10.1103/physreva.32.3435. [DOI] [PubMed] [Google Scholar]
- 30.Silver MS, Joseph RI, Hoult DI. Highly selective Pi/2 and Pi-pulse generation. J Magn Reson. 1984;59:347–351. [Google Scholar]
- 31.de Graaf R. In vivo NMR spectroscopy: principles and techniques. New York: John Wiley & Sons; 1998. [Google Scholar]
- 32.Sonnewald U, Muller TB, Westergaard N, Unsgard G, Petersen SB, Schousboe A. Nmr spectroscopic study of cell cultures of astrocytes and neurons exposed to hypoxia-compartmentation of astrocyte metabolism. Neurochem Int. 1994;24:473–483. doi: 10.1016/0197-0186(94)90095-7. [DOI] [PubMed] [Google Scholar]
- 33.Zeng JY, Hirai K, Yang GY, Ying WH, Swanson RA, Kelly M, Mayer M, James TL, Litt L. Using P-31 NMR spectroscopy at 14. 1 Tesla to investigate PARP-1 associated energy failure and metabolic rescue in cerebrocortical slices. J Bioenerg Biomembr. 2004;36:415–419. doi: 10.1023/B:JOBB.0000041777.07640.64. [DOI] [PubMed] [Google Scholar]
- 34.Lei H, Zhu XH, Zhang XL, Ugurbil K, Chen W. In vivo 31P magnetic resonance spectroscopy of human brain at 7 T: an initial experience. Magn Reson Med. 2003;49:199–205. doi: 10.1002/mrm.10379. [DOI] [PubMed] [Google Scholar]
- 35.Lu M, Zhang Y, Ugurbil K, Chen W, Zhu XH. In vitro and in vivo studies of 17O NMR sensitivity at 9.4 and 16. 4 T. Magn Reson Med. 2013;69:1523–1527. doi: 10.1002/mrm.24386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lu M, Zhang Y, Ugurbil K, Chen W, Zhu XH. Quantitative comparison of 31P relaxation time and NMR sensitivity between 9.4T and 16.4T. Proceedings of the 20th Annual Meeting of ISMRM; Melbourne, Australia. 2012. p. 4423. [Google Scholar]
- 37.Qiao H, Zhang X, Zhu XH, Du F, Chen W. In vivo 31P MRS of human brain at high/ultrahigh fields: a quantitative comparison of NMR detection sensitivity and spectral resolution between 4 T and 7 T. Magn Reson Imaging. 2006;24:1281–1286. doi: 10.1016/j.mri.2006.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lowry OH, Passonneau JV, Rock MK. The stability of pyridine nucleotides. J Biol Chem. 1961;236:2756–2759. [PubMed] [Google Scholar]
- 39.Jacobson KB, Kaplan NO. Pyridine coenzymes of subcellular tissue fractions. J Biol Chem. 1957;226:603–613. [PubMed] [Google Scholar]
- 40.Lowry OH, Passonneau JV, Schulz DW, Rock MK. The measurement of pyridine nucleotides by enzymatic cycling. J Biol Chem. 1961;236:2746–2755. [PubMed] [Google Scholar]
- 41.Guarneri R, Bonavita V. Nicotinamide adenine dinucleotides in the developing rat brain. Brain Res. 1966;2:145–150. doi: 10.1016/0006-8993(66)90019-9. [DOI] [PubMed] [Google Scholar]
- 42.Klaidman LK, Leung AC, Adams JD. High-performance liquid chromatography analysis of oxidized and reduced pyridine dinucleotides in specific brain regions. Anal Biochem. 1995;228:312–317. doi: 10.1006/abio.1995.1356. [DOI] [PubMed] [Google Scholar]
- 43.Cosi C, Marien M. Decreases in mouse brain NAD+ and ATP induced by 1-methyl-4-phenyl-1, 2,3,6-tetrahydropyridine (MPTP): prevention by the poly(ADP-ribose) polymerase inhibitor, benzamide. Brain Res. 1998;809:58–67. doi: 10.1016/s0006-8993(98)00829-4. [DOI] [PubMed] [Google Scholar]
- 44.Klaidman LK, Mukherjee SK, Adams JD., Jr Oxidative changes in brain pyridine nucleotides and neuroprotection using nicotinamide. Biochim Biophys Acta. 2001;1525:136–148. doi: 10.1016/s0304-4165(00)00181-1. [DOI] [PubMed] [Google Scholar]
- 45.Mack TG, Reiner M, Beirowski B, et al. Wallerian degeneration of injured axons and synapses is delayed by a Ube4b/Nmnat chimeric gene. Nat Neurosci. 2001;4:1199–1206. doi: 10.1038/nn770. [DOI] [PubMed] [Google Scholar]
- 46.Kannurpatti SS, Sanganahalli BG, Mishra S, Joshi PG, Joshi NB. Glutamate- induced differential mitochondrial response in young and adult rats. Neurochem Int. 2004;44:361–369. doi: 10.1016/s0197-0186(03)00164-5. [DOI] [PubMed] [Google Scholar]
- 47.Wang J, He Z. NAD and axon degeneration: from the Wlds gene to neurochemistry. Cell Adh Migr. 2009;3:77–87. doi: 10.4161/cam.3.1.7483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Pittelli M, Formentini L, Faraco G, et al. Inhibition of nicotinamide phosphoribosyltransferase: cellular bioenergetics reveals a mitochondrial insensitive NAD pool. J Biol Chem. 2010;285:34106–34114. doi: 10.1074/jbc.M110.136739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wilhelm F, Hirrlinger J. The NAD+/NADH redox state in astrocytes: independent control of the NAD+ and NADH content. J Neurosci Res. 2011;89:1956–1964. doi: 10.1002/jnr.22638. [DOI] [PubMed] [Google Scholar]
- 50.Canto C, Houtkooper RH, Pirinen E, et al. The NAD+ precursor nicotinamide riboside enhances oxidative metabolism and protects against high-fat diet-induced obesity. Cell Metab. 2012;15:838–847. doi: 10.1016/j.cmet.2012.04.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Salek RM, Pears MR, Cooper JD, Mitchison HM, Pearce DA, Mortishire-Smith RJ, Griffin JL. A metabolomic comparison of mouse models of the neuronal ceroid lipofuscinoses. J Biomol NMR. 2011;49:175–184. doi: 10.1007/s10858-011-9491-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Zhu XH, Lu M, Zhang Y, Chen W. In vivo 31P MRS imaging of intracellular NAD contents and NAD+/NADH redox states in normal and ischemic brains. Proceedings of the 21st Annual Meeting of ISMRM; Salt Lake City, Utah, USA. 2013. p. 861. [Google Scholar]
- 53.Zhu XH, Lu M, Lee BY, Ugurbil K, Chen W. In vivo MR study of intracellular NAD contents and redox state in healthy human brain. Proceedings of the 21st Annual Meeting of ISMRM; Salt Lake City, Utah, USA. 2013. p. 859. [Google Scholar]
- 54.Sies H. Metabolic compartmentation. London: Academic Press; 1982. [Google Scholar]
- 55.Siesjo BK. Brain energy metabolism. New York: Wiley; 1978. pp. 101–110. [Google Scholar]
- 56.Feeney J, Birdsall B, Roberts GC, Burgen AS. 31P NMR studies of NADPH and NADP+ binding to L. casei dihydrofolate reductase. Nature. 1975;257:564–566. doi: 10.1038/257564a0. [DOI] [PubMed] [Google Scholar]
- 57.Mas MT, Colman RF. Phosphorus-31 nuclear magnetic resonance studies of the binding of nucleotides to NADP+-specific isocitrate dehydrogenase. Biochemistry. 1984;23:1675–1683. doi: 10.1021/bi00303a015. [DOI] [PubMed] [Google Scholar]
- 58.Fan TW-M. Metabolite profiling by one- and two-dimensional NMR analysis of complex mixtures. Progr Nucl Magn Reson Spectrosc. 1996;28:161–219. [Google Scholar]
- 59.Navon G, Shulman RG, Yamane T, Eccleshall TR, Lam KB, Baronofsky JJ, Marmur J. Phosphorus-31 nuclear magnetic resonance studies of wild-type and glycolytic pathway mutants of Saccharomyces cerevisiae. Biochemistry. 1979;18:4487–4499. doi: 10.1021/bi00588a006. [DOI] [PubMed] [Google Scholar]
- 60.Blumenstein M, Raftery MA. 31P and 13C nuclear magnetic resonance studies of nicotinamide-adenine dinucleotide and related compounds. Biochemistry. 1972;11:1643–1648. doi: 10.1021/bi00759a017. [DOI] [PubMed] [Google Scholar]
- 61.Marshall I, Higinbotham J, Bruce S, Freise A. Use of Voigt lineshape for quantification of in vivo 1H spectra. Magn Reson Med. 1997;37:651–657. doi: 10.1002/mrm.1910370504. [DOI] [PubMed] [Google Scholar]
- 62.Du F, Zhu XH, Zhang Y, Friedman M, Zhang N, Ugurbil K, Chen W. Tightly coupled brain activity and cerebral ATP metabolic rate. Proc Natl Acad Sci USA. 2008;105:6409–6414. doi: 10.1073/pnas.0710766105. [DOI] [PMC free article] [PubMed] [Google Scholar]