Abstract
Titratable systems are common tools in metabolic engineering to tune the levels of enzymes and cellular components as part of pathway optimization. For nonmodel microorganisms with limited genetic tools, inducible sugar utilization pathways offer built-in titratable systems. However, these pathways can exhibit undesirable single-cell behaviors that hamper the uniform and tunable control of gene expression. Here, we applied mathematical modeling and single-cell measurements of l-arabinose utilization in Escherichia coli to systematically explore how sugar utilization pathways can be altered to achieve desirable inducible properties. We found that different pathway alterations, such as the removal of catabolism, constitutive expression of high-affinity or low-affinity transporters, or further deletion of the other transporters, came with trade-offs specific to each alteration. For instance, sugar catabolism improved the uniformity and linearity of the response at the cost of requiring higher sugar concentrations to induce the pathway. Within these alterations, we also found that a uniform and linear response could be achieved with a single alteration: constitutively expressing the high-affinity transporter. Equivalent modifications to the d-xylose utilization pathway yielded similar responses, demonstrating the applicability of our observations. Overall, our findings indicate that there is no ideal set of typical alterations when co-opting natural utilization pathways for titratable control and suggest design rules for manipulating these pathways to advance basic genetic studies and the metabolic engineering of microorganisms for optimized chemical production.
Keywords: carbon catabolism, Escherichia coli, feedback, inducible systems, linearization, systems biology
Metabolic engineering requires the optimization of native and heterologous pathways in order to maximize the yield of the desired chemical product, prevent the buildup of toxic intermediates, and maintain cell viability. A common strategy is finely tuning the expression of each cellular component using titratable systems.1−3 These systems rely on exogenous inducer molecules to tune the expression levels of regulated genes; by varying the concentration of the inducer, the expression levels of the gene can be manipulated without additional genetic modifications to the host organism. A number of titratable systems are available that were derived from or inspired by natural processes—including nutrient utilization pathways,2−5 riboswitches,6−9 antibiotic resistance cassettes,10−12 quorum sensing,13 and light sensing.14
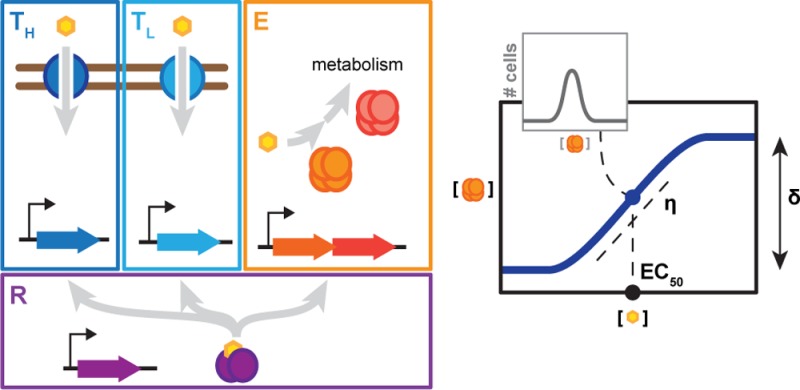
Metabolic engineering has been more frequently adopting nonmodel organisms that already possess desired pathways or have adapted to environments that parallel production conditions.15 Achieving titratable control in these organisms is more challenging because of limited genetic tools as well as growth conditions that perturb the stability and function of the inducers or regulators. However, these organisms often encode multiple sugar utilization pathways that can serve as ready-made titratable systems.16−25 Sugar utilization pathways are generally composed of transporters that import the sugar into the cytoplasm, catabolic enzymes that shunt the sugar into central metabolism, and regulators that activate the expression of the transporters and the enzymes when bound to the sugar (Figure 1A). Furthermore, pathways often respond to their individual sugar, offering orthogonal systems for the coordinated optimization of gene expression.
Figure 1.
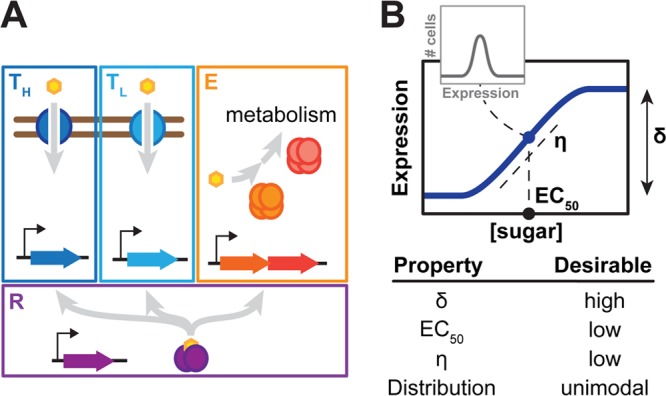
Co-opting sugar utilization pathways for titratable control of gene expression. (A) Components of inducible sugar utilization pathways. High affinity (TH) and low-affinity (TL) transporters import the sugar into the cell, while catabolic enzymes (E) shunt the sugar into central metabolism. Transcription regulators (R) up-regulate the expression of the transporters and the enzymes, but only in the presence of the sugar. (B) Desirable properties for a titratable response. These properties include a uniform response at all inducer concentrations, a large dynamic range (high δ), low inducer concentrations to induce the pathway (low EC50), and strong linearity (low η).
The drawback of co-opting natural utilization pathways is their potential to exhibit undesirable behaviors. While an ideal titratable response should be uniform and linear (Figure 1B), sugar utilization pathways have been shown to exhibit bimodal, sharp responses that prevent fine-tuning of expression levels in all cells of the population.26−30 These responses can be attributed to positive feedback within the pathway, which emerges from the sugar inducing the transporters that import more sugar into the cell.27,29,31,32 The pathways also possess negative feedback from induction of the catabolic enzymes that break down the sugar.33 While negative feedback would be expected to counterbalance positive feedback,33,34 sugar catabolism also degrades the inducing sugar. With all of these contributing factors, a fundamental question is how to modify a given pathway to achieve a desirable titratable response.
A powerful model has been the l-arabinose utilization pathway in Escherichia coli. This pathway encodes one high-affinity transporter (encoded within the araFGH operon) and one low affinity transporter (encoded by the araE gene), is well characterized, and has been regularly used for inducible control. This pathway has also been shown to exhibit a bimodal response, complicating its use as a titratable system.26 Accordingly, previous efforts sought to eliminate bimodality through the overexpression of one transporter along with multiple alterations to the pathway. Khlebnikov and co-workers demonstrated that heterologously expressing the low-affinity transporter AraE could remove bimodality, which required disrupting both endogenous transporters.35,36 Separately, Morgan-Kiss and co-workers demonstrated that heterologously expressing a substrate-relaxed mutant of the lactose transporter could eliminate bimodality in a strain lacking the l-arabinose transporters and catabolic enzymes.37 As a result, the consensus is that overexpressing a transporter and stripping away almost all native components of the pathway should be performed to achieve titratable control. While these studies laid the groundwork for generating utilization pathways with titratable responses, they called for extensive genetic manipulations (i.e., plasmid-based expression of a transporter, disruption of multiple genetic loci) that may be difficult to achieve in nonmodel organisms and may not reflect ideal configurations for titratable control. In addition, a systematic analysis of all pathway alterations remains to be performed, which could reveal other configurations that require fewer modifications or generate a more desirable titratable response.
Here, we systematically evaluated how natural utilization pathways can be altered to achieve titratable control. Mathematical modeling and experimental probing of the l-arabinose utilization pathway revealed distinct trade-offs when altering the pathway: (i) constitutively expressing the low affinity-transporter yielded the most linear response but required additional modifications to eliminate bimodality, (ii) constitutively expressing one transporter and deleting the other transporter had both positive and negative effects on the response properties specific to the selected transporter, and (iii) sugar catabolism linearized the response and reduced the extent of bimodality at the cost of elevated sugar concentrations to induce the pathway. Within these trade-offs, one of the most desirable responses came from a single alteration: constitutively expressing the high-affinity transporter. Furthermore, maintaining sugar catabolism improved the linearity of the response at higher cell densities, perceivably due to negative feedback through depletion of the exogenous sugar. Similar trends were observed for the d-xylose utilization pathway, suggesting broad applicability of our findings. These insights demonstrate that there is no perfect set of typical alterations when co-opting sugar utilization pathways, wherein the optimal configuration will depend on the specific demands placed on the titratable system.
Results and Discussion
We considered four metrics to assess the desirability of the response (Figure 1B): the extent of bimodality (the number of peaks in the fluorescence distribution), the dynamic range of the response (δ, measured as the ratio of expression levels at full and no induction), the inducer concentration to achieve half-maximal induction (EC50), and the steepness of the response curve (η, measured as a Hill coefficient). An ideal titratable system would exhibit uniform expression across the cell population at all inducer concentrations, a large dynamic range, a low inducer concentration to achieve half-maximal induction, and a low Hill coefficient reflecting the steepness of the response curve. We used these metrics as the basis to evaluate the predicted or measured behaviors of sugar utilization.
Simple Mathematical Model of Sugar Utilization
We built a simple mathematical model of sugar utilization to qualitatively explore how different alterations to the pathway influence the response properties (see Supporting Information). This model was composed of two transporters that import sugar into the cell, one enzyme that breaks down the sugar, and one regulator that binds the sugar and subsequently activates the expression of the transporters and the enzyme. This general configuration captures the l-arabinose utilization pathway and many other pathways found in microorganisms.16−25 Parameter values were selected for one high-affinity/low-capacity transporter and one low-affinity/high-capacity transporter at biologically relevant expression strengths and activities to yield a bistable response (Figure 2, see Supporting Information). This configuration parallels the l-arabinose utilization pathway and creates an undesired behavior for titratable control.
Figure 2.
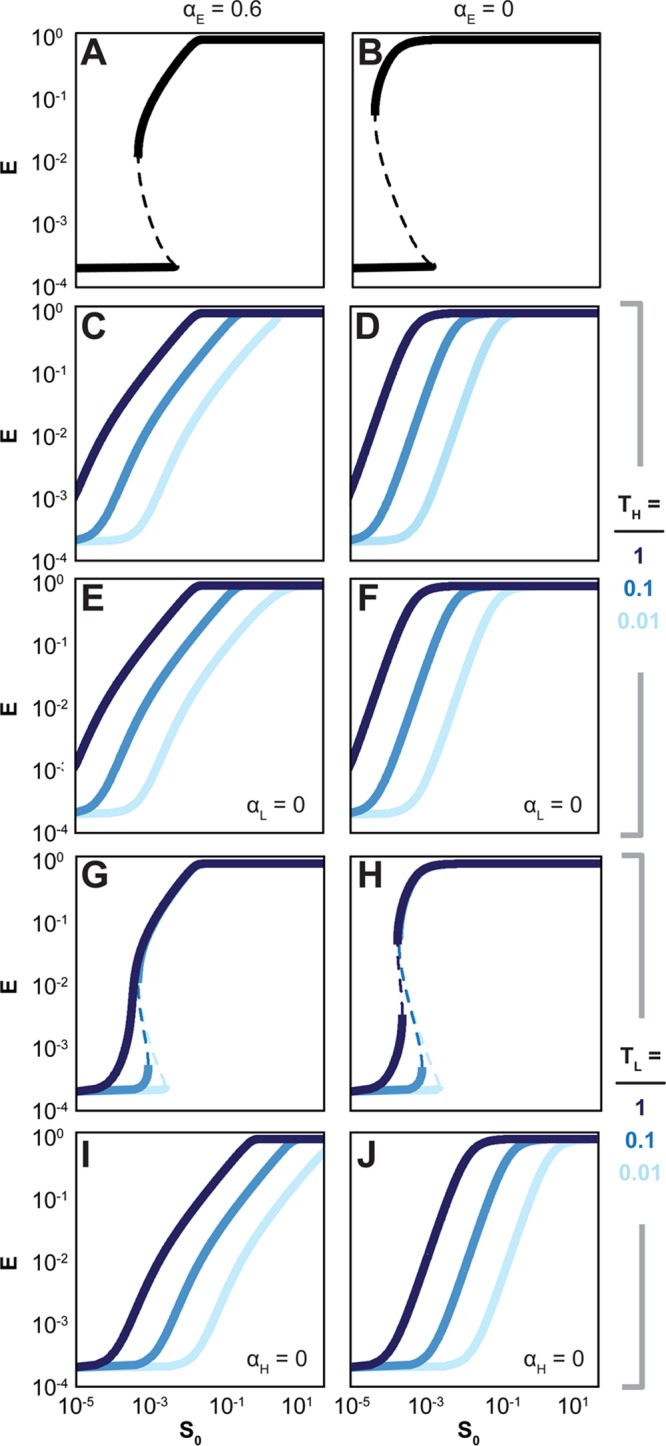
Simple mathematical model predicts trade-offs when altering the pathway structure. (A) The model assumes a base pathway comprising a high-affinity/low-capacity transporter (TH) and a low-affinity/high-capacity transporter (TL) that import extracellular sugar (S0) into the cell, a catabolic enzyme (E) that degrades the sugar, and a constitutively expressed regulator that upregulates the expression of the transporters and the enzymes when bound to the sugar. The steady-state expression levels of the enzyme are reported as a function of extracellular sugar concentration. Note that all variables were nondimensionalized as part of the model derivation. Dashed lines indicate bifurcation regions. To alter the pathway, TH was constitutively expressed (C,D) and the activity of TL was further eliminated (E,F), TL was constitutively expressed (G,H) and the activity of TH was further eliminated (I,J), and the activity of the catabolic enzymes was eliminated (B,D,F,H,J). Three strengths of constitutive expression were selected for TH and TL (low, light blue; medium, blue; high, dark blue). See Supporting Information (SI) for more details.
Experimentally Probing l-arabinose Utilization to Explore Model Predictions
We concurrently altered and assessed the l-arabinose utilization pathway in E. coli K-12. This pathway was attractive because of its extensive characterization,38 its widespread use as a titratable system,2 and its bimodal response that prevents titratable control.26,35,37 The pathway comprises three enzymes (encoded by araBAD) that shunt l-arabinose into the pentose phosphate pathway, a low-affinity transporter (encoded by araE), a high-affinity transporter (encoded by araFGH), and a dual transcription regulator (encoded by araC) that upregulates the expression of all other pathway components when bound to l-arabinose (SI Figure S1A). A third l-arabinose-responsive gene (araJ) encodes a putative transporter, although this gene appears to contribute negligibly to the pathway response39,40 and thus was not considered in our analyses.
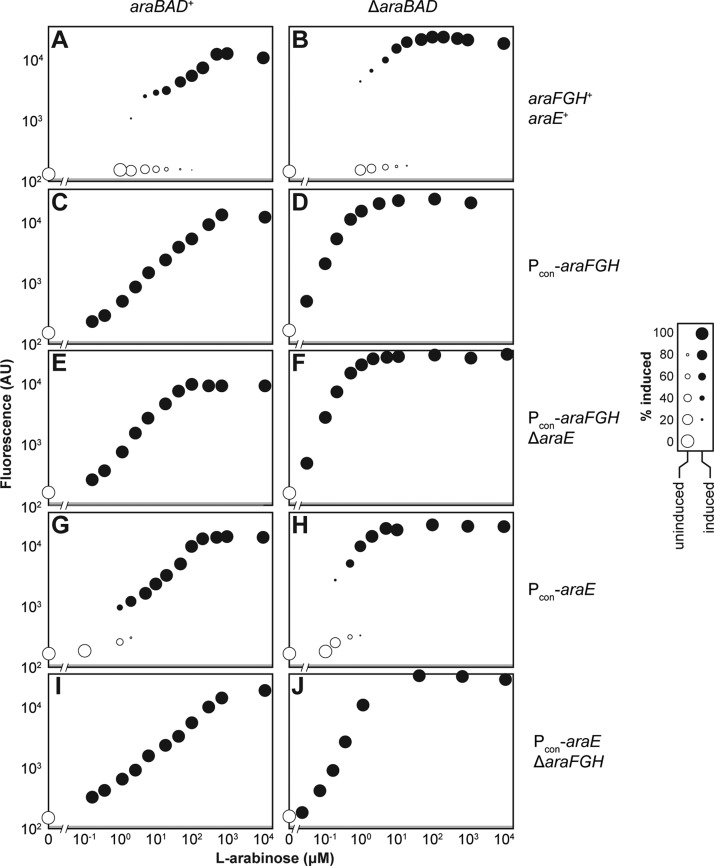
To measure the response to l-arabinose, we equipped the wild type (WT) strain of E. coli MG1655 with a low-copy plasmid encoding the araB promoter upstream of the green fluorescent protein (GFP) gene.41 The associated strain was then grown for 6 h in a defined medium supplemented with different concentrations of l-arabinose to mid log phase (ABS600 ∼ 0.4) and subjected to flow cytometry analysis (SI Figure S2). The incubation time was selected such that longer incubation times would yield similar fluorescence distributions (SI Figure S3). Figure 3 displays representative response curves while Table 1 reports the calculated response metrics. The response curves are depicted as dot plots to capture the extent of bimodality within each fluorescence distribution (the relative size of each dot) and the fluorescence of each subpopulation (vertical location of each dot). Following this approach, the WT strain yielded a bimodal response across a wide range of l-arabinose concentrations (Figure 3A, Table 1) similar to previous observations.35,37
Figure 3.
Probing alterations to the l-arabinose utilization pathway in E. coli. The wild type pathway (A) was subjected to different alterations: araFGH was constitutively expressed (Pcon-araFGH) (C,D) and araE was further deleted (ΔaraE) (E,F), araE was constitutively expressed (Pcon-araE) (G,H) and araFGH was further deleted (ΔaraFGH) (I,J), and araBAD was deleted (ΔaraBAD) (B,D,F,H,J). Each designated strain was back-diluted into M9 minimal medium supplemented with the indicated concentration of l-arabinose and grown for 6 h to ABS600 ∼ 0.4 prior to flow cytometry analysis. For unimodal distributions, the resulting mean fluorescence is plotted. For bimodal distributions, two dots are plotted to represent the mean fluorescence and the relative number of cells in the induced (black) and uninduced (white) subpopulations (see SI Figure S2 for more details on the flow cytometry analysis). The diameter of each dot is directly proportional to the fraction of cells in that subpopulation. Gray boxes indicate the limit of detection due to autofluorescence. Each dot plot is representative of at least three independent experiments conducted on separate days. See Table 1 for the response metrics that account for the replicate experiments.
Table 1. Response Metrics for Each Alteration of the l-arabinose Utilization Pathway in E. colia.
| alteration | bimodality (Y/n) | δ | EC50 (μM) | η |
|---|---|---|---|---|
| none (WT) | Y | 958 ± 118 | 205 ×/÷ 2.08 | 0.89 ± 0.19 |
| ΔaraBAD | Y | 1023 ± 235 | 9.8 ×/÷ 1.17 | 1.56 ± 0.14 |
| Pcon-araFGH | n | 290 ± 114 | 160 ×/÷ 1.47 | 0.96 ± 0.06 |
| Pcon-araFGH ΔaraBAD | n | 900 ± 288 | 0.54 ×/÷ 1.20 | 1.44 ± 0.07 |
| Pcon-araFGH ΔaraE | n | 262 ± 17 | 56 ×/÷ 1.16 | 1.18 ± 0.03 |
| Pcon-araFGH ΔaraE ΔaraBAD | n | 1440 ± 300 | 0.48 ×/÷ 1.15 | 1.65 ± 0.03 |
| Pcon-araE | Y | 828 ± 282 | 284 ×/÷ 1.02 | 0.75 ± 0.04 |
| Pcon-araE ΔaraBAD | Y | 1351 ± 265 | 0.86 ×/÷ 1.08 | 3.27 ± 0.30 |
| Pcon-araE ΔaraFGH | n | 737 ± 323 | 626 ×/÷ 1.56 | 0.76 ± 0.02 |
| Pcon-araE ΔaraFGH ΔaraBAD | n | 728 ± 407 | 7.5 ×/÷ 1.04 | 1.67 ± 0.09 |
| Pcon-araE ΔaraFGH (ABS600 ∼ 0.004) | n | 517 ± 141 | 10.1 ×/÷ 1.13 | 1.47 ± 0.03 |
| Pcon-araE ΔaraFGH ΔaraBAD (ABS600 ∼ 0.004) | n | 663 ± 128 | 7.1 ×/÷ 1.10 | 1.86 ± 0.01 |
| Pcon-araE ΔaraFGH (ABS600 ∼ 0.04) | n | 371 ± 91 | 21.2 ×/÷ 1.13 | 1.25 ± 0.10 |
| Pcon-araE ΔaraFGH ΔaraBAD (ABS600 ∼ 0.04) | n | 512 ± 78 | 8.6 ×/÷ 1.32 | 1.78 ± 0.08 |
| Pcon-araE ΔaraFGH (ABS600 ∼ 1.0) | n | 1060 ± 161 | 2050 ×/÷ 1.07 | 0.73 ± 0.01 |
| Pcon-araE ΔaraFGH ΔaraBAD (ABS600 ∼ 1.0) | n | 2410 ± 590 | 7.7 ×/÷ 1.19 | 1.64 ± 0.02 |
Listed values are the mean and S.E.M. (dynamic range, δ; Hill coefficient, η) or the geometric mean and geometric S.E.M. (effective concentration to achieve 50% induction, EC50) for three independent experiments conducted on separate days. All values reflect cultures grown to ABS600 ∼ 0.4 unless indicated otherwise. The dynamic range was calculated as the ratio of the maximal to minimal mean fluorescence of the entire population, with autofluorescence subtracted from each value. The large error associated with the dynamic range can be attributed to basal levels approaching autofluorescence of cells lacking the reporter plasmid.
Constitutively Expressing the High-Affinity Transporter More Readily Generates a Uniform Response
We considered different alterations to sugar utilization pathways that were previously applied: constitutively expressing one of the transporters, deleting the other transporter, and deleting the catabolic genes.35−37 From a network perspective, each alteration affects feedback within the pathway: constitutively expressing or deleting the transporter genes disrupts positive feedback, whereas deleting the catabolic genes disrupts negative feedback. While differential growth on the sugar could also impart feedback,42 we found that the addition of l-arabinose did not have a major impact on growth rates for any of the pathway alterations (SI Table S1).
We first explored the impact of constitutively expressing either transporter to partially disrupt positive feedback in the pathway. Within the model, we replaced the regulator-dependent expression term for either transporter with different constant values. We found that all evaluated expression strengths of the high-affinity transporter eliminated the bifurcation region (Figure 2C). In contrast, only the highest expression strength of the low-affinity transporter eliminated the bifurcation region (Figure 2G). In both cases, increasing the promoter strength reduced the EC50 value by allowing greater sugar import at lower extracellular concentrations. Because positive feedback is required for bistability, the model predictions suggest that the high-affinity transporter rather than the low-affinity transporter primarily drives bistability, at least under the selected parameter set.
To experimentally probe model predictions, we replaced the native araF or araE promoter with a medium-strength, synthetic promoter (Pcon-araFGH or Pcon-araE) and measured the response to l-arabinose (Figure 3C,G). Paralleling model predictions, constitutively expressing the high-affinity transporter eliminated bimodality, whereas constitutively expressing the araE low-affinity transporter reduced but did not eliminate bimodality. These results clearly demonstrate that (i) constitutively expressing the high-affinity transporter araFGH more readily generated a uniform response and (ii) only a single modification was required to fully convert a bimodal response into a uniform response.
Trade-offs when Deleting One Transporter
We next explored the impact of deleting one of the transporters when the other transporter was constitutively expressed. Within the model, the second transporter was removed by setting its maximal activity (αH, αL) equal to zero. The resulting impact on the predicted response was mixed and specific to the transporter (Figure 2E,I). Removing the high-affinity transporter from the pathway with a constitutively expressed low-affinity transporter eliminated the bifurcation region but also shifted the curves to higher extracellular sugar concentrations (Figure 2I). This effect may be attributed to the high-affinity transporter allowing sugar import at lower sugar concentrations while driving positive feedback within the pathway. In support of model predictions, deletion of the araFGH operon (ΔaraFGH) from the l-arabinose pathway with constitutively expressed araE resulted in a uniform response with a modest but statistically significant increase in the EC50 value (p-value = 0.019) (Figure 3I, Table 1).
The model predicted that removing the low-affinity transporter from the pathway constitutively expressing the high-affinity transporter had a negligible effect (compare parts C and E in Figure 2). While this may suggest that the low-affinity transporter is poorly induced for our parameter set, the low-affinity transporter alone could mediate full induction of the pathway at high extracellular sugar concentrations (SI Figure S4). Deletion of araE (ΔaraE) from the l-arabinose utilization pathway constitutively expressing araFGH also maintained the uniform response (Figure 3E). However, there was a significant decrease in the EC50 value (p-value = 0.008) and a significant increase in the Hill coefficient (p-value = 0.003). These changes would suggest that the low-affinity transporter contributes more than that predicted by the model by extending the concentration range that titrates the response. These changes also suggest that deletion of the low-affinity transporter poses a distinct trade-off: a lower EC50 value at the cost of a sharper response.
Trade-offs when Eliminating Sugar Catabolism
We next explored the impact of removing sugar catabolism. Previous work concluded that catabolism posed a barrier to a titratable response by breaking down the inducing molecule.37 Separately, sugar catabolism was predicted to entirely eliminate bistability,33 suggesting conflicting contributions. To examine the impact of removing catabolism in the model, we set the activity of the enzyme equal to zero (αE = 0) and evaluated the impact on the response metrics for all pathway configurations (Figure 2B, D, F, H, J). The model predicted both positive and negative effects of removing catabolism. As a positive effect, removing sugar catabolism lowered the apparent EC50 value by preventing the intracellular breakdown of the sugar. As two negative effects, removing sugar catabolism enhanced the propensity for bistability and sharpened the response. Both negative effects can be attributed to sugar catabolism conferring negative feedback on the pathway similar to negative feedback in transcriptional circuits.34,43,44
To test these predictions, we deleted the araBAD operon (ΔaraBAD) from all strains and measured the single-cell response curves (Figure 3B, D, F, H, J; Table 1). For all pathways (Figure 3), the response metrics aligned with model predictions. In particular, removing l-arabinose catabolism significantly lowered the EC50 value (p-values = 1 × 10–6 to 0.008), with over 100-fold differences in some cases. Furthermore, removing l-arabinose catabolism sharpened the response (p-values = 3 × 10–5 to 0.005) and increased the propensity for bimodality. Finally, removing l-arabinose catabolism did not have a consistent impact on the dynamic range, where a statistically significant increase was observed for only two strains (Pcon-araFGH, p-value = 0.027; Pcon-araFGH ΔaraE, p-value = 0.010) (Table 1). Thus, we conclude that removing l-arabinose catabolism poses a major trade-off between the amount of sugar necessary to induce the pathway and the sharpness of the response.
Breakdown of the Sugar Can Help Linearize the Response
Catabolism can deplete the reserve of sugar in the medium, which has been viewed as a barrier to the generation of titratable systems.37 However, such depletion would form negative feedback by depleting the available sugar to induce the pathway, potentially benefiting the response. To explore these potential effects, we first modified the simple model to allow for the depletion of the extracellular sugar through catabolism (see Supporting Information). The resulting model was then employed to predict the response in the presence of catabolism. As part of the model, we could specify the relative volume of the cells to the medium (ν), which dictates in part the rate of depletion. We specifically focused on the pathway with the constitutively expressed low-affinity transporter (TL = 0.02) and the deleted high-affinity transporter (αH = 0) that yielded a graded response in the presence or absence of sugar catabolism. The model predicted that depletion of the extracellular sugar flattened the curve and elevated the EC50 value (Figure 4A). High depletion (ν = 0.01) was detrimental based on the sharp response close to saturating sugar concentrations, although intermediate depletion (ν < 0.01) improved the overall linearity of the response.
Figure 4.
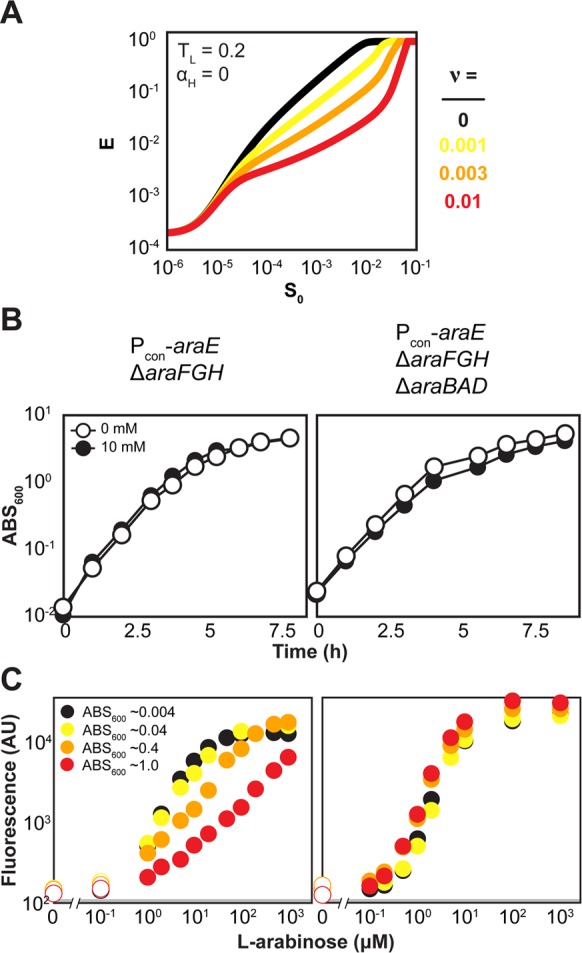
Effect of cell density in the presence or absence of sugar catabolism. (A) Model predictions for the pathway with a constitutively expressed low-affinity transporter (TL = 0.2) and the deleted high-affinity transporter (αH = 0) when accounting for depletion of extracellular sugar through catabolism. Each simulation was conducted to τ = 10. The different curves reflect the relative volume of the cells to the medium (ν). Note that all variables were nondimensionalized as part of the model derivation. See Supporting Information for more details. (B) Growth curves for the Pcon-araE ΔaraFGH strain with or without (ΔaraBAD) sugar catabolism in defined medium with or without 10 mM l-arabinose. Each value represents the mean of three independent experiments. The SEM for each measurement was smaller than the symbol. (C) Representative dot plots for both strains in log phase grown to the indicated final cell densities. See Figure 3 for more information on the dot plots. Each dot plot is representative of at least three experiments conducted from independent colonies. See Table 1 for the response metrics that account for the replicate experiments.
To test these predictions, we cultured the Pcon-araFGH ΔaraE and Pcon-araFGH ΔaraE ΔaraBAD strains for 6 h to final cell densities ranging from ABS600 ∼ 0.004 to ABS600 ∼ 1.0 (Figure 4B). Our reasoning was that extracellular l-arabinose would be more depleted at higher densities, but only in the strain with catabolism. For this strain, we observed higher EC50 values and lower Hill coefficients with increasing cell densities, paralleling model predictions (Figure 4C, Table 1). For the strain lacking catabolism, we observed similar EC50 values and Hill coefficients for all cell densities. These findings provide further support for a surprising benefit of sugar catabolism at higher densities and offer a separate form of negative feedback in sugar utilization that may generate more desirable titratable responses. A notable downside to this strategy is that the extent of induction peaks and then decreases over time at higher cell densities (SI Figure S5), potentially complicating the tuning of expression levels.
Similar Trends When Linearizing the Response to d-xylose
To extend the generality of our insights, we focused on the d-xylose utilization pathway in E. coli. Similar to the l-arabinose utilization pathway, the d-xylose utilization pathway encodes a high-affinity transporter and a low-affinity transporter, a transcriptional activator that recognizes d-xylose, and enzymes that shunt d-xylose into the pentose phosphate pathway (Figure S1B). Also paralleling the l-arabinose utilization pathway, the d-xylose utilization pathway exhibits a bimodal response when tracking the activity of the xylA promoter (Figure 5A).
Figure 5.
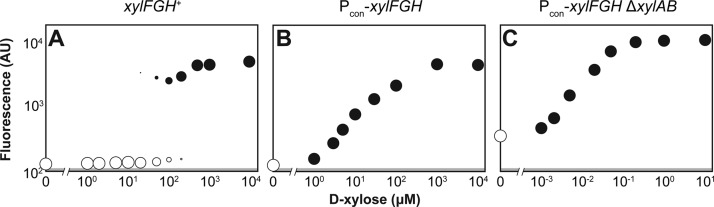
Linearizing the response to d-xylose. The wild type E. coli strain (A), the strain constitutively expressing the high-affinity transporter xylFGH (B), and the strain constitutively expressing the high-affinity transporter xylFGH and lacking the catabolic operon xylAB (C) each harbored the reporter plasmid pUA66-pxylA. The designated strain was back-diluted into M9 minimal medium supplemented with the indicated concentration of d-xylose and grown for 6 h to ABS600 ∼ 0.4 prior to flow cytometry analysis. See Figure 3 for more information on the dot plots. Each dot plot is representative of at least three experiments conducted from independent colonies.
We first asked how constitutively expressing the native high-affinity transporter (xylFGH) impacts the response. Paralleling the l-arabinose utilization pathway, constitutively expressing the endogenous copy of xylFGH resulted in a graded response at all examined d-xylose concentrations (Figure 5B). We next deleted the catabolic operon (xylAB) to evaluate the impact of removing d-xylose catabolism. Further paralleling the l-arabinose utilization pathway, deletion of the catabolic operon significantly reduced the EC50 value (99.8 μM ×/÷ 2.20 to 0.033 μM ×/÷ 1.10, p-value = 0.0014) at the cost of an increased Hill coefficient (1.00 ± 0.08 to 1.58 ± 0.24, p-value = 0.019) (Figure 5B). Collectively, we were able to generate a linear response to d-xylose through a single alteration and observed similar trade-offs when further deleting sugar catabolism, all matching our observations for the l-arabinose utilization pathway.
Design Rules to Engineer Sugar Utilization Pathways for Titratable Control
Overall, our combination of mathematical modeling and experimental probing of l-arabinose and d-xylose utilization suggest general design rules when co-opting natural sugar utilization pathways as titratable systems. The principal rule is that there is no single, perfect set of alterations within the commonly used set that we investigated. Instead, each alteration comes with specific trade-offs beyond the required number of genomic alterations. Accordingly, the best set of alterations will depend on the demands of the desired titratable system. For instance, systems that rely on expensive inducers would opt for modifications that minimize the EC50 value, whereas systems that require fine-tuning would minimize the Hill coefficient. The trade-offs principally applied to the EC50 value and the Hill coefficient, whereas alterations did not predictably impact the dynamic range.
The next rule pertains to the need for a uniform response free of bimodality. A uniform response can be most readily achieved by constitutively expressing the high-affinity transporter rather than the low-affinity transporter. Theoretically, sufficient expression of either transporter can eliminate bimodality, although the high-affinity transporter could be expressed at much lower levels. The advantage of this strategy is that lower expression conserves cellular resources and limits the toxicity of overexpressing membrane proteins.
The third rule relates to trade-offs associated with removing one transporter when the other is constitutively expressed. Removing the high-affinity transporter can help eliminate bimodality at the potential cost of a higher EC50 value, whereas removing the low-affinity transporter reduces the EC50 value at the cost of a sharper response. An alternative would be constitutively expressing the second transporter, which could be explored in future studies.
A final rule pertains to sugar catabolism. Aside from requiring higher sugar concentrations to induce the pathway, sugar catabolism helps reduce the extent of bimodality and linearizes the response. Linearization may be further enhanced when cultures are grown to higher cell densities. Achieving consistent densities between experiments may be challenging and entry into stationary phase may alter pathway activity (SI Figure S5). Furthermore, sugar catabolism may perturb central metabolism as part of metabolic engineering that complicates the results. However, the enhanced linearity would offer finely tuned control over gene expression that may be essential when precise pathway optimization is needed.
The design rules described above were extracted from a simple model and probing of l-arabinose utilization. The rules also applied to the d-xylose utilization pathway, suggesting broader applicability. However, many utilization pathways exhibit variations on the simple pathway, such as anabolic pathways45 or pathways that are induced by metabolic intermediates.46 Further analysis of these pathways will offer insights into the desirability of their natural responses and any required manipulations. Separately, we relied on a more restrained parameter set to probe alterations. Further interrogating parameter space may reveal other parameters and design rules tailored to the behavior of the native pathway. With additional insights, a set of more detailed design principles could be developed. The end result will be reliable means to convert the myriad of sugar utilization pathways in the microbial world into versatile titratable systems for fundamental genetic studies and for the engineering of microorganisms with optimized metabolic processes.
Methods
Bacterial Strains and Plasmids
All strains used in this work were derived from Escherichia coli K-12 substrain MG1655 and are listed in SI Table S2. With the exception of [ΔxylAB PxylF]::[cat Pcon], all genome modifications were achieved by PCR amplifying the bla or cat resistance cassette from pKD3 and recombineering the linear DNA into NM400 through mini-λ-mediated recombination.47 The corresponding oligonucleotides are listed in SI Table S4. To insert the constitutive promoters, the promoter sequence (J23110 from the Registry of Standard Biological Parts) was included in one of the primers used to amplify the resistance cassette followed by a second set of primers to add the homology arms for recombination. Successful recombinants were verified by PCR and by sequencing. The genomic locus with the resistance cassette was then transferred to MG1655 by P1 transduction. In the case of ΔaraBAD::cat, the cat cassette was excised with the pCP20 plasmid to allow for the subsequent insertion of the cat cassette as part of the replacement of the promoters for araE or for araFGH.48 All P1 transductions were verified by PCR. In the case of [ΔxylAB PxylF]::[cat Pcon], the amplified cat cassette was recombineered directly into MG1655 using pDK46.
Once generated, each strain was transformed with the pUA66-ParaB or pUA66-PxylA reporter plasmid encoding the low-copy sc101 origin-of-replication, the promoter region of the araBAD operon or the xylAB operon, respectively, and a downstream copy of gfpmut2 with a strong ribosome-binding site sequence.41 The reporter plasmids along with the cloning and recombination plasmids are listed in SI Table S3. Each reporter plasmid offers a balance between maximizing the fluorescence for high sensitivity and minimizing the copy number to limit titration of the transcription regulators AraC and XylR.49
Growth Conditions and Media
Strains harboring the reporter plasmid were streaked out from glycerol stocks onto LB plates supplemented with appropriate antibiotics. Single colonies were then inoculated in 2 mL of M9 minimal medium (1X M9 salts, 10 μg/mL thiamine, 2 mM MgSO4, 0.1 mM CaCl2 supplemented with 0.4% glycerol, 0.2% casamino acids, and 0.25 μg/mL kanamycin) and grown overnight at 250 rpm and 37 °C. The overnight cultures were then back-diluted into 2 mL of the same medium with varying concentrations of the indicated sugar and grown under the same conditions for 6 h to a final ABS600 of ∼ 0.4 unless indicated otherwise. Cell density measurements were performed on a Nanodrop 2000c (Thermo Scientific). For the time-course experiments (SI Figure S3), cultures were grown for the indicated time to the same final ABS600 of ∼ 0.4.
Flow Cytometry Analysis
Cells were diluted 1:100 in 1× PBS and run on an Accuri C6 flow cytometer (Becton Dickinson) equipped with CFlow plate sampler, a 488 nm laser, and a 530 ± 15 nm bandpass filter. Cells were gated based on forward scatter (FSC-H) and side scatter (SSC-H) using a gate set based on experiments with DRAQ5 dye (Thermo Scientific). A lower cutoff of 11 500 au for FSC-H and 500 au for SSC-H was used to eliminate the appearance of excessive noise. At least 20 000 cells were collected for each sample. See SI Figure S2 for more information on the analysis.
Curve Fitting to Extract Performance Metrics
The Hill equation (Y = a*Xn/(Kn + Xn) + b, where a, K, and n are fit constants and b is the fluorescence in the absence of the inducing sugar) was used to fit the mean fluorescence values (Y) across the different applied concentrations of applied sugar (X). Curve fitting was performed using the least-squares approach with the natural log of the measured and predicted mean fluorescence values. Of the fit values, n is the Hill coefficient (η), K is the EC50 value, and (a + b – AF)/(b – AF) is the dynamic range (δ) (where AF is autofluorescence of the cells harboring the pUA66 plasmid).
Mathematical Modeling
All simulations were conducted in MATLAB. The ordinary differential equations were integrated using the Euler method. The stable and unstable steady-states were calculated by implementing the arc-length continuation method. The details of the model can be found in Supporting Information, including its derivation and the selected values for the model parameters.
Statistical Analyses
P-values were calculated using the student t test with unequal variance when comparing all parameter metrics. The test used one tail for expected changes between metrics (e.g., an increase in the Hill coefficient) and two tails when no changes were expected. EC50 values were assumed to follow a log-normal distribution.
Acknowledgments
This work was supported by an Undergraduate Research Grant (to K.E.B.), start-up funds from North Carolina State University (to C.L.B.), a mentoring mini-grant from the ADVANCE D-3 program (to C.L.B.), a Doctoral Dissertation Fellowship awarded to K.B., and grants from the National Institutes of Health (GM086865), the National Science Foundation (CBET-0425882, CBET-0644792) and the Minnesota Supercomputing Institute. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number OCI-1053575.
Supporting Information Available
Figures S1–S5, Tables S1–S4, and a detailed description of the simple mathematical model. This material is available free of charge via the Internet at http://pubs.acs.org.
Author Present Address
§ (K.B.) Division of Immunobiology and Center for Systems Immunology Cincinnati Children’s Hospital Medical Center 231 Albert Sabin Way Cincinnati, OH 45229.
Author Contributions
C.L.B. and T.A. conceived of the study; T.A. and K.E.B. performed the experiments; C.L.B. and T.A. designed and interpreted the experiments; K.B. performed and interpreted the modeling; K.B., Y.K., and C.L.B. designed the model; and C.L.B., T.A. and K.B. wrote the manuscript.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Temme K.; Zhao D.; Voigt C. A. (2012) Refactoring the nitrogen fixation gene cluster from Klebsiella oxytoca. Proc. Natl. Acad. Sci. U.S.A. 109, 7085–7090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guzman L. M.; Belin D.; Carson M. J.; Beckwith J. (1995) Tight regulation, modulation, and high-level expression by vectors containing the arabinose PBAD promoter. J. Bacteriol. 177, 4121–4130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Boer H. A.; Comstock L. J.; Vasser M. (1983) The tac promoter: A functional hybrid derived from the trp and lac promoters. Proc. Natl. Acad. Sci. U.S.A. 80, 21–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber W.; Stelling J.; Rimann M.; Keller B.; Daoud-El Baba M.; Weber C. C.; Aubel D.; Fussenegger M. (2007) A synthetic time-delay circuit in mammalian cells and mice. Proc. Natl. Acad. Sci. U.S.A. 104, 2643–2648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hawkins K. M.; Smolke C. D. (2006) The regulatory roles of the galactose permease and kinase in the induction response of the GAL network in Saccharomyces cerevisiae. J. Biol. Chem. 281, 13485–13492. [DOI] [PubMed] [Google Scholar]
- Topp S.; Reynoso C. M. K.; Seeliger J. C.; Goldlust I. S.; Desai S. K.; Murat D.; Shen A.; Puri A. W.; Komeili A.; Bertozzi C. R.; Scott J. R.; Gallivan J. P. (2010) Synthetic riboswitches that induce gene expression in diverse bacterial species. Appl. Environ. Microbiol. 76, 7881–7884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wieland M.; Benz A.; Klauser B.; Hartig J. S. (2009) Artificial ribozyme switches containing natural riboswitch aptamer domains. Angew. Chem., Int. Ed. Engl. 48, 2715–2718. [DOI] [PubMed] [Google Scholar]
- Suess B.; Hanson S.; Berens C.; Fink B.; Schroeder R.; Hillen W. (2003) Conditional gene expression by controlling translation with tetracycline-binding aptamers. Nucleic Acids Res. 31, 1853–1858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharma V.; Nomura Y.; Yokobayashi Y. (2008) Engineering complex riboswitch regulation by dual genetic selection. J. Am. Chem. Soc. 130, 16310–16315. [DOI] [PubMed] [Google Scholar]
- Weber W.; Fux C.; Daoud-el Baba M.; Keller B.; Weber C. C.; Kramer B. P.; Heinzen C.; Aubel D.; Bailey J. E.; Fussenegger M. (2002) Macrolide-based transgene control in mammalian cells and mice. Nat. Biotechnol. 20, 901–907. [DOI] [PubMed] [Google Scholar]
- Gossen M.; Bujard H. (1992) Tight control of gene expression in mammalian cells by tetracycline-responsive promoters. Proc. Natl. Acad. Sci. U.S.A. 89, 5547–5551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volzing K.; Biliouris K.; Kaznessis Y. N. (2011) proTeOn and proTeOff, new protein devices that inducibly activate bacterial gene expression. ACS Chem. Biol. 6, 1107–1116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neddermann P.; Gargioli C.; Muraglia E.; Sambucini S.; Bonelli F.; De Francesco R.; Cortese R. (2003) A novel, inducible, eukaryotic gene expression system based on the quorum-sensing transcription factor TraR. EMBO Rep. 4, 159–165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levskaya A.; Chevalier A. A.; Tabor J. J.; Simpson Z. B.; Lavery L. A.; Levy M.; Davidson E. A.; Scouras A.; Ellington A. D.; Marcotte E. M.; Voigt C. A. (2005) Synthetic biology: Engineering Escherichia coli to see light. Nature 438, 441–442. [DOI] [PubMed] [Google Scholar]
- Alper H.; Stephanopoulos G. (2009) Engineering for biofuels: exploiting innate microbial capacity or importing biosynthetic potential?. Nat. Rev. Microbiol. 7, 715–723. [DOI] [PubMed] [Google Scholar]
- Joshua C. J.; Dahl R.; Benke P. I.; Keasling J. D. (2011) Absence of diauxie during simultaneous utilization of glucose and xylose by Sulfolobus acidocaldarius. J. Bacteriol. 193, 1293–1301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnsen U.; Dambeck M.; Zaiss H.; Fuhrer T.; Soppa J.; Sauer U.; Schönheit P. (2009) d-xylose degradation pathway in the halophilic archaeon Haloferax volcanii. J. Biol. Chem. 284, 27290–27303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng N.; Ao X.; Liang Y. X.; She Q. (2011) Archaeal promoter architecture and mechanism of gene activation. Biochem. Soc. Trans. 39, 99–103. [DOI] [PubMed] [Google Scholar]
- Cardona S. T.; Mueller C. L.; Valvano M. A. (2006) Identification of essential operons with a rhamnose-inducible promoter in Burkholderia cenocepacia. Appl. Environ. Microbiol. 72, 2547–2555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlegel A.; Böhm A.; Lee S.-J.; Peist R.; Decker K.; Boos W. (2002) Network regulation of the Escherichia coli maltose system. J. Mol. Microbiol. Biotechnol. 4, 301–307. [PubMed] [Google Scholar]
- Peri K. G.; Goldie H.; Waygood E. B. (1990) Cloning and characterization of the N-acetylglucosamine operon of Escherichia coli. Biochem. Cell Biol. 68, 123–137. [DOI] [PubMed] [Google Scholar]
- Tong S.; Porco A.; Isturiz T.; Conway T. (1996) Cloning and molecular genetic characterization of the Escherichia coli gntR, gntK, and gntU genes of GntI, the main system for gluconate metabolism. J. Bacteriol. 178, 3260–3269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lubelska J. M.; Jonuscheit M.; Schleper C.; Albers S.-V.; Driessen A. J. M. (2006) Regulation of expression of the arabinose and glucose transporter genes in the thermophilic archaeon Sulfolobus solfataricus. Extremophiles 10, 383–391. [DOI] [PubMed] [Google Scholar]
- Song S.; Park C. (1997) Organization and regulation of the d-xylose operons in Escherichia coli K-12: XylR acts as a transcriptional activator. J. Bacteriol. 179, 7025–7032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moralejo P.; Egan S. M.; Hidalgo E.; Aguilar J. (1993) Sequencing and characterization of a gene cluster encoding the enzymes for l-rhamnose metabolism in Escherichia coli. J. Bacteriol. 175, 5585–5594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegele D. A.; Hu J. C. (1997) Gene expression from plasmids containing the araBAD promoter at subsaturating inducer concentrations represents mixed populations. Proc. Natl. Acad. Sci. U.S.A. 94, 8168–8172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novick A.; Weiner M. (1957) Enzyme induction as an all-or-none phenomenon. Proc. Natl. Acad. Sci. U.S.A. 43, 553–566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohn M.; Horibata K. (1959) Analysis of the differentiation and of the heterogeneity within a population of Escherichia coli undergoing induced β-galactosidase synthesis. J. Bacteriol. 78, 613–623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ozbudak E. M.; Thattai M.; Lim H. N.; Shraiman B. I.; van Oudenaarden A. (2004) Multistability in the lactose utilization network of Escherichia coli. Nature 427, 737–740. [DOI] [PubMed] [Google Scholar]
- Acar M.; Becskei A.; van Oudenaarden A. (2005) Enhancement of cellular memory by reducing stochastic transitions. Nature 435, 228–232. [DOI] [PubMed] [Google Scholar]
- Kuhlman T.; Zhang Z.; Saier M. H. Jr; Hwa T. (2007) Combinatorial transcriptional control of the lactose operon of Escherichia coli. Proc. Natl. Acad. Sci. U.S.A. 104, 6043–6048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setty Y.; Mayo A. E.; Surette M. G.; Alon U. (2003) Detailed map of a cis-regulatory input function. Proc. Natl. Acad. Sci. U.S.A. 100, 7702–7707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishna S.; Semsey S.; Sneppen K. (2007) Combinatorics of feedback in cellular uptake and metabolism of small molecules. Proc. Natl. Acad. Sci. U.S.A. 104, 20815–20819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian X.-J.; Zhang X.-P.; Liu F.; Wang W. (2009) Interlinking positive and negative feedback loops creates a tunable motif in gene regulatory networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 80, 011926. [DOI] [PubMed] [Google Scholar]
- Khlebnikov A.; Datsenko K. A.; Skaug T.; Wanner B. L.; Keasling J. D. (2001) Homogeneous expression of the PBAD promoter in Escherichia coli by constitutive expression of the low-affinity high-capacity AraE transporter. Microbiology 147, 3241–3247. [DOI] [PubMed] [Google Scholar]
- Khlebnikov A.; Risa O.; Skaug T.; Carrier T. A.; Keasling J. D. (2000) Regulatable arabinose-inducible gene expression system with consistent control in all cells of a culture. J. Bacteriol. 182, 7029–7034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morgan-Kiss R. M.; Wadler C.; Cronan J. E. Jr. (2002) Long-term and homogeneous regulation of the Escherichia coli araBAD promoter by use of a lactose transporter of relaxed specificity. Proc. Natl. Acad. Sci. U.S.A. 99, 7373–7377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schleif R. (2010) AraC protein, regulation of the l-arabinose operon in Escherichia coli, and the light switch mechanism of AraC action. FEMS Microbiol. Rev. 34, 779–796. [DOI] [PubMed] [Google Scholar]
- Reeder T.; Schleif R. (1991) Mapping, sequence, and apparent lack of function of araJ, a gene of the Escherichia coli arabinose regulon. J. Bacteriol. 173, 7765–7771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hendrickson W.; Stoner C.; Schleif R. (1990) Characterization of the Escherichia coli araFGH and araJ promoters. J. Mol. Biol. 215, 497–510. [DOI] [PubMed] [Google Scholar]
- Zaslaver A.; Bren A.; Ronen M.; Itzkovitz S.; Kikoin I.; Shavit S.; Liebermeister W.; Surette M. G.; Alon U. (2006) A comprehensive library of fluorescent transcriptional reporters for Escherichia coli. Nat. Methods 3, 623–628. [DOI] [PubMed] [Google Scholar]
- Tan C.; Marguet P.; You L. (2009) Emergent bistability by a growth-modulating positive feedback circuit. Nat. Chem. Biol. 5, 842–848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevozhay D.; Adams R. M.; Murphy K. F.; Josic K.; Balázsi G. (2009) Negative autoregulation linearizes the dose-response and suppresses the heterogeneity of gene expression. Proc. Natl. Acad. Sci. U.S.A. 106, 5123–5128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madar D.; Dekel E.; Bren A.; Alon U. (2011) Negative auto-regulation increases the input dynamic-range of the arabinose system of Escherichia coli. BMC Syst. Biol. 5, 111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weickert M. J.; Adhya S. (1993) The galactose regulon of Escherichia coli. Mol. Microbiol. 10, 245–251. [DOI] [PubMed] [Google Scholar]
- Yildirim N.; Mackey M. C. (2003) Feedback regulation in the lactose operon: a mathematical modeling study and comparison with experimental data. Biophys. J. 84, 2841–2851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Court D. L.; Swaminathan S.; Yu D.; Wilson H.; Baker T.; Bubunenko M.; Sawitzke J.; Sharan S. K. (2003) Mini-lambda: a tractable system for chromosome and BAC engineering. Gene 315, 63–69. [DOI] [PubMed] [Google Scholar]
- Cherepanov P. P.; Wackernagel W. (1995) Gene disruption in Escherichia coli: TcR and KmR cassettes with the option of Flp-catalyzed excision of the antibiotic-resistance determinant. Gene 158, 9–14. [DOI] [PubMed] [Google Scholar]
- Del Vecchio D.; Ninfa A. J.; Sontag E. D. (2008) Modular cell biology: Retroactivity and insulation. Mol. Syst. Biol. 4, 161. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.