The fitness value of information

Abstract

Communication and information are central concepts in evolutionary biology. In fact, it is hard to find an area of biology where these concepts are not used. However, quantifying the information transferred in biological interactions has been difficult. How much information is transferred when the first spring rainfall hits a dormant seed, or when a chick begs for food from its parent? One measure that is commonly used in such cases is fitness value: by how much, on average, an individual’s fitness would increase if it behaved optimally with the new information, compared to its average fitness without the information. Another measure, often used to describe neural responses to sensory stimuli, is the mutual information—a measure of reduction in uncertainty, as introduced by Shannon in communication theory. However, mutual information has generally not been considered to be an appropriate measure for describing developmental or behavioral responses at the organismal level, because it is blind to function; it does not distinguish between relevant and irrelevant information. In this paper we show that there is in fact a surprisingly tight connection between these two measures in the important context of evolution in an uncertain environment. In this case, a useful measure of fitness benefit is the increase in the long-term growth rate, or the fold increase in number of surviving lineages. We show that in many cases the fitness value of a developmental cue, when measured this way, is exactly equal to the reduction in uncertainty about the environment, as described by the mutual information.

1 Introduction

Information is a central organizing concept in our understanding of biological systems at every scale. Our DNA digitally encodes information about how to create an organism—information that was refined over generations through the process of natural selection (Maynard Smith, 1999). Sensory systems are used to acquire information about the environment, and the brain processes and stores that information. A variety of learning mechanisms allow animals to flexibly act upon the information they receive. Signals like the peacock’s tail, the honeybee waggle dance, and human language are used to convey information about the signaler or the environment to other individuals (Maynard Smith and Harper, 2003).

In the study of human communication and data transfer, information is typically measured using entropy and mutual information (Wiener, 1948; Shannon, 1948; Cover and Thomas, 1991). Entropy is a statistical measure of the amount of uncertainty about some outcome, like whether it will rain tomorrow or not, which has to do with the number of different possible outcomes and the chance each one has to occur. Mutual information measures the reduction in uncertainty about that outcome after the observation of a cue, like the presence or absence of clouds in the sky. In some fields of biology, such as neurobiology, information is naturally and usefully measured with the same information-theoretic quantities (Borst and Theunissen, 1999). However, information theoretic measures have seen substantially less use in evolutionary biology, behavioral ecology, and related areas. Why is this? One problem is that measures of entropy do not directly address information quality; they do not distinguish between relevant and irrelevant information. When we think about fitness consequences we care very much about relevant and irrelevant information. For example, from an information-theoretic standpoint one has the same amount of information if one knows the timing of sunrise on Mars as one has if one knows the timing of sunrise on Earth. Yet individuals of few if any Earthbound species find the timing of sunrise on Mars relevant to their survival. Information measures based on entropy have therefore been deemed irrelevant to the evolutionary ecology of information. Instead evolutionary biologists and behavioral ecologists tend to focus on decision-theoretic measures such as the expected value of perfect information or the expected value of sample information (Savage, 1954; Good, 1967; Winkler, 1972; Gould, 1974; Ramsey, 1990), with value often measured in terms of fitness consequences (Stephens and Krebs, 1986; Stephens, 1989; Lachmann and Bergstrom, 2004).

The disconnect between information-theoretic and decision-theoretic measures is perplexing. Entropy and mutual information appear to measure information quantity while reflecting nothing about fitness consequences; the expected value of information measures fitness consequences but has nothing to do with the actual length or information quantity of a message. But early work in population genetics (Haldane, 1957; Kimura, 1961; Felsenstein, 1971, 1978) and recent analyses of evolution in fluctuating environments (Bergstrom and Lachmann, 2004; Kussell and Leibler, 2005) hint at a possible relation between information and fitness. What is this relation? Information theorists since Kelly (1956) have observed that in special circumstances, information value and information-theoretic measures may be related. Here we argue that these special circumstances are exactly those about which biologists should be most concerned: they include the context of evolution by natural selection in an changing, unpredictable environment.

Most organisms experience some kind of stochasticity in the environment, but short-lived inhabitants of extreme habitats are particularly vulnerable to its vagaries. A case in point is desert annual plants: once they germinate, they have just one chance to reproduce, and in many years there simply is not enough rain. Their adaptive solution is to sometimes delay germination for a year or more, so that each plant’s seeds will germinate over a spread of several years, rather than all together—a strategy known as risk-spreading or bet-hedging (Cohen, 1966; Cooper and Kaplan, 1982; Seger and Brockmann, 1987). This strategy, though it allows a lineage to persist through drought years, is somewhat wasteful; all the seeds that do happen to germinate in a drought year die with no chance of reproducing. What if, instead, seeds were sensitive to environmental cues that could help predict the chance of a drought in the coming year? The bet-hedging strategy could be improved, by adjusting the probability of germination in response to that cue, according to the conditional probability of a drought (Cohen, 1967; Haccou and Iwasa, 1995). How does this improved strategy translate into increased fitness, and how does that relate to the amount of information the cue conveys about the environment? We present a simple model of evolution in an uncertain environment, and calculate the increase in Darwinian fitness that is made possible by responding to a cue conveying information about the environmental state. We show that in certain cases this fitness value of information is exactly equal to the mutual information between the cue and the environment. More generally, we find that this mutual information, which seemingly fails to take anything about organismal fitness into account, nonetheless imposes an upper bound on the fitness value of information.

2 Two measures of information

Environmental cues can help organisms living in an uncertain environment predict the future state of the environment, and thereby can allow them to choose an appropriate phenotype for the conditions that they will face. We will consider a population of annual organisms living in a variable environment. The environmental state E and the environmental cue C are correlated random variables independently drawn every year; both are common to all individuals, so that all individuals encounter the same conditions in a given year. We might measure the information conveyed by the environmental cue C in two different ways.

The typical approach in statistical physics, communication engineering, neurobiology, and related fields is to use an information-theoretic measure such as the mutual information. The mutual information describes the extent to which a cue reduces the uncertainty about the environment, measured in terms of entropy. Following Cover and Thomas (1991), we define the entropy of the random variable E representing the environmental state as

$$H(E)=-\sum _{e}p(e)logp(e),$$

where p(e) is the probability of observing the state e. The more different states of the environment that are possible, and the closer those states are to equally likely, the higher the uncertainty about which state will actually occur. After the organism observes a cue, the chances of each environmental state may change. We define the conditional entropy of the environment E, once the random variable C representing the cue has been observed, as

$$H(E\mid C)=-\sum _{c}p(c)\sum _{e}p(e\mid c)logp(e\mid c),$$

where p(c) is the probability of observing cue c, and p(e|c) is the conditional probability that the environment is in state e, given that cue c has been observed. This is a measure of the remaining uncertainty about the state of the environment, once a cue has been observed.

Definition: The mutual information between a cue C and a random environmental state E measures how much the cue reduces the uncertainty about the state E: thus I(E; C) = H(E) − H(E|C).

If the cue is completely unrelated to the state of the environment, then the uncertainty about the environment remains the same after the cue has been observed, and the mutual information is zero. However, if there is some relationship between them, then the cue reduces the uncertainty about the environment, so the mutual information is positive. At best, a perfectly informative cue would exactly reveal the state of the environment; the remaining uncertainty would be zero and the mutual information between the cue and the environment would be exactly the amount of uncertainty about the environment.

The entropy measure is most familiar to ecologists as the Shannon index of species diversity, which takes into account the number of different species and the frequency of each (Shannon, 1948). The more different species are present, and the closer they are to equally frequent, the higher the species diversity. Consider a field ecologist observing random individuals in a particular habitat, and writing down the species of each individual as it is observed. The more different species are present in the habitat, the more different sequences of species are possible. However, sequences in which a rare species is observed many times and a common species is observed just a few times are quite unlikely. The number of sequences that are likely to actually occur thus depends also on the frequency of each species. For example, if there are just two species that are equally frequent, the most likely sequences of ten observations will have five individuals of one species and five of the other; there are 10!/(5!5!) = 252 such sequences. In contrast, if there are just two species, but one is nine times more frequent than the other, the most likely sequences of ten observations will have just one individual of the rare species; there are only 10/(9!1!) = 10 such sequences. If we consider very long sequences of observations, the number of likely sequences is close to 2^HN, where H is the diversity index and N is the number of individuals observed. With each new observation, the number of possible sequences is multiplied by the number of species, but the number of likely sequences increases by a factor of 2^H. Thus the diversity index H can be interpreted as the fold increase in likely outcomes with each additional observation—a measure of the uncertainty about the next species to be observed.

When we are observing individuals that live in different habitats, we can either ignore the habitat and measure the diversity of all individuals pooled together, or we can measure the diversity within each habitat. If we measure within-habitat diversity, and then average across habitats according to the number of individuals observed in each habitat, we will usually find a lower diversity than we would by pooling across habitats. The only case where the average within-habitat diversity will be as high as the overall diversity is when habitat plays no role—the frequency of each species is the same in the different habitats. The difference between the overall diversity and the average within-habitat diversity is the mutual information between habitat and species: how much uncertainty about which species will be encountered next is removed, if we know the habitat in which the encounter takes place?

Another approach, common in decision theory, economics, behavioral ecology, and related fields, is to look at the expected value of information: how information improves the expected payoff to a decision-maker (Gould, 1974). We write the maximal fitness obtainable without a signal as F(E) = max_xΣ_e p(e)f (x, e), where x is a strategy, and f (x, e) is the fitness of that strategy when the environmental state e occurs. Similarly, we write the optimal fitness attainable with a signal F(E|C) = Σ_c p(c) max_xc Σ_e p(e|c)f (x_c, e) where x_c is a strategy used in response to the cue c.

Definition: The decision-theoretic value of information that a cue C provides about the state of the world E is defined as the difference between the maximum expected payoff or fitness that a decision-maker can obtain by conditioning on C, and the maximum expected payoff that could be obtained without conditioning on C. This is written as ΔF(E; C) = F(E|C) − F(E).

2.1 An illustrative example

To illustrate the difference between the two measures of information described above, we start with a simplified model. The environment has two possible states, such as wet and dry years, and each organism has two possible phenotypes into which it can develop. Fitness depends on the match of phenotype to environment, as follows:

$$\begin{array}{ccc}& \text{Phenotype}{\varphi }_1& \text{Phenotype}{\varphi }_2\\ \text{Environment}{e}_1& 5& 1\\ \text{Environment}{e}_2& 1& 3\end{array}$$

Given that the probability of environmental state e₁ is p, and of state e₂ is (1 − p), what should these individuals do in the absence of information about the condition of the environment? The organism maximizes its single-generation expected fitness by developing into phenotype ϕ₁ if p > 1/3, and into phenotype ϕ₂ otherwise. This is optimal because 5 · p+1 · (1−p) > 1 · p+3 · (1−p) when p > 1/3. The payoff earned with this strategy would be F(E) = max[5p+(1−p), p+3(1−p)].

$$F(E)=\{\begin{array}{cc}5p+(1-p)& \text{for}p\ge \frac{1}{3}\\ p+3(1-p)& \text{for}p<\frac{1}{3}\end{array}$$ (1)

Now we suppose that there is a perfectly informative environmental cue C which accurately reveals the state E of the environment. How do we measure the information provided by this cue?

Within an information-theoretic framework, we measure the amount of information in the cue by calculating mutual information between the cue and the environment; this measures how much the cue tells us about the environment. Since the cue is perfectly informative, the conditional uncertainty about the environment once the cue is observed is zero: H(E|C) = 0. The mutual information is therefore

$$I(E;C)=H(E)-H(E\mid C)=H(E)=-\mathit{p}logp-(1-p)log(1-p).$$ (2)

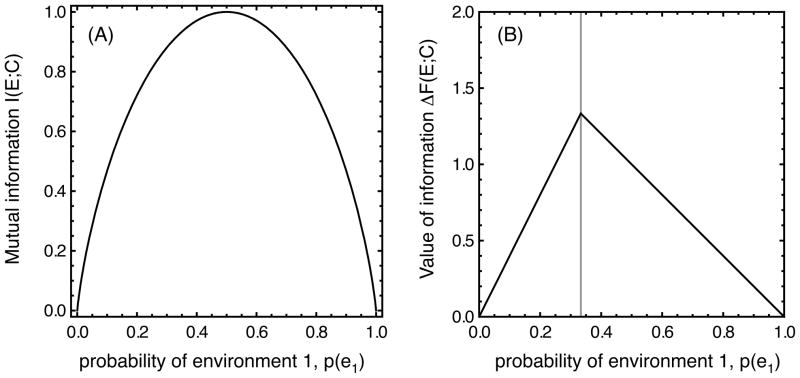
Figure 1A plots the mutual information between cue and environment as a function of the probability p that environment e₁ occurs.

Figure 1.

Two different measures of the information in a cue are commonly used. (A) The mutual information between the cue and the environment measures the reduction in environmental uncertainty once the cue has been observed. (B) The decision-theoretic value of information measures the change in expected fitness that is made possible by using the cue.

Within a decision theoretic framework, we measure the value of the information in the cue by calculating how much the ability to detect the cue improves the expected fitness of the organism. When an organism receives the cue, it can always develop the appropriate phenotype for the environment, and thus obtain a single-generation expected fitness of F(E|C) = 5p + 3(1 − p) = 3 + 2p. The decision-theoretic value of information in this case is therefore

$$\begin{array}{l}\mathrm{\Delta }F(E;C)=F(E\mid C)-F(E)\\ =\{\begin{array}{ll}2-2p\hfill & \text{for}p\ge \frac{1}{3}\hfill \\ 4p\hfill & \text{for}p<\frac{1}{3}\hfill \end{array}\end{array}$$ (3)

By using the cue, the organism increases its single-generation expected fitness by the decision-theoretic measure of the value of information. This quantity, illustrated in Figure 1B, differs considerably from the information-theoretic measure of mutual information shown in Figure 1A. Not only do the graphs take on different forms, but their units of measurement differ. Mutual information is measured in bits, whereas the value of information is measured in fitness units.

3 The fitness value of information

In the previous section, we measured the value of information by its effect on expected fitness over a single generation. But as many authors have shown (Dempster, 1955; Haldane and Jayakar, 1963; Cohen, 1966; Lewontin and Cohen, 1969; Gillespie, 1973; Yoshimura and Jansen, 1996), organisms will not always be selected to use a strategy that maximizes their fitness in a single generation. Instead, a better proxy for the likely outcome of evolution is to think of organisms as maximizing the long-term growth rate of their lineage. This distinction is critical when the environment changes from one generation to the next, and affects all individuals within one generation in the same way—as, for example, with drought or abundant spring rains. Under these circumstances, maximizing the long-term growth rate over a very large number of generations is equivalent to maximizing the expected value of the logarithm of the fitness in a single generation.

From an evolutionary perspective, it therefore makes sense to define the value of a cue not in terms of single-generation fitness consequences, but rather in terms of the increase in long-term growth rate it makes possible. Let g(x) = Σ_e p(e) log f (x, e) be the expected long-term growth rate of a strategy x. We write the maximum long-term growth rate obtainable without a cue as G(E) = max_xΣ_e p(e) log f (x, e). Similarly, we write the maximum long-term growth rate attainable with a cue as G(E|C) = Σ_c p(c) max_xc Σ_e p(e|c) log f (x_c, e).

Definition: The fitness value of information ΔG(E; C) associated with a cue or signal is the greatest fitness decrement or cost that would be favored by natural selection in exchange for the ability to detect and respond to this cue: ΔG(E; C) = G(E|C)−G(E).

3.1 Proportional betting

To explore the connection between environmental uncertainty and long-term growth rate, we will first look at an even simpler example, where the organism survives only if it matches its phenotype to the environment perfectly.

$$\begin{array}{ccc}& \text{Phenotype}{\varphi }_1& \text{Phenotype}{\varphi }_2\\ \text{Environment}{e}_1& 7& 0\\ \text{Environment}{e}_2& 0& 7/2\end{array}$$

In the short run, individuals maximize expected fitness by employing the highest-payoff phenotype only. But we can immediately see that the long-run fitness of lineage is not maximized in the same way: playing only one strategy will inevitably lead to a year with zero fitness and consequent extinction for the lineage. Thus organisms will be selected to hedge their bets, randomizing which of the two phenotypes they adopt (Cooper and Kaplan, 1982; Seger and Brockmann, 1987).

If environment e₁ occurs with probability p and environment e₂ occurs with probability (1 − p), with what probability should an individual adopt each phenotype? As we consider a larger and larger span of generations, a larger and larger fraction of the probability is taken up by “typical sequences” of environments, in which environment e₁ occurs around N p times, and environment e₂ occurs around N (1 − p) times (Cover and Thomas, 1991). A strategy that maximizes the growth rate over these typical sequences will, with very high probability, be the one that is observed as the result of natural selection (Robson et al., 1999). To find this genotype, let us assume a genotype that develops with probability x into phenotype ϕ₁ and with probability (1 − x) into phenotype ϕ₂; the population growth over a typical sequence of N events will be (7 x)^Np(7/2 (1 − x))^N(1−p). Maximizing the population growth is equivalent to maximizing the per-generation exponent of growth, or the log of the expression divided by N:

$$\begin{array}{l}g(x)=plog(7x)+(1-p)log(7/2(1-x))\\ =plog(x)+(1-p)log(1-x)+plog(7)+(1-p)log(7/2).\end{array}$$ (4)

The only part of this equation that depends on x is p log(x)+(1−p) log(1−x), so any dependence on the fitnesses when the organism properly matches the environments (i.e. on the values “7” and “7/2”) has dropped out. The maximum occurs when x = p, a strategy called proportional betting. With this strategy, organisms develop into the two phenotypes in proportion to the probabilities of the two environments — and these optimal proportions do not depend on the fitness benefits (Cover and Thomas, 1991). The optimal growth rate is thus

$$\begin{array}{l}G(E)=plog(p)+(1-p)log(1-p)+plog7+(1-p)log(7/2)\\ =plog7+(1-p)log(7/2)-H(E).\end{array}$$ (5)

3.2 Uncertainty and optimal growth

To understand the connection between environmental uncertainty and optimal growth more fully, it is instructive to generalize the simple model above to include several different environments and phenotypes. Let us assume that there are n environments, and that for each environment there is one optimal phenotype. The payoff for phenotype ϕ_e in environment e is d_e, and the payoff for any other phenotype in environment e is 0. Let the probability of environment e occurring be p(e), and the probability of developing into phenotype ϕ_e be x(e). Then the growth rate of the lineage over a typical sequence of environments, in which environment e occurs approximately Np(e) times, is Π_e(d_ex(e))^Np(e). Again, instead of maximizing the above expression, we can maximize its log, divided by N:

$$\begin{array}{l}g(x)=\sum _{e}p(e)log(d_{e}x(e))\\ =\sum _{e}p(e)log{d}_e+\sum _{e}p(e)logx(e)\end{array}$$ (6)

The left part does not depend on the strategy x, so we just need to maximize the right part, which as before is independent of the fitness values d_e in the different environments. But instead of simply giving the solution, let us rewrite the above expression as

$$\begin{array}{l}g(x)=\sum _{e}p(e)log{d}_e+\left(\sum _{e}p(e)logp(e)-\sum _{e}p(e)logp(e)\right)+\sum _{e}p(e)logx(e)\\ =\sum _{e}p(e)log{d}_e+\sum _{e}p(e)logp(e)-\sum _{e}p(e)log\frac{p(e)}{x(e)}\\ =\sum _{e}p(e)log{d}_e-H(E)-D_{KL}(p\Vert x).\end{array}$$ (7)

The term D_KL(p||x) ≡; _e p(e) log(p(e)/x(e)) is the Kullback-Leibler divergence (K-L divergence) between the distribution of environments and the distribution of phenotypes. The K-L divergence, also known as the relative entropy, quantifies how greatly a given distribution x(e) varies from a reference distribution p(e). To illustrate its meaning, we return to the example of a field ecologist recording the species of each individual as it is observed. If the true frequencies of each species are given by the distribution p(s), then the most likely sequences of observations are the ones where each species s is observed in proportion to its frequency, n(s)/N ≈ p(s). The observed frequency of each species is thus the maximum likelihood estimate for the true frequency of each species. However, other types of sequences are possible, where the observed frequency of each species q(s) = n(s)/N does not match the true frequency—leading the ecologist to an incorrect estimate. How often does this happen? As long as the total number of observations N is large, the probability of observing a sequence with species frequencies q when the true species frequencies in the habitat are p is approximately 2^−D(q||p)N. As the number of observations grows, deviations from p become less and less likely. The Kullback-Leibler divergence is a measure of the deviation of a distribution p from another distribution q, which reflects how unlikely it is that we would observe species frequencies q when the true frequencies are p.

The representation of the growth rate given in Equation 7 allows us to generalize and interpret the results of the previous section. We note that the term D_KL(p||x) is the only part of the expression for g(x) that depends on the organism’s choice of strategy; this is zero when x(e) = p(e). Therefore the optimal assignment of phenotypes will be a proportional betting strategy, and and will achieve a growth rate of

$$G(E)=\sum _{e}p(e)log{d}_e-H(E),$$ (8)

similar to Equation 5 above. When the distribution of phenotypes is x(e) instead of the optimal p(e), then the growth rate per generation will be reduced by D_KL(p||x).

Furthermore, if the organism knew exactly what the environment would be at every generation, it would choose the optimal phenotype every time. The growth rate would then be Π_e(d_e)^Np(e), corresponding to an average log growth rate of Σ_e p(e) log d_e. Comparing this quantity to Equation 8, we see that the growth rate associated with the proportional betting strategy is equal to the growth rate that could be achieved with full information, minus the entropy of the unknown environmental state. At least for this special case, environmental uncertainty reduces the log growth rate by an amount equal to the entropy of the environment!

3.3 The illustrative example, revisited

In the previous two sections, we assumed that organisms can only survive when they choose exactly the right phenotype for the environment. In general, however, choosing the wrong phenotype need not be fatal. How does this affect the optimal growth rate, and the fitness value of information?

Let us return to the first example presented in Section 2.1; in this example the wrong phenotype had a fitness of 1 instead of 0. Now the expected log growth rate in the absence of a cue is g(x) = p log(4x + 1) + (1 − p) log(3 − 2x) and here, organisms will not follow a strict proportional-betting strategy. Instead, the optimal strategy x^* will be to always develop into a single phenotype when p is near 0 or 1, and to hedge bets when p takes on an intermediate value:

$$x^{\ast }(p)=\{\begin{array}{lll}0\hfill & \text{for}p\le \frac{1}{7}\hfill & \text{always}\text{phenotype}{\varphi }_2\hfill \\ \frac{7p-1}{4}\hfill & \text{for}\frac{1}{7}<p<\frac{5}{7}\hfill & \text{bet}-\text{hedging}\text{between}1\text{and}2\hfill \\ 1\hfill & \text{for}\frac{5}{7}\le p\hfill & \text{always}\text{phenotype}{\varphi }_1\hfill \end{array}$$ (9)

This yields a growth rate without the cue of

$$G(E)=\{\begin{array}{ll}(1-p)log3\hfill & \text{for}p\le \frac{1}{7}\hfill \\ plog7+(1-p)log\frac{7}{2}-H(E)\hfill & \text{for}\frac{1}{7}<p<\frac{5}{7}\hfill \\ plog5\hfill & \text{for}p\ge \frac{5}{7}\hfill \end{array}$$ (10)

If organisms could sense a cue that perfectly revealed the state of the environment, all individuals could develop as the phenotype which matches the environment, and we would see a log growth rate of G(E|C) = p log(5) + (1 − p) log(3). The difference in expected log fitness — and thus the fitness value of information — is given by:

$$\mathrm{\Delta }G(E;C)=\{\begin{array}{ll}plog5\hfill & \text{for}p\le \frac{1}{7}\hfill \\ H(E)+plog5/7+(1-p)log6/7\hfill & \text{for}\frac{1}{7}<p<\frac{5}{7}\hfill \\ (1-p)log3\hfill & \text{for}p\ge \frac{5}{7}\hfill \end{array}$$ (11)

In the central region, where $\frac{1}{7}<p<\frac{5}{7}$, the fitness value of information is equal to the entropy of the environment plus a linear function of the probability of each environment: p log 5/7 + (1 − p) log 6/7. Outside the range, when the optimal strategy invests in only one of the phenotypes, the value of the cue depends linearly on the probability of each environment: p log 5 or (1 − p) log 3. Since in this region the strategy used is identical to the strategy optimizing fitness in a single generation, the value of the cue is just like the difference in long term growth rate when optimizing over only a single generation. Calculus reveals that the function is continuous and once continuously differentiable everywhere. The fitness value of information for the cue appears to be related to the mutual information between the cue and environment. In the next sections, we present a general model that will allow us to quantify and interpret that relationship.

3.4 Effective proportional betting

In order to explore the connection between fitness value and information, we will develop a general model based on the one presented in Section 3.2, but which relaxes the assumption that developing the wrong phenotype is always fatal. Let us again assume that an organism has to make a developmental decision between n possible phenotypes, each of which is a best match to one of n environments. Each environmental state e occurs with probability p(e), and the fitness of phenotype ϕ in environment e is f(ϕ, e). The best match for environment e is phenotype ϕ_e; that is, max_ϕ [f (ϕ, e)] = f (ϕ_e, e). The strategy x defines the probability x(ϕ) that an individual will develop into phenotype ϕ. We want to find the strategy that maximizes the expected long-term growth rate, g(x) = Σ_e p(e) log Σ_ϕ f (ϕ, e)x(ϕ).

In a previous paper (Donaldson-Matasci et al., 2008), we introduced a method for calculating optimal bet-hedging strategies that will prove useful in the present analysis. What follows is a very brief outline of the method; full details are provided in the previous paper.

We first define a set of hypothetical “extremist” phenotypes which fit the model of Section 3.2, so that each hypothetical phenotype ${\varphi }_e^{\prime }$ is ideally adapted to one environment e, where it has fitness d_e, but fails to survive in any other environment. We next aim to describe each actual phenotype ϕ as a bet-hedging strategy combining the hypothetical phenotypes ${\varphi }_e^{\prime }$. That is, we would like to find fitnesses d_e for the extremist phenotypes and mixing strategies s(e|ϕ) across extremist phenotypes such that

$$f(\varphi ,e)=s(e\mid \varphi )d_e$$ (12)

for all environments e and phenotypes ϕ. For each phenotype ϕ, the strategy s(e|ϕ) describes the bet-hedging proportions of hypothetical phenotypes ${\varphi }_e^{\prime }$ that would produce the same fitness, measured separately for each environment. This problem is equivalent to defining the fitness matrix F, with entries F_ϕe = f(ϕ, e), as a product of two unknown matrices: S, with entries S_ϕe = s(e|ϕ), and D, with diagonal entries D_ee = d_e and 0 elsewhere. Solving for these two matrices is straightforward and can almost always be done uniquely (Donaldson-Matasci et al., 2008).

The advantage of this approach is that it will allow easy comparison to the simplified model presented in Section 3.2, which highlights the connection between growth rate and uncertainty. We can express a strategy x as a row vector x⃗, with each element x_φ = x(φ) representing the probability of developing phenotype φ. To describe the strategy’s fitness in any particular environment e, we need simply look at the eth element of the vector x⃗ F:

$$f(x,e)={[\overrightarrow{x}\mathbf{SD}]}_e={[\overrightarrow{x}\mathbf{S}]}_e{d}_e=y(e)d_e.$$ (13)

This means that the strategy x, which produces each phenotype ϕ with probability x(ϕ), is exactly equivalent to a strategy y that produces each hypothetical phenotype ${\varphi }_e^{\prime }$ with probability y(e) = [x⃗ S]_e. We can write down the long-term growth rate for a lineage that uses strategy x by calculating the growth rate for the equivalent strategy y:

$$\begin{array}{l}g(x)=\sum _{e}p(e)logf(x,e)\\ =\sum _{e}p(e)logy(e)d_e\\ =\sum _{e}p(e)log{d}_e-H(E)-D_{KL}(p\Vert y).\end{array}$$ (14)

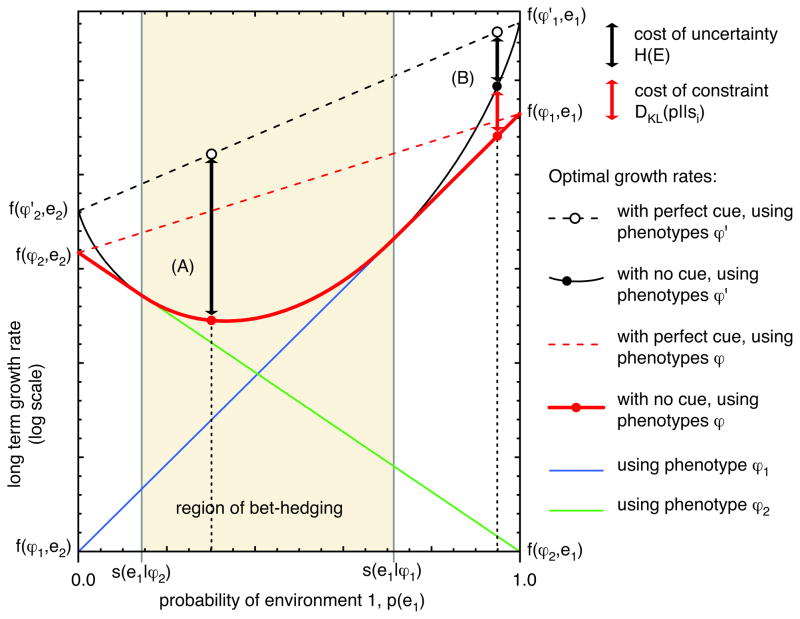
This equation is very similar to Equation 7, except that instead of measuring the Kullback-Leibler divergence of the strategy x from the environmental distribution, we measure the divergence of the effective strategy y from the environmental distribution. The maximum growth rate that can be achieved occurs when y(e) = [x⃗ S]_e = p(e), in which case D_KL(p||y) = 0 (see Figure 2A.) If there is no strategy x that can achieve this, then the strategy that minimizes the Kullback-Leibler divergence is optimal (see Figure 2B.) If we think of the effective strategy y as representing the effective bets the strategy is placing on each environment, then we see that the optimal strategy effectively does proportional betting—or as close as it can get.

Figure 2.

Maximal growth rate when choosing the wrong phenotype is not fatal. The red solid line indicates the maximal growth rate using the two phenotypes ϕ₁ and ϕ₂. The black solid line is the growth rate that could be achieved with an unconstrained strategy, using the hypothetical phenotypes ${\varphi }_1^{\prime }$ and ${\varphi }_2^{\prime }$. Since the hypothetical phenotypes are fatal in the wrong environment, the optimal unconstrained strategy always uses proportional betting. In contrast, the optimal constrained strategy bet-hedges only in an intermediate range of environmental frequencies, labeled the “region of bet-hedging”. Outside that region, it uses the single phenotype that does best on average. (A) Within the region of bet-hedging, the constrained strategy does just as well as the unconstrained strategy. Compared to an unconstrained strategy that can perfectly predict the environment, both strategies incur a cost of uncertainty equal to the entropy of the environment H(E) (see Equations 8 and 15.) (B) Outside the region of bet-hedging, the constrained strategy does worse than the constrained strategy, since it cannot bet-hedge anymore. It always uses phenotype ϕ₁ on the right of the region, where environment e₁ is more common, and ϕ₂ on the left. The growth rate achieved is therefore exactly as with the decision-theoretic strategy, optimizing fitness in just one generation. In this case, the constrained strategy pays not only the cost of uncertainty, H(E), but also a cost of constraint that arises from the inability to bet strongly enough on the most common environment. This constraint further reduces the growth rate by the Kullback-Leibler divergence D_KL(p||s_i), which gets larger as we get farther from the boundary of the region of bet-hedging (see Equation 14.)

The optimal growth rate for a strategy that effectively does proportional betting is therefore

$$G(E)=\sum _{e}p(e)log{d}_e-H(E)$$ (15)

just as it was for a diagonal fitness matrix (Equation 8.) Thus, even when choosing the wrong phenotype is not fatal, the optimal growth rate is limited by the entropy of the environment. However, the first term is no longer the growth rate that could be achieved if individuals could predict the environment perfectly. Instead, it is the growth rate that could be achieved if individuals could predict each environment e perfectly, and instead of using the actual phenotype ϕ_e with fitness f(ϕ_e, e), they could use the higher-fitness hypothetical phenotype ${\varphi }_e^{\prime }$ with fitness d_e. The value of perfect information is therefore the reduction in entropy it facilitates, H(E), plus a negative term that reflects the fitness cost due to the fact that individuals are in practice restricted to the actual phenotypes rather than the hypothetical ones, Σ_e p(e) log f (ϕ, e)/d_e (for example, see Equation 11.)

3.5 Information and fitness value

Until now, we have considered only cues that allow individuals to predict the state of the environment perfectly. We would now like to calculate the value of a partially informative cue.

All individuals within a generation observe the same environmental cue c, which occurs with probability p(c). Once that cue has been observed, the probability of each environmental state is given by the conditional probability distribution, p(e|c). A conditional strategy x specifies the probability of developing into each phenotype ϕ, after observing the cue c: x(ϕ|c). This can be represented as a matrix X, with entries X_cϕ = x(ϕ|c). To describe the strategy’s fitness in a particular environment e, after a cue c has been observed, we can look at the c-th row and the e-th column of the matrix XF:

$$f(x,e)={[\mathbf{XSD}]}_{ce}={[\mathbf{XS}]}_{ce}{d}_e=y(e\mid c)d_e.$$ (16)

This shows that a conditional strategy y which produces the hypothetical phenotype ${\varphi }_e^{\prime }$ with probability y(e|c) = [XS]_ce, conditional on observing the cue c, is exactly equivalent to the conditional strategy x. The growth rate of the strategy x can therefore be written as:

$$\begin{array}{l}g(x)=\sum _c{p}_c\sum _{e}p(e\mid c)log\sum _{\varphi }x(\varphi \mid c)f(\varphi ,e)\\ =\sum _c{p}_c\sum _{e}p(e\mid c)logy(e\mid c)d_e\\ =\sum _{e}p(e)log{d}_e-H(E\mid C)-D_{KL}(p(e\mid c)\Vert y(e\mid c)),\end{array}$$ (17)

which is like a conditional version of Equation 14. Instead of the uncertainty of the environment H(E), we have the conditional uncertainty after observing a cue, H(E|C). Instead of the relative entropy D_KL(p||y), we measure the conditional relative entropy D_KL(p(e|c)||y(e|c)), which reflects the difference between the bets the strategy effectively places on environments and the environmental probabilities, conditional on which cue is observed. As usual, the best strategy is effective proportional betting, conditional on the cue, but this may not always be possible.

What is the fitness value of the cue C? First of all, consider the situation where a bet-hedging strategy can effectively do proportional betting, both without the cue and with each possible cue. Then the Kullback-Leibler divergence terms in Equations 14 and 17 are always zero. We can therefore write:

$$\begin{array}{l}\mathrm{\Delta }G(E;C)=G(E\mid C)-G(E)\\ =\left(\sum _{e}p(e\mid c)log{d}_e-H(E\mid C)\right)-\left(\sum _{e}p(e)log{d}_e-H(E)\right)\\ =H(E)-H(E\mid C)=I(E;C).\end{array}$$ (18)

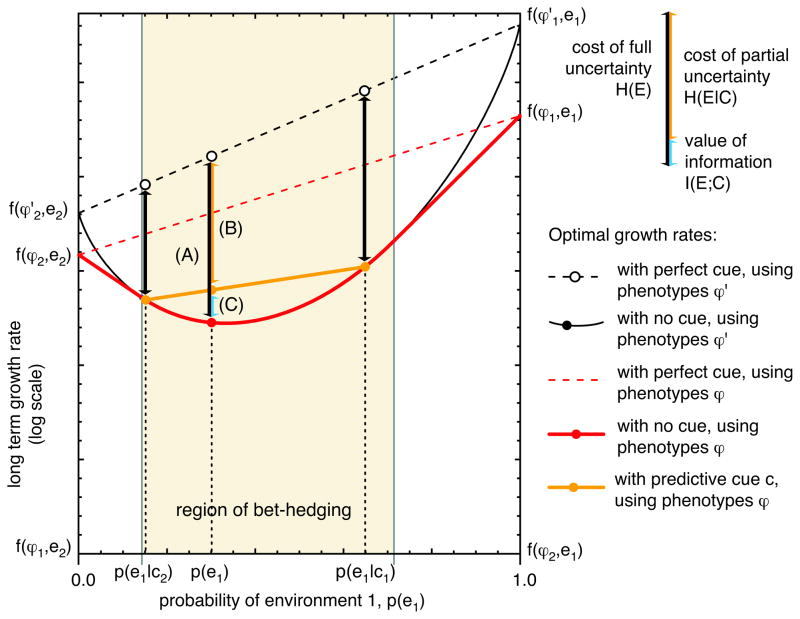
The value of receiving a cue—when effective proportional betting is possible—is exactly the mutual information between the cue and the environment (see Figure 3.)

Figure 3.

When the optimal strategy is to bet-hedge, both with and without a cue, the fitness value of information is equal to the mutual information between the cue and the environment. We calculate the value of a partially informative cue by looking at the reduction in growth rate, as in Figure 2, relative to a perfectly informed, unconstrained strategy. (A) With no cue at all, the cost of uncertainty is equal to the entropy of the environment H(E). (B) Once a particular cue c_i has been observed then the reduction in growth rate is just the cost of uncertainty, H(E|c_i). Averaging across the different cues, the reduction in growth rate for a strategy using a partially informative cue is simply the conditional entropy H(E|C). (C) The fitness value of information is, in this case, the amount by which the cue reduces uncertainty about the environment — that is, exactly the mutual information between the cue and the environment (see Equation 18.)

Now let us consider the more general situation, where effective proportional betting may not be possible. Let y^* be the best possible effective betting strategy when no cue is available, and let $y_C^{\ast }$ be the best possible effective betting strategy when the cue C is available. The fitness value of information is then

$$\begin{array}{l}\mathrm{\Delta }G(E;C)=G(E\mid C)-G(E)\\ =I(E;C)-\left(D_{KL}(p(e\mid c)\Vert y_C^{\ast }(e\mid c))-D_{KL}(p\Vert y^{\ast })\right).\end{array}$$ (19)

We would like to show that the mutual information I(E; C) is an upper bound for the fitness value of information ΔG(E; C). That means we need to show that the right-hand term is never negative: the cost of constraining the unconditional strategy cannot be greater than the cost of constraining the conditional strategy. We’ll do this in two steps. First of all, we define the unconditional strategy $y_C^{\ast }(e)={\sum }_{c}p(c)y_C^{\ast }(e\mid c)$ as the strategy an observer would see, watching someone play $y_C^{\ast }(e\mid c)$ in response to the cues c, but without observing the cues. The first step is to show that this marginal strategy can be no farther from the marginal distribution of environments than the conditional strategy is from the conditional distribution of environments. We can write the Kullback-Leibler divergence between the two joint distributions over cues and environments in two different ways:

$$\begin{array}{l}{D}_{KL}(p(e,c)\Vert y_C^{\ast }(e,c))=D_{KL}(p(c\mid e)\Vert y_C^{\ast }(c\mid e)+D_{KL}(p(e)\Vert y_C^{\ast }(e))\\ =D_{KL}(p(e\mid c)\Vert y_C^{\ast }(e\mid c)+D_{KL}(p(c)\Vert y_C^{\ast }(c)).\end{array}$$ (20)

However, the marginal distribution over cues is the same for the two distributions, because $y_C^{\ast }$ is defined in terms of the way it responds to cues generated according to the distribution p. This means the last term is zero, so

$$\begin{array}{l}{D}_{KL}(p(e\mid c)\Vert y_C^{\ast }(e\mid c)=D_{KL}(p(c\mid e)\Vert y_C^{\ast }(c\mid e)+D_{KL}(p(e)\Vert y_C^{\ast }(e))\\ D_{KL}(p(e\mid c)\Vert y_C^{\ast }(e\mid c)-D_{KL}(p(e)\Vert y_C^{\ast }(e))=D_{KL}(p(c\mid e)\Vert y_C^{\ast }(c\mid e)\ge 0\end{array}$$ (21)

as desired. Finally, we note that since y^* is defined as the optimal unconditional strategy for the environmental distribution p, $D_{KL}(p(e)\Vert y^{\ast }(e))\le D_{KL}(p(e)\Vert y_C^{\ast }(e))$. This shows that the fitness value of a cue cannot exceed the mutual information between that cue and the environment:

$$\begin{array}{l}\mathrm{\Delta }G(E;C)=I(E;C)-(D_{KL}(p(e\mid c)\Vert y_C^{\ast }(e\mid c))-D_{KL}(p\Vert y^{\ast }))\\ \le I(E;C)-(D_{KL}(p(e\mid c)\Vert y_C^{\ast }(e\mid c))-D_{KL}(p\Vert y_C^{\ast }))\\ \le I(E;C).\end{array}$$ (22)

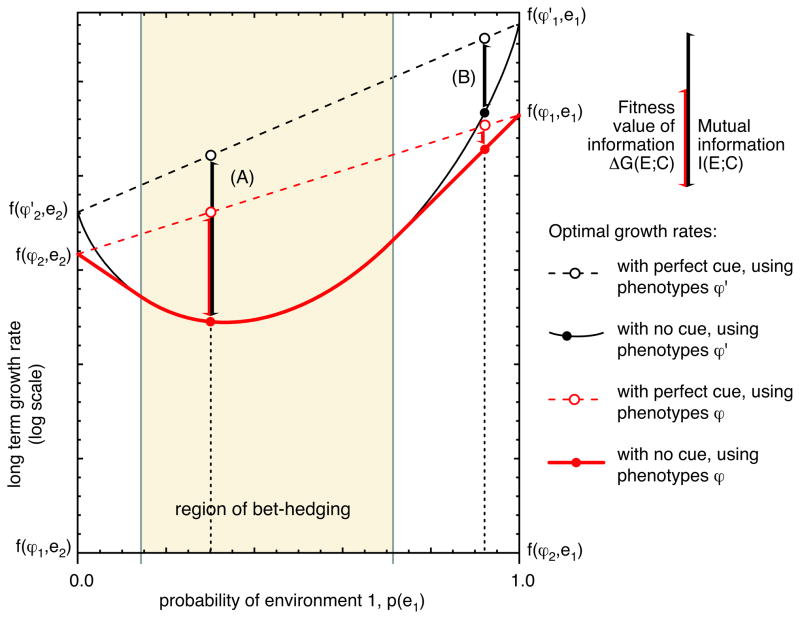
Figure 3 illustrates a case where the fitness value of the cue is exactly equal to the information it conveys; Figure 4 illustrates two cases in which the fitness value of the cue is strictly less than the information it contains.

Figure 4.

The mutual information between a cue and the environment is an upper bound on the fitness value of that information. For an unconstrained strategy, using the extremist phenotypes ϕ′, the value of a cue is exactly equal to the information it conveys. We illustrate two cases of a constrained strategy where the value of information is strictly less than the amount of information. (A) For example, say that the optimal strategy without a cue would be to bet-hedge; the optimal response to a perfectly informative cue would be to choose the single best phenotype ϕ₁ or ϕ₂. For an unconstrained strategy, the value of this perfect cue would be equal to the mutual information. The fitness value for the constrained strategy is lower, because although it can achieve just the same growth rate as the unconstrained strategy without information, once information is available the unconstrained strategy can do better. (B) If there is no bet-hedging even without a cue, then the constrained strategy does worse both with and without the cue. The value of the cue using a constrained strategy is thus not directly comparable to the value of the cue when using an unconstrained strategy. However, we prove in the text that the difference in growth rates for the constrained strategy cannot exceed the difference in growth rates for the unconstrained strategy (see Equation 22.)

4 Discussion

Many organisms living in a fluctuating environment show remarkable plasticity in life history traits. Desert annual plants often fail to germinate in their first year, on the chance that future conditions will be better (Philippi, 1993; Clauss and Venable, 2000). Similarly, some insects and crustaceans can enter diapause to wait out unfavorable conditions (Danforth, 1999; Philippi et al., 2001). For amphibians and fish, there is a trade-off between producing a few large eggs or many small ones; if the smallest eggs can only survive under the best conditions, this can provide an incentive to make eggs of variable size (Crump, 1981; Koops et al., 2003). Furthermore, some amphibians that breed in temporary pools show extremely variable time to metamorphosis, because the pools sometimes dry up before the tadpoles mature (Lane and Mahony, 2002; Morey and Reznick, 2004). Aphids and some plants can switch between sexual and asexual modes of reproduction depending on environmental conditions and uncertainty (Berg and Redbo-Torstensson, 1998; Halkett et al., 2004). In all these cases, the observed variation in life histories is thought to be an adaptation to environmental variability; the best studies show a quantitative agreement between the amount of observed plasticity and what is predicted to be optimal (Venable, 2007; Simons, 2009). However, it is often difficult to tell empirically whether the life history variation is produced randomly, as in bet-hedging, or in response to predictive environmental cues (Morey and Reznick, 2004; Philippi, 1993; Clauss and Venable, 2000; Adondakis and Venable, 2004); in some cases, it may actually be a combination of both mechanisms (Richter-Boix et al., 2006).

In this paper, we examined the adaptive value of responding to predictive cues in the context of environmental uncertainty. We have shown that the fitness value of using information about the environment gained from predictive cues is intimately related to the amount of information the cues carry about the environment. Under appropriate circumstances, the fitness benefit of being able to detect and respond to a cue is exactly equal to the mutual information between the cue and the environment. More generally, the mutual information provides an upper bound on the fitness value of responding to the cue. These results are surprising, in that the mutual information measure seemingly takes into account nothing about the fitness structure of the environment.

Why do we observe this connection between the fitness value of information and the mutual information? To answer that question, it helps take a closer look at the information-theoretic definition of information: information is the reduction of uncertainty, where uncertainty measures the number of states a system might be in. Thus mutual information between the world and a cue is the fold reduction in uncertainty about the world after the cue is received. For example, if a system could be in any of six equiprobable states, and a cue serves to narrow the realm of possibility to just three of these, the cue provides a twofold reduction in uncertainty. For reasons of convenience, information is measured as the logarithm of the fold reduction in uncertainty. Logarithmic units ensure that the measure is additive, so that for example we can add the information received by two successive cues to calculate the total information gained (Nyquist, 1924; Hartley, 1928; Shannon, 1948). Thus while information concepts are often thought to be linked with the famous sum −Σp log(p), the fundamental concept is not a particular mathematical formula. Rather, it is the notion that information measures the fold reduction in uncertainty about the possible states of the world.

With this view, it is easier to see why information bears a close relation to biological fitness. For simplicity, consider an extreme example in which individuals survive only if their phenotype matches the environment exactly, and suppose that there are ten possible environments that occur with equal probability. In the absence of any cue about the environment, the best the organism can do is randomly choose one of the ten possible phenotypes with equal probability. Only one tenth of the individuals will then survive, since only a tenth will match the environment with their phenotype. If a cue conveys 1 bit of information and thus reduces the uncertainty about the environment twofold, the environment can be only in one of five possible states. The organism will now choose randomly one of five possible phenotypes, and now a fifth of the population will survive — a twofold increase in fitness, or a gain of 1 bit in the log of the growth rate.

What happens when the environments are not equiprobable? In this case we can understand the connection between information and fitness by looking to long sequences of environments and the theory of typical sequences. The theory tells us that almost surely one of the “typical sequences” — those sequences in which the environments occur in their expected frequencies — will occur (Cover and Thomas, 1991). Moreover, all typical sequences occur with equal probability. Thus a lineage is selected to divide its members equally among all typical sequences. Since any one mistake in phenotype is lethal, only a fraction of these lineages, namely those that have just the right sequence of phenotypes, will survive. The number of typical sequences in this case is exactly 2^NH(E) where N is the number of generations in the sequence and H(E) is the entropy of the environment. Correspondingly, the fraction of surviving lineages will be 2^−NH(E). If a cue C is received that reduces the uncertainty of the environments by I(E; C), then the fraction of surviving lineages can be increased by exactly 2^NI(E;C). This is analogous to the situation in communication: if we need to encode a string of symbols that are not equiprobable, we turn to a long sequence of such symbols. Our code then needs only to be efficient for representing typical sequences of symbols, and those typical sequences occur with equal probability. The number of such sequences is 2^NH, where N is the length and H is the entropy of the symbols. If the message recipient also obtains side information related to the message itself, then the mutual information I between the message and the side information measures the reduction in the number of possible messages that need to be encoded by the transmitter. This number of messages is reduced exactly 2^NI-fold by the presence of the side information.

Finally, what happens when having the wrong phenotype is not lethal, but simply decreases fitness? In this case, we can no longer simply count the number of lineages that have the correct sequence of phenotypes to determine the fraction that survive. However, we can transform the system into one where this is possible, by constructing an alternate set of hypothetical phenotypes that survive in just one environment, and expressing everything in terms of those phenotypes. We imagine that, instead of an individual developing a single phenotype, it develops a certain combination of the alternate phenotypes; instead of following lineages of individuals, we follow lineages of these alternate phenotypes. The fraction that survive without information is, at best, 2^−NH(E), while the fraction that survive with information is, at best, 2^−NH(E|C). The mutual information I(E; C) places an upper limit on the fold increase of lineages that survive when a cue is available.

We can now see why the concept of information is the same across different disciplines. In communication theory, the transmission of information is the reduction of uncertainty about what signals will come through a channel, from an initial set of all possible signals down to the post hoc set of signals actually received. In thermodynamics, a decrease in entropy refers to the fold reduction in the number of states that a system can be in. In evolutionary biology, the fitness value of a cue about an uncertain environment refers to the fold increase in the number of surviving lineages made possible by responding to the cue.