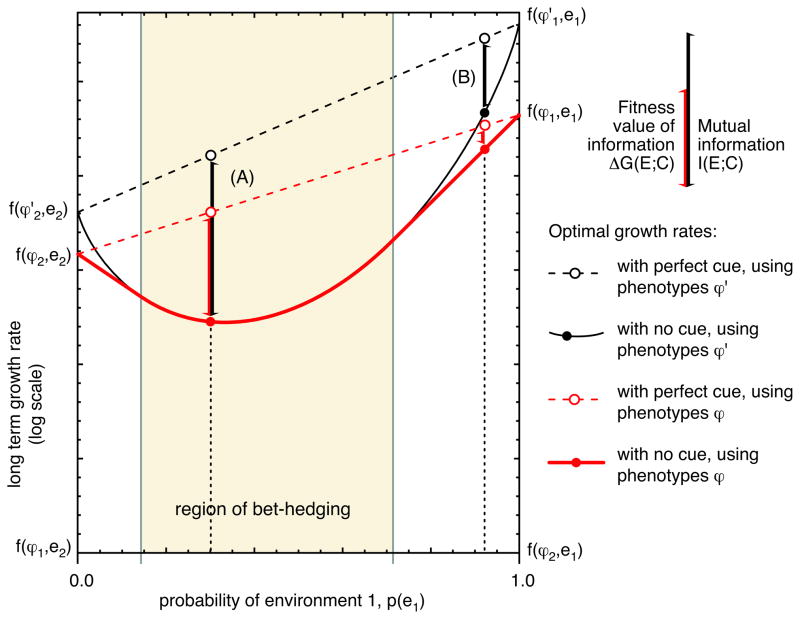
Figure 4.
The mutual information between a cue and the environment is an upper bound on the fitness value of that information. For an unconstrained strategy, using the extremist phenotypes ϕ′, the value of a cue is exactly equal to the information it conveys. We illustrate two cases of a constrained strategy where the value of information is strictly less than the amount of information. (A) For example, say that the optimal strategy without a cue would be to bet-hedge; the optimal response to a perfectly informative cue would be to choose the single best phenotype ϕ1 or ϕ2. For an unconstrained strategy, the value of this perfect cue would be equal to the mutual information. The fitness value for the constrained strategy is lower, because although it can achieve just the same growth rate as the unconstrained strategy without information, once information is available the unconstrained strategy can do better. (B) If there is no bet-hedging even without a cue, then the constrained strategy does worse both with and without the cue. The value of the cue using a constrained strategy is thus not directly comparable to the value of the cue when using an unconstrained strategy. However, we prove in the text that the difference in growth rates for the constrained strategy cannot exceed the difference in growth rates for the unconstrained strategy (see Equation 22.)