Microfluidic-based speckle analysis for sensitive measurement of erythrocyte aggregation: A comparison of four methods for detection of elevated erythrocyte aggregation in diabetic rat blood

Abstract

Biochemical alterations in the plasma and red blood cell (RBC) membrane of diabetic blood lead to excessive erythrocyte aggregation (EA). EA would significantly impede the blood flow and increase the vascular flow resistance contributing to peripheral vascular diseases. In this study, a simple microfluidic-based method is proposed to achieve sensitive detection of hyperaggregation. When a blood sample is delivered into the device, images of blood flows are obtained with a short exposure time for a relatively long measuring time. A micro-particle image velocimetry technique was employed to monitor variation of the flow rate of blood as a function of time. Given that EA formation in the channel creates clear speckle patterns, the EA extent can be estimated by calculating a speckle area (A_Speckle) through a normalized autocovariance function. The hematocrit effect is assessed by comparing optical images transmitted through blood samples. EA variations caused by dextran treatment are quantitatively evaluated using characteristic time (λ_Speckle) obtained by fitting the variations of A_Speckle. Other indices including number of RBCs in an aggregate (N_RBC), characteristic time of erythrocyte sedimentation rate (λ_ESR), and aggregation index estimated from ultrasound signals (AI_Echo) are determined under different EA conditions using conventional techniques. The four different methods are applied to diabetic blood samples to compare their indices under hyperaggregation conditions. It is found that the proposed method can detect variation of EA reasonably, compared with conventional measurement techniques. These experimental demonstrations support the notion that the proposed method is capable of effectively monitoring the biophysical properties of diabetic blood.

I. INTRODUCTION

Blood is a concentrated suspension of erythrocytes or red blood cells (RBCs), leukocytes, platelets, and protein macromolecules in plasma.¹ Erythrocytes are the most important component of blood because they occupy approximately 45% of the physiological volume concentration (hematocrit), as well as furnish tissues with oxygen and nitric oxide, and receive carbon dioxide in return.² In plasma, erythrocytes are prone to form rouleaux (RBC aggregates) and 3D networks as a reversible process. The extent of erythrocyte aggregation (EA) is mainly affected by force balance; an aggregating force induced by the presence of macromolecules, and disaggregating forces including the negative surface charge and shear force developed in blood flows.³ This phenomenon is of interest in hemorheology, because the shear dependence of viscosity is mainly attributed to EA. Specifically, large rouleaux formations under low shear condition lead to the elevation of blood viscosity. Hyperaggregation has been considered to significantly impede blood flow in blood vessels and increase vascular flow resistance.^4,5 In addition, elevated EA is somewhat correlated with various cardiovascular diseases (CVDs)^6,7 and diabetes mellitus (DM).^8,9

Several assessment techniques to quantify EA can be classified into direct measurement^10–12 and indirect measurements in terms of data acquisition. Indirect measurement techniques include erythrocyte sedimentation rate (ESR),^13,14 ultrasonic,^15–18 electrorheological,¹⁹ and light transmission or reflection methods.^20,21 The aforementioned techniques have merits and demerits in complexity and practicality.²²

Various EA-related phenomena have been directly investigated using microscopic observation methods.^11,23 For example, EA alteration changed the thickness of a cell-free layer by modifying the lateral migration of RBCs.^24,25 The formation and break up of rouleaux in rectangular polydimethylsiloxane (PDMS) channels were observed using a time-resolved scanning confocal microscopy.²⁶ To directly evaluate the degree of EA, the plasma gaps in the captured blood images were detected based on digital image-processing techniques.^10,27 By employing the Mehri's image-processing method and micro-particle image velocimetry (micro-PIV) technique, information about the size and flow velocity of RBC aggregates in the micro channel were simultaneously measured.^28,29 Although direct assessment techniques can figure out the size and dynamic motions of rouleaux, the hematocrit of blood samples should be adjusted to less than 10% for accurate quantification of EA.^12,30

Consequently, the degree of EA has mostly been measured indirectly under various physiological conditions. The ESR, which was first described by Westergren in 1921,³¹ represents the sedimentation rate in units of millimeters per hour by measuring the distance from the meniscus to the top of the column of sedimented erythrocytes in a 200 mm glass tube with a 2.5 mm in diameter for 1 h. The ESR measurement with minor modifications has been widely used clinically as a nonspecific indicator of inflammation in the diagnosis of chronic diseases.^32,33 The ESR value highly depends on physiological conditions, such as plasma protein and hematocrit. Especially, it significantly reflects the degree of EA.¹³ However, the conventional ESR method provides only a mean ESR value for each blood sample. The measurement accuracy of the ESR method is influenced by several factors including the installation angle and surface condition of specimen tubes.

Sigel et al. first observed that the ultrasonic backscattering of blood flows was dependent on shear rate.³⁴ Subsequently, ultrasonic investigations of blood samples have been attractively adopted as a means of EA measurement technique. Under static, steady, and pulsatile flow conditions, it was demonstrated that EA formation strongly contributes to the intensity of ultrasound signals.^17,35,36 Based on these results, the ultrasonic method has been employed under various in vivo physiological conditions to indicate EA formation.³⁷ However, measurement is restricted on superficial vessels, and ultrasonic signal requires calibration as a function of flow speed under steady flow conditions.

Electrical properties of blood are also changed due to hemorheological variations. Some methods for monitoring the electrical property have been employed to obtain information about the degree and time course of EA.^38,39 However, the electrical measurement of EA is not clearly and fully understood yet.⁴⁰ Especially, the electrical conductance cannot solely reflect the aggregation process. Further studies are necessary to understand the mechanisms of how EA formation affects the electrical properties of RBC suspensions.⁴¹

Compared with the aforementioned assessment methods, light intensity (LI) analysis, which utilizes either transmitted or back-scattered light through RBCs under a specific condition, has been widely used.⁴² Prior to EA measurement, rouleaux are completely disaggregated as separate RBCs at a high shear condition. The LI is then recorded after a sudden decrement in shear rate.^43,44 Based on the measurement of light transmittance or reflectance, several commercially available instruments exist, in which cone-plate or rotational Couette shearing systems are used to adjust shear rate conditions.^21,45 However, rotational flows are somewhat different from real blood flow in blood vessels. In addition, the rotational shearing systems are expensive and require cleaning after each measurement.

To measure LI of a laser beam scattered or transmitted by RBCs, microfluidic devices can also be used to obtain several aggregation parameters. These devices have distinctive advantages, including small sample volume and high sensitivity.^40,44 However, it is required for them to measure the pressure and LI separately for monitoring the hemodynamic information accurately.

Speckles can be observed by light illumination due to random light scattering from particles. Considering that speckle parameters such as size, contrast, intensity, and polarization contain information on scattering media, aggregations of polystyrene-microspheres⁴⁶ and platelets⁴⁷ were investigated by analyzing their speckle patterns. By applying speckle analysis to the captured optical images of blood flows, the EA can be quantified.

In the present study, a speckle analysis of blood flows in a microfluidic device is proposed to simply and precisely measure the EA extent through a label-free operation. The present speckle analysis method is compared with other EA measurement techniques, including direct measurement, modified ESR method, and ultrasonic imaging technique to validate the performance of the proposed method. To depict the EA extent under various hemorheological conditions, the representative index of each method is determined. Finally, the proposed method and other conventional techniques are applied to measure the hyperaggregation of diabetic blood extracted from rat samples to demonstrate the proposed technique.

II. MATERIALS AND METHODS

A. Fabrication of the microfluidic device

A rectangular master replica mold (height = 50 μm) was fabricated using MEMS technologies based on soft lithography and deep reactive-ion etching. As shown in Fig. 5(a), the microfluidic device has a straight channel (width = 1 mm, length = 10 mm). After pouring PDMS (Sylgard 184, Dow Corning, USA) on the silicon mold, it was cured at 80 °C for 3 h. Thereafter, a PDMS block was peeled off from the silicon mold. The channel has an inlet and outlet made with a puncher of 1 mm in diameter. After oxygen-plasma treatment (CUTE, Femto Science, Korea), the microfluidic device was finally prepared by bonding the PDMS block with a glass substrate.

FIG. 5.

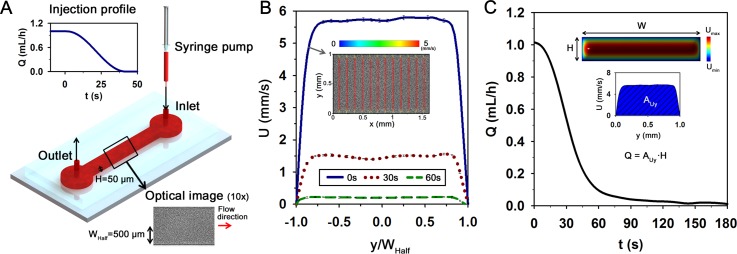
Flow condition in the microfluidic channel. (a) Schematic diagram of the microfluidic channel. The channel has a width (W) of 1000 μm and a height (H) of 50 μm. Blood is supplied into the channel using a programmable syringe pump with decreasing flow rate from 1 to 0 ml/h. (b) Variations of axial velocity profile at t = 0, 30, and 60 s. An instantaneous velocity field superimposed on the corresponding flow image at t = 0 s is represented in the inset. Normalized position (y/W_Half) depicts the lateral position in the channel. (c) Temporal variation of flow rate (Q) estimated by Eq. (2). Representations, depicting a 3D analytical velocity distribution of Poiseuille flow in the rectangular channel and a calculation of Q, are inserted.

B. Blood preparation

Male Sprague-Dawley (SD) rats (14 to 15 weeks old) were anesthetized with an intramuscular injection of ketamine (100 mg/kg) and xylazine (10 mg/kg). All blood samples, collected through an abdominal aortic puncture, were anticoagulated using ethylenediaminetetraacetic acid (EDTA) dipotassium salt (1.5 mg of EDTA per 1 ml of blood). The collected blood samples were separated into RBCs and plasma through centrifugation. Subsequently, the buffy layer was removed. Five different hematocrit (Ht) levels from 10% to 50% with intervals of 10% were tested in this study to check the effect of hematocrit. Each hematocrit level of blood samples was precisely set by carefully mixing RBCs with autologous plasma. To change RBC aggregability, Dextran 500 (molecular mass 450–550 kDa; Sigma Aldrich, USA) was dissolved in phosphate buffered saline (PBS; pH 7.4, Bio Solution, Korea) solution to be the concentration of 6%, and then autologous plasma was mixed to make plasma-dextran concentrations of 0%, 0.3%, 0.6%, and 1.2% for testing. Each experiment was repeated in three different samples. Plasma-dextran mixture solutions with different concentrations were mixed with RBCs to have a hematocrit level of 40%. All procedures performed on animal models were approved by the Animal Care and Ethics Committee of POSTECH, and the methods were carried out in accordance with the approved guidelines.

C. Experimental setup for speckle analysis

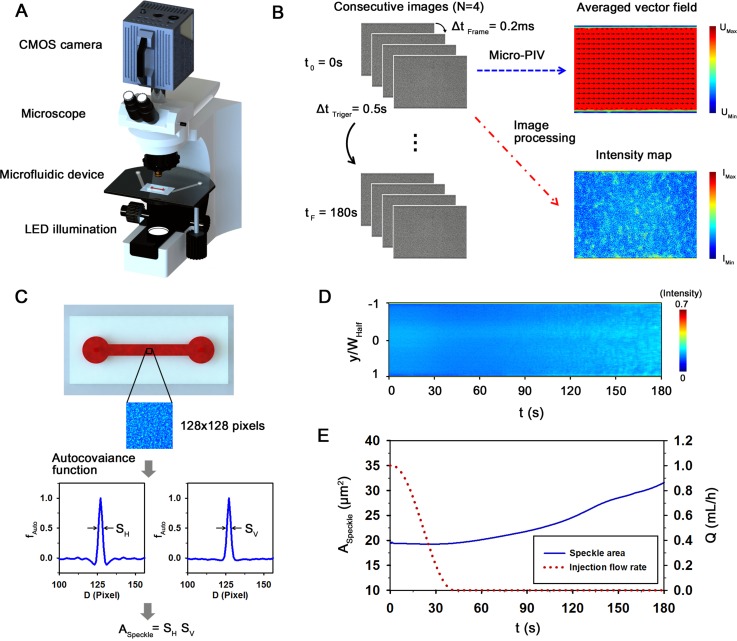
As shown in Fig. 1(a), the microfluidic device was mounted on an optical microscope (Nikon, Tokyo, Japan) with 10× objective lens (NA of 0.25). According to decrease of injection profile from 1 to 0 ml/h (Fig. 5(a)), the blood samples were supplied into the microfluidic device by using a syringe pump (neMESYS, Centoni Gmbh, Germany) with a 1 ml plastic syringe (BD; Becton Dickinson, Franklin Lakes, USA). A high-speed CMOS camera (FASTCAM SA 1.1, Photron Ltd., San Diego, USA) was used to acquire four consecutive images of blood flows at a frame rate of 5000 fps. An array-type, high-powered light-emitting diode (LED; BXRA-50C2600-B-00, Bridgelux) was employed as an illumination source. Trigger signals of the CMOS camera and the LED pulses were synchronized by using a delay generator (model 555, BNC, USA) with a trigger rate of 2 Hz. All experiments were conducted at room temperature of 25 °C.

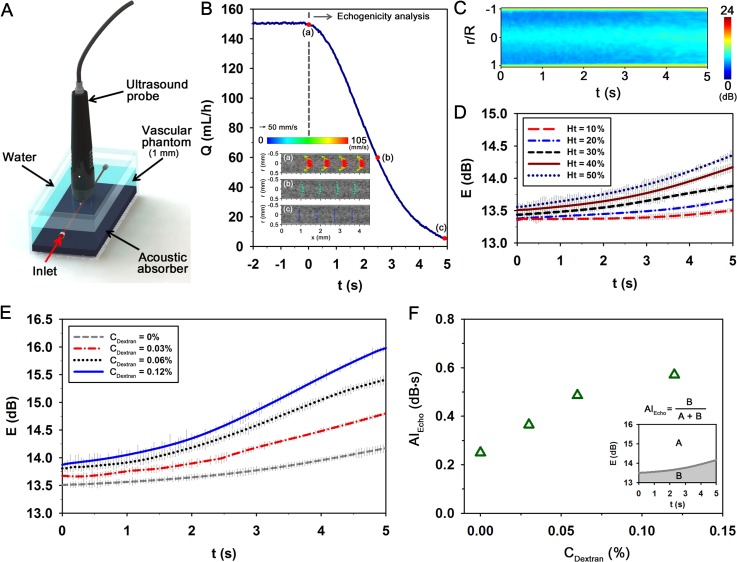
FIG. 1.

A proposed microfluidic-based measurement method to detect the elevated erythrocyte aggregation of diabetic blood. (a) Schematic of the measurement system composed of a microscope equipped with CMOS camera, microfluidic device, and LED illumination system. A delay generator synchronizes the trigger signals of the CMOS camera and the LED system. (b) Data processing procedure. A micro-particle image velocimetry (PIV) technique is applied to four consecutive flow images acquired at a high frame rate (Δt_Frame = 0.2 ms) to measure velocity fields. By adjusting trigger signals, the image acquisition process is repeated with a frequency of 2 Hz (Δt_Triger = 0.5 s) for a total time (t_F) of 180 s. Time-averaged mean velocity field and intensity map are used to minimize adverse errors. (c) Procedure to calculate the average size of speckles in an image of 128 × 128 pixels in size. The horizontal and vertical profiles are calculated by using the normalized autocovariance function (f_Auto). The full width at half maximum of f_Auto provides the size of speckle pattern. The average speckle area (A_Speckle) is evaluated by multiplying the horizontal and vertical speckle sizes. (d) Temporal variation of light intensity along the channel width. Speckle patterns are clearly appeared in the channel with the lapse of time. (e) Variations of A_Speckle and the injection flow rate (Q) of the syringe pump. The flow rate is decreased from 1 to 0 ml/h to induce EA formation.

D. Micro-PIV technique for flow rate measurement in a microchannel

Before applying the cross-correlation PIV algorithm to each image pair, the captured optical images of blood flows were cropped into images of 320 × 520 pixels. The spatial resolution is about 2.024 μm/pixel. To enhance the signal-to-noise ratio of the cross-correlation map, the captured flow images were processed using digital image-processing techniques. The detailed procedure and the image-processing techniques used in the present study were well described in our previous studies.^48,49 The size of each interrogation window was 32 × 16 pixels with 50% overlapping for all experimental conditions. The obtained velocity fields were filtered by using a 3 × 3 median kernel. Velocity profiles in the microchannel were obtained by averaging the velocity fields along the axial direction (x-axis).

As depicted in the insets of Fig. 5(c), the velocity field information in the rectangular channel has a 3D distribution. However, the micro-PIV technique can only measure the 2D velocity field in the measurement plane. Considering the fact that the micro-PIV technique illuminates the whole measurement volume through the entire depth of the microfluidic channel, the measurement plane has a certain thickness.⁴⁸ This thickness is typically expressed in terms of the depth of correlation (δ_C) as expressed by⁵⁰

$${\delta }_{\mathrm{C}}=2{\left\{\frac{(1-\sqrt{\epsilon })}{\sqrt{\epsilon }}\left[\frac{{{\mathrm{n}}_0}^2{{\mathrm{d}}_{\mathrm{p}}}^2}{{4\mathrm{\text{NA}}}^2}+\frac{5.95(\mathrm{M}+{1)}^2{\mathrm{L}}^2{\mathrm{n}}^4}{{16\mathrm{M}}^2{\mathrm{\text{NA}}}^4}\right]\right\}}^{1/2},$$ (1)

where d_p is the particle diameter, L is the wavelength of illumination light, M is the image magnification, n is the refractive index of the air, and NA is the numerical aperture of the lens. ε denotes the relative threshold over which particles no longer contribute to the evaluation of displacement-correlation peak. This threshold is normally set as 0.01. In the present study, δ_C is estimated to be about 100 μm based on the peak wavelength of LED light (λ = 440 nm) and the average size of RBCs (d_p = 8 μm). Given that the δ_C is larger than the microchannel height, all particles inside the channel may contribute to the micro-PIV measurement. Therefore, it can be postulated that the measured velocity information represents the mean velocity of RBCs in the whole depth. Based on this assumption, flow rate (Q) in the microchannel can be estimated by following equation:

$$\mathrm{Q}={\int }_0^{\mathrm{W}}\mathrm{U}\left(\mathrm{y}\right)\text{dy}\times \mathrm{H},$$ (2)

where U(y) is the velocity profile at a specific lateral position (y). To explain how Q is calculated using the profile data, an inset is included in Fig. 5(c).

E. Microscopic observation for EA measurement

A chamber (height = 10 μm), containing blood samples (100 μl; Ht = 20%) that were anticoagulated with EDTA, was mounted on an inverted optical microscope (Zeiss, Germany) attached with a high-speed CMOS camera (FASTCAM-ultima APX camera, Photron Ltd.). Optical images of blood samples were magnified with a 100× objective lens (NA of 1.3). The camera has a spatial resolution of 1024 × 1024 pixels corresponding to 0.269 μm/pixel. To measure the number of RBCs in an aggregate, the area of each rouleaux in binary images was divided by the mean area of a single RBC. Similar to Mehri's method,²⁹ each aggregate in binary images is labeled for better distinction. The binary images were obtained by thresholding with an optimal value evaluated by using the Otsu's algorithm.⁵¹ In this analysis, monodispersed RBCs were manually excluded.

F. ESR procedure

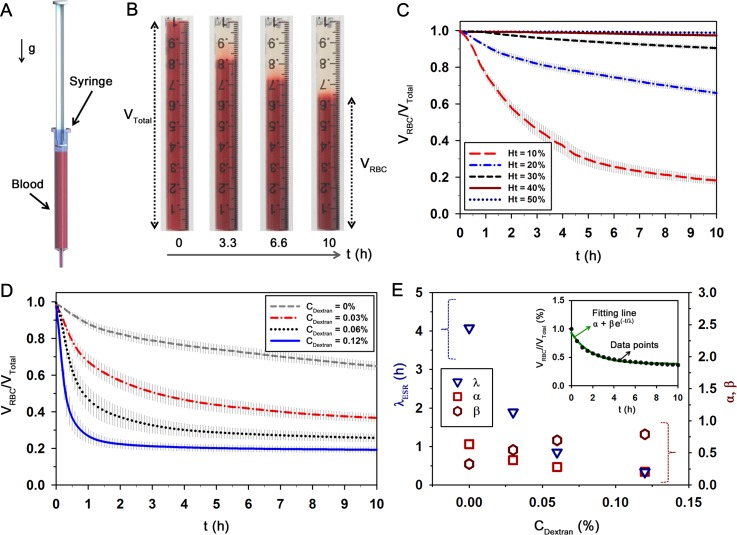
The ESR value was measured using a 1 ml plastic syringe (BD). After loading a blood sample (1 ml) in the disposable syringe, the syringe was disposed in an inverted vertical posture (Fig. 3(a)). Snap shot of the syringe were continuously captured with a digital camera (D700, Nikon, Japan) at intervals of 5 min for 10 h. Boundaries between the sedimented RBCs and RBC-depleted plasma were detected through an image-processing technique based on Canny's method.⁵²

FIG. 3.

Modified ESR method to measure erythrocyte aggregation. (a) Schematic diagram of the ESR measurement method. After loading a blood sample in the disposable syringe (1 ml), the syringe is vertically disposed at an inverted position. (b) Typical images showing the sedimentation of RBCs in a blood sample with a total volume of V_Total = 1 ml with respect to time (t). The volume of the sedimented RBCs (V_RBC) is gradually decreased with the lapse of time. Temporal variations of V_RBC/V_Total with respect to (c) hematocrit (Ht) and (d) dextran concentration (C_Dextran) at Ht = 20%. (e) Quantitative evaluations of λ_ESR, α, and β according to C_Dextran. Data points (C_Dextran = 0.03%) and a fitting curve determined by Eq. (5) are included in the inset. Each data set indicates the mean value and standard deviation evaluated from three test samples.

G. Ultrasonic imaging system for EA and flow rate measurements

To measure EA level using ultrasound signals, ultrasonic images of blood flows were acquired with a 35-MHz mechanical sector-scan probe (Capistrano Labs., San Clemente, CA, USA) at a frame rate of 30 fps with a sector angle of 20°. A vascular phantom with an inner diameter of 1 mm was used to minimize acoustic discrepancy at the tube wall. The details of the vascular phantom were described in our previous study.⁴⁹ The measurement section over the agarose vascular phantom was covered with water to facilitate acoustic transmission. The center of the lumen was positioned at the focal length of the transducer (11.8 mm). Blood sample was supplied into the vascular phantom by a syringe pump (neMESYS) with a 5 ml plastic syringe (BD). To quantify the degree of EA with respect to aggregability, the spatial distribution of mean echogenicity in the whole tube was measured. Before the measurement, a high shear condition was applied to completely disaggregate the rouleaux. The shear rate was then suddenly reduced to induce the formation of EA. For clear comparison, speckle images were quantitatively depicted in decibels (dB) using the ratio of the blood signals to PBS signals.

Flow rate (Q) was estimated using velocity field information obtained by a speckle image velocimetry (SIV) technique.⁴⁹ Before applying the SIV technique to ultrasonic images of blood flows, the ultrasonic images captured around the lumen were cropped into images of 320 × 84 pixels in size. The detailed procedure and the image-processing techniques were described in our previous studies.^49,53 The size of each interrogation window was fixed to 128 × 16 pixels with 50% overlapping. The obtained velocity vectors were filtered using a 3 × 3 median kernel. By averaging velocity vectors along with the flow direction, instantaneous velocity profile was obtained. The flow rate was calculated through the following equation based on a fitting model:

$$\mathrm{Q}={\pi \mathrm{R}}^2{\mathrm{U}}_{\text{Max}}\frac{\mathrm{K}}{\mathrm{K}+2},$$ (3)

where U_Max is the maximum velocity at the vessel center, and R represents the vessel radius. A bluntness index (K) describes the flatness of the velocity profile. For instance, the K value for a parabolic velocity profile is 2. As the velocity profile becomes a blunt shape, K value increases.

H. Preparation procedure of diabetic rat samples

Type 1 diabetes with hyperglycemia can be easily induced via streptozotocin (STZ) injection because a single high dose of STZ removes endogenous insulin production and glycemic control by destroying pancreatic beta cells.⁵⁴ In this study, SD rats (14 weeks old) were treated via intraperitoneal injection of STZ (65 mg/kg in sterile saline) under anesthesia with isoflurane and oxygen. Rat samples were initially fasted for 24 h prior to a STZ injection, and then fasted for another 24 h. After three days of recovery, blood samples were collected through an abdominal aortic puncture and then the samples were anticoagulated with EDTA.

III. THE PROPOSED METHOD TO MEASURE EA BASED ON SPECKLE ANALYSIS

As illustrated in Fig. 1(a), the experimental setup is composed of a microscope equipped with a CMOS camera, a microfluidic device with a straight channel, and LED illumination system. A programmable syringe pump was used to deliver blood samples into the microfluidic device. The range of shear rate established in the microfluidic device is relatively high to induce EA; for instance, the shear rate is about 1300 s⁻¹ when blood flow of 1 ml/h passes through the microfluidic device. For inducing the EA formation, the flow rate of blood was rapidly reduced by adjusting the syringe pump. However, the transient responses in the microfluidic systems give rise to slightly different hemodynamic conditions, compared with the injection flow rate of the syringe pump. In order to accurately monitor the hemodynamic condition during the experiment, velocity fields of blood flows in the micro channel were measured using a micro-PIV system. The detailed procedure of the micro-PIV technique is described in Sec. II D. The LED illumination enables RBCs to be used as tracer particles.

Fig. 1(b) illustrates a schematic of experimental procedure of the speckle analysis method. For the micro-PIV measurements, images of blood flows were acquired with a CMOS camera for a relatively long time (10 s–100 s) to quantify the extent of the EA. For this reason, a predetermined number of frames were saved to the memory of the camera, when a trigger signal generated by a delay generator was input to the camera. In this study, four images were consecutively acquired with a frame interval (Δt_Frame) of 0.2 ms. The time interval between every two trigger signals (Δt_Triger) is 0.5 s and the total measuring time is approximately 180 s. To measure the EA and flow velocity at a specific time with minimizing errors, the time-averaged velocity field and intensity map were obtained by averaging three instantaneous velocity fields and four images with a time interval Δt_Frame of 0.2 ms.

As shown in the intensity map of Fig. 1(b), speckle patterns are clearly appeared due to the EA formation. To estimate the average speckle size of blood images, the normalized autocovariance function was calculated in the image plane.^47,55 A sufficient sampling of speckles is required in an image to obtain reliable statistical evaluation. Hence, the region of interest (ROI) of 128 × 128 pixels was selected at the center of the channel (0.26 mm in the channel width of 1 mm). The intensity autocorrelation function is determined by the following equation:

$${\mathit{C}}_{\mathit{I}}(\Delta \mathit{x},\Delta \mathit{y})=\frac{{\mathit{\text{FT}}}^{-1}\left[{\left|\mathit{\text{FT}}\left[\mathit{I}(\mathit{x},\mathit{y})\right]\right|}^2\right]-{〈\mathit{I}(\mathit{x},\mathit{y})〉}^2}{〈{\mathit{I}(\mathit{x},\mathit{y})}^2〉-{〈\mathit{I}(\mathit{x},\mathit{y})〉}^2},$$ (4)

where I(x,y) is the intensity value in the image plane (x,y). Δx = x₁ − x₂ and Δy = y₁ − y₂; (x₁,y₁) and (x₂,y₂) are two specific positions. FT indicates the Fourier transformation and the symbol ⟨⟩ represents the spatial averaging over the image. C_I(Δx,0) and C_I(0,Δy) are the horizontal and vertical profiles of C_I(Δx,Δy), respectively. By applying Eq. (4) to ROIs in the channel, the normalized autocovariance functions (f_Auto) along the horizontal and vertical directions are obtained (Fig. 1(c)). Then, the full width at half maximum of the calculated f_Auto provides the information on the representative size of the speckle pattern. Therefore, the average speckle area (A_Speckle) can be calculated by multiplying the horizontal and vertical speckle sizes (A_Speckle = S_H × S_V). This speckle analysis enables one to measure EA under relatively various hematocrit conditions, compared to other techniques based on image-processing techniques.^10,27–29

Figs. 1(d) and 1(e) show the temporal variations of intensity distribution along with the channel width (y/W_Half), speckle area (A_Speckle) for RBCs suspended in plasma-dextran mixture with a concentration of 0.06% (Ht = 40%), and injection flow rate (Q) of the syringe pump. As the flow rate decreases from 1 to 0 ml/h, the EA formation is promoted. Therefore, the blood image becomes to have clear and bright speckles. As shown in Fig. 1(e), A_Speckle gradually increases with the lapse of time. This result indicates that A_Speckle can be used as an indicator to evaluate EA formation.

IV. RESULTS AND DISCUSSION

A. Microscopic observation method

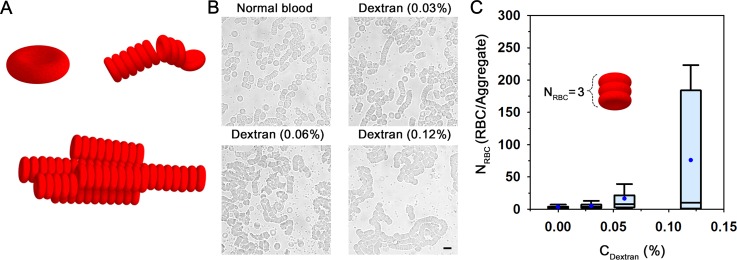
As depicted in Fig. 2(a), RBCs can be classified into three states depending on shear condition and RBC aggregability. At a high shear rate (above 100 s⁻¹) or low aggregability, most RBCs are generally monodispersed. Some smaller and deformed aggregates are present at shear rates ranging from 17 to 51 s⁻¹ or moderate aggregability. For low shear rate (below 8.5 s⁻¹) with high aggregability, the formation of large 3D complex rouleaux (clumping) is promoted.

FIG. 2.

Microscopic observation to measure erythrocyte aggregation. (a) Schematic representation for three different states of RBCs: monodispersed RBCs, smaller and deformed aggregates, and large 3D complex rouleaux. (b) Microscopic images of blood samples anticoagulated with EDTA. To enhance RBC aggregability, the mixtures of dextran solution and autologous plasma at concentrations of 0%, 0.03%, 0.06%, and 0.12% are used. (c) Variation of the number of RBCs in an aggregate (N_RBC) according to dextran concentration (C_Dextran) in blood samples (Ht = 10%). A schematic representation depicting N_RBC of 3 is included. The line in the box plot represents the median value, and the box length denotes the interquartile range. The lines emanating from the box indicate the minimum and maximum values in the dataset. Blue dots indicate the mean value evaluated from three test samples.

Fig. 2(b) shows typical optical images of blood samples in the chamber according to the treated dextran concentration. Blood samples treated with plasma-dextran mixture are compared with normal blood. RBCs in the normal plasma exhibit relatively small rouleaux and separated RBCs. As the dextran concentration increases, the rouleaux scale increases. This phenomenon can be explained by depletion theory; a thin layer, depleted of the dextran (long-chain macromolecules) between the surface of RBCs and the bulk dextran solution, reduces the osmotic force in the vicinity of RBCs, leading to a tendency for adjacent RBCs to come together.^5,56

To compare the degree of EA according to the dextran concentration (C_Dextran), the number of RBCs in an aggregate (N_RBC) was measured as depicted by the results in a box plot representation (Fig. 2(c)). The mean value of N_RBC significantly increases as C_Dextran increases. However, the range between the upper and lower quartiles becomes larger as C_Dextran increases because various sizes of rouleaux are observed under relatively high EA conditions. The dependence of local hematocrit on the size of rouleaux seems to attribute to this large interquartile range.

B. Modified ESR method

As shown in Fig. 3(a), RBCs in vertically disposed syringe are sedimented by gravity. Considering that the sedimentation rate is closely affected by the fibrinogen variations caused by inflammation and infection, EA variation can be estimated through a detailed analysis of ESR. Fig. 3(b) shows representative images of a blood sample with a total volume (V_Total = 1 ml) during RBC sedimentation (RBCs in normal plasma, Ht = 20%). As expected, the volume of the sedimented RBCs (V_RBC) is gradually decreased with the lapse of time. Given that the ESR is increased with a decrease in hematocrit,¹³ temporal variations of V_RBC were measured with respect to the hematocrit to check the effect of hematocrit, before quantifying the level of EA (Fig. 3(c)). The decreasing tendency of V_RBC is considerably accentuated at low hematocrit conditions. The variations of V_RBC at high hematocrit of 40% and 50% are not noticeable for long period over 10 h, but the V_RBC at 10% hematocrit is abruptly reduced with somewhat large standard deviation. Based on these results, the hematocrit was adjusted to be 20% for effective measurement of EA using ESR.

Like the microscopic observation method, different aggregability of RBCs caused by mixing dextran solution with different concentrations was measured through the ESR method. As represented in Fig. 3(d), V_RBC is largely reduced, as C_Dextran increases. Considering that all samples treated with the dextran have 20% hematocrit, the volume ratio (V_RBC/V_Total) may reach to 0.2 after all. However, the variation trend is somewhat different, depending on C_Dextran. For the normal blood (C_Dextran = 0%), V_RBC/V_Total almost linearly decreases for 10 h. However, the V_RBC/V_Total at the highest concentration (C_Dextran = 0.12%) is saturated at 0.2 in a short time. In order to evaluate the variation of ESR according to physiological conditions, V_RBC/V_Total is approximately modeled as follows:

$${\mathrm{V}}_{\text{RBC}}{/\mathrm{V}}_{\text{Total}}=\alpha +{\beta \mathrm{e}}^{(-\mathrm{t}/\lambda )},$$ (5)

where t is the measurement time. Three fitting parameters, namely, initial value (α), fitting constant (β), and characteristic time (λ_ESR) can be determined through regression analysis. Fig. 3(e) compares the variations of three fitting parameters estimated according to C_Dextran. As a typical example, a V_RBC/V_Total at the C_Dextran of 0.03% and its fitting curve (α = 0.38, β = 0.55, and λ_ESR = 1.89 h) are depicted in the right top inset of Fig. 3(e). λ_ESR tends to decrease as C_Dextran increases. This result indicates that completing the sedimentation of RBCs in a disposable syringe is faster for the RBCs mixed with high dextran molecules. However, other fitting parameters are inconsistent according to C_Dextran due to different V_RBC/V_Total variation trends. This discrepancy in fitting parameters (α and β) may lead to somewhat incorrect fitting of λ_ESR, because the fitting parameters depend on one another. The dextran treatment has been known to increase the viscosity of solution. Thus, increase in plasma viscosity caused by dextran treatment also enhances the sedimentation velocity.

C. Ultrasonic imaging method

Ultrasonic images of blood flows are mainly made from backscattering of RBCs. In particular, the presence of RBC aggregates significantly enhances the backscattering power (echogenicity). Based on this relationship, ultrasound signals of blood samples passing through the vascular phantom were measured using a transducer for the estimation of EA (Fig. 4(a)). During the EA measurement, hemodynamic information in the channel was monitored by employing the SIV technique. Fig. 4(b) shows variation of flow rate (Q) estimated by Eq. (3). Insets (a)–(c) in the bottom left of Fig. 4(b) show velocity fields captured at specific times [(a) t = 0 s, (b) t = 2.5 s, and (c) t = 5 s]. Fig. 4(c) shows the temporal variation of the echogenicity distribution along the radial direction (C_Dextran = 0.12% and Ht = 40%). As the flow rate in the vascular phantom decreases, the bright region around the tube center expands. These results signify that the decrease in shear force facilitates the EA formation and propagates it from the tube center toward the vessel wall.

FIG. 4.

Ultrasonic imaging method to measure erythrocyte aggregation. (a) Schematic diagram of the ultrasound imaging system. Blood is delivered into the vascular phantom with an inner diameter of 1 mm. An acoustic absorber is placed in the bottom of the phantom to minimize ultrasound artifacts. (b) Variation of flow rate (Q) estimated based on the results of speckle image velocimetry measurement. Typical velocity fields at specific times of [(a)–(c) t = 0, 2.5, and 5 s]. (c) Temporal variation of the echogenicity distribution measured along the radial direction. Temporal variations of the mean echogenicity (e) in the whole tube with respect to (d) hematocrit (Ht) and (e) dextran concentration (C_Dextran) at Ht = 40%. (f) Quantitative evaluation of aggregation index (AI_Echo) according to C_Dextran. An explanation depicting AI_Echo using the data (C_Dextran = 0.03%) is included. Each data set indicates the mean value and standard deviation evaluated from three test samples.

Taking into account the fact that the ultrasonic backscattering signals are dependent on the hematocrit,^57,58 the effect of hematocrit on the temporal variation of echogenicity (E) was investigated. Similar to previous studies, the dependence of E on hematocrit is clearly shown in Fig. 4(d). Specifically, the increasing tendency with respect to time becomes more pronounced at higher hematocrit conditions, and the final value at 5 s becomes higher as the hematocrit increases. However, this effect is not linearly proportional to the hematocrit. In light of hematocrit level under normal physiological conditions, the 40% hematocrit was used to evaluate the EA using ultrasound modality.

Fig. 4(e) shows the temporal variations of E for four different C_Dextran conditions. The dextran treatment significantly accentuates the increasing tendency of E caused by the ascertained intercellular interactions. The initial E value at 0 s and the final value at 5 s also increase as the C_Dextran increases. For quantification of these variations, an aggregation index (AI_Echo) is evaluated using a following mathematical equation:

$${\text{AI}}_{\text{Echo}}=\frac{{\int }_0^{\mathrm{t}}\mathrm{E}\left(t\right)dt-{\mathrm{E}}_{\text{Min}}\mathrm{t}}{{(\mathrm{E}}_{\text{Max}}-{\mathrm{E}}_{\text{Min}})\mathrm{t}},$$ (6)

where t represents the total measurement time (5 s). E_Max and E_Min are the maximum and minimum echogenicity in the data analysis. In this study, E_Max and E_Min are set as 13 and 16 dB for convenience. Fig. 4(f) shows variations in the estimated AI_Echo with respect to C_dextran. For the explanation, an inset depicting the AI_Echo at the C_Dextran of 0.03% is included in the bottom right of Fig. 4(f). As expected, the increasing tendency of AI_Echo is evident along with increases in C_Dextran. This finding indicates that the dextran treatment seems to promote the formation and propagation of EA under a defined hemodynamic condition. However, the elevated aggregability caused by dextran treatment can disturb complete disaggregation under high flow rates prior to EA measurement because the tube center has a relatively low shear rate. This effect may result in increase in the initial value of E at a high C_Dextran condition.

D. Microfluidic-based method

Variation of flow condition in the microchannel (Fig. 5(a)) was monitored during the measurement of EA using the micro-PIV technique. Fig. 5(b) shows the velocity profiles of RBCs suspended in autologous plasma (Ht = 40%) at different elapsed times (t = 0, 30, and 60 s) along the normalized lateral position (y/W_Half). The representative velocity field superimposed on the corresponding blood image in the microchannel is also included in Fig. 5(b). The velocity vectors in the middle region of the channel are quite blunt. This bluntness results from the low aspect ratio (H/W) of the rectangular microchannel. The flow rate measured by Eq. (2) is decreased as time lapses. Although the general variation trend is similar to the injection profile of the syringe pump, a certain discrepancy is observed because of the transient response in the microfluidic system (Fig. 5(c)).

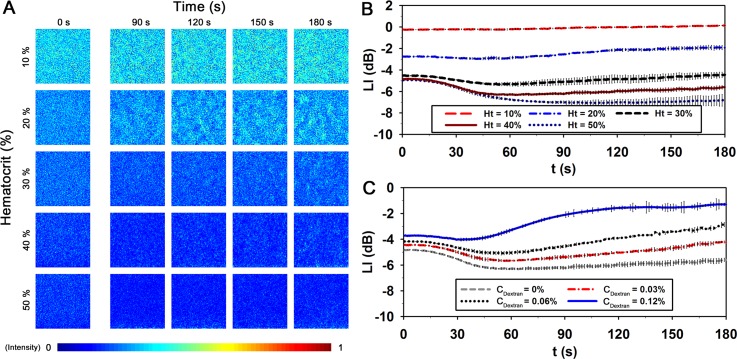
Likewise other conventional methods, the dependence of hematocrit was also investigated by using the microfluidic device. Fig. 6(a) shows images of RBCs in autologous plasma with respect to lapsed time and hematocrit. The optical images of blood flows are usually affected by the light transmitted through the migrating RBCs in the channel. Thus, such images become darker as hematocrit increases. The formation of EA, which results from the decrease in flow rate, creates speckle patterns accompanied with an increase in intensity. However, these variations are not so noticeable for the two cases of 10% and 50% hematocrits. For 10% hematocrit, the intensity difference between the blood samples and the background is difficult to distinguish due to the small number of RBCs. On the other hand, too many RBCs in the microchannel disturb the light transmission for the case of 50% hematocrit.

FIG. 6.

Temporal variation of blood flows in the microfluidic channel with respect to hematocrit and dextran treatment. (a) Speckle images of blood samples with respect to hematocrit level and elapsed time. The size of each image is 150 pixels, corresponding to 303.6 μm in physical dimension. Temporal variations of light intensity (LI) at the center of the channel with respect to (b) hematocrit (Ht), and (c) dextran concentration (C_Dextran). The LI is expressed in decibels (dB) to depict the ratio of the blood to the background intensities. Each data set indicates the mean value and standard deviation evaluated from three test samples.

For detailed quantitative analysis, light intensity (LI) transmitted through the channel was measured with respect to hematocrit. Like the echogenicity analysis, the LI value is also expressed in decibels (dB) to depict the ratio of the blood to the background intensities. As shown in Fig. 6(b), LI highly depends on hematocrit. LI has low values at high hematocrit conditions. For the 10% hematocrit, the LI value is almost similar to the background intensity, and the variation of LI is not clear during the measurement. However, when the hematocrit ranges from 20% to 50%, the LI value reduces during the initial state (0–45 s). This decreasing trend is accentuated by the increase in hematocrit. This enhancement may be attributed to the shift of Doppler-frequency experienced by the photons scattered from the flowing particles.^59,60 The decrease in flow velocity may reduce the light scattered from RBCs. Eventually, the reduction of scattering light may lead to the decrease of LI during the initial state. After 60 s, the LI values are increased for all hematocrit conditions due to the EA formation. The increment of LI is largest at the 20% hematocrit. As the hematocrit increases, the increasing trend of LI is attenuated. In the consideration of normal hematocrit level, the hematocrit was fixed at 40% to examine the effect of the dextran treatment on EA. Fig. 6(c) shows the temporal variations of LI with respect to C_Dextran. The LI values are also decreased at the initial state for all C_Dextran. Although the increasing trend of LI is promoted by the dextran treatment after 60 s, it is difficult to precisely measure the degree of EA at high aggregability conditions.

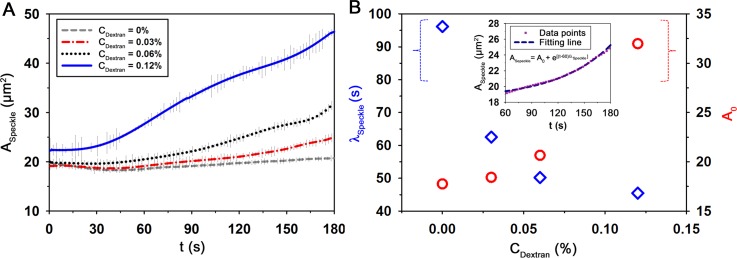
Thus, the variations of EA according to C_Dextran were measured through the speckle analysis based on the microfluidic measurement method (Fig. 7(a)). The difference in the degree of EA is clearly shown for all C_Dextran conditions. The ascertained C_Dextran tends to enhance the increasing trend of the A_Speckle. To quantify this increasing trend, the two fitting parameters, including initial value (A₀) and characteristic time (λ_Speckle), are obtained by approximately fitting the variation of A_Speckle using the following equation:

$${\mathrm{A}}_{\text{Speckle}}={\mathrm{A}}_0+{\mathrm{e}}^{[(\mathrm{t}–60){/\lambda }_{\text{Speeckle}}]},$$ (7)

where t is the measurement time. In order to minimize the effect of Doppler-frequency shift, the regression analysis was conducted after 60 s. Fig. 7(b) shows the variations of A₀ and λ_Speckle with respect to C_Dextran. As a typical example, A_Speckle at the C_Dextran of 0.03% and its fitting curve (A₀ = 18.4 μm² and λ_Speckle = 62.5 s) are included in the inset of Fig. 7(b). As the C_Dextran increases, λ_Speckle is reduced and A₀ is ascended. It means that high dextran molecules create clear speckle patterns in a short time. From these results, we can see that λ_Speckle can be used to reasonably estimate the extent of EA under various physiological conditions.

FIG. 7.

Speckle analysis method to measure erythrocyte aggregation. (a) Temporal variations of the average speckle area (A_Speckle) at Ht = 40% with respect to dextran concentration (C_Dextran). (b) Quantitative evaluations of the characteristic time (λ_Speckle) and A₀ obtained by Eq. (7) according to C_Dextran. Data points (C_Dextran = 0.03%) and its fitting curve are included. Each data set indicates the mean value and standard deviation evaluated from three test samples.

E. Detection of diabetic blood

Using the aforementioned four different assessment techniques, representative indices including N_RBC, λ_ESR, AI_Echo, and λ_Speckle were determined to quantitatively analyze the extent of EA. The obtained results clarify that these indices reasonably estimate the variations of EA under various hemorheological conditions. For clinical demonstration of the proposed method, the performances of the four indices in detecting different EA extent of diabetic blood were assessed.

DM is a metabolic disorder characterized by high blood sugar (hyperglycemia) resulted from either low insulin level or high insulin resistance in body cells. When blood is exposed under a hyperglycemic condition, biochemical plasma components and RBC membranes are changed. DM gives rise to the excessive EA which contributes to impaired microcirculatory flow⁸ and implicates the development of CVDs.⁶¹ To evaluate the elevated EA of diabetic blood using the four indices, blood samples were collected from STZ-induced diabetic rat models. Prior to the measurement of EA, glucose concentration of blood was measured using an Accu-Chek^® Sensor instrument with test strips (Roche Diagnostics, Mannheim, Germany). As summarized in Table I, the glucose concentrations of the DM blood samples are about 2.4 times larger than those of the control group.

TABLE I.

Comparison of various EA indices between normal and diabetic blood samples. Each value represents mean ± standard deviation.

	Control	DM	P-value
Blood sugar (mg/dl)	184.0 ± 2.6	434.3 ± 41.4	0.0010
NRBC (RBC/aggregate)	3.1 ± 2.0	16.4 ± 4.5	0.0186
λESR (h)	4.08 ± 0.34	1.10 ± 0.41	0.0014
AIEcho (dB s)	0.25 ± 0.03	0.42 ± 0.08	0.0572
λSpeckle (s)	96.1 ± 3.8	54.8 ± 9.3	0.0044

The four indices for the DM blood samples are considerably different from those for the control group (Table I). Specifically, N_RBC and AI_Echo for the DM are about 3 and 1.4 times higher compared with those for the control. On the other hand, λ_ESR and λ_Speckle for the DM are 3.7 times and 1.8 times lower than those for the control. These experimental results demonstrate that the four indices can reasonably detect the EA variation caused by DM. However, the N_RBC exhibits a rather large standard deviation because the average size of rouleaux is highly dependent on adjacent RBCs at local positions. Although λ_ESR has the smallest P-value among the four indices, this technique needs to measure for a relatively long time. For the case of AI_Echo, blood samples should be delivered at a high flow rate to completely disaggregate the rouleaux before the EA measurement. Therefore, a large volume of blood sample is essentially required to deliver samples into the vessel. Although the Couette system can induce a large shear rate condition with a small sample volume, the environment is somewhat different from the EA formed in blood vessels. Given that λ_Speckle can be obtained from a relatively small sample volume in a short time, speckle analysis based on the microfluidic measurement method has several distinctive advantages in detecting excessive EA caused by DM. However, this technique is hampered by the dependence of hematocrit and requires several devices such as camera, LED illumination system, and so on. Therefore, further advances in some aspects, such as eliminating the hematocrit effect and simplifying the measurement devices, are required in the near future.

V. CONCLUSION

This study proposed a simple speckle analysis based on the microfluidic measurement method to detect the hyperaggregation caused by DM. This proposed method can acquire microscopic images of blood flow in microfluidics with a short exposure time for a long time. EA formation was induced by reducing the injection flow rate via a programmable syringe pump. In order to monitor the temporal variation of flow conditions in the microchannel, a micro-PIV velocity field measurement technique was applied to the captured flow images. Before conducting the speckle analysis, the variations in LI and the hematocrit effect were assessed. By calculating the normalized autocovariance function, the variation of speckle area (A_Speckle) was evaluated during the measurement. The characteristic time of speckle patterns (λ_Speckle) was obtained by approximately fitting the variation of A_Speckle to quantitatively analyze the degree of the EA. The variation of λ_Speckle was demonstrated under different EA conditions caused by the dextran treatment. Other indices (N_RBC, λ_ESR, and AI_Echo) were also determined through other widely used conventional methods including the microscopic observation, modified ESR, and ultrasonic imaging methods to compare with the corresponding results measured by the proposed method. From the present experimental results, we can infer that the proposed method can reasonably detect EA changes caused by DM compared with conventional methods. This microfluidic-based measurement method has a strong potential as a useful tool for evaluating the variations in biophysical properties of blood samples collected from patients with DM or various cardiovascular diseases.