Biased diffusion in three-dimensional comb-like structures

Abstract

In this paper, we study biased diffusion of point Brownian particles in a three-dimensional comb-like structure formed by a main cylindrical tube with identical periodic cylindrical dead ends. It is assumed that the dead ends are thin cylinders whose radius is much smaller than both the radius of the main tube and the distance between neighboring dead ends. It is also assumed that in the main tube, the particle, in addition to its regular diffusion, moves with a uniform constant drift velocity. For such a system, we develop a formalism that allows us to derive analytical expressions for the Laplace transforms of the first two moments of the particle displacement along the main tube axis. Inverting these Laplace transforms numerically, one can find the time dependences of the two moments for arbitrary values of both the drift velocity and the dead-end length, including the limiting case of infinitely long dead ends, where the unbiased diffusion becomes anomalous at sufficiently long times. The expressions for the Laplace transforms are used to find the effective drift velocity and diffusivity of the particle as functions of its drift velocity in the main tube and the tube geometric parameters. As might be expected from common-sense arguments, the effective drift velocity monotonically decreases from the initial drift velocity to zero as the dead-end length increases from zero to infinity. The effective diffusivity is a more complex, non-monotonic function of the dead-end length. As this length increases from zero to infinity, the effective diffusivity first decreases, reaches a minimum, and then increases approaching a plateau value which is proportional to the square of the particle drift velocity in the main tube.

I. INTRODUCTION

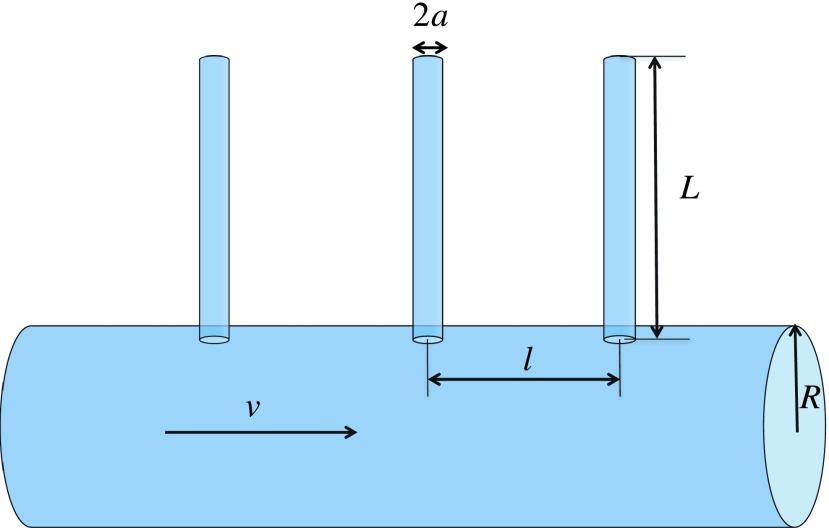
This paper deals with biased diffusion of point Brownian particles in a comb-like structure formed by a main cylindrical tube of radius R with identical periodic cylindrical dead ends of radius a and length L, separated by distance l (see Fig. 1). It is assumed that both the distance l between neighboring dead ends and radius R of the main tube significantly exceed the dead-end radius, a < < l, R, whereas the dead-end length may be arbitrary, L ≥ 0. In our recent paper,¹ we studied unbiased diffusion in such comb-like structures. An exciting feature of this process is that diffusion can be both normal and anomalous depending on whether the dead end length L is finite or infinite. The theory developed in Ref. 1 provides an analytical solution for the Laplace transform of the mean square displacement of a particle diffusing in such a system. Inverting this Laplace transform, one can find the time dependence of the mean square displacement over the entire range of time for arbitrary values of the geometric parameters a,  l,  R, and L. The solution for the Laplace transform not only describes effective normal and anomalous diffusions at long times but also shows the existence of intermediate anomalous diffusion^2–6 when the dead end length L is finite, but sufficiently long. The present work extends the theory to the case of biased diffusion, where a uniform constant external force F acts on the particle in the main tube. As a result, in the main tube, the particle, in addition to its regular diffusion with diffusivity D₀, moves with a constant drift velocity v, v ≥ 0, which is proportional to the biasing force, $v=D_{0}F/\left(k_{B}T\right)$, where k_BT is the product of the Boltzmann constant and absolute temperature. The goal of the theory is to predict the dependences of the first two moments of the particle displacement on time, as well as on the drift velocity v and the geometric parameters of the system. We will see that these time dependences are qualitatively different depending on whether L is finite or infinite.

FIG. 1.

Schematic representation of a comb-like structure formed by a main cylindrical tube of radius R and periodic thin cylindrical dead ends of radius a and length L, separated by distance l.

The model of particle transport in comb-like structures has been used in discussing different biological processes. Examples include transport in dendritic spines,^7–10 intratissue transport of water and other substances,^11–13 extracellular transport in brain,^14–18 and tumor development.¹⁹ This model was also used to describe transport in soils^20–24 and linear porous media.^25–32 Goldhirsch and Gefen³³ and Weiss and Havlin^34,35 proposed this model as a toy model of transport in disordered networks.^36,37 Finally, we note that transport in comb-like structures is a special case of a more general problem of transport in quasi-one-dimensional systems of periodically varying geometry, the so-called entropic transport, which has attracted attention of many researchers because of its importance in various applications (see recent review articles^38–43 and references therein).

The present study focuses on the first two moments of the particle displacement along the tube axis and, more specifically, on how these moments depend on time, the drift velocity, and the geometric parameters of the system. When developing a theory of transport in three-dimensional comb-like structures, one has to describe the particle entry into the dead ends and to characterize the duration of its stay in the dead end. To be more precise, one needs to know the probability densities of the particle lifetime in the main tube and in the dead end. Finding these probability densities is an extremely complicated problem. An approach that allows one to overcome the difficulties is proposed in Ref. 30. The approach involves two approximations: (1) one can find the probability density of the particle lifetime in the main tube by using boundary homogenization⁴⁴ which is an approximate replacement of non-uniform boundary conditions on the tube wall by an effective uniform boundary condition with a properly chosen trapping rate. (2) An approximate solution for the probability density of the particle lifetime in the dead end can be obtained by applying the formalism developed in papers cited in Ref. 45. The two above mentioned approximations are used in Ref. 1 devoted to unbiased diffusion in comb-like structures. In the rest of this section, we briefly discuss main ideas of the theory developed in Ref. 1, as well as some relations which are used in our further analysis.

The formalism developed in Ref. 1 allowed us to find an analytical solution for the Laplace transform of the mean square displacement of the particle along the tube axis in time t, $〈x^2\left(t\right)〉$, which is applicable for an arbitrary dead-end length L. The solution shows that after some relaxation time, $〈x^2\left(t\right)〉$ approaches its long-time asymptotic behavior, which is qualitatively different depending on whether L is finite or infinite. When L is finite, the asymptotic behavior is normal diffusion characterized by the effective diffusivity, D_eff, so that

$${\displaystyle 〈x^2\left(t\right)〉=2D_{\mathit{eff}}t,t\to \infty ,}$$ (1.1)

with the effective diffusivity given by

$${\displaystyle D_{\mathit{eff}}=D_0{f}_m^{\mathit{eq}}.}$$ (1.2)

Here, $f_m^{\mathit{eq}}$ is the equilibrium probability of finding the particle in the main tube (mobile (m) state), where it can propagate along the tube axis,

$${\displaystyle f_m^{\mathit{eq}}=\frac{V_m}{V_m+V_{\mathit{de}}}=\frac{R^{2}l}{R^{2}l+a^{2}L},}$$ (1.3)

with the notations V_m = πR²l and V_de = πa²L for the volume of the main tube per a dead end and the dead-end volume, respectively.

When L is infinite, the asymptotic behavior is anomalous subdiffusion,

$${\displaystyle 〈x^2\left(t\right)〉=2D_0\frac{V_m}{A_{\mathit{de}}}\sqrt{\frac{t}{\pi D_{\mathit{de}}}}=2D_0\frac{R^{2}l}{a^2}\sqrt{\frac{t}{\pi D_{\mathit{de}}}},t\to \infty ,}$$ (1.4)

where A_de = πa² is the dead-end entrance area, and D_de is the particle diffusivity in the dead ends, which may differ from its counterpart D₀ in the main tube. In what follows, we refer to the cases of finite and infinite L as normal and anomalous regimes, respectively. The solution obtained in Ref. 1 also shows that intermediate anomalous subdiffusion, $〈x^2\left(t\right)〉\propto t^{1/2}$, can be observed during transient behavior to normal diffusion at very long times. This happens only when the dead-end length L is large enough.

The central idea of the formalism developed in Ref. 1 exploits the fact that the particle propagates along the tube axis only when it is in the main tube, which we therefore refer to as a mobile state of the particle. The dead ends (de) are considered as a particle immobile state, since by entering a dead end, the particle interrupts its propagation along the tube axis. The transitions between the two states are described by the kinetic scheme

$${\displaystyle m€\mathit{de}.}$$ (1.5)

Let t_m(t) be the cumulative time spent by the particle in the mobile state, conditional on that the total observation time is t, t_m(t) ≤ t. Time t_m(t) is a random variable. In Ref. 1, we derived an expression for the double Laplace transform of the conditional probability density of time t_m, $\phi \left(\left.t_m\right|t\right)$, denoted by $\hat{\phi }\left(\sigma ,s\right)$,

$${\displaystyle \hat{\phi }\left(\sigma ,s\right)={\int }_0^{\infty }{e}^{-st}dt{\int }_0^t{e}^{-\sigma t_m}\phi \left(\left.t_m\right|t\right)d{t}_m={\int }_0^{\infty }{\int }_0^{\infty }{e}^{-\sigma t_m-st}\phi \left(\left.t_m\right|t\right)d{t}_{m}dt,}$$ (1.6)

where we have used the fact that $\phi \left(\left.t_m\right|t\right)=0$ for t_m > t. The expression gives $\hat{\phi }\left(\sigma ,s\right)$ in terms of the Laplace transforms of the probability densities of the particle lifetimes in the mobile state, w_m(t), and in the dead ends, w_de(t),

$${\displaystyle {\hat{w}}_{m,de}\left(s\right)={\int }_0^{\infty }{e}^{-st}{w}_{m,de}\left(t\right)dt.}$$ (1.7)

Assuming that the particle starts in the mobile state, we obtained

$${\displaystyle \hat{\phi }\left(\sigma ,s\right)=\frac{s\left(1-{\hat{w}}_m(s+\sigma ){\hat{w}}_{\mathit{de}}\left(s\right)\right)+\sigma {\hat{w}}_m(s+\sigma )\left(1-{\hat{w}}_{\mathit{de}}\left(s\right)\right)}{s(s+\sigma )\left(1-{\hat{w}}_m(s+\sigma ){\hat{w}}_{\mathit{de}}\left(s\right)\right)}.}$$ (1.8)

Having in hand the double Laplace transform of $\phi \left(\left.t_m\right|t\right)$, one can find the Laplace transform of any moment of time t_m(t) defined as

$${\displaystyle 〈t_m^n\left(t\right)〉={\int }_0^t{t}_m^n\phi \left(\left.t_m\right|t\right)d{t}_m,n=0,1,2,...,}$$ (1.9)

using the relation between $〈{\hat{t}}_m^n\left(s\right)〉$ and $\hat{\phi }\left(\sigma ,s\right)$,

$${\displaystyle 〈{\hat{t}}_m^n\left(s\right)〉={\int }_0^{\infty }{e}^{-st}〈t_m^n\left(t\right)〉dt={\left(-1\right)}^n{\left.\frac{{\partial }^n\hat{\phi }\left(\sigma ,s\right)}{\partial {\sigma }^n}\right|}_{\sigma =0}.}$$ (1.10)

As shown in Ref. 1, the probability density w_m(t) is a single exponential, w_m(t) = k_me^−k_mt, where the rate constant k_m is

$${\displaystyle k_m=\frac{4D_{0}a}{V_m}.}$$ (1.11)

Therefore, the Laplace transform of w_m(t) is given by

$${\displaystyle {\hat{w}}_m\left(s\right)=\frac{k_m}{s+k_m}.}$$ (1.12)

It is also shown that the Laplace transform of the probability density of the particle lifetime in the dead end has the form

$${\displaystyle {\hat{w}}_{\mathit{de}}\left(s\right)=\frac{{\kappa }_{\mathit{de}}}{{\kappa }_{\mathit{de}}+\sqrt{s{D}_{\mathit{de}}}tanh\left(L\sqrt{s/D_{\mathit{de}}}\right)},}$$ (1.13)

where the parameter κ_de is given by

$${\displaystyle {\kappa }_{\mathit{de}}=\frac{4D_0}{\pi a}.}$$ (1.14)

The probability densities of the particle lifetimes in both mobile and immobile states are independent of the particle drift velocity in the main tube.³² As a consequence, the conditional probability density $\phi \left(\left.t_m\right|t\right)$ is also velocity-independent. Therefore, in what follows, we use the above relations to analyze biased diffusion of the particles in comb-like structures. To this end, we derive expressions for the Laplace transforms of the first two moments of the particle displacement along the tube axis. Inverting these transforms numerically, one can find the time dependences of the moments for arbitrary values of the dead-end length L and the drift velocity v. These dependences are used to study the time dependences of the effective velocity and diffusivity of the particle as functions of L and v.

The outline of this paper is as follows. General expressions for the Laplace transforms of the first two moments of the particle displacement are derived in Sec. II. Time dependences of the mean displacement and the effective velocity are discussed in Sec. III. Section IV is devoted to the effective diffusivity. Finally, we summarize obtained results and make some concluding remarks in Sec. V.

II. GENERAL RELATIONS

In this section, we derive general relations between the first two moments of the particle displacement along the tube axis in time t and the first two moments of the cumulative time t_m(t), which the particle spent in the mobile state. Since the particle propagates along the tube axis (in the x-direction) only when it is in the mobile state, the particle propagator G(x, t), which is the probability density of finding the displacement equal to x at time t, can be written as

$${\displaystyle G(x,t)={\int }_0^t{G}_v(x,t_m)\phi \left(\left.t_m\right|t\right)d{t}_m,}$$ (2.1)

where G_v(x, t) is the axial propagator of the particle diffusing in a cylindrical tube with no dead ends in the presence of the drift velocity v,

$${\displaystyle G_v(x,t)=\frac{1}{\sqrt{4\pi D_{0}t}}{e}^{-{\left(x-vt\right)}^2/\left(4D_{0}t\right)}.}$$ (2.2)

Both propagators become the δ-function as t → 0, G(x, 0) = G_v(x, 0) = δ(x), since the displacement vanishes at t = 0.

The propagator in Eq. (2.1) is used to find the moments $〈x^m\left(t\right)〉$ of the particle displacement in time t,

$${\displaystyle 〈x^m\left(t\right)〉={\int }_{-\infty }^{\infty }{x}^{m}G(x,t)dx={\int }_0^t\left[{\int }_{-\infty }^{\infty }{x}^m{G}_v(x,t_m)dx\right]\phi \left(\left.t_m\right|t\right)d{t}_m.}$$ (2.3)

To find the mean displacement, $〈x\left(t\right)〉$, we use the relation

$${\displaystyle {\int }_{-\infty }^{\infty }x{G}_v(x,t)dx=vt.}$$ (2.4)

Substituting this into Eq. (2.3) with m = 1, we obtain

$${\displaystyle 〈x\left(t\right)〉=v〈t_m\left(t\right)〉,}$$ (2.5)

as might be expected based on the common-sense arguments.

Similarly, we find the mean square displacement in time t, $〈x^2\left(t\right)〉$, by substituting the relation

$${\displaystyle {\int }_{-\infty }^{\infty }{x}^2{G}_v(x,t)dx=v^2{t}^2+2D_{0}t}$$ (2.6)

into Eq. (2.3) with m = 2. The result is

$${\displaystyle 〈x^2\left(t\right)〉=v^2〈t_m^2\left(t\right)〉+2D_0〈t_m\left(t\right)〉.}$$ (2.7)

As follows from Eqs. (2.5) and (2.7), the variance of the displacement in time t, ${\sigma }_x^2\left(t\right)$, is related to the variance of the cumulative time spent by the particle in the mobile state, ${\sigma }_{t_m}^2\left(t\right)$, by the relation

$${\displaystyle {\sigma }_x^2\left(t\right)=〈x^2\left(t\right)〉-{〈x\left(t\right)〉}^2=2D_0〈t_m\left(t\right)〉+v^2{\sigma }_{t_m}^2\left(t\right),}$$ (2.8)

where the variance ${\sigma }_{t_m}^2\left(t\right)$ is

$${\displaystyle {\sigma }_{t_m}^2\left(t\right)=〈t_m^2\left(t\right)〉-{〈t_m\left(t\right)〉}^2.}$$ (2.9)

We assume that the particle starts in the mobile state, so that the double Laplace transform of the probability density $\phi \left(\left.t_m\right|t\right)$ is given by Eq. (1.8). Using Eq. (1.12), we can write $\hat{\phi }\left(\sigma ,s\right)$ as

$${\displaystyle \hat{\phi }\left(\sigma ,s\right)=\frac{1}{s\left[1+\frac{\sigma }{s+k_m\left(1-{\hat{w}}_{\mathit{de}}\left(s\right)\right)}\right]}.}$$ (2.10)

According to Eq. (1.10), the Laplace transforms of the first two moments of the cumulative time t_m(t) are

$${\displaystyle 〈{\hat{t}}_m\left(s\right)〉=\frac{1}{s\left[s+k_m\left(1-{\hat{w}}_{\mathit{de}}\left(s\right)\right)\right]}}$$ (2.11)

and

$${\displaystyle 〈{\hat{t}}_m^2\left(s\right)〉=\frac{2}{s{\left[s+k_m\left(1-{\hat{w}}_{\mathit{de}}\left(s\right)\right)\right]}^2}.}$$ (2.12)

Correspondingly, the Laplace transforms of the first two moments of the particle displacement, Eqs. (2.5) and (2.7), are given by

$${\displaystyle 〈\hat{x}\left(s\right)〉=\frac{v}{s\left[s+k_m\left(1-{\hat{w}}_{\mathit{de}}\left(s\right)\right)\right]}}$$ (2.13)

and

$${\displaystyle 〈{\hat{x}}^2\left(s\right)〉=\frac{2}{s\left[s+k_m\left(1-{\hat{w}}_{\mathit{de}}\left(s\right)\right)\right]}\times \hspace{0.17em}\left[\frac{v^2}{s+k_m\left(1-{\hat{w}}_{\mathit{de}}\left(s\right)\right)}+D_0\right].}$$ (2.14)

In what follows, the Laplace transforms in Eqs. (2.13) and (2.14) are used to analyze the particle motion at different values of the drift velocity v and the dead-end length L, which enters into the Laplace transform of the probability density w_de(t), given in Eq. (1.13).

III. MEAN DISPLACEMENT AND EFFECTIVE DRIFT VELOCITY

As follows from Eqs. (2.5) and (2.7), the time dependence of the mean displacement, $〈x\left(t\right)〉=v〈t_m\left(t\right)〉$, is identical to that of the mean square displacement in the absence of the drift velocity, ${\left.〈x^2\left(t\right)〉\right|}_{v=0}=2D_0〈t_m\left(t\right)〉$. The latter is discussed in detail in Ref. 1. Therefore, here we only briefly outline some features of the time dependence $〈x\left(t\right)〉$, focusing on the difference between the normal (finite L) and anomalous (infinite L) regimes.

Substituting ${\hat{w}}_{\mathit{de}}\left(s\right)$ in Eq. (1.13) into Eq. (2.13), we find that the Laplace transform of the mean displacement is

$${\displaystyle 〈\hat{x}\left(s\right)〉=\frac{v\left[{\kappa }_{\mathit{de}}+\sqrt{s{D}_{\mathit{de}}}tanh\left(L\sqrt{s/D_{\mathit{de}}}\right)\right]}{s\left[s{\kappa }_{\mathit{de}}+\left(s+k_m\right)\sqrt{s{D}_{\mathit{de}}}tanh\left(L\sqrt{s/D_{\mathit{de}}}\right)\right]}.}$$ (3.1)

The asymptotic behavior of this transform at large and small values of the Laplace parameter s is used to find the short- and long-time behavior of $〈x\left(t\right)〉$, respectively. In the former case, we have

$${\displaystyle 〈\hat{x}\left(s\right)〉=\frac{v}{s^2},s\to \infty .}$$ (3.2)

Inverting this transform, we obtain

$${\displaystyle 〈x\left(t\right)〉=vt,t\to 0,}$$ (3.3)

as might be expected since the particle starts in the mobile state.

The long-time behavior of $〈x\left(t\right)〉$ is qualitatively different depending on whether L is finite or infinite. When L is finite (the normal regime), we have

$${\displaystyle 〈\hat{x}\left(s\right)〉=\frac{v{\kappa }_{\mathit{de}}}{s^2\left({\kappa }_{\mathit{de}}+k_{m}L\right)},s\to 0.}$$ (3.4)

Using Eqs. (1.11) and (1.14), one can check that the ratio ${\kappa }_{\mathit{de}}/\left({\kappa }_{\mathit{de}}+k_{m}L\right)$ is the equilibrium probability of finding the particle in the mobile state defined in Eq. (1.3),

$${\displaystyle \frac{{\kappa }_{\mathit{de}}}{\left({\kappa }_{\mathit{de}}+k_{m}L\right)}=\frac{V_m}{V_m+V_{\mathit{de}}}=f_m^{\mathit{eq}}.}$$ (3.5)

This allows us to write Eq. (3.4) as

$${\displaystyle 〈\hat{x}\left(s\right)〉=\frac{v_{\mathit{eff}}}{s^2},s\to 0,}$$ (3.6)

where v_eff is the effective drift velocity given by

$${\displaystyle v_{\mathit{eff}}=v{f}_m^{\mathit{eq}}=\frac{v{V}_m}{V_m+V_{\mathit{de}}}.}$$ (3.7)

Inverting the Laplace transform in Eq. (3.6), we find that the long-time behavior of the mean displacement in the normal regime is

$${\displaystyle 〈x\left(t\right)〉=v_{\mathit{eff}}t,t\to \infty .}$$ (3.8)

In the anomalous regime (L = ∞), the Laplace transform in Eq. (3.1) simplifies and takes the form

$${\displaystyle 〈\hat{x}\left(s\right)〉=\frac{v\left({\kappa }_{\mathit{de}}+\sqrt{s{D}_{\mathit{de}}}\hspace{0.17em}\right)}{s\left[s{\kappa }_{\mathit{de}}+\left(s+k_m\right)\sqrt{s{D}_{\mathit{de}}}\right]}.}$$ (3.9)

In the small-s limit, this reduces to

$${\displaystyle 〈\hat{x}\left(s\right)〉=\frac{v{\kappa }_{\mathit{de}}}{k_m\sqrt{D_{\mathit{de}}}{s}^{3/2}}=\frac{v{V}_m}{A_{\mathit{de}}\sqrt{D_{\mathit{de}}}{s}^{3/2}},s\to 0,}$$ (3.10)

where we have used the expressions for k_m and κ_de in Eqs. (1.11) and (1.14). We find the long-time behavior of $〈x\left(t\right)〉$ in the anomalous regime by inverting the Laplace transform $〈\hat{x}\left(s\right)〉$ above. The result is

$${\displaystyle 〈x\left(t\right)〉=v\frac{2V_m}{A_{\mathit{de}}}\sqrt{\frac{t}{\pi D_{\mathit{de}}}},t\to \infty .}$$ (3.11)

To summarize, at long times, the mean displacement increases linearly with time in the normal regime and as the square root of time in the anomalous regime. Note that the long-time asymptotic behavior of the mean displacement, $〈x\left(t\right)〉\propto \sqrt{t}$, agrees with the corresponding asymptotic result obtained by Weiss and Havlin³⁴ who studied random walk on a comb-like structure with infinite teeth.

We define the effective drift velocity, v_eff(t), as the ratio of the mean displacement in time t to this time,

$${\displaystyle v_{\mathit{eff}}\left(t\right)=\frac{〈x\left(t\right)〉}{t}=v\frac{〈t_m\left(t\right)〉}{t}=v{f}_m\left(t\right).}$$ (3.12)

Here, $f_m\left(t\right)=〈t_m\left(t\right)〉/t$ is the fraction of time spent by the particle in the mobile state, conditional on that the total observation time is t. This function was introduced in Ref. 1, where one can find plots illustrating the time-dependence of f_m(t) for several values of the dead-end length L, including L = ∞. As t → ∞, f_m(t) tends to the equilibrium probability of finding the particle in the mobile state, $f_m^{\mathit{eq}}$. From Eq. (1.3), one can see that the equilibrium probability is a monotonically decreasing function of L that approaches zero as L → ∞, i.e., it vanishes in the anomalous regime. In this regime, as t → ∞, f_m(t) and hence the effective velocity v_eff(t) tend to zero as $1/\sqrt{t}$,

$${\displaystyle v_{\mathit{eff}}\left(t\right)=v\frac{2V_m}{A_{\mathit{de}}\sqrt{\pi D_{\mathit{de}}t}},t\to \infty .}$$ (3.13)

This is the reason why $〈x\left(t\right)〉\propto \sqrt{t}$ in Eq. (3.11). Thus, as t → ∞, the effective drift velocity vanishes in the anomalous regime and remains finite in the normal regime, where it is given by Eq. (3.7).

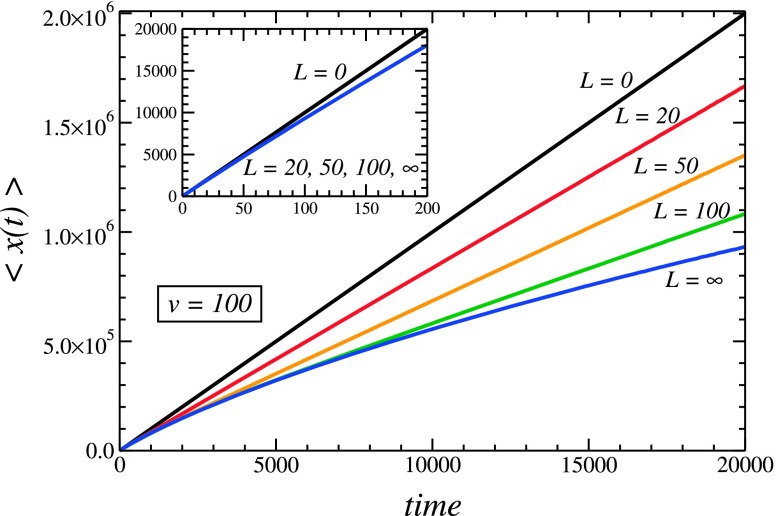
Figure 2 illustrates the time dependence of the mean displacement for several values of the dead-end length, L = 20, 50, 100, and ∞, in dimensionless units. For comparison, we also show the linear dependence, $〈x\left(t\right)〉=vt$, in a tube with no dead ends (L = 0). The dependences were obtained by numerically inverting the Laplace transforms in Eqs. (3.1) and (3.9) in the normal and anomalous regimes, respectively. Other parameters, in dimensionless units, were v = 100, R = l = D₀ = D_de = 1, and a = 0.1. According to Eqs. (1.11) and (1.14), this leads to k_m = 0.4/π and κ_de = 40/π. One can see that the mean displacement for a given time decreases as the dead-end length L increases. The initial parts of the dependences shown in the inset coincide for all L shown in the figure because, at sufficiently small times, particles are able to explore only the small fractions of the dead-end tubes that are close to the dead-end entrance. Therefore, the dependences are not sensitive to the dead end lengths.

FIG. 2.

The mean displacement $〈x\left(t\right)〉$ as a function of time for several values of the dead-end length L (the values of L, in dimensionless units, are given near the curves). Other parameters, in dimensionless units, are v = 100, R = l = D₀ = D_de = 1, and a = 0.1. The dependences were obtained by numerically inverting the Laplace transforms in Eqs. (3.1) and (3.9) in the normal and anomalous regimes, respectively. The inset shows the mean displacement at short times, where all the curves with L≠0 collapse to the same curve since the particle is ”unaware” about the length of the dead ends on these times.

IV. EFFECTIVE DIFFUSIVITY

Consider time-dependent effective diffusivity of the particle, denoted by D(t|L, v), which is defined as

$${\displaystyle D\left(t\right|L,v)=\frac{1}{2t}\left(〈x^2\left(t\right)〉-{〈x\left(t\right)〉}^2\right)=\frac{{\sigma }_x^2\left(t\right)}{2t}.}$$ (4.1)

Using Eq. (2.8), D(t|L, v) can be written in the form

$${\displaystyle D\left(t\right|L,v)=D_0{f}_m\left(t\right)+v^2\frac{{\sigma }_{t_m}^2\left(t\right)}{2t},}$$ (4.2)

where the variance ${\sigma }_{t_m}^2\left(t\right)$ is given by Eq. (2.9). The two terms contributing into D(t|L, v) have different origins: the first term, proportional to D₀, is due to the particle intrinsic diffusion in the x-direction during the mean cumulative time $〈t_m\left(t\right)〉$ spent by the particle in the mobile state. The second term, proportional to v², is due to fluctuations of the cumulative time spent by the particle in the mobile state around its mean value $〈t_m\left(t\right)〉$.

At short times (t → 0), t_m(t) = t. As a consequence, f_m(t) = 1 and ${\sigma }_{t_m}^2\left(t\right)=0$. This leads to

$${\displaystyle D\left(t\right|L,v)=D_0,t\to 0,}$$ (4.3)

as might be expected, since the particle starts in the main tube. As t → ∞, D(t|L, v) approaches its long-time limiting value, denoted by D_eff(L, v),

$${\displaystyle D_{\mathit{eff}}(L,v)=\underset{t\to \infty }{lim}D\left(t\right|L,v)=D_0{f}_m^{\mathit{eq}}+v^2\underset{t\to \infty }{lim}\frac{{\sigma }_{t_m}^2\left(t\right)}{2t}.}$$ (4.4)

While the short-time behavior of the time-dependent effective diffusivity is universal, its long-time behavior in the normal (finite L) and anomalous (infinite L) regimes is different.

To analyze the long-time behavior of D(t|L, v), we need to know the long-time behavior of the first two moments of the cumulative time t_m(t). According to Eqs. (2.11) and (2.12), their Laplace transforms are related by a simple relation

$${\displaystyle 〈{\hat{t}}_m^2\left(s\right)〉=2s{〈{\hat{t}}_m\left(s\right)〉}^2.}$$ (4.5)

The Laplace transform of the mean cumulative time, $〈{\hat{t}}_m\left(s\right)〉$, can be obtained by substituting into Eq. (2.11) the expression for ${\hat{w}}_{\mathit{de}}\left(s\right)$ in Eq. (1.13). The result is

$${\displaystyle 〈{\hat{t}}_m\left(s\right)〉=\frac{{\kappa }_{\mathit{de}}+\sqrt{s{D}_{\mathit{de}}}tanh\left(L\sqrt{s/D_{\mathit{de}}}\right)}{s\left[s{\kappa }_{\mathit{de}}+\left(s+k_m\right)\sqrt{s{D}_{\mathit{de}}}tanh\left(L\sqrt{s/D_{\mathit{de}}}\right)\right]}.}$$ (4.6)

Below, we consider the long-time behavior of the effective diffusivity in the normal and anomalous regimes separately, beginning with the latter case, where Eq. (4.6) reduces to

$${\displaystyle 〈{\hat{t}}_m\left(s\right)〉=\frac{{\kappa }_{\mathit{de}}+\sqrt{s{D}_{\mathit{de}}}}{s\left[s{\kappa }_{\mathit{de}}+\left(s+k_m\right)\sqrt{s{D}_{\mathit{de}}}\right]}.}$$ (4.7)

To find the long-time behavior of $〈t_m\left(t\right)〉$ in the anomalous regime, we use the small-s behavior of its Laplace transform, Eq. (4.7),

$${\displaystyle 〈{\hat{t}}_m\left(s\right)〉=\frac{V_m}{A_{\mathit{de}}\sqrt{D_{\mathit{de}}}{s}^{3/2}},s\to 0,}$$ (4.8)

where the relations in Eqs. (1.11) and (1.14) have been used. Inverting this Laplace transform, we arrive at

$${\displaystyle 〈t_m\left(t\right)〉=\frac{2V_m}{A_{\mathit{de}}}\sqrt{\frac{t}{\pi D_{\mathit{de}}}},t\to \infty .}$$ (4.9)

The small-s behavior of $〈{\hat{t}}_m^2\left(s\right)〉$ can be found by substituting $〈{\hat{t}}_m\left(s\right)〉$ in Eq. (4.8) into Eq. (4.5). This leads to

$${\displaystyle 〈{\hat{t}}_m^2\left(s\right)〉=\frac{2V_m^2}{A_{\mathit{de}}^2{D}_{\mathit{de}}{s}^2},s\to 0.}$$ (4.10)

Inverting this, we obtain

$${\displaystyle 〈t_m^2\left(t\right)〉=\frac{2V_m^2}{A_{\mathit{de}}^2{D}_{\mathit{de}}}t,t\to \infty .}$$ (4.11)

We use the expressions in Eqs. (4.9) and (4.11) to find the long time behavior of the variance ${\sigma }_{t_m}^2\left(t\right)$ by Eq. (2.9),

$${\displaystyle {\sigma }_{t_m}^2\left(t\right)=\frac{2t{V}_m^2}{A_{\mathit{de}}^2{D}_{\mathit{de}}}\left(1-\frac{2}{\pi }\right),t\to \infty .}$$ (4.12)

Substituting this into Eq. (4.4) and using the fact that $f_m^{\mathit{eq}}\to 0$ as L → ∞, we arrive at the following expression for the effective diffusivity in the anomalous (a) regime, denoted by $D_{\mathit{eff}}^{\left(a\right)}\left(v\right)$,

$${\displaystyle D_{\mathit{eff}}^{\left(a\right)}\left(v\right)=\frac{v^2{V}_m^2}{A_{\mathit{de}}^2{D}_{\mathit{de}}}\left(1-\frac{2}{\pi }\right).}$$ (4.13)

This expression shows that $D_{\mathit{eff}}^{\left(a\right)}\left(v\right)$ can be both smaller and larger than D₀ depending on the magnitude of the drift velocity v. There is a special value of the drift velocity, denoted by v^*, for which $D_{\mathit{eff}}^{\left(a\right)}\left(v^{*}\right)=D_0$,

$${\displaystyle v^{*}=\frac{A_{\mathit{de}}}{V_m}\sqrt{\frac{D_0{D}_{\mathit{de}}}{1-2/\pi }}.}$$ (4.14)

Thus, as L increases from zero to infinity, D_eff(L, v) varies from D₀ to $D_{\mathit{eff}}^{\left(a\right)}\left(v\right)$, which is smaller than D₀, when v < v^*, equal to D₀, when v = v^*, and larger than D₀, when v > v^*.

To study D_eff(L, v) at finite values of the dead-end length L, we repeat the above calculations using $〈{\hat{t}}_m\left(s\right)〉$ in Eq. (4.6). As s → 0, this Laplace transform reduces to

$${\displaystyle 〈{\hat{t}}_m\left(s\right)〉=\frac{1}{s^2}{f}_m^{\mathit{eq}}+\frac{1}{s}\mathrm{\Delta }t,s\to 0,}$$ (4.15)

where time Δt is given by

$${\displaystyle \mathrm{\Delta }t=f_m^{\mathit{eq}}\left(1-f_m^{\mathit{eq}}\right)\left(〈{\tau }_{\mathit{de}}〉+\frac{L^2}{3D_{\mathit{de}}}\right),}$$ (4.16)

and $〈{\tau }_{\mathit{de}}〉$ is the mean particle lifetime in the dead end,¹

$${\displaystyle 〈{\tau }_{\mathit{de}}〉=\frac{L}{{\kappa }_{\mathit{de}}}=\frac{\pi aL}{4D_0}.}$$ (4.17)

This, together with Eq. (1.3), allows us to write time Δt in term of the geometric parameters of the system,

$${\displaystyle \mathrm{\Delta }t=\frac{V_m{V}_{\mathit{de}}}{{\left(V_m+V_{\mathit{de}}\right)}^2}\left(\frac{\pi aL}{4D_0}+\frac{L^2}{3D_{\mathit{de}}}\right).}$$ (4.18)

Inverting the Laplace transform in Eq. (4.15), we obtain

$${\displaystyle 〈{\hat{t}}_m\left(t\right)〉=t{f}_m^{\mathit{eq}}+\mathrm{\Delta }t,t\to \infty .}$$ (4.19)

We find the small-s behavior of $〈{\hat{t}}_m^2\left(s\right)〉$ by substituting $〈{\hat{t}}_m\left(s\right)〉$ in Eq. (4.15) into Eq. (4.5). The results are

$${\displaystyle 〈{\hat{t}}_m^2\left(s\right)〉=\frac{2}{s^3}{\left(f_m^{\mathit{eq}}\right)}^2+\frac{4}{s^2}\mathrm{\Delta }t{f}_m^{\mathit{eq}},s\to 0.}$$ (4.20)

Inverting this Laplace transform, we obtain the long-time behavior of $〈t_m^2\left(t\right)〉$,

$${\displaystyle 〈t_m^2\left(t\right)〉={\left(t{f}_m^{\mathit{eq}}\right)}^2+4t\mathrm{\Delta }t{f}_m^{\mathit{eq}},t\to \infty .}$$ (4.21)

Then, the variance ${\sigma }_{t_m}^2\left(t\right)$, Eq. (2.9), at long times is given by

$${\displaystyle {\sigma }_{t_m}^2\left(t\right)=2t\mathrm{\Delta }t{f}_m^{\mathit{eq}},t\to \infty .}$$ (4.22)

Substituting ${\sigma }_{t_m}^2\left(t\right)$ above into Eq. (4.4), we arrive at the following expression for the effective diffusivity in the normal regime:

$${\displaystyle D_{\mathit{eff}}(L,v)=\left(D_0+v^2\mathrm{\Delta }t\right)f_m^{\mathit{eq}}.}$$ (4.23)

Explicit dependence of the effective diffusivity on the geometric parameters of the system can be obtained by substituting into Eq. (4.23) the expressions for $f_m^{\mathit{eq}}$ and Δt given in Eqs. (1.3) and (4.18). This leads to

$${\displaystyle D_{\mathit{eff}}(L,v)=\frac{V_m}{V_m+\pi a^{2}L}\left[D_0+v^2\frac{V_m\pi a^{2}L}{{\left(V_m+\pi a^{2}L\right)}^2}\left(\frac{\pi aL}{4D_0}+\frac{L^2}{3D_{\mathit{de}}}\right)\right],}$$ (4.24)

which is one of the main results of this paper. At L = 0, the effective diffusivity is equal to D₀ for all v, as it must be in a cylindrical tube without dead ends.

At v = 0, the expression in Eq. (4.23) reduces to the result for the effective diffusivity in the absence of the drift velocity obtained in Ref. 1, $D_{\mathit{eff}}(L,0)=D_0{f}_m^{\mathit{eq}}$, which describes monotonic decrease of D_eff(L, 0) from D₀ at L = 0 to zero as L → ∞. At v≠0, D_eff(L, v) is a non-monotonic function of L. Using Eq. (4.24), one can check that the derivative ∂D_eff(L, v)/∂L changes its sign from negative to positive as the dead-end length L increases from zero to infinity. Thus, D_eff(L, v) first decreases at small values of L, reaches a minimum, and then increases approaching its limiting value D_eff(∞, v), which is given by

$${\displaystyle D_{\mathit{eff}}(\infty ,v)=\frac{v^2{V}_m^2}{3A_{\mathit{de}}^2{D}_{\mathit{de}}}.}$$ (4.25)

Note that D_eff(∞, v) is smaller than $D_{\mathit{eff}}^{\left(a\right)}\left(v\right)$ given in Eq. (4.13). The ratio of the two effective diffusivities is

$${\displaystyle \frac{D_{\mathit{eff}}^{\left(a\right)}\left(v\right)}{D_{\mathit{eff}}(\infty ,v)}=3\left(1-\frac{2}{\pi }\right)=\frac{1-2/\pi }{1-2/3}>1.}$$ (4.26)

The fact that the two effective diffusivities differ is not surprising, since they are obtained using different expressions for $〈{\hat{t}}_m\left(s\right)〉$ given in Eqs. (4.6) and (4.7). The expression for D_eff(L, v) is obtained starting from Eq. (4.15) for the small-s behavior of $〈{\hat{t}}_m\left(s\right)〉$, which assumes that sL²/D_de ≪ 1, or L² ≪ D_det, while $D_{\mathit{eff}}^{\left(a\right)}\left(v\right)$ is obtained assuming that sL²/D_de ≫ 1, or L² ≫ D_det. This is the reason why $D_{\mathit{eff}}^{\left(a\right)}\left(v\right)$ is larger than D_eff(∞, v).

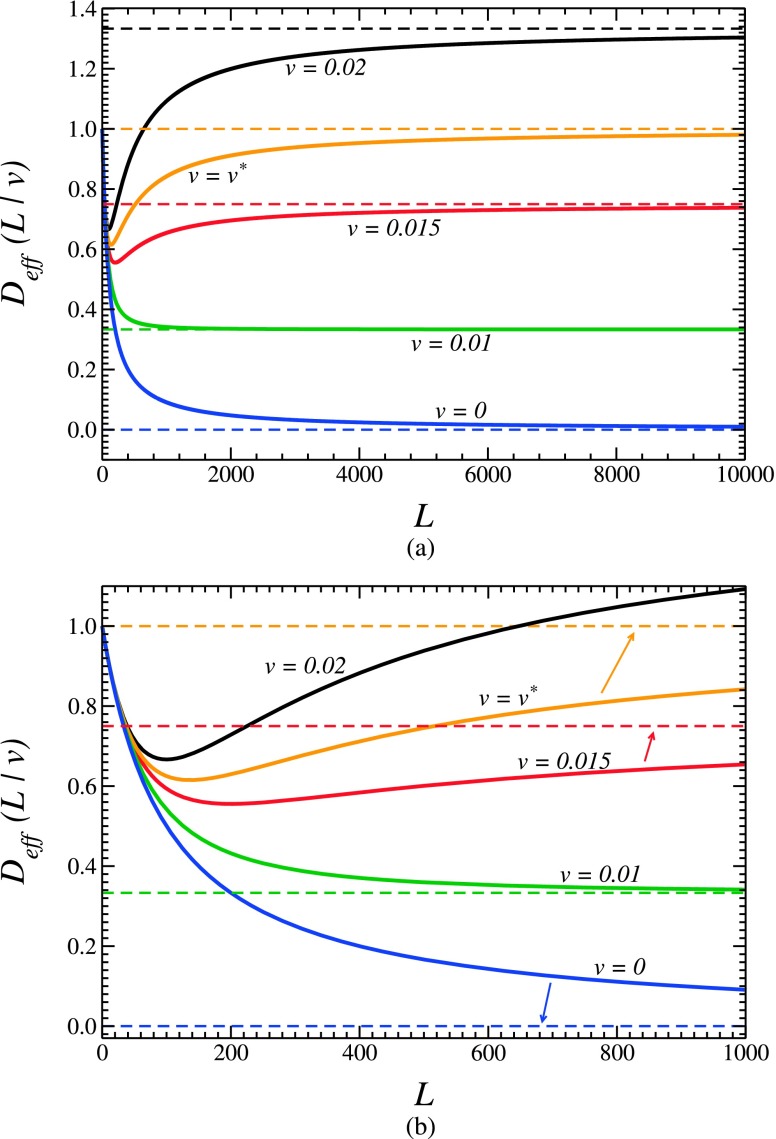
The non-monotonic L-dependence of the effective diffusivity, D_eff(L, v), at v≠0 is illustrated in Fig. 3. As v decreases, the minimum becomes flatter and flatter, and D_eff(L, v) approaches D_eff(L, 0) which is a monotonically decreasing function of L. The curves are drawn using Eq. (4.24) for the drift velocity values indicated near the curves; velocity v^* is given by Eq. (4.14). Other parameters, in dimensionless units, are R = l = D₀ = D_de = 1 and a = 0.1.

FIG. 3.

The effective diffusivity, D_eff(L, v), as a function of the dead-end length, L, for several values of the drift velocity, v, indicated near the curves in dimensionless units. Velocity v^* is given by Eq. (4.14). Other parameters, in dimensionless units, are R = l = D₀ = D_de = 1 and a = 0.1. The curves are drawn using Eq. (4.24). Dashed straight lines show the values of the effective diffusivity in the anomalous regime, $D_{\mathit{eff}}^{\left(a\right)}\left(v\right)$, given in Eq. (4.13). Panels (a) and (b) show the same curves at different length scales. D_eff(L, v) is a non-monotonic function of L, which first decreases with L, reaches a minimum, and then increases approaching its asymptotic value $D_{\mathit{eff}}^{\left(a\right)}\left(v\right)$. As the drift velocity v decreases, the minimum becomes flatter and flatter, and D_eff(L, v) approaches D_eff(L, 0) which is a monotonically decreasing function of L.

The transition of the effective diffusivity from D₀ at short times to its long-time asymptotic behavior D_eff(L, v), in the normal regime, and $D_{\mathit{eff}}^{\left(a\right)}\left(v\right)$, in the anomalous regime, is described by the time-dependent effective diffusivity, D(t|L, v), given in Eq. (4.2). The first term in this equation is the time-dependent effective diffusivity at v = 0, D(t|L, 0) = D₀f_m(t). This term is a decreasing function of time, since f_m(t) monotonically decreases with time from unity to $f_m^{\mathit{eq}}$, Eq. (1.3), as time increases from zero to infinity. The second term, $v^2{\sigma }_{t_m}^2\left(t\right)/\left(2t\right)$, increases with time from zero at t = 0 to its long-time limiting value, which is equal to $v^2\mathrm{\Delta }t{f}_m^{\mathit{eq}}$ in the normal regime (see Eq. (4.22)) and $v^2{V}_m^2\left(1-2/\pi \right)/\left(A_{\mathit{de}}^2{D}_{\mathit{de}}\right)$ in the anomalous regime (see Eq. (4.12)). It can be shown that at short times (t → 0), the first term decays linearly in time, $D_0{f}_m\left(t\right)\approx D_0\left(1-k_{m}t/2\right)$, while the second term grows as t². As a consequence, D(t|L, v) always decreases with time at short times. At longer times, the time-dependent effective diffusivity can be both monotonic and non-monotonic functions of time.

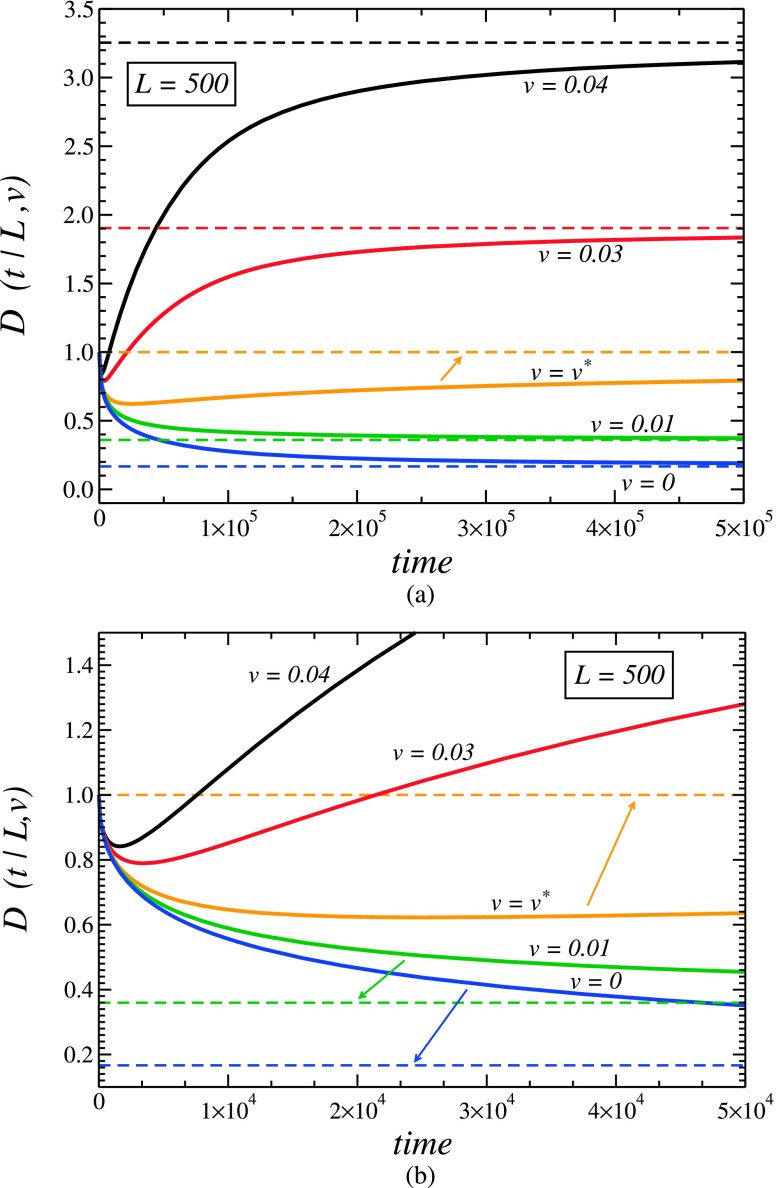
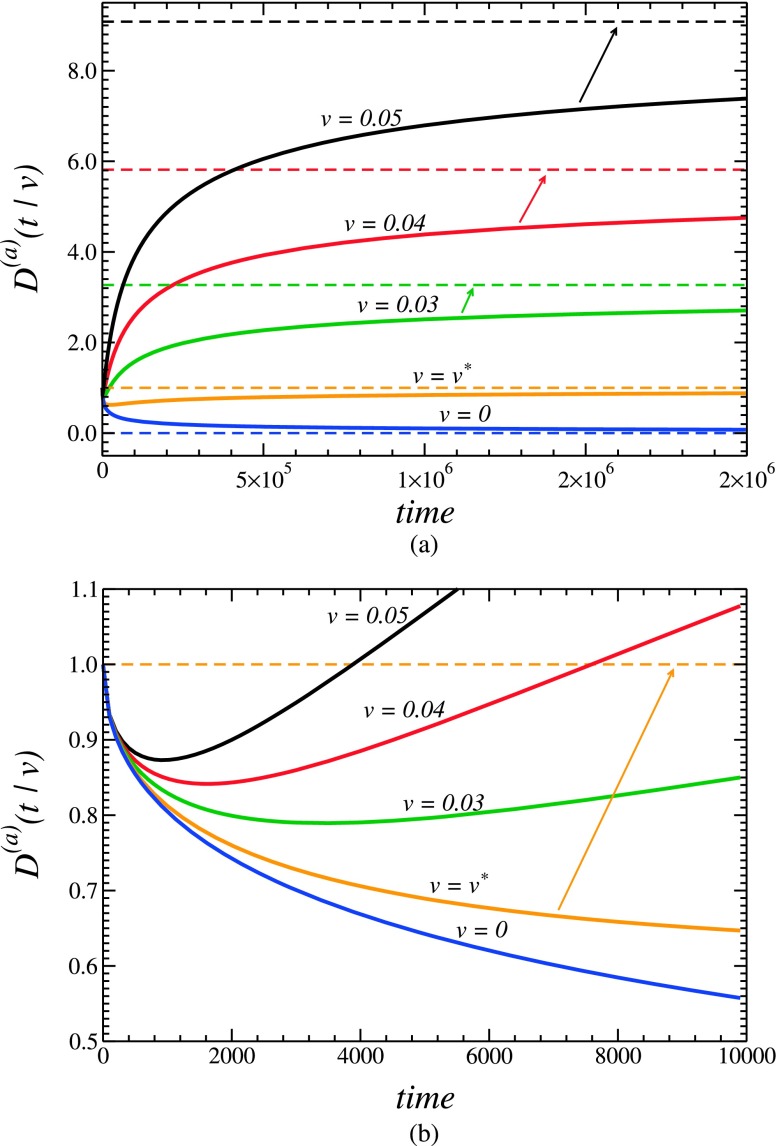
The transient behavior of the effective diffusivity is illustrated in Fig. 4. The curves are drawn using Eq. (4.2). Functions f_m(t) and ${\sigma }_{t_m}^2\left(t\right)$, entering into Eq. (4.2), are obtained by substituting numerically inverted Laplace transforms of $〈t_m〉$ and $〈t_m^2〉$, Eqs. (4.6) and (4.5), into the definitions of f_m(t) and ${\sigma }_{t_m}^2\left(t\right)$ in Eqs. (3.12) and (2.9), respectively. The dependences are shown for L = 500, R = l = D₀ = D_de = 1, and a = 0.1, and the drift velocity values are indicated near the curves (all parameter values are in dimensionless units).

FIG. 4.

Transient behavior of the effective diffusivity, D(t|L, v), for several values of the drift velocity, v, indicated near the curves, and L = 500, in dimensionless units. Other parameters, in dimensionless units, are R = l = D₀ = D_de = 1 and a = 0.1. Dashed straight lines are the corresponding values of D_eff(L, v) = D(∞|L, v), given in Eq. (4.25). The curves are drawn using Eq. (4.2) with functions f_m(t) and ${\sigma }_{t_m}^2\left(t\right)$ found using their definitions in Eqs. (3.12) and (2.9). The first two moments of the cumulative time t_m(t) entering into these definitions are obtained by numerically inverting their Laplace transforms in Eqs. (4.6) and (4.5), respectively. Panels (a) and (b) show the same curves on different time scales.

Similar dependences in the anomalous regime (L = ∞), where the time-dependent diffusivity is denoted by D^(a)(t|v), are shown in Fig. 5. The difference between the curves shown in Figs. 4 and 5 is due to the difference in the expressions for the Laplace transform of the mean cumulative time $〈{\hat{t}}_m\left(s\right)〉$, which are used to draw the curves. While the former curves are drawn using $〈{\hat{t}}_m\left(s\right)〉$ in Eq. (4.6), the latter curves are drawn using $〈{\hat{t}}_m\left(s\right)〉$ in Eq. (4.7).

FIG. 5.

Transient behavior of the effective diffusivity, D^(a)(t|v), in the anomalous regime. The curves shown in this figure are analogous to those shown in Fig. 4. The difference between the curves shown in the two figures is in the expressions for the Laplace transform of the mean cumulative time $〈{\hat{t}}_m\left(s\right)〉$, which are used to draw the curves. While the curves in Fig. 4 are drawn using $〈{\hat{t}}_m\left(s\right)〉$ in Eq. (4.6), here the curves are drawn using $〈{\hat{t}}_m\left(s\right)〉$ in Eq. (4.7).

Concluding this section, we consider the ratio of the square root of the displacement variance to the mean displacement, $\sqrt{{\sigma }_x^2\left(t\right)}/〈x\left(t\right)〉$. In a cylindrical tube without dead ends, $〈x\left(t\right)〉=vt$, ${\sigma }_x^2\left(t\right)=2D_{0}t$, and the ratio is given by

$${\displaystyle \frac{\sqrt{{\sigma }_x^2\left(t\right)}}{〈x\left(t\right)〉}=\frac{1}{v}\sqrt{\frac{2D_0}{t}}.}$$ (4.27)

This shows that in a tube without dead ends, the ratio monotonically decreases from infinity to zero as time goes from zero to infinity.

The expression in Eq. (4.27) also describes the short-time behavior of the ratio in the presence of dead ends, since the particle starts in the main tube. The long-time behaviors of the ratio in the normal and anomalous regimes are qualitatively different. In the normal regime at long times, we have $〈x\left(t\right)〉=v_{\mathit{eff}}t$, ${\sigma }_x^2\left(t\right)=2D_{\mathit{eff}}(L,v)t$, and the ratio is given by Eq. (4.27), in which v and D₀ are replaced by v_eff and D_eff(L, v), respectively,

$${\displaystyle \frac{\sqrt{{\sigma }_x^2\left(t\right)}}{〈x\left(t\right)〉}=\frac{1}{v_{\mathit{eff}}}\sqrt{\frac{2D_{\mathit{eff}}(L,v)}{t}},t\to \infty .}$$ (4.28)

The situation is qualitatively different in the anomalous regime. Here, the long time behavior of the displacement variance is

$${\displaystyle {\sigma }_x^2\left(t\right)=2D_{\mathit{eff}}^{\left(a\right)}\left(v\right)t=\frac{2v^2{V}_m^2}{A_{\mathit{de}}^2{D}_{\mathit{de}}}\left(1-\frac{2}{\pi }\right)t,t\to \infty .}$$ (4.29)

Using this and the long time behavior of $〈x\left(t\right)〉$ given by Eq. (3.11), we obtain

$${\displaystyle \frac{\sqrt{{\sigma }_x^2\left(t\right)}}{〈x\left(t\right)〉}=\sqrt{\frac{\pi }{2}-1},t\to \infty .}$$ (4.30)

Thus, in the anomalous regime, as t → ∞, the ratio approaches a constant value, whereas in the normal regime, the ratio at long times approaches zero as $1/\sqrt{t}$. Interestingly enough, the ratio in Eq. (4.30) is a universal constant in the sense that it is independent of the particle diffusivity, D₀, and drift velocity, v, as well as the geometric parameters, R,  l, and a, of the tube.

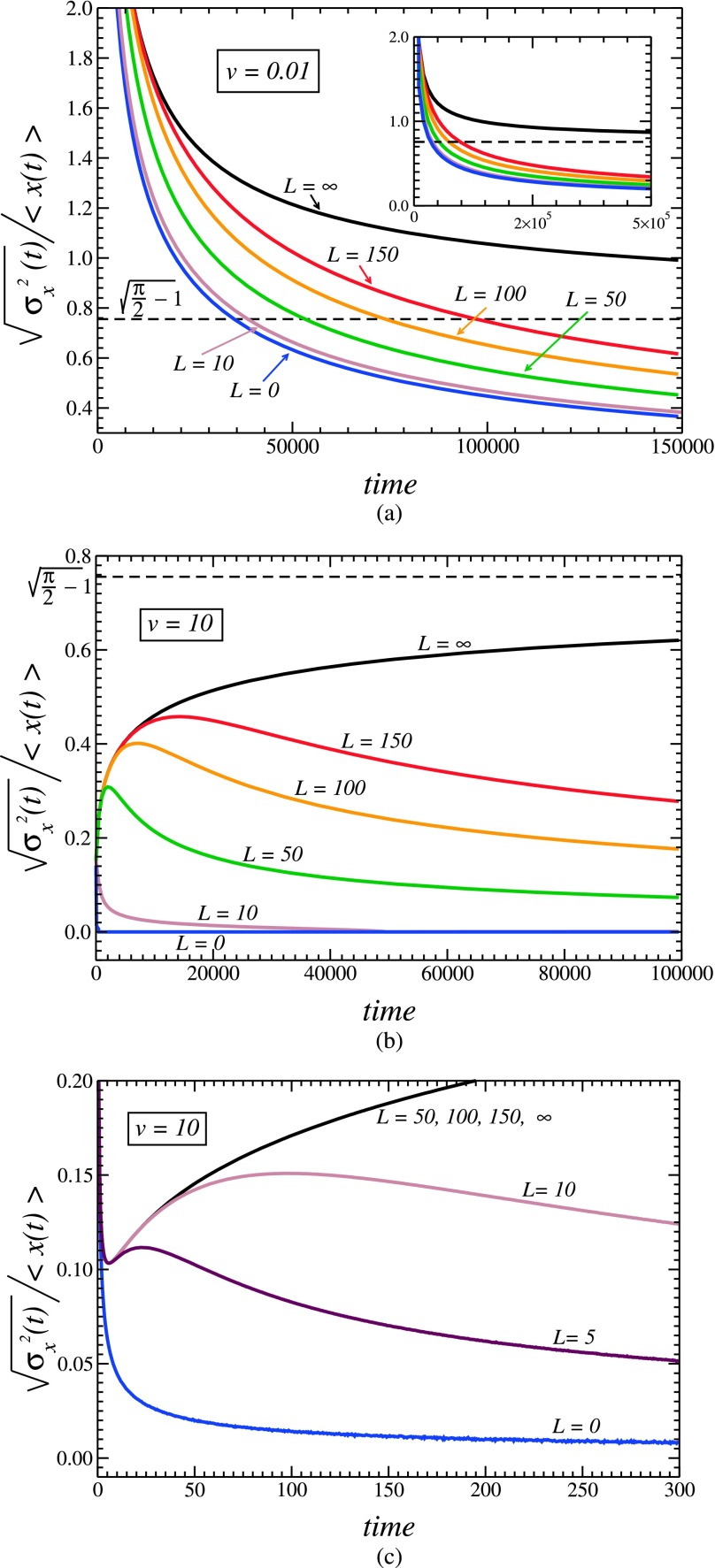
The time dependence of the ratio is illustrated in Fig. 6 for several values of the dead-end length L at v = 0.1 (panel (a)) and v = 10 (panels (b) and (c)). One can see that depending on v and L, this time dependence can be qualitatively different. It can be a monotonically decreasing function of time (see panel (a)) or it can go from infinity to its long-time limiting value non-monotonically (see panels (b) and (c)), having a minimum and a maximum (in the normal regime) or only a minimum (in the anomalous regime) in-between.

FIG. 6.

Time dependence of the ratio $\sqrt{{\sigma }_x^2\left(t\right)}/〈x\left(t\right)〉$ at v = 0.01 (panel (a)) and v = 10 (panels (b) and (c)) for several values of the dead-end length, L, indicated near the curves. In the normal regime (finite L), all curves go from infinity to zero, whereas in the anomalous regime (infinite L), the curves go from infinity to $\sqrt{\left(\pi -2\right)/2}$. When v is not too small, the curves are non-monotonic, having a minimum and a maximum in the normal regime and only a minimum in the anomalous regime. Panels (b) and (c) show the same curves on different time scales. The only exception is the curve for L = 5, which is shown only in panel (c) to illustrate the minimum and maximum in the time dependence of the ratio $\sqrt{{\sigma }_x^2\left(t\right)}/〈x\left(t\right)〉$. In panel (c), all the curves with L = 50,  100,  150, and ∞ collapse to the same curve since the particle is “unaware” about the length of the dead ends on these times.

Finally, we note that the effective diffusivity in Eq. (4.24) can be written as

$${\displaystyle D_{\mathit{eff}}(L,v)=D_0{f}_m^{\mathit{eq}}+v^2{\left(f_m^{\mathit{eq}}\right)}^3\left(\frac{\pi aL}{4D_0}+\frac{L^2}{3D_{\mathit{de}}}\right).}$$ (4.31)

This expression looks similar to that for the Aris-Taylor dispersion⁴⁶ of a Brownian particle advected by a laminar flow in a tube, when the particle can reversibly bind to the tube wall.⁴⁷ In addition, a similar velocity dependence of the effective diffusivity was obtained for a particle that randomly jumps between two states in which it moves with different drift velocities.⁴⁸ The resemblance of these expressions for the effective diffusivity is not surprising. The reason is that the velocity dependence of the effective diffusivity in all these cases, as well as Aris-Taylor dispersion, has the same origin. The effect is due to the fluctuations of times spent by the particle in states, where it moves with different velocities, about their average values.

V. CONCLUDING REMARKS

To summarize, one of the main results of this paper is the general expressions in Eqs. (2.13) and (2.14) for the Laplace transforms of the first two moments of the particle displacement in the comb-like structure shown in Fig. 1. The expressions are applicable for all values of the particle drift velocity v in the main tube and for arbitrary values of the tube geometric parameters, R,  l,  a, and L, on condition that both the distance l between neighboring dead ends and radius R of the main tube significantly exceed the dead-end radius, a < < l,  R. Inverting these Laplace transforms numerically, one can find the moments of the displacement as functions of time. We use the expressions in Eqs. (2.13) and (2.14) to study the time dependences of the effective drift velocity and diffusivity of the particle as functions of the drift velocity v and the geometric parameters of the tube.

Our special attention is on the dependences of the quantities of interest on the dead-end length L, including the case of infinitely long dead ends, where unbiased diffusion (v = 0) becomes anomalous at sufficiently long times. In this limiting case, the long-time behavior of the mean square displacement is given by $〈x^2\left(t\right)〉\propto t^{1/2}$, and hence, the effective diffusivity vanishes, as t → ∞, as $1/\sqrt{t}$. At the same time, when L is finite, $〈x^2\left(t\right)〉$ grows linearly with time, $〈x^2\left(t\right)〉\propto t$, as t → ∞, and hence, the effective diffusivity of the particle remains finite.

In the presence of a bias (v≠0), the difference between the normal (L≠∞) and anomalous (L = ∞) regimes manifests itself in the time dependences of the mean displacement, $〈x\left(t\right)〉$, and the effective velocity, v_eff(t) = 〈x(t)〉/t. In the normal regime, at long times, the mean displacement linearly grows with time, $〈x\left(t\right)〉=v_{\mathit{eff}}t$, with finite effective drift velocity v_eff, given in Eq. (3.7). In the anomalous regime, the mean displacement grows at long times as $\sqrt{t}$, and hence, the effective velocity vanishes, as t → ∞, as $1/\sqrt{t}$, Eq. (3.13).

In contrast, the effective diffusivity in the anomalous regime does not vanish and remains finite as t → ∞, as the effective diffusivity in the normal regime does. The limiting (t → ∞) values of the effective diffusivity in the two regimes are given in Eqs. (4.13) and (4.24). The time dependences of the effective diffusivities in both regimes may be qualitatively different, depending on the magnitude of the particle drift velocity v in the main tube. The dependences are monotonic at sufficiently low drift velocities and non-monotonic at high velocities, as illustrated in Figs. 4 and 5.

To obtain the above mentioned results, we extended the formalism developed in Ref. 1 for unbiased diffusion to the case where the diffusion is biased. Since a < < l, the particle displacement along the tube axis changes only when the particle is in the main tube. Based on this, we propose a two-step strategy for finding the moments of the displacement. First, we present the moments of the displacement in terms of the moments of the cumulative time spent by the particle in the main tube. Then, we find the moments of the cumulative time and use them to find the moments of the displacement. What is important is that the moments of the cumulative time can be readily found by considering a simple two-state problem, described by the kinetic scheme in Eq. (1.5). We believe that the two-step strategy described above can be useful for the analysis of other similar problems, where the particle/system jumps between two states.