Abstract
Mild cognitive impairment (MCI) is a neurological condition related to early stages of dementia including Alzheimer’s disease (AD). This study investigates the potential of measures of transfer entropy in scalp EEG for effectively discriminating between normal aging, MCI, and AD participants. Resting EEG records from 48 age-matched participants (mean age 75.7 years)—15 normal controls (NC), 16 MCI, and 17 early AD—are examined. The mean temporal delays corresponding to peaks in inter-regional transfer entropy are computed and used as features to discriminate between the three groups of participants. Three-way classification schemes based on binary support vector machine models demonstrate overall discrimination accuracies of 91.7—93.8%, depending on the protocol condition. These results demonstrate the potential for EEG transfer entropy measures as biomarkers in identifying early MCI and AD. Moreover, the analyses based on short data segments (two minutes) render the method practical for a primary care setting.
Keywords: early Alzheimer’s disease, mild cognitive impairment, EEG-based diagnosis, transfer entropy
1. INTRODUCTION
Mild cognitive impairment (MCI) is an old age memory and cognition disruption and a departure from normal aging. Amnestic MCI is often an early stage of dementia such as Alzheimer’s disease (AD) [Petersen 2001, Petersen 2003]. Identifying MCI state enables early intervention. Development of a simple EEG-based screening method for MCI for use in the primary care setting would be a valuable tool in the research and treatment of both disorders.
Transfer entropy is an information theoretic measure that quantifies the statistical coherence between systems evolving in time [Schreiber 2000, Hlaváčková-Schindler 2007]. While standard time delayed mutual information fails to distinguish information that is actually exchanged from shared information due to common history and input signals, transfer entropy is able to effectively distinguish driving and responding elements and to detect asymmetry in the interaction of subsystems [Schreiber 2000]. The fact that it is non-symmetric enables one to infer the direction of information flow. Transfer entropy reduces to Granger causality for processes in which the output variable depends linearly on its own previous values (i.e., vector auto-regressive processes) and Gaussian variables [Barnett 2009]. Transfer entropy has been applied to many different fields, including neuroscience, systems biology, bioinformatics, environmental sciences, climatology, engineering, finance, astronomy, Earth and space sciences, and astronomy. Transfer entropy has been used for estimation of functional connectivity of neurons [Lizier 2011, Vicente 2011] and social influence in social networks. Recent studies indicate that cognitive declines in MCI and AD may manifest as reduced complexity and perturbations in EEG synchrony [Dauwels 2010, Stam 2003, Stam 2005, Stam 2007]. Much work has been done to show the group differences between different cognitive statuses. However, group differences often are not sufficient to establish the initial evaluation of subjects with cognitive impairment in the routine clinical practice [Jelic 2009]. This work aims to develop easy neural indicators to diagnose and predict cognitive decline pre-clinically, such as among people with subjective memory complaints.
While various studies have investigated applications of entropy and complexity measures of scalp EEG for discrimination of cognitive deficits [Dauwels 2010, Sneddon 2005, Zhao 2007, McBride 2013a, McBride 2013b, McBride 2014a, McBride 2014b], the investigation on transfer entropy of EEG has been limited. Transfer entropy is a means to characterize exchange of information between two signal sources. Based on the hypothesis that the cognitive disruption of AD or MCI may affect the information exchange between two areas of the brain, this work aims to explore the application of transfer entropy of scalp of scalp EEG to diagnose AD and MCI. In this study, inter-regional EEG dynamics in MCI and AD during rest and a simple counting task are examined. Transfer entropy-based measures are studied as features to discriminate cognitive impairment of MCI and AD. Few researchers have investigated transfer entropy of scalp EEG. To the authors’ best knowledge, this article is the first study on transfer entropy analysis of scalp EEG for AD and MCI participants.
2. METHODS
2.1. Data
The EEG data used in this study were collected in the laboratory of Dr. Yang Jiang of the Behavioral Science Department and Sanders-Brown Center on Aging at the University of Kentucky (UK) College of Medicine. Participants between the ages of 60 and 90 years were recruited from a study cohort of cognitively normal older adults followed by the Alzheimer’s Disease Center (ADC) of the UK College of Medicine [Schmitt 2012]. MCI patients were recruited from the Memory Disorders Clinic of the ADC. Normal older participants are screened regularly and when screenings indicate possible cognitive decline they are referred to the ADC’s Research Memory Disorders Clinic. MCI and AD participants were diagnosed and recruited by cognitive neurologists Drs. C. Smith and G. Jicha at the UK ADC Clinical Core and from its Research Memory Disorders Clinic. All participants provided written informed consent before participation. This study was approved by the Institutional Research Board (IRB) of the University of Kentucky. The database includes 15 NC, 16 MCI, and 17 AD participants. The mean ages for NC, MCI, and AD participants are 75.7 years (SD 5.5 years), 74.6 years (SD 9.0 years), and 76.7 years (SD 5.2 years), respectively.
All MCI participants belonged to the amnestic subtype. In addition, a few of the MCI participants also presented with executive dysfunction. Differences between single- and multiple-domain MCI subtypes are not the focus of the current study. A list of neurological assessments used to make MCI/AD diagnoses is provided in Table 1. Means (standard deviations) for MMSE scores were 29.43 (0.73), 27.40 (2.00), and 24.26 (2.42) for the NC, MCI, and AD groups, respectively. MCI and early AD participants’ EEG data were recorded as soon as possible after diagnoses were made. Patients with stroke or seizure history were not included.
Table 1.
UK-ADC Uniform Research Battery of Cognitive Tests and Other Evaluations
|
General Cognitive Measures MMSE; Kokmen Test Clinical Dementia Rating (CDR) |
Baseline Only National Adult Reading Test* |
|
Attention/Executive Domain Measures Trail Making Tests A & B WAIS-R Digit Span & Digit Symbol |
Medical Evaluation Physical exam* Neurological exam* Medical history* Medications Nutritional supplements Food Frequency Questionnaire (FFQ) |
|
Memory Domain Measures WMS Logical Memory I & II California Verbal Learning Test* | |
|
Language Domain Measures COWAT* Animal & Vegetable Fluency Boston Naming |
Psychiatric Evaluation Neuropsychiatric Inventory Questionnaire (NPI-Q) Geriatric Depression Scale (GDS) |
|
Visual/Spatial Domain Measures CERAD Figures |
Functional Ability Measures Functional Assessment Questionnaire (FAQ) SF-36* ADCS-ADL* |
Additional test measures or expanded content beyond UDS core measures
Participants were connected to 64- or 32-channel EEG caps using a Neuroscan II system (10–20 montage). In either case, only the 32 common channels were recorded. EEG data were recorded under a protocol using three different non-memory-task conditions. These included (1) resting with eyes open for 5 min (REO condition), (2) resting with eyes closed while counting backwards by ones for 10 min while tapping a finger (counting task), and (3) resting with eyes closed for 10 min (REC condition). The EEG recording was performed without interruption at the same appointment for each subject. EEG data were acquired at 500 Hz. The 32 EEG channels included 2 ocular channels that were used to determine the dominant eye blink frequency. Notch filters were used to remove dominant eye blink frequencies and to remove 60 Hz frequencies, which may have been amplified by background electronic devices. A simple 2nd order Butterworth filter was used to attenuate frequencies greater than 200 Hz.
2.2. Transfer Entropy
Information can be defined mathematically as that which decreases uncertainty [Sneddon 2007]. Entropy, being a measure of the uncertainty in a system, can therefore be used to mathematically quantify the basic amount of information in time series [Sneddon 2007]. For example, the average number of bits required to optimally encode independent samples of a discrete variable x, which follows a probability distribution function px, is given by the classical definition for Shannon entropy:
| (1) |
where the sum extends over all possible states xi(i = 1, …, N) that the random variable x can assume. The base of the logarithm depends only on the units used for measuring information; thus, it will be dropped in further equations. If a different distribution is used, there will be an excess number of bits and the information will not be optimally encoded [Schreiber 2000]. The excess number of bits that will be encoded if a different distribution function q is used is given by the Kullback entropy [Kullback 1959]:
| (2) |
The mutual information of two random variables x and y with joint probability distribution function px, can be viewed as the excess amount of code produced when the two variables are assumed to be independent. That is, assuming px,y(xi, yj) = px(xi)py(yj). Mutual information Mxy between the variables x and y is thus the Kullback entropy given the assumption of independence between the two variables:
| (3) |
where the random variable y can assume states yj (j = 1, …, M). Mutual information thus provides an intuitive means for quantifying the deviation from independence of two random variables. Note that mutual information Mxy is symmetric under the exchange of x and y and therefore does not contain any information regarding the directional transfer of information (which may relate to causal effect) [Lizier 2010].
Suppose that the variables x and y are generated by two separate but coupled systems. An entropy rate S1 can be defined as the amount of additional information required to represent the current value xn of the random variable x given the value of both variables at an observation d steps in the past:
| (4) |
where pxnxn−d,yn−d is the joint probability function for the observations xn, xn−d, and yn−d, and pxn|xn−d,yn−d is the conditional probability function for xn given xn−d and yn−d. Further suppose that the value of the current observation xn of the random variable x is independent of the value of the random variable y observed d steps in the past (yn−d). The entropy rate in this case would then reduce to the following:
| (5) |
where pxn|xn−d is the conditional probability function for xn given xn−d. The incorrectness of this assumption can then be express as the difference S2 – S1 between the two entropy rates presented in Equations (4) and (5). This difference in entropy is then termed transfer entropy [Schreiber 2000]:
| (6) |
Substituting the definitions for the conditional probabilities given in Equations (7) and (8), Equation (6) reduces to Equation (9):
| (7) |
| (8) |
| (9) |
where pxn−d,yn−d is the joint probability of variables xn−d given yn−d, and pxn,xn−d is the joint probability of variables xn given xn−d. The transfer entropy is explicitly not symmetric since it measures the degree of dependence of x on y and not vice versa. Thus, . Note that the definition of transfer entropy here follows the definition in [Schreiber 2000]. Recently, Wibral et al. proposed an improved definition of transfer entropy to better measure the delay effect [Wibral 2013]. The differences between the two definitions shall be investigated in future research.
2.3. Peak Inter-regional Transfer Entropy Delays (PITEDs)
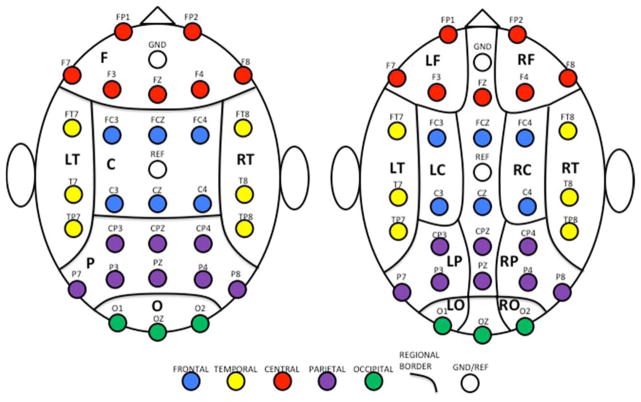
The 30 channels were grouped into 14 scalp regions based their arrangement and location on the scalp. The regions included: (1) left frontal (LF); (2) right frontal (RF); (3) frontal (F = LF + RF + channel FZ); (4) left temporal (LT); (5) right temporal (RT); (6) left central (LC); (7) right central (RC); (8) central (C = LC + RC + channels FCZ and CZ); (9) left parietal (LP); (10) right parietal (RP); (11) parietal (P = LP + RP + channels CPZ and PZ); (12) left occipital (LO); (13) right occipital (RO); and (14) occipital (O = LO + RO + channel OZ).). Note that left and right regions do not include central line channels; see Fig. 1 for regional boundaries.
Fig. 1.
Regional and Subregional Boundaries for Electrodes. Left: major regions; right: subregions. LF=left frontal; RF=right frontal; F=frontal; LT=left temporal; RT=right temporal; LC=left central; RC=right central; C=central; LP=left parietal; RP=right parietal; P=parietal; O=occipital. Note that central line channels (those with Z in the designation) are excluded from L/R subregions.
Peak values and peak delays are the most important characteristics of transfer entropy. Since channels have different magnitudes, peak values may not accurately reflect the effect of the measurements of information exchange between regions. We chose to use peak delay as the features since they are not influenced by magnitudes of the channels. First, transfer entropies were computed for each directional, pairwise combination of 30 channels (2 ocular channels excluded) for each protocol condition. The first two minutes of data for each protocol condition was used. Entropies were computed for delays of 0.002 through 1 second in 0.002-second steps. The delay at which the transfer entropy was greatest in magnitude was noted as the peak delay. Then, the inter-region delay for a directional pairing of regions (for example, region X → region Y) was computed as the average of all the delays for each channel in region X to each channel in region Y; see Equation (10),
| (10) |
where is the peak delay for channel i in region X to channel j in region Y, Nx is the number of channels in region X, and Ny is the number of channels in region Y. Note that inter-regional delays were defined for two different regions and they were not computed between a major region (C, F, O, P, or R) and any of its sub-regions. For example, the peak inter-regional delays for F→LF or LF→F were not computed. Thus, a total of 166 directional, mean peak inter-regional transfer entropy delays (PITEDs) were determined for each protocol condition.
2.4. Classification
For each protocol condition (REO, REC, or counting), we performed two types of classifications: first, binary classifications were conducted to discriminate (1) MCI vs. NC, (2) AD vs. NC, and (3) MCI vs. AD; and then a three-way classification was performed based on the binary classification results to determine which of the three groups a given record belonged to. The three-way classification scheme allows for the differentiation of the three groups without a priori knowledge that individuals fall into two of the three groups. Note that results of all classifications (both binary and three-way) were based on leave-one-out cross-validation (LOOCV) to avoid overfitting. For binary classifications, we used the support vector machine (SVM) functions in MATLAB™ [MathWorks 2013] with quadratic kernel functions. A three-way classification scheme is constructed by combining the outcomes of the binary classifiers using the pairwise coupling approach proposed by Hastie and Tibshirani [Hastie 1998]. For a given record, binary SVM classifiers (i.e., MCI vs. NC, AD vs. NC, and MCI vs. AD) are trained using all other available records and then applied to the given record. If two out of three of the SVM binary classifiers classify a record as belonging to class i, then the final decision of the three-way classifier is to classify the record as belonging to class i. Otherwise, the probability that a record belongs to each class, Pi, i = 1,2,3, is then estimated via pairwise coupling and then the final decision of the three-way classifier is to choose the class corresponding to the largest probability, argmaxi(Pi).
2.5. Feature Selection
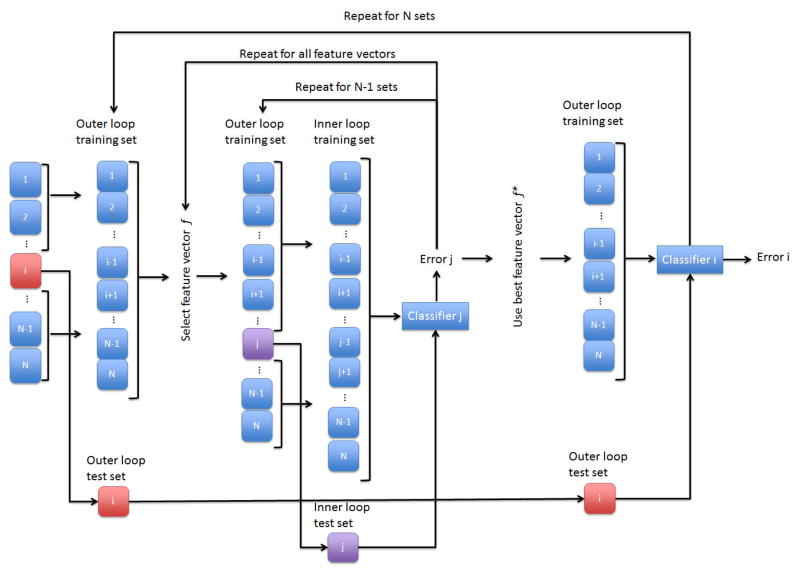
Feature selection was performed for each of three binary discrimination problems ((1) MCI vs. NC, (2) AD vs. NC, and (3) MCI vs. AD) for each protocol condition; see the schematic process in Fig. 2. We used the support vector machine (SVM) functions in MATLAB™ [MathWorks 2013] as the binary classifier. Quadratic kernel functions were used in all discriminations and the cost coefficient was held constant at unity. Nested leave-one-out cross-validation (LOOCV) loops were used to avoid overfitting while suggesting and testing different combinations of PITEDs as features [Bishop 2008, Nowotny 2014]. The inner loop generated a list of suggested combinations via a forward, high-score, features selection method where combinations were scored using LOOCV accuracy of SVM model predictions from a smaller, randomized, subset of records [Bishop 2008]. The outer loop determined the LOOCV accuracy of combinations suggested by the inner loop for all available records. The discriminatory power of individual PITEDs was then assessed based on how often they appeared in the 100 best performing combinations tested in the outer loop simulation.
Fig. 2.
Schematic feature selection process.
2.6. Statistical Significance
Monte Carlo permutation testing was used to assess the statistical significance of the LOOCV accuracies of the binary classifiers. Specifically, a random sample of 10,000 permutations of shuffled labels indicating groups (NC, MCI, or AD) was used to estimate a 95% confidence interval for the probability that the leave-one-out cross-validation accuracies obtained were due to chance. The p-values presented were determined using this method [Nichols 2001].
3. RESULTS
3.1. Binary Discrimination Results
Two-sample Student’s t-distribution tests (unequal variance) are performed on group means of PITEDs selected as features for binary classifiers in order to determine if observed differences are significant enough to infer a linear separability at the population level. Such an inference would require large differences between group means and small variation within groups. It should be noted that inferences are dependent on the assumption of representative samples.
3.1.1. MCI vs. NC
Results for LOOCV accuracies for each binary classifier are presented in Table 2 along with the selected features. Accuracies presented are obtained using selected features. For the REO condition, MCI participants demonstrate a lower PITED for occipital region to right frontal region coupled with an increased PITED from the frontal region to the left occipital region, compared to normal controls. An increased central-to-frontal PITED is also observed for MCI participants. Most of the selected features for the counting task include PITEDs of directed information transfer to the occipital region. For the REC condition, the pathway of right frontal to right temporal to right parietal to occipital appears discriminate MCI participants. Ninety-five percent confidence intervals for the corresponding p-values are determined via Monte Carlo permutation testing. LOOCV accuracies of 93.6% (p-value <0.0032), 90.3% (p-value <0.0182), and 87.1% (p-value <0.0321) are achieved for MCI vs. NC discrimination for the REO condition, counting task, and REC condition, respectively.
Table 2.
Group Comparisons of Selected Features for Binary Classifiers
| Condition | MCI vs. NC | AD vs. NC | AD vs. MCI | |||
|---|---|---|---|---|---|---|
| REO | Selected Features | Group Means | Selected Features | Group Means | Selected Features | Group Means |
| O→RF | MCI<NC | LT→F | AD>NC | LT→LF | MCI<AD*** | |
| F→LO | MCI>NC | RO→LC | AD>NC | RO→LC | MCI>AD | |
| C→F | MCI>NC | F→LT | AD<NC | P→LO | MCI<AD | |
| acc. (sens., spec.): | acc. (sens., spec.): | acc. (sens., spec.): | ||||
| 93.6% (100%, 86.7%) | 93.8% (100%, 86.7%) | 90.9% (93.8%, 88.2%) | ||||
| 95% CI for p-value: | 95% CI for p-value: | 95% CI for p-value: | ||||
| (0.0001, 0.0032) | (0.0031, 0.0043) | (0.0097, 0.0118) | ||||
| Counting Task | Selected Features | Group Means | Selected Features | Group Means | Selected Features | Group Means |
| RF→LP | MCI>NC | RP→LO | AD>NC*** | RP→LO | MCI<AD** | |
| P→LT | MCI<NC | RO→LO | AD>NC* | RP→O | MCI<AD*** | |
| LP→LO | MCI<NC | LF→LO | AD>NC* | LF→LT | MCI<AD* | |
| acc. (sens., spec.): | acc. (sens., spec.): | acc. (sens., spec.): | ||||
| 90.3% (93.8%, 86.7%) | 90.6& (82.4%, 100%) | 90.9% (88.2%, 93.8%) | ||||
| 95% CI for p-value: | 95% CI for p-value: | 95% CI for p-value: | ||||
| (0.00138, 0.0182) | (0.0020, 0.0110) | (0.0032, 0.0195) | ||||
| REC | Selected Features | Group Means | Selected Features | Group Means | Selected Features | Group Means |
| LO→RF | MCI>NC** | LT→RC | AD<NC | RF→RT | MCI<AD* | |
| C→RT | MCI<NC** | O→LF | AD>NC | LC→O | MCI<AD | |
| RT→RP | MCI>NC | LO→LT | AD<NC | RP→O | MCI<AD | |
| acc. (sens., spec.): | acc. (sens., spec.): | acc. (sens., spec.): | ||||
| 87.1% (87.5%, 86.7%) | 87.5% (82.4%, 93.3%) | 81.8% (100%, 64.7%) | ||||
| 95% CI for p-value: | 95% CI for p-value: | 95% CI for p-value: | ||||
| (0.0057, 0.0321) | (0.0211, 0.0324) | (0.0162, 0.0373) | ||||
p< 0.05
p<0.01,
p<0.001.
Feature designations are preceded by regional indices: LF=left frontal; RF=right frontal; F=frontal; LT=left temporal; RT=right temporal; LC=left central; RC=right central; C=central; LP=left parietal; RP=right parietal; P=parietal; LO=left occipital; RO=right occipital; O=occipital; see Fig. 1 for regional boundaries. REO = resting with eyes open; REC = resting with eyes closed. acc.=accuracy, sens.=sensitivity, and spec.=specificity.
3.1.2. AD vs. NC
Compared to normal controls, AD participants demonstrate a significantly greater left temporal-to-frontal PITED coupled with a decrease in frontal-to-left temporal PITED during the REO condition. A greater right occipital-to-left central PITED is also observed for AD participants. A LOOCV accuracy of 93.8% (p-value <0.0043) is achieved for the REO condition based on these differences. During the counting task, AD participants demonstrate significantly increased PITEDs for right parietal-to-left occipital, left frontal-to-left occipital, and right occipital-to-left occipital. These observations allow for a LOOCV accuracy of 90.6% (p-value <0.0110) for AD vs. NC discrimination during the counting task. When resting with eyes closed, AD participants demonstrated an increase in occipital-to-left frontal PITED and a decrease in left temporal-to-right central PITED coupled with a decrease in left occipital-to-left temporal PTITED. An accuracy of 87.5% (p-value <0.0324) is achieved for the REC condition.
3.1.3. MCI vs. AD
For the REO condition, AD participants demonstrate a significantly greater left temporal-to-left frontal PITED compared to MCI participants. This appears to closely follow the observation of increased left temporal-to-frontal PITED in AD participants compared to normal controls. Interestingly, during the REO condition, the right occipital-to-left central PITED is greater for AD participants compared to NC participants but lower for AD participants compared to MCI participants. There is also an observed increase in parietal-to-left occipital PITED for AD participants. A LOOCV accuracy of 90.9% (p-value <0.0118) for MCI vs. AD discrimination is achieved based on these observations for the eyes open resting condition. MCI vs. AD LOOCV accuracies of 84.5% (p-value <0.0195) and 81.8% (p-value <0.0373) are achieved for the counting task and REC condition, respectively. During the counting task, AD participants demonstrate significantly increased right occipital-to-left central PITED compared to MCI participants and NC participants. AD participants also have significantly higher right parietal-to-occipital and left frontal-to-left temporal PITEDs. While resting with eyes closed, AD participants and higher right frontal-to-right temporal, left central-to-occipital, and right parietal-to-occipital PITEDs.
3.2. Three-way Classification Results
Table 3 is a contingency table that shows the performance of the three-way classification for the REO condition. One participant from each group is misclassified using data from the REO condition: one NC participant is misclassified as AD, one MCI participant is misclassified as NC, and one AD participant is misclassified as MCI. Overall, the accuracy is 93.8%.
Table 3.
Contingency Table of 3-Way Classification Results for REO Condition Using PITEDs.
| Predicted Classes | |||||
|---|---|---|---|---|---|
| NC | MCI | AD | |||
| True Classes | NC | 14 | 0 | 1 | 93.3% |
| MCI | 1 | 15 | 0 | 93.8% | |
| AD | 0 | 1 | 16 | 94.1% | |
| 93.3% | 93.8% | 94.1% | Overall Acc.: 93.8% | ||
Table 4 shows a summary of the three-way classification results for the counting task. All NC participants are correctly classified. Two MCI participants are misclassified as NC participants. Two AD participants are also misclassified, one as MCI and one as NC. Thus, 100% of those predicted as AD are AD, 93.3% of those predicted to be MCI are MCI, and 83.3% of those predicted to belong to the NC group are actually NC participants. The resulting overall accuracy is 91.7%.
Table 4.
Contingency Table of 3-Way Classification Results for Counting Task Using PITEDs.
| Predicted Classes | |||||
|---|---|---|---|---|---|
| NC | MCI | AD | |||
| True Classes | NC | 15 | 0 | 0 | 100% |
| MCI | 2 | 14 | 0 | 87.5% | |
| AD | 1 | 1 | 15 | 88.2% | |
| 83.3% | 93.3% | 100% | Overall Acc.: 91.7% | ||
Results for the REC condition are very similar to those of the REO condition and are presented in Table 5. Comparing Tables 3 and 5, the only differences are that a NC participant is misclassified as MCI instead of being misclassified as AD and an MCI participant is also misclassified as NC. The overall accuracy for the REC condition is the same as for the counting task at 91.7%.
Table 5.
Contingency Table of 3-Way Classification Results for REC Condition Using PITEDs.
| Predicted Classes | |||||
|---|---|---|---|---|---|
| NC | MCI | AD | |||
| True Classes | NC | 14 | 1 | 0 | 93.3% |
| MCI | 1 | 14 | 1 | 87.5% | |
| AD | 0 | 1 | 16 | 94.1% | |
| 93.3% | 87.5% | 94.1% | Overall Acc.: 91.7% | ||
4. DISCUSSION
4.1. Contextualization of Results
In this study, average delays corresponding to maximized transfer entropy between EEG channels of different scalp regions are examined in normal aging, MCI, and early AD participants. We have analyzed EEG data collected using three different EEG protocols: resting eyes open condition, resting eyes closed condition, and a simple cognitive task of counting backwards by ones. Accuracies of 93.6–97.0% (using the three EEG protocol conditions) are achieved for binary classifications between the three groups using features from average peak inter-regional transfer entropy delays (PITEDs). A three-way classification scheme is also derived from the binary classifiers based on pairwise coupling, with overall accuracies of 91.7–93.8% (using the three EEG protocol conditions). The resting-state protocols reflect default mode networking activity in the brain and have shown promise in clinical application of AD [Vecchio 2013]. Counting and other cognitive protocols reflect task related network in the brain. Both method have demonstrated the EEG biomarkers’ are associated with AD pathology [Olichney 2013].
As observed in previous studies [Baker 2008, Huang 2000, Iqbal 2005, Rossini 2006], features that successfully discriminate between AD and NC, may not be able to discriminate between MCI and NC or between AD and MCI. As such, previous studies often investigated the three binary classification problems using different sets of features for each classification. Moreover, none of the aforementioned studies reported three-way classification between NC, MCI, and AD participants. A three-way classification model was constructed by combining the binary classifiers in [McBride 2014b], where the results demonstrate overall discrimination accuracies of 83.3%, 85.4%, and 79.2% for resting eyes open, counting eyes closed, and resting eyes closed protocols, respectively. Therefore, the encouraging results of three-way classifications in this work indicate the robustness of the transfer entropy measures. The three-way classification scheme may be used for differentiation of the three groups without a priori knowledge that individuals fall into two of the three groups. In contrast to the previous studies on differences between the cognitive groups, this work classifies participants at the individual level, which is the case when a patient comes into a doctor’s office. Moreover, the individualized analysis also makes it easy to test these EEG markers against known biomarkers and known cognitive tests.
The most significant results indicate that the transmission of electrophysiological activity at the parietal electrode site to early visual cortex is delayed in AD patients compared to those in MCI or in NC. The disruption of white matter connections has been linked to delayed reaction times or processing speed in the brain [Gold 2007]. Recent evidence has shown that white matter lesion and Alzheimer’s Tau pathology at the parietal lobe both contribute to development of AD [Hertze 2013]. The current entropy results of delayed parietal activity in AD are consistent with AD pathology. In addition, it is also well-known that medial temporal cortex, important structure for memory, is among the earliest to be affected in AD pathology. Our second most significant result showed delayed activity from left temporal cortex to left frontal in AD compared to that in NC during resting eyes open state. This result indicates the deficits in the default-mode network between left temporal-frontal communication. With further validation, these parietal and temporal activity-related EEG indicators are likely promising markers with clinical implication of AD progression. In addition, individual EEG indicators among normal older adults may be used as a predictor for risk factor of AD.
4.2. Limitations and Future Work
The current method cannot be readily applied to the clinical setting since it requires 30 EEG channels, making setup time an issue. Fewer electrodes would be ideal for more convenient application. Another shortcoming of the current studies is the need for a larger sample size. Future work should examine the developed EEG indicators against known biomarkers (e.g., cerebrospinal fluid proteins) in a larger sample size. Future work should also investigate whether the EEG indicators bear longitudinal changes over relatively short time periods at the individual level. Future work may also consider data fusion of the features from different conditions to allow synergies between the features.
5. CONCLUSIONS
Analysis of EEG inter-channel transfer entropy allows for observations of patterns in the complexity and synchrony of EEG data. Specifically, the features proposed here are intended to represent trends in the delay of the transfer of the information present in EEG signals between major regions of the scalp. The successful discrimination between the three groups of EEG records (NC, MCI, and AD) are the result of differences in the dynamics of the distribution of information in EEG voltages across the scalp in resting states and during a simple cognitive task. It is possible the observed differences in these information dynamics may be influenced by alterations in the functional organization of the brain as a result of cognitive decline.
The results of this pilot study suggest the potential for the use of features representing inter-regional EEG transfer entropy relationships as a means for objectively discriminating between normal older, MCI, and AD participants.
Acknowledgments
Research was sponsored in part by the Laboratory Directed Research and Development Program of Oak Ridge National Laboratory, managed by UT-Battelle, LLC, for the US Department of Energy under Contract No. DE-AC05-00OR22725; by the NSF under grant numbers CMMI-0845753 and CMMI-1234155; and in part by the NIH under grants NIH P30 AG028383 to UK Sanders-Brown Center on Aging, NIH AG00986 to YJ, and NIH NCRR UL1RR033173 to UK Center for Clinical and Translational Science. The contributions to this paper by N. B. Munro were prepared while acting in her own independent capacities and not on behalf of UT-Battelle, LLC, or its affiliates or successors, or Oak Ridge National Laboratory, or the US Department of Energy. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the funding agencies.
We deeply thank Dr. David Wekstein of the UK Alzheimer’s Research Center for his key role in getting the collaboration between ORNL and UK in place to make the pilot study possible. We thank A. Lawson, E. Walsh, J. Lianekhammy, S. Kaiser, C. Black, K. Tran, and L. Broster at the University of Kentucky for their assistance in data acquisition and database management, and Schmitt, F, Kryscio, R, and Abner, E at the Biostatics Core at the UK aging center for providing MMSE scores of some participants.
Footnotes
CONFLICTS OF INTEREST
The authors have no conflicts of interest to declare.
Contributor Information
Joseph McBride, Email: jmcbrid4@utk.edu, Department of Mechanical, Aerospace, and Biomedical Engineering, University of Tennessee, Knoxville, Knoxville, TN 37996, USA.
Xiaopeng Zhao, Email: xzhao9@utk.edu, Department of Mechanical, Aerospace, and Biomedical Engineering, National Institute of Mathematical and Biological Synthesis, University of Tennessee, Knoxville, Knoxville, TN 37996, USA.
Nancy Munro, Email: nbmunroconsulting@comcast.net, Research Scientist, retired, Oak Ridge Nation Laboratory, Oak Ridge, TN 37831-6418, USA.
Gregory Jicha, Email: gajich2@email.uky.edu, Sanders-Brown Center on Aging, Department of Neurology, University of Kentucky College of Medicine, Lexington, KY 40356, USA.
Charles Smith, Email: csmith@mri.uky.edu, Sanders-Brown Center on Aging, Department of Neurology, University of Kentucky College of Medicine, Lexington, KY 40356, USA.
Yang Jiang, Email: yjiang@uky.edu, Department of Behavioral Science, Sanders-Brown Center on Aging, University of Kentucky College of Medicine, Lexington, KY 40356, USA.
References
- [Baker2008].Baker M, Akrofi K, Schiffer R, O’Boyle MW. EEG patterns in mild cognitive impairment (MCI) patients. Open Neuroimag J. 2008;2:52–55. doi: 10.2174/1874440000802010052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [Barnett2009].Barnett L. Granger causality and transfer entropy are equivalent for Gaussian variables. Phys Rev Lett. 2009;103:238701. doi: 10.1103/PhysRevLett.103.238701. [DOI] [PubMed] [Google Scholar]
- [Bishop 2008].Bishop C. Neural Networks for Pattern Recognition. Oxford Univ. Press; 2008. pp. 295–329. [Google Scholar]
- [Dauwels 2010].Dauwels J, Vialatte FA, Cichocki A. Diagnosis of Alzheimer’s disease from EEG signals: where are we standing? Curr Alzheimer Res. 2010 Sep;7(6):487–505. doi: 10.2174/156720510792231720. [DOI] [PubMed] [Google Scholar]
- [Hastie 1998].Hastie T, Tibshirani R. Classification by pairwise coupling. Ann Statist. 1998;26:451–471. [Google Scholar]
- [Hlaváčková 2007].Hlaváčková-Schindler K, Palus M, Vejmelka M, Bhattacharya J. Causality detection based on information-theoretic approaches in time series analysis. Phys Rep. 2007;441:1–46. [Google Scholar]
- [Huang 2000].Huang C, Wahlund L, Dierks T, Julin P, Winblad B, Jelic V. Discrimination of Alzheimer’s disease and mild cognitive impairment by equivalent EEG sources: a cross-sectional and longitudinal study. Clin Neurophysiol. 2000;111:1961–1967. doi: 10.1016/s1388-2457(00)00454-5. [DOI] [PubMed] [Google Scholar]
- [Iqbal 2005].Iqbal K, Alonso AC, Chen S, Chohan MO, El-Akkad E, Gong CX, Khatoon S, Li B, Liu F, Rahman A, Tanikuai H, Grundke-Iqbal I. Tau pathology in Alzheimer’s disease and other tauopathies. Biochim Biophys Acta. 2005;1793:198–210. doi: 10.1016/j.bbadis.2004.09.008. [DOI] [PubMed] [Google Scholar]
- [Jelic 2009].Jelic V, Kowalski J. Evidence-based evaluation of diagnostic accuracy of resting EEG in dementia and mild cognitive impairment. Clin EEG Neurosci. 2009;40:129–142. doi: 10.1177/155005940904000211. [DOI] [PubMed] [Google Scholar]
- [Kullback 1959].Kullback S. Information Theory and Statistics. New York, NY: Wiley; 1959. [Google Scholar]
- [Lake 2002].Lake D, Richmann J, Griffin M, Moorman J. Sample entropy analysis of neonatal heart rate variability. Am J Physiol. 2002;283(3):R789–R797. doi: 10.1152/ajpregu.00069.2002. [DOI] [PubMed] [Google Scholar]
- [Lizier 2008].Lizier J, Prokopenko M, Zomaya A. Local information transfer as a spatiotemporal filter for complex systems. Phys Rev. 2008;77 doi: 10.1103/PhysRevE.77.026110. [DOI] [PubMed] [Google Scholar]
- [Lizier 2010].Lizier JT, Prokopenko M. Differentiating information transfer and causal effect. European Physical Journal B. 2010;73:605–615. [Google Scholar]
- [Lizier 2011].Lizier J, Heinzle J, Horstmann A, Haynes J, Prokopenko M. Multivariate information-theoretic measures reveal directed information structure and task relevant changes in fMRI connectivity. J Comput Neurosci. 2011;30:85–107. doi: 10.1007/s10827-010-0271-2. [DOI] [PubMed] [Google Scholar]
- [Mathworks 2013].MathWorks. [Accessed Feb. 2013];MATLAB. Available at mathworks.com/products/matlab.
- [McBride 2013a].McBride J, Zhao X, Munro N, Smith C, Jicha G, Jiang Y. Resting EEG discrimination of early stage Alzheimer’s disease from normal aging using inter-channel coherence network graphs. Ann Biomed Eng. 2013;41:1233–42. doi: 10.1007/s10439-013-0788-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [McBride 2013b].McBride J, Zhao X, Nichols T, Vagnini V, Munro N, Berry D, Jiang Y. Scalp EEG-based discrimination of cognitive deficits after traumatic brain injury using event-related Tsallis entropy analysis. IEEE Trans Biomed Eng. 2013;60:90–96. doi: 10.1109/TBME.2012.2223698. [DOI] [PubMed] [Google Scholar]
- [McBride 2014a].McBride J, Zhao X, Munro N, Jicha G, Schmitt F, Kryscio R, Smith C, Jiang Y. Sugihara causality analysis of scalp EEG for detection of early Alzheimer’s disease. doi: 10.1016/j.nicl.2014.12.005. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [McBride 2014b].McBride J, Zhao X, Munro N, Smith C, Jicha G, Hively L, Broster L, Schmitt F, Kryscio R, Jiang Y. Spectral and complexity analysis of scalp EEG characteristics for mild cognitive impairment and early Alzheimer’s disease. Comput Meth Prog Bio. 2014;114:153–163. doi: 10.1016/j.cmpb.2014.01.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [Nichols 2001].Nichols T, Holmes A. Nonparametric permutation tests for functional neuroimaging: a primer with examples. Hum Brain Map. 2001;15:1–25. doi: 10.1002/hbm.1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [Nowotny 2014].Nowotny T. Two challenges of correct validation in pattern recognition. Frontiers in Robotics and AI. 2014;1:Article 5, 1–6. [Google Scholar]
- [Petersen 2001].Petersen RC, Doody R, Kurz A, Mohs RC, Morris JC, Rabins PV, Ritchie K, Rossor M, Thal L, Winblad B. Current concepts in mild cognitive impairment. Arch Neurol. 2001;58:1985–1992. doi: 10.1001/archneur.58.12.1985. [DOI] [PubMed] [Google Scholar]
- [Petersen 2003].Petersen RC. Mild cognitive impairment. New York, NY: Oxford Press; 2003. [Google Scholar]
- [Rossini 2006].Rossini PM, Del Percio C, Pasqualetti P, Cassetta E, Binetti G, Dal Forno G, Ferreri F, Frisoni G, Chiovenda P, Miniussi C, Paris L, Tombini M, Vecchio F, Babiloni C. Conversion from mild cognitive impairment to Alzheimer’s disease is predicted by source and coherence of brain electroencephalography rhythms. Neuroscience. 2006;143:793–803. doi: 10.1016/j.neuroscience.2006.08.049. [DOI] [PubMed] [Google Scholar]
- [Schmitt 2012].Schmitt F, Nelson P, Abner E, Scheff S, Jicha G, Smith C, Cooper G, Mendiondo M, Danner D, van Eldik L, Caban-Holt A, Lovell M, Kryscio R. University of Kentucky Sanders-Brown healthy brain aging volunteers: donor characteristics, procedures and neuropathology. Curr Alzheimer Res. 2012;9:724–733. doi: 10.2174/156720512801322591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [Schreiber 2000].Schreiber T. Measuring information transfer. Phys Rev Lett. 2000;85:461–464. doi: 10.1103/PhysRevLett.85.461. [DOI] [PubMed] [Google Scholar]
- [Sneddon 2005].Sneddon, Shankle RW, Hara J, Rodriguez A, Horrman D, Saha U. EEG detection of early Alzheimer’s disease using psychophysical tasks. Clin EEG Neurosci. 2005;36(3):141–150. doi: 10.1177/155005940503600304. [DOI] [PubMed] [Google Scholar]
- [Sneddon 2007].Sneddon R. The Tsallis entropy of natural information. Physica A. 2007;386(1):101–118. [Google Scholar]
- [Stam 2003].Stam CJ, van der Made Y, Pijnenburg YA, Scheltens P. EEG synchronization in mild cognitive impairment and Alzheimer’s disease. Acta Neurol Scand. 2003;108:90–96. doi: 10.1034/j.1600-0404.2003.02067.x. [DOI] [PubMed] [Google Scholar]
- [Stam 2005].Stam CJ, Montex T, Jones BF, Rombouts SA, van der Made Y, Pijnenburg YA, Scheltens P. Disturbed fluctuations of resting state EEG synchronization in Alzheimer’s disease. Clin Neurophysiol. 2005;116:708–715. doi: 10.1016/j.clinph.2004.09.022. [DOI] [PubMed] [Google Scholar]
- [Stam 2007].Stam CJ, Jones BF, Nolte G, Breakspear M, Scheltens P. Small-world networks and functional connectivity in Alzheimer’s disease. Cerebral Cortex. 2007;17:92–99. doi: 10.1093/cercor/bhj127. [DOI] [PubMed] [Google Scholar]
- [Vecchio 2013].Vecchio F, Babiloni C, Lizio R, de Fallani FV, Blinowska K, Verrienti G, Frisoni G, Rossini PM. Resting state cortical EEG rhythms in Alzheimer’s disease: toward EEG markers for clinical applications: a review. Suppl Clin Neurophysiol. 2013;62:223–36. doi: 10.1016/b978-0-7020-5307-8.00015-6. [DOI] [PubMed] [Google Scholar]
- [Olichney 2013].Olichney JM, Pak J, Salmon DP, Yang J-C, Gahagan T, Nowacki R, et al. Abnormal P600 word repetition effect in elderly persons with preclinical Alzheimer’s disease. Cognitive Neuroscience. 2013;1(1):1–9. doi: 10.1080/17588928.2013.838945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [Vicente 2011].Vicente R, Vibral M, Lindner M, Pipa G. Transfer entropy—a model-free measure of effective connectivity for the neurosciences. J Comput Neurosci. 2011;30:45–67. doi: 10.1007/s10827-010-0262-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [Wibral 2013].Wibral M, Pampu N, Priesemann V, Siebenhühner F, Seiwert H, et al. Measuring Information-Transfer Delays. PLoS ONE. 2013;8(2):e55809. doi: 10.1371/journal.pone.0055809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [Zhao 2007].Zhao P, Van-Eetvelt P, Goh C, Hudson N, Wimalaratna S, Ifeachor E. Characterization of EEGs in Alzheimer’s disease using information theoretic methods. Proc IEEE Eng Med Biol Soc. 2007;2007:512705131. doi: 10.1109/IEMBS.2007.4353494. [DOI] [PubMed] [Google Scholar]
- [Gold 2007].Gold B, Powell DK, Liang X, Jiang Y, Hardy PA. Speed of lexical decision correlates with diffusion anisotropy in left parietal and frontal white matter: evidence from diffusion tensor imaging. Neuropsychologia. 2007;45:2439–2446. doi: 10.1016/j.neuropsychologia.2007.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [Hertze 2013].Hertze J, Palmqvist S, Minthon L, Hansson O. Tau Pathology and Parietal White Matter Lesions Have Independent but Synergistic Effects on Early Development of Alzheimer’s Disease. Dementia and Geriatric Cognitive Disorders Extra. 2013;3(1):113–122. doi: 10.1159/000348353. [DOI] [PMC free article] [PubMed] [Google Scholar]