Significance
Switching surface topographic patterns in a dynamic way controls properties such as friction, sticking–release, light reflection, aero- and hydrodynamics, self-cleaning, and touch experience. We present a method to make coatings which are initially flat but form a spiked surface structure under light exposure. The surface turns flat again immediately as the light switches off. The polydomain liquid crystal provides a convenient method that makes fabrication of responsive coatings significantly easier than previous methods. The polydomain texture is simulated by finite elements and the topographic deformation can be understood in terms of director-dependent absorption and related changes in local order. Moreover, the dynamic creation of free volume further enhances the surface modulation to the record value of 24% of the film thickness.
Keywords: surface dynamics, self-organization, switchable jagged surfaces, polydomain liquid crystal polymer, light activation
Abstract
In this work we propose randomly ordered polydomain nematic liquid crystal polymer networks to reversibly generate notable jagged relief patterns at a polymer coating surface by light illumination. The domain size is controlled by the addition of traces of partly insoluble fluorinated acrylate. The photoresponse of the coating is induced by a small amount of copolymerized azobenzene monomers. Upon exposure to UV light, azobenzene undergoes trans to cis isomerization, resulting in a change in molecular order and packing within each domain. The extent of this effect and its directionality depends on the domain orientation. Localized to domain level, this morphological change forms large 3D spikes at the surface with a modulation amplitude of more than 20% of the initial thickness. The process is reversible; the surface topographical patterns erase within 10 s by stopping the light exposure. A finite element model is applied to simulate the surface topography changes of the polydomain coating. The simulations describe the formation of the topographic features in terms of light absorption and isomerization process as a function of the director orientation. The random director distribution leads to surface structures which were found to be in close agreement with the ones measured by interference microscopy. The effect of domain size on surface roughness and depth modulation was explored and related to the internal mechanical constraints. The use of nematic liquid crystal polydomains confined in a polymer network largely simplifies the fabrication of smart coatings with a prominent triggered topographic response.
In nature, living creatures have developed a series of motion and surviving strategies based on unique topographic patterns on their surfaces. The surface topographies range from static patterns as, for instance, found on the leaves of the lotus flower, repelling water and dirt particles, to the dynamic structures that appear under certain conditions as found in many mammals. An example is the pilomotor reflex at the skin of mammals which creates insulation in cold conditions and provides protection by scaring away predators when the body appears larger. To date, many studies have been devoted to the use of static surface topographies fabricated by wrinkling (1, 2), embossing (3), or lithography. However, there is an increasing demand to make these surface structures switchable in modern applications, such as adjustable gas and water flow behavior at corrugated surfaces (4), autonomously adjusting lenses (5), controlled wettability (6), and modulated optics such as scattering, diffraction, or reflection (7–9). Also, the mechanical properties can be altered by the appearance or disappearance of protrusions at the surface (10, 11), such as friction, stick, and adhesion which manifest themselves in, e.g., haptic applications (12).
Our focus here is to develop dynamic topographic patterns at surfaces that can be switched on and off in response to an external trigger. From literature it is known that a focused polarized laser spot induces surface wrinkling in azobenzene modified linear polymer films (13, 14). However, many applications require polymers that can be switched over a much larger area under relatively moderate illumination intensities. In addition, we introduce the concept of a cross-linked coating which improves thermal properties and the resistance against wear under abrasive conditions. The elastic properties of the polymer network provide reversibility to the systems where the structures evolve and disappear by switching the light source on and off. Recently we published on the light-induced formation of dynamic protrusions in a system that consists of alternating homeotropic and chiral–nematic liquid crystal network molecules modified with azobenzene moieties (15). Although the effects are spectacular, the procedure to make these films is complicated and requires space-modulated electrical fields to produce localized homeotropic alignment. Another method we proposed is based on chiral liquid crystals that adapt a so-called fingerprint configuration (16). It is formed in the cholesteric phase of a liquid crystal monomer mixture by carefully balancing the chiral force that rotates molecules along their helix axis and the anchoring force at the substrate which acts as an unwinding force to promote the homeotropic (perpendicular) orientation. Although we can here eliminate the lithographic patterning and the additional electric field to align the molecules, large efforts are devoted seeking for the delicate balance between the two distinct forces and set limits to, for instance, the coating thickness which should be on the order of half the periodicity of the molecular helix.
A big step forward to the applicability of dynamic surfaces would be a method to produce this functionality in a simple coating process. Thereto we report here on a general approach to fabricate dynamic surface topographies through the self-assembling process in a liquid crystal polymer coating. The method is based on the formation of polydomain nematic liquid crystals. The employment of polydomain liquid crystals distinguishes itself from conventional liquid crystal applications, such as in displays, where a monolithic molecular alignment is desired. In polydomain liquid crystals, molecules are aligned in a discrete domain region instead of over the entire area. Throughout the coating, domains are randomly distributed with various alignments ranging from uniaxial and parallel to the surface with different orientations in the plane of the layer, tilted to the plane of the film with various tilt angles to domains with a (close to) homeotropic orientation.
To further support our understanding of the underlying actuation mechanisms, a finite element model is used to simulate the 3D surface topography changes of the polydomain liquid crystal coatings. A nonlinear light absorption model is used to account for the attenuation of UV light and the corresponding isomerization process of the azobenzene molecules. Photoinduced strains of the liquid crystal domains are linked to the generation of cis isomers. Constraints from the substrate, together with interactions between domains with different liquid crystal alignment, lead to the surface profiles that are found to be in close agreement with the experimental results.
Results and Discussion
Liquid crystals in their nematic phase tend to align along a common vector , called the director. The degree and accuracy in which they align depends on many conditions. Important parameters are the state and preparation of the substrates and the purity of the liquid crystal mixture with respect to homogeneity, the presence of particles, and/or phase-separated compounds. For instance, substrates provided with an anisotropic surface, as a unidirectionally rubbed polyimide coating, give a nicely uniaxial monodomain liquid crystal layer under the condition that there are no contaminating particles present in the liquid crystal mixture or at the surface. This is the configuration that is of most interest for many, mostly optical, applications of these materials. In this paper we adversely explore the use of a polydomain liquid crystal layer. Here the layer breaks up in domains with varying directors, often connected by disclinations where the director might describe a complex rotation on its transition from one domain into the other. To have control over the formation of the domains and their sizes, we have dispersed a small concentration of a nonsoluble monomer into the liquid crystal monomer mixture. The phase-separated monomer droplets disturb the long-range molecular order of the liquid crystal and nucleate domain formation. The obtained polydomain state in the liquid crystal is frozen by polymerization of the liquid crystal using UV light. Simultaneously the droplets with the nonsoluble monomer become polymerized.
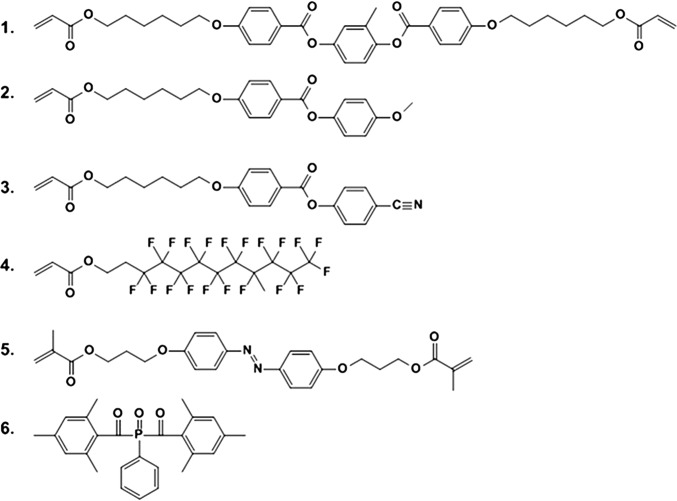
The mixtures that form polydomain polymerizable liquid crystal coatings were composed from a set of liquid crystal monomers provided with some additives as given in Fig. 1. Monomers 1–3 exhibit a nematic liquid crystal phase providing the molecular alignment. This mixture of mono- and diacrylates has been chosen such that it has good processing properties in the monomeric state, such as a low crystalline melting temperature, good solubility in organic solvents, and a wide nematic phase after evaporation of the solvent. The presence and concentration of the cross-linking diacrylate 1 regulates some important mechanical properties in the polymeric state such as a glass temperature above room temperature, thermal resistance against loss of order upon heating, and a measurable formation of protrusions upon activation. Fluorinated monomer 4 is added in low concentration. It reduces the surface energy of the coating (Fig. S1). However, because of its limited solubility in the liquid crystal acrylate monomers it remains partly undissolved and becomes randomly dispersed as reactive droplets in the liquid crystal medium after evaporation of the solvent. It therefore stimulates the formation of the domains in the monomeric state. The domain size is controlled by the concentration of this compound. After polymerization of the mixture this compound remains dispersed as small polymerized droplets chemically attached to the ordered polymer network. The reactive azobenzene monomer 5 is added to make the polymer sensitive for photoactuation. From previous studies we know that already a concentration as low as 2 wt % is sufficient to provide significant effects (15, 16). In this study we used 5 wt % of 5. Photoinitiator 6 is chosen as it can initiate the photopolymerization by light exposure with wavelengths >400 nm preventing undesired activation of the azobenzene compound at this stage of the process. This mixture is dissolved in dichloromethane and spin-coated on clean glass without an alignment layer but provided with a covalently coupled acrylated silane to promote adhesion. This silane has a weak tendency to orient liquid crystal molecules perpendicular to the surface. After polymerization the polymer coating is hard and glassy and adheres firmly to the glass substrate.
Fig. 1.
Monomers applied for the coating formulation.
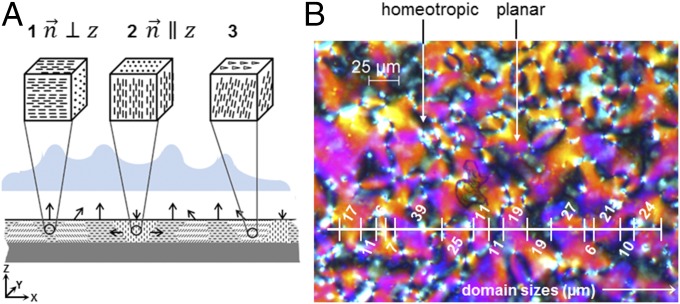
A cross-sectional schematic view of a polydomain liquid crystal is presented in Fig. 2A. Although we realize that this figure is oversimplified, it shows the basic principle. Each domain has its own specific orientation. The director can be parallel, perpendicular, or tilted with diverse angles and directions to the substrate as shown in Fig. 2 A, 1, 2, 3, respectively. From domain to domain, molecules align differently without any preference for a specific orientation. A typical sample is shown in Fig. 2B as observed by microscopy between crossed polarizers. The purple-colored areas correspond to domains with a (close to) planar alignment and the director close to 45° with the polarizer axes. These areas have a retardation, as defined by the product of thickness and birefringence, of around 1,000 nm and have colors that can be found in the second-order region on the Michel–Lžvy interference color chart (17). The other colors represent either areas with a tilted alignment with respect to the surface or with respect to the polarizer axes. Most black regions between crossed polarizers remain black upon rotation, meaning that they have a homeotropic orientation. A large variation in the domain size is observed. In this specific sample, measured along an arbitrary line, the smallest domain is about 7 µm whereas the largest domain is found to be 5 times larger.
Fig. 2.
Representation of polydomain liquid crystal networks (LCNs). (A) Schematic representation of the predicted deformation of the polydomain liquid crystal. From A, 1 to A, 3, molecules are aligned in a uniaxial (1), homeotropic (2), and tilted (3) manner. The arrows illustrate the direction of expansion propensities upon actuation and the blue inset illustrates the anticipated formation of surface structures. (B) Polarized optical microscopy images of a polydomain texture as observed between crossed polarizers. Bright regions correspond to planar or tilted regions and the black and whitish areas to regions where the orientation is (close to) homeotropic. In some black regions the orientation is tilted or planar with the x–y projection of the director parallel to one of the polarizer axes.
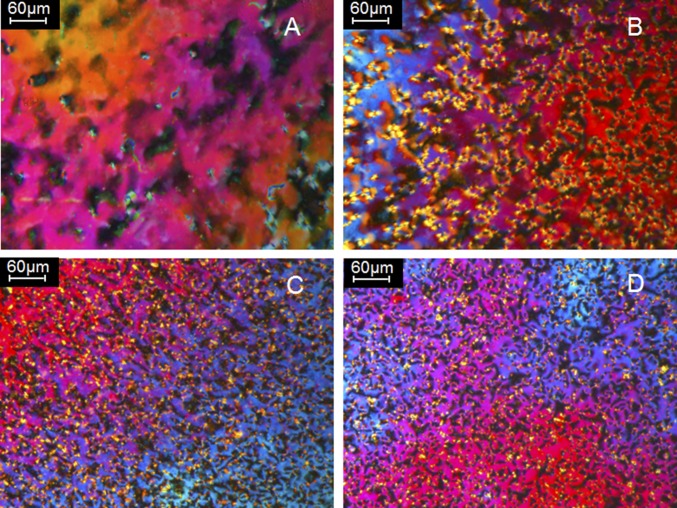
The domain size can be controlled by the concentration of the fluorinated monomer 4. The defects caused by the undissolved dispersed droplets of this monomer disturb long-range order. An increasing concentration, within the appropriate range, causes smaller domain sizes. Polarized optical microscopy images in Fig. 3 A–D show the effect of the concentration of 4 on the domain size. Large domains, on the order of 50 µm, are found at a concentration of 0.1 wt % 4 (in fact, no phase-separated areas are observed anymore at this low concentration) and smaller domains, on the order of 10 µm, at a concentration of 1.5 wt %. In our further study we keep the domain size in the range of 5–20 µm.
Fig. 3.
Polarized optical microscopy images of the polydomain textures observed between crossed polarizers as a function of the concentration of fluorinated acrylate. The concentration of fluorinated acrylate is (A) 0.1 wt %, (B) 0.5 wt %, (C) 1.0 wt %, and (D) 2.0 wt %.
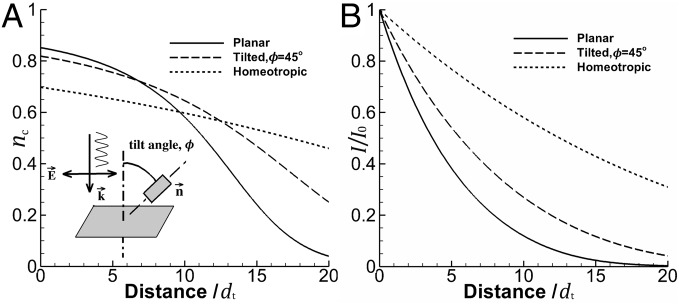
The photomechanical effect is induced by the azobenzene monomer 5 (18–24). The azobenzene unit has two isomeric states. In its elongated trans state this molecule is rod-like and complies with the orientation of the liquid crystal moieties. When the film is exposed to UV light the bent cis state of azobenzene is populated. The trans-to-cis isomerization results in a reduction of the molecular order parameter (S) and a decrease in the density of the liquid crystal network by the creation of free volume. The reduction of S results in an anisotropic deformation where molecules tend to contract along and expand perpendicular to it. Whereas the deformation is restricted in the x–y plane by the rigid substrate, both effects act simultaneously on the deformation in the z direction. Furthermore, depending on the orientation of the molecules with respect to the direction of the incoming light, the light absorption is different (for the orientations of the molecules, see the schematic representation in Fig. 2A). Using Eqs. 1–6 (Materials and Methods), we selected three representative light penetration schemes using the parameters α = 30, β = 3, η = 3, and S = 0.7. Note that these parameters are chosen for illustration purposes only; the actual parameters used in the simulations were fitted to the measured transmitted light intensities (vide infra). Fig. 4 shows the attenuation of the UV light and the changes of the fraction of cis along the light-propagating path in the photostationary state for a coating with thickness , where is the attenuation length for the azobenzene in the trans state. With light incoming along the normal z, the most pronounced absorption is found when the molecules are aligned in the x–y plane (). In contrast, the lowest absorption occurs where because the average direction of molecules is along the propagating direction of the light, so that the molecules are nearly perpendicular to the electric field vector in the electromagnetic wave and therefore absorb less energy. The result is that the trans-to-cis conversion is highest for the planar orientation near the surface, but reduces sharply at larger depths where the concentration of cis remains low. It is worth noting that even for the homeotropic case there is still generation of cis due to the order parameter S < 1 in Eq. 4 and the consequent absorption by the off-axis azobenzene moieties.
Fig. 4.
Profiles of (A) the fraction of cis molecules and (B) the reduced intensity against the light-propagating distance reduced by the attenuation length dt. The cases for planar, homeotropic, and 45° tilt angle are generated using α = 30, β = 3, η = 3, and S = 0.7.
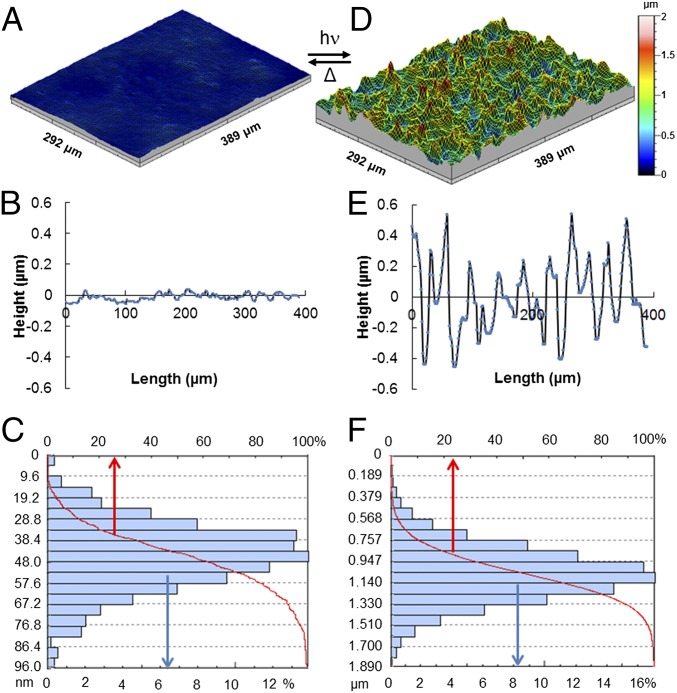
Before UV actuation of the polydomain coating, the initial coating surface was analyzed by interference microscopy. Results are shown in Fig. 5 A and B. A minor surface relief of around 40 nm is observed. This small relief is attributed to the Marangoni effect in the monomeric phase. The surface energy difference between planar and the more perpendicular aligned molecules drives the molecules to accumulate slightly in the lower surface energy regions where (25). From the distance between the maxima in this curve, one can conclude that the homeotropic domains are randomly distributed and between 10 and 100 µm apart, corresponding to the characteristics distances observed by polarization microscopy.
Fig. 5.
Interference microscope images of polydomain liquid crystal polymer surfaces. (A) Three-dimensional image of the initial flat state, (B) its surface profile, and (C) its distribution of the surface height difference Zt and the corresponding Abbott–Firestone curve. (D) Three-dimensional image of the UV activated surface topographies, (E) its surface profile relative to the average activated surface height, and (F) its distribution of the surface height difference Zt and the corresponding Abbott–Firestone curve. Arrows in the plot indicate the corresponding x axes.
The surface structure is formed immediately as the sample is subjected to UV exposure. A reference kinetic measurement is provided in SI Text (Fig. S2), showing the structure evolving within 10 s. An indirect method further validates the switching speed by measuring the change of friction of two coatings sheared against each other. As soon as the light is switched on, the surface spikes form and the dynamic friction increases within seconds. An example of the transient change in friction is shown in Fig. S3.
The surfaces activated by UV exposure are shown in Fig. 5 D and E. In this specific sample the average of the depth modulation ψ is 23%, with defined as , where is the height difference (depth) from the peak to the valley of the adjacent profile and is the initial coating thickness of 5 μm. As is obvious from Fig. 5 D and E, there is a broad distribution of ψ over the sample. The distribution histogram in Fig. 5F shows the density of the depth distribution of the entire coating surface in Fig. 5D. Various surface heights ranging from 0.4 to 1.9 µm are observed. The origin of this broad distribution is related to the distribution in over the sample. However, one should also take into account that the domains cannot behave as individual entities. They are mechanically connected to each other in a continuous polymer network. Nevertheless, the domains with are expected to be in the valleys of the surface and the domains with are expected in the top, as anticipated in Fig. 2A. The domains with adjacent to domains with are expected to form the highest tops as they benefit from the lateral forces exerted by the domains.
A standard methodology to quantify surface roughness is by using the so-called Abbott–Firestone curve (also known as bearing ratio curve) (26). In Fig. 5 C and F the upper horizontal axis relates to the cumulative probability density function of ψ derived from the height distribution histogram. In tribology the statistics around physical features of the formed profile are generally quantified by the kurtosis value as a measure of the sharpness of the profile (27, 28). The transition between a wavy surface profile and a spiky surface occurs at a value of 3. Generally, spiky surfaces will have a high kurtosis value ( > 3) and the more moderately undulating surfaces a low value ( < 3). In our sample, the kurtosis value as derived from Fig. 5C is 2.95 for the close to flat inactivated surface. In the activated surface it becomes 3.65 (Fig. 5F) as the more spiky structures are formed. This means that the coating transfers from a surface with “shallow tips” to a surface with relatively “sharp hills” when irradiated with UV light. Relaxation to the flat surface occurs also within about 10 s (Fig. S2), therefore the measurements are carried out in situ during light irradiation. For further confirmation of the surface changes we used the silicone rubber replication method by molding the activated surface structure (29). The fast restoration of the surface topography is related to the viscoelastic free-volume relaxation rather than to the cis- back to trans isomerization.
To validate the experimental results in terms of the assumed mechanistic model we simulated the polydomain structure using the methodology provided in Materials and Methods. Necessary input parameters are the dimensionless numbers α and β, the order parameter of the liquid crystal network S, the quantum efficiency ratio η, and the attenuation length for the trans state . The source light is diffuse and propagates normal to the top surface. The order parameter S is taken to be 0.7, a typical value for glassy liquid crystal polymers (30). For the ratio of quantum efficiencies η we use an estimated value of 3 from ref. 31. Now one can calculate α, β, and by comparing the calculated and measured transmitted light intensity for different source intensities. The experiments were done for a sample with a thickness of 7.7 µm, 5 wt % azobenzene, and various incoming intensities. The best-fitted model parameters were found to be α = 54.9, β = 14.3 for the illumination intensity of 600 mW⋅cm−2 and the attenuation length = 0.998 µm. Details on the fitting procedure can be found in Fig. S4 and Table S1.
For the mechanical properties, Young’s moduli were measured to be = 989 MPa and = 422 MPa. The Poisson ratio for liquid crystal glassy polymers is in the range 0.3–0.4 (30). Here we adopt = = 0.3. The shear modulus along the director direction is chosen to be equal to /(2 + 2) = 380 MPa. A group of checkerboard-style polydomain coatings was simulated using a mesh of 2,500,000 hexahedral elements and 2,761,011 nodes. The domains are simplified to have a cuboid shape with square in-plane dimensions. Various structures were constructed with a thickness of 5 µm and an in-plane domain size ranging from 2.5 to 20 µm. For each domain the director orientation is randomly chosen by picking the tilt angle ϕ and the azimuth angle θ from a uniform distribution between 0 and 180° and between 0 and 360°, respectively (Fig. S5). The values of the optomechanical coupling parameters, and , are calibrated by comparing the predicted surface profiles of the polydomain coatings with the measured data from Fig. 5E. The calibration was done by keeping their ratio = unchanged and then varying one of them. The is reported to range from 0.4 (32) to 0.7 (33). Here, we adopt = 0.6. A larger than 0.5 indicates that there is a volume increase after UV exposure for each domain due to a positive photoinduced volumetric strain = ( + 2. This corresponds to the measured density decrease of a similar freestanding liquid crystal film (29). An agreeable correlation between the predicted and measured surface profiles of a domain size of 15 µm was found for = −0.22 and = 0.13. These values were also adopted for the other domain sizes. Fig. 6 A, B, and D shows the 3D surface corrugation profile superimposed by a contour plot for the displacement along the thickness direction (in µm) for domain sizes of 5 and 15 µm. Corresponding surface profiles for these structures are shown in Fig. 6 C and E, respectively. Results for domain sizes of 2.5, 10, and 20 µm can be found in Figs. S6–S8.
Fig. 6.
Predicted activated 3D surface profiles with a contour plot for the displacement along the thickness direction uz (in micrometers) and the corresponding surface profile relative to the average activated surface height. The domain size for A–C and D and E are 5 and 15 µm, respectively.
Clearly, the coatings with small domain sizes were found to generate protrusions that are rougher and spikier compared with the coatings with larger domain sizes, which was supported by the prediction of the surface roughness (Fig. S9). Furthermore, to quantify the effect of the domain size on the surface height difference, we computed the average depth modulation (34) (Fig. S10). The reason for the decreased depth modulation with decreasing domain size is related to the increased level of constraint that the domains impose on each other. Another manifestation of the mechanical constraints was found to be present in situations where planar domains were surrounded by domains with directors close to homeotropic, leading to an enhancement of the planar domain’s surface expansion. Finally, we study the effect of the film thickness (normalized by the attenuation length on the Wenzel roughness and average depth modulation in Fig. S11. The results show a strong (linear) dependence of the depth modulation and a weak dependence of the roughness on the film thickness, as expected from dimensional arguments.
In conclusion, we have described a self-assembling design to create surface-responsive coatings based on photopolymerized nematic liquid crystal networks. By illumination with UV light, the coating undergoes a change from a flat state to a jagged state where random surface topographical textures are formed. To realize this, we formed a polydomain liquid crystal film attached to a solid substrate. The molecules are aligned only within the region of the domain but the domains alter their molecular orientation with respect to each other. The domain size is controlled by the concentration of a nonsoluble polymerizable additive. This method paves a simple and effective way to fabricate smart coatings without involving tedious lithography, external magnetic or electrical fields, or extra coating layers. The activated coatings exhibit a significant depth modulation of more than 20% with a large distribution. A finite element model was developed to predict the topographic changes of the polydomain structure as a function of the director-dependent UV absorption and trans–cis conversion, which was found to be in close agreement with the experiments. A reduction in domain size was found to lead to smaller profile height differences due to enhanced mechanical constraints. An indication of the switching speed was obtained by measuring the kinetic friction coefficient during cycling of the coating between a flat and an activated jagged state. The transition from low to high friction forces suggests a switching speed of 5 s. We anticipate the use of these dynamic surfaces with variable friction and surface area for haptic applications, e.g., to provide feedback of touch input, or in robotic manipulation controlling grip and release of objects (35).
Materials and Methods
Materials.
Fig. 1 shows the components for our reactive mixtures. Liquid crystal monomers 1–3 were obtained from Merck UK. Fluorinated monomer 4 was obtained from Sigma-Aldrich. Photoresponsive monomer 5 was custom-synthesized by Syncom (Groningen). Photoinitiator 6 was purchased from Ciba Specialty Chemicals. Typically, thin films were fabricated from a mixture containing 31.5 wt % 1, 45 wt % 2, and 15 wt % 3, 1.5 wt % 4, 5 wt % 5, 2 wt % 6. For reference measurements the concentration of compound 4 was varied while keeping the ratio of the others the same. The constituents were mixed by dissolving in dichloromethane. Differential scanning calorimetry results show that this mixture has a melting temperature of 40°C, above which it becomes nematic. Above 60°C the mixture is isotropic.
Sample Preparation.
Glass substrates are cleaned by a 5-min dip in acetone under stirring, 5 min in propanol-2 under stirring, flushed with demi water, followed by drying with a nitrogen flow. To promote the adhesion of the polymer on glass, the surface was treated using a vapor-phase reaction with Silane A-174 (methacryloxypropyltrimethoxysilane; Sigma-Aldrich). A 33 wt % concentration of monomer mixture dissolved in dichloromethane is spin-coated on the glass plates. Spin-coating conditions are speed 1,500 rpm, acceleration 50 rpm⋅s−1, and duration 20 s. After evaporation of the solvent the mixture is still in its monotropic (supercooled) nematic state at room temperature. The sample was cured at 36 °C by UV exposure for 5 min with an intensity of 400 mW⋅cm−2 in N2 atmosphere using a mercury lamp (Exfo Omnicure S2000) equipped with a cutoff filter transmitting light >400 nm (Newport FSQ-GG400 filter). The samples were postbaked at 120 °C under N2 to ensure full conversion of the acrylate monomers. By UV-VIS we checked that the azobenzene has kept its trans configuration (Fig. S12). The thickness of the final polymer coating is 5 µm.
Sample Characterization.
The polydomain liquid crystal film is checked by polarized microscopy (Leica). The formation of topographical surface elements is actuated by a 30-min exposure to a mercury lamp (Exfo; intensity 600 mW⋅cm−2). The sample is overexposed to reach its final structure but the time was chosen to allow sufficient time for manipulation during further experiments while being sure that equilibrium was reached. The surface topography is measured using interference microscopy (Fogal Nanotech Zoomsurf). The profile of the water droplet on the liquid crystal coatings is measured by a contact angle device (Dataphysics OCA-20). Surface friction is measured by sliding two liquid crystal coating surfaces against each other in the activated and inactivated state. The home-built measuring system has been published before (16). The modulus is tested by a dynamic mechanical analysis tool from TA Instruments (DMA Q800).
Modeling.
In light-induced actuation of liquid crystal polymers, the orientation of the director vector plays a key role in (i) the director-dependent absorption of light, and in (ii) the generation of director-aligned anisotropic deformation. To study these effects for polydomain liquid crystal coatings, we have developed a finite element model to predict the changes in 3D surface topography as a result of the director-dependent attenuation of UV light. It is assumed that the magnitude of the optomechanical effect is linearly proportional to the fraction of cis, (36). The coefficients of the photoinduced strain tensor with respect to the local coordinate system read
with the local axis aligned with the director . With respect to this local reference frame, the liquid crystal polymer is assumed to be transversely isotropic with the rotational symmetry axis pointing along the director. The components of the photoresponsivity tensor are given by
with referring to the contraction along the director and to the expansion in the plane perpendicular to it. The constitutive relation of the material reads
where are the components of the elastic stiffness tensor, the components of the elastic strain tensor, and those of the total strain tensor. There are five independent mechanical properties for a transversely isotropic material, namely Young’s modulus parallel to the director , its perpendicular counterpart , the Poisson ratio corresponding to a contraction perpendicular to when an extension is applied along , its counterpart in the isotropic plane , and the shear modulus parallel to the director . After the UV actuation, the different director orientations in neighboring domains lead to a mismatch between the local deformations. Additionally, the constraint from the substrate suppresses the in-plane deformation of the coating. Thus, internal stresses are generated due to these effects so that the final topography is a result of the superposition of the photoinduced and elastic (mismatch) strains.
To calculate the fraction of cis isomers after UV illumination, the nonlinear light absorption model proposed by Corbett and Warner (37) was adopted. Director-dependent absorption was introduced by using a polarization coefficient ζ (38).The coupled equations describing the evolution of the reduced intensity, defined as the local light intensity divided by that of the source light = , and the fraction of trans, and cis, , are given by
| [1] |
| [2] |
where the origin of the z axis is located at the bottom of the coating (at the substrate) and its positive direction points upward toward the light source. Two dimensionless parameters α and β are used to measure the level of incident intensity and τ is the average lifetime of the cis molecules.
The isomerization process consists of three contributions: light-induced trans-to-cis forward reaction, light-induced cis-to-trans back-reaction, and thermally activated back-reaction with a rate of 1/τ. The and are the attenuation lengths for trans and cis, respectively. They are related to the ratio between the quantum efficiencies of trans and cis η by
| [3] |
The parameter ζ is the polarization coefficient for diffuse light illumination (38)
| [4] |
where is the second Legendre polynomial and S is the order parameter of the liquid crystal polymer. The ϕ is the angle between the director and the propagating direction . The incorporation of the polarization coefficient ζ enables us to take into account the difference in light attenuation between domains with different director alignments. We assume the director in each domain will remain unchanged through the thickness, leading to a constant ζ per domain.
One can obtain the time-evolution history of and by solving the nonlinear coupled differential Eqs. 1 and 2 subjected to the boundary conditions at the top surface of the coating and = 1 at . In this paper, we only account for the photostationary state, i.e., the state in which the forward-reaction rate equals the sum of the two back-reactions. The values for the trans and cis fractions at the photostationary state can be obtained by equating the right-hand side of Eq. 1 to zero, resulting in
| [5] |
By substituting Eq. 5 into [2], the reduced intensity through the thickness is given by the nonlinear equation (37):
| [6] |
One can solve Eq. 6 to find the depth profile of the reduced intensity and then substitute it into Eq. 5 to obtain the fraction of trans and cis through the thickness.
Supplementary Material
Acknowledgments
The results presented are part of a research program financed by the Dutch Polymer Institute, Project 775.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. P.P.-M. is a guest editor invited by the Editorial Board.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1419312112/-/DCSupplemental.
References
- 1.Trujillo V, Kim J, Hayward RC. Creasing instability of surface-attached hydrogels. Soft Matter. 2008;4(3):564–569. doi: 10.1039/b713263h. [DOI] [PubMed] [Google Scholar]
- 2.Edmondson S, Frieda K, Comrie JE, Onck PR, Huck WTS. Buckling in quasi-2D polymers. Adv Mater. 2006;18(6):724–728. [Google Scholar]
- 3.Hermans K, et al. Highly efficient surface relief formation via photoembossing of a supramolecular polymer. Macromol Chem Phys. 2008;209(20):2094–2099. [Google Scholar]
- 4.Meijer HEH, Singh MK, Kang TG, Den Toonder JMJ, Anderson PD. Passive and active mixing in microfluidic devices. Macromol Symp. 2009;279(1):201–209. [Google Scholar]
- 5.Dong L, Agarwal AK, Beebe DJ, Jiang H. Adaptive liquid microlenses activated by stimuli-responsive hydrogels. Nature. 2006;442(7102):551–554. doi: 10.1038/nature05024. [DOI] [PubMed] [Google Scholar]
- 6.Onda T, Shibuichi S, Satoh N, Tsujii K. Super-water-repellent fractal surfaces. Langmuir. 1996;12(9):2125–2127. [Google Scholar]
- 7.Ibn-Elhaj M, Schadt M. Optical polymer thin films with isotropic and anisotropic nano-corrugated surface topologies. Nature. 2001;410(6830):796–799. doi: 10.1038/35071039. [DOI] [PubMed] [Google Scholar]
- 8.Schift H, et al. Surface structuring of textile fibers using roll embossing. J.Microelectron Eng. 2006;83(4-9):855–858. [Google Scholar]
- 9.de Jong TM, de Boer DKG, Bastiaansen CWM. Surface-relief and polarization gratings for solar concentrators. Opt Express. 2011;19(16):15127–15142. doi: 10.1364/OE.19.015127. [DOI] [PubMed] [Google Scholar]
- 10.Pettersson U, Jacobson S. Textured surfaces for improved lubrication at high pressure and lowsliding speed of roller/piston in hydraulic motors. Tribol Int. 2007;40(2):355–359. [Google Scholar]
- 11.Wakuda M, Yamauchi Y, Kanzaki S, Yasuda Y. Effect of surface texturing on friction reduction between ceramic and steel materials under lubricated sliding contact. Wear. 2003;254(3-4):356–363. [Google Scholar]
- 12.Mavoidis C, Pfeiffer C, Celestino J, Bar-Cohen Y. 2000. Controlled compliance haptic interface using electro-rheological fluids. 26th Biennial Mechanisms and Robotics Conference, ed Kazerounian KSM (American Society of Mechanical Engineers, Pennsylvania State University, State College, PA), 3987(40):300–310.
- 13.Sailer M, Fernández R, Lu X, Barrett CJ. High levels of molecular orientation of surface azo chromophores can be optically induced even in a wet biological environment. Phys Chem Chem Phys. 2013;15(46):19985–19989. doi: 10.1039/c3cp52873a. [DOI] [PubMed] [Google Scholar]
- 14.Kumar J, et al. Photoinduced fabrication of complex surface relief structures on azobenzene functionalized polymers. Bull Mater Sci. 1999;22(3):443–445. [Google Scholar]
- 15.Liu D, Bastiaansen CWM, den Toonder JMJ, Broer DJ. Photo-switchable surface topologies in chiral nematic coatings. Angew Chem Int Ed Engl. 2012;51(4):892–896. doi: 10.1002/anie.201105101. [DOI] [PubMed] [Google Scholar]
- 16.Liu D, Broer DJ. Self-assembled dynamic 3D fingerprints in liquid-crystal coatings towards controllable friction and adhesion. Angew Chem Int Ed Engl. 2014;53(18):4542–4546. doi: 10.1002/anie.201400370. [DOI] [PubMed] [Google Scholar]
- 17.Jakli A, Saupe A. One- and Two-Dimensional Fluids: Properties of Smectic, Lamellar and Columnar Liquid Crystals. CRC Press, Taylor and Francis Group; Boca Raton, FL: 2006. p. 175. [Google Scholar]
- 18.Yu HF, Dong C, Zhou W, Kobayasi T, Yang H. Wrinkled liquid-crystalline microparticle-enhanced photoresponse of PDLC-like films by coupling with mechanical stretching. Small. 2011;7(21):3039–3045. doi: 10.1002/smll.201101098. [DOI] [PubMed] [Google Scholar]
- 19.Camacho-Lopez M, Finkelmann H, Palffy-Muhoray P, Shelley M. Fast liquid-crystal elastomer swims into the dark. Nat Mater. 2004;3(5):307–310. doi: 10.1038/nmat1118. [DOI] [PubMed] [Google Scholar]
- 20.White TJ, Serak SV, Tabiryan NV, Vaia RA, Bunning TJ. Polarization-controlled, photodriven bending in monodomain liquid crystal elastomer cantilevers. J Mater Chem. 2009;19(8):1080–1085. [Google Scholar]
- 21.Yu Y, Nakano M, Ikeda T. Photomechanics: Directed bending of a polymer film by light. Nature. 2003;425(6954):145–145. doi: 10.1038/425145a. [DOI] [PubMed] [Google Scholar]
- 22.Kosa T, et al. Light-induced liquid crystallinity. Nature. 2012;485(7398):347–349. doi: 10.1038/nature11122. [DOI] [PubMed] [Google Scholar]
- 23.van Oosten CL, Bastiaansen CWM, Broer DJ. Printed artificial cilia from liquid-crystal network actuators modularly driven by light. Nat Mater. 2009;8(8):677–682. doi: 10.1038/nmat2487. [DOI] [PubMed] [Google Scholar]
- 24.Finkelmann H, Nishikawa E, Pereira GG, Warner M. A new opto-mechanical effect in solids. Phys. Rev. Lett. 2001;87(1):015501–015501-4. doi: 10.1103/PhysRevLett.87.015501. [DOI] [PubMed] [Google Scholar]
- 25.Eelkema R, et al. Molecular machines: Nanomotor rotates microscale objects. Nature. 2006;440(7081):163–163. doi: 10.1038/440163a. [DOI] [PubMed] [Google Scholar]
- 26.Abbott EJ, Firestone FA. Specifying surface quality: A method based on accurate measurement and comparison. Mech Eng. 1933;55:569–572. [Google Scholar]
- 27.Bhushan B. In: Modern Tribology Handbook. Bhushan B, editor. CRC Press, Taylor and Francis Group; Boca Raton, FL: 2000. pp. 49–114. [Google Scholar]
- 28.Davim JP. Surface Integrity in Machining. Springer; London: 2010. pp. 37–66. [Google Scholar]
- 29.Liu D, Bastiaansen CWM, Den Toonder JMJ, Broer DJ. Light-induced formation of dynamic and permanent surface topologies in chiral–nematic polymer networks. Macromolecules. 2012;45(19):8005–8012. [Google Scholar]
- 30.Heynderickx I, Broer DJ, Van Den Boom H, Teesselink WJD. Liquid-crystalline ordering in polymeric networks as studied by polarized Raman scattering. J Polym Sci Part B: Polym Phys. 1992;30(2):215–220. [Google Scholar]
- 31.Yager KG, Barrett CJ. In: Azobenzene Polymers for Photonic Applications. Smart Light-Responsive Materials: Azobenzene-Containing Polymers and Liquid Crystals. Yue Z, Ikeda T, editors. John Wiley & Sons, Inc.; Hoboken, NJ: 2009. pp. 1–27. [Google Scholar]
- 32.van Oosten CL, Harris KD, Bastiaansen CWM, Broer DJ. Glassy photomechanical liquid-crystal network actuators for microscale devices. Eur Phys J E Soft Matter. 2007;23(3):329–336. doi: 10.1140/epje/i2007-10196-1. [DOI] [PubMed] [Google Scholar]
- 33.Smith ML, Lee KM, White TJ, Vaia RA. Design of polarization-dependent, flexural-torsional deformation in photo responsive liquid crystalline polymer networks. Soft Matter. 2014;10(9):1400–1410. doi: 10.1039/c3sm51865e. [DOI] [PubMed] [Google Scholar]
- 34.Gadelmawla ES, Koura MM, Maksoud TMA, Elewa IM, Soliman HH. Roughness parameters. J Mater Process Technol. 2002;123(1):133–145. [Google Scholar]
- 35.Bar-Cohen Y. Nature as a model for mimicking and inspiration of new technologies. International Journal of Aeronautical and Space sciences. 2012;13(1):1–13. [Google Scholar]
- 36.Van Oosten CL, et al. Bending dynamics and directionality reversal in liquid crystal network photoactuators. Macromolecules. 2008;41(22):8592–8596. [Google Scholar]
- 37.Corbett D, Warner M. Bleaching and stimulated recovery of dyes and of photocantilevers. Phys Rev E Stat Nonlin Soft Matter Phys. 2008;77(5 Pt 1):051710–051721. doi: 10.1103/PhysRevE.77.051710. [DOI] [PubMed] [Google Scholar]
- 38.Corbett D, Warner M. Polarization dependence of optically driven polydomain elastomer mechanics. Phys Rev E Stat Nonlin Soft Matter Phys. 2008;78(6 Pt 1):061701–061714. doi: 10.1103/PhysRevE.78.061701. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.