Gait and speed selection in slender inertial swimmers

Significance

Swimming relies on linking internal neural dynamics to body mechanics and environmental hydrodynamics. To characterize this in an integrative setting we present a minimal theoretical framework that synthesizes the roles of passive body elasticity, hydrodynamics, muscular activation, and proprioceptive sensory feedback in inertial swimmers. Our findings quantitatively explain a range of classic experimental observations linking gait and speed in a range of swimming fish. Our calculations also yield a mechanism for how elastohydrodynamic resonances lead to optimal gait selection. Finally, we show that a self-organized propulsive gait can be achieved via a proprioceptive mechanism wherein local muscle activation is driven by shape change, without the need for a central pattern generator, suggestive of ways to engineer robotic swimmers.

Abstract

Inertial swimmers use flexural movements to push water and generate thrust. We quantify this dynamical process for a slender body in a fluid by accounting for passive elasticity and hydrodynamics and active muscular force generation and proprioception. Our coupled elastohydrodynamic model takes the form of a nonlinear eigenvalue problem for the swimming speed and locomotion gait. The solution of this problem shows that swimmers use quantized resonant interactions with the fluid environment to enhance speed and efficiency. Thus, a fish is like an optimized diode that converts a prescribed alternating transverse motion to forward motion. Our results also allow for a broad comparative view of swimming locomotion and provide a mechanistic basis for the empirical relation linking the swimmer’s speed U, length L, and tail beat frequency f, given by $U/L\sim f$ [Bainbridge R (1958) J Exp Biol 35:109–133]. Furthermore, we show that a simple form of proprioceptive sensory feedback, wherein local muscle activation is function of body curvature, suffices to drive elastic instabilities associated with thrust production and leads to a spontaneous swimming gait without the need for a central pattern generator. Taken together, our results provide a simple mechanistic view of swimming consistent with natural observations and suggest ways to engineer artificial swimmers for optimal performance.

Understanding locomotory behavior requires that we integrate the neural control of muscular dynamics with the body mechanics of the organism as it interacts with the environment. Simultaneously, we must also account for sensory feedback from the environment and from the organism’s sense of its own shape. However, translating these concepts to quantitative theories is challenging because of the variety of organism sizes and shapes and the complexity of their physical and biological environment. Therefore, investigations typically focus on specific organisms and try to glean principles that might be of broader relevance. In the context of terrestrial locomotion, recent experimental and theoretical work on the undulating worm Caenorhabditis elegans (1) shows that proprioceptive feedback suffices to coordinate undulatory motions. Complementing these studies, general theoretical models have explored the conditions under which coordinated crawling occurs in a coupled brain–body–environment system (2). These models explain observations in larvae of Drosophila melanogaster, showing how a sensorimotor coupling that links brain, body, and environment can robustly lead to crawling in a range of conditions.

Translating these ideas to macroscopic aquatic locomotion, when inertia dominates viscous forces, is a formidable challenge owing to the presence of complex hydrodynamic nonlinearities, which must be coupled to body mechanics and neural dynamics of proprioceptive and sensory feedback. The hydrodynamics of swimming has been the subject of a variety of studies for more than half a century from experimental (3–6), theoretical (7–11), and computational (12–19) perspectives. Recently there has been growing interest in integrating these physical approaches with neurobiological models using coupled neuromechanical simulations (20) and biomimetic devices (21, 22) to study developmental and evolutionary aspects of the problem. Indeed, when a dead fish is dragged through water it flutters and moves in a manner reminiscent of a live, swimming fish (23). Similarly, a passive flexible foil whose tip is subject to oscillations can generate thrust (11, 22). These observations suggest that the nervous system can work in close conjunction with and profits from elastohydrodynamic effects. Locomotion then emerges via a continuous interaction between embodiment and environment orchestrated by sensory feedback (21, 24). However, the role of proprioception, the body’s sense of self, is typically not accounted for in these studies, leaving open the two-way coupling that links neural dynamics to muscular movements to changes in body shape, which in turn modulates neural dynamics.

Here we build on a classic theory for inertial locomotion of a slender body (9, 10) by accounting for body elasticity, hydrodynamics and viscous boundary layer effects, muscle activity, and proprioceptive feedback. Our model complements previous large-scale simulations of these dynamical processes in a simple setting that allows for a transparent view of the various mechanisms at play and links the average swimming velocity to body deformations as solution of a nonlinear eigenvalue problem. Our results show that elastohydrodynamic resonances yield a mechanism for optimal gait selection. Furthermore, our theory quantitatively agrees with experimental data for swimming fish (3) and provides a theoretical basis for the empirical relation $U/L\sim f$. Finally, we show that a minimal proprioceptive feedback loop based on local body curvature is sufficient to trigger and maintain undulatory swimming, leading to a self-organized gait and speed.

Mathematical Model

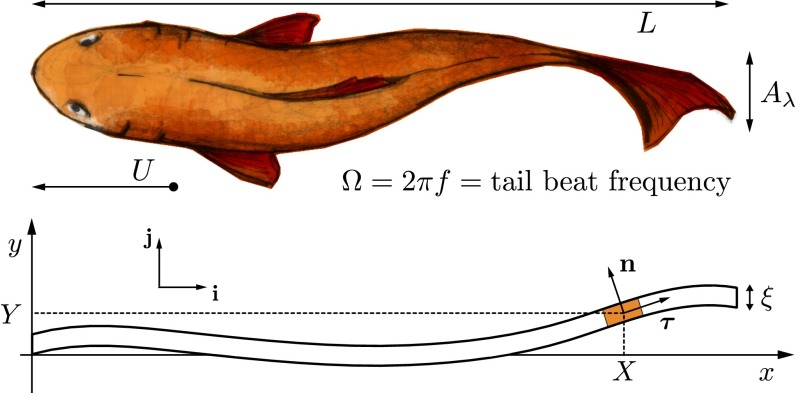
For simplicity, we focus on 2D swimming gaits, neglecting 3D effects, an approximation that is effective in characterizing many of the salient aspects of aquatic locomotion (15, 25). We model the fish as a neutrally buoyant, slender elastic sheet of density ${\rho }_s$, length L, and thickness $\mathit{\xi }$, characterized by a small aspect ratio $L\gg \mathit{\xi }$. We assume that the filament is aligned with the x direction and moving in the negative x region with velocity U (Fig. 1). Muscle-driven transverse undulations of the body in the y direction induce locomotion by generating reactive forces associated with the inertial acceleration of fluid.

Fig. 1.

Schematic showing the notation used in a moving frame of reference: A thin sheet of thickness $\mathit{\xi }$ and length L moves with velocity U in the negative x direction, through undulatory motions characterized by tail beat amplitude $A_{\lambda }$ (in dimensionless notation $\lambda =A_{\lambda }/L$). Unit vectors are denoted by $\mathbf{i}$ and $\mathbf{j}$.

Equations of Motion.

We denote an infinitesimal element of the fish by $\mathbf{R}\left(x,t\right)=X\left(x,t\right)\mathbf{i}+Y\left(x,t\right)\mathbf{j}$ with respect to a coordinate frame moving with the fish speed U. Assuming small deformations of the slender body so that ${\partial }_{x}Y\ll 1$, and ${\partial }_{x}X=1+O{\left({\partial }_{x}Y\right)}^2$, we may use Cartesian rather than arc-length-based coordinates to write down the equations of motion for the fish. Then, the momentum balance reads

$${\mathit{\rho }}_s\mathit{\xi }\left({\partial }_t^2\mathbf{R}-{\partial }_{t}U\mathbf{i}\right)={\partial }_x\left(T\mathit{\tau }+N\mathbf{n}\right)+\mathrm{\Delta }P\mathbf{n}+\sigma \mathit{\tau }.$$ [1]

Here the first term of the right-hand side represents the local divergence of the internal stresses, with $T\mathit{\tau }$ being the tangential stress resultant along $\mathit{\tau }={\partial }_{x}X\mathbf{i}+{\partial }_{x}Y\mathbf{j}$ and $N\mathbf{n}$ being the normal stress resultant along $\mathbf{n}=-{\partial }_{x}Y\mathbf{i}+{\partial }_{x}X\mathbf{j}$ at a transversal section of the fish. The second term on the right-hand side represents the pressure difference $\mathrm{\Delta }P$ across the body of the fish and the third term corresponds to the tangential shear stress $\mathit{\sigma }$ associated with moving through a viscous fluid.

We project Eq. 1 into the horizontal and vertical direction, retaining terms to second order

$${\rho }_s\xi {\partial }_{t}U={\partial }_x\left(N{\partial }_{x}Y-T\right)+\mathrm{\Delta }P{\partial }_{x}Y-\sigma$$ [2]

$${\rho }_s\xi {\partial }_t^{2}Y={\partial }_x\left(T{\partial }_{x}Y+N\right)+\mathrm{\Delta }P+\mathit{\sigma }{\partial }_{x}Y.$$ [3]

Because the plate is slightly deflected, U is almost uniform, and we can spatially average the horizontal velocity so that Eq. 2 becomes

$${\rho }_s\xi {\partial }_{t}U=\frac{1}{L}{\displaystyle \underset{0}{\overset{L}{\int }}\left(\mathrm{\Delta }P{\partial }_{x}Y-\sigma \right)dx,}$$ [4]

where tension ${T|}_{x=0,L}=0$ and normal forces ${N|}_{x=0,L}=0$ because the ends of the fish are free.

To close this system, we need to prescribe expressions for the internal stresses owing to passive elasticity, active muscular forces, hydrodynamic reactions from the fluid in the normal and tangential directions, and proprioceptive sensory feedback that links body shape to active force generation.

Passive Elasticity, Muscular Activity, and Proprioception.

The dependence of the internal stress resultants T and N on the elastic properties of the material that constitutes the fish follows from balancing the torque M on an infinitesimal section of the sheet (26). Ignoring the effects of rotatory inertia (an assumption that we can justify a posteriori) yields

$$N=-{\partial }_{x}M.$$ [5]

For slender bodies, the internal moment M may be additively decomposed (10) into the sum of a linear elastic response $M_e$, a viscous response $M_v$, owing to the hydrated flesh of the fish, an active torque $M_a$, generated by muscular activity (27), and a proprioceptive feedback torque $M_f$:

$$M=M_e+M_v+M_a+M_f.$$ [6]

For small deformations, the elastic torque is proportional to the body curvature approximated by ${\partial }_x^{2}Y$, so that (26)

$$M_e=B{\partial }_x^{2}Y\left(x,t\right),$$ [7]

where $B\left(x\right)=EI\left(x\right)$ is the local bending stiffness characterized by Young’s modulus E and second moment of inertia $I\left(x\right)$. The functional form of $B\left(x\right)$ is chosen here to fit the experimental measurements reported in (6) (Supporting Information). We assume that the active torque $M_a$ compensates for the viscous torque $M_v$ and further that the internal viscous losses are small compared with the external frictional losses, and so we neglect it. We approximate the active torque using the traveling wave form (28)

$$M_a=A\sin \left(\mathrm{\Omega }t-Qx\right)F\left(x\right),$$ [8]

where A is the amplitude, $\mathrm{\Omega }$ is the active angular frequency, Q the wavenumber, and $F\left(x\right)$ is a function determining the swimming pattern (anguilliform, carangiform, etc). We set $F\left(x\right)$ to be proportional to the bending stiffness (Supporting Information), motivated by the fact that $B\left(x\right)$ is related to the body thickness, and therefore to the muscle volume and torque. Eq. 8 is tantamount to assuming that a central pattern generator is responsible for the initiation and maintenance of a wave of muscular activity (17).

Although we will use a traveling wave of active torque for part of our study of self-propelled swimming, this approach is not altogether satisfactory, because it does not provide any insight on the mechanisms that lead to such a wave. Alternatively, muscular torques may be related to an excitatory and inhibitory neural network driven by the proprioception of the fish shape. This is biologically motivated by the fact that body deformations are detected by stretch receptor neurons in organisms such as lampreys and variations in curvature have been found to affect muscular activity (29). It is also not an accident that from a mathematical perspective curvature is naturally invariant with respect to translation and rotation of the midline of the fish. Therefore, here the proprioceptive feedback torque is given by

$$M_f=\mathcal{X}{\partial }_x^{2}Y\left(x,t-\mathrm{\Delta }\right),$$ [9]

where $\mathcal{X}$ is the strength of the response to the stimulus ${\partial }_x^{2}Y$ and $\mathrm{\Delta }$ is a temporal delay that effectively accounts for the temporal dynamics of the excitatory–inhibitory neural network underlying proprioception (29).

For a self-propelled swimmer the extremities are free of forces and torques. This implies that ${M|}_{x=0,L}=0$ and ${{\partial }_{x}M|}_{x=0,L}=0$. Because the bending stiffness vanishes at the smooth tips, this is automatically satisfied, but in general we enforce these conditions by independently setting ${M_e|}_{x=0,L}=0$, ${M_a|}_{x=0,L}=0$, ${M_f|}_{x=0,L}=0$, ${{\partial }_x{M}_e|}_{x=0,L}=0$, ${{\partial }_x{M}_a|}_{x=0,L}=0$, ${{\partial }_x{M}_f|}_{x=0,L}=0$ so that

$${{\partial }_x^{2}Y|}_{x=0,L}={{\partial }_x^{3}Y|}_{x=0,L}=0.$$ [10]

Finally, to determine T we project Eq. 1 in the x direction and note that the fish can be regarded as an inextensible sheet, therefore subject to the condition ${\left({\partial }_x\mathbf{R}\right)}^2=1$. Differentiating this relation with respect to time twice, and using Eq. 1, at leading order, this yields

$$T=\frac{x}{L}{\displaystyle \underset{0}{\overset{L}{\int }}\sigma dx}-{\displaystyle \underset{0}{\overset{x}{\int }}\sigma dx}.$$ [11]

Hydrodynamic Drag and Thrust.

To compute the tangential and normal stresses $\mathit{\sigma }$ and $\mathrm{\Delta }P$ induced by the flow, we note that at high Reynolds numbers $\left(Re=UL/\mathit{\nu }\gg 1\right)$ the viscous shear is confined to a thin boundary layer around the body. For small deformations and slopes of the midline, the wall shear stress along the fish may be approximated by the Blasius boundary layer over a flat plate (30):

$$\sigma =2\mathit{ϵ}{\rho }_f\sqrt{\frac{\nu U^3}{x}},$$ [12]

where ${\rho }_f$ and $\mathit{\nu }$ are, respectively, the fluid density and kinematic viscosity, $\mathit{ϵ}=0.332$ is a dimensionless constant, and we have accounted for a boundary layer on each side. Substituting this result into Eq. 11 yields the tension

$$T=4\mathit{ϵ}{\rho }_f\sqrt{\frac{\nu U^3}{L}}\left(x-\sqrt{xL}\right).$$ [13]

The pressure difference $\mathrm{\Delta }P$ is dominated by effectively irrotational and inviscid flow away from the boundary layer. If we further assume that the longitudinal velocity along the fish is slowly varying, following refs. 31 and 32 we can write

$$\mathrm{\Delta }P=-{\rho }_{f}UC\left[\gamma \right]k\left(s\right)\left({\partial }_{t}Y+U{\partial }_{x}Y\right)-L{\rho }_{f}n\left(s\right){\partial }_t^{2}Y,$$ [14]

with $s=x/L$, and $k\left(s\right)=2\sqrt{\left(1-s\right)/s}$ and $n\left(s\right)=2\sqrt{\left(1-s\right)s}$ are dimensionless functions, and $C\left[\mathit{\gamma }\right]$ is the Theodorsen functional (31, 33) that quantifies the unsteadiness of the flow. Indeed, this function captures the effects of an oscillatory trailing vortex sheet on the hydrodynamic loads acting on a flat plate, as a function of the reduced frequency $\mathit{\gamma }$ of the wake. In the case of steady flow $\gamma \to 0$ and $C\left[\gamma \right]\to 1$. Here, for simplicity we set $C\left[\gamma \right]=1$, noting that a more accurate calculation would slightly change the results quantitatively, but not qualitatively (32). In Eq. 14 each of the three terms has a simple meaning: the first corresponds to an effective damping term proportional to the local transverse velocity ${\partial }_{t}Y$, owing to the exchange of momentum with the flow, the second corresponds to a lift or resistive force term proportional to the local slope ${\partial }_{x}Y$ and that scales as ${\rho }_f{U}^2$, and the third corresponds to an added mass term that is proportional to the body acceleration ${\partial }_t^{2}Y$ and the fluid density.

Our complete model consists of Eqs. 3 and 4 subject to the boundary conditions (Eq. 10) and some initial conditions. This allows us to transparently see the role of namely passive elasticity (Eq. 7), muscular activity coordinated via the central pattern generator (Eq. 8), proprioceptive sensimotor feedback (Eq. 9), and both viscous (Eqs. 12 and 13) and inertial (Eq. 14) hydrodynamic effects.

Analysis and Results.

To make the system of equations dimensionless, we scale all lengths by the fish length L and the velocity by the slowest bending wave of wavelength $2\pi L$, such that $U_b=\sqrt{\overline{B}/\left({\rho }_s\xi L^2\right)}$, where $\overline{B}$ is the average bending stiffness of the fish. We define the scaled length $s=x/L$, vertical displacement $h=Y/L$, time $\tau =U_{b}t/L$, and velocity $u=U/U_b$. Furthermore, by defining $\rho ={\rho }_{f}L/\left({\rho }_s\xi \right)$, the bending Reynolds number $R{e}^b={\left(16{\mathit{ϵ}}^2\right)}^{-1}\left(L{U}_b/\nu \right)$ with $\mathit{ϵ}=0.332$ as in Eq. 12, the scaled bending stiffness $b=B/\overline{B}$, active torque $m_a=M_{a}L/\overline{B}$, and proprioceptive torque $m_f=M_{f}L/\overline{B}$, we can write the dimensionless form of Eqs. 3 and 4 as

$${\partial }_{\tau }u=-\rho C\left[\gamma \right]\left(u^2{I}_1+u{I}_2\right)-\rho I_3-\frac{1}{\sqrt{R{e}^b}}\rho u^{3/2}$$ [15]

$$\left(1+\rho n\left(s\right)\right){\partial }_{\tau }^{2}h=-\rho ukC\left[\gamma \right]\left({\partial }_{\tau }h+u{\partial }_{s}h\right)-{\partial }_s^2\left(b\left(s\right){\partial }_s^{2}h+m_a+m_f\right)+\frac{1}{\sqrt{R{e}^b}}\rho u^{3/2}\left({\partial }_{s}h+\left(s-\sqrt{s}\right){\partial }_s^{2}h\right),$$ [16]

where

$$I_1={\displaystyle \underset{0}{\overset{1}{\int }}{\left({\partial }_{s}h\right)}^{2}k\left(s\right)ds,I_2}={\displaystyle \underset{0}{\overset{1}{\int }}k\left(s\right){\partial }_{s}h{\partial }_{\tau }hds,I_3}={\displaystyle \underset{0}{\overset{1}{\int }}n\left(s\right){\partial }_{s}h{\partial }_{\tau }^{2}hds}.$$ [17]

The integral $I_1>0$ is the pressure drag, the integral $I_2$ is the damping term, and $I_3$ corresponds to the added mass effect and is primarily responsible for the generation of thrust. This allows us to see how active (or proprioceptive) torque in Eq. 16 induces lateral undulations that generate thrust through the integrals $I_1$, $I_2$, and $I_3$ as long as their weighted sum is negative and large enough to counterbalance the viscous shear due to the boundary layer, as detailed in Eq. 15.

Active Swimming Without Proprioception.

We first consider the case of active swimming when the central pattern generator is fully responsible for driving and maintaining a traveling wave of muscle torque without proprioception (i.e., $m_f=0$). At steady state, swimming velocity u is a constant. Furthermore, the transverse oscillations governed by h respond with one temporal frequency that is slaved to the driving torque $m_a$ at leading order. Therefore, we can separate temporal and spatial variables by studying solutions of the form $h\left(s,\tau \right)=e^{i\omega \tau }\eta \left(s\right)+c.c.$, where $\omega =\mathrm{\Omega }L/U_b$ is the dimensionless active angular frequency, $\eta \left(s\right)=\theta \left(s\right)+i\varphi \left(s\right)$ is a complex variable, and the complex conjugate $c.c.$ ensures that h is real at all times. Substituting the above definition of h into Eqs. 15–17 we obtain a nonlinear eigenvalue problem for the velocity u and the gait $h\left(s,\tau \right)$ of the fish that reads, in complex notation,

$$\begin{array}{c}\frac{1}{\sqrt{R{e}^b}}\rho u^{3/2}=-2k\left(s\right)C\left[\gamma \right]\rho u^2{\displaystyle \underset{0}{\overset{1}{\int }}\left[{\left({\partial }_s\theta \right)}^2+{\left({\partial }_s\varphi \right)}^2\right]ds}\\ -2k\left(s\right)C\left[\gamma \right]\rho \omega u{\displaystyle \underset{0}{\overset{1}{\int }}\left({\partial }_s\varphi \theta -{\partial }_s\theta \varphi \right)ds}\\ +2n\left(s\right)\rho {\omega }^2{\displaystyle \underset{0}{\overset{1}{\int }}\left(\theta {\partial }_s\theta +\varphi {\partial }_s\varphi \right)ds}\end{array}$$ [18]

$$\begin{array}{c}-{\omega }^2\left(1+n\left(s\right)\rho \right)\eta =-\rho k\left(s\right)C\left[\gamma \right]u\left(i\omega \eta +u{\partial }_s\eta \right)\\ -{\partial }_s^2\left(b\left(s\right){\partial }_s^2\eta -\frac{a}{2i}F\left(s\right)e^{-iqs}\right)\\ +\frac{1}{\sqrt{R{e}^b}}\rho u^{3/2}\left(-{\partial }_s\eta +\left(\sqrt{s}-s\right){\partial }_s^2\eta \right),\end{array}$$ [19]

where $q=QL$ and $a=AL/\overline{B}$ are, respectively, the dimensionless wavenumber and amplitude. Because the fish is free of forces and torques at its ends, the system of eight ordinary differential equations (ODEs) embodied in Eq. 19 must be accompanied by some boundary conditions that are given by ${\partial }_s^2\eta \left(\mathrm{0,1}\right)=0$ and ${\partial }_s^3\eta \left(\mathrm{0,1}\right)=0$ (see Eq. 10) and the integral constraint Eq. 18. We solve this problem using the continuation algorithm AUTO (34) to determine the dependence of the scaled speed u and gait $h\left(s,\tau \right)$ of the fish as a function of the bending Reynolds number $R{e}^b$, as well as the wavenumber q and frequency $\mathit{\omega }$ of the driving torque $m_a$.

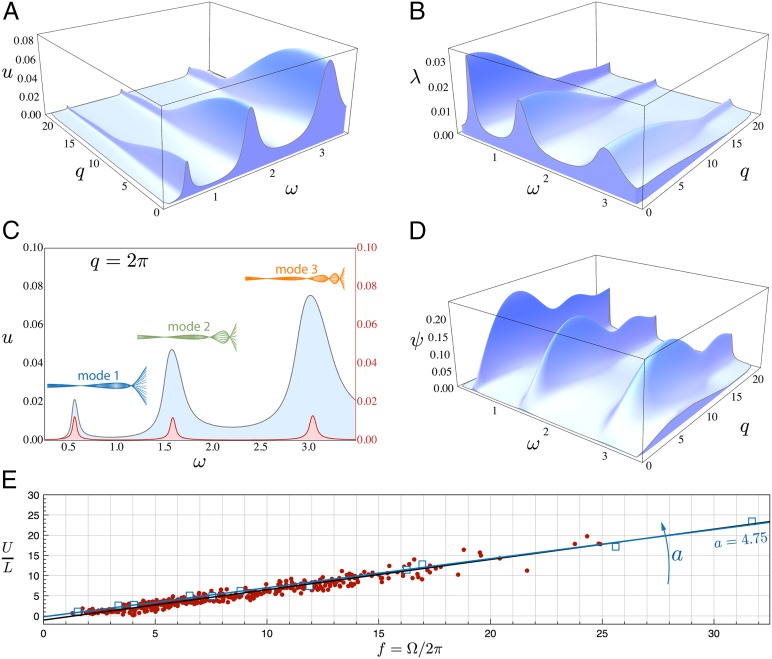
In Fig. 2A we show the dependence of the swimming velocity u for an active swimmer characterized by $R{e}^b=3.5\cdot {10}^4$, $\rho =300$ (corresponding to a fish of $L\sim 4.5$ cm with the same density as that of the surrounding water) and actuated with $a=1$ as a function of the scaled forcing wavenumber q and frequency $\mathit{\omega }$. We see that the locomotion velocity u is not a monotonic function of the active frequency $\mathit{\omega }$ and the wavenumber q, but instead shows clear localized peaks at particular values of $\mathit{\omega }$ and q. These hallmarks of a resonance are coincident with maxima in the tail oscillation amplitude $\mathit{\lambda }$, as shown in Fig. 2B.

Fig. 2.

Active swimming. (A) Velocity u, (B) tail amplitude $\mathit{\lambda }$, and (D) slip efficiency $\psi =u/c$ as functions of the angular frequency $\mathit{\omega }$ and wavenumber q characterizing the active torque $m_a$, obtained by solving Eqs. 15–17 with $m_f=0$, ${\rho }_f$=${\rho }_s$=1000 kg/m³, $\mathit{\nu }$ =${10}^{-6}$ m²/s, $R{e}^b$=3.5$\cdot {10}^4$, $\mathit{\rho }$ = 300, a = 1. (C) Comparison between the active swimmer with q = $2\pi$ (gray line) and the corresponding passive sheet (red line). For each resonance peak, a representative active swimmer’s midline gait is reported. (E) Comparison with experimental data. Red circles represent dace, trout, and goldfish of different size (3). Blue squares correspond to the resonant peaks of active swimmers of different size (3$\cdot {10}^4\le R{e}^b\le$ 4$\cdot {10}^4$) simulated with $a=4.75$, $q=2\pi$. Black and blue lines represent data fits ($U/L$=${\alpha }_{a}f$+${\beta }_a$, see SI) for, respectively, experiments and simulations.

To further clarify this observation, we consider the case of a biomimetic swimmer: a flexible sheet that is forced at its leading edge via an oscillating torque (11, 22, 23). In our model this corresponds to letting $m_a=\left(a/2\right)\sin \left(\omega \tau \right){\mathit{\delta }}_k\left[x\right]$, where ${\mathit{\delta }}_k[\cdot ]$ is the Kronecker delta. Equivalently, this can be achieved by modifying the boundary conditions Eq. 10 so that ${{\partial }_x^{2}h|}_{x=0}=a/2$. Solving the associated eigenvalue problem, we find that the passive sheet has a series of characteristic resonance peaks in the velocity shown in Fig. 2C. These steady-state results are consistent with experiments and transient computations of thrust production in a foil that is excited at its tip (11, 22, 23). Indeed, the fundamental resonance frequencies of the passive sheet activated at its leading edge and those of the fully actuated swimmer are coincident, as shown in in Fig. 2C together with representative midline traces for each mode. Our observations are also consistent with numerical computations of transient swimming (17), which show that for a fixed frequency of muscle activation waves there exist optimal elastic properties (characterized by an effective bending stiffness) that maximize the organism’s swimming speed. Our model predicts that such optimal elastic properties are the ones for which the imposed frequency is resonant.

Moving from a characterization of the speed and gait of the inertial swimmer as a function of the driving torque, we turn to a simple measure of locomotor efficiency as embodied in the slip efficiency $\psi =u/c$, where $c=\omega /q$ is the wave speed. In Fig. 2D we show $\psi \left(\omega ,q\right)$ and again see resonance peaks for a set of different $\mathit{\omega }$ along which there is an optimal wavenumber q that dictates the maximum.

A simple physical interpretation of this resonant response follows by recognizing an analogy between swimming and the flag flutter (32). A flag converts steady input flow into an oscillatory output via an instability known as 1:1 resonance. Physically, the flow couples the two lowest oscillator modes of the system so that as the fluid velocity is increased the corresponding frequencies approach each other. When they coincide energy is transferred from the flow into the flag, causing it to flutter; indeed, this is a fairly general instability mechanism in hydroelastic systems (35). A fish works in reverse, converting flexural oscillations into steady motion. This is most effectively achieved when the fish’s muscular activation sets the surrounding fluid into motion in a way such that the flow reaction is resonant with the body’s modes of passive hydroflexural oscillations. This 1:1 resonance condition is responsible for the peaks illustrated in Figs. 2 and 3. This duality between fishes and flags shows that the kinematic swimming waves (see modes 1, 2, and 3 in Figs. 2 and 3) are associated with the body’s flexural modes and selected via the actuation frequency f but are independent of the driving wavenumber q.

Fig. 3.

Proprioceptive swimming. (A) Families of self-propelled feedback-driven solutions as functions of $\mathit{\delta }$ and $\mathit{\chi }$, in the proximity of the natural resonance frequencies (passive sheet, red line), obtained by solving Eqs. 15–17 with $m_f\ne 0$ (Eq. 9), $m_a=0$, ${\rho }_f$ = ${\rho }_s$ = 1,000 kg/m³, $R{e}^b$ = 3.5$\cdot {10}^4$, $\mathit{\rho }$ = 300. For each resonance peak, a representative proprioceptive swimmer’s midline trace is reported. (B) The locomotion velocity u and (C) the tail amplitude $\mathit{\lambda }$ as functions of $\mathit{\delta }$ and $\mathit{\chi }$. In A–C the blue, green, and orange surfaces are associated with the first, second, and third resonance peak. The maximum velocity and tail amplitude are located at $\omega \delta =\pi /2$.

Comparison with Experiments.

We start by showing that our theory is consistent with a recent comparative analysis of macroscopic swimming (25). In the laminar regime, balancing the propulsive term with the viscous drag in Eq. 15 yields $\rho I_3\sim \rho u^{3/2}/\sqrt{{Re}^b}$. Expressing the vertical displacement as $h\sim e^{i\omega \tau }\gamma \left(s\right)\lambda$, where $\gamma \left(s\right)$ is a bounded function, implies that $I_3\sim {\lambda }^2{\omega }^2$. In dimensionless notation, this reads $Re\sim S{w}^{4/3}$, where the output Reynolds number is $Re=UL/\nu$ and the input swimming number is $Sw=f{A}_{\lambda }L/\nu$. In the turbulent regime, the balance of the propulsive term with the pressure drag in Eq. 15 yields $\rho I_3\sim \rho u^2{I}_1$. In dimensionless notation this leads to $U/L\sim f$, providing a mechanistic explanation for Bainbridge’s empirical relation (3). By recalling that $A_{\lambda }/L$ is approximately constant (3, 6) (Figs. 2B and 3C), we obtain $Re\sim Sw$, consistent with ref. 25 (Supporting Information). This explains why, as noticed by Bainbridge himself (1), a linear data fit is not accurate for frequencies approximately $f\le 5$ Hz. Indeed, in this regime the scaling law $Re\sim S{w}^{4/3}$ holds, whence the frequency and speed are nonlinearly related.

Our minimal model is consistent with ref. 25 but goes beyond it by allowing for a quantitative comparison with experiments (3) on dace, trout, and goldfish swimming to relate their rescaled speed $U/L$ to their tail beat frequency $\mathrm{\Omega }$. In terms of our theory, we solve the nonlinear eigenvalue problem Eqs. 18 and 19 by varying $\mathrm{\Omega }$ (or its scaled analog $\mathit{\omega }$) as a continuation parameter and follow the peak velocities of the swimmers as a function of the fish size. In Fig. 2E we show that $U/L={\alpha }_a\mathrm{\Omega }/2\pi$, where ${\alpha }_a$ approaches the experimental value of $\sim 0.75$ when the scaled amplitude of the swimmer approaches $a=4.75$ (Supporting Information). Analyzing our results in terms of the Strouhal number $St=\lambda \omega /\left(2\pi u\right)$, which mixes the input variables $\lambda ,\omega$ and output variable u, we find that $St$ associated with the velocity peaks is also in agreement with experimental observations (25, 36) that show that $0.1\lesssim St\lesssim 0.4$ (Supporting Information).

Thus, we envision a mechanism wherein the fish can rescale its bending stiffness and thus continuously shift its own passive resonance frequencies $U_b/L$ and the corresponding velocity peaks associated with active swimming. This effectively hides the resonance peaks and can be achieved via an extra contribution to the active torque proportional to ${\partial }_s^{2}h$ (similar to the passive elastic torque $b{\partial }_s^{2}h$). This may be related to the suggestion that negative muscular work is used by swimmers to vary their effective body stiffness (37). Altogether, our findings explain a range of prior observations of comparative swimming and further suggest that fish can tune their swimming regimes to take advantage of resonant interactions by flexing their elastic bodies optimally.

Proprioceptively Driven Locomotion.

Having seen how a traveling wave of muscular torques driven by a central pattern generator leads to resonant interactions in a swimmer, a natural question that arises is whether such a wave can be created spontaneously using only a local dynamical rule such as the minimal proprioceptive sensorimotor feedback torque $M_f$ given by Eq. 9.

To see whether this is possible, we set $m_a=0$ in Eq. 16 and then vary the scaled feedback strength $\chi =\mathcal{X}L/\overline{B}$ and the scaled delay $\delta =U\mathrm{\Delta }/L$. By substituting $h=e^{i\omega \tau }\eta \left(s\right)+c.c.$ into Eqs. 15–17 we obtain a modified nonlinear eigenvalue problem for proprioception driven swimming (Supporting Information). To solve this problem we start by inducing an initial instability assuming $m_a=\left(a/2\right)\sin \left(\omega \tau \right){\mathit{\delta }}_k\left[x\right]$ with $a=1$ at the leading edge. Then we use a two-parameter continuation scheme to gradually reduce a until it vanishes while increasing $\mathit{\chi }$ from zero to its designated value. In Fig. 3 we see that self-propelled feedback-driven solutions exist only in the proximity of the natural resonance frequencies of the fish, and swimming performance is modulated by both $\mathit{\delta }$ and $\mathit{\chi }$. Thus, by controlling the strength $\mathit{\chi }$ or the delay according to $0\le \omega \delta \le \pi$, the swimmer can vary its velocity u and tail amplitude $\mathit{\lambda }$ from zero to a maximum at $\omega \delta =\pi /2$ (Fig. 3A and Supporting Information). This allows us to see that the proprioceptive torque $m_f$ effectively acts on the body stiffness, shifting the resonance peaks (Fig. 3A). Indeed, the feedback strength $\mathit{\chi }$ may be regarded as a way to control the effective negative muscle work (37). The class of solutions determined by the parameters $\mathit{\delta }$ and $\mathit{\chi }$ produces nested performance surfaces (Fig. 3 B and C), each of them associated with a resonance peak, with multiple swimming regimes possible for a given pair $\mathit{\delta }$, $\mathit{\chi }$. This suggests a control mechanism that allows proprioceptive swimmers to continuously switch to higher frequencies, increasing their speed while maintaining their tail amplitude approximately constant, as experimentally observed (1, 6). Although we have assumed $\mathit{\chi }$ and $\mathit{\delta }$ to be constant, when they are functions of space they can be used to reproduce specific swimming patterns with complex gaits.

More generally, because locomotion is the product of the simultaneous action of central pattern generator and proprioception, we also solve Eqs. 15–17 with $m_a\ne 0$ and $m_f\ne 0$ (Eqs. 8 and 9). Our results indicate that the resonant character of optimal gaits persists, although the proprioceptive term quantitatively modifies the output swimming velocity u by sharpening or broadening the resonant peaks as a function of the parameters $\mathit{\delta }$, $\mathit{\chi }$ (Supporting Information). Our results show that the simple form of Eq. 9 suffices to yield self-organized propulsive gaits, hinting at robotics applications while also suggestive of the role of local sensory feedback mechanisms for gait evolution in developing organisms.

Discussion

Our simple 2D description for speed and gait selection in swimming accounts for passive elasticity and hydrodynamic drag and thrust, as well as coordinated muscular activity and proprioceptive sensory feedback, and thus allows us to dissect the roles of the physical and biological subsystems in a minimal self-consistent setting. Our study thus complements recent large-scale simulations by providing a mechanistic perspective on how a flexing fish converts transverse oscillations to steady swimming but goes beyond them by having the ability to provide comparative qualitative insights. Thus, for a prescribed traveling wave of muscular torques our observations of quantized resonance peaks of speed and efficiency have a simple interpretation: They are dictated by the flexural deformation modes of the elastic body, thus linking the instability mechanism for flag flutter (32) to resonant swimming. Our theory also allows us to provide a quantitative mechanistic explanation for the now-classic experimental observations of Bainbridge (3). Finally, we show that a local proprioceptive rule that links muscular torque to the local shape with a temporal delay is sufficient to trigger a spontaneous elastic instability that leads to thrust production, without the need for a central pattern generator, and is consistent with the hypothesis of negative muscle work and modified stiffness (37). Our study is thus a step in integrating neural dynamics, mechanics, and flow in the context of locomotory behavior.