Microdroplet fusion mass spectrometry for fast reaction kinetics

Significance

Time-resolved mass spectrometry is a powerful approach for identifying reaction intermediates and measuring reaction kinetics, yet one critical limitation is temporal resolution. Here, we describe microdroplet fusion mass spectrometry on timescales as short as microseconds. In our approach, two high-speed streams of liquid microdroplets collide to make fused droplets of 13 ± 6 μm in diameter, where the reactants are mixed in a negligible time. After a short flying time of 50 μs or less during which the reaction proceeds, the fused droplets enter a mass spectrometer for chemical analysis of intermediates and reaction products. This enables observation of early events of various fast chemical reactions in the liquid phase.

Abstract

We investigated the fusion of high-speed liquid droplets as a way to record the kinetics of liquid-phase chemical reactions on the order of microseconds. Two streams of micrometer-size droplets collide with one another. The droplets that fused (13 μm in diameter) at the intersection of the two streams entered the heated capillary inlet of a mass spectrometer. The mass spectrum was recorded as a function of the distance x between the mass spectrometer inlet and the droplet fusion center. Fused droplet trajectories were imaged with a high-speed camera, revealing that the droplet fusion occurred approximately within a 500-μm radius from the droplet fusion center and both the size and the speed of the fused droplets remained relatively constant as they traveled from the droplet fusion center to the mass spectrometer inlet. Evidence is presented that the reaction effectively stops upon entering the heated inlet of the mass spectrometer. Thus, the reaction time was proportional to x and could be measured and manipulated by controlling the distance x. Kinetic studies were carried out in fused water droplets for acid-induced unfolding of cytochrome c and hydrogen–deuterium exchange in bradykinin. The kinetics of the former revealed the slowing of the unfolding rates at the early stage of the reaction within 50 μs. The hydrogen–deuterium exchange revealed the existence of two distinct populations with fast and slow exchange rates. These studies demonstrated the power of this technique to detect reaction intermediates in fused liquid droplets with microsecond temporal resolution.

Time-resolved measurements of reaction intermediates are crucial for understanding the fast kinetics of chemical reactions. Various approaches have been implemented to improve the temporal resolution of kinetic measurements in liquid reactions (1, 2), which are often limited by the mixing time. One approach for improving the mixing time involves the use of turbulent flow to increase the shear stress in fluid channels (3). Another approach is to stimulate the rapid initiation of a reaction by photo-triggered initiation (4), electron transfer (5), or temperature jump/rise (6). A small-size reactor was also used for rapid mixing so that the time required for diffusion-dependent mixing is minimized (7–10).

Among various methods for detecting reaction intermediates, mass spectrometry has been a powerful tool for probing reaction products because it can discriminate similar species by their mass-to-charge ratio while simultaneously measuring multiple species. Time-resolved mass spectrometry (11) has been widely used for measuring the kinetics of protein–ligand complexation, organometallic compound formation, and enzyme-catalyzed processes. Despite these efforts for improving temporal resolution, time-resolved mass spectrometry has been limited to the millisecond timescale, with a recent achievement of 300 μs (12).

A major obstacle for improving the timescale of kinetic measurements in the liquid phase involves the diffusion-limited mixing time of reactants in bulk solution. Carroll and Hidrovo (13) reported that a substantial improvement in mixing time could be achieved by colliding liquid droplets through inertial mixing. They used droplets ranging from 90 μm to 115 μm in diameter that were traveling at a speed of ∼0.5 m/s to achieve a mixing time of ∼600 μs. Because the mixing time under the inertial mixing is proportional to the system’s length scale and inversely proportional to the speed of colliding droplets (13), the mixing time can be further reduced to microseconds by decreasing droplet size and increasing collision speed. In this study, we generated micrometer-size liquid droplets of 13 ± 6 μm in diameter using pressurized nebulizing nitrogen gas. The propulsive force from the pressurized gas formed a stream of high-speed liquid droplets traveling in air at a speed of 84 ± 18 m/s. The collision of two high-speed streams of micrometer-size liquid droplets allowed for their rapid mixing, estimated to be less than a few microseconds. The resulting fused droplets were directed to a mass spectrometer that determined the masses of intermediates and final reaction products. Thus, the mixing time is expected to be essentially negligible in comparison with the travel time of the fused droplet to the inlet of the mass spectrometer.

The reaction progressed as the fused droplet traveled in air to the inlet of the mass spectrometer. Once inside the heated inlet, the reaction was effectively complete. Although this might seem surprising, evidence for this behavior will be presented later, based on the observation of first-order kinetics of a known reaction. The fusion events and the distribution of droplet speeds were characterized by recording images with a camera running at 120,000 frames per second (fps). The fast mixing of micrometer-size liquid droplets traveling at a high speed enabled kinetic measurement with 3-μs temporal resolution and a dead time less than a few microseconds. We applied this technique to measure the kinetics on the microsecond timescale of the acid-induced unfolding of cytochrome c and the hydrogen–deuterium exchange (HDX) in the 9-aa peptide bradykinin.

Results

Droplet Fusion and Reaction Time.

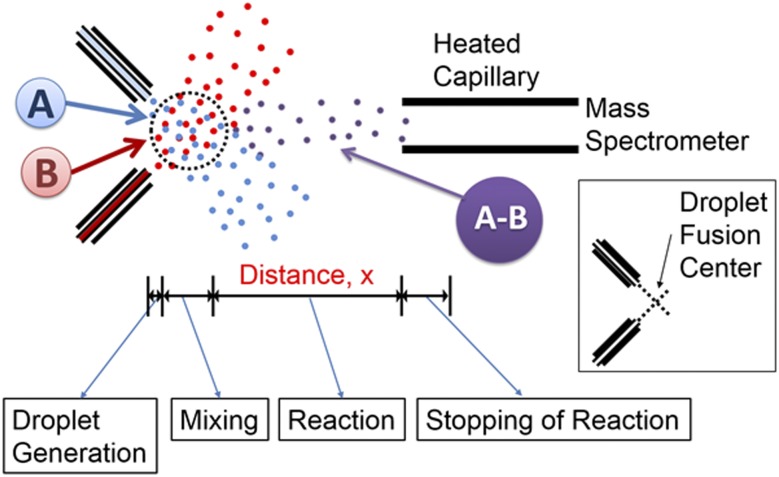
Fig. 1 shows a schematic of the experimental setup. Micrometer-size liquid droplets were generated by the atomization of bulk solutions with a turbulent nebulizing gas (dry N₂) at 120 psi. The droplets were charged to promote Coulomb fission inside the vacuum of the mass spectrometer (14) by applying a voltage of 5 kV to each syringe. The intersection of the two droplet streams was defined as the droplet fusion center, as shown in Fig. 1, Inset. Chemical reactions were initiated by the fusion of droplets containing each reactant, denoted as A and B in Fig. 1. The reaction seemed to stop as the droplets entered the heated mass spectrometer inlet capillary, which causes a sudden transition from molecules in the droplet to bare ions in the gas phase. The distance between the droplet fusion center and the mass spectrometer inlet is defined as x in Fig. 1, from which the corresponding reaction time in the droplets is determined. Kinetics of the reactions were monitored by mass spectrometry by recording the reaction intermediates and products for different values of the distance x.

Fig. 1.

Schematic (not to scale) of experimental setup for studying reaction kinetics in fused droplets. (Inset) The definition of the droplet fusion center, which is the intersection of the two droplet streams. Most fusion events take place in a circle (dotted black) of about 500 μm surrounding the droplet fusion center.

The position of the two sprays and the alignment of the stream of fused droplets to the mass spectrometry inlet strongly influence both the strength and the stability of the mass spectrometry signal. Before each kinetic measurement, the alignment was checked by centering the stream of fused droplets directed to the mass spectrometer inlet and monitoring the stability of the signal. As the travel distance increases, the ion signal decreases. To account for this change, each ion peak is normalized to the total ion signal.

The reaction time in the fused droplet was determined by the time the fused droplets spent traveling before reaching the heated inlet of the mass spectrometer. The typical method used for measuring droplet speed is Doppler anemometry (15, 16). Although this method allows the measurement of droplet speed, as well as size, in a spatially resolved manner, it fails to capture the collision and fusion of droplets as well as the trajectories of individual fused droplets. We opted to use a high-speed optical camera (Phantom v1610; Vision Research) to image the generation, fusion, and trajectories of the generated droplets. Fig. S1 illustrates the camera setup. Movies S1 and S2 are movies of the droplet fusion and real-time tracking of individual fused droplets. The movies were recorded at 120,000 fps and played at 10 fps. The time gap between each image was 8.33 μs. For tracking the individual fused droplets a series of image analyses was carried out as shown in Fig. S2. About 70% of the droplets generated from each source underwent fusion (see, for example, the blue- and green-colored droplets in Fig. S3E). Droplets not undergoing fusion travel off-axis and did not enter the mass spectrometer. The droplet size distribution is centered around 13 μm. About 93% of the fusion occurred within about 500 μm of the droplet fusion center, which defined the start distance and start time of the reaction. In these studies we examined pure water droplets and found their evaporation during transit time was negligible; that is, the size of the droplet was essentially unchanged during the time of observation (less than 50 μs). Data supporting the near constancy of the fused droplet size are presented in Table S1.

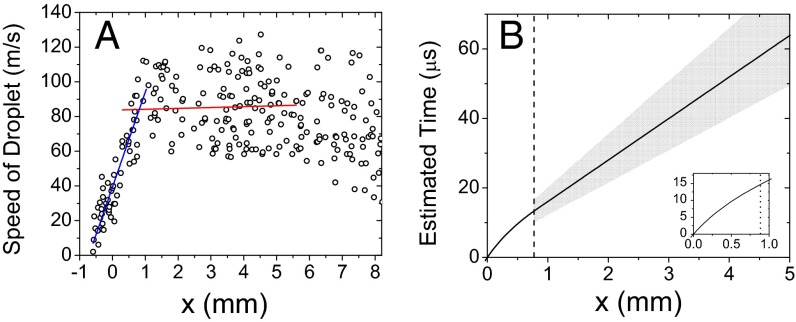
The distribution of droplet speeds was determined by tracking 243 droplets. Fig. 2A shows the results plotted as a function of the distance x. The droplets were accelerated by the pressure of the flowing nebulizing gas (dry N₂) at a constant value up to 0.8 mm from droplet fusion center. After passing through the distance of 0.8 mm from the droplet fusion center, the droplets remained at a relatively constant speed. Given this observation, the droplet speeds, v, in meters per second were fitted in two separate regions to straight lines: from 0 ≤ x < 0.8 mm to the expression v = 39.3 + 54.8x and from 0.8 ≤ x ≤ 5.0 mm to v = 83.7 + 0.5x. From the fitted speed values, estimated reaction times were calculated by integrating the speed over distance x. Fig. 2B shows a plot of calculated reaction time as a function of x, illustrating that the reaction time was linearly proportional to traveled distance x for 0.8 mm ≤ x ≤ 5.0 mm where almost all of the kinetic measurements were conducted. The speed of fused droplets at the range between 0.8 mm and 5.0 mm exhibited an SD of 18 m/s for the average speed of 84 m/s, which corresponds to a 21% uncertainty in estimating the speed of the fused droplets as well as the reaction time, indicated as the gray area in Fig. 2B.

Fig. 2.

Speed of fused liquid droplets as a function of distance x between the droplet fusion center and the mass spectrometer inlet. (A) Speed of liquid droplets (blue line, linear fit for 0 ≤ x < 0.8 mm; red line, linear fit for 0.8 ≤ x ≤ 5.0 mm) and (B) estimated reaction time in the fused liquid droplets calculated from the measured speeds in A. In B the inset shows the curvature for 0 ≤ x ≤ 1.2 mm for clarity and the vertical dotted line indicates x = 0.8 mm. The gray region shows the uncertainty of the estimated time.

A short mixing time is critical for the analysis of fast reaction kinetics. A simple calculation involving only diffusion would suggest the mixing time of 19 ms (see Supporting Information for the calculation). However, the mixing time, caused by inertial mixing (13), is much less. To ensure that solution mixing was complete before the initiation of kinetic measurements in fused droplets, the reaction rate in the droplets was measured using a standard chemical reaction for characterizing the performance of the kinetic apparatus. The reaction between 2, 6-dichloro-phenolindophenol (DCIP) and ascorbic acid has been used widely to measure reaction rates in the liquid phase (17–19). Water droplets containing 1 μM DCIP were fused with water droplets containing 100 μM ascorbic acid to provide pseudo-first-order kinetics based on the excess concentration of ascorbic acid compared with DCIP.

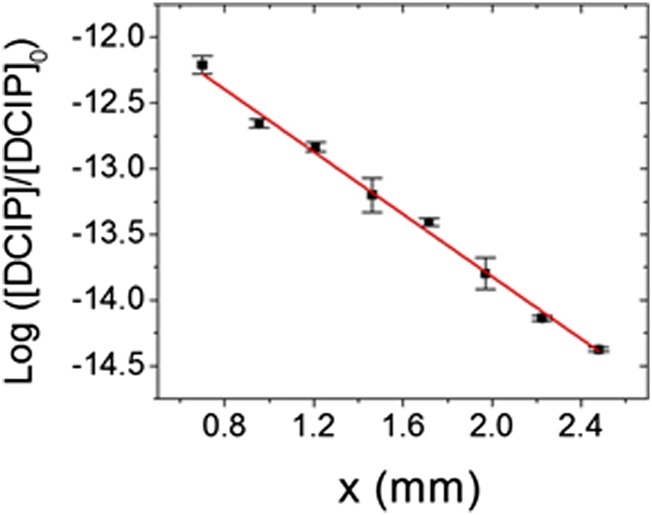
Fig. 3 shows the plot of the concentration of the remaining DCIP over the initial concentration of DCIP in a log scale as a function of the distance x. The linear relationship (R² = 99.4%) between the two axes indicates that the rate of reduction of DCIP was constant, regardless of x, starting from 0.7 mm. This linear relationship (i.e., constant reaction rate) indicated that the mixing of the two droplets was nearly complete before x = 0.7 mm and that the reaction was suddenly halted upon entering the heated inlet of the mass spectrometer. Otherwise, the linear dependence shown in Fig. 3 would not be expected to be valid. Thus, we are forced to conclude that (i) mixing takes place quite rapidly on the timescale of our measurements, (ii) evaporation does not play a significant role in determining the kinetics we observe during the flight time of the aqueous fused droplet to the mass spectrometer inlet, and (iii) the reaction is essentially stopped when the droplet enters the heated inlet of the mass spectrometer. This last conclusion is also what has been observed by Bain et al. (20) in their study of the Hantzsch synthesis of 1,4-dihydropyridines in electrosprayed droplets containing ethanol as the solvent.

Fig. 3.

Logarithmic plot of the concentration of DCIP divided by the initial concentration of DCIP as a function of the distance x. The error bars represent one SD using triplicate measurements.

The measured rate constant was determined to be 1.0 ± 0.2 × 10⁵ s⁻¹. This estimate is based on the slope found in Fig. 3 and the relation between distance traveled and time identified in Fig. 2. It is also based on the idea that the reaction stops upon entering the mass spectrometer. Further support for this assertion is provided by some past electrospray studies. Miller et al. (21) investigated the base-catalyzed Claisen–Schmidt condensation of 1-indanone with 4-chlorobenzaldehyde and thiamine-catalyzed benzoin condensation. For each reaction system a methanolic solution of the reactants was electrosprayed. The droplets were collected and analyzed by UV/visible absorption spectroscopy for the formation of products and these results were compared with a mass spectrometric analysis of the droplets. It was found in both cases that the reaction had essentially reached completion before entering the mass spectrometer. Thus, it seems that the rapid evaporation of microdroplets inside the mass spectrometer stops this reaction rather than accelerates it. We assume that other reactions we study behave in the same manner, although it is known that in some cases the temperature of the capillary inlet does influence the product yield. This implies that in some cases further reaction does occur inside the heated inlet and we cannot exclude this possibility in other reactions.

Kinetics of Acid-Induced Cytochrome c Unfolding.

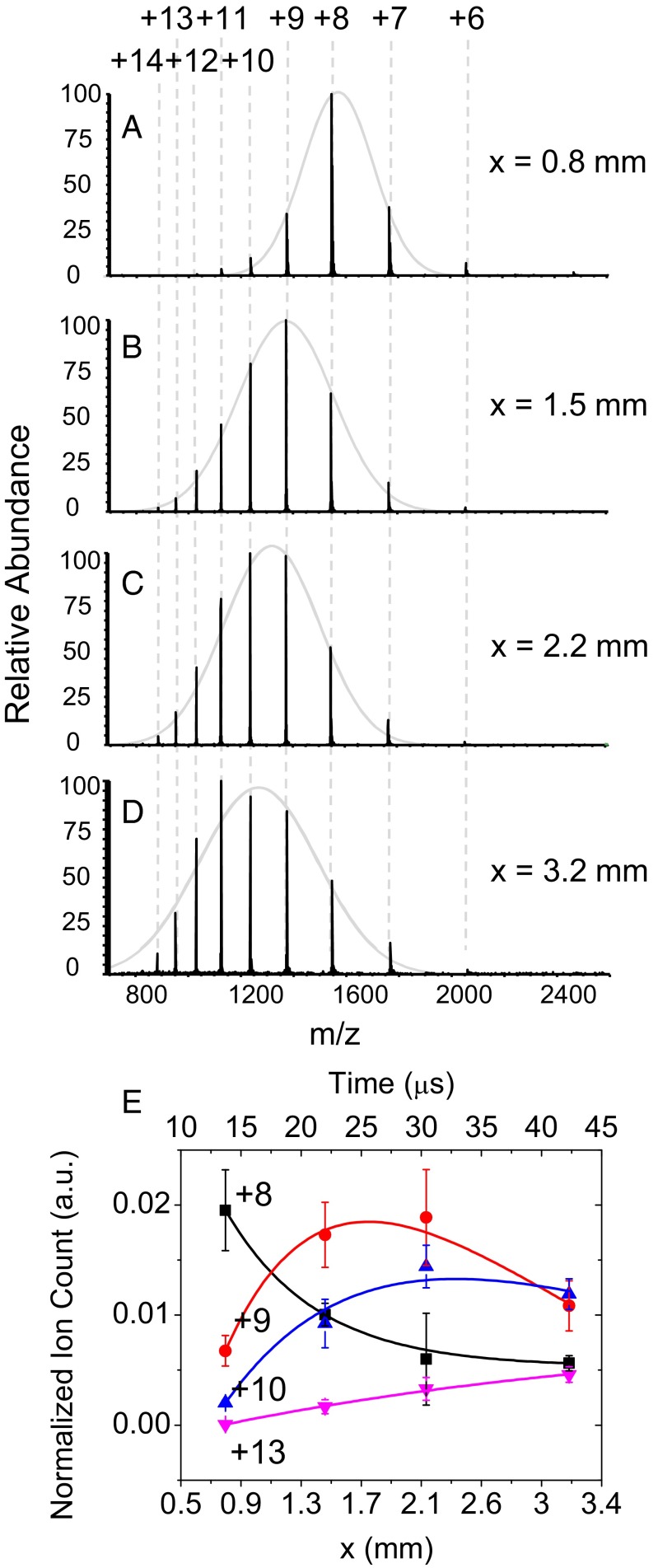
Acid-induced unfolding of cytochrome c was chosen for a proof-of-principle experiment because this process has been previously well characterized (10, 22–27) at different pH values (Fig. S4). Mass spectrometry provides useful information about protein folding and unfolding through changes in charge state (26). We examined the kinetics of acid-induced unfolding of cytochrome c by fusing water droplets containing cytochrome c solution with water droplets containing 1% (vol/vol) hydrochloric acid (pH 0.84). Fig. 4 shows the recorded kinetics of cytochrome c unfolding induced by the pH change. Fig. 4A shows typical mass spectra of the acid-induced cytochrome c unfolding at different distances x. In separate experiments we found that cytochrome c in the folded state at pH 7.0 exhibited a mass spectrum centered at +8 charges (Fig. S4A). At x = 0.8 mm, the mass spectrum of cytochrome c showed a folded spectrum of charge state having a maximum of +8 charges (Fig. 4A). Again, this observation supports the contention that the progress of the reaction is stopped by entering the heated inlet of the mass spectrometer. As the distance x increased to 1.5 mm, higher states such as +10, +11, and +12 began to appear (Fig. 4B), and +9 became the maximum peak, indicating appearance of unfolded intermediates. At 2.2 mm, even higher charge states, such as +13 and +14, showed up, with +10 being the maximum peak (Fig. 4C); low charge states, such as +6, were almost gone. At 3.2 mm, the charge state of +10 became the maximum peak (Fig. 4D). This gradual transition from low to high charge states is typical behavior of a protein as it unfolds. The completely unfolded charge state of cytochrome c typically shows a distribution centered with +17 charges (22). Cytochrome c in this experiment did not reach this value because of the short timescale of the present kinetic measurements. The envelopes of the mass spectra were fitted to a Gaussian curve for a quantitative analysis of the charge states. The calculated FWHM of the fitted Gaussian curve at x = 0.8 mm, 1.5 mm, 2.2 mm, and 3.2 mm were 317.1 ± 12.0, 427.7 ± 20.0, 431.9 ± 49.6, and 534.0 ± 39.3 m/z, respectively. The FWHM increased as the distance and corresponding reaction time increased. This widening of the observed charge distribution indicates the increase of slightly different unfolding states.

Fig. 4.

Kinetics of acid-induced cytochrome c unfolding. (A–D) Mass spectra of cytochrome c acquired from the fusion of droplets containing 10 μM cytochrome c and the other with 1% (vol/vol) HCl (pH 0.84) while the distance x is varied. The charge state +n denotes the protein ion of [cytochrome c + nH]ⁿ⁺. Gray solid lines are Gaussian fits to each spectrum. (E) Normalized ion counts of different charge states of +8 (black square), +9 (red circle), +10 (blue triangle), and +13 (magenta triangle). The axis on bottom and top shows the distance x and corresponding time using the distance-to-time conversion factor found from Fig. 2B. Sold lines are biexponential fits to the data. The error bars represent one SD from three independent measurements.

Fig. 4E shows a plot of ion count intensities for the peaks +8, +9, +10, and +13 normalized by the total ion current at each distance x. The corresponding reaction times are shown on the top horizontal axis of Fig. 4E, using the time-to-distance conversion established in Fig. 2B. Protein folding and unfolding generally follows simple exponential kinetics that are sufficiently described by two exponential terms (23, 28). The cytochrome c unfolding kinetics in Fig. 4B exhibits three types of behavior often observed in protein unfolding (10): (i) monophasic exponential decay of the lowest charge state, (ii) exponential rise and decay of intermediate charge states, and (iii) monophasic exponential rise of the highest observed charge state. In Fig. 4E solid lines are biexponential fits to the data according to I(t) = A₀ + A₁ exp(−t/τ₁) + A₂ exp(−t/τ₂) using the Levenberg–Marquardt algorithm (29) to find the optimal least-squares fit.

Whereas the folded charge state of +8 exponentially decayed with a time constant of 7.5 ± 0.6 μs, the charge states +9 and +10 exhibited exponential rises with 12.7 ± 1.4 μs and 20.5 ± 0.7 μs time constants, respectively, followed by exponential decays with a similar time constant of 23.6 ± 0.6 μs and 22.5 ± 4.4 μs for +9 and +10. The +13 charge state underwent a monophasic exponential rise with a time constant of 39.0 ± 13.2 μs, indicating cytochrome c gradually enters into an unfolded state as the distance and corresponding reaction time increases. Interestingly, the time constant for the decay term increased as charge states increased. The present data show the initial progression of cytochrome c unfolding to reveal intermediate charge states observed at a short timescale of ∼25 μs.

Kinetics of HDX in Bradykinin.

HDX combined with mass spectrometry is a useful technique for exploring higher-order structural changes of proteins and peptides (30, 31). The HDX rate is determined by solvent accessibility of deuterium to labile hydrogen atoms in the protein, revealing information about the protein conformational structure. Here we recorded the HDX kinetics for a simple 9-aa peptide, bradykinin, a dilator of blood vessel (32), with microsecond temporal resolution. Bradykinin (Arg-Pro-Pro-Gly-Phe-Ser-Pro-Phe-Arg) has the structure shown in Fig. S5.

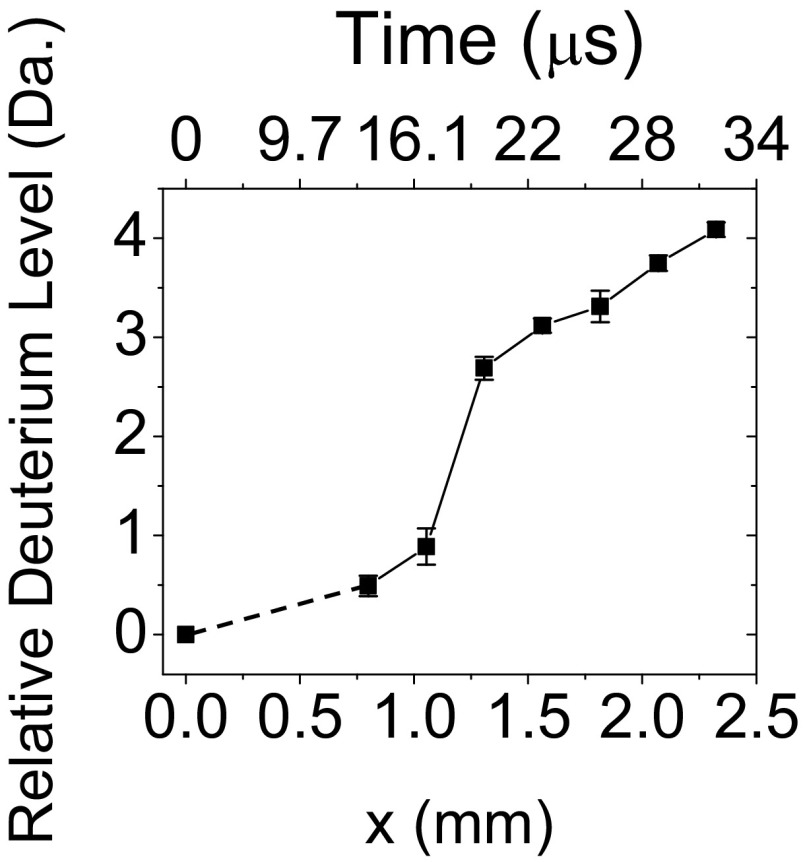
Fig. S6 shows mass spectra as a function of distance when water droplets of 1 μM bradykinin were fused with a 99.9% D₂O droplets. We observed a gradual increase of mass as deuterium replaced labile hydrogen atoms in doubly charged bradykinin. There was an initial exchange of deuterium for hydrogen in bradykinin between x = 0.8 mm and 1.054 mm, corresponding to reaction time of 13.7 μs and 16.7 μs. Then, a fast exchange of two deuterium atoms for hydrogen atoms occurred between x = 1.054 mm (16.7 μs) and 1.308 mm (19.7 μs). This fast exchange was followed by a relatively slow deuterium exchange at distances of x = 1.308 mm (19.7 μs) and longer.

Fig. 5 shows the calculated average number of incorporated deuterium atoms in bradykinin plotted as a function of distance x and corresponding converted reaction times (top axis). The calculation was carried out first by calculating the centroid value C at each time point t according to C(t) = Σ_i (m/z)_i I_i/Σ_i I_i, where I_i is the spectral intensity at the corresponding (m/z)_i value. Then, the average number of incorporated deuterium atoms D was calculated by taking the difference of each centroid value from the centroid value calculated from the mass spectrum of deuterium-free bradykinin according to $D\left(t\right)=C\left(t\right)-C_{free}.$ The charged states and the necessary adjustment for the charge carrier, hydrogen in this case, was taken into account for these calculations. The guide line between x = 0 and 0.8 mm is dotted because the number of exchanged deuterium atoms at point x = 0 mm was derived from bradykinin with no deuterium exchange, not from the direct kinetic measurement at the position x = 0 mm. This was because of the physical limitation of approaching the droplet fusion center to the mass spectrometer inlet. These data clearly show the existence of an initial rapid deuterium exchange until 17 μs followed by three slow deuterium exchanges until 32 μs.

Fig. 5.

Kinetics of HDX in bradykinin. Droplets with 1 μM of bradykinin solution were fused with droplets containing 99.9% D₂O. The plot shows the calculated average number of deuterium atoms incorporated in bradykinin as a function of distance x and converted reaction time (line to guide the eyes). The error bars correspond to ± one SD from triplicate measurements.

Discussion and Conclusions

We have developed a mass spectrometry platform based on droplet fusion for fast kinetic studies. Fused droplets have been used previously in mass spectrometry (33–35) but not for kinetic measurements. The droplet generation and fusion platform, combined with mass spectrometric detection, allows for kinetic measurements at microsecond temporal resolution, which has not yet been achieved with conventional time-resolved mass spectrometry. The processes of droplet generation, fusion, and transport to the mass spectrometer were characterized by real-time imaging of the fused droplets with a high-speed camera. We found that the size and the speed of fused droplets remained relatively constant in the region where kinetic measurements were conducted. Thus, the reaction time in the droplets was largely proportional to the distance traveled between the time of fusion and the time the fused droplet entered the heated capillary inlet of the mass spectrometer. We applied this droplet-fusion platform to investigate the kinetics of acid-induced cytochrome c unfolding and HDX in bradykinin. We argue that this platform can be widely applied to learn about transient reaction intermediates in liquid droplets on the microsecond timescale.

The fused liquid droplets had a diameter of 13 ± 6 μm. Our time resolution was as short as 3 μs. The dead time of mixing was less than a few microseconds, and the speed of the fused droplets was 84 ± 18 m/s. About 93% of the collisions and fusions of the crossed streams of droplets occurred within a 500-μm radius from droplet fusion center. After passing from the mixing zone, the fused droplets underwent little to no additional fusion events, allowing the start time of the reaction to be well defined. The stop time was taken as the point of entry into the heated capillary inlet of the mass spectrometer. This statement agrees with previous studies (21) and is supported by the linear dependence of the reaction rate of DCIP with ascorbic acid on distance traveled. It is possible that rapid adiabatic cooling of the droplet or even precipitation of compounds inside the droplet inside the heated capillary inlet is responsible for the rapid stopping mechanism, but this matter requires further study.

The kinetics of acid-induced cytochrome c unfolding from one charge state to the next observed in the present investigation qualitatively agrees with previously reported studies of the unfolding kinetics of this protein (10). It is interesting that the time constant increased as the charge state increased during the unfolding event. In several cases reported in previous studies the time constant or rate constant remained the same when fitted with exponential curves (28). In other cases, protein unfolding kinetics exhibited a rapid initial unfolding followed by a decrease in the folding rate (36). It is unclear whether the slower unfolding we observed was limited to the early unfolding or held for the entire unfolding event because our measurements were carried out for only ∼40 μs. Nevertheless, fleeting intermediate charge states were clearly observed in this study.

We also investigated HDX in doubly charged bradykinin for which we observed at the shortest times that we measure (13.7 μs and 16.7 μs) one HDX followed soon thereafter (19.7 μs) by two HDXs, followed by the addition of another deuterium. We cannot identify which sites are responsible for this behavior but we offer a speculation in Supporting Information. In any event, our ability to distinguish between the rates of different hydrogen-atom exchange sites was made possible by the high temporal resolution and short initial dead time of our fused-droplet approach.

It is becoming well established that the reaction rate in microdroplets is remarkably faster than the same reaction in bulk solution (20, 21, 37–39). Moreover, in some cases products are found in the droplet reactions that are different from those in the bulk (40). Consequently, it would be a mistake to believe that reactions in microdroplets simply mirror that in bulk, although the major pathways so far seem to be often the same. The behavior of reactions in microdroplets has been attributed to continuous desolvation (evaporation) of the microdroplet and the spatial effects of microdroplet confinement in which charged, polar, and hydrophobic species are concentrated on the outside of the microdroplet. We also observe this strong enhancement of the reaction rate in the systems we investigated. For example, in the reaction of DCIP with ascorbic acid the bulk reaction rate has been measured to be 1.16 ± 0.03 × 10² s⁻¹ (17) and 1.12 ± 0.02 × 10² s⁻¹ (18), which should be compared with our measured value 1.0 ± 0.2 × 10⁵ s⁻¹. At first sight, this thousandfold enhancement of the reaction rate seems to be a large discrepancy but is actually smaller than that reported for other reactions. For example, Bain et al. (20) studied the Hantzsch synthesis of 1,4-dihydropyridines and compared the time for product formation by electrospray (on the order of milliseconds) to that in the bulk (on the order of 5 h). This result corresponds to an acceleration factor of more than six orders of magnitude.

In our case, we know evaporation is playing a minor role because the size of the microdroplet is essentially unchanged during its flight time (Table S1). Thus, the present study strongly supports the idea that the accelerated reaction rate for the systems we have studied originates from microdroplet confinement. This same mechanism agrees with a previous study by Fallah-Araghi et al. (39) in which they reacted a nonfluorescent amine with a very weakly fluorescent aldehyde to form a fluorescent imine in water droplets (16–68 μm in diameter) surrounded by fluorinated oil. Again, a significant enhancement in reaction rate compared with the bulk was observed, and the rate was reported to be inversely proportional to the radius of the microdroplet. Clearly, these results have many important possible implications ranging from the kinetics of reactions inside a cell to the possible role confinement has played in the origin of life (39, 41, 42).

It is also interesting to compare our rate for cytochrome c unfolding on the timescale of tens of microseconds with that found by Rob and Wilson (10) using a microreactor followed by electrospray ionization (ESI) mass spectrometry on the timescale of tens of milliseconds. The experiments, however, are not comparable. The size of the microchannel of their reactor was 155 ± 2 μm, producing a much larger liquid-flow size than in our studies. Because microdroplet size does affect the extent of acceleration of the reaction rate, these results are not necessarily inconsistent.

The power of high temporal resolution of the present fused droplet kinetic apparatus allowed the detection of reaction intermediates even under the condition of accelerated reaction.

The present approach for fast kinetic measurements still has some limitations; further improvements are to be expected. The uncertainty of the fused droplet speed (84 ± 18 m/s) causes a 21% uncertainty in the reaction times. The uncertainty in the location of the droplet (which is around 500 μm) adds another uncertainty of few microseconds in the reaction times. The kinetic information is not yet refined but clearly shows the evolution of the reaction. These limitations might be overcome in part by changing the method for generating high-speed droplets from the current electrospray type to a more controlled type, such as a piezoelectric droplet generator. Another approach is to use an airflow guide (43). Despite these limitations, the present study demonstrates that our approach holds much promise as a general means for studying the kinetics of rapid solution-phase reactions in droplets.

Materials and Methods

Chemicals and Sample Preparation.

Horse heart cytochrome c, deuterium oxide, ascorbic acid, 2, 6-dichlorophenolindophenol, and hydrochloric acid were purchased from Sigma-Aldrich. HPLC-grade methanol and water were purchased from Fisher Scientific. Cytochrome c was dissolved in pure water at a stock concentration of 1 mM and diluted to a working concentration of 100 μM before each experiment. Bradykinin was prepared at a stock concentration of 1 mM in pure water and diluted to a working concentration of 1 μM.

Droplet-Fusion Mass Spectrometry.

A Thermo Scientific LTQ Orbitrap XL Hybrid Ion Trap-Orbitrap mass spectrometer was used. The cone and capillary voltages were set to 80 V and 120 V, respectively. The capillary temperature was set to 275 °C. A voltage of 5 kV was applied to the metal tips of two syringes for inducing ESI of the analytes and facilitating the atomization of the liquid droplets. The syringes were connected to two separate capillaries entering into two crossed ESI-like spray sources. The two ESI-like spray sources were equipped with X-Y-Z micro positioning on a linear and angular stage for the accurate alignment of the two streams of droplets. The angle between the two spray sources was set between 60° and 78°. The optimal angle was 78°, which showed the highest probability of droplet fusion and straight trajectories of the fused droplets to the inlet of the mass spectrometer. The distance between the two capillaries was set in a range of 0.5–3 mm, depending on the angle of the two spray sources. The alignment of the two capillary sources was carried out before each experiment by adjusting the angle and distance. This alignment was important for ensuring the fusion of the majority of the incident droplets and maximizing the fraction of droplets that have a linear trajectory toward the mass spectrometer inlet. The solutions containing analytes were infused with a syringe pump (Harvard Apparatus) at a flow rate of 30 μL/min for both syringes. The pressure of the dry N₂ nebulizing gas is 120 psi, and in each case the inner and outer capillary diameters are 100 μm and 360 μm.

Kinetic Measurement Between DCIP and Ascorbic Acid.

The kinetic measurement between DCIP and ascorbic acid was carried out as described in ref. 19. Briefly, solutions of DCIP at 1 μM and ascorbic acid at 100 μM were infused to the droplet fusion mass spectrometry using two separate syringes at a flow rate of 30 μL/min. The reduction of DCIP by ascorbic acid lowered the concentration of DCIP as the redox reaction progressed. A reaction rate constant was calculated by measuring remaining concentration of DCIP and calculating the ratio of the remaining DCIP over the initial concentration of the DCIP. The slope of the log of the ratio as a function of converted progression time gives the pseudo-first-order rate constant.