Abstract
We compare the effectiveness of short tandem repeat (STR) and single nucleotide polymorphism (SNP) genotypes for estimating pairwise relatedness, using molecular data and pedigree records from a captive Chinese rhesus macaque population at the California National Primate Research Center. We find that a panel of 81 SNPs is as effective at estimating first-order kin relationships as a panel of 14 highly polymorphic STRs. We note, however, that the selected STRs provide more precise predictions of relatedness than the selected SNPs, and may be preferred in contexts that require the discrimination of kin related more distantly than first-order relatives. Additionally, we compare the performance of three commonly used relatedness estimation algorithms, and find that the Wang [2002] algorithm outperforms other algorithms when analyzing STR data, while the Queller and Goodnight [1994] algorithm outperforms other algorithms when analyzing SNP data. Future research is needed to address the number of SNPs required to reach the discriminatory power of a standard STR panel in relatedness estimation for primate colony management.
Keywords: Macaca, relatedness estimation, STR, SNP, colony management, kinship
Introduction
Variable levels of relatedness among experimental subjects in biomedical research are capable of obscuring treatment effects. When the use of highly inbred or identical twins is not practical, as in research involving non-human primates, only unrelated or very remotely related subjects should be used in any given experiment. While the use of pedigree information for determination of kin relationships remains a gold standard, it is sometimes necessary for investigators to determine relatedness estimates among animals that are wild-caught or are acquired without sufficient pedigree information to determine kin relationships. In these circumstances, the coefficient of relatedness (r) can be estimated from molecular markers, notably short tandem repeats (STRs) and single nucleotide polymorphisms (SNPs).
The STR loci normally chosen for estimating r are those that are highly polymorphic [Estoup et al. 2002], while most SNPs are typically di-allelic and exhibit a maximum heterozygosity of 0.50. The higher information content of STRs necessitates the use of a greater number of high-frequency SNPs to obtain equivalent discriminatory power [Butler et al. 2007]. Butler et al. [2007] use model-based methods to conclude that approximately 40–60 SNPs are required to obtain the discriminatory power of 13–15 STRs.
The use of SNPs for the purpose of estimating relatedness is motivated primarily by more cost-effective data acquisition [Morin et al. 2004], despite the lower per-marker information content. Notably, however, SNPs are also more likely than STRs to reflect allelic identity by descent (i.e., homology), rather than only identity by state (i.e., homoplasy), since the average mutation rate of SNPs is approximately one-hundred thousand times lower than that of STRs [Butler et al. 2007], which are characterized by a high incidence of repeat-number expansion and contraction.
No empirical comparisons of the effectiveness of SNPs and STRs for relatedness estimation in non-human primates have been reported thus far. However, some comparisons of the effectiveness of STRs and SNPs in estimating relatedness have been conducted in the domain of human parentage analysis [Dario et al. 2009], especially for forensic investigation [Butler et al. 2007]. It is not immediately obvious if the results of these human studies can be directly applied to non-human primates, particularly when levels of inbreeding are high. Likewise, there have been several comparative studies of SNPs and STRs for the purposes of estimating relatedness in species of interest to the agricultural industry, for example in wild sockeye salmon [Hauser et al. 2011], Atlantic salmon [Glover et al. 2010], and in livestock to clarify breed history and to manage and preserve domesticated strains [Li et al. 2007]. Again, we note that the very different life histories of these species obscure the direct application of these studies to primate colony genetic management.
There has been much research addressing the relative performance of various algorithms for estimating pairwise relatedness [Csilléry et al. 2006], yet we are unaware of any empirical comparisons of these algorithms using both SNP and STR data for relatedness estimation in primate colonies. It is clear that properly distinguishing degrees of relatedness within captive breeding colonies is vital to proper management, regardless of species [Eding 2001]. The primary goal of this research is to compare and assess the effectiveness of established SNP and STR panels for relatedness estimation in Chinese rhesus macaques. We utilize multiple descriptive and inferential statistical techniques to investigate the relative performance of SNPs and STRs in predicting pedigree-based relationships. Additionally, we investigate the relative performance of the Queller and Goodnight [1994], Lynch and Ritland [1999], and Wang [2002] algorithms for relatedness estimation using each type of molecular marker. A detailed description of specific research goals is included in the methods section.
Methods
The relevant phases of this research had institutional approval (IACUC) and adhered to the American Society of Primatologists principles for the ethical treatment of primates.
Estimating r Using Pedigree Data
The California National Primate Research Center (CNPRC) has kept detailed birth records for 162 Chinese rhesus macaques bred in its Super Specific Pathogen-Free colony in the form of parent-offspring trios. Descent v2.0.2 [Hagen 2005] was used to transform the trio records into a comprehensive pedigree, from which a pairwise relatedness matrix between all possible pairs of the 162 Chinese rhesus macaques was constructed. This primary matrix was reduced to a 31x31 matrix representing all animals for which both SNP and STR data were available. The estimates of r based on breeding records were then used to evaluate the accuracy of r estimates based on SNP and STR genotype data. These pedigree estimates are not exact indices of relatedness due to both the possibility of missing trio information, and the fact that r estimated through pedigree data is a maximum likelihood estimate, about which there is variance, especially for categories of kin other than parent-offspring. Given the above constraints, pedigree estimates of r remain the best information available by which one can assess the accuracy of r as estimated from molecular markers.
Genotyping
The Molecular Anthropology Laboratory (MAL) at the University of California, Davis maintains data files containing STR and SNP genotypes for Chinese SSPF rhesus macaques in the CNPRC breeding colony. STR genotype data for the Chinese rhesus macaques were produced by the Veterinary Genetics Laboratory, at University of California, Davis, using the methods described in Kanthaswamy et al. [2006]. The same animals were genotyped using the 96 SNP genetic management (GM) panel developed by the Genetics and Genomic Working Group of the National Non-human Primate Research Consortium [Kanthaswamy et al. 2009; Ferguson et al., in press]. DNA samples were extracted from blood collected in EDTA vacutainer tubes using conventional methods, adjusted to 60 ng/ul and genotyped using the BeadXpress assay on the Illumina GoldenGate™ platform at the Technology Core of the UC Davis Genome Center. SNP genotypes were validated according to Satkoski Trask et al. [2011].
To maximize the power of the comparison, relatedness estimates were calculated for all Chinese SSPF rhesus macaques at the CNPRC for which STR genotype data, SNP genotype data, and pedigree information were available. At least 90% complete genotypes for the 14 STR loci (i.e. missing data did not exceed 2 of 28 alleles) and 100% complete genotypes for 81 SNP loci could be assigned to 31 of these animals. Only 81 of the 96 SNPs in the genetic management panel were used for estimating r, because 15 of the SNPs either exhibited missing genotypes for many animals, or exhibited a frequency of exactly 1.0 (9 of the 96 SNPs are polymorphic for Indian, but not Chinese rhesus macaques) and were therefore uninformative for relatedness estimation. The number of observed alleles, in addition to the observed and expected heterozygosity of each STR and SNP, are provided in Appendices 1 and 2, respectively. The mean observed and expected heterozygosity of the utilized STRs were 0.89 and 0.84 (respectively), and the mean observed and expected heterozygosity of the utilized SNPs were 0.39 and 0.43.
Estimating r using Molecular Markers
We utilized two programs to estimate r from molecular markers. For the most basic comparative analyses of SNPs and STRs, we utilized the SPAGeDi program [Hardy and Vekemans 2002] to implement the Queller and Goodnight [1994], Lynch and Ritland [1999], and Wang [2002] algorithms for relatedness estimation. For more complex sub-sampling analysis, we developed a relatedness estimation program using the statistical computing program R version 2.12.1 (R Development Core Team 2010), which implements the Lynch and Ritland [1999] regression algorithm. We chose to utilize the Lynch and Ritland [1999] algorithm a priori from literature review, before we compared the output of multiple algorithms using this data set, as it has been one of the most widely used methods of relatedness estimation and has aided in the creation of a variety of programs meant to simplify and streamline the process of exploring population stratification, inbreeding, and pairwise relatedness [Wang 2011; Kalinowski 2006]. Retrospectively, the Lynch and Ritland [1999] algorithm did not perform as well at estimation as other algorithms; however, the relative performance of SNPs and STRs under the Lynch and Ritland [1999] was similar to the relative performance of SNPs and STRs under the other reviewed algorithms. It should be noted that all of the algorithms utilized in this study permit negative estimates of r, which simply indicate that the given pair of unrelated animals share fewer alleles in common than an average pair of unrelated animals in the same population.
While aspects of this study could be completed using the SPAGeDi program, evaluation of the number of SNPs needed to discriminate various orders of relatedness requires several thousand iterations and manipulations of the relatedness estimation algorithm, a task that is much more easily implemented by the R script developed for this project (see Supplementary Materials §1). The R script used in this study utilizes the Genepop file format [Rousset 2008] as an input, and outputs a 4-dimensional array of relatedness estimates, which is composed of the pairwise relatedness estimates of all animals in the Genepop file, using from 1 SNP to 81 SNPs, for 100 random orderings of these SNPs. The R script employed in this study was validated by calculating the product-moment correlation, 0.9946, between relatedness estimates generated by our base script and those generated by the same algorithm in the commonly used SPAGeDi program [Hardy and Vekemans 2002].
Specific Objectives
The specific objectives of the present study are to: 1) evaluate the distributions of SNP-based and STR-based estimates of r in first-order, second-order, and third-order kin relationships, and in unrelated individuals, in a sample of Chinese-origin rhesus macaques (Macaca mulatta) at the CNPRC, 2) evaluate the distribution of difference between pedigree based estimates of r and both SNP-based and STR-based estimates of r, 3) calculate the product-moment correlation between pedigree based estimates of r and both STR-based and SNP-based estimates of r, controlling for non-independence of cases with QAP (Quadratic Assignment Procedure), 4) compare the predictive power of STRs and SNPs in distinguishing first-order relationships using matrix logistic regression, which is designed specifically for use in cases where data is provided in pairwise matrices, to control for possible interdependencies, 5) compare the ability of SNP-based and STR-based modelsto predict pedigree relationships, using AICc (corrected Akaike information criterion) and BIC (Bayesian information criterion) for formal model comparison, 6) compare the relative performance of three relatedness estimating algorithms (Lynch and Ritland [1999], Wang [2002], and Queller and Goodnight [1994]), and 7) identify the number of SNPs required to discriminate various order of kin, by implementing an algorithm to iteratively re-calculate r using an increasing number of SNPs.
Data Analysis
We conducted all data analyses using the Lynch and Ritland [1999] algorithm, unless otherwise indicated in the study description.
To address objective 1, data corresponding to estimates of r = 0.5, 0.25, 0.125, and 0.0 in the pedigree matrix were extracted from both the SNP and STR matrices. Estimates of r based on SNPs and STRs were compared within each category of relatedness (r = 0.5, 0.25, 0.125, and 0.0).
To address objective 2, kernel density estimates of the difference between each of the two molecular marker estimates and pedigree estimates of r were computed and plotted using the density function in the stats library in R. Confidence intervals were calculated using the HPDI (Highest Posterior Density Intervals) function in the rethinking package in R [McElreath 2012].
To address objective 3, we calculated the product-moment correlation between the matrix of pedigree relatedness estimates and the matrices of relatedness estimates calculated from molecular markers. The product-moment correlation is a measure of the linear relationship between two variables that reflects the direction and strength of a relationship, but not the slope; the data may still contain non-linear relationships that the product-moment correlation will not reflect. Because data in pairwise matrices, such as the matrices of relatedness utilized in this study, are non-independent, it is possible that spurious structures in the data drive correlations between the matrix of estimates derived from pedigrees and those derived from molecular markers. To determine the statistical significance of our results, a QAP test [Krackhardt 1987] was performed using the SNA package in R [Butts 2010]. After first calculating the product-moment correlation between two matrices, the rows and columns of one matrix are randomly reordered (permuted) and the product-moment correlation between the two matrices is recalculated. This procedure was repeated ten thousand times to obtain a distribution of correlation values. The probability that a correlation of the magnitude observed is spurious, due to a lack of independence in the data, is determined by comparing the original correlation to the resulting distribution.
To address objective 4, we used the netlogit (logistic regression for network data) function in the SNA package in R [Butts 2010] to model the ability of SNP-based and STR-based relatedness estimates to predict first-order pedigree relationships (r >=0.5, expressed as a binary variable). This method of data analysis carries with it the cost of significantly reduced resolution in our dependent variable, but provides an excellent direct comparison of the differential ability of SNPs and STRs to categorically predict animals as first-order kin. This method of data analysis allows for estimates of false positive and false negative rates, and also controls for possible dependencies in the data through QAP permutation.
To address objectives 5 and 6, we employed three forms of modeling to compare the relative performance of SNPs and STRs, using each of the three algorithms compared for estimating relatedness in this study. In order to maintain full resolution of our dependent variable, we utilized linear regression with a logistic response curve. Additionally, we employed ordered logistic regression, using the polr function in the MASS package in R, to compare the ability of SNPs and STRs to classify pairwise relatedness estimates into ordered categories (first-order kin, second-order kin, third-order kin, and non-kin). Finally, we utilized standard logistic regression to compare the ability of SNPs and STRs to discriminate first-order kin from other categories with each of the three relatedness estimation algorithms. We then conducted formal model comparisons of SNP-based and STR-based models using AICc and BIC in the bbmle package in R [Bolker 2012]. Unlike the use of p or r2 values to compare models (which are ad hoc methods), AICc and BIC are model comparison metrics derived from information theory [Burnham and Anderson 2002], and are the gold standard tools for statistical model evaluation. For the purposes of this study, AICc and BIC weights can be loosely understood as indicating the posterior probability that the specified model family minimizes out-of-sample prediction errors [McElreath 2011].
To address objective 7, we utilized the R script developed for this project to compute relatedness using an increasing number of SNPs, in order to investigate the number of SNPs required to effectively discriminate various orders of kin. The R script operates by randomly ordering the 81 SNPs, then iteratively recalculating pairwise relatedness between focal individuals using an increasing number of SNPs (in this case from 1 SNP to 81 SNPs). The algorithm repeats this process for all pairwise comparisons of the 31 Chinese Rhesus macaques using 100 random orderings of SNPs for each pairwise comparison to ensure that the SNP order contributes minimal bias to interpretation.
Results
Comparing Estimates of r between SNPs and STRs
Table 1 shows the mean values and standard deviations of SNP-based and STR-based estimates of r for which the pedigree data indicate relationships of r equal 0.5, 0.25, 0.125, and 0.0.
Table 1.
Means and Standard Deviations of r estimates based on SNPs and STRs in first-order, second-order, and third-order kin, and unrelated individuals (as calculated through pedigrees).
| Pedigree Relationship | N | SNP: Mean(r) | STR: Mean(r) | SNP: SD(r) | STR: SD(r) |
|---|---|---|---|---|---|
| 0.5 | 20 | 0.43369 | 0.396343 | 0.091193 | 0.088345 |
| 0.25 | 27 | 0.120589 | 0.085252 | 0.154994 | 0.102221 |
| 0.125 | 42 | 0.005701 | −0.01018 | 0.092786 | 0.081974 |
| 0.0 | 349 | −0.08049 | −0.07368 | 0.115119 | 0.063504 |
Both STRs and SNPs predict mean estimates of relatedness well below the expected values indicated by the pedigree data, but our R script includes the alleles of the individuals being compared in the calculation of population allele frequency. More accurate estimates could be generated by calculating population allele frequencies from a secondary data set in which the focal individuals do not appear, or by re-calculating the population allele frequency from the data but iteratively removing the focal pairs’ alleles for each relatedness estimate. However, both of these methods allow an individual to possess an allele that has no described frequency in the population, leading to a failure of the Lynch and Ritland [1999] algorithm. In most circumstances, the purpose of estimating r is not to precisely determine the true relatedness coefficients, but rather to discriminate close kin from unrelated, or remotely related individuals. Accordingly, the R script has been optimized to function reliably.
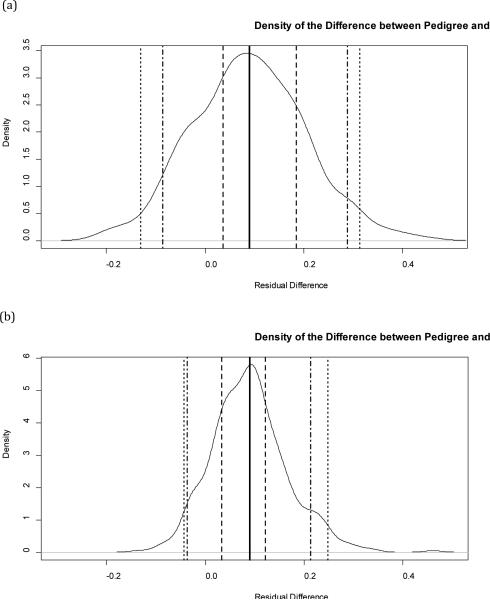
Although SNP-based and STR-based estimates of r have very similar mean differences from the pedigree based estimates (in general, both under-predict relatedness for the reasons described above), the density of difference between STR-based estimates and pedigree-based estimates of r is concentrated in a much smaller area near the mean than the density of difference between SNP-based estimates and pedigree-based estimates of r, as illustrated in Figure 1.
Figure 1.
Kernel Density Estimates
The data presented in Table 2 indicate that the deviation of STR-based estimates of relatedness from pedigree-based estimates of relatedness is smaller than that of SNP-based estimates.
Correlation between Pedigree Estimates of r and Molecular Marker Estimates of r
The level of arbitrariness in interpreting product-moment correlations requires that they be evaluated according to context and purpose. In the present study, other contributing factors such as imperfect pedigree information (e.g. errors in paternity assignment) and the degree of randomness inherent in the actual relatedness coefficient between relationships other than parent-offspring might decrease the product-moment correlation below 1. Despite these factors, the product-moment correlation between SNP-based estimates of r and pedigree-based estimates of r was 0.71, and the product-moment correlation between STR-based estimates of r and pedigree-based estimates of r was 0.80. These results suggest that both SNP-based and STR-based estimates of relatedness correlate strongly with pedigree estimates of relatedness. In both cases the entire distribution of re-calculated product-moment correlation between permuted matrices lies well below the product-moment correlation between the matrices of observed data (QAP p < 0.0001), which provides confidence that the correlation observed between matrices cannot be explained by spurious dependencies.
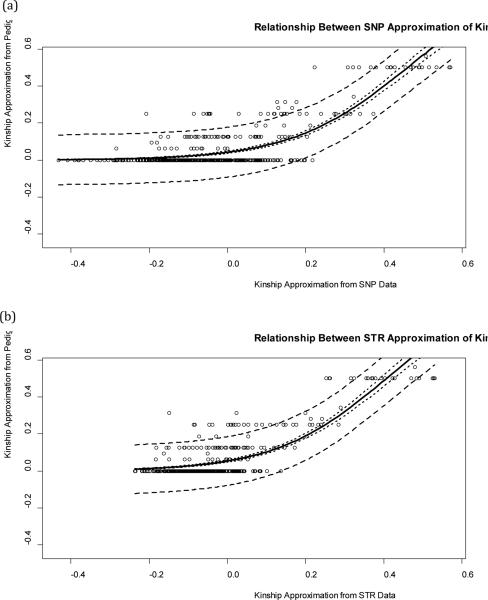
Regression of Pedigree Estimates on Molecular Marker Estimates
While a linear relationship between estimates of relatedness from molecular markers and pedigree data is expected, Figure 2 illustrates that linear models are sub-optimal for describing this relationship.
Figure 2.
Logistic Modeling
It is important to note that while the dependent variable is constrained to values between 0 and 1, the independent variable is unconstrained. Additionally, non-kin relationships in the data far outnumber kin relationships, leading to non-normally distributed data. A smooth spline curve suggested that modeling the mean with a logistic model would be optimal; we utilize three forms of logistic regression below to address our research questions.
1. The Network Logistic Regression Model
The netlogit function in the SNA package for R [Butts 2010] controls for network dependencies in the data, at the cost of reduced resolution in the dependent variable, which must be collapsed to a binary variable of first-order kin (r=0.5) or non-first-order kin (r<0.5). The results from matrix logistic regression show that SNP and STR genotype data predict first-order relatedness with indistinguishable error rates. Conditional on the pedigree information being true, both SNPs and STRs correctly predicted 442 of 444 non-first-order kin relationships, and 18 of 21 first-order kin relationships, leading to a false negative rate of 0.1428, and a false positive rate of 0.00455, QAP p < 0.0001.
2. Gaussian, Proportional Odds Logistic, and Logistic Regression Models
Since both the QAP test and the matrix logistic regression indicated that the magnitude of interdependence in our data is negligible, we utilized three other forms of model fitting, using methods that do not control for interdependencies in the data. In one case, we maintained full resolution in the dependent variable and fit Gaussian models with logistic response curves to the data; in the second case, we coded the dependent variable using ordered categories: unrelated (r<0.125), third-order kin (r=0.125), second-order kin (r=0.25), and first-order kin (r=0.5), and fit models using proportional odds logistic regression; and finally, we coded the dependent variable as a binary variable of first-order kin or non-first-order kin, and used standard logistic regression to compare the performance of SNPs and STRs. In each analysis, we compare the performance of STR and SNP genotype data, using the Queller and Goodnight [1994], Lynch and Ritland [1999], and Wang [2002] algorithms. We use AICc and BIC to formally compare the SNP-based and STR-based models. These analyses indicate that while both STRs and SNPs effectively predict pedigree estimates of relatedness, STRs explain more variation and are highly preferred by both AICc and BIC (information theoretic weights of ~100%) as shown in Table 3. Our main result, that 14 STRs outperform 81 SNPs in relatedness estimation, is robust to the particular algorithm utilized in relatedness estimation, as 8 out of 9 models indicate that STRs outperform SNPs in relatedness estimation (Table 3). The Wang [2002] algorithm appears to outperform all other algorithms for STR data, and the Queller and Goodnight [1994] algorithm performs best for SNP data in two of three cases.
Identifying the Number of SNPs Required to Discriminate Various Orders of Kin
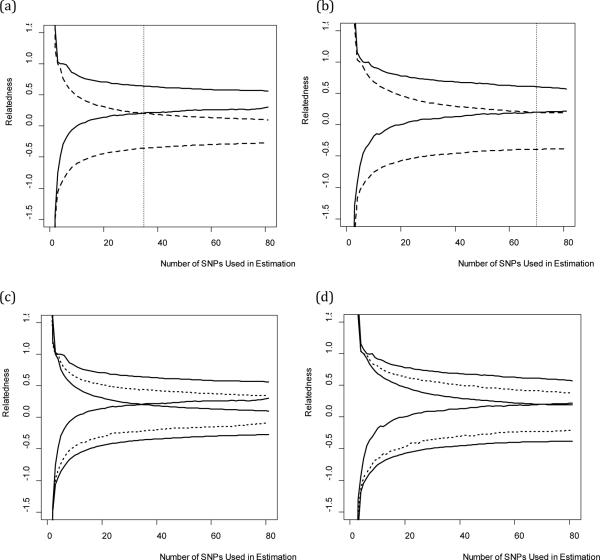
Figure 3 illustrates the decline in the variance of estimates of relatedness as an increasing number of SNPs are utilized in the estimation process. Figure 3a illustrates that at least 35 SNPs are required to separate the central 90% confidence intervals of first-order kin and non-kin; in other words, when 35 SNPs were used to estimate relatedness in this sample, less than 5% of first-order kin fall within the 90% confidence interval of non-kin, and vice versa. Figure 3b illustrates that 70 SNPs are required to separate the 98% confidence intervals of first-order kin and non-kin, indicating that less than 1% of first-order kin fall within the 98% confidence interval of non-kin, and vice versa.
Figure 3.
Estimating Relatedness Using an Increasing Number of SNPs
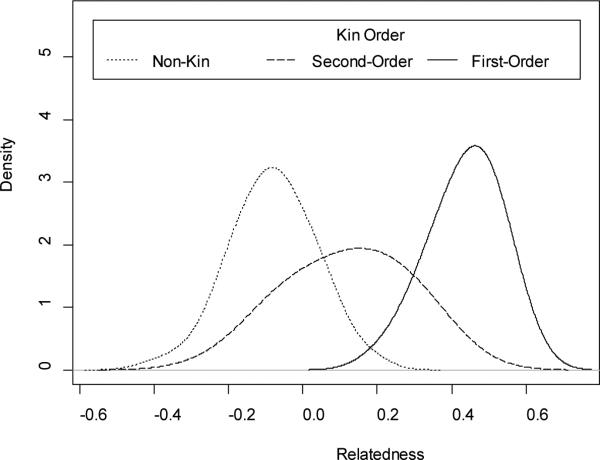
Figure 3c and Figure 3d indicate that greater than 81 SNPs are required to effectively discriminate the 90% and 98% confidence intervals (respectively) of second-order kin from the confidence intervals of first-order kin or non-kin. Future research should be designed to investigate the number of SNPs required to separate the distributions of second-order kin from other kin classes. It is important to note, that although 81 SNPs are not sufficient to fully separate the 90% or 98% confidence intervals of second-order kin from first-order kin or non-kin, probabilistic assignment of kin categories can be accomplished by computing the probability density of an observed relatedness estimate from each of the three (approximately) Gaussian distributions corresponding to each order of kin (see Figure 4), divided by the total probability density across all three distributions (if we assume, for simplicity, that these are the only classes of kin possible).
Figure 4.
Density of Relatedness Estimates (81 SNPs)
For example, in the empirical data utilized in this study, the Gaussian approximation of the first-order kin distribution is mean=0.43, sd= 0.09, the Gaussian approximation of the second-order kin distribution is mean=0.12, sd=0.15, and the Gaussian approximation of the non-kin distribution is mean= −0.08, sd=0.11. If one were to observe a relatedness estimate of r=0.2, one could compute the probability density of this observation under each of the above Gaussian distributions (0.17, 2.3, and 0.14, respectively), and divide by the summed probability density across all distributions (2.61), and conclude with approximately 88% certainty that the pair of animals are second-order kin (5% non-kin, and 7% first-order kin). The choice to use any ambiguously classified animal could then be based on cost-benefit analysis.
Discussion
Within each order of kin (r = 0.5, 0.25, 0.125, and 0.0) as defined by pedigree data, 14 STRs produce less variation in estimates of r than 81 SNPs. The product-moment correlation between the STR-based estimates of relatedness and the pedigree-based estimates of relatedness was 1.13 times as large as the product-moment correlation between the SNP-based estimates of relatedness and the pedigree-based estimates of relatedness. Formal model comparison using AICc and BIC suggests that when using a small set of polymorphic markers, STRs are better overall predictors of relatedness than SNPs, in that STR-based models show less deviance than SNP-based models, and predict pedigree relatedness with smaller residuals. These results are only valid in this particular data set, with these particular sets of STRs and SNPs; future analysis in other macaque populations with larger numbers of molecular markers is needed to investigate the extent to which our observations are more widely generalizable.
However, our results are consistent with previous model-based studies that have found STRs to be better predictors of relatedness than SNPs [Butler et al. 2007], probably because STRs are more highly polymorphic than SNPs. However, the product-moment correlations calculated between both STR-based and SNP-based estimates of relatedness and pedigree-based estimates of relatedness were quite high. Both SNP-based and STR-based estimates of relatedness are sufficient to distinguish first-order kin from lesser-related and unrelated individuals, and do so with identical error rates. This suggests that SNP-based estimates of r may be adequate for estimating kinship in primate colonies, especially when it is only necessary to distinguish first-order kin from more remotely related individuals.
The effectiveness of both STRs and SNPs in reliably estimating r depends on the standard error of the estimate of r, a function of the number of loci used and their frequencies. The lowest standard error in estimates of r achievable is approximately 1/√N(m-1) where N and m are the numbers of loci employed and the number of equally frequent alleles, respectively [Lynch and Ritland 1999]. A standard error of 0.1 (100 SNPs with minor allele frequencies (MAFs) of 0.5, or 20 STRs with 5 equally frequent alleles) should assure discrimination among most first-order and second-order relatives and unrelated individuals. While this level was achieved by STRs for first-order kin, second-order kin, and unrelated individuals, the standard error of r estimated from SNPs exceeded 0.1 for second-order kin.
Further work remains to be done to identify the number of SNPs required to effectively estimate relatedness for more remote classes of kin and for Indian rhesus macaques, the most prevalent subspecies at the National Primate Research Centers. The additional 15 SNPs excluded for use in this study of Chinese rhesus, in addition to the increased heterozygosity of the other 81 SNPs, may substantially improve SNP-based estimation of relatedness in Indian rhesus macaques.
Conclusions and Future Directions
The decision to use STRs over SNPs in estimating kinship for primate colony management or experimental research design may be motivated by a desire for extra precision, and might be a reasonable strategy when it is necessary to distinguish kin relations more distant than first-order. However, if it is only necessary to distinguish first-order kin relationships from all other relationships, the use of the SNP panel described in this paper for relatedness estimation in the context of primate colony management is defensible, provided that the SNPs are sufficiently variable in the study population to provide relevant information about relatedness.
It remains possible that adding additional SNPs to a panel, or selecting SNPs with greater variance, might lead to more accurate estimates of relatedness in rhesus macaques than a standard panel of STRs without incurring greater costs. Because the number of available SNP loci exceeds that of STR loci overall, SNPs with sufficiently high MAFs will likely be identified for use in primate colony management. Future empirical research should be designed to evaluate the number of highly variable SNP loci required to effectively discriminate various orders of kin.
Supplementary Material
Acknowledgements
The authors wish to express their substantial thanks to the other members of the Genetics and Genomics Working Group of the National Nonhuman Primate Research Consortium (L. Cox, R. Wiseman, D. O'Connor, R. Palermo, J. Nylander, C.J. Dubay, Z.P. Johnson, M.G. Katze, L.S. Kean, G.M. Miller, E.J. Vallender, and J. Rogers) for their comments and suggestions during the development of this study. The genetic tests reported here developed out of discussions within the Genetics and Genomics Working Group, and the authors wish to thank all who contributed to that process. Funding for the development of this SNP assay was provided by the Office of Research Infrastructure Programs in the Office of the Director, NIH. This work began when that organization was part of the Comparative Medicine program of the National Center for Research Resources, NIH. We wish to express our sincere thanks to Dr. John Harding for his consistent and valuable support of the Genetics and Genomics Working Group and all its activities.
Finally, we wish to thank Anthony Di Fiore and two anonymous reviewers for very helpful critiques and recommendations.
Footnotes
Author Contributions Box
Cody Ross – designed research, performed research, analyzed data, programming, wrote paper
Jessica A. Weise – wrote paper, edited paper
Sarah Bonnar – wrote paper
David Nolin – analyzed data, edited paper
Jessica S. Trask – edited paper, contributed data, developed SNP panel
David Glenn Smith – conceived study, edited paper, contributed data, developed SNP panel
Betsy Ferguson - developed SNP panel, edited paper
James Ha - contributed data
H. Michael Kubisch - contributed data
Amanda Vinson – contributed data, edited paper
Sree Kanthaswamy – contributed data, edited paper, developed SNP panel
References
- Amorim A, Pereira L. Pros and cons in the use of SNPs in forensic kinship investigation: a comparative analysis with STRs. Forensic Science Int. 2005;150(1):17–21. doi: 10.1016/j.forsciint.2004.06.018. [DOI] [PubMed] [Google Scholar]
- Andrade MC, Penedo MC, Ward T, et al. Determination of genetic status in a closed colony of rhesus monkeys (Macaca mulatta). Primates. 2004;45:183–186. doi: 10.1007/s10329-004-0084-x. [DOI] [PubMed] [Google Scholar]
- Bolker B. bbmle: Tools for general maximum likelihood estimation. R package version 1.0.4.1. 2012 [Google Scholar]
- Burnham K, Anderson D. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach. 2nd edition. Springer-Verlag; 2002. [Google Scholar]
- Butler JM, Coble MD, Vallone PM. STRs vs. SNPs: thoughts on the future of forensic DNA testing. Forensic Sci Med Pathol. 2007:200–205. doi: 10.1007/s12024-007-0018-1. [DOI] [PubMed] [Google Scholar]
- Butts CT. sna: Tools for Social Network Analysis. R package version 2.1. 2010 [Google Scholar]
- Csilléry K, Johnson T, Beraldi D, et al. Genetics. 2006;173(4):2091–2101. doi: 10.1534/genetics.106.057331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dario P, Ribeiro T, Espinheira R, et al. SNPs in paternity investigation: The simple future. Forensic Science International: Genetics Supplement Series. 2009;2(1):127–128. [Google Scholar]
- Domingo-Roura X, Lopez-Giraldez T, Shinohara M, et al. Hypervariable Microsatellite Loci in the Japanese Macaque (Macaca fuscata) Conserved in Related Species. American Journal of Primatology. 1997;43:357–360. doi: 10.1002/(SICI)1098-2345(1997)43:4<357::AID-AJP7>3.0.CO;2-W. [DOI] [PubMed] [Google Scholar]
- Eding H, Meuwissen T. Marker-based estimates of between and within population kinships for the conservation of genetic diversity. Animal Breeding and Genetics. 2001;118:141–159. [Google Scholar]
- Estoup A, Jarne P, Cornuet JM. Homoplasy and mutation model at microsatellite loci and their consequences for population genetics analysis. Molecular Ecology. 2002;11(9):1591–1604. doi: 10.1046/j.1365-294x.2002.01576.x. [DOI] [PubMed] [Google Scholar]
- Glover KA, Hansen MM, Lien S, et al. A comparison of SNP and STR loci for delineating population structure and performing individual genetic assignment. BMC Genetics. 2010;11(2):1–12. doi: 10.1186/1471-2156-11-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagen EH. Descent. Version 2.0. 2005 Retrieved from http://itb.biologie.hu-berlin.de/~hagen/Descent/
- Hardy OJ, Vekemans X. SPAGeDi: a versatile computer program to analyse spatial genetic structure at the individual or population levels. Molecular Ecology Notes. 2002;2:618–620. [Google Scholar]
- Hauser L, Baird M, Hilborn R, et al. An empirical comparison of SNPs and microsatellites for parentage and kinship assignment in a wild sockeye salmon (Oncorhynchus nerka) population. Molecular Ecology Resources. 2011;11:150–161. doi: 10.1111/j.1755-0998.2010.02961.x. [DOI] [PubMed] [Google Scholar]
- Kalinowski ST, Wagner AP, Taper ML. ML-RELATE: A Computer Program for Maximum Likelihood Estimation of Relatedness and Relationship. Molecular Ecology Notes. 2006;6(2):576–579. [Google Scholar]
- Kanthaswamy S, von Dollen A, Kurushima JD, et al. Microsatellite markers for standardized genetic management of captive colonies of rhesus macaques (Macaca mulatta). American Journal of Primatology. 2006;68(1):73–95. doi: 10.1002/ajp.20207. [DOI] [PubMed] [Google Scholar]
- Kanthaswamy S, Capitanio JP, Dubay CJ, et al. Resources for Genetic Management and Genomics Research on Non-Human Primates at the National Primate Research Centers (NPRCs). Journal of Medical Primatology. 2009;38:17–23. doi: 10.1111/j.1600-0684.2009.00371.x. [DOI] [PubMed] [Google Scholar]
- Krackhardt D. QAP partialling as a test of spuriousness. Social Networks. 1987;9:171–186. [Google Scholar]
- Li M, Ismo S, Timo T, et al. A Comparison of Approaches to Estimate the Inbreeding Coefficient and Pairwise Relatedness Using Genomic and Pedigree Data in a Sheep Population. PLoS ONE. 2011;6(11):e26256. doi: 10.1371/journal.pone.0026256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, Ritland K. Estimation of Pairwise Relatedness with Molecular Markers. Genetics. 1999;152:1753–1766. doi: 10.1093/genetics/152.4.1753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McElreath R. rethinking. R package version 1.02. 2012 [Google Scholar]
- McElreath R. Statistical Rethinking: A Mostly Bayesian Course in Mostly Non-Bayesian Statistics. 2011. URL xcelab.net/rm/?page_id=598. [Google Scholar]
- Morin P, Luikart G, Wayne RK, et al. SNPs in ecology, evolution and conservation. Trends in Ecology and Evolution. 2004;19(4):208–216. [Google Scholar]
- Rousset F. Genepop'007: a complete reimplementation of the Genepop software for Windows and Linux. Molecular Ecology Resources. 2008;8:103–106. doi: 10.1111/j.1471-8286.2007.01931.x. [DOI] [PubMed] [Google Scholar]
- R Development Core Team . R: A language and environment for statistical computing. R Foundation for Statistical Computing. Vienna, Austria: 2010. ISBN 3-900051-07-0, URL http://www.R-project.org/ [Google Scholar]
- Satkoski Trask JA, Garnica WT, Kanthaswamy S, et al. 4040 Novel SNPs for genomic analysis in the rhesus macaque (Macaca mulatta). Genomics. 2011;98:352–358. doi: 10.1016/j.ygeno.2011.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith DG, Kanthaswamy S, Viray J, et al. Additional Highly Polymorphic Microsatellite (STR) Loci for Estimating Kinship in Rhesus Macaques (Macaca mulatta). American Journal of Primatology. 2000;50:1–7. doi: 10.1002/(SICI)1098-2345(200001)50:1<1::AID-AJP1>3.0.CO;2-T. [DOI] [PubMed] [Google Scholar]
- Wang J. COANCESTRY: a program for simulating, estimating, and analyzing relatedness and inbreeding coefficients. Molecular Ecology Resources. 2011;11(1):141–145. doi: 10.1111/j.1755-0998.2010.02885.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.