Checking Fine and Gray Subdistribution Hazards Model with Cumulative Sums of Residuals

Abstract

Recently, Fine and Gray (1999) proposed a semi-parametric proportional regression model for the subdistribution hazard function which has been used extensively for analyzing competing risks data. However, failure of model adequacy could lead to severe bias in parameter estimation, and only a limited contribution has been made to check the model assumptions. In this paper, we present a class of analytical methods and graphical approaches for checking the assumptions of Fine and Gray’s model. The proposed goodness-of-fit test procedures are based on the cumulative sums of residuals, which validate the model in three aspects: (1) proportionality of hazard ratio, (2) the linear functional form and (3) the link function. For each assumption testing, we provide a p-values and a visualized plot against the null hypothesis using a simulation-based approach. We also consider an omnibus test for overall evaluation against any model misspecification. The proposed tests perform well in simulation studies and are illustrated with two real data examples.

1 Introduction

Competing risks data arise in medical studies where patients may experience failure from multiple causes, and failure from one cause precludes observation of failure from the other causes. Fine and Gray (1999) proposed a semi-parametric proportional subdistribution hazards model (FG model). It can be applied to evaluate the effects of covariates on the cumulative incidence function directly. The FG model has been using extensively in cancer studies, epidemiological studies, and many other biomedical studies (Scrucca et al, 2007; Wolbers et al, 2009; Kim, 2007; Lau et al, 2009). Similarly to the Cox regression model for the regular time to event data (Lin et al, 1993), the FG model may also fail in three ways: (1) the proportional hazards assumption does not hold, i.e. the subdistribution hazard ratio is time-variant; (2) the functional forms of individual covariates in the exponent of the model are misspecified; (3) the link function, i.e. the exponential form for the subdistribution hazard ratio is not appropriate. It is well known that violation of any one of these three model assumptions, required for the Cox proportional hazards model, may lead to severely biased effect for the statistical inference (Lin et al, 1993).

Although it is important to validate the FG model, only limited contributions have been made to check the model assumptions. For checking the proportionality assumption, Zhou et al (2013) proposed a simple goodness-of-fit test by adding a time dependent covariate, and showed through a simulation study that this simple test performed well. However, the power of this simple test may depend on the specific pattern of the covariate effect over time, under the alternative models. Scheike and Zhang (2008) considered a goodness-of-fit test by estimating the regression effect nonparametrically over time based on their direct binomial modeling approach. In general, such nonparametric goodness-of-fit tests may have lower power compared to the specific alternative model based test. Perme and Andersen (2008) proposed using a pseudo-value approach to test the proportionality assumption and a linear functional form of individual covariates for right censored competing risks data. Pseudo-observations are often calculated for a pre-fixed set of time-points. Some computation issues may occur when one needs to calculate the pseudo-observations for a large set of time points. Pseudo-value based goodness-of-fit tests may be difficult to employ when the censoring distribution depends on some continuous covariates.

Martingale residual based goodness-of-fit test has been well developed for checking the Cox model (Andersen et al, 1993). Alternatively, Lin et al (1993) proposed a goodness-of-fit test based on cumulative sums of martingale residuals to check the proportionality assumption, functional forms of covariates effect, and the link function in the Cox model for right censored survival data. In this paper, we extend their approach (Lin et al, 1993) to the right censored competing risks data, using the cumulative sums of residuals to check the FG model. For checking the proportionality assumption, we propose using the score process, which is a special case of the cumulative sums of residuals on time. Compared to the approach of adding a time-dependent variable (Zhou et al, 2013), our proposed test has a better performance when the trend of the covariate effect is not modeled correctly over time. We also propose using the cumulative sums of residuals on covariates values to check the linearity and the link function assumption of the FG model. All tests proposed in this study are based on a simulation based approach for the null limiting distribution of the test process. Besides the numerical results, we provide each test with a diagnostic plot for the visual checking. An omnibus test accumulating the residuals on time and covariate value simultaneously, is considered to evaluate the validation of FG model in an overall view.

In section 2, we briefly introduce the background of FG model and some techniques which will be used for the model checking. In section 3, we examine the performance of the proposed method through simulation studies. In the simulation studies, we test against each of the assumptions with some commonly seen alternatives. We show the application of the proposed approach to two real datasets in section 4 and conclude with discussion in section 5.

2 Model checking techniques

Let T and C be the underlying time to event and censoring, and X = T ∧ C. Δ = {T ≤ C} is the non-censoring indicator, and 3 represents cause of failure. We usually observe i.i.d. (X_i, Δ_i, Δ_i ε_i), where Δ_iε_i contains the information of both censoring and cause of failure. For the competing risk data, one quantity of interest is the cumulative incidence function, the probability of failure due to one specific cause (assuming to be cause 1),

$$F_1(t)=P(T_i\le t,{\epsilon }_i=1)={\int }_0^{t}S(u^{-})d{\mathit{\Lambda }}_1(u),$$

where S(t) is the overall survival function and Λ₁ (t) is the cumulative cause-specific hazard for cause 1. Fine and Gray (1999) proposed a semi-parametric proportional regression model for the subdistribution hazard function

$${\lambda }_1^{\ast }(t\mid \mathbf{Z})={\lambda }_{10}^{\ast }(t)exp\{{\mathit{\beta }}^{\top }\mathit{Z}\},$$ (1)

where ${\lambda }_{10}^{\ast }(t)$ is the baseline subdistribution hazard, β are the covariates effect for Z. Let $N_i^1(1)=𝟙\{T_i\le t,{\epsilon }_i=1\}$ be the cause specific counting process, $Y_i^1(t)=1-N_i^1(t^{-1})$ is the risk set associated with the subdistribution hazard. When the right censoring is present, $N_i^1(t)$ and $Y_i^1(t)$ will not be fully observed. Recently, Fine and Gray (1999) proposed using the inverse probability of censoring weighting technique (IPCW) with a time-dependent weight function w_i(t, G_c) = r_i(t)G_c(t)/G_c(T_i ∧ t), where r_i(t) = 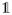{C_i ≤ T_i ∧ t} and G_c(t) is the survival function for the censoring distribution. It is easy to see both $w_i(t,{\widehat{G}}_c){dN}_i^1(t)$ and $w_i(t,{\widehat{G}}_c)Y_i^1(t)$ are computable for all time t. IPCW can be generalized to allow the dependency between C and Z as suggested in Fine and Gray (1999). In this study, we estimate G_c(t) nonparametrically using the Kaplan-Meier estimator, denoted as Ĝ_c(t), or Ĝ_c for simplicity. The score equation and information matrix can be obtained by taking the first and negative second derivative of the partial likelihood:

$$\begin{array}{l}\mathit{U}(\mathit{\beta })=\sum _{i=1}^n{\int }_0^{\infty }\left\{{\mathit{Z}}_i-\frac{{\mathit{S}}_1(\mathit{\beta },t)}{S_0(\mathit{\beta },t)}\right\}{w}_i(t,{\widehat{G}}_c){dN}_i^1(t),\\ \mathit{I}(\mathit{\beta })=\sum _{i=1}^n{\int }_0^{\infty }\left[\frac{{\mathit{S}}_2(\mathit{\beta },t)}{S_0(\mathit{\beta },t)}-{\left\{\frac{{\mathit{S}}_1(\mathit{\beta },t)}{S_0(\mathit{\beta },t)}\right\}}^{\otimes 2}\right]w_i(t,{\widehat{G}}_c){dN}_i^1(t),\end{array}$$

where ⊗ denotes the Kronecker product and

$${\mathit{S}}_k(\mathit{\beta },t)=\sum _{i=1}^n{w}_i(u,{\widehat{G}}_c)Y_i(u){\mathit{Z}}_i^{\otimes k}exp\{{\mathit{\beta }}^{\top }{\mathit{Z}}_i\},\text{for}k=0,1,2.$$

The β is estimated by solving the score equation U(β̂) = 0, and the cumulative baseline subdistribution function, ${\mathit{\Lambda }}_{10}^{\ast }(t)={\int }_0^t{\lambda }_{10}^{\ast }(u)du$ is estimated by

$${\widehat{\mathit{\Lambda }}}_{10}^{\ast }(t)=\sum _{i=1}^n{\int }_0^t\frac{w_i(u,{\widehat{G}}_c){dN}_i^1(u)}{S_0(\widehat{\mathit{\beta }},u)}.$$

Under the null hypothesis of FG model, the differences between the weighted counting processes and their respective intensity functions are

$$w_i(u,{\widehat{G}}_c){dM}_i^1(t)=w_i(u,{\widehat{G}}_c){dN}_i^1(t)-w_i(u,{\widehat{G}}_c)Y_i^1(t)exp({\mathit{\beta }}_0^{\top }{\mathit{Z}}_i)d{\mathit{\Lambda }}_{10}^{\ast }(t).$$ (2)

Most importantly, $w_i(u,{\widehat{G}}_c){dM}_i^1(t)$ is a zero-mean Gaussian process. The residuals are defined as

$$w_i(t,{\widehat{G}}_c)d{\widehat{M}}_i^1(t)=w_i(t,{\widehat{G}}_c){dN}_i^1(t)-w_i(t,{\widehat{G}}_c)Y_i^1(t)exp({\widehat{\mathit{\beta }}}^{\top }{\mathit{Z}}_i)d{\widehat{\mathit{\Lambda }}}_{10}^{\ast }(t).$$ (3)

2.1 Checking the proportional hazards assumption

We use the observed score process U(β̂, t) for checking the proportional hazards assumption. It can be shown that the score process equals to a special form of the cumulative sums of residuals over time:

$$\mathit{U}(\widehat{\mathit{\beta }},t)=\sum _{i=1}^n{\int }_0^t{\mathit{Z}}_i{w}_i(u,{\widehat{G}}_c)d{\widehat{M}}_i^1(u),$$

Under the null hypothesis that FG model is valid, by involving the equation (2) and (3) we obtain

$$\begin{array}{l}U(\widehat{\mathit{\beta }},t)=\sum _{i=1}^n{\int }_0^t{\mathit{Z}}_i{w}_i(u,{\widehat{G}}_c)\left\{{dN}_i^1(u)-Y_i^1(u)exp({\widehat{\mathit{\beta }}}^{\top }{\mathit{Z}}_i)d{\widehat{\mathit{\Lambda }}}_{10}^{\ast }(u)\right\}\\ =\sum _{i=1}^n{\int }_0^t{\mathit{Z}}_i{w}_i(u,{\widehat{G}}_c){dM}_i^1(u)-\sum _{i=1}^n{\int }_0^t{\mathit{Z}}_i{w}_i(u,{\widehat{G}}_c)Y_i^1(u)\left\{exp({\widehat{\mathit{\beta }}}^{\top }{\mathit{Z}}_i)d{\widehat{\mathit{\Lambda }}}_{10}^{\ast }(u)-exp({\mathit{\beta }}_0^{\top }{\mathit{Z}}_i)d{\widehat{\mathit{\Lambda }}}_{10}^{\ast }(u)\right\}\end{array}$$

By the Taylor expansions of U(β̂, t) at β₀ and some arguments, the observed score process is shown to be asymptotically equivalent to the summation of n independent and identically distributed random processes,

$$\mathit{U}(\widehat{\mathit{\beta }},t)=\sum _i^n{\mathit{W}}_i^{(p)}({\mathit{\beta }}_0,t)+o_p(1),$$

where the explicit form of ${\mathit{W}}_i^{(p)}(\mathit{\beta },t)$ and a detailed derivation of the limiting distribution under the FG model can be found in the Appendix. The limiting distributional of $w_i(u,{\widehat{G}}_c)M_i^1(u)$ is asymptotically equivalent to the limiting distribution of $w_i(u,{\widehat{G}}_c)N_i^1(u)V_i$, where $w_i(u,{\widehat{G}}_c)N_i^1(u)$ is the observed counting process and V_i, i = 1, …, n, are i.i.d. standard normal variables (Lin et al, 1993). Therefore, ${\mathit{W}}_i^{(p)}$ is replaced by the product of ${\widehat{\mathit{W}}}_i^{(p)}$ and a normal variable V_i, where ${\widehat{\mathit{W}}}_i^{(p)}$ is a plug-in estimator for ${\mathit{W}}_i^{(p)}({\mathit{\beta }}_0,t)$.

To check the proportionality assumption for the jth covariate, we consider the score process

$$B_j^{(p)}(t)={\{I_{jj}^{-1}(\widehat{\mathit{\beta }})\}}^{1/2}{U}_j(\widehat{\mathit{\beta }},t),\text{for}j=1,\dots ,m,$$

where U_j and $I_{jj}^{-1}$ are the jth element and jth diagonal element of U and I⁻¹, respectively, and m is the total number of covariates. Under the FG model, $B_j^{(p)}(t)$ is, asymptotically, a zero-mean Gaussian process and has the same limiting distributions as

$${\{I_{jj}^{-1}(\widehat{\mathit{\beta }})\}}^{1/2}\sum _i^n{\widehat{W}}_{ij}^{(p)}(\widehat{\mathit{\beta }},t)V_i,$$

and ${\widehat{W}}_{ij}^{(p)}$ is the jth element of ${\widehat{\mathit{W}}}_i^{(p)}=({\widehat{W}}_{i1}^{(p)},\cdots ,{\widehat{W}}_{im}^{(p)})$. Resampling techniques can be used for the supremum test over a fixed time interval. Let

$$b_j^{(k)}=\underset{t}{sup}\left|{\{I_{jj}^{-1}(\widehat{\mathit{\beta }})\}}^{1/2}\sum _i^n{\widehat{W}}_{ij}^{(p)}(\widehat{\mathit{\beta }},t)V_i^{(k)}\right|,\text{for}k=1,\dots ,K,$$

where K is the total number of realizations. The p-value of proposed test can be approximated by

$$\frac{1}{K}\sum _{k=1}^K𝟙\left\{\underset{t}{sup}\left|B_j^{(p)}(t)\right|\ge b_j^{(k)}\right\}.$$

We can also plot the observed score process $B_j^{(p)}(t)$ versus the follow-up time. Under the null hypothesis, $B_j^{(p)}(t)$ asymptotically equals to a zero-mean Gaussian process, which fluctuates randomly around zero. To access how unusual the observed process is, we may plot it along with a few simulated limiting processes under FG model. If the proportionality assumption is invalid, the observed process will be isolated above or below those simulated processes for some time periods.

To evaluate the overall proportionality assumption, we consider

$$\underset{t}{sup}\sum _{j=1}^m\left|{\left\{I_{jj}^{-1}(\widehat{\mathit{\beta }})\right\}}^{1/2}{U}_j(\widehat{\mathit{\beta }},t)\right|.$$

The overall plot and the p-value of the supremum test can be generated exactly the same as we check the proportionality for a single covariate.

2.2 Checking the functional form and the link function

To check the functional form of jth covariate, we consider

$$B_j^{(f)}(z_j)=\sum _{i=1}^n{\int }_0^{\infty }𝟙\{Z_{ij}\le z_j\}{w}_i(u,{\widehat{G}}_c)d{\widehat{M}}_i^1(u),\text{for}j=1,\dots ,m,$$

and to check the link function, we consider

$$B^{(l)}(x)=\sum _{i=1}^n{\int }_0^{\infty }𝟙\left\{{\widehat{\mathit{\beta }}}^{\top }{\mathit{Z}}_i\le x\right\}{w}_i(u,{\widehat{G}}_c)d{\widehat{M}}_i^1(u).$$

Both processes are cumulative sums of residuals with respect to the covariate values. For the linear functional form, we focus on the change of each single covariate value. For the link function, we catch the value change of all covariates simultaneously by (β̂^TZ), which reflects on the adequacy of link function. Similarly as the process proposed for checking the proportionality of subdistribution hazards, we can show that, under the FG model, these two processes asymptotically equals to zero-mean Gaussian processes. The limiting processes can be simulated as well (see Appendix for details). Resampling techniques can be used to estimate the p-values the supremum tests. Plotting the observed process and a few simulated limiting processes under the FG model versus the covariate values can be used for visually checking the linearity of functional form and the link function.

2.3 An omnibus test for each covariate

Summing up the residuals, with respect to t and z simultaneously, would offer a global checking of the model. Consider

$${\mathit{B}}^{(o)}(t,\mathit{z})=\sum _{i=1}^n{\int }_0^t𝟙\{{\mathit{Z}}_i\le \mathit{z}\}{w}_i(u,{\widehat{G}}_c)d{\widehat{M}}_i^1(u),$$

Since B^(o)(t, z) is, asymptotically, a zero-mean Gaussian process under the null hypothesis of the FG model (see Appendix for details), we can construct a lack of fit test based on resampling techniques as well. Plotting the observed process over t and z simultaneously would give an omnibus view on model adequacy. But since it is a high-dimensional plot, some technical issues need to be considered, which are not pursued in this study.

3 Simulation study

We evaluated the performance of the proposed approaches by simulation studies. The simulation studies were designed in two aspects: first, we tested the proportional hazards assumption, which used the cumulative residuals with respect to time; second, we tested the linear functional form and the link function, which used the cumulative residual with respect to covariate values (note that only continuous covariate will be considered here). All simulation studies were designed for 15% and 30% censoring, with total sample sizes of 50, 100 and 300, respectively. All censoring time were generated independently from a uniform random variable, U(0, τ], where τ was used to adjust the censoring rate. For each setting, we replicated 5000 repeated samples for the type I error rate and 2000 samples for the power of the proposed tests. Significance level α was set at 0.05 throughout the simulation study unless otherwise specified.

3.1 proportional hazards assumption

Suppose we have two groups in a univariate model with the only covariate Z. Half of the subjects belong to group 1 (Z = 1) and the other half belong to group 2(Z = 0). The type I error rate was evaluated under the null hypothesis with the data generated from the FG model. Respectively, the cumulative incidence functions for cause 1 and cause 2 are:

$$\begin{array}{l}{F}_1(t\mid Z)=1-{\{1-p_1(1-e^{-t})\}}^{exp(\beta Z)},\\ F_2(t\mid Z)={(1-p_1)}^{exp(\beta Z)}\left[1-e^{\{-texp(\beta Z)\}}\right]\end{array}$$

where p₁ = F₁(∞|Z = 0) is the cumulative incidence probability of cause 1 for Z = 0 as t goes to infinity, and it was set to be 0.66, and β was set to be 0.2 with F₁(∞|Z = 1) = 0.73. We first determined the cause of event by generating a uniform variable u_i ~ U[0, 1]. If u_i ≤ F₁(∞|z_i), then the cause of failure was set ε_i = 1, and the failure time was generated from F₁(t|z_i)/F₁(∞|z_i) using inverse distribution method; otherwise, the failure time was generated from F₂(t|z_i)/F₂(∞|z_i). The Table 1 shows the type I error under the null hypothesis. The type I error rates were consistently close to the nominal level when the sample sizes were getting large.

Table 1.

Type I Error for Testing the Proportional Hazards Assumption

n	c(%)	Type I
50	15	0.0624
50	30	0.0642
100	15	0.0606
100	30	0.0564
300	15	0.0536
300	30	0.0536

Under the alternative hypothesis, the proportional hazards assumption does not hold. We consider following alternative subdistribution hazards for the cause 1,

$${\lambda }_1^{\ast }(t\mid Z)={\lambda }_{10}^{\ast }(t)exp\{\beta (t)Z\},$$ (4)

where β(t) counts the time-varying treatment effect. To study the power of our proposed test, we generated data from two types of β(t). We assume the treatment effect has a linear function of time t, i.e. β(t) = β + θt. The baseline subdistribution hazard function in model (4) was set to

$${\lambda }_{10}^{\ast }(t)=\gamma exp(\rho t).$$

A uniform variable u was generated from U(0, 1) to determine the cause of event, and we fixed the probability of cause 1 at 0.66, for simplicity. If u ≤ 0.66, the failure time was generated from F₁(t|Z); otherwise, the failure time was generated from F₂(t|Z). The cumulative incidence function of cause 1 equals to

$$F_1(t\mid Z)=1-exp\{-{\mathit{\Lambda }}_1^{\ast }(t\mid Z)\}=1-exp\left[-{\int }_0^t\gamma exp\{(\rho +\theta Z)s+\beta Z\}ds\right].$$

The failure time of cause 2 was generated from an exponential distribution with rate exp(αZ), given F₂(∞|Z) = 1 − F₁(∞|Z). Here we set β = 0, θ = −8, ρ = −5, α = 2 and α = −0.5. In parallel to the proposed approach, we also fitted the same data using Fine and Gray’s model with β(t) = t, log(t), and t² (Zhou et al, 2013). Table 2 shows that when the treatment has a linear time-varying effect, fitting time-varying Fine and Gray’s model with linear effect gave the highest power. The proposed test and the other two time-varying effect models performed slightly worse than the liner effect model, but all had very reasonable power. From the results, we can see that if the form of treatment effect is correctly specified, it would have the largest power. But when the treatment effect is misspecified, our test would give a comparable and even better power.

Table 2.

Estimated Power for Testing Proportional Hazards Assumption

n	c(%)	Proposed	t	t2	log(t)
50	15	0.3260	0.4305	0.2800	0.2700
50	30	0.2100	0.2815	0.2215	0.1795
100	15	0.5560	0.7840	0.5490	0.4495
100	30	0.3920	0.5870	0.4405	0.3085
300	15	0.9590	0.9985	0.9295	0.8910
300	30	0.8420	0.9780	0.8775	0.7365

In practice, the treatment effect may have a more complicated relationship with time. For example, the treatment has two different effects before and after time t₀, where t₀ is unknown. To evaluate the performance of proposed test under this situation, the data were generated from model (4) with treatment effect β(t) = β₁ 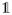(t ≤ t₀) + β₂ 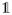(t > t₀). For simplicity, we assume ${\lambda }_{10}^{\ast }(t)=1$, therefore

$$F_1(t\mid Z)=1-exp\left[-{\int }_0^{t}exp\{Z{\beta }_1𝟙(u\le t_0)+Z{\beta }_2𝟙(u>t_0)\}du\right].$$

The treatment effects, β₁ and β₂ were set as 1 and 0.2, respectively, and t₀ was set as 0.5. The results in Table 3 show the power of our proposed test and the tests based on fitting Fine and Gray’s model with three different time-varying effects. In this case, our proposed test produced better power than any of the tests based on a pre-specified alternative form of the covariate effect.

Table 3.

Estimated Power for Testing Proportional Hazards Assumption

n	c(%)	Proposed	t	t2	log(t)
50	15	0.3510	0.2450	0.1450	0.2565
50	30	0.2045	0.1680	0.1385	0.1785
100	15	0.5770	0.4350	0.2275	0.4050
100	30	0.3760	0.3215	0.2050	0.2560
300	15	0.9715	0.9125	0.4930	0.8775
300	30	0.8025	0.7620	0.3835	0.5905

3.2 Linear functional form and link function

We use the cumulative sums of residuals over covariate values for testing both the linear functional form and the link function. The former sums up the values for each individual covariate, while the latter sums up the combination of all covariates. To study the type I error rate, the data were generated from model (1) with a single covariate Z, where Z = {0, ⋯, 9}, with equal proportions. Here we set β = 0.2. Table 4 shows that the type I error rates were consistently close to the nominal level.

Table 4.

Type I Error and Estimated Power for Testing the Functional Form and the Link Function

n	c(%)	Type I	Test Function Form	Test Link Function
50	15	0.0568	0.1575	0.1325
50	30	0.0556	0.2055	0.1350
100	15	0.0514	0.2505	0.2240
100	30	0.0566	0.3945	0.2170
300	15	0.0478	0.6055	0.7210
300	30	0.0506	0.8645	0.6755

The linear functional form fails when the covariates do not linearly correspond to the log of the subdistribution hazard ratio. To test the validation of functional form, the failure time of cause 1 was generated from

$${\lambda }_1^{\ast }(t\mid Z)={\lambda }_{10}^{\ast }(t)exp\{{\beta }_{1}Z+{\beta }_2{Z}^2\},$$ (5)

with β₁ = 0.8 and β₂ = −0.1. Failure times of cause 2 were generated from the exponential distribution with the rate of exp(−0.5). The rate of cause 1 was pre-set at 0.6. We fitted the data using FG model (1) with the covariate Z. Table 4 shows that our proposed test for the validation of the linear functional form has sufficient power and that the power increases when the sample size increases.

The misspecification of the link function means the exponential form in model (1) is inappropriate. For example, if the data is from an additive model, the test should give strong evidence of model misspecification. We generated the failure time of cause 1 from

$${\lambda }_1^{\ast }(t\mid Z)=\alpha (t)+\beta Z.$$ (6)

For simplicity, we assume α(t) = 0.03, which is a constant, and Z = {0, ⋯, 9} with equal proportions. We set β = 0.5. The failure times of cause 2 were generated from an exponential distribution with the rate of exp(−0.5). The rate of cause 1 was pre-set at 0.6. We fitted the data to the FG model (1) with the covariate Z. It is clear that this model is misspecified. Table 4 shows the power of our proposed test for validation of the link function of the FG model. We can see the test is very reliable when sample size is getting large.

4 Real data example

We now apply the proposed testing approaches to two real data examples. The p-values of the supremum tests throughout this section are based on 1000 replications. In each graphical display, the observed process is indicated by a solid curve and the first 10 simulated processes are plotted in dash curves. Comparing to the simulated curves, we can distinguish the observed curve if the model assumption is not appropriate.

4.1 BMT data

We considered data from the Center for International Blood and Marrow Transplant Research (CIBMTR), on acute myeloid leukemia (AML) patients, who are older than 50 years, and had alternative donor hematopoietic transplants in first complete remission (Weisdorf et al, 2013). The CIBMTR is comprised of clinical and basic scientists who share data on their blood and bone marrow transplant patients, with the CIBMTR Data Collection Center located at the Medical College of Wisconsin. The CIBMTR has a repository of information regarding the results of transplants at more than 450 transplant centers worldwide. For the illustrative purpose, the data set used for our example consists of patients who received a 8/8 HLA-matched unrelated donor transplant (URD: N=440) or an umbilical cord blood transplant (UCB: N=204). The two competing events are leukemia relapse and treatment-related mortality (TRM), which is defined as death without relapse. The CIBMTR study (Weisdorf et al, 2013) identified that donor type had a time-varying effect on the TRM. The variables considered in this example are donor type (GP (main interest of the study): 1 for 8/8 URD versus 0 for UCB) and patient age (AGE: median=59 (range: 50 – 76) years old). We fit this BMT data to a Fine and Gray’s model for TRM with two covariates: GP and AGE. The parameter estimates are β̂(GP) = −0.287 (P = 0.054) and β̂(AGE) = 0.012 (P = 0.346).

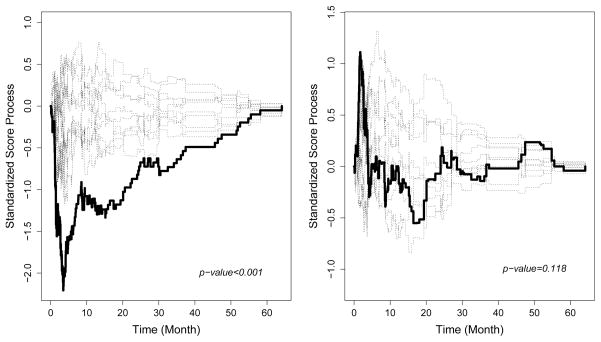
First, we checked the proportionality of two covariates GP and AGE. The p-values of the supremum test are < 0.001 and 0.118, respectively, which indicate that the proportional hazards assumption of AGE is reasonable, but the proportional hazards assumption of GP is strongly violated. Figure 1 displays the score process for the covariates of GP and AGE, respectively. For GP, the observed process severely departs from the simulated process in the early time period since transplant, which indicates that the donor type had a strong time-varying effect on TRM. For the early time departure of the covariate effect (Figure 1), we suggest adding a time-varying covariate γ × log(t). Applying the crr() function in R-cmprsk package suggested by Zhou et al (2013), we obtained γ̂(GP) = 0.565 (P < 0.001). The observed score process of AGE sits well within the simulated score process which indicates that the proportional hazards assumption of AGE does not violate. Also, we noticed that the conclusion from the p-value and graphical approach are consistent. When the proportionality assumption of the FG model is violated, more flexible alternative regression models for the competing risks data need to be considered, which allow some covariates to have time-varying effect (see Scheike et al (2008); Scheike and Zhang (2008)).

Fig. 1.

Plot of Standardized Score Process for GP and AGE in the BMT Data

We also checked the adequacy of functional form and link function. Both linear functional form and link function are satisfied. We do not recommend testing the functional form for the donor type, since it only has 2 levels and discussing the linearity is not very meaningful. Table 5 gives a summary of the p-values for checking each assumption based on the supremum test.

Table 5.

p -values of Checking Fine and Gray’s Model in BMT Data

	GP	AGE	overall
Proportionality	< 0.001	0.118	0.001
Functional form	–	0.896	-
Link function	-	-	0.954

4.2 PBC data

Next, we looked at an example violates the linear functional form. Mayo Clinic developed a database for patients with primary biliary cirrhosis (PBC) of the liver conducted between 1974 and 1984. The data and the description of the PBC dataset were given in Appendix of Fleming and Harrington (1991). Of the 418 patients, 161 died, which was the main interest of the study. 25 patients had a liver transplantation, and 232 patients were censored at the end of the study (without a liver transplantation). This data were used by Dickson et al (1989) building a Cox model with five covariates, log(bilirubin), log(protime), log(albumin), age and odema. Treating a liver transplant and all others as censored observations. Lin et al (1993) demonstrated that the use of the untransformed bilirubin was inappropriate because the fitted model overestimated the hazard at low bilirubin values and suggested a log transformation. Since patients could die after the liver transplantation, and the liver transplant may be correlated with the death rate, we treat the liver transplantation as the competing event for illustrative purpose. In this section, we reanalyze the data in a competing risks setting by using Fine and Gray’s subdistribution hazards model, and checking the assumptions of the FG model.

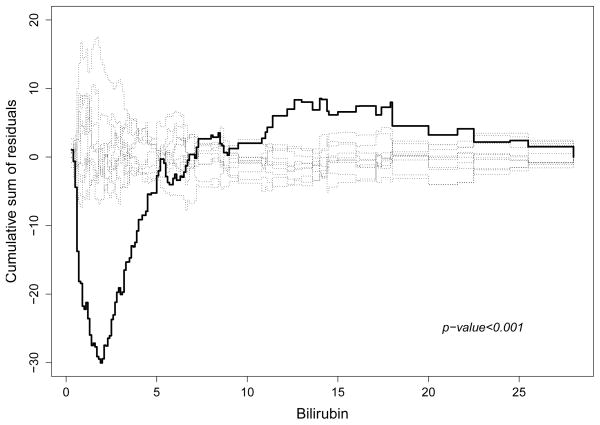
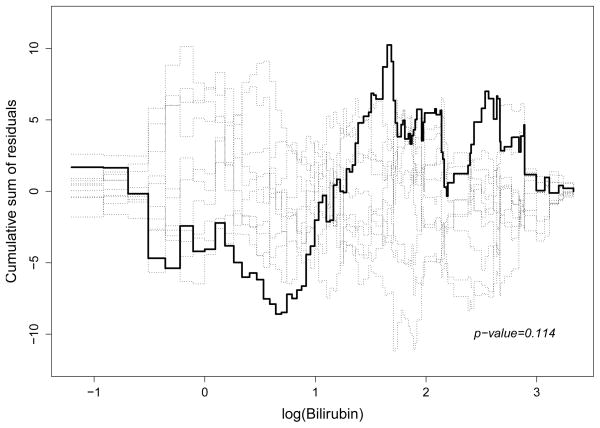
We first consider fitting the Fine and Gray’s model (1) with covariates bilirubin, log(protime), log(albumin), age and odema. The parameter estimates are 0.044, 0.966, 0.109, −2.558 and 3.507 respectively, and all are significant, with P < 0.05. Figure 2 shows the plot of the cumulative residuals against bilirubin. The fitted model extremely overestimates the subdistribution hazard for the low bilirubin values with P < 0.001. The pattern of the plot suggests a log transformation is needed. Figure 3 shows the plot of the cumulative residuals against log(bilirubin), which is a much better functional form (P = 0.114). Additional analysis indicates that the functional forms for the remaining covariates and the link function are appropriate (see Table 6).

Fig. 2.

Plot of Cumulative Residuals vs bilirubin in the PBC Data

Fig. 3.

Plot of Cumulative Residuals vs log(bilirubin) in the PBC Data

Table 6.

p -values of Checking the Fine and Gray’s Model in the PBC Data

	age	oedema	log(bili)	log(albumin)	log(protime)	overall
prop	0.469	0.019	0.071	0.119	0.007	0.006
func	0.180	0.349	0.114	0.515	0.239	-
link	-	-	-	-	-	0.290

Our proposed test shows that the proportional hazards assumption was not satisfied for oedema and log(protime) with P = 0.019 and 0.007, respectively (see Table 6). The plots of their score processes against time confirm our test conclusion as well (plots are omitted here). The p-value of overall proportional test is 0.006, which means the non-proportionality should be corrected. Again, we can consider fitting this PBC data with some more flexible alternative models, which allow some covariates to have time-varying effects (see Scheike et al (2008); Scheike and Zhang (2008)).

Lin et al (1993) checked the Cox model with cumulative sums of martingale-based residuals for the PBC data treating 25 liver transplantations as the censored subjects, and derived similar conclusions since it only counts 13% (25/186) of total events. This shows our proposed goodness-of-fit tests can be used for the model validation for the Fine and Gray’s proportional subdistribution hazards model.

5 Conclusion and discussion

In this paper, we presented a dynamic model diagnostics approach for checking the Fine and Gray’s model based on cumulative sums of residuals. Specifically, we checked the proportionality of the hazards function, the linearity of the functional form, and the link function. We proposed different test statistics for each specific testing purpose, and derived the asymptotic properties under the null hypothesis that the Fine and Gray’s model is valid. The three different test statistics were written into a general form, and more details of this were provided in the Appendix. For each proposed test, we also presented a graphical method for visually checking the model assumptions, which also provided some useful information on how the model assumption was violated.

When any one of the Fine and Gray model assumptions is violated, one needs to consider an alternative regression model. Only a limited goodness-of-fit test has been considered for these flexible models. Scheike et al (2008) and Scheike and Zhang (2008) proposed a class of flexible regression models which allow some covariates to have time-varying effects, and have some alternative link functions. In such situations an important issue would be to subsequently check the adequacy of the extended model. Actually some of the extended models could be also validated using the cumulative sums of residuals. For example, when proportional hazards assumption is invalid, we may consider the time-varying treatment effect as β(t) = β + θt. In this case, the cumulative sums of residuals would involve the time-varying term and the limiting distribution under the null hypothesis needs to be derived. This could be an extension of our current work and further studies are needed.

One issue for using the resampling techniques is the extensive computational time. We use 1000 replicates in most of our studies, but some studies need more replicates to obtain reliable p-values for the supremum-type test (Lin et al, 1993). We implemented the most computational intensive calculation in C++ for its speed and wrapped it by R via the interface between R and C++ for its flexibility. The code implementing the analysis is available upon request, and a user-friendly R package is under development for future release.

Appendix

Consider the following partial sums of residuals

$$B(t,x)=\sum _{i=1}^n{\int }_0^{t}f(x,{\mathit{Z}}_i,\mathit{v},p)w_i(u,{\widehat{G}}_c)d{\widehat{M}}_i^1(u),$$

where f(x, Z_i, v, p) = (v^⊤Z_i)^p 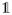(v^⊤Z_i ≤ x). Here v is a vector with same dimension of covariates Z, and p = 0 or 1. Under the null hypothesis that the FG model is valid,

$$\begin{array}{l}B(t,x)=\sum _{i=1}^n{\int }_0^{t}f(x,{\mathit{Z}}_i,\mathit{v},p)w_i(u,{\widehat{G}}_c)\left\{{dN}_i^1(u)-Y_i^1(u)exp({\widehat{\mathit{\beta }}}^{\top }{\mathit{Z}}_i)d{\widehat{\mathit{\Lambda }}}_{10}^{\ast }(u)\right\}\\ =\sum _{i=1}^n{\int }_0^{t}f(x,{\mathit{Z}}_i,\mathit{v},p)w_i(u,{\widehat{G}}_c){dM}_i^1(u)\\ -\sum _{i=1}^n{\int }_0^{t}f(x,{\mathit{Z}}_i,\mathit{v},p)w_i(u,{\widehat{G}}_c)Y_i^1(u)\left\{exp({\widehat{\mathit{\beta }}}^{\top }{\mathit{Z}}_i)d{\widehat{\mathit{\Lambda }}}_{10}^{\ast }(u)-exp({\mathit{\beta }}_0^{\top }{\mathit{Z}}_i)d{\mathit{\Lambda }}_{10}^{\ast }(u)\right\}\\ =\sum _{i=1}^n{\int }_0^{t}f(x,{\mathit{Z}}_i,\mathit{v},p)w_i(u,{\widehat{G}}_c){dM}_i^1(u)\end{array}$$ (7)

$$-\sum _{i=1}^n{\int }_0^{t}f(x,{\mathit{Z}}_i,\mathit{v},p)w_i(u,{\widehat{G}}_c)Y_i^1(u)exp({\mathit{\beta }}_0^{\top }{\mathit{Z}}_i){\mathit{Z}}_i^{\top }d{\widehat{\mathit{\Lambda }}}_{10}^{\ast }(u)\left(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0\right)$$ (8)

$$-\sum _{i=1}^n{\int }_0^{t}f(x,{\mathit{Z}}_i,\mathit{v},p)w_i(u,{\widehat{G}}_c)Y_i^1(u)exp({\mathit{\beta }}_0^{\top }{\mathit{Z}}_i)\left\{d{\widehat{\mathit{\Lambda }}}_{10}^{\ast }(u)-d{\mathit{\Lambda }}_{10}^{\ast }(u)\right\}+o_p(1).$$ (9)

Taking the Taylor expansion of U(β̂, t) at β₀, we can obtain

$$n^{1/2}(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0)={\mathit{\Omega }}^{-1}\{n^{-1/2}\mathit{U}({\mathit{\beta }}_0)\}+o_p(1),$$

where Ω = lim_n→∞ I(β₀)/n and asymptotically U(β₀) can be expressed as the sum of n independent and identically distributed random variables, i.e. $n^{-1/2}\mathit{U}({\mathit{\beta }}_0)=n^{-1/2}{\sum }_{i=1}^n({\mathit{\eta }}_{\mathit{i}}+{\mathit{\psi }}_{\mathit{i}})+o_p(1)$ (for explicit expressions of η_i and ψ_i see Fine and Gray (1999)). Since η_i contributes the majority of the variability, so we call η_i major term and ψ_i minor term. Both η_i and ψ_i are zero-mean Gaussian processes. Therefore

$$n^{1/2}(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0)={\mathit{\Omega }}^{-1}\left\{n^{-1/2}\sum _{i=1}^n({\mathit{\eta }}_{\mathit{i}}+{\mathit{\psi }}_{\mathit{i}})\right\}+o_p(1).$$ (10)

Recall that

$${\widehat{\mathit{\Lambda }}}_{10}^{\ast }(t)=\sum _{i=1}^n{\int }_0^t\frac{w_i(u,{\widehat{G}}_c){dN}_i^1(u)}{S_0(\widehat{\mathit{\beta }},u)},$$

therefore

$$n^{1/2}\left\{{\widehat{\mathit{\Lambda }}}_{10}^{\ast }(t)-{\mathit{\Lambda }}_{10}^{\ast }(t)\right\}=n^{1/2}\sum _{i=1}^n{\int }_0^t\left\{\frac{1}{S_0(\widehat{\mathit{\beta }},u)}-\frac{1}{S_0({\mathit{\beta }}_0,u)}\right\}{w}_i(u,{\widehat{G}}_c){dN}_i^1(u)$$ (11)

$$+n^{1/2}\left\{\sum _{i=1}^n{\int }_0^t\frac{1}{S_0({\mathit{\beta }}_0,u)}{w}_i(u,{\widehat{G}}_c){dN}_i^1(u)-{\mathit{\Lambda }}_{10}^{\ast }(t)\right\}.$$ (12)

Further more, for (11), taking the Taylor expansion of 1/S₀(β̂, u) at β₀, we can obtain

$$(11)=-\sum _{i=1}^n{\int }_0^t\frac{{\mathit{S}}_1^{\top }({\mathit{\beta }}_0,u)}{{\{S_0({\mathit{\beta }}_0,u)\}}^2}{w}_i(u,{\widehat{G}}_c){dN}_i^1(u)n^{1/2}(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0)+o_p(1).$$ (13)

For (12),

$$\begin{array}{l}(12)=n^{1/2}\sum _{i=1}^n{\int }_0^t\frac{w_i(u,{\widehat{G}}_c){dM}_i^1(u)}{S_0({\mathit{\beta }}_0,u)}\\ =n^{1/2}\sum _{i=1}^n{\int }_0^t\frac{w_i(u,G_c){dM}_i^1(u)}{S_0({\mathit{\beta }}_0,u)}+n^{1/2}\sum _{i=1}^n{\int }_0^t\frac{\{w_i(u,{\widehat{G}}_c)-w_i(u,G_c)\}{dM}_i^1(u)}{S_0({\mathit{\beta }}_0,u)}\\ =n^{1/2}\sum _{i=1}^n{\int }_0^t\frac{w_i(u,G_c){dM}_i^1(u)}{S_0({\mathit{\beta }}_0,u)}-n^{1/2}\sum _{i=1}^n{\int }_0^{\infty }\frac{Q(u,t)}{{\sum }_{l=1}^n𝟙(X_i\ge u)}{dM}_i^c(u)+o_p(1),\end{array}$$

where

$$\begin{array}{c}Q(u,t)=\sum _{j=1}^n{\int }_0^t\frac{𝟙(X_j\le u\le s)}{S_0({\mathit{\beta }}_0,s)}{w}_i(s,{\widehat{G}}_c){dM}_i^1(s),\\ {dM}_i^c(u)=𝟙(X_i\le t,{\mathit{\Delta }}_i=0)-{\int }_0^t𝟙(X_i\ge u)d{\widehat{\mathit{\Lambda }}}^c(u),\\ {\widehat{\mathit{\Lambda }}}^c(u)={\int }_0^t\frac{d{\sum }_{i=1}^n𝟙(X_i\le t,{\mathit{\Delta }}_i=0)}{{\sum }_{i=1}^n𝟙(X_i\ge u)}.\end{array}$$

Plug (11) and (12) into (9) we have

$$(9)=-\sum _{i=1}^n{\int }_0^{t}f(x,{\mathit{Z}}_i,\mathit{v},p)\frac{w_i(u,{\widehat{G}}_c)Y_i^1(u)exp({\mathit{\beta }}_0^{\top }{\mathit{Z}}_i)}{S_0({\mathit{\beta }}_0,u)}\sum _{l=1}^n{w}_l(u,{\widehat{G}}_c){dM}_l^1(u)$$ (14)

$$+\sum _{i=1}^n{\int }_0^{t}f(x,{\mathit{Z}}_i,\mathit{v},p)w_i(u,{\widehat{G}}_c)Y_i^1(u)exp({\mathit{\beta }}_0^{\top }{\mathit{Z}}_i)\frac{{\mathit{S}}_1^{\top }({\mathit{\beta }}_0,u)}{S_0({\mathit{\beta }}_0,u)}d{\mathit{\Lambda }}_{10}^{\ast }(u)\left(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0\right)$$ (15)

$$-\sum _{i=1}^n{\int }_0^{\infty }f(x,{\mathit{Z}}_i,\mathit{v},p)w_i(u,{\widehat{G}}_c)Y_i^1(u)exp({\mathit{\beta }}_0^{\top }{\mathit{Z}}_i)\frac{{\sum }_{j=1}^{n}Q(u,t){dM}_j^c(u)}{{\sum }_{l=1}^n𝟙(X_i\ge u)}+o_p(1).$$ (16)

Under the asymptotic regularity conditions:

$$\underset{n\to \infty }{lim}{n}^{-1}{\mathit{S}}_k(\mathit{\beta },t)\stackrel{p}{\to }{\mathit{s}}_k(\mathit{\beta },t),\underset{n\to \infty }{lim}Q(u,t)\stackrel{P}{\to }q(u,t),\underset{n\to \infty }{lim}{n}^{-1}\sum _{l=1}^n𝟙(X_i\ge u)\stackrel{p}{\to }y(t)$$

Exchange summation on (14) and combine with (7). When $n\stackrel{p}{\to }\infty$,

$$(7)+(14)=n^{-1}\sum _{i=1}^n{\int }_0^t\{f(x,{\mathit{Z}}_i,\mathit{v},p)-g({\mathit{\beta }}_0,u,x)\}{w}_i(u,G_c){dM}_i^1(u)+o_p(1),$$

where

$$g({\mathit{\beta }}_0,u,x)=\frac{1}{s_0({\mathit{\beta }}_0,u)}\sum _{l=1}^{n}f(x,{\mathit{Z}}_l,\mathit{v},p)w_l(u,G_c)Y_l^1(u)exp({\mathit{\beta }}_0^{\top }{\mathit{Z}}_l).$$

Combine (8) and (15). When $n\stackrel{p}{\to }\infty$,

$$\begin{array}{l}(8)+(15)=-\sum _{i=1}^n{\int }_0^{t}f(x,{\mathit{Z}}_i,\mathit{v},p)w_i(u,G_c)Y_i^1(u)exp({\mathit{\beta }}_0^{\top }{\mathit{Z}}_i){\left\{{\mathit{Z}}_i-\frac{s_1({\mathit{\beta }}_0,u)}{s_0({\mathit{\beta }}_0,u)}\right\}}^{\top }d{\mathit{\Lambda }}_{10}^{\ast }(u)\left(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0\right)+o_p(1)\\ =n^{-1}\sum _{i=1}^n\left\{{\mathit{C}}^{\top }({\mathit{\beta }}_0,t,x)\right\}{\mathit{\Omega }}^{-1}({\mathit{\eta }}_{\mathit{i}}+{\mathit{\psi }}_{\mathit{i}})+o_p(1),\end{array}$$

where

$$\mathit{C}({\mathit{\beta }}_0,t,x)=-\sum _{i=1}^n{\int }_0^{t}f(x,{\mathit{Z}}_i,\mathit{v},p)w_i(u,G_c)Y_i^1(u)exp({\mathit{\beta }}_0^{\top }{\mathit{Z}}_i)\left\{{\mathit{Z}}_i-\frac{s_1({\mathit{\beta }}_0,u)}{s_0({\mathit{\beta }}_0,u)}\right\}d{\mathit{\Lambda }}_{10}^{\ast }(u).$$

Exchange summation on (16). When $n\stackrel{p}{\to }\infty$,

$$(16)=n^{-1}\sum _{i=1}^n{\int }_0^{\infty }\frac{q(u,t)}{y(u)}v({\mathit{\beta }}_0,u,x){dM}_i^c(u)+o_p(1)=n^{-1}\sum _{i=1}^n{q}_i^{(f)}(t,x)+o_p(1)$$

where

$$v({\mathit{\beta }}_0,u,x)=\sum _{j=1}^{n}f(x,{\mathit{Z}}_j,\mathit{v},p)w_j(u,{\widehat{G}}_c)Y_j^1(u)exp({\mathit{\beta }}_0^{\top }{\mathit{Z}}_j).$$

So

$$B(t,x)=n^{-1}\sum _{i=1}^n\{W_i(t,x)\}+o_p(1),$$

where

$$W_i(t,x)={\int }_0^t\{f(x,{\mathit{Z}}_i,\mathit{v},p)-g({\mathit{\beta }}_0,u,x)\}{w}_i(u,G_c){dM}_i^1(u)+{\mathit{C}}^{\top }({\mathit{\beta }}_0,t,x){\mathit{\Omega }}^{-1}({\mathit{\eta }}_{\mathit{i}}+{\mathit{\psi }}_{\mathit{i}})-q_i^{(f)}(t,x),$$ (17)

which can be consistently estimated by the plug-in estimators.

Test proportional subdistribution hazards assumption:

To check the proportional subdistribution hazards assumption, we consider the score process U_j (β̂, t) for each covariate, which can be written as

$$U_j(\widehat{\mathit{\beta }},t)=\sum _{i=1}^n{\int }_0^t{Z}_{ij}{w}_i(u,{\widehat{G}}_c)d{\widehat{M}}_i^1(u),j=1,\cdots ,m.$$

It is a special case of the general form B(t, x) with x = ∞, p = 1 and v has 1 in jth element and 0 elsewhere. Under the null hypothesis,

$$U_j(\widehat{\mathit{\beta }},t)=n^{-1}\sum _{i=1}^n[{\int }_0^t\left\{Z_{ij}-\frac{s_{1j}({\mathit{\beta }}_0,u)}{s_0({\mathit{\beta }}_0,u)}\right\}{w}_i(u,G_c){dM}_i^1(u)+{\mathit{C}}_j^{\top }(t){\mathit{\Omega }}^{-1}({\mathit{\eta }}_i+{\mathit{\psi }}_i)-q_i^{(f)}(t,x)]+o_p(1),$$

where s_1j (β₀, u) is the jth element of s₁(β, u) and

$${\mathit{C}}_j(t)=-\sum _{i=1}^n{\int }_0^t{Z}_{ij}{w}_i(u,G_c)Y_i^1(u)exp({\mathit{\beta }}_0^{\top }{\mathit{Z}}_i)\left\{{\mathit{Z}}_i-\frac{{\mathit{s}}_1({\mathit{\beta }}_0,u)}{s_0({\mathit{\beta }}_0,u)}\right\}d{\mathit{\Lambda }}_{10}^{\ast }(u).$$

In practice, we standardized the process by multiplying $I_{jj}^{-1}(\widehat{\mathit{\beta }})$, and denoted $B_j^{(p)}(t)=I_{jj}^{-1}(\widehat{\mathit{\beta }})U_j(\widehat{\mathit{\beta }},t)$ in the text.

Test linear functional form

To test the linear functional form for the jth covariate, we consider

$$B_j^{(f)}(x)=\sum _{i=1}^n{\int }_0^{\infty }𝟙\{Z_{ij}\le x\}{w}_i(u,{\widehat{G}}_c)d{\widehat{M}}_i^1(u),j=1,\cdots ,m$$

which is a special case of the general form B(t, x) when t = ∞, p = 0, and v has 1 in jth element and 0 elsewhere. Under the null hypothesis,

$$B_j^{(f)}(x)=n^{-1}\sum _{i=1}^n[{\int }_0^{\infty }\{𝟙(Z_{ij}\le x)-g_j(u,x)\}{w}_i(u,G_c)d{M}_i(u)+{\mathit{C}}_j^{\top }(x){\mathit{\Omega }}^{-1}({\mathit{\eta }}_i+{\mathit{\psi }}_i)-q_i^{(f)}(t,x)]+o_p(1),$$

where

$$\begin{array}{c}{g}_j(u,x)=\frac{1}{s_0({\mathit{\beta }}_0,u)}\sum _{l=1}^n𝟙(Z_{lj}\le x)w_l(u,G_c)Y_l^1(u)exp({\mathit{\beta }}_0^{\top }{\mathit{Z}}_l),\\ {\mathit{C}}_j(x)=-\sum _{l=1}^n{\int }_0^{\infty }𝟙(Z_{lj}\le x)w_l(u,G_c)Y_l^1(u)exp({\mathit{\beta }}_0^{\top }{\mathit{Z}}_l)\left\{{\mathit{Z}}_l-\frac{{\mathit{s}}_1({\mathit{\beta }}_0,u)}{s_0({\mathit{\beta }}_0,u)}\right\}d{\mathit{\Lambda }}_{10}^{\ast }(u).\end{array}$$

Test link function

To test the link function, we consider

$$B^{(l)}(x)=\sum _{i=1}^n{\int }_0^{\infty }𝟙\left\{{\widehat{\mathit{\beta }}}^{\top }{\mathit{Z}}_i\le x\right\}{w}_i(u,{\widehat{G}}_c)d{\widehat{M}}_i^1(u).$$

In this case, t = ∞, p = 0 and v = β̂. Under the null hypothesis, the test statistic has exactly the same format as the test statistic in the linear functional form, except the indictor function is replaced by 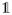{β̂^⊤Z_i ≤ x}. Note, if there is only one covariate, checking the function is equivalent to checking the functional form of the covariate.

Omnibus test

Here we consider

$${\mathit{B}}^{(o)}(t,\mathit{z})=\sum _{i=1}^n{\int }_0^t𝟙\{{\mathit{Z}}_i\le \mathit{z}\}{w}_i(u,{\widehat{G}}_c)d{\widehat{M}}_i^1(u).$$

For the jth covariate is of interest for testing, the jth element in B^(o)(t, x) is the statistic we look for,

$$B_j^{(o)}(t,x)=\sum _{i=1}^n{\int }_0^t𝟙\{Z_{ij}\le x\}{w}_i(u,{\widehat{G}}_c)d{\widehat{M}}_i^1(u),$$

which is a special case of the general form B(t, x) when p = 0 and and v has 1 in jth element and 0 elsewhere. The omnibus test also can be viewed as recording each linear function test through the time span. Under the null hypothesis,

$$B_j^{(o)}(t,x)=n^{-1}\sum _{i=1}^n[{\int }_0^t\{𝟙(Z_{ij}\le x)-g_j(u,x)\}{w}_i(u,G_c)d{M}_i(u)+\sum _{i=1}^n{\mathit{C}}_j^{\top }(t,x){\mathit{\Omega }}^{-1}({\mathit{\eta }}_i+{\mathit{\psi }}_i)-q_i^{(f)}(t,x)]+o_p(1),$$

where

$$\begin{array}{c}{g}_j(u,x)=\frac{1}{s_0({\mathit{\beta }}_0,u)}\sum _{l=1}^n𝟙(Z_{lj}\le x)w_l(u,G_c)Y_l^1(u)exp({\mathit{\beta }}_0^{\top }{\mathit{Z}}_l),\\ {\mathit{C}}_j(t,x)=-\sum _{l=1}^n{\int }_0^t𝟙(Z_{lj}\le x)w_l(u,G_c)Y_l^1(u)exp({\mathit{\beta }}_0^{\top }\mathit{Z})\left\{{\mathit{Z}}_l-\frac{{\mathit{s}}_1({\mathit{\beta }}_0,u)}{s_0({\mathit{\beta }}_0,u)}\right\}d{\mathit{\Lambda }}_{10}^{\ast }(u).\end{array}$$