Maximum entropy estimation of Glutamate and Glutamine in MR spectroscopic imaging

Abstract

Magnetic resonance spectroscopic imaging (MRSI) is often used to estimate the concentration of several brain metabolites. Abnormalities in these concentrations can indicate specific pathology, which can be quite useful in understanding the disease mechanism underlying those changes. Due to higher concentration, metabolites such as N-acetylaspartate (NAA), Creatine (Cr) and Choline (Cho) can be readily estimated using standard Fourier transform techniques. However, metabolites such as Glutamate (Glu) and Glutamine (Gln) occur in significantly lower concentrations and their resonance peaks are very close to each other making it di!cult to accurately estimate their concentrations (separately). In this work, we propose to use the theory of ‘Spectral Zooming’ or high-resolution spectral analysis to separate the Glutamate and Glutamine peaks and accurately estimate their concentrations. The method works by estimating a unique power spectral density, which corresponds to the maximum entropy solution of a zero-mean stationary Gaussian process. We demonstrate our estimation technique on several physical phantom data sets as well as on in-vivo brain spectroscopic imaging data. The proposed technique is quite general and can be used to estimate the concentration of any other metabolite of interest.³

1 Introduction

MR spectroscopic imaging (MRSI) also known as chemical shift imaging (CSI) is a clinical imaging tool used to spatially map tissue metabolites in-vivo to investigate neurobiology and cancer. In particular, it has been used to measure the amount of specific tissue metabolites in the brain. Each metabolite appears at a specific frequency (measured in parts-per-million or ppm), and each one reflects specific cellular and biochemical processes. For example, NAA is a neuronal marker, while Creatine provides a measure of energy stores and Choline is a measure of cellular turnover and is elevated in tumors and inflammatory processes. Similarly, Glutamate (Glu), which is a major excitatory neurotransmitter has been shown to play a role in several neurological disorders [1]. Similarly, Glutamine (Gln), which is converted to Glutamate by the neuronal cellular processes has also been found to be abnormal in schizophrenia [2]. However, accurate estimation of these metabolites (Glu and Gln) from proton MRSI signal is still an area of active research. In particular, these metabolites have similar resonance frequencies as seen on a standard 3T clinical scanner, i.e. their peaks are too close to each other and hence accurate estimation is di!cult using standard processing techniques.

2 Our contribution

Separate estimation of Glutamate and Glutamine concentration from one dimensional in-vivo brain MRS data obtained from a 3T scanner is quite challenging. Standard basis fitting algorithms such as LCModel provide a combined estimate of Glu and Gln (referred to as Glx in the literature), due to its inability to resolve the two peaks [3]. In this work, we propose a novel method to obtain a separate estimate of Glutamate and Glutamine based on the theory of high resolution spectral analysis. The method works by estimating the power spectral density (PSD), which corresponds to the maximum entropy solution of a zero-mean stationary Gaussian process. To obtain a robust estimate of the concentrations, we compute several PSD’s of these metabolites from a moving window of the measured data. Further, we propose to use concepts from wavelet theory (Morlet wavelets) to preprocess the time domain data, which aids in removing low frequency baseline trends as well as noise from the signal. We demonstrate the robustness of our method on several phantom data sets along with several human in-vivo single and multi-voxel (MRSI) data sets.

3 Methods

3.1 MR Spectroscopy

In magnetic resonance spectroscopy, nuclei resonate at a frequency (ν) given by the Larmor equation ν = γB₀, where B₀ is the strength of the external magnetic field, and γ is a nucleus specific gyromagnetic ratio. The resonant frequency of a molecule depends on its chemical structure, which is exploited in MRS to obtain information about the concentration of a particular metabolite. In particular, let M₀ be the magnetization vector of a tissue sample placed in an external magnetic field B₀. Following the application of a 90° radio-frequency pulse (or any other acquisition sequence such as PRESS or STEAM), the magnetization vector M₀ is tipped in the transverse x–y plane and starts to precess about B₀ at the Larmor frequency resulting in decay of the signal with time as measured in the x–y plane. This decay is referred to as the free-induction-decay (FID), and is mathematically given by a combination of damped complex sinusoids: $S(t)=\int p(\omega )exp(-i\omega t)exp(-t/T_2^{\ast })d\omega$, where p(ω) represents one or more Lorentzian line shape function whose amplitude, width, etc. reveals spectroscopic information about the spin system under investigation and S(t) is the measured complex signal. The frequency contents of S(t) can be estimated using the Fourier transform, which also allows to estimate the concentration of several metabolites present in the tissue.

The most abundant metabolite present in the brain is water, whose concentration is about 10,000 times higher than that of other metabolites, which dominates the measured signal. Thus, to get ‘visible’ spectra of other metabolites, a water suppression pulse is typically applied prior to the acquisition of the actual time domain signal. This allows for accurate estimation of NAA, Cho and Cr. Yet, due to lower concentration of Glu and Gln in the brain and the fact that their frequency peaks are very close to each other, it is in general quite di!cult to obtain an accurate estimate of each of these metabolites. Nevertheless, there have been few methods proposed for proper estimation of Glutamine in the brain. For example, in [4], the authors use a 4T magnet for proper separation of the peaks, while the authors in [5] study different echo-times (TE) on a phantom data set with a 3T magnet to determine the best sequence parameters for peak separation. Both methods use the LCModel software package [6] to determine the concentration of Glu and Gln, which works by fitting a basis of known metabolite spectra to the measured data. While the separation of the Glu and Gln peaks can be seen distinctly on scanners with magnetic strength of 4T and above due to increased spectral dispersion, existing techniques fail to characterize Glutamine on data acquired on a 3T scanner. The current work proposes a maximum entropy based method to obtain the power spectral density (and consequently the concentrations) of Glutamate and Glutamine by spectrally zooming into a small frequency range of 2.20 to 2.50 ppm.

3.2 High resolution spectral analysis using maximal entropy

Consider a discrete-time zero-mean stationary process {y₀, y₁, …, y_N−1, …}, y_t ∈ (the set of complex numbers), and let $r(k)=E(y_t{y}_{t-k}^{\ast })$, k ∈ 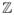be the co-variance lags. Then the power spectral density (PSD) function can be written as $f(\theta )={\sum }_{k=-\infty }^{\infty }r(k)e^{-i\theta k}$, where θ ∈ [π, −π). Spectral estimation refers to the problem of estimating f(θ) when only a finite-sized observation record {y₀, y₁, …, y_N−1}, N < ∞ of the time series is available. Standard techniques for the estimation of f(θ) include methods based on Fourier transform as well as other well-known methods such as ESPIRT and MUSIC [7]. However, recent work done by [8] allows high resolution spectral estimation or ‘spectral zooming’ by generalizing the relation between the Toeplitz structure of the state covariance matrix of a filter and the theory of Szego orthogonal polynomials.

Below, we briefly describe the theory of high resolution of spectral analysis. Consider the input-to-state filter given by the following state transition equation: x_k = Ax_k−1 + By_k, where {x₀, x₁, …, x_N, ..} are the states and {y₀, y₁, …, y_N, ..} is the sequence of input measurements. The transfer function for this filter is given by G(z) = (I − z⁻¹A)⁻¹B, for appropriate choice of matrices A and B. A positive semi-definite matrix R is the state covariance of the above filter, i.e. $R=E(x_k{x}_k^{\ast })$, if and only if it satisfies the following identity: R − ARA^* = BH + H^*B^*, for some row-vector H with A^* being the conjugate transpose of matrix A [8]. When the state covariance matrix R has a Toeplitz structure, it can be used to estimate the power spectral density of the data. For appropriate choice of the filter matrices A and B, the input-to-state filter works as a magnifying glass, amplifying the harmonics in a particular frequency interval. The shape of the filter is determined from the eigenvalues of A.

The entropy of a system with probability distribution function p(x), x ∈ ℝⁿ is given by: ∫ −p(x) log p(x)dx, which quantifies the amount of information contained in the random variable x. For a zero-mean Gaussian process, the entropy itself is unbounded, however, the entropy rate is bounded from above and is given by: $\frac{1}{4\pi }{\int }_{-\pi }^{\pi }logf(\theta )d\theta +C$, where f(θ) is the power spectral density function. Given the state statistics in the form of a covariance matrix R, the power spectrum with the maximum entropy rate is the candidate with the maximal information content (among all possible solutions). Such a power spectrum can be obtained from the following cost function [9]:

$$f_{me}(\theta )=arg\underset{f(\theta )}{max}\left({\int }_{-\pi }^{\pi }logf(\theta )d\theta \mid {\int }_{-\pi }^{\pi }G(e^{i\theta })f(\theta )G(e^{-i\theta })d\theta =R\right).$$ (1)

If we assume that the time series is a zero-mean Gaussian stochastic process with a transfer function given by G(z) = G(e^iθ), then the above cost function has a closed form solution and the maximum entropy solution is given by [9]:

$$\begin{array}{ll}\hfill f_{me}(\theta )& =P{(e^{i\theta })}^{-1}\mathit{\Omega }{(P{(e^{i\theta })}^{-1})}^{\ast },\text{where}P(e^{i\theta })=\mathit{\Gamma }G(e^{i\theta }),\\ \hfill \mathit{\Omega }& =\mathit{\Gamma }R{\mathit{\Gamma }}^{\ast },\text{and}\mathit{\Gamma }={(B^{\ast }{R}^{-1}B)}^{-1}{B}^{\ast }{R}^{-1}.\end{array}$$ (2)

Given the time-domain signal, the above formulation can be used to estimate the power spectral density (PSD) function in the frequency range of interest. To reduce the effect of noise and for robust estimation, we use a concept similar to short-time-Fourier transform, i.e., we use several subsequences of the data {y_i, y_i+1, …y_k} to obtain the corresponding estimates of the PSD function. A cumulative distribution function (cdf) is then computed for each PSD followed by averaging of the cdf’s to obtain a single average cdf function. Derivative of this function gives the final PSD function, from which the concentration of the relevant metabolite is obtained by computing the area under the peaks.

4 Experiments

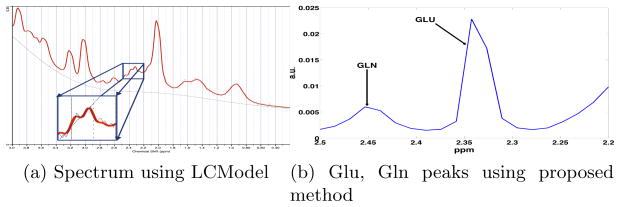
The Glutamate and Glutamine resonances occur in the region 2.20 to 2.50 ppm. Thus, this is the region where we perform “spectral zooming” as shown in Figure 1. Standard techniques such as LCModel, find it di!cult to separate the Glutamate and Glutamine peaks due to overlapping resonances (Figure 1a), however, the proposed method of high-resolution spectral analysis enables one to separate these peaks (Figure 1b). To test the effectiveness and robustness of our method, we performed three different experiments. First, to validate our method, we used data acquired from a physical phantom where we knew the exact concentration of Glu and Gln. The second experiment involved estimation of Glu/Gln from a single voxel in 8 human subjects, while in the third experiment we show the estimation of these metabolites on MRSI data (an entire axial slice).

Fig. 1.

(a) Metabolite spectra estimated using LCModel [6] from a single voxel with data from in-vivo human brain. Notice that the Glu and Gln peaks (zoomed rectangular region) are indistinguishable. (b) Using the proposed high resolution spectral analysis, the two peaks can be easily separated.

Data acquisition

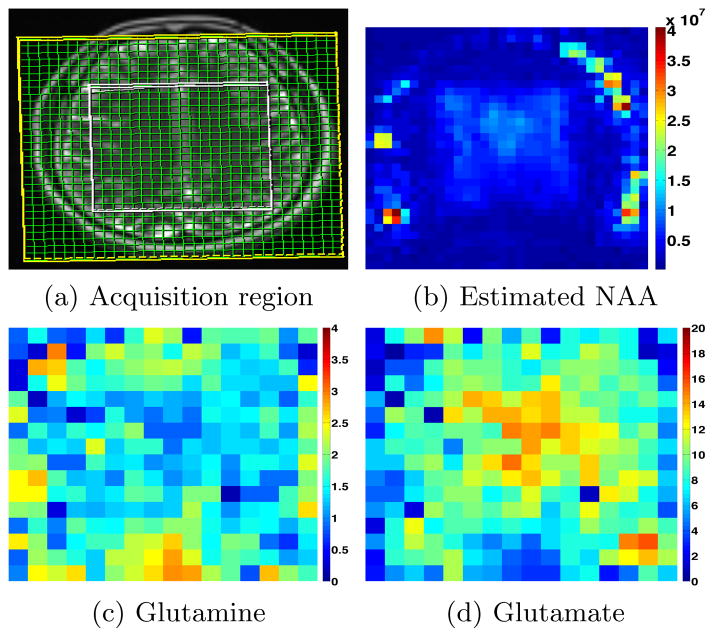
Single voxel spectroscopy data (for phantom) was acquired on a 3T Siemens scanner using a point-resolved spin-echo sequence (PRESS) sequence [10] with the following scan parameters: TE=30ms, 8cc voxel size, dwell-time of 1 ms, and N=512 time points. For the water-suppressed signal, we collected 64 repetitions while for the water un-suppressed signal we obtained 16 repetitions. For human in-vivo data, similar parameters were used, except N=1024 and dwell-time was 0.5 ms. In the case of MRSI data, an axial slice was acquired using a spiral CSI acquisition sequence [11] with TE=50ms, N = 512 time points and spatial resolution of 8mm × 8mm × 16 mm (imaging matrix of 32 × 32). In order to avoid contamination due to the lipid signal from the skull, only the tissue within a rectangular region of the brain was excited (even though acquisition was done in the entire slice), see Figure 3 for more details.

Fig. 3.

(a) Region within the white rectangle is excited, while data is collected at each grid point (green). (b) Estimated NAA concentration from the water suppressed signal. (c) and (d) Estimated Glutamine and Glutamate respectively (arbitrary units) within the excitation box (white).

All data were pre-processed with the following steps: (a) The distortion from eddy currents was corrected by a point by point phase correction of the time domain signal using the unsuppressed water signal as a reference. (b) If the initial phase of the FID was not zero, we corrected the spectra for “phasing” errors [12]. (c) Removal of residual water signal and baseline trends was achieved by applying a wavelet transform to the time domain data. In particular, we used Morlet wavelet to filter the time domain signal and the subsequent analysis was done on this filtered data. (d) The window size used in the estimation of PSD was 400. Each subsequence was obtained by moving the window by 5 time points. The estimation technique was not sensitive to any of these parameters. Further, we used 5 eigenvalues for the Jordan matrix A which provided su!cient pass-band for the filter. The matrices A and B were chosen as given in [9].

4.1 Phantom data

Three different phantoms were created each containing 10 mM of NAA and Cr along with the following concentration of Glu and Gln respectively: 1). 6 mM of Glu and 6 mM of Gln, 2). 12 mM of Glu and 3 mM of Gln, 3). 12mM of Glu and 6 mM of Gln. Data pre-processing was done as described earlier and equation 2 was used to “zoom-into” the frequency range [2.20 to 2.50] ppm to separate the Glu and Gln peaks. Concentration was estimated by computing the area under each of the peaks. LCModel (LCM) was also used to estimate the concentrations. The following table gives the estimated concentrations for each of the three phantoms: The results show that for equal concentration of Glu and Gln, the proposed method is quite accurate whereas for unequal proportions, the estimation deviates slightly from the true value. LCModel (LCM), however, fails completely to estimate the concentrations.

Table 1.

Glu and Gln concentration (mM) estimation on Phantom data

	Phantom 1			Phantom 2			Phantom 3
	Actual	Estimated	LCM	Actual	Estimated	LCM	Actual	Estimated	LCM
Glu	6	6	2.83	12	13.57	6.97	12	10.63	5.1
Gln	6	5.86	1.29	3	4.09	0.80	6	5.04	1.49

4.2 Single voxel in-vivo data

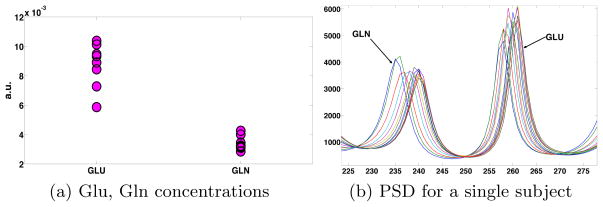
A single 8cc voxel located in the posterior cingulate gyrus of each subject was scanned. Using the proposed technique, we estimated the Glu and Gln concentrations as shown in Figure 2(a). As expected, the Gln concentration is 2–3 times lower than that of Glu. Also shown in Figure 2(b) are the estimated PSD functions for one subject obtained from each of the subsequences (data over a moving window) as described earlier. The maxima of the estimated PSD functions show a small shift as we use a shifted subsequence of the data for each estimation as well as due to noise in the data and the estimation process. Note that, such an estimation of Gln would not be possible using LCModel (see Figure 1(a)).

Fig. 2.

(a) Glutamate and Glutamine concentrations in eight healthy subjects. (b) Power spectral density functions estimated for a single subject. Each curve represents the estimated PSD obtained from a shifted subsequence (window) of data.

4.3 MRSI data

MRSI data was acquired in the brain region shown in Figure 3. Using the proposed technique, we estimated Glu, Gln and NAA in each of the voxels. Note that, the tissue outside the white box was not excited to avoid contamination due to the strong lipid signal, however, data is generally acquired in the entire field-of-view (green grid). As expected, the concentration of Glutamate is higher than that of Glutamine and the estimation of NAA demonstrates that data is very noisy outside the excitation window (white box).

We should point out that, in general, the concentrations are reported in several different ways in the literature. One way is to report the absolute concentration in mM (milli molar) [12] (requires several correction factors as well as consideration of gray/white volume fractions). Another popular method is to use the concentration of creatine (or water) as a reference to obtain a ratio. Alternatively, the area under the peak is also used as an estimate of the concentration, which is what we use in this work for our in-vivo data (since this work is essentially a proof of concept).

5 Conclusion and limitations

In this work, we proposed a novel method based on high resolution spectral analysis to estimate the power spectral density (PSD) corresponding to glutamate and glutamine from MR spectroscopy data. This method can be used to estimate the PSD of any metabolite of interest, but in this work, we only show its application to estimate Glu and Gln peaks. In particular, we propose to estimate the PSD with the maximum entropy given the covariance function of an appropriate filter. To the best of our knowledge, this is a novel and first application of this technique to estimate Glu and Gln peaks from in-vivo human brain data. We validated our method on three physical phantom data sets and also reported preliminary results on eight human subjects. In addition, as a proof of concept, we also reported results on MRSI data from human subject. We should note that, very few methods have been able to reliably estimate Glu and Gln concentrations from data acquired on a 3T scanner.

A few limitations of this work, which we would like to acknowledge: (a) Estimation of absolute concentration as given in [12]. (b) Accounting for gray-white volume fractions needs to be done for proper estimation of the concentration at each voxel.