From gross anatomy to the nanomorphome: stereological tools provide a paradigm for advancing research in quantitative morphomics

Abstract

The terms morphome and morphomics are not new but, recently, a group of morphologists and cell biologists has given them clear definitions and emphasised their integral importance in systems biology. By analogy to other ‘-omes’, the morphome refers to the distribution of matter within 3-dimensional (3D) space. It equates to the totality of morphological features within a biological system (virus, single cell, multicellular organism or populations thereof) and morphomics is the systematic study of those structures. Morphomics research has the potential to generate ‘big data’ because it includes all imaging techniques at all levels of achievable resolution and all structural scales from gross anatomy and medical imaging, via optical and electron microscopy, to molecular characterisation. As with other ‘-omics’, quantification is an important part of morphomics and, because biological systems exist and operate in 3D space, precise descriptions of form, content and spatial relationships require the quantification of structure in 3D. Revealing and quantifying structural detail inside the specimen is achieved currently in two main ways: (i) by some form of reconstruction from serial physical or tomographic slices or (ii) by using randomly-sampled sections and simple test probes (points, lines, areas, volumes) to derive stereological estimates of global and/or individual quantities. The latter include volumes, surfaces, lengths and numbers of interesting features and spatial relationships between them. This article emphasises the value of stereological design, sampling principles and estimation tools as a template for combining with alternative imaging techniques to tackle the ‘big data’ issue and advance knowledge and understanding of the morphome. The combination of stereology, TEM and immunogold cytochemistry provides a practical illustration of how this has been achieved in the sub-field of nanomorphomics. Applying these quantitative tools/techniques in a carefully managed study design offers us a deeper appreciation of the spatiotemporal relationships between the genome, metabolome and morphome which are integral to systems biology.

Introduction

By convention, the suffix ‘-ome’ refers to the total complement of some component (molecule, molecular assemblage, membrane, organelle, cell, tissue, organ) of a biological system (virus, cell, organism). An early usage was the term chondriome, which referred to the total complement of mitochondria in a cell. More recently, use of the suffix has included terms such as genome, epigenome, transcriptome, proteome, glycome, lipidome, metabolome and physiome. In addition, the suffix ‘-omics’ identifies the corresponding fields of study. Thus, the genome represents the entire complement of genes and genetic material within a biological system and genomics is the field of study that applies DNA technology and bioinformatics to identify genome structure and function.

The epigenome refers to chemical changes to DNA and histones which lead to changes in genome function and gene expression. In the same way, the transcriptome is the totality of RNA species synthesised by a system. As this is influenced by the genes that are being expressed, the transcriptome can vary qualitatively and quantitatively depending on natural or experimental conditions. Therefore, transcriptomics embraces the quantitative study of the expression levels of mRNAs utilising microarray, reverse transcription polymerase chain reaction and RNA-seq technologies. Like the epigenome, the other ‘-omes’ vary with time and the natural or artificial treatments to which the system is exposed (the exposome).

These areas of study have developed from different disciplines (biochemistry, genetics and physiology) but each seeks to understand biological processes by identifying, quantifying and recording individual molecules or supramolecular assemblages. They also embrace quantification by applying the tools of descriptive and inferential statistics in order to identify significant changes in, say, expression levels. However, a more comprehensive and inclusive understanding of biological systems warrants an approach which embraces all the biomedical disciplines (including anatomy/morphology) and provides a spatiotemporal context within which all the ‘-omes’ operate. Information about structure is required at multiple levels of resolution in order to understand better the processes by which systems alter with time, experimental treatment or environmental insult. Integrating this information with that obtained from other ‘-omics’ approaches provides the basis for understanding systems biology (Fig.1).

Figure 1.

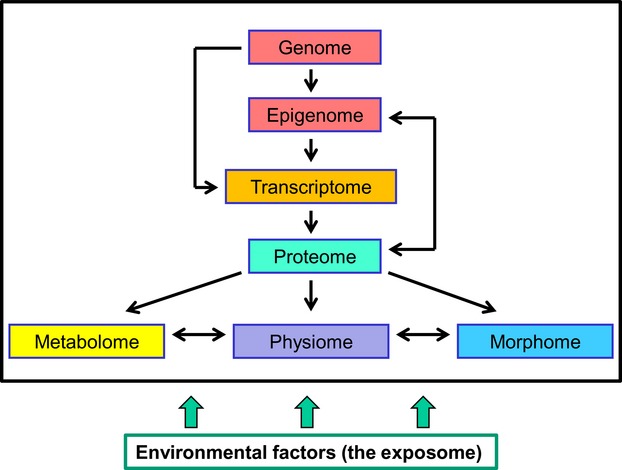
Morphomics as an integral part of systems biology. The genome is essentially constant but the epigenome is more variable and influences the transcriptome, proteome, metabolome, physiome and morphome. As well as the proteome, the glycome and lipidome (not shown) will affect the metabolome, physiome and morphome. All may be influenced in turn by the exposome (the totality of environmental conditions to which the system becomes exposed). This simple and incomplete representation serves to emphasise that all these fields have roles to play in furthering our understanding of biological systems and how they alter under various conditions.

Bringing it all back ‘-ome’ – the concept of the morphome

Until recently, we lacked terms that refer to the total content of structures at each successive level of biological organisation and to the field which describes and quantifies them and identifies their functional correlates. The terms anatome and anatomics are not suitable because they are etymologically awkward: anatomy describes an activity and literally means ‘cutting up’, as it has the Greek affixes ana- (up) and -tomy (cutting) as its roots (Mayhew, 2013). Morphome and morphomics provide a more appropriate pair of alternatives.

The term morphome is not new but, until recently, it had been applied inconsistently in biology and biomedicine and without any encompassing definition or concept. It has been adopted, for example, to investigate selected organs and organisms (Surkova et al. 2008; Englesbe et al. 2012; Düring et al. 2013). More recently, however, the terms morphome and morphomics have been given clearer definitions and wider utility (Lucocq et al. 2015).

By analogy to other ‘-omes’, the morphome refers to the total complement of morphological features within a biological system and morphomics to the systematic study of the qualitative and quantitative attributes of those structures. It follows that morphomics includes techniques spanning all attainable levels of resolution from the macroscopic (e.g. surface anatomy, dissection, surgery, medical imaging) to the microscopic and nanoscopic (all forms of optical and electron microscopy). Of course, quantification is an important part of this field. Indeed, precise descriptions of form and content require the quantification of structure in 3D space by estimating the global and/or individual volumes, surface areas, lengths and numbers of interesting features and the spatial relationships between them. In short, the morphome defines any biological object examined by all imaging methods and at all levels of organisation (Lucocq et al. 2015).

To achieve the systematic, detailed and quantitative description of a biological system, each level of structural organisation within it will warrant application of appropriate tools and techniques. Also, each level of organisation will provide a subset of the complete morphome. For instance, qualitative and quantitative analyses of structure at the macroscopic level might be termed macromorphomics, whereas complementary analyses at the microscopic level might be termed micromorphomics. Those at the nanoscale have been termed nanomorphomics (Lucocq et al. 2015).

Revealing structural detail – the consequences of sectioning/slicing

It is self-evident that biological systems exist and operate within 3D space. However, to reveal their internal structure, we usually apply some form of sectioning or slicing (whether physical/mechanical, optical, tomographic or medical) and this process (Fig.2) has practical consequences:

Figure 2.

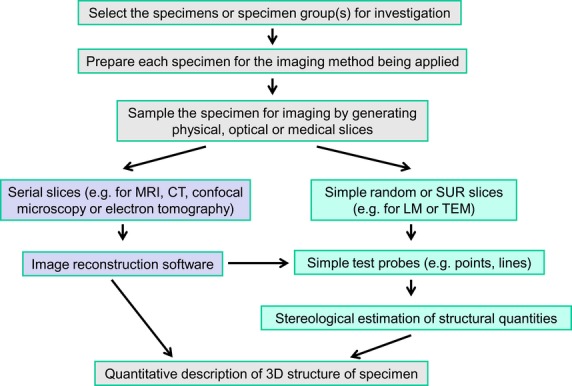
Quantifying 3D morphology. A morphomics study will require decisions about the specimen(s) to be examined and imaging techniques with which to visualise them. Some form of sectioning/slicing (physical, optical, medical, tomographic) will be applied and may involve serial slices or random (SUR or simple random) slices. The former allows reconstruction of 3D structure and the latter extrapolation via stereological methods. Some forms of image reconstruction (e.g. MRI, CT, electron tomography and micro-CT) also permit stereological quantification. The outcome is a quantitative description of the 3D morphology of the specimen(s). CT, computed tomography; MRI, magnetic resonance imaging.

1. It can limit substantially both the number of specimens (e.g. animals or parts thereof) and the fractions of specimens that can be examined. Consequently, we need to be confident that the selected specimens are an unbiased subset of the population and that the specimen fractions examined fairly reflect the whole. This implies that sampling specimens is of cardinal importance. Indeed, it is often a practical necessity. For example, preparing specimens for light microscopy (LM) and transmission electron microscopy (TEM) requires thin-section microtomy to improve lateral resolution in the final image.

2. Slicing often reduces 3D reality to a set of 2-dimensional (2D) or planar representations. Volumes (cm³) are represented on section planes as profile areas (cm²), surfaces (such as membranes or other interfaces, cm²) appear as linear features (known as boundary traces, cm¹) and linear structures (nerve fibres, blood vessels, ducts, filaments, etc., cm¹) and the numbers of particulate structures (e.g. cells and nuclei, cm⁰) both appear as numbers of transections or profiles (cm⁰). In short, the representations of 3D objects on section planes do not possess, in general, the sizes, shapes or numbers of the objects themselves.

It follows from these considerations that quantitative tools should permit the reconstruction or extrapolation of 3D quantities from the distorted impressions displayed on 2D images (Fig.2). Failure to undertake this step holds the danger of impairing or frustrating the ability to draw hard (biologically useful) interpretations. Advances in technology have extended considerably the range of techniques available for generating slice images and quantifying them. The range of resolutions now available to morphomics researchers has created a ‘big data’ problem. To exploit the full potential of these advances, and reduce the accompanying problem, the fundamental importance of random sampling, unbiased quantification and correct interpretation of slice images must be recognised and accepted.

It is of some concern that the slice image is sometimes viewed as a starting point for analysis rather than an intermediate step in a more extensive sampling and quantification scheme. Yet we cannot appreciate the quality of a sample of images (especially the degree of bias) without knowing the selection process by which those images were generated. With the increasing quest for high-throughput imaging technologies, it is important not to lose sight of the fact that ease and speed of data acquisition per se are not enough. In short, regardless of whether a study is quantitative or qualitative, methods for correlating structure and function must strive to be objective, precise (reliable, reproducible) and unbiased (accurate, valid).

Dealing with the consequences of sectioning/slicing – the small specimen fraction

The solution to the problem of ensuring that the fraction of specimen examined is a fair reflection of the whole is either to resort to exhaustive serial sectioning or to adopt some form of random sampling (Fig.2). Serial sectioning can be technically demanding (see below) and, though less comprehensive in terms of specimen coverage, random sampling schemes (Mayhew, 2008) are, by definition, unbiased selection schemes (Stuart, 1976).

In practice, random sampling includes every stage of the procedure for collecting and preparing specimens for examination. In comparative studies, the first stage involves selecting sets of specimens (e.g. individual animals or cell culture replicates) from one or more groups (e.g. control and treated). In the case of LM and TEM studies, the sampling hierarchy or sampling cascade is usually multistage and includes selecting suitably processed blocks from each specimen, cutting histological and/or other thin sections or taking optical or tomographic sections and, finally, selecting microscopical fields of view. It is important to appreciate that such a cascade of sampling stages is analogous to a chain and its links. The chain is only as strong as its weakest link. By the same token, the quality of the final sample is only as good as the choices made at each stage of the sampling cascade. For illustrations of multistage sampling schemes applied to mammalian lung, see Hsia et al. (2010).

It is worth noting also that, in this context, the term ‘random’ has several elements associated with it, viz. specimen selection, location or position and direction or orientation. Individual items (e.g. laboratory rats) drawn from a biological population display natural differences and this must be accounted for in the study design by replication, i.e. by selecting more than one individual from each study group (e.g. control and treated). Randomising the position and orientation of samples within individual specimens (e.g. rat liver) is relevant because biological structure is neither purely homogeneous (i.e. uniform in appearance regardless of position) nor purely isotropic (i.e. uniform in appearance regardless of orientation). One only has to think of a polarised structure such as a skeletal muscle fibre or the gradient of morphology along the small intestine to appreciate this. But even a relatively homogeneous structure such as the liver varies internally with position. If a system was both homogeneous and isotropic, a sample comprising just a single arbitrary plane of sectioning might suffice for some purposes. It hardly needs to be said that biological structures do not exhibit such properties because heterogeneity and anisotropy are reflections of the structural order demanded by function and its local compartmentalisation. Furthermore, a single arbitrary section plane will not allow us to reconstruct 3D content and will make stereological estimation of certain quantities, notably particle number, impracticable.

Random sampling for position may be undertaken in various ways and, although all forms are unbiased, they may vary in precision and, hence, efficiency depending on specimen heterogeneity (Stuart, 1976; Cochran, 1977; Mayhew & Sharma, 1984; Mayhew, 2008; Hsia et al. 2010). Two alternatives are considered below: simple or independent uniform random sampling and systematic uniform random (SUR) sampling.

Simple or independent uniform random sampling

This conforms to the ‘lottery principle’ because the specimen is sampled independently with the aid of some sort of random number generator (e.g. a random number table, the roll of a dice, the flip of a coin). Though unbiased, this type of random sampling does not guarantee even coverage of the entire specimen and some parts of it may be oversampled and others undersampled (Mayhew, 2008). Consequently, where sample items are located very close to each other, more work is undertaken in order to obtain essentially the same information and this tends to reduce sampling efficiency. In fact, this tendency increases with specimen heterogeneity.

SUR sampling

To improve sampling efficiency, it is preferable to spread the sampling items evenly and widely throughout the specimen so that all parts are covered uniformly and each is more likely to present new information. For this, SUR sampling can be undertaken. Here, the position of the first item is chosen randomly (Fig.3) but a previously selected pattern (the sampling interval) determines the positions of other items (Mayhew, 2008). In almost every situation, SUR sampling is more efficient than simple random sampling because it gives more even coverage across the entire specimen and this is especially pertinent when the specimen is heterogeneous (Gundersen & Jensen, 1987; Gundersen et al. 1999; Hsia et al. 2010). Despite the sampling pattern, SUR sampling retains its unbiasedness because it gives all parts an equal chance of selection (Mayhew, 2008). It is useful to remember that SUR sampling can be implemented at any stage of a sampling cascade (Fig.4).

Figure 3.

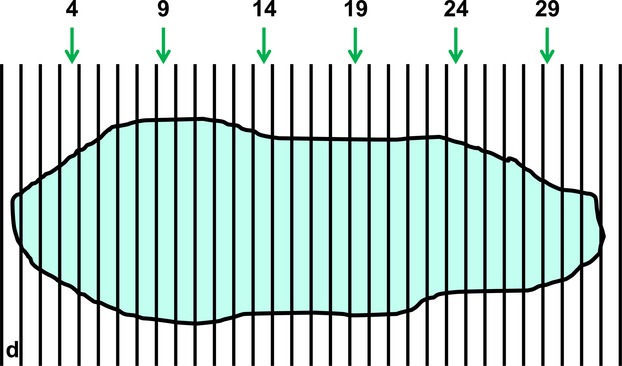
The principle of SUR sampling: sub-sampling from an exhaustive set of serial slices. In many forms of tomography, the whole specimen (or a part thereof) is reconstructed from an exhaustive set of serial slices through it. The slices might be obtained mechanically, optically or by medical imaging. Where 3D structural quantities are required from the specimen, it is much more efficient to make stereological estimates based on a SUR subset of these slices. Here, a specimen (e.g. an organ) has been serially cut into just 32 slices of thickness d with a random start position between 0 and d. Taking a SUR sample of every 5th slice with a random start between 1 and 5 (here, 4) yields slices 4, 9, 14, 19, 24 and 29. Using the right-facing section plane of each slice as the viewing plane, the resulting precision of estimation (for, say, specimen volume) is unlikely to overwhelm the natural variation between independent specimens belonging to the same study group. Indeed, the total observed variation (equal to the natural variation + estimation precision) depends more crucially on the number of specimens examined within a group.

Figure 4.

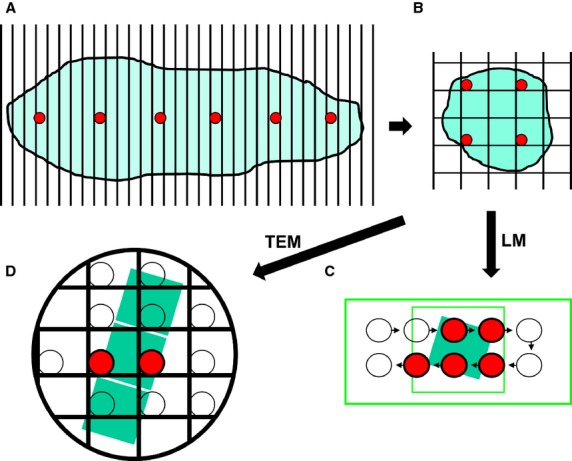
SUR sampling undertaken as part of a sampling cascade. Here, a multistage SUR sampling cascade is applied to a specimen in four stages. Stage A: the specimen is cut into serial slices and every 5th slice (red circles) is selected for further sampling. Stage B: each of the selected slices is overlaid with a quadratic lattice and SUR sampled to obtain tissue pieces (red circles). The selected tissue pieces are sub-sampled to provide sections for LM and TEM. Stage C: an SUR sample of LM fields of view (highlighted red circles) is obtained by moving the microscope stage at step intervals in x- and y-directions across each chosen section. Stage D: a ribbon of TEM sections is placed on copper grid and an SUR sample of fields of view from one section is obtained (highlighted red circles, middle section).

It is worthy of note that the efficiency of SUR sampling can be compromised if the sampling interval happens to coincide with a natural pattern within the specimen itself. Fortunately, this potential difficulty is easy to avoid provided we are aware of the specimen pattern (e.g. that of the sarcomere units along a muscle fibre). All that is required is to choose a sampling interval that does not coincide with the periodicity of the specimen pattern or with some whole-number multiple of it (Mayhew, 2008).

Sampling schemes for handling specimen orientation or polarisation by randomising the directions of physical sectioning are discussed below (see Stereology and its tools).

Dealing with the consequences of sectioning/slicing – obtaining 3D information

Ensuring that quantification is 3D rather than 2D is tackled currently in two main ways. The first is by reconstruction techniques such as serial sectioning or tomographic reconstruction. The second way is by extrapolation using the sampling and estimation tools of stereology (Fig.2). Each approach has its limitations and benefits. Although reconstructions are costly in terms of time and limit the numbers and sizes of samples that can be analysed, they provide valuable and visual 3D information about spatial relationships and connectivities. Stereology does not provide this but its cost-benefits mean that reasonably precise quantitative information can be obtained from more samples with greater efficiency. Although these approaches have developed somewhat independently, it is worth noting that they are not mutually exclusive but can be, and have been, used together.

Reconstruction techniques

Serial physical sectioning has a number of attendant technical problems associated with the physical sectioning process itself (compression, knife score marks, section damage/loss, etc.), specimen hardness (e.g. due to mineralisation) and maintaining faithful registration of sections. At the LM level, these can be avoided by optical sectioning using high numerical aperture lenses or imaging modes such as confocal microscopy, super-resolution microscopy and scanned light sheet microscopy (Hess et al. 2006; Rust et al. 2006; Keller et al. 2008; Silvestri et al. 2012; Hedde & Nienhaus, 2014). The problems of serial physical sectioning are even more severe at the TEM level where the production of ultrathin (30–90 nm thick) sections renders the process rather time-consuming and less efficient (for a truly impressive application, see White et al. 1986). These issues can be solved in part by sparse reconstruction based on a hierarchical sampling scheme and combining reconstruction of partial volumes with stereological estimation (Nava et al. 2014).

It is worth noting also that physical ultrathin sectioning underlies various forms of array tomography in which ribbons of such sections are deposited on suitable substrates and viewed by scanning electron microscopy (SEM, see Micheva & Smith, 2007; Wacker & Schroeder, 2013). Alternatively, the uncoated block faces of serial sections prepared for TEM can be examined using SEM in backscattering mode (Denk & Horstmann, 2004). Molecular characterisation can be achieved by combining array tomography and immunocytochemistry with SEM or TEM (Micheva et al. 2010; Kay et al. 2013). Software is available for 3D reconstruction and for quantification (e.g. Kay et al. 2013).

As alternative approaches, types of ‘optical’ sectioning are available in the guise of electron tomography (McIntosh et al. 2005; Vanhecke et al. 2007; Vijayakrishnan et al. 2013), scanning transmission electron microscopy tomography (STEM tomography, see Aoyama et al. 2008; Baudoin et al. 2013) and micro-computed tomography (micro-CT, see Vasilescu et al. 2013; Danz et al. 2014), thereby avoiding the need to cut serial physical slices. Spatial information is retained by making images of the specimen at different tilt angles and then merging them to generate a 3D reconstruction (e.g. see Leis et al. 2008). The technique can be combined with pre-embedding labelling using nanogold particles for immunolocalisation.

In electron tomography, tilting of the specimen occurs around an axis which is orthogonal to the electron beam, the entire content of a section (200–300 nm thickness) is always in focus, and the tilting ensures that structures within it can be viewed from different directions. From the thick sections, stacks can be reconstructed from faithfully registered, parallel sections separated by only 2–10 nm in the z-direction and such stacks are also very attractive from a stereological perspective (Vanhecke et al. 2007; Mayhew et al. 2009). Again, software is available for reconstruction and allows quantification (e.g. Kremer et al. 1996).

Initially, electron tomography was applied to conventional and cryofixed specimens embedded in resin but, latterly, cryofixed samples and sections have been imaged in the frozen state. More recent developments include focused ion beam/scanning electron microscopy (FIB/SEM) tomography where a specimen sample is milled repeatedly with the ion beam and the block face, rather than the section, imaged using SEM. Though having lower resolving power than electron tomography, FIB/SEM permits 3D analysis of larger volumes including whole cell volumes (Villinger et al. 2012; Blazquez-Llorca et al. 2013; Drobne, 2013; Kizilyaprak et al. 2014; Narayan et al. 2014). Recently, increases in speed and automation have been combined with region-of-interest sampling (Narayan et al. 2014) and this could be adapted to achieve SUR sampling of sub-volumes at high-resolution. A similar approach, serial block-face SEM, uses a sectioning device placed within the SEM to slice and record images successively (Hughes et al. 2014). STEM tomography (Yakushevska et al. 2007; Aoyama et al. 2008; Baudoin et al. 2013) can be used also to obtain a tilt series of images through an entire cell using 1-μm-thick sections.

X-rays may be used to image specimens at different levels of organisation from molecules to whole organisms. Soft X-ray tomography (Carzaniga et al. 2014; Duke et al. 2014) is analogous to electron tomography in that specimens are tilted during imaging: the penetration depth is about 10 μm and resolution about 20–40 nm. Computed tomography (CT) also involves the interaction of X-radiation with the biological specimen and, to produce a 3D image, a set of 2D projections is required. In micro-CT, these are usually taken with X-ray source and detector at a fixed position and the specimen rotated around its long axis. Image displays are not confined to axial images but, instead, software programmes can be used to build a stack of slices. This allows non-destructive sectioning and imaging of specimens at multiple resolutions down to about 2 μm. Recently, the technique has been employed to scan the whole mouse lung at high resolution and then regionally sample at even higher resolution (Vasilescu et al. 2013). Stereological tools were used to assess whole organ structure and estimates compared with others obtained by conventional histology on the same lungs. Similar developments have been made with slices obtained using magnetic resonance imaging (MRI) and Cavalieri sectioning or array tomography (Mayhew & Olsen, 1991; Roberts et al. 1993; Gong et al. 2000; Kopeikina et al. 2013).

Stereology and its tools

Over the past 50 years, research in the morphological sciences has benefitted from the development, refinement and application of the principles of stereology (Weibel, 1979; Howard & Reed, 2005; Mayhew, 2006; Nyengaard & Gundersen, 2006; Hsia et al. 2010; Tschanz et al. 2014). The special emphasis accorded to stereology reflects the peculiar problems associated with interpreting 2D structural quantities abstracted from images appearing on physical and optical slices through biological specimens. However, the continuing and increasing usage of the methods stems from conviction as well as practical necessity. The benefits of stereology derive from at least four sources:

1. Stereological sampling and estimation tools generate 3D (hard) quantitative information (including the volumes, surface areas and numbers of compartments or particulate objects) which facilitates the biological interpretation of structural alterations. Generating 2D structural data (transectional areas, boundary lengths and numbers of profiles) is simply not an acceptable general route to describing the 3D spatial morphome.

2. Stereological 3D information is accurate (unbiased) and can be acquired with reasonable levels of precision. Precision, but not accuracy, can be improved by doing more (e.g. by increasing sample sizes). Few other morphometric approaches offer these twin advantages.

3. Stereological tools and principles are cheap to apply and 3D information can be gathered without using expensive measuring devices or high-precision technologies. The approach is, therefore, cost-effective and can also be efficient in terms of precision per unit of effort (e.g. per hour).

4. All levels of biological organisation (from the molecular to the organic or organismal) can be investigated and quantitative data obtained from slices of widely different thicknesses (from, say, 1-cm organ slices or MRI slice images, via 3- to 30-μm LM sections and 30- to 100-nm TEM slices to 2- to 10-nm-thick electron tomographic slices).

The essence of stereology is to apply random (preferably SUR) sampling schemes to the specimen and produce slice images that are probed by simple geometrical features (Fig.2) and, thereby, generate good estimates of the sizes, numbers and spatial arrangements of structures. Strictly speaking, estimates are obtained from the viewing plane of the slice and will not require correction provided there are no projection effects through the section thickness. Although pioneered for use with physical slices, stereological principles are just as valid for slice images generated by other means, including medical imaging techniques (e.g. MRI, computer-assisted tomography including micro-CT, positron emission tomography, ultrasonography), optical sectioning (e.g. by confocal scanning microscopy) or electron tomographic ‘optical’ sectioning.

Stereological tools offer unbiased estimates of volume, surface, length and number on aggregate compartments or individual items from organelles to cells and organs. There are, in addition, powerful estimators that can estimate sizes and numbers and their distribution within specimens.

The validity and efficiency of these estimates are determined by a design-based approach to sampling over the entire sampling cascade (Fig.4) and most of the underlying stereological estimators are astonishingly simple if random sampling is performed. The stereological tools have been applied successfully to characterise 3D structure in a host of different systems at different levels of structural organisation and in combination with diverse imaging techniques (for only a few examples, see Weibel & Knight, 1964; Blouin et al. 1977; Williams & Cope, 1981; Henery & Mayhew, 1989; Mayhew et al. 1993; Roberts et al. 1993; Mayhew & Astle, 1997; Gong et al. 2000; Ochs et al. 2001; Lawlor et al. 2002; Hyde et al. 2004; Jinno & Kosaka, 2004; McCullough & Lucocq, 2005; Vanhecke et al. 2007; Eisele et al. 2008; Knust et al. 2009; Heilmann et al. 2012; Vasilescu et al. 2013).

Most 3D quantities can be derived from slice images easily and with relatively little effort. Indeed, volumes, surface areas, lengths and numbers of objects can all be estimated without making any measurements at all! Instead, random test probes (lattices of areas, lines and points) thrown on suitably randomised section planes are used as a basis for classifying and counting chance events (Weibel, 1979; Howard & Reed, 2005). For example, on slices through cells, we can estimate the surface area of ER cisternae membranes by counting sites at which test line probes intersect the traces of membranes seen on the slices, and the volume of the cell (or an intracellular compartment) can be estimated by counting test point probes which fall on the sections through it. The number of cells can be estimated by counting them in a type of volume probe called a disector, which consists of a pair of parallel slices a known distance apart (Sterio, 1984; Gundersen, 1986). In all these cases, relative quantities are estimated as component densities (e.g. volume or numerical density) which can be converted into absolute quantities if the reference volume (e.g. organ volume) is determined. An attraction of SUR sampling is that it selects a fixed fraction of the specimen and, hence, of the components within it. This is the basis of the fractionator, a tool for counting particles in a specimen without needing to know section thickness or the reference volume or the distance between the slice planes of a disector (Gundersen, 1986, 2002; Hyde et al. 2004). Although the fractionator is optimal for particle counting, the reference volume is required when global volumes, surfaces and lengths are required.

Clearly, counting lattice points is not a very precise way of estimating the areas of slices through a cell or other object. Similarly, counting intersection sites is not a very precise way of estimating the length of a membrane trace. However, it is worth emphasising that, in biology, these sources of imprecision often have negligible impact on total study variation. This is because they must be balanced against other sources of experimental error including sampling variation and, ultimately, the natural differences (biological variation) existing between individuals (e.g. between one animal and the next). Often, the latter is the major contributor to total study variation, and the most effective way of dealing with the precision of the final estimate for a group of individuals is to increase the number of individuals and not the precision of estimation made on each individual (Shay, 1975; Gundersen & Østerby, 1981; Gupta et al. 1983; Mühlfeld et al. 2010). This is easier to achieve in the stereological context than in the reconstruction methods mentioned above. The bottom line is this: a commonsense approach to study design is to ensure that the introduced errors (ascribable to sampling accuracy and estimation precision) do not account for the major share of total variation (including the biological variation).

As stated already, the sampling schemes used in stereology are of general utility and work on the basis that random sampling allows each item or location/orientation within a specimen an equal chance of being chosen. Again, although simple random sampling is adequate, SUR sampling is often more efficient (Mayhew, 2008). It should be noted, however, that obtaining efficient and unbiased stereological estimates of certain quantities (notably, membrane surface areas, filament/tubule lengths and layer thicknesses) requires the production of sets of sections and test probes which are not only positioned but also oriented randomly. The latter is achievable by producing section sets that are isotropic uniform random (IUR) in 3D space or, applying to sections sets, test line probes which are IUR in 3D. IUR simply means randomised so that all positions, and all orientations, are equally probable.

One way of aiming for IUR sections is to randomise the orientations of tissue pieces during embedding (Stringer et al. 1982). More robust schemes which include elements of systematic sampling and provide IUR sections are the isector (ideal for small specimens embedded for TEM, Nyengaard & Gundersen, 1992), the orientator and orthogonal triplet probe (both useful for highly anisotropic structures, Mattfeldt et al. 1985, 1990) and vertical sectioning (efficient for investigating polarised surfaces, Baddeley et al. 1986). The latter generates sections which are isotropic only in 2D but all these sampling tools can be used with test grids whose designs ensure that test lines are IUR in 3D (see Mayhew, 2008 for further illustrations). Finally, IUR and vertical sections can be combined with particle selection tools to determine individual or total volumes and total numbers.

Biological variation and the issue of replication

In biology, independent sampling items (whether animals or parts thereof) differ because of natural variation. As a consequence, comparative studies require information about the levels of variability within and between study groups. This is achieved by replication, i.e. by having more than one independent sampling item (specimen) in each study group. The minimum number of specimens needed in each group depends on several factors, including the variability within each study group and the magnitude of the group differences being tested for statistical significance at a given probability level (often P < 0.05). In many (but not all) cases, a sensible sample size would be five to six specimens in each group. More rigorous estimates of sample size may be obtained after undertaking small pilot studies with two to three specimens in each group (Gundersen & Østerby, 1981; Gupta et al. 1983).

A potential problem with the newer imaging and slicing technologies is that of the cost and time limitations of generating complete reconstructions from exhaustive serial slice images. When 3D quantitative structural data are required, the danger of undertaking exhaustive reconstruction of a single specimen at the expense of replication can be offset by sub-sampling from the exhaustive slice sets. SUR sampling is a powerful and efficient approach in this context (Fig.3). For example, stereological estimates of specimen volume can be obtained from a set of just five to six SUR slices with a precision of about 5% or less (Gundersen & Jensen, 1987; Henery & Mayhew, 1989).

Stereology, TEM and immunogold cytochemistry

Comprehensive investigation of systems biology via morphomics requires application of imaging modalities that reveal structure at multiple resolution scales. Nanomorphomics is the sub-field of morphomics devoted to the systematic study of morphology at the nanoscale and an important element of nanomorphomics is the combination of immunolabelling and TEM. Combined with the sampling and estimation tools of stereology, TEM offers a paradigm for quantifying structure at nanoscale resolution (Howard & Reed, 2005; Nyengaard & Gundersen, 2006; Lucocq, 2012; Lucocq & Hacker, 2013). The procedures have had a significant impact on the quantification of organelles and cell compartments and, recently, their use has been extended to mapping the spatial distributions and intensities of labelled molecules and nanoparticles across tissue and cell compartments (see Mühlfeld et al. 2007; Mayhew & Lucocq, 2008; Mayhew et al. 2009; Mayhew, 2011; Rothen-Rutishauser et al. 2014).

Immunogold cytochemistry or immunoEM (Griffiths, 1993; Amiry-Moghaddam & Ottersen, 2013; Griffiths & Lucocq, 2014) is an important tool in cell biology applicable to ultrathin TEM sections. The ultimate goal of quantitative immunoEM is to estimate numbers of target molecules (usually peptides, proteins or protein complexes) in biological systems and to map their spatial distributions within them. This provides a route to integrate morphomics with proteomics. Target molecules are bound specifically to affinity markers (primary antibodies) and then detected and localised with visualisation probes (usually colloidal gold particles bound to protein A). While TEM provides high-resolution images of gold particles and cell compartments, the particles themselves are electron dense, countable and available in different sizes and these attributes facilitate the quantification of one or more defined targets in cell compartments. To achieve this, stereological tools are used to estimate local intensities of labelling/co-labelling and labelling distributions across various compartments (Mayhew & Lucocq, 2008, 2011; Lucocq & Gawden-Bone, 2009, 2010; Mayhew et al. 2009). In combination with cryo-ET, the approach has the potential to overcome a bugbear of immunoEM, viz. that of reliably estimating labeling efficiency (Lucocq et al. 2015), by allowing a correlation of molecular density with gold labelling density.

During the past decade, new and more coherent ways of quantifying gold labelling within cells have been developed (for a recent review, see Mayhew, 2011). The efficiency and validity of the methods rely on sound principles of specimen sampling, event counting using test probes and inferential statistics. These include random selection of items at each stage of a sampling cascade, stereological analysis of cell ultrastructure, unbiased particle counting and statistical evaluation of an appropriate null hypothesis. Depending on the aims/objectives of a given investigation, a compendium of approaches now allows of the following possibilities:

1. We can test whether a target molecule shows preferential labelling by mapping the localisation of gold particles across relevant compartments (Mayhew et al. 2002).

2. Using data from wild-type and knockdown/knockout control cells, we can correct raw gold particle counts, estimate specific labelling densities and then test for preferential labelling (Lucocq & Gawden-Bone, 2010).

3. We can map the distributions of a given target in two or more groups of cells (which differ in type or treatment) to test whether there are shifts in compartment labelling (Mayhew & Desoye, 2004).

4. Using a variant of (3), we can undertake multiple-labelling studies to test whether different target molecules co-localise (Mayhew & Lucocq, 2011). This is achievable by utilising more than one size of gold particle or other electron-dense nanoparticles distinguishable by virtue of differences in shape (see Philimonenko et al. 2014).

5. In studies involving target translocation, we can map absolute numbers of gold particles over compartments at specific positions within dividing, oriented or polarised cells (Lucocq & Gawden-Bone, 2009).

The development of methods for quantitative immunoEM illustrates the power and potential of random sampling designs and stereological analysis for improving the quality of quantitative datasets and extending our knowledge base in a given area. Now, let us consider the requirements of such studies in the context of broader morphomics research. The paradigm is a series of steps integrated into a multistage cascade sampling scheme and followed by quantification (Fig.5). Four main decision steps can be envisaged:

Figure 5.

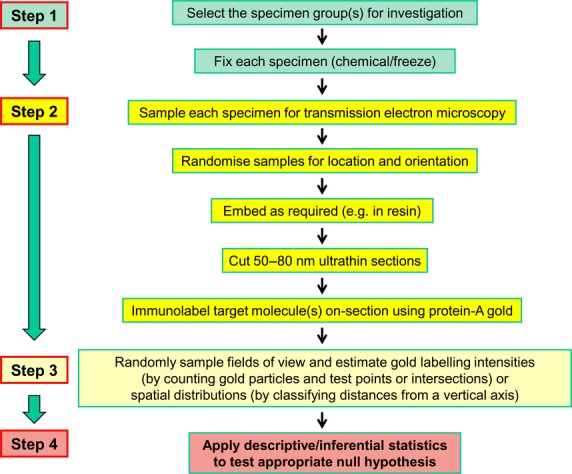
Workflow for a study involving stereology, TEM and post-embedding immunogold cytochemistry. Four main decision steps are identified in a multistage cascade sampling scheme followed by quantification. From the group(s) to be studied, a set of specimens is selected and these might be replicates of cell cultures, cells isolated from bodily fluids or whole cells removed from some tissue/organ (Step 1). Next, the specimen is prepared for examination by the chosen imaging technique (Step 2). With immunoEM, this involves fixing, embedding and sectioning specimens for TEM and then on-section labeling for immunogold cytochemistry. The steps may involve further sub-sampling of the specimens and randomisation of section location (SUR sampling) and orientation (IUR sampling). Finally, the method of quantification is chosen (Step 3). For immunoEM, this could involve using stereology to count (i) gold particles, (ii) test points and/or (iii) intersections between test lines and membrane traces. Again, these have random sampling requirements in terms of location and orientation. Finally, data handling involves using appropriate descriptive and inferential statistics (Step 4). Similar workflows can be adopted for other imaging modalities including electron tomography and micro-CT.

1. Step 1. From the population to be sampled, select the set of specimens for investigation. In the case of immunoEM, these might be replicates of cell cultures, cells isolated from bodily fluids such as blood or peritoneal exudates, or whole cells removed from some tissues/organs of some multicellular organisms. Random sampling will avoid selection bias.

2. Step 2. Choose the imaging technique. This will have associated with it particular technical procedures which prepare the specimens for investigation. Again, with immunoEM, this involves fixing, embedding and sectioning specimens for TEM and then post-embedding or on-section labelling for immunogold cytochemistry. These steps will involve further sub-sampling of the specimens (selecting embedded blocks for sectioning, selecting ultrathin sections for TEM imaging, selecting fields of view at appropriate magnification to permit accurate quantification) and, as we have seen, this may require randomisation of section orientation as well as section location.

3. Step 3. Choose the method of quantification. Here, this involves using stereological tools to obtain unbiased (accurate) estimates of numbers of gold particles, numbers of test point probes falling on organelle profiles and/or numbers of intersections between test line probes and membrane traces. Again, these have random sampling requirements in terms of location and orientation.

4. Step 4. The output data must be handled appropriately using the tools of descriptive and inferential statistics in order to test a pertinent null hypothesis.

Apart from TEM/immunogold cytochemistry, this strategy of sampling and stereological principles has been utilised in combination with other imaging modalities including confocal microscopy, MRI, micro-CT, and electron and array tomography (Mayhew & Olsen, 1991; Gong et al. 2000; Vanhecke et al. 2007; Vasilescu et al. 2012, 2013; Kopeikina et al. 2013; Rothen-Rutishauser et al. 2014). It has been used also with non-imaging diagnostic techniques such as acoustic rhinometry (Mayhew & O'Flynn, 1993).

Closing remarks

The aim of this article has been to emphasise the potential value of stereological tools and study designs as a template for advancing the study of morphomics and giving clearer descriptions of the morphome. Although, at first sight, newcomers might find the sampling and estimation requirements of stereology to be daunting, consider the following. Scientists have a responsibility to use the best tools and techniques that are available subject only to constraints of time and cost. Apart from sampling and estimation requirements, it is the case that different imaging modalities require their own preparative steps, including fixation and embedding, and detailed discussion of these potential sources of technical bias is beyond the scope of this review. Suffice it to say that special attention must be given to preserving specimen dimensions as close as possible to the native state. However, it is worth remembering that the validity of comparisons between specimens in different study groups will be retained provided that technical biases are constant between groups.

From a statistical viewpoint, the worth of sampling techniques and quantitative tools must be judged in terms of their precision, efficiency and degree of bias. At the time of writing, it is fair to state that stereology offers precise and flexible tools for obtaining 3D quantitative information about biological structures and, when applied with random sampling schemes, its tools can be unbiased and efficient. In comparative studies, the ability to analyse multiple specimens drawn from control and experimental populations is a real bonus as it allows us to take full account of natural or biological variation. It is no accident that stereological practice has been recommended as the ‘gold standard’ for quantifying structure in several areas of biomedical research, including cell biology (Nyengaard & Gundersen, 2006; Lucocq & Hacker, 2013) and studies on nervous tissue (Saper, 1996), kidney (Madsen, 1999; Nyengaard, 1999), placenta (Mayhew, 2006, 2008), heart (Mühlfeld et al. 2010) and lung (Hsia et al. 2010).

For morphomics research, the same effort to employ robust tools for sampling specimens and quantifying their 3D morphology should be undertaken to facilitate inter-study comparability and improve our capacity to interpret changes in functional morphology visualised by whatever means. How these powerful and sound procedures can be coupled with other microscale and nanoscale imaging methods in order to extend their use across different levels of resolution (fluorescence microscopy, correlative light-electron microscopy, super-resolution microscopy, cryo-electron tomography, FIB/SEM tomography, micro-CT, etc.) has been discussed elsewhere (Vanhecke et al. 2007; Koning & Koster, 2009; Vasilescu et al. 2013; Lucocq et al. 2015) or awaits future advances and applications. Certainly, applying stereological sampling and estimation tools to subsets of slices obtained via the new tomography-based technologies, should facilitate the efficiency of high-throughput microscopy.