Abstract
Key points
Rod photoreceptors play a key role in vision in dim light; in the mammalian retina, although rods are anatomically connected or coupled by gap junctions, a type of electrical synapse, the functional importance and regulation of rod coupling has remained elusive.
We have developed a new technique in the mouse: perforated patch-clamp recording of rod inner segments in isolated intact retinae maintained by superfusion.
We find that rod electrical coupling is controlled by a circadian clock and dopamine, and is weak during the day and stronger at night.
The results also indicate that the signal-to-noise ratio for a dim light response is increased at night because of coupling.
Our observations will provide a framework for understanding the daily variations in human vision as well as the basis of specific retinal malfunctions.
Abstract
Rod single-photon responses are critical for vision in dim light. Electrical coupling via gap junction channels shapes the light response properties of vertebrate photoreceptors, but the regulation of rod coupling and its impact on the single-photon response have remained unclear. To directly address these questions, we developed a perforated patch-clamp recording technique and recorded from single rod inner segments in isolated intact neural mouse retinae, maintained by superfusion. Experiments were conducted at different times of the day or under constant environmental conditions, at different times across the circadian cycle. We show that rod electrical coupling is regulated by a circadian clock and dopamine, so that coupling is weak during the day and strong at night. Altogether, patch-clamp recordings of single-photon responses in mouse rods, tracer coupling, receptive field measurements and pharmacological manipulations of gap junction and dopamine receptor activity provide compelling evidence that rod coupling is modulated in a circadian manner. These data are consistent with computer modelling. At night, single-photon responses are smaller due to coupling, but the signal-to-noise ratio for a dim (multiphoton) light response is increased at night because of signal averaging between coupled rods.
Introduction
Gap junction channels are phylogenetically ancient and ubiquitous mediators of cellular communication (Pereda et al. 2013). In the nervous system, gap junctions form electrical synapses, key elements of neural circuit function and signal processing (Bennett & Zukin, 2004; Hormuzdi et al. 2004; Pereda et al. 2013). However, in contrast to detailed knowledge of the mechanisms underlying chemical transmission, the regulation and functional significance of electrical synapses remain largely incomplete.
In the retina, cell–cell electrical coupling is a key determinant of light response properties of verteb-rate photoreceptors. Together with voltage-gated conductances, electrical coupling shapes the change in membrane potential initiated in the outer segment by the absorption of light and the subsequent development of photocurrent (Baylor et al. 1971, 1979; Burns & Arshavsky, 2005). Photoreceptor electrical coupling is proposed to play important roles in signal processing, including noise filtering, intensity coding, spatial processing and rod and cone signal mixing (Baylor et al. 1971; Lamb & Simon, 1976; Attwell et al. 1984; Tessier-Lavigne & Attwell, 1988; Hornstein et al. 2005; Zhang & Wu, 2005; Li et al. 2012). In lower vertebrates, photoreceptor coupling has been shown to be regulated by light, the retinal neuromodulator dopamine, and a circadian clock (Yang & Wu, 1989; Krizaj et al. 1998; Ribelayga et al. 2008; Li et al. 2009).
In mammals, electrical coupling between cones produces a dramatic increase in sensitivity and the signal-to-noise ratio (SNR; DeVries et al. 2002). Phosphorylation of the gap junction-forming protein connexin36 (Cx36) in photoreceptors is regulated by light and dopamine and may function as a key regulator of gap junction coupling (Li et al. 2013). Although the nature of the rod connexin has yet to be identified (Bloomfield & Völgyi, 2009; Li et al. 2013), the existence of gap junctions between rods has been clearly observed by electron microscopy (Raviola & Gilula, 1973; Tsukamoto et al. 2001). However, the functional significance of rod coupling remains elusive. On the one hand, a long-standing view in the field of visual neuroscience is that in the dark, rods should remain electrically isolated from one another in order to prevent loss of the single photon response and optimize the SNR (Taylor & Smith, 2004; Okawa & Sampath, 2007). On the other hand, electrophysiological data, including paired recordings from guinea-pig rods, have provided clear evidence that rods are electrically coupled via gap junctions (Hornstein et al. 2005; Li et al. 2012). Important open questions remain, however, as to whether rod electrical coupling preserves the single-photon response in individual rods and whether rod coupling is dynamically regulated.
To directly address these questions, we developed a perforated patch-clamp recording technique and recorded from single rod inner segments in isolated intact neural mouse retinae, maintained by superfusion, of the melatonin-proficient CBA/CaJ strain. We report that rod electrical coupling is regulated by a circadian clock and dopamine, so that coupling is weak during the day and strong at night. Importantly, we show that the increase in rod coupling at night only slightly affects the single photon response but increases the SNR for a dim light response. We argue that the strength and regulation of rod coupling in mouse may represent a general principle of retinal design in mammals, possibly reflecting retinal evolutionary history.
Methods
Ethical approval
The care and use of mice were in accordance with federal and institutional guidelines and conducted with the approval of the Institutional Animal Care and Use Committee (The University of Texas Health Science Centre Animal Welfare Committee).
Animals and lighting conditions
Adult CBA/CaJ mice (Jackson Laboratories, Bar Harbor, ME, USA), 2–6 months old, were housed in a 12 h light–12 h dark cycle (with lights on at 07.00 h) for at least 2 weeks before an experiment. Circadian conditions were created by keeping the mice in the dark for up to 48 h, with dark adaptation starting at the end of the light phase (19.00 h). We refer to the light phase between 07.00 and 19.00 h as the day (D), also defined as the period between zeitgeber time (ZT) 0 and ZT12, and the dark phase between 19.00 and 07.00 h as the night (N) or the period between ZT12 and ZT24. Accordingly, under circadian conditions, we refer to the subjective day (SD) as the period between circadian time (CT) 0 and CT12 that is, for most experiments between 12 and 24 h after the beginning of dark adaptation (SD1), and the subjective night (SN) as the period between CT12 and CT24, that is 24 and 36 h after the beginning of dark adaptation. Some recordings were also obtained during the second subjective day (SD2) that is, between 36 and 48 h after the beginning of dark adaptation. Manipulation of the animals and retinal tissue during the night or under circadian conditions were conducted under infrared light with the help of infrared goggles (D-321G-A; Night Optics USA, Huntington Beach, CA, USA).
Mouse neural retina preparation
Dark-adapted mice were anaesthetized with a mixture of ketamine and xylazine (100 mg kg−1 + 10 mg kg−1, respectively, i.m.), decapitated, and one eye was enucleated and rapidly placed in Ames’ medium with glutamine buffered with 23 mm NaHCO3 (Sigma-Aldrich, St Louis, MO, USA). We used only one eye for recording purposes. The second eye was either discarded or used for other histochemical experiments. Neural mouse retinae were isolated under infrared illumination with dual-unit Prowler Night Vision scopes (Meyers Electro Optics, Redmond, WA, USA). The intact neural mouse retina with photoreceptor side up was placed on a nylon mesh, clamped with a second nylon mesh and a plastic ring, and moved to a 2 ml chamber on the microscope stage. The retina was then superfused at 2 ml min−1 (turnover 1 min−1) with the bicarbonate-buffered Ames’ solution at 32 °C continuously gassed with 5% CO2–95% O2 to maintain pH at 7.4. Drugs were dissolved in Ames’ solution, and the pH was adjusted to 7.4 with NaHCO3 when required. All chemicals were purchased from Sigma-Aldrich or Fisher Scientific (Pittsburgh, PA, USA). The neural retina was superfused for 60 min in the dark before the start of electrical recording. Rod light responses were recorded in the intact mouse retina maintained in superfusion under dark-adapted conditions for 1–4 h.
Patch-clamp recording
Perforated patch-clamp recordings from rod inner segments in intact mouse neural retinae were obtained under continuous dark-adapted conditions in the subjective day and subjective night of a circadian cycle and in the day and night of a 12 h light–12 h dark cycle. The preparation and electrode tips were visualized with infrared (>900 nm) differential interference contrast (DIC) microscopy. Recordings (current-clamp configuration with I = 0) were obtained under visual control with a 3900A amplifier (Dagan Corporation, Minneapolis, MN, USA) using Clampex 10.2 software and digitized with a Digidata 1322A interface (Molecular Devices, Sunnyvale, CA, USA). Signals were filtered at 1 kHz with a four-pole Bessel filter and sampled at 1 kHz. Electrodes were fashioned from borosilicate glass capillaries (OD 1.2 mm, ID 0.69 mm, Sutter Instruments, Novato, CA, USA). The pipette solution contained (in mm) 10 KCl, 120 K-d-gluconate, 5 MgCl2, 5 Na2-ATP, and 1 Na3-GTP. The pH was adjusted to 7.25 with KOH and osmolarity to 265 mosmol l–1. Electrodes were backfilled with 25 μm β-escin (Sigma) with or without 4% Neurobiotin (Vector Laboratories, Burlingame, CA, USA) in standard electrode solution. The tip resistance measured in the bath was 15–20 MΩ. The liquid junction potential (∼15 mV) was not corrected. The seal resistance ranged from 1 to 20 GΩ. We used positive pressure to give electrode tips clean access to photoreceptor membrane. Following perforation, which typically developed within 10 min, the series resistance was 15–30 MΩ. In some experiments, and only when series resistance was ≤20 MΩ, rods were clamped at −35 mV, and the light-evoked membrane current was measured and/or the input resistance Ri was estimated from the change in resting current following a 20 ms voltage step from −35 to −50 mV. Occasionally, we recorded light responses from cones. Cones were identified based on their response sensitivity and kinetics and morphology following Neurobiotin injection. We excluded cone recordings from this study. However, we used our estimate of the cone resting membrane potential (RMP) in the resistive–capacitive model: −45.1 ± 2.2 mV (mean ± SEM; n = 8). A recent study has reported that rod–cone coupling increases spontaneously after obtaining intracellular access in mouse cones and that rundown of kinetics with time are often observed in patched rods (Asteriti et al. 2014). In our conditions, we observed a rundown in rod kinetics following intracellular access in less than 10% of the rods. This phenomenon typically developed within minutes, and the data obtained under these conditions were discarded. Differences between the technique used by Asteriti et al. and ours include a different perforating agent (Amphotericin-B vs. β-escin), the presence of ATP in our pipette solution and its absence in theirs, and a higher resistance of the pipettes we used (15–20 MΩ vs. 6–9 MΩ). The very stable recordings we were able to obtain allowed us to perform pharmacological manipulations of the rod light response, as illustrated in Figs10. Although we were able to maintain recording of a cell long enough to pharmacologically manipulate the rod voltage responses, slow baseline drift of a few millivolts in amplitude typically occurred during long recordings and prevented us from detecting significant differences between the experimental groups. However, we were able to demonstrate a day–night difference in the rod RMP because the potential was measured as soon as the membrane was perforated and because of the large number of rods recorded and averaged.
Figure 10.
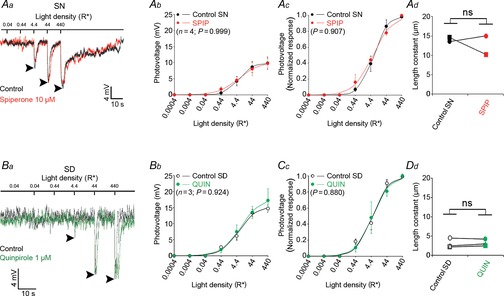
The effects of spiperone and quinpirole on the rod light response kinetics and receptor field size depend on time of day
A, blocking dopamine D2-like receptors during the subjective night (SN) does not affect the nighttime state. Examples of rod responses to a series of 20 ms full-field 500 nm light flashes of increasing intensity recorded under dark-adapted conditions during the SN under control conditions (no drug, dark trace) and following the application of the D2-like receptor antagonist spiperone (10 μm, > 10 min, red trace; Aa). Averaged (Ab) and normalized (Ac) intensity–response curves and receptive field size (Ad) of rods recorded during the SN under control conditions (black points and curves) and after ∼15 min application of spiperone (red points and curves). B, application of quinpirole during the subjective day (SD) had no effect on the rod light responses kinetics or receptive field size. Examples of rod responses to a series of 20 ms full-field 500 nm light flashes of increasing intensity recorded under dark-adapted conditions during the SD under control conditions (no drug, dark trace) and following the application of the D2-like receptor agonist quinpirole (1 μm, > 10 min, green trace; Ba). Averaged (Bb) and normalized (Bc) intensity–response curves and receptive field size (Bd) of rods recorded during the SD between CT06 and CT09, under control conditions (black points and curves) and after ∼15 min application of the D2-like receptor agonist quinpirole (green points and curves). The P values in Ab, Ac, Bb, and Bc were calculated for interactions between light density and treatment (control or drug; two-way ANOVA). ns, non-significant; P > 0.05; Student's paired t test). Arrowheads in Aa and Ba indicate the peak of the response under control conditions. Error bars, SEM (1 cell retina–1). Resting membrane potential was –43.5 mV (control) and –41.5 mV (spiperone) for cell in Aa, and –42.4 mV (control) and –41.6 mV (quinpirole) for cell in Ba.
We defined the time-to-peak as the time between the beginning of the light response and its maximum amplitude (i.e. the most negative value of the membrane potential); the response amplitude was the difference between the RMP and the membrane potential at the peak response; and the duration of the response was the duration of the hyperpolarization. The end of the response was thus set as the time the membrane potential equalled the initial resting potential for the first time following the light-evoked hyperpolarization (see Fig.4E for illustration).
Figure 4.
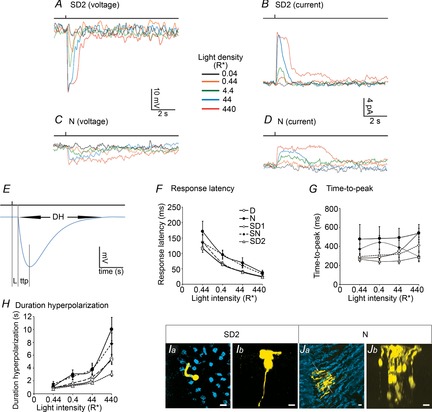
Rod light response kinetics during the second subjective day and the night
A–D, representative examples of light-evoked rod membrane voltage (A and C) and current (B and D) responses to a series of 20 ms full-field 500 nm light flashes of increasing intensity recorded during the second subjective day (SD2, CT06; A and B), and the night (N, ZT21; C and D). Resting membrane potential was –38.7 mV in A, and –45.3 mV in C. Holding current at –35 mV was 0.9 pA in B, and 5.4 pA in D. E, measures of the kinetics of the rod light response. L, response latency; ttp, time-to-peak; Dh, duration of hyperpolarization. Blue trace is an empirical photovoltage response of a rod in the form 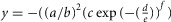 . F–H, kinetics of the rod light responses recorded during the D, N, SD1, SD2 and SN. Latency (F), time-to-peak (G), and duration of hyperpolarization (H) of the rod light responses are plotted as a function of light density. Shown are average data ± SEM from 10–35 cells. For each measurement, a two-way ANOVA was performed. The between-group factor was time of D (i.e. D, N, SD1, SD2 or SN) and the intra-group was flash intensity. ANOVA of the data presented in F revealed significant time of D effect (F(4,330) = 6.24, P < 0.001) and intensity effect (F(3,330) = 85.27, P < 0.001) but no time of D × intensity effect (F(12,330) = 0.59, P = 0.85). ANOVA of the data presented in G revealed significant time of D effect (F(4,330) = 6.24, P < 0.001) and intensity effect (F(3,330) = 85.27, P < 0.001) but no time of D × intensity effect (F(12,330) = 0.59, P = 0.85). ANOVA of the data presented in H revealed significant time of D effect (F(4,345) = 11.96, P < 0.001), intensity effect (F(3,345) = 67.09, P < 0.001) and time of D × intensity effect (F(12,345) = 2.48, P = 0.004). I and J, typical examples of Neurobiotin tracer coupling between photoreceptors obtained during the SD2 (Ia and b) and the N (Ja and b). Panels show confocal images of whole-mount retinae at the level of the cone inner segments (optical sections, 5 × 1 μm; Ia and Ja) and 3D projections of 70-μm thick Z-stacks of the outer nuclear layer of the same area (Ib and Jb). The distribution of the number of tracer coupled cells during the SD2 and N are illustrated in Fig.7G. Scale bars, 5 μm.
. F–H, kinetics of the rod light responses recorded during the D, N, SD1, SD2 and SN. Latency (F), time-to-peak (G), and duration of hyperpolarization (H) of the rod light responses are plotted as a function of light density. Shown are average data ± SEM from 10–35 cells. For each measurement, a two-way ANOVA was performed. The between-group factor was time of D (i.e. D, N, SD1, SD2 or SN) and the intra-group was flash intensity. ANOVA of the data presented in F revealed significant time of D effect (F(4,330) = 6.24, P < 0.001) and intensity effect (F(3,330) = 85.27, P < 0.001) but no time of D × intensity effect (F(12,330) = 0.59, P = 0.85). ANOVA of the data presented in G revealed significant time of D effect (F(4,330) = 6.24, P < 0.001) and intensity effect (F(3,330) = 85.27, P < 0.001) but no time of D × intensity effect (F(12,330) = 0.59, P = 0.85). ANOVA of the data presented in H revealed significant time of D effect (F(4,345) = 11.96, P < 0.001), intensity effect (F(3,345) = 67.09, P < 0.001) and time of D × intensity effect (F(12,345) = 2.48, P = 0.004). I and J, typical examples of Neurobiotin tracer coupling between photoreceptors obtained during the SD2 (Ia and b) and the N (Ja and b). Panels show confocal images of whole-mount retinae at the level of the cone inner segments (optical sections, 5 × 1 μm; Ia and Ja) and 3D projections of 70-μm thick Z-stacks of the outer nuclear layer of the same area (Ib and Jb). The distribution of the number of tracer coupled cells during the SD2 and N are illustrated in Fig.7G. Scale bars, 5 μm.
Light stimulation
A 175 W xenon arc lamp provided light for a single beam optical bench that provided full-field light stimulation. Calibrated neutral density filters and narrow-band interference filters were used to control light density and stimulus wavelength, respectively. Photoreceptors were stimulated with unpolarized, monochromatic (500 nm, 10 nm half-width) light, and the duration of the stimulus was 20 ms. Light density was measured using an IL-1700 radiometer (International Light, Newburyport, MA, USA). Stability of maximum output was checked weekly. The maximum, unattenuated photon density of the stimulus at 500 nm (i0–500) was 1.62 × 10−2 W cm−2, 5.49 × 1014 photons cm−2 s−1, or 8.23 × 106 photons μm−2 flash−1. This estimate was, however, revised to 4.43 × 106 photons μm−2 flash−1 following calibration of the light stimulus (see Fig.2 and below).
Figure 2.
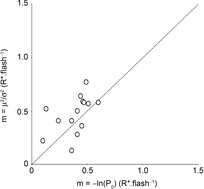
Calibration of the light stimulus by patch-clamp recordings
The photovoltage responses to a series of 70–150 flashes of light of fixed density (0.44 photons μm−2) were recorded during the early day (ZT00–06) for 14 rods (1 rod retina–1). The mean number of events per flash (m), that is, the mean number of isomerizations per rod per flash (R*), was determined by two different methods. The value of m was estimated from the natural logarithm of the observed probability of failure (P0; eqn 04) and from the ratio of the square of the peak of the ensemble mean (μ2) to the square of the peak ensemble variance (σ2; eqn 05). The figure illustrates the comparison of the calibration methods. Proximity to the dashed line (unity) indicates agreement between the two methods for individual rods. Estimates of m averaged 0.39 ± 0.04 (eqn 04) and 0.47 ± 0.05 (eqn 05; mean ± SEM). The value of m was set at 0.44R* at this attenuation.
To convert the photon density into the mean number of effective isomerizations per rod per flash (R*), we calculated the collecting area of a single rod (Ac), which is the effective cross-sectional area of the total pigment content of a photoreceptor for axially propagating light. For a light stimulus that directly reaches the rod outer segment (i.e. without travelling throughout the retina):
| 1 |
where dr0d is the rod density in the mouse retina (437,000 mm−2; Jeon et al. 1998), D(λ) is the axial optical density of rhodopsin in the outer segment, and γ is the quantum efficiency, with which a photon absorbed by a molecule of rhodopsin induces an isomerization. We calculated D(λ) as the product of the specific density per unit length (0.019 OD units μm−1 at 498 nm; Lyubarsky & Pugh, 1996) and the length of the rod outer segment (23.6 μm; Carter-Dawson & LaVail, 1979); thus D(λ) = 0.448. Therefore the fraction of light entering the outer segment that is absorbed is 1 – 10−D(λ) = 0.644. For the quantum efficiency of isomerization (γ), we adopted the conventional value of 67%. Thus, Ac = 0.987 μm; for simplification, Ac was set to 1.0 μm2. This estimate is within the range of published values of Ac (see Naarendorp et al. 2010 for instance). The calculated unattenuated photon density at 500 nm of a 20 ms flash (8.23 × 106 photons μm−2) was thus equivalent to 8.23 × 106R*. Calibration of the light stimulus (Fig.2) yielded an unattenuated value of R* slightly lower (4.43 × 106R*). Although the difference between these two estimates may have originated from the non-uniform focus of light along the rod outer segment and/or errors due to the different refraction indexes of air and water, these values remain very close. However, 4.43 × 106R* probably reflects light intensity under recordings conditions best, and therefore we used this estimate in our calculations.
Data analysis
Statistical analyses were performed with Clampfit 10.2 (Molecular Devices) and OriginPro 8.5.1 (OriginLab Corporation, Northampton, MA, USA). Results from the non-linear least-squares regression analysis are given ± SEM.
Our analysis of the rod light responses was performed assuming the quantal nature of light and the consequent Poisson variability of the rod responses. This type of analysis has been widely used by others in the field (Baylor et al. 1979; Schneeweis & Schnapf, 2000; Field & Rieke, 2002a2002a; Hornstein et al. 2005; Li et al. 2012).
For events K that follow a Poisson distribution with mean m per trial, the probability Pk that there will be K = k events per trial is:
| 2 |
For quantized rod responses, m is the mean number of isomerizations (K) per trial (in R*) and k = 0, 1, 2, …
The characteristics of the rod response to dim flashes were derived from 50–150 consecutive recordings from the same cell. Successes (responses) and failures (no responses) were discriminated by correlation with the ensemble event mean (μ, in mV). The ensemble peak variance (σ2, in mV2) is the increase in variance at the peak of the ensemble mean response (an example is shown in Fig.1E). The probability that there will be no event per trial equal to the probability of failure (K = 0) can be calculated from the ratio of the number of failures to the total number of flashes delivered and can be used to estimate m, according to:
| 3 |
or
| 4 |
Figure 1.
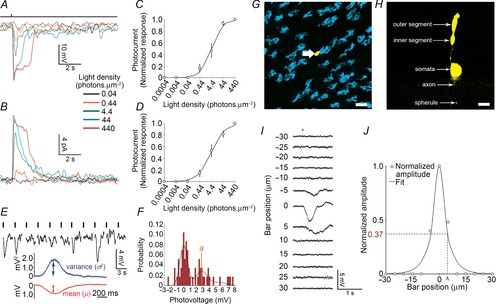
Rod light responses in the intact mouse retina
Rod light responses were recorded in the intact mouse retina during the morning (ZT00–06) under dark-adapted conditions (>1 h). A and B, representative examples of light-evoked rod membrane voltage (A) and current (B) responses to a series of 20 ms full-field 500 nm light flashes of increasing density ranging from 0.044 to 440 photons μm−2 obtained at ZT02. Flash monitor is shown on top of the traces. Bandwith DC to 50 Hz. RMP was –29.0 mV in A and –31.2 mV in E. Holding current was 7.5 pA in B. C and D, average normalized intensity–response curves of rods recorded under the conditions depicted in A and B. Error bars, SEM, n = 33 (C) and 4 (D) (1 cell retina−1). E and F, response variability to dim flashes and electrical coupling of the rods. Representative examples of rod responses to a series of repetitive 20 ms full-field 500 nm dim light flashes, illustrating amplitude fluctuations of a rod to dim light flashes (E) and the probability density calculated from 150 consecutive recordings from the same cell (F), some of which are illustrated in E. Vertical black bars indicate the timing of flashes in E. G and H, representative example of a Neurobiotin-filled single rod. Shown are a tangential section (optical sections 5 × 1 μm) at the level of the inner segment of the injected rod (G) and a perpendicular view of the 3D projection of a 70 μm thick Z-stack of the outer nuclear layer that includes the same cell (H). Cone inner segments are labelled with Dylight647-conjugated peanut agglutinin (PNA, blue; G). The different morphological parts of the injected rod are labelled (H). Note that, following iontophoresis of Neurobiotin into individual rods, the tracer (yellow) remained in the injected cell. Scale bars: 5 μm. I and J, measurement of the rod receptive field size. The receptive field size of single rods was measured by presenting a 5-μm thick slit of dim 500 nm light of fixed intensity for 50 ms and moving it by 5 μm every 3 s across the retinal surface using the Lucivid system. Representative examples of rod responses to the slit of light presented at different distances from the centre of the recorded cell are illustrated (I). Normalized response amplitudes plotted against distance of the slit from the centre of the recorded cell and fitted to an exponential equation are also illustrated (eqn 16; J). The length constant (λ) was used as a measure of the receptive field size.
In addition, m equals the ratio of the square of the ensemble event mean (μ) to the ensemble peak variance (σ2):
| 5 |
The event amplitude, a, can be estimated in different ways (Baylor et al. 1979): from μ and m, using the relation:
| 6 |
or from σ2:
| 7 |
A probability density function was computed from the distribution of the response amplitude to 50 or more flashes. The probability density, P(x), for a response with amplitude in the range x to x + Δx/2 is the sum of Gaussian components each with mean ka and an area weighted by the Poisson function (eqn 02; Baylor et al. 1979) and that follows the equation:
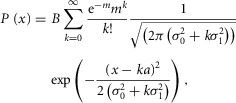 |
8 |
where m is the mean number of events per trial, k the number of events per trial (k = 0, 1, 2 or 3; for light stimuli < 1R* and k ≥ 4, 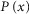 ≈ 0),
≈ 0), 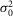 is rod intrinsic noise (in mV2),
is rod intrinsic noise (in mV2),  is the dispersion in the event amplitude (in mV2) and a is the single event amplitude (in mV). B is the bin width and is set to 0.2 mV.
is the dispersion in the event amplitude (in mV2) and a is the single event amplitude (in mV). B is the bin width and is set to 0.2 mV.  ,
,  , m, and a were allowed to vary.
, m, and a were allowed to vary.
The effective pool size of coupled rods (Ne) is the effective pool size that accounts for electrical coupling between photoreceptors, assuming ‘perfect coupling’, that is, that rod-to-rod junction conductance is infinite, and photon responses are equivalent in all coupled rods (Hornstein et al. 2005). Ne was calculated from different ways as explained below:
Assuming that only a single photoisomerization is required to elicit a unit electrical response, the mean number of photoisomerizations (= mean number of events, m, in units of R*) should be proportional to the number of coupled rods (Ne), the effective collecting area of a single rod (Ac) and light intensity:
| 9 |
where i is the flash density (photons μm−2) and Ac (μm2) is the effective collecting area of the outer segment of a single rod (= 1.0 μm2 from eqn 01).
With Ac (eqn 01 and i known, Ne can be calculated from eqn 09, after determining m (from eqn 04):
| 10 |
Ne can also be calculated from the square of the ensemble event mean (μ) and the variance of the event peak (σ2; Li et al. 2012), following the equation:
| 11 |
Finally, we defined the signal-to-noise ratio (SNR) as:
| 12 |
The peak amplitude of the rod light responses was plotted as a function of flash intensity using a Hill-type equation in the form:
| 13 |
where R is the response amplitude (in mV or pA), Rmax is the maximum response amplitude (in mV or pA), i is the stimulus intensity (in photons μm−2 or R*), i50%Rmax is the stimulus intensity needed to generate a response with half-maximal amplitude (in photons μm−2 or R*), and N is the Hill coefficient. Non-linear least-squares regression analysis was performed with N and i50%Rmax as free parameters. To fit absolute values of R, Rmax was a free parameter. To fit the normalized values of R, Rmax was set to 1.0. Residues from the non-linear regression of the normalized values were used to calculate the light density required to elicit 95% of Rmax (i95%Rmax).
The peak amplitude of the rod light responses measured at 440 photons μm−2 was plotted as a function of time of day using either of the following two methods.
(1). The symmetrical traditional COSINOR equation:
| 14 |
where y is the nth data point (response amplitude in mV), x the time of the nth data point (h), W the mean (mesor, in mV), Y the amplitude (equal to one-half of the sinusoid, in mV), Z the acrophase (in radians) and T the endogenous period (h). Non-linear least-squares regression analysis was performed with W, Y and Z as free parameters and T set to 24.0.
(2).The sum of an asymmetrical logistic function in the form:
| 15 |
where y is the nth data point (response amplitude in mV), x the time of the nth data point (h), y0 is the nadir of the rhythm (in mV), A is the peak of the rhythm (in mV), Sa is the slope of the ascending peak (in mV h−1), ϕa is the inflection point of the ascending peak (in h), Sd is the slope of the descending peak (in mV h−1), ϕd is the inflection point of the descending peak (in h), and w is the period (in h). y0, A, Sa, Sd, ϕa and ϕd were allowed to vary and w = 0, 24, 48. Best fit of the data in Fig.3E was obtained with y0 = 6.2 mV, A = 16.6 mV, Sa = 14.93 mV h−1, and Sd = −0.30 mV h−1.
Figure 3.
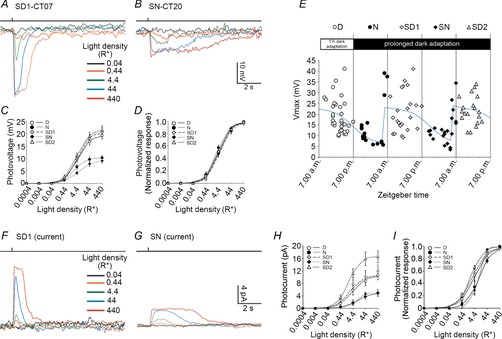
Circadian variations of the rod light response kinetics
A and B, representative examples of rod responses to a series of 20 ms full-field 500 nm light flashes of increasing intensity recorded under dark-adapted conditions during the subjective day-1 (SD1; A) or the subjective night (SN; B). Flash monitor is shown on top of the traces. Bandwith DC to 50 Hz. RMP was –26.3 mV for cell in A and –43.3 mV for cell in B. C and D, averaged (C) and normalized (D) intensity–response curves of rods recorded during the day (D), night (N), subjective day-1 (SD1), subjective night (SN) or subjective day-2 (SD2). Data collected within 2 h of the transition times were excluded from the analysis. Error bars, SEM, n = 29 (D), 13 (N), 19 (SD1), 12 (SN) and 17 (SD2) cells (1 cell retina–1). E, variation of the maximum amplitude of the rod photovoltage (Vmax) as a function of time in the dark. Individual values from 114 cells better fitted a function in the form of the sum of 3 logistic peak functions with identical shape and amplitude (blue curve, eqn 15, r2 = 0.36, P < 0.001) than the COSINOR function (not illustrated, eqn 14, r2 = 0.20, P < 0.001). F and G, representative examples of light-evoked rod current responses to a series of 20 ms full-field 500 nm light flashes of increasing intensity recorded during the first subjective day (SD1, CT01; F), and the subjective night (N, CT20; G). Holding current at –35 mV was –1.2 pA in F, and 1.9 pA in G. H and I, averaged (H) and normalized (I) intensity–response curves of rods recorded during the day (D), night (N), subjective day-1 (SD1), subjective night (SN) or subjective day-2 (SD2). Data collected within 2 h of the transition times were excluded from the analysis. Error bars, SEM, n = 4 (D), 3 (N), 7 (SD1), 5 (SN) and 7 (SD2) cells (1 cell retina–1).
Receptive field measurements
To assess the receptive field size of a rod, a 5-μm wide 150-μm long rectangular slit of dim 500 nm light of fixed intensity was presented for 50 ms and moved in 5-μm steps every 3 s across the retinal surface using a Lucivid XC-R miniature LCD colour system (MBF Bioscience, Willinston, VT, USA) hooked onto a microscope port. A 500 nm narrow-band interference filter (10 nm half-width) was positioned on the light path. Light intensity of the bar was adjusted so that to elicit a 2–4 mV response in the recorded rods when positioned on the receptive field centre during the day and thus corresponded to ∼2–4R*. The length constant (λ), a measure of the receptive field size of recorded cells (Lamb & Simon, 1976), was estimated from plotting the normalized response amplitudes against the stimulus position and fitting the data with the following equation:
| 16 |
where y is the nth data point (standardized response amplitude), |x| the absolute value of the position of the slit of light relative to the centre of the recorded rod, and λ the length constant (in μm). Non-linear least-squares regression analysis was performed with λ as a free parameter. For cells that elicited a light response only when the slit was positioned at their centre, λ default value was set to 2.5 μm (= slit half-width).
Tracer coupling
Tracer coupling was revealed by iontophoresis and cytochemical visualization of the biotinylated tracer Neurobiotin (Vector Laboratories, Burlingame, CA, USA). Micropipettes were backfilled with 4% (w/v) Neurobiotin in pipette solution that also contained 25 μm β-escin. To minimize the effects of light adaptation, tracer coupling experiments were separated from recording experiments. After perforation, the response of the cell to a single dim flash of light (44 photons μm−2) was recorded to confirm the photoreceptor type and the viability of the cell. Neurobiotin diffused into the recorded rod and coupled cells for 10–15 min. Typically two to three injections were made per retina. After the last injection, the retina was kept in the superfusion chamber in total darkness for 30 min, then rapidly immersed in a solution of 4% paraformaldehyde + 0.1% glutaraldehyde in 10 mm phosphate-buffered saline (PBS, 0.8% NaCl, pH 7.3) for 12 min at room temperature and postfixed in 4% paraformaldehyde in 10 mm PBS overnight at 4 °C. The retina was then washed in PBS and reacted for 2 days with Dylight488-conjugated strepavidin (5 μg ml−1, Jackson ImmunoResearch, West Grove, PA, USA) in 10 mm PBS that contained 0.5% Triton-X100 and 10 μg ml−1 Dylight647-conjugated peanut agglutinin (Invitrogen, Grand Island, NY, USA). Thereafter the retina was washed in PBS and flat-mounted on a microscope slide. Labelled photoreceptor cells could then be observed and digitally captured using a confocal microscope (Zeiss LSM510; Carl Zeiss Microscopy, LLC, Thornwood, NY, USA).
Rod network modelling
The effect of coupling on signal and noise was calculated assuming a network of perfectly coupled rods. The effect of coupling on the signal evoked by a light stimulus depends on the number of illuminated rods (M) and of coupled rods (Ne) in the network (Tessier-Lavigne & Attwell, 1988; Hornstein et al. 2005). If a stimulus illuminates M rods in the network, it will evoke a response V in each rod of the network (including the recorded rod), with:
| 17 |
and Vr = the response of an isolated rod illuminated by the same stimulus.
In addition, the variance of the voltage noise in the network 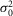 is related to that of an isolated rod
is related to that of an isolated rod 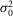 r:
r:
| 18 |
and the dispersion in the event amplitude 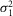 is related to that of an isolated rod
is related to that of an isolated rod 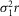 :
:
| 19 |
The values of 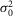 r,
r, 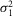 r, and ar (defined as the amplitude of the single photon response in an isolated rod) were measured in rods in the presence of MFA and estimated to be 0.36 mV2, 0.42 mV2 and 2.89 mV, respectively.
r, and ar (defined as the amplitude of the single photon response in an isolated rod) were measured in rods in the presence of MFA and estimated to be 0.36 mV2, 0.42 mV2 and 2.89 mV, respectively.
The probability density function of the rod response to a dim light stimulus of 0.44R* (eqn 08) was computed for various numbers of coupled rods (Ne, range 0–3). To express eqn 08 as a function of Ne, we substituted m with NeAci (eqn 09, or m = 0.44 Ne, with Ac = 1 μm2) and 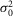 r,
r, 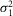 r, and ar with the values described above. Since the probability density functions calculated in this study were obtained for a light density equal to 0.44R*, we assumed that at that light density and for small Ne values (≤3), only 1 rod in the network was illuminated and that M/Ne ≈ 1/Ne. Thus, eqn 08 can be written as:
r, and ar with the values described above. Since the probability density functions calculated in this study were obtained for a light density equal to 0.44R*, we assumed that at that light density and for small Ne values (≤3), only 1 rod in the network was illuminated and that M/Ne ≈ 1/Ne. Thus, eqn 08 can be written as:
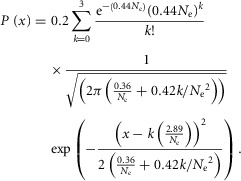 |
20 |
From eqn 20, the probability density function of the first component (k = 0, probability of failure) is:
 |
21 |
Let F0(x) be the cumulative probability density function, which can be written as:
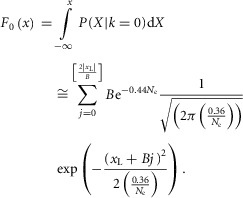 |
22 |
B is the bin size and xL is the minimal value of response amplitude. We chose B = 0.2 mV and xL = −3 mV to estimate F0(x) and plotted estimates for Ne ∈ [1,3]. It should be noted that the cumulative function, F0(x = ∞) is equal to 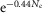 and was used to estimate P0.
and was used to estimate P0.
The effects of the number of rods illuminated (M) in the network of perfectly coupled rods (Ne) on the single photon response amplitude (a) and the SNR were modelled from eqns 12, 17, 18 and 19, with:
| 23 |
and
| 24 |
and 1.0 ≤ M ≤ Ne.
The effects of light intensity on the amplitude of the response in an illuminated rod were calculated for a stimulus restricted to the illuminated rod (M = 1) and for a stimulus covering the entire array of coupled rods (M = Ne), for Ne = 1.13 (daytime model) and Ne = 2.40 (nighttime model), using a modified version of eqn 13, with:
| 25 |
The maximal response amplitude (Rmax) in an electrically isolated rod that was measured in rods in the presence of MFA is 21.5 mV. For simplification, the Hill coefficient (N) was set to 1, the intensity to elicit 50% of the maximum response amplitude (i50%Rmax) was set to 6R* and for light densities < 1R*, we considered that M = 1, in both models.
Resistive–capacitive model of the mouse photoreceptor network
To test whether electrical coupling between rods and cones could modulate the rod light response kinetics, we developed a simplified capacitive and resistive model of electrically coupled mouse photoreceptors. We used a square lattice, with connections between nearest neighbours as an idealized description of the rod network in the mouse retina (see Fig.2). Given that rods outnumber cones by ∼33 to 1 in mouse retina (Jeon et al. 1998) and that each rod is coupled to one cone (Tsukamoto et al. 2001), we developed a model of idealized arrangement of the mouse photoreceptors. We then developed an equivalent electrical circuit of the lattice. Solving the behaviour of the rod network, taking into account the coupled rods and cones, would require precise measurements of the rod–rod and rod–cone gap junction resistance values as well as cone biophysical constants during day and night, which we have not been able to obtain. However, by making a series of rational assumptions, we were able to simplify the model to one that includes a cone and 30 rods, each coupled to the cone by a gap junction of resistance Rj(r–c). We assumed that for uniform light stimuli (R* ≥ 1), rods are isopotential, and thus no net current flows though the rod–rod gap junctions, thereby eliminating rod–rod coupling from the model. Similarly, we assumed that the rod–cone convergence is similar in every cone, and thus that no net current flows through the cone–cone gap junctions, thereby eliminating cone–cone coupling from the model. We also made the additional following assumptions: the membrane parameters are linear and uniform; the membrane resistance is constant and independent of the voltage (we excluded voltage-gated currents in our simplified model); the membrane resistance of the rod membrane is similar to that of the cone (Rmr ≈ Rmc); the membrane capacitance of the rod is similar to that of the cone (Cmr ≈ Cmc); the rod RMP is more positive than that of the cones (Cangiano et al. 2012); the photocurrent in rods is >> than that elicited in cones at the same light intensity, and thus the rod membrane potential drives the cone membrane potential when rod–cone coupling is strong. Based on these assumptions, we developed an equivalent resistive–capacitive model to determine the rod behaviour in response to uniform light stimuli in the presence of a coupled cone.
To simulate the photocurrent, we used a simulated current waveform as input in the form (Publio et al. 2009):
| 26 |
with iphoto the photocurrent (in pA) at any time t (in ms), X the amplitude of the photocurrent (in pA), b the inflection point at the decline of the peak, and τ1 and τ2 time constants (in ms). Equation 26 was adjusted with the amplitude and width values obtained from our voltage-clamp recording data of photoresponse measured during the day for the different light density values (4.4, 44 and 440R*) and used as the current injection function to model the rod or the cone photovoltage (V) as a function of current and time for various values of Rj(r–c). We set Rmc = Rmr = 2.4 GΩ, cone RMP = −45 mV, rod RMP = −30 mV, and Cmc = Cmr = 10 pF. Simulations of V were made in Mathlab Simscape 8.3 (MathWorks, Natick, MA, USA).
Results
Rod light responses in the isolated intact mouse retina
We have developed a new technique in mouse: voltage clamp of single photoreceptors in intact retinae maintained by superfusion (see Methods for details). The sensitivity, kinetics, and reliability of the rod responses to dim light flashes were determined during the daytime phase of a normal light–dark cycle (zeitgeber time (ZT) 00–12) under dark-adapted conditions (>1 h; Fig.1). Under these conditions, the RMP of the recorded rods was, on average, −33.9 ± 1.5 mV (mean ± SEM; n = 33), and their input resistance (Ri) was 2.51 ± 0.09 GΩ (mean ± SEM; n = 20). The mean holding current at −35 mV was, on average, −3.25 ± 2.67 pA (mean ± SEM; n = 4). Presentation of a brief flash of light (500 nm, 20 ms) evoked typical reduction in dark current and hyperpolarization of the membrane potential (Field & Rieke, 2002a; Cangiano et al. 2012). The amplitude of these events increased as a function of flash intensity (Fig.A and B). The amplitude of the rod light responses at the highest light density was on average 19.3 ± 1.4 mV (mean ± SEM; n = 33) or 10.6 ± 1.38 pA (mean ± SEM; n = 4). The relation between the peak response amplitude and intensity was fitted by a Hill-type equation (eqn 13; Fig.1C and D). The half-saturating intensity (i50%Rmax) was not significantly different between the two measurements (5.7 ± 0.4 photons μm−2 and 5.3 ± 1.2 photons μm−2 for voltage and current measurements, respectively; P = 0.34, Student's unpaired t test). The Hill coefficient (N) was also similar between the two measurements (0.90 ± 0.1 and 0.75 ± 0.1 for voltage and current measurements, respectively; P = 0.29, Student's unpaired t test). In addition, rod light responses started to saturate (95% of the maximum response; i95%Rmax) by ∼100–200 photons μm−2 (see Tables1 and 2, for details). Overall, the sensitivity and kinetics of the current and voltage responses to light compared favourably with those measured with suction (Field & Rieke, 2002a) and patch-clamp (Cangiano et al. 2012) electrodes in mouse retinal slices.
Table 1.
Properties of the mouse rod photovoltage under different experimental conditions
| D | SD1 | SD2 | N | SN | ZT/CT22–00 | ANOVA F(4,94) | P | |
|---|---|---|---|---|---|---|---|---|
| n | 33 | 19 | 17 | 13 | 13 | 13 | ||
| RMP | −33.9 | −30.9 | −30.0 | −35.8 | −38.7 | −28.27 | 2.50 | 0.050 |
| SEM | 1.5 | 1.8 | 1.75 | 3.3 | 2.31 | 3.27 | ||
| Observed Vmax | 19.29** | 20.57*** | 21.6*** | 10.31 | 9.07 | 23.19 | 11.46 | <0.0001 |
| SEM | 1.40 | 1.86 | 1.65 | 0.92 | 0.89 | 2.84 | ||
| Parameters obtained from fitting the absolute data to eqn 13 | ||||||||
| Vmax | 19.53*** | 20.62*** | 21.88*** | 10.24 | 9.37 | 23.68 | 17.17 | <0.0001 |
| SEM | 1.23 | 1.30 | 1.35 | 0.71 | 0.88 | 2.18 | ||
| N | 0.86 | 0.96 | 0.86 | 1.05 | 0.78 | 0.95 | 0.16 | 0.959 |
| SEM | 0.19 | 0.24 | 0.19 | 0.31 | 0.22 | 0.34 | ||
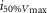 |
1.09E–06 | 1.11E–06 | 9.69E–07 | 5.67E–07 | 1.27E–06 | 1.21E–06 | ||
| SEM | 3.22E–07 | 3.17E–07 | 2.89E–07 | 1.91E–07 | 5.86E–07 | 5.05E–07 | ||
Log(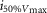 ) ) |
−5.96 | −5.95 | −6.01 | −6.25 | −5.90 | −5.92 | ||
| SEM | −1.76 | −1.70 | −1.79 | −2.10 | −2.72 | −2.47 | ||
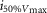 (photons cm−2) (photons cm−2) |
6.00 | 6.11 | 5.33 | 3.12 | 6.99 | 6.66 | 0.38 | 0.820 |
| SEM | 1.77 | 1.74 | 1.59 | 1.05 | 3.22 | 2.78 | ||
| Fit (r2) | 0.64 | 0.74 | 0.77 | 0.70 | 0.71 | 0.67 | ||
| Fit ANOVA | F(3,163) = 237.67 | F(3,95) = 207.3 | F(3,85) = 234.78 | F(3,63) = 122.76 | F(3,65) = 129.42 | F(3,65) = 101.85 | ||
| P | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | ||
| Parameters obtained from fitting the normalized data to eqn 13 | ||||||||
| Vmax (fixed) | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | ||
| SEM | — | — | — | — | — | — | ||
| N | 0.91 | 0.89 | 0.86 | 0.87 | 0.80 | 1.02 | 0.35 | 0.846 |
| SEM | 0.057 | 0.064 | 0.061 | 0.087 | 0.075 | 0.089 | ||
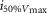 |
1.01E–06 | 1.23E–06 | 9.41E–07 | 7.64E–07 | 1.16E–06 | 1.20E–06 | ||
| SEM | 7.31E–08 | 1.06E–07 | 8.36E–08 | 9.65E–08 | 1.52E–07 | 1.04E–07 | ||
Log(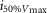 ) ) |
−6.00 | −5.91 | −6.03 | −6.12 | −5.94 | −5.92 | ||
| SEM | −0.43 | −0.51 | −0.54 | −0.77 | −0.78 | −0.51 | ||
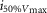 (photons cm−2) (photons cm−2) |
5.56 | 6.77 | 5.18 | 4.20 | 6.38 | 6.62 | 2.82 | 0.030 |
| SEM | 0.40 | 0.58 | 0.46 | 0.53 | 0.84 | 0.57 | ||
| Fit (r2) | 0.94 | 0.95 | 0.95 | 0.93 | 0.92 | 0.96 | ||
| Fit ANOVA | F(2,155) = 2856.75 | F(2,95) = 1910.47 | F(2,85) = 2032.24 | F(2,60) = 1023.31 | F(2,65) = 969.99 | F(2,65) = 1756.7 | ||
| P | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | ||
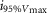 |
2.57E–05 | 3.39E–05 | 2.90E–05 | 2.26E–05 | 4.65E–05 | 2.16E–05 | ||
Log(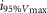 ) ) |
−4.59 | −4.47 | −4.54 | −4.65 | −4.33 | −4.67 | ||
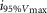 (photons cm−2) (photons cm−2) |
141 | 186 | 160 | 124 | 256 | 119 | ||
Observed Vmax is the value of the peak photoresponse measured with a flash of light density 440 photons μm−2. The light density to reach 95% of saturation (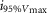 ) was calculated using the parameters obtained from fitting the normalized data to eqn 13. A one-way ANOVA was performed to compare the data from day (D), subjective day-1 (SD1), subjective day-2 (SD2), night (N), and subjective night (SN; right columns).
) was calculated using the parameters obtained from fitting the normalized data to eqn 13. A one-way ANOVA was performed to compare the data from day (D), subjective day-1 (SD1), subjective day-2 (SD2), night (N), and subjective night (SN; right columns).
P < 0.01
P < 0.001 when compared to respective N or SN (Tukey's post hoc test). Values collected during late N and late SN (ZT/CT22–00) are given for information but were not included in the ANOVA. RMP, resting membrane potential.
Table 2.
Properties of the mouse rod photocurrent under different experimental conditions
| D | SD1 | SD2 | N | SN | ZT/CT22–00 | ANOVA F(4,25) | P | |
|---|---|---|---|---|---|---|---|---|
| n | 4 | 7 | 7 | 3 | 5 | 9 | ||
| RMP | −29.9 | −24.3** | −32.1 | −43.9 | −42.4 | −27.2 | 7.22 | 0.0008 |
| SEM | 0.97 | 1.47 | 1.45 | 9.3 | 3.8 | 3.11 | ||
| Observed Imax | 10.55** | 11.94** | 16.59*** | 4.87 | 4.74 | 8.32 | 7.90 | 0.0005 |
| SEM | 1.38 | 1.94 | 1.94 | 1.12 | 0.62 | 1.09 | ||
| Parameters obtained from fitting the absolute data to eqn 13 | ||||||||
| Imax | 10.55 | 10.7* | 16.73*** | 5.23 | 4.84 | 8.60 | 13.67 | <0.0001 |
| SEM | 1.37 | 1.42 | 1.35 | 1.29 | 0.46 | 0.97 | ||
| N | 0.79 | 0.80 | 0.92 | 0.71 | 1.37 | 0.87 | 0.31 | 0.868 |
| SEM | 0.34 | 0.37 | 0.29 | 0.39 | 0.73 | 0.34 | ||
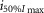 |
8.93E–07 | 5.74E–07 | 4.50E–07 | 2.74E–06 | 1.63E–06 | 1.36E–06 | ||
| SEM | 5.85E–07 | 4.06E–07 | 1.92E–07 | 3.16E–06 | 6.76E–07 | 7.14E–07 | ||
Log(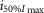 ) ) |
−6.05 | −6.24 | −6.35 | −5.56 | −5.79 | −5.87 | ||
| SEM | −3.96 | −4.41 | −2.71 | −6.41 | −2.40 | −3.08 | ||
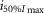 (photons cm−2) (photons cm−2) |
4.91 | 3.16 | 2.48 | 15.07 | 8.97 | 7.48 | 0.93 | 0.466 |
| SEM | 3.22 | 2.23 | 1.06 | 17.38 | 3.72 | 3.93 | ||
| Fit (r2) | 0.79 | 0.60 | 0.76 | 0.77 | 0.83 | 0.69 | ||
| Fit ANOVA | F(3,20) = 57.97 | F(3,35) = 48.21 | F(3,35) = 102.15 | F(3,15) = 30.18 | F(3,25) = 81.32 | F(3,45) = 77.99 | ||
| P | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | ||
| Parameters obtained from fitting the normalized data to eqn 13 | ||||||||
| Vmax (fixed) | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | ||
| SEM | — | — | — | — | — | — | ||
| N | 0.75 | 0.74** | 0.9* | 0.86 | 1.49 | 0.92 | 4.66 | 0.0075 |
| SEM | 0.12 | 0.087 | 0.063 | 0.13 | 0.27 | 0.21 | ||
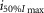 |
9.58E–07 | 6.80E–07 | 4.78E–07 | 2.27E–06 | 1.77E–06 | 8.64E–07 | ||
| SEM | 2.19E–07 | 1.20E–07 | 4.31E–08 | 4.65E–07 | 2.48E–07 | 2.29E–07 | ||
Log(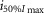 ) ) |
−6.02 | −6.17 | −6.32 | −5.64 | −5.75 | −6.06 | ||
| SEM | −1.38 | −1.09 | −0.57 | −1.16 | −0.81 | −1.61 | ||
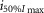 (photons cm−2) (photons cm−2) |
5.27** | 3.74** | 2.63*** | 12.49 | 9.74 | 4.75 | 14.38 | <0.0001 |
| SEM | 1.20 | 0.66 | 0.24 | 2.56 | 1.36 | 1.26 | ||
| Fit (r2) | 0.93 | 0.93 | 0.98 | 0.96 | 0.96 | 0.77 | ||
| Fit ANOVA | F(2,20) = | F(2,35) = | F(2,35) = | F(2,15) = | F(2,25) = | F(2,45) = | ||
| 342.58 | 613.9 | 2219.94 | 329.86 | 605.55 | 195.95 | |||
| P | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | ||
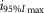 |
4.90E–05 | 3.65E–05 | 1.26E–05 | 7.00E–05 | 1.28E–05 | 2.13E–05 | ||
Log(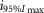 ) ) |
−4.31 | −4.44 | −4.90 | −4.15 | −4.89 | −4.67 | ||
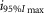 (photons cm−2) (photons cm−2) |
270 | 201 | 69 | 385 | 70 | 117 | ||
Observed Imax is the value of the peak photoresponse measured with a flash of light density 440 photons μm−2. The light density to reach 95% of saturation (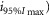 was calculated using the parameters obtained from fitting the normalized data to eqn 13. A one-way ANOVA was performed to compare the data from day (D), subjective day-1 (SD1), subjective day-2 (SD2), night (N), and subjective night (SN; right columns).
was calculated using the parameters obtained from fitting the normalized data to eqn 13. A one-way ANOVA was performed to compare the data from day (D), subjective day-1 (SD1), subjective day-2 (SD2), night (N), and subjective night (SN; right columns).
P < 0.05
P < 0.01
P < 0.001 when compared to respective N or SN (Tukey's post hoc test). Values collected during late N and late SN (ZT/CT22–00) are given for information but were not included in the ANOVA. RMP, resting membrane potential.
Single-photon responses in rods
To determine whether rods in the intact mouse retina are able to detect and process single quanta of light, we examined their responses to dim flashes of light. Figure E shows an example of trial-to-trial amplitude fluctuations of a rod from a series of consecutive flashes of light of fixed intensity, 0.44 photons μm−2 delivered at 0.2 Hz. The apparent trial-to-trial variability in the rod response to dim light stimuli has been shown to reflect both the quantal nature of light and the stochastic process of photon absorption (Baylor et al. 1979; Schneeweis & Schnapf, 2000; Field & Rieke, 2002a; Hornstein et al. 2005; Cangiano et al. 2012; Li et al. 2012). The behaviour of the rods was indeed characteristic of a quantized response: each quantal electrical event resulted from a single photoisomerization when photons were so scarce that either no photon elicited a response in the recorded rod (failures) or sometimes just one (successes) and occasionally more than one (Fig.1E). Consistent with a quantized response, the probability density function of the responses exhibited two major discrete peaks, one entered at 0 mV and the other at 2.6 mV (Fig.1F). Data were fitted by a convolution of the sum of Gaussian distributions weighted by a Poisson distribution (eqn 08). Best fit of the data shown in Fig.1F was obtained with the event amplitude (a) = 2.76 mV, the rod intrinsic noise (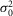 ) = 0.35 mV2, the dispersion in the event amplitude (
) = 0.35 mV2, the dispersion in the event amplitude (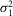 ) = 0.44 mV2 and mean number of events per trial (m) = 0.54. The average values of a,
) = 0.44 mV2 and mean number of events per trial (m) = 0.54. The average values of a, 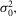
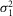 , and m estimated from the probability density function were 2.66 ± 0.58 mV, 0.20 ± 0.08 mV2, 0.34 ± 0.13 mV2, and 0.64 ± 0.19, respectively (mean ± SEM; n = 3). The insert in Fig.1E shows ensemble average photovoltage (red trace) and variance (blue trace) for responses to the 150 flashes, including those illustrated in Fig.1E. For the cell illustrated in Fig.1E, the mean peak hyperpolarization (μ) was 1.14 mV, and the mean peak variance (σ2) was 1.89 mV2. Average values of μ and σ2 were 0.99 ± 0.08 mV and 1.78 ± 0.24 mV, respectively (mean ± SEM; n = 3). Poisson statistics were used to further characterize the rod responses under dim light (see Methods for details).
, and m estimated from the probability density function were 2.66 ± 0.58 mV, 0.20 ± 0.08 mV2, 0.34 ± 0.13 mV2, and 0.64 ± 0.19, respectively (mean ± SEM; n = 3). The insert in Fig.1E shows ensemble average photovoltage (red trace) and variance (blue trace) for responses to the 150 flashes, including those illustrated in Fig.1E. For the cell illustrated in Fig.1E, the mean peak hyperpolarization (μ) was 1.14 mV, and the mean peak variance (σ2) was 1.89 mV2. Average values of μ and σ2 were 0.99 ± 0.08 mV and 1.78 ± 0.24 mV, respectively (mean ± SEM; n = 3). Poisson statistics were used to further characterize the rod responses under dim light (see Methods for details).
Photon density was converted into mean effective photoisomerizations per rod per flash (R*) for a flash of fixed dim intensity (0.44 photons μm−2) by calculating the effective collecting area of a single mouse rod under our conditions (Ac, 1.0 μm2; eqn 01) and estimating the mean number of events (m) from the observed probability of failure (P0; eqn 04) or from the ratio of the square of the ensemble mean amplitude (μ) to the ensemble event variance (σ2; eqn 05). The two calibration methods are compared in Fig.2. Collectively, they gave a value for R* at that light density of 0.44. The event amplitude, a, was estimated by different means, from the ratio of μ to m (eqn 06) or from the ratio of σ2 to μ (eqn 07), with values ranging from 1.5 to 2.5 mV (n = 3), in agreement with the values derived from the probability density function (see above). The SNR (eqn 12) ranged from 3.5 to 4.5 (n = 3). Our estimate of a is significantly larger than the ∼1 mV obtained from macaque (Hornstein et al. 2005) and guinea-pig (Li et al. 2012) rods, yet compares favourably with previous patch-clamp measurements of rods in mouse retinal slices (Cangiano et al. 2012).
The trial-to-trial variability of the rod light response to dim light flashes reflects the strength of rod electrical coupling, in that variability in the amplitude of the response to dim flashes is lower when electrical coupling is stronger because of signal averaging within the coupled network (Attwell et al. 1984; Hornstein et al. 2005; Li et al. 2012). Assuming perfect coupling, i.e. infinite coupling conductance, the number of effectively coupled rods (Ne) can be estimated from the ratio of –ln(P0) (eqn 10), or of μ2/σ2 (eqn 11), to the product of light density (i) and Ac. In the daytime and under dark-adapted conditions, Ne estimates ranged from 0.9 to 1.4 with both techniques (n = 3); a value close to 1 is consistent with weak or no coupling (Hornstein et al. 2005; Li et al. 2012), indicating that rods are weakly coupled or electrically isolated under these conditions. These calculations were confirmed by tracer coupling data and receptive field measurements. Indeed, following iontophoresis of Neurobiotin into single rods, tracer was restricted to the recorded cell, consistent with weak rod–gap junction coupling (Fig.1G and H). Also, the space constant (λ), a measure of the receptive field size of the recorded rod, was 4.03 ± 0.51 μm (mean ± SEM; n = 4; Fig.1I and J). This value compared well to the mouse rod cell diameter (∼2 μm) and is consistent with weak electrical coupling. Our observations indicate that in the intact mouse retina, where most synaptic connections are preserved between photoreceptors, dark-adapted rods respond to single photons of light. In the daytime, rods are essentially in a decoupled state or electrically isolated from other photoreceptors.
A circadian clock controls electrical coupling and the light response properties of mouse rods
We recorded the light responses of mouse rod photoreceptors under dark-adapted conditions at different times in a day–night cycle and under circadian conditions, during the first subjective day (subjective day-1), the subjective night, and the second subjective day (subjective day-2; see Methods for details). We found that the rod light responses during the subjective day-1 (Fig.3A and F) resembled those typically observed during the day under dark-adapted conditions (compare Fig.3A with Fig.1A and Fig.3F with Fig.1B). However, we found that the RMP was slightly more negative at night (−35.8 ± 3.3 mV; n = 13) or subjective night (−38.7 ± 2.31 mV; n = 13), compared to day (−33.9 ± 1.5 mV; n = 33), subjective day-1 (−30.9 ± 1.8 mV; n = 19) or subjective day-2 (−30.0 ± 1.75 mV; n = 17; one-way ANOVA, F(4,94) = 2.50, P = 0.050; see also Table2). The holding current at −35 mV did not significantly change between night (−3.67 ± 2.85 pA; n = 3), subjective night (−2.90 ± 0.99 pA; n = 5), day (−3.25 ± 2.67 pA; n = 4), subjective day-1 (−4.00 ± 1.22 pA; n = 7) or subjective day-2 (−3.01 ± 2.99 pA; n = 7; one-way ANOVA, F(4,23) = 0.51, P = 0.73).
Although rods appeared to be as sensitive to light during the subjective night as during the subjective day, as shown by no change in the photon density that elicited a response of half-maximal amplitude (i50%Rmax) or the Hill coefficient (N; Fig.3D and I, Tables1 and 2), the maximal peak amplitude of both the voltage (Vmax; Fig.3C; Table1) and the current (Imax) response (Fig.3H, Table2) were reduced by approximately half at night compared to daytime. In addition, the kinetics of the rod light responses were also slower and the duration of the responses lasted longer at night (Fig.4C and D) or subjective night (Fig.3B and G) compared to the day (Fig.1A and B) or subjective day (Figs3A and F, and 4A and B, and F–H). Plotting Vmax as a function of time in the dark showed that the day–night differences persisted under circadian conditions, with peak values around subjective dawn and trough values during the night and subjective night (Fig.3E), thereby revealing the control of the rod light responses by a circadian clock. Remarkably, the clock-induced change in rod kinetics was particularly steep at the night-to-day transition but was more gradual at the day-to-night transition. This suggests that the action of the clock on the rods primarily occurs in anticipation of daylight.
The decrease in amplitude and the slow time course of the rod responses at night may reflect the action of a clock at various regulatory sites. The observed change in Imax may be difficult to interpret, as we demonstrate below that rods are electrically coupled at night and therefore the current recorded at night represents the sum of local and axial currents and is likely to be distorted due to space clamp issues and inadequate voltage control. Yet the observed change in Imax may reflect an effect of the clock on the outer segment current. The decrease in Vmax at night could reflect an effect of a clock on the photocurrent, and/or rod electrical coupling, and/or a drop in the rod input resistance (Ri). These possibilities were later tested by using a gap junction antagonist and measuring Ri (see below).
The characteristics of the rod responses to dim light flashes were also different between the day (or subjective day) and the night (or subjective night; Fig.5). The rod single-photon responses were ∼50% more reliable at night compared to daytime, as evidenced by a lower observed probability of failure (P0) measured at night (Fig.5E). For a flash delivering 0.44R*, P0 was 61 ± 1% during the day or subjective day (n = 8) and 42 ± 4% at night or subjective night (n = 8; mean ± SEM, P < 0.001, Student's unpaired t test; Fig.5A, B and F; Tables3 and 4). In addition, the kinetics of the single-photon response were slower at night and subjective night compared to the daytime (Fig.5A and B; Tables3 and 4). Estimates of the event amplitude (a) were also significantly smaller at night and subjective night (∼1.0 mV) compared to day and subjective day (∼2.4 mV; Fig.5A–D, K and L; Tables3 and 4). However, the SNR was only slightly but significantly decreased between daytime (∼3) and nighttime (∼2), in part because of a reduction in the rod intrinsic noise (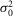 ) of similar amplitude at nighttime (Fig.5M and N; Tables3 and 4). The coupling-induced reduction in fluctuation noise is consistent with experimental and theoretical data from lower vertebrates (Lamb & Simon, 1976; Attwell et al. 1984; Tessier-Lavigne & Attwell, 1988). Thus, even if the event amplitude a decreased at night, the SNR was less affected by coupling at least in part because of the concomitant decrease in
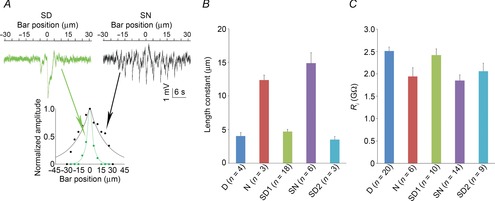
) of similar amplitude at nighttime (Fig.5M and N; Tables3 and 4). The coupling-induced reduction in fluctuation noise is consistent with experimental and theoretical data from lower vertebrates (Lamb & Simon, 1976; Attwell et al. 1984; Tessier-Lavigne & Attwell, 1988). Thus, even if the event amplitude a decreased at night, the SNR was less affected by coupling at least in part because of the concomitant decrease in 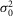 . Estimates of the effective pool size of coupled rods (Ne) were significantly higher at night and subjective night (∼2.5) compared to daytime (∼1.0; Fig.5J; Tables3 and 4). Because a reduction in trial-to-trial rod response amplitude variability has been clearly associated with an increase in rod coupling (Fain, 1975; Attwell et al. 1984; Hornstein et al. 2005; Li et al. 2012), and because Ne was significantly higher at night or subjective night compared to daytime, our data strongly suggest that electrical coupling between rods is increased at night in the mouse retina. Consistent with an increase in rod coupling at night, measurements of the rod input resistance (Ri) were lower by ∼23% and the rod receptive field size, as measured by the length constant, increased by ∼3-fold at night or subjective night compared to the daytime (Fig.6).
. Estimates of the effective pool size of coupled rods (Ne) were significantly higher at night and subjective night (∼2.5) compared to daytime (∼1.0; Fig.5J; Tables3 and 4). Because a reduction in trial-to-trial rod response amplitude variability has been clearly associated with an increase in rod coupling (Fain, 1975; Attwell et al. 1984; Hornstein et al. 2005; Li et al. 2012), and because Ne was significantly higher at night or subjective night compared to daytime, our data strongly suggest that electrical coupling between rods is increased at night in the mouse retina. Consistent with an increase in rod coupling at night, measurements of the rod input resistance (Ri) were lower by ∼23% and the rod receptive field size, as measured by the length constant, increased by ∼3-fold at night or subjective night compared to the daytime (Fig.6).
Figure 5.
Circadian variations of the rod light response properties and electrical coupling
A–D, response variability of rods to dim flashes during the subjective day and the subjective night. Representative examples of rod responses to series of repetitive 20 ms full-field 500 nm dim light flashes of density 0.44R*, illustrating amplitude fluctuations of a rod to dim light flashes (A and B) and the probability density calculated from 150 consecutive recordings from the same cells (C and D) obtained during the subjective day-1 (SD1; A and C) and subjective night (SN; B and D), some of which are illustrated in A and B, respectively. The peaks of the ensemble mean hyperpolarizations (μ) are 1.10 mV and 0.64 mV, and the peaks of the ensemble variance (σ2) are 2.53 mV2 and 0.75 mV2, in A and B, respectively. Vertical black bars indicate the timing of flashes in A and B. RMP was –32.1 mV in A and –31.9 mV in B. E, probability of failure (P0) as a function of light density and time of day. P0 was calculated from the series of photovoltage responses to 60–150 consecutive flashes of the same intensity. Light density values were 0.13, 0.25, 0.44, 1.26, 2.52, and 4.44R*. Data obtained during the day (D, n = 23) or subjective day (SD, n = 10) and night (N, n = 10) or subjective night (SN, n = 12) were pooled together (1 rod retina–1). Data were fitted to an equation in the form.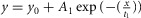 (continuous curves). Two-way ANOVA revealed significant time-of-day effect (F(1,55) = 11.19, P < 0.001), intensity effect (F(5,55) = 29.89, P < 0.001), and time-of-day × intensity effect (F(5,55) = 2.52, P < 0.05). We selected 0.44R* as the intensity to further study the rod response under dim light because at that density P0 oscillates around 0.5 and thus can be determined accurately, and any deviation from this value can be easily observed. Note that P0 falls rapidly towards 0 when light density > 1R*. F–N, properties of the mouse rod response to dim light stimuli during the day (D), subjective day-1 (SD1), subjective day-2 (SD2), night (N) or subjective night (SN). The photovoltage responses to a series of 60–150 flashes of light of fixed density (0.44R*) were recorded. Shown are average values of the probability of failure (P0; F), the peak ensemble mean (μ; G), the ensemble peak variance (σ2; H), the mean number of responses per flash (m; I), the number of effectively coupled rods (Ne; J), the estimated (K) or observed (L) mean amplitude of the single photon response (a), the dark noise (
(continuous curves). Two-way ANOVA revealed significant time-of-day effect (F(1,55) = 11.19, P < 0.001), intensity effect (F(5,55) = 29.89, P < 0.001), and time-of-day × intensity effect (F(5,55) = 2.52, P < 0.05). We selected 0.44R* as the intensity to further study the rod response under dim light because at that density P0 oscillates around 0.5 and thus can be determined accurately, and any deviation from this value can be easily observed. Note that P0 falls rapidly towards 0 when light density > 1R*. F–N, properties of the mouse rod response to dim light stimuli during the day (D), subjective day-1 (SD1), subjective day-2 (SD2), night (N) or subjective night (SN). The photovoltage responses to a series of 60–150 flashes of light of fixed density (0.44R*) were recorded. Shown are average values of the probability of failure (P0; F), the peak ensemble mean (μ; G), the ensemble peak variance (σ2; H), the mean number of responses per flash (m; I), the number of effectively coupled rods (Ne; J), the estimated (K) or observed (L) mean amplitude of the single photon response (a), the dark noise (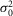 ; M), and the SNR (N) from cells recorded during the D (n = 3), SD1 (n = 3), SD2 (n = 2), N (n = 3) or SN (n = 5; 1 cell retina–1). For some of the parameters, different estimates were obtained from different equations illustrated as bars of different colour (see Methods for details and Tables3 and 4 for individual values). Error bars, SEM *P < 0.05, **P < 0.01, ***P < 0.001 (unpaired Student t test).
; M), and the SNR (N) from cells recorded during the D (n = 3), SD1 (n = 3), SD2 (n = 2), N (n = 3) or SN (n = 5; 1 cell retina–1). For some of the parameters, different estimates were obtained from different equations illustrated as bars of different colour (see Methods for details and Tables3 and 4 for individual values). Error bars, SEM *P < 0.05, **P < 0.01, ***P < 0.001 (unpaired Student t test).
Table 3.
Properties of the mouse rod response to dim light stimuli during the day or subjective day
| Cell | 37–12612001 | 37–12612015 | 37–12612020 | 43–12628004 | 42–12626025 | 49–12809006 | 116–13314005 | 54–12907020 | Average | SEM |
|---|---|---|---|---|---|---|---|---|---|---|
| Time | ZT05 | ZT08 | ZT10 | SD1–CT07 | SD1–CT08 | SD1–CT08 | SD2–CT05 | SD2–CT07 | ||
| Trials | 60 | 60 | 60 | 70 | 70 | 150 | 150 | 150 | ||
| P0 | 0.63 | 0.67 | 0.55 | 0.64 | 0.61 | 0.60 | 0.63 | 0.57 | 0.61 | 0.01 |
| μ (mV) | 1.14 | 0.94 | 0.89 | 1.87 | 1.12 | 0.96 | 1.10 | 1.43 | 1.18 | 0.11 |
| σ2 (mV) | 2.19 | 1.77 | 1.37 | 5.43 | 2.72 | 1.61 | 2.53 | 3.53 | 2.64 | 0.47 |
| m ( = −ln(P0)) | 0.46 | 0.40 | 0.60 | 0.45 | 0.49 | 0.51 | 0.46 | 0.56 | 0.49 | 0.02 |
| a ( = σ2/μ) | 1.92 | 1.88 | 1.54 | 2.90 | 2.43 | 1.68 | 2.30 | 2.47 | 2.14 | 0.16 |
| a ( = μ/m) | 2.47 | 2.35 | 1.49 | 4.19 | 2.27 | 1.88 | 2.38 | 2.54 | 2.45 | 0.28 |
| Ne ( = (−ln(P0)/iAc) | 1.05 | 0.91 | 1.36 | 1.01 | 1.12 | 1.16 | 1.05 | 1.28 | 1.12 | 0.05 |
| Ne ( = (μ2/σ2)/iAc) | 1.35 | 1.13 | 1.31 | 1.46 | 1.05 | 1.30 | 1.09 | 1.32 | 1.14 | 0.05 |
| Parameters obtained from fitting the data to eqn 08 | ||||||||||
| m | 0.54 | 0.37 | 1.00 | 0.92 | 0.77 | 0.73 | 0.67 | 1.14 | 0.77 | 0.09 |
| SEM | 0.10 | 0.09 | 0.11 | 0.12 | 0.11 | 0.24 | 0.08 | 0.15 | ||
| a (mV) | 2.76 | 3.61 | 1.60 | 2.50 | 2.94 | 2.50 | 2.56 | 2.32 | 2.60 | 0.20 |
| SEM | 0.26 | 0.36 | 0.05 | 0.15 | 0.14 | 0.53 | 0.15 | 0.15 | ||
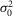 (mV) (mV) |
0.35 | 0.17 | 0.07 | 0.29 | 0.25 | 0.79 | 0.36 | 0.30 | 0.32 | 0.07 |
| SEM | 0.08 | 0.04 | 0.02 | 0.08 | 0.07 | 0.29 | 0.07 | 0.11 | ||
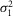 (mV) (mV) |
0.44 | 0.50 | 0.07 | 0.29 | 0.25 | 0.79 | 0.36 | 0.30 | 0.37 | 0.07 |
| SEM | 0.41 | 0.49 | 0.04 | 0.20 | 0.17 | 1.25 | 0.23 | 0.22 | ||
| SNR | 2.49 | 3.34 | 3.48 | 2.67 | 3.38 | 1.63 | 2.47 | 2.44 | 2.74 | 0.22 |
| Fit (r2) | 0.67 | 0.71 | 0.70 | 0.59 | 0.65 | 0.64 | 0.81 | 0.61 | ||
| Fit ANOVA-F(4,56) | 49.46 | 40.08 | 47.24 | 44.17 | 46.19 | 48.62 | 108.80 | 51.03 | ||
| P | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | ||
| Observed dark noise | ||||||||||
| Matched filtering | ||||||||||
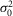 (mV) (mV) |
0.72 | 0.37 | 0.36 | 0.39 | 0.58 | 0.70 | 0.74 | 1.05 | 0.61 | 0.08 |
| SEM | 0.07 | 0.02 | 0.03 | 0.03 | 0.05 | 0.02 | 0.02 | 0.03 | ||
| All traces | ||||||||||
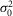 (mV) (mV) |
0.60 | 0.28 | 0.29 | 0.40 | 0.42 | 0.51 | 0.54 | 0.95 | 0.50 | 0.08 |
| SEM | 0.04 | 0.01 | 0.01 | 0.03 | 0.03 | 0.02 | 0.02 | 0.02 | ||
| Data of single photon measurements | ||||||||||
| Peak ampl. (mV) | 2.47 | 3.30 | 1.76 | 3.30 | 2.80 | 2.30 | 3.02 | 2.99 | 2.74 | 0.19 |
| Latency (ms) | 25 | 47 | 60 | 58 | 35 | 41 | 45 | 33 | 43 | 4 |
| Time-to-peak (ms) | 340 | 351 | 342 | 793 | 258 | 279 | 291 | 282 | 367 | 62 |
| Duration (ms) | 1070 | 1504 | 1304 | 2500 | 1595 | 901 | 1282 | 962 | 1390 | 181 |
The response characteristics to a series of 60 to 150 dim flashes of intensity 0.44R* presented at 0.2 Hz of 8 different cells recorded during the day (D), subjective day-1 (SD1) or subjective day-2 (SD2) are given. For each cell, the characteristics of the light responses were derived from Poisson statistics formulas (see Methods for details). Estimates from the dark noise (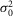 ) were obtained from eqn 08 but also from 2 other measurements. First,
) were obtained from eqn 08 but also from 2 other measurements. First, 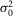 was estimated from the selection by matched filtering of the traces that did not show a response (failures) and second, from the entire set of traces, during the last 1 s of recording, that is after the light response has recovered. Data of the single photon measurements were obtained from averaged traces selected by matched filtering. Estimates from D, SD1, and SD2 were pooled together and averaged and are given ± SEM at the end of each line (right columns).
was estimated from the selection by matched filtering of the traces that did not show a response (failures) and second, from the entire set of traces, during the last 1 s of recording, that is after the light response has recovered. Data of the single photon measurements were obtained from averaged traces selected by matched filtering. Estimates from D, SD1, and SD2 were pooled together and averaged and are given ± SEM at the end of each line (right columns).
Table 4.
Properties of the mouse rod response to dim light stimuli during the night or subjective night
| Cell | 41–12620023 | 41–12620031 | 117–13322001 | 51–12814015 | 40–12620009 | 51–12814018 | 44–12703002 | 108–13222016 | Average | SEM | P value | D/N diff. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time | ZT16 | ZT17 | ZT18 | CT15 | CT15 | CT16 | CT16 | CT17 | (t test) | |||
| Trials | 76 | 53 | 139 | 150 | 150 | 150 | 60 | 150 | ||||
| P0 | 0.53 | 0.49 | 0.42 | 0.34 | 0.20 | 0.43 | 0.50 | 0.45 | 0.42 | 0.04 | 0.0003 | *** |
| μ (mV) | 0.33 | 0.31 | 0.96 | 0.64 | 0.91 | 0.81 | 0.82 | 0.46 | 0.66 | 0.11 | 0.0030 | ** |
| σ2 (mV) | 0.16 | 0.17 | 0.64 | 0.32 | 0.40 | 0.28 | 1.51 | 0.36 | 0.48 | 0.18 | 0.0006 | *** |
| m ( = −ln(P0)) | 0.63 | 0.71 | 0.87 | 1.08 | 1.61 | 0.84 | 0.69 | 0.80 | 0.90 | 0.13 | 0.0028 | ** |
| a ( = σ2/μ) | 0.48 | 0.55 | 0.67 | 0.50 | 0.44 | 0.35 | 1.84 | 0.78 | 0.70 | 0.20 | 0.0000 | *** |
| a ( = μ/m) | 0.52 | 0.43 | 1.11 | 0.59 | 0.57 | 0.96 | 1.18 | 0.58 | 0.74 | 0.12 | 0.0001 | *** |
| Ne ( = (−ln(P0)/iAc) | 1.44 | 1.62 | 1.97 | 2.45 | 3.66 | 1.92 | 1.58 | 1.81 | 2.06 | 0.29 | 0.0028 | ** |
| Ne ( = (μ2/σ2)/iAc) | 1.55 | 1.28 | 3.27 | 2.91 | 4.71 | 5.33 | 1.01 | 1.34 | 2.67 | 0.68 | 0.0302 | * |
| Parameters obtained from fitting the data to eqn 08 | ||||||||||||
| m | 0.79 | 1.06 | 0.96 | 1.38 | 1.98 | 1.16 | 0.58 | 1.46 | 1.17 | 0.18 | 0.0387 | * |
| SEM | 0.19 | 0.16 | 0.21 | 0.17 | 0.25 | 0.17 | 0.10 | 0.15 | ||||
| a (mV) | 0.77 | 0.83 | 1.10 | 0.77 | 0.73 | 1.51 | 2.74 | 0.96 | 1.17 | 0.28 | 0.0005 | ** |
| SEM | 0.14 | 0.08 | 0.21 | 0.07 | 0.03 | 0.12 | 0.19 | 0.06 | ||||
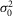 (mV) (mV) |
0.05 | 0.05 | 0.08 | 0.09 | 0.01 | 0.19 | 0.26 | 0.07 | 0.10 | 0.03 | 0.0146 | ** |
| SEM | 0.01 | 0.01 | 0.02 | 0.03 | 0.00 | 0.06 | 0.07 | 0.02 | ||||
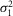 (mV) (mV) |
0.17 | 0.11 | 0.46 | 0.09 | 0.03 | 0.19 | 0.26 | 0.07 | 0.17 | 0.06 | 0.0388 | * |
| SEM | 0.11 | 0.07 | 0.25 | 0.05 | 0.01 | 0.14 | 0.24 | 0.04 | ||||
| SNR | 1.23 | 1.56 | 1.10 | 1.44 | 2.87 | 2.00 | 3.11 | 2.05 | 1.92 | 0.30 | 0.045 | * |
| Fit (r2) | 0.90 | 0.85 | 0.85 | 0.89 | 0.75 | 0.77 | 0.67 | 0.83 | ||||
| Fit ANOVA-F(4,56) | 141.52 | 94.79 | 102.25 | 147.05 | 47.12 | 76.12 | 41.35 | 95.37 | ||||
| P | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | ||||
| Observed dark noise | ||||||||||||
| Matched filtering | ||||||||||||
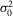 (mV) (mV) |
0.24 | 0.53 | 0.34 | 0.54 | 0.34 | 0.53 | 0.38 | 0.33 | 0.40 | 0.04 | 0.0405 | * |
| SEM | 0.01 | 0.03 | 0.02 | 0.02 | 0.02 | 0.03 | 0.02 | 0.02 | ||||
| All traces | ||||||||||||
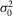 (mV) (mV) |
0.19 | 0.37 | 0.22 | 0.26 | 0.29 | 0.42 | 0.40 | 0.25 | 0.30 | 0.03 | 0.0297 | * |
| SEM | 0.01 | 0.03 | 0.01 | 0.01 | 0.00 | 0.01 | 0.02 | 0.01 | ||||
| Data of single photon measurements | ||||||||||||
| Peak ampl. (mV) | 0.84 | 0.87 | 1.95 | 1.07 | 0.92 | 1.41 | 1.07 | 0.68 | 1.10 | 0.14 | 0.0000 | *** |
| Latency (ms) | 35 | 102 | 73 | 36 | 35 | 36 | 41 | 88 | 56 | 10 | 0.2521 | ns |
| Time-to-peak (ms) | 241 | 325 | 853 | 282 | 198 | 391 | 301 | 624 | 402 | 79 | 0.7334 | ns |
| Duration (ms) | 1941 | 2140 | 4085 | 1678 | 1622 | 1771 | 1616 | 2388 | 2155 | 292 | 0.0428 | * |
The response characteristics to a series of 53 to 150 dim flashes of intensity 0.44R* presented at 0.2 Hz of 8 different cells recorded during the night (N) or subjective night (SN) are given. The characteristics of the light responses were determined as described in the legend of Table3. The nighttime characteristics of the rod light responses were compared with their respective daytime values listed on Table3 using the unpaired t test. The last 2 columns on the right list the P value of the test and the statistical significance; ns: not significant (P > 0.05)
P < 0.05
P < 0.01
P>0.001.
Figure 6.
Circadian variations of the rod receptive field size and input resistance (Ri)
A, circadian variations in the size of the receptive field. Representative examples of receptive field size measurements of single rods obtained during the subjective day-1 (SD1) and subjective night (SN). Cell RMP was –38.0 mV (SD1) and –43.0 mV (SN). B, average values of the space constant (λ) measured during the day (D), night (N), subjective day-1 (SD1), subjective day-2 (SD2), or subjective night (SN). A two-way ANOVA of the data was performed. The between-group factor was the type of lighting cycle (i.e. 12 h light–12 h dark cycle or circadian cycle) and the intra-group was time of D (D or N). ANOVA of the data revealed significant time of D effect (F(1,33) = 110.90, P < 0.001) but no type of lighting cycle effect (F(1,33) = 2.88, P = 0.10) or time of D × type of lighting cycle effect (F(1,33) = 1.29, P = 0.26). n is shown for each condition on the figure (1 cell retina). Error bars, SEM. C, comparison of Ri measurements obtained during the day (D), night (N), subjective day-1 (SD1), subjective day-2 (SD2), or subjective night (SN). Ri of the recorded rods was measured using a 5 mV voltage step (see Methods for details). A two-way ANOVA of the data was performed. The between-group factor was the type of lighting cycle (i.e. 12 h light–12 h dark cycle or circadian cycle) and the intra-group was time of D (D or N). ANOVA of the data revealed significant time of D effect (F(1,58) = 12.51, P < 0.001) but no type of lighting cycle effect (F(1,58) = 1.67, P = 0.20) or time of D × type of lighting cycle effect (F(1,58) = 0.35, P = 0.56). n is shown for each condition on the figure (1 cell retina–1). Error bars, SEM.
Pharmacological control of gap junction coupling
Pharmacological blockade of gap junctions brought additional evidence supporting an increase in rod electrical coupling at night. The gap junction antagonist meclofenamic acid (MFA, 50 μm; Pan et al. 2007) was applied (>10 min) after a control (no drug) recording was obtained, so that recordings before and after MFA application were obtained from the same cell. MFA had limited or no effect on the rod light responses and receptive field size during the subjective day (Fig.7A). However, application of MFA during the subjective night increased the rod light response amplitude and its variability by ∼2-fold and decreased the receptive field size by ∼3-fold (Fig.7B), so that they resembled those typically observed during the day (Fig.1) or subjective day (Fig.5). Application of MFA did not significantly shift the membrane voltage potential during subjective day-1: −40.1 ± 3.3 mV (control) vs. −40.8 ± 2.8 mV (MFA; mean ± SEM; n = 4; P = 0.27; Student's paired t test), or subjective night: −42.4 ± 4.3 mV (control) vs. −35.4 ± 4.17 mV (MFA; mean ± SEM; n = 8; P = 0.39; Student's paired t test). Also, the effects of MFA on the rod light responses and receptive field size were only partially reversible within 30 min (data not shown). Thus, MFA was sufficient to induce a daytime state, thereby confirming that rod coupling was weak during the day or subjective day and stronger at night or subjective night, but also suggesting that the primary effect of the clock on the circadian regulation of the rod light responses is via the modulation of gap junction coupling.
Figure 7.
The rod gap junction is a primary target of the circadian clock to control the rod light response
A and B, effects of the gap junction antagonist MFA on the rod responses (Aa–d, Ba–d) and rod receptive field size (Ae and Be) during the subjective day (SD; Aa–e) and the subjective night (SN; Ba–e). Shown are examples of amplitude fluctuation of rods to a full-field 500 nm light stimulus of fixed intensity (0.44R*) recorded under dark-adapted conditions (dark traces) and after ∼15 min application of MFA (blue traces) during the SD1 (Aa) or the SN (Ba) and rod responses to a series of 20 ms full-field 500 nm light flashes of increasing intensity during the SD1 (Ab) or the SN (Bb). RMP was –33.5 mV (control) and –32.3 mV (MFA) for cell in Aa, –39.9 mV (control) and –40.3 mV (MFA) for cell in Ab, –30.2 mV (control) and –33.4 mV (MFA) for cell in Ba, and –47.7 mV (control) and –41.9 mV (MFA) for cell in Bb. Also illustrated are averaged (Ac and Bc) and normalized (Ad and Bd) intensity–response curves and receptive field size (Ae and Be) of rods recorded during the D or SD (Ac–e) and N or SN (Bc–e) under control conditions (black points and curves) and after ∼15 min application of MFA (blue points and curves). Vertical black bars indicate the timing of flashes, and the probability of failure (P0) is given (Aa and Bb). The P value in Ac, Ad, Bc and Bd was calculated for interactions between light density and treatment (control or MFA; two-way ANOVA). In Ae and Be, ***P < 0.001, ns: non-significant (P > 0.05; paired Student t test). Error bars, SEM; n is shown for each condition on the figure (1 cell retina–1). All recordings were paired (i.e. same cell recorded before (control) and after (>10 min) MFA application). C–F, neurobiotin tracer coupling between photoreceptors under control conditions during the subjective day-1 (SD1; Ca and b) or the subjective night (SN; Da and b) and in the presence of MFA (50 μm, > 30 min) during the SD1 (Ea and b) or the SN (Fa and b). Coupled photoreceptor cells during SN included rods and cones (labelled with PNA, white arrows in Da). Panels show confocal images of whole-mount retinae at the level of the cone inner segments (optical sections, 5 × 1 μm; Ca, Da, Ea, Fa) and 3D projections of 70-μm thick Z-stacks of the outer nuclear layer of the same area (Cb, Db, Eb, Fb). Scale bars: 5 μm. G, distribution of the number of tracer coupled cells during the day (D), subjective day-1 (SD1), subjective day-2 (SD2), night (N) and subjective night (SN). n is shown for each condition on the figure. In the presence of MFA, tracer remained exclusively in the injected cell (D: n = 3; N: n = 3; SD1: n = 2; SN: n = 2; SD2: n = 3; not illustrated for clarity purposes).
Tracer coupling
In a complementary approach, we measured tracer coupling between rods during day, subjective day, night, and subjective night. The extent of tracer coupling during the subjective day was similar to that observed during daytime (Fig.1G and H) and was typically restricted to the injected cell (Figs4I and 7C and G). In a few cases (4 out of 14 injections), tracer coupled cells included a cone as well. In contrast, during the subjective night or night, tracer staining was found in numerous (range 11–27) rods and in cones (Figs4J and 7D and G), indicating strong rod coupling with neighbouring rods but also neighbouring cones. The average ratio of tracer-coupled cones to rods was 0.12 ± 0.03 (mean ± SEM, n = 6) at night or subjective night. Rod–cone coupling is functionally important because it represents a route for rod signals to enter cone pathways (Bloomfield & Dacheux, 2001; Field et al. 2005; Hornstein et al. 2005; Bloomfield & Völgyi, 2009). The functional importance of rod–cone coupling on the rod response remains tenuous, but it is conceivable that the strength of rod–cone coupling may modulate rod Ri and thereby the rod response (see below). In the presence of MFA (50 μm, > 30 min), rod tracer coupling was strictly restricted to the injected cell (Fig.7E and F), regardless of the time of day. Together these data provide electrophysiological and tracer coupling evidence that a circadian clock regulates rod electrical coupling. Rod coupling is weak during the day and stronger at night.
The circadian clock uses dopamine and D2-like receptors to control rod electrical coupling and light response kinetics
Retinal dopamine and dopamine D2-like receptors control photoreceptor electrical and tracer coupling in the retina of lower vertebrates (Krizaj et al. 1998; Ribelayga et al. 2008; Li et al. 2009), and similar actions are predicted in mouse based on tracer coupling and immunocytochemistry data (Ribelayga et al. 2008; Li et al. 2013). Application of the D2-like antagonist spiperone (10 μm, > 10 min) during the subjective day, when endogenous retinal dopamine levels are high (Iuvone et al. 2005), affected the rod light responses and the rod receptive field size so that they resembled those typically observed at night (Fig.8A). Application of spiperone usually produced longer light response durations compared to nighttime. This ‘super-night’ effect of spiperone is likely to be due to the fact that the antagonist blocks D2-like receptor activity while nighttime levels of dopamine are low but not insignificant and support some basal activity of the D2-like receptors. Detectable low levels of dopamine have been measured at night in the retina of many vertebrates, including mice (Iuvone et al. 2005). Application of MFA during the subjective day in the presence of spiperone blocked the effects of the D2-like receptor antagonist on the rod light responses and receptive field size (Figs8B and 9). Conversely, application of the D2-like receptor agonist quinpirole (1 μm, > 10 min) during the subjective night, when retinal dopamine levels are low (Iuvone et al. 2005), mimicked the daytime state (Fig.8C).
Figure 8.
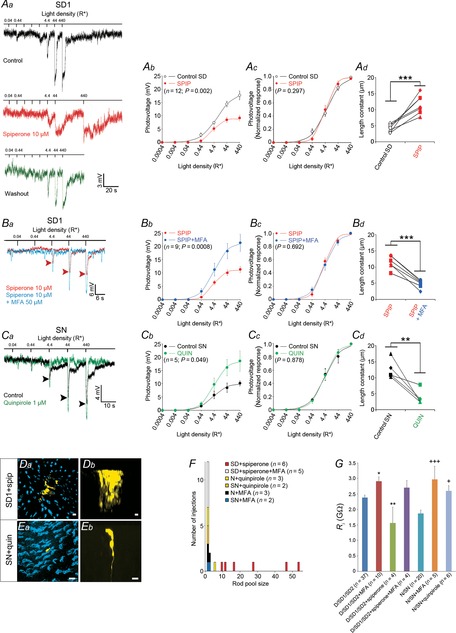
Dopamine D2-like receptor signalling mediates the effects of the clock on the rod light response properties and electrical coupling
A, blocking dopamine D2-like receptors during the subjective day (SD) mimics the nighttime state. Examples of rod responses to a series of 20 ms full-field 500 nm light flashes of increasing intensity recorded under dark-adapted conditions during the subjective day-1 (SD1) under control conditions (no drug, dark trace) and following the application of the D2-like receptor antagonist spiperone (10 μm, > 10 min, red trace; Aa). Partial recovery after washout (no drug, green trace) was after 15 min. Averaged (Ab) and normalized (Ac) intensity–response curves and receptive field size (Ad) of rods recorded during the day (D) or SD under control conditions (black points and curves) and after ∼15 min application of spiperone (red points and curves). B, MFA blocks the effects of spiperone. Representative example of rod responses to a series of 20 ms full-field 500 nm light flashes of increasing intensity recorded under dark-adapted conditions during the SD1 in the presence of spiperone (10 μm, > 15 min) before (red trace) and during application of MFA (50 μm, > 15 min, blue trace; Ba). Averaged (Bb) and normalized (Bc) intensity–response curves and receptive field size (Bd) of rods recorded during the D or SD after ∼15 min application of spiperone (red points and curves) and after ∼15 min application of spiperone and MFA (blue points and curves). C, activating dopamine D2-like receptors at night (N) mimics the daytime state. Example of rod responses to a series of 20 ms full-field 500 nm light flashes of increasing intensity recorded under dark-adapted conditions during the subjective night (SN) before (no drug, dark trace) and during application of the D2-like receptor agonist quinpirole (1 μm, > 10 min, green trace; Ca). Averaged (Cb) and normalized (Cc) intensity–response curves and receptive field size (Cd) of rods recorded during the N or SN under control conditions (black points and curves) and after ∼15 min application of quinpirole (green points and curves). Arrowheads in Ba and Ca indicate the peak of the response under spiperone and control conditions, respectively. RMP was –38.7 mV (control), –38.0 mV (spiperone) and –41.5 mV (washout) for cell in Aa, –47.2 mV (spiperone) and –38.6 mV (spiperone + MFA) for cell in Ba, and –36.3 mV (control) and –40.7 mV (quinpirole) for cell in Ca. Statistical analysis performed as described in Fig.7. All recordings were paired (i.e. same cell recorded before (control) and after (>10 min) drug application). D and E, neurobiotin tracer coupling between photoreceptors in the presence of spiperone (10 μm, > 30 min) during the SD1 (Da and b) or in the presence of quinpirole (1 μm, > 30 min) during the SN (Ea and b). Panel views and organization as in Fig.7C–F. Scale bars, 5 μm. F, distribution of the number of tracer coupled rods following the injection of single rods under the conditions illustrated in Aa, Ba and Ca and in the presence of MFA during the N or SN or during the SD together with spiperone. n is shown for each condition on the figure. G, effects of various pharmacological manipulations on Ri. Values from the D, SD1, and SD2 and from the N and SN and illustrated in Fig.6C were pooled together, respectively, and used as the control. During the daytime, MFA significantly increased and spiperone decreased Ri. However, the effects of spiperone on Ri were blocked by the co-application of MFA (one-way ANOVA, F(3,57) = 7.47, P < 0.001). At N, application of MFA or quinpirole significantly increased Ri (one-way ANOVA, F(2,30) = 9.57, P < 0.001). *P < 0.05, **P < 0.01 when compared to the D, SD1 and SD2; +P < 0.05, +++P < 0.001 when compared to the N and SN (Tukey's post hoc test). Shown are averaged measurements ± SEM from 4–37 cells (n is indicated for each condition on the figure).
Figure 9.
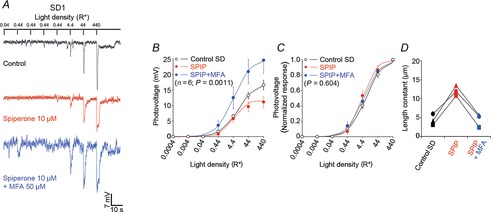
MFA reverses the effects of the D2-like receptor antagonist spiperone on the rod light response properties and receptor field size
A, examples of rod responses to a series of 20 ms full-field 500 nm light flashes of increasing intensity recorded under dark-adapted conditions during the subjective day-1 (SD1) under control conditions (no drug, dark trace), following the application of the D2-like receptor antagonist spiperone (10 μm, > 10 min, red trace), and following the subsequent application of spiperone together with the gap junction antagonist MFA (50 μm; > 10 min, blue trace). Resting membrane potential was –41.3 mV (control), –39.7 mV (spiperone) and –40.0 mV (spiperone + MFA). B and C, averaged (B) and normalized (C) intensity–response curves and receptive field size (D) of rods recorded during the SD1 under control conditions (black points and curves), after ∼15 min application of spiperone (red points and curves) and after ∼15 min of co-application of spiperone and MFA (blue points and curves). The P value in B and C was calculated for interactions between light density and treatment (control or drug; two-way ANOVA). In D, a one-way ANOVA of the data revealed significant difference between the experimental conditions (F(2,8) = 24.86, P < 0.01). n = 6 (B and C) and 3 (D). Error bars, SEM (1 cell retina–1).
The effects of spiperone and quinpirole depended on the time of day. Application of spiperone during the subjective night, when endogenous retinal dopamine levels are low, or of quinpirole during the subjective day, when dopamine levels are high, had no significant effect on the rod light response kinetics or the receptive field size (Fig.10). Furthermore, tracer coupling was extensive during the subjective day in the presence of spiperone and was restricted during the subjective night in the presence of quinpirole, indicating that pharmacological manipulation of the dopamine D2-like receptor affected tracer coupling of the rods (Fig.8D–F). Application of spiperone did not significantly affect the membrane voltage potential during the subjective day: −37.5 ± 2.5 mV (control) vs. −38.6 ± 2.9 mV (spiperone; mean ± SEM; n = 12; P = 0.78; Student's paired t test), or subjective night: −37.1 ± 5.0 mV (control) vs. −37.7 ± 4.9 mV (spiperone; mean ± SEM; n = 4; P = 0.62; Student's paired t test). Rod baseline voltage was also not significantly altered by application of quinpirole during subjective day: −39.4 ± 3.8 mV (control) vs. −34.6 ± 3.5 mV (quinpirole; mean ± SEM; n = 3; P = 0.41; Student's paired t test), or subjective night: −34.5 ± 3.0 mV (control) vs. −32.9 ± 2.0 mV (quinpirole; mean ± SEM; n = 4; P = 0.44; Student's paired t test). Application of MFA during subjective day in the presence of spiperone blocked the effects of the D2-like receptor antagonist on rod tracer coupling (Fig.8F). Finally, application of spiperone during day or subjective day decreased the rod input resistance (Ri), whereas application of quinpirole during night or subjective night increased Ri (Fig.8G). Collectively, these data provide evidence that a circadian clock uses dopamine to control rod function in the mammalian retina and dopamine primarily affects rod electrical coupling, thereby modulating the light responses of rods.
Rod–rod coupling – a computational model
The effects of rod–rod coupling on signal and noise were modelled for a network of coupled rods (Ne) and a number of illuminated cells in the network (M). Coupling was assumed to be ‘perfect’, that is the gap junction conductance between rods is infinite, and the light responses are equivalent in all coupled rods. For simplification, we excluded the cones from the analysis as they do not intrinsically respond to dim light stimuli. Modelling was based on previous studies (Baylor et al. 1979; Tessier-Lavigne & Attwell, 1988; Hornstein et al. 2005) and on our measurements of the rod light response kinetics obtained in the presence of MFA, that is, for individual rods (see Methods for details). We first calculated the probability density function for an intensity i = 0.44R* and a varying number of coupled rods (Ne) with the number of illuminated rods in the network (M) set to 1 (Fig.11A). With i = 0.44R*, it is expected that only one rod in a network of 2.40 coupled rods (2.4 × 0.44 ≈ 1) elicits a response at night, thereby allowing us to compare the experimental data to the model. Our experimental data fitted almost perfectly with the model for Ne = 1.13 (daytime value; Fig.11B) and for Ne = 2.40 (nighttime value; Fig.11C).
Figure 11.
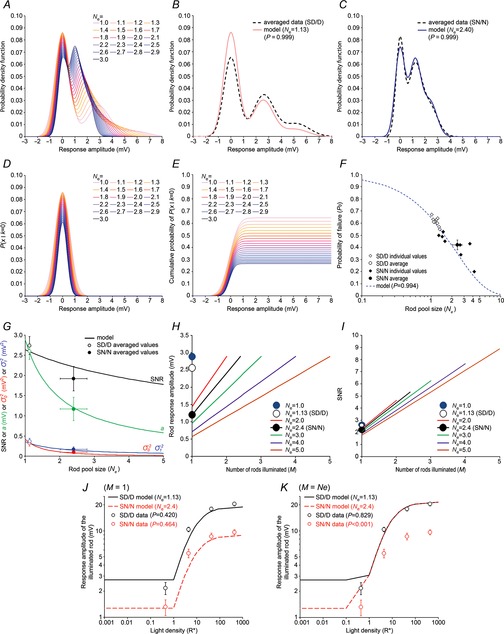
Rod network modelling
A, probability density function calculated for different numbers of coupled rods in the network (Ne). See eqn 20 (Methods) for details. B, probability density function calculated with eqn 20 for Ne = 1.13 (daytime model) and with eqn 08 using the averaged experimental values of m, a, 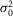 , and
, and 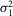 obtained during subjective day (SD) or day (D; Table3). P value was obtained from χ2 goodness of fit. C, probability density function calculated with eqn 20 for Ne = 2.40 (nighttime model) and with eqn 08 using the averaged experimental values of m, a,
obtained during subjective day (SD) or day (D; Table3). P value was obtained from χ2 goodness of fit. C, probability density function calculated with eqn 20 for Ne = 2.40 (nighttime model) and with eqn 08 using the averaged experimental values of m, a, 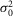 , and
, and 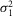 obtained during subjective night (SN) or night (N; Table4). P value was obtained from χ2 goodness of fit. D, probability density function of the first component (k = 0) calculated for Ne ∈ [1,3]. See eqn 21 (Methods) for details. E, cumulative density function of the first component (k = 0), F0(x), calculated for Ne ∈ [1,3]. See eqn 22 (Methods) for details. F0(x) =
obtained during subjective night (SN) or night (N; Table4). P value was obtained from χ2 goodness of fit. D, probability density function of the first component (k = 0) calculated for Ne ∈ [1,3]. See eqn 21 (Methods) for details. E, cumulative density function of the first component (k = 0), F0(x), calculated for Ne ∈ [1,3]. See eqn 22 (Methods) for details. F0(x) = 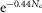 when
when 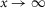 . F, individual experimental values of P0 and fitted values (P0 =
. F, individual experimental values of P0 and fitted values (P0 = 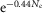 ) as a function of Ne. Averaged values are shown with error bars, SEM. P value was obtained from χ2 goodness of fit. G, calculated single photon response amplitude (a), variance of rod noise (
) as a function of Ne. Averaged values are shown with error bars, SEM. P value was obtained from χ2 goodness of fit. G, calculated single photon response amplitude (a), variance of rod noise (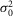 ) and of the single photon response (
) and of the single photon response (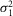 ), and SNR as a function of Ne, with M = 1 and i = 0.44R*. Averaged data obtained during the SD (or D; open circles) and SN (or N; filled circles) are illustrated for comparison (see Tables3 and 4 and eqns 23 and 24 in Methods for details). Error bars, SEM. H and I, rod response amplitude (H) and SNR (I), as a function of the number of rods illuminated (M) and calculated for Ne ∈ [1,5], with i = 1R* in each illuminated rod. Values obtained with Ne = 1.13 and Ne = 2.4 for M = 1 compare well with the values of a and of the SNR obtained during SD or D (a = 2.60 and SNR = 2.74) and SN or N (a = 1.17 and SNR = 1.92), respectively (Tables3 and 4). Note that both the response amplitude and the SNR decrease when Ne increases. However, for a given Ne, increasing the number of rods illuminated (M) increases the rod response towards a limit that equals its value in an isolated rod. The SNR also increases when M increases but beyond the limit set by an isolated rod when M approaches Ne. Thus, coupling reduces the rod response amplitude and SNR for small stimuli but is beneficial for the detection of large stimuli. J and K, light response amplitude of an illuminated rod as a function of light density (i) for a spatially restricted stimulus (M = 1; J) and for a full-field stimulus (M = Ne; K). Shown are curves calculated with Ne = 1.13 (daytime model) and Ne = 2.4 (nighttime model; see eqn 25 for details). The model predicts that for I < 1R*, an increase in coupling would lower the response amplitude whatever the extent of the stimulus because of the influence of the coupled rods. However, for i ≥ 1R*, coupling should affect the response amplitude only when the stimulus is restricted to the illuminated rod and should not affect the response amplitude when the stimulus covers the entire field. Experimental values obtained during SD or D (n = 65) and SN or N (n = 25) with full field stimuli of intensity i = 0.44, 4.4, 44 and 440R* are shown for comparison. As expected, SD or D values fitted well both models because the rods are essentially in a decoupled state during the SD or D. However, contrary to the prediction, SN or N values fitted well the model in J and poorly the model in K. See eqn 25 (Methods) for details. A density of 0.01 means that 1R* is elicited in the illuminated rod and that no response occurs in the 99 neighbouring rods. Error bars, SEM; P value was obtained from χ2 goodness of fit.
), and SNR as a function of Ne, with M = 1 and i = 0.44R*. Averaged data obtained during the SD (or D; open circles) and SN (or N; filled circles) are illustrated for comparison (see Tables3 and 4 and eqns 23 and 24 in Methods for details). Error bars, SEM. H and I, rod response amplitude (H) and SNR (I), as a function of the number of rods illuminated (M) and calculated for Ne ∈ [1,5], with i = 1R* in each illuminated rod. Values obtained with Ne = 1.13 and Ne = 2.4 for M = 1 compare well with the values of a and of the SNR obtained during SD or D (a = 2.60 and SNR = 2.74) and SN or N (a = 1.17 and SNR = 1.92), respectively (Tables3 and 4). Note that both the response amplitude and the SNR decrease when Ne increases. However, for a given Ne, increasing the number of rods illuminated (M) increases the rod response towards a limit that equals its value in an isolated rod. The SNR also increases when M increases but beyond the limit set by an isolated rod when M approaches Ne. Thus, coupling reduces the rod response amplitude and SNR for small stimuli but is beneficial for the detection of large stimuli. J and K, light response amplitude of an illuminated rod as a function of light density (i) for a spatially restricted stimulus (M = 1; J) and for a full-field stimulus (M = Ne; K). Shown are curves calculated with Ne = 1.13 (daytime model) and Ne = 2.4 (nighttime model; see eqn 25 for details). The model predicts that for I < 1R*, an increase in coupling would lower the response amplitude whatever the extent of the stimulus because of the influence of the coupled rods. However, for i ≥ 1R*, coupling should affect the response amplitude only when the stimulus is restricted to the illuminated rod and should not affect the response amplitude when the stimulus covers the entire field. Experimental values obtained during SD or D (n = 65) and SN or N (n = 25) with full field stimuli of intensity i = 0.44, 4.4, 44 and 440R* are shown for comparison. As expected, SD or D values fitted well both models because the rods are essentially in a decoupled state during the SD or D. However, contrary to the prediction, SN or N values fitted well the model in J and poorly the model in K. See eqn 25 (Methods) for details. A density of 0.01 means that 1R* is elicited in the illuminated rod and that no response occurs in the 99 neighbouring rods. Error bars, SEM; P value was obtained from χ2 goodness of fit.
In addition, we calculated the probability of failure (P0) from the probability density and cumulative density functions of the first component (k = 0) and observed a perfect fit of the experimental data with the calculated model (Fig.1D–F). These experiments confirm a major contribution of rod–rod coupling in shaping the probability density function and the probability of detecting a response when recording from the rod inner segment. We next modelled the behaviour of the single event amplitude (a), rod intrinsic noise (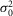 ), the dispersion in the single event amplitude (
), the dispersion in the single event amplitude (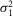 ), and the SNR for varying Ne and M set to 1. The model revealed that the increase in coupling at night we measured (Ne = 2.40) results in a ∼50% decrease in a but in only a ∼15% decrease in the SNR (Fig.1G). Although the model globally agrees with published studies (Tessier-Lavigne & Attwell, 1988; Hornstein et al. 2005) in that an increase in rod–rod coupling is detrimental to both a and the SNR, it also demonstrates that the modest coupling between rods we measured at night has less impact on the SNR.
), and the SNR for varying Ne and M set to 1. The model revealed that the increase in coupling at night we measured (Ne = 2.40) results in a ∼50% decrease in a but in only a ∼15% decrease in the SNR (Fig.1G). Although the model globally agrees with published studies (Tessier-Lavigne & Attwell, 1988; Hornstein et al. 2005) in that an increase in rod–rod coupling is detrimental to both a and the SNR, it also demonstrates that the modest coupling between rods we measured at night has less impact on the SNR.
We next modelled the rod light response amplitude and the SNR for varying numbers of illuminated rods in the network (M), with i = 1R* in each illuminated rod. The models in Fig.1H and I predict values of a and of the SNR that are very close to the experimental values. Also, in agreement with previous studies (Tessier-Lavigne & Attwell, 1988; Hornstein et al. 2005) and Fig.1G, the models confirm that under dim illumination, the rod response amplitude and the SNR are degraded when rods are coupled, and only a single rod in the network elicits a single photon response. However, both are improved when rods are coupled, and the stimulus covers more than one rod in the network. Overall, the conclusions drawn from our modelling studies are in agreement with the literature and confirm that under dim light, coupling is detrimental to the detection of small stimuli by rods but is actually beneficial for large stimuli (Tessier-Lavigne & Attwell, 1988; Hornstein et al. 2005; Li et al. 2012). However, our analysis also demonstrates that the extent of rod–rod coupling observed at night in the mouse retina does not prevent the rod single-photon response and has a limited impact on the SNR.
We next modelled the amplitude of the rod response as a function of the light density (i) for a spatially restricted stimulus (M = 1; Fig.1J) and for a large (full-field) stimulus (M = Ne; Fig.1K). The theory states that weak coupling should minimally affect the rod light response at any intensity and for any size of stimulus because of the minimal contribution of neighbouring cells. On the contrary, when rods are coupled, coupling is expected to have a maximal effect when the stimulus is focused and a minimal effect when the stimulus is uniform and all rods undergo the same voltage displacement and no current flows through the junctional resistances coupling the cells (Tessier-Lavigne & Attwell, 1988). The data collected during the day or subjective day fitted well to both models, consistent with the minimal influence of the neighbouring photoreceptor cells on the response of a rod when electrical coupling is weak (Fig.1J and K). The data collected at night or subjective night fitted well to both models as well for when i < 1R*, because at this light density, the stimulus is not uniform and can be considered as spatially restricted, in particular when Ne is small. However, contrary to the theory, the data we collected at night or subjective night using a full-field light stimulus of intensity i > 1R* better fitted the model for a spatially restricted stimulus (Fig.1J) than the model for a full-field stimulus (Fig.1K). Thus, our mathematical analysis of the rod network was able to predict the behaviour of the rod response during the day for any type of stimulus and intensity and during the night for dim and spatially restricted stimuli but fell short in providing an explanation for the behaviour of the rod light response at night for a large light stimulus of intensity i > 1R* (Fig.1J and K). The poor fit between the rod responses to bright uniform stimuli at night and our model may reflect the limitations of a model based solely on a network of perfectly coupled rods and that excluded cones. In fact, the rod response behaviour at night could be explained by the presence of cones coupled to rods through gap junctions that shunt the rod light response. To test this possibility, we developed a resistive–capacitive model of the mouse photoreceptor network (see below).
Resistive–capacitive model of the mouse photoreceptor network
We developed a simplified resistive–capacitive model to calculate whether electrical coupling between rods and cones would affect the kinetics of the rod light responses (see Methods for details). An idealized lattice of connected rods and cones in mouse retina was first drawn based on published anatomical data (Tsukamoto et al. 2001; Fig.12A). An equivalent resistive, capacitive and inductive model was then developed (Fig.12B) and simplified into a resistive–capacitive circuit (Fig.12C) by making a few reasonable assumptions. In particular, the model assumed that no net current should flow through the rod–rod gap junctions or the cone–cone gap junctions when the light stimulus is uniform (see Methods for details). In addition, the model assumed a value for the rod membrane resistance (Rmr) of 2.4 GΩ based on our own measurements of the instantaneous input resistance performed during the day (see Fig.6C) and a value for the cone membrane resistance (Rmc) identical to that of the rods. The rod membrane capacitance (Cmr) ranged from 8 to 10 pF based on our whole-cell recordings (data not shown) and was set to 10 pF. As mouse rods and cones have a similar cell volume, we set the cone membrane capacitance to 10 pF. We calculated reasonable limits of the rod–cone junctional conductance (Gj(r–c)) as follows. Both the phosphorylation state of connexin36 (Cx36), which mirrors the strength of photoreceptor electrical coupling, and photoreceptor tracer coupling vary through a 20-fold dynamic range between day and night (Ribelayga et al. 2008; Li et al. 2013). Assuming that (1) rod–cone coupling is primarily regulated by Cx36 phosphorylation; (2) that Gj(r–c) in mouse is close to the values reported in ground squirrel (∼100–200 pS; Li et al. 2010), and that these estimates were obtained during the day; and (3) that a 20-fold change in Cx36 phosphorylation between day and night reflects a 20-fold change in junction conductance, then the nighttime value of Gj(r–c) may be close to 200 × 20 = 4000 pS. Thus, the resistance of the rod–cone gap junction (Rj(r–c)) may theoretically vary between ∼10 GΩ during the day (weak coupling) and ∼0.3 GΩ at night (strong coupling).
Figure 12.
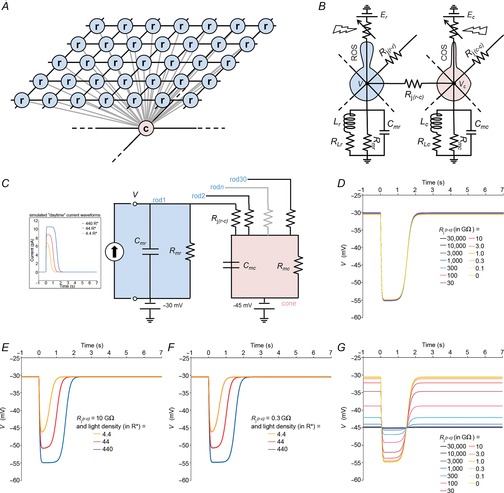
Resistive–capacitive model of the mouse photoreceptor network
A, idealized arrangement of the rods and cones in the mouse retina. Each rod (blue circles) is electrically coupled to its 4 closest neighbours and to 1 cone (pink circle). Each cone is coupled to most of the rods in its vicinity and to other cones as well. See Methods for details. B, an electrical equivalent resistive–capacitive–inductive circuit model of the photoreceptor network of the mouse. Cmc, cone membrane capacitance; Cmr, rod membrane capacitance; COS, cone outer segment; Ec, reversal potential of the cone light sensitive conductance; Er, reversal potential of the rod light sensitive conductance; Lc, cone inductance; Lr, rod inductance; RLc, cone shunt resistance; RLr, rod shunt resistance; Rj(c–c), cone–cone junction resistance; Rj(r–c), rod–cone junction resistance; Rj(r–r), rod–rod junction resistance; Rmc, cone membrane resistance; Rmr, rod membrane resistance; ROS, rod outer segment; V, rod membrane potential; Vc, cone membrane potential. C, a simplified equivalent resistive–capacitive circuit model of the mouse photoreceptor network we used for simulation of the rod membrane potential as a function of current and time. The cone compartment is connected to 30 rods. The RMP of the rod is set at –30 mV and that of the cone at –45 mV. Insert shows the simulated daytime current waveforms injected simultaneously in each of the rod compartments to simulate changes in the dark current caused by the phototransduction processes for a flash intensity of 4.4R*, 44R* or 440R*. Current peak is 7, 8.8 and 10.5 pA for flash intensities of 4.4R*, 44R* or 440R*, respectively. D, simulation of the rod membrane potential (c) as a function of time for different values of the rod–cone gap junction resistance (Rj(r–c)) ranging from 0 to 30,000 GΩ (≈ no coupling). Simulated daytime current for a flash of 440R*, Rmc = Rmr = 2.4 GΩ and Cmr = Cmc = 10 pF. Note that a change in Rj(r–c) does not significantly affect the rod RMP or the amplitude or kinetics of the response. Thus, the rod RMP and light response remain essentially unaffected by strength of rod–cone coupling. E and F, simulation of the rod membrane potential (V) as a function of time for different values of light density using daytime current functions when rods and cones are weakly coupled (Rj(r–c) = 10 GΩ at all 30 rod–cone gap junctions; E) or strongly coupled (Rj(r–c) = 0.3 GΩ at all 30 rod–cone gap junctions; F). The model predicts that when rods and cones are either weakly coupled (E) or strongly coupled (F), the simulated traces essentially mirror the current traces and resemble those recorded during the daytime and depicted in Figs1A and 3A. Rmc = Rmr = 2.4 GΩ and Cmr = Cmc = 10 pF. (G) Simulation of the cone membrane potential (Vc) as a function of time for different values of the rod–cone gap junction resistance (Rj(r–c)) ranging from 0 to 30,000 GΩ (≈ no coupling). Simulated daytime current waveforms for a flash of 440R* were injected simultaneously in each of the rod compartments, Rmc = Rmr = 2.4 GΩ and Cmr = Cmc = 10 pF. The cone photocurrent was ignored in the model (see Methods for details). Note the strong influence of the coupled rods on the cone polarization for Rj(r–c) ≤ 30 GΩ. Overall, the model predicts that the rod polarization and the speed and amplitude of the rod voltage response should remain essentially unaffected by the state of rod–cone coupling.
We simulated the membrane voltage (V) for a rod within the coupled network in response to a current injection mimicking the photocurrent elicited by a full-field flash of light (see Methods for details). We used a daytime current waveform to model the effects of rod–cone coupling on the rod voltage responses in the absence of any potential clock effect on the photocurrent. All the 30 rods electrically connected to the cone received the current injection simultaneously. We assumed that when Rj(r–c) = 30,000 GΩ, Rj(r–c) was high enough so that the recorded rod was electrically isolated from the cone. Under these conditions, the rod RMP was −30 mV and the amplitude of the current-evoked voltage response was close to −25 mV (Fig.2D). Increasing rod–cone coupling, or decreasing Rj(r–c), did not significantly change the rod RMP or the amplitude or kinetics of the response (Fig.2D). Thus, the model indicates that rod–cone coupling results in little attenuation of rod signals during full-field stimulation.
Assuming that Rj(r–c) = 10 GΩ was high enough to represent weak rod–cone electrical coupling, or the daytime state, and that Rj(r–c) = 0.3 GΩ was low enough to represent strong rod–cone electrical coupling, or the nighttime state, we then simulated the rod voltage for current injections mimicking the daytime current responses to flashes of increasing intensity (Fig.2E and F). With Rj(r–c) = 10 GΩ, we observed voltage responses that mirrored those of the simulated current and resembled the rod recordings obtained during the daytime (Fig.2G). With Rj(r–c) = 0.3 GΩ, the voltage responses were essentially undistinguishable from the ones obtained with Rj(r–c) = 10 GΩ in Fig.2E (Fig.2F). These observations support the interpretation of Fig.2D: change in rod–cone coupling does not significantly alter the rod RMP or response wave shape.
The reason why rod polarization and responses are not affected much by the strength of rod–cone coupling probably resides in the peculiar arrangement and connectivity pattern of rods and cones in mouse retina. A single cone is connected to ∼30 rods whereas each rod is connected to only one cone (Tsukamoto et al. 2001; Fig.2A). Because of the large number of rods connected to a cone, strong rod–cone coupling would be expected to drive the cone RMP towards that of the rods. In addition, for a full-field light stimulus, each rod would be receiving the same light flux, and this collective signal presumably would be transmitted very cleanly to the cone when rod–cone coupling is strong. As a result, one might expect that the cone would receive a robust signal from the rods and the full amplitude would be recorded from a single rod. Using the model, we directly tested the possibility that the cone voltage is driven by the rods by simulating the membrane voltage for the cone in response to a current injection in the rods (Fig.2G). When the cone was electrically isolated from the rods (Rj(r–c) = 30,000 GΩ), the cone membrane potential rested at −45 mV and no current-evoked voltage response was observed. Decreasing Rj(r–c) to 10,000 GΩ shifted the cone RMP towards that of the rod, i.e. more positive values, and a small current-evoked voltage response was observed. Further decreasing Rj(r–c) moved the cone RMP closer to that of an isolated rod (−30 mV) and increased the amplitude of the response (Fig.2G). The model indicates that within the range Rj(r–c) is expected to vary between day and night (0.3–10 GΩ), rods efficiently drive the cone RMP and light responses, whereas cones have little or no impact on the rod polarization or light responses.
Overall, the model demonstrates that the rod membrane polarization and response amplitude and kinetics are not affected much by the strength of rod–cone coupling (Fig.2D–F). Thus, the resistive–capacitive model provides weak support for an important role of rod–cone coupling in the linear modulation of the rod polarization and light response. Alternative mechanisms are likely to be at play to shape the rod responses (see Discussion below).
Discussion
Despite the presence of gap junctions between rods in most vertebrates (Bloomfield & Völgyi, 2009), the functional role and regulation of rod electrical coupling has remained largely unresolved. The functional significance of rod coupling has been particularly questioned in mammals, because rod coupling is expected to degrade the SNR and the detection of dim, focused-light stimuli (Tsukamoto et al. 2001; Taylor & Smith, 2004; Okawa & Sampath, 2007). However, recent work has provided undeniable evidence that mammalian rods are electrically coupled (Li et al. 2012).
This study provides evidence that mammalian rod coupling is dynamically regulated. Rod coupling is weak during the day and stronger at night. The coupled state of rods at night does not prevent rods from detecting single photons, even though the amplitude of the single event and the SNR are reduced. However, because of signal averaging in the network of coupled rods, the SNR for a dim (multiphoton) light response is increased. Therefore, the nocturnal increase in rod coupling represents a trade-off between the size of the rod response and the probability of detecting scarce photons. The possible physiological implications of this trade-off are further discussed below.
Our results also indicate that a circadian clock in mouse retina controls the light responses of rod photoreceptors and that the pathway of control includes dopamine, D2-like receptors, and gap junctions in rods. The clock controls the strength of rod coupling to anticipate the change in light intensity which accompanies the break of dawn (Fig.3E). When viewed from this perspective, the circadian clock, and not the dark-adapted state of the retina, is a key regulator of rod function.
The rod gap junction is a primary target of the clock to control rod electrical coupling and the rod light response
We report that the trial-to-trial variability of the rod light response amplitude to dim light flashes is lower at night and that the number of effectively coupled rods (Ne) is increased at night (Fig.5). Together with the increase in rod–tracer coupling and receptive field size observed at night (Figs6 and 7), and the excellent fit of the recording data to our model (Fig.1), our observations provide converging evidence that gap junction coupling between rods is low during the day and increased at night. In addition, our data indicate that the circadian clock controls some aspects of the phototransduction cascade. However, our observations that acute blockade of gap junction coupling with MFA during the subjective night (Fig.7), or during the subjective day in the presence of spiperone (Figs8 and 9), rapidly enlarged the rod response to a daytime state and reduced the rod receptive field size and tracer coupling suggest that the modulation of the photocurrent by the clock is likely to be secondary to modulation of gap junction conductance (this point is further discussed below). Thus, the current results confirm that mammalian rods are electrically coupled and provide insight into the mechanisms regulating rod coupling.
A clock effect on the collecting area of single rods (Ac) is unlikely because an increase in Ac at night would increase the sensitivity of the rods to light at all densities and shift the response–intensity curve to the left (lower light densities), which is not what we observed (Fig.3D; Tables1 and 2). Finally, a role for the circadian rhythm in rod disk shedding (LaVail, 1976) in the rhythmic control of the rod light responses is unlikely based on the fact that pharmacological manipulation of the rod light responses could be obtained on isolated neural retinae separated from the pigmented epithelium (Figs10).
A potential limitation of the present analysis is that it rests on the measurements obtained from patch-clamp recording of single rods. Recording from pairs of neighbouring rods would yield direct measurements of the rod–rod junction conductance (Gj). Yet our measurements of the mouse rod input resistance (Ri) and the demonstration that Ri changes between day and night (Figs6C and 8G) can be used to make an estimate of Gj. The input conductance (Gi, with Gi = 1/Ri) reflects both the junction conductance (Gj) and the membrane conductance (Gm). Assuming that Gm of dark-adapted mouse rods does not change significantly between the day and night (as suggested by the fact that MFA increases Gi to the same level day and night; Fig.8G), we can set an upper limit on Gj as the difference between Gi measured at night (Gi-N) and during the day in the presence of MFA (Gi-D + MFA). From the averaged data illustrated in Fig.8G, we can conclude Gj < Gi-N – Gi-D + MFA or Gj < (1/1.8) – (1/2.9) or Gj < 0.55 – 0.35 or Gj < 200 pS. These estimates are in good agreement, though slightly lower, than the average values of Gj between guinea-pig rods (386 pS; Li et al. 2012) and between ground squirrel cones (217 pS; Li & DeVries, 2004).
The nature of the connexin (Cx) expressed in mammalian rods is unknown (Bloomfield & Völgyi, 2009; Li et al. 2013), but it has been clearly identified as Cx35, which is the orthologue of mammalian Cx36, in lower vertebrates (Zhang & Wu, 2004; Bloomfield & Völgyi, 2009). Cx35/36 is expressed in the cones in all vertebrates studied so far, including the mouse (Bloomfield & Völgyi, 2009; Li et al. 2013) and primate (O'Brien et al. 2012). Cx36 has the lowest unitary conductance of all the Cxs at ∼15 pS (Srinivas et al. 1999; Bloomfield & Völgyi, 2009; Völgyi et al. 2013). A value of 200 pS for Gj translates into 200/15 = 14 open Cx36 channels. Assuming that ∼1% of the channels are open at any time (Teubner et al. 2000), 14 × 100 = 1400 channels would be required. If an entire plaque were composed of Cx36 channels at a density of ∼10,000 channels μm−2 (Caspar et al. 1977), 1400 channels would form a single gap junction plaque of area ∼0.14 μm2. Considering that each rod is electrically coupled to 1–4 neighbouring rods (Raviola & Gilula, 1973; Tsukamoto et al. 2001), our estimates of the size of a gap junction plaque between 2 coupled rods range from 0.035 to 0.14 μm2. These values are likely to be overestimated as each rod is also coupled to 1 cone (Tsukamoto et al. 2001, this study). Thus, calculation of gap junction size based on estimated Gj predicts small plaques and is consistent with results from electron microscopy (Raviola & Gilula, 1973; Tsukamoto et al. 2001) and immunohistochemical (O'Brien et al. 2012; Li et al. 2013) studies.
Do cones contribute to the circadian regulation of the rod light response?
Although rod–cone interactions are well established and convey fundamental properties of vision (Bloomfield & Dacheux, 2001; Field et al. 2005), the influence of cone photoreceptors on the rod light response remains largely unknown. Our data raise the possibility that rod–cone coupling may modulate the rod light response at night. Firstly, our tracer coupling data clearly indicate that mouse cones are tracer-coupled to rods (Fig.7D and J), in agreement with previously published work (Ribelayga et al. 2008; Li et al. 2013). Secondly, the hyperpolarization of the rods at night is consistent with strong rod–cone coupling because cones are much more hyperpolarized at rest than rods (Cangiano et al. 2012).
The simple ‘perfect coupling’ model is consistent with the well-accepted view that under full-field illumination, the effect of rod coupling should be maximal at intensities that deliver less than 1R* and minimal at intensities that deliver more than 1R*. This is because when light intensity elicits less than 1R*, the single-photon signal is averaged within the network of coupled rods. When light intensity is ≥1R*, the full-field stimulus becomes homogeneous, the rods are isopotential, and no net current should flow from rod to rod through gap junctions during illumination (Tessier-Lavigne & Attwell, 1988). However, as shown in Fig.3B and C, the maximum amplitude of the rod response (Vmax) measured at night or subjective night was ∼50% smaller than that measured in the day or subjective day (Fig.3C; Tables3 and 4), a result that cannot be explained only by the increase in rod–rod coupling (Fig.1J and K). In fact, the rod responses we recorded at night or subjective night behaved as if the light stimulus was spatially restricted (Fig.1J and K). Yet, as shown in Fig.7B, blocking the gap junctions with 50 μm MFA at night was sufficient to increase amplitude and induce a daytime state. In contrast, 50 μm MFA had minimal effect on the rod light responses when applied during the day (Fig.7A). Collectively, the effects of MFA indicate that the modulation of electrical coupling is key to the control of the rod light response amplitude.
One possibility to explain these surprising results is that rod–cone coupling affects the rod response to light. That is, the decrease in the rod Vmax at night may reflect the influence of rod–cone coupling because cones are less sensitive to light, have a higher threshold, and may act as ‘sinks’. In addition, because mouse cones rest at a much more hyperpolarized potential than rods (Cangiano et al. 2012), cones may hyperpolarize the rods at night and this in turn may affect the rod light response. The increased polarization of the rod membrane at night we report here is consistent with this possibility. However, in a simplified resistive–capacitive model (Fig.2), we calculated that strong rod–cone coupling would have little, if any, influence on the polarization of the rods or the amplitude of the rod voltage response. In addition, the model demonstrates that the properties of the resistive–capacitive network do not slow the rod response kinetics. Thus, the resistive–capacitive model cannot produce the major effects of the lower amplitude and wave shape of the rod response at night, indicating that rod–cone coupling does not play a major role in the linear modulation of the rod light response and that additional mechanisms are likely to be at play.
Does the clock control the outer segment current?
There is excellent quantitative agreement between the change in the current responses and the change in the voltage responses recorded in rods during subjective day or subjective night (Figs3 and 4). That is, the difference in the amplitude and time course of these currents appears to reproduce the major fraction of the change in amplitude and time course of voltage responses. It is therefore possible that the photocurrent we recorded at night is, despite the limitations of the patch-clamp technique, slower and of lower amplitude than that recorded during the day. However, increased electrical coupling at night should increase the amplitude of the current response in the recorded rod, and not decrease it. The reasoning is as follows. A voltage clamp located at the inner segment separates the outer segment current input on one side, from gap junction current inputs at the rod terminal on the other side; therefore the measured current due to the outer segment will not be affected by the extent of electrical coupling. The current arising from the gap junction-coupled cone and rods obviously will depend on the strength of coupling, but importantly it will augment the light-evoked current measured at the inner segment. The augmentation occurs because the coupled photoreceptors will not be well-clamped, and therefore during a full-field light stimulus the coupled cone–rods will hyperpolarize relative to the recorded rod. This relative hyperpolarization will induce a net outward current through the gap junctions in the recorded rod, and this outward current will add to the light-evoked outward current produced in the outer segment of the rod. Thus, coupling should increase the amplitude of the light response recorded by a voltage clamp at the inner segment, and therefore the large reduction in the light-evoked current (Fig.3) suggests a large circadian effect on the outer segment current, which in turn will produce a similar change in the light-evoked voltage response.
Whether the clock and/or dopamine directly control some of the elements of the transduction cascade or whether the modulation of the photocurrent is secondary to the modulation of rod–rod and/or rod–cone coupling remains to be determined. Indeed, the hyperpolarization of the rods at night is expected to change the level of internal calcium or some other molecule. Such a change might lead to a longer time constant for rhodopsin activation and/or calcium feedback to complete recovery from the light response (see Burns & Pugh, 2010, for review). Other mechanisms, such as changes in proteins that regulate the timing of response recovery may also be involved (Burns & Pugh, 2010). In addition, the increase in the duration of the near-peak (saturated) plateau at night is a highly non-linear transformation. This non-linearity could be caused by one or more of the components of the transduction cascade being driven above the level necessary to shut down the light-modulated ion channel, with the recovery phase components being unable to keep up. As a result the current through the light-modulated channel stays turned off for a longer time than for the weaker light fluxes. Also, modulation of voltage-gated channels may not be ruled out.
Although we cannot rule out the possibility that the clock uses dopamine to directly modulate some elements of the phototransduction cascade or some other mechanism, the absence of a noticeable effect of spiperone on the rod light responses in the presence of the gap junction blocker MFA indicates that this is unlikely (Figs8B and 9).
Further analysis of the involvement of electrical coupling in the smaller rod response and its wave shape at night will require a genetic approach, which we are currently developing. In particular we are planning to use a mouse model that lacks Cx36. Cx36 is clearly expressed in cones in mouse, but it is still unclear whether it is expressed in rods as well (Bloomfield & Völgyi, 2009). If the rod connexin is not Cx36, then Cx36−/− mice will still be useful to study the behaviour of the rods in the absence of the cone influence. Our recordings of the current light response under voltage clamp (Figs3 and 4), with all the limitations of potential space clamp problems, suggests a modulation of the photocurrent by the clock. The lack of electrical coupling between rods and cones that is expected in Cx36−/− mice will create favourable space clamp conditions to study the regulation of the rod photocurrent by the clock and dopamine in detail.
The Cx36−/− line is on a C57Bl/6 J background. Our preliminary data indicate that rod coupling is constitutively weak in C57Bl/6 J (N. Jin & C. P. Ribelayga, unpublished data). As a consequence, we are in the process of moving the null Cx36 allele to a CBA/CaJ background. Nonetheless, application of spiperone increases rod tracer coupling and decreases the amplitude and speed of the rod responses in C57Bl/6J mice, and we have observed that neither spiperone (n = 3) nor MFA (n = 3) has an effect on rod tracer coupling or the rod light responses in Cx36−/−/C57Bl/6J animals (N. Jin & C. P. Ribelayga, unpublished data). These preliminary data support the view that spiperone and MFA do not directly affect the kinetics of the photocurrent and that the modulation of the photocurrent and/or other regulators of the rod response by the clock/dopamine is likely to be a consequence of the change in electrical coupling.
Overall, our data demonstrate that rod electrical coupling and light responses are controlled by a circadian clock and dopamine. Mathematical modelling of the mouse photoreceptor network suggests that the properties of the resistive–capacitive circuit are not a major player in the control of the rod light responses. The mechanisms that contribute to the changes in amplitude and time course of the rod responses during the circadian cycle remain to be determined in future studies.
What is the functional importance of rod electrical coupling at night?
Although our study proposes a mechanism that controls rod coupling, much remains to be learned about the impact of rod coupling on signal processing in the retina at night. Our recordings show that modest coupling among mouse rods does not prevent rods from detecting single photons. In addition, the probability for a single rod to detect a single-photon response is increased by electrical coupling because the single-photon signal in one rod quickly spreads to the neighbouring cells through gap junctions, thus indicating that the single-photon response can propagate in the rod network. However, whether low-amplitude single-photon signals can be read out of the photoreceptor layer at night remains to be determined.
Under low scotopic conditions, rod signals are primarily conveyed to rod bipolar cells and then to cone bipolar cells and ganglion cells via AII amacrine cells (Bloomfield & Dacheux, 2001; Field et al. 2005). Rod–rod bipolar cell signal transfer is highly non-linear: a threshold mechanism filters out rod noise and selectively passes rod signals resulting from rare photon events (Field et al. 2005). Yet the efficiency of this mechanism is low and results in the elimination of a large fraction of the rod single-photon responses (Field & Rieke, 2002b2002b; Berntson et al. 2004). If the threshold mechanism of the rod–rod bipolar cell synapse were stationary, and not determined dynamically by mechanisms that sense the amplitude of the elementary responses and/or track the time of day, the reduction of the size of the rod response due to coupling at night would probably result in greater rejection by the threshold.
Could the rod–rod bipolar synapse adapt with time of day to adjust the non-linear threshold? On the one hand, studies based on the genetic manipulation of the rod response support the notion that the non-linear threshold mechanism at the rod–rod bipolar synapse is not controlled dynamically, at scotopic light levels (Okawa et al. 2010; Long et al. 2013). On the other hand, the discrepancy in the measurements of the synaptic gain between studies may indicate otherwise. Indeed, the height of the threshold has been estimated as low as 0.85 (Berntson et al. 2004) and as high as 1.2 (Field & Rieke, 2002b2002b) times the amplitude of the single-photon signal, resulting in rejection rates of 40% and 75%, respectively. Thus, to cope with the decrease in the single-photon response amplitude at night, the threshold would have to adjust and be 0.50 times below the amplitude of the signal recorded during the day (2.6 mV / 1.2 mV≈ 50%). We argue that it is possible that the rod–rod bipolar cell synaptic threshold mechanism is lowered at night in order to increase responsiveness to smaller presynaptic voltages. The lack of such plasticity would represent an exception to one of the most fundamental properties of neural circuits.
However, even if the threshold mechanism is not controlled dynamically, an increase in rod coupling may still be beneficial for the transmission of single photon events. Because of coupling and synaptic convergence (each rod bipolar cell contacts approximately 20–50 rods; Bloomfield & Dacheux, 2001; Taylor & Smith, 2004; Field et al. 2005), the coordinated response to a single photon in a network of coupled rods may in fact improve the reliability of the transmission of dim rod responses to rod bipolar cells by increasing the number of trials to pass the rod signal, even with a low probability of success at each individual synapse. Theoretical considerations and mathematical calculations have led to opposite conclusions as to whether rod coupling is detrimental (Taylor & Smith, 2004; Hornstein et al. 2005; Li et al. 2012) or beneficial (Tessier-Lavigne & Attwell, 1988) to the transmission of an elementary rod response to the rod bipolar cell and/or to the absolute visual threshold. The current consensus in the field is that coupling (along with a threshold non-linearity at the rod–rod bipolar synapse) reduces the amplitude of the single-photon response and lowers its SNR. Yet several lines of evidence argue in favour of a beneficial effect of rod coupling in dim light detection and/or a dynamic regulation of the rod–rod bipolar cell synaptic transfer with the time of day. For instance, the amplitude of the b-wave of the mouse scotopic electro-retinogram, which mostly reflects the activity of the rod bipolar cells, is increased at night (Baba et al. 2009). Also, the absolute visual threshold in humans follows a circadian rhythm and is decreased at night (Bassi & Powers, 1986). Future work will clarify the impact of rod coupling on the activity of second-order neurons in mouse retina. In particular, the activity of the rod–rod bipolar cell synapse will have to be evaluated at night.
The strength of rod coupling in mouse may represent a general principle of retinal design in mammals. Our estimate of the effective pool size of coupled rods (Ne) in the mouse retina (range 1–5.3) is within the range of those measured in the primate (range 1–5.9; Hornstein et al. 2005) and guinea-pig (range 1–12; Li et al. 2012) retinae. Similarly, the size of the pool of tracer-coupled rods in the mouse retina (1–26; this study) compares well with those in the macaque (range 1–10; Hornstein et al. 2005) and guinea-pig (range 1–21; Li et al. 2012) retinae. Based on these examples, it is noteworthy that the strength of rod coupling in mammals appears weak relative to lower vertebrates. Salamander rods, for instance, have Ne >> 10, and while single photons are able to elicit a photocurrent in the rod outer segment (Baylor et al. 1979), the low SNR prevents rods from transmitting single events (Zhang & Wu, 2004, 2005). We show here that the nocturnal increase in rod coupling in mouse retina does not prevent rods from detecting single photons and transmitting the signal to other coupled rods (Fig.5). Thus, an overall decrease in the strength of rod coupling during the evolution of vertebrates may reflect an adaptive strategy to increase visual sensitivity as mammals passed through a nocturnal ‘bottleneck’ (Gerkema et al. 2013).
Circadian clock control of rod coupling
The circadian clock regulation of retinal function is a robust mechanism that controls retinal processing of visual information according to the time of day (Iuvone et al. 2005; Storch et al. 2007; Mangel & Ribelayga, 2010; McMahon et al. 2014). Although it has been clearly established that the melatonin and dopamine systems in the retina are controlled by circadian clocks and play key roles in the circadian control of retinal function, their impact on retinal circuits is not well understood (Iuvone et al. 2005; Storch et al. 2007; Mangel & Ribelayga, 2010; McMahon et al. 2014). Previous work has shown that rod–cone coupling is regulated by a circadian clock and D2-like dopamine receptors in vertebrates (Krizaj et al. 1998; Ribelayga et al. 2008; Li et al. 2009, 2013; Ribelayga & Mangel, 2010). Our observations that a D2-like agonist or antagonist can manipulate the rod light response and coupling depending on the time of day (Fig.8) strongly support a role for dopamine in the circadian regulation of rod electrical coupling. Altogether, our studies and others are consistent with the view that dopamine is a daytime effector of a circadian clock that controls photoreceptor coupling in vertebrates in general. Conditional deletion of the key circadian clock component BMAL1 (Storch et al. 2007), or of tyrosine hydroxylase, the rate-limiting enzyme in dopamine synthesis (Jackson et al. 2012) in the retina, or of the D2/4 dopamine receptors (Nir et al. 2002) results in profound defects in retinal function, such as a decrease in light adaptation and sensitivity. As the absolute threshold for human vision varies over the course of the day (Bassi & Powers, 1986), it is likely that perturbations of this clock-controlled mechanism over retinal function in humans may have long-term consequences on vision in dim light. Therefore the dependence of the rod electrical coupling on time of day should be a key consideration in our efforts to understand vision under dim light.
Summary
We find that, in mouse retina, rod photoreceptors are more coupled at night compared to day. The nocturnal increase in rod coupling reduces the amplitude of the single-photon response and lowers its SNR, which is likely to reduce the probability of detection by downstream neurones. Yet strong rod coupling is expected to enhance the detection of multiple photons by post-receptor neurones because the SNR of an extended visual object is governed by the spatial correspondence between the object and the space constant of the electrical coupling (Tessier-Lavigne & Attwell, 1988).
The mouse has a larger ratio of lens diameter/postnodal distance, i.e. numerical aperture, than other mammalian species previously studied, including humans (Geng et al. 2011). This large numerical aperture gives the mouse rod a greater photon flux at a given scotopic background. Essentially, mouse rods see a multi-photon signal at some backgrounds where rods in another species only see single-photon signals. Thus, the advantage to rod coupling that we report here, that is, to sum and average signals from several rods, may be particularly helpful for mice in dim light.
The control of the strength of electrical coupling between the elements forming a neural circuit is a powerful means to modify the properties of that circuit (Hormuzdi et al. 2004; Pereda et al. 2013). Functional neuronal circuits underlie behaviours, many aspects of which are controlled by circadian clocks (Mohawk et al. 2012). Our observations suggest that electrical coupling between rods does not follow an ‘all-or-none’ principle. Rather, our data reflect a spectrum of coupling strengths. Rod electrical coupling is weak during the day and stronger at night. Dopaminergic drugs exaggerate these effects because a high dose of agonist will saturate the receptors beyond the daytime level of dopamine, and an antagonist may block residual trace amounts of dopamine present at night. MFA blocks at a different regulatory site, emphasizing that gap junctions are the end-point of the signalling pathway. Circadian clock regulation of electrical coupling may be a widespread mechanism for fine-tuning neural circuit properties and behaviour.
Acknowledgments
We thank Drs Stephen C. Massey, Stephen L. Mills, Iris Fahrenfort, Wei Li, Samuel M. Wu, John O'Brien, and John E. Dowling for critical discussion and reading of the manuscript. We thank Drs Gladys Ko and Zhijing Zhang for helping with the experiments. We thank Dr Kimberly A. Mankiewicz for editing.
Glossary
- CT
circadian time
- COS
cone outer segment
- Cx
connexin
- Cx36
connexin36
- DC
direct current
- MFA
meclofenamic acid
- N
night
- ns
not significant
- PBS
phosphate-buffered saline
- PNA
peanut agglutinin
- Quin
quinpirole
- RMP
resting membrane potential (in mV)
- ROS
rod outer segment
- SD
subjective day
- SD1
subjective day-1
- SD2
subjective day-2
- SN
subjective night
- SNR
signal-to-noise ratio
- Spip
spiperone
- ZT
zeitgeber time
Additional information
Competing interests
None declared.
Author contributions
Conception and design of the experiments: N.G. and C.P.R. Collection, analysis and interpretation of the data: N.G., A.Z.C. and C.P.R. Network modelling: A.Z.C., P.J.M. and C.P.R. Drafting of the article and revising it critically for important intellectual content: C.P.R. All authors have read and approved the final submission.
Funding
This work was supported by the National Institutes of Health (EY018640, EY010608, OD010768), the Hermann Eye Fund, and a Challenge Grant to The University of Texas Medical School at Houston from Research to Prevent Blindness.
References
- Asteriti S, Gargini C. Cangiano L. Mouse rods signal through gap junctions with cones. eLife. 2014;3:e01386. doi: 10.7554/eLife.01386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Attwell D, Wilson M. Wu SM. A quantitative analysis of interactions between photoreceptors in the salamander (Ambystoma) retina. J Physiol. 1984;352:703–737. doi: 10.1113/jphysiol.1984.sp015318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baba K, Pozdeyev N, Mazzoni F, Contreras–Alcantara S, Liu C, Kasamatsu M, Martinez–Merlos T, Strettoi E, Iuvone PM. Tosini G. Melatonin modulates visual function and cell viability in the mouse retina via the MT1 melatonin receptor. Proc Natl Acad Sci USA. 2009;106:15043–15048. doi: 10.1073/pnas.0904400106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassi CJ. Powers MK. Daily fluctuations in the detectability of dim lights by humans. Physiol Behav. 1986;38:871–877. doi: 10.1016/0031-9384(86)90056-9. [DOI] [PubMed] [Google Scholar]
- Baylor DA, Fuortes MG. O'Bryan PM. Electrical signaling in vertebrate photoreceptors. J Physiol. 1971;214:265–294. [Google Scholar]
- Baylor DA, Lamb TD. Yau KW. The membrane current of single rod outer segments. J Physiol. 1979;288:589–611. [PMC free article] [PubMed] [Google Scholar]
- Bennett VL. Zukin RS. Electrical coupling and neuronal synchronization in the mammalian brain. Neuron. 2004;41:495–511. doi: 10.1016/s0896-6273(04)00043-1. [DOI] [PubMed] [Google Scholar]
- Berntson A, Smith RG. Taylor WR. Transmission of single photon signals through a binary synapse in the mammalian retina. Vis Neurosci. 2004;21:693–702. doi: 10.1017/S0952523804215048. [DOI] [PubMed] [Google Scholar]
- Bloomfield SA. Dacheux RF. Rod vision: pathways and processing in the mammalian retina. Prog Retin Eye Res. 2001;20:351–384. doi: 10.1016/s1350-9462(00)00031-8. [DOI] [PubMed] [Google Scholar]
- Bloomfield SA. Völgyi B. The diverse functional roles and regulation of neuronal gap junctions in the retina. Nat Rev Neurosci. 2009;10:495–506. doi: 10.1038/nrn2636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burns ME. Arshavsky VY. Beyond counting photons: trials and trends in vertebrate visual transduction. Neuron. 2005;48:387–401. doi: 10.1016/j.neuron.2005.10.014. [DOI] [PubMed] [Google Scholar]
- Burns ME. Pugh EN., Jr Lessons from photoreceptors: Turning off G–protein signaling in living cell. Physiology. 2010;25:72–84. doi: 10.1152/physiol.00001.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cangiano L, Asteriti S, Cervetto L. Gargini C. The photovoltage of rods and cones in the dark-adapted mouse retina. J Physiol. 2012;590:3841–3855. doi: 10.1113/jphysiol.2011.226878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carter-Dawson LD. LaVail MM. Rods and cones in the mouse retina. I. Structural analysis of cell regeneration using light and electron microscopy. J Comp Neurol. 1979;188:245–262. doi: 10.1002/cne.901880204. [DOI] [PubMed] [Google Scholar]
- Caspar DL, Goodenough DA, Makowski L. Phillips WC. Gap junction structures. I. Correlated electron microscopy and x–ray diffraction. J Cell Biol. 1977;74:605–628. doi: 10.1083/jcb.74.2.605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeVries SH, Qi X, Smith RG, Makous W. Sterling P. Electrical coupling between mammalian cones. Curr Biol. 2002;12:1900–1907. doi: 10.1016/s0960-9822(02)01261-7. [DOI] [PubMed] [Google Scholar]
- Fain GL. Quantum sensitivity of rods in the toad retina. Science. 1975;187:838–841. doi: 10.1126/science.1114328. [DOI] [PubMed] [Google Scholar]
- Field GD. Rieke F. Mechanisms regulating variability of the single photon responses of mammalian rod photoreceptors. Neuron. 2002a;35:733–747. doi: 10.1016/s0896-6273(02)00822-x. [DOI] [PubMed] [Google Scholar]
- Field GD. Rieke F. Nonlinear signal transfer from mouse rods to bipolar cells and implications for visual sensitivity. Neuron. 2002b;34:773–785. doi: 10.1016/s0896-6273(02)00700-6. [DOI] [PubMed] [Google Scholar]
- Field GD, Sampath AP. Rieke F. Retinal processing near absolute threshold: from behavior to mechanism. Annu Rev Physiol. 2005;67:491–514. doi: 10.1146/annurev.physiol.67.031103.151256. [DOI] [PubMed] [Google Scholar]
- Geng Y, Schery LA, Sharma R, Dubra A, Ahmad K, Libby RT. Williams DR. Optical properties of the mouse eye. Biomed Opt Express. 2011;2:717–738. doi: 10.1364/BOE.2.000717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerkema MP, Davies WIL, Foster RG, Menaker M. Hut RA. The nocturnal bottleneck and the evolution of activity patterns in mammals. Proc Biol Sci. 2013;280:20130508. doi: 10.1098/rspb.2013.0508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hormuzdi SG, Filippov MA, Mitropoulou G, Monyer H. Bruzzone R. Electrical synapses: a dynamic signaling system that shapes the activity of neuronal networks. Biochim Biophys Acta. 2004;1662:113–137. doi: 10.1016/j.bbamem.2003.10.023. [DOI] [PubMed] [Google Scholar]
- Hornstein EP, Verweij J, Li PH. Schnapf JL. Gap–junctional coupling and absolute sensitivity of photoreceptors in macaque retina. J Neurosci. 2005;25:11201–11209. doi: 10.1523/JNEUROSCI.3416-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iuvone PM, Tosini G, Pozdeyev N, Haque R, Klein DC. Chaurasia SS. Circadian clocks, clock networks, arylalkylamine N–acetyltransferase, and melatonin in the retina. Prog Retin Eye Res. 2005;24:433–456. doi: 10.1016/j.preteyeres.2005.01.003. [DOI] [PubMed] [Google Scholar]
- Jackson CR, Ruan GX, Aseem F, Abey J, Gamble K, Stanwood G, Palmiter RD, Iuvone PM. McMahon DG. Retinal dopamine mediates multiple dimensions of light–adapted vision. J Neurosci. 2012;32:9359–9368. doi: 10.1523/JNEUROSCI.0711-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeon CJ, Strettoi E. Masland RH. The major cell populations of the mouse retina. J Neurosci. 1998;18:8936–8946. doi: 10.1523/JNEUROSCI.18-21-08936.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krizaj D, Gabriel R, Owen WG. Witkovsky P. Dopamine D2 receptor–mediated modulation of rod–cone coupling in the Xenopus retina. J Comp Neurol. 1998;398:529–538. [PMC free article] [PubMed] [Google Scholar]
- Lamb TD. Simon EJ. The relation between intercellular coupling and electrical noise in turtle photoreceptors. J Physiol. 1976;263:257–286. doi: 10.1113/jphysiol.1976.sp011631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LaVail MM. Rod outer segment disk shedding in rat retina: relationship to cyclic lighting. Science. 1976;194:1071–1074. doi: 10.1126/science.982063. [DOI] [PubMed] [Google Scholar]
- Li H, Chuang AZ. O'Brien J. Photoreceptor coupling is controlled by connexin35 phosphorylation in zebrafish retina. J Neurosci. 2009;29:15178–15186. doi: 10.1523/JNEUROSCI.3517-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, Zhang Z, Blackburn MR, Wang SW, Ribelayga CP. O'Brien J. Adenosine and dopamine receptors co-regulate photoreceptor coupling via gap junction phosphorylation in mouse retina. J Neurosci. 2013;33:3135–3150. doi: 10.1523/JNEUROSCI.2807-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li PH, Verweij J, Long JH. Schnapf JL. Gap–junctional coupling of mammalian rod photoreceptors and its effect on visual detection. J Neurosci. 2012;32:3552–3562. doi: 10.1523/JNEUROSCI.2144-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W. DeVries SH. Separate blue and green cone networks in the mammalian retina. Nat Neurosci. 2004;7:751–756. doi: 10.1038/nn1275. [DOI] [PubMed] [Google Scholar]
- Li W, Chen S. DeVries SH. A fast rod photoreceptor signalling pathway in the mammalian retina. Nat Neurosci. 2010;13:414–416. doi: 10.1038/nn.2507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long JH, Arshavsky VY. Burns ME. Absence of regulation by phosducin in retinal slices. PLoS One. 2013;8:e83970. doi: 10.1371/journal.pone.0083970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyubarsky AL. Pugh EN., Jr Recovery phase of the murine rod photoresponse reconstructed from electroretinographic recordings. J Neurosci. 1996;16:563–571. doi: 10.1523/JNEUROSCI.16-02-00563.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mangel SC. Ribelayga C. Comparative eye: The circadian clock in the retina regulates rod and cone pathways. In: Dana R, editor; Dartt DA, Besharse JC, editors. The Encyclopedia of the Eye. Vol. 1. Oxford: Elsevier; 2010. pp. 283–289. [Google Scholar]
- McMahon DG, Iuvone PM. Tosini G. Prog Retin Eye Res. 2014;39:58–76. doi: 10.1016/j.preteyeres.2013.12.001. Circadian organization of the mammalian retina: From gene regulation to physiology and diseases. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mohawk JA, Green CB. Takahashi JS. Central and peripheral circadian clocks in mammals. Annu Rev Neurosci. 2012;35:445–462. doi: 10.1146/annurev-neuro-060909-153128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naarendorp F, Esdaille TM, Banden SM, Andrews–Labenski J, Gross OP. Pugh EN., Jr Dark light, rod saturation, and the absolute and incremental sensitivity of mouse cone vision. J Neurosci. 2010;30:12495–12507. doi: 10.1523/JNEUROSCI.2186-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naka KI. Rushton WAH. The generation and spread of S–potentials in fish (Cyprinidae. J Physiol. 1967;192:437–461. doi: 10.1113/jphysiol.1967.sp008308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nir I, Harrison JM, Haque R, Low MJ, Grandy DK, Rubinstein M. Iuvone PM. Dysfunctional light-evoked regulation of cAMP in photoreceptors and abnormal retinal adaptation in mice lacking dopamine D4 receptors. J Neurosci. 2002;22:2063–2073. doi: 10.1523/JNEUROSCI.22-06-02063.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Brien JJ, Chen X, Macleish PR, O'Brien J. Massey SC. Photoreceptor coupling mediated by connexin36 in the primate retina. J Neurosci. 2012;32:4675–4687. doi: 10.1523/JNEUROSCI.4749-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okawa H, Miyagishima KJ, Arman AC, Hurley JB, Field GD. Sampath AP. Optimal processing of photoreceptor signals is required to maximize behavioural sensitivity. J Physiol. 2010;588:1947–1960. doi: 10.1113/jphysiol.2010.188573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okawa H. Sampath AP. Optimization of single-photon response transmission at the rod-to-rod bipolar synapse. Physiology (Bethesda) 2007;22:279–286. doi: 10.1152/physiol.00007.2007. [DOI] [PubMed] [Google Scholar]
- Pan F, Mills SL. Massey SC. Screening of gap junction antagonists on dye coupling in the rabbit retina. Vis Neurosci. 2007;24:609–628. doi: 10.1017/S0952523807070472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pereda AE, Curti S, Hoge G, Cachope R, Flores CE. Rash JE. Gap junction–mediated electrical transmission: Regulatory mechanisms and plasticity. Biochim Biophys Acta. 2013;1828:134–146. doi: 10.1016/j.bbamem.2012.05.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Publio R, Oliveira RF. Roque AC. A computational study on the role of gap junctions and rod Ih conductance in the enhancement of the dynamic range of the retina. PLoS One. 2009;4:e6970. doi: 10.1371/journal.pone.0006970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raviola E. Gilula NB. Gap junctions between photoreceptor cells in the vertebrate retina. Proc Natl Acad Sci USA. 1973;70:1677–1681. doi: 10.1073/pnas.70.6.1677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ribelayga C, Cao Y. Mangel SC. The circadian clock in the retina regulates rod–cone coupling. Neuron. 2008;59:790–801. doi: 10.1016/j.neuron.2008.07.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ribelayga C. Mangel SC. Identification of a circadian clock–controlled neural pathway in the rabbit retina. PLoS One. 2010;5:e11020. doi: 10.1371/journal.pone.0011020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneeweis DM. Schnapf JL. Noise and light adaptation in rods of the macaque monkey. Vis Neurosci. 2000;17:659–666. doi: 10.1017/s0952523800175017. [DOI] [PubMed] [Google Scholar]
- Srinivas M, Rozental R, Kojima T, Dermietzel R, Mehler M, Condorelli DF, Kessler JA. Spray DC. Functional properties of channels formed by the neuronal gap junction protein connexin36. J Neurosci. 1999;19:9848–9855. doi: 10.1523/JNEUROSCI.19-22-09848.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storch KF, Paz C, Signorovitch J, Raviola E, Pawlyk B, Li T. Weitz CJ. Intrinsic circadian clock of the mammalian retina: importance for retinal processing of visual information. Cell. 2007;130:730–741. doi: 10.1016/j.cell.2007.06.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor WR. Smith RG. Transmission of scotopic signals from the rod to rod–bipolar cell in the mammalian retina. Vision Res. 2004;44:3269–3276. doi: 10.1016/j.visres.2004.07.043. [DOI] [PubMed] [Google Scholar]
- Tessier-Lavigne M. Attwell D. The effect of photoreceptor coupling and synapse nonlinearity on signal:noise ratio in early visual processing. Proc R Soc Lond B Biol Sci. 1988;234:171–197. doi: 10.1098/rspb.1988.0043. [DOI] [PubMed] [Google Scholar]
- Teubner B, Degen J, Söhl G, Güldenagel M, Bukauskas FF, Trexler EB, Verselis VK, De Zeeuw CI, et al. Functional expression of the murine connexin 36 gene coding for a neuron–specific gap junctional protein. J Membr Biol. 2000;176:249–262. doi: 10.1007/s00232001094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsukamoto Y, Morigiwa K, Ueda M. Sterling P. Microcircuits for night vision in mouse retina. J Neurosci. 2001;21:8616–8623. doi: 10.1523/JNEUROSCI.21-21-08616.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Völgyi B, Kovacs–Oller T, Atlasz T, Wilhelm M. Gabriel R. Gap junctional coupling in the vertebrate retina: variations on one theme? Prog Retin Eye Res. 2013;34:1–18. doi: 10.1016/j.preteyeres.2012.12.002. [DOI] [PubMed] [Google Scholar]
- Yang XL. Wu SM. Modulation of rod–cone coupling by light. Science. 1989;244:352–354. doi: 10.1126/science.2711185. [DOI] [PubMed] [Google Scholar]
- Zhang J. Wu SM. Connexin35/36 gap junction proteins are expressed in photoreceptors of the tiger salamander retina. J Comp Neurol. 2004;470:1–12. doi: 10.1002/cne.10967. [DOI] [PubMed] [Google Scholar]
- Zhang J. Wu SM. Physiological properties of rod photoreceptor electrical coupling in the tiger salamander retina. J Physiol. 2005;564:849–862. doi: 10.1113/jphysiol.2005.082859. [DOI] [PMC free article] [PubMed] [Google Scholar]


