A Bayesian Graphical Model for Integrative Analysis of TCGA Data

Abstract

We integrate three TCGA data sets including measurements on matched DNA copy numbers (C), DNA methylation (M), and mRNA expression (E) over 500+ ovarian cancer samples. The integrative analysis is based on a Bayesian graphical model treating the three types of measurements as three vertices in a network. The graph is used as a convenient way to parameterize and display the dependence structure. Edges connecting vertices infer specific types of regulatory relationships. For example, an edge between M and E and a lack of edge between C and E implies methylation-controlled transcription, which is robust to copy number changes. In other words, the mRNA expression is sensitive to methylational variation but not copy number variation. We apply the graphical model to each of the genes in the TCGA data independently and provide a comprehensive list of inferred profiles. Examples are provided based on simulated data as well.

I. Introduction

Gene expression is a critical genetic process in which DNA is transcribed to RNA. Perturbation of transcription directly affects mRNA expression and hence the subsequent protein production, leading to pathological states. Genetic variations such as copy-number variations (CNVs) and DNA methylations frequently contribute to disrupted gene expression. CNVs result in an abnormal number of copies of DNA and thus change the gene expression level and associated phenotypes. For example, a higher copy number of CCL3L1 has been associated with lower susceptibility to HIV infection [1], and a low copy number of FCGR3B can increase susceptibility to systemic lupus erythematosus and similar inflammatory autoimmune disorders [2]. DNA methylation is a biochemical modification that adds a methyl group to the 5 position of the cytosine pyrimidine ring or the number 6 nitrogen of the adenine purine ring. There is strong evidence that abnormal hypermethylation at the gene promoter region results in transcriptional silencing of tumor suppressor genes. Also, aberrant DNA methylation patterns have been associated with a large number of human malignancies such as cancer, lupus, and a range of birth defects [3]. Therefore, elucidating tumor-specific methylation changes will shed light on potential clinical applications in cancer diagnosis, prognosis and therapeutics [4].

Current literature mainly focuses on the pair-wise integration, between CNVs and mRNA or between methylation and mRNA. Bussey et al. [5] computed Pearson’s correlation coefficients and tested the significance of correlations using false discovery rate (FDR) control. Waaijenborg et al. [6] proposed a penalized canonical correlation analysis to study genome-wide association between DNA copy number and mRNA expression. Menezes et al. [7] modeled the relationship of DNA copy number and mRNA expression by a linear model based on a modified correlation coefficient and an explorative Wilcoxon test. Choi et al. [8] described a Bayesian double-layered mixture model which directly modeled the stochastic nature of CNVs and identified abnormally expressed genes due to aberrant copy number. Etcheverry et al. [9] investigated the effect of methylation on mRNA expression in glioblastoma, and identified 13 genes that display an inverse correlation between methylation and mRNA expression using Perason’s correlation coefficient.

Since both CNVs and DNA methylation play important roles in mRNA expression, an integrated analysis that models all three platforms together is most appropriate. Denoting with C, M, and E the three platforms used to measure CNVs, methylation, and mRNA expression, we integrate data from all three platforms and present inference results as graphs that include C, M, and E as three vertices. In particular, we propose a Bayesian graphical model which imposes a probability distribution on the unknown networks and apply an autologistic prior to learn the dependence structure of three platforms through a graph. The vertices of the graph represent the platforms, and the presence or absence of edges indicates the presence or absence of conditional dependence between the platforms. For example, an edge between M and E and a lack of edge between C and E implies methylation-controlled transcription, which is robust to copy number changes. In other words, the mRNA expression is sensitive to methylational variation but not copy number variation. In this application, the use of a 3-node graphical model to represent the dependence structure of C, M and E is mainly chosen for convenience and for ease of display.

In the next Section, we give a brief overview of the ovarian cancer data to which we apply our integration analysis. In Section III, we introduce the proposed Bayesian graphical models along with MCMC simulation details. Section IV presents several simulation studies to evaluate the performance of the proposed model. In Section V, we report results based on the analysis of ovarian cancer data. We conclude with a discussion in Section VI.

II. TCGA Ovarian Cancer Data

Ovarian cancer is ranked as the fifth leading cause of death related to reproductive cancer in women. The Cancer Genome Atlas (TCGA) Research Network (http://cancergenome.nih.gov/) has examined more than 500 tumor samples and thousands of genes. The data is publically available online [10]. Special effort has been directed to produce matched measurements on DNA copy number (C), DNA methylation (M), and mRNA expressoin (E) for all the genes across the tumor samples. Taking advantage of this effort, we use the level 3 data of measurements on (C, M, E) for each gene with matched tumor samples. Specifically, let y_itg denote the measurement for gene g, on sample t, with platform i. Here i = 1, 2, 3 represents C, M, and E respectively, t indexes the T = 534 tumor samples, and g indexes the N = 9283 genes.

III. Probability Model

A. Sampling Model

We apply the proposed model for individual genes separately and thus drop the index g in subsequent discussion. For a single gene, the data is arranged in a 3 × T matrix Y = [y_it], i = 1, 2, 3 and t = 1, 2, …, T. We assume independence of measurements y_it across samples. The proposed model introduces latent trinary indicators e_it ∈ {−1, 0, 1}. The indicators have an interpretation as under-, regular and over-expression of the corresponding measurement. Using e_it we apply the mixture model proposed by Parmigiani et al. (2002) [11] for y_it. In words, we assume a mixture model with uniform, normal and uniform components corresponding to under-, regular and over-expression. The model is

$$(y_{\mathit{\text{it}}}-{\alpha }_t-{\mu }_i)|e_{\mathit{\text{it}}},{\mathit{\theta }}_{\mathit{\text{it}}}~I[e_{\mathit{\text{it}}}=-1]U(y_{\mathit{\text{it}}}|-k_{i-},0)+I[e_{\mathit{\text{it}}}=0]N(y_{\mathit{\text{it}}}|0,{\sigma }_i^2)+I[e_{\mathit{\text{it}}}=1]U(y_{\mathit{\text{it}}}|0,k_{i+}),$$ (1)

where I[·] is the indicator function, U(A) denotes a uniform distribution over the set A, and N(·, ·) denotes the normal distribution. The vector ${\mathit{\theta }}_{\mathit{\text{it}}}=({\alpha }_t,{\mu }_i,{\sigma }_i^2,k_{i-},k_{i+})$ collects all the other parameters. For example, α_t and μ_i are the random effects of sample t and platform i. We subsequently convert the trinary variable e_it to a binary variable z_it with p(e_it|z_it = 0) = δ₋₁(e_it), and

$$p(e_{\mathit{\text{it}}}=0|{\pi }_i,z_{\mathit{\text{it}}}=1)={\pi }_i,p(e_{\mathit{\text{it}}}=1|{\pi }_i,z_{\mathit{\text{it}}}=1)=1-{\pi }_i.$$

This conversion is devised to set up the following graphical model.

Denote V = {1, 2, 3} the set of three vertices representing C, M, and E. We use a graph on these three nodes to characterize the dependence structure across the three platforms. A graph is a pair G = {V, S} where S is a set of undirected edges {i, j}, i, j ∈ V. A graph G can be used to describe the conditional independence structure of a set of variables indexed by V, for example the binary indicators {z_it, i ∈ V} in the case of our application. The absence of an edge {i, j} indicates conditional independence of z_it, z_jt given the remaining variables z_kt, k ≠ i, k ≠ j. In the case of the three platforms the set of remaining variables reduces to just the third platform. Any joint probability model p(z_1t, z_2t, z_3t) that respects the dependence structure G can be written as (Besag, 1974 [12]):

$$p({\mathbf{z}}_t|\mathit{\beta },G)=p(0|\mathit{\beta },G)\times \text{exp}\{\sum _{i=1}^3{\beta }_i{z}_{\mathit{\text{it}}}+\sum _{\{i,j\}\in V;i<j}{\beta }_{ij}{z}_{\mathit{\text{it}}}{z}_{jt}\}$$ (2)

where z_t = (z_1t, z_2t.z_3t) and β = (β₁, β₂, β₃, β₁₂, β₂₃, β₁₃). Coefficients β_ij are non-zero only when the corresponding edge is included in the graph. Model (2) is known as the autologistic model.

Caragea and Kaiser [13] and Hughes et al. [14] proposed a centered parametrization of the autologistic model and argued that the centered version improves mixing of the Markov chain Monte Carlo (MCMC) posterior simulation and simplifies prior specification. The centered version is used in the form of

$$p({\mathbf{z}}_t|\mathit{\beta },G)=p(0|\mathit{\beta },G)\mathit{\text{exp}}\{\sum _{i=1}^3{\beta }_i{z}_{\mathit{\text{it}}}+\sum _{\{i,j\}\in V;i<j}{\beta }_{ij}(z_{\mathit{\text{it}}}-{\nu }_i)(z_{jt}-{\nu }_j\left)\right\},$$ (3)

where ν_i = exp(β_i)/{1 + exp(β_i)}.

The joint model factors as

$$p(\mathbf{Y},\mathbf{e},\mathbf{z},\mathit{\pi },\mathit{\theta },\mathit{\beta },G)=p(\mathbf{Y}|\mathbf{e},\mathit{\theta })p(\mathbf{e}|\mathbf{z},\mathit{\pi })p(\mathbf{z}|\mathit{\beta },G)p(\mathit{\theta })p(\mathit{\beta }|G)p(G)$$ (4)

We introduce the priors p(θ)p(β | G)p(G) next. Let Ga(a, b) denote a gamma distribution with mean a/b. We assume conditionally conjugate priors

$${\mu }_i~N(0,{\tau }_{\mu }),\frac{1}{{\sigma }_i^2}~\mathrm{G}\mathrm{a}({\gamma }_{\sigma },{\lambda }_{\sigma }),$$

$$\frac{1}{k_{i-}}~\mathrm{G}\mathrm{a}({\gamma }_{k_{i-}},{\lambda }_{k_{i-}}),\frac{1}{k_{i+}}~\mathrm{G}\mathrm{a}({\gamma }_{k_{i+}},{\lambda }_{k_{i+}}),$$

$${\beta }_{*}~N(0,{\sigma }_{\beta }^2),{\pi }_i~U(0,1),$$

where β_⋆ stands for the coefficients β_i, β_ij in (3). For the sample random effects α_t’s, we assume α_t ~ N(0, τ_α) subject to identifiability constraint ∑_t α_t = 0. Lastly, we define a prior p(G) as a uniform distribution over all possible graphs. With 3 vertices, we only need to consider up to 8 graphs. Each of the subgraphs is given a prior probability of 1/8.

B. Markov Chain Monte Carlo (MCMC) Simulations

We carry out posterior inference for model (4) using MCMC simulations. Each iteration of the MCMC scheme includes the following transition probabilities. We start by generating z_it from its complete conditional posterior. Following the update of z, we generate values for e from complete conditional posterior p(e | Y, α, z). If z_it = 0, the update is deterministic, e_it = −1. If z_it = 1, the update requires a Bernoulli draw for e_it = 0 versus e_it = 1. The update of parameters θ is straight-forward. Resampling G and the regression coefficients β could be challenging in larger graphs, essentially because of the difficult evaluation of the normalization constant p(0 | β, G) in (3) (see, e.g. [15]). However, here p(G) is only supported over 8 possible graphs, making the evaluation of the normalization constant straightforward. Thus, resampling G and β reduces to straightforward trans-dimensional MCMC as in [16].

IV. Simulation Study

To evaluate the proposed model, we examine the performance of our model with 3 simulated data sets, each with T = 300 samples, one true graph and a single gene. For each simulation, a true graph G is first generated as follows. For a pair of vertices {i, j}, we include the edge with probability 0.5. For each imputed edge {i, j}, we generate values of β_ij ~ N(μ₁, 0.5²) with μ₁ ~ U(−3, 3). We generate β_i ~ N(μ₂, 0.5²) with μ₂ ~ U(−0.5, 0.5). Then, we generate z for T = 300 samples. Since p(e_it|z_it = 0) = δ₋₁(e_it), and p(e_it = 0|π_i, z_it = 1) = π_i, p(e_it = 1|π_i, z_it = 1) = 1 − π_i, we first generate π_i ~ U(0.25, 0.75) and then generate e. Furthermore, we let μ_i = 0, σ_i = 0.316, k_i− = 5.556, k_i+ = 5.556 for each node, and generate α_t ~ N(0, 0.1²) subject to the identifiability criterion ∑_t α_t = 0. Lastly, the hyper-parameters are τ_α = 1, τ_μ = 1, γ_σ = 2, λ_σ = 0.1, γ_k+ = 10, λ_k+ = 50, γ_k− = 10, λ_k− = 50, ${\sigma }_{\beta }^2=10$.

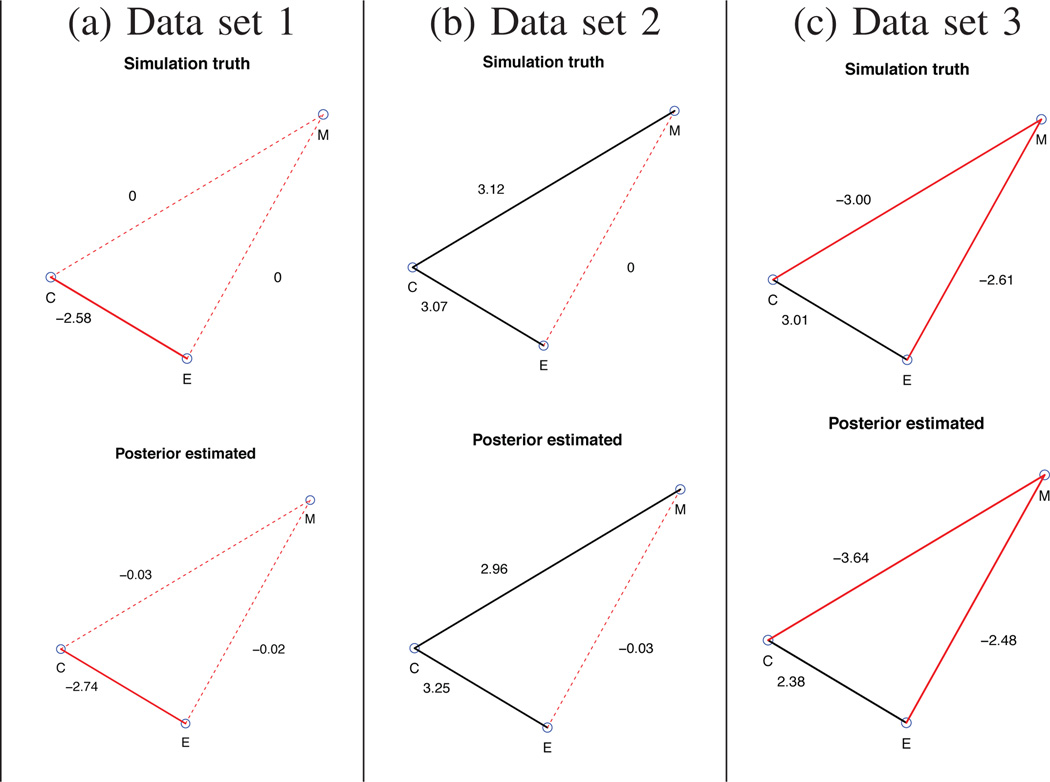
We implement our model to compute the posterior summaries for each simulated data set. The posterior estimates are obtained by MCMC posterior simulation with 5,000 iterations, of which 2,000 are burn-in. Since graph G is modeled as a random variable, we report the inference ξ = P(G = G₀ | data), where G₀ is the true graph in the simulation. For the three data sets ξ = 0.82, 0.86, and 1, respectively. We also report parameter estimates β̄ = E(β | Y) denoting the posterior mean for the autologistic coefficients.

From Figure 1, we can see that the estimated graph match the simulation truth for all three data sets. Here the estimated graph is the graph with highest posterior probability. We denote the positive and negative edges by black lines and red lines, respectively. The sign of β_ij has an intuitively appealing interpretation related to the effect of the j-th platform on the probability of presence of i-th platform, keeping the other platform fixed. Let z_−ij = z\{z_i, z_j}. We can show that β_ij is the log odds ratio of z_i and z_j through simple algebra, where β_ij > 0 implies that p(z_i = 1 | z_j = 1, z_−ij) > p(z_i = 1 | z_j = 0, z_−ij). See Figure 1 for the values of β’s.

Fig. 1.

The simulation truth versus the estimated graph for three simulated data set. Edge colors black and red represent positive and negative relationships. The solid line represents that the edge exists. The red dotted lines indicate that the corresponding edges do not exsit. The number next to each edge represents either the true value or the posterior mean of the autologistic coefficients β’s, 0 for the edges do not exist. The estimated graph based on posterior inference is identical to the simulation truth.

V. Ovarian Cancer DATA Analysis

We apply our model and inference method to one gene at a time using the ovarian cancer data described in Section II, aiming to recover the unknown dependence structure among the three platforms for each gene, and display it as a three-vertices graph. We carry out inference using the described MCMC posterior simulation and ran 5,000 iterations with 2,000 burn-in. We obtain a posterior estimate Ĝ of the unknown graph with the largest posterior probability.

An Excel table is provided as supplementary materials in which we present the posterior probability of each subgraph for each gene (https://sites.google.com/site/yanxunresearch). Genes are listed in descending order according to Pr(G = Ĝ | data). There are 142 genes whose Pr(G = Ĝ | data) > 0.4. When the cutoff is set to 0.6, there are 61 genes. For cutoff = 0.8, there are only 13 genes. From these 13 gene, we select two genes “ERLIN2” and “PIR” randomly to demonstrate the results.

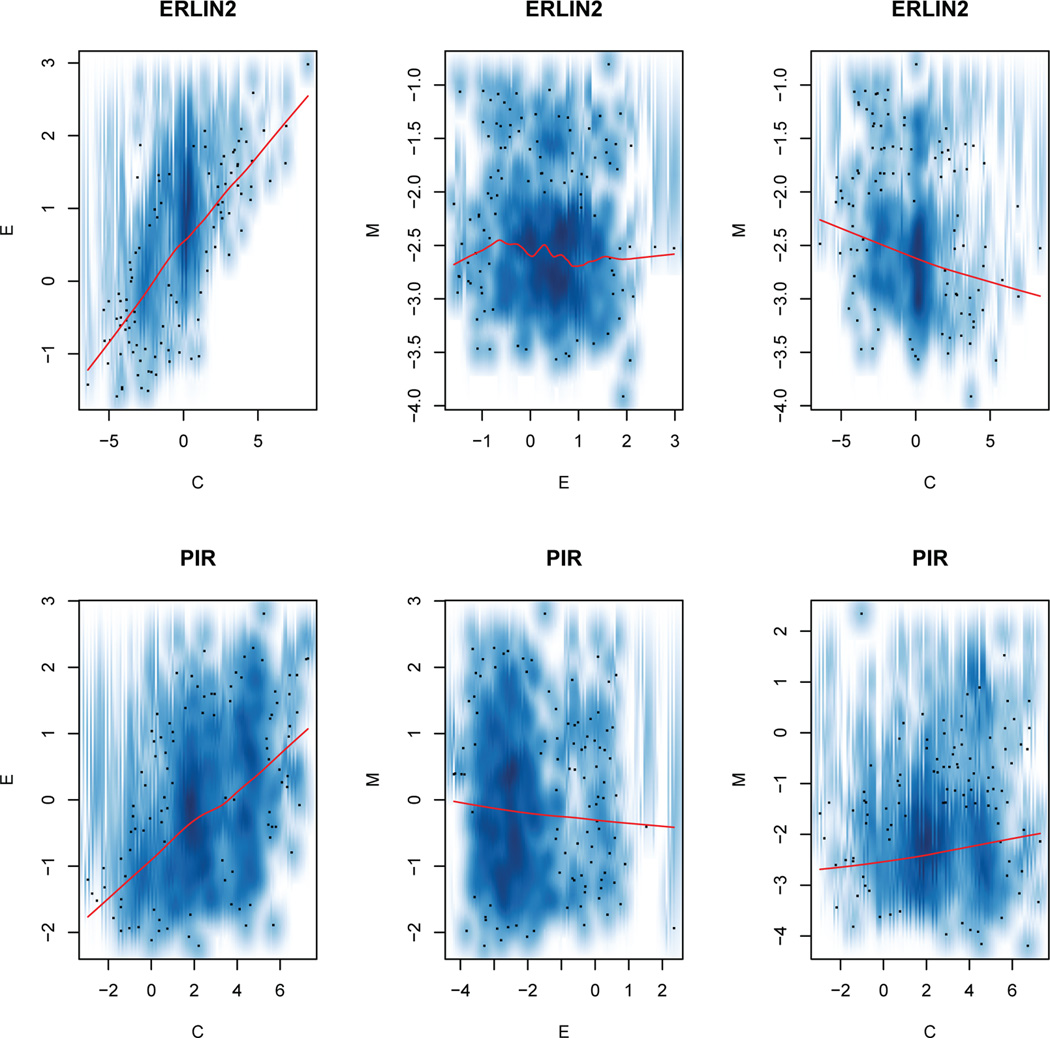
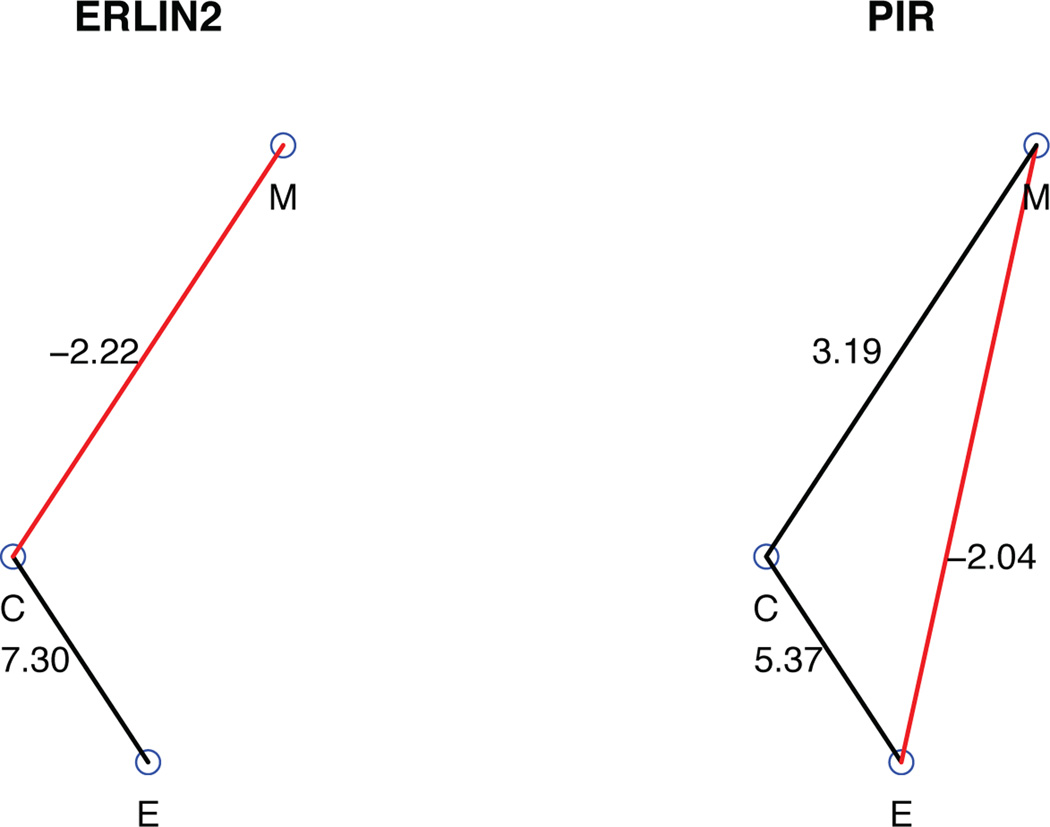
Figure 2 shows smooth scatter plots of the data for the two selected genes. Figure 3 displays the estimated graph for them. From these two figures, we can see that the actual trend exhibited in the scatter plot is consistent with our model estimation. For example, there is an obvious positive correlation between mRNA expression and CNVs for ERLIN2 in Figure 2 and the posterior mean given by our model for the mRNA expression-CNVs edge in Figure 3 is 7.30, indicating a strong positive correlation between the two platforms, which corresponds well with what we observed in Figure 2. This matching pattern is also observed for other cases. Overall, our model estimation corresponds well with the association observed among the platforms.

Fig. 2.

Smooth scatter plots of pairwise relationship among platforms C, M and E. The upper panel is for gene “ERLIN2”, the low panel is for gene “PIR”. The red line in each smooth scatter plot is the lowess smoother. Dots correspond to the raw expression measurements from the level three TCGA data.

Fig. 3.

Posterior estimated graphs for genes “ERLIN2” and “PIR”. Black edges represent positive relationships and red edges represent negative relationships. The number next to each edge is the posterior mean of β_ij.

VI. Discussion

We propose a Bayesian graphical model to describe the dependence structure of three genetic phenomena, CNVs, DNA methylation, and mRNA expression. The inferred graph gives a clear representation of the regulatory relationships involving the three genetic features. For example, the mRNA expression of gene ERLIN2 is sensitive to copy number changes but robust to DNA methylation, while the mRNA expression of gene PIR is sensitive to both copy number changes and DNA methylation. We are in the process of making a comprehensive list of these relationships using the entire TCGA data, expanding the effort to include more cancer types and more features such as microRNA and protein expression.