Abstract
Boron, an essential micronutrient, is transported in roots of Arabidopsis thaliana mainly by two different types of transporters, BORs and NIPs (nodulin26-like intrinsic proteins). Both are plasma membrane localized, but have distinct transport properties and patterns of cell type-specific accumulation with different polar localizations, which are likely to affect boron distribution. Here, we used mathematical modeling and an experimental determination to address boron distributions in the root. A computational model of the root is created at the cellular level, describing the boron transporters as observed experimentally. Boron is allowed to diffuse into roots, in cells and cell walls, and to be transported over plasma membranes, reflecting the properties of the different transporters. The model predicts that a region around the quiescent center has a higher concentration of soluble boron than other portions. To evaluate this prediction experimentally, we determined the boron distribution in roots using laser ablation-inductivity coupled plasma-mass spectrometry. The analysis indicated that the boron concentration is highest near the tip and is lower in the more proximal region of the meristem zone, similar to the pattern of soluble boron distribution predicted by the model. Our model also predicts that upward boron flux does not continuously increase from the root tip toward the mature region, indicating that boron taken up in the root tip is not efficiently transported to shoots. This suggests that root tip-absorbed boron is probably used for local root growth, and that instead it is the more mature root regions which have a greater role in transporting boron toward the shoots.
Keywords: Arabidopsis thaliana, Boron, LA-ICP-MS, Mathematical modeling, Polar localization, Transporter
Introduction
Plant growth depends on nutrient uptake. Understanding the mechanisms and regulation of nutrient uptake is of fundamental biological importance. The process is crucial for crop production, so its understanding is also essential to achieve an efficient usage of nutrients in agriculture (for a review, see Marschner 1995). A number of mineral nutrient transporters involved in nutrient uptake from the soil have been identified and characterized (for a review, see Dean et al. 2014). In many cases, a particular mineral nutrient is transported by several transporters with different transport properties, while different nutrient transporters can exhibit distinct, cell type-specific accumulation (for a review, see Slewinski 2011). For a nutrient to be taken up by roots and transported to shoots, it needs to be taken up into symplasts and then loaded into the xylem, an apoplastic space. Uptake by root cells and loading into the xylem are thus controlled by influx and efflux transport, respectively, and in many cases both processes are facilitated by distinct transporters with different properties.
Boron is an essential micronutrient for plants, but toxic in excess (Warington 1923; for a review, see Miwa and Fujiwara 2010). Its deficiency causes severe defects in vegetative and reproductive growth (for a review, see Shorrocks 1997), but excess boron also causes growth defects (for reviews, see Nable et al. 1997, Shorrocks 1997). Hence it is important for plant growth to maintain boron homeostasis. To achieve homeostasis, the spatial organization of transport processes plays a crucial role.
Boron is taken up from the soil by plant roots through an elaborate spatial network of transport proteins, which are expressed differently in each cell type and, moreover, can be localized in a highly polar fashion along the cells’ plasma membrane (PM). In Arabidopsis thaliana we have identified several transporters of boron that are required for efficient uptake by roots, transport to shoots, preferential distribution in shoots and excluding excess boron from roots (Takano et al. 2001, Takano et al. 2002, Takano et al. 2006, Miwa et al. 2007, Miwa and Fujiwara 2011, Miwa et al. 2013). Two main classes of boron transporters account for the facilitated transport of boron, in the form of boric acid, through the plant tissue: nodulin26-like intrinsic proteins (NIPs) allow for an increased unbiased bidirectional movement of boric acid across the PM, while BOR1/BOR2 account for a facilitated efflux of boric acid out of the cell into the cell wall. Specifically, NIP5;1 is required for efficient uptake of boron from soil to the root (Takano et al. 2006). BOR1 is an efflux transporter of boron and is required for efficient transport of boron from roots to shoots. BOR2, the closest homolog of BOR1, is important for root growth under low boron condition and enhances cross-linking of pectic polysaccharides in the cell wall (Miwa et al. 2013). In the aerial portion of plants, BOR1 and NIP6;1, the closest homolog of NIP5;1, play an important role for efficient preferential transport of boron to young portions of shoots (Takano et al. 2001, Tanaka et al. 2008).
Among the transporters identified, BOR1, BOR2 and NIP5;1 are important for boron transport in roots. These transporters have distinct cell type specificity of expression and polar localization patterns (Takano et al. 2010, Miwa et al. 2013). In general, BOR1 and BOR2 exhibit ‘inner’ localization while NIP5;1 exhibits ‘outer’ localization. We expect that the presence of different transporters with different properties in terms of cell specificity and polarity should give rise to a characteristic pattern of boron distribution in the root, and that such a pattern could affect the overall flux of boron through the organ. As boron passes through the plant tissue, it can get cross-linked and incorporated into the cell wall, which is essential for establishing correct cell wall properties and hence plant growth. Xylem loading is likewise essential, to deliver boron to the growing shoot and leaves. Nevertheless, in the root tip—in the absence of mature vascular systems—a striking level of complexity can be observed in the spatial patterning of the transporters, both on the cellular and on the tissue scale. It is as yet unclear what functionality or behavior this patterning manifests.
Despite the great advances in molecular and genetic studies on boron uptake in plants, until now we could only indirectly estimate how the removal or change of certain transporters would impact boron movements and concentrations within the root. Boron measurements have only been performed at the tissue or plant level or through xylem loading assays (Takano et al. 2002). Such coarse-grained data were valuable to estimate approximate behaviors of mutants, but cannot reveal boron distributions within tissues.
In this study, to elucidate the boron distribution pattern in the root tip, we adopted two different approaches, namely mathematical modeling and an experimental demonstration of the boron distribution in the root. For the mathematical modeling, we developed a description of the diffusion and BOR1/BOR2- and NIP5;1-facilitated boron transport in and across cells and cell walls in a structured root layout. A similar approach has been successfully adopted for the modeling of auxin transport (Grieneisen et al. 2007).
For the experimental approach, we utilized laser ablation-inductivity coupled plasma-mass spectrometry (LA-ICP-MS). This method was originally developed for the determination of elements in solid samples at micrometer-scale resolution (Audétat et al. 1998, Chi et al. 2002). LA-ICP-MS also allows us to obtain elemental distributions in biological samples (Wang et al. 1994, Punshon et al. 2004). Although the technique has a strength in being able to obtain high spatial resolution of the elemental distributions, the major drawback for the analysis of biological materials is the need for pre-treatments or fixation, which could affect the distribution of elements (Koelmel et al. 2013, da Silva and Arruda, 2013, Lefèvre et al. 2014). In the present study, we therefore developed a method to determine boron distribution in the root of A. thaliana without the need for fixation, by reducing the duration of the experiment.
Comparison of the simulation outputs and experimental data of the boron distribution in roots allowed us to propose that A. thaliana roots have two functional domains with different physiological roles in terms of boron transport and boron utilization.
Results and Discussion
Establishment of a spatial model to describe boron distribution in A. thaliana roots
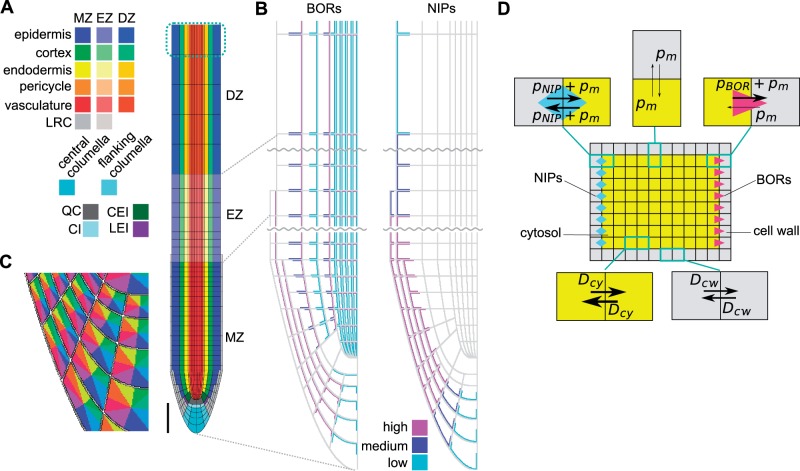
We constructed a two-dimensional model for boron transport within the spatial setting of the A. thaliana root, to assess what patterning would be expected in the Arabidopsis root when the combined action is taken into account of known (i) levels and localization of boron efflux facilitators (BOR1 and BOR2); (ii) levels and localization of NIP5;1, which enhances the diffusive (i.e. bidirectional) permeability of boron; and (iii) intracellular and extracellular diffusion of soluble boron. Many of the previous nutrient transport models describe cells as units containing only a single concentration value. Given the polar localization of the transporters, it is possible that boron concentrations within a cell or the cell wall could manifest spatial patterning. Hence, to be able to simulate such features, we took subcellular spatial structures explicitly into account. Given that only the soluble form of boron diffuses, is able to cross membranes and interacts with the transporters, we only consider this form within the model, ignoring all transitions between the soluble and solid form. Our computational framework thus describes boron diffusion within cells and within the cell wall, as well as BOR- and NIP-mediated boron transport across membranes. It does so by numerically solving partial differential equations with complex boundary conditions using alternating implicit direction methods, which have previously been extensively used to perform simulations on auxin dynamics (Grieneisen et al. 2007, Grieneisen et al. 2012). For further details on the equations and numerical simulations, see the Materials and Methods. More recently, modifications to the spatial layout of the root tip have been incorporated and used to take into account the more refined detail of the cell types of the root tip and stem cell niche, their shape and polarity (see also Cruz-Ramírez et al. 2012). We based, and further developed, the spatial layout of our current work on this advanced and validated layout. Our current spatial setting thus captures all cell types in the stem cell niche as well as overall differences in cell lengths at more proximal regions of the root (Fig. 1A). The root is therefore longitudionally divided into a meristem zone (MZ), an elongation zone (EZ) and a differentiation zone (DZ), as reported in Laskowski et al. (2008) with, moreover, variable cell lengths within the EZ.
Fig. 1.
Spatial diffusion model for boron transport simulation. (A) Root layout of the spatial model. The root consists of cell wall and cells, which are classified into 23 cell types. To describe the boundary condition at the proximal end of the plant, boron concentrations in the top cells that are surrounded by cyan dashed lines were fixed to zero, effectively capturing a shootward boron flux. MZ, meristem zone; EZ, elongation zone; DZ, differentiation zone, LRC, lateral root cap; QC, quiescent center; CEI, cortex/endodermis initial; CI, columella initial; LEI, lateral root cap/epidermis initial. Scale bar = 100 µm. (B) Layout of BORs and NIPs in the root. BORs and NIPs were localized in the boundary between cell walls (gray) and cells. BORs and NIPS were assigned three different intensities, based upon experimental observations. Each cell type has an identical transporter localization. (C) Each cell surface was divided into eight regions to allow for a detailed matching between experimental observations and the model regarding transporter localization. (D) Schematic diagram of diffusion and permeation within the spatial model. Cells and cell walls were built up from 0.5 µm square grid points, the minimum unit in the model. Arrows indicate diffusion or permeation between each grid point. For the parameters that were used in the simulations, see Table 1.
Critical to the outcome of the model is the positioning of the transporters, which, together with the spatial root context, results in the complex flux patterns underlying the concentration profiles. Through careful analysis of BOR1 and BOR2–green fluorescent protein (GFP) lines, and in accordance with previously published expression and localization patterns, we positioned these efflux facilitators on the cell membranes in a similar and characteristic manner, in which the simulated BORs represent all BORs in the root, and the simulated NIPs represent all the NIPs in the root (Fig. 1B; Takano et al. 2010, Miwa et al. 2013). BORs are mostly represented by BOR1 and BOR2, as these are the only two BOR transporters whose disruption causes a severe growth defect under low boron conditions among the seven members of BORs in A. thaliana (Takano et al. 2002, Miwa et al. 2013). NIPs are mostly represented by NIP5;1 as it is the only gene whose disruption causes a severe growth defect under low boron conditions among A. thaliana NIPs (Takano et al. 2006). To allow for polarized transporter localization, we divided the PM of each cell into eight distinct zones, depending on its orientation directed inwards or outwards, and upwards (shootwards) or downwards (rootwards) (Fig. 1C). This enabled us to analyze experimental images critically and incorporate in silico which of those eight zones, for each individual cell type, presented transporter localization. Note that the density of BOR proteins differs both between cell types and along the longitudinal axis of the root. We captured this in the model by assuming three distinct levels of efflux permeability strengths due to BOR action: high, medium and low. Similarly, we analyzed the NIP5;1 levels and localization patterns, and modeled what we considered the representative positions of these proteins, again subdividing their levels (and hence permeability strengths) into three categories. Regarding NIP5;1, some experimental images suggest that they might reside at low levels in the vascular tissue, although the experimental evidence is not conclusive. We have therefore considered both possibilities, as will be discussed below.
BORs were set to allow for unidirectional efflux transport of boron and for its transport to be dependent on the local concentration of boron within the cell at the PM, while NIPs were set to allow for bidirectional boron transport over the PM. Also a background boron permeability over the PM allows bidirectional diffusion of boron (Fig. 1D). Given the absence of any quantitative data from which saturation in boron transport could be derived, we here considered a purely linear relationship between observed transporter density and enhanced permeability, as well as between the soluble boron concentration and the flux over the PM. Note that as a consequence of such an assumption, different boron levels in the medium result in the same relative pattern in boron concentration in the model, scaled by the medium concentration used (as long as no changes in transporter levels or localization are explicitly introduced).
The simulations consider a fixed boron concentration in the medium, which then can diffuse into the cell wall that surrounds the root with a rate equal to the diffusion rate within the cell wall. In this study we focus on the very tip of the root, hence we do not simulate the xylem and its convective flow shootwards. The proximal boundary condition, however, is such that we allow soluble boron to flow out of the vasculature at the very end of the in silico root, as if it were connected to further vascular cells (for a detailed description of how this is implemented, see Cruz-Ramírez et al. 2012). In each simulation, we consider the initial concentrations within the whole root tissue to be zero, and, as boron from the medium starts to diffuse in, a pattern in boron distribution emerges. The profiles shown were obtained after allowing the simulation to achieve a steady-state distribution.
Predicted spatial distribution of soluble boron in the root
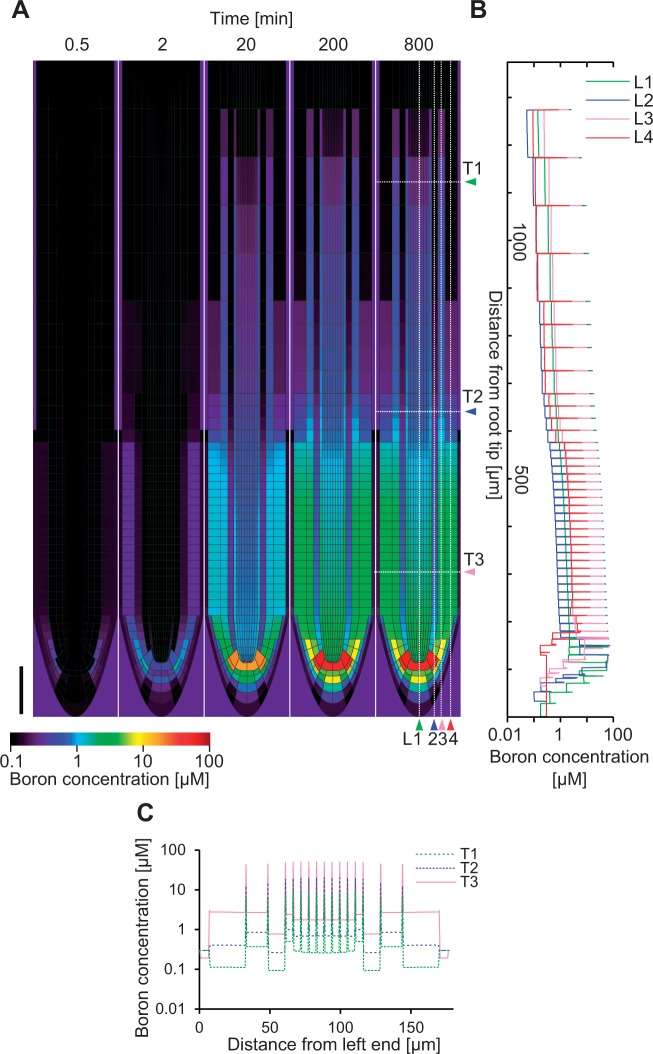
With the given settings, we simulated boron transport from the soil into the root. The concentration of boron in the medium was set to 0.3 µM, the initial concentration of boron in the root was set to 0 µM and transport dynamics were simulated until a steady state was reached (Fig. 2A). The resulting boron concentration profile exhibited a pattern in which the concentration near the root tip was higher than in the other portions of the root. The boron concentration in the cell wall was always much higher than that in the cells (Fig. 2B, C), which can be easily understood as BORs drive the efflux of boron into the cell wall, while NIPs affect import and export in an equal fashion. Cell wall concentration is therefore inevitably always higher than the cytosolic concentration. Combined with the polarized NIP localization, the high concentration of boron in the cell wall drives a large directed flux of boron into the inner neighboring cells. It accumulates in the quiescent center (QC), while the concentration of boron in the vascular tissue is also slightly higher than in the surrounding cell types. The overall concentration of boron becomes low in the upper portion of roots (see further discussion below). Such a pattern becomes apparent after 200 min from the initiation of the simulation, and does not change dramatically during the next 600 min (Fig. 2).
Fig. 2.
Simulation of boron distribution in roots. In the simulation, the root whose initial boron content was zero was immersed in a 0.3 µM boron medium. The simulation was run for 480,000 time steps, corresponding to 800 min of immersion. (A) Frames depict the temporal change in the spatial distribution of boron after the immersion. After 200 min the distribution pattern no longer changed. Scale bar = 100 µm. Boron profiles in longitudinal (L1–L4) and transversal (T1–T3) sections are also shown by a line graph in (B) and (C), respectively.
Boron determination of gel samples with LA-ICP-MS
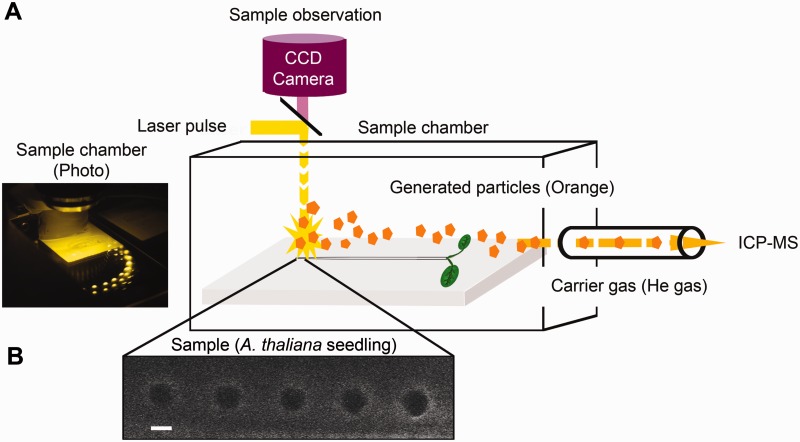
To determine experimentally the actual boron distribution in the roots of A. thaliana, we set up an LA-ICP-MS system as shown in Fig. 3. Plant materials were placed in the chamber in which a laser beam with an aperture of 10 µm is applied to the samples, and the ablated materials were then carried into the inductively coupled plasma-mass spectometer (ICP-MS) by He gas (600 ml min−1). The volume of the chamber and the passage to the ICP-MS is about 300 ml and the ablated materials are detected with about a 20 s delay from the moment of ablation. We continuously recorded an arbitrary value, in counts per second (cps), representing 11B detected per time. From those values, an arbitrary boron count for a laser beam shot could be calculated, by integrating the peak representing the ablation. The parameter setting of the LA-ICP-MS is described in Table 2.
Fig. 3.
Workflow of LA-ICP-MS analysis. (A) Five-day-old A. thaliana seedlings were placed in the chamber of the laser ablation apparatus. Observation through the CCD camera was used to select the position of the spots to be ablated. A laser beam of 10 µm in diameter was applied to the root, and ablated materials (orange) were drawn into the ICP-MS by the He carrier gas. (B) An image of A. thaliana roots after three rounds of ablation at the same positions. Dark circles represent the sampling spots of the laser ablation. The settings for spot diameter and spot spacing were 10 and 30 µm, respectively. Scale bar = 10 µm.
Table 2.
Parameters settings for LA-ICP-MS used in this study
| Laser ablation instrumentation | NWR-193X (ESI) |
|---|---|
| Laser type | ArF (wavelength 193 nm) |
| Carrier gas | He |
| Laser power | 5 mJ |
| Spot diameter | 10 µm |
| Frequency of laser pulse applied | 5 Hz |
| Wash-out time | 5 s |
| Laser irradiation time per spot (dwell time) | 5 s |
| Pulse duration | 5 ns |
| Time interval between spots | 20 s |
| Carrier gas flow | 600 ml min−1 |
Before analyzing plant samples, we first established the relationship between the count obtained through LA-ICP-MS analysis and the boron content in the samples. Boric acid under a series of solution concentrations was solidified with gellan gum [1.5% (w/v)] to form a sheet of gel with a thickness of 0.5 mm. Pieces of the gel sheet were subjected to LA-ICP-MS analysis. In one set of irradiation experiments, one spot on the sheet was irradiated by laser pulses of 5 ns 25 times within 5 s, followed by the irradiation of the next spot. Each spot then repeatedly received additional irradiation bombardments, until the signal produced by the irradiation became less than three times the background fluctuation. At that moment we assumed that the complete 0.5 mm deep column had been ablated. We then calculated the total count for each spot as the sum of the counts of all detectable shots at that spot. As indicated in Fig. 4A, the cumulative count from the LA-ICP-MS of such a set of shots at a single spot increases almost linearly in proportion to the concentration of boron in the gel. The conversion ratio of a signal count to the boric acid concentration in the gel is 953 counts µM−1 boric acid (Fig. 4A). In this experiment, the volume of the gels that were ablated is that of a cylinder of 10 µm in diameter having a depth of 500 µm. Given this volume, we estimate the ratio between the count obtained by LA-ICP-MS and the amount of ablated boron in the gel to be 4×10−5 fmol per count.
Fig. 4.
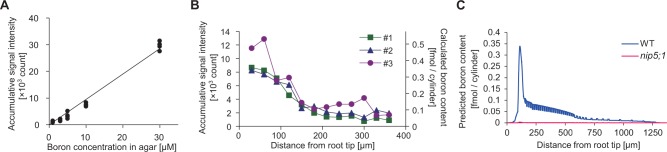
Quantitative analysis of boron distribution in A. thaliana roots by LA-ICP-MS. (A) Calibration curve for LA-ICP-MS. Data points and the linear regression line are shown. The slope of the linear regression and the volume of the ablated cylinder in the ICP-MS allowed calculation of a quantitative link between the count and the boron content: ‘boron content [fmol]’ = 4×10−5בaccumulative signal intensity [count]’. The coefficient of determination was 0.986. (B) Signal count of LA-ICP-MS and calculated boron content in the ablated cylinder at various positions from the tip of the root. Profiles obtained from three independent wild-type seedlings are shown. Note that no detectable signal was obtained from the nip5;1 mutant even though the same position in the root tip was ablated. (C) Predicted boron content if LA-ICP-MS were to be applied to the in silico root, intregrated over a 10 µm diameter at each position in the root at the 800 min time point.
Determination of boron in A. thaliana root using LA-ICP-MS
We then examined A. thaliana seedlings. Col-0 plants were grown for 5 d after germination on MGRL medium (Fujiwara et al. 1992), solidified with 1% (w/v) gellan gum containing 0.3 µM boric acid and subjected to the analysis. The very tip of the root was identified with the microscope attached to the laser ablation equipment, and from the tip 11 spots of 10 µm in diameter each were laser ablated, with 30 µm intervals between the centers of the spots. Ablation of the 11 spots was carried out in sequence, and the same sequence was repeated several times, until the signal intensity became less than three times the background fluctuation. Typically the fourth sequence gave a signal indistinguishable from the background level. The laser ablations were repeatedly done at precisely the same spots; we assured ourselves that after several shots the spots of the laser ablation were almost perfect circles of 10 µm in diameter (Fig. 3B). We therefore conclude that in most cases three shots at the same spot are sufficient to penetrate transversally completely through the root tissue.
The average counts for each spot from wild-type roots ranged between 1,500, in the proximal region of the roots where the signal was low, and 10,000, in the QC area (Fig. 4B). Using the conversion ratio of 4×10−5 fmol per count derived above, this is equivalent to 0.06–0.4 fmol and it is reasonable to assume that this amount of boron is derived from a cylinder of root tissue of 10 µm in diameter and the typical root thickness of 175 µm in length, which would make 0.06–0.4 fmol correspond to 4–30 pmol mm−3. Miwa et al. (2013) determined the total boron concentration in wild-type roots grown with 0.1 µM boric acid to be 0.39 mmol kg−1 DW. Assuming that the dry weight of the root is 15% of the fresh weight, the total amount of boron in a cylinder of root tissue 10 µm in diameter and 175 µm in length would be 0.8 fmol if boron were distributed homogeneously in roots, or 59 pmol mm−3. This is, depending on the location along the root, about 2–15 times higher than the amounts obtained from the LA-ICP-MS analysis, and on average 10 times higher. In the study by Miwa et al. (2013), the total concentration of boron in the whole root was determined for plants grown with 0.1 µM boric acid for 10–14 d. We should therefore take into consideration that at that stage of development it is likely that the majority of the root samples analyzed would be derived from the mature portion of the roots, for which we do not have LA-ICP-MS measurements. Another factor to take into account is that in the present analysis we used seedlings grown with 0.3 µM boric acid, so the total boron concentration in our samples is likely to be higher than what is to be expected with 0.1 µM boric acid.
Nevertheless, we conclude that the fraction of boron determined by LA-ICP-MS seems to represent only about, or less than, 10% of total boron in the cylinder. Under low boron supply, it is known that most of the boron in plants is present in the cell wall-bound form (Matoh et al. 1992). It is possible that LA-ICP-MS determines free soluble boron much more efficiently than the cell wall-bound boron, and that this is the underlying cause of the discrepancy. To support our assumption further, we determined the ratio of soluble boron to the total boron in roots grown with 0.3 µM boric acid, as described in the Materials and Methods. It was found that 14 ± 4% (mean ± SD, n = 3) of boron was in the soluble fraction, which is in reasonable agreement with our above-mentioned assumption.
To analyze further if this could make sense, we compared the experimental results with the mathematical simulation. We did this by calculating from the model the amount of boron that would be measured with the LA-ICP-MS method if the technique were to be applied to our in silico root. Given that in our LA-ICP-MS analysis we ablated root samples in the shape of a cylinder with a diameter of 10 µm and a depth of 175 µm, and the boron in this cylinder was taken into the ICP-MS for determination, we therefore calculated the predicted amount of boron that would be contained in a virtual cylinder, integrating boron concentrations over a 10 µm diameter and with a 175 µm depth, its hypothetical center positioned at any possible location along the in silico root (Fig. 4C). In support of the notion that the LA-ICP-MS analysis measures soluble boron, our modeling, which does not take bound boron into account, predicts very comparable boron amounts as measured in the experiments when using the final, equilibrium concentrations from the simulation. Furthermore, the model also predicted that in the absence of NIPs in the in silico root, the predicted boron concentrations would become very low (Fig. 4C). We therefore used our LA-ICP-MS analysis to look at the nip5;1 mutant, again grown with 0.3 µM boric acid. It did not provide us with any detectable signal, even though the same positions from the root tips were ablated as in the experiment with the wild type, suggesting that the amount of boron detectable with LA-ICP-MS is greatly reduced in the nip5;1 mutant, closely corresponding to the modeling prediction. In contrast, it has been determined by Takano et al. (2006) that the total boron in the nip5;1 mutant grown with 3 µM boric acid is reduced to 60% of that of the wild type, suggesting that reduction of the total amount of boron in the nip5;1 mutant is not so dramatic. Combining our observation with the fact that the boron that we simulate in our mathematical model is soluble boron only and the fact that in our LA-ICP-MS analysis the nip5;1 mutant did not give any detectable signal implies that boron determined through LA-ICP-MS probably represents soluble boron.
Based upon the above-mentioned observations and considerations, we therefore assumed that the boron determined by LA-ICP-MS predominantly represents the soluble fraction of boron in roots. We do not know at this moment why LA-ICP-MS specifically detects soluble boron rather than also measuring cell wall-bound boron. It may be that soluble boron is more readily ablated and efficiently taken into the ICP-MS, whereas the cell wall-bound boron is more resistant to ablation, or the ablated cell wall material may be less able to reach the ICP-MS for detection.
Determination of spatial distribution of boron along the distance from the root tip in A. thaliana roots
Experimental measurements on the wild type gave a boron distribution pattern along the distance from the root tip as shown in Fig. 4B. Boron was high in the first two shot positions and then gradually declined as the shots moved further away from the tip. We compared this distribution with the one predicted by the mathematical simulation, shown in Fig. 4C. The distribution obtained from the simulation is similar to the experimental data, with high boron levels at the root tip and a gradual decrease when moving away from the tip, as well as an equivalent concentration range, as discussed above. We acknowledge that the peak position and peak pattern are not identical between the simulation and the experimental data. This could be due to the difficulty in locating the tip of the roots in the LA-ICP-MS experiments or to detailed differences in the distribution of transporters in the in silico root. Overall, we concluded that the experimentally found boron distribution pattern is reasonably similar to the pattern predicted by the model. This suggests that our model is capturing the major features of boron transport and distribution in the root.
We also conclude from our LA-ICP-MS analysis and mathematical modeling that the boron concentration is high in the tip region of A. thaliana roots. Although we do not know what biological advantage high boron in the root tip region of roots provides, we would like to speculate on possible roles of this distribution. It was demonstrated 40 years ago that root elongation stops very quickly (within 30 min) after removal of boron from the medium (Kouch and Kumazawa 1975). Hence it is possible that a high boron concentration is required in the tip to maintain its growth. If indeed a high concentration of boron in the root tip is required for growth, this would create a risky situation, since a high concentration of boron is toxic to living organisms, irrespective of the kingdom. In fact, even relatively small fluctuations in the boron conditions could further augment high boron toxicity problems. In agreement with these findings, it has been established that high-boron-induced DNA damage and related cell death is predominantly observed in the tip regions (Sakamoto et al. 2011). It is possible that relatively strict regulation of boron homeostasis is needed to maintain high boron levels in the root tip while avoiding boron toxicity problems.
Consideration of the possible contribution of NIPs in the vascular tissues
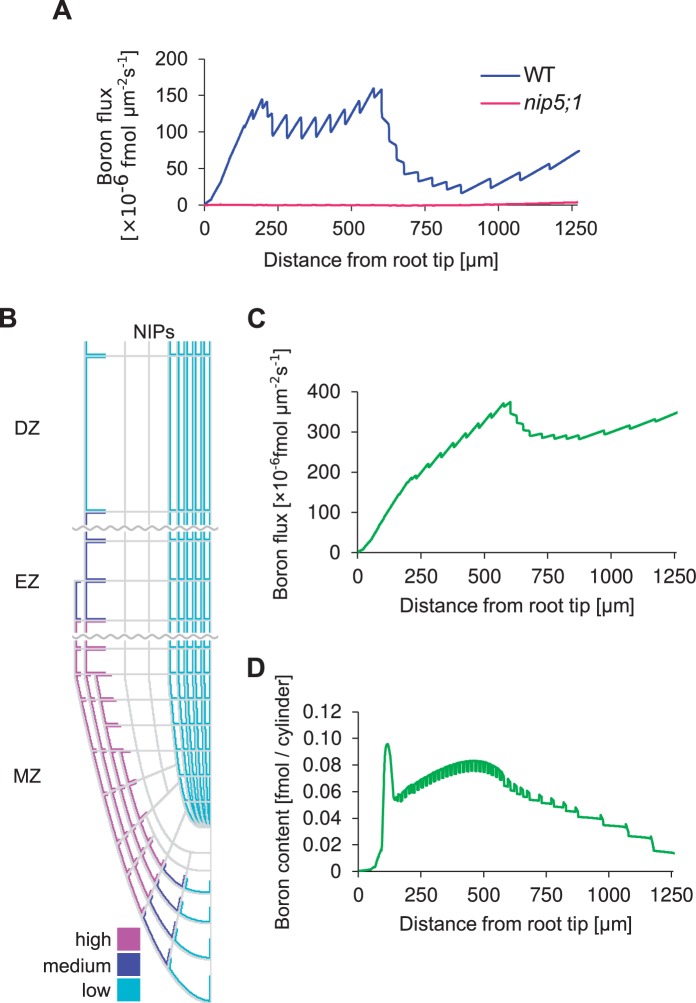
Our model also predicted very high boron concentrations in the vascular cell walls, presenting large differences between high apoplastic values vs. low cytoplasmic concentrations (Fig. 2B, C). This was due to the fact that in our model vascular cells were endowed with BOR proteins, but did not possess NIP transporters to enhance the uptake in the next cell shootwards. To analyze its implications, we studied the predicted resulting shootward fluxes within the root. Our mathematical model straightforwardly allows us to calculate the upward flux of boron along the distance from the root tip.
Surprisingly, we found that the net shootward fluxes were extremely low (Fig. 5A). The flux is reasonably high up to 500 µm from the tip, but it becomes very low in the region further away from the tip. This means that in this model, boron taken up by the tip of the roots is not efficiently transported shootwards, and a substantial portion of boron ‘leaks’ out back into soil from the cell wall in the more proximal region of the MZ. We considered that this scenario is conceptually strange, given that boron uptake requires energy and boron taken up by NIPs and BORs in the tip region at the expense of energy should thus be efficiently transported to shoots, by means of loading the xylem for further shootward transport (which only initiates around 2 mm from the tip, which is why it is not included in this model). In contrast, the model predicted that unused boron (i.e. the soluble boron that does get built into the cell wall in the MZ/EZ) would effectively become lost while being transported upwards (i.e. leave the root again), before it is able to reach the region where functional xylem starts.
Fig. 5.
Mathematical modeling analysis of the flux affected by NIPs in the stele. Simulations of a root whose initial boron content is zero, immersed in a 0.3 µM boron medium. Simulations were run for 480,000 time steps, corresponding to 800 min. (A) Net shootward boron flux for each longitudinal position along the root at the 800 min time point. (B) Layout of NIPs in the modified model. NIPs with low permeability were introduced into the stele and pericycle, with the intention of enhancing upward boron flux. The layout of BORs used in the model was identical to that of Fig. 1B. (C) Net shootward boron flux for each longitudinal position along the root at the 800 min time point. (D) Boron content as predicted by the modified model, if LA-ICP-MS were to be applied to the in silico root.
Given that this loss of boron is a direct consequence of the high boron levels in the vasculature and the outward flux through the apoplast it triggers, we hypothesized that weak vascular NIP5;1 signaling that could be observed in some images of NIP5;1–GFP lines might represent actual and functional vascular transporters. When we implemented this into the model, by positioning weak NIP transporter expression within the vascular tissue (Fig. 5B), we found that, in contrast to the previous results, simulations now predicted a high net shootward flux (Fig. 5C). Even low densities of NIP transporters were sufficient to cause a strong positive effect on shootward boron throughput. The reason for this is that now, instead of the root effectively loosing boron at each cell wall interface, diffusing apoplastically outwards back into the medium, the neighboring vascular cells are capable of taking up the soluble boron again, followed by directional transport due to polarly localized BOR1, bringing it into the cell wall to be taken up again by the next cell and so forth—all the way up until it reaches the point at which a functional xylem has been established.
Although the flux pattern predicted by our alternative hypothesis (Fig. 5C) indicated that the meristem and its intricate spatial network of transporters could function as an entry point of boron into the plant, the resulting concentration pattern turned out not to be in accordance with the experimentally measured values (Fig. 5D). Although it still correctly presented the characteristic high peak of soluble boron at the QC area of the root (like the LA-ICP-MS measurements), it now failed to show the subsequent decreasing pattern in soluble boron content. Instead, when following the boron concentration in the shootward direction, after a small decrease a subsequent strong increase in boron is predicted within the experimentally measured root area. We explored possible ways of ‘correcting’ this profile by means of various assumptions regarding NIP localization in the cortex and endodermis (data not shown), but found that this general feature of the profile was robust, due to the close link between boron containment and an increasing profile: boron enters everywhere along the root, and then gets transported upwards. If boron is not lost again during this process, more proximal cross-sections through the root must inevitably present larger boron fluxes. Increasing fluxes can only be accompanied by decreasing concentrations if there were a very steep shootward gradient in transport efficiency, requiring an accompanying steep gradient in transporter levels. The latter, however, is not observed experimentally. We therefore conclude that—contrary to what might previously have been expected—the root tip does not function as an entry gate to bring boron to the shoot.
Given that the LA-ICP-MS results are consistent with lack of NIP in the vasculature, this led us to conclude that boron transport in the root tip area does not give rise to a functional net flux shootwards, motivating us to reconsider the functional role of the root meristem tips regarding boron. Together with the prediction that root tip dynamics generate extremely high vascular cell wall concentrations, our combined experimental and theoretical results suggest that soluble boron in the cell wall of the root tip is seemingly more important than previously considered, possibly because of the high rate of new cell wall formation as a consequence of the high division rates in the MZ. This opens up further cell biological- and cell wall-related questions for future investigation.
These findings suggest a functional division in the root. The tip region takes up boron and accumulates it at the ‘tip’, but this boron does not contribute strongly to the transport to shoots. The boron requirement is known to be high in the growing portion of plants and it is reasonable for the root growth to maintain the boron in the tip for proper growth.
Conclusion
Our mathematical modeling and experimental determination of the boron distribution in A. thaliana roots demonstrated an accumulation of high boron in the tip of roots. We also concluded that two different functional domains are likely to be present in the roots in terms of boron uptake. In the tip, boron is taken up and used for growth, while boron transported to the aerial portion is taken up from more mature portions of the roots.
Materials and Methods
Simulation for boron transport in root
Simulations of boron transport in A. thaliana root were conducted using a grid-based two-dimensional spatial model. Our model consists of 2,751×355 square grid points, each representing 0.5×0.5 µm, giving rise to a root 175 µm in diameter, corresponding to our observations of typical roots. The framework of the model followed Grieneisen et al. (2007), in which the spatial auxin distribution in the root was analyzed by means of simulating diffusion and transport by auxin transporters. Each grid point is allocated to be part of the cytosol, cell wall or media; interfaces between the cytosol and cell wall represent membranes, and interfaces between media and the root represent the root–soil interface. BORs and NIPs, which are the boron efflux transporters and permeability facilitators, respectively, were located along the cytosolic boundaries according to observed localization patterns of recombinant proteins (Takano et al. 2010, Kasai et al. 2011, Miwa et al. 2013). The layout of the root was improved from both the original and a more recent model (Grieneisen et al. 2007, Cruz-Ramírez et al. 2012), based on detailed experimental observations of A. thaliana roots (Fig. 1A). Boron diffusion and transport were calculated numerically on the discretized grid points. Diffusion and permeability were dealt with independently. Diffusion only takes place within cells or within the cell wall, and its rate depends on whether the grid points represent cell or cell wall. Permeability is involved whenever two grid points are separated by a PM. The permeability rates, which can be different for boron entering the cell compared with leaving the cell, depend on the type and density of the transporters that are located at that specific piece of PM (Fig. 1C). Reasonable parameter values are being used for both diffusion and permeability (Table 1).
Table 1.
Parameters for simulation
| Symbol | Description | Value | Unit | |||
|---|---|---|---|---|---|---|
| Δt | Time step | 0.1 | s | |||
| Δx | Space step | 0.5 | µm | |||
| Dcy | Boron diffusion constant in cytosol | 1100 | µm2 s−1 | |||
| Dcw | Boron diffusion constant in cell wall | 73.3 | µm2 s−1 | |||
| pm | Membrane permeability of boron | 0.01 | µm s−1 | |||
| Symbol | Description | High | Medium | Low | Unit | |
| pNIP | Boron permeability facilitated by NIP | 1.5 | 0.6 | 0.3 | µm s−1 | |
| pBOR | Boron efflux permeability facilitated by BOR | 1.5 | 0.6 | 0.3 | µm s−1 | |
Specifically, soluble boron is allowed to diffuse freely within cells, as well as within the apoplast, at a lower rate. Diffusion occurs in accordance with Fick’s law:
where represents the flux of boron within a contiguous space, D is the diffusion coefficient, and represents the local gradient in soluble boron levels. The diffusion rate of boron in the cytoplasm was assumed to be 1,100 µm2 s−1, based on the boron diffusion rate in water (Goli et al. 2010). The diffusion in the cell wall was assumed to be 15 times slower than in the cytoplasm, based on measurements of carboxyfluorescein diffusion (Kramer et al. 2007), which is expected to have a negative charge in the cell wall, as is the case for boric acid.
However, whilst soluble boron can diffuse freely within cells and apoplastic spaces, the cell membrane represents a barrier to boron diffusive flux. The PM is represented in our model by the interfaces between grid points representing the cellular compartments and the apoplastic cell wall. We consider a small level of ‘leakage’ across the membrane, which is incorporated as a background permeability term (), without directional preference. When NIP is localized at a membrane interface, this enhances the bidirectional passage (), while the BOR family transporters facilitate only the efflux of soluble boron out of the cell (). Thus, the flux of soluble boron across the cell membrane is described in our simulations by the following equation:
where is the inward-directed unit vector perpendicular to the membrane, and represent the soluble boron concentrations immediately adjacent to the membrane, at the cytosolic and cell wall side, respectively, represents the permeability rate due to NIP, and represents the efflux permeability rate due to BOR. Note that if transporters are present (so that and take up non-zero values), three possible levels for the permeability due to BORs and NIPs can be assigned, high, medium or low, reflecting observed differences among tissue types in the localization intensity of the recombinant protein (Fig. 1B).
Laser ablation-inductively coupled plasma-mass spectrometry (LA-ICP-MS) analysis
The boron concentration was measured using an ICP-MS (model SPQ9700; Seiko instrument Industry), interfaced with a laser ablation system (New Wave Research UP 213). Laser ablation was performed in line scanning mode; the other ablation parameters are summarized in Table 2. Spots on the roots were observed with confocal microscope optics (FV1000; Olympus). The ICP-MS was set up in time-resolved analysis mode and the resultant boron amounts were reported in cps. The data were plotted and the total count of the boron signal was calculated using ImageJ 1.46r by manual identification of the shapes of the peaks. A peak was defined as having a >3-fold larger area than the background. Baselines were determined as the averages of the highest and lowest background cps values during the 5 s before and after the peak. Signals with an area less than three times the background were considered to be background themselves and treated as non-detectable.
Sample preparation for LA-ICP-MS
Wild-type (Col-0) A. thaliana seeds were sterilized with 10% (v/v) bleach and 0.1% (v/v) Co-op K soft dish detergent (CO-OP Co., Ltd.), and grown on MGRL plates containing 2% (w/v) sucrose, 0.3 µM boric acid and 1.0% (w/v) gellan gum (Wako Pure Chemical, Inc.), under controlled environmental conditions (at 22°C under a 16 h light/8 h dark cycle), as described previously (Fujiwara et al. 1992, Takano et al. 2006, Miwa et al. 2013). The whole seedlings at 5 d after germination were placed on glass slides attached by double-sided adhesive tape (Nichiban Co., Ltd.), and used for LA-ICP-MS analysis. Ablating the double-sided adhesive tape confirmed that the tape did not contain detectable boron. Since no suitable matrix-matched internal control for A. thaliana seedlings was available, we alternatively prepared 1.5% (w/v) gellan gum MGRL plates containing different concentration of boric acid (0, 0.3, 3, 5, 10 and 30 µM) for calibration standards. The resultant pieces of solidified gellan gum or A. thaliana whole seedlings were immediately placed on the glass slides and used for further LA-ICP-MS analysis.
Determination of soluble boron fraction
Arabdiopsis thaliana wild-type seedlings at 5 d after germination grown on MGRL medium containing 0.3 µM boric acid were used for compartmental analysis. The sample preparation was conducted according to Dannel et al. (1998) with modifications. About 100 mg of fresh root materials were frozen and thawed to burst the cell wall, and centrifuged at 14,000 r.p.m. for 10 min. The supernatant was taken as the soluble fraction and the resultant cell pellet was rinsed with double-distilled water four times. Rinsed material containing cell wall-bound boron and the resultant soluble fractions were digested with nitric acid and applied for further ICP-MS analysis. The ratio of boron in the soluble fraction was calculated as the amounts of boron in the soluble fraction/combined amounts of boron in the soluble fraction and the pellet.
Funding
This work was supported by the Japan Society for the Promotion of Science (JSPS) [Grant-in-Aid for Scientific Research No. 21228002 to T.F.]; the UK Biological and Biotechnology Research Council (BBSRC) [to V.A.G. and A.F.M.M. via grant BB/J004553/1 to the John Innes Centre].
Acknowledgments
The authors would like to thank Y. Kawara for excellent technical assistance, and T. Hakoyama for help with LA-ICP-MS.
Glossary
Abbreviations
- DZ
differentiation zone
- EZ elongation zone; GFP
green fluorescent protein
- ICP-MS
inductively coupled plasma-mass spectrometry
- LA-ICP-MS
laser ablation-inductively coupled plasma-mass spectrometry
- MZ
meristem zone
- NIP
nodulin26-like intrinsic protein
- PM
plasma membrane
- QC
quiescent center
Disclosures
The authors have no conflicts of interest to declare.
References
- Audétat A, Günther D, Heinrich CA. Formation of a magnetic–hydrothermal ore deposit: insights with LA-ICP-MS analysis of fluid inclusions. Science. 1998;279:2091–2094. doi: 10.1126/science.279.5359.2091. [DOI] [PubMed] [Google Scholar]
- Chi PH, Ko FH, Hsu CT, Chen HL, Yang CK, Sun YC, et al. Direct impurity analysis of semiconductor photoresist samples with laser ablation ICP-MS. J. Anal. Atom. Spectrom. 2002;17:358–365. [Google Scholar]
- Cruz-Ramírez A, Díaz-Triviño S, Blilou I, Grieneisen VA, Sozzani R, Zamioudis C, et al. A bistable circuit involving SCARECROW–RETINOBLASTOMA integrates cues to inform asymmetric stem cell division. Cell. 2012;150:1002–1015. doi: 10.1016/j.cell.2012.07.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- da Silva MA, Arruda MA. Laser ablation (imaging) for mapping and determining Se and S in sunflower leaves. Metallomics. 2013;5:62–67. doi: 10.1039/c2mt20154b. [DOI] [PubMed] [Google Scholar]
- Dannel F, Pfeffer H, Römheld V. Compartmentation of boron in roots and leaves of sunflower as affected by boron supply. Plant Physiol. 1998;153:615–622. [Google Scholar]
- Dean P, Major P, Nakjang S, Hirt RP, Embley TM. Transport proteins of parasitic protists and their role in nutrient salvage. Front. Plant Sci. 2014;5:1–13. doi: 10.3389/fpls.2014.00153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fujiwara T, Hirai MY, Chino M, Komeda Y, Naito S. Effects of sulfur nutrition on expression of the soybean seed storage protein genes in transgenic petunia. Plant Physiol. 1992;99:263–268. doi: 10.1104/pp.99.1.263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grieneisen VA, Xu J, Maree AFM, Hogeweg P, Scheres B. Auxin transport is sufficient to generate a maximum and gradient guiding root growth. Nature. 2007;449:1008–1013. doi: 10.1038/nature06215. [DOI] [PubMed] [Google Scholar]
- Grieneisen VA, Scheres B, Hogeweg P, Marée AF. Morphogengineering roots: comparing mechanisms of morphogen gradient formation. BMC Syst. Biol. 2012;14:6–37. doi: 10.1186/1752-0509-6-37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goli E, Hiemstra T, Van Riemsdijk WH, Rahnemaie R, Malakouti MJ. Diffusion of neutran and ionic species in charged membranes: boric acid, arsenite and water. Anal. Chem. 2010;82:8438–8445. doi: 10.1021/ac1009436. [DOI] [PubMed] [Google Scholar]
- Kasai K, Takano J, Miwa K, Toyoda A, Fujiwara T. High boron-induced ubiquitination regulates vacuolar sorting of the BOR1 borate transporter in Arabidopsis thaliana. J. Biol. Chem. 2011;286:6175–6183. doi: 10.1074/jbc.M110.184929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koelmel J, Leland T, Wang H, Amarasiriwardena D, Xing B. Investigation of gold nanoparticles uptake and their tissue level distribution in rice plants by laser ablation-inductively coupled-mass spectrometry. Environ. Pollut. 2013;174:222–228. doi: 10.1016/j.envpol.2012.11.026. [DOI] [PubMed] [Google Scholar]
- Kouchi H, Kumazawa K. Anatomical responses of root tips to boron deficiency. I. Effect of boron deficiency on cellular growth and development in root tips. Soil Sci. Plant Nutr. 1975;21:137–150. [Google Scholar]
- Kramer EM, Frazer NL, Baskin TI. Measurement of diffusion within the cell wall in living roots of Arabidopsis thaliana. J. Exp. Bot. 2007;58:3005–3015. doi: 10.1093/jxb/erm155. [DOI] [PubMed] [Google Scholar]
- Laskowski M, Grieneisen VA, Hofhuis H, Hove CA, Hogeweg P, Marée AF, et al. Root system architecture from coupling cell shape to auxin transport. PLoS Biol. 2008;6:e307. doi: 10.1371/journal.pbio.0060307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lefèvre I, Vogel-Mikuš K, Jeromel L, Vavpetič P, Planchon S, Arčon I, et al. Differential cadmium and zinc distribution in relation to physiological impact in the leaves of the accumulating Zygophyllum fabago L. Plant Cell Environ. 2014;37:1299–1320. doi: 10.1111/pce.12234. [DOI] [PubMed] [Google Scholar]
- Marschner H. 1995 Mineral Nutrition of Higher Plants, 2nd edn. Academic Press, San Diego. [Google Scholar]
- Matoh T, Ishigaki K, Mizutani M, Matsunaga W, Takabe K. Boron nutrition of cultured tobacco BY-2 cells. I. Requirement for and intracellular localization of boron and selection of cells that tolerate low levels of boron. Plant Cell Physiol. 1992;33:1135–1141. [Google Scholar]
- Miwa K, Fujiwara T. Boron transport in plants: co-ordinated regulation of transporters. Ann. Bot. 2010;105:1103–1108. doi: 10.1093/aob/mcq044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miwa K, Fujiwara T. Role of overexpressed BOR4, a boron exporter, in tolerance to high level of boron in shoots. Soil Sci. Plant Nutr. 2011;57:558–565. [Google Scholar]
- Miwa K, Takano J, Omori H, Seki M, Shonozaki K, Fujiwara T. Plants tolerant of high boron levels. Science. 2007;318:1417. doi: 10.1126/science.1146634. [DOI] [PubMed] [Google Scholar]
- Miwa K, Wakuta S, Takeda S, Ide K, Takano J, Naito S, et al. Roles of BOR2, a boron exporter, in cross linking of Rhamnogalactuonan II and root elongation under boron limitation in Arabidopsis. Plant Physiol. 2013;163:1699–1709. doi: 10.1104/pp.113.225995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nable RO, Bañuelos GS, Paull JG. Boron toxicity. Plant Soil. 1997;193:181–198. [Google Scholar]
- Punshon T, Jackson BP, Bertsch PM, Burger J. Mass loading of nickel and uranium on plant surfaces: application of laser ablation-ICP-MS. J. Environ. Monit. 2004;6:153–159. doi: 10.1039/b310878c. [DOI] [PubMed] [Google Scholar]
- Sakamoto T, Inui YT, Uraguchi S, Yoshizumi T, Matsunaga S, Mastui M, et al. Condensin II alleviates DNA damage and is essential for tolerance of boron overload stress in Arabidopsis. Plant Cell. 2011;23:3533–3546. doi: 10.1105/tpc.111.086314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shorrocks VM. The occurrence and correction of boron deficiency. Plant Soil. 1997;193:121–148. [Google Scholar]
- Slewinski TL. Diverse functional roles of monosaccaride transporters and their homologs in vascular plants: a physiological perspective. Mol. Plant. 2011;4:641–662. doi: 10.1093/mp/ssr051. [DOI] [PubMed] [Google Scholar]
- Takano J, Noguchi K, Yasumori M, Kobayashi M, Gajdos Z, Miwa K, et al. Arabidopsis boron transporter for xylem loading. Nature. 2002;420:337–340. doi: 10.1038/nature01139. [DOI] [PubMed] [Google Scholar]
- Takano J, Tanaka M, Toyoda A, Miwa K, Kasai K, Fuji K, et al. Polar localization and degradation of Arabidopsis boron transporters through distinct trafficking pathways. Proc. Natl Acad. Sci. USA. 2010;107:5220–5225. doi: 10.1073/pnas.0910744107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takano J, Wada M, Ludewig U, Schaaf G, von Wirén N, Fujiwara T. The Arabidopsis major intrinsic protein NIP5;1 is essential for efficient boron uptake and plant development under boron limitation. Plant Cell. 2006;18:1498–1509. doi: 10.1105/tpc.106.041640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takano J, Yamagami M, Noguchi K, Hayashi H, Fujiwara T. Preferential translocation of boron to young leaves in Arabidopsis thaliana regulated by the BOR1 gene. Soil Sci. Plant Nutr. 2001;47:345–357. [Google Scholar]
- Tanaka M, Wallace IS, Takano J, Roberts DM, Fujiwara T. NIP6;1 is a boric acid channel for preferential transport of boron to growing shoot tissues in Arabidopsis. Plant Cell. 2008;20:2860–2875. doi: 10.1105/tpc.108.058628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S, Brown R, Gray DJ. Application of laser ablation-ICP-MS to the spatially resolved micro-analysis of biological tissue. Appl. Spectrosc. 1994;48:1321–1325. [Google Scholar]
- Warington K. The effect of boric acid and borax on the broad bean and certain other plants. Ann. Bot. 1923;37:629–672. [Google Scholar]