Power reduction and the radial limit of stall delay in revolving wings of different aspect ratio

Abstract

Airplanes and helicopters use high aspect ratio wings to reduce the power required to fly, but must operate at low angle of attack to prevent flow separation and stall. Animals capable of slow sustained flight, such as hummingbirds, have low aspect ratio wings and flap their wings at high angle of attack without stalling. Instead, they generate an attached vortex along the leading edge of the wing that elevates lift. Previous studies have demonstrated that this vortex and high lift can be reproduced by revolving the animal wing at the same angle of attack. How do flapping and revolving animal wings delay stall and reduce power? It has been hypothesized that stall delay derives from having a short radial distance between the shoulder joint and wing tip, measured in chord lengths. This non-dimensional measure of wing length represents the relative magnitude of inertial forces versus rotational accelerations operating in the boundary layer of revolving and flapping wings. Here we show for a suite of aspect ratios, which represent both animal and aircraft wings, that the attachment of the leading edge vortex on a revolving wing is determined by wing aspect ratio, defined with respect to the centre of revolution. At high angle of attack, the vortex remains attached when the local radius is shorter than four chord lengths and separates outboard on higher aspect ratio wings. This radial stall limit explains why revolving high aspect ratio wings (of helicopters) require less power compared with low aspect ratio wings (of hummingbirds) at low angle of attack and vice versa at high angle of attack.

1. Introduction

Hovering animals, such as hummingbirds, can operate their wings at extreme angles of attack because they generate an attached leading edge vortex [1,2] (LEV; figure 1a). The LEV is a convergent solution for generating elevated lift (figure 1b) at high angle of attack in both flapping animal wings [4–8] and spinning seed flight [9]. The wings of these organisms move in different ways and have diverse wing morphologies ranging from essentially stiff to passive aeroelastic wings to articulated feathered wings under muscular control. Which features of wing morphology and wingbeat motion facilitate the generation of an attached LEV? Several studies confirm that a similar attached LEV is formed when a wing revolves, either unidirectionally around an axis, or reciprocates by flapping back and forth around a hinge [6,10,11]. This similarity between revolving and flapping animal wings forms the foundation of the quasi-steady model of animal flight in which a revolving wing estimates flapping wing performance [6,12].

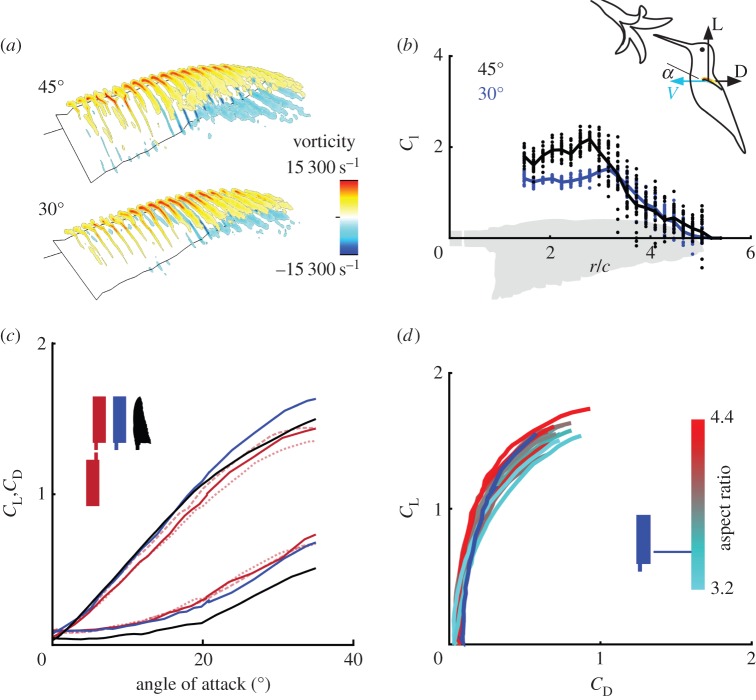
Figure 1.

Revolving hummingbird wings generate a stable LEV, and can be modelled with a rectangular model wing. (a) The average vorticity concentration above a Calypte anna wing at Re = 13 000 reveals an attached LEV at 30° and 45° angle of attack (α). (b) The distribution of vortex lift coefficient, C_l, calculated based on local circulation and chord length, shows vortex lift drops when radius, r, divided by chord length, c, is larger than approximately 3 (line, average; points, instantaneous values). (c) A single rectangular model hummingbird wing with aspect ratio 3.5 and 6% camber (see Material and methods) generates somewhat more lift (C_L) and drag (C_D) than a single C. anna wing (Re = 14 000; n = 5). The effect of a double versus single winged rotor is a small reduction in lift and an increase in drag. We contrasted double winged rotor measurements with aspect ratio 3.5 (solid red line; Re = 11 000) with 3.0 (dotted light red line; Re = 13 000) and 4.0 (dashed light red line; Re = 13 000) to show the effect on lift and drag. (d) The lift and drag values of the rectangular model hummingbird wing fall in the range of lift and drag values generated by the wings of 12 hummingbird species. Hummingbird lift-drag data have been adapted from Kruyt et al. [3].

A key observation is that the instantaneous vertical lift force and aerodynamic torque (due to drag) of a flapping animal wing, is similar to the values generated by the same wing revolving at the same instantaneous angle of attack and angular velocity [6,12]. Whereas this quasi-steady model of a flapping wing does not capture the aerodynamic effects that occur during stroke reversal, it does predict the overall aerodynamic performance well, in particular during the midstroke when wing acceleration is small [3,6,12–18]. During midstroke, hummingbird wingbeat kinematics closely approximates constant wing revolution [3,19]. In vivo recordings in rufous hummingbirds show this quasi-steady flapping phase is of particular importance during the downstroke when up to 75% of the lift is generated [1,20]. At midstroke an attached LEV elevates lift [1,2], which has been confirmed for 12 other hummingbird species by revolving hummingbird wings continuously [3].

Hummingbirds have a very similar wing shape across species and there are only small differences in aspect ratio: R/c = 3.7 ± 0.3 (n = 65; [11]). Small variation nonetheless influences aerodynamic power when hummingbird wings are tested in revolution [3]. This result was not predicted by an earlier study with revolving model insect-wings, which suggested that even large changes in aspect ratio have minimal effect on lift and drag at high angle of attack, but the study did not consider aerodynamic power [14]. At lower angle of attack and higher Reynolds number, Re (inertial versus viscous force in the airflow [21]), aspect ratio is arguably the most important design parameter for optimizing the performance of an airplane [21] or helicopter [22]. It remains unclear how aspect ratio influences aerodynamic performance of all these wings at high angle of attack.

For flapping and revolving wings, it has been proposed that the effect of aspect ratio needs to be considered in concert with wing motion [11]. At high angle of attack, low Re experiments with unidirectionally (constant) and reciprocating (flapping) revolving fly wings show that LEV attachment depends on aspect ratio with respect to the centre of rotation, R/c, wing radius, R, divided by chord, c [11,23]. This non-dimensional ratio is equivalent to the Rossby number of a (unidirectional or reciprocating) revolving wing. Low values imply that rotational accelerations operating in the boundary layer are significant compared to inertial forces, which helps the LEV to remain attached [11,24]. These studies of LEV attachment manipulated the radial distance between the base of a constant aspect ratio wing and its centre of rotation, but not wing aspect ratio itself.

Here we compare real and model hummingbird wings of aspect ratio 2–10 using a wing to test how aspect ratio with respect to the centre of rotation, R/c, influences aerodynamic performance at low versus high angle of attack.

2. Material and methods

To test the effect of aspect ratio with respect to the centre of rotation, we use a wing spinner and PIV flow measurement set-up that have been described in an earlier study of comparative hummingbird wing performance [3]. A detailed description of the set-up can be found in the electronic supplementary material, figure S1.

2.1. Hummingbird wing preparation

Wings from previously collected specimens of Anna's hummingbirds (Calypte anna) were removed from the (proximal) base of the humerus and dried in fully spread position to resemble wing morphology during hovering flight [3]. We removed minimal amounts of wing material to glue the wing base into a square plastic tube aligned with the innermost secondary feather. The square tube was mounted on a square rod attached to the variable pitch mechanism of the spinner. We then selected five right wings that had least imperfections in the feathers due to wear, molt and preparation (electronic supplementary material, figure S1a). When necessary, gaps were closed using a minimal amount of hairspray applied locally with a pin; we sprayed the solution in a cup, soaked the head of the pin in it and applied minimal amounts with the pin to fix particular barbs. Finally, we artificially groomed (preened) the feathers with our fingers and an entomological pin to close small gaps. Each wing's out-of-centre mass was carefully counterbalanced with an opposing plastic mount filled with lead fishing weights. Each mount was fitted with a minimally protruding hooklet at the base that enabled securing the wing and counterweight with an orthodontic rubber band.

2.2. Model wing design and validation

The rectangular model wings were made of carbon fibre with a constant cord of 15 mm, thickness of 0.4 mm and camber of 6% (similar to hummingbird wings [25]), which resulted in negligible deformation. The aerofoil has a thin square leading edge and a smooth surface, see the electronic supplementary material, figure S2. The aspect ratio of these model wings are 2, 3, 4, 5, 6.5, 8 and 10. Comparison of the lift and drag of a single model wing (aspect ratio 3.5, Re = 11 000) with a single C. anna wing (n = 5, average aspect ratio 4.1, Re = 14 000) shows they generate similar lift and drag versus α (figure 1c). Comparison of model wings with the average lift-drag data for 12 hummingbirds species matches even more, figure 1d, similar to the ProxDynamics Black Hornet rotor tested in an earlier study [3]. Comparison of model wings with aspect ratio 3.0, 3.5 and 4.0 (figure 1c) shows that these wings generate similar lift and drag values at similar Reynolds numbers. Not surprisingly, the more slender model wing generates more lift for similar drag and thus requires less power to support weight, which is consistent with our earlier observations that slender hummingbird wings need less power [3]. We found that hummingbird wings and low aspect ratio model wings could be spun without vibration by balancing them with a counterweight. High aspect ratio model wings, however, vibrated due to the relatively large eccentric aerodynamic forces at the larger outward radius of gyration of the wing [26]. We therefore tested all model wings in pairs, which balances the aerodynamic and inertial forces such that the set-up did not vibrate. Each wing pair was carefully balanced by gluing small lead fishing weights at the lower surface into one of the plastic mounts. This paired configuration better approximated the ‘solidity’ of the ‘actuator disc’ of a hummingbird wing beating at 180° amplitude [22,27]. The higher induced flow through the disc lowers angle of angle of attack [22] and hence lift, and also tilts lift backward, which increases drag (figure 1c).

2.3. Wing spinner torque and force measurement

The torque of low Reynolds number wings is difficult to measure in air. Earlier revolving model wings of various aspect ratios supposedly required no power to spin at low angle of attack because of spurious negative torques [14]. Our automated wing spinner has been designed to resolve this problem so that it can measure torque. To account for coupling effects, we applied combinations of lift and torque to build a 9 × 9 calibration matrix with increased resolution around zero lift and torque to accommodate low Reynolds number measurements. These calibrations were repeated five times before and after the measurements. Average calibration bias over all measurement points was 5.0% on torque and 1.0% on lift. The lift force range was between 0.03 × 10⁻³ N and 5.73 N, and the torque range was between 0. 013 × 10⁻³ Nm and 0.246 Nm [3].

The computer-run wing spinner autonomously controlled wing tip Reynolds number and angle of attack. Two brushless motors (AXi2212/34 and AXi2208/20, Model Motors) were selected to extend the RPM and torque range of the spinner (electronic speed controller; M-Drive-18, Motortron System Inc.). The spinner axle was hollow and suspended with ball bearings in an aluminium housing. The wings were fitted to a variable pitch propeller mechanism to vary angle of attack, which was controlled by a servo-actuated push–pull rod running through the axle (servo control; ServoCenter v. 3.1, Yost Engineering). Every angle of attack measurement loop consisted of an upward leg during which α was increased until the maximum was attained, after which α was reduced during the downward leg until it reached the minimum value. Three complete loops enabled us to check for hysteresis effects, which we did not find. The distance between the rotation axis and the wing root, d, was 9.5 mm. This offset was incorporated in the Reynolds number Re = ρ2πf(R + d)c/μ (air density, ρ, spinning frequency, f, wing length, R and dynamic viscosity, μ). The dynamic viscosity was calculated based on the measured air temperature using Sutherland's equation [28].

We calculate aerodynamic lift, C_L, and drag coefficient, C_D, by dividing lift by 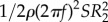and drag due to torque by 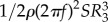using air density, ρ, spinning frequency, f, wing area, S and the radii of second and third moments of area R₂ and R₃, to account for the velocity gradient along the wing span [10,26]. Zero angle of attack was defined as the point of zero lift, based on the zero intercept of the C_L − α curve. We calculated the capability to lift weight with a unit aerodynamic power by computing power factor .

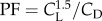2.4. Particle image velocimetry-based flow measurement

We measured the flow field around the wings using phase-locked particle image velocimetry (PIV) to characterize the radial extent of stall delay on the upper surface. We recorded either 20 (model wings) or 25 (C. anna hummingbird wings) phase-locked image pairs in two-dimensional planes along the span of the spinning wing at 19–22 equidistant stations. We automatically moved the imaging plane along the span using a linear actuator that traversed the spinner and its mounted wing through a laser sheet. Both the laser and the PIV camera were triggered when the wing passed in front of a camera (electronic supplementary material, figure S1b,d). Image pairs were cross-correlated using DaVis software (v. 7.4, LaVision GmbH) using a multi-pass cross-correlation procedure consisting of a first pass on a 128 × 128 pixel grid (0% overlap) and then two passes on a finer 64 × 64 pixel grid (75% overlap). The vortex lift distribution was calculated by integrating the vorticity field to determine local circulation, Γ, at each spanwise station. We omitted the area below the wing, where laser illumination was insufficient, from the area of integration. We cut off vorticity below a threshold level based on free-stream vorticity noise measured in front of the wing. From the circulation, we computed local vortex lift coefficients as C_l = 2Γ/Vc using local wing velocity, V and chord length, c. For the hummingbird wing, we used the local wing chord.

2.5. Aspect ratio, Reynolds number and angle of attack range

We sampled lift and drag 600 times for each angle (α = 0° up to 60°; stepsize 1° for α < 20° and 3° for α ≥ 20°) of five C. anna wings (Re = 14 000) and the model wings (Re = 5000–25 000, stepsize 4000). The wide range of revolving wings represent a quasi-steady model for the hovering insects [5], bats [7] and birds [1,2,8] for which a stable LEV has been found during the midstroke. Additional experimental details can be found in the electronic supplementary material.

3. Results and discussion

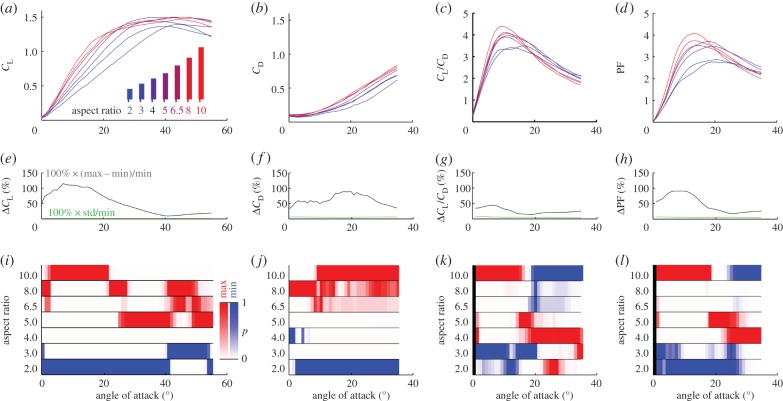
Lift and drag coefficients were determined for nine revolving model wings ranging in aspect ratio from 2 to 10 using a wing spinner (figure 2). These comparative force measurements show that revolving model wings with an aspect ratio of 4, similar to hummingbirds (figure 1c), outperform model wings with an aspect ratio of 10 at angle of attack beyond 20° (figure 2). At lower angle of attack, aspect ratio 10 wings outperform those of 4. We find this at the typical Re for hummingbirds of 13 000 (electronic supplementary material, figure S4) and on average across Re 9000–25 000 (figure 2; electronic supplementary material, figure S5). The maximum lift coefficient, C_L, is similar for all aspect ratios independent of Re [14], figure 2a, but is two times higher than found for with translating wings [6,11,29]. By contrast, lift slope (gradient), dC_L/dα, increases strongly with aspect ratio [14], figure 2a, which causes pronounced differences in C_L at identical α [21,22]. Whereas none of the revolving wings experience stall in the form of a drop in lift around α = 15°, as found for fixed wings [18], the aspect ratio 6.5, 8 and 10 wings do experience a drop in lift gradient beyond 20°. The factor 6.8, 8.8 and 9.5 drops in gradient, of the approximately linear segments α = 25°–40° versus 1°–15°, suggest that these slender wings are partially stalled. Partial stall also helps explain why the resultant force angle of high aspect ratio wings point further backward and approximate values for inefficient flat plates (figure 3a). Similar findings have been made for inverted cambered aerofoils with separated flow, which also have higher drag, and thus better approximate flat plates [3]. Drag coefficient, C_D, increases with aspect ratio at identical α, similar to fixed rectangular wings at similar low Re [29,30]. At much higher Re, drag is known to decrease with aspect ratio in accordance with fixed-wing theory [21]. One explanation for the discrepancy is based on the observation that profile drag of fixed wings is similar to induced drag at low Re [29,31]. Low aspect ratio suppresses flow separation, which lowers profile drag more than it increases induced drag and, as a result, total drag goes down with aspect ratio [29,32]. In addition, rotating wings presumably experience less boundary layer separation at low angle of attack than fixed wings, owing to rotational flow effects [33,34], and thus lower profile drag. To evaluate the impact of low drag due to low aspect ratio on hover performance, we compare power factor [11], PF = C_L^1.5/C_D. Power factor is the non-dimensional aerodynamic ratio of the weight that a wing can support for a unit power in hover. How do power requirements in hummingbirds and helicopters compare? During hover, hummingbirds need to flap their wings back and forth, which cost additional inertial power that can be minimized by flapping slower [18]. Similarly, their muscles can operate at higher power density if they can contract at an optimal, intermediate, speed [35]. Hummingbirds thus benefit from flapping slower to support their body weight, for which they need a high C_L at high α, because it reduces the overall hover power. The motors of helicopters, on the other hand, perform better at relatively high angular velocity, which affords them to operate at lower C_L at lower α. The aspect ratio 10 wings, typical of helicopters, require up to 48% less power to support weight than aspect ratio 2 wings at α < 20° (figures 2f and 3). By contrast, aspect ratio 4 wings, typical of hummingbirds [3], require up to 21% less power than aspect ratio 10 wings for α > 20°. The great divide in aerodynamic power can help explain why revolving helicopter blades (α < 20°) are slender and hovering animal wings are stubby (α > 20°). Is there a similar divide in stall performance across aspect ratios?

Figure 2.

Aspect ratio 10 model wings perform better below 20° angle of attack, whereas aspect ratio 4 wings do better above 20°. (a–d) Lift, drag, glide ratio, and power factor versus angle of attack as a function of aspect ratio, averaged over Re = 9000–25 000. Aspect ratio 4 wings combine near maximal lift, and intermediate drag, which maximizes power factor beyond 20°. The relative difference between minimum and maximum lift (e) drag (f) glide ratio (g) and power factor (h) among wings is substantial (green line, std calibration accuracy for reference). The optimal aspect ratio to obtain maximum (red) versus minimum (blue) lift (i), drag (j), glide ratio (k) and power factor (l), depends on angle of attack. The colour intensity corresponds with the p-value of the Wilcoxon rank-sum test for aspect ratio at constant angle of attack (black area; see the electronic supplementary material, figure S4).

Figure 3.

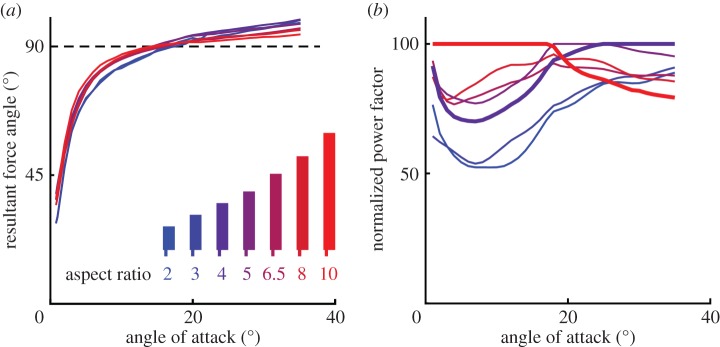
Model wings with aspect ratio 4, close to values for hummingbird wings, perform well at incidence beyond 20°. (a) High aspect ratio wings best approximate the resultant force angle predicted by the quasi-steady model for flat plates, because of their relatively high drag. (b) Reynolds averaged power factor among aspect ratio wings is compared with the wing that attains maximum power factor at every incidence (100%). This normalized power factor shows that aspect ratio 10 wings perform best below 20° angle of attack, but do poorly at higher incidence; aspect ratio 4 wings provide the best trade-off above 20°.

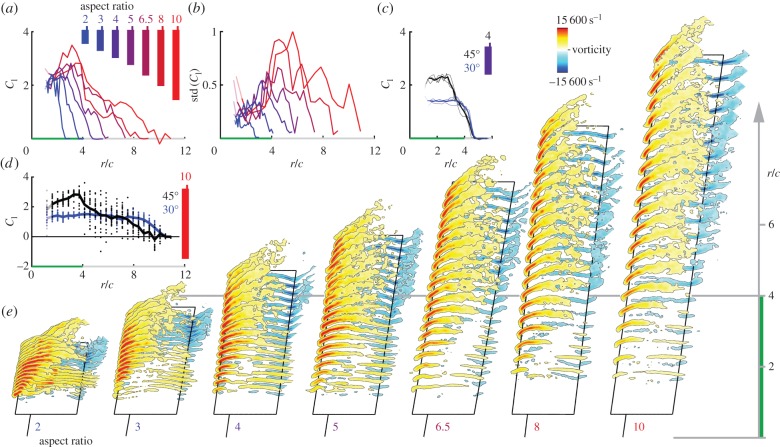
Delayed stall is concentrated inboard near the centre of rotation of each revolving wing irrespective of aspect ratio and Re (figure 4; electronic supplementary material, figure S6 and S7). The radial limit of stall delay, r/c < 4, corresponds with comparable maximal lift coefficients for all wings. Outboard vortex lift distribution drops at α = 45° (figure 4a,d). This drop in vortex lift implies the wing stalls outboard, which is confirmed by high standard deviation for r/c > 4 (figure 4b,d). The strong radial difference in LEV dynamics—inboard attachment versus outboard separation—is further evident from flow fields. Both the vorticity field (figure 4e) and a robust vortex identification scheme (electronic supplementary material, figure S8) confirm that the LEV is attached along the upper surface inboard, whereas it is detached outboard. At outboard stations vortex shedding leads to smeared-out positive vorticity (time-averaged) at the leading edge and negative vorticity at the trailing edge (figure 4e), which we dynamically illustrate in electronic supplementary material, movie S1. At the wingtip, the airflow further separates and forms a tip vortex that merges with the wake. The thickness of the near wake is much larger outboard of r/c ∼ 4 (figure 5). This increase in wake thickness results from vortex detachment at the leading edge of the wing, which results in stagnant flow above the wing that is dragged along, causing momentum loss with respect to the wing. Inboard stall delay, corresponding with an attached LEV, results in a much thinner wake velocity profile (figure 5b), and thus a much lower local profile drag [18]. Comparison of the stagnant flow area at α = 45° confirms that stall delay occurs at inboard radii for which r/c < 4 for all revolving wings (figure 5c). This reduces profile drag [18] of low aspect ratio wings and explains why they generate less drag and higher power factor at high α, compared to high aspect ratio wings (figures 2a–d and 3).

Figure 4.

The LEV remains attached and lift is elevated at radii up to four chord lengths at 45° (highlighted with a green bar). Vorticity is integrated (excluding the lower surface) at Re = 13 000 to approximate lift of model wings. (a,b) The average local vortex lift coefficient, C_l, steeply decreases for r/c > 4, whereas standard deviation increases. At the first station the hub is visible, which increases std artificially (semitransparent). (c) The vortex lift distribution is Re insensitive (thin lines, Re = 5000, 13 000, 25 000; thick line, average) and similar to C. anna (figure 1b). (d) When the angle of attack of an aspect ratio 10 wing increases from 30° to 45° vortex lift increases inboard of r/c ∼ 4 and lift starts to fluctuate outboard (line, average; points, instantaneous values). (e) Average vorticity concentration reveals an attached LEV inboard of r/c ∼ 4. Outboard vortices detach from the leading (yellow) and trailing edge (blue).

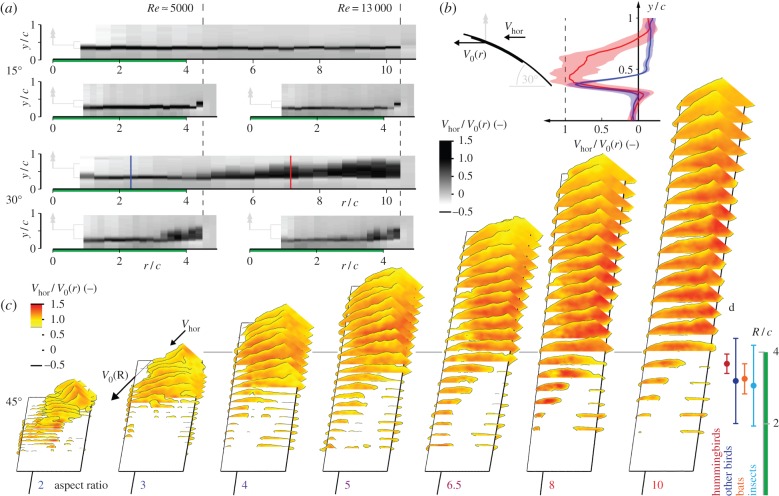
Figure 5.

At high angle of attack the near wake is thick at radii beyond four chord lengths, because the flow separates from the upper surface. Distributions of horizontal speed (V_hor) at 1/8th chord behind the revolving wing (local wing speed, V₀(r)) at Re = 13 000 illustrate this. (a) At 15° the wake is formed by an attached boundary layer, which thins with radially increasing local Re for aspect ratio 10 wings (above)—but not for aspect ratio 4 wings at Re 5000 (below left) and Re 13 000 (below right). The lack of radial effect due to Re on aspect ratio 4 wings help show that r/c effects dominate over local Re on the aspect ratio 10 wing at 30°. (b) The wake velocity profile at 30° thickens and fluctuates outboard (line, average; area, std; radial position, see (a)). (c) Outboard of r/c ∼ 4 the revolving wings drag a large volume of stagnant air along at 45° (clipped at 1/8th chord beyond trailing edge). (d) The mean R/c of hummingbirds (n = 65), other birds (n = 117), bats (n = 39) and insects (n = 98) is between 3 and 4 [11], facilitating stall delay.

Our experiments show that wing revolution and aspect ratio mediate stall delay in concert up to wing radii of about four chord lengths. This effect of aspect ratio with respect to the centre of rotation on stall delay was first demonstrated by extending the radius of a constant aspect ratio wing at Re 110–14 000 [11]. This was later tested and confirmed for Re 1400 [23]. We now confirm this for a more relevant manipulation, by varying the aspect ratio of a rectangular wing with a constant centre of rotation at Re up to 25 000; this range of aspect ratios includes the wings of micro-helicopters, quadcopters, hummingbirds [3,36] and hovering animals in general [5,7,8]. Whereas the earlier study considered only one wing revolution [11], this study now shows that stall delay is also robust to continuous revolution within a radial limit of four chord lengths—for all combinations of aspect ratio and Reynolds numbers studied here. Similar stall delay has been demonstrated for radii up to three chord lengths at the much larger scales of propellers and rotors that operate at Re = 250 000 up to millions [37–39]. This finding contrasts an earlier study by Ellington using spinning flat plates [40], the cambered plates tested here perform much better, suggesting that camber might help delay stall at Reynolds numbers beyond the laminar flow regime of insects. At the lower Reynolds numbers of insects, CFD studies find that the LEV is unstable outboard on flat, high aspect ratio, wings [41,42]. Notwithstanding significant differences in laminar versus turbulent boundary layers, scale analysis for all of these wings show that centrifugal and Coriolis accelerations in the boundary layer contribute to stall delay across scales [11,33,34,37,43]. The average wing aspect ratio of hummingbirds, and many other birds, bats and insects falls between 3 and 4 [11] (figure 5d). Our findings suggest that this intermediate aspect ratio can help keep their LEVs in place during slow-hovering flight, in particular at midstroke when revolving a wing approximates flapping [6,12]. The peak power efficiency of revolving aspect ratio 4 wings coincides with the aspect ratio of hummingbird wings, which is 3.7 on average (s.d. = 0.3; n = 65; figure 5d). Whereas our measurements show that revolving aspect ratio 4 ‘hummingbird wings’ outperform aspect ratio 10 ‘helicopter wings’ at high angle of attack, they also show that aspect ratio 10 ‘helicopter wings’ perform better at low angle of attack. This functional divide between low and high angle of attack performance helps explain aspect ratio differences in nature versus technology and can thus guide drone design.

Funding statement

This work was supported by NWO-ALW grant no. 817.02.012.