Abstract
Robust motor behaviors emerge from neuromechanical interactions that are nonlinear, have delays, and contain redundant neural and biomechanical components. For example, in standing balance a subject’s muscle activity (neural control) decreases as stance width (biomechanics) increases when responding to a lateral perturbation, yet the center-of-mass motion (behavior) is nearly identical regardless of stance width. We present stability radius, a technique from robust control theory, to overcome the limitations of classical stability analysis tools, such as gain margin, which are insufficient for predicting how concurrent changes in both biomechanics (plant) and neural control (controller) affect system behavior. We first present the theory and then an application to a neuromechanical model of frontal-plane standing balance with delayed feedback. We show that stability radius can quantify differences in the sensitivity of system behavior to parameter changes, and predict that narrowing stance width increases system robustness. We further demonstrate that selecting combinations of stance width (biomechanics) and feedback gains (neural control) that have the same stability radius produce similar center-of-mass behavior in simulation. Therefore, stability radius may provide a useful tool for understanding neuromechanical interactions in movement and could aid in the design of devices and therapies for improving motor function.
1 Introduction
Biological systems are composed of many complex, interacting components and as Aristotle remarked over two millennia ago “…the whole is something beside the parts.” Even with sophisticated computational models, behaviors resulting from such interactions are difficult to analyze and compare using tools from classical control theory that divide a system’s dynamics into components that are to be controlled (plant) and those that are added to achieve a desired behavior (controller). For example, neuromechanical models of human movement contain redundant biomechanical and inherently delayed neural feedback control components that can change concurrently in order to achieve a desired behavior. Unfortunately, classical stability analysis tools, such as gain margin [1], cannot be used to compare behavior across neuromechanical conditions where both biomechanics (plant) and neural control (controller) change during a task. To overcome these challenges we introduce the technique of stability radius, an approach that builds upon eigenvalue analysis as a compact representation of dynamical behavior.
The technique of stability radius is useful for identifying different sets of parameter values that can produce similar behaviors, or quantifying the sensitivity of a system’s stability to parameter changes. The mathematical theory is derived from the fields of pseudospectral analysis [2, 3] and robust control [4, 5]. Initially developed for linear time invariant systems, it has been expanded to systems with feedback delays [6–8]. Many techniques for stability analysis, such as Lyapunov’s indirect method, utilize eigenvalues to classify the stability of dynamical behavior. However, the eigenvalues by themselves do not indicate sensitivity of stability to perturbations, modeling errors or parameter changes. Furthermore, it may be difficult to calculate eigenvalues for some systems, e.g. delayed systems having an infinite number of eigenvalues. Instead of using eigenvalues directly to characterize stability, the stability radius gives a scalar measure of the smallest change to any system parameter that would result in instability. This provides a single measure to compare stability of one system against itself as parameters change, as well as against entirely different systems. Stability radius can also be used to test the sensitivity of system stability to model parameters. This single number can be used to classify a system’s dynamical behavior on a relative scale of stability and to predict system responses across different modeling conditions.
Given these characteristics, stability radius may be well suited to quantify changes in stability due to changes in biomechanical and neural feedback parameters in neuromechanical systems. Neuromechanical systems in different biomechanical contexts can achieve similar motor performance by altering biomechanical configuration, neural strategy, or both [9]. Experiments in the upper extremity suggest that changes in biomechanical configuration and neural control are the result of a neural strategy to maximize stability in the presence of a disturbance [10–12]. Here, our application of the stability radius to the control of frontal-plane balance control is motivated by the experimental observation that subjects respond to support surface translations in the frontal-plane with nearly identical center-of-mass motion regardless of their stance width [13]; however, muscle activity is observed to decrease as stance width increases, demonstrating a concurrent change in neural control [13–15]. We propose that the similar behavior observed across stance widths during standing balance may be the result of a neural strategy to select feedback gains that maximize stability for a given stance width. Previously, we developed a model of frontal-plane balance that demonstrated increasing stance width necessitates decreasing delayed feedback gains to maintain stability [16]. However, using classical stability analysis we were not able to compare stability across biomechanical contexts and could not quantify the contribution of neural versus biomechanical parameters in achieving a given behavior. This was because traditional tools to compare stability, such as gain margin, are formulated based on the premise that the stability of the plant, or musculoskeletal system in our case, is fixed and only alterations to control affect stability.
Here we present the theoretical background and context to introduce the stability radius technique for a linearized system with and without delays. Next, we apply this technique to our frontal-plane model of balance control [16] to illustrate its utility in characterizing changes in stability from different delayed feedback gains (controller parameters) and stance widths (plant parameters). We use stability radius to identify feedback gains that produce either maximum stability or similar performance across stance widths, i.e. postural configurations. We show that model feedback parameters that have the same stability radius across postural configurations also produce similar trajectories in simulations. The stability radius therefore predicts how neural control and biomechanical parameters interact to produce a desired behavior.
2 Theory
We introduce stability radius as a robust measure of the sensitivity of a system’s asymptotic stability to parameter changes. Starting with the linearized equations of motion we provide a brief overview of how to identify the characteristic equation and the eigenvalues for non-delayed and delayed systems. Next, we introduce ε-pseudospectra as a method to analyze the sensitivity of eigenvalues to parameter changes. Finally, we connect the concepts of stability and ε-pseudospectra to give a definition of stability radius.
2.1 Characteristic equation
Here we show how to generate a characteristic equation for a large class of ordinary differential equations (ODEs) with delays. We start our discussion assuming the dynamic equations are linear and first-order. This can be achieved for nonlinear systems by linearizing the ODE about an equilibrium point using Taylor-series expansion and converting higher-order linear ODEs into a system of first-order ODEs [17]. We first show how to generate the characteristic equation for a linear system of first-order ODEs without delays and then expand this to delayed systems.
A system of linear, constant-coefficient, first-order ODEs can be described with a system matrix, A, and state vector, x.
| (1) |
The deterministic solution for this system is a matrix exponential (2), which can be evaluated by writing the system as (3) where the new matrices are the result of the eigenvalue decomposition, A=UΛU−1.
| (2) |
| (3) |
The matrix, Λ, is a diagonal matrix whose elements are the eigenvalues of the matrix, A, and are found algebraically by solving for the roots of the characteristic equation (4) [17].
| (4) |
A similar method can be applied to linear, constant-coefficient, delayed differential equations (DDE) of the retarded type (5). A retarded DDE has delays only in differential terms whose order is less than the maximum differential order of the system. This form of equation can be written where the terms collected in matrix, Ak, are associated with the k-th delay, τk.
| (5) |
The characteristic equation for the delayed system (6) now includes exponential terms [18]. The addition of transcendental functions results in an infinite number of solutions to this characteristic equation [19]; therefore, DDEs of this form will have an infinite number of eigenvalues.
| (6) |
2.2 System stability
Eigenvalues are critical descriptors of a dynamical system’s stability. We first give an overview of the definition of eigenvalues of a matrix, show how this leads to a characteristic equation and then define asymptotic stability.
The eigenvalues of a system are the set of complex values, λ∈C, for a matrix, A∈Cn×n, associated with eigenvectors, v∈Cn≠0, that satisfy (7).
| (7) |
After rewriting (7) we require that solutions for eigenvalues and eigenvectors non-trivially satisfy the following relation.
| (8) |
For (8) to hold and satisfy v≠0, then the resulting matrix of (A−λI) must be singular. In other words, if the inverse existed (i.e. the matrix was non-singular) then v=0, which violates the definition of the eigenvector. Thus, to ensure that the matrix is singular its determinant must be zero. This leads to the characteristic equation for a matrix, which is identical in form to the characteristic equation of an ODE (4).
| (9) |
In linear ODEs, with or without delays, eigenvalues are the exponential constants that define the time evolution of the system behavior. Eigenvalues with positive real part are considered unstable, because as time advances the eventual behavior of the system will tend to depart from equilibrium. Thus, asymptotic stability of a linear system is defined by all eigenvalues having strictly negative real part. Similarly, this definition of asymptotic stability may be extended to the class of non-linear ODEs with Lyapunov’s Indirect Method, which states that the eigenvalues of the linearized system about an equilibrium point describe the system’s stability if the eigenvalues are not identically zero [20].
2.3 ε-pseudospectra
Here we define ε-pseudospectra and show its relationship to eigenvalues. We give equations for calculating ε-pseudospectra and then describe how this gives a measure of sensitivity of eigenvalues to parameter changes.
The sensitivity of an eigenvalue to parameter change can be found by comparing eigenvalues of the original system to new eigenvalues calculated from a system with altered parameters. For a specified magnitude of parameter change there are a set of new eigenvalues, which are displaced by some amount compared to the eigenvalues of the original system. This set of new eigenvalues (10) is the ε-pseudospectra for a corresponding set of parameter perturbations, E∈Cn×n, whose magnitude is less than a specified value, ε. The magnitude of the perturbation matrix, E, can be evaluated using any matrix norm and we will use the Frobenius norm, or 2-norm. Thus, the distribution of ε-pseudospectra about the eigenvalue give a measure of sensitivity to a specified amount of parameter change.
| (10) |
An alternate definition, to avoid calculating eigenvalues directly, is to use the knowledge that the ε-pseudospectra are the perturbed eigenvalues, z=λ+δ. First, consider the definition of the new eigenvalues, with normalized eigenvectors, |v|=1.
| (11) |
Next, the parameter perturbation matrix is defined as, E=suv*, with s<ε, and |u|=1. Here we use the notation of a superscript asterisk to designate the complex conjugate of v as v*. Then, we introduce the resolvent (12) of the matrix, A, at a scalar value, z∈C [3].
| (12) |
Note that the resolvent evaluated at the eigenvalues of A will produce a singular matrix having a norm with infinite magnitude. Furthermore, the norm of the resolvent evaluated away from the eigenvalues will, by definition, be non-singular and finite. Using these definitions equation (11) can be rewritten as (2.3) in terms of the resolvent and the definition of the parameter perturbation.
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
Taking the norm of (2.3) relates the magnitude of the resolvent to the the magnitude of the parameter change. This is accomplished by using the property of a norm that |X||Y|≥|XY|.
| (18) |
| (19) |
| (20) |
Finally, the ε-pseudospectra are now defined as the values for which the inverse of the resolvent is less than a specified magnitude of parameter perturbation.
| (21) |
This form also allows for a compact extension to ODEs with delays by using the resolvent for delayed differential equations [8].
| (22) |
Simplified calculation of the ε-pseudospectra can be achieved by using the Frobenius norm, or matrix 2-norm, in conjunction with properties of singular value decomposition (SVD). A property of the SVD is that the largest singular value, smax, of a matrix, B, is equivalent to the matrix’s Frobenius norm. In addition, the largest singular value, smax, of a matrix’s inverse is equal to the inverse of the smallest singular value, smin.
| (23) |
Substituting (22) into (21) and using the relations of (23) results in a compact and stable method to numerically calculate the ε-pseudospectra for non-delayed (k=0) and delayed (k>0) systems.
| (24) |
The ε-pseudospectra are the values of z that satisfy (24). The value of the resolvent can be computed by evaluating the left-hand side of (24) at a desired grid of values over a region of the complex plane. The resulting surface will have valleys with a minimum zero value about the eigenvalues. Narrow valleys suggest eigenvalues that are less sensitive to parameter change while wide valleys correspond to the eigenvalues that are most sensitive to parameter change. Therefore, the ε-pseudospectra correspond to the open subset of the complex plane bounded by the level curve formed by the norm of the resolvent equal to ε−1.
2.4 Stability radius
We now present the complex stability radius with unstructured parameter perturbation using the concepts of stability and ε-pseudospectra. The mathematical definition is extended to the delayed case and presented in a form that can be implemented numerically.
Stability radius is defined as the smallest change to a system parameter that results in shifting eigenvalues so that the corresponding system is unstable. In terms of the ε-pseudospectra this is equivalent to finding the smallest magnitude of parameter change where the pseudospectral set is grown to just contain part of the positive right-half complex plane. When the parameter perturbation is allowed to be a complex value the mathematical definition of stability radius is:
| (25) |
| (26) |
| (27) |
This can be further simplified by minimizing |R(z)|−1 in place of ε. In addition, we can restrict the minimization to only pseudospectral values strictly on the boundary of stability, ℝ(z)=0.
| (28) |
Finally, using properties of the SVD (23) and the extended resolvent (22) we can write a compact and stable method to numerically calculate the complex stability radius for non-delayed (k=0) and delayed (k>0) systems. Therefore, minimization can be achieved quickly by evaluating the SVD of the characteristic equation only over values on the imaginary axis.
| (29) |
3 Application
We present an application of stability radius to identify how changes in delayed feedback gains and stance width affect frontal-plane balance control. Subjects during standing balance respond to support surface translations in the frontal-plane with nearly identical center-of-mass motion regardless of their stance width [14]; however, muscle activity is observed to decrease as stance width increases, demonstrating a change in neural control [13]. We used stability radius as a tool to analyze the changes in stability due to different stance widths and delayed feedback gains.
First, we give an overview of a mathematical model of frontal-plane standing balance. Using this model we show the steps necessary to calculate the stability radius for a set of parameters. Then, we use stability radius to identify the feedback gains that produce the maximum stability at nominal stance width and the feedback gains that produce similar stability radius at narrow and wide stance width. Finally, we compare simulated center-of-mass responses at narrow and wide stance width using the feedback gains identified to have the same stability radius.
3.1 Model
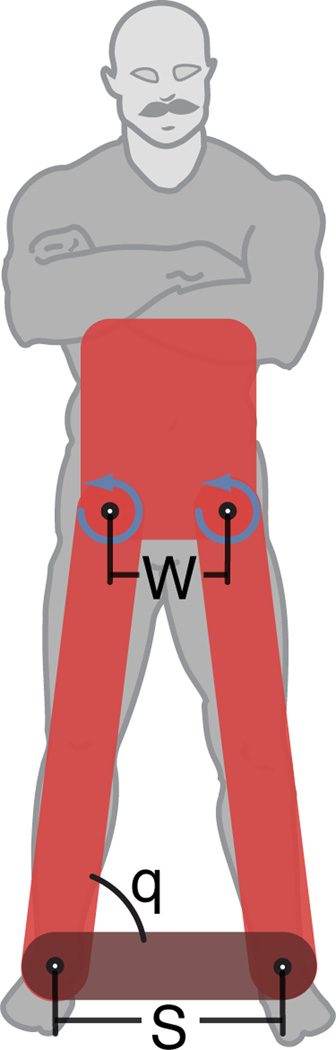
We examined a delayed second order system that modeled human frontal-plane standing balance as a four-bar linkage (Fig 1) with ankle angle, q, using scaled anthropometric parameters based on healthy adults.
| (30) |
Inertial, I, coriolis, V, and gravitational, G, terms were included in the closed-chain, nonlinear equations of motion. Total joint torque applied at the hips necessary to maintain the initial configuration was generated by feedback gains of position, kp, and velocity, kv, with a delay, τ, and geometric scaling, (S is stance width, W is hip width). Nominal parameters for the model were selected based on average anthropometric values of height (1.8 m), mass (72 kg), and delay (100 ms). Further details of the model can be found in Bingham et al. 2011 [16].
Figure 1.
Frontal-plane model of human mediolateral balance control. Frontal-plane motion of the body was modeled as a four-bar linkage. Two bars represented the legs, the third bar was the torso, and the fourth bar was the ground. Perturbations were applied as initial conditions in lieu of ground translations. Important parameters of the model were the hip width (W), stance width (S), and ankle angle (q).
3.2 Analysis
The system (30) was first linearized about the symmetric equilibrium condition to generate a linear system of first order equations with states, x= [q:q]T.
| (31) |
Next, using (6) the characteristic equation for the system was formed.
| (32) |
We explored the stability of the system at the nominal stance width (S/W=1) by computing the dominant eigenvalues across all feasible pairs of delayed feedback gains. Previously identified stability boundaries were used to restrict feedback gains that produced unstable dynamics [16]. Across this region, we examined each stable gain pair in a 100×100 grid. First, we verified stability by ensuring that none of the roots of the characteristic equation had a positive real part, which was accomplished by using the Cauchy residue theorem and evaluating a path integral over the right-half plane to determine that there was no residual [21]. To numerically evaluate the path integral and to determine the values of a limited set of eigenvalues for each solution we used Cauchy’s argument principle and a modification to the Lehmer polynomial root finding algorithm [19, 22].
For representative cases, we computed the ε-pseudospectra to investigate the sensitivity of the dominant eigenvalues to perturbations. For each case, the magnitude of the resolvent was evaluated across a grid of complex values and these magnitudes were plotted as level sets to illustrate the pseudospectral variations across the level of perturbation (1.0×10−3<ε<2.0).
The stability radius (33) for each stable, delayed feedback gain pair was also calculated for each of 16 stance widths ranging from S/W=0.5 to 2.0. Each stability radius result was solved using a bisection line search over the set of complex values along the imaginary axis to identify the minimum value of the argument.
| (33) |
To compare the relative stability of feedback gain pairs within the same stance width the stability radius was compared across all feasible gain values at the nominal stance width (S/W=1.0). A single pair of delayed feedback gains was selected that resulted in the maximum stability radius for the model at nominal stance width.
To compare the relative stability of feedback gain pairs across stance widths, kp and kv gains were found that resulted in the same stability radius across stance widths. Across the range of stance ratios the largest common stability radius was identified and for each stance width the associated delayed feedback gain pair was recorded.
Finally, to test the behaviors resulting from the selected feedback gains, we simulated the motions of the COM using the fully nonlinear equations of motion in both narrow and wide stances. An initial velocity disturbance was imposed (q0 = [0 rad, 0.1 rad/s]) to the model at narrow (S/W=0.5) and wide (S/W=2.0) stance widths using the respective delayed feedback gain pairs associated with the same stability radius value.
4 Results
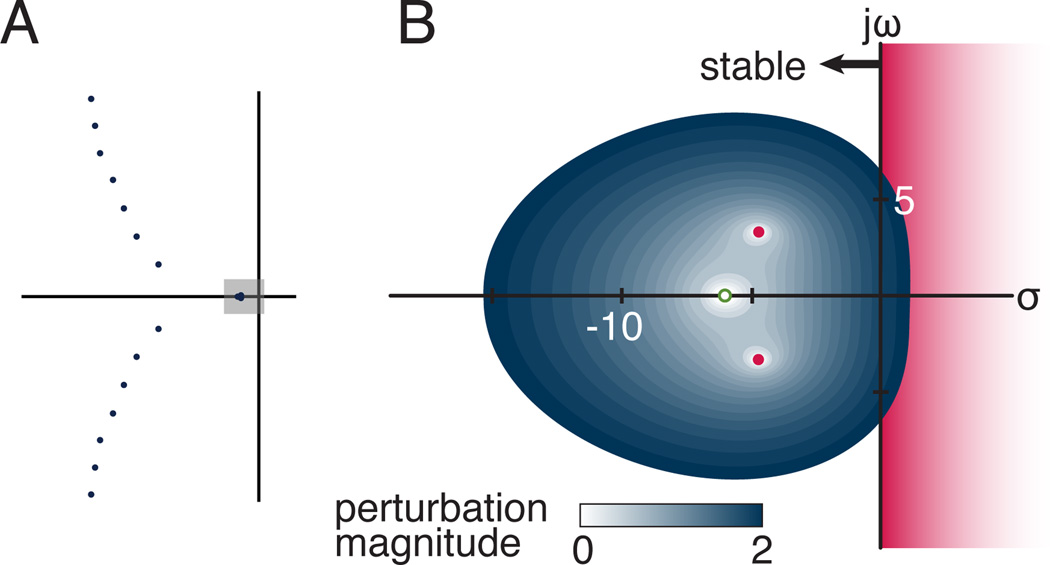
A pattern of three stable dominant eigenvalues was found for all stable feedback gains for the model at the nominal stance width (Fig. 2).
Figure 2.
Eigenvalues and pseudospectra for a single feedback gain pair at the nominal stance width. (A) A subset of the infinite number of eigenvalues for the delayed four-bar linkage model (S/W=2, kp=243 N-m/rad, and kv=57 N-m/rad/s). Shaded box is complex region surrounding the three dominant eigenvalues and enlarged in (B) The pseudospectra corresponding to a perturbation that caused the eigenvalues to go unstable is represented by dotted lines. The value of the smallest perturbation to cause any of the eigenvalues to go unstable was the stability radius for this system. For the neuromechanical system modeled here, the more negative eigenvalue (unfilled dot) went unstable at a lower level of perturbation than the dominant eigenvalues that were closer to the imaginary axis (filled dots).
As the perturbation ε increased in the stable range from 0.0 to 0.8, the ε-pseudospectra of these eigenvalues demonstrated that the most positive eigenvalue was often least sensitive to parameter changes (Fig. 2). That is, an eigenvalue further from the imaginary axis (Fig. 2B) was more sensitive to the imposed perturbation, crossing the imaginary axis first and rendering the system unstable.
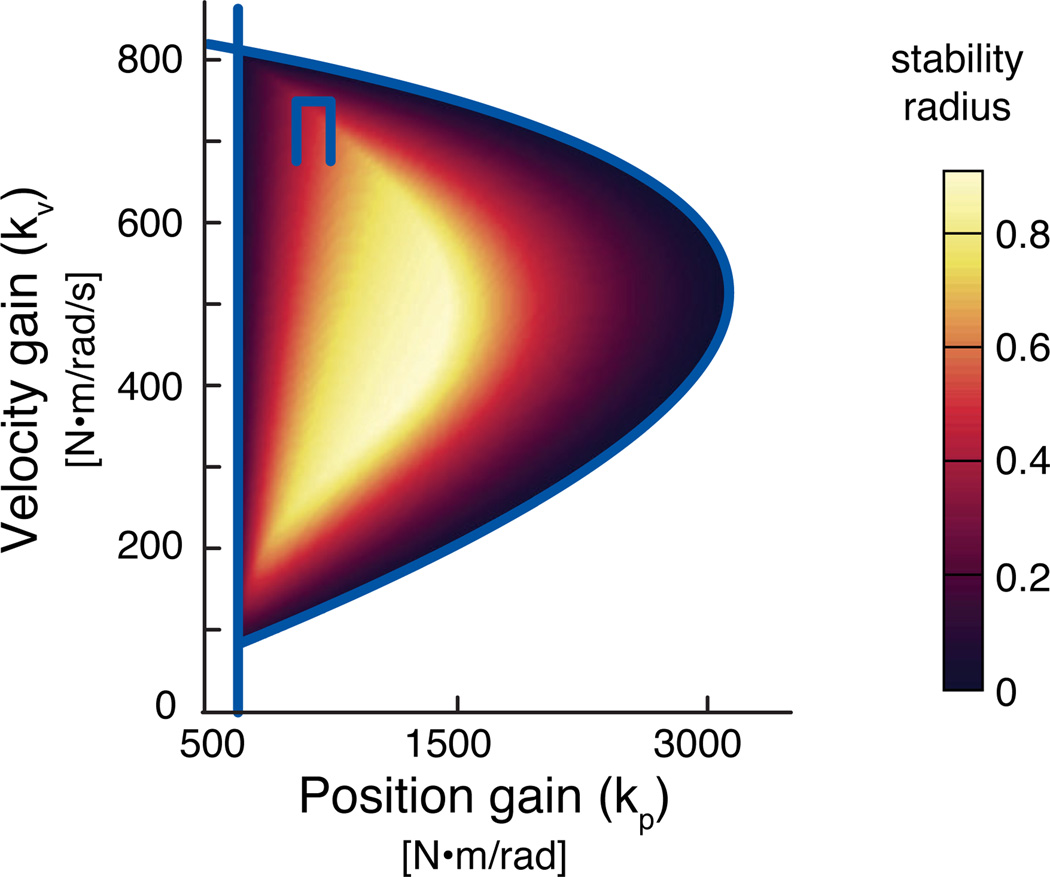
Across all stable feedback gain pairs in the nominal stance width, the stability radius was found to be lowest at the boundaries and highest for mid-range gain values (Fig. 3). The maximum stability radius (r=0.92) at the nominal stance (S/W=1.0) was found when kp=1540 N-m/rad and kv=405 N-m/rad/s. This stable feedback gain pair produced system behavior that was least sensitive to changes in system parameters.
Figure 3.
Stability radius across all stable feedback gains at the nominal stance width. The solid lines giving a D-shaped boundary encloses the range of all stable feedback gains at the nominal stance width (S/W=1.0). Shaded intensity represents the value of the stability radius for each stable gain pair. Lighter values have greater stability radius and resulted in system behavior that was less sensitive to parameter variations.
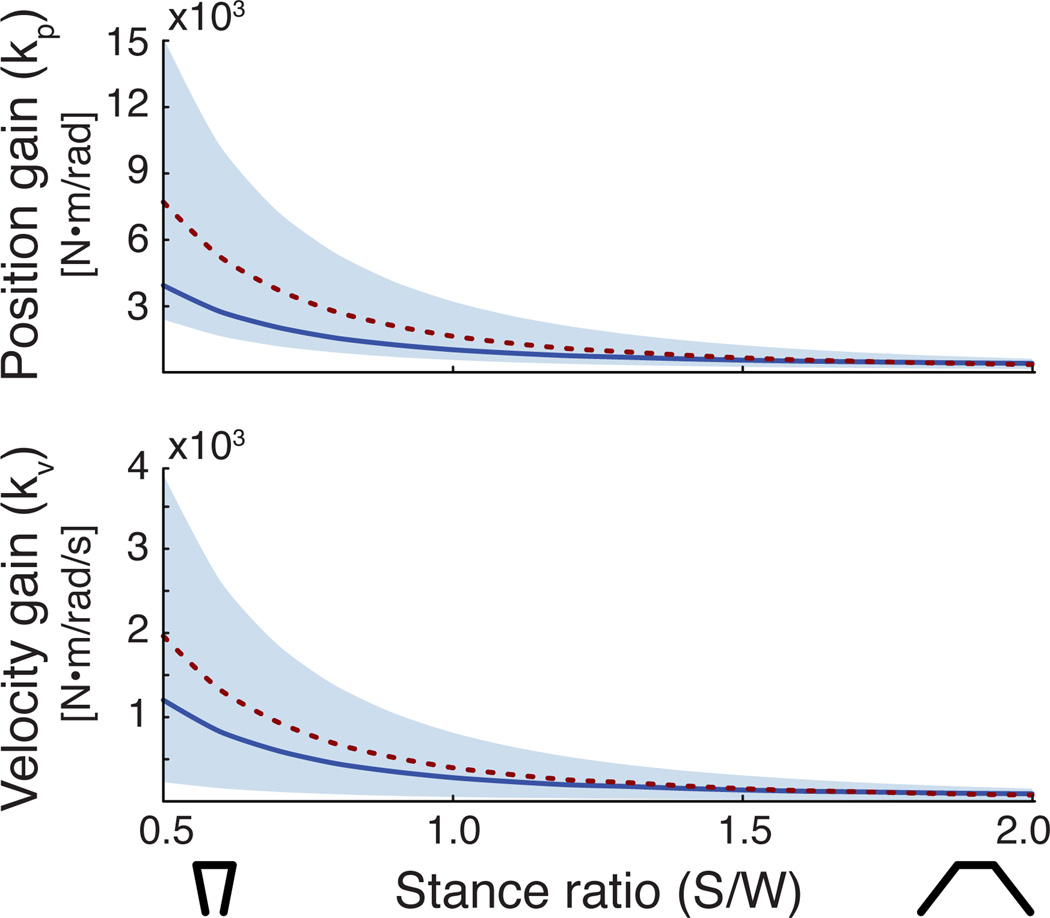
Maximum stability radius was found to decrease as stance width increased. Maximum stability radius at narrow stance (r=0.93 at S/W=0.5) was associated with larger feedback gains (kp=7312 N-m/rad, kv=1982 N-m/rad/s) and stability radius at wide stance (r=0.89 at S/W=2.0) had smaller feedback gains (kp=323 N-m/rad, kv=79 N-m/rad/s) (dotted line in Fig. 4). Narrow stance was found to be less sensitive to parameter perturbations than wide stance.
Figure 4.
Stable feedback gains across stance width. The shaded regions defined all stable feedback gains across stance widths. The dotted line indicates the feedback gain pairs that produced maximum stability radius across stance widths. The solid line indicates the feedback gain values that produced the same stability radius (r=0.8) across stance widths.
The feedback gains kp and kv that maintained the same stability radius (r=0.8) increased by over 16× from wide (kp=243 N/rad and kv=57 N/rad/s) to narrow (kp=3951 N-m/rad and kv=1201 N-m/rad/s) stance (solid line in Fig. 4). This similar level of stability radius was found to be associated with gains that were within the mid-range of feasible feedback gains.
Simulations of the model at narrow and wide stance using feedback gains with the same stability radius (r=0.8) produced similar center-of-mass kinematics (Fig. 5). Trajectories of the center-of-mass position were characterized by a near critically damped response in both cases.
Figure 5.
Simulated center-of-mass position across stance widths using feedback gains that produce the same stability radius. (A) Although feedback gain values differed substantially across stance widths, the resulting center-of-mass motion produced in response to a change in the initial state of the system was similar in narrow (solid) and wide (dotted) stance widths when feedback gains with the same stability radius were used. (B) The resulting torque necessary to generate the center-of-mass response was an order of magnitude smaller for the wide stance compared to the narrow stance.
5 Discussion
Here we demonstrated that stability radius is a useful metric for comparing behavior across neuromechanical conditions where both biomechanics (plant) and neural control (controller) change during a task. Similar to previous applications of stability radius [4, 23] we identified the most robust neural feedback gains (controller parameters) for a given stance width (plant parameter). In addition, we used stability radius to quantify and predict how concurrent changes in neural control and biomechanical configuration affected system behavior. Using stability radius we identified the underlying delayed neural feedback gains associated with a stance width that produced similar center-of-mass behavior. Stability radius may provide insight into the neuromechanical interactions governing robust balance control by identifying the neural control parameters that yield the same stability radius across changes in biomechanical configuration. This type of analysis could be extended to understanding general principles of neuromotor control.
In contrast to typical stability analyses that explore tolerable delays, in our application the delay was a fixed parameter reflecting measured neural conduction and processing time. Standard delayed-system analyses pose a problem of finding the maximum delay for which the system is stable [18, 24] or the sensitivity of stability to delays [7]. In contrast, delays in neuromechanical systems are remarkably invariant to system changes [13, 25]. Thus, the problem is to identify how variations in system parameters, and not changes in delay, cause instability. Stability radius is particularly useful for delayed systems, because it is not necessary to explicitly compute any of the infinite number of eigenvalues associated with a delayed system.
The application of stability radius to a simple neuromechanical model of balance control with delayed neural feedback improved our ability to compare postural behaviors across biomechanical configurations. In our prior work using eigenvalue analysis, it was only possible to determine the set of feedback gains that produced stable behaviors at each stance width and to compare the relative stability of each solution within a stance width using the gain margin [16]. However, it was not possible to compare stability across stance widths without performing explicit forward simulations of the system using the different parameter values. This was because the gain margin is computed with respect to the boundary of stability, which was specific to each stance width. Thus, gain margin does not take into account the changes in stability due to changes in configuration, and provides only a relative measure of stability within a stance width. In contrast, the stability radius is an absolute measurement of system behavior which allows comparisons of feedback gains across stance widths. For example, whereas the maximum gain margin was identical across stance widths, the stability radius demonstrated that narrow stance widths are actually more robust to parameter variations, consistent with our previous simulation results [16].
We show that changes in system behavior due to perturbations to the state variables of the model are described by the stability radius. Previously we demonstrated that precise tuning of delayed neural feedback gains were necessary to produce similar behaviors across stance widths, but we lacked a method to prospectively select the appropriate gains that generated a desired behavior [16]. We replicated the experimentally-observed similarity in center-of-mass kinematics across stance widths in response to imposed motion of the support surface by selecting feedback parameters with the same stability radii across stance widths. Thus, feedback gains and stance widths that reduced the sensitivity of the behavior to parameter variation were the same as those that led to similar responses to physical perturbations. Although the similarity in center-of-mass kinematics could be the result of the nervous system selecting robust feedback gains it is also possible that the nervous system selects the trajectory itself to produce robust behaviors.
Our results support the hypothesis that the nervous system may employ a neural strategy for selecting feedback gains and biomechanical configurations that reduces the sensitivity to parameter variation arising from sensory noise or imperfect control. The feedback gains in the model that produced maximum stability radius were in the mid-range of possible stable values, consistent with the feedback gain values identified by fitting the model to experimental data [16]. Similarly, research in upper-extremity control also suggests that motor strategies are selected that reduce sensitivity to parameter variation in dexterous tasks [26, 27].
Our results corroborate the idea that stability is maximized in unstable motor tasks, and stability radius could contribute to a better understanding of how increased stability is achieved. Previously, arm impedance has been shown to increase by muscle co-contraction when generating forces in an unstable environment [10, 28, 29]. However, limb impedance can be altered by both muscle activity [30] as well as limb configuration [11]. Using stability radius, the contribution of muscle activity and limb configuration on stability could be dissociated. This may be useful for understanding modulation of feedback gains in a given context, as well as the selection of a particular configuration or strategy to achieve a desired behavior.
Our current formulation for stability radius assumes a conservative estimate of how parameters affect the stability of a neuromechanical system. Our perturbation to the system, E, assumed that the musculoskeletal and neural feedback gain parameters were equally variable. In this unstructured case, all parameters contributed equally to the stability radius, leading to a conservative estimate. It is possible to structure the parameter perturbations so that only specific parameters are affected [2, 23, 31]. Such a weighting may be useful in cases where some parameters are known to a greater accuracy and are unlikely to be perturbed, e.g. mass of the body, and could lead to a less conservative stability radius estimate. We also assumed that perturbations to parameters could be complex valued, which begs the question: When do real-world parameters have complex value? While the perturbations to system parameters are almost always real-valued, it is possible that imposing complex-valued perturbations could reveal how transient changes in parameters, e.g. oscillations from sensory noise, may further alter stability [3, 32]. In cases where it is reasonable to assume that parameter perturbations are only achieved through real values, such as uncertainty in knowing limb inertia, the perturbations can be restricted to only real values using a slightly more complicated minimization technique to identify the stability radius [4, 33].
Using stability radius to assess a system’s behavior is limited to those systems that can be mathematically modeled and their equilibria determined. This restricts the analysis to local behavior determined by the fixed points of the dynamical system. Therefore, stability radius is only descriptive of the local stability and does not explain the global stability of a system. Fortunately this does not encumber the method any more than other traditional stability methods (e.g. Lyapunov’s indirect method) when examining nonlinear systems as the local stability of the nonlinear and linearized systems are equivalent at the equilibria [20]. Furthermore, stability radius quantifies the sensitivity of an equilibrium point to perturbations or modeling uncertainties, which quantifies the degree to which the linearized system predicts behavior away from the equilibrium.
It is important to note that the application presented in this paper is a first step in verifying stability radius as a useful method for analyzing robustness of biological systems in general. To fully validate this method, its applicability should be verified across multiple tasks and conditions. We propose that this method may be directly applied to station-keeping behaviors, such as maintaining balance during standing [16], maintaining a constant force in an unstable environment [34], or fixating on a visual target [35]. Cyclical behaviors, such as locomotion, breathing or heart-beat, would require additional steps in order to apply the stability radius technique such as the application of Floquet theory; the resulting system could then be analyzed using the methods presented in this paper.
It is important to note that the application presented is a first step in verifying stability radius as a useful method for analyzing robustness of biological systems. To fully validate this method, its applicability should be verified across multiple tasks and conditions. We propose that this method may be directly applied to station-keeping behaviors, such as maintaining balance during standing [16], maintaining a constant force in an unstable environment [34], or fixating on a visual target [35]. Cyclical behaviors, such as locomotion, breathing or heart-beat, would require additional steps in order to apply the stability radius technique. We propose that cyclical systems could be transformed into the necessary form using Floquet theory and the resulting system could be analyzed using the methods presented in this paper.
To conclude, stability radius has many benefits over using eigenvalues alone for analysis of neuromechanical systems. Specifically, we were able to quantify the effect of both biomechanical and neural parameters on the stability of frontal-plane standing balance. Stability radius is generalizable and can be applied to a variety of complex systems that may be nonlinear and have delays. Thus, stability radius lends itself to additional applications that were not explored in the example presented in this paper. Stability radius can be used as a tool for bifurcation analysis to identify critical parameter values that cause large changes in system behavior [36]. Often the parameters in neuromechanical models are unknown, using stability radius to determine the sensitivity of stability to these parameters can help to identify error bounds and simulation accuracy [37]. Determining muscle activation and musculoskeletal parameters that reproduce observed behaviors is often achieved through optimization [38–40]. However, simulations based on the optimized parameters are often unstable, which affects the ability to produce forward simulations over a long duration [41]. This affects the ability to perform dynamic optimization of parameters that rely on completion of a movement [42]. In contrast, selection of muscle activation patterns that produce a system with stable eigenvalues generate simulations that are stable and can be run for much longer simulation times [43, 44]. Further, parameters selected based on stability criteria result in responses to perturbations that are more similar to experimentally-measured responses than those found using minimum muscle stress criteria alone [43]. Stability radius could be used as an additional optimization criterion to identify parameters that generate stable behaviors, which would improve both optimization speed, as well as identifying parameters that could generate more physiologically-realistic behaviors. In short, stability radius offers a metric for quantifying the stability and dynamical responses of parameters within, and across, individuals, which offers a useful tool for the analysis of neuromechanical systems. In contrast to classical stability analyses from control theory, stability radius can concurrently evaluate the effect of active and passive mechanisms affecting system stability; this could be an important tool for the design of assistive and rehabilitative devices for improving motor function.
Acknowledgment
This work was funded by NIH R01 NS053822 and HD04922 to LHT. The authors would like to thank Andrew Sawers, J. Lucas McKay, Hongchul Sohn, Stacie Chvatal, Nathan Bunderson and Thomas Burkholder for their feedback and critical insight.
Contributor Information
Jeffrey T. Bingham, Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA, USA
Lena H. Ting, Wallace H. Coulter Department of Biomedical Engineering, Georgia Institute of Technology and Emory University, Atlanta, GA, USA, lting@emory.edu
References
- 1.Dorf RC, Bishop RH. Modern Control Systems, 9th ed. plus 0.5em minus 0.4em. Upper Saddle River, NJ: Prentice-Hall; 2000. [Google Scholar]
- 2.Hinrichsen D, Pritchard A. Mathematical Systems Theory I: Modelling State Space Analysis, Stability and Robustness, 2nd ed. plus 0.5em minus 0.4em. Berlin, Heidelberg: Springer Verlag; 2005. [Google Scholar]
- 3.Trefethen LN, Embree M. Spectra and Pseudospectra: The Behavior of Nonnormal Matrices and Operators. plus 0.5em minus 0.4em. Princeton, NJ: Princeton University Press; 2005. [Google Scholar]
- 4.Hinrichsen D, Pritchard A. Stability radii of linear systems. Systems & Control Letters. 1986 Feb;7(1):1–10. [Google Scholar]
- 5.Martin J. State-space measures for stability robustness. IEEE Transactions on Automatic Control. 1987 Jun;32(6):509–512. [Google Scholar]
- 6.Verriest S-iNEI, Dugard L. Stability and Robust Stability of Time-Delay Systems : A Guided Tour. Stability and Control of Time-delay Systems. 1998:1–71. [Google Scholar]
- 7.Michiels W, Fridman E, Niculescu S-i. Robustness assessment via stability radii in delay parameters. International Journal of Robust and Nonlinear Control. 2009 Sep;19(13):1405–1426. [Google Scholar]
- 8.Michiels W, Green K, Wagenknecht T, Niculescu S-I. Pseudospectra and stability radii for analytic matrix functions with application to time-delay systems. Linear Algebra and its Applications. 2006 Oct;418(1):315–335. [Google Scholar]
- 9.Ting LH, McKay JL. Neuromechanics of muscle synergies for posture and movement. Current opinion in neurobiology. 2007 Dec;17(6):622–628. doi: 10.1016/j.conb.2008.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Selen LP, Franklin DW, Wolpert DM. Impedance control reduces instability that arises from motor noise. Journal of Neuroscience. 2009;29(40):12 606–12 616. doi: 10.1523/JNEUROSCI.2826-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Trumbower RD, Krutky MA, Yang B-S, Perreault EJ. Use of self-selected postures to regulate multi-joint stiffness during unconstrained tasks. PloS One. 2009;4(5):e5411. doi: 10.1371/journal.pone.0005411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Rancourt D, Hogan N. Stability in force-production tasks. Journal of motor behavior. 2001 Jun;33(2):193–204. doi: 10.1080/00222890109603150. [DOI] [PubMed] [Google Scholar]
- 13.Henry SM, Fung J, Horak FB. Effect of stance width on multidirectional postural responses. Journal of neurophysiology. 2001 Feb;85(2):559–570. doi: 10.1152/jn.2001.85.2.559. [DOI] [PubMed] [Google Scholar]
- 14.Torres-Oviedo G, Macpherson JM, Ting LH. Muscle synergy organization is robust across a variety of postural perturbations. Journal of neurophysiology. 2006 Sep;96(3):1530–1546. doi: 10.1152/jn.00810.2005. [DOI] [PubMed] [Google Scholar]
- 15.Torres-Oviedo G, Ting LH. Subject-specific muscle synergies in human balance control are consistent across different biomechanical contexts. Journal of Neurophysiology. 2010;103(6):3084–3098. doi: 10.1152/jn.00960.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bingham JT, Choi JT, Ting LH. Stability in a frontal plane model of balance requires coupled changes to postural configuration and neural feedback control. Journal of neurophysiology. 2011 Jul;106(1):437–448. doi: 10.1152/jn.00010.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Strang G. Introduction to Applied Mathematics. plus 0.5em minus 0.4em. Wellesley, MA: Wellesley-Cambridge Press; 1986. [Google Scholar]
- 18.Sipahi R, Niculescu S, Abdallah CT, Michiels W. Stability and Stabilization of Systems with Time Delay. IEEE Control Systems. 2011 Feb;31(1):38–65. [Google Scholar]
- 19.Wu Z, Michiels W. Reliably computing all characteristic roots of delay differential equations in a given right half plane using a spectral method. Journal of Computational and Applied Mathematics. 2012 Mar;236(9):2499–2514. [Google Scholar]
- 20.Khalil HK. Nonlinear Systems, 3rd ed. plus 0.5em minus 0.4em. Upper Saddle River, NJ: Prentice-Hall; 2002. [Google Scholar]
- 21.Wunsch DA. Complex variables with applications, 2nd ed. plus 0.5em minus 0.4em. Addison Wesley; 1993. [Google Scholar]
- 22.Lehmer DH. A Machine Method for Solving Polynomial Equations. Journal of the ACM. 1961 Apr;8(2):151–162. [Google Scholar]
- 23.Hinrichsen D, Pritchard A. Stability radius for structured perturbations and the algebraic Riccati equation. Systems & Control Letters. 1986 Dec;8(2):105–113. [Google Scholar]
- 24.Sieber J, Krauskopf B. Extending the permissible control loop latency for the controlled inverted pendulum. Dynamical Systems. 2005 Jun;20(2):189–199. [Google Scholar]
- 25.Henry SM, Fung J, Horak FB. EMG responses to maintain stance during multidirectional surface translations. Journal of Neurophysiology. 1998;80(4):1939–1950. doi: 10.1152/jn.1998.80.4.1939. [DOI] [PubMed] [Google Scholar]
- 26.Sternad D, Abe MO, Hu X, Müller H. Neuromotor noise, error tolerance and velocity-dependent costs in skilled performance. PLoS computational biology. 2011 Oct;7(9):e1002159. doi: 10.1371/journal.pcbi.1002159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bays PM, Wolpert DM. Computational principles of sensorimotor control that minimize uncertainty and variability. The Journal of physiology. 2007 Jan;578(Pt 2):387–396. doi: 10.1113/jphysiol.2006.120121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Perreault EJ, Kirsch RF, Crago PE. Multijoint dynamics and postural stability of the human arm. 2004;157(4):507–517. doi: 10.1007/s00221-004-1864-7. [DOI] [PubMed] [Google Scholar]
- 29.Hogan N. The mechanics of multi-joint posture and movement control. Biological Cybernetics. 1985;52(5):315–331. doi: 10.1007/BF00355754. [DOI] [PubMed] [Google Scholar]
- 30.Krutky Ma, Ravichandran VJ, Trumbower RD, Perreault EJ. Interactions between limb and environmental mechanics influence stretch reflex sensitivity in the human arm. Journal of neurophysiology. 2010 Jan;103(1):429–440. doi: 10.1152/jn.00679.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wagenknecht T, Michiels W, Green K. Structured pseudospectra for nonlinear eigenvalue problems. Journal of Computational and Applied Mathematics. 2008 Mar;212(2):245–259. [Google Scholar]
- 32.Hinrichsen D, Pritchard A. A note on some differences between real and complex stability radii. Systems & Control Letters. 1990 Jun;14(5):401–408. [Google Scholar]
- 33.Qiu L, Bernhardsson B, Rantzer A, Davison E, Young P, Doyle J. A formula for computation of the real stability radius. Automatica. 1995 Jun;31(6):879–890. [Google Scholar]
- 34.Valero-Cuevas FJ, Smaby N, Venkadesan M, Peterson M, Wright T. The strength-dexterity test as a measure of dynamic pinch performance. J Biomech. 2003;36(2):265–270. doi: 10.1016/s0021-9290(02)00340-8. [DOI] [PubMed] [Google Scholar]
- 35.Chen-Harris H, Joiner WM, Ethier V, Zee DS, Shadmehr R. Adaptive control of saccades via internal feedback. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2008 Mar;28(11):2804–2813. doi: 10.1523/JNEUROSCI.5300-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Verdaasdonk BW, Koopman HFJM, van Gils SA, van der Helm FCT. Bifurcation and stability analysis in musculoskeletal systems: a study in human stance. Biological cybernetics. 2004 Jul;91(1):48–62. doi: 10.1007/s00422-004-0494-2. [DOI] [PubMed] [Google Scholar]
- 37.Ackland DC, Lin Y-C, Pandy MG. Sensitivity of model predictions of muscle function to changes in moment arms and muscle-tendon properties: a Monte-Carlo analysis. Journal of biomechanics. 2012 May;45(8):1463–1471. doi: 10.1016/j.jbiomech.2012.02.023. [DOI] [PubMed] [Google Scholar]
- 38.Thelen DG, Anderson FC. Using computed muscle control to generate forward dynamic simulations of human walking from experimental data. Journal of Biomechanics. 2006 Jan;39(6):1107–1115. doi: 10.1016/j.jbiomech.2005.02.010. [DOI] [PubMed] [Google Scholar]
- 39.Remy CD, Thelen DG. Optimal estimation of dynamically consistent kinematics and kinetics for forward dynamic simulation of gait. Journal of biomechanical engineering. 2009 Mar;131(3):031005. doi: 10.1115/1.3005148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Anderson FC, Pandy MG. Static and dynamic optimization solutions for gait are practically equivalent. Journal of biomechanics. 2001 Feb;34(2):153–161. doi: 10.1016/s0021-9290(00)00155-x. [DOI] [PubMed] [Google Scholar]
- 41.Neptune RR. Optimization algorithm performance in determining optimal controls in human movement analyses. Journal of biomechanical engineering. 1999 Apr;121(2):249–252. doi: 10.1115/1.2835111. [DOI] [PubMed] [Google Scholar]
- 42.van den Bogert AJ, Blana D, Heinrich D. Implicit methods for efficient musculoskeletal simulation and optimal control. Procedia IUTAM. 2011 Jan;2(2011):297–316. doi: 10.1016/j.piutam.2011.04.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Bunderson NE, McKay JL, Ting LH, Burkholder TJ. Directional constraint of endpoint force emerges from hindlimb anatomy. J Exp Biol. 2010;213(Pt 12):2131–2141. doi: 10.1242/jeb.037879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Bunderson NE, Burkholder TJ, Ting LH. Reduction of neuromuscular redundancy for postural force generation using an intrinsic stability criterion. Journal of biomechanics. 2008 Jan;41(7):1537–1544. doi: 10.1016/j.jbiomech.2008.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]