A stochastic agent-based model of pathogen propagation in dynamic multi-relational social networks

Abstract

We describe a general framework for modeling and stochastic simulation of epidemics in realistic dynamic social networks, which incorporates heterogeneity in the types of individuals, types of interconnecting risk-bearing relationships, and types of pathogens transmitted across them. Dynamism is supported through arrival and departure processes, continuous restructuring of risk relationships, and changes to pathogen infectiousness, as mandated by natural history; dynamism is regulated through constraints on the local agency of individual nodes and their risk behaviors, while simulation trajectories are validated using system-wide metrics. To illustrate its utility, we present a case study that applies the proposed framework towards a simulation of HIV in artificial networks of intravenous drug users (IDUs) modeled using data collected in the Social Factors for HIV Risk survey.

1 Introduction

Modeling the propagation of pathogens through risk-bearing interactions of actors in a social network is an emerging perspective in epidemiology, particularly in HIV research [Goforth and Berleant, 1994, Bell et al., 2002, Goodreau, 2006]. Approaches such as these shift our view of risk away from individuals to collective social bodies as the carriers and transmitters of infection. The subject of study here then is “risk networks”, comprised of populations whose social interconnections signify particular “risk behaviors” that bear a potential for pathogen transmission. In the context of HIV, some examples of risk behaviors include social relationships which result in drug injection equipment sharing, and sexual relationships in the context of drug use. Although HIV will be used as a case study, the model presented in this paper is general enough to be applied towards the simulation of any epidemiological scenario in which disease transmission is driven by pairwise risk behaviors across a speci able set of relationship types. Risk networks are now widely recognized as critical factors in understanding infection patterns, as they define the natural environment in which risk behaviors occur, and through which the propagation of infection proceeds [Friedman et al., 1997, Bachanas et al., 2002]. The value of network-based simulation then, is that it can make the dynamic structures of risk visible and compelling [Hsieh et al., 2006], and help further a change in perspective to one that sees collectivities (and their respective forms and dynamics) as health actors with specific and identifiable structures of risk.

For reasons of cost, most risk network studies are relatively small in scale compared to the size of the overall communities they seek to understand. Even large-scale network studies manage to interview only a small portion of the ambient risk network; e.g. the study of Social Factors for HIV Risk (SFHR) conducted in Brooklyn, New York, in the early 1990s involved interviews with several hundred people [Friedman, 1999] out of the 30,000-80,000 IDUs in Brooklyn at the time. In contrast, simulation allows researchers to operate at the scale of the phenomenon of interest. While simulation is necessarily far from perfect and not a substitute for direct research, when based on detailed data and constructed to conform closely to known, short-term social dynamics, it can potentially provide suggestions and even tentative conclusions about critical health phenomenon at a time depth and social scale not possible in direct empirical research. Considerable prior work exists in which agent based modeling (ABM) is applied to questions of infectious disease epidemiology (see e.g. Nikolai and Madey [2009] for a recent review of ABM toolkits).

Most previous ABM efforts consider spatial models [Bian, 2004, Dunham, 2005, Lopez-Paredes et al., 2012, Luke et al., 2005] wherein social networks are implicit through spatial proximity; networks restructure themselves dynamically as actors move (coming in and out of pairwise contact). The EpiSimS system [Stroud et al., 2007], for example, considers social contact to define a network over which the spread of pandemics may be explored via simulation. Spatial contact-based stochastic agent models have also been used to study problems of infectious disease, including Enzootic Bovine Leukemia [Bagni et al., 2002], smallpox [Eidelson and Lustick, 2004], SARS [Huang et al., 2004], and influenza [Yoneyama and Krishnamoorthy, 2012]. ABM has even been used to evaluate the impact of the adoption of health care innovations [Dunn and Gallego, 2010], and intervention strategy efficacies [Huang et al., 2010]. One strength of explicitly spatial approaches is that the micro-level movements/behaviors of individuals drive the simulation trajectory forward over time, and the parameters specifying these behaviors can be drawn from distributions that have been calibrated to behavioral profile data collected from the population modeled. A weakness of spatial models, however, is that macro-level network characteristics—e.g. degree distribution, and triangle prevalence or “transitivity” (the latter not preserved in Markov movement paradigms)—cannot be easily controlled through the course of the simulation without impinging on actor agency (though for recent progress relating spatial models with small-world network structure see Huang et al. [2005, 2009]).

Exemplary of research efforts to generate networks having specified macro-level characteristics include the work of Hamill and Gilbert [2009], wherein artificial networks are generated to mimic structural characteristics observed in real-world social networks (e.g. sparseness, short distances, searchability, fat tails, assortativeness, transitivity, and clustering). Such efforts are part of a long line of inquiry concerning the problem of generating random networks having characteristics of social networks seen “in the wild”—see Watts and Strogatz [1998], Barabasi and Albert [1999] and Dorogovtsev and Mendes [2003] for example. The problem of generating random k-regular graphs (i.e. thefficase where the degree distribution is uniform) has been the subject of a sequence of results starting with the work of Bender and Canfield [1978], the switching process of McKay and Wormald [1990], and the configuration model [Bollobas, 1980, Bollobas, 2001]. The more difficult problem of generating random graphs satisfying a specified univariate degree distribution (over all nodes), or bivariate degree distribution (over all edges) remains a subject of ongoing inquiry. General speaking, the unbalanced (power-law) degree sequences of social networks mandate the development of inhomogeneous random graph models [Bollob as and Riordan, 2008]. The problem of efficiently generating networks with a specific non-uniform degree sequence (across all nodes) is a well-known difficult problem that has received considerable attention in recent years [Bayati et al., 2010, Blitzstein and Diaconis, 2011, Chatterjee et al., 2011], and the problem of generating graphs with a prescribed joint degree distribution has only been recently addressed by Stanton and Pinar [2011] using Markov chain techniques.

Complicating matters further is the fact that the plausibility of an artificially generated social network rests on more than merely the extent to which its univariate and bivariate degree distributions reflect those observed in the real-world population being modeled. Many other aspects of network structure might influence the likelihood of edge formation. One such example arises when individual nodes are assumed to have associated attributes (e.g. gender), since then attribute homophily may exert a bias on edge likelihoods (e.g. if same gender or opposite gender links are more predominant in the population/relationship being modeled). Another example arises in the presence of small scale structural effects like transitivity (the bias to edges forming between two individuals who share a network neighbor). To determine the extent to which edge formation is influenced by phenomena such as attribute homophily or relation transitivity, one may employ the techniques of Exponential Random Graph Modeling (ERGM), which were originally put forth by Holland and Leinhardt [1981] and Frank and Strauss [1986], with estimation questions settled recently by Snijders et al. [2006]. ERGM models of networks can be used to generate artificial networks [Goodreau, 2007, Goodreau et al., 2009, Kolaczyk, 2010, Lieberman, 2012]. As described by Goodreau, such studies can also create dynamic networks where the connections between node actors are periodically reassigned according to a given distribution of pair-wise likelihoods [Goodreau, 2011]. As such, ERGM networks can be made to “evolve” over time, though at the cost of readily controllable actor agency. One strength of ERGM simulation models then is that macro-level network characteristics (e.g. the network's instantaneous degree distribution) drive the simulation trajectory over time, and these characteristics may be calibrated against measurements of the actual population being modeled. A weakness of ERGM simulation models, on the other hand, is that the micro-level behaviors of individuals (implicit in edge restructuring) cannot be readily controlled and made to reflect the known behavioral profiles exhibited in the population being modeled. Indeed, when discussing their future efforts, Snijders et all refer to the need for “stochastic actor-based models for network dynamics” [Snijders et al., 2010]. As Snijders describes it, networks gain their dynamism as actors come and go from the network, and when they change their mutual connections due to:

... the structural positions of the actors within the network—e.g., when friends of friends become friends—characteristics of the actors (“actor covariates”), characteristics of pairs of actors (“dyadic covariates”), and residual random influences representing unexplained influences [Snijders et al., 2010, p. 44].

What is needed is a framework in which macro-level network characteristics and individual micro-level behavioral profiles both play a role. Such a framework is developed and presented here, specifically for application towards the study of disease epidemiology. The framework is designed with the following guiding principles in mind:

• like ABM-based simulations, we want to maintain an actor-based environment, where actions which determine network dynamism originate in characteristics of the nodes themselves. Such actor-based dynamism should include risk behaviors, length of network participation, and when and how to establish new network connections or get rid of prior ones.

• like ERGM-based simulations, we want link creation to reflect node-specific attributes (such as gender, age, ethnicity/race), and local structural tendencies (e.g. network transitivity), so that our dynamic network remains “real-world viable” over long simulation trajectories, even while individual nodes/actors enter or leave the network.

• like ABM-based simulations, we want our actors to exhibit individual behavior patterns (beyond node-specific characteristics such as age, or gender) parametrized from a distribution of possibilities, and to allow for different modalities of participation (such as one might see from two very different classes of network actors who are otherwise indistinguishable on the basis node characteristics).

• like ERGM-based models, we want to be able to control for network-level factors affecting overall network dynamism, such as bounded deviation from a specific network-wide degree distribution. And finally,

• like ABM-based simulations, we want to be able to simulate large networks, to determine whether factors of scale influence network dynamics and infection trajectories over simulation time, and to examine simulation results on a scale of the phenomena of interest.

Towards this, Marshall et al. [2012] have recently made progress by demonstrating an ABM approach that considers both macro-level network characteristics and individual micro-level behavioral profiles, in the context of their work on HIV interventions in IDU risk networks. In this paper we present a case study that extends the approach of Marshall et al., providing an illustrative application of our general-purpose framework for epidemiological modeling which considers multi-pathogen multi-layer networks by synthesizing both ERGM and ABM approaches. A more detailed comparison of features is given as part of the case study (see Section 5, pp.20).

The framework is presented in stages. We begin, in Section 2, by considering static risk networks. First, in Subsection 2.1, we describe how a population survey can be used to obtain a description of a concrete real-world risk network, and how from this one may determine which attributes (of individuals) exert the greatest influence on the formation of risk relationships. In Subsection 2.2, we present the derivation of an (m, l, p) statistical network model — in effect, a distribution over the space of all static networks, which reflects the properties of the concrete risk network being modeled. In Subsection 2.3, we discuss how one may use a statistical network model to generate new (static) artificial risk networks. Finally, in Subsection 2.4, we address the need to validate generated artificial risk networks against the original real-world risk network from which the generative model was distilled. To simulate infection across these networks, the framework is extended in Section 3 to permit each of p distinct types of pathogens to flow between individuals via any of the l different types of risk relationships. Lastly, in Section 4, network dynamism is captured via node arrival and departure processes, incremental changes to individual risk relationship structures, and node aging. Fifinally, to illustrate the efficacy of the proposed framework, we apply it towards a case study of HIV in injection drug user (IDU) communities where drug equipment sharing and sex in the context of drug use are the principal risk events underlying the transmission of HIV, the case study and associated simulation results are presented in Section 5.

Throughout this exposition, we adhere to certain notational conventions. Sets will be denoted by capital letters, A, B, C, etc., and will be indexed by integer variables i, j, k, etc. Elements within sets will be written in lower case Roman letters, a, b, c, etc. Distributions will usually be expressed as α, β, γ, etc. Types or proper names will be represented in script $\mathcal{A},\mathcal{B},\mathcal{C}$, etc. In an exposition where a set or function, (e.g. the actors V ) must be considered time-dependent, the temporal index will appear as a superscript, (causing us to write V^t for the set of actors at time t). In situations where a set or function (e.g. the infectiousness curve I) is being seen in the context of a particular layer, attribute, or pathogen type, this dependency will be made clear in the subscript of the variable, (e.g. I_j,k is the infectiousness curve of pathogen k via risk acts in layer j). Both superscripts (for time) and subscripts (for context) will be employed simultaneously when referencing sets or functions that are both time and context dependent (e.g. $N_j^t\left(v\right)$ is the set of neighbors of actor v within network layer j at time t). A function f whose domain is D and range is R will be declared so by the statement f : D → R. Set differences are indicated using the \ operator.

2 Modeling network structure

We view a risk network as an l-layer combinatorial fabric, weaving together a set of n individuals, each of whom has m attributes, and may host one or more of p distinct types of pathogens. In what follows, we present how a real-world risk network is described (2.1), modeled statistically (2.2), and how the statistical network model can be subsequently used to sample new artificial risk networks (2.3) that can be validated against the original real-world network (2.4).

2.1 Obtaining data on real-world risk networks

In a survey of a population V, each constituent individual v is interrogated regarding a fixed set of m attributes X = {x₁,. . . x_m}, e.g., x₁ could be gender, while x₂ might be age, etc. We assume that each variable x_i (for i = 1,. . ., m) is categorical, taking values from a nite set U_i that is known in advance (e.g. U₁ could be {Male, Female}, while U₂ might be 21AndUnder, Over21}). Each node attribute x_i (i = 1,. . ., m) is seen as a function x_i : V → U_i.

Yet to model a risk network, the survey must go beyond individual attributes and collect data on the risk relationships between them. The relationships of interest might be of several concrete types ${\mathcal{I}}_1,{\mathcal{I}}_2,\dots ,{\mathcal{I}}_l$. For example, ${\mathcal{I}}_1$ might be the relationship of “sharing injection equipment with”, while ${\mathcal{I}}_2$ relationships could embody “sexual partnership”, etc. In practice, during the survey, each individual v from V is questioned about their risk relationships for each type ${\mathcal{I}}_j$ (for j = 1,. . ., l), and is asked to provide sufficient information with which to identify the individuals N_j(v) ⊆ V with whom v enjoys a type ${\mathcal{I}}_j$ relationship. In other words, the survey must be capable of capturing ego network data that, in turn, can be aggregated to produce a network whose structural features are representative of the topological characteristics of the risk network as a whole. The data thus collected is used to define a degree $d_j\left(v\right)\stackrel{\mathrm{def}}{=}\mid N_j\left(v\right)\mid$ for each individual v, the value of this quantity is the number of ${\mathcal{I}}_j$ relationships that v has. The set of all pairwise relationships, at each network layer j = 1,. . ., l is then expressible as $E_j={\bigcup }_{v\in V}{N}_j\left(v\right)$.

Finally, the survey must produce data on the prevalence and distribution of the pathogens of interest, which may be of several distinct types ${\mathcal{P}}_1,{\mathcal{P}}_2,\dots ,{\mathcal{P}}_p$. Specifying the instantaneous state of a risk network thus requires a collection of p concrete sets of individuals A₁, A₂,. . ., A_p ⊆ V where A_k is the set of individuals who are positive for pathogen type ${\mathcal{P}}_k$ (k = 1, 2,. . ., p).

Collecting the above elements, we define a risk network to be an (m + 2l + p + 1) tuple $\mathcal{D}\stackrel{\mathrm{def}}{=}(x_i,V,E_j,A_k,d_j)$ where i = 1,. . ., m, j = 1,. . ., l, k = 1,. . ., p.

2.2 Defining a statistical network model

In modeling a risk network $\mathcal{D}$, the question arises as to the contents of the model, and particularly, which m attributes X = {x₁,. . . x_m} to consider. Questions of determinate variables (and their relative importance), are of paramount importance to our modeling process. In particular, we need to determine which individual attributes were important to the formation of the network, and to know how these attributes rank relative to one another.

Recently, the statistical analysis of network data has been advanced considerably by the introduction of Exponential Random Graph Modeling (ERGM), which provides researchers with an alternative to the simple cross-tabulation of network link data. ERGM is a statistical technique aimed at determining the extent to which the likelihood of network linkages appears to be biased towards (or against) the creation of specified network substructures, above and beyond what is expected by chance occurrence. Such substructures can be as simple as the tendency of “like” nodes to be connected (at a greater rate than expected by a random distribution of connections), or as complex as specific structures of connection between several individuals [Bearman et al., 2004]. The theoretical basis for ERGM analysis was laid down by Holland and Leinhardt [1981] and Frank and Strauss [1986], with estimation questions finally settled only recently [Snijders et al., 2006]. Readers can find a detailed exposition of ERGM in Goodreau [2007], Goodreau et al. [2009], Kolaczyk [2010].

To begin the process of parameterizing the models, we apply ERGM analysis to the data set $\mathcal{D}$ obtained from the survey. The outcome of such analysis is the m most influential attributes X = {x₁,. . . x_m}, together with weights that quantify their relative influence. In addition, we use ERGM to evaluate the influence of significant network substructures. These can be as simple as edge reciprocity or network transitivity, or as complex as those discussed by Bearman and colleagues [Bearman et al., 2004]. Here we consider only the influence of triadic closure (i.e. transitivity) on link formation in each of the l network layers, these l weights are denoted $w_j^{\Delta }$ (for j = 1,. . ., l). Triadic closure was found to be in the SFHR network data on which the case study of our framework is based. SFHR considered risk relationships between intravenous drug users which were based on equipment co-use, and the stigmatized nature of the pairwise relationships clearly leads to a bias towards triad formation (if A co-uses with B and C, then B and C are more likely to co-use together). In other networks, such as those where the edge relation signifies sexual intercourse, no bias towards transitivity is seen. ¹

Attribute Distributions. Given a risk network $\mathcal{D}=(x_i,V,E_j,A_k,d_j)$ where i = 1,. . ., m; j = 1,. . ., l, k = 1,. . ., p, we can from each of the attributes x_i (i = 1,. . ., m), determine a univariate attribute distribution α_i : U_i → [0, 1] for i = 1, 2,. . ., m, where for u ∈ U_i,

$${\alpha }_i\left(u\right)\stackrel{\mathrm{def}}{=}\frac{1}{\mid V\mid }\mid x_i^{-1}\left(u\right)\mid .$$

If a chi-squared test reveals a significant level of association to be present between α_i and α_i′ (for i ≠ i′), then the categorical attribute variables x_i and x_i′ are coalesced into a new joint variable x* defined over the Cartesian product of categorical spaces U_i × U_i′. The joint distribution α* over a suitably binned U_i × U_i′ is used whenever we need to sample a pairs of values (x_i, x_i′). In this manner, we may inductively coalesce all attributes which show significant pairwise dependencies. Given this strategy, in what follows we simplify the exposition by assuming that {α_i | i = 1,. . ., m} is a set of pairwise independent distributions.

Next, each set of type-${\mathcal{I}}_j$ relationships E_j (for j = 1, 2,. . ., l) is used to define a bivariate attribute distribution β_i,j : U_i × U_i → [0, 1] for i = 1, 2,. . ., m, where for each u₁, u₂ ∈ U_i,

$${\beta }_{i,j}(u_1,u_2)\stackrel{\mathrm{def}}{=}\frac{1}{\mid E_j\mid }\mid (x_i^{-1}\left(u_1\right)\times x_i^{-1}\left(u_2\right))\cap E_j\mid ,$$

Degree Distributions. Next, we model the layer-j degree distribution for the population, taking care to account for the fact that individual attributes and degrees are often related.² To capture this, we determine a suitable partition of the Cartesian product of the categorical spaces U_i (i = 1,. . ., m)

$${\mathcal{C}}_1^j\bigsqcup {\mathcal{C}}_2^j\bigsqcup \dots \bigsqcup {\mathcal{C}}_s^j\bigsqcup \dots \bigsqcup {\mathcal{C}}_{S_j}^j=\prod _{i=1}^m{U}_i.$$

Informally, each of the ${\mathcal{C}}_s^j(s=1,\dots ,S_j)$ represents a distinct class of individuals, where classes are differentiated from one another because they exhibit different “ideal layer-j degree” distributions. In practice, the value of S_j and the definition of each class ${\mathcal{C}}_s(S=1,\dots ,S_j)$ is determined by performing a statistical analysis to discover which univariate attributes appear to significantly influence vertex degree (in layer j). From the results of such an analysis, classes are suitably defined so that the individuals within a single class can be assumed to draw their ideal layer-j degree from a distribution that is independent of their individual attribute values.

Since the set $\{{\mathcal{C}}_s^k\mid s=1,\dots ,S_j\}$ is a partition of ${\prod }_{i=1}^m{U}_i$, and every v ∈ V has attributes (x₁(v), x₂(v),. . ., x_m(v)) which lie in exactly one of the S_j classes, we obtain a natural classification function $f_j^{\mathcal{C}}:V\to \{1,2,\dots ,S_j\}$. Given such a classification function, the individuals V in a risk network can be naturally partitioned by class:

$$V\left({\mathcal{C}}_1^j\right)\bigsqcup V\left({\mathcal{C}}_2^j\right)\bigsqcup \dots \bigsqcup V\left({\mathcal{C}}_s^j\right)\bigsqcup \dots \bigsqcup V\left({\mathcal{C}}_{S_j}^j\right)=V$$

where $V\left({\mathcal{C}}_s^j\right)\stackrel{\mathrm{def}}{=}\{v\in V\mid f_j^{\mathcal{C}}\left(v\right)=s\}$.

Each layer-j degree class ${\mathcal{C}}_s(s=1,\dots ,S_j)$ exhibits its own univariate degree distribution ${\chi }_{j;s}:\mathbb{Z}\times \mathbb{Z}\to \mathbb{R}$ where for every pair of integers a < b, and s ∈ {1,. . ., S_j}:

$${\chi }_{j;s}(a,b)\stackrel{\mathrm{def}}{=}\frac{\mid \{v\in V\left({\mathcal{C}}_s^j\right)\mid a\le d_j\left(v\right)<b\}\mid }{\mid V\left({\mathcal{C}}_s^j\right)\mid }.$$

In general, the layer-j degree distributions χ_j;s(a, b) for different classes s may differ from one another, and may differ from the overall “class-neutral” layer-j degree distribution

$${\chi }_{j;\ast }(a,b)\stackrel{\mathrm{def}}{=}\frac{\mid \{v\in V\mid a\le d_j\left(v\right)<b\}\mid }{\mid V\mid }.$$

If a chi-squared test reveals a significant level of association to be present between the class-neutral degree distributions of two layers, say χ_j;* and χ_j′;*, (for j ≠ j′), then the degree distributions of the two layers j and j′ must be coalesced into a new joint variable χ* over the Cartesian product $\mathbb{N}\times \mathbb{N}$, using a common refinement of the classification schemes $\{{\mathcal{C}}_s\mid s=1,\dots ,S_j\}$ and $\{{\mathcal{C}}_s^{\prime }\mid s=1,\dots ,S_{j^{\prime }}\}$. The distribution χ* is used to simultaneously sample a pair of degrees (for network layers j and j′). In this manner, we may (for the purpose of degree sampling) inductively coalesce all network layers which show significant pairwise dependency in their degree distributions. Given this strategy, without loss of generality, in what follows we simplify the exposition by assuming that the set {χ_j;* | j = 1,. . ., l} consists of pairwise independent distributions. The degree distribution in layer j is captured by the set of pairs

$${\mathbb{X}}_j\stackrel{\mathrm{def}}{=}\{({\mathcal{C}}_s^j,{\chi }_{j;s})\mid s=1,2,ldots,S_j\}$$

which functiofinally specifies a distribution for each of the classes in $\{{\mathcal{C}}_s\mid s=1,\dots ,S_j\}$.

For each j = 1,. . ., l we also define a bivariate degree distribution $\stackrel{=}{{\chi }_j}:{(\mathbb{Z}\times \mathbb{Z})}^2\to \mathbb{R}$ where for every 4-tuple of integers a < b, a′ < b′

$$\stackrel{=}{{\chi }_j}(a,b,a^{\prime },b^{\prime })\stackrel{\mathrm{def}}{=}\frac{\mid \{e\in E_j\mid e=(u,v);a\le d_j\left(u\right)<b;a^{\prime }\le d_j\left(v\right)<b^{\prime }\}\mid }{\mid E_j\mid }.$$

Pathogen Distributions. For each of the p pathogen types ${\mathcal{P}}_k$ (k = 1, 2,. . ., p), we model its prevalence, taking care to account for the fact that individual attributes and pathogen prevalences are often related.³ To capture this, we determine a suitable partition of the cartesian product of the categorical spaces U_i (i = 1,. . ., m)

$${\mathcal{B}}_1^k\bigsqcup {\mathcal{B}}_2^k\bigsqcup \dots \bigsqcup {\mathcal{B}}_r^k\bigsqcup \dots \bigsqcup {\mathcal{B}}_{R_k}^k=\prod _{i=1}^m{U}_i.$$

Informally, each of the ${\mathcal{B}}_r^k(r=1,\dots ,R_k)$ represents a distinct class of individuals, where classes are differentiated from one another because they exhibit different“pathogen-k prevalence” levels. In practice, the value of R_k and the definition of each class ${\mathcal{B}}_r(r=1,\dots ,R_k)$ is determined by performing a statistical analysis to discover which univariate attributes appear to significantly influence pathogen prevalence (with respect to pathogen k). From the results of such an analysis, classes are suitably defined so that the individuals in a single class can be assumed to draw their pathogen-k infection status via a Bernoulli trial whose outcome is positive with a constant probability that is independent of the individual's attributes.

Since the set $\{{\mathcal{B}}_r\mid r=1,\dots ,R_k\}$ is a partition of ${\prod }_{i=1}^m{U}_i$, and every v ∈ V has attributes (x₁(v), x₂(v),. . ., x_m(v)) which lie in exactly one of the R_k classes, we obtain a natural classification function $f_k^{\mathcal{B}}:V\to \{1,2,\dots ,R_k\}$. Given such a classifying function, the individuals V in a risk network may be partitioned by class:

$$V\left({\mathcal{B}}_1^k\right)\bigsqcup V\left({\mathcal{B}}_2^k\right)\bigsqcup \dots \bigsqcup V\left({\mathcal{B}}_r^k\right)\bigsqcup \dots \bigsqcup V\left({\mathcal{B}}_{R_k}^k\right)=V$$

where $V\left({\mathcal{B}}_r^k\right)\stackrel{\mathrm{def}}{=}\{v\in V\mid {\int }_k^{\mathcal{B}}\left(v\right)=r\}$.

Each pathogen-k prevalence class ${\mathcal{B}}_r(r=1,\dots ,R_k)$ exhibits its own pathogen prevalence $p_{k;r}\in \mathbb{R}$ where for every k = 1, 2,. . ., p, and r ∈ {1,. . ., R_k}:

$$p_{k;r}\stackrel{\mathrm{def}}{=}\frac{\mid A_k\cap V\left({\mathcal{B}}_r^k\right)\mid }{\mid V\left({\mathcal{B}}_r^k\right)\mid }.$$

where

$$A_k\stackrel{\mathrm{def}}{=}\{v\in V\mid v\text{is positive for pathogen}k\}.$$

The prevalence of pathogen k is captured by the set of pairs

$${\mathbb{P}}_k\stackrel{\mathrm{def}}{=}\{({\mathcal{B}}_r^k,p_{k;r})\mid r=1,2,\dots ,R_k\}$$

which functionally specifies a distribution for each of the classes in $\{{\mathcal{B}}_r\mid r=1,\dots ,R_k\}$.

The statistical network model $\mathcal{M}\left(\mathcal{D}\right)$ of risk network $\mathcal{D}$ is the (m + (m + 2)l + p)-tuple:

$$\mathcal{M}\left(\mathcal{D}\right)\stackrel{\mathrm{def}}{=}({\alpha }_i,{\beta }_{i,j},{\mathbb{X}}_j,{\stackrel{=}{\chi }}_j,{\mathbb{P}}_k)i=1,\dots ,m;j=1,\dots ,l;k=1,\dots p$$

2.3 Generating networks from a statistical network model

Given a statistical network model $\mathcal{M}$, procedure MakeNetwork (Listing 1) instantiates a new artificial risk network of size n, using $\mathcal{M}$ as a statistical guideline.

In the first phase (line 1 of Listing 1), the MakePopulation procedure is called (Listing 2), which in turn, creates n individuals, assigning each of their m attributes independently at random, using the univariate distributions α₁,. . ., α_m (lines 4,5). Then (lines 7-10) the degree distributions ${\mathbb{X}}_j$ are used to assign each individual an ideal ego network size, or ideal degree, d_j(v), based on v's ideal layer-j degree class s, for each of the layers j = 1,. . ., l. Justification for individuals having an intrinsic ideal degree comes from prior work on the emergence of “roles” within risk networks [Friedman et al., 1998, Curtis et al., 1995, Romero-Severson et al., 2012].

In the second phase (line 2 of Listing 1), the MakePathogens procedure is called (see Listing 3), which in turn, distributes each of the p types of pathogens (line 2) to each of the individuals in V (line 3), in a manner that reflects the specified prevalence levels for the particular pathogen type (lines 4-7), based on v's pathogen-k prevalence class t, for each of the pathogen k = 1,. . ., p.

In the third phase (line 3 of Listing 1), the MakeRelations procedure creates risk relationships between individuals (see Listing 4). To do this, it initializes the layer j neighbors (line 3) of each node v_i (line 2) to be the empty set (line 4), and then schedules d_j(v_i) executions of AddEdge for each node v_i at each layer j (lines 5-6). Because all calls to AddEdge are at times < 1, MakeRelations need only wait until time 1 before aggregating the set of all edges (line 8).

Each execution of AddEdge is in the context of a given vertex v, layer j, and time t (Listing 5). The procedure first computes the set $C_j^t\left(v\right)$ of candidate new layer-j neighbors of v (line 2), proceeding only if this is nonempty (line 3). It then (i) computes the layer j edge deficit for each candidate vertex c (line 5), taking this to be the difference between v's ideal degree d_j(v) and actual degree $\mid N_j^t\left(v\right)\mid$, rescaled into the interval [0, 1] by composing with the smooth squashing function $e^{\frac{-1}{x}}$. The squashing function approaches 1 as x → ∞ and 0 as x → 0⁺. The quantity a_δ(c) is thus close to 1 whenever $\mid N_j^t\left(c\right)\mid \ll d_j\left(c\right)$ and becomes 0 once c's actual degree $\mid N_j^t\left(c\right)\mid$ attains its ideal value d_j(c). The selection of candidate c is also influenced by (ii) the actual degrees of v and c (line 6), with respect to the bivariate degree distribution $\stackrel{=}{{\chi }_j}$ (suitably binned to 2∊-sized buckets). Likewise (iii) the joint attributes of v and c influence the candidate selection (line 7), reflecting the bivariate attribute distributions β_i,j. Finally, (iv) each new triangle arising from the addition of edge (v, c) contributes $(w_j^{\Delta }-1)$ to the total triadic bias (line 8) which is accumulated in $a_{\Delta }^t\left(c\right)$. The factors (i)-(iv) are used to construct a probability distribution $p_j^t$ over the set of candidate new layer-j neighbors (lines 9,10), using which one of the candidates w is selected (line 11). The edge (v, w) is then added to network layer j by augmenting the set of layer j edges emanating from v (line 13).

2.4 Validating generated networks

We have shown how, from a network survey, one may specify a real-world risk network $\mathcal{D}$ (see Section 2.1), and from $\mathcal{D}$ derive a statistical network model $\mathcal{M}$ (see Section 2.2), and then use the model $\mathcal{M}$ to sample new artificial risk networks ${\mathcal{D}}_1^{\prime },{\mathcal{D}}_2^{\prime },{\mathcal{D}}_3^{\prime },\dots$ (see Section 2.3). We now present techniques to quantify the divergence between the original real risk network $\mathcal{D}$ and a generated artificial risk network(s) ${\mathcal{D}}^{\prime }$. These techniques shall be particularly relevant to assessing the possible degeneracy of model $\mathcal{M}$, i.e. its potential inability to generate networks that reflect characteristics of the network from which the model was derived.

We begin by considering how one may measure the similarity or difference between two (m, l, p) statistical network models

$$\begin{array}{cc}\hfill {\mathcal{M}}_1=& {({\alpha }_i,{\beta }_{i,j},{\mathbb{X}}_j,\stackrel{=}{{\chi }_j},{\mathbb{P}}_k)}_{i=1,\dots ,m;j=1,\dots ,l;k=1,\dots ,p}\hfill \\ \hfill {\mathcal{M}}_2=& {({\alpha }_i^{\prime },{\beta }_{i,j}^{\prime },{\mathbb{X}}_j^{\prime },\stackrel{=}{{\chi }_j^{\prime }},{\mathbb{P}}_k^{\prime })}_{i=1,\dots ,m;j=1,\dots ,l;k=1,\dots ,p}.\hfill \end{array}$$

Because ${\mathcal{M}}_1$ and ${\mathcal{M}}_2$ each consist of a set of distributions, the two models are readily comparable only if the domains of these distributions agree. In particular, for two models to be comparable it is necessary that

$$\begin{array}{c}\hfill Domain\left({\alpha }_i\right)=Domain\left({\alpha }_i^{\prime }\right)\hfill \\ \hfill Domain\left({\beta }_{i,j}\right)=Domain\left({\beta }_{i,j}^{\prime }\right)\hfill \end{array}$$

for all i = 1,. . ., m, j = 1,. . ., l. Likewise, the set of ideal layer-j degree classes (referred to via ${\mathbb{X}}_j$ and ${\mathbb{X}}_j^{\prime }$), and pathogen-k prevalence classes (referred to via ${\mathbb{P}}_k^{\prime }$ and ${\mathbb{P}}_k^{\prime }$) must be compatible:

$$\begin{array}{c}\hfill Domain\left({\mathbb{X}}_j\right)=Domain\left({\mathbb{X}}_j^{\prime }\right)\hfill \\ \hfill Domain\left({\mathbb{P}}_k\right)=Domain\left({\mathbb{P}}_k^{\prime }\right).\hfill \end{array}$$

for all j = 1,. . ., l, k = 1,. . ., p. The above conditions can be met by any pair of (m, l, p) statistical network models by using a suitable common refinement of the categorical spaces U_i and $U_i^{\prime }$ (for i = 1,. . ., m), classifications ${\mathbb{X}}_j,{\mathbb{X}}_j^{\prime }$ (for j = 1,. . ., l), and ${\mathbb{P}}_k,{\mathbb{P}}_k^{\prime }$ (for k = 1,. . ., p).

Given two comparable models how might one quantify their similarity or difference?

Since statistical network models are tuples of distributions, we begin by considering how one may assess the similarity between two probability distributions f, f′ over a common set X. Many approaches exist, including histogram intersection [Barla et al., 2003], Chi-square statistic [Read, 1993], quadratic form distance, match distance, Kolmogorov-Smirnov distance [Stephens, 1974], earth mover's distance, Kullback-Leibler divergence—sometimes now called information divergence, information gain, relative entropy—see Kullback and Leibler [1951], and Jensen-Shannon divergence—also known as information radius or IRad. Here we shall chose to measure the difference between two probability distributions as

$$\Delta (f,f^{\prime })\stackrel{\mathrm{def}}{=}\sqrt{IRad(f,f^{\prime })}$$

because by doing so, we obtain a metric space on the set of all probability distributions over an underlying set [Endres and Schindelin, 2003, Österreicher and Vajda, 2003]. The IRad of two distributions is defined to be their mean Kullback-Leibler divergence from their average (as distributions). Applying this to the constituent distributions in the two models, we get

$$\begin{array}{cc}\hfill \Delta ({\alpha }_i,{\alpha }_i^{\prime })& \stackrel{\mathrm{def}}{=}\sqrt{\sum _{x\in U_i}{a}_i\left(x\right)\log \frac{{\alpha }_i\left(x\right)}{{\stackrel{‒}{\alpha }}_i\left(x\right)}+{\alpha }_i^{\prime }\left(x\right)\log \frac{{\alpha }_i^{\prime }\left(x\right)}{{\stackrel{‒}{\alpha }}_i\left(x\right)}}\hfill \\ \hfill \Delta ({\beta }_{i,j},{\beta }_{i,j}^{\prime })& \stackrel{\mathrm{def}}{=}\sqrt{\sum _{(x,y)\in U_i\times U_i}{\beta }_{i,j}(x,y)\log \frac{{\beta }_{i,j}(x.y)}{{\stackrel{‒}{\beta }}_{i,j}(x,y)}+{\beta }_{i,j}^{\prime }(x,y)\log \frac{{\beta }_{i,j}^{\prime }(x,y)}{{\stackrel{‒}{\beta }}_{i,j}(x,y)}}\hfill \end{array}$$

where ${\stackrel{‒}{\alpha }}_i$ is the average of α_i and ${\alpha }_i^{\prime }$ (as a distribution over U_i), and ${\stackrel{‒}{\beta }}_{i,j}$ is the average of β_i,j and ${\beta }_{i,j}^{\prime }$ (as a distribution over U_i × U_i). Analogous distance measures may be defined between the two models’ bivariate degree distributions $\stackrel{=}{{\chi }_j}$ and $\stackrel{=}{{\chi }_j^{\prime }}$, as well as between corresponding in-class univariate degree distributions χ_j;s and ${\chi }_{j;s}^{\prime }$ (taken from ${\mathbb{X}}_j$ and ${\mathbb{X}}_j^{\prime }$, respectively). Because these distributions are defined over identical partitions $\{{\mathcal{C}}_s^j\mid s=1,\dots ,S_j\}$ of ${\prod }_{i=1}^m{U}_i$ we can aggregate the distances by summing the divergences between corresponding class distributions:

$$\Delta ({\mathbb{X}}_j,{\mathbb{X}}_j^{\prime })\stackrel{\mathrm{def}}{=}\sum _{s=1}^{S_j}\Delta ({\chi }_j,{\chi }_j^{\prime }).$$

Having defined the distance between corresponding distributions in the two models, we use the L_∞ norm to extend to a de nition of distance between statistical network models:

$${\Delta }^{\ast }({\mathcal{M}}_1,{\mathcal{M}}_2)\stackrel{\mathrm{def}}{=}\max \left(\underset{i=1}{\overset{m}{\max }}\Delta ({\alpha }_i,{\alpha }_i^{\prime }),\underset{j=1}{\overset{l}{\max }}\underset{i=1}{\overset{m}{\max }}\Delta ({\beta }_{i,j},{\beta }_{i,j}^{\prime }),\underset{j=1}{\overset{l}{\max }}\Delta ({\mathbb{X}}_j,{\mathbb{X}}_j^{\prime })\underset{j=1}{\overset{l}{\max }}\Delta (\stackrel{=}{{\chi }_j},\stackrel{=}{{\chi }_j^{\prime }},\right)$$ (1)

By considering the worst-case divergences of all constituent distributions within the two models, we hope to produce a holistic assessment of the relative validity of each model against the other [Bharathy and Silverman, 2013].

The distance between two risk networks $\mathcal{D}$ and ${\mathcal{D}}^{\prime }$ (which have comparable models), is now taken as

$$\Delta (\mathcal{D},{\mathcal{D}}^{\prime })\stackrel{\mathrm{def}}{=}{\Delta }^{\ast }(\mathcal{M}\left(\mathcal{D}\right),\mathcal{M}\left({\mathcal{D}}^{\prime }\right)).$$ (2)

Note that by not incorporating divergences of pathogen prevalence rates p_k (interpreted as Bernoulli distribution parameters) into the de nition of Δ*, we ensure that $\Delta (\mathcal{D},{\mathcal{D}}^{\prime })$ measures the extent to which $\mathcal{D},{\mathcal{D}}^{\prime }$ differ as networks, the pathogen prevalence rates in the two risk networks $\mathcal{D},{\mathcal{D}}^{\prime }$ may diverge arbitrarily without influencing the value of $\Delta (\mathcal{D},{\mathcal{D}}^{\prime })$.

We have thus transformed the set of all risk networks generated from comparable statistical network models into a metric space in which distance is inverse to similarity in network structure. In practice, the metric Δ (on risk networks) will allow us to detect when an (artificial) generated network ${\mathcal{D}}^{\prime }$ is very different from the surveyed (real-world) risk network $\mathcal{D}$ from which the generative statistical network model $\mathcal{M}\left(\mathcal{D}\right)$ was defined. By using rejection sampling techniques [Robert and Casella, 2005] we may ensure that the artificial networks which are used as starting points of our simulation are not exceptionally different from the real-world networks from which our statistical network models are derived.

In the context of dynamic network simulation (to be described), Δ will allow us to keep track of the extent of structural divergence between the initial artificial risk network ${\mathcal{D}}^{\prime }$ and its instantaneous evolute ${\mathcal{D}}_t^{\prime }$ at time t (over the course of the simulation trajectory). If at some point (in time) in the simulation trajectory, we discover that ${\mathcal{D}}^{\prime }$ and ${\mathcal{D}}_t^{\prime }$ are significantly different (i.e. $\Delta ({\mathcal{D}}^{\prime },{\mathcal{D}}_t^{\prime })$ exceeds some prescribed threshold), the de nition of Δ permits us to dissect the contributions of the constituent distributions in $\mathcal{M}\left({\mathcal{D}}_t^{\prime }\right)$ and $\mathcal{M}\left({\mathcal{D}}^{\prime }\right)$ to determine what aspects of the models are most responsible for the divergence. In such circumstances, either the trajectory can be discarded (because it has produced an exceptional network)—a form of rejection sampling from the space of all system trajectories, or, alternatively, the dynamism model parameters (to be described) may be altered to allow less drift in the risk network's structure over time.

Next, in Section 3, we shall extend the model to support pathogen dynamics. Then, in Section 4, we extend it further to capture the dynamic evolution of network topologies.

3 Modeling pathogens: the risk process

An individual v's infection status may change with respect to a pathogen ${\mathcal{P}}_k$ (for some k in 1,. . ., p) when v engages in risk behaviors (via layer j relationships, j = 1,. . ., l) with a risk partner w who is positive for ${\mathcal{P}}_k$. We refer to aspects of the framework which speak to such events, as the risk process for pathogen ${\mathcal{P}}_k$, the details of which are described in what follows. While the description is from the vantage point of a fixed layer j and time t, it applies to all layers j = 1,. . ., l at all times t > 1. At a given time t, each individual is represented as a node v ∈ V^t within a network

$${\mathcal{D}}^t\stackrel{\mathrm{def}}{=}(x_i^t,V^t,E_j^t,A_k^t,,d_j){}_{i=1},\dots ,m;j=1,\dots ,l;k=1,\dots ,p.$$

The set $N_j^t\left(v\right)\subseteq V^t$ represents the potential layer j risk partners for v within a fixed temporal window of duration Θ_j, i.e. during the time [t, t + Θ_j). Typically, Θ_j is related to the definition of edge relation in the survey, e.g. in SFHR, subjects were asked for the number of risk behavior partners they had in the past 30 days so Θ₁ would be taken as 1 month.

Individual v has the propensity to sporadically engage in risk acts across layer j of their network, with a partner randomly chosen from $N_j^t\left(v\right)$. In anticipation of this, when a node v first enters the network, we assign it a propensity $r_j^R\left(v\right)$ for risk activities in layer j. This number is assumed to be time-invariant for each individual, and is randomly chosen from the positive reals using a truncated Gaussian [Robert, 1995] with (time-invariant) mean ${\mu }_j^R$ and (time-invariant) standard deviation ${\sigma }_j^R$. A Gaussian distribution was adopted in order to allow for controllable variation (across individuals) in the appetite for risk acts (per network layer j). The selection of $t_j^R\left(v\right)$ occurs independently for all individuals v and layers j. The quantity $t_j^R\left(v\right)∕\mid N_j^t\left(v\right)\mid$ represents the expected time between successive layer j risk impulses experienced by v. Statistically speaking, one may say that on average, every $t_j^R\left(v\right)$ months, individual v is expected to have engaged in roughly $\mid N_j^t\left(v\right)\mid \approx d_j\left(v\right)$ risk events via layer j edges. Following previous work on the outcomes of HIV transmission in the context of unsafe sex, risk impulse streams are generated by independent Poisson processes operating at each individual v [Barta et al., 2010, Xia et al., 2012]. To achieve the above characteristics (regarding mean times between impulses) in a memoryless fashion, the time between successive risk impulses follows an exponential distribution with rate $\mid N_j^t\left(v\right)\mid ∕t_j^R\left(v\right)$. Upon experiencing a layer j risk impulse at time t, node v selects a partner w uniformly atj random from its layer j neighbors $N_j^t\left(v\right)$, and engages in a mutual layer j risk act with w. In applications where Poisson processes are not good models of risk impulse streams, a different class of stochastic processes could be instrumented at each node, with $\mid N_j^t\left(v\right)\mid ∕t_j^R\left(v\right)$ serving as an parameter regulating the process’ intensity.

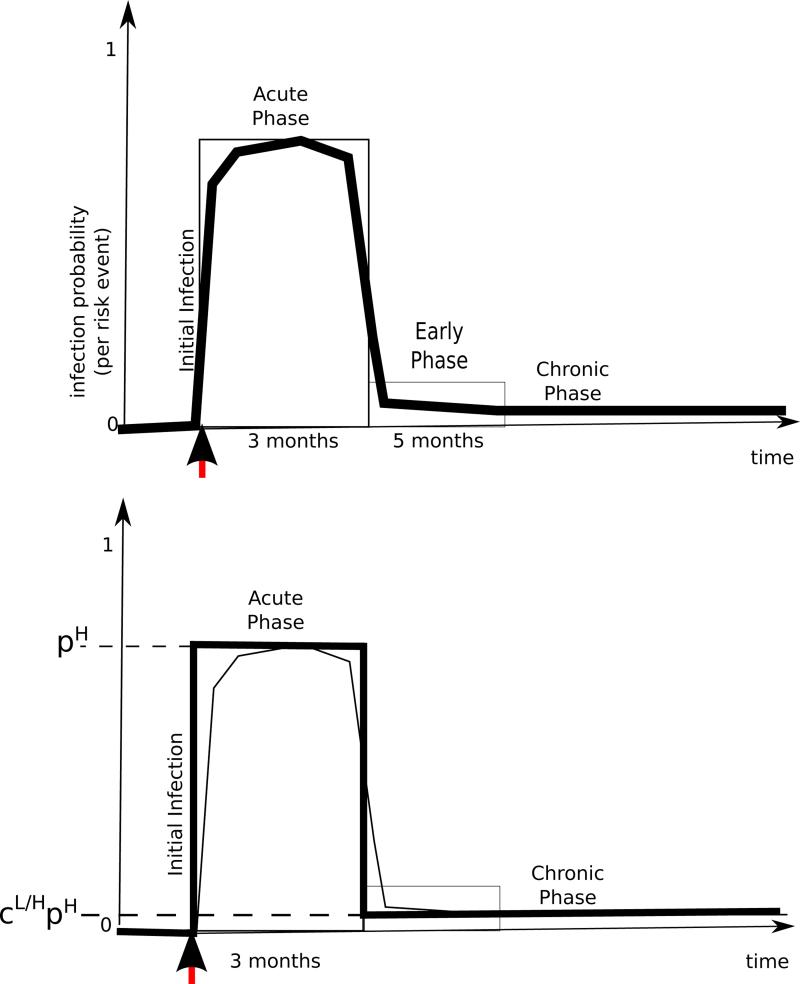
During a layer j risk act involving v and w, one or more of the pathogens ${\mathcal{P}}_k$ (for k = 1,. . ., p) may propagate. The likelihood of this is taken to be 0 if both individuals have the same infection status, i.e. when both $v,w\notin A_k^t$ or when both $v,w\in A_k^t$. If the individuals are serodiscordant with respect to pathogen ${\mathcal{P}}_k$ (i.e. precisely one of them is infected), then the probability of transmission is modeled using an infectiousness curve I_j,k. For concreteness of exposition, let's assume v is positive for pathogen ${\mathcal{P}}_k$ while w is not. The infectiousness curve I_j,k then maps the age of v's infection (with respect to ${\mathcal{P}}_k$) to the probability of the pathogen's transmission during a layer j risk act. To support this within the model, it is necessary for the risk network representation to be augmented so as to maintain information about the time when individuals first become positive for each pathogen ${\mathcal{P}}_k$. We record this information via p functions $t_k^{+}:A_k^t\to \mathbb{R}$ (for k = 1,. . ., p). Fifinally, the susceptibility of w to becoming infected by pathogen k may be impacted by the infection status of w with respect to another pathogen k′ ∈ {1,. . ., p} where k′ ≠ k. We capture this via a scalar susceptibility multiplier γ_k,k′ ∈ [0, + ∞) which amplifies or dimishes the transmission likelihood mandated the infectiousness curve. ⁴ Aggregating these factors, we get that the probability of w becoming infected by v during a single layer j risk act involving the pair (v, w) is

$$\max (0,\min (1,I_{j,k}^{+}\left(t_k^{+}\left(v\right)\right)\cdot \prod _{w\in A_{k^{\prime }}}{\gamma }_{k,k^{\prime }}))$$

While it is easy to update $t_k^{+}$ during the course of a trajectory (i.e. as previously uninfected nodes acquire the pathogen), we must also specify the infection times for individuals who were chosen to be infected at the very outset of the simulation, i.e. in the MakePathogens procedure (see Listing 3). We do this for each v in V¹ by initializing $t_k^{+}\left(v\right)$ to a value selected uniformly at random from the interval $[1-T_k^{+},1]$, the values $T_k^{+}$ are new model parameters (k = 1,. . ., p).

The 2l parameters ${\mu }_j^R$ and ${\sigma }_j^R$ (for j = 1,. . ., l) are added to the model, as are the p initialization parameters $T_k^{+}$ (k = 1,. . ., p) and the lp infectiousness curves I_j,k (for j = 1,. . ., l and k = 1,. . ., p) that capture the time dependencies of transmission risks of pathogen ${\mathcal{P}}_k$ via layer j risk acts. The model is thus augmented to support the risk process via the parameters below.

4 Modeling network dynamism

In the next section, we extend the model to include additional parameters that specify the mechanisms governing network evolution over time, capturing the fact that:

1. An individual's risk partnerships may change if and when they decide to abandon an existing risk partner (or when the risk partner decides to abandon them). Loss of risk partners may cause individual social instability, inducing the individual to seek new risk partners. We refer to the losing and gaining risk partners as the churn process, it is the subject of Section 4.1.

2. The population may change because an individual enters or leaves the risk network. We refer to this as the population process, it is the subject of Section 4.2.

3. As individuals age over time, this may alter their risk partner preferences. We refer to this as the aging process, it is the subject of Section 4.3.

Each of the three processes are described below. While the narrative is written from the vantage point of a single layer j of the risk network the processes described are replicated and operate concurrently at each of the j = 1,. . ., l layers.

4.1 The churn process

While the set $N_j^t\left(v\right)$ represents the potential layer j risk partners for v at time t, it is possible for individuals to abandon (or be abandoned by) their risk partners over time. Social instability due to a loss of layer j risk partners may induce individuals to seek new risk partners to compensate for loss of social context. The central premise of our model concerning partner “churn” is the idea that each individual v has an ideal degree d_j(v), which is the ideal size of v's ego network in layer j, based on v's stable personality. This is reflected in the fact that the ideal degree at layer j is selected using the degree distribution ${\mathbb{X}}_j$ in procedure MakePopulation (lines 8-10 of Listing 2). While d_j is permitted to vary over the population, here it is assumed to be fixed over time. ⁵

On the other hand, the actual membership (and cardinality) of v's layer j risk partners $N_j^t\left(v\right)$ is permitted to vary with time, albeit in a controlled fashion to be described in what follows.

Each individual v has the propensity to change the membership of $N_j^t\left(v\right)$, in an act we refer to as “churn”. At creation time, each node v is assigned propensity for churn $t_j^C\left(v\right)$. In the current model, this number is assumed to be time-invariant for each individual, and is randomly chosen from the positive reals using a truncated Gaussian [Robert, 1995] with (time invariant) mean ${\mu }_j^C$ and

Param	Description	Units/Range
${\mu }_j^R$	Mean time between inter layer j risk impulses	Months
${\sigma }_j^R$	Inter layer j risk impulse std. dev.	Months
$T_k^{+}$	Age interval for initial ${\mathcal{P}}_k$ infections.	Months
$I_{j,k}^{+}$	Infectiousness curve for ${\mathcal{P}}_k$ via layer j.	Fcn. of age
γk,k′	Multiplier for susceptibility to pathogen k given prior infection by k′ ∈ {1,...,p}; k′ ≠ k.	Scalar

(time invariant) standard deviation ${\sigma }_j^C$. A Gaussian distribution was used to allow for controlled variation (across individuals) in their appetite for churn acts (per network layer j). In the present model, the selection of $t_j^C\left(v\right)$ occurs independently, for all individuals v and layers j.

The quantity $t_j^C\left(v\right)∕\mid N_j^t\left(v\right)\mid$ represents the mean time between successive churn impulses experienced by v. Statistically speaking, on average every $t_j^C\left(v\right)$ months, individual v is expected to have engaged in $\mid N_j^t\left(v\right)\mid \approx d_j\left(v\right)$ churn events at layer j. The churn impulse stream is generated by independent Poisson processes operating at each individual. To achieve the desired characteristics (regarding mean times between impulses) in a memoryless fashion, the time between successive churn impulses in the Poisson process must follow an exponential distribution with rate $\mid N_j^t\left(v\right)\mid ∕t_j^C\left(v\right)$.

Upon experiencing a layer j churn impulse at time t, node v engages in a Bernoulli trial, responding to the impulse by adding a partner with probability

$$p_{j+}^t\left(v\right)\stackrel{\mathrm{def}}{=}\frac{{\left(\frac{\mid N_j^t\left(v\right)\mid +1}{d_j\left(v\right)+1}\right)}^{w_j^S}}{{\left(\frac{\mid N_j^t\left(v\right)\mid +1}{d_j\left(v\right)+1}\right)}^{w_j^S}+1}$$

or abandoning an existing partner with probability $p_{j-1}^t\stackrel{\mathrm{def}}{=}1-p_{j+}^t$.

Note that $p_{j+}^t\left(v\right)=1∕2$ whenever $\mid N_j^t\left(v\right)\mid =d_j\left(v\right)$, and that

$$\begin{array}{cc}\hfill d_j\left(v\right)-\mid N_j^t\left(v\right)\mid \to \infty & \Rightarrow p_{j+}^t\left(v\right)\to 1\hfill \\ \hfill \mid N_j^t\left(v\right)\mid -d_j\left(v\right)\to \infty & \Rightarrow p_{j+}^t\left(v\right)\to 0.\hfill \end{array}$$

In short, edge loss becomes ever more likely the more actual degree exceeds ideal degree, while edge gain becomes ever more likely the more ideal degree exceeds actual degree. When ideal degree equals actual degree, edge loss and edge gain are equally likely choices in response to a churn event. The parameter $w_j^S$ controls the rate at which $p_{j+}^t\left(v\right)$ approaches the limits asserted above, and so determines how closely individual nodes adhere to their ideal degree over the course of their network lifetimes. Justification for an individual seeking to maintain an intrinsic ideal degree comes from prior work on network “roles” and the correlations between role and ego network size [Friedman et al., 1998, Curtis et al., 1995, Romero-Severson et al., 2012].

If the Bernoulli trial due to a churn impulse at v triggers abandonment of a risk partner, the partner to be abandoned is selected uniformly at random from $N_j^t\left(v\right)$. If the Bernoulli trial triggers adding a partner, the new partner is selected by calling a modi ed version of AddEdge in which the bias due to degree constraints has been modi ed (compare with line 5 of Listing 2) as follows:

$$a_{\delta }\left(C\right):=\frac{{\left(\frac{\mid N_j^t\left(c\right)\mid +1}{d_j\left(c\right)+1}\right)}^{w_j^S}}{{\left(\frac{\mid N_j^t\left(c\right)\mid +1}{d_j\left(c\right)+1}\right)}^{w_j^S}+1}$$

Note that a_δ (c) = 1/2 whenever $\mid N_j^t\left(c\right)\mid =d_j\left(c\right)$, and that

$$\begin{array}{cc}\hfill d_j\left(c\right)-\mid N_j^t\left(c\right)\mid \to \infty & \Rightarrow a_{\delta }\left(c\right)\to 1\hfill \\ \hfill \mid N_j^t\left(c\right)\mid -d_j\left(c\right)\to \infty & \Rightarrow a_{\delta }\left(c\right)\to 0.\hfill \end{array}$$

implying that a candidate c which is experiencing a layer j degree deficit is more likely to be chosen as the terminus of the new edge from v, compared to a candidate c′ who is experiencing a layer j degree surplus.

The 3l parameters added to the model in support of the churn process are summarized below.

Param	Description	Units/Range
${\mu }_j^C$	Layer j churn interval mean	Months
${\sigma }_j^C$	Layer j churn interval std. dev.	Months
$w_j^S$	Layer j degree stability bias	Positive real

In practice, setting the churn propensity parameters aboveffican be tricky for modelers. Setting these parameters empirically requires data on the distribution of the duration of risk relationships. Given that subjects are more able to describe existing risk relationships than ones that have ended, the age of existing risk relationships can be used as a proxy for this. In the case study presented later, for example, we determined that risk partners were held as such for an average of 5 years (with a standard deviation 3 years). Accordingly, we took ${\mu }_1^C=5.0$ and ${\sigma }_1^C=3.0$, this ensured that actors chose their individual churn behavior from a distribution that allowed for a turnover (for their entire personal network) ranging from less than 2 years to 8 years or more.

4.2 The population process

The population of the risk network is controlled by both aggregate-level and individual-level processes. We refer to these respectively, as macroscopic and microscopic controls, each is treated separately below.

Macroscopic population controls

To support population growth/decline over time, we extend the dynamism model to include a new parameter r_p which captures the growth/decline of the population every 10 years (120 months). Taking r_p = 100, for example, indicates that the population should double every decade. Taking r_p = –25, on the other hand, specifies that a quarter of the population is lost every ten years. The parameter r_p is a new addition to the model. Suppose the initial population is n₁, and the population at time t is n_t. If r_p > 0, the population process creates

$$V^{+}\stackrel{\mathrm{def}}{=}{(1+r_p)}^{1∕120}{n}_1-n_t$$

new individuals in each month interval (t, t + 1]. If r_p < 0, then the population process removes

$$V^{-}\stackrel{\mathrm{def}}{=}{n}_t-{(1-r_p)}^{1∕120}{n}_1$$

existing individuals in each month interval (t, t + 1].

Microscopic population controls

In addition to the macroscopic trends in population represented by the r_p parameter, the individual agency of nodes may drive them to leave the network. Each node v has an associated “lifetime” (within the risk network), which we denote as L(v) months. The value of L(v) is set when node v is created (i.e. enters the risk network), and is selected by randomly drawing a positive real from a truncated distribution [Robert, 1995] that is the weighted sum of two Gaussians:

$$pdf(L\left(v\right)=x)=f_{tr}{e}^{-{\delta }_{tr}{(x-{\mu }_{tr})}^2}+(1-f_{tr})e^{-{\sigma }_{st}{(x-{\mu }_{st})}^2}$$

In effect, a bimodal distribution is used to model a population consisting of two types of nodes: transient nodes (which occur with relative frequency f_tr), and steady nodes (which occur with relative frequency 1 – f_tr). Transient nodes have lifetimes which are derived from a Gaussian distribution with mean σ_tr and standard deviation σ_tr, steady nodes have lifetimes which are derived from a Gaussian distribution with mean μ_st and standard deviation σ_st. Typically, μ_{st > > μtr}. An individual v who was created at time b(v) removes themself from all layers of the network at time b(v) + L(v), v is replaced if/when mandated by the macroscopic population process described in the previous section. The parameters μ_tr, σ_tr, μ_st, σ_st are assumed to be time-invariant, and are new additions to the model. Such a model enables one to confirm through simulation emerging understanding of the impact of episodic risk behaviors on epidemics (see Alam et al. [2012], Zhang et al. [2012]).

The 6 parameters added to the model in support of the population process, are summarized in the table that follows.

Param	Description	Units/Range
rp	Population growth rate every 10 years	Percentage (real)
ftr	Fraction that are “transient”	Between 0 and 1
μtr	Mean duration of transients' lifetimes	Months
σtr	Std. dev. of transients' lifetimes	Months
μst	Mean duration of steadies' lifetimes	Months
σst	Std. dev. of steadies' lifetimes	Months

4.3 The aging process

Each individual, when created, is assigned values for attributes x_i (for i = 1,. . ., m) by random sampling from the corresponding distribution α_i. Of these attributes, some may be time dependent. In particular, if one of the x_i variables represents categorical age, then it would be incorrect for the model to assume that an individual remains the same age over the course of the network trajectory. The resulting inaccuracy is of potential consequence, since age plays a role in edge formation through the corresponding bivariate distributions β_i,j, which contribute to the propensities of layer j edges being created in the course of a network's evolution. It is therefore important to update any age-related attributes (from among the x_i) over time, so that they accurately change as time passes. We refer to this continuous updating of time-varying attributes as the aging process.

5 A case study: HIV in IDU networks

Having developed a general framework for modeling dynamic risk networks, here we apply it to network data collected in the Social Factors and HIV Risk (SFHR) survey, using this as a test case for the framework presented above. We are interested in the extent to which simulations within this context yield realistic approximations of what is known about historical HIV infection rates among Injecting Drug User (IDU) networks in New York City in the earlier years of the epidemic. Conducted between 1990 and 1993, SFHR was a cross-sectional, mixed methods project that asked 767 out-of-treatment injecting drug users (IDUs) about their risk networks and HIV risk behaviors in the prior 30 days. Interested in both individuals’ network composition (namely, the presence of high-risk partners) and sociometric risk position, the SFHR study produced major findings relevant to risk populations with high HIV prevalence [Friedman et al., 1998, 2007, Goldstein et al., 1995, Des Jarlais et al., 1998, Jose et al., 1993, Kottiri et al., 2002, Neaigus et al., 1994, 1995]. SFHR documented 92 connected components among 767 subjects (connected by 662 edges), including a 105-member 2-core within a large connected component of 230 individuals. Subjects located within the 2-core were more likely to be infected with HIV [Friedman et al., 1997], causing study authors to emphasized the importance of HIV prevention within densely-connected portions of the network. The SFHR study was also among the first studies of IDU communities to document network substructures and their relationship to HIV infection/transmission [Friedman et al., 2010].

In the case study presented here, artificial networks of 1000, 5000, 10,000 and 25,000 nodes are generated using a model derived from the SFHR network survey, and these artificial networks are simulated over 15 year periods. We note that the risk network modeled on this data necessarily consists of just l = 1 layers, wherein edges represent equipment-sharing during drug co-use during the last ₁ = 30 days. In addition, this model only considers p = 1 pathogens, namely ${\mathcal{P}}_1=\mathrm{HIV}$.

As described above, ERGM analysis of the SFHR data was used to isolate actor attributes that contributed most significantly to the network topology as a whole, and produced the following multivariate model for the network (see also [Dombrowski et al., 2013a].

Attribute	θ	p-value
Transitive closure	3.592	***
Gender homophily (all)	0.058	0.566
Race/Ethnic homophily (all)	1.205	***
Age homophily (all)	0.367	**
Number of injection partners	0.460	***

^***(p < 0.001)

^**(p < 0.01)

Beyond the selection of attributes, the θ coefficients in the table above represent log-odds exponents that allow the weighting of model factors in the edge formation process. Thus raceffican be seen as e^{1.205–0.460} (or, 2.11) times more important than number of injection partners in determining risk partners. We note here that transitive closure turned out to be the most significant factor in determining the given patterns of edge formation, followed by race/ethnic homophily, degree homophily, and age homophily. The ERGM analysis provided the value $w_1^{\Delta }=3.592$ to capture the influence of triadic closure on link formation. Gender homophily—which appeared significant when examined in univariate analysis of the data—failed to be significant in the multivariate model. The remaining parameterization of the model from the SFHR study using the above attributes is presented in detail in the Appendix (section 7).

The simulations in this case study share several features in common with the concurrent work of Marshall et al. [2012], who apply an ABM approach to model HIV transmission in IDU networks, towards understanding the historical impact of various HIV interventions. Where Marshall et al. consider just five discrete classes of individuals in constructing their networks (IDU, Non-IDU, Non-User MSM, Non-User WSW, and the “general population”), the case study here allows edge formation to be biased in ways that reflect fine-grained pairwise distributions of gender, age, race, and the degrees of the endpoints { precisely the set of individual attributes determined by ERGM analysis to be significant influencers of edge formation likelihood. In addition, we take into account network-structural factors, in particular triadic closure, which ERGM also frequently shows to exert a significant influence on edge formation. In short, we have sought to reach beyond evident limitations which arise when “social norms and the network and individual properties that shape who forms a relationship with whom are not considered” (see [Marshall et al., 2012, p.12]). Although Marshall et. al consider the transmission of HIV via two different types of risk behavior (syringe sharing and unprotected intercourse), these risk behaviors appear to take place along edges in the same network layer. In our case study, we too consider a single pathogen (HIV) and just one network layer (where the edge relation represents injection drug equipment co-use), however, multi-layer multi-pathogen aspects of the general framework are exercised using artificial scenarios derived from this “Baseline Scenario” (see Section 5.1.3). While Marshall et al. devote considerable attention to the modeling of HIV interventions, we do not consider the topic here, choosing to calibrate our model instead on the subsaturation levels at which HIV prevalence stabilized in New York City's IDU community in the early 1990s. Most of all, for us, the case study primarily represents a realistic illustration of the expressive power of the proposed general-purpose framework for modeling multi-pathogen epidemiology on multi-layer risk networks.

5.1 Simulation experiments

Having captured the SFHR data to create a statistical network model (hereafter referred to as the HIV/IDU model), new artificial networks which follow the SFHR topology were generated, and these networks were made the subject of stochastic simulation. We note that since the mean in-network lifetimes of individuals was taken to be μ_st = 60 months (standard deviation σ_st = 48 months), the total number of distinct individuals which participated in these networks over the in 15 years was far greater than the number of nodes present at any given time. For example, in the 10,000 node networks, the total number of simulated network participants over the duration of the simulation was closer to 10,000 × 180/60 = 30,000. Given that 30,000 individual nodes participated in the network, each with an average degree of 3.4 and an average churn rate set to the duration of their participation in the network (i.e. 60 months) such that each node would on average churn through his/her entire set of connections completely over the course of their participation in the network, and so we estimate that (30,000 × 3.4 initial connections) + (30,000 × 3.4 churned connections)=204,000 total edge changes took place over the course of the 15 year simulation for the 10,000 nodefinetworks. Further, with a risk rate of μ_R =1 month, each of these edges was (on average) subject to a risk event monthly, from which we estimate that each simulation trial of 10,000 nodes entailed approximately 37 million risk events across which HIV infection could have taken place.

5.1.1 Validating the Simulations against “Ground Truth”

Since each simulation starts with an artificial network ${\mathcal{D}}^{\prime }$ generated via a statistical model $\mathcal{M}\left(\mathcal{D}\right)$ that is based on the SFHR dataset $\mathcal{D}$, one might ask how similar the artificial networks ${\mathcal{D}}^{\prime }$ generated were to original SFHR network $\mathcal{D}$ from which the model $\mathcal{M}\left(\mathcal{D}\right)$ was derived. According to the framework's guidelines, this similarity $\Delta ({\mathcal{D}}^{\prime },\mathcal{D})$ may be estimated via the Shannon-Jensen divergence between the corresponding constituent distributions of $\mathcal{M}\left(\mathcal{D}\right)$ and $\mathcal{M}\left({\mathcal{D}}^{\prime }\right)$, as indicated in expressions (1) and (2). Following this guideline, we conducted 10⁶ independent trials, each of which generated an artificial network ${\mathcal{D}}^{\prime }$ of size 1,000. In all these trials, the artificial network always exhibited $\Delta ({\mathcal{D}}^{\prime },\mathcal{D})\le {10}^{-2}$.

Of particular interest for us was the extent to which the dynamic networks would achieve HIV-prevalence stabilization at rates known for New York City at the time [Des Jarlais et al., 2011]. In all but the smallest simulation scenario (1000 individuals), HIV prevalence in the simulations was found to stabilize at 40% and the rise very gradually thereafter over the next 15 years. This is commensurate with the history of the HIV epidemic in New York City's IDU networks during its early stages around 1990 [Des Jarlais et al., 2011, 2005, 1998, 1989]. It also agrees with the ground truth of the SFHR data set itself, wherein 40% of the 767 subjects in the population sample were found to be HIV positive (50% in the 1-core, and 36% in the periphery).

To compare the quality of the artificial risk networks generated (as starting points of the simulation) to those that would be generated by an ERGM-based approach, we created 10³ initial networks of size 10,000 using ERGM, and 10³ using the proposed ABM procedure MakeNetwork given in Listing 1, both parameterized by statistical network data derived from the SFHR study. We then computed pairwise divergences between all 10⁶ pairs of networks generated by ERGM, all 10⁶ pairs of networks generated by MakeNetwork, and all 10⁶ heterogenous pairs of models (one generated by ERGM and the other by MakeNetwork). All three sets of 10⁶ numbers exhibited comparable means (0.03 ± 0.005) and least upper bounds (0.1 ± 0.02). From this experiment, we concluded that the proposed ABM procedure MakeNetwork produces networks whose quality is commensurate to networks generated by ERGM.

5.1.2 Continuous Model Validation

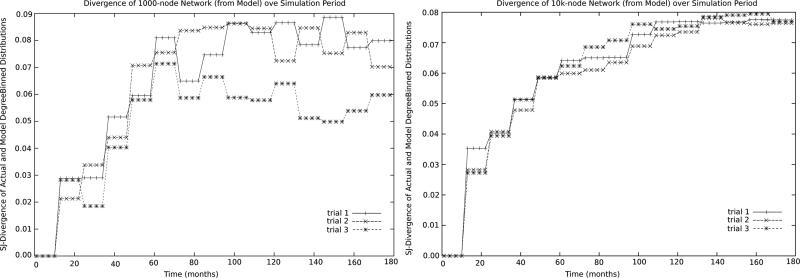
In the case study, we tracked the values of Δ across each simulation trajectory, finding the univariate degree distributions $\mathbb{X}$ to be the only characteristic that diverged by more than 0.0015 across the trajectory. As seen in Figures 1 / 2, the divergence of $\mathbb{X}$ distributions over the course of the trajectories remained bounded by Δ < 0.09. In Figure 3, the left graph shows the divergence of $\mathbb{X}$ as a function of time for three trials of a 1,000 node dynamic network, the right graph shows the same quantity at a scale of 10,000 nodes. As can be seen, the Δ is bounded by 0.09 for both small and large networks, though larger networks exhibit less variance across trials (consistent with the wide variation shown by the 1000 nodefinetwork throughout these experiments, and shown here for three trials to allow for detail that is lost in aggregating large numbers of trials).

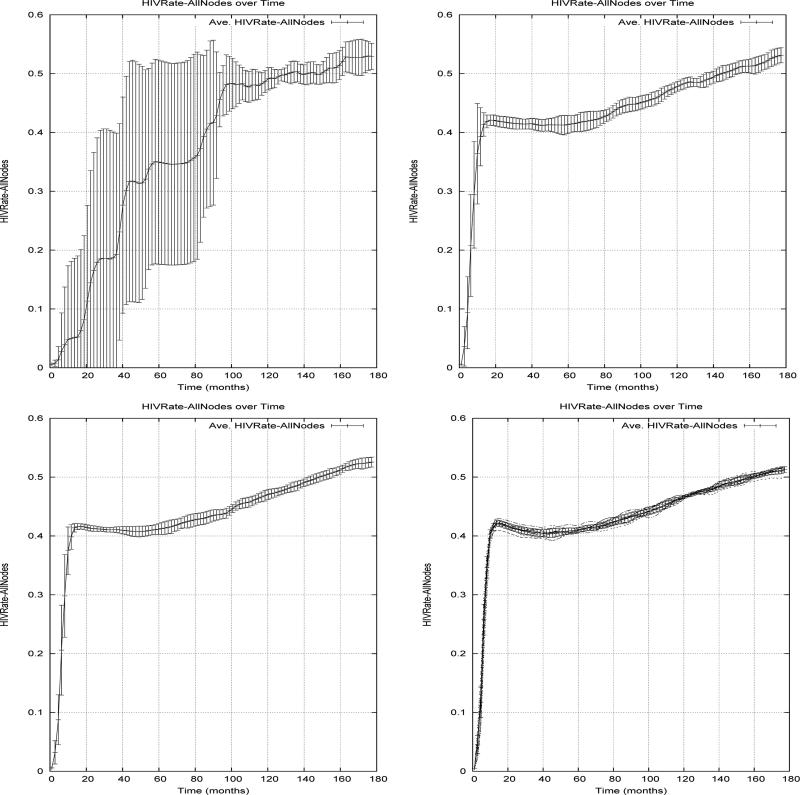
Figure 1. HIV prevalence in SFHR-based networks of size 1000, 5000, 10,000 and 25,000.

Figure 1 shows the HIV prevalence (over time) in 15 year simulations of ten independently generated networks of various sizes based on the HIV/IDU model. The bars in the graph indicate the range of findings across these ten trials. We note that in all but the smallest of these graphs, an initial infection rate of 0.5% HIV spreads throughout the network in 12-18 months to a prevalence level of roughly 40%. From here, it remains relatively stable, rising to 50% over the next 15 years.

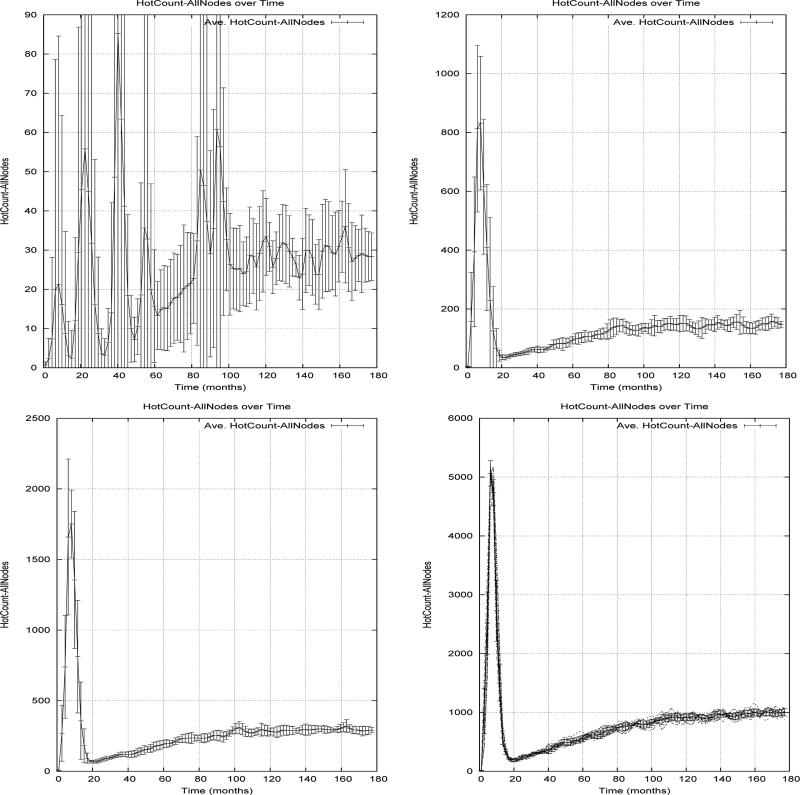
Figure 2. New HIV infections over time in networks of size 1000, 5000, 10,000 and 25,000.

Figure 2 shows the number of highly infectious nodes (over time) in 15 year simulations of ten independently generated networks based on the HIV/IDU model. All but the first of these graphs show that a surge of acute infections appears roughly 10 months into the simulation, encompassing roughly 20% of all individuals. In the 10 months after the initial spike, the acute infections dissipate, and the network returns to having relatively few acute infections (approximately 3%). This low but steady rate of new infections over time, together with the stabilization of HIV shown in Figure 1 demonstrates that while the network continues to produce new infections over time, they fail to propagate through the network, as suggested by Friedman and the original SFHR investigators [Friedman et al., 2000].

Figure 3.

Divergence Δ of $\mathbb{X}$ over 18mo for 1k (left), 10k (right) nodefinetworks on 3 trials.

To give the reader a sense of the extent to which Δ < 0.09) acts as a control on the dynamic network, we note that in such a situation, the expected absolute value of the difference between of actual and ideal degrees is 0.3 (edges). When compared to the network model's expected degree of 3.4 edges (per node), we deem this to be an acceptable level of deviation.⁶ These nodes will seek to return to their ideal degree at a rate dictated by the $w_j^S$ parameter, but at any given time, a significant number of nodes can be expected to show this high level of variation. ⁷

5.1.3 Experiments with Derived artificial Multi-Layer Multi-Pathogen Scenarios

Because our case study is based on a network model developed from the SFHR network data, which concerns the prevalence of a single pathogen (HIV) and the structure of one risk network layer (IDU needle co-use), the case study presented so far is less comprehensive than the mathematical framework. The latter is designed to support much more general multi-layer multi-pathogen settings. To ensure that all aspects of the mathematical framework are justified and sufficiently tested, multi-layer multi-pathogen case studies are required. However, because the results of unrelated complex multi-layer multi-pathogen case studies would be difficult to validate against one another, here we consider 4 artificial scenarios, systematically derived from the SFHR model.

For brevity, we report only on the mean HIV rate (over 10 trials) observed in each of the four artificial scenarios, at the end of a 60 month simulation of a network of 10,000 nodes. This prevalence rate is compared with the mean rate observed in the “Base Scenario” simulations of the true SFHR network model (see previous Section 5.1). The artificial scenarios use the same settings as the Base Scenario, and change only very few parameters related to numbers of layers and pathogen types, as specifically indicated.

Base Scenario: Here there is a single (l = 1) risk network layer based on the SFHR model and a single (p = 1) type of pathogen (HIV) which uses this network layer to propagate. As can be seen from the bottom right graph of Figure 1, the average prevalence rate of HIV in a 10,000 nodefinetwork after 60 months was seen to be approximately 42%.

Artificial Scenario 1: Here there are multiple (l > 1) risk network layers each with structure based on the SFHR network model, but constructed independently of one another following procedure MakeRelations (see Listing 1). There is a single (p = 1) type of pathogen which behaves like HIV in terms of infectiousness curves. This pathogen simultaneously uses all l > 1 network layers to propagate. The mean time between risk acts in each layer is taken to be 1/l of the value in the Base Scenario, implying that although the pathogen uses all l layers to propagate, its rate of propagation within each layer is reduced in inverse proportion to l.

To interpret the outcomes for artificial Scenario 1 (see table above), we begin by noting that in the Base Scenario, 42% of the population is infected, while 58% is uninfected. When the second network layer is added, an additional 28% becomes infected (that is, 48% of the previously uninfected 58%), leaving just 30% now uninfected. When the third network layer is added, an additional 11% becomes infected (that is, 36% of the previously uninfected 30%), leaving just 19% now uninfected. When the fourth network layer is added, an additional 8% becomes infected (that is, 42% of the previously uninfected 19%). Thus we observe that with each additional network layer roughly 40% (between 36% and 48%) of the previously uninfected nodes become reachable to the pathogen. This is expected, since each of the network layers is structured independently, and with just one layer, roughly 40% of the network was infected. Slowing down the risk act rate does not retard pathogen transmission because even with 4 layers and each layer operating at 1/4 of the Base Scenario's risk rate, we expect the pathogen's progress through each layer to be comparable to what is experienced in the Base Scenario at month 60/4=15—but as the bottom right graph of Figure 1 shows, the Base Scenario has already stabilized to roughly 40% prevalence by month 15.

Artificial Scenario 1.

Multiple layers, One pathogen

Number of layers	Pathogen 1 prevalence at 60 months
l = 2 (and p = 1)	70%
l = 3 (and p = 1)	81%
l = 4 (and p = 1)	89%
Base Scenario (p = 1 and l = 1)	42%

Artificial Scenario 2: Here there is a single (l = 1) risk network layer with structure based on the SFHR network model. There are multiple (p “> 1) types of pathogens, all of which individually behave like HIV, but must share the single risk network layer to propagate. Cross-pathogen susceptability multipliers γ_k,k′ are all taken as 1, meaning that prior infection by k′ neither enhances nor reduces susceptibility to pathogen k (k ≠ k′). The mean time between risk acts in the layer is taken to be the same as that in the Base Scenario, meaning that every time a risk event occurs between two vertices, upto p > 1 types of pathogens may be simultaneously and independently transmitted between the two parties.

The outcomes for artificial Scenario 2 (see table above) show that all pathogens reach roughly the same prevalence levels in 60 months as was manifested in the Base Scenario. Also listed is the correlation coefficient r(k, k′) between infection status for pathogen k versus k′ (for k ≠ k′), we see that the average value of the correlation (across all distinct pairs k, k′) is quite high (though it decreases slightly as the number of pathogens increases). This indicates that network structural features are at play which cause “clumping” of all pathogen infections (independent of type).

Artificial Scenario 2.

Multiple pathogens, One layer

Number of Pathogens	Average prevalence at 60 months (across all p pathogens)	Ave. pairwise correlation of pathogen occurrence
p = 2 (and l = 1)	42%	0.86
p = 3 (and l = 1)	43%	0.76
p = 4 (and l = 1)	44%	0.72
Base Scenario (p = 1 and l = 1)	42%

Artificial Scenario 3: Here there are multiple (l > 1) risk network layers each with structure based on the SFHR network model, but constructed independently of one another following procedure MakeRelations (see Listing 1). There are multiple (p > 1) types of pathogens, all of which individually behave like HIV, but with each having its own dedicated mode of propagation (embodied in a separate risk network layer), i.e. p = l. Cross-pathogen susceptability multipliers γ_k,k′ are all taken as 1, meaning that prior infection by k′ neither enhances nor reduces susceptibility to pathogen k (k ≠ k′). The mean time between risk acts for each layer is taken to be the same as that in the Base Scenario. Since each risk event occurs in a layer, and each layer is devoted to a single pathogen type, when a risk event occurs between two vertices, at most one type of pathogen may be transmitted. However, since all l = p layers are operating independently, all p pathogens propagate concurrently through the population, albeit with each pathogen making use of its own dedicated risk network layer.

The outcomes for artificial Scenario 3 (see table above) show that all pathogens reach roughly the same prevalence levels in 60 months as was observed in the Base Scenario. However, in examining the correlation r(k, k′) between infection status for pathogen k versus k′ (for k ≠ k′), we see that the average value of the correlation (across all distinct pairs k, k′) is now quite low. This indicates that shared network structural features that were at play in artificial Scenario 2 are disrupted when the pathogens are forced to travel across multiple independently constructed risk network layers.

Artificial Scenario 3.

Multiple layers, Multiple non-inreracting pathogens

Number of Pathogens p Number of Layers l	Average prevalence at 60 months (across all p pathogens)	Ave. pairwise correlation of pathogen occurrence
p = l = 2	42%	0.12
p = l = 3	43%	−0.11
p = l = 4	42%	0.08
Base Scenario (p = l = 1)	42%

Artificial Scenario 4: This scenario is identical to scenario 3, except that cross-pathogen susceptability multipliers γ_k,k′ are all taken as 0. This means that prior infection by pathogen k′ makes an individual immune to pathogen k (k ≠ k′).

The outcomes for artificial Scenario 4 (see table above) show that the pathogens considered collectively, reach roughly the same prevalence levels in 60 months as was observed in the Base Scenario. That is, 2 21% ≈ 3 × 15% ≈ 4 × 12% ≈ 42%. This is expected, since cross-pathogen susceptability multipliers force the p pathogens to share host infection opportunities between them.

Artificial Scenario 4.

Multiple layers, Multiple inreracting pathogens

Number of Pathogens p Number of Layers l	Average prevalence at 60 months (across all p pathogens)
p = l = 2	22%
p = l = 3	15%
p = l = 4	12%
Base Scenario (p = l = 1)	42%

Taken together, these four artificial scenarios, and the plausible explanations for the outcomes observed in each of them, provide us with a measure of confidence in our framework's general applicability to epidemiological modeling involving multi-pathogen multi-layer risk networks.

6 Conclusions

Simulations of artificial risk networks generated by the HIV/IDU model exhibited stabilization of HIV prevalence to sub-saturation levels similar to those observed historically in IDU networks in New York City during the early stages of the HIV epidemic [Des Jarlais et al., 2011, 2005, 1998, 1989]. Simulations in which the virulence of the pathogen was raised (modeled as an overall increase in the likelihood of transmission in any given risk event) showed little change to overall stabilization levels for networks of 5000+ nodes—a truly counter-intuitive finding, given that so much public health effort is directed to lowering individual risk in stemming the spread of HIV. Of interest is that stabilization manifests in networks of 5000 to 25,000 nodes, but is not clear in smaller networks, the 1000 node network shows little evidence of HIV stabilization, and a wide range of prevalence rates at any given time when examined across independent simulation trials. The framework developed here was able to reveal historical HIV prevalence trajectories through the simulation of dynamic risk networks which reflected both known (micro) IDU behavioral profiles and (macro) structural characteristics of a real-world risk network, as recorded in the SFHR survey, as such, it represents a significant step forward in our ability to model and simulate the dynamics of infectious disease.

More generally, we note that while traditional social network research continues to produce considerable data on infection profiles, and equally detailed data on the broad demographic and behavioral profiles of at-risk communities and their risk behaviors, such research has not—and for reasons of cost often cannot—produce long-term, dynamic data on these same populations. At best, it provides snapshots of social processes within risk networks that are otherwise known to be in a state of flux. The general framework presented here—demonstrated through a real case study of HIV in IDU networks—shows that simulation provides an opportunity to understand the long-term dynamics of risk networks themselves. Looking to the future, the framework opens the door to understanding how the specific patterns of risk-bearing relationships came to be the way they are, how infections move (and do not move) across these topologies, where risk networks and the infections they contain are going in the future, and what the impacts of various interventions might be.

Figure 4.

(Top) Infectiousness of HIV as a function of age of infection, (Bottom) A simpli ed two-parameter representation.

Algorithm 1.

Procedure MakeNetwork

	Input: statistical network model ${({\alpha }_i,{\beta }_{i,j},{\mathbb{X}}_j,\stackrel{=}{{\chi }_j},{\mathbb{P}}_k)}_{i=1,\dots ,m;j=1,\dots ,l;k=1,\dots ,p}$; population size n.
	Output: risk network (xi, V, Ej, Ak, dj)i=1,...,m;j=1,...l;k=1,...,p.
1	({xi}, {dj}, V) ← MakePopulation${(n,\left\{{\alpha }_i\right\},\left\{{\mathbb{X}}_j\right\})}_{i=1,..,m;j=1..l}$
2	{Ak} ← MakePathogens${(V,\left\{{\mathbb{P}}_k\right\})}_{k=1..p}$
3	E ← MakeRelations${(\left\{{\beta }_{i,j}\right\},\left\{\stackrel{=}{{\chi }_j}\right\},\left\{x_i\right\},\left\{d_j\right\},V)}_{i=1,,,m;j=1..l}$
4	return (xi, V, Ej, Ak, dj)i=1,...,m;j=1,...,l;k=1,...,p.

Algorithm 2.

Procedure MakePopulation

	Input: pop. size n, attribute distributions {αi}i=1..m, degree distributions ${\left\{{\mathbb{X}}_j\right\}}_{j=1..l}$.
	Output: ({xi}, {dj}, V)i=1..m;j=1..l.
1	V = {v1, v2, . . ., vn}.
2	foreach vk in V do
3	// Set the attributes of individual vk.
4	foreach i in 1...m do
5	xi(vk) := an element of Ui randomly selected via αi.
6	// Set individual vk's ideal ego net size at each layer.
7	foreach j in 1...l do
8	$s≔f_j^C\left(v\right)$, the layer-j ideal degree class of vk.
9	τ := χj;s the corresponding layer-j ideal degree distribution, taken from $Range\left({\mathbb{X}}_j\right)$.
10	dj(vk) := an integer randomly chosen via pdf τ.
11	return ({xi}, {dj}, V)i=1..m;j=1..i.

Algorithm 3.

Procedure MakePathogens

	Input: population V, pathogen prevalences ${\left\{{\mathbb{P}}_k\right\}}_{k=1..p}$
	Output: {Ak}k=1..p
1	A1 = A2 = ... Ap = $\varnothing$
2	foreach k in 1... p do
3	foreach vi in V do
4	$t≔f_k^{\mathcal{B}}\left(v\right)$, identifying the pathogen-k class of vi in Domain$\left({\mathbb{P}}_k\right)$.
5	τ := pk;t the corresponding pathogen-k prevalence rate in Range$\left({\mathbb{P}}_k\right)$.
6	if Random(0, 1) < τ then
7	Ak := Ak ∪ {vi}
8	return {Ak}k=1..p

Algorithm 4.

Procedure MakeRelations

	Input: bivariate attribute distributions {βi,j}i=1..m;j=1..l, bivariate degree distributions ${\left\{\stackrel{=}{{\chi }_j}\right\}}_{j=1,,l}$, individual attributes {xi}i=1..m and ideal degrees {dj}j=1..l, the population V
	Output: E
1	$E=\varnothing$
2	foreach i in 1... |V| do
3	foreach j =1...l do
4	$N_j\left(v_i\right)≔\varnothing$.
5	foreach e = 1...dj(v) do
6	Schedule AddEdge(vi, j) to take place at time $\frac{1}{ei+1}$.
7	Wait until time 1.
8	$E≔{\bigcup }_{i=1}^{\mid V\mid }{\bigcup }_{w\in N\left(v_i\right)}\left\{(v,w)\right\}$
9	return E

Algorithm 5.

procedure AddEdge

	Input: individual v, layer j.
1	// Determine candidate new neighbors for v.
2	$C_j^t\left(v\right)≔V_j^t\backslash (N_j^t\left(v\right)\cup \left\{v\right\})$.
3	if $\mid C_j^t\left(v\right)\mid >0$ then
4	foreach c in $C_j^t\left(v\right)$ do
5	Compute the bias due to degree constraints:
	$a_{\delta }^t\left(c\right)≔\{\begin{array}{cc}{e}^{-1∕(d_j\left(v\right)-\mid N_j^t\left(v\right)\mid )}\hfill & \mid N_j^t\left(u\right)\mid <d_j\left(u\right)\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$
6	Compute the bias due to the bivariate degree distribution:
	$a_{\chi }^t(v,c)≔\stackrel{=}{{\chi }_j}(\mid N_j^t\left(v\right)\mid -∊,\mid N_j^t\left(v\right)\mid +∊,\mid N_j^t\left(c\right)\mid -∊,\mid N_j^t\left(c\right)\mid +∊)$.
7	Compute the bias due to bivariate attribute distributions:
	$a_{\beta }^t\left(c\right)≔{\prod }_{i=1}^m{\beta }_{i,j}(x_i\left(v\right),x_i\left(c\right))$.
8	Compute the bias due to triadic closures:
	$a_{\Delta }^t\left(c\right)≔\zeta (w_j^{\Delta }-1)\cdot {\Delta }_j^t(v,c)$
	where ${\Delta }_j^t(v,c)=\#$ layer j triangles formed on adding layer j edge (v, c).
9	Compute propensity of edge (v, c) as the product of 4 biases:
	$w_j^t\left(c\right)≔a_{\delta }^t\left(c\right)\cdot a_{\chi }^t\left(c\right)\cdot a_{\alpha }^t\left(c\right)\cdot a_{\Delta }^t\left(c\right)$.
10	Normalize propensity to obtain a distribution over $C_j^t\left(v\right):$:
	$p_j^t\left(c\right)≔\frac{{\omega }_j^t\left(c\right)}{{\sum }_{c^{\prime }\in C_j^t\left(v\right)}{\omega }_j^t\left(c^{\prime }\right)}$.
11	w := choose from $C_j^t\left(v\right)$ randomly according to distribution $p_j^t$.
12	// Add the layer j edge connecting v to w.
13	$N_j^t\left(v\right)≔N_j^t\left(v\right)\cup \left\{(v,w)\right\}$

7 Appendix: Model Parameterizations

The following parameters were taken from the SFHR data and used in the case study above:

7.1 Static Network

In the context of this work, by applying ERGM analysis to the risk network $\mathcal{D}$ obtained from the SFHR survey data, we determined that m = 4 individual attributes exerted significant influence on the likelihood of edge formation. The names and categorical ranges of each of these significant attributes X = {x₁,. . . x₄} are tabulated below, a full exposition of their derivation by ERGM analysis is available [Dombrowski et al., 2013b]. The univariate and bivariate distributions of Gender, Ethnicity, AgeBinned, and DegreeBinned are tabulated below. Fifinally, as 39% of individuals in the SFHR risk network were HIV+, in the corresponding statistical network model we take p = 0.39.

Significant attributes (as determined by ERGM)

Name	Possible values (Ui)
x1 : Gender	{Male, Female}
x2 : Ethnicity	{White, Hispanic, African-American, Other}
x3 : AgeBinned	{[15-20), [20-25), [25-30), [30-35), [35-40), [40-45), [45-50), [50-55)}
x4 : DegreeBinned	{[0-2), [2-4), [4-10), [10-20)}

Gender univariate α₁

	Male	Female
α1	540/767	227/767

Ethnicity univariate α₂

	White	Hispanic	African-American	Other
α2	243/767	206/767	311/767	7/767

AgeBinned univariate α₃

	[15-20)	[20-25)	[25-30)	[30-35)	[35-40)	[40-45)	[45-50)	[50-55)
α3	6/767	32/767	158/767	172/767	198/767	159/767	23/767	19/767

DegreeBinned univariate χ

	[0-2)	[2-4)	[4-10)	[10-20)
χ	322/767	221/767	161/767	63/767

Gender bivariate β₁

β1	Male	Female
Male	94/145	51/145
Female	76/127	51/127

Ethnicity bivariate β₂

β2	White	Hispanic	African-American	Other
White	115/178	18/178	43/178	7/178
Black	11/157	112/157	31/157	7/157
Hispanic	32/175	25/175	117/175	1/175
Other	2/7	4/7	1/7	0

AgeBinned univariate β₃

β3	[15-20)	[20-25)	[25-30)	[30-35)	[35-40)	[40-45)	[45-50)	[50-55)
[15-20)	1/4	1/4	2/4	0	0	0	0	0
[20-25)	1/26	1/26	7/26	6/26	7/26	3/26	1/26	0
[25-30)	1/147	8/147	41/147	45/147	38/147	12/147	2/147	0
[30-35)	0	5/153	33/153	50/153	43/153	16/153	5/153	1/153
[35-40)	0	4/161	20/161	41/161	56/161	29/161	6/161	5/161
[40-45)	0	2/137	14/137	27/137	44/137	40/137	3/137	7/137
[45-50)	0	0	2/20	6/20	6/20	4/20	2/20	0
[50-55)	0	0	0	2/14	6/14	4/14	0	2/14

DegreeBinned univariate $\stackrel{=}{\chi }$

$\stackrel{=}{\chi }$	[0-2)	[2-4)	[4-10)	[10-20)
[0-2)	77/158	37/158	29/158	15/158
[2-4)	57/203	77/203	40/203	29/203
[4-10)	42/195	50/195	64/195	39/195
[10-20)	15/100	23/100	31/100	31/100

7.2 Pathogen model for HIV/IDU

Inter risk impulse interval mean μ_R was set in accordance with the SFHR data set. Given that the criteria for connection in the SFHR survey was “a risk event in the last 30 days” [Friedman, 1999, p.115], the risk parameter μ_R was set to 1.0 months, so that nodes would draw from a distribution of risk profiles centered at one risk event per month per risk partner. With a mean degree of 3.4, this means, in effect, that the average actor will engage 3-4 risk events in a 30 day period. Further description in the SFHR documentation points to a wide range of risk behavior rates. SFHR interview subjects reported an average of 112 monthly injections (not all of which, obviously, involved a risk event), with a standard deviation of 139 [Friedman, 1999] p. 120. Taking the latter as our guide, we set the inter risk impulse interval standard deviation σ_R to 1.0 months, such that the variation in risk was roughly equal to the overall rate. This produced a truncated distribution with a near at distribution between 0 and 2, and long but diminishing tail for rates greater than 2 risk events per number of risk partners per month.

In the case of HIV, the infectiousness curveffican be approximated as function of infection age that decreasing sharply at approximately three months, and remains at low levels until approximately eight years later [Cates et al., 1997, Kahn and Walker, 1998, Lyles et al., 2007]. We use this information to construct two-parameter infectiousness function I_j,1. Given that we know the infectiousness drop sharply approximately 3 months after the time of initial infection, we approximate the infectiousness curve I_j,1 by a step function whose value is $p_j^H$ for the 3 month high infectiousness, or “acute” phase, and $c_j^{L∕H}\cdot p_j^H$ thereafter, in the low infectiousness or “chronic” phase. We note here that $c_j^{L∕H}\ll 1$. With such a model, if $t-t_1^{+}\left(v\right)\le 3$ then with probability $p_j^H$ individual w acquires HIV from v during the layer j risk act. If, on the other hand, $t-t_1^{+}\left(v\right)>3$, then the transmission occurs with a much smaller probability $c_j^{L∕H}\cdot p_j^H$. In either case, if w acquires HIV during the layer j risk act, then w is added to $A_1^t$ and we set its infection time $t_1^{+}\left(w\right)≔t$. To support such a model of HIV pathogen transmission, the 2 parameters $p_1^H$ and $c_1^{L∕H}$ must be specified.

The infection probability in infectious period p_H was initially inteded as a tuning parameter such that, once the other parameters had been set according to the SFHR data, a series of trials could be undertaken in simulated networks and the transmission parameter set such that the simulated HIV rates for the SFHR settings regularly matched those of the SFHR sample (i.e. 40%). This proved unnecessarily complex, as variations in the infectiousness probability had little effect on the overall HIV rates. In the end, we used a mean rate of risk for equipment co-use during periods of high infectousness of 5% chance of infection per risk event. Rates at low as 2% and as high as 10% showed only small effect in overall infection rates. While no precise data are available for HIV per-event risk rates, Hagan and colleagues found that HCV risk among IDU showed a 3 to 5 fold increase in seroconversion ratesand a risk factor of 5.9 for those who shared drug preparation equipment or syringes [Hagan et al., 2001].

The reduction in infectiousness post 3 months c_L/H, was taken to be 1/100, as an estimate for a wide range of published measures, from 1/20th to 1/1000th, based on comparisons between periods of high and low infectiousness [Daar et al., 1991, Kahn and Walker, 1998].

The infection interval T₊ for individuals initially HIV+ was taken to be three weeks, as an approximation for published a range of estimates from 9 to 14 weeks [Daar et al., 1991, Kahn and Walker, 1998].

7.3 Network dynamism model for HIV/IDU

The rate at which network actors changed their current list of risk partners churn interval mean μ_C was taken to reflect a network wherein risk partners are held as such for an average of 5 years. Justification for this [Friedman, 1999, p. 130] includes the fact that, 53 percent of the network noted that they had known all of their network for at least a year, and 43 percent of the network felt “very close” to some or all of their network. Ethnographic reports from the SFHR network [Curtis et al., 1995] note considerable longevity to risk partnerships (see also [Friedman, 1999] chapter 3). Here again, where wide variation in individual characteristics obtained, we set the churn interval standard deviation σ_C=3.0 years to ensure that actors chose their individual churn behavior from a distribution that allowed for rapid turn overs of less than 2 years (for their entire personal network) to long-term partnerships (of 8 years or more). It was later discovered that the changes to μ_C and σ_C had little effect on the simulation outcomes with respect to asymptotic HIV rates.

The degree stability bias w_S determined how closely individual nodes maintained their degree over the course of their participation in the network. On the whole, the justification for a fixed degree comes from prior work on drug scene “roles” [Friedman et al., 1998, Curtis et al., 1995]. While, obviously, no direct parameter settings can be drawn from the data described by Friedman et al and Curtis et al, the function used to determine the effects of the parameter, and the original parameter setting of 2.9 was designed such that variations from initial degree by roughly 30 % were very likely to be corrected. It was discovered that the changes to w_S little effect on the simulation outcomes with respect to asymptotic HIV rates.

The macroscopic population process growth rate r_P =0 was set thereby specifying a constant population size, although certainly individuals were leaving and entering throughout (see below).

While a number of individuals in the SFHR study had few partners, or would be considered marginal members of the network itself, there is also a wealth of ethnographic reports on very short-term visitors to the network [Friedman et al., 1998, Curtis et al., 1995]. As far as we know, no solid estimates of the proportion of these transient participants is given, nor would we expect the number to be uniform across sub-networks in New York City. A “drug market” zone like that studied by the SFHR project is likely to have a greater proportion of transient members than a smaller, let public network. We took the fraction of individuals that are “transient” f_tr=0, as a base-line in the simulations here.

As with network churn, a dearth of diachronic data meant that we relied heavily for these parameter settings on ethnographic observation and the experience of project co-authors in the SFHR network. While many of the SFHR network members had been injectors for longer than 9 years, this does not mean that their they participated in the same IDU network for that entire time. For this reason, the settings were made identical to the churn settings above, mean duration of steadies’ lifetimes μ_st=5.0 years, and standard deviation of steadies’ lifetimes σ_st=3.0 years, so that participation varied widely from 2-8 years for “steady” participants.