Skip to main content
PMC home page
Acta Crystallographica Section F: Structural Biology Communications logoLink to Acta Crystallographica Section F: Structural Biology Communications
. 2015 Mar 30;71(Pt 4):358–370. doi: 10.1107/S2053230X15005348

Large-volume protein crystal growth for neutron macromolecular crystallography

Joseph D Ng a,b,*, James K Baird c, Leighton Coates d, Juan M Garcia-Ruiz e, Teresa A Hodge c, Sijay Huang c
PMCID: PMC4388167  PMID: 25849493

Growing large-volume crystals are necessary and important for neutron macromolecular crystallography. Experimental strategies, techniques and theoretical considerations for protein crystal growth are reviewed.

Keywords: large-volume crystals, neutron macromolecular crystallography

Abstract

Neutron macromolecular crystallography (NMC) is the prevailing method for the accurate determination of the positions of H atoms in macromolecules. As neutron sources are becoming more available to general users, finding means to optimize the growth of protein crystals to sizes suitable for NMC is extremely important. Historically, much has been learned about growing crystals for X-ray diffraction. However, owing to new-generation synchrotron X-ray facilities and sensitive detectors, protein crystal sizes as small as in the nano-range have become adequate for structure determination, lessening the necessity to grow large crystals. Here, some of the approaches, techniques and considerations for the growth of crystals to significant dimensions that are now relevant to NMC are revisited. These include experimental strategies utilizing solubility diagrams, ripening effects, classical crystallization techniques, microgravity and theoretical considerations.

1. Introduction  

Neutron macromolecular crystallography (NMC) is a powerful method to obtain the accurate positioning of H atoms in biological structures of 50–175 kDa molecular weight from neutron data collected to near-atomic resolution (1.5–2.5 Å; Blakeley et al., 2008 ▶). Macromolecules will primarily refer to proteins unless stated otherwise. H atoms constitute 50% of the protein atoms but they scatter X-rays weakly, such that their positions can only be accurately identified at a resolution higher than 1.0 Å. Most three-dimensional macromolecular structures have been determined by X-ray crystallography within the resolution range 1.5–2.0 Å (RCSB Protein Data Bank). As a result, there is very little knowledge of the location of H atoms and water molecules in 99% of the structures determined to date. Knowing the hydrogen positions in macromolecules and in interacting water molecules is necessary to completely understand the reaction mechanisms, pathways and structure–function relationships among proteins and their important binding partners. Therefore, it is invaluable to obtain macromolecular structures that can provide unique and complementary insights into the hydrogen-bonding interactions, protonation states, catalytic mechanisms and hydration states of biological structures that are not available from X-ray analysis alone.

The primary limiting factor in obtaining a neutron crystallographic macromolecular structure rests on the success of growing protein crystals of adequate size and quality. Large-volume protein crystals are required to overcome the weak flux associated with neutron sources (Coates et al., 2001 ▶; Teixeira et al., 2008 ▶). NMC is dependent on scattering by the atomic nuclei providing information on the location of H atoms from the protein, its substrates and surrounding water. The present protein crystal volume prerequisite for neutron diffraction is at least 0.1 mm3 (Blakeley et al., 2008 ▶; Howard et al., 2011 ▶; Weber et al., 2013 ▶). In most cases a larger protein crystal (∼0.5 mm3 for nonperdeuterated proteins) is needed for successful neutron analysis. These substantial crystal sizes are not necessary for X-ray structure determination because of the accessibility of intense synchrotron focused-beam sources and sensitive X-ray detectors.

Globally, there are only a handful of neutron facilities available for single macromolecular crystal diffraction. LADI-III (Blakeley et al., 2010 ▶) at the Institut Laue–Langevin, Grenoble, France is a quasi-Laue diffractometer that is able to collect high-resolution data between 1.5 and 2.5 Å. It has been repositioned closer to the cold neutron source, thereby increasing the incident neutron flux considerably. The ability to collect data at cryogenic temperatures of around 100 K has also just been added to the instrument. Several newly constructed neutron beamlines have also recently come online such as the Biological Diffractometer (BIODIFF) at the FRM II reactor in Garching, Germany. BIODIFF is designed to analyze crystals with large unit-cell sizes with a monochromatic neutron source. In the United States, the macromolecular diffractometers MaNDi (Coates et al., 2010 ▶) and IMAGINE (Meilleur et al., 2013 ▶) instruments are available at Oak Ridge National Laboratory (ORNL). MaNDi is equipped with the capability to conduct cryo-data collection and to use crystals with large unit-cell sizes. In Japan, the IBIX instrument at J-PARC has been operational since December 2008. All of these facilities have significantly increased the availability of neutron diffraction beamtime to the global user community. Even though high-power neutron sources with state-of-the-art facilities are becoming more available with faster data-collection capabilities, the large crystal size requirement still persists.

Extended protein crystal growth to acquire large volumes has been very challenging because macromolecules are usually dynamic and flexible, and as a result contain inherent heterogeneity (Malkin & Thorne, 2004 ▶) despite the extent of their purity. In addition, the presence of partially denatured protein most often poisons the growing surface (Ng, Kuznetsov et al., 1997 ▶). Nonetheless, a small number of protein neutron crystallographic structures have been determined to date compared with those deciphered using X-rays. Less than 75 nonredundant neutron structures have been deposited in the RCSB Protein Data Bank at present compared with over 90 000 deciphered using X-rays. All of the macromolecular structures that have been obtained by neutron crystallography are listed in Table 1 ▶, which gives their PDB codes, space groups and determined resolutions.

Table 1. Crystallographic structures determined to date by neutron crystallography.

  Macromolecule PDB code Space group Resolution ()
1 Achromobacter protease I 4gpg P1 1.90
2 Antifreeze protein (type III) 3qf6 P212121 1.85
3 Apo D-xylose isomerase 3kcj I222 1.80
4 Aspartic proteinase 2jji P21 1.57
5 Aspartic proteinase 2jjj P21 1.00
6 B-DNA decamer d(CCATTAATGG)2 1wqz P21 3.00
7 -Lactamase Toho-1 R274N/R276N double mutant (perdeuterated) 2xqz P3221 2.10
8 -Lactamase Toho-1 E166A/R274N/R276N triple mutant 2wyx P3221 2.10
9 -Lactamase Toho-1 R274N/R276N double mutant (perdeuterated) in complex with fully deuterated boronic acid (BZB) 4c3q P3221 2.20
10 Bovine pancreatic ribonuclease A 3a1r P21 1.70
11 Bovine pancreatic trypsin inhibitor 5pti P212121 1.00
12 Carbonmonoxymyoglobin 2mb5 P21 1.80
13 Concanavalin A 1c57 I222 2.40
14 Concanavalin A 2yz4 I222 2.20
15 Crambin 4fc1 P21 1.10
16 Crambin (H/D-exchanged) 3u7t P21 0.85
17 Cytochrome c peroxidase 3r98 P212121 2.40
18 Cytochrome c peroxidase (compound I intermediate) 4cvj P212121 2.50
19 D-Xylose isomerase 2gve I222 2.20
20 D-Xylose isomerase in complex with two Ni2+ cations and perdeuterated D-sorbitol 4dvo I222 2.00
21 D-Xylose isomerase in complex with two Cd2+ cations and d12-D--glucose 3kcl I222 2.00
22 D-Xylose isomerase in complex with two Ni2+ cations and d12-D-glucose 3kco I222 1.80
23 Deoxy human hemoglobin 2dxm P21 2.10
24 Dihydrofolate reductase (Escherichia coli) bound to the anticancer drug methotrexate 2inq P61 2.20
25 Diisopropyl fluorophosphatase 3byc P212121 2.20
26 Diisopropyl fluorophosphatase (DFPase) (perdeuterated) 3kgg P212121 2.10
27 Dissimilatory sulfite reductase D (DsrD) 1wq2 P212121 2.40
28 Endothiapepsin complexed with transition-state analogue inhibitor H261 1gkt P21 2.10
29 Endothiapepsin in complex with a gem-diol inhibitor 2vs2 P21 2.00
30 Ferric cytochrome c peroxidase 4cvi P212121 2.41
31 Get5 ubiquitin-like domain 4goc P212121 2.40
32 Hen egg-white lysozyme 1lzn P1 1.70
33 HIV-1 protease in complex with the clinical inhibitor amprenavir (perdeuterated) 4jec P21212 2.00
34 HIV-1 protease in complex with the potent inhibitor KNI-272 2zye P21212 1.90
35 Human carbonic anhydrase II 3kkx P21 2.00
36 Human transthyretin 3u2j P21212 2.00
37 Human transthyretin 3u2i P21212 1.70
38 Human transthyretin (TTR) at room temperature 4pvm P21212 2.00
39 Inorganic pyrophosphatase 3q3l C2 2.50
40 Insulin 2zpp I213 2.50
41 Insulin 3ins H3 1.50
42 Insulin (porcine 2Zn2+) 3fhp H3 2.00
43 Leucine and valine methyl-protonated type III antifreeze 4ny6 P212121 1.85
44 Lysozyme in D2O (wild type, human) 2zwb P212121 1.80
45 Magnesium-activated inorganic pyrophosphatase 3q46 H32 0.99
46 Major urinary protein I 1i05 P43212 2.00
47 Myoglobin (fully perdeuterated) 1cq2 P21 2.00
48 Oxidized amicyanin 3l45 P21 1.80
49 Oxymyoglobin 1mbd P21 1.40
50 Photoactive yellow protein (PYP) 2zoi P63 1.50
51 Photoactive yellow protein (PYP) 2qws P63 2.50
52 PKGI in complex with cGMP 4qxk P41212 2.20
53 Porcine pancreatic elastase complexed with the potent peptidyl inhibitor FR130180 3hgn P212121 1.65
54 Ribonuclease A with uridine vanadate 6rsa P21 2.00
55 Rubredoxin (fully perdeuterated) 3kyx P212121 1.68
56 Rubredoxin (fully perdeuterated) 3kyy P212121 1.10
57 Rubredoxin (perdeuterated oxidized form) from Pyrococcus furiosus 4ar3 P212121 1.05
58 Rubredoxin (perdeuterated) 4k9f P212121 1.75
59 Rubredoxin (wild type) from P. furiosus 1vcx P212121 1.50
60 Rubredoxin from P. furiosus (perdeuterated) 4ar4 P212121 1.38
61 Rubredoxin mutant 1iu5 P212121 1.50
62 Rubredoxin mutant from P. furiosus 1iu6 P212121 1.60
63 Saccharide-free concanavalin A 1xqn I222 2.50
64 Sperm whale met-myoglobin 1l2k P21 1.50
65 Streptomyces rubiginosus D-xylose isomerase in complex with two Cd2+ ions and cyclic -L-arabinose 4qdp I222 2.00
66 S. rubiginosus D-xylose isomerase in complex with two Ni2+ ions and linear L-arabinose 4qdw I222 1.80
67 Trypsin 1ntp P212121 1.80
68 Trypsin complexed with BPTI (bovine pancreatic trypsin inhibitor) 3otj I222 2.15
69 Urate oxidase in complex with 8-azaxanthine 4n3m I222 1.90
70 Urate oxidase in complex with 8-hydroxyxanthine 4n9m I222 2.30
71 Urate oxidase in complex with 8-hydroxyxanthine 4n9s I222 1.06
72 Xylose isomerase E186Q mutant (cyclic glucose bound) 4lnc I222 2.19
73 Z-DNA 3qba P212121 1.53
74 Z-DNA hexamer CGCGCG 1v9g P212121 1.80
Open in a new tab

Obtaining large-volume crystals begins with the same common approach as used for crystallizing any macromolecules out of solution. The general strategy for protein crystallization is to reduce the solubility of the macromolecule in the solvent such that an extreme supersaturation state is achieved with respect to the protein. There are a number of devices and procedures to bring a protein solution into a supersaturated state (for reviews, see McPherson, 1999 ▶; Ducruix & Giegé, 1999 ▶; Ng & García-Ruiz, 2006 ▶; McPherson & Cudney, 2014 ▶; Loll, 2014 ▶) and ultimately lead to a large crystal after appropriate optimization. The most commonly used in obtaining protein crystals are the batch and vapor-diffusion methods (Cudney & Patel, 1994 ▶; Bergfors, 2007 ▶). Batch crystallization entails the direct mixing of an undersaturated protein solution with a precipitant solution (Rayment, 2002 ▶; Chayen et al., 1990 ▶). In vapor diffusion, an undersaturated protein solution is mixed with precipitants in a droplet and the resulting mixture is allowed to evaporate in a closed system against a reservoir solution containing the precipitant (Benvenuti & Mangani, 2007 ▶). At this point there is a high probability that critical nuclei will spontaneously form in solution. Counter-diffusion crystallization in restricted geometry is also a well known method to screen and optimize conditions for protein crystallization (García-Ruiz, 2003 ▶). In counter-diffusion equilibration, samples of the precipitating agent and protein solution are arranged in juxtaposition to one another inside a volume-constrained capillary. The two solutions are set to diffuse against each other in a convection-minimized environment, resulting in a spatial–temporal gradient of supersaturation along the length of the capillary (García-Ruiz, 2003 ▶; Otálora et al., 2009 ▶). This technique has been successfully used for in situ X-ray diffraction analyses for structure determination (Gavira et al., 2002 ▶; Ng, Stevens et al., 2008 ▶; Ng et al., 2003 ▶). Regardless of the initial approach to find early crystallization conditions, strategic efforts and consideration must be made to optimize ongoing crystallization processes to attain maximum crystal volume. Here, we will review some established experimental tools, approaches and observations associated with large crystal growth for neutron crystallography. These include the use of phase-diagram information, counter-diffusion crystallization, Ostwald ripening, microgravity and essential manipulations once protein crystals suitable for neutron crystallization have been obtained.

2. Phase diagram-guided crystallization  

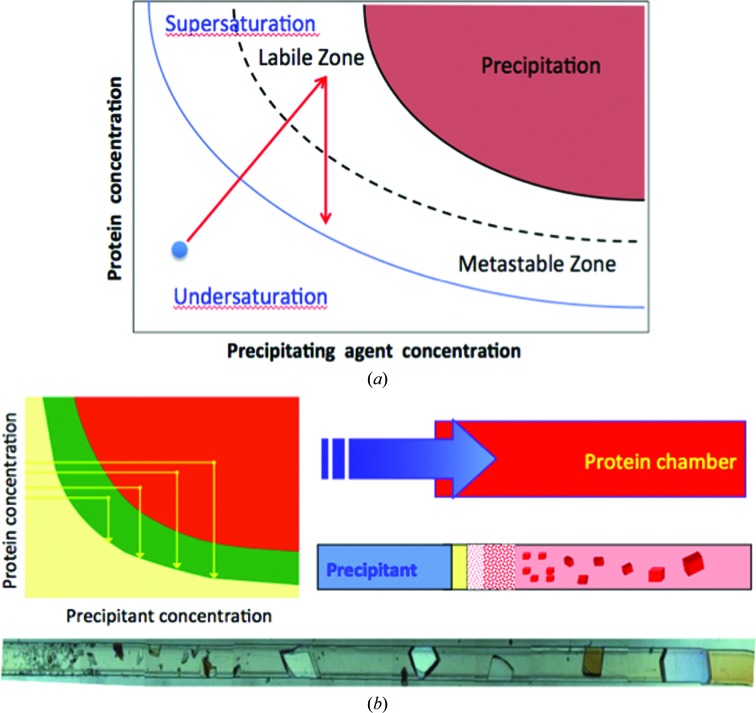
Knowledge of protein solubility from phase-diagram information can be most useful in finding optimal nucleation and growth conditions. While obtaining phase diagrams may not be necessary to obtain crystals for conventional X-ray crystallographic determination, knowing the solubility barriers of a protein is important in cultivating crystals to a maximum size for neutron crystallography. Lysozyme and a DNA decamer are examples of macromolecules for which phase diagrams were essential in obtaining crystals suitable for neutron crystallographic determination (Iwai et al., 2008 ▶; Niimura, 2010 ▶). A protein phase diagram describes the liquid and solid states of the macromolecule as a function of chemical or physical variables that affect the solubility of the protein (for a review, see Rupp, 2015 ▶). Most commonly used are the precipitant or additive concentration, pH, temperature or ionic strength. As shown in Fig. 1 ▶(a), the solubility and supersolubility curve divide the plot into regions, namely the undersaturated zone for protein concentrations below the solubility barrier and the supersaturated zone for protein concentrations greater than the solubility. This supersaturated region is itself divided into the labile zone at larger supersaturation values, where nucleation occurs instantaneously, and the metastable zone, where the nucleation probability varies between 0 (on the solubility curve) and 1 (on the supersolubility curve) (Ng et al., 1996 ▶).

Figure 1.

Figure 1

Open in a new tab

Schematic phase diagram and solubility measurements. (a) displays the solubility diagram of a protein versus the concentration of precipitant. The solubility curve (solid line) where the waiting time for nucleation is infinite and the supersolubility curve (dashed line) where the probability of nucleation is 1 are the boundaries of the metastable region. The arrows illustrate the pathway of a solution that crystallizes in a typical vapor-diffusion experiment. The blue dot marks the condition at the beginning of the equilibration process. Note that in a vapor-diffusion experiment the solution moves out of equilibrium until supersaturation is reached. The labile zone is where nucleation occurs and the metastable zone is defined by an absence of nucleation but the crystal will continue to grow. Beyond the labile zone is the precipitation area where proteins will amorphously come out of solution. The quality and size of the crystals depends on how fast the solution moves across the metastable zone, i.e. it depends on the rate of change of supersaturation, a variable that it is difficult to control. (b) describes a counterdiffusion experiment in which the precipitant solution diffuses across a long capillary containing the protein solution. This creates a pattern of supersaturation values across the capillary that varies from very high (thus a high flow of nucleation of amorphous particles or small crystals) to very low (thus forming very few crystal of large size) as shown by the subsequent pathways at different times shown in the solubility diagram. Note that in this case the solution moves towards equilibrium, towards low supersaturation located in the metastable region, thus creating large crystals at the end of experiment. The case is exemplified by the growth of thaumatin crystals grow by counter-diffusion inside a microfluidic cell (Ng et al., 2008 ▶).

A phase diagram for conventional crystallization (Fig. 1 ▶ a) highlights the extreme supersaturation region often referred to as the labile region (Miers & Isaac, 1907 ▶; Feigelson, 1988 ▶). A lower value of supersaturation is present in the metastable region, where nucleation events are few and crystal growth is favorable. In traditional protein crystallization screens, chemical reagents in buffered solution can be randomly, systematically or selectively chosen to mix and equilibrate with varying protein concentrations. In this process, a supersaturated condition targeting a single labile region for spontaneous nucleation and the metastable region for the greatest crystal growth can be acquired. Upon evaluation of a phase diagram for a targeted protein, one can strategically maneuver between nucleation and crystal-growth conditions (Fig. 1 ▶ a) as a strategic crystallization approach to obtain large-volume crystals suitable for neutron diffraction.

There are many procedures to obtain information for a protein phase diagram (Cacioppo & Pusey, 1991 ▶; Asherie, 2004 ▶; Dunuwila & Berglund, 1997 ▶). The most commonly applied phase diagrams are two-dimensional, with only one independent variable, although multidimensional diagrams also exist (Ewing et al., 1994 ▶; Sauter et al., 1999 ▶; Rakel et al., 2014 ▶). Here, we will only discuss single independent variable diagrams. To establish a phase diagram, one must first determine the solubility of the protein as a function of the ambient conditions; that is, the concentration of protein in the solution at equilibrium under a certain chemical condition. The most classical method to determine solubility for a phase diagram is to measure protein concentrations at equilibrium under saturated and undersaturated conditions (Sazaki et al., 1996 ▶; Haire & Blow, 2001 ▶; Gray et al., 2001 ▶; Ewing et al., 1994 ▶). One may obtain solubility data points by placing protein crystals in a protein-free solution of interest while gently stirring the solution. As a function of time, the soluble protein concentration is measured from the absorbance (A 280) or by using the bicinchoninic acid assay (BCA; Smith et al., 1985 ▶) to determine how much of the protein in the crystals has dissolved back into solution. Concurrently, the targeted protein is set up against a supersaturated solution (Asherie, 2004 ▶). During the equilibration process, the protein concentration as a function of time is measured as described for the undersaturated equilibration process. The point where the protein concentrations converge for the supersaturated and undersaturated equilibration is the solubility of the protein for the selected condition (C eq). The equilibrium method can provide valuable information on protein solubility and phase transitions; however, the technique requires significant amounts of protein material (up to gram quantities) and time.

The use of Michaelson interferometry has been an effective tool in obtaining protein solubility data (Sazaki et al., 1996 ▶; Gray et al., 2001 ▶; Nakazato, 2008 ▶), requiring less time and material than the equilibrium technique. By measuring the changes in surface and concentration gradient solution interference fringes in the presence of small crystals, accurate estimates of protein solubility are achievable. Lysozyme has been the most well reported protein used in interferometry measurements, in which surface fringe movements were correlated with crystal growth or dissolution as a function of a variable condition (i.e. temperature). Consequently, informative solubility curves can be derived for selected conditions and used to adjust crystal-growth conditions to obtain optimized crystal volumes.

Thermally and chemically stable proteins are convenient and are often preferred candidates for large-volume crystallization. These include proteins derived from thermophilic organisms or mesophilic proteins that are functionally and structurally tolerant to wide temperature changes (i.e. plant storage proteins, proteases, nucleases etc.). In this case, temperature can be exploited as a useful variable in keeping the crystallization solution metastable during the growth process. One successful approach in using temperature-controlled ripening processes to grow protein crystals suitable for NMC is the use of a semi-automated protein crystal-growth arrangement coupled to a custom-made quartz crystal-growth cell with a microscope temperature-controlled system (Budayova-Spano et al., 2007 ▶). This approach includes seeding a protein solution in a predetermined crystallization condition and observing in situ growth or dissolution as a function of temperature under batch equilibration. Upon fine temperature changes, the areas of the phase diagram can be qualitatively identified. Large-volume crystals of perdeuterated urate oxidase (Uox) have successfully been obtained using this method. By carefully controlling and optimizing the crystallization conditions for Uox around its metastable zone (with no occurrence of spontaneous nucleation), the neutron crystallographic structure of Uox was determined from crystals grown by temperature adjustments (Budayova-Spano et al., 2007 ▶; Oksanen et al., 2009 ▶).

3. Counter-diffusion crystallization  

Protein crystallization by counter-diffusion in restricted geometry is an effective technique to obtain macromolecular crystals suitable for neutron crystallography. Contrary to conventional techniques such as vapor diffusion, varying supersaturation conditions leading to protein precipitation, nucleation and crystal growth can be obtained simultaneously in a capillary channel, as exemplified in Fig. 1 ▶(b) using the model protein thaumatin (Ng, Clark et al., 2008 ▶). Crystals obtained by this technique are a consequence of selective growth conditions from different supersaturation environments (García-Ruiz, 2003 ▶; Ng et al., 2003 ▶; García-Ruiz & Ng, 2006 ▶). The crystals can grow out to the diameter of the capillary and can be directly analyzed by X-ray radiation in situ without ever touching the crystals (Ng, Clark et al., 2008 ▶; Ng et al., 2003 ▶; Gavira et al., 2002 ▶; Ng & García-Ruiz, 2006 ▶; Ng, Stevens et al., 2008 ▶).

The counter-diffusion crystallization procedure is able to compose a continuous supersaturation gradient. During the diffusion process, a supersaturation state with respect to the protein can be attained in the labile region while crystal growth can occur in a continuous range in the metastable area of the phase diagram (Fig. 1 ▶ b). Hence, crystal formation is caused by the progression of a nucleation front resulting from the nonlinear interplay between mass transport, protein crystal nucleation and growth (García-Ruiz et al., 2001 ▶; Carotenuto et al., 2002 ▶).

The implementation of counter-diffusion crystallization relies on the maximum reduction of convection allowing diffusion to govern the mass-transport process along the length of the protein chamber. In practice, the optimal supersaturation gradient achieved is dependent on minimizing the ratio between buoyant and viscous forces. The quality of this diffusive scenario can be described by the nondimensional Grashof number (N G) used in fluid-dynamic studies with the following relationship,

3.

where d is the characteristic dimension of the system, ρ is the density of the fluid, δρ/δC is the density gradient, ΔC is the change in concentration, g is the gravity value and u is the viscosity of the solution (García-Ruiz, 2003 ▶). We have shown that proteins with different molecular weights and isoelectric points can be crystallized by counter-diffusion crystallization under a wide range of chemical and physical conditions (Ng et al., 2003 ▶).

There are some advantages to consider in this approach. Single nucleation and maximum crystal growth can be experimentally revealed along the length of the capillary since the equilibration process passes through the labile and metastable conditions along a solubility gradient. Therefore, optimization for the growth of large crystal volumes filling up the entire diameter of the capillary can be realised without solubility data. Secondly, diffraction analysis can be performed in situ without physical handling of the crystals (Ng, Clark et al., 2008 ▶; Gavira et al., 2002 ▶). Crystals that grow across the diameter of the capillary are attached to the chamber walls and are immobilized. Therefore, X-ray or neutron diffraction can be performed without the need to separately mount the crystals, minimizing damage from physical manipulation, particularly for large fragile crystals. Thirdly, crystals grown in the capillary can undergo soaking of ligands, metals, cryogenic preservatives (Gavira et al., 2002 ▶) and the exchange of H2O for D2O to prepare for neutron diffraction (discussed in the next section).

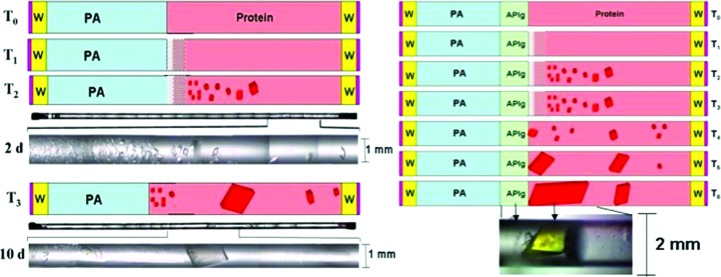
When crystals must be grown with large diameters (>0.3 mm), high-viscosity precipitants are preferred and, in some cases, are accompanied by the strategic placement of agarose-gel plugs. The initial arrangement is prepared similarly to the free-interface diffusion (FID) crystallization technique, in which the same geometry is used. Typical FID preparations can be considered as batch experiments conducted with very slow mixing (Otálora & García-Ruiz, 1997 ▶; García-Ruiz & Otálora, 1997 ▶). As shown in Fig. 2 ▶, a supersaturation gradient can be observed in the large-diameter channel similar to that observed in a narrow channel.

Figure 2.

Figure 2

Open in a new tab

Schematic diagram of capillary configuration for large-volume crystal growth. The capillary, used as a growth cell, is filled with protein solution (pink) to about half of its volume, followed by an equal volume of the solution of the precipitating agent (PA). Both ends of the capillary are sealed with soft wax (W) and enamel varnish (red). T 0 to T 6 indicate time progression within a span of about 30 d of equilibration. Actual photographs of the entire tube and IPP crystals grown out of a supersaturation gradient are shown in black and white 2 and 10 d after the start of the experiment. The left panel shows the case with no initial barrier between the protein and precipitant solutions. The right panel shows equilibration with a transparent agarose plug (APlg) separating the protein and the precipitant solution.

4. Ostwald ripening  

Ostwald ripening is a process in which larger stable particles grow at the expense of smaller ones such that a more stable thermodynamic state is established (Veesler et al., 1994 ▶; Ostwald, 1897 ▶; Mullin, 1993 ▶). While this process was discovered and observed in small-molecule crystallization, it has not been well documented for proteins. However, characteristic features of Ostwald ripening have been observed for macromolecules in which depletion zones were present as larger crystals grow at the expense of smaller ones. These proteins include α-amylase, TBSV, thermostable AspRS (Ng et al., 1996 ▶) and lysozyme (Streets & Quake, 2010 ▶). In these cases, large-volume crystals can be achieved when conditions for Ostwald ripening are permitted. The ripening behavior of thermostable AspRS has been particularly well observed and crystals measuring up to 1 mm in the longest dimension were subsequently obtained (Ng et al., 1996 ▶).

Ostwald ripening is often observed with large-volume crystal growth in counter-diffusion equilibration. When the diameter of the crystallization capillary is large (>0.3 mm), convective mixing may follow the formation of a supersaturated gradient along the length of the crystallization chamber. This was the case for large-volume protein crystal growth of a hyperthermophilic inorganic pyrophos­phatase (IPPase; Hughes et al., 2012 ▶). Below, a scenario in which large IPPase crystals were achievable is described (Fig. 2 ▶).

Conditions for initial crystallization were already known in which small crystals of IPPase were obtained from vapor-diffusion sparse-matrix screens. Concentrated protein solution was loaded into a quartz capillary by syringe aspiration with syringe diameters ranging from 1 to 2 mm. It is worth noting that one must use quartz capillaries for neutron diffraction because borosilicate glass strongly scatters neutrons. In addition, the protein concentration required for counter-diffusion crystallization is approximately twice that needed in vapor-diffusion or batch processes. Fig. 2 ▶ illustrates the progress of equilibration accompanied by the observation of the actual protein crystals obtained. Several significant results were produced. The precipitant contained a minimal concentration of 30% 2-methyl-2,4-pentanediol (MPD; Anand et al., 2002 ▶) and was sufficient to achieve a ratio between buoyancy and viscous forces (1) allowing diffusion to govern the mass-transport process despite the large tube volume. This was evident by the supersaturation gradient obtained giving rise to a precipitation front closest to the precipitant interface and the progression from high to low nucleation of crystal growth along the length of the capillary. When the capillary diameters are large, the presence of additives that can increase the viscosity of the solution is important to sustain a diffusion-limiting process. Reagents such as glycerol, PEG and general cryoprotectants have been shown to be effective.

A single crystal filling the entire diameter of the capillary can be obtained within 10 d. During the initial course of equilibration, crystals are observed to grow along the length of the capillary. However, slow mixing shortly occurs and the existing crystals undergo Ostwald-like ripening, in which depletion zones form around the growing crystals that eventually fill up the capillary. To avoid osmotic shock, agarose plugs are implemented dividing the protein and precipitating solutions prior to initializing the crystallization process. Consequently, a large single crystal usually grows on and sometimes into the agarose plug.

5. Deuteration  

Once a large-volume crystal has been obtained, one must prepare the crystal for diffraction by D2O exchange without compromising the quality of the crystals. This is because the large incoherent scattering background of hydrogen can reduce the integrated signal to noise ratio of Bragg peaks. Approaches to remedy this issue include the complete replace­ment of H atoms with deuterium (Shu et al., 2000 ▶) and D2O exchange with H2O by vapor exchange or by soaking procedures (Niimura & Bau, 2008 ▶). Here, we will discuss exchanging H2O with D2O in the capillary geometry without any physical manipulation of the protein crystal.

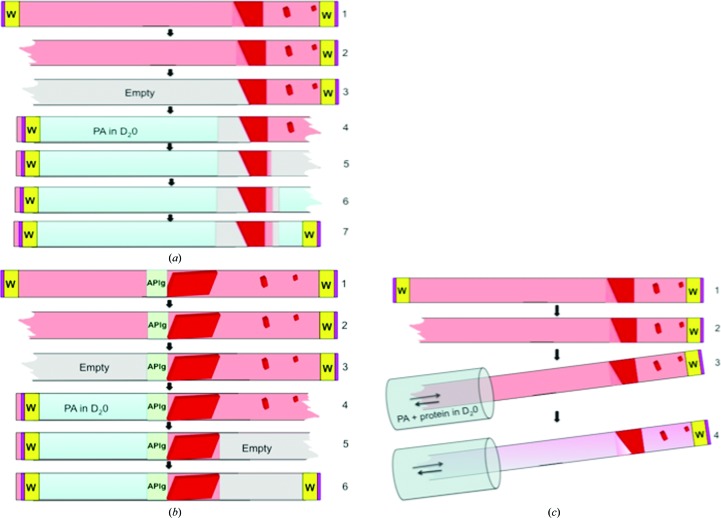
When crystals are grown in capillaries, it is easy to remove the mother liquor and carefully equilibrate the targeted protein with an equivalent solution containing D2O. This is performed by carefully excising the ends of the capillaries and withdrawing all of the solution and smaller crystals, leaving the targeted crystal immobilized with some residual mother liquor. The capillary is then filled from both sides with deuterated solution, leaving an adequate gap between the solution and the crystals to allow vapor diffusion (Fig. 3 ▶ a). The capillaries are then sealed again and this process can be repeated several times during the course of D2O exchange.

Figure 3.

Figure 3

Open in a new tab

Procedure for deuterium exchange in capillaries. Large-volume crystals grown or mounted in a large-diameter (>0.3 mm) quartz capillary can undergo D2O exchange quite readily. In the case where the crystals are grown in situ, the capillary ends can be excised and the solutions withdrawn one end at a time and replaced with precipitating agent (PA) in D2O (a). The exchanging D2O solution is placed close to the targeted crystal, leaving an air gap for vapor diffusion. When there is an agarose plug separating the precipitant and protein solutions, the precipitant is simply replaced with the D2O solution filled against the agarose plug while the other end is left empty (b). D2O exchanges can also directly diffuse into the existing precipitant solution with a solution containing deuterated precipitating agent and protein (c).

Crystals obtained in the presence of an agarose plug are preferred because slow exchange of new solutions through a porous barrier minimizes physical and chemical stress. The deuterated solutions are replaced as described before and directly placed against the agarose plug, allowing free liquid diffusion (Fig. 3 ▶ b). A final alternative for effective D2O exchange is simply to use free-interface diffusion against a solution containing similar concentrations of the protein and precipitant as the mother liquor. In a typical protein crystal, 66% of the H atoms in the unit cell can be exchanged for deuterium. The percentage that can exchange within the protein is much lower, at approximately 26%. Highly stable nonflexible domains resist deuterium exchange, giving data on protein dynamics. It is thought that the bulk solvent in the crystal rapidly exchanges with D2O. However, many experimenters perform deuterium exchanges for days with several exchanges to assure the adequate replacement of dissociable H atoms by deuterium.

6. Cryogenic neutron protein crystallography  

In X-ray crystallography, collecting diffraction data at synchrotron and home X-ray sources under cryogenic conditions (near liquid-nitrogen temperature; Hope, 1988 ▶) has become routine. Protein crystals that are cryocooled have reduced radiation damage by X-rays and consequently a significant improvement of resolution in data collection can be obtained with a single crystal (Garman & McSweeney, 2007 ▶). In contrast to X-ray radiation, protein crystals are not damaged by thermal neutron diffraction. Presently, most neutron diffraction analyses are conducted at ambient temperatures, with minimal or no radiation damage as long as the crystals are chemically and thermally stable during data collection. However, collecting neutron diffraction data requires a very extended exposure time, ranging from 6 to 18 h per image. This means that the data-acquisition time can be on the order of days to weeks. In comparison, capturing X-ray diffraction images usually requires only seconds per image, and can even be much faster with the recent development of shutterless cameras. In the interest of performing NMC with protein crystals that may not be chemically or thermally robust, trapping short-lived intermediates or reducing atomic displacement parameters, cryogenic neutron protein crystallography is necessary. In addition, other important crystallo­graphic rationales for neutron cryogenic data collection include the desire to compare X-ray and neutron structures at the same temperature (Juers & Weik, 2011 ▶), measure the impact of radiation damage and determine its influence on X-ray/neutron joint refinement. The study of cryocrystallography for crystals of suitable size for neutron studies is still in its nascent stage and there is no systematic study to date that has examined the ability to cryocool a large crystal for neutron studies as a function of its size, solvent content, cooling kinetics and cryoprotecting agents. In contrast, there are extensive reports on cryocooling methods and approaches for crystals appropriate for X-ray crystallography, and the principles of these techniques may be considered for large-volume crystals (Juers & Matthews, 2004a ▶,b ▶; Garman & Owen, 2007 ▶; Garman & Doublié, 2003 ▶; Borgstahl et al., 2000 ▶). We will focus our discussion here on reporting approaches that have been recently performed on neutron beamlines that are amendable to neutron cryocrystallography.

To date, only three protein cryogenic neutron structures have been reported. These include concanavalin A (Blakeley et al., 2004 ▶), Toho-1 β-lactamase (Coates et al., 2014 ▶) and ferric cytochrome c peroxidase (Casadei et al., 2014 ▶). Cryo-treating large-volume crystals has been thought to be very difficult if not impossible. The difficulty lies in selecting proper cryosolutions, soaking protocols and rates of supercooling crystals without disrupting the crystal quality (i.e. increasing the mosaicity). Even though there are many techniques and approaches for the cryogenic preparation of protein crystals for X-ray studies (Hope, 1988 ▶; Kitago et al., 2005 ▶), detailed studies on the cryocooling of large-volume crystals have not been well documented and there are no standard procedures to prepare protein crystals for cryogenic neutron data collection.

Cryogenic neutron data collection for protein crystals has recently become available at BIODIFF at the FRM II and MaNDi at the Spallation Neutron Source, ORNL. The Toho-1 β-lactamase was the first perdeuterated cryogenic protein–ligand complex to be captured at 100°C using NMC (Coates et al., 2014 ▶). In this case, crystals of about 1 mm3 were grown by a batch method and were exposed to a cryogenic solution (in this case 30% perdeuterated trehalose) very briefly (30 s). The crystal was then flash-cooled immediately with a liquid-nitrogen open-flow cryostream. Short soaking times (in seconds) for the large protein crystals produced better results than crystals that underwent long sequential soaks in cryoprotective solutions. This was also the case for hyperthermophilic IPPase, where crystals of greater than 1 mm3 in volume were analyzed with X-rays under cryogenic conditions as a function of soaking time. Quick soaks (<30 s) followed by flash-cooling provided the best results as determined by mosaicity and resolution-limit measurements. In addition to Toho-1 β-lactamase and IPPase, we have observed for other large-volume protein crystals (>1 mm3) that regardless of solvent content, space group and cryopreservative solutions, crystal integrity was retained much better for crystals that underwent quick cryo-soaks followed by flash-cooling compared with those that underwent extensive cryo-soaks followed by storage in liquid nitrogen (unpublished results). BIODIFF uses a large cylindrical neutron-sensitive area detector that completely surrounds the crystal in the presence of a cryostream. This system shows that cryogenic neutron crystallography can be highly feasible using standard equipment and procedures. Other neutron facilities are now also being equipped with cryogenic capabilities (see §1). Neutron cryocrystallography will be necessary in the future as many biologically relevant proteins are temperature and chemically labile. As neutron facilities are still limited, extended storage and transportation periods will be required while waiting for data-collection opportunities. More studies aimed at the development of cryopreservation for large-volume crystals will be needed in the future.

7. Microgravity  

Protein crystal growth under microgravity has been shown to produce larger and higher quality protein crystals compared with those obtained on earth (Day & McPherson, 1992 ▶; Ng et al., 2002 ▶; Ng, 2002 ▶; DeLucas et al., 1999 ▶; Lorber et al., 2002 ▶; Ng, Lorber et al., 1997 ▶). While microgravity protein crystal-growth experiments have been curtailed in the US and Europe in the past ten years, the International Space Station (ISS) has been recently used as a platform, managed by the Center for the Advancement of Science in Space (CASIS), to grow large-volume protein crystals for X-ray and neutron crystallography. Space X, an American space-transport services company, can now provide lift vehicles to the ISS delivering protein crystallization experiments. While obtaining large protein crystals may not be as important now as it was in the past for X-ray crystallography, it is absolutely necessary for NMC today. Microgravity may play a critical role in obtaining protein crystals suitable for NMC that would not otherwise be possible on earth. When protein crystals grow to large volumes in the presence of gravity, lattice defects or irregularities accumulate owing to convective mixing and sedimentation during the equilibration process. In microgravity, molecules will traverse the crystallization chamber at a very slow rate, providing more time for crystal lattice alignment and thus producing a higher quality crystal.

The protein IPPase was recently crystallized by counter-diffusion equilibration in large-diameter (2 mm) quartz capillaries on the ISS for six months, the longest duration of time for any protein crystal-growth experiment using the counter-diffusion geometry as described earlier. Large crystal volumes were obtained growing across the length of the capillary as a result of a progressive nucleation front.

Reflecting the values of the viscosity normally used in protein crystallization, pure diffusive mass transport can only be assured for capillary diameters of 2 µm considering the diffusive scenario determined by the Grashof number (1). For a diameter of 2000 µm as used in neutron diffusion experiments there is a strong contribution of convection to mass-transport processes, in particular for a solid crystalline phase form, unless highly viscous protein solutions or gels are used. Alternatively, one can use microgravity. This is clearly shown in Fig. 4 ▶, which shows the well separated large-volume crystals grown from microgravity compared with those grown on earth. The details of this work will be reported elsewhere. This method of growing large-volume crystals holds promise for obtaining protein crystals suitable for NMC that would otherwise not be possible on earth.

Figure 4.

Figure 4

Open in a new tab

Quartz capillaries containing crystals grown under microgravity in space (a) and crystals grown on earth (b). All capillaries are 50 mm in length and have an inner diameter of 2 mm. In both cases the starting precipitating solution is located on the left. Both space and earth crystallization experiments were prepared with the same proteins, concentrations, loading protocols, locations and laboratory and environmental conditions. For a canonical counter-diffusion experiment, the protein solution should diffuse from left to right, creating a supersaturation wave that moves across the capillary with increasing width and decreasing amplitude (García-Ruiz et al., 2001 ▶). Thus, the number of crystals should decrease and the size of the crystals should increase along the length of the capillary (left to right). This spatial–temporal gradient of supersaturation is clearly observed in the capillaries of the microgravity-grown crystals (a) while it is not observed in the capillaries with earth-grown crystals. The reason is that capillaries of 2 mm in diameter are too large to reduce convective flow, as expected from simple fluid-dynamics considerations. Typical crystals grown in space are shown under polarized light (c).

8. Theoretical considerations on protein crystal size  

In the sections above, we have focused on laboratory methods for controlling parameters that would be conducive to the growth of large crystals. Theory can also serve as a guide. It can be shown, for example, that some of the difficulties encountered in obtaining large protein crystals are owing to the peculiar dependence of the free energy of dissolution of a protein crystal on its size. The free energy is a function of the charge on the protein molecule, however, which suggests that the proper adjustment of pH can be an effective method for controlling the free energy.

Consider the size, a, of a microscopic crystal of a substance, such as glucose, whose molecules are uncharged in aqueous solution. The free energy of dissolution, ΔG(a), of the crystal is given by (Rowe & Baird, 2007 ▶),

8.

where m(a) is the solubility in mg ml−1 of a crystal of radius a, m s is the solubility of the crystal when it has reached macroscopic size, v is the molecular volume of glucose, γo is the interfacial energy at the crystal/solution boundary, T is the temperature in Kelvin and k B is Boltzmann’s constant. The quantity m s can be identified with the experimentally observed ‘bulk solubility’ or the ‘solubility limit’ of the protein. The condition for a crystal of microscopic size a to be in equilibrium with the growth solution is ΔG(a) = 0. According to (2), this can occur for finite values of a only if the growth solution is supersaturated in glucose, i.e. m(a) > m s. As the crystal grows in size, it takes up more glucose molecules from the solution, so the ambient concentration m(a) falls and the supersaturation, defined by m(a)/m s, diminishes. As the crystal reaches its final macroscopic size, regarded mathematically as a→∞, its solubility m(a) approaches m s.

In contrast to molecules of glucose, the molecules of a water-soluble protein are charged when they are dissolved in a pH-buffered aqueous growth solution. Depending upon the pH, the functional groups responsible for the charges on protein molecules are (Baird & Kim, 2002 ▶): (i) the COOH and NH3 + amino-acid groups at the ends of the polypeptide chain and (ii) the acid/base groups in the side chains of certain amino-acid residues, specifically lysine, arginine, histidine, tyrosine, aspartic acid, glutamic acid and also cysteine when it is not forming a disulfide bond to another cysteine. Not only are the protein molecules in solution charged, but so also are the crystals formed from these molecules (Lee et al., 2001 ▶). The charges on the crystals are most likely to be on the surface and occur whenever a protein molecule in the crystal is oriented so that one or more of its ionizable groups comes in contact with the growth solution.

The crystal surface thus contains a number of acidic sites, HA, and a number of basic sites, B. The acid sites ionize according to

8.

The fraction θ of the HA sites which are in the charged form A− depends upon the pH and is given by

8.

where pK a = −logK a and K a is the acid ionization constant of HA. By contrast, the basic sites, B, when in acid form, BH+, ionize according to

8.

The fraction θ of the basic sites B which are in the charged form BH+ is given by

8.

where K a is the acid ionization constant of BH+.

The presence of ionizable sites on the crystal surface contributes to the free energy of the crystal (Rowe & Baird, 2007 ▶). These contributions augment the interfacial tension γo, which appears in (2). The contributions, which are both energetic and entropic, are as follows.

  • (i) The surface charges on the crystal attract ions of opposite sign in the growth solution and repel ions of like sign. This displacement of ions away from their original random positions in the growth solution has the effect of decreasing the entropy at the crystal/solution interface. The decrease in entropy increases the free energy.

  • (ii) By attracting oppositely charged ions and repelling like charged ions, the crystal surface builds up electrostatic energy. This stored electrostatic energy makes a negative contribution to the free energy.

  • (iii) According to (4) and (6), when the value of the pH equals the value of the pK a of an ionizable group on the surface, half of the sites of this particular type will be in the charged form and half will be in the uncharged form. In this situation, H+ ions can hop between charged sites and uncharged sites. This mixing of charged and uncharged sites increases the entropy of the crystal surface and makes a negative contribution to the free energy.

When the above three contributions are taken into account, the free energy of dissolution of the crystal assumes the form (Hodge, 2014 ▶)

8.

where the overall interfacial energy Inline graphic is given by (Rowe & Baird, 2007 ▶)

8.

In (7), u is the number of charged groups on a protein molecule and σ is the charge density on the surface of the crystal. Both u and σ are evaluated at the prevailing pH. The other electrostatic parameters are ∊, the dielectric constant of water; ∊o, the dielectric constant of vacuum; and κ, the reciprocal of the Debye length. In the case of an aqueous solution at T = 298 K with NaCl serving as the electrolyte,

8.

where c is the molar concentration of NaCl (Rowe & Baird, 2007 ▶). In (8), we have assumed that the growth-solution pH is close to the pK a value of one of the ionizable groups on the surface of the crystal. The surface density of this group is Γ. All other groups with pK a values lower than the value of the pH will be present in their basic forms, either B or A−. All ionizable groups with pK a values greater than this pH will be present in their acid forms, either BH+ or HA. The ionizations of groups with pK a values distant from the growth solution pH are saturated and are essentially independent of the pH. The contributions of these groups to the free energy are included in the surface charge density σ and also in the background interfacial tension γo.

(7) was derived by solving the Poisson–Boltzmann equation in the Debye–Hückel approximation (Rowe & Baird, 2007 ▶), which limits its quantitative application to electrolytes with concentrations c < 0.1 M. A numerical integration of the Poisson–Boltzmann equation would be required to extend the range of applicability of the theory to concentrations in excess of 0.1 M. Although c = 0.1 M is about a factor of ten below that ordinarily employed in crystal-growth solutions, we can still draw some qualitative conclusions by comparing (2) and (7).

Our discussion of (2) indicates that an uncharged crystal of microscopic size (i.e. a ≪ ∞) cannot be in equilibrium [ΔG(a) = 0] with a growth solution where the ambient concentration m(a) equals the bulk solubility m s. Such a crystal will dissolve. The molecules released will diffuse through the growth solution and precipitate onto the surfaces of any larger crystals which are present. As explained above, this process is called Ostwald ripening. By contrast, when σ ≠ 0, (7) predicts that a crystal of microscopic size, a ≪ ∞, can be at equilibrium [ΔG(a) = 0] with an ambient concentration m(a) equal to the bulk solubility m s. To find this condition, we set the left-hand side of (7) to zero and let m(a) = m s on the right. These restrictions force the bracket on the right-hand side of (7) to be zero. The value of a which makes the bracket zero is (Hodge, 2014 ▶)

8.

where

8.

(10) predicts the size a of a protein crystal which is in equilibrium with a growth solution where the protein concentration is equal to the bulk solubility m s. Since the ambient concentration equals the bulk solubility, such a solution cannot support any net exchange of mass with crystals of this size. In the absence of a net exchange of mass, the process of Ostwald ripening is frustrated, which may explain why Ostwald ripening is not well documented in protein crystallization. Until one or more of the three variables pH, temperature and salt concentration are changed, the crystal remains stuck in equilibrium with the growth solution.

It is apparent from (10) that a > 0 for β > 1/2. Experimentally, the values of a predicted by (10) make sense, however, only within the range (3v/4π)1/3 < a < a max, where (3v/4π)1/3 is an estimate of the size of a protein molecule and a max is the size of a single crystal consisting of all of the protein which at the beginning of the experiment was in excess of m s V, where V is the volume of the growth solution. At β = 1/2, (10) has a singular point where a becomes very large. For values of β only slightly greater than 1/2, a diminishes rapidly, numerically reaching the molecular limit a = (3v/4π)1/3 as β approaches unity. Hence, crystals of macroscopic size are to be expected only for those values of β which are in close proximity to β = 1/2. This tight restriction may explain why large protein crystals are so rare.

At temperature T = 298 K, the dielectric constant of water is ∊ = 78.54 (Rowe & Baird, 2007 ▶). If we consider lysozyme as a model protein, then at an NaCl concentration of c = 0.05 M the value of σ will be no greater than 2 µC cm−2 (Kim et al., 2003 ▶). When (9) is used to calculate κ, and the values of κ, T, ∊ and σ are substituted into (11), we find that β = 1/2 when 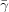Inline graphic = 0.4 mJ m−2. This estimate of 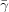Inline graphic is close to the values of the interfacial energy calculated from the results of experiments where the rate of advance of a macroscopic crystal facet was determined optically (Malkin et al., 1999 ▶). According to (8), this moderate value of 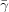Inline graphic can be expected to occur for values of θ between the limits θ = 0, where 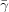Inline graphic has its maximum value of 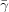Inline graphic = γo, and θ = 1, where 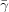Inline graphic = −∞. The latter is an unphysical value of 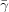Inline graphic corresponding to an ionizable group with a pK a value far from the prevailing pH. As pointed out, the contributions of such groups are not represented by (8) but are included within σ and γo. In order to achieve β = 1/2, a value of θ near 1/2 would seem to be a good compromise. According to (4) and (6), the value θ = 1/2 occurs when the pH equals the pK a of one of the ionizable groups on the protein molecule. Hence, in the absence of complications, such as the effect of pH on nucleation, (10) makes the simple prediction that to obtain large protein crystals the pH of the growth solution should be adjusted to a value which is close to the pK a of one the ionizable groups on the protein molecular chain.

The theory explicitly takes into account only the effects of protein molecular charge on crystal size. The effects of the short-range van der Waals forces acting between the protein molecules and the crystal are subsumed within the interfacial energy parameter γo. This simple approximation is forced on the theory because the details of the distance dependence of the van der Waals forces cannot be treated analytically within the Debye–Hückel approximation that gives rise to (7). Nevertheless, for all distances short of molecular contacts, the electrostatic forces can be expected to dominate the van der Waals interactions. For this reason, the electrostatic theory can be expected to have some predictive power, albeit perhaps only qualitative. Finally, for the case where m(a) is not too much greater than m s, the theory predicts additional values of a besides the one given by (10) which make ΔG(a) = 0. The conditions appropriate for this additional case must be determined numerically and are currently under investigation.

9. Conclusion  

Funding agencies from different countries have invested considerable resources in building structural repositories of three-dimensional protein structures (over 90 000 to date), yet 50% of the atoms in these structures are comprised of hydrogen and are invisible in most X-ray structures. Therefore, the role of H atoms in protein structures is severely understudied. The precise locations of H atoms cannot be experimentally determined by biochemical methods or by X-ray crystallography in the average resolution range, but can be definitively located using neutron diffraction. Despite the development and renovation of powerful neutron sources, protein crystal size remains a bottleneck for NMC. The knowledge of current techniques to grow large crystals and understanding how they grow will be critical to future neutron crystallographic studies.

Acknowledgments

Information acquired here was from research supported by the Center for the Advancement of Science in Space (CASIS; GA-2013-100). The Office of Biological and Environmental Research supported research at the Oak Ridge National Laboratory Center for Structural Molecular Biology (CSMB), using facilities supported by the Scientific User Facilities Division, Office of Basic Energy Sciences, United States Department of Energy. JMGR acknowledges the ‘Factoría de Cristalización’ (Consolider Ingenio 2010, Spanish MINECO) and Excellence project RNM5384 of Junta de Andalucía. We thank Mr Jorge Barcena for his assistance in the preparation of this manuscript.

References

  1. Anand, K., Pal, D. & Hilgenfeld, R. (2002). An overview on 2-methyl-2,4-pentanediol in crystallization and in crystals of biological macromolecules. Acta Cryst. D58, 1722–1728. [DOI] [PMC free article] [PubMed]
  2. Asherie, N. (2004). Protein crystallization and phase diagrams. Methods, 34, 266–272. [DOI] [PubMed]
  3. Baird, J. K. & Kim, Y. W. (2002). Theory of the nucleation of protein macromolecular ions. Mol. Phys. 100, 1855–1866.
  4. Benvenuti, M. & Mangani, S. (2007). Crystallization of soluble proteins in vapor diffusion for X-ray crystallography. Nature Protoc. 2, 1633–1651. [DOI] [PubMed]
  5. Bergfors, T. (2007). Screening and optimization methods for nonautomated crystallization laboratories. Methods Mol. Biol. 363, 131–151. [DOI] [PubMed]
  6. Blakeley, M. P., Kalb, A. J., Helliwell, J. R. & Myles, D. A. (2004). The 15 K neutron structure of saccharide-free concanavalin A. Proc. Natl Acad. Sci. USA, 101, 16405–16410. [DOI] [PMC free article] [PubMed]
  7. Blakeley, M. P., Langan, P., Niimura, N. & Podjarny, A. (2008). Neutron crystallography: opportunities, challenges, and limitations. Curr. Opin. Struct. Biol. 18, 593–600. [DOI] [PMC free article] [PubMed]
  8. Blakeley, M. P., Teixeira, S. C. M., Petit-Haertlein, I., Hazemann, I., Mitschler, A., Haertlein, M., Howard, E. & Podjarny, A. D. (2010). Neutron macromolecular crystallography with LADI-III. Acta Cryst. D66, 1198–1205. [DOI] [PubMed]
  9. Borgstahl, G. E., Pokross, M., Chehab, R., Sekher, A. & Snell, E. H. (2000). Cryo-trapping the six-coordinate, distorted-octahedral active site of manganese superoxide dismutase. J. Mol. Biol. 296, 951–959. [DOI] [PubMed]
  10. Budayova-Spano, M., Dauvergne, F., Audiffren, M., Bactivelane, T. & Cusack, S. (2007). A methodology and an instrument for the temperature-controlled optimization of crystal growth. Acta Cryst. D63, 339–347. [DOI] [PubMed]
  11. Cacioppo, E. & Pusey, M. L. (1991). The solubility of the tetragonal form of hen egg white lysozyme from pH 4.0 to 5.4. J. Cryst. Growth, 114, 286–292.
  12. Carotenuto, L., Piccolo, C., Castagnolo, D., Lappa, M., Tortora, A. & Garcìa-Ruiz, J. M. (2002). Experimental observations and numerical modelling of diffusion-driven crystallisation processes. Acta Cryst. D58, 1628–1632. [DOI] [PubMed]
  13. Casadei, C. M., Gumiero, A., Metcalfe, C. L., Murphy, E. J., Basran, J., Concilio, M. G., Teixeira, S. C. M., Schrader, T. E., Fielding, A. J., Ostermann, A., Blakeley, M. P., Raven, E. L. & Moody, P. C. E. (2014). Neutron cryo-crystallography captures the protonation state of ferryl heme in a peroxidase. Science, 345, 193–197. [DOI] [PubMed]
  14. Chayen, N. E., Shaw Stewart, P. D., Maeder, D. L. & Blow, D. M. (1990). An automated system for micro-batch protein crystallization and screening. J. Appl. Cryst. 23, 297–302.
  15. Coates, L., Erskine, P. T., Wood, S. P., Myles, D. A. A. & Cooper, J. B. (2001). A neutron Laue diffraction study of endothiapepsin: implications for the aspartic proteinase mechanism. Biochemistry, 40, 13149–13157. [DOI] [PubMed]
  16. Coates, L., Stoica, A. D., Hoffmann, C., Richards, J. & Cooper, R. (2010). The macromolecular neutron diffractometer (MaNDi) at the Spallation Neutron Source, Oak Ridge: enhanced optics design, high-resolution neutron detectors and simulated diffraction. J. Appl. Cryst. 43, 570–577.
  17. Coates, L., Tomanicek, S., Schrader, T. E., Weiss, K. L., Ng, J. D., Jüttner, P. & Ostermann, A. (2014). Cryogenic neutron protein crystallography: routine methods and potential benefits. J. Appl. Cryst. 47, 1431–1434.
  18. Cudney, B. & Patel, S. (1994). Crystallization as a tool for bioseparation. Am. Biotechnol. Lab. 12(7), 42. [PubMed]
  19. Day, J. & McPherson, A. (1992). Macromolecular crystal growth experiments on International Microgravity Laboratory-1. Protein Sci. 1, 1254–1268. [DOI] [PMC free article] [PubMed]
  20. DeLucas, L. J., Moore, K. M. & Long, M. M. (1999). Protein crystal growth and the International Space Station. Gravit. Space Biol. Bull. 12, 39–45. [PubMed]
  21. Ducruix, A. & Giegé, R. (1999). Crystallization of Nucleic Acids and Proteins: A Practical Approach. Oxford University Press.
  22. Dunuwila, D. D. & Berglund, K. A. (1997). ATR FTIR spectroscopy for in situ measurement of supersaturation. J. Cryst. Growth, 179, 185–193.
  23. Ewing, F., Forsythe, E. & Pusey, M. (1994). Orthorhombic lysozyme solubility. Acta Cryst. D50, 424–428. [DOI] [PubMed]
  24. Feigelson, R. S. (1988). The relevance of small molecule crystal growth theories and techniques to the growth of biological macromolecules. J. Cryst. Growth, 90, 1–13.
  25. García-Ruiz, J. M. (2003). Counterdiffusion methods for macromolecular crystallization. Methods Enzymol. 368, 130–154. [DOI] [PubMed]
  26. García-Ruiz, J. M. & Ng, J. D. (2006). Protein Crystallization Strategies for Structural Genomics, edited by N. E. Chayen, ch. 5. La Jolla: International University Line.
  27. García-Ruiz, J. M. & Otálora, F. (1997). Crystal growth studies in microgravity with the APCF. II. Image analysis studies. J. Cryst. Growth, 182, 155–167.
  28. García-Ruiz, J. M., Otálora, F., Novella, M. L., Gavira, J. A., Sauter, C. & Vidal, O. (2001). A supersaturation wave of protein crystallization. J. Cryst. Growth, 232, 149–155.
  29. Garman, E. F. & Doublié, S. (2003). Cryocooling of macromolecular crystals: optimization methods. Methods Enzymol. 368, 188–216. [DOI] [PubMed]
  30. Garman, E. F. & McSweeney, S. M. (2007). Progress in research into radiation damage in cryo-cooled macromolecular crystals. J. Synchrotron Rad. 14, 1–3. [DOI] [PubMed]
  31. Garman, E. & Owen, R. L. (2007). Cryocrystallography of macromolecules: practice and optimization. Methods Mol. Biol. 364, 1–18. [DOI] [PubMed]
  32. Gavira, J. A., Toh, D., Lopéz-Jaramillo, J., García-Ruíz, J. M. & Ng, J. D. (2002). Ab initio crystallographic structure determination of insulin from protein to electron density without crystal handling. Acta Cryst. D58, 1147–1154. [DOI] [PubMed]
  33. Gray, R. J., Hou, W. B., Kudryavtsev, A. B. & DeLucas, L. J. (2001). A new approach to the measurement of protein solubility by Michaelson interferometry. J. Cryst. Growth, 232, 10–16.
  34. Haire, L. F. & Blow, D. M. (2001). A novel spin filter method for the measurement of solubility. J. Cryst. Growth, 232, 17–20.
  35. Hodge, T. A. (2014). A Size Limit for Protein Crystals, Chemistry. MS thesis, University of Alabama in Huntsville, Huntsville, Alabama, USA.
  36. Hope, H. (1988). Cryocrystallography of biological macromolecules: a generally applicable method. Acta Cryst. B44, 22–26. [DOI] [PubMed]
  37. Howard, E. I., Blakeley, M. P., Haertlein, M., Petit-Haertlein, I., Mitschler, A., Fisher, S. J., Cousido-Siah, A., Salvay, A. G., Popov, A., Muller-Dieckmann, C., Petrova, T. & Podjarny, A. (2011). Neutron structure of type-III antifreeze protein allows the reconstruction of AFP-ice interface. J. Mol. Recognit. 24, 724–732. [DOI] [PubMed]
  38. Hughes, R. C., Coates, L., Blakeley, M. P., Tomanicek, S. J., Langan, P., Kovalevsky, A. Y., García-Ruiz, J. M. & Ng, J. D. (2012). Inorganic pyrophosphatase crystals from Thermococcus thioreducens for X-ray and neutron diffraction. Acta Cryst. F68, 1482–1487. [DOI] [PMC free article] [PubMed]
  39. Iwai, W., Yagi, D., Ishikawa, T., Ohnishi, Y., Tanaka, I. & Niimura, N. (2008). Crystallization and evaluation of hen egg-white lysozyme crystals for protein pH titration in the crystalline state. J. Synchrotron Rad. 15, 312–315. [DOI] [PMC free article] [PubMed]
  40. Juers, D. H. & Matthews, B. W. (2004a). The role of solvent transport in cryo-annealing of macromolecular crystals. Acta Cryst. D60, 412–421. [DOI] [PubMed]
  41. Juers, D. H. & Matthews, B. W. (2004b). Cryo-cooling in macromolecular crystallography: advantages, disadvantages and optimization. Q. Rev. Biophys. 37, 105–119. [DOI] [PubMed]
  42. Juers, D. H. & Weik, M. (2011). Similarities and differences in radiation damage at 100 K versus 160 K in a crystal of thermolysin. J. Synchrotron Rad. 18, 329–337. [DOI] [PubMed]
  43. Kim, Y. W., Barlow, D. A., Caraballo, K. G. & Baird, J. K. (2003). Kinetics of supersaturation decay in the crystallization of lysozyme. Mol. Phys. 101, 2677–2686.
  44. Kitago, Y., Watanabe, N. & Tanaka, I. (2005). Structure determination of a novel protein by sulfur SAD using chromium radiation in combination with a new crystal-mounting method. Acta Cryst. D61, 1013–1021. [DOI] [PubMed]
  45. Lee, H.-M., Kim, Y. W. & Baird, J. K. (2001). Electrophoretic mobility and zeta-potential of lysozyme crystals in aqueous solutions of some 1:1 electrolytes. J. Cryst. Growth, 232, 294–300.
  46. Loll, P. J. (2014). Membrane proteins, detergents and crystals: what is the state of the art? Acta Cryst. F70, 1576–1583. [DOI] [PMC free article] [PubMed]
  47. Lorber, B., Théobald-Dietrich, A., Charron, C., Sauter, C., Ng, J. D., Zhu, D.-W. & Giegé, R. (2002). From conventional crystallization to better crystals from space: a review on pilot crystallogenesis studies with aspartyl-tRNA synthetases. Acta Cryst. D58, 1674–1680. [DOI] [PubMed]
  48. Malkin, A. J., Kuznetsov, Y. G., Lucas, R. W. & McPherson, A. (1999). Surface processes in the crystallization of turnip yellow mosaic virus visualized by atomic force microscopy. J. Struct. Biol. 127, 35–43. [DOI] [PubMed]
  49. Malkin, A. J. & Thorne, R. E. (2004). Growth and disorder of macromolecular crystals: insights from atomic force microscopy and X-ray diffraction studies. Methods, 34, 273–299. [DOI] [PubMed]
  50. McPherson, A. (1999). Crystallization of Biological Macromolecules. Cold Spring Harbor Laboratory Press.
  51. McPherson, A. & Cudney, B. (2014). Optimization of crystallization conditions for biological macromolecules. Acta Cryst. F70, 1445–1467. [DOI] [PMC free article] [PubMed]
  52. Meilleur, F., Munshi, P., Robertson, L., Stoica, A. D., Crow, L., Kovalevsky, A., Koritsanszky, T., Chakoumakos, B. C., Blessing, R. & Myles, D. A. A. (2013). The IMAGINE instrument: first neutron protein structure and new capabilities for neutron macromolecular crystallography. Acta Cryst. D69, 2157–2160. [DOI] [PubMed]
  53. Miers, H. A. & Isaac, F. (1907). The spontaneous crystallisation of binary mixtures. Experiments on salol and betol. Proc. R. Soc. Lond. Ser. A, 79, 322–351.
  54. Mullin, J. W. (1993). Crystallization, 3rd ed. Oxford: Butterworth-Heinemann.
  55. Nakazato, K. (2008). Method of measuring protein solubility, process for producing crystal and apparatus therefore. US Patent No. 7416708 B2.
  56. Ng, J. D., Clark, P. J., Stevens, R. C. & Kuhn, P. (2008). In situ X-ray analysis of protein crystals in low-birefringent and X-ray transmissive plastic microchannels. Acta Cryst. D64, 189–197. [DOI] [PubMed]
  57. Ng, J. D. & García-Ruiz, J. M. (2006). Counter-diffusion capillary crystallization for structural genomics. Trends Drug Discov. 3, 36.
  58. Ng, J. D., Gavira, J. A. & García-Ruiz, J. M. (2003). Protein crystallization by capillary counterdiffusion for applied crystallo­graphic structure determination. J. Struct. Biol. 142, 218–231. [DOI] [PubMed]
  59. Ng, J. D., Kuznetsov, Y. G., Malkin, A. J., Keith, G., Giegé, R. & McPherson, A. (1997). Visualization of RNA crystal growth by atomic force microscopy. Nucleic Acids Res. 25, 2582–2588. [DOI] [PMC free article] [PubMed]
  60. Ng, J. D., Lorber, B., Giegé, R., Koszelak, S., Day, J., Greenwood, A. & McPherson, A. (1997). Comparative analysis of thaumatin crystals grown on earth and in microgravity. Acta Cryst. D53, 724–733. [PubMed]
  61. Ng, J. D., Lorber, B., Witz, J., Théobald-Dietrich, A., Kern, D. & Giegé, R. (1996). The crystallization of biological macromolecules from precipitates: evidence for Ostwald ripening. J. Cryst. Growth, 168, 50–62.
  62. Ng, J. D. (2002). Space-grown protein crystals are more useful for structure determination. Ann. N. Y. Acad. Sci. 974, 598–609. [DOI] [PubMed]
  63. Ng, J. D., Sauter, C., Lorber, B., Kirkland, N., Arnez, J. & Giegé, R. (2002). Comparative analysis of space-grown and earth-grown crystals of an aminoacyl-tRNA synthetase: space-grown crystals are more useful for structural determination. Acta Cryst. D58, 645–652. [DOI] [PubMed]
  64. Ng, J. D., Stevens, R. C. & Kuhn, P. (2008). Protein crystallization in restricted geometry: advancing old ideas for modern times in structural proteomics. Methods Mol. Biol. 426, 363–376. [DOI] [PubMed]
  65. Niimura, N. (2010). Neutron Scattering in Biology: Techniques and Applications, edited by J. Fitter, T. Gutberlet & J. Katsaras, pp. 43–62. Dordrecht: Springer.
  66. Niimura, N. & Bau, R. (2008). Neutron protein crystallography: beyond the folding structure of biological macromolecules. Acta Cryst. A64, 12–22. [DOI] [PubMed]
  67. Oksanen, E., Blakeley, M. P., Bonneté, F., Dauvergne, M. T., Dauvergne, F. & Budayova-Spano, M. (2009). Large crystal growth by thermal control allows combined X-ray and neutron crystallographic studies to elucidate the protonation states in Aspergillus flavus urate oxidase. J. R. Soc. Interface, 6, S599–S610. [DOI] [PMC free article] [PubMed]
  68. Ostwald, W. (1897). Studien über die Bildung und Umwandlung fester Körper. Z. Phys. Chem. 22, 289–330.
  69. Otálora, F. & García-Ruiz, J. M. (1997). Crystal growth studies in microgravity with the APCF. I. Computer simulation of transport dynamics. J. Cryst. Growth, 182, 141–154.
  70. Otálora, F., Gavira, J. A., Ng, J. D. & García-Ruiz, J. M. (2009). Counterdiffusion methods applied to protein crystallization. Prog. Biophys. Mol. Biol. 101, 26–37. [DOI] [PubMed]
  71. Rakel, N., Baum, M. & Hubbuch, J. (2014). Moving through three-dimensional phase diagrams of monoclonal antibodies. Biotechnol. Prog. 30, 1103–1113. [DOI] [PubMed]
  72. Rayment, I. (2002). Small-scale batch crystallization of proteins revisited. Structure, 10, 147–151. [DOI] [PubMed]
  73. Rowe, J. D. & Baird, J. K. (2007). Reduced capillary length scale in the application of Ostwald ripening theory to the coarsening of charged colloidal crystals in electrolyte solutions. Int. J. Thermophys. 28, 855–864.
  74. Rupp, B. (2015). Origin and use of crystallization phase diagrams. Acta Cryst. F71, 247–260. [DOI] [PMC free article] [PubMed]
  75. Sauter, C., Lorber, B., Kern, D., Cavarelli, J., Moras, D. & Giegé, R. (1999). Crystallogenesis studies on yeast aspartyl-tRNA synthetase: use of phase diagram to improve crystal quality. Acta Cryst. D55, 149–156. [DOI] [PubMed]
  76. Sazaki, G., Kurihara, K., Nakada, T., Miyashita, S. & Komatsu, H. (1996). A novel approach to the solubility measurement of protein crystals by two-beam interferometry. J. Cryst. Growth, 169, 355–360.
  77. Shu, F., Ramakrishnan, V. & Schoenborn, B. P. (2000). Enhanced visibility of hydrogen atoms by neutron crystallography on fully deuterated myoglobin. Proc. Natl Acad. Sci. USA, 97, 3872–3877. [DOI] [PMC free article] [PubMed]
  78. Smith, P. K., Krohn, R. I., Hermanson, G. T., Mallia, A. K., Gartner, F. H., Provenzano, M. D., Fujimoto, E. K., Goeke, N. M., Olson, B. J. & Klenk, D. C. (1985). Measurement of protein using bicinchoninic acid. Anal. Biochem. 150, 76–85. [DOI] [PubMed]
  79. Streets, A. M. & Quake, S. R. (2010). Ostwald ripening of clusters during protein crystallization. Phys. Rev. Lett. 104, 178102. [DOI] [PMC free article] [PubMed]
  80. Teixeira, S. C. et al. (2008). New sources and instrumentation for neutrons in biology. Chem. Phys. 345, 133–151. [DOI] [PMC free article] [PubMed]
  81. Veesler, S., Marcq, S., Lafont, S., Astier, J. P. & Boistelle, R. (1994). Influence of polydispersity on protein crystallization: a quasi-elastic light-scattering study applied to α-amylase. Acta Cryst. D50, 355–360. [DOI] [PubMed]
  82. Weber, I. T., Waltman, M. J., Mustyakimov, M., Blakeley, M. P., Keen, D. A., Ghosh, A. K., Langan, P. & Kovalevsky, A. Y. (2013). Joint X-ray/neutron crystallographic study of HIV-1 protease with clinical inhibitor amprenavir: insights for drug design. J. Med. Chem. 56, 5631–5635. [DOI] [PMC free article] [PubMed]

Articles from Acta Crystallographica. Section F, Structural Biology Communications are provided here courtesy of International Union of Crystallography

RESOURCES