Representation of pitch chroma by multi-peak spectral tuning in human auditory cortex

Abstract

Musical notes played at octave intervals (i.e., having the same pitch chroma) are perceived as similar. This well-known perceptual phenomenon lays at the foundation of melody recognition and music perception, yet its neural underpinnings remain largely unknown to date. Using fMRI with high sensitivity and spatial resolution, we examined the contribution of multi-peak spectral tuning to the neural representation of pitch chroma in human auditory cortex in two experiments. In experiment 1, our estimation of population spectral tuning curves from the responses to natural sounds confirmed—with new data—our recent results on the existence of cortical ensemble responses finely tuned to multiple frequencies at one octave distance (Moerel et al., 2013). In experiment 2, we fitted a mathematical model consisting of a pitch chroma and height component to explain the measured fMRI responses to piano notes. This analysis revealed that the octave-tuned populations—but not other cortical populations—harbored a neural representation of musical notes according to their pitch chroma. These results indicate that responses of auditory cortical populations selectively tuned to multiple frequencies at one octave distance predict well the perceptual similarity of musical notes with the same chroma, beyond the physical (frequency) distance of notes.

Introduction

Human experience of musical notes is influenced by two relevant perceptual dimensions. The first is the pitch height, which relates to the physical (frequency) dimension along which notes can be ordered from low to high. The second is the pitch chroma, related to the similarity of musical notes at octave intervals (i.e., notes with fundamental frequency [f₀] at a 2:1 ratio; Shepard, 1982). Pitch chroma is central to melody recognition and music perception. The fundamental importance of the octave interval in perception is illustrated by the observation that it is the only interval common to nearly all musical scales ever evolved (Randel, 2003). Infants already generalize a melody across octaves (Demany and Armand, 1984), and even monkeys assign a special status to octaves, judging melodies transposed by multiples of octaves as being more similar to the original than non-integer transpositions (Wright et al., 2000). The widespread occurrence, early onset, and generalization beyond the human species of octave perception suggest that a mechanism for the explicit representation of octave frequency intervals may be present in the brain.

To date, the neural underpinnings of pitch chroma perception remain largely unknown. Throughout the auditory system, neurons are described by their characteristic frequency (CF), which is the frequency to which they respond best. Auditory neurons are spatially ordered according to their CF, resulting in tonotopic maps. This topographic organization of frequency is maintained in the various auditory relays (King and Nelken, 2009; Merzenich and Brugge, 1973; Merzenich et al., 1975) and can be examined non-invasively in the human auditory cortex using functional MRI (fMRI; Da Costa et al., 2011; Formisano et al., 2003; Humphries et al., 2010). Beyond the tonotopic organization (i.e., main peak of a voxel's spectral profile), a large part of auditory cortical neurons (Kadia and Wang, 2003) and auditory voxels' receptive fields (Moerel et al., 2013) are tuned to multiple frequency bands. In a recent study, we performed a data-driven identification of voxels with a similar pattern of multi-peaked spectral tuning and hypothesized that resulting spectral tuning patterns may be useful for auditory perception. For example, a cluster of voxels with broad spectral tuning resulting from our analysis could process overall sound energy, the harmonic tuning in another cluster could serve to parse harmonic sounds (such as speech) from a noisy background, and fine-grained tuning to multiple octaves as seen in yet another cluster (“octave cluster”) may contribute to the human percept of octave similarity (Moerel et al., 2013; see Fig. 1 and below for further elaboration on this “spectral” hypothesis and a discussion of possible alternative “temporal” mechanisms). However, these hypotheses have yet to be tested. That is, it is not clear whether these different clusters of spectral tuning patterns, consistently observed inhuman auditory cortex, have any meaning from a perceptual and behavioral point of view.

Fig. 1.

Hypothesized neural mechanism for pitch chroma perception. Incoming musical sounds—such as piano notes (left)—are filtered according to the voxels' spectral tuning curves. While voxels with single-peaked spectral tuning curves only respond to musical notes that are f₀-matched with their CF (top row), octave-tuned voxels additionally respond to sounds whose f₀ matches the voxel's octave-related spectral peaks (bottom row). In this manner, octave-tuned voxels respond similar to sounds whose f₀ differs precisely one or more octaves (i.e., C₄ and C₅, or E₄ and E₅).

Here we hypothesized that the fine-grained spectral tuning to multiple octaves in the human auditory cortex relates to the pitch chroma percept of musical notes. Specifically, we reasoned that the voxels' tuning reflects the spectral neural filtering of incoming sounds (see Fig. 1). While voxels with single-peaked spectral tuning curves only respond to musical notes that are f₀-matched with their CF (top row of Fig. 1), octave-tuned voxels are predicted to additionally display a responses to sounds whose f₀ matches the voxel's octave-related spectral peaks (bottom row of Fig. 1). For example, an octave-tuned voxel with a CF of 262 Hz (see voxel 3 in Fig. 1) will respond strongly to CF-matched piano note C₄, but also to notes—such as C₅—whose f₀ matches the voxel's octave-related spectral peaks (f₀ of C₅ = 524 Hz, which is 2*voxels' CF). An octave-tuned voxel with a CF of 330 Hz (see voxel 4 in Fig. 1) will respond strongly to piano notes E₄ and E₅ (with f₀ of 1*CF = 330 Hz and 2*CF = 660 Hz, respectively) and weaker to C₄ and C₅. In this manner, octave-tuned voxels respond more similar to sounds with an f₀ differing precisely one or more octaves than to sounds with an f₀ at other musical intervals, generating a representation according to the pitch chroma of these sounds.

We tested our hypothesis using data from two experiments (see Fig. 2a and b, respectively) where we used ultra-high field functional MRI (7 T) to measure auditory cortical responses to sounds. In experiment 1 (see Fig. 2a), we measured the brain's responses to a large set of natural sounds and estimated population spectral tuning curves for voxels in the sound frequency domain (i.e., population receptive fields; see top and middle row of Fig. 2a). In a data-driven manner, we identified those locations that displayed sensitivity to multiple frequency bands at one octave distance from each other (i.e., octave-tuned locations; see bottom row of Fig. 2a). In experiment 2, we measured—in the same subjects—the brain responses to piano notes using fMRI (see top row of Fig. 2b). Then we fitted the responses to piano notes (spanning three octaves) with a mathematical model (Briley et al., 2013)consisting of a pitch chroma and a pitch height component (Shepard, 1982; see middle and bottom row of Fig. 2b, and Fig. 1c of Briley et al., 2013). We expected that in the octave-tuned locations (as identified in experiment 1)—but not in other parts of auditory cortex—responses would be significantly explained by the pitch chroma component of the model, reflecting that in these locations the response to notes at a distance of one octave was more similar than the response to notes at other musical intervals.

Fig. 2.

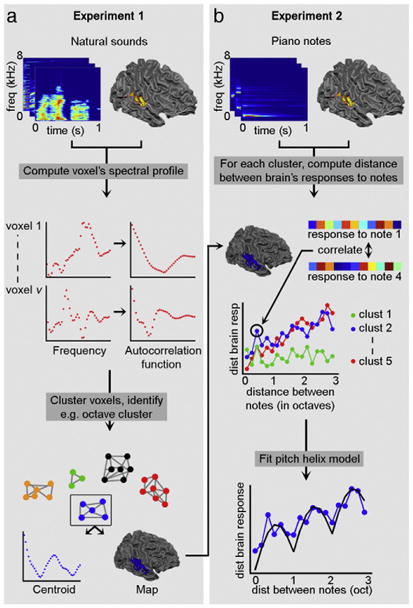
Overview of the performed analysis. (a) In experiment 1, the voxels' spectral tuning curve profile (referred to as its spectral profile, i.e., its frequency preference) was computed based on brain responses to natural sounds (top and middle row). The autocorrelation of these spectral profiles was submitted to a clustering algorithm, producing groups of voxels (i.e., clusters) with similar frequency modulation preference (bottom row). The clusters are characterized by a centroid and map. (b) In experiment 2, brain responses to piano notes spanning three octaves were collected (top row). The dissimilarity (or distance) between brain responses to these notes was computed for each cluster resulting from experiment 1 (middle row). These distances were then fitted with a “pitch helix” model (bottom row), which assumed that the distance between musical notes depended on their relative pitch height and relative pitch chroma.

Materials and methods

Subjects

Six subjects participated in this study (mean age [SD] = 29.5 [5.5]; three males and three females). The subjects reported to have normal hearing, had no history of hearing disorder/impairments or neurological disease, and gave informed consent before commencement of the measurements. The Institutional Review Board for human subject research at the University of Minnesota granted approval for the study.

Stimuli

The stimuli consisted of recordings of 72 natural sounds (including human speech, animal cries, musical instruments, and tool sounds) and 18 piano notes. The piano notes were sampled from an online database (University of Iowa Musical Instrument Samples; http://theremin.music.uiowa.edu/MIS.html; accessed on 11 July 2012) and consisted of six musical notes (i.e., C, D, E, G^b, A^b, and B^b) sampled from three octaves (C₄ = 262Hz, C₅ = 523 Hz, and C₆ = 1047 Hz). Sounds were sampled at 16 kHz and their duration was 1000 ms. Sound onset and offset were ramped with a 10 ms linear slope, and their energy (RMS) levels were equalized. Before starting the experiment, with the earbuds in place, the subjects rated the perceived loudness of the piano notes. That is, the highest piano note (B^b₆) was played in combination with each of the other notes. The subjects adjusted the loudness of this second note until they perceived it as equally loud as B^b₆. During the experiment, the piano notes were played at these individually and subject-specific loudness adjustments, with the purpose of equalizing the perceived loudness across notes. Sounds were presented using the fMRI-compatible S14 model earphones of Sensimetrics Corporation (www.sens.com), with a linear frequency transfer up to 8 kHz.

Magnetic resonance imaging

Data were acquired on a 7T whole body system driven by a Siemens console using a head gradient insert operating at up to 80 mT/m with a slew rate of 333 T/m/s. A head RF coil (single transmit, 16 receive channels) was used to acquire anatomical (T1 weighted) and functional (T2*-weighted BOLD) images. T1-weighted (1 mm isotropic) images were acquired using a modified MPRAGE sequence (TR = 2500 ms; TI = 1500 ms; TE = 3.67 ms). Proton density (PD) images were acquired together with the T1-weighted images (both acquisitions are interleaved in the modified MPRAGE sequence) and were used to minimize inhomogeneities in T1-weighted images (van de Moortele et al., 2009). The acquisition time for these anatomical scans was ∼ 7 minutes.

T2*-weighted functional data were acquired using a clustered Echo Planar Imaging (EPI) technique. The experiments were designed according to a fast event-related scheme. The acquisition parameters were as follows: TR = 2600 ms; time of acquisition [TA] = 1200 ms; TE = 30 ms; number of slices = 31; GRAPPA acceleration X3; partial Fourier 6/8; voxel size = 1.5 × 1.5 × 1.5 mm³. In experiment 1, 72 natural sounds were presented one time per run for three runs in total (run 1/3/5). In experiment 2, 18 different piano notes were presented 4 times per run for three runs in total (run 2/4/6). Within each run, sounds were randomly spaced at a jittered interstimulus interval of 2, 3, or 4 TRs and presented—with additional random jitter—in the silent gap between acquisitions. This clustered imaging paradigm with jittered sound representation represents a trade-off between reducing the confounding effects of scanner noise (Langers et al., 2014) and a time-efficient data collection (as required for estimating responses to a large set of natural sounds). Zero trials (trials where no sound was presented, 5% of the trials), and catch trials (trials in which the sound which was just heard was presented, 8% and 5% of the trials in experiments 1 and 2, respectively) were included. Subjects were instructed to perform a one-back task, and were required to respond with a button press when a sound was repeated. Catch trials were excluded from the analysis. Each run lasted approximately 10 min. Functional and anatomical data were analyzed with BrainVoyager QX. Preprocessing consisted of slice scan-time correction (with sinc interpolation), 3-dimensional motion correction, and temporal high pass filtering (removing drifts of 7 cycles or less per run). Functional data were co-registered to the anatomical data and normalized in Talairach space (Talairach and Tournoux, 1988). Functional data were resampled (with sinc interpolation) in the normalized space at a resolution of 1 mm isotropic. Anatomical volumes were also used to derive gray matter segmentations, indicating the border between white and gray matter. Using this border, inflated hemispheres of the individual subjects were obtained.

Computing the spectral profile of each cortical location

Based on the responses to natural sounds as collected in experiment 1, we calculated the voxels' spectral tuning curve (referred to below as the voxel's spectral profile, which is the frequency preference of each voxel; see first/second row of Fig. 2a) using customized Matlab code (Moerel et al., 2012, 2013) (www.mathworks.com). In this analysis, the sounds are passed through a biologically plausible computational model of auditory processing (Chi et al., 2005) that characterizes them according to their frequency content W (N × B; where N = number of sounds and B = number of frequency bins). We calculated the fMRI response Y ([N × V], where V = number of voxels) to the sounds by first computing noise regressors on the data (Kay et al., 2013) (http://kendrickkay.net/GLMdenoise/; noise regressors extracted on both experiments), and adding these regressors to the analysis as described before (Moerel et al., 2012). By combining the sounds frequency representation W with the fMRI response matrix Y, the voxels' spectral preferences (matrix R [B × V], where V = number of voxels) is obtained as the relevance vector machine (RVM) solution to the linear problem:

$$Y_j=\mathbf{W}.R_j$$ (1)

where each element i of the vector R_j describes the contribution of the frequency bin i to the overall response of voxel j (see left-most graphs of the second row of Fig. 2a for two example voxels). Tonotopic maps were created by logarithmically mapping the maximum of R_j to a red-yellow-green-blue color scale. Group maps were created by first optimizing alignment across subjects using cortex based alignment (CBA; Goebel et al., 2006) and subsequent averaging across subjects.

Assessing the validity of voxels' spectral profiles

We assessed the validity of the spectral profiles by evaluating their ability to predict responses to the piano notes as collected in experiment 2. Note that this part of the analysis is not shown in Fig. 2 as it serves solely as a quality check. Specifically, we used the spectral profile of each voxel j to predict the response Ŷ_j to the 18 notes as:

$${\widehat{Y}}_j=\mathbf{W}.R_j$$ (2)

where R_j [N × B] is the frequency representation of the musical notes (N = 18). For each sound i, we computed the correlation between predicted response Ŷ_i [1 × V] and measured fMRI responses to all piano notes Y. Rank r_i measures whether predicted response Ŷ_i was correctly matched with measured response Y_i. Thus, a rank of 1 indicates perfect prediction, while a rank of N would be the worst outcome. Prediction accuracy P_i of each sound was defined as

$$P_i=1-\frac{r_i-1}{N-1}$$ (3)

Values of P_i range between 0 and 1, with perfect prediction = 1 and chance = 0.5. The statistical significance of the prediction accuracy was obtained by randomly permuting N in matrix Y and repeating the analysis (200 permutations). The voxels' tuning profiles as estimated on responses to natural sounds (experiment 1) predicted responses to the piano notes in experiment 2 above chance both at group level (mean [SE] = 0.60 [0.04], p < 0.05; t-test after Fisher transformation) and in a subset of individuals (p < 0.05 for S3 and S5, p < 0.1 for S2 and S6, permutation tests).

Identification of octave-tuned locations

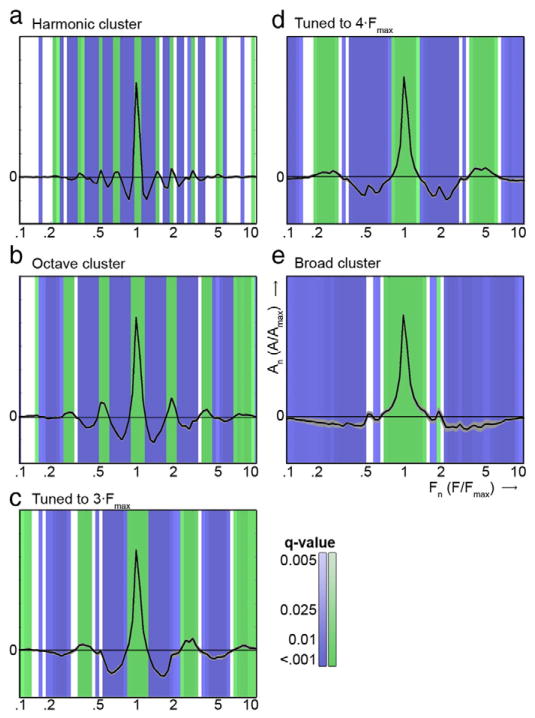
Next, we characterized the voxels' spectral profiles by dividing them into groups of similar spectral tuning using a clustering analysis (bottom row of Fig. 2a). Details of this clustering analysis can be found in Moerel et al. (2013). We computed the correlation between the normalized autocorrelation profiles of the voxels' profiles R_j (see middle row of Fig. 2a), which reflects the voxels' preferences to spectral modulations independent of the frequency of the main peak. We obtained a fully data-driven subdivision of this network into spatially non-overlapping clusters (i.e., groups of voxels) with the Louvain algorithm for each individual (Blondel et al., 2008; Rubinov and Sporns, 2011) (http://www.brain-connectivity-toolbox.net). We computed the characteristic profile (i.e., the centroid) of each resulting cluster as follows. We normalized each voxel's spectral profile by expressing all amplitude and frequency values as ratios with respect to its amplitude maximum and the frequency at that maximum. Thus, the abscissa and ordinate became, respectively, F_n = F/F_max and A_n = A/A_max, where F_n and A_n were the normalized values (Moerel et al., 2013; Schwartz et al., 2003). This normalization ensures that both maximum and additional frequency peaks align across spectral profiles of different voxels (the voxels' CF is at 1 × F_max). Cluster centroids per individual were computed by averaging these normalized spectral profiles of the voxels per cluster. Matching clusters across subjects were identified as those clusters whose centroids had the highest correlation to each other, and group centroids were obtained by averaging matching cluster centroids across subjects (see Fig. 3). At each normalized frequency bin, group centroids were tested for significant deviation from zero (one sample t-test; results FDR corrected for multiple comparisons).

Fig. 3.

Clusters' centroids characterizing the five extracted clusters. The centroids' main peak represents the main frequency peak (aligned across voxels), and additional peaks show the presence of sensitivity to additional frequency bands at consistent spectral intervals. Positive and negative significant deviations from zero are color coded in green and blue, respectively. Grey areas show the standard error in extracted centroids across the six subjects. (a–e) The harmonic cluster, the octave cluster, the cluster tuned to 3 × F_max, the cluster tuned to 4 × F_max, and the broadly tuned cluster, respectively.

Evaluation of the cluster-specific representation of piano notes

To investigate whether voxels in the octave cluster represented the pitch chroma and/or pitch height of piano notes, we performed the following analysis. For each cluster (i.e., for each group of voxels with similar spectral modulation tuning, as defined by experiment 1), we computed the distance between the brain's responses to piano notes (see middle row of Fig. 2b). This was achieved by selecting for each cluster c the voxels belonging to that cluster V_c. Then for each piano note P_k, we identified a subset of voxels V_c,k whose main tonotopic peak coincided with the main frequency of P_k ± 0.1 octave (i.e., frequency-matched voxels) and computed the distance between each combination of notes P_k,l as (1 - linear correlation between Y_k and Y_l). Here, Y_k and Y_l reflect the fMRI response to piano notes P_k and P_l, respectively, in the combined set of voxels V_c,k and V_c,l. The group analysis was conducted by concatenating voxels across subjects before computing the distance between each combination of notes.

Pitch height and pitch chroma effects were assessed by fitting the observed distances between piano notes with a combined sinusoidal and linear “pitch helix” model (Shepard, 1982), where the sinusoidal and linear component reflect the pitch chroma and pitch height dimension, respectively (Briley et al., 2013; see black line in bottom row of Fig. 2b, and Fig. 1c of Briley et al., 2013). The model was defined by

$$D(\mathit{\Delta }M)=a.|sin(\pi .\mathit{\Delta }M)|+b.\mathit{\Delta }M+c$$ (4)

Here, D(ΔM) reflects the observed distance in brain responses to two piano notes normalized between (0,1), and ΔM represents the musical distance between these notes in octaves. Parameters a and b are scaling factors for the sinusoidal and linear components of the function, and c is a constant that fits the mean of D(ΔM). The model was fit in 5-fold cross-validation. The 1/5 of ΔM observations not used in model fitting per fold was used for model fit evaluation, by computing the correlation between predicted ΔM and observed ΔM. Statistical significance of the model fit and model parameters a and b was assessed by comparing the obtained correlation between predicted and observed ΔM and model parameters to the correlation and parameters obtained from permutation testing (1000 permutations of the labels ΔM).

For each subject, we selected a varying number of voxels to compute the distance in brain responses to piano notes. Voxel selection was based on the correlation of the voxels' spectral profile to the centroid of cluster c (range of approximately 500–3500 voxels selected). Per subject, the number of voxels used was selected as the set of voxels that generated the highest model fit (assessed as the correlation between predicted ΔM and observed ΔM) in any of the clusters. Thus, the number of voxels selected was different across subjects but stable within a subject across clusters. On average, we selected 134 voxels/note (2412 voxels/cluster; minimum = 45 voxels/note for S2; maximum =185 voxels/note for S6).

Individual octave maps (see Fig. 4c and Supplementary Figure S1c) show the location of the frequency-matched octave-tuned voxels selected in that subject and reflect the correlation of the profile of those voxels with the centroid of the octave cluster. Group octave maps were created by transferring individual maps to CBA space and using them to create a probabilistic map. This probabilistic map reflects for each voxel how often it is included in individual maps.

Fig. 4.

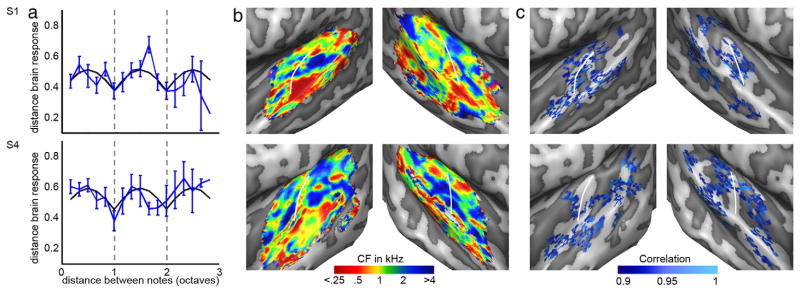
Model fit, tonotopy, and octave map for two individuals. (a) Blue lines show the observed distance between musical notes across three octaves in the octave cluster. The error bars reflect the standard error across note combinations. Black lines show the best model fit. Grey dotted lines show a musical distance of one and two octaves. (b–c) Tonotopy and octave map. The octave maps show the correlation between the voxel's profile and the centroid of the octave cluster. The white lines indicate HG. See Supplementary Figure 1 for the remaining four subjects.

Results

Estimation of voxels' spectral profiles and tonotopic maps

Both natural sounds (experiment 1) and piano notes (experiment 2) evoked strong responses throughout the superior temporal plane. The activated regions included early auditory areas along Heschl's gyrus (HG), and surrounding regions on Heschl's sulcus (HS), planum polare (PP), planum temporale (PT), along the superior temporal gyrus (STG), and on the posterior superior temporal sulcus (STS). Based on the maximum of the estimated voxels' spectral profiles (experiment 1), we extracted tonotopic maps in individual subjects (Fig. 4b and Supplementary Figure 1b) and at group level (Fig. 5a). At group level, and visible in most individual hemispheres, we observed the high–low–high tonotopic pattern characteristic for human primary auditory cortex (PAC; Da Costa et al., 2011; Formisano et al., 2003; Humphries et al., 2010). That is, on top of HG or at its immediate proximity in HS, a region preferring low frequencies was consistently observed. Anterior (on HG and on the first transverse sulcus [FTS]) and posterior (on HS and anterior PT) to this main low frequency region, regions preferring high frequencies were situated. Beyond the main high–low–high gradient, additional frequency clusters were observed on PP, PT, and STG/STS. These regions may reflect additional frequency gradients, possibly indicating the location of belt and parabelt auditory fields (see Moerel et al., 2014).

Fig. 5.

Group tonotopy and octave map. (a) Consistent with results of previous studies, group tonotopic maps (averaged across six subjects) displayed a large low frequency region near Heschl's gyrus (HG), bordered anteriorly and posteriorly by regions preferring higher frequencies. b: The group octave map is a probabilistic map that counts the occurrences of each voxel in the octave map across individual subjects. The map was smoothed and thresholded to show voxels that were selected in > 2.6 subjects. The white lines indicate HG. (c) Histograms show the distribution of CF values in the tonotopy map (black line) and in the octave map (red line), separate for the left and right hemisphere. The black and red line show the mean across subjects, and the shaded areas reflect the standard error across subjects. The blue shaded regions represent the range of f₀ present in the piano notes.

Cluster extraction and identification of octave voxels

Next, we used a data-driven algorithm (Blondel et al., 2008; Rubinov and Sporns, 2011) to divide the voxels into separate clusters according to their type of spectral tuning (see Moerel et al., 2013). The algorithm extracted five clusters in 5 of the 6 subjects, and four clusters in the remaining subject (S5). The characteristic profiles (i.e., centroids) of the clusters were highly consistent across subjects (mean [SD] correlation between matching and non-matching centroids = 0.99 [0.01] and 0.78 [0.06], respectively). In accordance with our previous results (Moerel et al., 2013), we found a broadly tuned cluster, a cluster with an additional peak around 4 × F_max, a cluster tuned to 3 × F_max, and a cluster tuned to harmonically related frequencies (see Fig. 3). As expected, voxels in one of these clusters were tuned to multiple frequency bands at one octave interval from each other (Fig. 3b). In the subject for which four clusters were extracted (S5), the cluster with an additional peak around 4 × F_max was absent.

Cluster-specific pitch helix model fit

For each cluster as assessed on data from experiment 1, we tested for the presence of a pitch chroma and height representation in data from experiment 2. That is, we fitted the “pitch helix” model to responses to the musical piano notes as recorded in experiment 2 separately for each cluster.

The “pitch helix” model significantly fitted the data of the octave cluster in 5 out of 6 individual subjects (r = 0.22/0.20/0.16/0.20/0.13/0.19 for S1–S6; p < 0.01 in S1,p < 0.05 in S2, S3, S4, and S6, p = 0.08 in S5; see Fig. 4a and top row of Supplementary Figure 2). In 4 out of 6 subjects (S1, S3, S4, and S6), the sinusoidal component a of the model was significantly higher than chance (p < 0.05; see middle row in Supplementary Figure 2), reflecting the smaller distance in responses to notes at octave interval compared to notes at other musical intervals (i.e., pitch chroma; see Fig. 4a). In the remaining subject (S2), the linear component b of the model was significant (p < 0.05; see top row of Supplementary Figure 1 and bottom row of Supplementary Figure 2), reflecting the increase in distance in response to notes at increasing musical interval (i.e., pitch height). The pitch model did not significantly fit the data in the four non-octave clusters. Two exceptions were cluster 3 (cluster tuned to 3 × F_max) in S3 (r = 0.24; p < 0.05; parameter b significant) and cluster 1 (harmonic cluster) in S6 (r = 0.18, p < 0.05; parameter a significant).

At group level, the “pitch helix” model significantly fitted the data of the octave cluster (r = 0.40, p < 0.01; see Fig. 6 and top row of Supplementary Figure 3). This significant fit was due to the sinusoidal (i.e., pitch chroma) component of the model, which was significantly higher than chance (a = 0.23, p < 0.01; see middle row of Supplementary Figure 3). The linear contribution to the fit was small (b = 0.02) and did not reach statistical significance (see bottom row of Supplementary Figure 3). Thus, at group level, the responses to piano notes in the octave cluster are well represented by the sinusoidal “pitch chroma” component of the model. In the other four clusters, the model fit was substantially lower (r = 0.09/0.11/–0.16/0.11, respectively, for the other four clusters). Neither the model fit nor the model parameters were statistically significant for these non-octave clusters (see Fig. 6 and Supplementary Figure 3).

Fig. 6.

Group model fit across clusters. Colored lines show the observed distance between musical notes across three octaves, separate for each cluster. That is, the harmonic, octave, 3 × F_max, 4 × F_max, and broad cluster are shown inmagenta, blue, red, cyan, and green, respectively. The error bars reflect the standard error across note combinations. Black lines show the best model fit. Grey dotted lines show a musical distance of one and two octaves.

Cortical location of octave voxels

Fig. 4c shows the spatial distribution of the octave-tuned voxels selected for the pitch helix model fit in two individuals (see Supplementary Figure 1c for the maps of the remaining subjects). At individual subject level, the octave-tuned voxels are distributed throughout the superior temporal plane. The group maps display the presence of across-subject similarities within this distributed pattern (Fig. 5b). At group level, octave-tuned voxels are localized bilaterally along HG, extending into middle and lateral HS. Bilateral octave regions are present on middle STG and on PT/posterior STG. In the right hemisphere, regions of octave-tuned voxels can be observed on anterior STG. We further explored the location of the octave-tuned voxels by comparing it to extracted tonotopic maps. While the full tonotopic map displayed a 1/f distribution of CF values, the octave-tuned voxels occupied only the subset of CF values matching the f₀ of piano notes (C₄ = 262 Hz to B^b₆ = 1865 Hz; Fig. 5c). Note that this result is driven by our analysis, as only frequency-matched octave voxels were selected (f₀ of note ± 0.1 octave; see Evaluation of the Cluster-Specific Representation of Piano Notes section). Bilaterally, the octave cluster occupied the main low frequency region (<0.5 kHz) on HG as well as part of the higher frequency (between 0.5 and 2 kHz) regions immediately anterior and posterior to it. The additional octave regions on PT/posterior STG and on anterior STG occupied regions of both low and higher frequency preference.

Discussion

We used 7-T fMRI to investigate the representation of musical notes in the human auditory cortex. First, we confirmed our previous results (Moerel et al., 2013) by showing that a subset of cortical populations displayed spectral tuning to multiple frequency bands at exactly one octave distance. Second, we revealed that these neuronal populations represent piano notes according to their pitch chroma, as they responded similarly to notes one octave apart and differently to notes at other musical intervals.

Octave-tuned populations in human auditory cortex

The results of experiment 1 replicated our previous observation of auditory cortical populations tuned to multiple frequencies at exactly one octave. As we measured fMRI voxels containing hundreds of neurons at a temporal resolution in the range of seconds, the observed octave-tuned locations could result from several patterns of neuronal tuning. Kadia and Wang (2003) showed the existence of multi-peaked neurons in primate A1, describing neurons with harmonically related frequency peaks. A similar mechanism may be in place for octave tuning, such that our octave-tuned voxels may reflect multi-peaked mechanisms operating at the level of single neurons. Alternatively, an octave-tuned voxel could reflect the complex spatial average of spectral profiles of many simple, single-peaked neurons. To advance our understanding regarding the neuronal tuning underlying our octave-tuned clusters, a well-controlled exploration of non-linear and combination-sensitive tuning to the multiple frequency bands within these profiles is needed. Based on the current results, we can conclude that, irrespective of the underlying neuronal mechanism, at population (i.e., voxel) level, octave-tuned information can be read out.

Interpretation of pitch helix model fit

In experiment 2, we showed that a mathematical model (Briley et al., 2013), consisting of a sinusoidal (i.e., circular) and linear component reflecting pitch chroma and pitch height, respectively (“pitch helix” model; Shepard, 1982), significantly fit the responses to piano notes in octave-tuned locations. This fit was driven—at group level and in four out of six individuals—by the pitch chroma component of the model. These results indicate that the representation of pitch chroma is supported by auditory cortical neuronal populations selectively and finely tuned to frequency bands at octave intervals (see bottom row of Fig. 1). The pitch height component of the model was not significant at group level or in the majority of individuals, suggesting that the neural mechanisms supporting pitch chroma perception do not underlie the percept of pitch height. A likely mechanism representing pitch height is the tonotopic organization of the auditory system (i.e., the voxels' CF), possibly operating at early (i.e., pre-cortical) stages in the auditory hierarchy. In our analysis, we purposefully represented voxels irrespective of their CF, and clustered voxels throughout the auditory cortex according to modulation patterns in their spectral tuning beyond their main frequency preference. As such, the voxel's tonotopic responses—and presumably the sounds' pitch height representation—were removed at the clustering stage of our analysis.

Mechanisms of human pitch perception

The coding of pitch in the auditory system has been debated for well over a century (de Cheveigné, 2005). Place models of pitch perception suggest that the spatial representation of sound frequency in the cochlea (tonotopy) underlies the representation of the spectral components of a stimulus. This representation may then be matched to (cortical) templates, each with a pitch label. Pitch is assigned as the label of the best-matching template (de Cheveigné, 2005). This model is challenged by a number of findings showing that pitch can be perceived based on sounds that do not contain spectral pitch information, such as sounds consisting fully of unresolved harmonics, or regular-interval noise (RIN; Griffiths and Hall, 2012). RIN is created by starting with random noise, taking and delaying a copy of it by a set time interval, and adding it back to the sound. By repeating this process, a sound with pronounced pitch is created that does not contain stable, harmonically related peaks in its auditory spectrum (Yost, 1996; Patterson et al., 2002). These observations prompted the development of time models of pitch perception (de Cheveigné, 2005; Patterson, 1994; Patterson et al., 1996), which rely on the precise spike timing in the auditory nerve. Pitch is represented as the main peak in the autocorrelation of spike timing. Support for time models comes from the observation that pitch perception degrades at frequencies higher than 4–5 kHz, which is assumed to be the upper limit of phase locking in the human auditory nerve (Oxenham, 2012). However, recent studies showed that pitch can only be extracted based on temporal cues that originate from the correct place in the cochlea (Oxenham et al., 2004) and that pitch can be extracted based on sounds that exclusively contain information above currently accepted limits of neural phase locking (Oxenham et al., 2011). These observations suggest that pitch perception may be supported by a combination of spectral and temporal mechanisms.

The neuronal populations finely tuned to multiple octaves, as shown to contribute to a representation of pitch chroma in our results, could function as templates corresponding to a specific pitch chroma. Note that such “octave templates” do not necessarily rely on spectral information (de Cheveigné, 2005). The piano notes employed in this study contained congruent spectral and temporal information and both types of information could serve as input to the octave-based neuronal filters. To explore this further, it would be interesting to examine how the octave templates in human auditory cortex represent the pitch chroma of sounds that do not contain spectral pitch cues (e.g. RIN sounds; see The Cortical Representation of Pitch section).

While octave-tuned neuronal populations represent pitch chroma, they could not act as general pitch templates as presupposed by the place model. Instead, the neuronal populations finely tuned to spectral ranges at harmonic intervals, as observed in previous work (Moerel et al., 2013) and replicated in the current study, could undertake such a role. Future work may test this hypothesis by examining the response in these neuronal populations during stimulation with spectrally diverse sounds that elicit the same pitch (e.g. examine how these neuronal populations represent sounds with a missing fundamental).

The cortical representation of pitch

Previous studies of human pitch representation have sought for a cortical region that responded preferentially to artificial sounds associated with pitch, using for example RIN as opposed to control sounds with no pitch (Griffiths and Hall, 2012). These studies observed a region with stronger responses to pitch than to non-pitch sounds in lateral HG (Hall et al., 2006, and Patterson et al., 2002; but see reports of medial HG in Griffiths et al., 2010; Krumbholz et al., 2003; and an argument for anterior PT in Barker et al., 2012). This region has been linked to the “pitch region” found by Bendor and Wang (2005), which was shown to contain neurons that respond to spectrally dissimilar stimuli as long as these sounds have the same pitch. Our study and results diverge from these previous studies of cortical pitch representation. While previous studies explored the processing of pitch as a characteristic of an individual sound, we approached the topic from a fundamentally different angle by exploring how the relation between a set of sounds is represented in cortical regions with specific spectral tuning. Our results and conclusions focus specifically on pitch chroma, which forms only a part of the entire pitch percept.

Two previous human studies relate closely to the explorations in the current study. First, a study by Warren et al. (2003) specifically sought to disentangle cortical processing of pitch chroma from processing of pitch height. They observed stronger responses to changes in pitch chroma and pitch height anterior and posterior to PAC, respectively, and concluded that pitch chroma was processed anterior to PAC while pitch height was processed in posterior regions. Instead, our results showed octave-tuned locations throughout the supra-temporal plane. Although anterior STG was included (in agreement with Warren et al., 2003), we also observed regions on PT and posterior STG which according to Warren et al. (2003) should be involved in processing of pitch height. These partially opposing conclusions may result from the radically different experimental and analysis approaches used in the two studies. We reported similarity in response patterns across changes in chroma and height, rather than the main activation level reported by Warren et al. (2003). Furthermore, in our study pitch chroma changes were always accompanied by pitch height changes, making a direct comparison across studies impossible.

Second, in human auditory cortex, a correlate of octave similarity was shown using electroencephalography (EEG; Briley et al., 2013). In this study, cortical responses adapted to RIN sounds at octave distance but not to RIN sounds at other musical intervals, following the sounds' pitch chroma. The authors concluded that auditory cortex contains a representation of pitch chroma. While this conclusion is in accordance with our observations, there are several discrepancies between studies. For example, Briley et al. (2013) did not observe EEG adaptation in response to pure tone stimuli. Instead, both our hypothesized filtering model and observations in humans (Ward, 1954) suggest that pitch chroma perception is preserved when processing pure tones. Moreover, the pitch chroma results of Briley et al. (2013) are based on RIN stimuli designed to uniformly activate the tonotopically arranged cochlear nerve neurons (Patterson et al., 2002). Thus, in order to explain the results of Briley et al. (2013), the octave-based neuronal populations should be able to operate on temporal cues as well as on spectral information. Further explorations are needed in order to determine the cues based on which the “octave templates” as observed in the current study can function. Overall, while both studies reached the same conclusion, the underlying mechanisms may be different. Such co-existence of two mechanisms of pitch perception is not impossible and has in fact been proposed to exist based on human psychophysics and marmoset electrophysiology (dual-pitch processing mechanism; Bendor et al., 2012; Carlyon and Shackleton, 1994). In order to link these studies, it may be interesting in future work (1) to evaluate how octave-tuned voxels respond to pure tones and RIN sounds across variations in pitch chroma and (2) to explore the voxels' receptive fields and resulting “preferred RIN repetition rate”map based on RIN stimuli with different repetition rate and pitch.

Pitch chroma representation includes primary auditory cortex

In individual hemispheres, octave-tuned locations were distributed throughout the supra-temporal plane. However, at group level commonalities in octave-tuned maps were apparent. These maps may reflect a distributed nature of the neuronal correlates of pitch chroma processing and suggest that the processing of pitch chroma cannot be pinpointed to one auditory cortical field. Octave voxels were localized bilaterally on HG, occupying part of the main low frequency region on HG and part of the high-frequency locations immediately anterior and posterior to it. To date, there is no consensus on how to interpret human tonotopy maps in terms of underlying auditory fields (Baumann et al., 2013; Da Costa et al., 2011; Langers and van Dijk, 2012; Moerel et al., 2014). However, these varying interpretations agree, supported by results from cytoarchitectonic studies (Galaburda and Sanides, 1980; Morosan et al., 2001) and explorations of myelin-related MRI contrast (De Martino et al., 2014; Dick et al., 2012), that the human PAC (including at least two auditory subfields hA1 and hR) occupies part of the main high–low–high frequency gradient centered on HG (Baumann et al., 2013; Langers and van Dijk, 2012; Moerel et al., 2012). Therefore, we interpret the octave-tuned locations observed on HG as included within human PAC. In this region, the sound representation followed the human percept rather than the linear increase in the sounds' frequency content and thereby it contributes to a complex and relatively abstract sound representation.

This conclusion conflicts with a strictly hierarchical view of auditory processing. Hierarchical models of auditory perception suggest that lower processing levels such as the PAC are limited to low-level acoustic feature analysis (Rauschecker et al., 1995; Wessinger et al., 2001). Processing complexity is proposed to increase when moving towards anterior and lateral locations (e.g., anterior and middle STG; Rauschecker and Scott, 2009), and in these regions, a more abstract and perceptual sound representation may emerge (Belin et al., 2000; Binder et al., 2000; Warren et al., 2003). While our results conflict with a strictly hierarchical view of auditory processing, they add to the accumulating evidence that the PAC—the earliest auditory cortical region—is much more than a simple sensory feature detector. For example, recent studies showed that 25–50% of A1 neurons in the awake mammal were shown to be unresponsive to simple tones and instead to respond only to a complex combination of sound features (Sadagopan and Wang, 2009), that feature tuning in A1 neurons is strongly modulated by context and task demands (David et al., 2012; Fritz et al., 2003), and that early cortical levels are involved in creating an abstract representation of speech sounds (Formisano et al., 2008). Together, these results suggest that auditory regions as early as the primary auditory cortex are more than simple sensory feature detectors and instead contribute to “perceptual” sound representations. Beyond PAC, octave-tuned locations included middle and lateral HS bilaterally, middle STG and PT/posterior STG bilaterally, and anterior STG (mainly in the right hemisphere). Based on these observations, we suggest that a spatially distributed pathway extending both anteriorly and posteriorly from PAC preserves a representation of pitch chroma.

Future directions

The existence of a biological substrate for the percept of pitch chroma does not imply that these filters are inborn and unchanging with experience. In fact, it is entirely feasible that these finely tuned neuronal populations, and accordingly the octave percept, change and mature with sound exposure early in life. Consequently, it would be interesting to evaluate whether similarly tuned neuronal populations can be observed in young children. Furthermore, exploring brain plasticity by investigating musicians is of interest, as such studies could reveal whether with training other musical intervals may become equally hard-wired in the brain. Beyond octave tuning, it would be fascinating to explore how other types of fine-grained spectral tuning may contribute to auditory perception. In a recent review, a view was put forward in which finegrained frequency tuning underlies the emergence of an abstract sound representation (Wang, 2013). Specifically, it was suggested that a fundamental organizational principle of the auditory cortex is based on harmonicity. Harmonically tuned neural populations may function to extract the pitch and harmonic structures from a complex sound. A future challenge would be to explore whether and how the harmonically tuned populations in human auditory cortex could support such a task.