Emergence of Rich-Club Topology and Coordinated Dynamics in Development of Hippocampal Functional Networks In Vitro

Abstract

Recent studies demonstrated that the anatomical network of the human brain shows a “rich-club” organization. This complex topological feature implies that highly connected regions, hubs of the large-scale brain network, are more densely interconnected with each other than expected by chance. Rich-club nodes were traversed by a majority of short paths between peripheral regions, underlining their potential importance for efficient global exchange of information between functionally specialized areas of the brain. Network hubs have also been described at the microscale of brain connectivity (so-called “hub neurons”). Their role in shaping synchronous dynamics and forming microcircuit wiring during development, however, is not yet fully understood. The present study aimed to investigate the role of hubs during network development, using multi-electrode arrays and functional connectivity analysis during spontaneous multi-unit activity (MUA) of dissociated primary mouse hippocampal neurons. Over the first 4 weeks in vitro, functional connectivity significantly increased in strength, density, and size, with mature networks demonstrating a robust modular and small-world topology. As expected by a “rich-get-richer” growth rule of network evolution, MUA graphs were found to form rich-clubs at an early stage in development (14 DIV). Later on, rich-club nodes were a consistent topological feature of MUA graphs, demonstrating high nodal strength, efficiency, and centrality. Rich-club nodes were also found to be crucial for MUA dynamics. They often served as broker of spontaneous activity flow, confirming that hub nodes and rich-clubs may play an important role in coordinating functional dynamics at the microcircuit level.

Introduction

Graph theoretical analysis has provided a compelling body of evidence that neuronal systems at the macroscopic scale exhibit complex topological properties. Whole-brain graphs derived from diffusion tensor imaging, functional magnetic resonance imaging, or electroencephalography have indicated that brain graphs have a hierarchical, modular structure, with low average shortest path lengths between all pairs of the network, high average nodal clustering, and a few high-degree nodes or hubs (Bullmore and Sporns, 2009).

Recently, it was demonstrated that the structural network of the human brain has a “rich-club” organization (van den Heuvel et al., 2011). This complex topological feature implies that highly connected nodes are more densely interconnected with each other than expected by chance (Colizza et al., 2006). It has also been reported that the rich-club is a relatively high-cost component of brain networks: the wiring cost or connection distance was greater between rich nodes than between less well connected nodes in the periphery and rich-club nodes had higher levels of metabolic energy consumption than peripheral nodes (Collin et al., 2014). In this context, it has been argued that maintaining such a network component may be the result of a trade-off between biological cost and topological value in brain network evolution, i.e., rich-clubs may confer advantages to the brain's computational performance (Crossley et al., 2013; Senden et al., 2014).

There is also growing evidence for functional network hubs at a cellular scale (Yu et al., 2008; Shimono and Beggs, 2014). Using two-photon calcium imaging and post hoc morphological classification of cells to probe the mechanisms of spontaneous synchronization in rodent hippocampal networks in vitro, it was demonstrated that some glutamatergic and GABAergic cells contained an above average number of “functional connections,” i.e., high statistical dependencies between their firing activity (Bonifazi et al., 2009). Stimulation experiments further confirmed the role of GABAergic hub cells for orchestrating dynamic synchronous network oscillations. It is tempting to speculate that a specific class of these cells may actually be organized in a rich-club (Cossart, 2014). Experimental evidence in favor of the idea that hub cells form distinct subpopulations and an elite group in mature networks comes from studies that used genetic fate mapping. Results indicated that some cells preferentially connect to each other, if they share similar birthdates (Picardo et al., 2011) or embryonic origin (Deguchi et al., 2011).

Cultures of dissociated neurons have been recognized as an attractive model system to probe self-organizational properties of neuronal cell assemblies and thereby better understand the complexity of brain networks (Shein-Idelson et al., 2011). There is now evidence for the emergence of complex network architectures, such as small-worldness, in more mature neuronal networks in vitro (Downes et al., 2012). Applying graph metrics previously tested at the macroscale of brain connectivity, we investigated the role of hubs and rich-clubs during network formation in dissociated hippocampal cultures. Using inter-electrode coupling during spontaneous multi-unit activity as a metric of functional connectivity, we find that rich-clubs emerge early in development and later on represent an important building block of mature network topology and dynamics.

Materials and Methods

Overview

The rationale of the present study was to quantify the growth and topological structure of neuronal functional networks during periods of high spontaneous activity in the first 4 weeks in vitro. Using weekly multi-electrode array recordings in dissociated primary hippocampal cultures, we observed that spontaneous network-wide activity of cultures emerged after 10–14 days in vitro (DIV) which is in line with previous studies (Chiappalone et al., 2006; Wagenaar et al., 2006). Raw extracellular activity of all electrodes/cultures and their spectral properties were examined carefully and had to pass a stringent quality control to be included in further analyses. Recordings with excess line noise on multiple channels on one recording day were excluded. This resulted in a longitudinal dataset (14–28 DIV, n = 6) and a dataset from more mature networks at 28 DIV (n = 10). Functional connectivity was estimated as inter-channel cross-covariance between each pair of electrodes during sequences of high multi-unit activity (MUA). We thresholded the cross-covariance matrix to construct graphs representing functional network organization during each burst of MUA and analyzed the complex topological properties of these networks. We then investigated the relationships between network topology and developmental age and between topology and synchronized dynamics of neuronal cultures.

Multi-electrode array culture preparation

Primary cultures of dissociated hippocampal neurons were prepared from embryonic day (E) 17–18 mice of either sex. Cells at this developmental stage can be assumed to be postmitotic, i.e., cells are fully differentiated and incapable of undergoing further division (Götz and Huttner, 2005). Hippocampi were dissected from E17.5 mouse embryos (two to four, pooled) and transferred to papain (10 units/ml; Worthington) for 22 min at 37°C. Cells were manually dispersed in DMEM containing 10% v/v fetal bovine serum and centrifuged twice at 400 × g for 3.5 min; any organizational structure or connectivity of cells present at E17–E18 was destroyed during this step. The final pellet was resuspended in Neurobasal (NB)/B27 supplemented with 0.5 mm glutamine (Invitrogen), and dissociated cells were seeded in the center of poly-d-lysine/laminin-coated multi-electrode arrays (MEAs) containing 600 μl full Neurobasal medium at a density of 310 ± 130 cells/mm² (mean ± SD; n = 10 cultures; cell count at 2 DIV). Zero-evaporation lids (Potter and DeMarse, 2001) were fitted and the MEAs housed in tissue culture incubators maintained and humidified at 37°C and 5% CO₂/95% air. At 3–4 DIV, cultures were fed by replacing 200 μl medium with prewarmed, fresh full Neurobasal medium. Cultures were subsequently fed using the same method after each recording, equating to a one-third medium change twice per week.

Pharmacology.

At more mature stages of development (28 DIV), TTX control experiments were performed. TTX was applied by replacing 1/10th volume (60 μl) of medium with 10 × solution (in NB/B27) to give a final concentration of 1 μm.

Electrophysiological recording and preprocessing

Recording setting.

Recordings started at 7–8 DIV and continued during the first 4 weeks of development (7, 10, 14, 17, 21, 24, and 28 DIV). Ten minutes of spontaneous extracellular neuronal activity in 10 cell cultures was recorded by a MEA system supplied by Multi Channel Systems (60MEA200/30-Ti, 59 titanium nitride electrodes, 30 μm diameter, 200 μm spacing, internal reference electrode). Assuming recording sensitivity within a 15 μm radius around the electrode (Brewer et al., 2009), on average one to three neurons contributed to the signal of each electrode. The signal was sampled at 25 kHz and stored using a 64-channel data-acquisition board (MC Card; Multi Channel Systems) and the acquisition software MC Rack (Multi Channel Systems). For all further analysis, data were converted into a MATLAB-readable format (The MathWorks) using the MC Data Tool (Multi Channel Systems). The first minute of each recording was discarded from analysis, allowing cultures to stabilize.

Burst detection.

To test overall comparability of our dataset with previous studies, we searched developing cultures for population bursts (i.e., repetitive spiking across multiple electrodes of the array). The broadband extracellular signal was bandpass filtered (third-order Butterworth, 600–8000 Hz) and thresholded to detect extracellular spike waveforms. A spike detection threshold of 5 × SD below background noise was calculated for each channel separately with an imposed 2.0 ms refractory period after each detected spike. As indicated by previous studies (Wagenaar et al., 2006), spike waveforms were observed to occasionally overlap and hence spike sorting of the data was not attempted. Population bursts were defined by the following three-step approach. First, spike times were downsampled to 1 kHz resolution and activity of all electrodes averaged over windows of 10 ms into one vector. This vector was then searched for clusters of activity (<60 ms inter-event interval). If activity within clusters occurred on at least six electrodes and contained at least 50 spikes, a population burst was defined. Bursts closer than 200 ms were merged. The majority of cultures showed population bursts at 14 DIV, hence all our analyses started from this day onward.

MUA sequence detection.

Functional connectivity was calculated on the filtered extracellular signal during periods of high MUA, which we will here refer to as “‘MUA sequences’.” To detect MUA sequences, all signals were first filtered (500–3000 Hz), downsampled (1 kHz), rectified, and summed over all electrodes into one vector (similar to the previously described burst detection scheme). This vector was then mean subtracted and individual peak detection thresholds used to detect activity peaks (minimum peak height: 5 × SD above the average MUA signal; peak-to-peak distance: 50 ms; MATLAB function: findpeaks). MUA sequence start and end times were defined as the zero-crossings of the population vector before and after the respective peak(s). For subsequent functional connectivity analysis, we extended sequence windows to 80 ms, ensuring that the detected peak kept its central position in the sequence and that activity on the boundaries (i.e., the time between onset, or offset, and respective zero-crossings of the MUA signal) remained below a second lower bound threshold (minimum peak height × 0.5). Filtering operations were performed using default settings of the FieldTrip Toolbox (http://www.ru.nl/neuroimaging/fieldtrip/).

Spectral properties.

A time-frequency analysis of the spectral properties of extracellular neuronal activity during bursting activity was estimated using a continuous wavelet transform and by applying a bank of Morlet wavelets (frequency range: 4–100 Hz in 2 Hz steps; Torrence and Compo, 1998). Development of overall broadband power over recording DIVs was computed for two functionally distinct broadband signals, the frequency range of LFPs (4–100 Hz), and the frequency range of MUA (500–3000 Hz; MATLAB function: bandpower).

Connectivity analyses

The term functional connectivity generally refers to the covariation of fluctuations in neural activity recorded from multiple sites (Aertsen and Gerstein, 1985). A great variety of methods has been proposed to estimate the spatiotemporal organization of spontaneous synchronous activity using multi-electrode recordings of in vitro slices (Beggs and Plenz, 2003; Gireesh and Plenz, 2008; Pajevic and Plenz, 2009; Carmeli et al., 2013) and dissociated neurons (Chiappalone et al., 2006; Wagenaar et al., 2006; Bettencourt et al., 2007; Srinivas et al., 2007; Ham et al., 2008; Raichman and Ben-Jacob, 2008; Sun et al., 2010; Downes et al., 2012; Maccione et al., 2012). Most of these studies used either the firing profiles of extracellularly derived spiking neurons or related population dynamics in the LFP as the basis for their analyses. However, there is currently no gold standard for optimal estimation of functional connectivity at the microscale.

In the present study, we calculated functional connectivity of developing primary hippocampal cultures during MUA sequences. MUA was estimated by the high-frequency component of the extracellular signal (500–3000 Hz; Einevoll et al., 2007, 2013). Restricting functional connectivity analysis to activity during MUA sequences assured that time series were as wide-sense stationary as possible (Downes et al., 2012), and that transient functional networks were sufficiently large to be characterized using graph theory. Coupling of filtered multi-electrode signals was estimated by calculating the normalized inter-channel cross-covariance (MATLAB function: xcov). The cross-covariance is the cross-correlation function of the two mean-subtracted input signals x and y (and lag l). Connectivity strength R was defined as the maximum cross-covariance value within a lag of ±15 ms. We excluded values at zero-lag to mitigate potential spurious correlations caused by volume conduction, i.e., to limit the possibility of two electrodes picking up activity from the exact same neuronal source. Symmetric all-to-all association matrices were estimated for each MUA sequence separately. Analysis of MUA functional connectivity circumvents the problem of picking specific thresholds for the extracellular signal, as one would do for single-unit detection, and further avoids dealing with varying spike waveforms across maturation or spike-sorting issues associated with overlapping waveforms (Harris et al., 2000; Bar-Gad et al., 2001; Pazienti and Grün, 2006; Wagenaar et al., 2006; Baltz et al., 2010). We note, that neither a reconstruction of network activity at single-cell resolution, nor a reconstruction of the synaptic connectome from the observed activity patterns, was in scope of the present study. Future studies should also test to what extent periods of lower activity, currently excluded from our analysis, contain complementary information on the underlying functional network organization.

Significance of functional connectivity and thresholding schemes.

Transforming an all-to-all association matrix into an MUA graph requires testing for the significance of connections. This step has to be carefully balanced with the assumptions underlying network comparisons, if applicable.

First, basic functional connectivity metrics (degree, density, and size of largest connected component) were calculated across a range of absolute thresholds (range of absolute thresholds: 0.05–1.0, in steps of 0.05; calculated for each MUA sequence) removing all connectivity weights below a fixed threshold value. Basic connectivity metrics were estimated on the overall MUA graphs and averaged over all absolute thresholds to quantify changes across developmental age.

Second, complex topological metrics (rich-club, modularity, and small-worldness) were calculated for the largest connected component of MUA graphs derived from proportionally thresholded matrices (range of proportional thresholds: 2–40% density, in steps of 2%; calculated for each MUA sequence). Proportional thresholding and normalization by randomized surrogate graphs allowed testing for the consistency of metrics across a range of network densities, and improved comparability between MUA graphs.

To ensure consistency over development and to calculate the edge age of mature networks, average functional connectivity was benchmarked against a set of surrogate data derived from a simple block permutation scheme (Malmersjö et al., 2013). In brief, for each MUA sequence individual electrode time series were split at a randomly chosen time point t. Resulting blocks were swapped, cross-covariance recalculated, values pooled over all MUA sequences, and the 95th percentile derived. The common significance threshold for average connectivity was the mean of the 95th percentile coefficients, averaged over all cultures and days.

Graph metrics

Graph theory was used to characterize graph topology over development for MUA functional connectivity of each detected MUA sequence and connectivity averaged over all MUA sequences. In the following paragraphs, we describe in detail which metrics were calculated.

Basic connectivity metrics.

Global MUA functional connectivity strength was defined as the mean of all connection weights R (calculated separately for each sequence). Nodal strength was defined as the sum over R for each node i. Further metrics on overall networks included the average degree (mean of the number of connections linked to each node), network density (percentage of realized connections), and size of the largest connected component (ratio of the number of connected nodes to the maximal possible size of the network).

For the largest connected component, we calculated nodal clustering coefficient (the number of triangular connections between node i's nearest neighbors divided by the maximal possible number of such connections), path length (the minimum number of edges to get from node i to node j), nodal efficiency (inverse of the mean of the minimum path length of a node i and all other nodes), and betweenness centrality (fraction of shortest paths between any two nodes in the network that pass through node i). To estimate similarity of MUA functional connectivity, we calculated pairwise Spearman correlations between edge vectors derived from the upper triangle of the 59 × 59 cross-covariance matrix across all MUA sequences.

Hubs and hub-score.

Previous studies already introduced the concept of hubs at the microscale of brain connectivity, suggesting the existence of hub neurons (Morgan and Soltesz, 2008; Bonifazi et al., 2009; Sun et al., 2010). Hub nodes are generally referred to as a subset of nodes demonstrating above average centrality in the network, such as a high number of edges or nodes with short average path length. In addition to this classic definition, we here define a “hub-score” for the centrality of nodes over time. For functional connectivity of all selected MUA sequences, we first estimated four nodal metrics (nodal strength, betweenness centrality, local efficiency, and participation coefficient; see description below). In a second step, metrics were averaged over all MUA sequences and ranked, and it was determined whether nodes belonged to the top 20% within each category. Finally, results were summarized in a hub-score, ranging from 0 to 4 (for nodes that belonged to the top 20% of all four categories). Hub-scores were tested against a null distribution of values derived by randomly shuffling and averaging nodal hub affiliations (1000 iterations). Nodes with consistently high hub-scores (>99th percentile of surrogate data) were defined as average hubs. The hub-score metric was calculated for graphs derived from MUA functional connectivity thresholded by an absolute weight threshold (median + 1.5 × SD above pooled connectivity weights of each sequence).

Modularity.

Modular community structure of MUA graphs was assessed by a standard community detection algorithm (Blondel et al., 2008). For each MUA graph the modularity index Q was calculated, describing how well the network can be separated into subdivisions of nonoverlapping partitions, by maximizing the number of within-module edges and minimizing the number of between-module edges. In addition to assessment of MUA graph community structure, the role of individual nodes in intermodular and intramodular connectivity was calculated, using the participation coefficient P and the within-module degree z (Guimerà and Amaral, 2005). The participation coefficient P of node i is as follows:

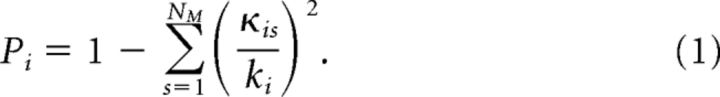Here κ_is is the sum of all edges linking node i to all other nodes of module s; k_i is the degree of node i. A node i with P_i close to 1 has many connections to other modules in the network, whereas P_i close to 0 means maximal within-module connectivity of node i. The within-module degree z-score Z_i measures how well node i is connected to other nodes in the module to which it belongs:

κ_i is the number of links of node i to all other nodes of the module s_i node to which i belongs, κ̄_si is the average over all nodes in the module s_i, and σ_ksi is the SD of κ in module s_i (Guimerà and Amaral, 2005).

Small-worldness.

Networks demonstrate a small-world organization if the ratio of the normalized clustering coefficient (γ), defined as C/C_random, is larger than 1; the ratio of the normalized path length (λ), defined as L/L_random, approaches 1; and the ratio γ/λ = σ is therefore >1 (Watts and Strogatz, 1998; Humphries and Gurney, 2008). C_random and L_random represent the average clustering coefficient and average path length of a set of randomly rewired surrogate graphs (100 iterations), with the same size and degree distribution as the original network (Maslov and Sneppen, 2002). Of note, the present study estimated clustering and path length (and respective surrogates) only for the largest connected component of MUA graphs. Results calculated on functional connectivity estimated for each MUA sequence were further compared with results from functional connectivity averaged over MUA sequences.

Rich-club.

This is the main analysis of the study aimed at characterizing the core properties of MUA graphs. An MUA graph G was defined as having a rich-club organization, if the hub nodes of G were more strongly connected with each other than expected by their high degree k alone (Zhou and Mondragón, 2004; Colizza et al., 2006). For binary connectivity matrices, the rich-club coefficient Φ at a specific k level is calculated by first removing nodes with degree ≤ k from the network and then computing the ratio of all extant connections between nodes to the total number of all possible connections between them as follows:

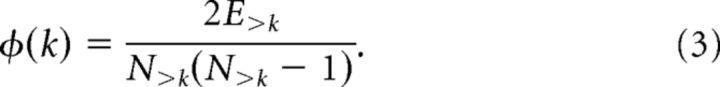Rich-club coefficients are normalized by comparing them to appropriately randomized surrogate networks, assuring that those networks were connected and had comparable degree distributions and degree sequences (Maslov and Sneppen, 2002). In the present study, each rich-club coefficient was normalized against 100 surrogate networks. For each k level a normalized rich-club coefficient Φ_norm (k) was calculated by dividing Φ (k) by an average Φ_random (k). Significance of Φ_norm (k) was tested at each k level by comparing Φ (k) to a distribution of Φ_random (k) values derived from surrogate network analysis:

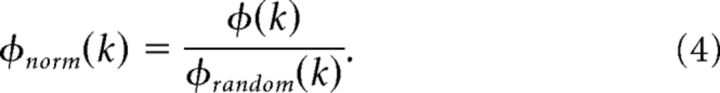MUA rich-club organization was also benchmarked by comparison to model graphs constructed by a “preferential attachment” growth rule (Barabasi and Albert, 1999), here referred to as the BA model. Starting with two nodes initially, BA model networks were constructed by iteratively attaching new nodes to already existing nodes with the probability of connection weighted by their total degree k, until graphs reached a size of 59 nodes (corresponding to the maximum number of nodes an empirical MUA graph could have). For simplicity, we only compared BA models at one connection density (10%) with mature MUA graphs (28 DIV).

Development of rich-clubs.

We observed that functional connectivity and graph topology of cultures underwent substantial variations—even between MUA sequences of the same recording day. To allow characterization of rich-clubs across development, we hence defined the most consistent “average rich-club” for each network. For each sequence, we first derived graphs by thresholding MUA functional connectivity (single-weight threshold: median + 1.5 × SD above pooled connectivity weights of each sequence), then picked the maximal Φ_norm (k) and classified nodes as either belonging to the rich-club or the periphery. In a second step, nodal affiliations were averaged to measure the consistency of rich-club memberships for each node. The significance of rich-club affiliation was tested against a null distribution of values derived by randomly shuffling and averaging nodal rich-club memberships over time (1000 iterations). Nodes with highly consistent rich-club membership, significantly exceeding surrogate data (99th percentile cutoff), were defined collectively as the average rich-club. Connectivity strength of the average rich-club nodes was tracked back in time and compared with the average connectivity strength of peripheral nodes that were not consistently members of the average rich-club. To estimate connectivity growth, we fitted four parameter logistic models to average connectivity of rich-club and peripheral nodes over development, using the following equation (MATLAB function: fit):

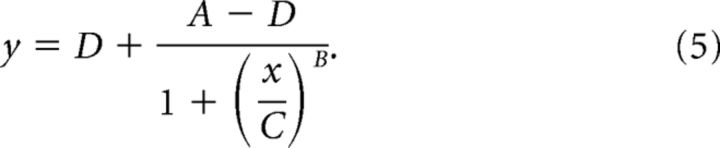A defines the lower asymptote, B the Hill's slope between the bottom and top of the curve (referring to the steepness of the curve), C the inflection point on the curve (i.e., the point where the curve changes direction), and D the upper asymptote. In an alternative approach, less dependent on the choice of a maximal Φ_norm (k) or number of rich-club nodes, we collated average MUA functional connectivity over days in vitro and calculated relative edge age as a function of connectivity strength at 28 DIV. MUA functional connectivity at each recording day was averaged over 50 sequences and thresholded by a common significance threshold (mean of the 95th percentiles of the surrogate data).

MUA flow analysis

There is now a large body of literature that investigated the temporal propagation dynamics of neuronal activity measured via local field potentials and repetitive spike sequences (Abeles and Gerstein, 1988; Beggs and Plenz, 2003; Ikegaya et al., 2004; Hahn et al., 2010; Sun et al., 2010; Priesemann et al., 2013, 2014). Here we make a first attempt toward the integration of the temporal propagation of activity during MUA sequences and graph topology. We therefore combined propagation dynamics, later referred to as “temporal flow profiles”, with nodal graph topological metrics observed during each MUA sequence (defined by a fixed window length of 80 ms). First, temporal flow profiles were defined as an ordered temporal sequence consisting of electrode peak times, T_max, of electrodes that showed at least some minimum level of MUA (amplitude deflection at T_max > 2). Electrode position within the temporal sequence was determined by estimating relative ranks among all included electrodes. Similarity of temporal flow profiles was estimated by pairwise Spearman correlation. Temporal propagation structure of each MUA sequence was subsequently binned, assigning electrodes to three broad temporal classes: electrodes that demonstrated high activity early on in the MUA sequence were termed “leaders” (T_max before or equal to 33rd percentile of temporal flow values), electrodes that showed highest activity in close proximity to the relative mean of electrode peak times were termed “brokers” (T_max between 33rd and 66th percentile), and electrodes with a late peak in MUA in the sequence were termed “followers” (T_max after 66th percentile). To relate temporal profiles with key topological metrics, we calculated MUA graph topology (using a threshold of median + 1.5 × SD above pooled connectivity weights of each sequence) and derived the percentage of rich-club nodes classified as leader, broker, or follower nodes for each MUA sequence.

Statistical analysis

All statistical analyses were performed using SPSS (Version 20) or MATLAB (The MathWorks). Longitudinal development across days in vitro was tested using repeated-measures ANOVA, including only cultures that passed quality control criteria on all five successive recording days. Two-tailed Wilcoxon signed rank tests were used for node statistics, in particular for the comparison of rich-club and peripheral nodes and nodal dynamics. Graph metrics and surrogates for binary networks were calculated using algorithms of the Brain Connectivity Toolbox (Rubinov and Sporns, 2010). BA model networks were constructed using MATLAB code described previously (Bounova and de Weck, 2012). For comparison of functional connectivity metrics over development we restricted analysis to 50 MUA sequences per culture. Error bars in figures represent SEM, unless stated otherwise.

Results

Development of spontaneous activity

The present study followed the development of neuronal activity in dissociated primary hippocampal neurons over the first 4 weeks in vitro. Apparently, randomly occurring single-spike activity was observed as early as 7 DIV. More organized, longer lasting epochs of repetitive, synchronous neuronal activity across multiple sites, i.e., population bursts (Fig. 1C), emerged later and were detected in most cultures from 14 DIV onward. We found a main effect of age on the frequency of population bursts (repeated-measures ANOVA: longitudinal dataset, n = 6 cultures; F_(4,20) = 6.51, p = 0.002; Fig. 2A). Spectral analysis of electrophysiological signals during epochs of population bursts (Fig. 1E) demonstrated rhythmic fluctuations across a range of low frequencies of the local field (4–100 Hz) as well as prominent high-frequency extracellular spike waveforms. Overall, there was a significant increase in broadband spectral power in the LFP frequency range (F_(1.1,5.4) = 23.41, p = 0.004; Fig. 2B), but not in the MUA frequency range (500–3000 Hz), as a function of age.

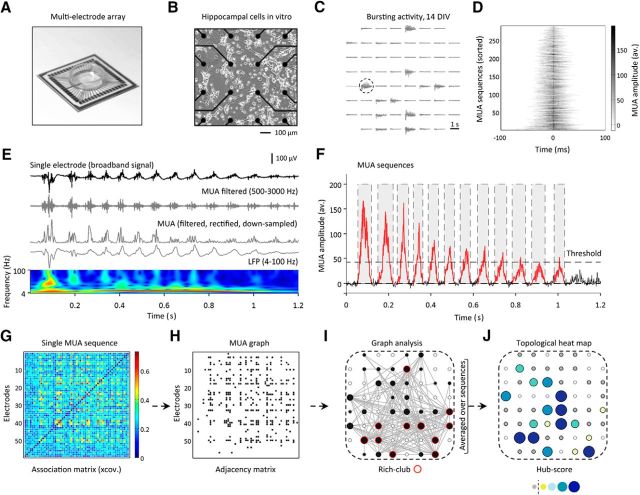
Figure 1.

Analysis of in vitro neuronal networks using MEAs. A, Example MEA used for recording of spontaneous neuronal activity of hippocampal cells in vitro. B, Zoom in on the 16 most central electrodes and cells at 7 DIV. C, Cultures exhibited a great repertoire of spontaneous bursting activity from 14 DIV onward. Traces depict the extracellular signature of a single population burst at 14 DIV (broadband signal). D, Functional connectivity was calculated during epochs of high MUA (“MUA sequences”). Average MUA temporal waveforms (summed over all electrodes) are shown for explanatory MUA sequences of varying duration; MUA sequences were centered according to their respective maxima (±100 ms). E, Depicts the broadband time series, the filtered MUA signal (500–3000 Hz), the rectified and downsampled MUA signal (1 kHz), and the LFP (4–100 Hz) of the channel and epoch marked in C. A continuous wavelet transform of the LFP signal demonstrates rhythmic oscillations at lower frequencies. F, MUA sequences were detected on an average time series, containing the filtered, downsampled, and rectified MUA signal summed over all electrodes. The average time series was mean subtracted and MUA sequence start and end times defined as the zero-crossings before and after the detected peak(s) (peak threshold height: 5 × SD above the average MUA signal). For functional connectivity analysis, we used MUA sequences defined by a window length of 80 ms. G–I, Full functional connectivity matrix for a single MUA sequence (G), the same matrix after thresholding (H), and the corresponding MUA graph in physical MEA space (I). J, Hub structure of MUA sequences was summarized in a topological heat map showing that some nodes had consistently high hub-scores over multiple individually variable sequences of multi-unit activity.

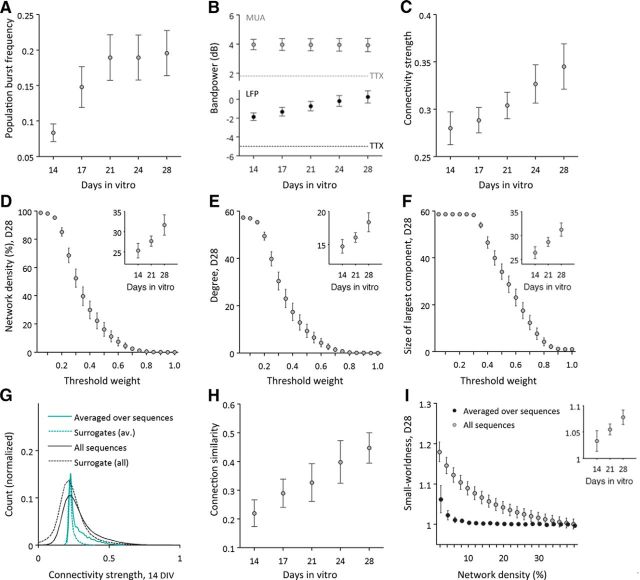
Figure 2.

Developmental changes in MUA functional connectivity. A, All cultures demonstrated regular bursting activity and the frequency of population bursts increased strongly until 21 DIV. B, At all times, spectral power in the MUA (gray) and LFP (black) frequency range was found to be stronger than power of 28 DIV control recordings with TTX (dashed lines). Overall bandpower of the LFP frequency range increased with development. C, MUA functional connectivity also increased significantly with age. D–F, Basic network metrics of overall MUA graphs were computed over a range of absolute thresholds. Large graphs depict metrics of cultures at 28 DIV as a function of thresholds, with weight thresholds ranging from 0.05 to 1. Overall MUA graph density (D), degree (E), and size (F) of its largest component increased significantly with maturation (depicted for 14, 21, and 28 DIV in the insets of each part). G, Functional connectivity at 14 DIV, both averaged over and separately for all MUA sequences, was significantly stronger than surrogate connectivity data calculated on shuffled MUA time series. H, Functional connectivity demonstrated variations across MUA sequences, but became significantly more (self-)similar with development. I, Functional connectivity of neuronal cultures also demonstrated a small-world configuration that was >1 for a range of connection probabilities, but less pronounced for connectivity averaged over MUA sequences.

To confirm that observed population bursting activity and MUA sequences were actually mediated by action potentials, we performed control analyses on cultures at 28 DIV treated with TTX. Pharmacological treatment largely diminished spontaneous activity [n = 3 cultures; LFP power (before/after TTX; mean ± SD): −3.53 ± 1.38 dB/−5.02 ± 1.22 dB; MUA power: 2.10 ± 0.24 dB/1.80 ± 0.36 dB; Fig. 2B], and neither population bursts nor organized MUA sequences could be detected. The reported developmental changes in MUA functional connectivity parameters are therefore likely to represent changes in neuronal function rather than originating from nonbiological sources.

Development of functional connectivity

To quantitatively describe the formation of neuronal functional connectivity with development, we estimated lagged inter-channel cross-covariance over MUA sequences for each culture and each recording day in vitro. The spatiotemporal structure of MUA functional connectivity, estimated by pairwise Spearman correlations between all edge weights across all detected MUA sequences (for each recording day/culture), varied strongly in young cultures [14 DIV (mean ± SD): 0.21 ± 0.11], but similarity increased steadily with maturation (n = 6 cultures; F_(4,20) = 7.96, p = 0.001; Fig. 2H). Over development, recordings from all neuronal cultures also demonstrated a robust increase in functional connectivity strength (F_(1.4,6.9) = 9.14, p = 0.015; Fig. 2C). Maturation of MUA functional connectivity was paralleled by increases in overall graph density (n = 6 cultures; repeated-measures ANOVA; F_(1.3,6.7) = 7.27, p = 0.027; Fig. 2D, inset), degree (F_(1.3,6.7) = 7.27, p = 0.027; Fig. 2E, inset), and size of the largest connected component (F_(1.4,6.8) = 10.28, p = 0.012; Fig. 2F, inset). Inter-electrode coupling of MUA time series thereby deviated significantly from connectivity estimates computed on shuffled MUA time series (14 DIV, Wilcoxon signed rank test: p = 0.031; Fig. 2G).

The main analysis on developmental changes in MUA topology was estimated over a range of proportional thresholds (averaged over 2–40% connection density) and MUA sequences with a fixed window size of 80 ms. MUA graphs demonstrated increases in modularity (Q/Q_random: F_(4,20) = 4.30, p = 0.011; data not shown) and small-worldness (σ > 1) across a range of network densities (Fig. 2I, large graph); the increase of σ with age, however, was not significant (Fig. 2I, inset; F_(4,20) = 1.60, p = 0.21). Small-worldness of mature networks (28 DIV) was more pronounced for functional connectivity of individual MUA sequences, rather than for connectivity averaged over MUA sequences (n = 10 cultures; Wilcoxon signed rank test: p = 0.013; Fig. 2I).

Development of hub architecture and rich-club

Most MUA graphs were found to have a clique of hub nodes that demonstrated strong connectivity early in development (14 DIV), which maintained a central position in MUA graph topology throughout network evolution [Spearman correlation coefficients over individual culture's hub-scores (mean ± SD): 0.73 ± 0.06; Fig. 3A,E]. Graphs derived from MUA functional connectivity also demonstrated a rich-club organization (Fig. 3B–D). Normalized rich-club coefficients tended to decrease with development (Φ_norm averaged over 2–40% densities and k-levels; F_(1.3,6.3) = 6.21, p = 0.040; Fig. 3C), and were found to be less prominent, if estimated on average connectivity instead of connectivity of single MUA sequences at 28 DIV (average over density thresholds; Wilcoxon signed rank test: p = 0.001; data not shown). Results on development of rich-club topology, as reported here for the largest connected component of MUA graphs, were highly consistent with results for comparable metrics calculated on the overall networks.

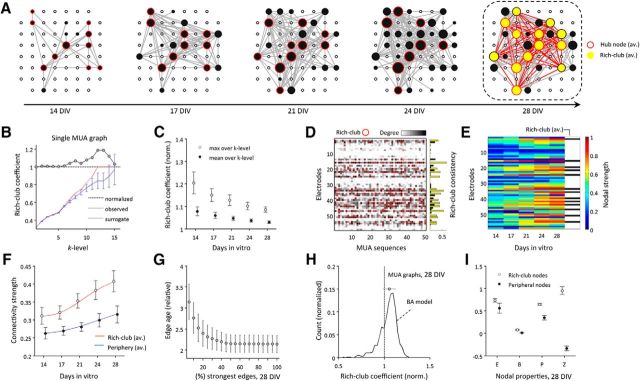
Figure 3.

Rich-club organization of MUA functional connectivity. A, Display of averaged functional connectivity during the first 4 weeks in vitro. For visualization purposes, connectivity at 28 DIV was thresholded with a high absolute weight threshold (median + 1.5 × SD); the same weight was used to threshold connectivity of all previous recording days. Depicted node size is proportional to the degree of average MUA connectivity; yellow nodes indicate the average rich-club at 28 DIV. B, Rich-club organization derived for MUA functional connectivity of a single MUA sequence. C, Normalized rich-club coefficients tend to decrease over development; depicted rich-club coefficients are averaged over a range of proportional thresholds (2–40% connection density). D, The nodes affiliated to the MUA rich-club varied across sequences; red circles indicate rich-club nodes derived from the maximal normalized rich-club coefficient. A rich-club consistency cutoff was used to define the average rich-club (yellow bars), and to separate stable rich-club nodes from nodes that were only occasionally classified as rich-club (black bars). E, Tracking back in time how connectivity strength of mature (average) rich-clubs developed, we found that hub nodes that end up in the mature rich-club were likely to form their strong connectivity early in development. F, To quantify differences in growth trajectories, logistic models were fitted to development of connectivity of nodes belonging to either the average rich-club or periphery. Members of the mature (average) rich-club demonstrated earlier and faster growth of connectivity than more peripheral nodes. G, Strongest average connectivity at 28 DIV also scaled with edge age, mirroring principles similar to what would be expected by a rich-get-richer network growth rule (H). H, Depicts normalized rich-club coefficients (averaged over k-levels) for all MUA graphs at 28 DIV and BA model networks, both at 10% connection density. I, Rich clubs of mature MUA graphs (28 DIV) also comprised nodes with significantly higher efficiency (E), betweenness centrality (B), participation coefficient (P), and higher within-module degree z-score (Z) than nodes of the periphery. B, H, and I show mean values ± SDs.

Mature average rich-clubs (28 DIV) comprised nodes with significantly higher nodal strength (n = 10 cultures; Wilcoxon signed rank test: p = 0.005), efficiency (p = 0.005), betweenness centrality (p = 0.005), participation coefficient (p = 0.005), and higher within-module z-score (p = 0.005; Fig. 3I) than peripheral nodes. We note that the compared nodal topological metrics were positively correlated with each other [Pearson's correlation between all average nodal metrics (mean ± SD): 0.70 ± 0.18].

Having defined a consistent average rich-club at 28 DIV, we also investigated its development in more detail by tracking back in time to delineate the history of each average rich-club node from the first recording session in the experimental series (Fig. 3E,F). Nodes that were destined to become part of the average rich-club in maturity were typically the first nodes in the array to demonstrate strong connectivity (Fig. 3A,E). Quantifying growth of mature average rich-clubs by logistic models (Fig. 3F), we found that connectivity of mature rich-club members also demonstrated a steeper [Hill's slope (B): 3.66 (average rich-club) vs 2.66 (periphery)] and earlier increase in connectivity strength (inflection point (Fig. 3C: 3.67 vs 5.51) compared with connectivity of peripheral nodes. Likewise, strongest connections in mature networks were found to be older than peripheral edges (Fig. 3G). Finally, we compared rich-club organization of 28 DIV MUA graphs (n = 10 cultures; values averaged over all k-levels; 50 graphs per culture) with rich-club organization as observed in a set of BA model networks (1000 realizations; 10% connection density; 59 nodes). MUA functional connectivity demonstrated similar average rich-club coefficients as model networks (Fig. 3H), but less strong variability. Direct statistical comparison between networks, however, was hampered due to the varying size of MUA graphs.

Dynamics of mature rich-clubs

Developing primary hippocampal cultures demonstrated MUA of varying spatiotemporal complexity. The majority of more mature MUA sequences spread over the array in a wave-like manner (Fig. 4A). To further quantify the dynamical signatures of observed activity, we defined “temporal flow profiles” by tracking the relative peak time of (active) electrodes during each MUA sequence. We then compared temporal flow profiles across all sequences by calculating pairwise Spearman correlations (Fig. 4C). Similarity analysis revealed distinct, yet overlapping classes of temporal dynamics. Averaging over multiple MUA sequences clearly diluted the fine spatiotemporal structure inherent to most of these activity patterns (Fig. 4B). The relatively short length of recordings in the present study, however, limited a more detailed analysis of subclasses of MUA sequences and their variability.

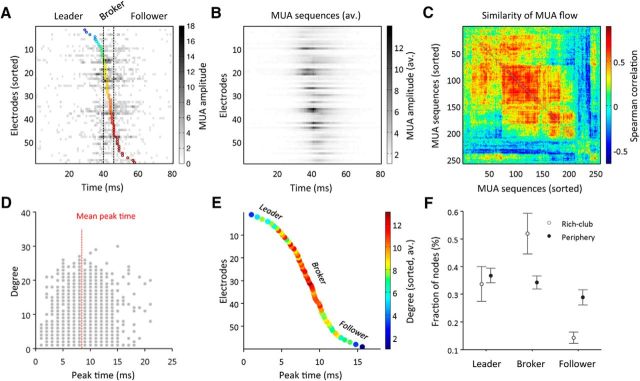
Figure 4.

Analysis of MUA propagation and rich-club dynamics. A, MUA propagated in varying spatiotemporal sequences over the MEA. Flow of MUA during these sequences was estimated by tracking the exact time when activity peaked in each electrode. Depicts the “temporal flow profile” for a single MUA sequence; the coloring of each circle indicates the respective peak time detected for each electrode. B, C, Similarity analysis across temporal flow profiles indicated that MUA sequences were not identical, but could be grouped into different classes of spatiotemporal dynamics. The similarity matrix in C was reordered to group more similar sequences in closer proximity. Averaging MUA over multiple sequences still revealed the predominant flow of activity, but clearly diluted finer patterns. D, E, To test for a potential relationship between MUA dynamics and graph topology, we combined temporal flow profiles with nodal graph topological metrics. We found that nodal degree of MUA graphs was highest for electrodes located in a broker position, i.e., near the center of the MUA propagation chain. D, Depicts the relationship between electrode peak times and nodal degree over 50 MUA sequences of a single culture at 28 DIV. The average temporal flow-to-degree relationship (of the same culture) is demonstrated in E; coloring indicates the average nodal degree. F, Concurrent analysis of MUA temporal dynamics and graph topology demonstrated that rich-club hubs were among the nodes that were most frequently classified as brokers of spontaneous activity. F, Shows mean values ± SDs (n = 10 cultures).

To test potential links between MUA temporal dynamics and transient organization of functional connectivity, we combined the information about electrode peak times (i.e., temporal flow profiles) with nodal graph topological metrics for each MUA sequence (using a fixed window length of 80 ms to define each sequence). We found that nodal degree was highest for electrodes located in close proximity to the relative mean of peak times in the propagation chain (Fig. 4D). Compared with nodes in this broker position, initiation sites or leaders of activity (i.e., electrodes which peaked early in the MUA sequence), as well as followers (i.e., electrodes that peaked late in the MUA sequence), demonstrated on average lower connectivity (Fig. 4E). Interestingly, rich-club members comprised the majority of nodes that were classified as brokers of spontaneous activity (n = 10 cultures; Wilcoxon signed rank test: p = 0.005; Fig. 4F). Conversely, peripheral nodes were significantly more often classified as followers (p = 0.005).

Discussion

The present study investigated spontaneous activity of developing neuronal networks derived from dissociated E17–E18 mouse hippocampal neurons, using MEA recordings in vitro. In line with previous research, cultures developed (1) rich patterns of neuronal dynamics over the period of 7–28 DIV, with functional network growth manifesting in (2) an overall increase in functional connectivity strength, degree, density, and size (14–28 DIV). MUA graphs demonstrated (3) the early presence of hubs and a rich-club organization in functional connectivity, indicating a nontrivial community structure among hub nodes. Connectivity of mature average rich-clubs was found to be (4) significantly older than connectivity of peripheral nodes, suggesting that graphs evolve similar to models of preferential attachment growth. Finally, members of the rich-club were also proportionally more likely to be classified as broker nodes (5), routing spontaneous neuronal activity. We speculate that rich-club connectivity constitutes a critical topological component in the formation of microcircuits, representing a self-organized architecture for orchestrating neuronal activity in mature networks.

Spontaneous activity in developing neural networks

From 14 DIV onward, most cultures examined in the present study exhibited a mixture of activity patterns, comprising few isolated high-amplitude units and epochs of massively parallel MUA. Correlated spontaneous activity has been described as a common feature of many developing neuronal networks and suggested to contribute to the establishment and refinement of efficient mature microcircuits, such as sensory maps and motor circuits (Spitzer, 2006; Blankenship and Feller, 2010; Feldt et al., 2011; Egorov and Draguhn, 2013; Kirkby et al., 2013).

In agreement with previous reports, we found a significant increase in recurrent synchronous spiking activity (“population bursts”) with maturation (van Pelt et al., 2004; Chiappalone et al., 2006; Wagenaar et al., 2006), and an increase in broadband power in the frequency range of the local field potential (Gireesh and Plenz, 2008). In the developing hippocampus, emergence of global, synapse-driven, “giant depolarizing potentials” (GDPs) has been described at the end of the first postnatal week (Ben-Ari et al., 1989; Crépel et al., 2007). GDPs are proposed to coincide with early formation of functional synaptic connections and outgrowth of axons and dendrites shortly after birth (Minkwitz, 1976; Ben-Ari, 2001). GDPs in immature hippocampal networks were suggested to rely on the excitatory action of immature GABA transmission (Ben-Ari, 2002), and can be blocked by ionotropic glutamate and antagonists of GABA_A receptors (Leinekugel et al., 1997; Allène et al., 2008). The occurrence of recurrent spike sequences across multiple electrodes in immature circuits, as observed in this study, hence very likely reflects activity accompanying the formation of structural synapse ensembles of cells (Abeles and Gerstein, 1988). Having reported an increase in overall similarity of MUA sequences with age, the present study also provides evidence for the emergence of an increasingly efficient and stable synaptic backbone of connectivity in more mature cultures. However, results also indicate that MUA sequences are likely to be organized in subfamilies of functional dynamics with precise temporal structures (Beggs and Plenz, 2004; Sun et al., 2010). The exact mechanisms and driving forces behind initiation of such distinct temporal complexes and their spatiotemporal orchestration within neuronal networks require further experimental investigation and new modeling efforts (Ellender and Paulsen, 2010; Orlandi et al., 2013).

Development of functional connectivity

Our analysis focused on the development of neuronal functional networks in vitro, in particular the emergence of hubs and rich-club connectivity. Functional connectivity was calculated on a frequency band closely related to spiking activity (500–3000 Hz). This method advantageously circumvented spike-sorting issues commonly associated with classification of single-unit activity across multiple recordings. A key challenge to graph analysis of functional connectivity remains to decide on a reliable benchmark for significance tests of functional connectivity. This becomes of even greater importance when graph analysis is applied to developmental settings, with new connections forming, connection weights and projection directionality changing, and global network structure adapting to endogenous or exogenous factors. We demonstrated that connectivity during MUA sequences is significantly stronger than surrogate data at 14 DIV (and thereafter) and we estimated key network metrics across a range of connection densities to avoid analytical biases (potentially) caused by the choice of threshold. In this context, it is also important to acknowledge that structural network formation starts even before neuronal networks demonstrate their typical spiking activity—with growing axons connecting cells structurally and communicating via gap junctions. Quantitatively testing the development of in vitro synaptic connectivity, a recent study demonstrated that cultures of rat hippocampal and cortical neurons start responding to external electrical stimulation already at around 2 DIV, and then rapidly develop toward a cohesive network within the first 5 days after plating (Soriano et al., 2008). For E17 or E19 cultures, the same study reported a fully developed “giant component” at around 5 DIV. Putting our results in context of these findings suggests that functional connectivity patterns, as observed for the developmental period of the present study, are snapshots of a structural (synaptic) network that is still “under construction” and that increasingly becomes functional with maturation (Nakanishi and Kukita, 1998). The coexistence of observed patterns could also imply some sort of metastability or intrinsic mechanism that explores the repertoire of activity states inherent to the network (Sasaki et al., 2007). It may further indicate that, although local synaptic connectivity is suggested to become dense in adulthood (Braitenberg and Schüz, 1998), functional connectivity orchestrated on top of a subset of structural connectivity remains sparse—keeping the cost of functional information processing low (Bullmore and Sporns, 2009). Rich-club nodes acting as brokers in neuronal communication may not only enable efficient transfer of information across the network, but also play an important role in switching between different network states.

Complexity in developing neural networks

A key question for modern systems neuroscience is whether modeling systems, as used in this study, will help to better understand the ontogenetic and phylogenetic evolution of the brain's complexity. Results of our study confirm previous reports that generic mechanisms of neuronal self-organization and network formation may indeed be observed in this experimental setting (Shein-Idelson et al., 2011). As found on the macroscale of the brain (Achard et al., 2006), we confirm a modular, small-world architecture with high nodal clustering for networks of functional connectivity at the microscale of neuronal cultures in vitro (Bettencourt et al., 2007; Pajevic and Plenz, 2009; Gerhard et al., 2011; Downes et al., 2012).

It is noteworthy that the developmental scenario observed here, in which clusters of neurons become functionally active, more connected, and progressively globally integrated, does not necessarily imply that topological complexity emerges from an originally random network organization (Gritsun et al., 2012). In line with this reasoning, a small-world network organization was recently reported to be present even before brains become fully operational (e.g., in preterm brains of neonates; van den Heuvel et al., 2014). In this context, it is tempting to speculate that there are intrinsic genetic programs that drive basic network layouts by preconfiguring “connectivity blueprints” required for the subsequent development of more specific functionality of brain circuits (Sur and Rubenstein, 2005). Removal of some structural randomness inherent to neuronal connectivity at birth, however, most likely takes place throughout maturation via pruning and activity-dependent refinement of connectivity.

The present study also confirmed the presence of hubs in early neuronal development (Bonifazi et al., 2009; Varier and Kaiser, 2011). We add to the literature that these hubs are likely to be organized in rich-clubs, a structure that has been described at the macroscale of the human brain (van den Heuvel and Sporns, 2011), and for other nervous systems (Towlson et al., 2013). rich-clubs were maintained throughout maturation, suggesting that these nodes may have a key developmental role. Mature rich-clubs comprised not only nodes with disproportionally stronger connectivity strength and degree, but were also shown to be of great importance for routing of spontaneous activity flow in the network. Rich-club nodes show pivotal similarities with GABAergic hub neurons (Bonifazi et al., 2009). Future studies may further investigate their role in modulating oscillatory activity and classifying sensory data into behaviorally and computationally tractable information (Rowland and Moser, 2014). Hub nodes, preferentially connected within a rich-club subnetwork, demonstrating complex neuronal morphologies and maintaining long-range connections among each other, may represent an organizational feature both microscales and macroscales of brain connectivity have in common (Beul et al., 2014; Buzsáki and Mizuseki, 2014; Scholtens et al., 2014).

Conclusion

The present study aimed at investigating the role of hubs and rich-clubs throughout functional network development using functional connectivity during episodes of high spontaneous neuronal activity of dissociated primary hippocampal neurons in vitro. Emergence of functional connectivity manifested in a significant increase in average connectivity strength, degree, density, and network size. Functional connectivity graphs demonstrated high clustering and a modular small-world organization with a pronounced rich-club organization, which was central to the networks. Hubs, comprising the mature rich-club, connected early, demonstrating structural similarities to network models grown by a rich-get-richer rule. Moreover, rich-club nodes of mature networks frequently acted as brokers for spontaneous multi-unit activity, suggesting a role of rich-clubs for orchestrating coordinated activity in the network.

Notes

Supplemental material and datasets used for this article are freely available at https://github.com/MSchroeter/Rich_club_topology_in_developing_neuronal_networks. This material has not been peer reviewed.