ϒ Spike-Field Coherence in a Population of Olfactory Bulb Neurons Differentiates between Odors Irrespective of Associated Outcome

Abstract

Studies in different sensory systems indicate that short spike patterns within a spike train that carry items of sensory information can be extracted from the overall train by using field potential oscillations as a reference (Kayser et al., 2012; Panzeri et al., 2014). Here we test the hypothesis that the local field potential (LFP) provides the temporal reference frame needed to differentiate between odors regardless of associated outcome. Experiments were performed in the olfactory system of the mouse (Mus musculus) where the mitral/tufted (M/T) cell spike rate develops differential responses to rewarded and unrewarded odors as the animal learns to associate one of the odors with a reward in a go–no go behavioral task. We found that coherence of spiking in M/T cells with the ϒ LFP (65 to 95 Hz) differentiates between odors regardless of the associated behavioral outcome of odor presentation.

Introduction

A key question is how sensory systems achieve parallel processing within a neuronal network transmitting different units of information (Christensen et al., 1998; Kayser et al., 2012; Gire et al., 2013b; Panzeri et al., 2014). Early in the olfactory system, spikes of mitral/tufted (M/T) cells appear to convey sharply different units of information (Christensen et al., 1998; Cury and Uchida, 2010; Blumhagen et al., 2011; Doucette et al., 2011; Shusterman et al., 2011; Gschwend et al., 2012; Gire et al., 2013a); spikes precisely locked to the rhythmic sniff cycle are postulated to convey information on odor identity (“what is the odor?”; Davison and Katz, 2007; Cury and Uchida, 2010; Shusterman et al., 2011; Gschwend et al., 2012; Gire et al., 2013a), and changes in spike rate convey information on the differential treatment of the rewarded odor (“is the odor rewarded?”; Doucette et al., 2011; Gire et al., 2013a). However, it is unclear whether these and other features of the odor stimulus are conveyed in parallel by the network of M/T neurons within the olfactory bulb (OB), the first central signal processing area in the olfactory system.

Based on the understanding that the aggregate neural activity that underlies the local field potential (LFP) can be used for segmentation of neuronal activity to extract specific items of information (Ito et al., 2011; Buzsáki and Watson, 2012), we formulate the hypothesis that the LFP provides the temporal reference frame needed to extract information from the spike train of M/T neurons that can be used to differentiate between odors regardless of the associated outcome. To test this hypothesis, we record LFP and M/T cell spiking in go–no go experiments where the mouse learned to respond to one odor (rewarded) and not to an unrewarded odor. In this go–no go experiment, the odors do not elicit a divergent spike rate response at the beginning of the session, but the spike responses become divergent as the mouse learns to differentiate the odors (Doucette and Restrepo, 2008; Doucette et al., 2011). Thus spike rate conveys information on odor reward. We postulate that spike-field coherence provides information to differentiate between odors regardless of associated outcome.

Importantly in the insect olfactory system, when an odor is presented, it induces transient ϒ frequency oscillation in the neural population of the antennal lobe (equivalent to the mammalian OB), and silencing ϒ oscillation interferes with discrimination of closely related odorants (Stopfer et al., 1997; Laurent, 2002; Perez-Orive et al., 2002; Christensen et al., 2003). In mammals, ϒ LFP responses in the OB are thought to carry information on odor identity (Nusser et al., 2001; Beshel et al., 2007; Lepousez and Lledo, 2013; Kay, 2014). In addition, in the θ frequency, the LFP partially follows sniffing (Grosmaitre et al., 2007; Rosero and Aylwin, 2011; Gschwend et al., 2012; Khan et al., 2012), and sniffing has been postulated to provide a temporal basis to extract odor identity (Cury and Uchida, 2010; Shusterman et al., 2011; Wachowiak, 2011; Blauvelt et al., 2013). Finally, neuronal oscillation related to the LFP has been implicated to underlie extraction of information on odor identity (Laurent, 2002; Brody and Hopfield, 2003). Together, these studies raise the question of whether the field potential can be used to read out information on properties such as odor identity when M/T cell spike firing is largely involved in conveying information on whether the odor is rewarded (Doucette and Restrepo, 2008; Doucette et al., 2011). We find that ϒ LFP coherence with M/T cell spiking provides information to differentiate between odors regardless of associated outcome.

Materials and Methods

Animals and tetrode implantation.

We followed methods used previously for OB microarray implantation (Doucette et al., 2011) with modifications for use of tetrodes (Felsen and Mainen, 2008). Briefly male 8- to 13-week-old C57BL/6 mice were anesthetized with an intraperitoneal injection of ketamine (100 mg/kg) and xylazine (10 mg/kg). Mice were implanted with one ground screw inserted 1 mm posterior from the bregma and 1 mm away from the midline, and four tetrodes were inserted in the OB 4 mm anterior to bregma and 0.5 mm lateral from the midline. Tetrodes were lowered to an average depth between 1.8 and 2.0 mm targeting the ventral M/T cell layer (Doucette and Restrepo, 2008). Each tetrode consisted of four polyimide-coated nichrome wires (Sandvik; single-wire diameter, 12 μm) connected to a 16 channel electrode interface board (EIB-16; Neuralynx). Recording was performed during implantation to ensure optimal placement within the ventral M/T cell layer.

For the optogenetic experiments we used OMP-hChR2V mice where the coding sequence for olfactory marking protein (OMP) was replaced with a human codon optimized version of channelrhodopsin-2 (H134R), fused to Venus YFP (Li et al., 2014). The optotetrodes included one glass tube for the optic fiber and four tetrodes that consisted of four polymide-coated nichrome wires (diameter, 12.5 μm; Sandvik) gold plated to an impedance of 0.2–0.4 MΩ. Tetrodes were connected and glass tube was glued through an EIB-16 interface board (Neuralynx). The optotetrodes were implanted targeting the mitral cell layer in the OB determined by M/T cell firing (depth, 1800–2200 μm; Doucette et al., 2011) and sealed to the bone by dental acrylic. Optotetrodes were implanted in nine mice.

All animal procedures were performed under a protocol approved by the Institutional Animal Care and Use Committee of the University of Colorado Anschutz Medical Campus.

In vivo electrophysiological recordings for light stimulation.

We followed the procedures in our previous study (Li et al., 2014). Briefly, during recording, the mouse was freely moving in a chamber (11.6 × 9.7 × 9.4 cm deep). The signals recorded from the tetrodes were sent to a headstage (LP16CH; Tucker-Davis Technologies) and a 16 channel amplifier (Model 3500, A-M Systems; bandpass, 1–5000 Hz, 2000× gain), and were sampled at 24 kHz by a DT3010 analog-to-digital (A/D) card (Data Translation).

Light was delivered via a diode-pumped, solid-state laser (473 nm; Shanghai Laser and Optics Century). The power was measured to be 19.5–21.5 mW for pulses of 5–200 ms. Light stimulation was triggered by the recording program, which sent a signal to a stimulator (Master 8, A.M.P.I.). Temporal parameters were as follows: five light pulses per trial; 10–200 ms pulse duration. Light pulses were presented for 12 trials with an intertrial interval of 20 s, 60 pulses for each duration. Light activation was not synchronized with sniff.

Go–no go and go–go behavioral tasks.

We used instrumental conditioning in freely moving mice in the Slotnick olfactometer (Bodyak and Slotnick, 1999; Abraham et al., 2004; Doucette et al., 2011). Briefly, for go–no go tasks, the water-deprived mice were required to enter the odor port and start licking on the water delivery tube, and obtained water reinforcement after licking this tube for 2 s in trials involving the reinforced odor. When exposed to the unreinforced odor, they quit licking because of the substantial effort required for licking the tube. Presence in the odor port was detected by breaking the light path of a photodiode, and licking was detected by closing a circuit between the water tube and the grounded floor of the cage (Slotnick and Restrepo, 2005). Figure 1A shows an example of monitoring licking, sniffing, and the tetrode signal during the odor exposure trial. As shown in Figure 1B of Doucette et al. 2011, there is a minimal difference in sniffing frequency in the first 2 s after the addition of the reinforced versus the unreinforced odor. All mice were first trained to distinguish 10% isoamyl acetate (v/v; reinforced odor, S+) versus mineral oil (unreinforced odor, S−). The animal's performance was evaluated in blocks of 20 trials (10 reinforced and 10 unreinforced presented at random), and each session included 6–10 blocks. Each block's percent correct value represents the percentage of trials in which the odors were correctly discriminated and associated with the appropriate behavioral action. Once the animal learned to discriminate between isoamyl acetate and air in one to three sessions, they were ready for the go–no go novel odor discrimination task. For novel odor discrimination in go–no go experiments, we used odors that we found stimulated ventral M/T cells in previous work (Doucette et al., 2011). One to three days after the animals performed the “forward” go–no go session, the S+ (rewarded) and S− (unrewarded) odors were reversed in a “reversed” go–no go session. Finally, in go–go experiments, the animal was required to enter the odor port and start licking, and obtained water reward in 70% of trials if they licked for 2 s during exposure to either of the two odors. The following compounds were used as S+/S− odors in the go–no go experiments (or S−/S+ odors in the reversal) and as one of the two odors in the go–go experiments: phenyl acetate/2-butanone, acetophenone/octaldehyde, heptanoic acid/ethyl propionate and 1-nonanol/2-undecanone.

Figure 1.

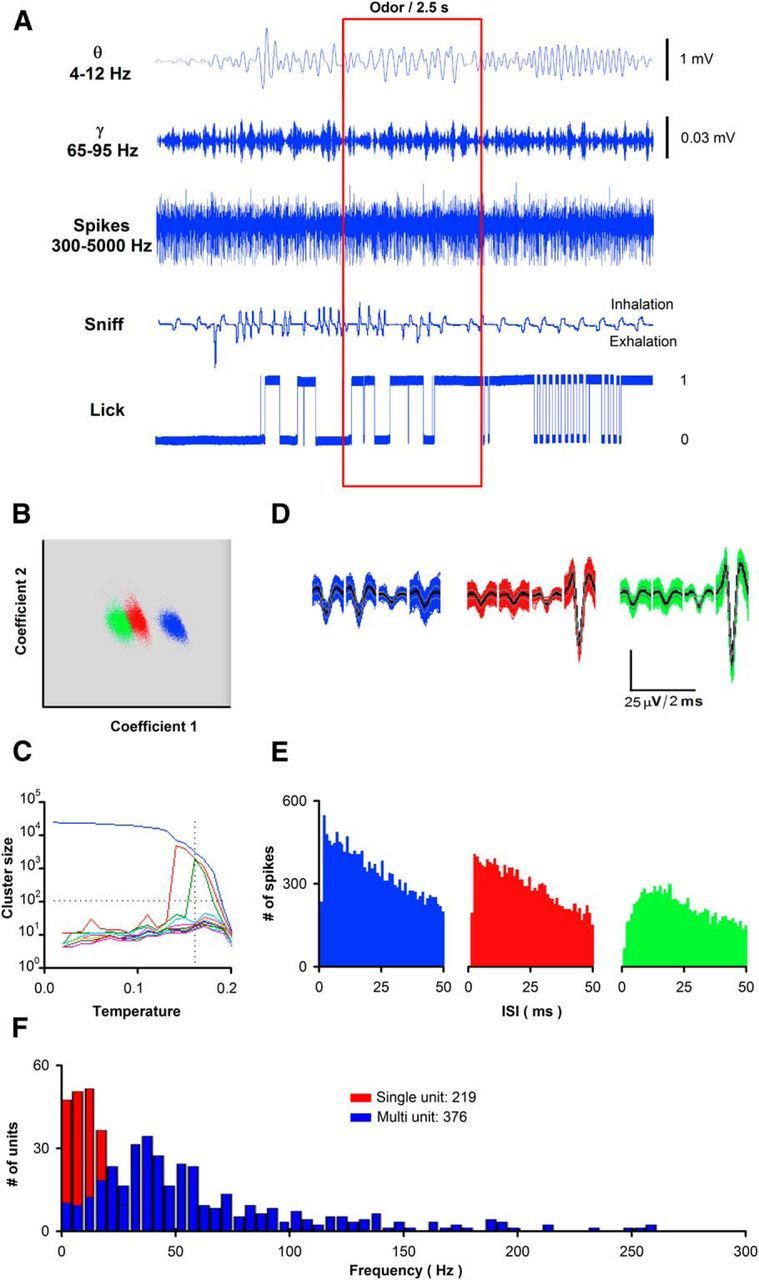
Data acquisition during awake behavior recording. A, Example of data recorded during each trial. Raw data were recorded at 24 kHz. LFP data were obtained by filtering in different frequency ranges. Spike data were obtained by digitally filtering the raw data from 300 to 5000 Hz. Sniff pressure measurement is filtered by >2 Hz. Recording of lick status was performed digitally, ranging from licking at a value of one and no licking at a value of zero. B–E, Example of spike detection and sorting using superparamagnetic clustering (Quiroga et al., 2004) of extracellular voltage recorded in tetrodes resulting in separation of one single unit and two multi units. B, Separation of tetrode spikes shown in D into three different units. The two coefficients were wavelets in two of the electrodes in the tetrode. C, Temperature chosen under paramagnetic clustering to obtain three different units (the meaning of temperature under paramagnetic clustering is explained in Quiroga et al. (2004)). D, Spiking by the three units separated using the data in B. E, Interspike interval histograms for the three units. F, Histogram for single units (red) and multiunits (blue) separated using the superparamagnetic clustering from 76 sessions.

Odor delivery.

We performed measurements of odor delivery using a photoionization detector (mini-PID; Aurora Scientific; Doucette et al., 2011). Odor delivery occurred 0.3 s after turning the odor delivery valve on, and the timing was corrected to zero at the time for odor delivery.

Monitoring sniffing.

Sniffs and unit activity were simultaneously recorded in 10 mice in go–no go and go–go experiments. As described in previous publications (Doucette et al., 2011; Gire et al., 2013a), surgical procedures for cannula implantation were based upon the work of Wesson et al. (2008). Briefly, animals were anesthetized as described above, and lidocaine was injected into the epidermis above the frontal nasal bone as a local anesthetic. An incision was made down the midline, and the skull was cleaned with 3% H₂O₂. Next, a hole was drilled 1 mm anterior to the frontal/nasal fissure and 1 mm lateral from the midline using a dental drill. A hollow cannula made from a cut 21 g needle was then lowered into the hole and fixed in place with nail acrylic. Sniffing was detected by recording intranasal pressure through the implanted nasal cannula connected to a pressure sensor (Model 24PCEFA6G(EA), 0–0.5 psi; Honeywell) via polyethylene tubing. Voltage reporting on pressure transients was amplified 100-fold using a 3000 amplifier from A-M systems, digitized using a DT3010 A/D card from Data Translation in a computer and sampled at 24 kHz. Each sniff was detected as occurring at the point for the transition from exhalation to inhalation.

Recording setup.

The recording setup is as described previously (Doucette and Restrepo, 2008; Doucette et al., 2011; Gire et al., 2013a), with the exception that in this study a screw was used to provide ground at the brain surface to record both LFP and spikes. The output of the four tetrodes was directed to a Tucker-Davis Technologies 1× gain headstage that was in turn connected to an A-M Systems 3600 amplifier. The signal from the four tetrodes was amplified 2000 times before outputting to a Data Translation DT3010 A/D card in a computer. Data were acquired at 24 kHz with custom software written in MATLAB (MathWorks). Sniffing and digitized behavioral events from the Slotnick olfactometer (licks, presence of the mouse in the odor port, and odor on) were also acquired in real time (Fig. 1A).

Offline LFP processing and spike clustering.

Data were filtered digitally with a Butterworth filter from 4 to 100 Hz for LFP and 300 to 3000 Hz for spike detection using the MATLAB filtfilt function with zero phase shift (Fig. 1A). For the LFP, θ was filtered at 4–12 Hz and ϒ at 65–95 Hz, and the LFP signals were averaged per block. Custom software written in MATLAB was used to threshold spikes in each channel at three times the standard deviation. Every thresholded spike (24 points at 24 kHz) was imported into a second program where we clustered the waveforms of similar shape by performing wavelet decomposition and superparamagnetic clustering using the method and MATLAB software developed by Quiroga et al. (2004) as described previously (Doucette et al., 2011; Gire et al., 2013a), modified to process tetrode data. We defined a single unit using the criterion of finding <3% of the spikes in the refractory period of 2 ms in the interspike interval histogram (usually <1% of spikes violated the 2 ms refractory period; Fig. 1B–E). On average, we obtained four multiunits and two single units per experiment (Fig. 1F). Data from single units and multiunits were used for data analysis. Power spectral density of LFP was estimated in MATLAB using methods of Kay and Lazzara (2010). The LFPs recorded from the different electrodes in an implant were averaged per session.

Spike-field coherence.

We estimated coherence to test the relationship between spike firing and LFP (or sniff and LFP). Coherency is a method to estimate at each frequency (f) the extent of amplitude covariation and matching phase relationship between two signals (Jarvis and Mitra, 2001; Womelsdorf et al., 2006). In coherency, the Fourier transforms of the two signals (x and y, e.g., spikes and LFP) are used to calculate multitaper estimates for the spectrum [S_x(f) and S_y(f)] and the cross-spectrum [S_xy(f); calculated as by Womelsdorf et al. (2006))]. Spectra and cross-spectra are averaged over trials before calculating the coherency [C_xy(f)]: C_xy(f) = S_xy(f)/[S_x(f) S_y(f)]^1/2. Coherency is a complex number, and the absolute value is termed coherence and has a value of one if the two signals have substantial phase and amplitude covariation relationship, while the coherence is zero if phase relationship and amplitude covariation do not match at a specific frequency (Jarvis and Mitra, 2001; Womelsdorf et al., 2006). For the assessment of coherence, we used windows of ±500 ms for θ and ± 250 ms for gamma frequency. These windows were moved over the data in steps of 100 or 50 ms, respectively. For each window, we applied mutitaper analysis of coherence involving the multiplication of data segments with multiple tapers before Fourier transformation to achieve optimal spectral concentration. Tapering effectively concentrates spectral estimates across a specified frequency band and allows estimation of the statistical error of coherence. We used a time-bandwidth product of three and five tapers (and using five and nine yielded a similar result; data not shown). Spike-field coherence was calculated using spectra and cross spectra of the spikes and LFP in θ and γ frequencies, and sniff-field coherency was calculated using the LFP and sniff in the θ frequency. The spikes were convolved with a normal distribution (σ = 4 ms). The estimation of coherence with MATLAB was tested using simulated data. The magnitude of the odor-elicited changes of the coherence was in a similar magnitude to changes in the visual system (Womelsdorf et al., 2006). Finally, the measure we used of spike-field coherence is biased by relatively large changes in spike rate (Vinck et al., 2012). However, this is not a problem for the present study because the changes in the firing rate elicited by odors are relatively small (Fig. 2B) and because we find a substantial differential response to odor in spike-field coherence in early blocks in a session, when there are few differential responses to odor in the overall spike response (see Figs. 2D,E, 7B,C).

Figure 2.

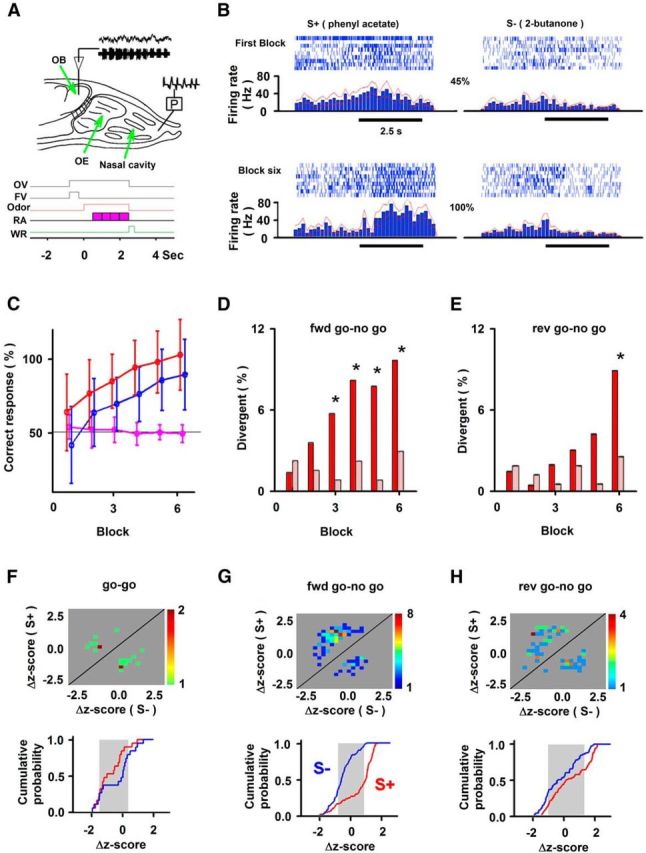
Divergent overall spike responsiveness of M/T cells to rewarded (S+) and unrewarded (S−) odors in different behavioral tasks: forward go–no go (fwd), reversed go–no go (rev), and go–go. A, Setup for the experiment and time course for trials in the odor discrimination task. OE, Olfactory epithelium; P, pressure. Bottom, The odor valve (OV) and final valve (FV) open simultaneously, directing air to exhaust, and later the FV turns off, eliciting the odor on. The animal must lick for the rewarded odor on the water delivery tube for four periods (pink blocks) in the response area (RA). If the animal licks for S+ it receives a water reward (WR). B, Example showing spiking and peristimulus time histograms during the first block and sixth block in the forward go–no go task (each block has ∼10 S+ and 10 S− trials; the best is the block when odors elicit the largest difference in spiking rate). The percentage of correct behavior (45 and 100%) is shown in the middle. C, Percentage of correct behavioral responses in forward go–no go (red; 33 sessions), reversed go–no go (blue; 25 sessions), and go–go (magenta; 18 sessions; mean ± SD) sessions. D, E, Percentage of units responding differentially to S+ and S− for forward (D) and reversed (E) go–no go (red) or go–go (light red) sessions. Asterisks indicate statistical significance (χ², p < 0.05). F–H, Quantification of firing rates in all blocks with differential spike responses for S+ versus S− in go–go (F), forward go–no go (G), and reversed go–no go (H) sessions. Top, Pseudocolor histogram showing the number of differentially responsive blocks with different S+ and S− induced firing rate changes. The firing rate was quantified as the Δz-score: change in firing rate induced by odor stimulation divided by the SD of firing rate before odor addition. Bottom, Cumulative probability for S+ (red) and S− (blue) odors for the Δz-score for the same blocks. Gray shows the average SD in Δz-scores for all odor responses. Values from paired-sample t tests for S+ versus S− in cumulative probability plots are as follows: F, go–go, p > 0.05, t = −1.1, df = 100; G, forward go–no go, p < 0.001, t = 8.3, df = 107; H, reversed go–go, p < 0.05, t = 2.5, df = 71.

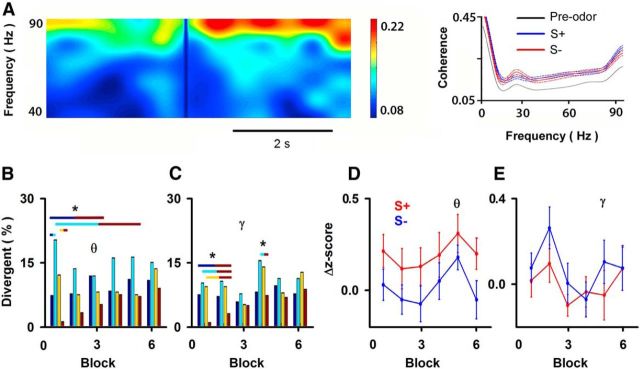
Figure 7.

Spike-field coherence measured in the same sessions as for Figure 2. A, Example of odor-induced change in coherence with pseudocolor showing odor-induced change in coherence in a block with 10 S+ (acetophenone). Right, Average spike-field coherence calculated for 2 s before addition of the odor (black line) or after addition of the rewarded odor (S+, blue line) or the unrewarded odor (S−, red line) for the block including the 10 S+ trials shown on the left. The dashed lines are 1 SEM. B, C, Divergence of coherence (coh) responses to S+ versus S− [dark blue, forward (fwd) go–no go coherence; light blue, reversed (rev) go–no go coherence; yellow, go–go coherence; red, forward go–no go spike (spk) rate (from Fig. 2D). In determining divergence, the spike-field coherence was averaged within a block over either the θ frequency (4–12 Hz; B) or the ϒ frequency (65–95 Hz; C). Asterisks indicate that a χ² test indicated that the percentage of divergent responses differed between the different sessions. D, E, Δz-score for all the units in the study as a function of block number within the session (mean ± SEM). The correlation coefficients (σ) and their p values are as follows: D, θ frequency (4–12 Hz), reinforced odor (S+, blue), σ = 0.04, p > 0.05; unreinforced odor (S−, red), σ = 0.04, p > 0.05; E, ϒ frequency (65–95 Hz), reinforced odor (S+, blue), σ = −0.02, p > 0.05; unreinforced odor (S−, red), σ = −0.05, p > 0.05.

Analysis of odor-elicited changes in firing rate, LFP power, and coherence.

Analysis for odor-induced changes in the rate of firing of neurons, the power of LFP, and coherence was performed using custom-written MATLAB programs tested previously using simulated data (Doucette and Restrepo, 2008; Doucette et al., 2011). Briefly, for each behavioral session, a t test was used to classify a unit as “divergent” within a block when the responses to the rewarded odor and the unrewarded odor were statistically different (see Figs. 2D,E, 4D, 6C,D, 7B,C). The calculated t test p values were corrected for multiple comparisons using the false discovery rate (FDR; Curran-Everett, 2000). FDR is a statistical method used previously by our group (Doucette and Restrepo, 2008) that is suitable for testing significant differences in large data sets and does not require independent data (Benjamini and Yekutieli, 2001, 2005). Using this method, we calculated a p value for statistical significance (pFDR). This is particularly relevant to awake behaving recording, where a subset of the units fire in a related manner. Differences between behavioral sessions (e.g., forward go–no go vs go–go) in each block in the number of units diverging in odor responses for the data in Figures 2, D and E, 4D, and 7, B and C, were tested using χ² corrected for multiple comparisons with FDR.

Figure 4.

Sniff-locked responses of M/T cells to different odors. A, Example of spike firing of an M/T cell aligned along the record of the sniff measured as a change in pressure in the nose. Right, One of the sniffs is shown. The red horizontal line is where the sniff-locked firing rate was determined. B, Pseudocolor displaying the Δz-score for the changes in firing rate elicited by two different odors (S+, top; S−, bottom). Time during the trial is shown in the abscissa, and the ordinate shows the time after the start of inhalation (0–100 ms). C, Examples of discrimination success for the S+ and S− odors in two different M/T cells. The left M/T cell responded differentially to the two odors in the sixth block, but not in the first block. The right M/T cell did not respond differentially to the two odors. D, Percentage of divergent units. The asterisks shows a statistically significant difference between go–no go (dark color) and go–go sessions (light color) tested with χ² and FDR. E, F, Pseudocolor histogram for the Δz-score of the sniff-locked response to the S+ and S− trials in blocks differentially responsive to S+ and S− (E) and the cumulative probabilities for the same blocks (F). The gray background in the cumulative probability graph (F) shows the average SD for the Δz-scores for rewarded and unrewarded odors. A paired-sample t test indicates that the cumulative probability for rewarded odors is different from that for unrewarded odors (p < 0001, t = 8.6, df = 79).

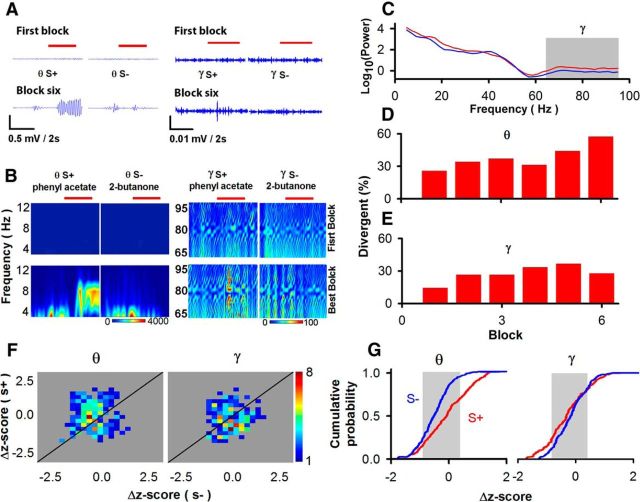
Figure 6.

Responses of the LFP in the OB to odors in the forward go–no go behavioral test measured in the same experiments as for the data in Figure 2, D and G. A, Example showing θ and ϒ LFP responses to rewarded (S+, phenyl acetate) and unrewarded (S−, 2-butanone) odors in the go–no go task. Red lines show when odors were presented. B, Power for the Fourier transform of the θ and ϒ LFP responses in a single block (10 S+ and 10 S− trials). C, Average power spectrum for 10 S+ trials (blue, baseline average for 2 s before odor addition; red, average for 2 s during odor addition). D, E, divergent responses to the rewarded and unrewarded odors for θ (D) and ϒ (E) frequencies. F, G, Pseudocolor histograms for the Δz-score of the θ and ϒ LFP responses to the S+ and S− trials in blocks differentially responsive to S+ and S− (F) and cumulative probability θ and ϒ LFP responsiveness for the S+ and S− trials of LFP (G). The gray background in F shows the average SD for the Δz-scores for responsive and unresponsive odor trials. A paired-sample t test indicated that the dependence of the cumulative probability of the Δz-score for rewards and correct rejections was significantly different for θ (p < 0.001, t = 4, df = 147) but not for ϒ (p > 0.05, t = −0.95, df = 110) frequencies, but values were relatively small compared to the SD (gray background).

To obtain more thorough information and show all the data for the differential responses, the Δz-score was computed for the change in firing rate (see Figs. 2, 4), LFP (Fig. 6), and coherence (Fig. 8). Δz-score was calculated by measuring in each block of 20 trails the change in any of these parameters elicited by odor stimulation for 2 s divided by the SD of the parameter 2 s before odor addition. As in the past (Doucette and Restrepo, 2008), there were no differences in the Δz-scores under the different conditions before the addition of the odor. Figures 2F–H (top), 3A, 4E, 6F, and 8, A, C, and E, report, for blocks that were differentially responsive to S+ and S−, pseudocolor histograms of the Δz-scores for S+ versus Δz-scores for S−. Figures 2F–H (bottom), 3B, 4F, 6G, and 8, B, D, and F, report the cumulative histograms for the Δz-score for either S+ or S−. The difference in the cumulative histograms for S+ and S− was tested with paired-sample t tests. In these figures, the Δz-score was included for blocks where there were different Δz-scores for each block for each unit (block unit) or for each LFP for each unit (block LFP). Table 1 shows the number of block units or block LFPs used in each of these figures. For the behavioral experiments not requiring measurement of sniff (see Figs. 2, 6, 7, 8), the number of animals and sessions are as follows: go–no go forward, 20 animals, 33 sessions; reversed go–no go, 20 animals, 25 sessions; go–go sessions, 5 animals, 18 sessions. For the experiments requiring measurement of sniff (see Fig. 4), the number of animals and sessions are 12 animals and 36 sessions for go–no go sessions, and 3 animals and 12 sessions for go–go sessions.

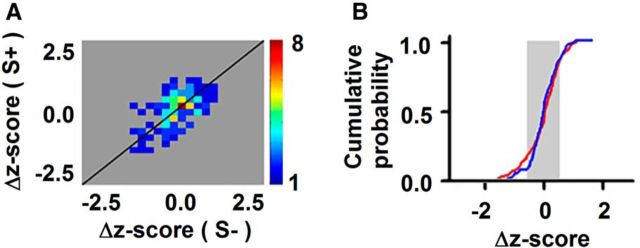
Figure 8.

Pseudocolor histograms and cumulative probabilities of the Δz-scores for the spike-field coherence. Pseudocolor histogram for the Δz-score of the θ and ϒ coherence responses to the S+ and S− trials in blocks differentially responsive to S+ and S−. B, Cumulative probability for the θ and ϒ coherence as a function of the change in coherence elicited by odors in responsive odor (S+) and unresponsive odor trials (S−) in these blocks. In B, the gray background shows the average SD for coherence for all odor trials. The dependence of the cumulative probability on coherence was not different for responsive and unresponsive odors for ϒ, but was different for θ, indicated by paired-sample t test (ϒ, p > 0.05, t = −0.2, df = 115; θ, p < 0.001, t = 4.2, df = 115). C–F, The same items shown in A and B for reversed go–no go (C, D) and go–go [E, F; paired-sample t test, p > 0.05 for go–no go reversed for ϒ (t = −0.2, df = 86) and θ (t = 0.5, df = 182; C, D) and for go–go for ϒ (p > 0.05, t = 0.9, df = 86) and θ (t = −1.6, df = 86); E, F].

Figure 3.

Analysis of spike firing in all forward go–no go sessions for the first block that shows no significant difference for S+ responses compared to S− responses. This figure is relevant to Figure 2G, which shows a similar analysis of spike firing in blocks where there is a statistically significant difference for S+ compared to S−. A, Pseudocolor histogram for the number of responses at different Δz-scores for the first block. The firing rate was quantified as the Δz-score: the change in firing rate induced by odor stimulation divided by the SD of firing rate before odor addition. B, Cumulative probability for S+ (red) and S− (blue) odors for the first block. The gray background shows the average SD for the odor responses to S+ and S− odors in the same block. The S+ cumulative probability does not differ from the S− cumulative probability (paired-sample t test, p > 0.05, t = −0.4, df = 154).

Table 1.

Number of block units with differential responses included in the Δz-score plots for the different figures

Figure/parameter/behavioral experiment	Number of units/LFPs	Number of block units (of block LFP)	Number of block units (block LFPs) with differential responses
Fig. 2F/firing rate/go–go	151	906	19
Fig. 2G/firing rate/forward go–no go	251	1426	108
Fig. 2H/firing rate/reversed go–no go	193	1123	72
Fig. 4E,F/sniff-locked firing rate/go–no go	271	1613	80
No figurea/sniff-locked firing rate/go–no go	105	630	0
Fig. 6F,G/θ LFP/go–no go	33	475	98
Fig. 6F,G/¡ LFP/go–no go	33	475	66
Fig. 8A,B/θ coherence/forward go–no go	251	1426	116
Fig. 8A,B/¡ coherence/forward go–no go	251	1426	87
Fig. 8C,D/θ coherence/reversed go–no go	193	1123	183
Fig. 8C,D/¡ coherence/reversed go–no go	193	1123	112
Fig. 8E,F/θ coherence/go–go	148	888	87
Fig. 8E,F/¡ coherence/go–go	148	888	92

^aNo figure was shown because there were no divergent block units.

In addition, for the go–no go forward session, the overall population responsiveness including data from all units in all sessions was studied by using principal component analysis (PCA; see Fig. 9) as performed previously (Doucette and Restrepo, 2008). Briefly, we calculated the PCA in 0.15 s intervals throughout the trial using either the number of spikes or the ϒ spike-field coherence. These measures were calculated for the 20 trials in the block (10 S+ and 10 S−) for all the units recorded from in all the experiments, and were normalized by dividing by the mean of the measure in the 2 s before odor addition. Then the normalized measures were centered to have mean zero and scaled to have an SD of one. The principal components in each time interval were then calculated using the same algorithm as in the princomp function in MATLAB. The input to princomp for each time interval was these normalized measures entered into a two-dimensional matrix with 20 rows corresponding to the 10 S+ and 10 S− trials and 151 columns corresponding to the units recorded from in all experiments. The output of the PCA in each time interval was a matrix of 20 rows corresponding to S+ and S− trials and 151 columns corresponding to principal component scores.

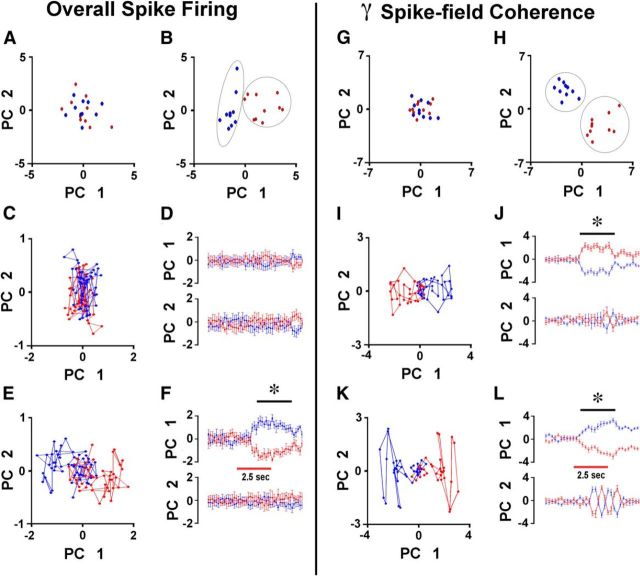
Figure 9.

A–L, PCA of the spike odor responses (A–F) and ϒ spike-field coherence responses (G–L) calculated using data from all the forward go–no go sessions. PCA was evaluated in all trials within the first block (A, C, D, G, I, J) or for a block in the middle of the session (B, E, F, H, K, L). A, B, G, and H show all the first and second PCA scores (PC1 and PC2) for an example of one of the time intervals before (A, G) or during (B, H) the addition of odor in a middle block. C, E, I, and K show the means for the two PC scores calculated at time intervals before and after the addition of odor within a trial during the first block (C, I) or the middle block (E, K). D, F, J, and L show the averages (±SEM) for the first two scores as a function of time within a trial during the first block (D, J) or the middle block (F, L; one-way ANOVA for PC1 in overall spike firing, D, F_(1,378) = 3.4, p > 0.05; F, F_(1,378) = 482, p < 0.001; one-way ANOVA for PC1 in ϒ spike LFP coherence, J, F_(1,218) = 597, p < 0.001; F, F_(1,218) = 864, p < 0.001).

Finally, for spike-field coherence in the go–no go sessions, we apply a linear classifier to decode sensory stimulus from the ϒ spike-field coherence activity of all recorded units (Quiroga et al., 2007; Quiroga and Panzeri, 2009). This was performed in the first and middle 20 trial blocks to decode which odor (rewarded, S+, or unrewarded, S−) was the mouse exposed to on a trial-by-trial basis. For decoding and generating a confusion matrix, the crossval function in MATLAB was used with stratified 10-fold cross-validation using linear discriminant analysis. The input to crossval was the normalized ϒ spike-field coherence for 151 units in nine 0.15 s time intervals starting 0.15 s after odor addition for each of the 20 trials in the block (20 trials by nine time intervals equals 180 entries per unit). In addition, the identity of the odor (S+ or S−) was provided as input.

As described by Quiroga et al. (2007), decoding results were plotted in the form of “confusion matrices.” The values in a given row and column of this 2 × 2 confusion matrix represent the (normalized) number of times a presentation of the S+ or S− odors are predicted to be S+ or S−. If the decoding is perfect, S+ and S− for all trials and the confusion matrix should have entries equal to one along the negative slope diagonal and zero everywhere else. Performance at chance levels should be reflected in a matrix in which each entry has equal probability. Decoding performance was quantified as the percentage of correct predictions, which is the mean of the diagonal of the confusion matrix. For statistical analysis of getting k or more hits by chance, we quantified the number of hits (that is, the average of the diagonal in the confusion matrix) and used a Bernoulli test based on the binomial distribution to obtain a p value (Quiroga et al., 2007). Finally, we determined the dependence of decoding performance on the number of units by repeating the analysis 10 times with different numbers of units. A random permutation of the order of the units was performed before the subset of units was drawn out for each of these runs.

Calculation of responsive and divergent percentages and Δz-scores for sniff-locked responses.

The method of Cury and Uchida (2010) was used to estimate sniff-locked firing. Briefly, using sniff data, the start of each sniff was detected. The spike firing was determined in 12 intervals from −25 to 100 ms after the air entered the nose. Sniff-locked spiking patterns were then calculated as performed by Cury and Uchida (2010) for both the average sniff-locked firing rate and for sniff-locked changes in temporal responses (Cury and Uchida, 2010, their Fig. 1E). In our experiment, we found odor-induced changes in the sniff-locked average rate, and very few sniff-locked changes in temporal responses. Because of this, the data were calculated using sniff-locked average rate. The sniff-locked average rate was calculated within each sniff, and the sniff-locked rate was averaged from trial to trial over the entire time course. This was done on a trial-by-trial basis, generating the sniff-locked firing rate that was used to calculate responsive and divergent percentages and Δz-scores. A template-matching algorithm (Shusterman et al., 2011) was used to evaluate discrimination success.

Results

Overall spiking from M/T cells develops differential responsiveness as the animal learns to lick for the rewarded odor

To simultaneously obtain information on M/T cell responses, LFP, and sniffing, we implanted tetrodes in the OB and recorded sniffing (Figs. 1, 2A). In a go–no go behavioral task, mice were provided water if they licked for 2 s for the rewarded odor (Bodyak and Slotnick, 1999; Abraham et al., 2004; Doucette et al., 2011). Figure 2B shows an example of odor-induced changes in the firing rate that increased as the animal learned to differentiate between odors in a go–no go session. In this figure, data are shown for firing rate in an experiment where the animal responded correctly to 45% of the trials during the first block and 100% of the trials in the sixth block. Importantly, as expected from previous studies (Doucette and Restrepo, 2008; Doucette et al., 2011), when all blocks are surveyed for all sessions as the animal developed differential licking to the odors (Fig. 2C), a fraction of M/T cells developed, in the latter blocks, a differential odor response in the forward go–no go experiments (Fig. 2D, red bars) and also in “reversed” sessions, where the odor that was rewarded in the “forward” session was made unrewarded (and vice versa; Fig. 2E, red bars).

We then tested the response of the units in go–go experiments, where the animals were given water reward for licking in 70% of the trials regardless of which of the two odors was presented. In contrast with the results in the go–no go sessions, where licking for one of the odors but not the other is rewarded, in the go–go experiment M/T cells did not develop a larger differential response to the odors in the latter blocks (Fig. 2D,E, light red bars); a χ² test indicates that in the latter blocks there are statistical differences in the number of divergent responses for go–no go and go–go sessions (p < pFDR; pFDR was >0.02 in Fig. 2D,E; for details of data analysis, see Materials and Methods, Table 1). Thus, differential spiking rate response to the odors increased throughout the session only when odors were differentially rewarded.

In go–no go sessions, units tend to respond to the rewarded odor with increases in firing rate

To further extract information on how the animal was responding in go–no go and go–go sessions, we calculated the Δz-score in each block, defined as the change in firing rate induced by odor stimulation divided by the SD of firing rate before odor addition. We then generated plots to obtain information on how the units respond in blocks where there is a statistically identified differential response to rewarded and unrewarded odors using this Δz-score (for details on statistics, see Materials and Methods, Table 1). The complementary plots were a pseudocolor histogram for the number of blocks where a unit responded differentially with different Δz-scores for rewarded and unrewarded odors (Figs. 2G,H, top) and a cumulative histogram that shows the relationship of the Δz-scores for rewarded versus unrewarded odors for all these differential blocks (Figs. 2G,H, bottom).

These complementary plots showed that odors did not elicit randomly in some M/T units an increase in the firing rate and in others a decrease as expected for odor identification (Yokoi et al., 1995; Mori et al., 1999; Nagayama et al., 2004; Rinberg et al., 2006; Davison and Katz, 2007; Bathellier et al., 2008; Fantana et al., 2008; Khan et al., 2008; Gschwend et al., 2012; Kato et al., 2012). In contrast, for these go–no go experiments, the firing rate tended to increase when the mouse was exposed to the rewarded odor, as shown by a tendency for a positive Δz-score for S+ and a decrease in spiking for the unrewarded odor (a tendency for a negative Δz-score for S−; Fig. 2G,H). Indeed, the cumulative probability of the Δz-score (Fig. 2G,H, bottom) was different for the S+ and S− odors (paired-sample t tests, Fig. 2G, p < 0.001, t = 8.3, df = 107; H, p < 0.05, t = 2.5, df = 71). In contrast, there was a random distribution of Δz-scores for responses to the two odors in blocks where there was no differential response in the go–no go experiments (Fig. 3A,B) and in differentially responsive blocks in the go–go experiments (Fig. 2F). Indeed, paired-sample t test revealed no difference between S+ and S− for blocks where there was no differential response in the go–no go experiments (Fig. 3B; p > 0.05, t = −0.4, df = 154) and in go–go experiments (Fig. 2F, bottom; p > 0.05, t = −1.1, df = 100).

Thus, spike rates of M/T cells convey information on odor reward. However, the M/T cells are expected to convey information to differentiate between odors regardless of associated outcome such as odor identity and odor intensity. Because of this, we sought to determine whether the information to differentiate between odors regardless of associated outcome could be extracted from M/T cell spiking either by the sniff-locked spikes (David et al., 2009; Cury and Uchida, 2010; Shusterman et al., 2011; Blauvelt et al., 2013) or by extracting spikes that are coherent (Womelsdorf et al., 2006) with neuronal activity reflected by the LFP in the olfactory bulb.

Sniff-locked M/T cell firing becomes differentially responsive to odor in the go–no go task, but not in the go–go task

Importantly a fraction of M/T cells have been proposed to carry information on odor identity through sniff-locked transient changes in firing (Cury and Uchida, 2010; Shusterman et al., 2011; Gschwend et al., 2012; Blauvelt et al., 2013). However, it is not known whether sniff-locked M/T cell firing responsive to odor identity (as opposed to odor reward) occurs during learning when there are strong odor reward-induced changes in the overall firing rate (Doucette and Restrepo, 2008; Doucette et al., 2011). Figure 4 shows that during go–no go learning, sniff-locked firing does take place in a subset of M/T cells. Figure 4B is an example showing that there are differential sniff-locked odor responses to the two odors. In addition, Figure 4C (left) shows that for this specific neuron, there is a significant change in odor discrimination success calculated from the changes of spike firing from −25 to 100 ms after the sniff delivers odor (discrimination success is calculated as indicated in the experimental procedures).

Indeed, ∼10% of 271 units responded differentially with sniff-locked responses to the two odors in the go–no go sessions (Fig. 4D, red bar). Importantly, as in overall firing (Figs. 2D,E), for sniff-locked odor-induced changes in firing rate represented by the Δz-score, the rewarded odors tended to elicit responses with more increases in firing than the unrewarded odors (Figs. 4E,F). Indeed, the cumulative probability of the Δz-score (Fig. 4F) was different for the S+ and S− odors (paired-sample t test, p < 0001, t = 8.6, df = 79). In addition, odors did not elicit differential increases in sniff-locked spikes in go–go sessions (Fig. 4D, pink bars). Statistical comparison of the percentages of differential responses to S+ and S− in go–no go divergent sessions and go–go sessions revealed a difference in odor divergence for the last block (Fig. 4D, compare red bars, pink bars), indicated by p < 0.001 (pFDR = 0.008) in the χ² test for the last block. Thus, in the go–no go behavior, the sniff-locked responses follow odor reward.

LFP conveys information to differentiate between odors regardless of associated outcome

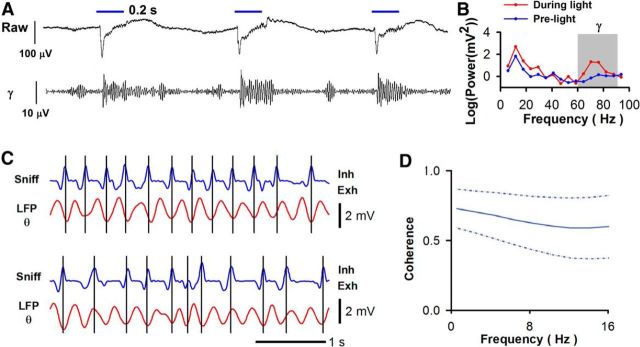
We next determined whether the information to differentiate between odors regardless of associated outcome could be extracted from M/T cell spiking by extracting spikes coherent (Womelsdorf et al., 2006) with OB aggregate neuronal activity reflected by the LFP (Ito et al., 2011; Buzsáki and Moser, 2013). The possibility that the field potential can be used to extract the information carried by M/T cell sniff-locked spike firing is particularly relevant because studies have previously suggested that ϒ LFP (65–95 Hz) responds differentially to odors (Kay, 2014; Martin and Ravel, 2014). Indeed, stimulation with light of the glomerular input in mice expressing channelrhodopsin-2 in the axons of the olfactory sensory neurons elicited a robust ϒ LFP response (Fig. 5A,B). In addition, we also studied θ LFP (4–12 Hz) because it is somewhat, but not always, related to sniffs (Kay, 2005; Grosmaitre et al., 2007; Khan et al., 2012; Manabe and Mori, 2013). Indeed Figure 5C shows examples of the relationship of sniffs and θ LFP, and Figure 5D shows that there was a strong coherence of the sniff and the LFP. As a result we decided to determine, using coherence of LFP and M/T cell spikes, whether the neural activity underlying the LFP can provide a temporal reference to pull out particular information from spikes.

Figure 5.

Dependence of the ϒ LFP on odor input and relation of the θ LFP to sniffs. A, Response of the ϒ LFP to light activation of glomerular input in OMP-hChR2V mice expressing channelrhodopsin-2 in the axons of olfactory sensory neurons. Top, Recording of the LFP with low-pass filtering at 3 kHz. Bottom, LFP filtered in the ϒ range (65–95 Hz). B, Frequency dependence of the LFP power 0.2 s before (blue) and during (red) light exposure of the glomerular layer. C, Examples of the θ LFP and the sniff. D, Coherence for the θ LFP and the sniff (20 sessions). The dashed lines show the SEM.

Figure 6A–C shows examples of typical LFP responses in the θ and ϒ frequencies to rewarded (S+) and unrewarded (S−) odors in the forward go–no go task in the first and sixth blocks. As expected from previous studies (Martin et al., 2004; Kay, 2014), in all blocks, including the first block, there was a significant fraction of LFP θ and ϒ responses divergent to the rewarded and unrewarded odors (Figs. 6D,E). In addition, the change in the power of the LFP elicited by unrewarded and rewarded odors in all blocks where the LFP was different for these two odors took place by both increases and decreases (Fig. 6F). Interestingly, the cumulative probability of the Δz-score for the ϒ LFP when the animal responded to the rewarded (S+) odor was not largely shifted along the Δz-score axis compared to the cumulative probability curve for the unrewarded odor (S−); the shift along the Δz-score axis was much smaller than the SD of the ϒ LFP power (Fig. 6G, gray). Indeed, the cumulative histograms for rewarded versus unrewarded odors were significantly different for θ, but not for ϒ LFP (paired-sample t test for θ, p < 0.001, t = 4, df = 147; ϒ, p > 0.05, t = −0.95, df = 110). The fact that LFP responses were both positive and negative in the Δz-scores in Figure 6, F and G, raises the question of whether coherence of the LFP with spike firing (spike-field coherence; Womelsdorf et al., 2006) could convey information relevant to differentiate between odors, regardless of associated outcome.

Response of ϒ spike-field coherence to odors is consistent with conveying information to differentiate between odors, regardless of associated outcome

Spike-field coherence changes as a function of time during the trials. Figure 7A shows an example where addition of the rewarded odor elicited an increase in a block in coherence in the ϒ frequency. Testing for differences in spike-field coherence with a t test revealed that there were ∼10% of the blocks where the spike-field coherence for the θ or ϒ LFP differed between rewarded and unrewarded odors in go–no go and go–go experiments (Fig. 7B,C). In contrast, the percentage of divergence between rewarded and unrewarded odors for spike-field coherence for the θ or ϒ LFP calculated in the 2 s before odor addition was 0%. As expected for information on features such as odor identity or intensity, which should be conveyed whenever the odor is presented, the odor-induced changes in divergence between rewarded and unrewarded trials in spike-field coherence took place for all blocks including the first block (Figs. 7B,C). Indeed, for the spike-field coherence with the θ and ϒ LFPs, the divergence in the responses between rewarded and unrewarded odors for forward go–no go, reversed go–no go, and go–go sessions (Figs. 7B,C, dark blue, light blue, yellow, respectively) was statistically different from the divergence for the first few blocks for the S+/S− odor-induced divergence of responses in overall spike rate (Figs. 7B,C, red; p < pFDR, pFDR for θ coherence = 0.05, dark blue–red, light blue–red; pFDR for θ coherence = 0.01, yellow–red; pFDR for ϒ coherence = 0.05, dark blue–red, light blue–red, pFDR for ϒ coherence = 0.02, yellow–red). In addition, unlike the behavioral response that increases during the session (Fig. 2C), the Δz-score for spike-field coherence did not tend to change during the session (Figs. 7D,E). Divergence in all blocks including the first block and a lack of a change in the Δz-score is consistent with conveying information to differentiate between odors regardless of associated outcome.

In anesthetized animals where responses of M/T cells to odors through changes in spike rate are clearly elicited by odor identity, the responses are increases in some cells and decreases in others (Yokoi et al., 1995; Mori et al., 1999; Nagayama et al., 2004; Rinberg et al., 2006; Davison and Katz, 2007; Bathellier et al., 2008; Fantana et al., 2008; Khan et al., 2008; Gschwend et al., 2012; Kato et al., 2012). Figure 8, A, C, and E, shows that the coherence responses to the odors were also found to be either increases or decreases. This is in sharp difference with the overall spike rate odor responses, where in the go–no go trials there was a tendency for an increase in Δz-score for the rewarded odor and a decrease for the unrewarded odor (Figs. 2G,H, top). Because of this, on average, the cumulative histograms should overlap for S+ and S−. We studied this issue by plotting the cumulative histograms for Δz-scores for the rewarded (S+) versus unrewarded (S−) odors (Figs. 8B,D,F). For both θ and ϒ spike-field coherence, the variation in cumulative histograms between S+ and S− (red and blue lines) was smaller than the SD of odor-induced changes in spike-field coherence (gray background). However, there was a minor difference between θ and ϒ spike-field coherence. The cumulative histograms were not statistically significantly different between S+ and S− for ϒ spike-field coherence (paired-sample t test, forward, p > 0.05, t = −0.2, df = 115; reversed go–no go, p > 0.05, t = −0.2, df = 86; go–go, p > 0.05, t = 0.9, df = 86). However, the cumulative histograms for S+ and S− were different for θ spike-field coherence for forward go–no go sessions (paired-sample t test, p < 0.001, t = 4.2, df = 115), but not different for reversed go–no go (p > 0.05, t = 0.5, df = 182) and go–go sessions (p > 0.05, t = −1.6, df = 86). Therefore, the lack of a difference in cumulative histograms between the rewarded (S+) and the unrewarded (S−) Δz-scores supports the possibility that ϒ spike-field coherence conveys information to differentiate between odors regardless of associated outcome.

Finally, of the 212 units recorded from in the sixth block of the session, 18 units (8.5%) responded divergently in the overall spike rate, and 22 or 16 units (10.4 or 7.5%) responded divergently in the θ or ϒ spike-field coherence. Of these divergent units, two multiunits and one single unit responded divergently to both the overall firing rate and θ or ϒ spike-field coherence.

ϒ spike-field coherence extracts information on an odor property that is not affected by learning during the go–no go session

To analyze the difference between responses of the rate of spike firing and responses of ϒ spike-field coherence to the odors using all the data, we performed PCA including all sessions (Fig. 9). The first principal component score allows for differentiation of the odor responses when performed on the ϒ spike-field coherence (Fig. 9I–L). Interestingly, this divergent coherence response to the odors takes place not only in blocks in the middle of the session (Figs. 9K,L), but also in the first block (Figs. 9I,J), as indicated by one-way ANOVA for principal component 1 (PC1) in ϒ spike-field coherence (J, F_(1,218) = 597, p < 0.001; L, F_(1,218) = 864, p < 0.001). This is consistent with ϒ spike-field coherence conveying information to differentiate between odors regardless of associated outcome. In contrast, the differential response to the odors in the PCA of the overall rate of spike firing does not take place in the first block (Figs. 9C,D), but does take place clearly in the middle of the session (Figs. 9E,F), consistent with learning during the session to convey information on odor reward through the overall rate of spike firing. One-way ANOVA for PC1 in overall spike firing in the first block (Fig. 9D) is not significant (F_(1,378) = 3.4, p > 0.05), but it is significant in the middle block (Fig. 9F; F_(1,378) = 482, p < 0.001). This is consistent with learning which odor is rewarded.

ϒ spike-field coherence can be used to predict stimulus in the go–no go session

The clear separation of S+ and S− odors in each trial shown in Figure 9H, suggests that a trained observer could predict the odor stimulus based on the ϒ spike-field coherence of the neurons in our study. A linear discriminant decoding analysis was performed to obtain information on whether ϒ spike-field coherence can be used to predict odor stimulus (S+ vs S−) on a trial-by-trial basis in the go–no go experiment with a focus on whether there was a difference between discrimination performance in the first and middle blocks. Figure 10A shows decoding performance in a confusion matrix (see Materials and Methods). The input to the decoding algorithm was the ϒ spike-field coherence values for the first nine 0.15 s time intervals after addition of the odor for all the units recorded in the forward go–no go sessions in the 20 trials in each block (10 S+ and 10 S− trials). The percentages of hits for the first block and middle block were 96.7 and 96.1%, respectively. They are significantly better than chance (p < 10⁻²⁰, Bernoulli test; see Materials and Methods). Figure 10, B and C, shows the relationship of the decoding performance (B) and its p value in the Bernoulli test (C) and the number of units provided to the decoding algorithm. The performance was similar for both the first and middle blocks, and it was better than chance (p < 0.05) with more than five units. This decoding analysis shows that the information in ϒ spike-field coherence can be used to predict the odor stimulus as well in the first block of 20 trials, as in the middle block of the go–no go session.

Figure 10.

Trial-by-trial decoding performance for the ϒ spike-field coherence data in the first and middle blocks of the go–no go experiments. A, Confusion matrix showing the decoding performance for the different stimuli (S+ and S− odors) for the different blocks. B, Relationship of the decoding performance on the number of units whose ϒ spike-field coherence data were provided to the decoding algorithm. C, p values for the data in B calculated using a Bernoulli test. When computed before odor addition, the p values were >0.05. Finally, when evaluated using the overall spike rate, the decoding performance was 55% (p = 0.21) for the first block and 58% (p = 0.16) for the middle block. For chance, the decoding performance was 50%.

Discussion

Our data indicate that the coherence of changes in spiking and oscillatory network activity in the ϒ LFP conveys information to differentiate between odors, regardless of associated outcome, whereas the overall firing rate for M/T cells largely conveys information on differential treatment of the rewarded odor that may encode for odor value or top-down attention to the rewarded odor (Fig. 11). The ϒ spike-field coherence may be carrying information on odor features such as identity or intensity that are detected from the beginning of a go–no go odor-learning session. Alternatively, ϒ spike-field coherence may not change during the behavioral session because it codes for value and reward in a mix of positive and negative coding schemes. Regardless, we find that ϒ LFP coherence with M/T cell spiking provides information to differentiate between odors regardless of associated outcome.

Figure 11.

The diagram shows a model consistent with the results indicating that the firing of action potentials in the MT cells carries information for odor reward (is the odor rewarded?), and an odor feature that carries information to differentiate between odors regardless of associated outcome, which could be odor identity or intensity, is carried by coherence between spike firing and the ϒ LFP. OE, Olfactory epithelium.

In anesthetized animals, M/T cells respond strongly to odor identity through increases or decreases in the firing rate (Yokoi et al., 1995; Mori et al., 1999; Nagayama et al., 2004; Rinberg et al., 2006; Davison and Katz, 2007; Bathellier et al., 2008; Fantana et al., 2008; Khan et al., 2008; Gschwend et al., 2012; Kato et al., 2012). Importantly, the presence of distinct groups for each odor in PCA indicates that in these animals, M/T cells in the OB respond differentially to multiple odorants (Bathellier et al., 2008; Kato et al., 2012). In addition, recording of M/T cell responses in anesthetized animals to intermediate mixtures indicates that representation of an odor can be morphed to the representation of another odor through summation of components (Khan et al., 2008). Thus, studies in anesthetized rodents solidly show that spike firing by M/T cells can carry information on odor identity.

However, in contrast with studies in zebrafish (Blumhagen et al., 2011) and invertebrates (Stopfer et al., 1997; Laurent, 2002; Christensen et al., 2003), experiments in awake mammals indicate that overall changes in M/T cell firing do not necessarily carry information on odor identity. Indeed, the odor-induced changes in firing rate are, in some awake rodent studies, sparse or absent (Rinberg et al., 2006; Davison and Katz, 2007; Gschwend et al., 2012; Blauvelt et al., 2013; Wachowiak et al., 2013), but in other studies there are odor-induced increases or decreases in the overall firing rate of 10–80% of the M/T cells (Doucette and Restrepo, 2008; Fuentes et al., 2008; Doucette et al., 2011; see also Cury and Uchida, 2010; Shusterman et al., 2011). Importantly, changing behavioral paradigms from passive odorant exposure to active odorant exposure during a two-alternative forced choice (2AFC) odor discrimination task elicits changes in the firing rate responses to odors (Fuentes et al., 2008), suggesting that the responses of changes in overall spike firing do not represent odor identity.

Here we provide additional data supporting that in an awake rodent, spike firing in the majority of divergent units does not carry information on odor identity, but rather carries information on odor value or top-down attention to the rewarded odor. Thus, as shown in a previous study (Doucette and Restrepo, 2008), when the two odors are switched from rewarded (S+) to unrewarded (S−) in a go–no go odor discrimination task, the tendency to elicit an increase in firing as a response to the S+ odor switches to a decrease after the reversal (and vice versa) (compare Figs. 2G, forward, and 2H, reversal). This radical switch is not expected for odor identity, but is consistent with the response of a subset of units to a change in odor reward upon reversal. Consistent with conveying information on odor reward when the responses of the overall population of neurons was analyzed by PCA, we found for overall spike firing that there is no divergent PCA response in the first block, but there is a clear differential response for S+ versus S− in a block in the middle of the session (Fig. 9A–F). Finally, we show that if the animal is engaged in a go–go task where both odors are rewarded, the number of neurons responding differentially to the odors with overall changes in spike firing is relatively small (compare go–no go and go–go in Figs. 2D and 2E). These findings indicate that for the majority of divergent units overall spike responses to odors do not carry information on odor identity, but carry information on odor value. Nevertheless, a small number of units responded differentially in all blocks in the go–go task and these units could carry information on odor identity or another odor feature that does not change while learning whether an odor is rewarded (also see Doucette and Restrepo, 2008, their Fig. 4A).

We show that the number of divergent neurons for the overall spiking rate are low at the beginning of the three different task types and that this number greatly increases by block 6 of the go–no go tasks (Fig. 2). This finding could be explained by improved odor discrimination during a discrimination task. However, Doucette et al. (2008) showed in their Figure 6 that a unit that developed an inhibitory response to an unrewarded odor in a go–no go behavioral task developed an excitatory response to this odor when it was made the rewarded odor. That change in the polarity of the response is not consistent with simply improved odor discrimination and indicates that changes in firing rate from the majority of the M/T cells carry information on odor reward. However, this does not rule out that a subset of M/T cells convey information on odor identity through changes in spike rate. In fact, the small number of M/T units that respond to the odor in the go–go experiments could be a subset of neurons that respond to odor identity with a change in firing rate. Indeed, comparison of the pseudocolor histograms for the go–no go tasks (Figs. 2G,H) with that of the go–go task (Fig. 2F) suggests that this small number of mitral cells respond to odors in the go–no go task as well.

The finding that M/T cell spike rates respond to odor value raises the question of whether information to differentiate between odors regardless of associated outcome is conveyed by the M/T cells. Previous studies suggested that sniff-locked M/T cell firing conveys information on odor identity (Cury and Uchida, 2010; Shusterman et al., 2011; Gschwend et al., 2012; Blauvelt et al., 2013). To provide information on whether the sniff-locked spiking conveys information on odor identity in the go–no go and go–go tasks, we measured sniffing and spike firing in these experiments. In the go–no go task, response to the rewarded (S+) odor tended to be an increase in sniff-locked firing, whereas the response to unrewarded (S−) odors tended to be a decrease (Fig. 4F). In addition, there were no sniff-locked differential responses to odors in the go–go task where both odors are rewarded (Fig. 4D). Thus, in these experiments, sniff-locked responses to odors do not carry information on odor identity, but likely carry information on odor value.

In contrast, past experiments studying sniff-locked spike responses to odors suggest that these carry information on odor identity (Cury and Uchida, 2010; Shusterman et al., 2011; Gschwend et al., 2012). The behavioral condition of the mice in these previous studies is different from that in ours. In the experiments of Shusterman et al. (2011) and Gschwend et al. (2012), the animal was exposed to an odor without a behavioral outcome depending on the identity of the odor. On the other hand, in the study by Cury and Uchida (2010), the animals underwent either an active 2AFC behavior where the animals were given water for correct odor choices or a passive task where the animals received water for all odors. It is likely that in these studies the sniff-locked spike firing was carrying information on odor identity because PCA in the study by Cury and Uchida (2010) suggests that there is distinct separation in the principal component space for different odors. However, given that our study clearly indicates that in our behavioral conditions the sniff-locked spike firing does not transfer information on odor identity, future studies should be performed to determine whether sniff-locked spike firing conveys information under certain behavioral demands.

Therefore, in our studies, neither overall spike firing nor sniff-locked spike firing carries information to differentiate between odors, regardless of associated outcome. On the other hand, as in previous studies in rodents (Kay, 2014; Martin and Ravel, 2014), we find that the ϒ LFP is stimulated by olfactory input (Figs. 5A,B) and responds differentially to odors (Fig. 6D). In addition, spike phase synchronization in the ϒ band differs between odorant stimuli for a subset of recorded M/T cells (Fig. 7C). A local or distal readout process that is sensitive to ϒ phase synchronization could use this information to discriminate between or identify odorants. Indeed, analyzing coherence between the ϒ LFP and M/C cell spike firing (ϒ spike-field coherence), we show that a subset of spikes in M/C neurons transmit information that is not affected by associated outcome (Figs. 7, 8). Thus, although overall spike firing in the first block of a go–no go session does not respond differentially to the rewarded and unrewarded odors (Figs. 2D,E), ϒ spike-field coherence responds differentially to the odors in the first block (Fig. 7C). Consistent with this finding, PCA and trial-by-trial decoding of ϒ spike-field coherence shows a clear differential response in the first block in the go–no go task (Figs. 9I,J, 10). These experiments show that ϒ spike-field coherence does not carry information on odor value according to a positive reward-coding scheme as observed for spike rates, and suggests that the ϒ-band phase synchronization of this subset of M/T cell spikes conveys information on a feature such as odor identity or intensity.

Thus, our data indicate that the activity of neuronal populations reflected by the ϒ LFP provides the temporal reference frame needed to decode odor features that do not carry information on odor reward. This odor feature could be odor identity or intensity. The mechanism of downstream readout of these spike-field coherence patterns likely involves comparison of M/T cell spikes with some of the aggregate neural activity conveyed by the LFP. Future studies should examine how this information can be pulled out downstream from the OB and whether ϒ spike-field coherence patterns convey information on odor identity. This will likely take place in downstream signal processing similar to signal processing in the dorsal telencephalon circuit in the zebrafish OB (Yaksi et al., 2009) and is likely to involve the feedback circuit from the piriform cortex because optogenetic activation of this cortical feedback elicits a sustained increase in ϒ spike firing in piriform cortex (Boyd et al., 2012). Future work with optogenetics with the cortical feedback circuit could yield information on the causality of M/T cell ϒ spike-field coherence.