Too old to have children? Lessons from natural fertility populations

Abstract

STUDY QUESTION

Is it possible to construct an age curve denoting the ages above which women are biologically too old to reproduce?

SUMMARY ANSWER

We constructed a curve based on the distribution of female age at last birth in natural fertility populations reflecting the ages above which women have become biologically too old to have children.

WHAT IS KNOWN ALREADY

The median age at last birth (ALB) for females is ∼40–41 years of age across a range of natural fertility populations. This suggests that there is a fairly universal pattern of age-related fertility decline. However, little is known about the distribution of female ALB and in the present era of modern birth control, it is impossible to assess the age-specific distribution of ALB. Reliable information is lacking that could benefit couples who envisage delaying childbearing.

STUDY DESIGN, SIZE, DURATION

This study is a review of high-quality historical data sets of natural fertility populations in which the distributions of female age at last birth were analysed. The studies selected used a retrospective cohort design where women were followed as they age through their reproductive years.

PARTICIPANTS/MATERIALS, SETTING, METHODS

Using a common set of eligibility criteria, large data files of natural fertility populations were prepared such that the analysis could be performed in parallel across all populations. Data on the ALB and confounding variables are presented as box and whisker plots denoting the 5th, 25th, 50th, 75th and 95th percentile distribution of the age at last birth for each population. The analysis includes the estimation of Kaplan–Meier curves for age at last birth of each population. The hazard curve for ALB was obtained by plotting the smoothed hazard curve of each population and taking the lowest hazard within a time period of at least 5 years. This lowest hazard curve was then transformed into a cumulative distribution function representing the composite curve of the end of biological fertility. This curve was based on the data from three of the six populations, having the lowest hazards of end of fertility.

MAIN RESULTS AND THE ROLE OF CHANCE

We selected six natural fertility populations comprising 58 051 eligible women. While these populations represent different historical time periods, the distribution of the ages at last birth is remarkably similar. The curve denoting the end of fertility indicates that <3% of women had their last birth at age 20 years meaning that almost 98% were able to have at least one child thereafter. The cumulative curve for the end of fertility slowly increases from 4.5% at age 25 years, 7% at age 30 years, 12% at age 35 years and 20% at age 38 years. Thereafter, it rises rapidly to about 50% at age 41, almost 90% at age 45 years and approaching 100% at age 50 years.

LIMITATIONS, REASONS FOR CAUTION

It may be argued that these historical fertility data do not apply to the present time; however, the age-dependent decline in fertility is similar to current populations and is consistent with the pattern seen in women treated by donor insemination. Furthermore, for reproductive ageing, we note that it is unlikely that such a conserved biological process with a high degree of heritability would have changed significantly within a century or two.

WIDER IMPLICATIONS OF THE FINDINGS

We argue that the age-specific ALB curve can be used to counsel couples who envisage having children in the future. Our findings challenge the unsubstantiated pessimism regarding the possibility of natural conception after age 35 years.

STUDY FUNDING/COMPETING INTEREST(S)

No external funding was either sought or obtained for this study. There are no conflicts of interest to be declared.

Introduction

Since the general availability of effective contraception in the late 1960s, motherhood has become an issue of personal preferences instead of biology (van de Kaa, 1987). Women could decide to continue schooling and acquire a profession before thinking of having children. One of the consequences of this choice was the significant postponement of childbearing in Western societies (Lutz et al., 2003). The problem with this delay is that fertility—the biological capacity to reproduce—starts to decline around age 25–30 years (Wood, 1989; Van Noord-Zaadstra et al., 1992). Most women still decide to delay having children and the question is: how long can they wait?

The age at which fertility declines to a level where it becomes impossible to conceive a pregnancy leading to live birth is associated with the biological age at last birth (ALB): the age at last birth when no contraceptive measures have been used to limit family size. In the present era of modern birth control, it is impossible to assess the age-specific distribution of ALB. In developed countries many fertile women and men are childless by choice and if not, most of them want a family of one or two children only and prevent conception thereafter. Accordingly, we do not observe in modern populations the ages when the biological capacity to have children ends.

The pattern of fertility decline can best be studied in so-called natural fertility populations where no deliberate attempt is made to limit family size (Henry, 1961, 1965). These populations lived before the so-called demographic fertility transition (Chesnais, 1992) when couples intentionally restricted the number of children, first by measures such as withdrawal, abstinence, the use of condoms, prolonged breastfeeding or induced abortion (McLaren, 1990), and since the 1960s by modern contraceptive methods including the ‘pill’, intrauterine device and sterilization. As we demonstrated previously (Te Velde and Pearson, 2002), the evolving practice of birth control enabling parents to prevent the birth of additional children after they have achieved their preferred family size first resulted in earlier ALB. Demographic fertility transition started at the end of the 18th century in France and spread throughout Europe and the rest of the Western world during the 19th and beginning of the 20th century. It was related to increasing life expectancy and a greater valuation of children. This pattern started gradually and was adopted first by the educated residents in cities and then later among the working class and in rural areas. Given that this transformation occurred slowly, it is impossible to identify a specific year or period when it started or was completed. Natural fertility populations existed all over the world until the 18th–19th centuries. Also in the recent past as well as at present, there have been populations where contraception is not practised for religious and cultural reasons (Tietze, 1957; Rahman and Menken, 1993; O'Connor et al., 1998).

The similarity of the median female ALB at ages 40–41 years in most natural fertility populations (Bongaarts, 1982) suggests that there is a universal pattern of age-related fertility decline. However, this has only been assessed in small data sets (Tietze, 1957; Trussell and Wilson, 1985; Menken et al., 1986). Recently, electronic databases describing the reproductive events of large natural fertility populations have become available and offer the opportunity to study the distribution of ALB more reliably. These data sets are not only larger but also they allow analysts to apply identical sample inclusion criteria and identical methods of analysis.

The aim of this study is 2-fold. The first is to review and analyse data files from natural fertility populations with respect to the distribution of ALB. Apart from shared biological determinants, the ALB distribution in natural fertility populations may be confounded by behavioural, socio-medical and historical factors such as (‘period’) effects, age at marriage, birth spacing, the level of secondary infertility and parity. These factors have to be taken into account as they may change the distribution of ALB (Leridon, 1977). The second aim is to construct an age curve that describes ages above which women are not biologically able to have children. To achieve this aim, we combine several data sets matching with the lowest chance of reaching ALB. The resulting curve is likely to be least influenced by confounding factors and therefore best reflects the biological process of fertility decline. Hereafter, we call this the biological ALB curve.

Materials and Methods

Selection of databases

We used a variety of sources to identify databases with potentially useful information on ALB: an overview of international historical micro-data presented by the International Micro-data Access group (Kelly Hall et al., 2000), a review of databases that could be used for bio-demographic studies in historical demography that reside in publicly available computerized genealogical data resources (Gavrilova and Gavrilova, 1999), an inventory of large-scale, public databases of life histories from the past drawn from a questionnaire by the International Commission for Historical Demography (International Commission for Historical Demography, 2010), and an overview of databases participating in the European Historical Population Samples Network (European Science Foundation, 2012). In selecting populations from these sources we applied the following criteria:

1. The database had to contain information on individuals/couples from a natural fertility population.

2. The number of first-time married women who remained with their partner until age 50 years had to be sufficiently large (arbitrarily n = 1000 or more).

3. The distribution of ALB had to be available or, if the woman remained childless, her age at marriage had to be known.

4. The database had to include more than a strictly local population in order to avoid bias related to women giving birth outside their natural community of residence.

5. The data set had to be accessible in electronic form.

Methods of analysis

ALB, the main outcome, is presented as box and whisker plots denoting the 5th, 25th, 50th, 75th and 95th percentile of the ALB distribution for each of the selected populations. The demographic features possibly affecting the ALB distribution including year of birth, age at marriage, number of children and birth spacing are presented in the same manner. In addition, the level of childlessness was determined for each population. Since we know from the literature that age at marriage might be inversely related to ALB (Menken et al., 1986), we also analysed the impact of age at marriage on ALB and the other parameters. Because the initial level of the biological ALB curve also depends on the level of childlessness in a population, we had to exclude databases for populations with obvious under-representation of childless women.

The biological ALB curve began with the construction of a Kaplan–Meier curve for each population with ALB as the time variable for parous women. For women who had no children, no ALB could be observed. Nevertheless, these women might have had one or more children and consequently have had an ALB if they had been married at a younger age. Therefore, we included them in the analysis by assuming that their chances of having an ALB at the ages before their marriage were equal to the chances of the women who were married at those ages (i.e. left censored observations). Thus, the Kaplan–Meier analysis was performed with the time axis running backwards from age 50 years, by censoring childless women at their age at marriage. For the composite curve we did not use the absolute level of the Kaplan–Meier curves, because at every age the Kaplan–Meier curve is accumulating the levels of previous ages, which may differ considerably between populations, e.g. due to differences in age at marriage or childlessness. Instead, we used the hazard function, which reflects the risk of having reached the end of fertility at a given age, provided it did not happen before that age. A smoothed hazard curve for each population was derived by using a smoothing spline with 10 degrees of freedom. The hazard curve of biological fertility was obtained by plotting the smoothed hazard curve of each population against age and taking the lowest hazard within a time window of at least 5 years of the assessed populations. This resulted in a composite curve of lowest hazards against age for each population. Finally, this composite lowest hazard curve was transformed into a cumulative distribution function ( = 1 – survival function), representing our estimate of the biological ALB curve. For this last step it is necessary to know the level of childlessness at the start of the curve and we decided to base this level on the average of the population-specific Kaplan–Meier curves at age 20 years.

Results

The first aim was to review the ALB distribution in large data sets of natural fertility populations in Western countries. We found six data sets that fulfilled our selection criteria.

1. A database collected by the French demographer Louis Henry contains a representative survey of the French population between 1670 and 1830. It is based on parish registers before the French Revolution and on civil registrations after the French Revolution. All vital life events had been counted in a sample of 378 parishes, and all families were fully reconstituted in a sub-sample of 40 parishes. This sub-sample was limited to rural France (86% of the total population was rural in 1750). A computerized file became available in 2001. This file includes >106 000 children born between 1670 and 1819 from 34 800 marriages. We used data of first marriages occurring before 1790. Database label: France

2. The Registre de la population du Québec Ancien at the Université de Montréal, Canada (RPQA) is based on marriage, baptism and burial certificates from 153 catholic parishes of preindustrial Québec from the onset of settling in 1608 up to 1850 (Desjardins, 1998). Familial biographies were constructed by linking baptismal certificates of children to the marriage, baptismal and burial certificates of their parents. Overall, the database includes ∼712 000 certificates prior to the 19th century. The population of this area remained almost completely closed until the 19th century; consequently missing observations were infrequent. In this study we included couples married in the period 1638–1796. Database label: Old Quebec

3. The German database is based on Ortssippenbuch—literally ‘book of local kinsmen’—and contains a collection of village genealogies. Because the individual codes allowed the linkage of the couple information to all children born, the genealogies could be reorganized into the same logical scheme as a traditional family reconstitution (Knodel, 1987, 1988). Knodel primarily used the data sets of 6 of 14 villages. In these six villages, data on the vital life events (birth, marriage and death) of all families were recorded in the parish registers. In this data set couples were included who married between 1651 and 1889; most of them married in the 18th or 19th century. Database label: Germany

4. The LINKS database, hosted by the International Institute of Social History in Amsterdam, is a database in construction, aiming at the reconstruction of all 19th and early 20th century families in the Netherlands on the basis of the nationwide birth, death and marriage registration since 1811 (Mandemakers, 2009). The data used here cover two of the eleven Dutch provinces, Zeeland and Drenthe, for which data entry has been completed. The database is based on ∼250 000 marriages registered in the 168 municipalities of these two provinces between 1812 and 1922, on 838 000 births registered between 1812 and 1902, and on 937 000 deaths registered between 1812 and 1952. Given the different observation windows for birth, marriage and death records, we restricted the analysis to marriages contracted in the years 1812–1893 for women born before 1850. By studying data for a whole province and including only couples for which the dates of marriage and death of both partners were registered in the province, the problem of missing observations due to inter-municipal migrations is greatly reduced. Database label: Netherlands

5. The Utah Population Database (UDBP) is one of the world's most comprehensive computerized genealogies. In the mid-1970s over 185 000 three-generation families were identified on Family Group Sheets from the archives of the Utah Family History Library, each with at least one member having had a vital life event (birth, marriage or death) on the Mormon Pioneer Trail or in Utah (Smith et al., 2002). These families have been linked into multigenerational families. The genealogy provides data on migrants to Utah and their Utah descendants for >1.6 million individuals born from the 1780s to the mid-1970s. The UPDB includes also individuals who have lived in other states and countries and describes families with and without an affiliation to the Church of Jesus Christ of Latter-day Saints (Mormons). Polygamy was practised in Utah but only by a small proportion of the population. In our analysis we could differentiate between polygamous and monogamous couples and used the latter (the vast majority) for our analysis. We analyse individuals born between 1750 and 1864, and married between 1773 and 1875. This period is selected because they still lived during a time when effective contraceptive methods were not yet available. Accordingly, their family formation patterns reflect natural fertility conditions. In the Utah case, the number of descendants who contribute to genealogical data will be larger in pedigrees where fertility is high. In the primary data the notation of ‘no issue’ indicating that no children were born to a couple was recorded incompletely. Database label: Utah

6. The BALSAC demographic database (Bouchard et al., 1989) consists of the first marriages of women born between 1840 and 1899 in the Saguenay-Lac-St-Jean (SLSJ) region in Québec, Canada, and their spouses, who married and died in the region. The SLSJ region became populated by colonists from the nearby Charlevoix region around the middle of the 19th century and their data from church registers (Roman-Catholic) on birth, baptism, marriage and death are contained in the database. The demographic fertility transition occurred relatively late in this region, in 1946–1955 among farmers and in 1931–1935 for all other professions (Bouchard and Roy, 1991). For this reason, the birth cohorts chosen were restricted to those from before 1900. Database label: QUEBEC/SLSJ

After selecting first-time married women who remained with their partner until age 50, we found 58 051 women eligible collectively across all six data sets: 3 518 from France, 11 402 from Utah, 10 817 from Old Quebec, 2651 from Quebec SLSJ, 28 097 from the Netherlands and 1566 from the Knodel database in Germany. Three of the databases—Old Quebec, Quebec SLSJ and Utah—share an important characteristic: they relate to the demographic history of frontier populations.

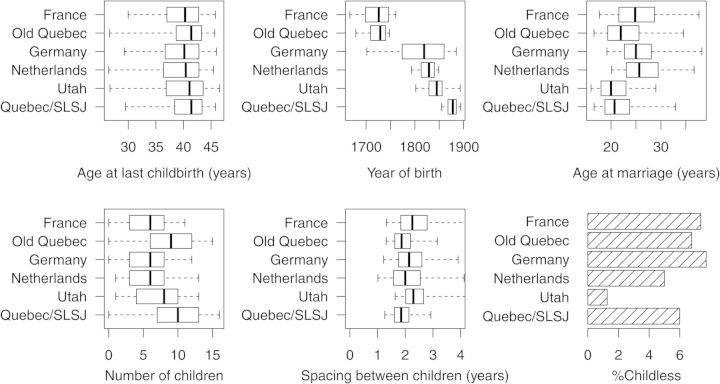
ALB and the related demographic parameters are depicted in Fig. 1. Large differences exist between the populations with regard to the historical time during which they lived: the oldest (from France and Old Quebec) in the second half of the 17th century and the youngest (Quebec/SLSJ) in the second half of the 19th century; a difference of about 200 years. Nevertheless, the distribution of ALB is similar for all populations with median values of 40.3 years for France; 41.4 years for Old Quebec; 40.1 years for Germany; 40.4 years for the Netherlands; 41.1 years for Utah and 41.4 years for Quebec, SLSJ. With regard to the prevalence of childlessness (Fig. 1), the very low level in the Utah database of about 1.5% is exceptional due to the genealogical focus of the Utah data. In the other databases, the level of childlessness varies from about 5% in the Netherlands to around 8% in Germany.

Figure 1.

Distribution of the demographic and fertility parameters in the six populations. Boxes: P25, P50 and P75; whiskers: P5 and P95. SLSJ: Saguenay-Lac-St-Jean region of Quebec.

Supplementary data, Table SI depicts the distribution of the same parameters for the quartiles of ‘year of birth’ shown in Fig. 1. ALB showed a decreasing trend in more recent birth cohorts in all populations except the Netherlands. No trend was seen in the number of children in any of the populations except for Utah in the youngest cohorts. There were no trends in average birth spacing except for a tendency of shorter spacing in recent cohorts in Germany. The level of childlessness did not show a trend over time, except for a decline in the Netherlands.

In Table I the distribution of ALB and the related fertility parameters for the oldest birth quartile of the six populations is shown against five categories for age at marriage: 15–20, 20–25, 25–30, 30–35 and 35–60 years. A clear positive (and expected) trend between early age at marriage and increasing parity was present. There was no trend, however, between age at marriage and ALB. For example, women who married early and had many children did not have an advanced ALB in comparison to women who married late. The level of childlessness became higher at later age at marriage in most populations while the average spacing became shorter.

Table I.

Fertility parameters (median with interquartile range) of the oldest birth year quartiles split by categories of age at marriage.

Age at marriage (years)	France	Old Quebec	Germany	Netherlands	Utah	Quebec/SLSJ
Age at last childbirth (years)a
(15,20)	38.7 (34.3–41.9)	41.4 (38.8–43.3)	39.4 (36.2–42.4)	39.4 (33.7–42.3)	41.8 (38.8–43.8)	41.1 (37.9–43.2)
(20,25)	39.9 (36.0–42.4)	41.4 (38.7–43.3)	39.2 (34.3–42.4)	40.2 (35.0–42.8)	42.1 (39.2–44.2)	41.3 (37.7–43.3)
(25,30)	40.1 (36.2–42.7)	41.3 (38.4–43.2)	40.1 (36.4–42.8)	40.3 (36.0–42.7)	42.1 (39.3–44.2)	41.4 (38.3–43.4)
(30,35)	40.7 (37.4–43.1)	41.0 (38.0–42.9)	39.8 (36.2–42.5)	40.5 (37.5–42.7)	42.0 (39.8–44.0)	41.0 (38.0–43.1)
(35,60)	40.8 (38.2–43.6)	40.8 (37.3–42.6)	40.9 (38.3–43.0)	41.9 (39.9–43.5)	42.6 (41.5–45.4)	40.4 (38.9–42.4)
Number of children
(15,20)	8.0 (5.0–9.25)	12.0 (9.0–14.0)	9.0 (6.0–10.0)	9.0 (5.0–12.0)	10.0 (8.0–12.0)	12.0 (9.0–14.0)
(20,25)	7.0 (5.0–9.0)	10.0 (8.0–12.0)	7.0 (4.0–9.0)	7.0 (5.0–10.0)	8.0 (6.0–10.0)	10.0 (8.0–12.0)
(25,30)	5.0 (3.5–7.0)	7.0 (5.0–9.0)	6.0 (4.0–8.0)	6.0 (3.0–8.0)	6.0 (5.0–8.0)	7.0 (6.0–9.0)
(30,35)	4.0 (2.0–6.0)	5.0 (3.0–6.0)	4.0 (2.0–5.0)	4.0 (2.0–6.0)	4.0 (3.0–6.0)	5.0 (3.0–7.0)
(35,60)	1.0 (0.0–3.0)	1.0 (0.0–2.25)	1.0 (0.0–3.0)	2.0 (1.0–3.0)	3.0 (2.0–4.0)	0.0 (0.0–2.0)
Average spacing between children (years)
(15,20)	2.57 (2.21–3.21)	1.92 (1.67–2.21)	2.33 (1.98–2.74)	2.03 (1.63–2.54)	2.32 (2.06–2.66)	1.88 (1.63–2.15)
(20,25)	2.29 (1.9–2.79)	1.86 (1.62–2.18)	2.18 (1.82–2.65)	2.07 (1.66–2.63)	2.27 (1.99–2.65)	1.84 (1.61–2.12)
(25,30)	2.17 (1.81–2.7)	1.84 (1.59–2.16)	2.13 (1.76–2.54)	2.03 (1.6–2.56)	2.19 (1.89–2.67)	1.84 (1.56–2.11)
(30,35)	2.02 (1.63–2.61)	1.76 (1.49–2.09)	1.94 (1.56–2.4)	1.88 (1.47–2.4)	2.19 (1.77–2.7)	1.79 (1.53–2.09)
(35,60)	1.8 (1.33–2.38)	1.66 (1.37–2.18)	1.71 (1.21–2.29)	1.61 (1.2–2.14)	1.85 (1.23–2.63)	1.55 (1.32–2.02)
Childlessness (%)
(15,20)	3.0 (1.7–5.0)	3.2 (2.7–3.9)	5.2 (2.1–11.5)	5.0 (3.9–6.3)	2.4 (1.9–2.9)	3.6 (2.6–4.9)
(20,25)	4.1 (3.1–5.4)	4.5 (3.9–5.2)	4.3 (3.0–6.3)	4.4 (4.1–4.8)	1.5 (1.1–2.1)	3.5 (2.5–4.9)
(25,30)	4.8 (3.6–6.4)	5.9 (4.9–7.1)	6.0 (4.2–8.6)	4.5 (4.1–4.9)	0.85 (0.34–1.9)	5.0 (2.9–8.4)
(30,35)	8.8 (6.3–12.0)	10.8 (8.6–13.4)	11.8 (7.3–18.2)	5.7 (5.0–6.4)	1.2 (0.21–4.7)	11.3 (6.2–19.3)
(35,60)	37.8 (32.1–43.8)	48.6 (44.1–53.1)	29.5 (21.9–38.2)	8.7 (7.6–10.0)	2.4 (0.13–14.4)	53.3 (43.4–62.9)

SLSJ, Saguenay-Lac-St-Jean region of Quebec

^aEstimates for age at last childbirth derived from Kaplan–Meier analysis with left censoring for age at marriage (see Methods)

The second aim was to establish the biological ALB curve. For this analysis the oldest birth quartile in each population was selected, and we excluded the Utah database as this population had a clear under-representation of childless women. First, Kaplan–Meier curves for ALB were constructed (see Fig. 2A). The chance that ALB occurs before the age of 20 years appears to be similar, around 2%. However, at higher ages, ALB curves start to diverge indicating that non-biological factors played a role in altering the pattern of ALB. For example, at age 35 years, the proportion of women having had their last birth varied from about 12% in Old Quebec and Quebec/ SLSJ to about 24% in the Netherlands. In Fig. 2B, the smoothed hazard curves are shown. The age-specific differences between populations are more marked on this scale and the curves cross at various ages. Until about age 42, Old Quebec and Quebec/ SLSJ have the lowest hazards while beyond 42 years, the minimum is achieved in France.

Figure 2.

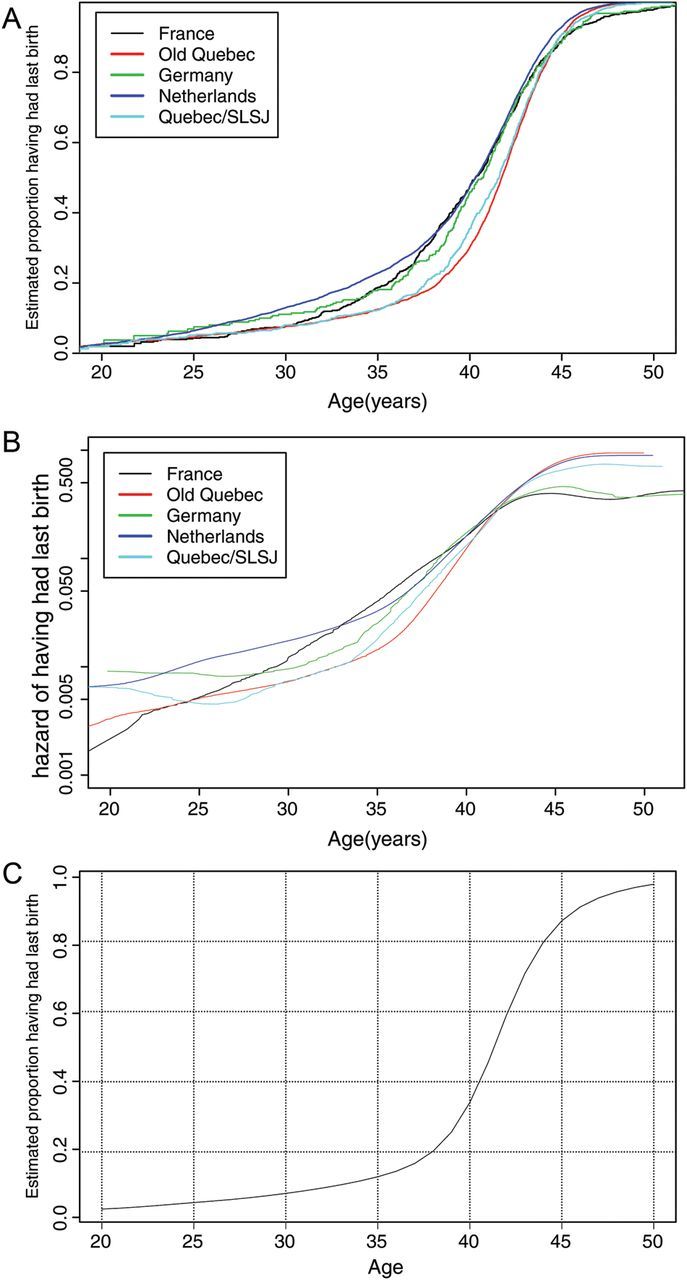
(A) Cumulative age at last birth (ALB) curves for the oldest birth quartile of the five selected populations. Kaplan–Meier curves using left censoring at age at marriage. (B) Smoothed hazard curves for ALB, for the oldest birth quartile of the five selected populations. (C) The biological ALB curve based on the minimal hazard at each age for the oldest birth quartile of the five selected populations.

Figure 2C shows the biological ALB curve that is obtained by taking the lowest hazard of ALB over an age period of at least 5 years of the five selected populations and assuming the level of childlessness at age 20 to be the average of the five populations (2.4%).

Discussion

The birth of the last child is the last noticeably major reproductive event for women living under natural fertility conditions. Nine months before she had her last effective conception leading to the birth of her last child; hence at that time she was still fertile. At some point in time during the course of gestation or the subsequent period of post-partum amenorrhoea caused by breastfeeding, she must have lost the capacity of achieving effective conceptions because thereafter, she is no longer able to have a live birth. In surveys where both the return of menses and the duration of breastfeeding were recorded, it has been shown that the period of post-partum amenorrhoea on average lasted for about 1 year (Leridon, 1977; Leridon and Ferry, 1985). The ALB is approximately between the age at last conception when she is still fertile (the ALB minus 9 months) and the time she has become definitely infertile (the ALB plus 1 year). Therefore, we may consider this age (ALB) as a proxy for the end of female fertility. There is no reason to assume that nulliparous women are different in this respect from multiparous women. While the ALB theoretically marks the imminent end of the couple's joint reproductive capacity, the female contribution is far more important (Minneau and Trussell, 1982; Menken et al., 1986). We follow the convention in demography of attributing the couple's fertility to the woman.

The first aim of our study was to review and analyse the distribution of ALB in large computerized data sets of natural fertility populations in Western countries. We selected data sets from six natural fertility populations. Although the oldest and youngest population lived 200 years apart, the distribution of ALB is remarkably similar (Fig. 1) demonstrating the universal pattern of the age-related fertility decline. From the boxes and whiskers plots it is obvious that the ALB distributions are skewed to the left in all populations. In a previous study we found a strikingly similar distribution of ALB in one of the populations selected in this study (Quebec/SLSJ) and of age at menopause in a contemporary population, suggesting that both are the consequence of the same process (Te Velde and Pearson, 2002). The left skew in both studies suggests that a considerable proportion of women exhibit premature or early ovarian failure and consequently early ALB and early age at menopause.

The three frontier populations selected in our search—Old Quebec, Quebec/SLSJ and Utah—share three important characteristics: the women married earlier and thus started to reproduce at younger ages, they had the highest parity and they continued to reproduce for longer corresponding with a later ALB. In frontier populations there are fewer intentional checks on reproduction; consequently the reproductive potential is more effectively used (Moreau et al., 2011) than in the established populations living in Germany, France and the Netherlands. The striking low level of childlessness in the Utah database is due to its genealogical nature by which selective non-inclusion of childless women occurs. Moreover, reproduction is for a significant part a heritable process (see later), thus selecting the more fertile descendants.

Was the effect of the demographic transition already noticeable in the populations selected? Not when we look at the number of children which showed no time trend, with Utah as the only exception (see Supplementary data, Table SI: Number of children). However, there was a consistent trend of earlier ALB in the later birth quartiles (see Supplementary data, Table SI: Age at last childbirth).

In a previous study we demonstrated that the first major decision Dutch women took after their newly found freedom by the introduction of the ‘pill’ in the 1970s, was not to have fewer children but to have no children at an advanced reproductive age (Te Velde and Pearson, 2002). This result is in line with studies in historical populations showing that the number of children ever born declined almost entirely as a result of stopping behaviour, when women were ending their reproductive period earlier (Knodel, 1987; Reher and Sanz-Gimeno, 2007; Van Poppel et al., 2012). Since we focus on the biological age-dependent fertility decline we, therefore, only used data from the oldest birth quartiles.

Lowering the age of first reproduction increases the number of subsequent children being born (Moreau et al., 2011). In Table I, where the effect of age at marriage is analysed, this expected trend is again observed.

It has been suggested (Trussell and Wilson, 1985; Menken et al., 1986) that there is a ‘a childbearing-induced sterility’ implying that as more children were born, the earlier the ALB and the earlier the onset of infertility, and consequently that women who married later were more fertile at that age than women who had married early. Possible explanations for such an association relate to the higher chance of secondary infertility due to the increased probability of post-partum or post-abortion infections leading to tubal disease as the number of children born increases. However, we could not confirm such an association in the much larger populations selected by us: earlier age at marriage did not lead to earlier ALB, with France as the only exception (see Table I under: Age at last childbirth). Another explanation for the differences found between the Menken curves and ours is that Menken et al. (1986) had to use an estimate of the reference age within 5-year intervals to plot a curve on. The position of these reference ages may have greatly influenced the level of the curve, given the sharp increase in level with age from 35 years onwards. In contrast, we were able to use exact ages for each individual woman. Apparently, the method needed to plot a curve based on 5-year intervals in the Menken et al. (1986) data and the necessity to correct for dependency of ALB on the age at marriage have resulted in a curve differing from ours.

The second aim is to establish the biological ALB curve: the age above which women have become biologically too old to conceive of a pregnancy leading to live birth. The frontier populations—Old Quebec and Quebec/SLSJ—contribute most to this curve until age 42 years; thereafter the data from France are the most influential in affecting the curve (see Fig. 2B).

The biological ALB curve of Fig. 2C demonstrates that the age-related loss of fertility rises slowly until somewhere between ages 35 and 40 after which it rises rapidly.

The prevailing concept of fertility decline assumes that the age-dependent loss of fertility is determined by the continuous depletion of the pool of oocytes stored in both ovaries during fetal life, leading first to a decrease of fertility and its subsequent expiration followed ∼10 years later by menopause (Te Velde and Pearson, 2002). Thus, apparently ALB and age at menopause denote different stages of the same biological process of reproductive ageing. Several studies point to the strong heritable component of age at menopause with a polygenic pattern of inheritance (De Bruin et al., 2001; Van Asselt et al., 2004; Murabito et al., 2005). A Finnish study in a 19th century fertility population demonstrated a similar heritability for ALB (Pettay et al., 2005).

With regard to the strengths and weaknesses of our study, we consider a strength is that our data are not from one single place and time period, as in most previous studies, but from a variety of countries and time periods, each having their own demographic specificity which might have had an effect on fertility patterns (marriage, health and mortality characteristics). Nonetheless, the distribution of the ALB was remarkably similar suggesting that there is a universal pattern of age-related fertility decline. Moreover, our data set is much larger than in previous reports and collected from countries with complete and well-functioning registration systems, thus leading to more reliable outcomes than in earlier studies. We have applied sophisticated statistical techniques to derive our fertility estimates.

With regard to possible weaknesses we cannot exclude missing observations caused by (temporary) outmigration, during which period children may have been born outside the study area, or by under-registration of children who were born alive but died before being registered as a live birth. Furthermore, still-born children are usually not included in these data and it is possible that unfavourable factors in the past that resulted in a stillbirth could, under the present medical conditions, have led to a live birth. The consequence of these problems would be the same namely that the fertility curve derived underestimates the present reality.

More fundamentally, it is questionable whether applying conclusions drawn from natural populations living 150–200 years ago to the present time is justified. For example, as deliveries and abortions now occur in more favourable environments, the prevalence of infections after these events most probably has declined. With regard to sexually transmitted diseases we can only speculate: sexual promiscuity probably has increased but treatment is certainly more efficient. There has been widespread anxiety about the adverse effect of environmental pollutants on sperm quality during the last 50 years (Carlsen et al., 1992), which, however, has not been confirmed (Bonde et al., 2011) whereas during the last 2–5 decades population fertility did not change (Te Velde et al., 2010). The so-called ‘relaxed reproductive selection hypothesis’ argues that since family size decreased markedly during the 20th century, the proportion of births from the biologically most fertile couples is likely to have decreased (Czeizel and Rothman, 2002). This and the introduction of assisted reproduction technologies enabling infertile couples to reproduce may have increased the level of infertility in the population (Joffe, 2003).

In favour of extrapolation of data from natural populations to the present time is the fact that also in contemporary natural populations, the age-dependent decline of fertility appears to be comparable to the biological ALB curve of Fig. 2C, for example in the Hutterite population living in the first half of the 20th century (Tietze, 1957; Larsen and Yan, 2000) and among currently married non-contracepting women in several parts of the world (Rahman and Menken, 1993; O'Connor et al., 1998). Also, the age-dependent decline in fertility of couples treated by donor insemination is in line with the biological fertility curve (Van Noord-Zaadstra et al., 1992). Indeed, it seems unlikely that a biological phenomenon with a high degree of heritability would have noticeably changed within 1–2 centuries, i.e. a maximum of 4–8 generations.

Apart from biological factors, the frequency of coitus, showing an age-related decline across the life course (Brewis and Meyer, 2005), is also an important determinant for the occurrence of pregnancy (Stanford and Dunson, 2007). In this respect, couples from historical populations differ from modern couples who have finally taken the decision to have their first child. First, with regard to motivation: modern couples probably attempt to have more frequent intercourse than women from historical populations who became pregnant with their last child by chance rather than by intention. Second, there is more information about the frequency and timing of intercourse during the fertile window of the menstrual cycle than in the past. Using this information may well enhance the likelihood of spontaneous pregnancy (Stanford et al., 2003; Dunson et al., 2004; Rothman et al., 2013). The biological ALB curve as currently constructed may therefore provide an overly conservative estimate for the prospects for later-age conceptions for modern couples who have delayed childbearing and who seek to conceive without medical interventions.

What lessons can be learnt from the pattern of age-related decline in natural fertility populations? At present, age at childbearing has been delayed considerably since the contraceptive revolution of the 1960s. Presently, the mean maternal age at first birth is approaching age 30 in several European countries and many women deliver their first child at age 35 or older. Several studies show that most women are not aware of the fact that delaying childbearing increases the risk of infertility (Schmidt, 2010) and that the risk of abortion, chromosomal aberrations and pregnancy complications steeply increases with age (Heffner, 2004). Moreover, many women erroneously believe that IVF can always address the fertility complications associated with advancing age (Maheshwari et al., 2008). At the same time, however, others believe there is an age at which women are too old to conceive (Billari et al., 2011). Under these circumstances the question raised in the title of our manuscript ‘Too old to have children?’ is relevant. Regrettably, there are no reliable biological markers that accurately portend the onset of reproductive failure. Irregular menstrual cycles and hot flushes signifying imminent menopause represent symptoms that arise too late to be offered as a predictive measures because sterility is likely to have started already years earlier, when the menstrual pattern was still regular and hormone levels deviated little from the standard (van Zonneveld et al., 2003).

The biological ALB curve proposed here can be used as a tool to counsel women who are considering or are actually delaying childbearing. This information will be most beneficial provided the woman is told that the age-related chances of success are averages: for any individual woman these chances may be higher or lower, depending on the characteristics of the woman. Reports suggesting that the determination of anti-Mullerian hormone (AMH) can already be used to individualize such predictions have to be regarded as overly optimistic at this time (Loh and Maheshwari, 2011). For example, the result from a recent long-term study focussing on the age at menopause as a marker for the end of reproduction (Broer et al., 2011) demonstrates that young women with very low AMH levels have menopause about 2 years earlier than the average age of 51: it is dubious whether such knowledge will change the reproductive intentions of young women. Female age is the only realistic information available at present for estimating the magnitude of the reproductive ageing process. The biological ALB curve demonstrates that the average chance of involuntarily childlessness slowly increases to 12% at 35 and 20% at age 38. From there this chance sharply rises to 50% at about 41 and reaches almost 90% at age 45.

The biological ALB curve reveals several important lessons. For example, for women aged 32–34 who still have a very good chance of bearing children although their risk of childlessness has tripled since age 25 and will increase substantially more after age 35, the lesson is: do not wait much longer, certainly not if you want more than one child. At the same time, the curve contradicts the occasionally exaggerated pessimism about women who intend (or by circumstances are forced) to have children in their late thirties (Twenge, 2013). For them the lesson is: you still have a good chance to succeed if you don't wait any longer. For women in their early forties the lesson is: just try, your chances are still far from hopeless. Since the success rate of IVF demonstrates a similar age-related decline as the chance of a natural pregnancy (Malizia et al., 2009), women should also be told that the idea of IVF reversing the effect of age is a mistaken belief.

In conclusion, we evaluated six large natural fertility populations from a range of historical periods and locations, and found substantial resemblance in the age distribution of ALB. We constructed a biological ALB curve that can be used as a counselling tool for couples who envisage delaying their age of childbearing.

Supplementary data

Supplementary data are available at http://humrep.oxfordjournals.org/.

Authors' roles

M.J.C.E., E.R.t.V. and D.F.H. conceived the idea of the study and its design, E.R.t.V. wrote the manuscript, M.J.C.E. is responsible for the methodology and performed the analyses, F.v.P., K.R.S. and H.L. collected the demographic databases and made them accessible for analysis. All authors contributed intellectually to the final version of the manuscript.

Funding

No external funding was either sought or obtained for this study.

Conflict of interest

None declared.