Abstract
In magnetic materials, the Pauli exclusion principle typically drives anti-alignment between electron spins on neighbouring species resulting in antiferromagnetic behaviour. Ferromagnetism exhibiting spontaneous spin alignment is a fairly rare behaviour, but once materialized is often associated with itinerant electrons in metals. Here we predict and rationalize robust ferromagnetism in an insulating oxide perovskite structure based on the popular titanate series. In half-doped layered titanates, the combination of Jahn–Teller and oxygen breathing motions opens a band gap and creates an unusual charge and orbital ordering of the Ti d electrons. It is argued that this intriguingly intricate electronic network favours the elusive inter-site ferromagnetic (FM) ordering, on the basis of intra-site Hund's rules. Finally, we find that the layered oxides are also ferroelectric with a spontaneous polarization approaching that of BaTiO3. The concepts are general and design principles of the technologically desirable FM ferroelectric multiferroics are presented.
 Magnetic insulators often display antiferromagnetic ordering owing to implications from the Pauli exclusion principle. Here, the authors predict ferromagnetism on the basis of intra-site Hund's rules in ferroelectric titanate superlattices showing charge and Jahn–Teller induced orbital orderings.
Magnetic insulators often display antiferromagnetic ordering owing to implications from the Pauli exclusion principle. Here, the authors predict ferromagnetism on the basis of intra-site Hund's rules in ferroelectric titanate superlattices showing charge and Jahn–Teller induced orbital orderings.
Perovskite oxides exhibit a fascinating range of physical properties, including ferroelectricity, (anti)ferromagnetism (AFM), superconductivity and magnetoresistance. This diverse behaviour is appealing for both fundamental and applied investigations, and has resulted in an intense global research effort over the past few decades. Many of these functional properties manifest due to the complex and subtle interplay between spin, charge, orbital and lattice degrees of freedom in perovskites1,2,3,4. Of the perovskites, the doped manganites have become a prototypical playground for the study of this interplay. Just considering the case of half-doping, that is, 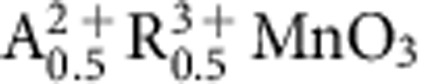 , where A2+ is a divalent alkaline earth metal ion and R3+ is a trivalent rare earth ion, manganites exhibit a rich variety of electronic phases. For example, half-doped manganites can display ferromagnetic (FM) or A-type AFM metallic behaviour5,6,7 or more commonly a CE-type AFM Mott insulating phase8,9 associated with two different charge orderings (rocksalt10 and columnar11) and two different orbital orderings (‘ferro’ and ‘antiferro’ Mn d eg orderings12). The preferred electronic phase appears to be strongly dependent on the A2+ and R3+ cation sizes and whether they appear disordered (such as with Ca and La/Pr) or layered (such as for Ba and La/Tb/Y5,10,12) in the crystal.
, where A2+ is a divalent alkaline earth metal ion and R3+ is a trivalent rare earth ion, manganites exhibit a rich variety of electronic phases. For example, half-doped manganites can display ferromagnetic (FM) or A-type AFM metallic behaviour5,6,7 or more commonly a CE-type AFM Mott insulating phase8,9 associated with two different charge orderings (rocksalt10 and columnar11) and two different orbital orderings (‘ferro’ and ‘antiferro’ Mn d eg orderings12). The preferred electronic phase appears to be strongly dependent on the A2+ and R3+ cation sizes and whether they appear disordered (such as with Ca and La/Pr) or layered (such as for Ba and La/Tb/Y5,10,12) in the crystal.
In this regard, it is interesting to compare the physics of the half-doped manganites, with that of the half-doped titanates. At the bulk level, the A2+ and R3+ cations are found to naturally disorder13,14 in the titanates, and typically no charge and orbital-ordered Mott insulating phase is observed at half-doping15. An exception has been recently discovered for the case of very small A2+-cations, such as Ca0.5Lu0.5TiO3, where a rocksalt charge-ordered and dxy t2g orbital-ordered Mott insulating phase was recently proposed16. On the other hand, in layered superlattices consisting of a repeating unit of k layers of A2+TiO3 with l layers of R3+TiO3, exotic behaviour such as an interface two-dimensional (2D) electron gas17, which can be FM18 and superconducting19 has been reported.
Here we consider half-doped titanates in short-period [001] superlattice form (k=l=1) (see Fig. 1), which can in principle be artificially grown using modern layer-by-layer growth techniques (see for instance refs. 20, 21 and references within). This case resembles a bulk-like double perovskite, where every Ti ion shares the same mixed environment at odds with thicker superlattices. A careful first principles investigation (see Methods) including all possible degrees of freedom reveals an unexpected FM and ferroelectric insulating ground state. The electronic structure exhibits an intricate orbital and charge ordering, which is argued to be at the heart of the observed ferromagnetism. A symmetry lowering structural distortion enabling this particular orbital ordering is also found to drive the ferroelectricity. The results appear rather general across the whole A2+TiO3-R3+TiO3 (k=l=1) series, being shared by a wide variety of combination of cations with a large variation of cationic sizes. This has allowed for universal physical principles to be rationalized and new multiferroic design guidelines to be proposed. The subtle interplay between electronic and structural degrees of freedom are compared with the manganites and novel features are highlighted.
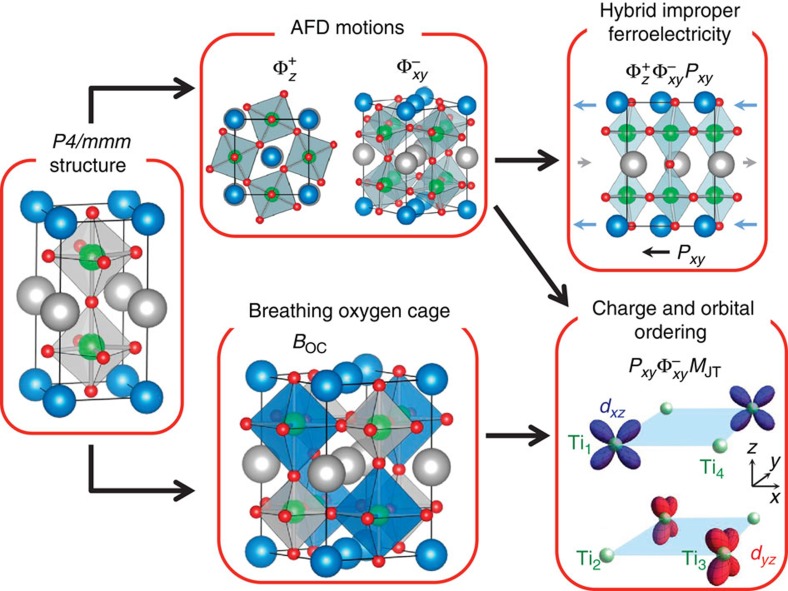
Figure 1. Superlattice geometry, major structural distortions, and resulting ferroelectric, charge and orbital ordering.
The A2+TiO3-R3+TiO3 digital superlattice 10-atom high-symmetry tetragonal P4/mmm reference structure undergoes two major structural distortions: AFD motions and a breathing oxygen cage distortion. The rocksalt arrangement of large (blue) and small (grey) octahedral cages of the breathing distortion are shown in the 20-atom cell. The AFD motions induce ferroelectricity through a unique anharmonic coupling to an in-plane polar mode. The combination of the AFD motions and breathing oxygen cage allows for an unusual charge and orbital ordering. Blue, grey, red and green spheres represent R3+, A2+, O and Ti, respectively. Distortions are exaggerated for illustrative purposes.
Results
Ferroelectricity
To unravel the unexpected ferroelectric and FM behaviour, we begin by focussing on the atomic structure of the A2+TiO3-R3+TiO3 superlattice (see Fig. 1). Unless stated otherwise the results presented throughout, although qualitatively similar across the whole series (see Supplementary Tables 3 and 4), are presented for the case of SmTiO3-SrTiO3. In all cases, we find a P21 symmetry ground state that consists of a complex combination of several lattice distortions (see Table 1) of the high-symmetry (P4/mmm) cube-on-cube double perovskite. Out of all the distortions, the largest in amplitude are oxygen octahedral rotations, both in-phase around the out-of-plane (z) axis, 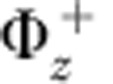 and anti-phase around the in-plane (x and y) axes,
and anti-phase around the in-plane (x and y) axes, 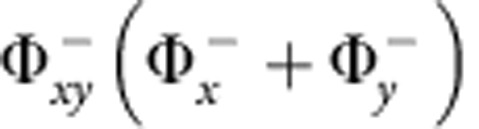 . These so-called antiferrodistortive (AFD) motions are ubiquitous in perovskites, appearing through steric effects described by the Goldschmidt tolerance factor22. The particular AFD pattern found here, a−a−c+ in Glazer’s notations23, is the most common pattern shown by perovskites24, certainly with tolerance factors between 0.8–1.0, the case studied here. This particular AFD pattern is stabilized over others in simple bulk perovskites through unique anharmonic couplings allowing the subsequent appearance of anti-polar A-cation motions25,26,27, located at the zone-boundary of the cubic ABO3 Brillouin zone. In the A2+TiO3-R3+TiO3 digital superlattices, this A- and R-cation motion transforms to the zone-centre, becoming polar in nature. The precise form of the anharmonic coupling is trilinear,
. These so-called antiferrodistortive (AFD) motions are ubiquitous in perovskites, appearing through steric effects described by the Goldschmidt tolerance factor22. The particular AFD pattern found here, a−a−c+ in Glazer’s notations23, is the most common pattern shown by perovskites24, certainly with tolerance factors between 0.8–1.0, the case studied here. This particular AFD pattern is stabilized over others in simple bulk perovskites through unique anharmonic couplings allowing the subsequent appearance of anti-polar A-cation motions25,26,27, located at the zone-boundary of the cubic ABO3 Brillouin zone. In the A2+TiO3-R3+TiO3 digital superlattices, this A- and R-cation motion transforms to the zone-centre, becoming polar in nature. The precise form of the anharmonic coupling is trilinear, 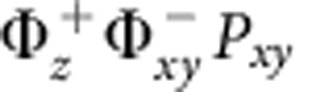 , which is the signature of the so-called rotationally driven hybrid improper ferroelectricity28,29,30,31,32. Indeed, we calculate all superlattices to exhibit spontaneous polarizations in the range of 7–23 μC cm−2 (see for example Table 1), approaching that of BaTiO3, which is among the highest reported in hybrid improper ferroelectrics. Since the Pxy mode has a ‘ferri’-like character of the A-and R-cation motion (see Fig. 1), the large polarization is achieved by maximizing the mode polarity through choosing A- and R-cations not only with asymmetric cation sizes33 but also here thanks to significantly distinct Born effective charges (or valences in the simplest picture).
, which is the signature of the so-called rotationally driven hybrid improper ferroelectricity28,29,30,31,32. Indeed, we calculate all superlattices to exhibit spontaneous polarizations in the range of 7–23 μC cm−2 (see for example Table 1), approaching that of BaTiO3, which is among the highest reported in hybrid improper ferroelectrics. Since the Pxy mode has a ‘ferri’-like character of the A-and R-cation motion (see Fig. 1), the large polarization is achieved by maximizing the mode polarity through choosing A- and R-cations not only with asymmetric cation sizes33 but also here thanks to significantly distinct Born effective charges (or valences in the simplest picture).
Table 1. Key quantities for a selection of A2+TiO3-R2+TiO3 superlattices.
| R3+, A2+ |
Q |
P | Δ | ΔE | ||||
|---|---|---|---|---|---|---|---|---|
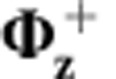 |
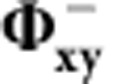 |
Pxy | BOC | MJT | ||||
| Sm, Sr | 0.96 | 1.19 | 0.56 | 0.10 | 0.04 | 14.9 | 0.46 | 20.1 |
| Y, Sr | 1.10 | 1.30 | 0.66 | 0.11 | 0.04 | 16.7 | 0.57 | 18.0 |
| Tm, Sr | 1.18 | 1.36 | 0.72 | 0.11 | 0.03 | 18.2 | 0.63 | 16.4 |
| Sm, Ba | 0.75 | 0.96 | 0.48 | 0.13 | 0.07 | 18.6 | 0.50 | 18.5 |
| Y, Ba | 0.95 | 1.08 | 0.59 | 0.14 | 0.07 | 21.2 | 0.60 | 13.9 |
| Tm, Ba | 1.05 | 1.16 | 0.65 | 0.16 | 0.07 | 23.4 | 0.66 | 10.5 |
AFD, antiferrodistortive; AFM, antiferromagnetism.
Amplitude Q (Å) of lattice distortions (in-phase 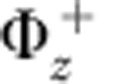 and anti-phase
and anti-phase 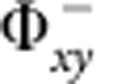 AFD motions, polar mode Pxy, Jahn–Teller mode appearing at the M-point of the cubic Brillouin zone MJT and breathing oxygen cage BOC), polarization P (μC cm−2), band gap Δ (eV) and gain of energy for FM versus AFM solution (see Methods) per 20-atom formula unit ΔE (meV).
AFD motions, polar mode Pxy, Jahn–Teller mode appearing at the M-point of the cubic Brillouin zone MJT and breathing oxygen cage BOC), polarization P (μC cm−2), band gap Δ (eV) and gain of energy for FM versus AFM solution (see Methods) per 20-atom formula unit ΔE (meV).
Charge ordering
A necessary requirement of ferroelectricity is to be electronically insulating, which is not a priori obvious in these half-doped titanates. Allowing only AFD motions yields a metastable system with the usual Pmc21 symmetry (equivalent to Pnma but for the superlattice). Within this symmetry, the system is metallic and all Ti ions share the same magnetic moment by symmetry (roughly 0.45 μB per Ti site). However, we observe an electronic instability leading to an incipient charge ordering between the four Ti sites. Indeed, releasing the symmetry constraint on the electronic wavefunction while keeping the atoms fixed to a Pmc21 structure produces an energy gain due to an incipient d1–d0 charge ordering. Relaxing the geometry produces the P21 ground state with the appearance of a related breathing BOC motion, which expands or contracts the oxygen octahedra in nearest neighbour unit cells (see Fig. 1 and Table 1). This breathing distortion does not lift the degeneracy of the t2g levels of the Ti atoms at the centre of each octahedra, but does lift the degeneracy between Ti sites, amplifying the charge ordering, and helping render the superlattices insulating. The charge ordering mimics the rocksalt pattern, and hence appears at the R-point (M-point) of the cubic (tetragonal) Brillouin zone, maximizing the distance between the more highly charged d0 Ti4+ ions. Please see Supplementary Note 1, and associated Supplementary Tables 6 and 8, for further discussion on the breathing mode and charge ordering.
Orbital ordering
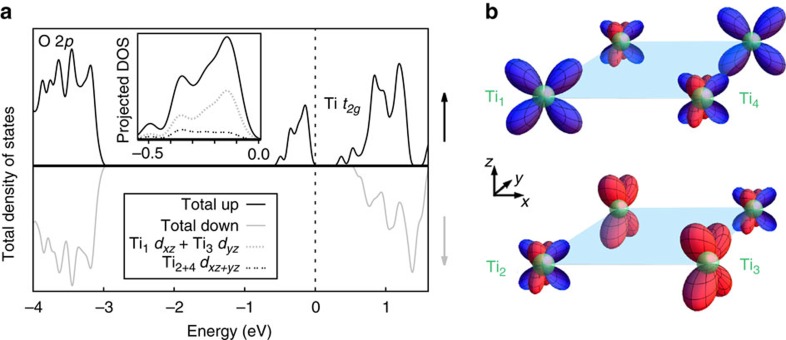
This charge-ordered insulating state is indeed found, as indicated through the spin-resolved density of states (DOS), as presented for the FM solution in Fig. 2 (for the full projected DOS see Supplementary Fig. 1). The states near the Fermi level exhibit Ti d character, while the O 2p states appear deeper into the valence. A band gap separates an occupied spin-polarized ‘split-off’ band from the remaining unoccupied Ti d conduction band. This ‘split-off’ valence is found to consist of 2 bands with the majority of weight located at 2 different Ti sites, out of the 4 possible Ti sites in total in the 20-atom unit cell (see Fig. 1). These two sites are surrounded by the expanded oxygen octahedra, which we label the Ti d1 sites, as opposed to the two other Ti d0 sites surrounded by a contracted oxygen octahedra. Interestingly the orbital occupation of the two d1 sites are different with one showing dxz and the other dyz character. The resulting orbital ordering corresponds to the same pattern, albeit with half the sites empty, as that achieved through a Jahn–Teller distortion appearing at the M-point of the cubic Brillouin zone (MJT). This lattice distortion is indeed observed in the ground state (see Table 1). In fact it is found that the AFD motion themselves can achieve this orbital ordering, in absence of the MJT, by lowering the symmetry of the bulk (superlattice) cubic (tetragonal) reference phase to orthorhombic (monoclinic). Indeed, similarly to the improper appearance of the polar A-cation motions, the AFD motions also drive the appearance of the MJT distortion through another trilinear coupling, 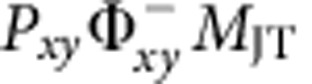 34. The fact that the AFD motions produce the same orbital ordering as the MJT distortion is simply a consequence of this symmetry relation.
34. The fact that the AFD motions produce the same orbital ordering as the MJT distortion is simply a consequence of this symmetry relation.
Figure 2. Electronic structure–charge and orbital ordering.
(a) Total and projected spin-polarized DOS. The upper panel (solid black), and lower panel (solid grey) correspond to up and down spins, respectively. The vertical dashed line represents the Fermi level. The Projected DOS in the inset compares the Ti1 dxz+Ti3 dyz (grey fine dashed lines) with the Ti2+4 dxz+yz (black dashed lines) DOS of the spin-split-off state. (b) Sketch of the resulting orbital ordering. Green spheres represent Ti sites, and red and blue lobes represent dyz and dxz orbitals, respectively.
Interestingly, we find that the charge ordering is not exactly the ideal case of d1–d0. Defining m as the magnitude of the local magnetic moment, we find a d(1−m)–dm ordering, with a significant weight on the nominally d0 sites (0.11<m<0.18 depending on the A- and R-species), displaying a mixed dxz–dyz character. The system remains insulating despite this delocalized state, through a strong hybridization of the two occupied Ti d bands. The resulting intricate and entangled charge and orbital ordering is sketched in Fig. 2.
Magnetic ordering
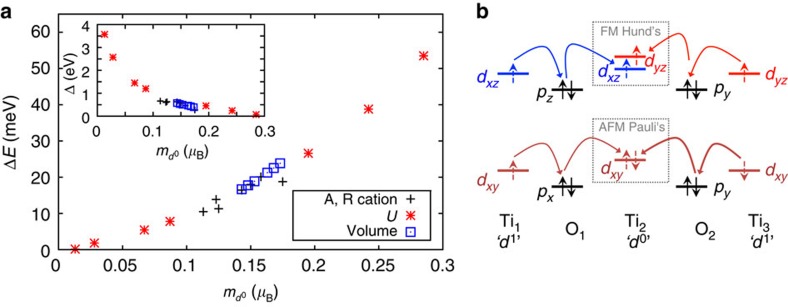
Having discussed the lattice, charge and orbital degrees of freedom, and their coupling, we move to the final degree of freedom—spin. Various magnetic orderings (see methods and Supplementary Tables 4 and 5) were studied, and in all cases and chemistries the FM state was unexpectedly found to be the lowest in energy. In an attempt to understand the origin of this rare insulating FM ground state, we observe a universal trend across A2+TiO3-R3+TiO3 superlattices with all A- and R-species and various applied perturbations. This trend is shown in Fig. 3, where it is seen that the energy difference between AFM and FM states, or more simply the strength of the FM exchange, is clearly strongly dependent on the spin density of d electrons on the nominally d0 sites. Indeed, as the system tends to the ideal charge ordering d1–d0, the FM and AFM energies tend to equilibrate. Therefore, in this regime, the spins on the two d1 sites are completely decoupled. However, as the d0-site electrons become populated, the FM exchange strengthens. This key observation indicates that the FM exchange mechanism relies on a real intra-site spin exchange on the nominally d0 sites, rather than a virtual direct exchange between d1 sites. We propose the intra-site FM spin exchange as Hund’s rule (see Fig. 3).
Figure 3. Insights into magnetic interactions.
(a) Energy gain of FM compared with AFM state (see Methods) per 20-atom formula unit, ΔE, as a function of the moment on the d0 sites, md0. Inset: band gap Δ versus md0. The different points correspond to various perturbations of the superlattice, including varying the A- and R-cation species, the on-site Coulomb repulsion U and the volume of the cell. (b) Simplified spin exchange diagram between nearest neighbour d1 sites (Ti1 and Ti3) via a d0-site (Ti2). The curved arrows represent inter-site spin hopping through oxygen ions, and the dashed box represents intra-site spin-exchange via Hund’s rules, in the case of dxz–dyz orbital ordering due to AFD motions, or Pauli's exclusion principle, in the case of dxy orbital ordering in the absence of AFD motions.
The explanation of the FM interaction between d1 sites relies on two simple arguments, sketched in Fig. 3 (for simplicity in the following, we only consider the four Ti sites of Fig. 2, but the same arguments hold when including all neighbours in 3D). First, due to covalency effects, the electron on the Ti1 (d1) site delocalizes partly on the neighbouring Ti2 and Ti4 (d0) sites necessarily with the same spin (since it is the same electron) and the analogous occurs to the electron on the Ti3 (d1) site. Second, due to the orbital ordering, the charges on Ti2 (and equivalently Ti4) that originate independently from Ti1 and Ti3 populate a different orbital (dxz and dyz respectively). In the same spirit as Hund’s rule of maximum multiplicity, which maximizes the spin of an electron configuration of an atom, a FM solution of the 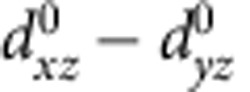 spins becomes the ground state. This rule minimizes the intra-site Coulombic energy. The FM solution relies on both kinetic and Coulomb contributions, to delocalize the spin-polarized d1 electrons partially on the d0 sites and to align the d0 intra-site spins, respectively. In this regard, it resembles a double (kinetic+Coulomb) exchange, even if in an insulator. This FM mechanism in d0–d1 charge-ordered systems, which has been previously overlooked, extends the list of di–dj charge orderings considered within the Goodenough–Kanamori rules8,35,36.
spins becomes the ground state. This rule minimizes the intra-site Coulombic energy. The FM solution relies on both kinetic and Coulomb contributions, to delocalize the spin-polarized d1 electrons partially on the d0 sites and to align the d0 intra-site spins, respectively. In this regard, it resembles a double (kinetic+Coulomb) exchange, even if in an insulator. This FM mechanism in d0–d1 charge-ordered systems, which has been previously overlooked, extends the list of di–dj charge orderings considered within the Goodenough–Kanamori rules8,35,36.
We performed two computational experiments to further support this picture. In the first computational experiment, we took the ground state structure and artificially modified the magnitude of the MJT distortion (leaving all other lattice modes unchanged). Eventually at a huge MJT distortion (50 times larger than the ground state magnitude, but similar in size to the prototypical Jahn–Teller system LaMnO3), the 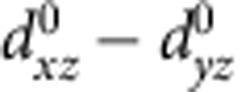 splitting (see Fig. 3) is so large that only one of the orbitals becomes populated at each d0-site, removing the Hund’s interaction and producing an AFM ground state. In the second case, the AFD motions were artificially neglected (along with all other motions except BOC). The tetragonal symmetry can still lead to an insulating charge-ordered state but now with dxy orbital ordering, once an unrealistically large on-site Coulomb repulsion U (>7 eV) is enforced37. We have reproduced this constraint and find that the AFM solution now becomes the ground state. This can again be understood through the intra-site spin exchange on the nominally d0 sites (see Fig. 3). An anti-alignment of spins on the intra-site
splitting (see Fig. 3) is so large that only one of the orbitals becomes populated at each d0-site, removing the Hund’s interaction and producing an AFM ground state. In the second case, the AFD motions were artificially neglected (along with all other motions except BOC). The tetragonal symmetry can still lead to an insulating charge-ordered state but now with dxy orbital ordering, once an unrealistically large on-site Coulomb repulsion U (>7 eV) is enforced37. We have reproduced this constraint and find that the AFM solution now becomes the ground state. This can again be understood through the intra-site spin exchange on the nominally d0 sites (see Fig. 3). An anti-alignment of spins on the intra-site 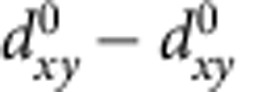 orbitals (and hence on the inter-site
orbitals (and hence on the inter-site 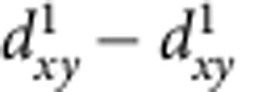 orbitals) is favoured from Pauli’s exclusion principles—now that the same orbital (spacial coordinate) is occupied, opposite electron spins are favoured. Therefore the combination of charge ordering at the R-point, via breathing oxygen cage motions, and orbital ordering at the M-point, via AFD and MJT motions (but not too large), of the cubic Brillouin zone are the key to realize the FM ground state.
orbitals) is favoured from Pauli’s exclusion principles—now that the same orbital (spacial coordinate) is occupied, opposite electron spins are favoured. Therefore the combination of charge ordering at the R-point, via breathing oxygen cage motions, and orbital ordering at the M-point, via AFD and MJT motions (but not too large), of the cubic Brillouin zone are the key to realize the FM ground state.
Discussion
We note the FM mechanism here is distinct from the FM behaviour found in some R3+TiO3 bulk compounds (for R from Gd to Yb). To illustrate, for example, we note the FM coupling becomes stronger as the A size decreases and band gap38 increases in bulk R3+TiO3 compounds. This is seen through a transition from AFM to FM and then a rise in FM TC with decreasing A size39. The reverse trend is observed here, where the FM coupling strengthens with increasing A-cation size and decreasing band gap.
It is interesting finally to compare the FM solution of the half-doped titanates, to the (A-type or E-type) AFM solution of the half-doped manganites. The magnetic ordering is likely different due to the superexchange interaction in the manganites between the half-filled core t2g electrons on every Mn site. This superexchange path is clearly cutoff by the rocksalt arrangement of d0 sites in the titanates studied here. A FM insulating phase of the manganites does exist for the specific case of Pr1−xCaxMnO3 with doping x≈0.2 (refs 40, 41, 42), where a FM exchange wins due to a particular eg orbital polaron ordering43, not completely dissimilar to the t2g case here, using the Goodenough–Kanamori rules8,35,36.
Having rationalized the key concepts underlying the FM and ferroelectric behaviour, we can propose some basic design rules and suggest alternative materials to achieve a similar multiferroic state. To ensure an insulating ground state, the smaller the A- and R-cations the larger the band gap, consistent with the recent observation of insulating Ca0.5Lu0.5TiO3 (ref. 16). Maximizing the ferroelectric polarization can be achieved by choosing the greatest asymmetry in both the Born charge and size of the A- and R-cations. Regarding ferromagnetism, the exchange coupling constant J, and hence the FM TC, increases the greater the delocalization of charges onto the nominally d0 sites, which can be altered with strain and A-site chemistry as shown in Fig. 3. It could be interesting to test the same concepts on other B-cations such as the 4d and 5d transition metals, d9–d10 systems such as the cuprates, which can be viewed as a d1–d0 hole charge ordering, or d6–d7 systems with ordering of the single eg electron instead of the t2g in the titanates. Here we might expect a similar type of entangled charge and orbital orderings leading to unexpected ferromagnetism. We hope that this study might encourage the search for related novel electronic phases within these systems.
Methods
First principles calculations
Here we describe a three-step first principles strategy for the titanate calculations. (i) Initially hybrid functional calculations, using the B1WC functional44 within the Crystal code45, were performed on bulk titanates (YTiO3, LaTiO3, SrTiO3 and BaTiO3) and compared with experiment (see Supplementary Table 1). The details of the pseudopotentials and basis sets for La, Sr, Ti and O can be found in ref. 46, while for Ba and Y details can be found in refs. 47, 48 respectively. (ii) Once verified on the bulk, hybrid functional calculations were performed on several representative R3+TiO3-A2+TiO3 superlattices. Ground states were determined through condensing various lattice instabilities and recalculating phonon frequencies. Band gaps and FM and AFM energies were computed on the ground states. (iii) To make the calculations computationally tractable, and allow simulation of many more chemistries, GGA+U calculations49, using the PBEsol functional50 and projector augmented wave potentials within the VASP code51, were performed on the relaxed hybrid functional superlattice ground state structures. The on-site Coulomb repulsion U was fitted to simultaneously reproduce the band gap and spin flip energy of the hybrid functionals, and minimize atomic forces (see Supplementary Table 2), with a value of U=3.0 eV found to be appropriate. This allowed for full structural relaxation using GGA+U on a wide-range of R3+TiO3-A2+TiO3 structures (R3+: La, Pr, Sm, Y, Tm, Lu; A2+: Sr, Ba, Ca and we also include Eu2+—see Supplementary Table 7). We used a 5 × 5 × 3 Monkhorst-Pack k-point mesh to model the 20-atom cell and a plane wave cutoff of 500 eV. All lattice vectors were fully relaxed. Small to moderate in-plane strains resembling thin film epitaxy were not found to alter the qualitative findings presented. Structural optimizations were performed until the difference of forces were <10−6 eV Å−1 and the energy difference between conjugate gradient steps became lower <10−8 eV. Note: we do not consider R f-electrons explicitly to simplify calculations, since in practice the 4f-electrons order at much lower temperatures than the 3d-electrons. We have tested explicitly including f-electrons and find that the results are not affected. Unless stated otherwise the AFM ordering presented is the simplest AFM configuration between first-neighbour d1 sites allowed within the 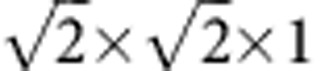 20-atom cell. For longer range AFM orderings 2 × 2 × 1 and
20-atom cell. For longer range AFM orderings 2 × 2 × 1 and 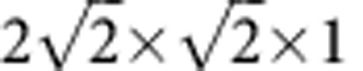 , 40-atom supercells were relaxed with all possible spin orderings considered, including the CE-type. AFM orderings requiring cell doubling out-of-plane (80 atoms) were additionally checked (see Supplementary Table 5). Atomic positions were relaxed for all AFM orderings. The polarization was computed using the Berry phase approach as implemented in VASP. The amplitude Q (Å) of lattice distortions, was determined through the symmetry-mode analysis using the AMPLIMODES software52.
, 40-atom supercells were relaxed with all possible spin orderings considered, including the CE-type. AFM orderings requiring cell doubling out-of-plane (80 atoms) were additionally checked (see Supplementary Table 5). Atomic positions were relaxed for all AFM orderings. The polarization was computed using the Berry phase approach as implemented in VASP. The amplitude Q (Å) of lattice distortions, was determined through the symmetry-mode analysis using the AMPLIMODES software52.
Author contributions
All authors contributed extensively to the work presented in this paper.
Additional information
How to cite this article: Bristowe, N. C. et al. Ferromagnetism induced by entangled charge and orbital orderings in ferroelectric titanate perovskites. Nat. Commun. 6:6677 doi: 10.1038/ncomms7677 (2015).
Supplementary Material
Supplementary Figure 1, Supplementary Tables 1-8, Supplementary Note 1 and Supplementary References.
Acknowledgments
We acknowledge stimulating discussions with N. Spaldin and C. Ederer and support from the ARC project TheMoTherm and FNRS project HiT4FiT. Ph.G. acknowledges Research Professorship from the Francqui foundation and N.C.B. a Research Fellowship from the Royal Commission for the Exhibition of 1851. Calculations have been performed within the PRACE projects TheoMoMuLaM and TheDeNoMo. They also took advantage of the Céci-HPC facilities funded by F.R.S.-FNRS (Grant No 2.5020.1) and the Tier-1 supercomputer of the Fédération Wallonie-Bruxelles funded by the Walloon Region (grant no 1117545).
Footnotes
The authors declare no competing financial interest.
References
- Zubko P., Gariglio S., Gabay M., Ghosez P. & Triscone J.-M. Interface physics in complex oxide heterostructures. Annu. Rev. Condens. Matter Phys. 2, 141–165 (2011) . [Google Scholar]
- Hwang H. et al. Emergent phenomena at oxide interfaces. Nat. Mater. 11, 103–113 (2012) . [DOI] [PubMed] [Google Scholar]
- Tokura Y. & Nagaosa N. Orbital physics in transition-metal oxides. Science 288, 462–468 (2000) . [DOI] [PubMed] [Google Scholar]
- Dagotto E. Complexity in strongly correlated electronic systems. Science 309, 257–262 (2005) . [DOI] [PubMed] [Google Scholar]
- Millange F., Caignaert V., Domenges B., Raveau B. & Suard E. Order-disorder phenomena in new LaBaMn2O6−x CMR perovskites. Crystal and magnetic structure. Chem. Mater. 10, 1974–1983 (1998) . [Google Scholar]
- Millange F., Suard E., Caignaert V. & Raveau B. YBaMn2O5: crystal and magnetic structure reinvestigation. Mater. Res. Bull. 34, 1–9 (1999) . [Google Scholar]
- Nakajima T., Kageyama H. & Ueda Y. Successive phase transitions in a metal-ordered manganite perovskite YBaMn2O6. J. Phys. Chem. Solids 63, 913–916 (2002) . [Google Scholar]
- Goodenough J. B. Theory of the role of covalence in the perovskite-type manganites [La,M(II)]MnO3. Phys. Rev 100, 564 (1955) . [Google Scholar]
- Wollan E. & Koehler W. Neutron diffraction study of the magnetic properties of the series of perovskite-type compounds [La1−xCax]MnO3. Phys. Rev. 100, 545 (1955) . [Google Scholar]
- Williams A. J. & Attfield J. P. Alternative charge-order polymorph for half-doped manganites in TbBaMn2O6. Phys. Rev. B 66, 220405 (2002) . [Google Scholar]
- Radaelli P., Cox D., Marezio M. & Cheong S. Charge, orbital, and magnetic ordering in La0.5Ca0.5MnO3. Phys. Rev. B 55, 3015 (1997) . [Google Scholar]
- Williams A. J. & Attfield J. P. Ferro-orbital order in the charge-and cation-ordered manganite YBaMn2O6. Phys. Rev. B 72, 024436 (2005) . [Google Scholar]
- Ju H., Eylem C., Peng J., Eichhorn B. & Greene R. Metal-insulator transitions and weak ferromagnetism in the electron-correlated system Nd1−xCaxTiO3. Phys. Rev. B 49, 13335 (1994) . [DOI] [PubMed] [Google Scholar]
- Eylem C. et al. Structural, magnetic, and transport properties of RxBa1−xTiO3−δ solid solutions, where R=La, Nd, Gd, Er, and Y: rare-earth-dependent metal-to-semiconductor transitions. Chem. Mater. 4, 1038–1046 (1992) . [Google Scholar]
- Tokura Y. et al. Filling dependence of electronic properties on the verge of metal-Mott-insulator transition in Sr1−xLaxTiO3. Phys. Rev. Lett. 70, 2126 (1993) . [DOI] [PubMed] [Google Scholar]
- Komarek A. et al. Evidence for charge and orbital order in the doped titanates RE1−xCaxTiO3 (RE=Y, Er, Lu) arXiv preprint arXiv:1109.0234 (2011) .
- Ohtomo A., Muller D., Grazul J. & Hwang H. Y. Artificial charge-modulationin atomic-scale perovskite titanate superlattices. Nature 419, 378–380 (2002) . [DOI] [PubMed] [Google Scholar]
- Okamoto S. & Millis A. J. Electronic reconstruction at an interface between a mott insulator and a band insulator. Nature 428, 630–633 (2004) . [DOI] [PubMed] [Google Scholar]
- Biscaras J. et al. Two-dimensional superconductivity at a Mott insulator/band insulator interface LaTiO3/SrTiO3. Nat. Commun. 1, 89 (2010) . [DOI] [PubMed] [Google Scholar]
- Martin L., Chu Y.-H. & Ramesh R. Advances in the growth and characterization of magnetic, ferroelectric, and multiferroic oxide thin films. Mat. Sci. Eng. R-Rep. 68, 89–133 (2010) . [Google Scholar]
- Martin L. W. & Schlom D. G. Advanced synthesis techniques and routes to new single-phase multiferroics. Curr. Opin. Solid State Mater. Sci. 16, 199–215 (2012) . [Google Scholar]
- Goldschmidt V. M. Die gesetze der krystallochemie. Naturwissenschaften 14, 477–485 (1926) . [Google Scholar]
- Glazer A. The classification of tilted octahedra in perovskites. Acta Crystallogr. B 28, 3384–3392 (1972) . [Google Scholar]
- Lufaso M. W. & Woodward P. M. Prediction of the crystal structures of perovskites using the software program spuds. Acta Crystallogr. B 57, 725–738 (2001) . [DOI] [PubMed] [Google Scholar]
- Miao N., Bristowe N. C., Xu B., Verstraete M. J. & Ghosez P. First-principles study of the lattice dynamical properties of strontium ruthenate. J. Phys.: Condens. Matter 26, 035401 (2014) . [DOI] [PubMed] [Google Scholar]
- Thomas N. W. The compositional dependence of octahedral tilting in orthorhombic and tetragonal perovskites. Acta Crystallogr. B 52, 16–31 (1996) . [Google Scholar]
- Woodward P. M. Octahedral tilting in perovskites. ii. structure stabilizing forces. Acta Crystallogr. B 53, 44–66 (1997) . [Google Scholar]
- Bousquet E. et al. Improper ferroelectricity in perovskite oxide artificial superlattices. Nature 452, 732–736 (2008) . [DOI] [PubMed] [Google Scholar]
- Benedek N. A. & Fennie C. J. Hybrid improper ferroelectricity: a mechanism for controllable polarization-magnetization coupling. Phys. Rev. Lett. 106, 107204 (2011) . [DOI] [PubMed] [Google Scholar]
- Fukushima T., Stroppa A., Picozzi S. & Perez-Mato J. M. Large ferroelectric polarization in the new double perovskite NaLaMnWO6 induced by non-polar instabilities. Phys. Chem. Chem. Phys. 13, 12186–12190 (2011) . [DOI] [PubMed] [Google Scholar]
- Benedek N. A., Mulder A. T. & Fennie C. J. Polar octahedral rotations: a path to new multifunctional materials. J. Solid State Chem. 195, 11–20 (2012) . [Google Scholar]
- Rondinelli J. M. & Fennie C. J. Octahedral rotation-induced ferroelectricity in cation ordered perovskites. Adv. Mater. 24, 1961–1968 (2012) . [DOI] [PubMed] [Google Scholar]
- Mulder A. T., Benedek N. A., Rondinelli J. M. & Fennie C. J. Turning ABO3 antiferroelectrics into ferroelectrics: design rules for practical rotation-driven ferroelectricity in double perovskites and A3B2O7 ruddlesden-popper compounds. Adv. Funct. Mater. 23, 4810–4820 (2013) . [Google Scholar]
- Varignon J., Bristowe N. C., Bousquet E. & Ghosez P. Coupling and electrical control of structural, orbital and magnetic orders in perovskites. arXiv preprint arXiv:1409.8422 (2014) . [DOI] [PMC free article] [PubMed]
- Goodenough J. B. An interpretation of the magnetic properties of the perovskite-type mixed crystals La1−xSrxCoO3−λ. J. Phys. Chem. Solids 6, 287–297 (1958) . [Google Scholar]
- Kanamori J. Superexchange interaction and symmetry properties of electron orbitals. J. Phys. Chem. Solids 10, 87–98 (1959) . [Google Scholar]
- Pentcheva R. & Pickett W. E. Correlation-driven charge order at the interface between a mott and a band insulator. Phys. Rev. Lett. 99, 016802 (2007) . [DOI] [PubMed] [Google Scholar]
- Okimoto Y., Katsufuji T., Okada Y., Arima T. & Tokura Y. Optical spectra in (La,Y)TiO3: variation of Mott-Hubbard gap features with change of electron correlation and band filling. Phys. Rev. B 51, 9581 (1995) . [DOI] [PubMed] [Google Scholar]
- Komarek A. et al. Magnetoelastic coupling in RTiO3 (R= La, Nd, Sm, Gd, Y) investigated with diffraction techniques and thermal expansion measurements. Phys. Rev. B 75, 224402 (2007) . [Google Scholar]
- Jirak Z., Krupička S., Šimša Z., Dlouha M. & Vratislav S. Neutron diffraction study of Pr1−xCaxMnO3 perovskites. J. Magn. Magn. Mater. 53, 153–166 (1985) . [Google Scholar]
- Tomioka Y., Asamitsu A., Moritomo Y., Kuwahara H. & Tokura Y. Collapse of a charge-ordered state under a magnetic field in Pr1/2Sr1/2MnO3. Phys. Rev. Lett. 74, 5108 (1995) . [DOI] [PubMed] [Google Scholar]
- Yoshizawa H., Kawano H., Tomioka Y. & Tokura Y. Neutron-diffraction study of the magnetic-field-induced metal-insulator transition in Pr0.7Ca0.3MnO3. Phys. Rev. B 52, R13145 (1995) . [DOI] [PubMed] [Google Scholar]
- Mizokawa T., Khomskii D. & Sawatzky G. Orbital polarons and ferromagnetic insulators in manganites. Phys. Rev. B 63, 024403 (2000) . [Google Scholar]
- Bilc D. et al. Hybrid exchange-correlation functional for accurate prediction of the electronic and structural properties of ferroelectric oxides. Phys. Rev. B 77, 165107 (2008) . [Google Scholar]
- Dovesi R. et al. Crystal: a computational tool for the ab initio study of the electronic properties of crystals. Z. Kristallogr. 220, 571–573 (2005) . [Google Scholar]
- Delugas P. et al. Spontaneous 2-dimensional carrier confinement at the n-type SrTiO3/LaAlO3 interface. Phys. Rev. Lett. 106, 166807 (2011) . [DOI] [PubMed] [Google Scholar]
- Piskunov S., Heifets E., Eglitis R. & Borstel G. Bulk properties and electronic structure of SrTiO3, BaTiO3, PbTiO3 perovskites: an ab initio HF/DFT study. Comp. Mat. Sci. 29, 165–178 (2004) . [Google Scholar]
- Varignon J., Petit S., Gellé A. & Lepetit M. B. An ab initio study of magneto-electric coupling of YMnO3. J. Phys.: Condens. Matter 25, 496004 (2013) . [DOI] [PubMed] [Google Scholar]
- Liechtenstein A., Anisimov V. & Zaanen J. Density-functional theory and strong interactions: orbital ordering in Mott-Hubbard insulators. Phys. Rev. B 52, 5467 (1995) . [DOI] [PubMed] [Google Scholar]
- Perdew J. P. et al. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 100, 136406 (2008) . [DOI] [PubMed] [Google Scholar]
- Kresse G. & Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996) . [DOI] [PubMed] [Google Scholar]
- Orobengoa D., Capillas C., Aroyo M. I. & Perez-Mato J. M. Amplimodes: symmetry-mode analysis on the bilbao crystallographic server. J. Appl. Crystallogr. 42, 820–833 (2009) . [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Figure 1, Supplementary Tables 1-8, Supplementary Note 1 and Supplementary References.