Electrostatically optimized Ras-binding Ral guanine dissociation stimulator mutants increase the rate of association by stabilizing the encounter complex

Abstract

Association of two proteins can be described as a two-step process, with the formation of an encounter complex followed by desolvation and establishment of a tight complex. Here, by using the computer algorithm pare, we designed a set of mutants of the Ras effector protein Ral guanine nucleotide dissociation stimulator (RalGDS) with optimized electrostatic steering. The fastest binding RalGDS mutant, M26K,D47K,E54K, binds Ras 14-fold faster and 25-fold tighter compared with WT. A linear correlation was found between the calculated and experimental data, with a correlation coefficient of 0.97 and a slope of 0.65 for the 24 mutants produced. The data suggest that increased electrostatic steering specifically stabilizes the encounter complex and transition state. This conclusion is backed up by Φ analysis of the encounter complex and transition state of the RalGDS^{M26K,D47K,E54K}/Ras complex, with both values being close to 1. Upon further formation of the final complex, the increased Coulombic interactions are probably counterbalanced by the cost of desolvation of charges, keeping the dissociation rate constant almost unchanged. This mechanism is also reflected by the mutual compensation of enthalpy and entropy changes quantified by isothermal titration calorimetry. The binding constants of the faster binding RalGDS mutants toward Ras are similar to those of Raf, the most prominent Ras effector, suggesting that the design methodology may be used to switch between signal transduction pathways.

Members of the Ras-related superfamily of GTP-binding proteins are small, 20- to 25-kDa proteins that bind guanine nucleotides very tightly and cycle between an inactive GDP-bound and an active GTP-bound state (1, 2). In the GTP-bound state, Ras proteins can interact with effector molecules as downstream targets, thereby communicating signals into different pathways (3). In recent years, many effector molecules, such as c-Raf, Ral guanine dissociation stimulator (RalGDS), AF6, and phosphatidylinositol 3-kinase have been identified. These effectors do not share biological functions or sequence homology except for the common Ras-binding domain (RBD). This domain is responsible for binding to the effector region of Ras·GTP. The structures of all RBDs resolved so far share a common fold that is similar to that of ubiquitin (reviewed in ref. 4). Despite these structural similarities, biochemical studies have shown that the various effector RBDs interact with proteins of the Ras family with different affinities that dictate the specificity of the interaction (5).

An important feature of Ras/effector RBD interactions is the high charge complementarity found between the proteins in the complex. Ras has a net negatively charged binding site, whereas the effector RBDs have a net positively charged binding site. As a result, the rate of association between them was found to be very high and contributes significantly to the affinity of the complex (6, 7). Furthermore, differences in binding affinities for some of the Ras/effector complexes are a consequence of different association rate constants, with the dissociation rate constants being at a similar range (6, 7). For example, the high, nanomolar affinity of the binding of Raf-RBD to Ras is attributed to the very high k_on value, which stems from the strong electrostatic complementarity between the Ras/Raf-RBD binding sites. In contrast, the electrostatic complementarity between Ras and RalGDS-RBD binding sites is poor, accounting for their slower rate of association and lower affinity. It seems that the rate of association is of major importance in determining the affinity and specificity of Ras/effector interactions.

According to the concept of electrostatic steering, two proteins first diffuse randomly in solution until they reach a point where they feel the electrostatic field of each other. Then the proteins come together by directional diffusion until they form a low affinity encounter complex (8–11). The nature of the interactions stabilizing the encounter complex has been discussed frequently (12, 13). Most often, the encounter complex is not observed experimentally, but is assigned from theoretical considerations. However, this two-step reaction could be assigned experimentally to the association of Ras and effector RBDs (6, 7, 14, 15) as presented in Scheme 1,

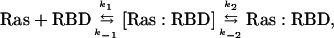where Ras and RBD are the free proteins, [Ras:RBD] is the encounter complex, and Ras:RBD is the final complex.

The RalGDS-RBD/Ras interaction is well suited for teaching researchers about the nature of the encounter complex, because it can be directly observed by using stopped-flow experiments. Here, we used a protein design strategy to optimize the electrostatic complementarity between these two proteins through the introduction of charged mutations at the vicinity of, but outside, the binding site (16) to determine the influence of electrostatic steering on the different steps along the association pathway while keeping the influence on short-range effects as low as possible. The design and implementation of these mutants and subsequent analysis of their influence on binding is the subject of this paper.

Methods

Site-Directed Mutagenesis. The introduction of single lysine mutations into pGEX-2T:RalGDS-RBD was done by using the QuikChange site-directed mutagenesis kit (Stratagene), with pGEX-2T:RalGDS-RBD^WT as a template. For double and higher-order lysine mutants, the corresponding pGEX-2T:RalGDS-RBD mutant was used as a template. All mutants were verified by sequence analysis. The alanine mutants were available from earlier studies (7, 17).

Protein Expression and Purification. RalGDS-RBD^WT and mutant proteins were expressed as described earlier (7, 17). Ha-Ras (here termed Ras) was cloned in Ptac vector and expressed by using Escherichia coli CK600K cells. The expressed Ras protein was purified, and the bound nucleotide was exchanged for the nonhydrolyzable nucleotides 5′-guanosyl-β, γ-imidotriphosphate (GppNHp) or 2′,3′-N-methylanthraniloyl-GppNHp (mGppHHp) as described (18). The protein concentrations of Ras and RalGDS-RBD were measured by the Bradford method.

Calculation of Association Rate Constants. k_on values of the mutant RalGDS-RBD/Ras complexes were calculated relative to the experimental value of the WT complex by using the computer program pare as described (16). For calculations, it is assumed that the association is directly related to the magnitude of electrostatic forces between the two proteins, which is calculated in terms of electrostatic energy of interaction as presented in refs. 11 and 16. Calculations were done under the same ionic strength as the relevant measurements. Coordinates for calculations of the RalGDS-RBD/Ras complex and for the individual proteins were taken from its x-ray structure (19). All mutations were modeled by using swiss pdb viewer (20).

Stopped-Flow Measurements. Measurements of association rate constants were done by using an SM17 apparatus (Applied Photophysics, Surrey, U.K.) by rapid mixing of 0.5 μM Ras bound to mGppNHp and 5–200 μM RalGDS-RBD. N- methylanthraniloyl nucleotides were excited at 360 nm, and the fluorescence was recorded through a 408-nm cutoff filter. Binding of RalGDS-RBD to Ras was detected by a change in the fluorescence of the N-methylanthraniloyl nucleotide as described earlier (6, 7). Because RalGDS-RBD was in >10-fold molar excess, an exponential equation was fitted to the fluorescence traces according to pseudofirst-order kinetics. The resulting inverse time constant corresponds to the observed rate constant k_obs within an experimental error of 10–20%. Unless indicated otherwise, all measurements were done in buffer containing 15 mM Hepes (pH 7.4) and 5 mM MgCl₂ at 25°C.

Isothermal Titration Calorimetry (ITC). The thermodynamic parameters of Ras/effector interactions were determined by using an ITC (MCS-ITC, MicroCal, Amherst, MA) as described (21). In all experiments, the effector RBDs were placed into the cell at concentrations varying between 10 and 80 μM, depending on the expected association constant. The concentration of Ras·GppNHp in the syringe was 10-fold higher compared with the effector concentration in the cell. Data evaluation was done as described in ref. 5, yielding ΔG° and ΔH° values with 0.2 kcal/mol error bars each. For the n value, defined as the stoichiometry of the Ras/effector complex, an experimental error of 0.1 was obtained. All ITC experiments were carried out at 25°C in 15 mM Hepes buffer, pH 7.4/5 mM MgCl₂.

Results

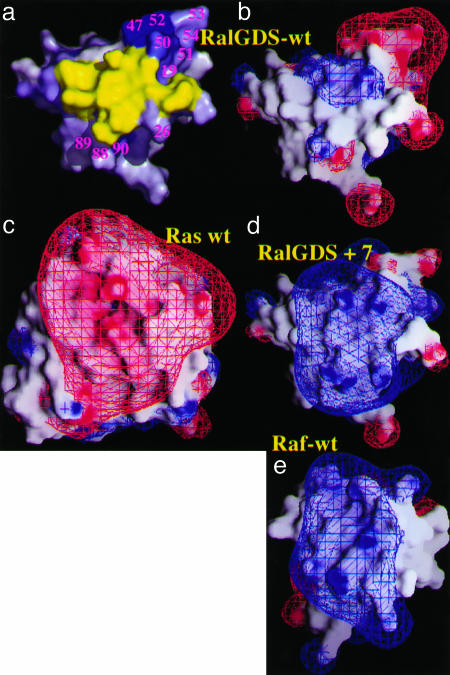
The association rate constant between a pair of proteins has been shown to depend on electrostatic steering, which is related to the electrostatic complementarity of the two binding proteins. Although Ras is mainly negatively charged in its effector binding region, RalGDS-RBD has a mixed charge surface as presented in Fig. 1. Some weak positive charge is calculated at the center of the Ras binding site, whereas a strong negatively charged patch is observed at the periphery. In contrast, Raf-RBD (Fig. 1e) has a strong positive potential in and around the Ras binding site. The charge distribution of RalGDS-RBD indicates that the introduction of additional positive charges within RalGDS-RBD has the potential to increase the electrostatic interaction energy between RalGDS and Ras (Fig. 1d) and thereby increasing the rate of their association.

Fig. 1.

Surface representation of the Ras binding site of RalGDS-RBD and Raf-RBD. (a) The residues on RalGDS-RBD probed for faster association. The residues are color-coded scaled to the calculated change in the association rate constant, from white (no increase) to blue (large increase). The values are from Fig. 2. The yellow patch denotes the binding interface. (b–e) The electrostatic potentials on the binding surfaces of Ras, RalGDS-RBD^WT, RalGDS-RBD^{M26K,D47K,E54K,D90K} mutant, and Raf-RBD^WT are depicted with grasp, with the contours drawn at 2 kT per electron at 0.018 mM NaCl (blue for positive and red for negative) by using only full charges (including for GTP and Mg⁺²).

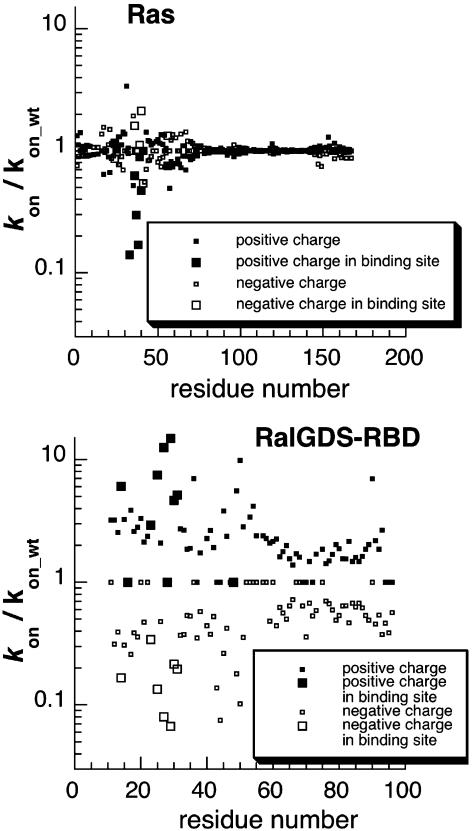
Design and Production of Faster Binding RalGDS-RBD Mutants. In the first step of calculation, a positive or negative charge was assigned to all side-chains along the Ras or RalGDS-RBD sequences, and the increase in association rate was calculated by using pare (Fig. 2). The calculations show that the potential to increase the rate of association by mutation of Ras is limited, whereas mutations on RalGDS-RBD have a major potential to increase k_on. This finding reflects the charge distribution of the respective binding sites, which is negatively charged on Ras and neutral on RalGDS-RBD; it also explains why only mutations to a positive charge on RalGDS-RBD have the potential to increase association significantly. Two “hot-spot” regions for association on RalGDS-RBD were identified: One is between residues 25–29, and the second is between residues 47–52 (Figs. 1a and 2). The latter regions are not located within the interface and are therefore good candidates for mutagenesis if changes in the binding site are to be avoided. The most promising residues for faster binding were mutated in silico to Lys and minimized; the contribution of multiple mutant rotomers to association was calculated. To keep dissociation rates constant, only residues that are surface-exposed and located at the vicinity of, but outside, the binding site were further considered for mutagenesis. The final calculated k_on values are given in Table 2, which is published as supporting information on the PNAS web site. Mutations to Lys of uncharged single amino acid residues located at the vicinity of the Ras binding site (S18K, L19K, M26K, L51K, N88K, and Y89K) are calculated to lead to accelerations between 1.7- and 4.5-fold, whereas mutations of negatively charged residues to Lys (E54K and D90K) are predicted to result in a 3- to 5.5-fold increase of the association rate constants. The largest effect on the rate of association was predicted for the RalGDS-RBD mutant D47K (10-fold).

Fig. 2.

Calculating the effect of a charge mutation along the protein sequence. To produce this figure, the program pare was modified to simulate single point charge mutations. Each residue was introduced with a positive or negative charge. Then the relative rate of association was recalculated. The process was repeated for all residues along the polypeptide chain of both proteins. The location of the binding site is marked. The calculations were done at an ionic strength of 0.018 M.

Based on our predictions, mutations were introduced into RalGDS-RBD by using site-directed mutagenesis, and the corresponding proteins were produced. The mutant proteins were purified by using standard methodology, yielding soluble proteins in comparable amounts to those of WT. Because mutations may cause a destabilization of the protein structure, some of the mutant proteins were evaluated for their thermal stability by differential scanning calorimetry (data not shown). No significant changes in the shape of the melting curve or in the melting temperature were measured, indicating that these mutations do not cause large structural changes.

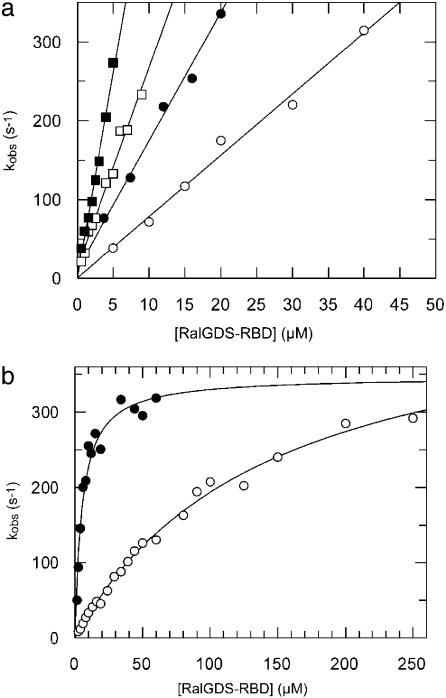
Kinetic Investigation of Mutant Complexes. The interaction of RalGDS-RBD with Ras was measured by using a stopped-flow as described earlier (6, 7). To keep Ras in an active conformation, the GTP in Ras was exchanged for the nonhydrolyzable nucleotide analogue GppNHp attached to the N-methylanthraniloyl group as a fluorescence label (Ras·mGppNHp). Under pseudofirst-order conditions (with the concentration of Ral-GDS-RBD being at least 10-fold higher than the Ras·mGppNHp concentration), the observed time-dependent fluorescence changes can be fitted to a single exponential equation. For a single-step reaction, the values of the observed rate constants (k_obs) increase linearly with increasing RBD concentration, as observed at low RBD concentrations (Fig. 3a). However, at higher RBD concentrations, the increase in k_obs lags behind the increase in concentration until saturation is reached at very high concentrations (Fig. 3b). According to a two-step mechanism shown in Scheme 1, the observed rate constant can be described as

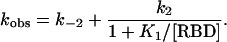[1]

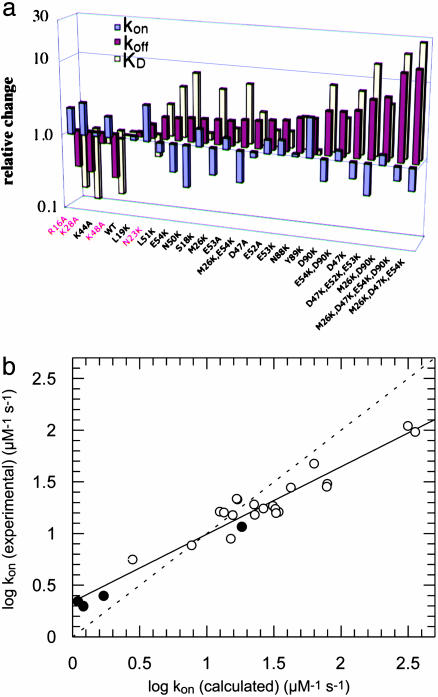
From Eq. 1, the equilibrium dissociation constant of the encounter complex K₁ = k_-1/k₁ is obtained. For RalGDS-RBD^WT binding to Ras·mGppNHp, K₁ was measured to be 134 μM, and the maximal rate (k₂) was 459 s^-1 at 10°C. Accordingly, the rate constant of association k_on = k₂/K₁ is 3.4 μM^-1·s^-1. At low RBD concentrations ([RBD] << K₁), Eq. 1 can be linearly approximated as k_obs = k_off + k_on × [RBD]. For the binding of RalGDS-RBD^WT to Ras·mGppNHp, the slope of the linear fit between k_obs and the concentration (at a range up to 40 μM) yields a k_on value of 2.5 μM^-1·s^-1. Thus, the association rate constants determined from saturation kinetics and from the linear approximation are similar. At higher temperatures, saturating protein concentrations lead to k_obs values that are too large to be measured by stopped-flow. Therefore, the association rate constants for all mutant proteins were determined from the linear regression at low RalGDS-RBD concentrations at 25°C, as in Fig. 3a. The dissociation rate constant was determined from a displacement experiment in which the Ras·mGppNHp-RalGDS-RBD complex was mixed in the stopped-flow apparatus with nonlabeled Ras·GppNHp at high molar excess. A summary of all of the measured association and dissociation rate constants is given in Fig. 4a (and Table 2), where mutant RalGDS-RBD proteins are ordered according to their relative values of k_on, showing also the relative values for k_off and K_D. In addition to the thus far designed mutants, we measured and calculated values of k_on for a number of interface mutants that were produced previously (17). Fig. 4b shows a plot of logk_on (experimental) versus logk_on (calculated) for all investigated RalGDS-RBD mutants. The slope of the linear fit between the calculated and experimental data are 0.65, with a correlation coefficient of 0.97. For low k_on values the calculations underestimate the association rate constants, and for high k_on values the calculations overestimate the association rate constants. The same relationship between calculated and experimental data holds for the four interface mutants investigated, as well as for faster and slower binding complexes. Thus, k_on seems to be affected only by the electrostatic contribution of the specific residue. The triple mutant RalGDS-RBD^{D47K,E52K,E53K} is a clear exception, with the calculated increase in k_on being 4,000-fold, but the actual measured value of k_on is only 5.6-fold faster relative to WT. However, the calculations did hold for the three individual single mutants making up this triple mutant protein, suggesting some structural perturbation of this triple mutant, which was not analyzed further.

Fig. 3.

Kinetic analysis of Ras·mGppNHp binding to RalGDS-RBD^WT and mutants. (a) Plot of the k_obs values against the concentration of RalGDS-RBD^WT(○), RalGDS-RBD^E53A (•), RalGDS-RBD^E54K,D90K (□), and RalGDS-RBD^M26K,D90K(▪). A linear fit leads to the k_on values. Measurements were performed at 25°C. (b) Plot of k_obs against the RalGDS-RBD concentration for the binding of Ras·mGppNHp to RalGDS-RBD^WT (○) and RalGDS-RBD^{M26K,D47K,E54K} (•). These measurements were performed at 10°C, and the curves were fitted according to Eq. 1.

Fig. 4.

(a) Relative values of k_on (red), k_off (blue), and K_D (yellow) for the binding of RalGDS-RBD mutants to Ras·mGppNHp at 25°C. The mutants are ordered with increasing k_on values. Interface mutants are designated in red. The relative values are normalized to the WT values at 25°C, i.e., k_on = 7.7 μM^-1·s^-1, k_off = 14.9 s^-1 and K_D = 1.9 μM. (b) Plot of calculated and experimentally determined values for the association rate constants. Interface mutants are designated as •. The correlation coefficient is 0.97 and the slope is 0.65. The dashed straight line has a slope of 1.

The picture for the rate of dissociation is somewhat more complex. Most k_off values of noninterface mutants vary around the WT value (<2-fold difference). All four interface mutants (R16A, K28A, K48A, and N23K on RalGDS-RBD) cause an increase in k_off by 2- to 3-fold (Fig. 4a), as may be expected. Still, a number of mutations of noninterface residues seem to change the values of k_off as well. RalGDS-RBD^Y89K causes an increase in k_off, whereas in several cases k_off is decreased (between 1.4- and 3.5-fold). For these mutants, both k_on and k_off contribute toward the overall higher affinity obtained. This result is especially pronounced for the N50K mutation. Replacing Asn with Lys can bring the side chain of this residue to a distance of 3–4 Å from a number of residues on Ras. The short-range interactions formed may contribute to the observed decrease in values of k_off. In this sense, analyzing mutations to Ala is much simpler because side-chains are deleted, whereas, for mutations to Lys a long side-chain is added, which may contribute to the formation of new interactions.

The association of Ras with RalGDS-RBD is a two-step process, which can be analyzed from the nonlinear concentration dependence of the observed rate constant (Fig. 3b). Producing faster binding RalGDS variants gave us the unique opportunity to investigate whether increasing electrostatic steering between two proteins affects the formation of the encounter complex or the rate of final complex formation. The association of the triple mutant RalGDS-RBD^{M26K,D47K,E54K} to Ras·mGppNHp has been followed up to high concentration and compared to the WT complex. The observed rate constants were plotted against the RalGDS-RBD concentration (Fig. 3b). Based on the two step-model (Eq. 1), the affinity of the encounter complex (K₁) was measured to be 5.3 μM and k₂ = 347 s^-1 for RalGDS-RBD^{M26K,D47K,E54K} compared with K₁ = 134 μM and k₂ = 459 s^-1 for the WT. Thus, the affinity of the encounter complex is increased roughly 25-fold, whereas k₂ (which is the rate of formation of the final complex out of the encounter complex) is almost unchanged. This experiment confirms that the engineered increase in electrostatic attraction between RalGDS-RBD and Ras specifically affects the affinity of the encounter complex. One should keep in mind that all of the mutations are located outside the actual binding site.

Activation Energy of the Interaction Between Ras and RalGDS-RBD Mutants. According to transition state theory, the relationship between the relative change in association rate constant upon mutation and the difference in free energy between the unbound proteins and the transition state is given by the following equation:

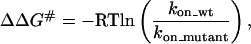[2]

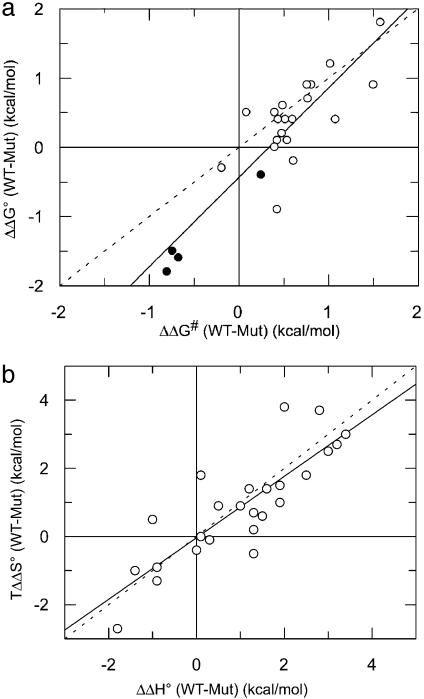
where ΔΔG^# is the change in activation energy upon mutation. Although absolute values of ΔG^# of second order reactions are difficult to interpret, changes in ΔΔG^# are easier to discuss because they probe only the difference between a mutant and the WT in respect to the transition state (13, 21, 22). The activation energy for the fastest associating RalGDS-RBD mutant is decreased by 1.5 kcal/mol, which corresponds approximately to the change in the free energy of binding. Fig. 5a is a plot of changes in activation energy between WT and mutant complexes [ΔΔG^# (WT-Mut)] and changes in free energy as determined from ITC [ΔΔG° (WT-Mut)]. The slope of a linear fit was 1.3, with a correlation coefficient of 0.88. The ratio between ΔΔG^# and ΔΔG°, also termed the Bronsted (β) value, indicates the extent of bond making and breaking in the transition state. In the case presented here, it is clear that for charged mutations located outside the binding site the interaction is made at the transition state, implying their long-range nature. Moreover, these results show that the increase in binding affinity stemming from the faster rate of association is mainly the result of decreasing the energy barrier for association, whereas the energy barrier for dissociation is about constant. A similar observation was made for the interactions between barnase and barstar and the TEM–BLIP complex (11, 13).

Fig. 5.

(a) Plot of changes in activation energy (ΔΔG^#) and changes in free energy (ΔΔG°) between WT and mutant RalGDS-RBD/Ras·mGppNHp complexes. The slope of a linear fit is 1.3, with a correlation coefficient of 0.91. (b) Changes in free enthalpy (ΔΔH°) plotted versus changes in entropy (TΔΔS°)of binding between WT and mutant RalGDS-RBD/Ras·mGppNHp complexes. The slope of a linear fit is 0.77, with a correlation coefficient of 0.81. Interface mutants are designated as •. The dashed straight lines have a slope of 1.

Thermodynamic Analysis of Mutant Complexes. To confirm the binding affinities obtained from the kinetic data, all RalGDS-RBD mutant complexes were investigated independently by using ITC, which provides direct measurements of ΔG° and ΔH° from which ΔS° is calculated (23). The results obtained for the mutant proteins are summarized in Table 2. In all cases, a 1:1 Ras/RalGDS complex formation was observed with n values at ≈1.0, showing that the predetermined Ras·GppNHp and Ral-GDS-RBD protein concentrations reflected the concentration of active protein throughout the experiments. The free energy values (ΔG°) obtained from the analysis of the kinetic stopped-flow data and those measured directly by using ITC experiments are in good agreement. The association process of RalGDS-RBD^WT to Ras·GppNHp was earlier reported to be driven by a favorable enthalpy change (5). This negative enthalpy change is observed also for the complex formation of all mutants. Values of ΔΔH° (WT-Mut) for all complexes are between -2 and 4 kcal/mol. No good correlation was found between ΔΔG° and either ΔΔH° or TΔΔS°, although a clear enthalpy/entropy compensation was observed (Fig. 5b). This enthalpy/entropy compensation has been often found in mutational studies (24, 25).

Discussion

The affinity of a protein complex can be described as the ratio between k_off and k_on. The rate of dissociation is influenced mainly by the magnitude of short-range interactions (ionic interactions, hydrogen bonds, and hydrophobic interactions), which are difficult to optimize through rational design. In contrast, the association reaction can be described more easily based on the classical rules of diffusion and electrostatics (26). It has been shown that the association rate correlates with the electrostatic energy of interaction between two molecules, which is calculated by using the algorithm pare (16). By implementing our design strategy on the Ras/RalGDS-RBD complex, it was possible to increase the rate of association of 7.7 μM^-1·s^-1 for the WT complex to >100 μM^-1·s^-1 for the RalGDS^{M26K,D47K,E54K} mutant. The kinetic parameters for RalGDS^WT, RalGDS^{M26K,D47K,E54K}, and Raf (which is the preferred effector of Ras) binding Ras are shown in Table 1. The kinetics of RalGDS^{M26K,D47K,E54K} (but not RalGDS^WT) binding Ras are similar to those measured for Raf, despite the lack of sequence similarity between RalGDS and Raf (both bind Ras at the same location). Ras is originally optimized to bind Raf fast. By electrostatic design of RalGDS, we succeeded to imitate the electrostatic picture of Raf on RalGDS (Fig. 1), achieving a similar kinetic profile. It should be emphasized that RalGDS was designed just from electrostatic principle without using Raf as a model. These results raise the possibility of kinetic control of cellular signal transduction in this case. Because we avoided mutating residues in the interface, the dissociation rate constant was less affected. As a consequence, a significant tightening of the Ras/RalGDS complex was achieved, from a K_D value of 1.9 μM for WT to 0.071 μM (27-fold) for RalGDS^{M26K,D47K,E54K}.

Table 1. Binding data for Ras/effector complexes.

Ras/effector complexes	K1, μM-1	kon, μM-1·s-1	k2, s-1
RalGDS WT	134.0	3.4	459
RalGDSM26K,D47K,E54K	5.3	65.0	347
Raf WT	9.2	52.0	480

RalGDS measurements were performed in a stopped-flow at 10°C, Raf at 15°C, and additional 125 mM NaCl because of the low solubility of Raf-RBD at low ionic strength.

A good correlation was found between the experimental versus calculated association rate constants. However, the absolute values differ, as reflected by the slope of 0.65 between the two (Fig. 4b). Interestingly, the correlation extends to both faster and slower binding mutants, associating with rates varying over a range of 55-fold (between RalGDS^{M26K,D47K,E54K} and RalGDS^K48A). Moreover, the same trend was observed independently on whether the mutations were located within or outside the binding site. Therefore, one has to conclude that the difference between the calculated versus measured values is related to a global feature of this interaction. pare calculates the electrostatic contribution toward the rate of association. These calculations yielded the exact values for diverse systems, such as antibody-antigen, RNase/inhibitor, AchE/inhibitor, and others (16, 27). The observation that for Ras/RalGSD, pare successfully predicted the trend of changes in the rate of association but fails in giving the exact values may show that a different electrostatic model has to be applied in this case or that this reaction is not purely diffusion limited but is partially reaction limited. For the RalGDS-RBD/Ras interaction, the latter explanation seems to be valid, because a dynamic equilibrium between two conformational states during binding is clearly resolved, with only one of them being present in the final complex (15). Thus, the RalGDS-RBD/Ras interaction can serve as a classic example for binding of a partially reaction limited protein–protein interaction. A hallmark of a partially reaction-limited reaction is the nonlinearity of the relation between the rate of association and the reactants concentrations, which is indeed the case for the RalGDS-RBD/Ras interaction investigated here. Therefore, in addition to the value of k_on, the data provide direct information about the stability of the encounter complex along the association pathway. Based on kinetic measurements at high RalGDS-RBD concentration, we were able to determine the affinity of the encounter complex with Ras·mGppNHp, which is 134 μM for the WT and 5.3 μM for RalGDS^{M26K,D47K,E54K}. In contrast to the increased stability of the encounter complex with increasing electrostatic energy of interaction, the rate of formation of the final complex, k₂, was hardly affected (459 s^-1 versus 347 s^-1 for the WT versus mutant proteins). A similar value of 480 s^-1 was measured for Raf interacting with Ras (Table 1 and Fig. 6, which is published as supporting information on the PNAS web site), again suggesting that k₂ is related to the rearrangement of Ras during association. These results can be analyzed by using Φ value analysis (28), where Φ_e =ΔΔG_e/ΔΔG_complex and F_# = DDG_#/ΔΔG_complex (e stands for the encounter complex). By using the experimental data for WT and the RalGDS^{M26K,D47K,E54K}/Ras complex (with ΔΔG_e, ΔΔG_#, and ΔΔG_complex calculated from K₁, k_on, and ΔG°, respectively), Φ_e = 1.9/1.8 = 1.05 and Φ_e = 1.57/1.8 = 0.87. These two Φ values demonstrate that increasing electrostatic steering by mutating residues located outside the binding site stabilizes the encounter complex and the transition state to a similar extent as they stabilized the final complex. Thus, the charge mutants have a long-range effect, which is not increased during binding.

Why did k₂ and k_-2 remain constant despite the increasing electrostatic attraction between the two proteins? In other words, why didn't we observe a gain in electrostatic energy upon moving from the encounter complex toward the final complex and vice versa? A possible explanation would be that the penalty paid for the desolvation of charges is apparently similar to the gain in Coulombic energy upon bringing them together (29, 30). The two-step pathway for association observed for the RalGDS-RBD/Ras interaction does not seem to be a unique case. Indirect evidence supports the notion that this mechanism is actually the common pathway for association, but in most cases the encounter complex is less pronounced and not easy to be measured directly (26).

The observations presented in this paper demonstrate that not only the contact area of proteins but also their periphery may be important for specific and efficient complex formation. By designing RalGDS mutants, we reached a tighter encounter complex and final Ras/effector complex, which has an almost identical dissociation constant as observed for the Ras/Raf system, in which high charge complementarity was demonstrated between the interfaces (Table 1). This finding is relevant for drug design, for which not only the contact site may be targeted but also neighboring protein surface patches. Finally, creating protein variants with a wide range of kinetic constants opens the possibility of investigating the biological impact of the dynamics of protein–protein interaction in general and for signal transduction mediated by cascades of protein–protein interactions in particular.